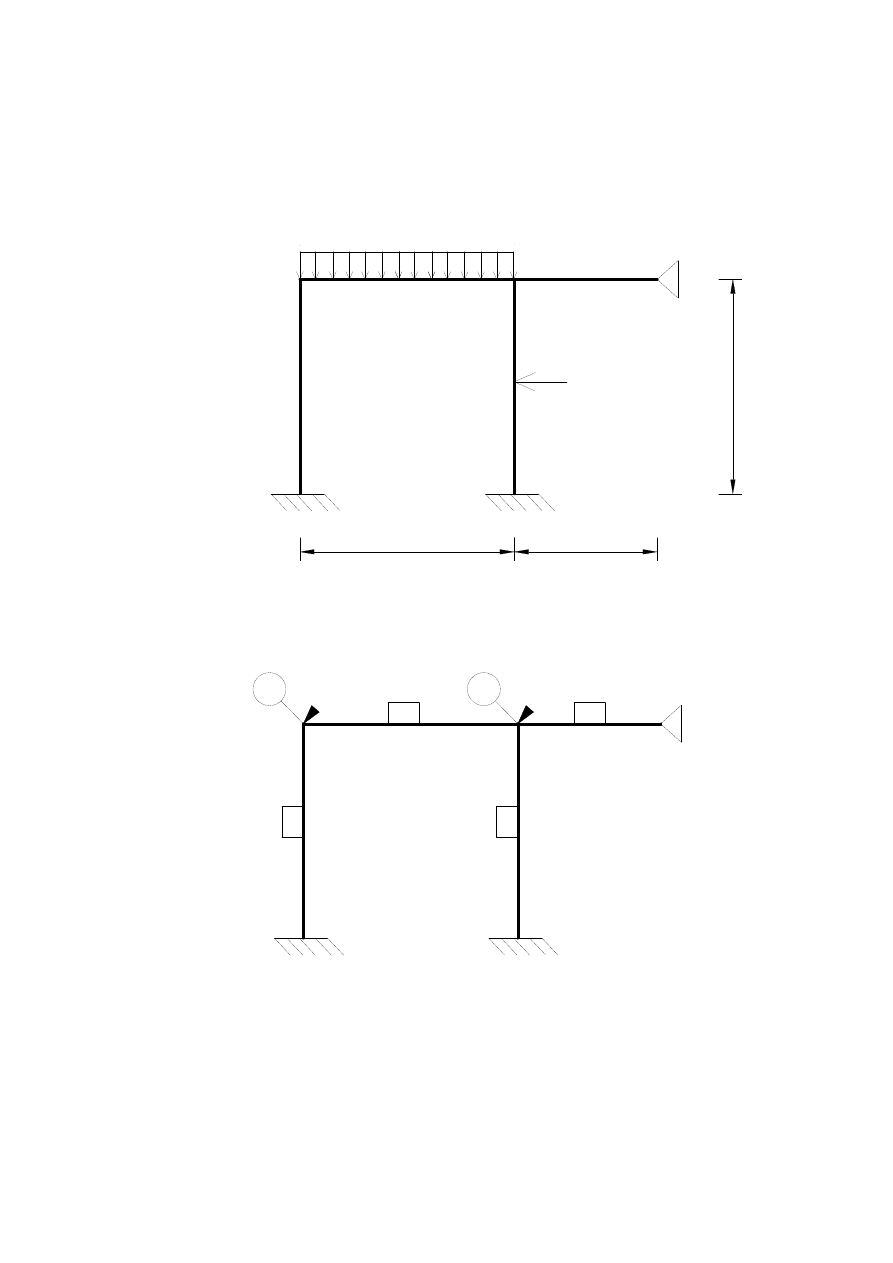
Rozwiazanie schematu statycznego metod

ą

przemieszcze

ń

:

Rozwi

ą

zujac układ metoda przemieszcze

ń

zało

ż

y

ć

,

ż

e wymiary przekrojów poprzecznych wszystkich

elementów s

ą

identyczne.

q

P

L

2L

3

L

Rys.1 Schemat konstrukcji

1

2

2

4

1

3

A

B

C

Rys.2 Układ podstawowy metody przemieszcze

ń

Konstrukcja jest dwukrotnie geometrycznie niewyznaczalna. Jedynymi niewiadomymi
geometryczneymi jakie nale

ż

y wyliczy

ć

s

ą

k

ą

ty obrotu wezłów 1 i 2.

Zapisujemy momenty w

ę

złowe dla poszczególnych pr

ę

tów korzystaj

ą

c z wzorów

transformacyjnych :

Φ

A

1

2E J

⋅

3L

φ

1

( )

⋅

=

Φ

1

1

2E J

⋅

3L

2

φ

1

( )

⋅

=

Φ

1

2

2E J

⋅

L

2

φ

1

φ

2

+

(

)

⋅

1

12

q

⋅

L

2

⋅

−

=

Φ

2

2

2E J

⋅

L

φ

1

2

φ

2

+

(

)

⋅

1

12

q

⋅

L

2

⋅

+

=

Φ

2

3

2 E

⋅

J

⋅

3 L

⋅

2

φ

2

⋅

( )

⋅

1

8

P

⋅

3

⋅

L

−

=

Φ

B

3

2E J

⋅

3L

φ

2

( )

⋅

1

8

P

⋅

3

⋅

L

+

=

Φ

2

4

3E J

⋅

2L

φ

2

( )

⋅

=

Zapisujemy równania równowagi momentów w wezlach :

.

M1

∑

0

=

Φ

1

1

Φ

1

2

+

0

=

.

M2

∑

0

=

Φ

2

2

Φ

2

3

+

Φ

2

4

+

0

=

Po podstawieniu wzorów na momenty otrzymujemy :

.

M1

∑

0

=

2E J

⋅

3L

2

φ

1

( )

⋅

2E J

⋅

L

2

φ

1

φ

2

+

(

)

⋅

+

1

12

q

⋅

L

2

⋅

−

0

=

2E J

⋅

L

φ

1

2

φ

2

+

(

)

⋅

1

12

q

⋅

L

2

⋅

+

2 E

⋅

J

⋅

3 L

⋅

2

φ

2

⋅

( )

⋅

+

1

8

P

⋅

3

⋅

L

−

3E J

⋅

2L

φ

2

( )

⋅

+

0

=

.

M2

∑

0

=

Po uporzadkowaniu :

.

M1

∑

0

=

E J

⋅

L

16

3

φ

1

2

φ

2

+













⋅

1

12

q

⋅

L

2

⋅

−

0

=

E J

⋅

L

2

φ

1

41

6

φ

2

+













⋅

1

12

q

⋅

L

2

⋅

+

1

8

P

⋅

3

⋅

L

−

0

=

.

M2

∑

0

=

Macierz sztywno

ś

ci i wyrazów wolnych:

K

E J

⋅

L

16

3

2

2

41

6





















⋅

=

E

D

1

12

−

q

⋅

L

2

⋅

1

12

q

⋅

L

2

⋅

1

8

P

⋅

3

⋅

L

−





















=

q

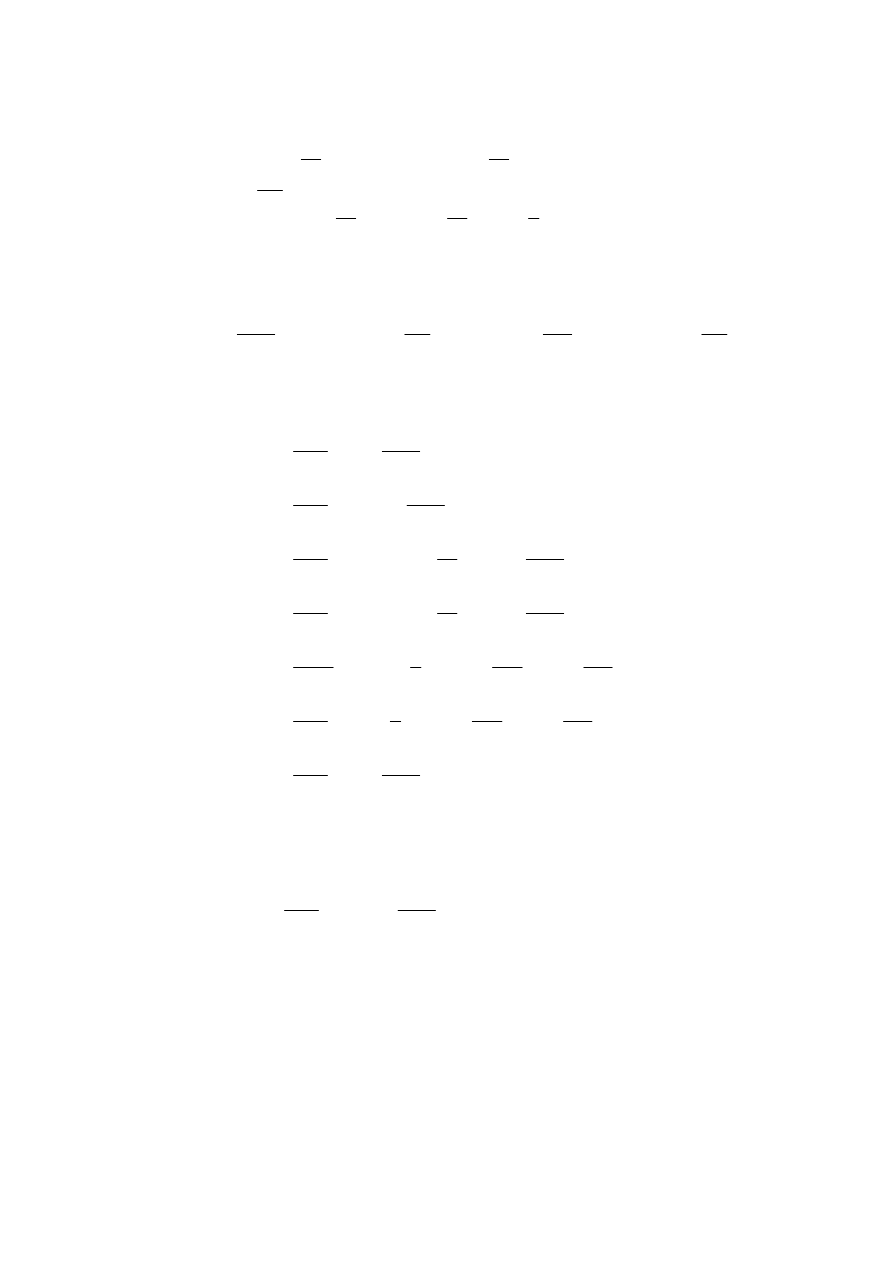
Układ równa

ń

zapisany macierzowo :

K X

⋅

D

+

0

=

E J

⋅

L

16

3

2

2

41

6





















⋅

φ

1

φ

2

















⋅

1

12

−

q

⋅

L

2

⋅

1

12

q

⋅

L

2

⋅

1

8

P

⋅

3

⋅

L

−





















+

0

0













=

Rozwi

ą

zuj

ą

c układ równa

ń

otrzymujemy nast

ę

puj

ą

ce warto

ś

ci k

ą

tów obrotu w

ę

złów :

φ

1

1

2336

53 q L

⋅

⋅

54 P

⋅

−

(

)

⋅

L

2

E J

⋅

⋅

=

φ

2

1

−

584

11 q L

⋅

⋅

36 P

⋅

−

(

)

⋅

L

2

E J

⋅

⋅

=

Rozwi

ą

zanie : momenty w

ę

złowe :

Φ

A

1

.

=

2E J

⋅

3L

φ

1

⋅

1

3504

L 53 q L

⋅

⋅

54 P

⋅

−

(

)

⋅

⋅

=

Φ

1

1

.

=

2E J

⋅

3L

2

φ

1

( )

⋅

1

1752

L 53 q L

⋅

⋅

54 P

⋅

−

(

)

⋅

⋅

=

Φ

1

2

.

=

2E J

⋅

L

2

φ

1

φ

2

+

(

)

⋅

1

12

q

⋅

L

2

⋅

−

1

−

1752

L 53 q L

⋅

⋅

54 P

⋅

−

(

)

⋅

⋅

=

Φ

2

2

.

=

2E J

⋅

L

φ

1

2

φ

2

+

(

)

⋅

1

12

q

⋅

L

2

⋅

+

1

3504

L 187 q L

⋅

⋅

702 P

⋅

+

(

)

⋅

⋅

=

Φ

2

3

.

=

2 E

⋅

J

⋅

3 L

⋅

2

φ

2

⋅

( )

⋅

1

8

P

⋅

3

⋅

L

−

11

−

438

q L

2

⋅

⋅

171

584

P L

⋅

⋅

−

=

Φ

B

3

.

=

2E J

⋅

3L

φ

2

( )

⋅

1

8

P

⋅

3

⋅

L

+

11

−

876

q L

2

⋅

⋅

243

584

P L

⋅

⋅

+

=

Φ

2

4

.

=

3E J

⋅

2L

φ

2

⋅

3

−

1168

L 11 q L

⋅

⋅

36 P

⋅

−

(

)

⋅

⋅

=

Moment w przekroju 1-1 wynosi wi

ę

c :

Φ

1

1

.

=

2E J

⋅

3L

2

φ

1

( )

⋅

1

1752

L 53 q L

⋅

⋅

54 P

⋅

−

(

)

⋅

⋅

=