The Discrete Time Control of a Three Phase 4

Wire PWM Inverter with Variable DC Link

Voltage and Battery Storage for PV

Application

Dipl. Ing. Said El-Barbari

and

Prof. Dr. W. Hofmann

CHEMNITZ UNIVERSITY OF

TECHNOLOGY

Department of Electrical Machines

and Derives

Abstract

The discrete time control of a three phase 4 wire PWM inverter with variable DC link voltage for
simultaneously supply of three phase and single phase load in transformerless stand alone
photovoltaic application with battery energy storage (BES) and LC output filter is described. The
whole system consists of a photovoltaic array, a battery energy storage, two step up boost converter
and three phase PWM voltage source inverter with a LC output Filter. The first boost converter is
controlled in such a way so that the battery will be always charged at the maximum power point
(MPP) when changes in the insulation or temperature are occurred. The second step up boost
converter is connected in series between the Battery energy storage and the DC link capacitor of the
PWM inverter. It controls the DC link capacitor voltage. The mathematical model of the linearized
system is first obtained. The discretized state space equation of the whole system is derived. A new
control method based on the dead beat control algorithm is implemented to control both the output
voltage of the LC filter and dc link capacitor voltage so that disturbance of the output voltage due to
load unbalances is eliminated. Simulation results for various operation conditions are presented to
verify the validity of the control method.

Summary

Nowadays more attention is paid to PV system and their related technology for domestic application
as well as in large central power stations. PV systems are advantageous because they are abundant,

pollution free and distributed through the earth. The only draw back is that the initial installation
cost is considerably high.

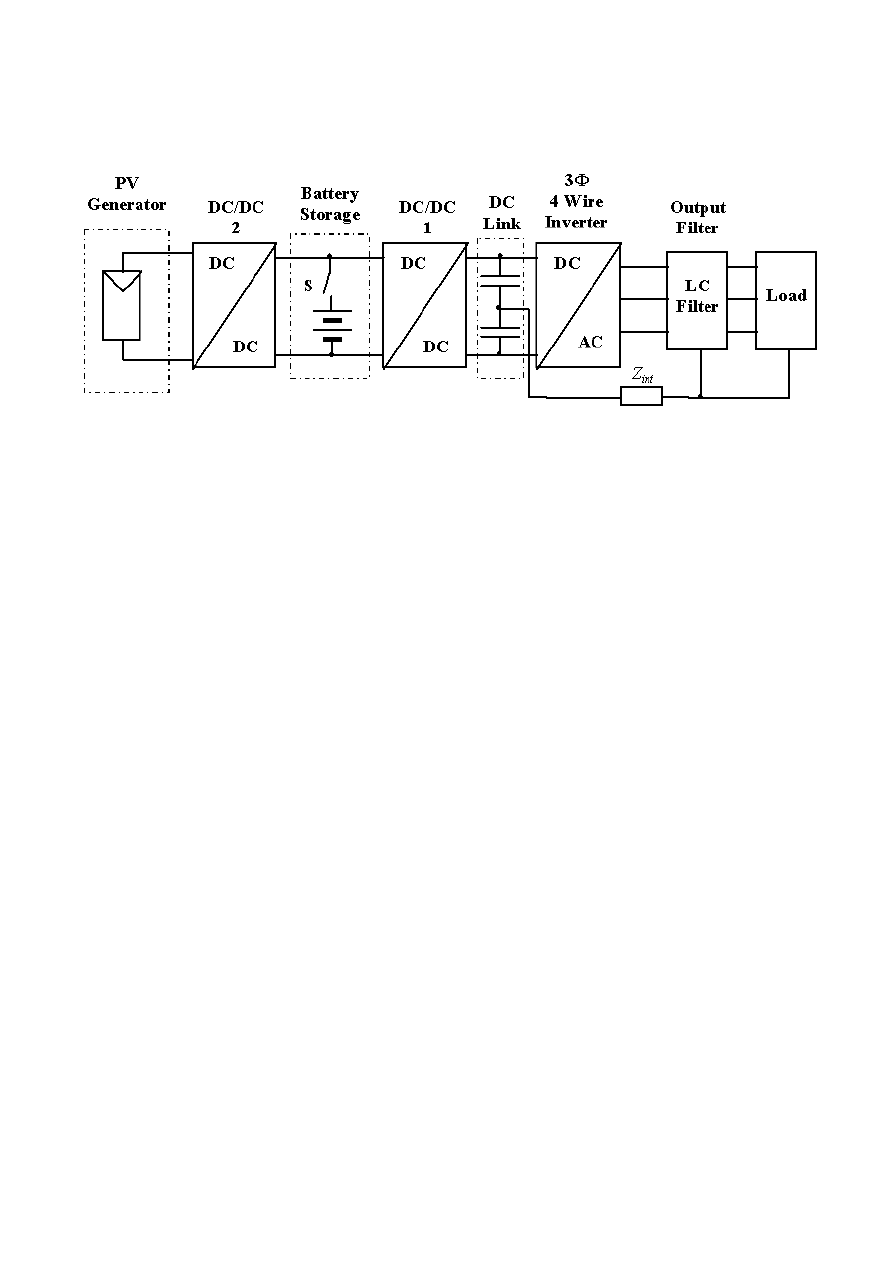
Figure 1 stand alone photovoltaic system with 3 phase 4 wire PWM voltage source inverter

Since the power generated by an array of PV panels is direct-current, it may be transformed, either
into a power with constant voltage for dc applications or into ac power. In both cases it is important
to draw as much energy as possible from the PV panel. The output power of PV generators vary
extensively with the weather conditions such as solar insulation, temperature and cloudy skies. To
obtain the maximum power from such an array under any weather condition it is necessary to
connect the PV array to a converter that can adapt itself to the changing V-I characteristic of the PV
generator (MPPT). In the system illustrated in Figure 1 this is provided by the DC/DC2. In this way
the battery will be always charged at the Maximum Power Point. The goal of the system illustrated
in figure 1 is to supply three as well as single phase loads of any art with constant amplitude
sinusoidal voltage and constant frequency. For this propose the neutral point of the LC output filter
and load is connected to the midpoint of the DC link capacitor bank. Due to load unbalances an
intruding current flows throw the impedance between the neutral point and midpoint and a voltage
drop occurs which distorts the symmetrical output voltage. To solve this problem the following
measurements were taken



a zero sequence current and voltage control is implemented



a DC/DC converter is used to control the DC link voltage according to load unbalances

In this way the symmetry of the output voltage is achieved and the linear region of the PWM
modulator of the DC/AC VSI (Voltage Source Inverter) is extended.

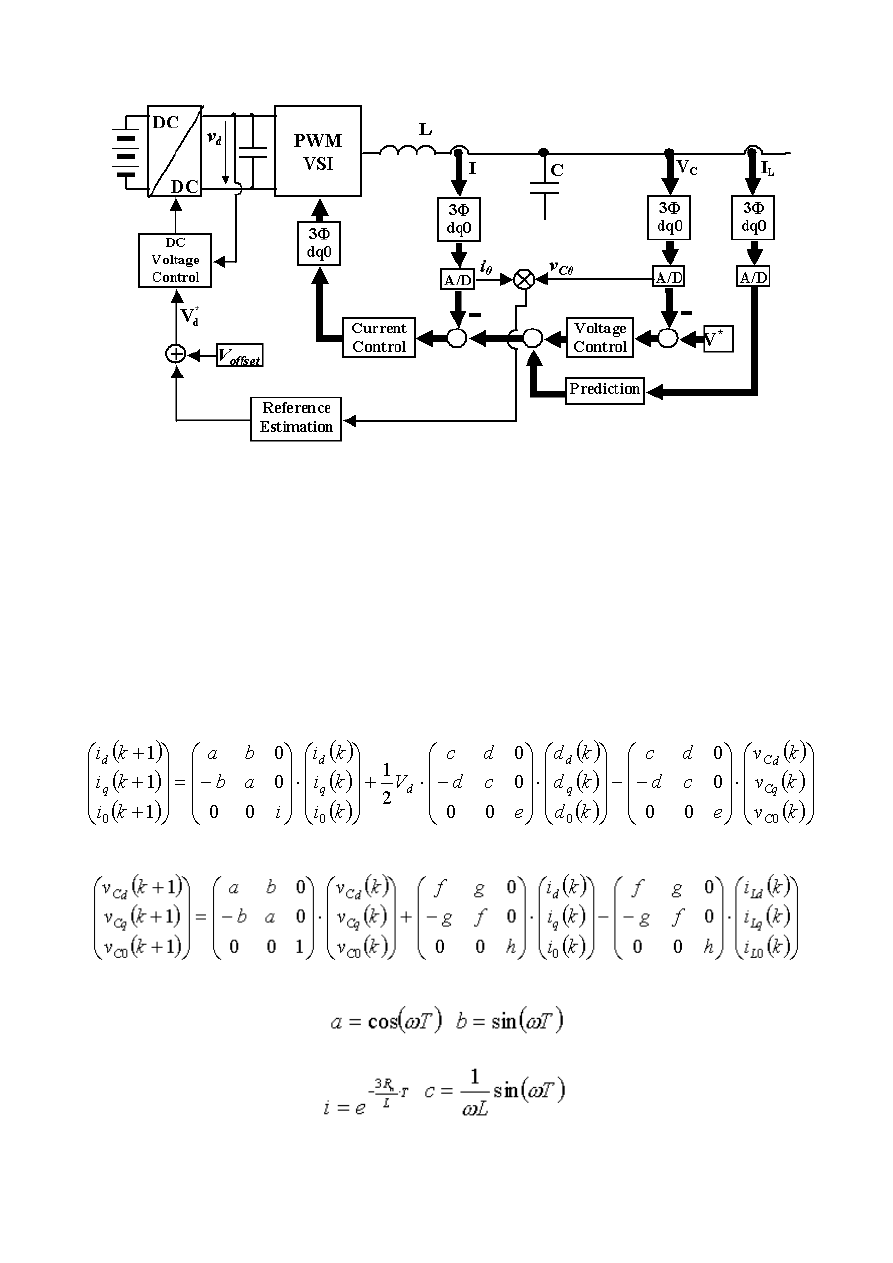
Figure 2 principle of the control method

Since the dead beat control strategy for single phase inverter was discussed in [4], [6] and [8] and
for three phase inverters in [1], [2], [3], [5] and [7], the dead beat control in [1] and [2] is adopted
and extended to mach for three phase 4 wire VSI. The control proposed of the VSI is illustrated in
Figure 2. It contains the current minor loop, voltage major loop, the DC link reference estimation
and the DC link voltage control loop. Here only a brief description of the current and voltage as
well as dc link control is intended since to describe them in details will exceed the limits of the
summary. The control of the VSI is designed in the synchronized dq0 frame. Equation (1) and (2)
describe the discrete system in the synchronized dq0 frame.

(1)

(2)

,

,

,

,

,

,

,

,

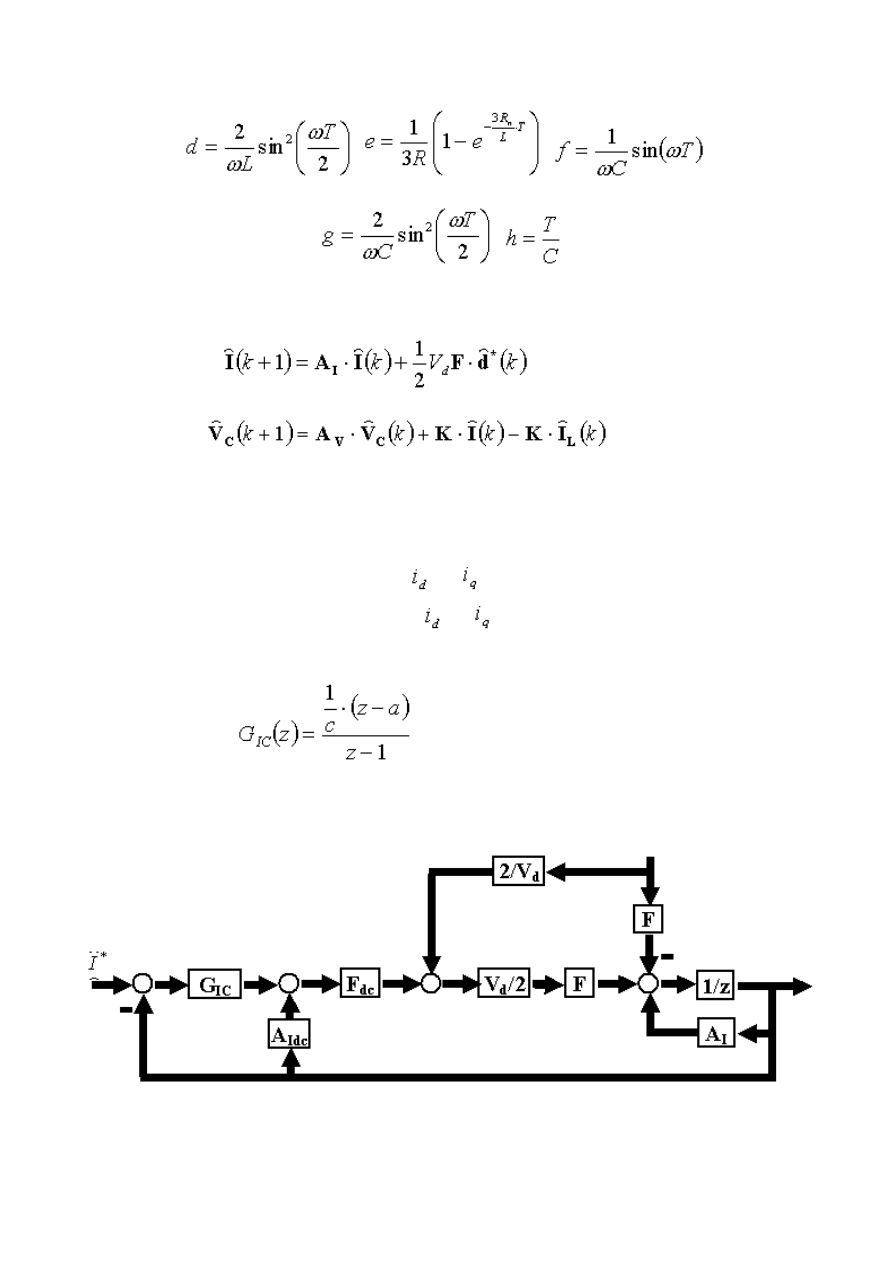
Equation (3) and (4) describe the system in vector form

(3)

(4)

Form these equations one can see that the d and the q variables are coupled with each other whereas
the 0 sequence is decoupled. To enhance the performance of the control loop the capacitor voltage

is fed forward as seen in figure 3. To control

and

separately the coupling elements b and d are

decoupled by the matrixes F

dc

and A

Idc

so that

and

depend only on a and c. After removing

the couplings, the dead beat controller G

IC

is provided.

(5)

Figure 3 principle of the current control loop

Since the inverter must quickly supply the load current I

L

to compensate the disturbance of the load,

the prediction of the load current is implemented, as shown in figure 2, so that the predicted load
current is given by ([1], [2])

(6)

In this way the target value of the load current is provided and thus the computation time delay is
compensated. The voltage major loop is constructed in the same manner. The same dead beat
control is also applied to the 0-scequence of currents and voltages except that, in the 0 control loop
no decouplings are needed.

The mathematical model of the DC/DC converter in the continuos conduction mode is established
and linearized ([9], [10]). The digital control is implemented [11] so that the DC link voltage will
follow a certain reference voltage which is given by

(7)

where

is given by

(8)

and K is a correction factor.

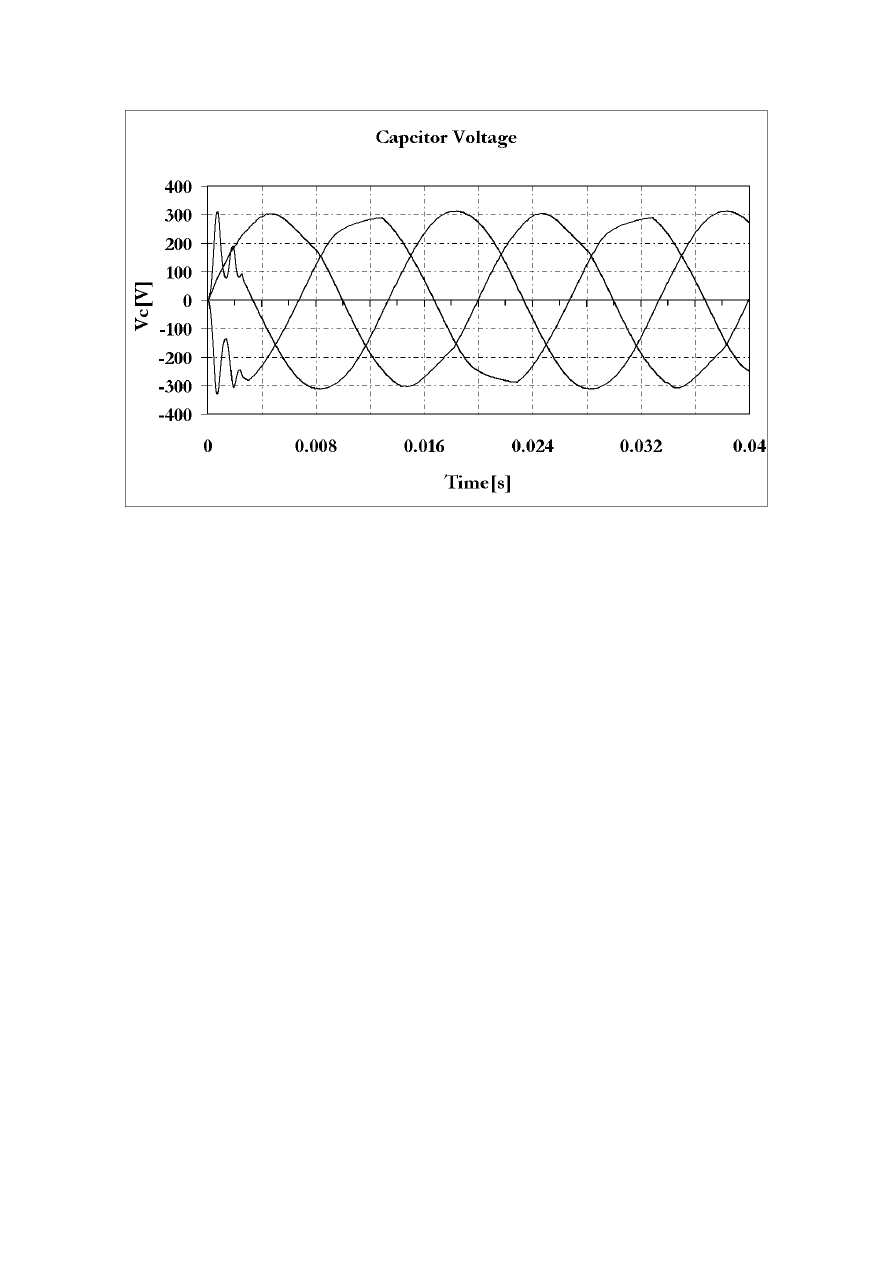
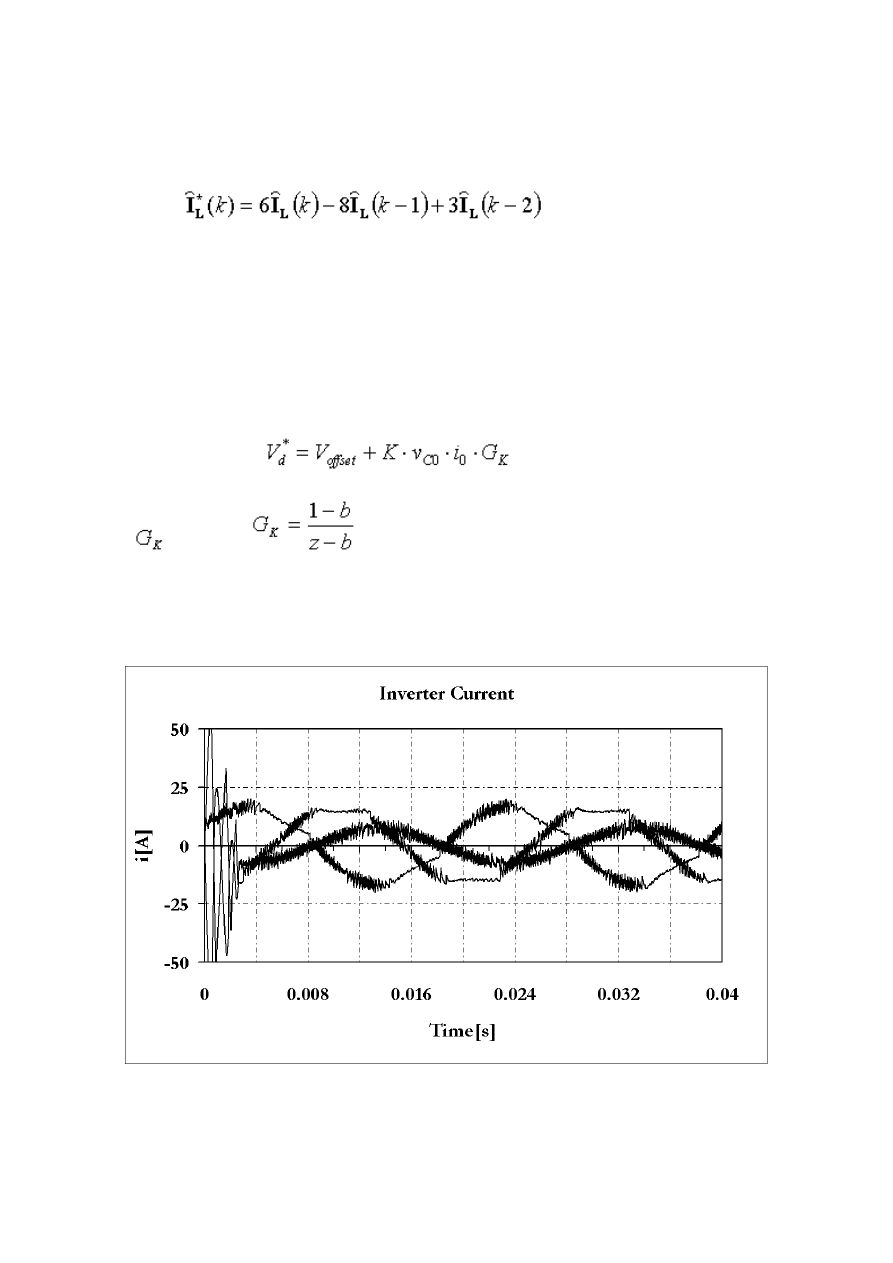
Figure 4 inverter current and capacitor voltage of the output filter with unbalanced load

(R

u

=R

v

=20



,R

w

=2000



) and uncontrolled DC link voltage

Figure 4 shows the simulation results of the dead beat control for unbalanced load with uncontrolled
dc link voltage. The distortion in the inverter currents occur when the control signals exceed the
linear region of the PWM modulator due to load unbalances. As a result, the capacitor voltage of
the output filter is also distorted. Figure 5 shows the simulation results when the DC-link voltage is
controlled. It shows the capacitor voltage of the output filter when the load changes from
(R

u

=R

v

=60



, R

w

=2000



) to (R

u

=R

v

=20



, R

w

=2000



) as indicated by an arrow in the lift hand

sub diagram. This shows the high dynamic performance of the introduced dead beat control method
as the disturbance of the output voltage is quickly compensated. The distortion of the output voltage
reduces gradually as a result of the controllable dc link voltage as indicated in the right hand sub
diagram.

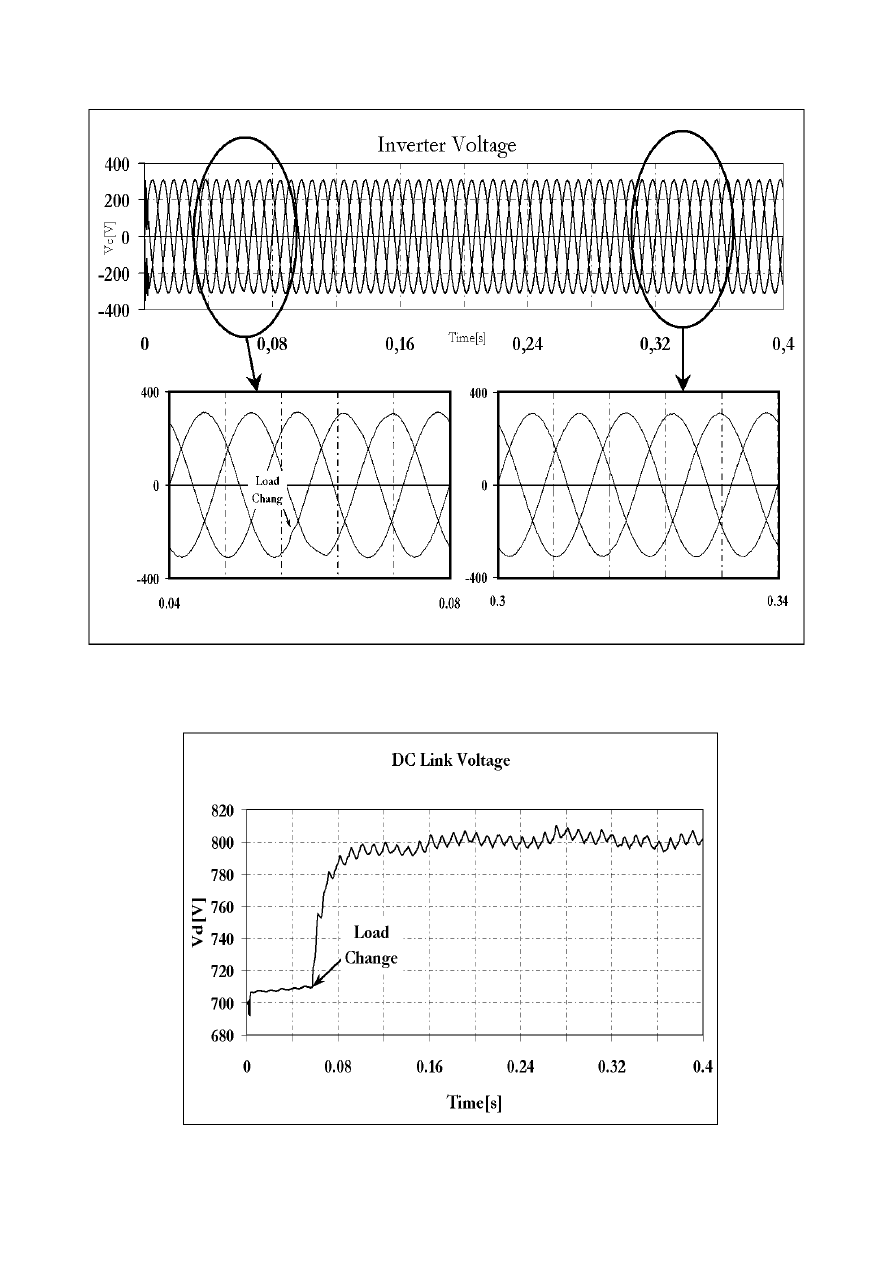
Figure 5 capacitor voltage of the output filter with unbalanced load and controlled DC link

voltage

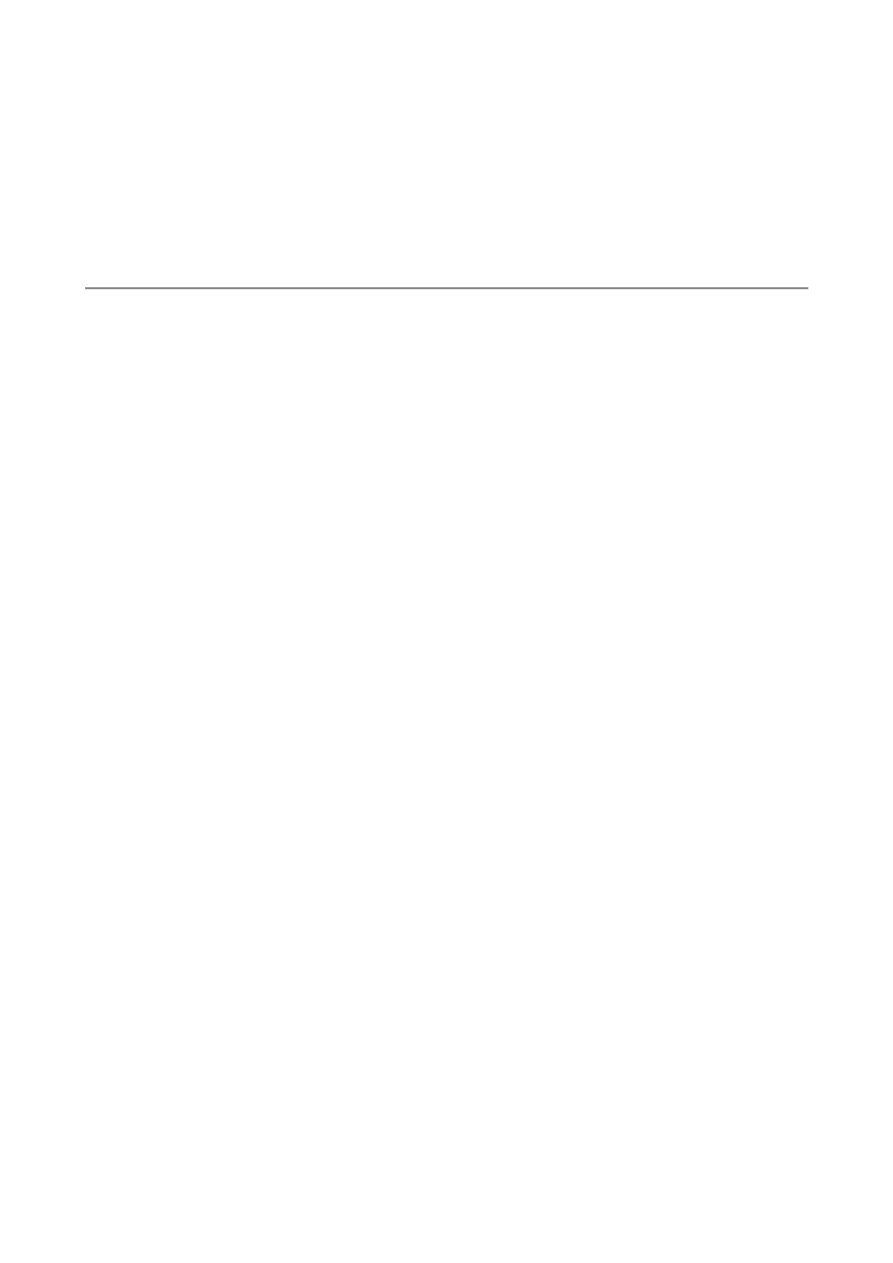
Figure 6 DC link Voltage

Diagram 6 shows the dc link voltage when the load changes and distortion in the output voltage
occurs. The dc link voltage increases to reduce the output voltage distortion. The oscillations in the
dc link voltage are due to the filter effect in the DC link reference estimation given by equation (8).
However; the oscillation portion is relatively small compared to the dc voltage portion, so that it
does not affect the output voltage.

References

[1] Takao Kawabata, Takeshi Miyashita and Yushin Yamamoto, "Digital Control of three-Phase
Inverter with LC Filter", IEEE Transactions on Power Electronics, Vol. 6, No. 1, January 1991, pp.
62-72.

[2] Takao Kawabata, Takeshi Miyashita and Yushin Yamamoto, "Dead Beat Control of three-
Phase PWM Inverter", IEEE Transactions on Power Electronics, Vol. 5, No. 1, January 1990, pp.
21-28.

[3] Osman Kükrer, "Deadbeat Control of a Three-Phase Inverter with an Output LC Filter", IEEE
Transactions on Power Electronics, Vol. 11, No. 1, January 1996, pp. 16-23.

[4] Chihchiang Hua and Richard G. Hoft, "Hight Performance Deadbeat Controlled PWM
Inverter using a Current Source Compensator for nonlinear loads", IEEE/PESC 23rd Anual, Toledo,
Spain 1992, pp. 443-450.

[5] Tomoki Yokoyama and Atsuo Kawamura, "Disturbance Observer Based Fully Digital
Controlled PWM Inverter for CVCF Operation", IEEE Transactions on Power Electronics, Vol. 9,
No. 5, September 1994, pp. 473-480.

[6] Atsuo Kawamura and Tomoki Yokoyama, "Comparison of Five Control Methods for Digitally
Feedback Controlled PWM Inverters", EPE Firenze 1991, Vol. 2, pp. 35-40.

[7] Youichi Ito and Shoichi Kawauchi, "Microprocessor-Based Robust Digital Control for UPS
with Three -Phase PWM Inverter", IEEE Transactions on Power Electronics, Vol. 10, No. 2, March
1995, pp. 196-204.

[8] Atsuo Kawamura, Toshimasa Haneyoshi and Richard G. Hoft, "Deadbeat Controlled PWM
Inverter with Parameter Estimation Using Only Voltage Sensor", IEEE Transactions on Power
Electronics, Vol. 3, No. 2, April 1988, pp. 118-125.

[9] P. R. K. Chetty "Current Injected Equivalent Circuit Approach to Modeling and Analysis of
Current Programmed Switching DC-DC Converters (Discontinuous Inductor Conduction Mode)",
IEEE Transactions on Industrial Applications, Vol. IA-18, No. 3, May/June 1982, pp. 295-299.

[10] Francisco Guinjoan, Javier Calvente, Alberto Poveda and Luis Martinez, "Large-Signal
Modeling and Simulation of Switching DC-DC Converter", IEEE Transactions on Power
Electronics, Vol. 12, No. 3, May 1997, pp. 485-494.

[11] F. Al-Hosini, ABB Corporate Research, Sweden, "An Aproximate Dead-Beat Control
stratigy for the disign of functions regulators in DC/DC Converters", EPE Trondheim 1997, Vol. 3,
pp. 155-160.