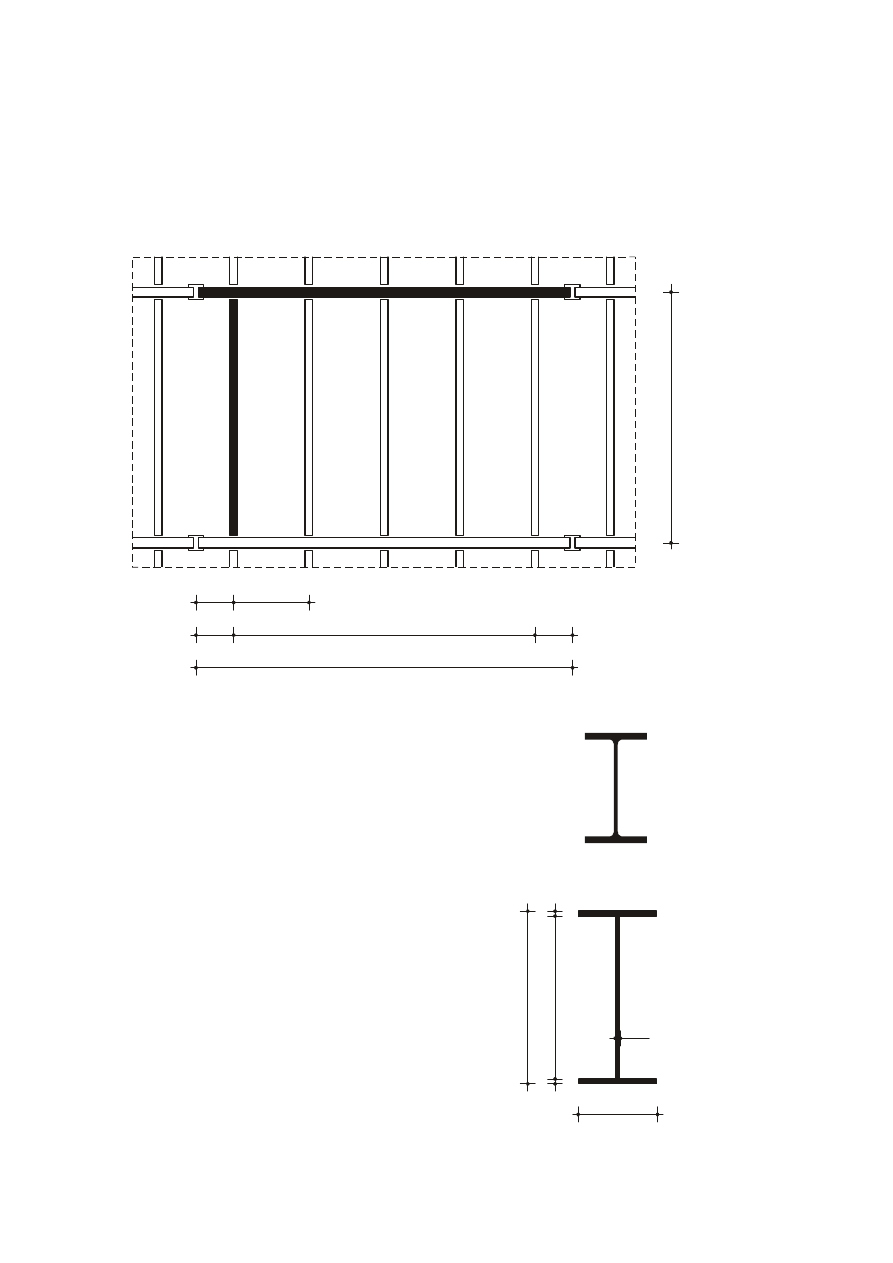
Geometria konstrukcji wsporczej stropu:

Długość belki:

B

6.4 m

⋅

:=

Liczba belek:

n

5

:=

Rozstaw belek:

a

1.8 m

⋅

:=

Długość dźwigara:

L

n a

⋅

9m

=

:=

B

a/2
a/2

a/2

a

(n-1) x a

n x a = L

Przekrój belki stropowej walcowanej:

A , I

y,b

b

Pole powierzchni:

Ab 45.9 cm

2

⋅

:=

Moment bezwładności:

Iy.b 5790 cm

4

⋅

:=

Przekrój spawany dźwigara:

t

f

b

f

t

f

h

w

t

w

h

Szerokość pasów:

bf 220 mm

⋅

:=

Grubość pasów:

tf 14 mm

⋅

:=

Wysokość środnika

hw 700 mm

⋅

:=

Grubość środnika:

tw 6 mm

⋅

:=

Obciążenie powierzchni stropu / grubość płyty stropowej:

Qk 4 kPa

⋅

:=

tc 120 mm

⋅

:=

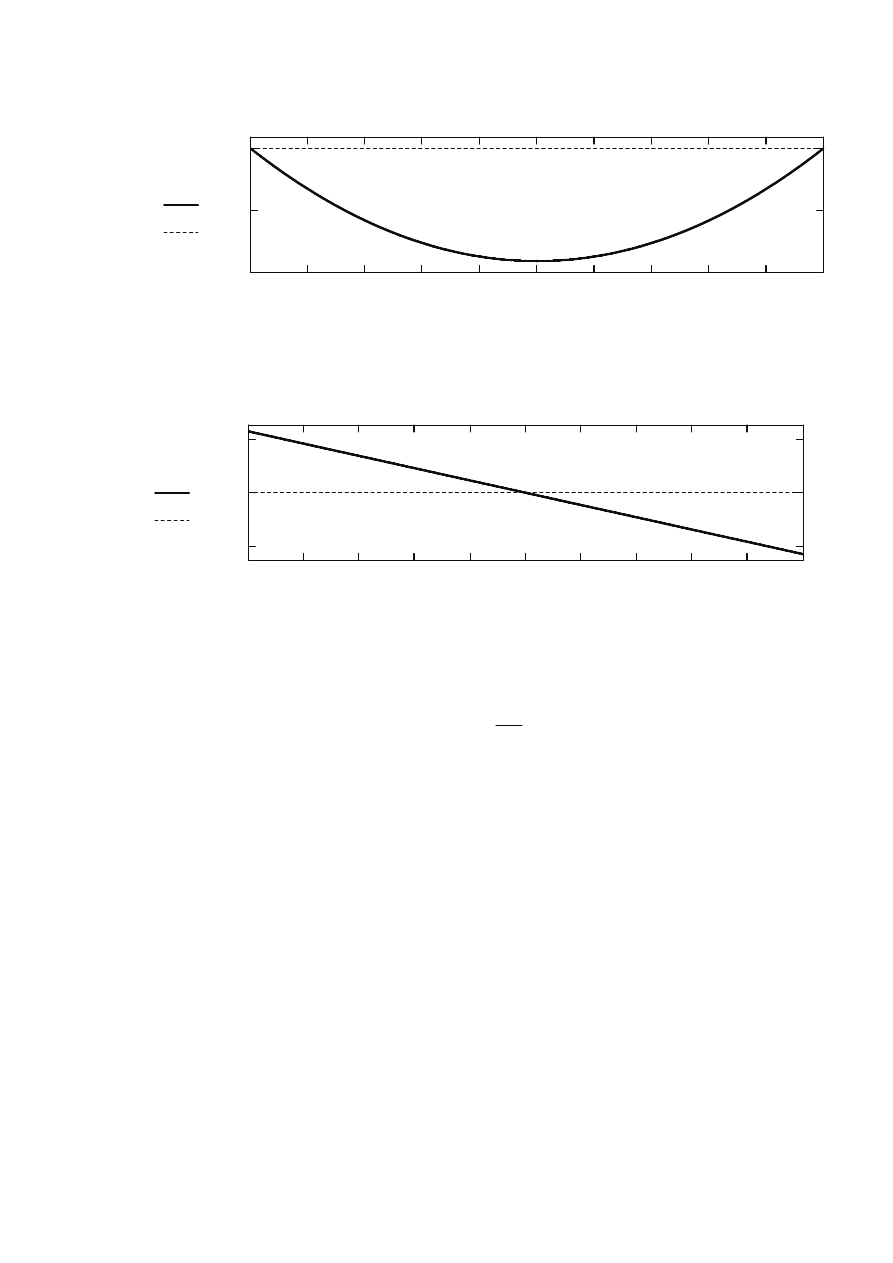
Wyniki obliczeń statycznych belki stropowej

Wykres momentu zginającego:

0

0.64

1.28

1.92

2.56

3.2

3.84

4.48

5.12

5.76

6.4

0

5 10

4

×

0

My x()
0

x

Moment w środku rozpiętości:

My 0.5 B

⋅

(

) 92.4 kNm

⋅

=

Wykres siły tnącej:

0

0.64

1.28

1.92

2.56

3.2

3.84

4.48

5.12

5.76

6.4

5

−

10

4

×

0

5 10

4

×

Vz x()
0

x

Siła tnąca przy podporze / reakcja podporowa:

Vz 0 m

⋅

(

) 57.7 kN

⋅

=

Ugięcie belki w środku rozpiętości:

Ugięcie dopuszczalne belki:

z 0.5 B

⋅

(

) 24.2 mm

⋅

=

B

250

25.6 mm

⋅

=

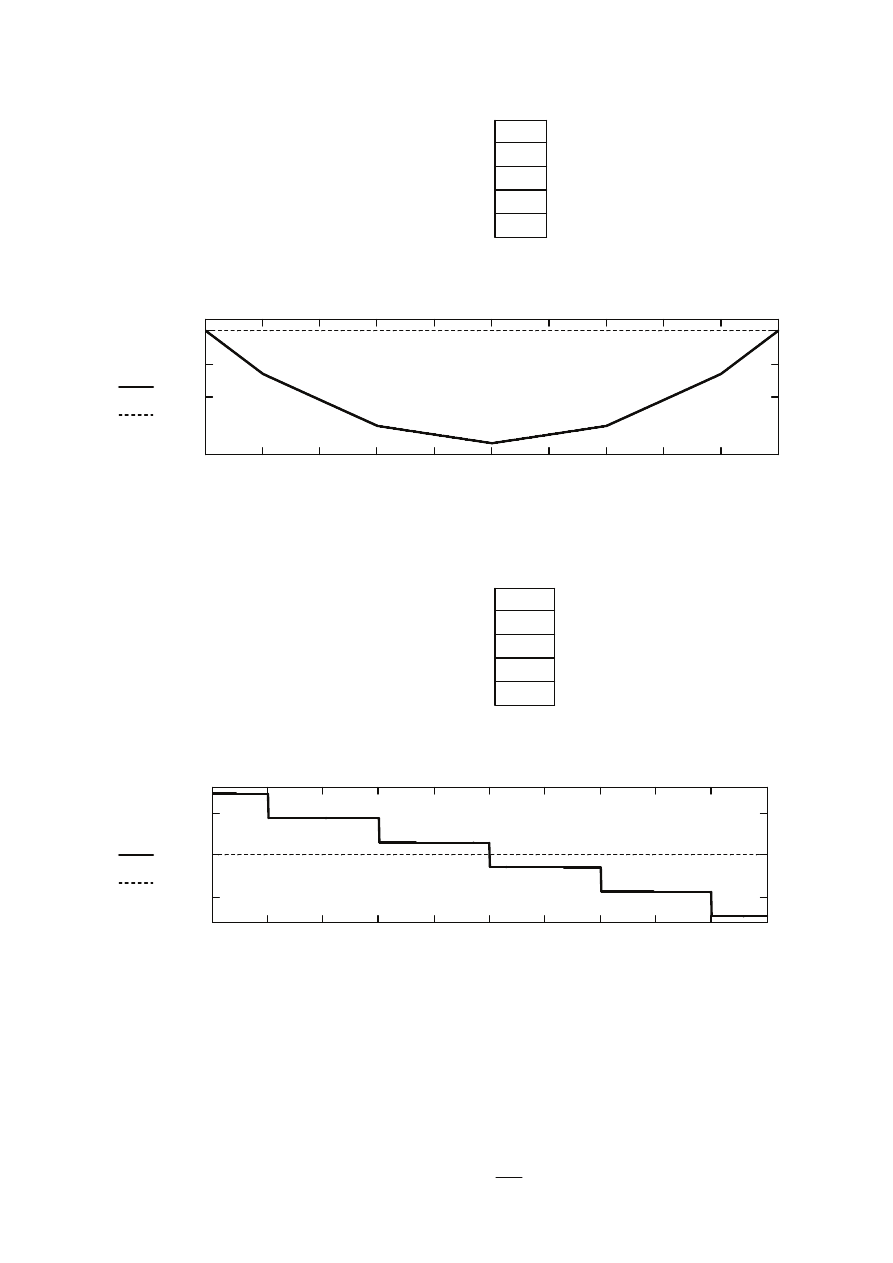
Wyniki obliczeń statycznych dźwigara

Przekroje, w których przyłożone jest obciążenie:

X

i

0.90
2.70

4.50

6.30

8.10

m

⋅

=

Wykres momentu zginającego:

0

0.9

1.8

2.7

3.6

4.5

5.4

6.3

7.2

8.1

9

0

4 10

5

×

2 10

5

×

0

My x()
0

x

Moment w środku rozpiętości:

My 0.5 L⋅

(

) 684.6 kNm

⋅

=

Momenty w miejscach przyłożenia sił skupionych

My X

i

( )

263.1
579.2

684.6

579.2

263.1

kNm

⋅

=

Wykres siły tnącej:

0

0.9

1.8

2.7

3.6

4.5

5.4

6.3

7.2

8.1

9

2

−

10

5

×

0

2 10

5

×

Vz x()
0

x

Reakcja podporowa

R 292.7 kN

⋅

=

Siła tnąca przed skrajną belką:

Vz 0 m

⋅

(

) 292.7 kN

⋅

=

Siła tnąca za skrajną belką:

Vz X

1

( )

176.5 kN

⋅

=

Ugięcie dźwigara w środku rozpiętości:

Ugięcie dopuszczalne dźwigara

z 0.5 L

⋅

(

) 21.1 mm

⋅

=

L

350

25.7 mm

⋅

=

kNm

kN m

⋅

:=

1. GEOMETRIA STROPU

Rozpiętość belek stropowych:

B

6.4 m

⋅

:=

Rozstaw belek stropowych:

a 1.8 m

⋅

:=

Liczba belek:

n 5

:=

Rozpiętość dźwigarów:

L n a

⋅

9m

=

:=

2. ZEBRANIE OBCIĄŻEŃ - BELKA STROPOWA

1. Obciążenia stałe: ciężar płyty 12 cm, ciężar warstw wykończenia 0,3 kN/m2, ciężar własny belki IPE270,

2. Obciążenia zmienne: obciążenie eksploatacyjne 4,0 kN/m2.

3. OBLICZENIA BELKI STROPOWEJ

1. Warunek nośności belki przy zginaniu,

2. warunek nośności przekroju przy ścinaniu,

3. sprawdzenie ugięć granicznych,

4. warunki nośności belki w miejscu połączenia z dźwigarem.

3.1 WARUNEK NOŚNOŚCI BELKI PRZY ZGINANIU

Moment zginający w belce:

(wyniki obliczeń statycznych wzięto z załączonego pliku)

My.Ed 92.4 kNm

⋅

:=

Przekrój: dwuteownik równoległościenny IP270E ze stali S235

Wysokość

h 270 mm

⋅

:=

Szerokość

b 135 mm

⋅

:=

Grubości części

tf 10.2 mm

⋅

:=

tw 6.6 mm

⋅

:=

Promień zaokrąglenia

r 15 mm

⋅

:=

Szerokość środnika

hw h 2 tf⋅

−

249.6 mm

⋅

=

:=

Granica plastyczności

fy 235 MPa

⋅

:=

ε

1

:=

Współczynniki częściowe

γM0 1.0

:=

γM1 1.0

:=

Klasa przekroju

środnik

h 2 r⋅

−

2 tf⋅

−

tw

33.273

=

<

72 ε

⋅

72

=

stopka

b tw

−

2 r⋅

−

2 tf⋅

4.824

=

<

9 ε

⋅

9

=

Przekrój przy zginaniu jest klasy 1.

Wskaźnik plastyczny przekroju

Wpl.y b tf⋅ h tf

−

( )

⋅

hw

2

tw

⋅

4

+

2 r

2

⋅

hw r

−

(

)

⋅

+

π

r

2

⋅

hw

2

4 3 π

⋅

−
3 π

⋅

r⋅

+













⋅

−

483.997 cm

3

⋅

=

:=

1z13

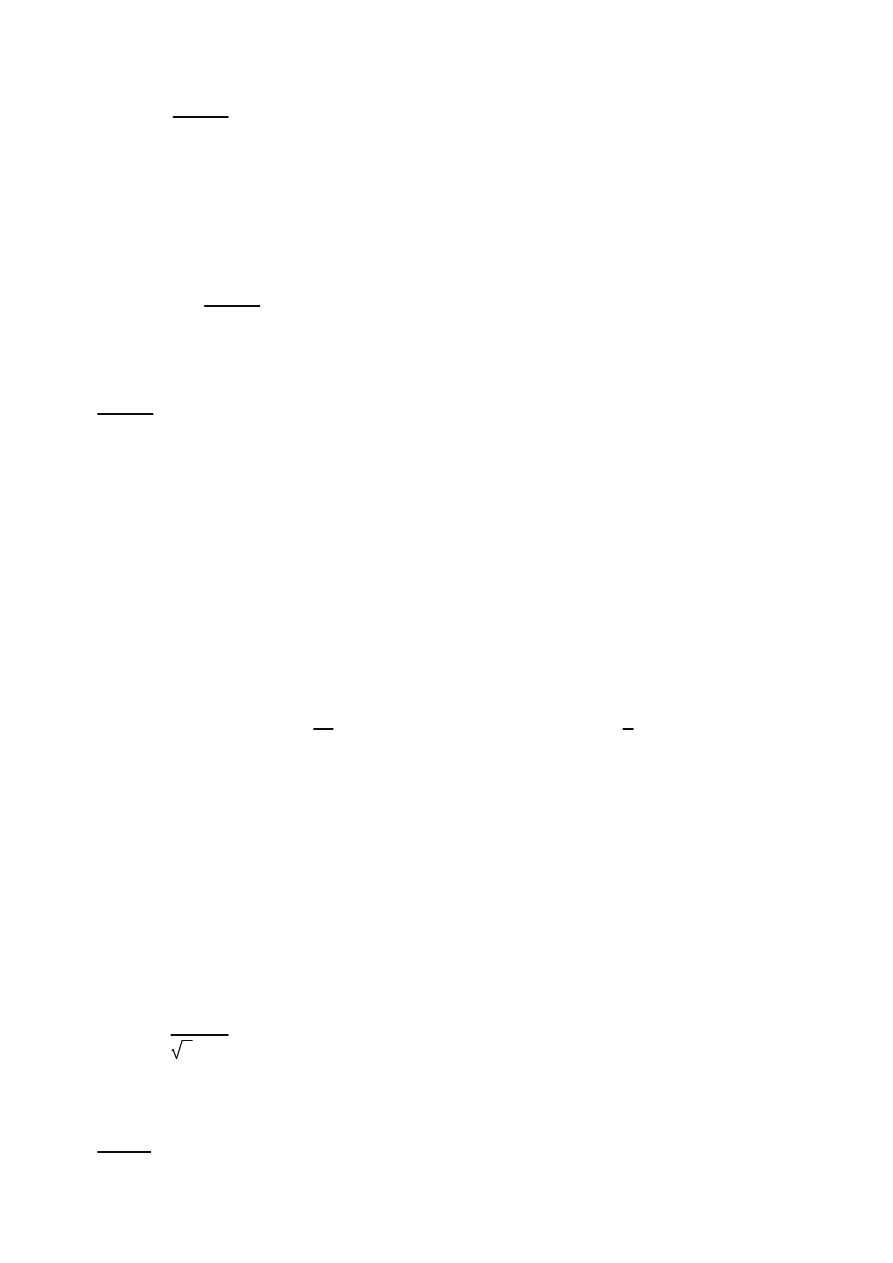
Nośność plastyczna przekroju:

Mc.y.Rd

Wpl.y fy

⋅

γM0

113.739 kNm

⋅

=

:=

Belka pasem górnym (ściskanym) jest stężona bocznie na całej długości. Pominięto zwichrzenie.

χLT 1

:=

Nośność zwichrzeniowa belki:

Mb.y.Rd χLT

Wpl.y fy

⋅

γM1

⋅

113.739 kNm

⋅

=

:=

Warunek stateczności elementu:

My.Ed

Mb.y.Rd

0.812

=

< 1,0

Warunek jest spełniony.

3.2 WARUNEK NOŚNOŚCI PRZEKROJU PRZY ŚCINANIU

Siła tnąca przy podporze

Vz.Ed 57.7 kN

⋅

:=

Sprawdzenie wrażliwości na miejscową utratę stateczności

współczynnik

η

1.2

:=

środnik

hw

tw

37.818

=

<

72

ε

η

⋅

60

=

Środnik nie jest wrażliwy na utratę stateczności miejscowej.

Pole brutto przekroju:

A

2 tf⋅ b⋅ h 2 tf⋅

−

(

)

tw

⋅

+

4 π

−

(

) r

2

⋅

+

45.945 cm

2

⋅

=

:=

Pole czynne przy ścinaniu

AV max A 2 b⋅ tf⋅

−

tf 2 r⋅ tw

+

(

)

⋅

+

η

hw

⋅

tw

⋅

,





22.138 cm

2

⋅

=

:=

Nośność plastyczna przekroju:

Vc.z.Rd

AV fy

⋅

3 γM0

⋅

300.365 kN

⋅

=

:=

Warunek wytrzymałości przekroju:

Vz.Ed

Vc.z.Rd

0.192

=

< 1,0

Warunek jest spełniony.

2z13

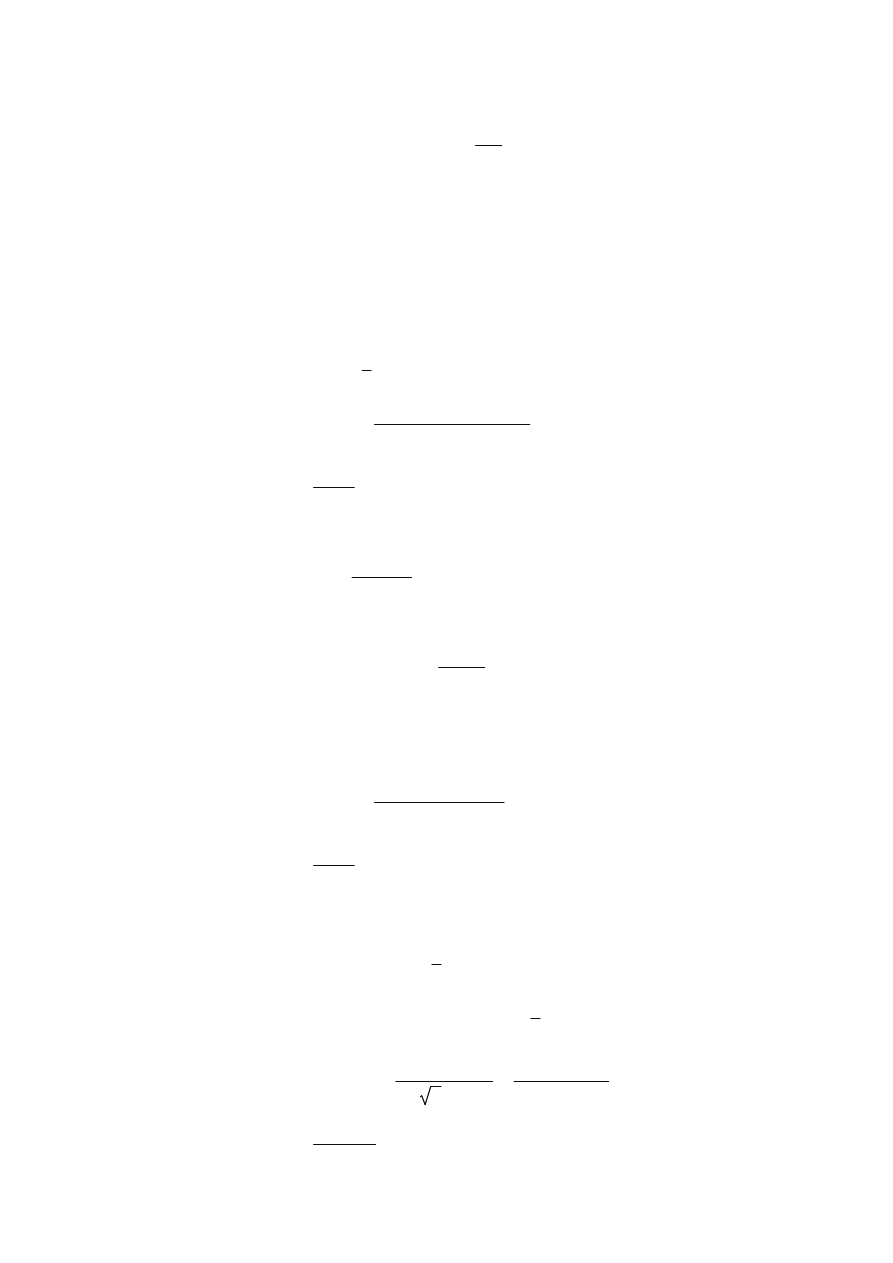
3.3 SPRAWDZENIE UGIĘĆ GRANICZNYCH

Ugięcie belki w środku rozpiętości:

Ugięcie dopuszczalne belki:

wmax 24.2 mm

⋅

:=

<

B

250

25.6 mm

⋅

=

Warunek jest spełniony.

3.4 WARUNKI NOŚNOŚCI BELKI W MIEJSCU POŁĄCZENIA Z DŹWIGAREM

Reakcja podporowa belki:

R Vz.Ed 57.7 kN

⋅

=

:=

Połączenie zakładkowe dociskowe (kategorii A). Przyjęto 2 śruby M16 kl. 8.8

Siła tnąca na jeden łącznik:

FEd

1
2

R

⋅

28.85 kN

⋅

=

:=

Nośność śruby na ścinanie:

Fv.Rd

0.6 161

⋅

mm

2

⋅

800

⋅

MPa

⋅

1.25

61.824 kN

⋅

=

:=

FEd

Fv.Rd

0.467

=

< 1,0

Warunek jest spełniony.

Nośność otworu na docisk:

αd

40 mm

⋅

3 18

⋅

mm

⋅

0.741

=

:=

αb min 1 αd

,

( )

0.741

=

:=

k1 min 2.5 2.8

40 mm

⋅

18 mm

⋅

⋅

1.7

−

,













2.5

=

:=

t

tw 6.6 mm

⋅

=

:=

d 16 mm

⋅

:=

Fb.Rd

k1 αb

⋅

d

⋅ t⋅ 360

⋅

MPa

⋅

1.25

56.32 kN

⋅

=

:=

FEd

Fb.Rd

0.512

=

< 1,0

Warunek jest spełniony.

Rozerwanie blokowe:

An.t

40 mm

⋅

d
2

−













tw

⋅

2.112 cm

2

⋅

=

:=

An.v

40 mm

⋅

110 mm

⋅

+

d

−

d
2

−













tw

⋅

8.316 cm

2

⋅

=

:=

Feff.1.Rd

An.v 235

⋅

MPa

⋅

3 1.0

⋅

An.t 360

⋅

MPa

⋅

1.25

+

173.655 kN

⋅

=

:=

R

Feff.1.Rd

0.332

=

< 1,0

Warunek jest spełniony.

3z13

Złożony stan naprężenia w miejscu podcięcia:

R 57.7 kN

⋅

=

M1 R 110

⋅

mm

⋅

6.347 kNm

⋅

=

:=

h1 h 40 mm

⋅

−

:=

b1

b
2

tw

2

−

64.2 mm

⋅

=

:=

zc

0.5 h1

2

⋅

tw

⋅

0.5 tf

2

⋅

b1

⋅

+

h1 tw

⋅

b1 tf⋅

+

8.188 cm

⋅

=

:=

Iy

h1

3

tw

⋅

tf

3

b1

⋅

+

12

h1 tw

⋅

zc

−

h1

2

+













2

⋅

+

b1 tf⋅ zc

−

tf
2

+













2

⋅

+

1222.307 cm

4

⋅

=

:=

Wy

Iy

h1 zc

−

82.521 cm

3

⋅

=

:=

τ

R

h1 tw

⋅

38.011 MPa

⋅

=

:=

σ

M1
Wy

76.914 MPa

⋅

=

:=

σred

σ

2

3 τ

2

⋅

+

101.243 MPa

⋅

=

:=

<

fy

γM0

235 MPa

⋅

=

Warunek jest spełniony.

4. OBLICZENIA DŹWIGARA

1. Warunek nośności dźwigara przy zginaniu,

2. warunek nośności przekroju przy ścinaniu,

3. sprawdzenie ugięć granicznych,

4. dobór żeber ze względu na ścinanie

5. połączenie dźwigara ze słupem.

4.1 WARUNEK NOŚNOŚCI DŹWIGARA PRZY ZGINANIU
Moment zginający w dźwigarze

My.Ed 685 kNm

⋅

:=

Przekrój: dwuteownik spawany 700x6/220x14 ze stali S275

Wysokość środnika

hw 700 mm

⋅

:=

Szerokość

b 220 mm

⋅

:=

Grubości części

tf 14 mm

⋅

:=

tw 6 mm

⋅

:=

h hw 2 tf⋅

+

:=

Granica plastyczności

fy 275 MPa

⋅

:=

ε

0.924

:=

Współczynniki częściowe

γM0 1.0

:=

γM1 1.0

:=

4z13

Klasa przekroju

środnik

hw

tw

116.667

=

>

124 ε

⋅

114.576

=

stopka

b tw

−

2 tf⋅

7.643

=

<

9 ε

⋅

8.316

=

Przekrój przy zginaniu jest klasy 4, przy czym wrazliwy na utratę stateczności jest tylko środnik.

Cechy przekroju brutto:

Iy

1

12

h

3

b

⋅

h 2 tf⋅

−

(

)

3

b tw

−

(

)

⋅

−









⋅

95668.645 cm

4

⋅

=

:=

A

2 tf⋅ b⋅ h 2 tf⋅

−

(

)

tw

⋅

+

103.6 cm

2

⋅

=

:=

Środnik

współczynnik rozkładu naprężeń normalnych na szerokości ścianki

ψ

1

−

:=

parametr niestateczności miejscowej: k

σ

23.9

:=

smukłość względna

λw

hw

tw

1

28.419 ε

⋅

kσ

⋅

⋅

:=

λw 0.909

=

współczynnik redukcyjny

ρw

λw 0.055 3 ψ

+

(

)

⋅

−

λw

2

:=

ρw 0.967

=

szerokość strefy ściskanej

bc

hw

1 ψ

−

:=

bc 350 mm

⋅

=

szerokości współpracujące

beff bc ρw

⋅

338.509 mm

⋅

=

:=

be.1 0.4 beff

⋅

135.404 mm

⋅

=

:=

be.2 0.6 beff

⋅

203.106 mm

⋅

=

:=

zmiana położenia środka ciężkości

∆

zc

tw bc beff

−

(

)

⋅

0.5 h

⋅

tf

−

be.1

−

0.5 bc beff

−

(

)

⋅

−





⋅

A tw bc beff

−

(

)

⋅

−

1.399 mm

⋅

=

:=

Cechy przekroju współpracującego:

Ieff.y Iy A ∆zc

2

⋅

+

1

12

bc beff

−

(

)

3

⋅

tw

⋅

−

1

−

( ) tw

⋅

bc beff

−

(

)

⋅

0.5 hw

⋅

∆

zc

+

be.1

−

0.5 bc beff

−

(

)

⋅

−





2

⋅

+

...

95365.828 cm

4

⋅

=

:=

Weff.y

Ieff.y

0.5 h

⋅

∆

zc

+

2609.908 cm

3

⋅

=

:=

5z13

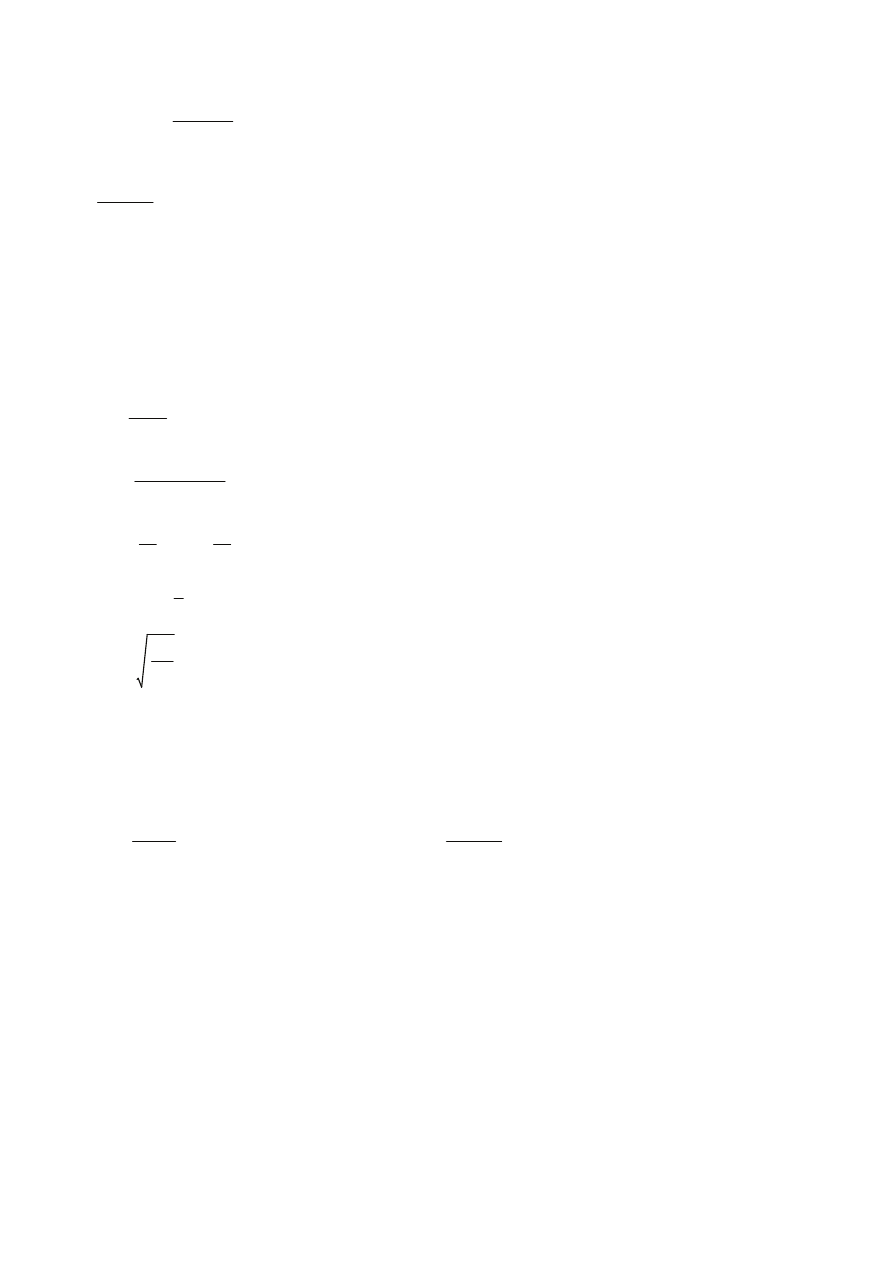
Nośność sprężysta przekroju:

Mc.y.Rd

Weff.y fy

⋅

γM0

717.725 kNm

⋅

=

:=

My.Ed

Mc.y.Rd

0.954

=

< 1,0

Warunek jest spełniony.

Zwichrzenie - metoda uproszczona

Lc 1.8 m

⋅

:=

ψ

579.2
684.6

0.846

=

:=

kc

1

1.33 0.33 ψ

⋅

−

0.952

=

:=

Iz.f

1

12

b

3

⋅

tf⋅

1

72

hw

⋅

tw

3

⋅

+

1242.477 cm

4

⋅

=

:=

Af b tf⋅

1
6

hw

⋅

tw

⋅

+

37.8 cm

2

⋅

=

:=

iz.f

Iz.f

Af

5.733 cm

⋅

=

:=

λ1 93.9 ε

⋅

86.764

=

:=

λc.0 0.4

:=

λf

Lc kc

⋅

iz.f λ1

⋅

0.344

=

:=

<

λc.0

Mc.y.Rd

My.Ed

⋅

0.419

=

Nie przekroczono granicznej wartości smukłości giętnej pasa przy wyboczeniu z płaszczyzny dźwigara. Warunek

stateczności elementu sprowadza się do warunku wytrzymałości przekroju. Warunek zatem jest spełniony.

6z13

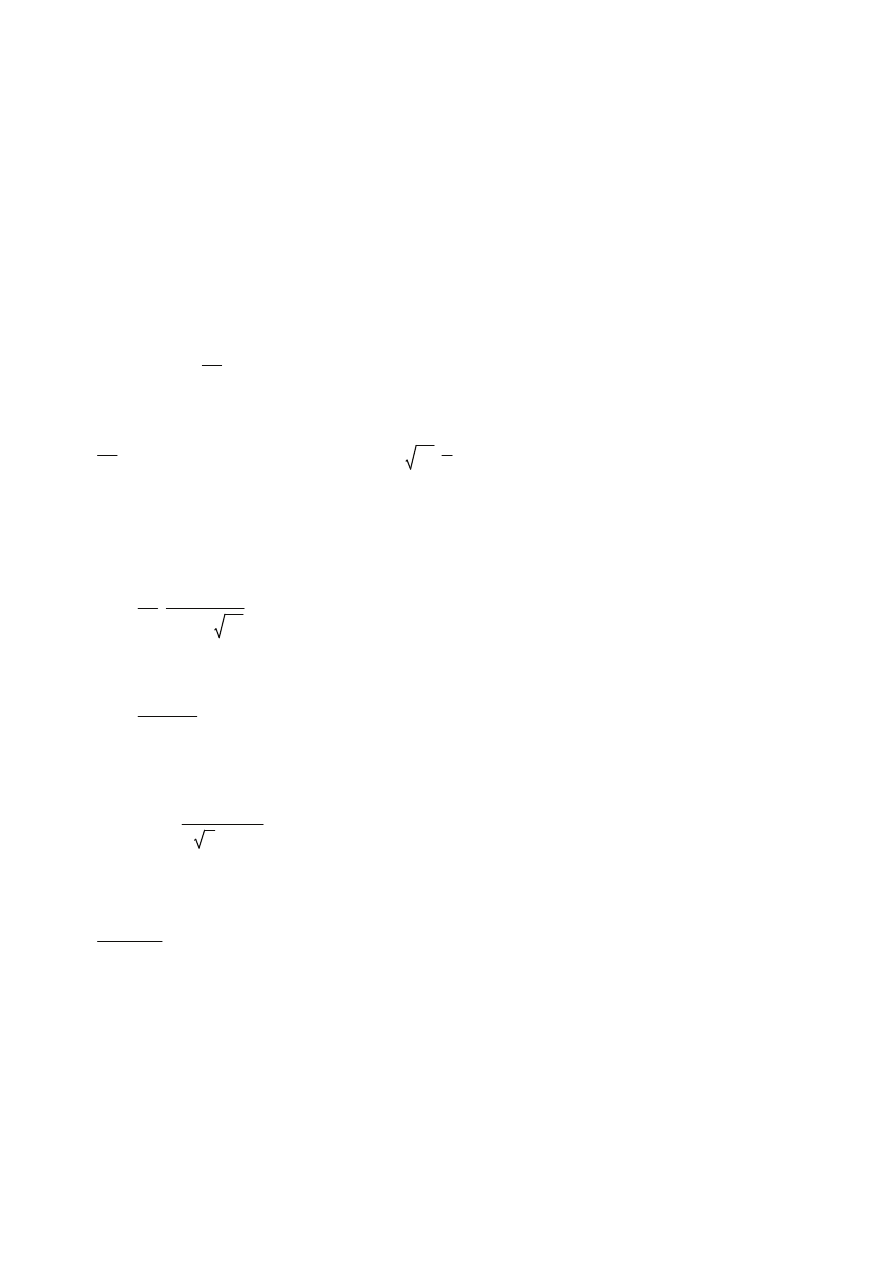
4.2 WARUNEK NOŚNOŚCI DŹWIGARA PRZY ŚCINANIU

Zastosowano żebra podporowe i pośrednie. Przy podporze przyjęto rozstaw obliczeniowy 900 mm, na długości

przęsła 1800 mm.

Panel środnika przy podporze:

a 900 mm

⋅

:=

hw 700 mm

⋅

=

Siła tnąca przy podporze

Vz.Ed.1 293 kN

⋅

:=

Parametr niestateczności:

kτ 5.34 4

hw

a













2

⋅

+

7.76

=

:=

Sprawdzenie wrażliwości na miejscową utratę stateczności

hw

tw

116.667

=

>

31 kτ

⋅

ε

η

⋅

66.493

=

Panel środnika jest wrażliwy na utratę stateczności przy ścinaniu.

Smukłość względna

λw

hw

tw

1

37.4 ε

⋅

kτ

⋅

⋅

1.212

=

:=

Współczynnik redukcyjny niestateczności

χw

1.37

0.7 λw

+

0.717

=

:=

Nośność wyboczeniowa środnika na ścinanie:

Vbw.Rd.1

χw hw

⋅

tw

⋅

fy

⋅

3 γM1

⋅

477.825 kN

⋅

=

:=

Warunek nośności na ścinanie panela:

Vz.Ed.1

Vbw.Rd.1

0.613

=

< 1,0

Warunek jest spełniony.

7z13

Panel środnika za pierwszą belką

a 1800 mm

⋅

:=

hw 700 mm

⋅

=

Siła tnąca za pierwszą belką

Vz.Ed.2 177 kN

⋅

:=

Parametr niestateczności:

kτ 5.34 4

hw

a













2

⋅

+

5.945

=

:=

Sprawdzenie wrażliwości na miejscową utratę stateczności

hw

tw

116.667

=

>

31 kτ

⋅

ε

η

⋅

58.2

=

Panel środnika jest wrażliwy na utratę stateczności przy ścinaniu.

Smukłość względna

λw

hw

tw

1

37.4 ε

⋅

kτ

⋅

⋅

1.385

=

:=

Współczynnik redukcyjny niestateczności

χw

1.37

0.7 λw

+

0.657

=

:=

Nośność wyboczeniowa środnika na ścinanie:

Vbw.Rd.2

χw hw

⋅

tw

⋅

fy

⋅

3 γM1

⋅

438.244 kN

⋅

=

:=

Warunek nośności na ścinanie panela:

Vz.Ed.2

Vbw.Rd.2

0.404

=

< 1,0

Warunek jest spełniony.

4.3 SPRAWDZENIE UGIĘĆ GRANICZNYCH

Ugięcie dźwigara w środku rozpiętości:

Ugięcie dopuszczalne dźwigara

wmax 21.1 mm

⋅

:=

<

L

350

25.7 mm

⋅

=

Warunek jest spełniony.

8z13

4.4. DOBÓR ŻEBER ZE WZGLĘDU NA ŚCINANIE

Żebro podporowe sztywne

Żebro podporowe przyjęto jako zdwojone żebro dwustronne z płaskownika 100x8, w odstępie osiowo 150 mm

bst 100 mm

⋅

:=

tst 8 mm

⋅

:=

e 150 mm

⋅

:=

bst

tst

12.5

=

<

14 ε

⋅

12.936

=

Żebro jest stateczne

Ast 2 bst

⋅

tst

⋅

16 cm

2

⋅

=

:=

>

4 hw

⋅

tw

2

⋅

e

6.72 cm

2

⋅

=

Warunek jest spełniony.

e 150 mm

⋅

=

>

hw

10

70 mm

⋅

=

Warunek jest spełniony.

Żebro przyjęto właściwie.

Żebro pośrednie sztywne

Przyjęto żebra pośrednie 100x8

a 900 mm

⋅

:=

hw 700 mm

⋅

=

Ist

1

12

2 bst

⋅

tw

+

(

)

3

⋅

tst

⋅

2.5 ε

⋅ tw

4

⋅

+

583.087 cm

4

⋅

=

:=

>

1.5

hw

3

tw

3

⋅

a

2

⋅

13.72 cm

4

⋅

=

Warunek jest spełniony.

Żebro przyjęto właściwie.

9z13

4.5 POŁĄCZENIE DŹWIGARA ZE SŁUPEM

Reakcja podporowa dźwigara:

R Vz.Ed.1 293 kN

⋅

=

:=

Połączenie zakładkowe dociskowe (kategorii A). Przyjęto 4 śruby M20 kl. 8.8, co 100 mm.

Siła tnąca na jeden łącznik:

FEd

1
4

R

⋅

73.25 kN

⋅

=

:=

Nośność śruby na ścinanie:

Fv.Rd

0.6 245

⋅

mm

2

⋅

800

⋅

MPa

⋅

1.25

94.08 kN

⋅

=

:=

FEd

Fv.Rd

0.779

=

< 1,0

Warunek jest spełniony.

Nośność otworu na docisk:

αd

100 mm

⋅

3 22

⋅

mm

⋅

1
4

−

1.265

=

:=

αb min 1 αd

,

( )

1

=

:=

k1 min 2.5 2.8

40 mm

⋅

22 mm

⋅

⋅

1.7

−

,













2.5

=

:=

t

tst 8 mm

⋅

=

:=

(grubość żeber podporowych)

d 20 mm

⋅

:=

Fb.Rd

k1 αb

⋅

d

⋅ t⋅ 430

⋅

MPa

⋅

1.25

137.6 kN

⋅

=

:=

FEd

Fb.Rd

0.532

=

< 1,0

Warunek jest spełniony.

10z13

5. OBLICZENIA SŁUPA ŚCISKANEGO MIMOŚRODOWO

Długość słupa swobodnie podpartego:

H 6.6 m

⋅

:=

Słup należy sprawdzić w dwóch przypadkach, gdy:

1. dźwigary obciążają słup osiowo,

2. dźwigary obciążają słup mimośrodowo (na jednym dźwigarze nie ma obciążenia zmiennego, Qk=0)

Przekrój: dwuteownik szerokostopowy HE220A ze stali S275

Wysokość

h 210 mm

⋅

:=

Szerokość

b 220 mm

⋅

:=

Grubości części

tf 11 mm

⋅

:=

tw 7 mm

⋅

:=

Promień zaokrąglenia

r 18 mm

⋅

:=

Szerokość środnika

hw h 2 tf⋅

−

188 mm

⋅

=

:=

Granica plastyczności

fy 275 MPa

⋅

:=

ε

1

:=

Klasa przekroju - ŚCISKANIE

środnik

hw 2 r⋅

−

tw

21.714

=

<

33 ε

⋅

33

=

pas

b tw

−

2 r⋅

−

2 tf⋅

8.045

=

<

9 ε

⋅

9

=

Przy ściskaniu przekrój jest klasy 1. Przy zginaniu czy zginaniu ze ściskaniem będzie on również klasy 1.

Przekrój zachowywać się bedzie plastycznie.

Momenty bezwładności

Iy 5409.701 cm

4

⋅

=

Iz 1954.561 cm

4

⋅

=

Iw 193266.08 cm

6

⋅

=

IT 21.671 cm

4

⋅

=

Wskaźniki plastyczne

Wpl.y 568.457 cm

3

⋅

=

Wpl.z 270.595 cm

3

⋅

=

Pole powierzchni

A 64.341 cm

2

⋅

=

Promienie bezwładności

iy 9.169 cm

⋅

=

iz 5.512 cm

⋅

=

io 10.698 cm

⋅

=

is 10.698 cm

⋅

=

Nośność charakterystyczna przekroju przy ściskaniu:

Nc.Rk A fy

⋅

1769.384 kN

⋅

=

:=

Nośność charakterystyczna przekroju przy zginaniu

Mc.y.Rk Wpl.y fy

⋅

156.326 kNm

⋅

=

:=

11z13

Siła krytyczna wyboczenia giętnego względem osi słabej

Ncr.z

π

2

E

⋅ Iz

⋅

H

2

929.994 kN

⋅

=

:=

Współczynnik wyboczenia:

λz

Nc.Rk

Ncr.z

1.379

=

:=

Φ

0.5 1 0.49 λz 0.2

−

(

)

⋅

+

λz

2

+









⋅

1.74

=

:=

χz

1

Φ

Φ

2

λz

2

−

+

0.357

=

:=

Moment krytyczny zwichrzenia (moment liniowo zmienny, ψ=0)

C1 1.879

:=

kz 1

:=

kw 1

:=

Mcr C1 Ncr.z

⋅

kz

kw









2

Iw

Iz

⋅

G IT

⋅

Ncr.z

+

⋅

296.121 kNm

⋅

=

:=

Współczynnik zwichrzenia:

λLT

Mc.y.Rk

Mcr

0.727

=

:=

Φ

0.5 1 0.34 λLT 0.4

−

(

)

⋅

+

0.75 λLT

2

⋅

+









⋅

0.753

=

:=

χLT

1

Φ

Φ

2

0.75 λLT

2

⋅

−

+

0.856

=

:=

5.1 PRZYPADEK 1: OBCIĄŻENIE OSIOWE

Reakcje z dźwigarów

R1 293 kN

⋅

:=

R2 293 kN

⋅

:=

NEd R1 R2

+

586 kN

⋅

=

:=

Warunek stateczności pręta ściskanego osiowo

NEd

χz

Nc.Rk

γM1

⋅

0.928

=

< 1,0

Warunek jest spełniony.

12z13

5.2 PRZYPADEK 2: OBCIĄŻENIE MIMOŚRODOWE

Reakcje z dźwigarów

R1 293 kN

⋅

:=

R2 120 kN

⋅

:=

(R.2 - ustalono jako reakcję dźwigara przy Qk=0)

Mimośród przyłożenia obciążenia z dźwigara na słup (odległość od osi słupa do płaszczyzny ścinania śrub)

e

h
2

105 mm

⋅

=

:=

NEd R1 R2

+

413 kN

⋅

=

:=

My.Ed R1 e⋅ R2 e⋅

−

18.165 kNm

⋅

=

:=

współczynnik interakcji (moment liniowo zmienny ψ=0)

CmLT 0.6

:=

kzy max 1

0.05 λz

⋅

CmLT 0.25

−

NEd

χz

Nc.Rk

γM1

⋅

⋅

−

1

0.05

CmLT 0.25

−

NEd

χz

Nc.Rk

γM1

⋅

⋅

−

,





















0.907

=

:=

Warunek stateczności pręta zginanego i ściskanego

NEd

χz

Nc.Rk

γM1

⋅

kzy

My.Ed

χLT

Mc.y.Rk

γM1

⋅

⋅

+

0.777

=

< 1,0

Warunek jest spełniony.

13z13