INSTYTUT KONSTRUKCJI MASZYN

PRACOWNIA

NAPĘDÓW HYDRAULICZNYCH

LABORATORIUM

NAPĘDÓW I STEROWANIA

HYDRAULICZNEGO I PNEUMATYCZNEGO

Temat: Badanie charakterystyk sprzęgła

hydrokinetycznego

Grupa: ........................ Zespół: .........................

Lp

Nazwisko i Imię

Ocena

Data

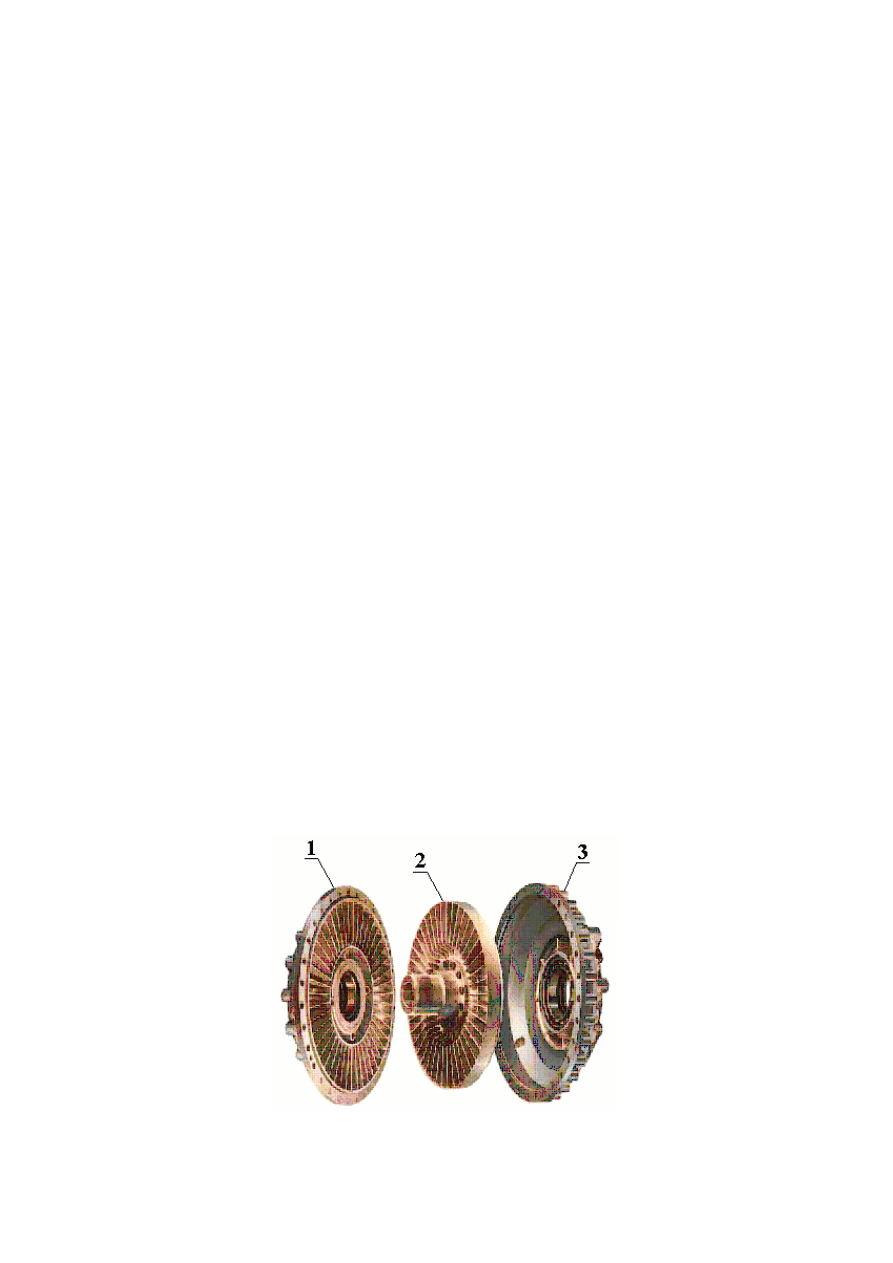
Wstęp

Przekładnie i sprzęgła hydrokinetyczne są wynalazkiem z początku XX w. Wówczas

transportem masowym był transport morski. Wtedy zastępowano wolnoobrotowe silniki parowe
szybkoobrotowymi turbinami parowymi. Ponieważ przy dużych obrotach śruby okrętowej
sprawność spadała tak, że przy 1,5 razy większej mocy nie uzyskiwano efektów lepszych niż
przy silnikach tłokowych, powstała konieczność zbudowania pomiędzy turbiną i śrubą okrętową
odpowiednich przekładni. Prace nad tym podjął w stoczni Vulkan w Szczecinie początkujący
inżynier Herman Fottinger. Zwrócił uwagę na możliwość wykorzystania pompy i turbiny
do zbudowania odpowiedniej przekładni. Mimo nieprzychylnych opinii ówczesnych wybitnych
specjalistów z dziedziny hydromechaniki utrzymujących, że wobec sprawności pomp wodnych
i turbin dochodzącej do 85%, maksymalna sprawność przekładni nie przekroczy 65% - prowadził
prace dalej, a w 1905 r. opatentował przekładnie i sprzęgła hydrokinetyczne. W 1909 r.
zastosowano przekładnię hydrokinetyczną o mocy 500 KM po próbach stanowiskowych na
statku, który wypłynął w próbny rejs. W 1932 r. wbudowano przekładnię hydrokinetyczną do
napędu wagonu motorowego na trasie Berlin-Hamburg, napędzanego silnikiem 600 KM. W 1930
r. zakłady Daimlera po raz pierwszy zastosowały sprzęgło hydrokinetyczne w samochodzie
osobowym.

Budowa i zasada pracy sprzęgła hydrokinetycznego

Sprzęgła są elementami napędu maszyn i mechanizmów przenoszącymi ruch obrotowy
z wału wejściowego - od strony silnika napędowego, na wał wyjściowy – od strony odbiornika.

Sprzęgło hydrokinetyczne składa się zasadniczo z trzech podstawowych elementów:

wirnika pompy, wirnika turbiny i obudowy. Wirniki wykonane są w postaci czasz wyposażonych
w szereg promieniowych łopatek. Wirnik pompy połączony jest z wałem wejściowym, a wirnik
turbiny z wałem wyjściowym. Obudowa, wewnątrz której znajdują się oba wirniki, wypełniona
jest cieczą roboczą.

Zasada pracy sprzęgła jest następująca: obracający się, napędzany zewnętrznym źródłem

energii wirnik pompy wprawia cząstki cieczy znajdujące się w kanałach międzyłopatkowych
w ruch wirowy dookoła osi obrotu wirnika. Pod wpływem powstających przy ruchu obrotowym
sił odśrodkowych działających na cząstki cieczy powstaje przepływ cieczy w kierunku od środka
do zewnątrz.

Rys.1. Sprzęgło hydrokinetyczne

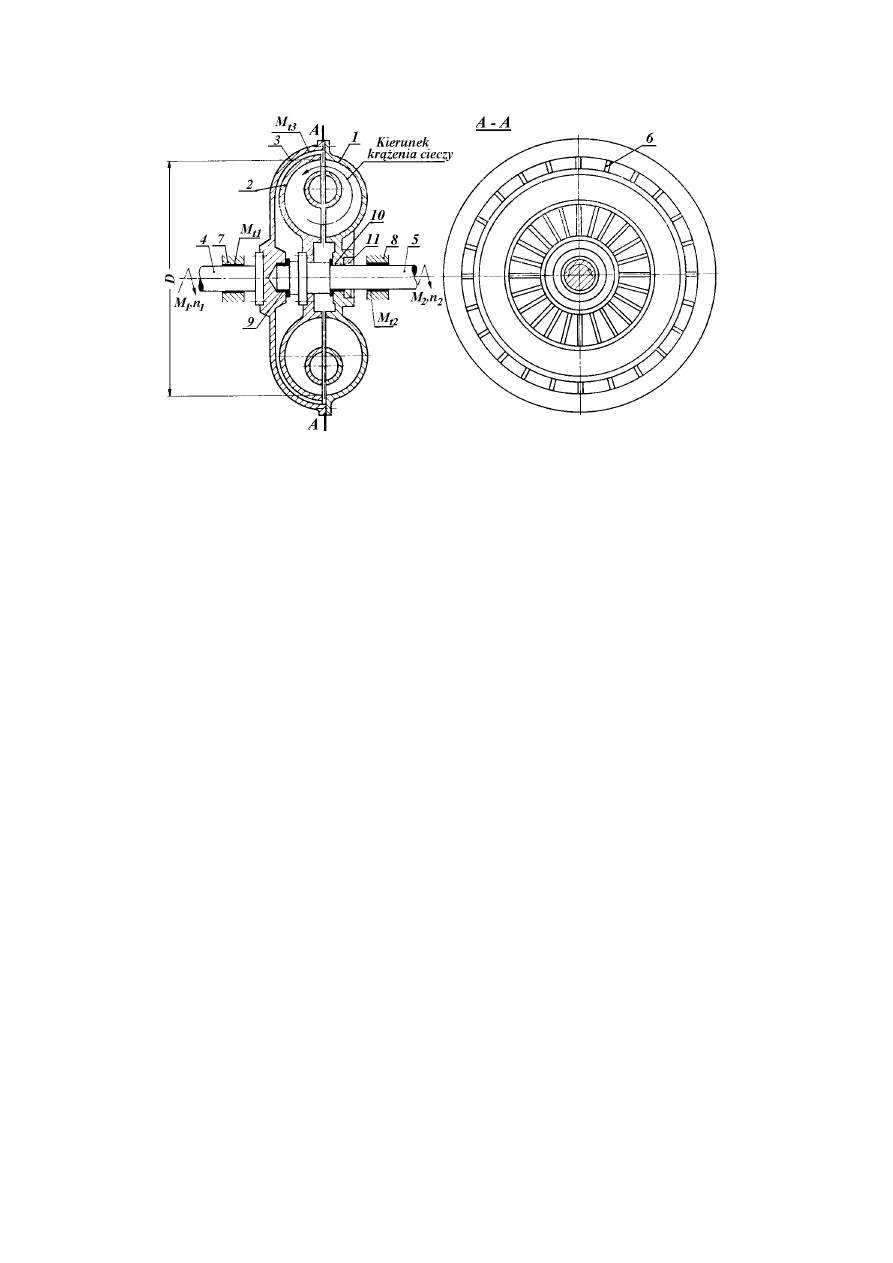
Rys.2. Sprzęgło hydrokinetyczna: 1 – wirnik pompy, 2 – wirnik turbiny, 3 – obudowa, 4 – wał

wejściowy, 5 – wał wyjściowy, 7 – łożysko wału wejściowego, 8 - łożysko wału wyjściowego, 9 -

łożysko wewnętrzne przekładni, 10 – łożysko obudowy przekładni, 11 – uszczelnienie, D – średnica

czynna

Przy

przepływie cieczy przez kanały międzyłopatkowe obracającego się wirnika pompy

w kierunku coraz większej średnicy, następuje przyspieszenie cząstek cieczy w kierunku
obwodowym i zwiększenie ich prędkości obwodowej. Jest to równoznaczne ze zwiększaniem
energii kinetycznej strumienia cieczy. Wychodzący z wirnika pompy strumień cieczy wpada
do wirnika turbiny. Tu przepływając wzdłuż kanałów międzyłopatkowych w kierunku coraz
mniejszej średnicy, cząstki cieczy muszą zmniejszyć swą prędkość obwodową. Wiąże się to ze
zmniejszaniem energii kinetycznej cieczy i powstawaniem reakcji strumienia na łopatki wirnika
turbiny (siły Coriolisa). Siły reakcji strumienia powodują obracanie się wirnika turbiny w
kierunku zgodnym z kierunkiem obrotów wirnika pompy. Wychodzący z wirnika turbiny
strumień cieczy wpada ponownie do wirnika pompy i w ten sposób obieg cieczy między
wirnikami odbywa się w sposób ciągły.

Ruch cieczy między wirnikami pompy i turbiny sprzęgła może zachodzić tylko wtedy,

gdy ciśnienie na wylocie z wirnika pompy jest większe od ciśnienia na wlocie, do wirnika
turbiny. Ponieważ ciśnienia te wywołane są siłami odśrodkowymi, proporcjonalnymi do
kwadratu prędkości obrotowych, zatem aby uzyskać krążenie cieczy między wirnikami prędkość
obrotowa wirnika pompy musi być większa od prędkości obrotowej wirnika turbiny. Im większa
będzie, różnica prędkości obrotowych obu wirników, tym większa będzie również i różnica
ciśnień na wylocie z wirnika pompy i na wlocie, do wirnika turbiny, a zatem i większa prędkość
krążenia cieczy. Od szybkości krążenia cieczy między wirnikami zależy z kolei wielkość reakcji
wywieranych przez strumień na łopatki wirników. Im szybkość ta jest większa, tym większe są
i reakcje, a zatem i momenty przenoszone przez sprzęgło.

Rozpatrując równanie momentów zewnętrznych działających na sprzęgło hydrokinety-

czne w ruchu ustalonym i pomijając niewielkie momenty oporów tarcia obudowy o otaczające
powietrze oraz momenty tarcia w łożyskach zewnętrznych wałów 4 i 5 można napisać

2

1

M

M

=

0

2

1

=

+

=

∑

M

M

M

Z

A zatem, dla sprzęgła hydrokinetycznego momenty na wale wejściowym i na wale

wyjściowym są równe. Dlatego też przełożenie dynamiczne sprzęgła wynosi

1

1

2

=

=

M

M

i

d

Natomiast przełożenie kinematyczne i

k

nie jest równe jedności i w dodatku jest zmienne w

zależności od warunków ruchu sprzęgła. Zgodnie z powyższym równaniem, przyjmując i

d

= 1

otrzymuje się

k

k

d

i

i

i

=

⋅

=

η

Jak wynika z powyższych rozważań wielkość momentu przenoszonego przez sprzęgło

zależy zarówno od prędkości obrotowej wirnika pompy, jak i od stosunku prędkości obrotowych
obu wirników, czyli od przełożenia kinematycznego i

k

przy jakim sprzęgło pracuje. Innymi

słowy dane sprzęgło hydrokinetyczne będzie pracować z różnym przełożeniem kinematycznym i

k

w zależności od prędkości obrotowej wirnika pompy i od wielkości momentu jakim jest

obciążone. Sprzęgło hydrokinetyczne nie może pracować przy przełożeniu kinematycznym i

k

=

1, gdyż wówczas prędkości obrotowe obu wirników byłyby równe i obieg cieczy między
wirnikami ustałby. Zatem aby była możliwa praca sprzęgła hydrokinetycznego musi występować
poślizg.

Charakterystyczna dla sprzęgieł hydrokinetycznych praca ze zmiennym (w zależności od

przenoszonego momentu i prędkości obrotowej wirnika pompy) przełożeniem kinematycznym
powoduje, że dla określenia własności danego sprzęgła konieczne jest podanie funkcji M

1

= f(i

k

),

przy czym funkcja ta jest inna dla różnych prędkości obrotowych wirnika pompy. Funkcje te
podaje się w formie wykresów, nazywanych charakterystykami sprzęgieł hydrokinetycznych.

Należą do nich:
ƒ

charakterystyka bezwymiarowa,

ƒ

charakterystyki wymiarowe, wśród których można z kolei wymienić:

− charakterystykę wymiarową dla stałej liczby obrotów wału wejściowego,
− charakterystykę uniwersalną,
− charakterystykę pełną.

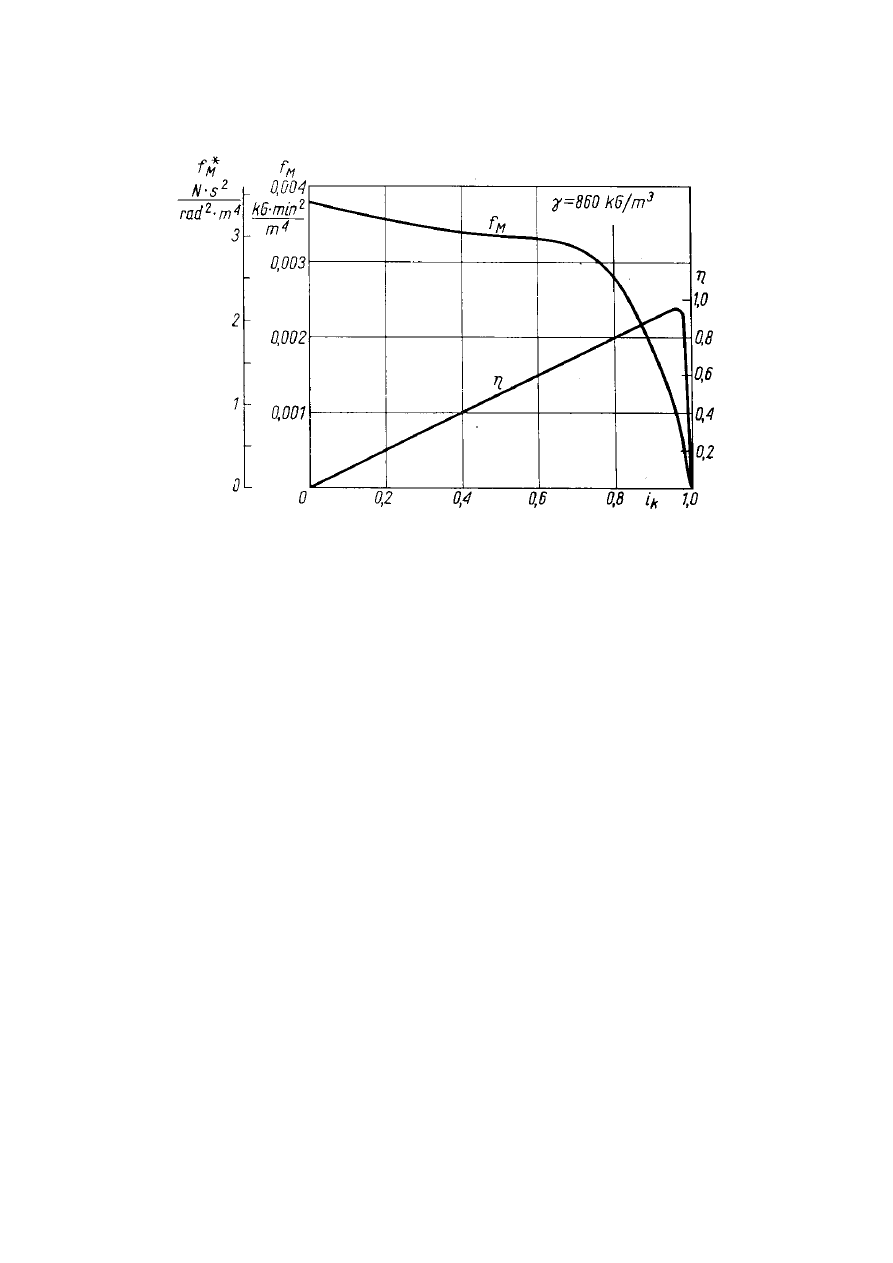
Charakterystyka bezwymiarowa

Rys.3. Charakterystyka bezwymiarowa sprzęgła hydrokinetycznego

Charakterystyka bezwymiarowa sprzęgła hydrokinetycznego przedstawia wykreślną

zależność współczynnika momentu

M

f

lub

λ i sprawności

η

w funkcji przełożenia

kinematycznego

k

i (rys.3). Charakterystyka taka odnosi się do całej rodziny sprzęgieł

podobnych, o różnych średnicach czynnych D, o ile zostaną zachowane warunki podobieństwa
sprzęgieł.
Dysponując charakterystyką bezwymiarową sprzęgła można po założeniu jego średnicy
czynnej D określić parametry pracy sprzęgła w danych warunkach obciążeniowych, korzystając
z wyprowadzonej w teorii podobieństwa zależności na moment przenoszony przez sprzęgło:

5

2

D

n

f

M

M

⋅

⋅

=

gdzie:

n – prędkość obrotowa wirnika pompy [obr/min],

D – średnica nominalna sprzęgła [m].

Można również dobrać wielkość średnicy czynnej sprzęgła odpowiedniego dla danych warunków
pracy.
Charakterystyka

sprzęgła i wartości współczynników

M

f

zależą przede wszystkim od

kształtu wirników, stosunków wymiarowych, liczby łopatek itp. Na charakterystykę ma równie
wpływ rodzaj cieczy roboczej. Ścisłe ustalenie charakterystyki sprzęgła możliwe jest tylko
doświadczalnie (przez przeprowadzenie badań wykonanego już sprzęgła lub jego modelu).
Istniejące metody obliczeń teoretycznych pozwalają na określenie charakterystyki sprzęgła
jedynie z pewnym przybliżeniem.
Charakterystyka

bezwymiarowa

sprzęgła jest bardzo wygodna w użyciu i umożliwia

porównywanie własności sprzęgieł niezależnie od ich wymiarów. Z charakterystyki
bezwymiarowej sprzęgła można określić tzw. wskaźnik sztywności sprzęgła oznaczany
symbolem Φ i będący stosunkiem współczynników momentu

M

f

przy

k

i = 0 oraz

k

i = 0,98

1

0

=

=

=

Φ

k

i

k

i

M

M

f

f

Łatwo udowodnić, że wskaźnik sztywności sprzęgła określa stosunek momentów obrotowych
przenoszonych przez sprzęgło przy danej prędkości obrotowej wału wejściowego: przy
zatrzymanym wale wyjściowym i przy przełożeniu kinematycznym

k

i = 0,98, które odpowiada

zazwyczaj normalnej pracy sprzęgła. Momenty przenoszone przez sprzęgło przy

k

i = 0 oraz

k

i = 0,98 można wyrazić w sposób następujący:

5

2

1

0

D

n

f

M

k

i

k

M

o

i

=

=

=

5

2

1

98

,

98

,

0

D

n

f

M

k

i

k

M

o

i

=

=

=

Stąd

Φ

=

=

=

98

,

0

0

k

k

i

i

M

M

Wielkość wskaźnika sztywności dla sprzęgieł hydrokinetycznych jest zależna od konstrukcji
sprzęgła i zawiera się zazwyczaj w granicach Φ = 4 – 16. Wielkość ta wpływa w sposób istotny
na warunki pracy sprzęgła z silnikiem, zwłaszcza przy rozruchu oraz przy napędzie maszyn o
dużym zakresie obciążeń.

Charakterystyka wymiarowa

Charakterystyka wymiarowa przy stałych obrotach wału wejściowego odnosi się do

sprzęgła o określonej średnicy czynnej D i przedstawia wykres momentu przenoszonego przez
sprzęgło w funkcji prędkości obrotowej wału wyjściowego dla stałej prędkości obrotowej wału
wejściowego. Charakterystyki takie podaje się dla sprzęgieł pracujących w urządzeniach
stacyjnych, gdzie sprzęgła często pracują przy stałej prędkości obrotowej wału wejściowego.

Charakterystykę wymiarową sprzęgła dla n

1

= const łatwo sporządzić, jeżeli dana jest

charakterystyka bezwymiarowa sprzęgła i jego średnica czynna D, Wówczas korzystając
z zależności

M

M

o

i

f

a

D

n

f

M

k

i

k

⋅

=

=

=

=

5

2

1

0

gdzie

5

2

1

D

n

a

=

oraz

k

i

⋅

=

1

2

ω

ω

rad/s

można podstawiając odpowiednie wartości

M

f

dla określonych

k

i

obliczyć odpowiadające

sobie wartości

M

i

2

ω

i sporządzić wykres.

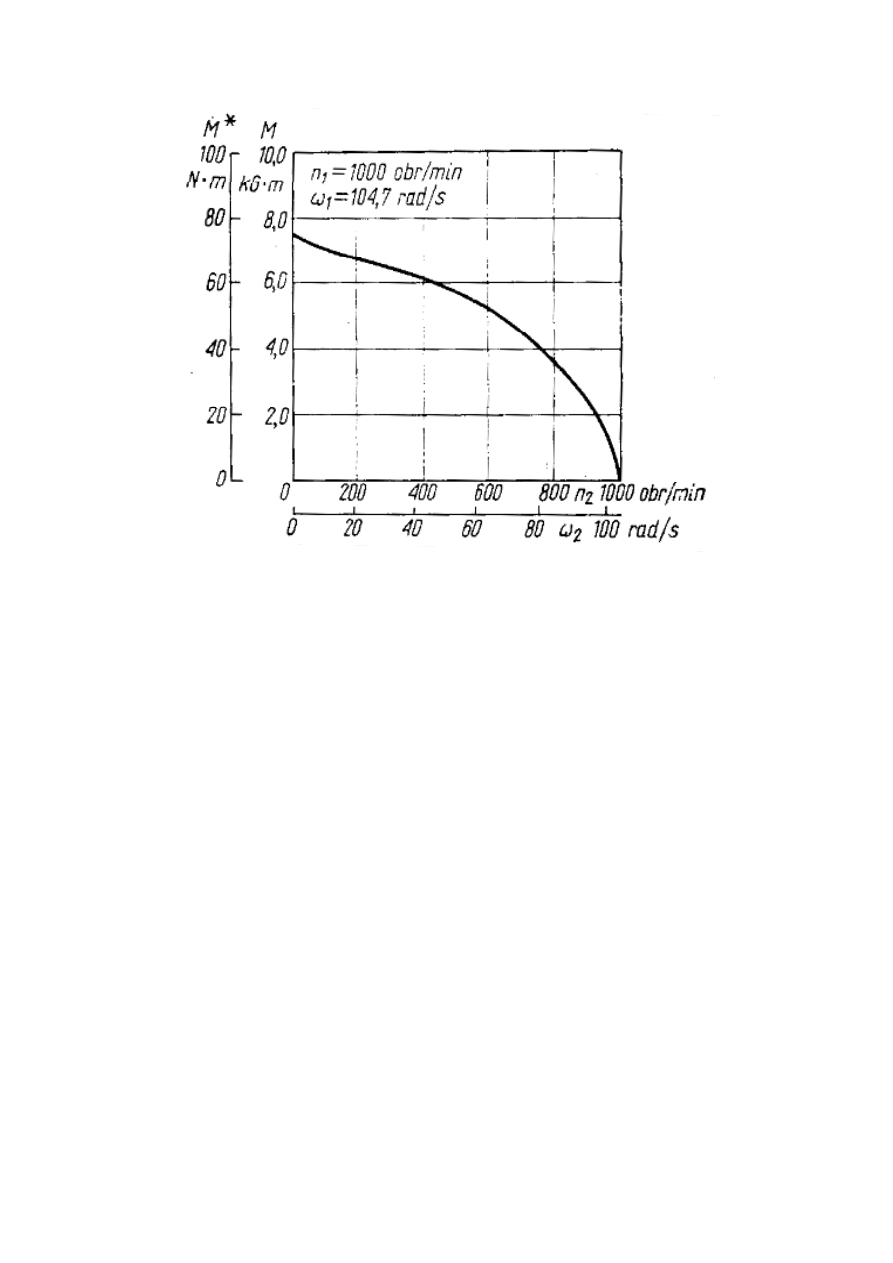
Rys.4. Charakterystyka wymiarowa sprzęgła hydrokinetycznego

przy stałych obrotach wału wejściowego (n

1

= const)

Charakterystyka uniwersalna sprzęgła hydrokinetycznego

Charakterystyka uniwersalna sprzęgła hydrokinetycznego odnosi się do sprzęgła

o określonej średnicy czynnej D i przedstawia wykres krzywych, momentów przenoszonych
przez sprzęgło przy stałych wartościach przełożenia kinematycznego, tj. wykres krzywych

)

(

1

ω

f

M

=

dla

const

i

k

=

Ten sposób przedstawiania własności sprzęgieł używany jest często przez wytwórnie

produkujące sprzęgła i można go spotkać w katalogach i prospektach fabrycznych. Wykres
krzywych

)

1

(

ω

f

M

=

dla

const

i

k

=

podawany jest zazwyczaj na podstawie badań

określonego sprzęgła, można go jednak również sporządzić obliczeniowo korzystając z
bezwymiarowej charakterystyki sprzęgła. Wychodząc z zależności

5

2

1

D

f

M

M

⋅

⋅

=

ω

dla sprzęgła o określonej średnicy czynnej D przy i

k

= const otrzymuje się

2

1

ω

⋅

= b

M

gdzie

5

D

f

b

M

⋅

=

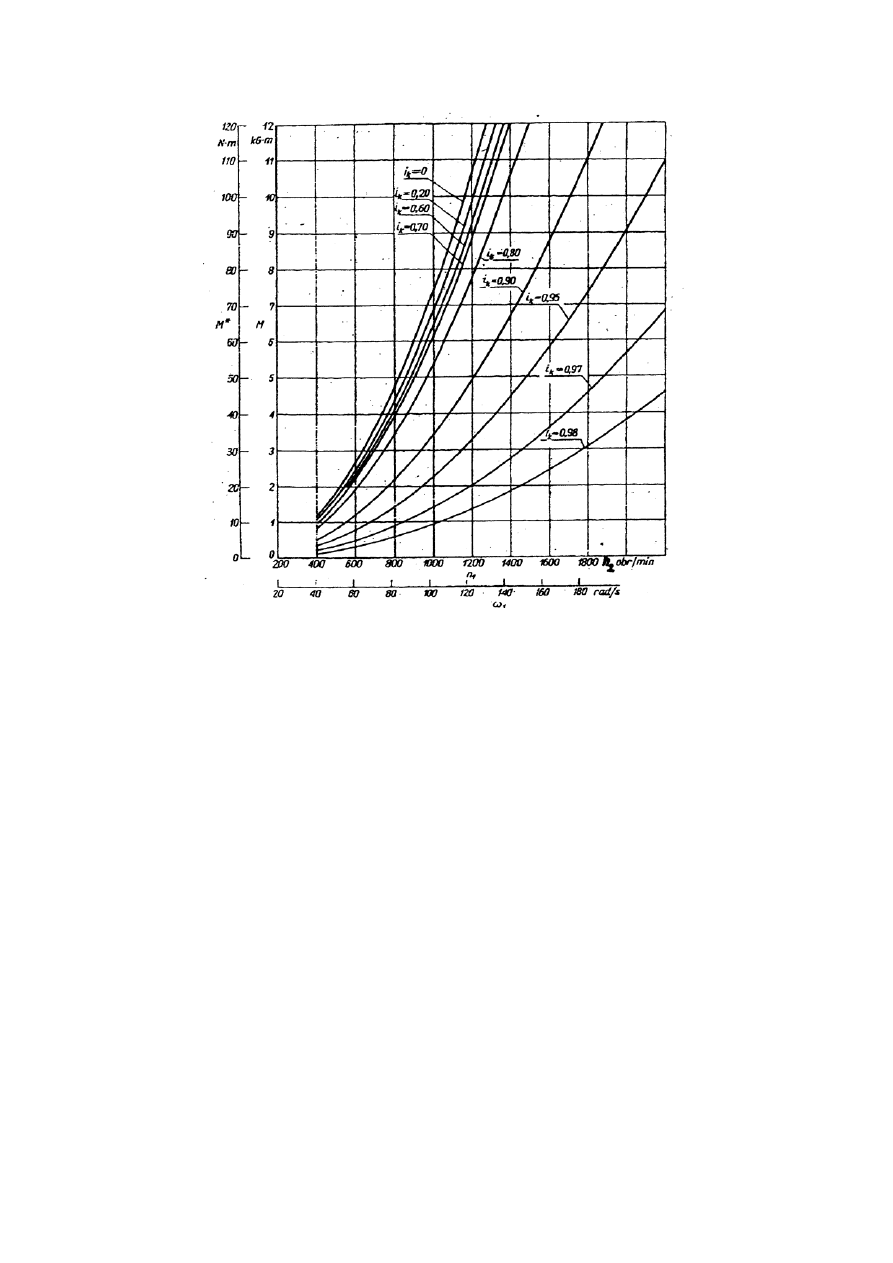
Rys.5. Charakterystyka uniwersalna sprzęgła hydrokinetycznego

Pełna charakterystyka sprzęgła hydrokinetycznego

Pełną charakterystykę sprzęgła hydrokinetycznego przedstawia wykres krzywych

)

(

2

n

f

M

=

dla

const

n

=

1

i

)

(

2

n

f

M

=

dla

const

i

k

=

. Wykres taki umożliwia

zorientowanie się w parametrach pracy sprzęgła przy różnych warunkach obciążeniowych.
Wykres pełnej charakterystyki może być sporządzony na podstawie charakterystyki
bezwymiarowej sprzęgła. Po ustaleniu średnicy czynnej sprzęgła oblicza się wartości momentów
przenoszonych przez sprzęgło przy różnych prędkościach obrotowych wirnika pompy i różnych
przełożeniach kinematycznych

k

i . Za każdym razem przy tym oblicza się odpowiednie prędkości

obrotowe wirnika turbiny n

2

ze wzoru

k

i

n

n

⋅

=

1

2

Krzywe

)

(

2

n

f

M

=

dla

const

n

=

1

mają przebieg podobny do przebiegu współczynnika

momentu

M

f

w funkcji

k

i . Krzywe

)

(

2

n

f

M

=

przy

const

i

k

=

są równocześnie krzywymi

stałej sprawności sprzęgła, gdyż

k

i

=

η

.

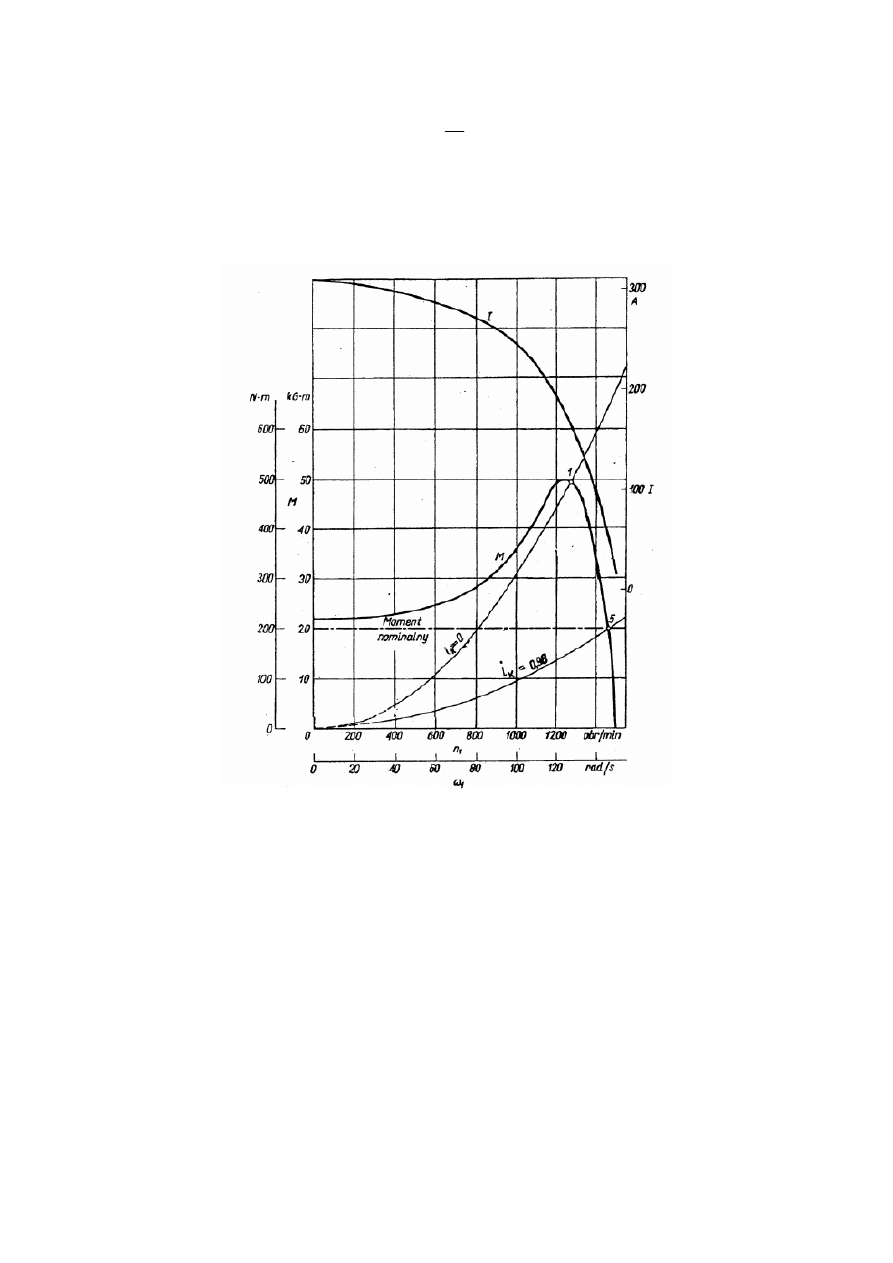
Rys.6. Pełna charakterystyka sprzęgła hydrokinetycznego

Wykres

pełnej charakterystyki sprzęgła umożliwia zorientowanie się, z jaką sprawnością

i przełożeniem kinematycznym będzie pracować dane sprzęgło w określonych warunkach ruchu.
Na przykład jeśli sprzęgło, którego charakterystykę podano na rysunku 6 ma przenosić moment
obrotowy M = 10 kGm przy prędkości obrotowej wału napędzanego n

2

= 2000 obr/min, wówczas

jak wynika z wykresu przełożenie kinematyczne sprzęgła wyniesie i

k

= 0,95 i taką samą wartość

osiągnie sprawność sprzęgła. Dysponując wykresami pełnych charakterystyk dla różnych
sprzęgieł można zawsze dobrać najkorzystniejszy typ sprzęgła dla danych warunków pracy.

Jak wynika z powyższych rozważań, wszystkie rodzaje charakterystyk sprzęgieł

hydrokinetycznych można z łatwością sporządzić, jeżeli znana jest charakterystyka
bezwymiarowa danej rodziny sprzęgieł. Dlatego też przy analizowaniu własności jakiegoś
sprzęgła zazwyczaj dąży się najpierw do ustalenia jego charakterystyki bezwymiarowej.
Charakterystykę bezwymiarową można otrzymać za pomocą badań danego sprzęgła. Jest
to metoda dająca najbardziej dokładne wyniki i przez to najbardziej pewna. Wadą jej jest
konieczność wykonania sprzęgła oraz dysponowania odpowiednimi urządzeniami do badań.
Oprócz tego można sporządzać charakterystykę bezwymiarową na drodze obliczeniowej po
założeniu kształtu i wymiarów wirników sprzęgła. Podstawową wadą metody obliczeniowej jest
to, że otrzymuje się wyniki przybliżone.

Charakterystyka sprzęgła hydrokinetycznego zależy nie tylko od kształtu, wymiarów

i konstrukcji wirników, ale również od ilości cieczy znajdującej się w obudowie sprzęgła. Ilość ta
określana jest tzw. stopniem napełnienia sprzęgła1jJ, przy czym

%

100

⋅

=

Ψ

c

i

V

V

gdzie:

i

V -ilość cieczy znajdująca się faktycznie wewnątrz sprzęgła,

c

V -ilość cieczy, jaka mieści się w całkowicie napełnionym sprzęgle.

Rys. 7. Charakterystyka silnika elektrycznego trójfazowego asynchronicznego z wirnikiem zwartym

z naniesioną charakterystyką uniwersalną sprzęgła hydrokinetycznego: I - natężenie prądu

pobieranego przez silnik, M – moment obrotowy na wale silnika, ik = 0 i ik = 0,98 - momenty

przenoszone przez sprzęgło przy ik = const, n1 – prędkość obrotowa wału silnika i wału wejściowego

sprzęgła.

Wszystkie sprzęgła tzw. zamknięte, to znaczy stanowiące hermetycznie zamknięty zbiornik

z cieczą, muszą być z konieczności sprzęgłami częściowo napełnionymi, w których stopień
napełnienia 1jJ=85~90%. Jest to spowodowane tym, że w czasie pracy sprzęgła ciecz roboczą
silnie nagrzewa się i zwiększa w związku z tym swą objętość, wypełniając poduszkę powietrzną
istniejącą wewnątrz sprzęgła. Przy całkowitym napełnieniu sprzęgła ciecz rozszerzając się
powodowałaby powstawanie bardzo wysokich ciśnień prowadzących do rozsadzania obudowy.
Jedynie sprzęgła pracujące z tzw. obiegiem cieczy, do których ciecz doprowadzana jest ze
zbiornika przez specjalną pompę, mogą być sprzęgłami całkowicie napełnionymi tj., w których
stopień napełnienia 1jJ=100%.

Zakres ćwiczenia:

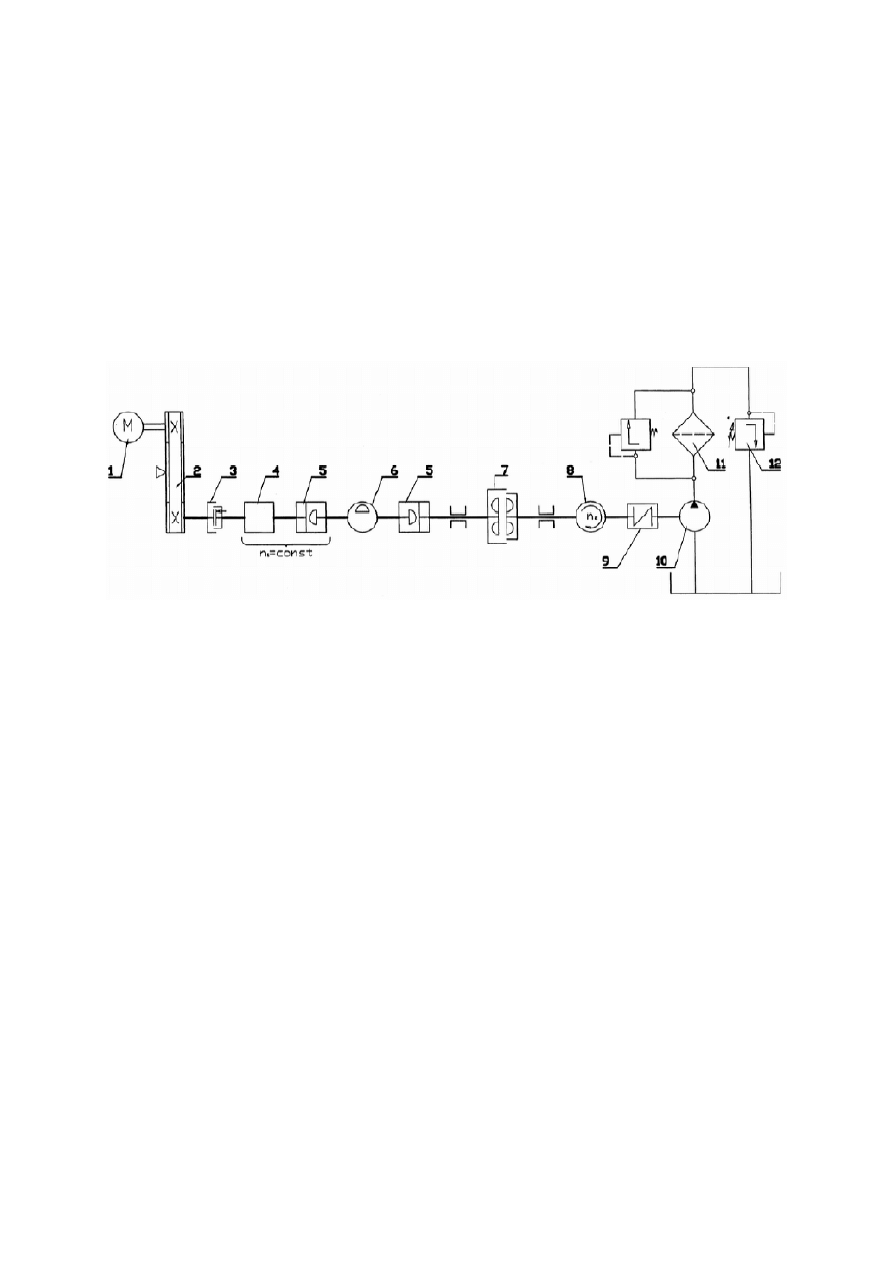
Program ćwiczenia obejmuje badania sprzęgła hydrokinetycznego SHB 22M na stanowisku,
którego schemat przedstawiony jest na rys. 8.

Dane techniczne sprzęgła:
- średnica czynna D = 0,370 [m]
- moc przenoszenia N = 22 [kW]
- nominalna prędkość obrotowa n = 1000 [obr/min]
- stopień napełnienia Ψ = 0,97
- gęstość cieczy ρ = 870 [kg/m3]

Rys.8. Schemat stanowiska do badania sprzęgła hydrokinetycznego: 1 – silnik asynchroniczny SZJe

76b, 2 – przekładnia pasowa, 3 – sprzęgło cierne jednostronne, 4 – skrzynia przekładniowa, 5 – sprzęgło

nierozłączne samonastawne SBG, 6 – przetwornik momentu obrotowego T1, 7 – sprzęgło

hydrokinetyczne SHB 22M, 8 – przetwornik prędkości obrotowej n

2

, 9 – sprzęgło podatne,

10 – pompa PNS-150, 11 – filtr, 12 – zawór DBW-30.

Warunki zaliczenia ćwiczenia:

− obecność na zajęciach laboratoryjnych,
− oddanie sprawozdania z ćwiczenia laboratoryjnego,
− umiejętność objaśnienia zasady działania wskazanego elementu.



Cel ćwiczenia:

1. Poznanie zasady działania sprzęgła hydrokinetycznego,
2. Wyznaczenie charakterystyk badanego sprzęgła.