International Research Journal of Finance and Economics
ISSN 1450-2887 Issue 14 (2008)
© EuroJournals Publishing, Inc. 2008
http://www.eurojournals.com/finance.htm

Incorporating Technical Analysis into

Behavioral Finance: A Field Experiment in the

Large Capitalization Firms of the Athens Stock Exchange

Dimitrios Vasiliou

Hellenic Open University, 4 Heiden Street, 10434, Athens, Greece

Nikolaos Eriotis

National and Kapodistrian University of Athens

5 Stadiou Street, 10562, Athens, Greece

Spyros Papathanasiou

Hellenic Open University, 2 Knossou Street, 17564 Palaio Faliro, Greece

E-mail: [e-mail]

Tel: [phone]; Fax: [phone]

Abstract

In this paper we try to apply Technical Analysis methodology into the Behavior

Theory for the large capitalization firms of the Athens Stock Exchange (ASE). In
Behavioural and in Technical Theory we observe a combination between fundamental
(rational) and psychological – emotional (irrational) factors. We use standards tests in
combination with bootstrap methodology under the AR(1) & GARCH(1,1) models. On the
whole, the results support a strong increase in trading rules performance over time. Hence
we notice the existence of the behavioral phenomenon in the large capitalization firms of
the Athens Stock Exchange.

Keywords: Behavioral Finance, Technical Analysis, Bootstrap.

JEL Classification Codes: G12, G14

1. Introduction

Technical analysis is a method of evaluating securities by analyzing the statistics generated by market
activity, such as past prices and volume. In other words, technical analysis tests historical data
attempting to establish specific rules for buying and selling securities with the objective of maximizing
profits and minimizing risk of loss. Technical analysts do not attempt to measure a security's intrinsic
value, but instead they use charts and indicators to identify patterns that can suggest future activity.
This kind of analysis attempts to understand the emotions in the market by studying the market itself.
Technical analysis includes a variety of forecasting techniques such as chart analysis, pattern
recognition analysis, seasonality and cycle analysis, and computerized technical trading systems.

The field of technical analysis is based on three assumptions: I) The market discounts

everything. Technical analysts believe that the company's fundamentals, along with broader economic
factors and market psychology, are all priced into the stock, removing the need to actually consider
these factors separately. II) Price moves in trends. This means that after a trend has been established,

101

International Research Journal of Finance and Economics - Issue 14 (2008)

the future price movement is more likely to be in the same direction as the trend than to be against it.
III) History tends to repeat itself. The repetitive nature of price movements is attributed to market
psychology. Hence, market participants tend to provide a consistent reaction to similar market over
time.

In efficient market models technical trading profits are not feasible because, by definition, in

efficient markets current prices reflect all available information (Working 1949, 1962, Fama 1970). In
addition, according to Jensen (1978) it is impossible to make net risk-adjusted profits of all transaction
costs by trading on the basis of past price history. So in efficient markets, therefore, any attempts to
make profits by exploiting currently available information are futile. Theoretically, the efficient
markets models rule out the existence of profitable technical trading rules. Contrariwise, models, such
as behavioral or feedback (De Long et al. 1990a, 1991, Shleifer and Summers 1990), noisy rational
expectations (Brown and Jennings 1989, Blume, Easley & O'Hara 1994), agent-based (Schmidt 2002),
disequilibrium (Beja and Goldman 1980), and chaos theory (Clyde & Osler 1997), suggest that
technical trading strategies may be profitable because they presume that price adjusts sluggishly to new
information due to noise, market power, humans irrational behavior, and chaos. In these models, thus,
there exist profitable trading opportunities that are not being exploited. So, the disagreement between
the efficient market and the other theoretical models makes empirical evidence a key consideration in
determining the profitability of technical trading strategies.

In recent years it has become more and more obvious that psychology plays an ever-more

important role in financial markets and also drives back the influence on the rational actions of stock
market participants. Behavioral Finance is a young field, with its formal beginnings in the 1980s. It is a
new approach into financial markets that has emerged, at least in part, in response to the difficulties
faced by the traditional – rational- paradigm. The logic of the homo oeconomicus is more and more
juxtaposed with the logic of the homo psychologicus. Behavioral economics incorporates insights from
other social sciences, such as psychology and sociology (Shiller 2003), into economic models, and
attempts to explain anomalies that defy standard economic analysis. Behavioral economics has to do
with complexities of human behavior. In broad terms, it argues that some financial phenomena can be
better understood using models in which some agents are not fully rational. Behavioral Finance is
showing that in an economy where rational and irrational traders interact, irrationality can have a
substantial and long-lived impact on prices. This field has also had success in explaining how certain
groups of investors behave, and in particular, what kinds of portfolios they choose to hold and how
they trade over time. The behavioral theory shows that if irrational traders cause deviations from
fundamental value, rational traders will often be powerless to do anything about it. In order to say more
about the structure of these deviations, behavioral models often assume a specific form of irrationality.

Overall, in the Behavioural Finance model it is observed rational and irrational expectations

about returns like Technical Analysis. In behavioral and in technical theory we observe a combination
between fundamental and psychological – emotional factors. Besides, in feedback or behavioral
models, traders buy when prices rise and sell when prices fall, like technical analysis. Behavioral
literature shows that sophisticated investors in Finland Stock Market were more likely to follow
momentum-trading strategies (Grinblatt & Keloharju 2000, 2001). In addition, Barber and Odean
(2000, 2001) and Odean (1999) find that individual investors trade excessively and expose themselves
to a high level of risk. Odean (1998a) finds that individual investors are more willing to recognize
paper gains than paper losses. Investors who are overconfident believe they can obtain large returns,
thus they trade often and they underestimate the associated risks (DeLong, Shleifer, Summers, and
Waldmann 1990, Kyle and Wang 1997, Odean 1998 and Wang 1998, 2001). Coval and Shumway
(2002) find that Chicago Board of Trade proprietary traders suffer from a loss-aversion bias. As we can
see we notice common elements in technical and behavioral theory.

In this paper we try to apply technical methodology into the behavior theory. The methodology

of this paper considers the changes in the returns to the Brock et al. (1992) one on FTSE/ASE-20 Index
of the Athens Stock Exchange (ASE) over the 1995–2005 (end) period. Furthermore, we investigate
the performance of various technical trading rules in the large capitalization firms of the Athens Stock

International Research Journal of Finance and Economics - Issue 14 (2008)

102

Exchange. The methodology that is going to be used for the analysis of the data is standard tests. In
addition, standard tests will be compared with the bootstrap methodology under the AR(1) &
GARCH(1,1) models inspired by Efron (1979), and Efron and Tibshirani (1986). By studying
FTSE/ASE-20 of ASE data, our paper examines how investor’s sophistication influences investing
behavior and technical trading performance.

This paper contributes to the existing literature by:
a) Investigating the relationship between Behavioral Finance and Technical Analysis.
b) Examining the previous relationship on the large capitalization firms of the Athens Stock

Exchange.

c) Investigating the performance of various technical trading in the large capitalization firms

of the Athens Stock Exchange

d) Extending previous literature on Behavioral Finance and Technical Analysis as well.
This paper is organized as follows: Section 2 outlines the technical trading rules used to test

market efficiency. Methodological issues are presented in section 3. Section 4 contains data &
empirical results and section 5 concludes the paper.

2. Literature Review

Fama and French (1988) test for the 1926 to 1985 period examined autocorrelations of daily and
weekly stock returns. They found significant statistical serial correlation in price series of small and
large firm portfolios of all New York Stock Exchange stocks, over various time horizons. Their state
”Our results add to mounting evidence that stock returns are predictable”. They estimated that 25-45%
of the variation of 3-5 year stock returns is predictable.

Wing-Keung Wong, Meher Manzur, Boon-Kiat Chew (2003) focuses on the role of technical

analysis in signalling the timing of stock market entry and exit. Test statistics are introduced to test the
performance of the most established trend followers, the moving average, and the most frequently used
counter-trend indicator, the relative strength index. Using Singapore data, the results indicate that the
indicators can be used to generate significantly positive return. It is found that member firms of
Singapore Stock Exchange (SES) tend to enjoy substantial profits by applying technical indicators.

Brock William, Lakonishok Josef, LeBaron Blake (1992), tested two of the simplest and most

popular trading rules-moving average and trading range break-by utilizing the Dow Jones Index from
1897-1986. Standard statistical analysis is extended through the use of bootstrap techniques. Overall,
their results provide strong support for the technical strategies. The returns obtained from these
strategies are not consistent with four popular null models: the random walk, the AR(1), the GARCH-
M, and the EGARCH.

Ki-Yeol Kwon and Richard J. Kish (2002) investigated an empirical analysis on technical

trading rules (the simple price moving average, the momentum, and trading volume) utilizing the
NYSE value-weighted index over the period 1962-1996. The methodologies employed include the
traditional t-test and residual bootstrap methodology utilizing random walk, GARCH-M and GARCH-
M with some instrument variables. The results indicate that the technical trading rules add a value to
capture profit opportunities over a buy-hold strategy.

Rodríguez, Sosvilla and Andrada (1999) in their paper judge whether some simple forms of

technical analysis as Variable Moving Average, Fixed Moving Average and Trading Range Break out
can predict stock price movements in the Madrid Stock Exchange. Their study covered the period from
January 1966 to October 1997. They used the daily data of the General Index of the Madrid Stock
Exchange and the bootstrap methodology. They state, “Our results provide strong support for
profitability of these technical trading rules.”

Balsara Nauzer, Carlson Kathleen and Narendar V. Rao, (1996), studied the behaviour of a

fixed-parameter technical trading rule as applied to four commodity futures contracts. They used the
dual moving average crossover rule to generate buy and sell signals. The evidence suggests that fixed-
parameter rules are inflexible, leading to wide swings in performance both across commodities and

103

International Research Journal of Finance and Economics - Issue 14 (2008)

time periods. They concluded, “These findings have powerful practical implications, in as much as
they recommend that traders be wary about using fixed-parameter mechanical trading systems”.

Neftci (1991) in his study supported that the usefulness of the well-defined rules of technical

analysis are useful in prediction. The first of the two interests of the study were to devise formal
algorithms to represent various forms of technical analysis and see if these rules are well defined. The
second interest was to discuss the conditions that technical analysis can capture properties of stock
prices by linear models of Wiener-Kolmogorov prediction theory. The author concludes, “Tests done
using Dow-Jones industrials for 1911-76 suggested that this may indeed be the case for the moving
average”.

Tian, Wan and Guo (2002) explored the predictability and profitability of technical trading

rules in markets with different efficiency levels; namely, the U.S. and China. In the case of the U.S.
they found rules to have no predictability after 1975, whereas their results give support of the technical
trading rules having both predictability and profitability for the Chinese markets across the 1990’s.

Cai, Cai and Keasey extended the analysis of Tian et al. in two ways. First, they wanted to see

if the conclusions extend to other markets – namely, the U.K., Hong Kong and Japan. Second, in the
case of China, they examined whether the predictability and profitability of technical trading rules
changed across the 1990’s. On the basis of daily data Tian et al’s results for the U.S. market are
supported by the results for a number of the main developed markets where the technical trading rules
had predictive ability during the 1970’s that disappeared by the 1990’s. Furthermore, the results
suggest that while technical trading rules had short-term predictive ability and profitability in the
Chinese stock markets during the 1990’s, this lessened as the decade progressed.

3. Methodological Issues

As we saw in this paper we try to apply technical methodology into the behavior theory. The
methodology of this paper considers the changes in the returns to the Brock et al. (1992) one on the
Athens Stock Exchange (FTSE/ASE-20 Index) over the 1995–2005 (end) period. Particularly, the
investigation of these technical strategies will be achieved by comparing the returns given by the buy
signals of the moving averages with the returns of the buy and hold method. Furthermore, the returns
given by the buy signals of the moving averages minus the returns of the sell signals of the moving
average with the returns of the buy and hold method will be compared. The hypothesis that the returns
of the buy and hold method with the returns of the moving average will be examined using the t-test
methodology. The moving averages give buy signal when the short term moving average crossover the
long-term moving average.

Firstly the methodology that is going to be used for the analysis of the data is t-test, which was

used in previous studies for the investigation of technical rules. (Levich, R. and L. Thomas 1993,
Gençay, R. 1998, Fernando Fernández-Rodríguez, SimóN Sosvilla-Rivero and Julián Andrada-Félix
1999, Fernandez-Rodriguez, F., Sosvilla-Rivero, S. and M. D. Garcia-Artiles 1997, Brown, D. P. and
R. H. Jennings 1989). The t-test is used in order to assess if the means of two data groups are
statistically different from each other in order to compare these means. The t-statistic is calculated by
the formulas:

(1)

(2)

International Research Journal of Finance and Economics - Issue 14 (2008)

104

where

2

is the square root of the variance of the returns, µ is the mean return for the buys, sells, buy-

and-hold-method, N is the number of signals for the buys, sells, observations.

The results of the t-test will help to accept the null hypothesis [there is no actual difference

between mean returns (buys, sells) or reject our null hypothesis (there is an actual difference the mean
returns)]. Therefore, the two hypotheses for the above test are the following:

Accept Null Hypothesis:

0

:

2

1

1

R

R

H

(3)

Reject Null Hypothesis:

0

:

2

1

2

R

R

H

Many times the assumptions of normality, stationary, and independent distributions, which are

required for t -tests do not hold for the examined data. As we will see these assumptions certainly do
not characterize the returns from the FTSE/ASE-20 Index of Athens Stock Exchange series (table 1).
Hence, we focus our concentration on the results from more appropriate bootstrap methodology.
Bootstrap method¬ology inspired by Efron (1979), Freedman (1984), Freedman and Peters (1984a,
1984b), and Efron and Tibshirani (1986). Following Brock et al. (1992), the problem above can be
solved using bootstrap methods (Efron and Tibshiarani, 1993). So we combine the standard t -test and
the bootstrap methodology. In any case, the t-test results are not significantly different from their
bootstrap counterparts.

Bootstrapping is a method, introduced by Efron (1979), for estimating the distributions of

statistics that are otherwise difficult or impossible to determine. This approach was introduced to the
finance literature by Brock et al. (1992) and has become the standard technique for assessing the
statistical significance of technical trading rule profitability (Kwon & Kish, 2002, Bessembinder &
Chan, 1998). The general idea behind the bootstrap is to use resampling to estimate an empirical
distribution for the statistic.

The bootstrap methodology is based on the comparison of conditional buy and sell returns

using the original FTSE/ASE-20 series with the conditional buy or sell returns generated from a
simulated series using two models. In the bootstrap procedure our model is to fit the original series to
obtain estimated parameters and residuals. We standardize the residuals using parameters standard
deviations for the error process. The estimated residuals are then redrawn with replacement to form a
scrambled residuals series, which is then used with the estimated parameters to form a new
representative series for the given model. By construction, the scrambled residual distribution will be
independent and identically distributed. Each of the simulation is based on 500 replications of the
model. This should provide a good approximation of the return distribution under the model. The null
hypothesis is rejected at the 5% percent level if returns obtained from the actual FTSE/ASE-20 Index
data are greater than the 5% percent cutoff of the simulated returns under the null model.

The first null model we fit is a AR(1) process:
r

t

=b+

1

r

t-1

+e

t

(4)

where is r

t

the t

th

day return and e

t

is independent and identically distributed.

The second null model we fit is a GARCH(1,1) process:
r

t

= + r

t-1

+e

t

h

t

=w+ae

2

t-1

+bh

t-1

(5)

e

t

= h

1/2

t

z

t

, z

t

~ N(0, 1)

where e

t

is an independent, identically distributed normal random variable, r

t

is the conditional

variance.

We use MATLAB 7.0 to estimate the parameters for the AR(1) model via OLS (Ordinary Least

Square) and for the GARCH(1,1) model using maximum likehood. Then we resample the standardized
residuals with replacement to create 500 replications of the model. The bootstrap methodology requires
high computer power and computer programming.

To test the significance of the trading rule excess returns the following hypothesis can be

stated:

105

International Research Journal of Finance and Economics - Issue 14 (2008)

0

1

H : XR XR *

H : XR > XR*

*

(6)

Under the null hypothesis, the trading rule excess return (XR) calculated from the original

series is less than or equal to the average trading rule return for the pseudo data samples ( XR * ). The
p-values from the bootstrap procedure are then used to determine whether the trading rule excess
returns are significantly greater than the average trading rule return given that the AR(1) and
GARCH(1,1) models.

4. Data and Empirical Results

4.1. Data

The data used in this paper spans the 1

st

January 1995 to 30

th

December 2005 period. The FTSE/ASE-

20 is the basic index of the Athens Stock Exchange (ASE). The FTSE/ASE-20 Index is constituted
from twenty stocks of the Athens Exchange with the largest capitalization. This index designed from
the Athens Stock Exchange with the co-operation of the London Stock Exchange and FTSE
International Limited. The FTSE/ASE-20 Index of the Athens Stock Exchange reflects, approximately,
53% of the overall capitalization. The database used is composed of 2,747 observations.

In this paper there will be an investigation for the period from 1995 to 2005. This is a very

important period for the Athens Stock Exchange as evidenced by i) three general elections, ii) the
worldwide crash in Hong-Kong in 1997, ii) the entry of Greece to the European Exchange Rates
Mechanism II (1998), iii) the readjustment of its macroeconomic variables in order to achieve the
criteria to become the 12

th

member of the ‘Euro Zone’, iv) the entry of Greece to the ‘Euro Zone’

(2001), v) the introduction of the Athens Derivatives Exchange (ADEX) since 1999, vi) the Athens
Stock Exchange institutional reform of 1995, 2001 & 2005 in an attempt to ease illiquidity problems
and foster an increased volume of transactions, and vii) the characterization of the Greek stock market
as a developed market since 2001.

Table 1 presents the summary statistics for the examined period. For this period, we define the

daily return as the difference in the natural logarithms of the price levels. We examine the distribution
characteristics using the following statistics: mean, standard deviation, skewness, kurtosis, and the
Jarque-Bera test for normality. As can be seen, these returns exhibit excessive kurtosis and skewness.
Besides, Jarque-Bera test rejects normality in the examined period.

Table 1: Descriptive Statistics

num:

2,747

max:

0.08680583

min:

-0.09604792

mean:

0.0005764197

median:

0.0001790130

range:

0.18285375

std:

0.016746064

skewness:

0.072433206

kurtosis:

6.845538657

jarquebera:

0.00169379697

jbpval:

0

Buy-Hold mean return

0.000575498

Technical analysis has been around for decades and through the years, traders have seen the

invention of hundreds of indicators. While some technical indicators are more popular than others, few
have proved to be as objective, reliable and useful as the moving average. This is the most common
method used to calculate the moving average of prices. A moving average is the average price of a

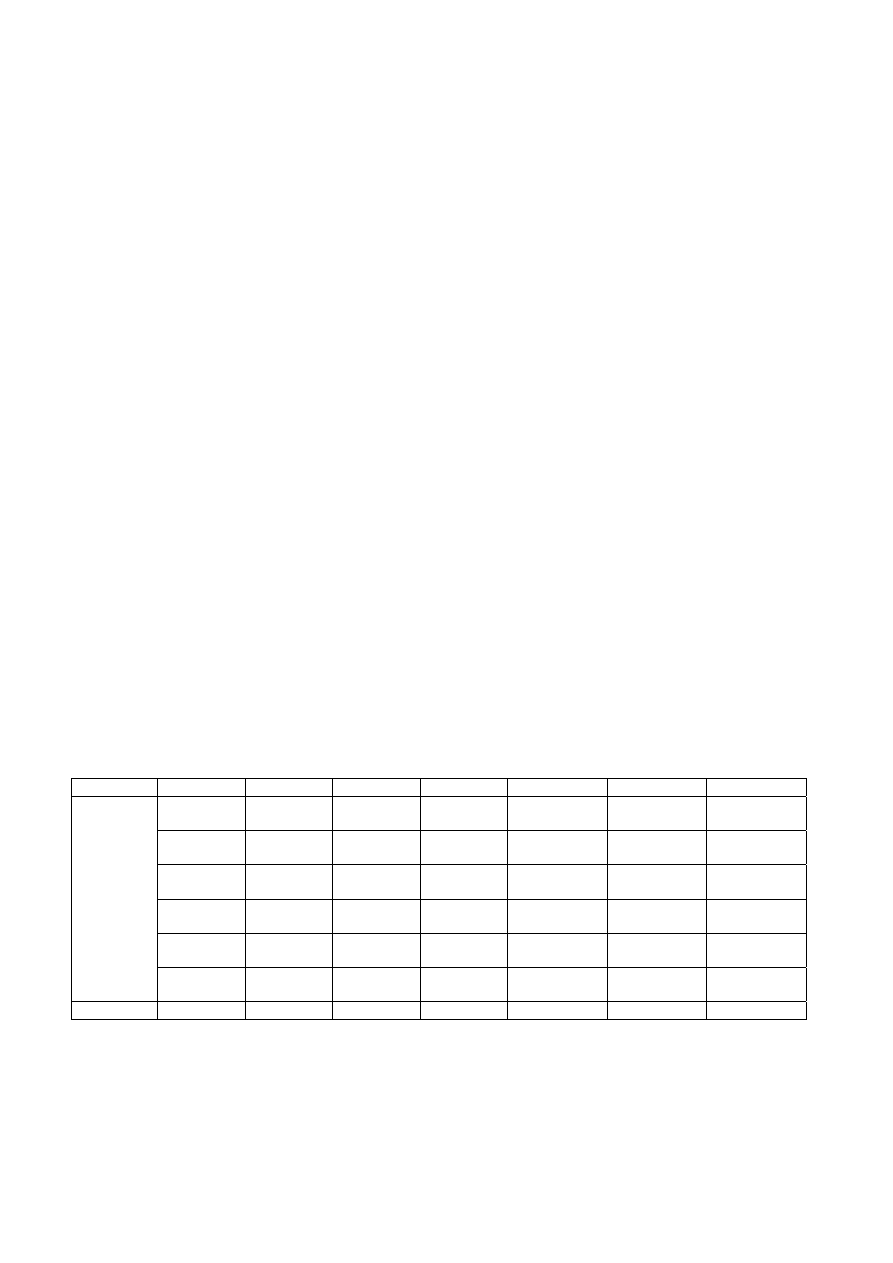
International Research Journal of Finance and Economics - Issue 14 (2008)

106

security over a set amount of time. It simply takes the sum of all of the past closing prices over the time
period and divides the result by the number of prices used in the calculation By plotting a security's
average price, the price movement is smoothed out. Once the day-to-day fluctuations are removed,
technical analysts are able to identify the true trend and increase the probability to work in their favor.
Increasing the number of time periods in the calculation is one of the best ways to gauge the strength of
the long-term trend and the likelihood that it will reverse. Typically, upward momentum is confirmed
when a short-term average crosses above a longer-term average. Downward momentum is confirmed
when a short-term average crosses below a long-term average.

These moving averages are used in this paper, as they are the most common used by the

technical analysts. We evaluate the following popular moving average rules: 1-9, 1-15, 1-30, 1-60, 1-
90 and 1-130 where the first number in each pair indicates the days in the short period and the second
number shows the days in the long period. Thus, the technical trading rules that are going to be
investigated and show the presence of behavioral finance in the largest capitalization firms
(FTSE/ASE-20 Index) of the Greek Stock Market are simple moving averages. We will follow similar
methodology with Brock et al. (1992) adding transaction costs. All transactions assume 0.08% (of the
investing capital) commission as entry (buy) fees and 0.08% as exit (sell) fee.

4.2. Technical Rules Results

As we know if technical analysis does not have any power to forecast price movements, then we
should observe that returns on days when the rules emit by signals do not differ appreciably from
returns on days when the rules emit sell signals.

Turning to the results for the six simple moving average trading rules shown in Table 2, we

note that there is a general trend of the profits being highly statistically significant in the examined
period. The rules differ by the length of the short and the long period. For example (1,130) indicates
that the short period is one day, the long period is 130 days. In columns 3 and 4 (table 2) we report the
number of buy "N(Buy)" and sell "N(Sell)" signals generated during the period. The (daily) mean buy
and sell returns are reported separately in columns 6 and 7. The last column "Buy-Sell" lists the
differences between the mean daily buy and sell returns. The t statistics for the Buy and Sell statistics
are computed using the following Brock et al. (1992) methodology.

Table 2:

Standard results for various types of simple moving averages

Period

Test

N(buy)

N(sell)

Sum

Buy

Sell

Buy-Sell

(1,9)

214

214

428

0.00105

-0.00046

0.00151

(4.44642)

(-2.23933)

(4.51016)

(1,15)

151

151

302

0.00101

-0.00042

0.00143

(4.23837)

(-2.06299)

(4.25171)

(1,30)

95

94

189

0.00091

-0.00032

0.00123

(3.69945)

(-1.67710)

(3.62803)

(1,60)

66

66

132

0.00074

-0.00014

0.00089

(2.89580)

(-0.92442)

(2.55586)

(1,90)

46

45

91

0.00080

-0.00025

0.00105

(3.07382)

(-1.45146)

(3.07567)

(1,130)

28

27

55

0.00071

-0.00020

0.00091

01/01/1995
To
12/30/2005

(2.71568)

(-1.25493)

(2.66785)

Average

0.000868901

-0.000298587

0.00116749

As we can see in Table 2, the mean buy-sell returns are all positive with an average daily return

of 0.117%, or 29% on annual base (250 trading days x 0.117%). In addition the buy-sell differences are
significantly positive (5% probability) for all rules and the t-tests for these differences are highly
significant rejecting the null hypothesis of equality with zero. [For 0.05 probability the upper (lower)
critical values of the t-test values are +(-) 1.960]. The mean buy returns are all positive with an average
daily return of 0.087%, which is about 22% on annual base (250 trading days x 0.087%). The t-

107

International Research Journal of Finance and Economics - Issue 14 (2008)

statistics reject the null hypothesis that the returns equal the unconditional returns (0.0575% from
Table 1). All the tests reject the null hypothesis that the returns equal the unconditional returns at the
5% significance level using a two-tailed test.

Constructively, our methodology combines rational and irrational (emotional) expectations

seem to beat the market performance (FTSE/ASE-20 Index of the Athens Stock Exchange). In
particular, buy-hold strategy (Table 1) give us about 14% per year (0.057% x 250 days) and using
moving averages strategy 29% for buy-sell method (250 trading days x 0. 0.117%) on annual base and
using buys method 22% (250 trading days x 0.0869%) yearly. So we notice abnormal returns over the
FTSE/ASE-20 Index of the Athens Stock Exchange benchmark.

4.3. Bootstrap Results

We further our analysis via the bootstrap methodology under the models of AR(1) and GARCH(1,1).
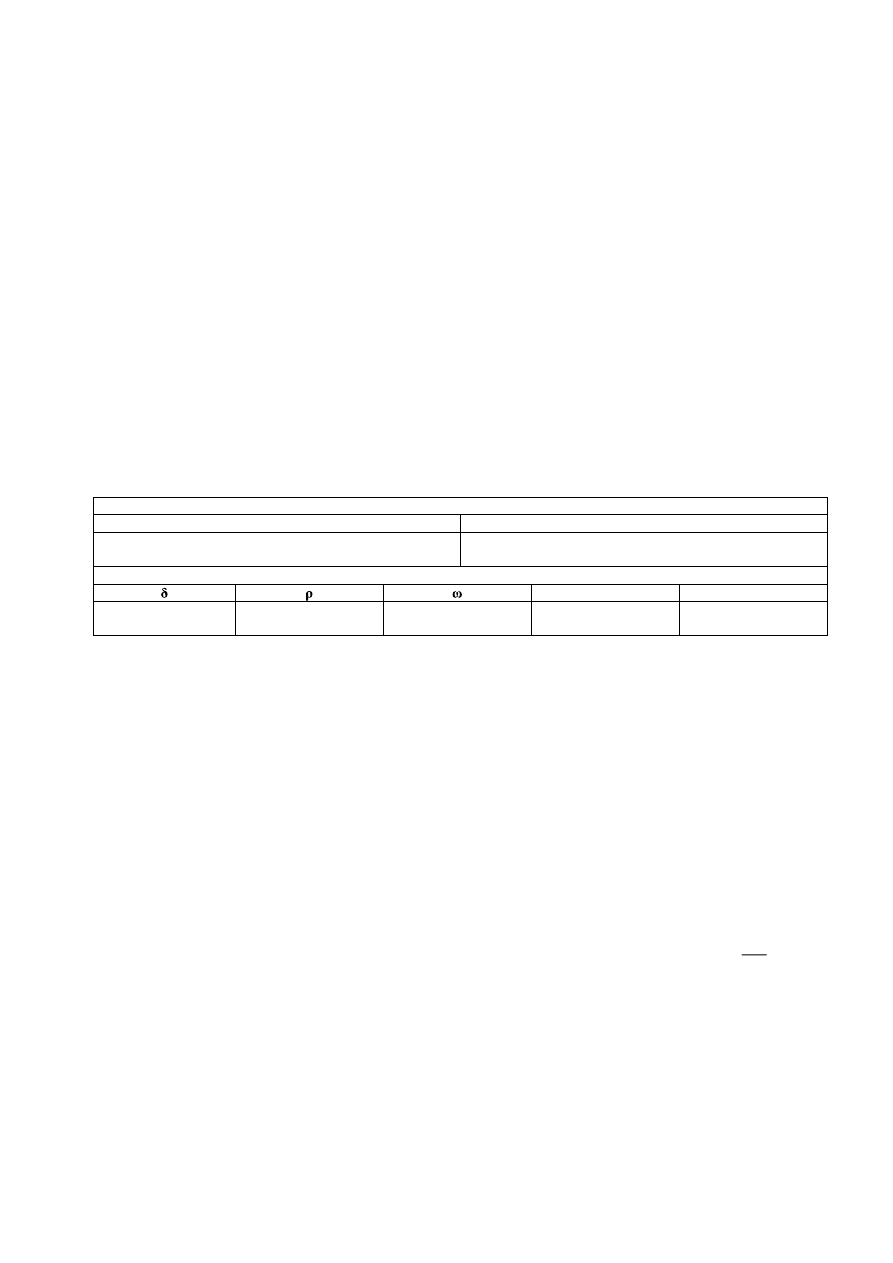
Table 3 presents the model fit parameters for the AR and GARCH models. In particular this table
contains estimation results for the AR(1) and GARCH models which will be used for comparison with
the actual FTSE/ASE-20 Index series of the Athens Stock Exchange.

Table 3: Parameter estimates for model

a)AR(1)

a

b

0.000470

0.177879

(1.483810)

(6.004976)

b)GARCH(1,1)

a

b

0.00045096

0.18429

3.6476e-006

0.12067

0.87253

(1.8995)

(9.4182)

(5.4973)

(14.4823)

(116.3168)

The AR(1) and GARCH(1,1) is estimated using OLS and maximum likehood. The numbers in parenthesis are t-ratios.

In Table 4 we present the results for the 6 rules we examined under the null models of AR(1)s

and GARCH(1,1) using bootstrap methodology. All the numbers presented in columns 4,5,6 are the
fractions of the simulated result which are larger than the results for the original FTSE/ASE-20 Index
of Athens Stock Exchange. The mean buy and sell returns are reported separately in columns 4 and 5.
The results for the returns are presented in the columns 4,5,6 are p-values. The p-values from the
bootstrap procedure are then used to determine whether the trading rule excess returns (simple moving
averages) are significantly greater than the average trading rule return given from original series. The
numbers in parenthesis in columns 4,5,6 show how many series from 500 replications are greater from
original returns. Hence the number in the column labelled “Buy”, which is (413), shows that 413 of the
simulated GARCH(1,1)s or gener¬ated a mean buy return as large as that from the original
FTSE/ASE-20 Index of Athens Stock Exchange. As we see from reported numbers in columns 4,5,6
most of the simulated AR(1)s and GARCH(1,1)s were greater than those from the FTSE/ASE-20 Index
of Athens Stock Exchange series. All the buy, sell and buy-sell are highly significant accepting the null
hypothesis. Under the null hypothesis, the trading rule excess return (XR) calculated from the original
series is less than or equal to the average trading rule return for the pseudo data samples ( XR * ). For
0.05 probability the p-value must be greater than 0.05 (p-value>0.05). The results for the returns are
consistent with the traditional tests presented earlier.

International Research Journal of Finance and Economics - Issue 14 (2008)

108

Table 4: Simulations for AR(1) & GARCH(1,1) tests for 500 replications

AR(1)

GARCH(1,1)

Period

Test

Results

Buy

Sell

Buy-Sell

Buy

Sell

Buy-Sell

01/01/1995

1

0.932

1

0.826

0.116

0.57

-

(1,9)

Fraction > FTSE/ASE-20

(500)

(466)

(500)

(413)

(58)

(285)

0.998

0.828

1

0.822

0.132

0.542

(1,15)

Fraction > FTSE/ASE-20

(499)

(414)

(500)

(411)

(66)

(271)

0.992

0.64

0.986

0.85

0.152

0.564

(1,30)

Fraction > FTSE/ASE-20

(496)

(320)

(493)

(425)

(76)

(282)

0.988

0.462

0.976

0.85

0.152

0.598

(1,60)

Fraction > FTSE/ASE-20

(494)

(231)

(488)

(425)

(76)

(299)

0.972

0.42

0.928

0.846

0.166

0.63

(1,90)

Fraction > FTSE/ASE-20

(486)

(210)

(464)

(423)

(83)

(315)

0.957

0.34

0.877

0.857

0.179

0.67

12/31/2005

(1,130)

Fraction > FTSE/ASE-20

(480)

(171)

(438)

(430)

(90)

(331)

Average

0.9847

0.6037

0.9613

0.842

0.1493

0.594

5. Conclusions

In the past few years there has been a burst of theoretical work modeling financial markets with less
than fully rational agents. These papers show that it is possible to think coherently about asset pricing
while incorporating aspects of human behavior. So it is found a persistent doubt about the assumption
of individual rationality. ehavioral Finance is new research field which combines psychological and
economic knowledge in a consistent way. In behavioral scientific financial market research, the
psychological analysis of individual human beings as market participants is deliberately placed at the
centre. Behavioral Finance is showing that in an economy where rational and irrational traders interact,
irrationality can have a substantial and long-lived impact on prices. Only this way for instance can
investors’ “illogical” or ”irrational” behaviour as well as interrelated price developments be made
transparent and understandable.

Basic assumption of the technical analysis models is that the company's fundamentals, along

with broader economic factors and market psychology, are all priced into the stock, removing the need
to actually consider these factors separately and the repetitive nature of price movements is attributed
to market psychology. In the behavioral finance model it is observed rational and irrational
expectations about returns like technical analysis. In behavioral and in technical theory we observe a
combination between fundamental and psychological – emotional factors.

In this paper we applied technical methodology into the behavior theory. So we conducted an

analysis about the presence of the behavioral phenomenon in the large capitalization firms of the
Athens Stock Exchange. In addition, we tried to determine how investor’s sophistication influences
investing behavior and technical trading performance. The methodology of this paper considers the
changes in the returns to the Brock et al. (1992) one on FTSE/ASE-20 Index of the Athens Stock
Exchange over the 1995–2005 (end) period. Furthermore, we investigated the performance of various
technical trading rules in the large capitalization firms of the Athens Stock Exchange. We used
technical analysis models such as moving averages into behavioral practice. Moving averages are used
to emphasize the direction of a trend and to smooth out price and volume fluctuations, or "noise” that
can confuse interpretation. We have evaluated the following popular moving averages rules: 1-9,1-15,
1-30, 1-60, 1-90, and 1-130 where the first number in each pair indicates the days in the short period
and the second number shows the days in the long period.

In our analysis we have used standards tests in combination with bootstrap methodology under

the AR(1) & GARCH(1,1) models. Using a bootstrapping technique with two common models for
stock market returns (AR(1), GARCH) we statistically tested the significance of the profits generated
by six common technical trading rules in 11 year period. Constructively, our methodology combines
rational and irrational (emotional) expectations seem to beat the market performance (FTSE/ASE-20

109

International Research Journal of Finance and Economics - Issue 14 (2008)

Index of the Athens Stock Exchange). In particular, buy-hold strategy (Table 1) give us about 14% per
year (0.057% x 250 days) and using moving averages strategy 29% for buy-sell method (250 trading
days x 0.117%) on annual base and using buys method 22% (250 trading days x 0.0869%) yearly. So
we have noticed abnormal returns over the FTSE/ASE-20 Index of the Athens Stock Exchange
benchmark. Thus, technical analysis and behavioral finance theory seem to exist in the Greek Stock
Market. The AR(1) and GARCH (1,1) show a similar trend, with p-values going be significant in
examined period.

On the whole, the six rules examined over two models showed that the results overwhelmingly

support a strong increase in trading rules performance over time. The examined trading rules are highly
profitable over the most recent eleven-year period. So we have notice the existence of the behavioral
phenomenon in the large capitalization firms of the Athens Stock Exchange.

International Research Journal of Finance and Economics - Issue 14 (2008)

110

References

[1]

Balsara Nauzer, Carlson Kathleen and Narendar V. Rao, (1996), “Unsystematic Futures Profits
with Technical Trading Rules: A case for flexibility", Journal Of Financial And Strategic
Decisions, 9,1, pp 57-66

[2]

Barber, Brad M. and Terrance Odean, (2000), Trading is hazardous to your wealth: The
common stock investment performance of individual investors, Journal of Finance, 55, pp 773-
806.

[3]

Barber, Brad M. and Terrance Odean, 2001, Boys will be boys: Gender, overconfidence, and
common stock investment, Quarterly Journal of Economics 116, pp 261-292.

[4]

Beja, A., and M. B. Goldman. (1980) "On the Dynamic Behavior of Prices in Disequilibrium."
Journal of Finance, 35, pp 235-248.

[5]

Bessembinder Hendrik

Chan Kalok (1998), “Market Efficiency and the Returns to

Technical Analysis”, Financial management, 27, 2, pp 5-17

[6]

Blume, L., D. Easley, and M. O'Hara (1994) "Market Statistics and Technical Analysis: The
Role of Volume." Journal of Finance, 49, pp 153-181.

[7]

Brown, D. P. and R. H. Jennings (1989) "On technical analysis", Review of Financial Studies,
2, pp 527-551.

[8]

Chen, Gong-Meng, Kenneth A. Kim, John R. Nofsinger, and Oliver M. Rui, "Does investor
sophistication influence investing behavior and trading performance? Evidence from China,"
working paper.

[9]

Cheol-Ho Park and Scott H. Irwin (2004), “The Profitability of Technical Analysis: A Review”
AgMAS Project Research Report No. 2004-04

[10]

Clyde, W. C. and C. L. Osler (1997) "Charting: Chaos theory in disguise?", Journal of Future
Markets, 17, pp 489-514.

[11]

Coval, Joshua D., and Tyler Shumway, (2002), “Do behavioral biases affect prices?”, Harvard
University working paper, September 2002

[12]

De Long, J. B., A. Shleifer, L. H. Summers, and R. J. Waldmann (1991), "The Survival of
Noise Traders in Financial Markets." Journal of Business, 64, pp 1-19.

[13]

De Long, J. B., A. Shleifer, L. H. Summers, and R. J. Waldmann, (1990a) "Noise Trader Risk
in Financial Markets." Journal of Political Economy, 98, pp 703-738.

[14]

De Long, J. B., A. Shleifer, L. H. Summers, and R. J. Waldmann, (1990b),"Positive Feedback
Investment Strategies and Destabilizing Rational Speculation." Journal of Finance, 45, pp 379-
395.

[15]

Efron, B. (1979) "Bootstrapping methods: Another look at the Jacknife", Annals of Statistics, 7,
pp 1-26.

[16]

Efron, B. and R. J. Tibshirani (1993), “An introduction to the bootstrap”, Chapman & Hall,
New York.

[17]

Efron, B.and R. Tibshirani, (1986), Bootstrap methods for standard errors, confidence intervals
and other measures of statistical accuracy, Statistical Science,1, pp54-77.

[18]

Fama E. and French K. (1988), “Permanent and Temporary Components of Stock Prices',
Journal of Political Economy, 96, 2, pp 246-274.

[19]

Fama E.(1970). Efficient Capital Markets: A Review of Theory and Empirical Work, Journal
of Finance, Volume 25, Is 2, Papers and Proceedings of the Twenty-Eighth Annual Meeting of
the American Finance Association New York, N.Y. December, 28-30, 1969, pp383-417.

[20]

Fama, E.F., Blume, M., (1966). “Filter rules and stock market trading”, Journal of Business, 39,
pp 226–241.

[21]

Fernandez-Rodriguez, F., Sosvilla-Rivero, S. and M. D. Garcia-Artiles (1997) "Using nearest
neighbour predictors to forecast the Spanish stock market", Investigaciones Economicas, 21, pp
75-91.

[22]

Fernando Fernández-Rodríguez, SimóN Sosvilla-Rivero and Julián Andrada-Félix (1999),
"Technical Analysis in the Madrid Stock Exchange", FEDEA –D.T.99-05, pp 1-29

111

International Research Journal of Finance and Economics - Issue 14 (2008)

[23]

Freedman, D (1984b), Bootstrapping an econometric model: Some empirical results, Journal of
Busi¬ness and Economic Statistics, 2, pp150-158

[24]

Freedman, D and S. Peters, (1984a), Bootstrapping a regression equation: Some empirical
results, Journal of the American Statistical Society, 79, pp 97-106.

[25]

Freedman, D., (1984), “On bootstrapping two-stage least squares estimates in stationary linear
models”, Annals of Statistics, 12, pp 827-842.

[26]

Gençay, R. (1998) "The predictability of securities returns with simple technical rules", Journal
of Empirical Finance, 5, pp 347-359.

[27]

Grinblatt, M., and M. Keloharju, (2000), “The investment behavior and performance of various
investor types: A study of Finland’s unique data set,” Journal of Financial Economics, 55, pp
43-67.

[28]

Grinblatt, M., and M. Keloharju, (2001), “How distance, language, and culture influence
stockholdings and trades” Journal of Finance, 56, pp 1053-1074.

[29]

Jensen, M. C. (1978), "Some Anomalous Evidence Regarding Market Efficiency." Journal of
Financial Economics, pp 695-101.

[30]

Jensen, M.J., Bennington, G., (1970). “Random walks and technical theories: Some additional
evidence”. Journal of. Finance, 25, 469–482.

[31]

Ki-Yeol Kwon and Richard J. Kish (2002), “Technical trading strategies and return
predictability: NYSE”, Applied Financial Economics, 12, 9, pp 639 - 653

[32]

Kyle, A., and F. A. Wang, (1997), Speculation duopoly with agreement to disagree: Can
overconfidence survive the market test?, Journal of Finance, 52, pp 2073-2090.

[33]

Levich, R. and L. Thomas (1993) "The significance of technical trading rule profits in the
foreign exchange market: A bootstrap approach", Journal of International Money and
Finance,12, pp 451-474.

[34]

Mamaysky Harry Andrew W. Lo and Jiang Wang (2000), “Foundations of technical analysis:
Computational algorithms, statistical inference, and empirical implementation”, Journal of
Finance, 40,4, 2000.

[35]

Neftci Salih N (1991) “Naive Trading Rules in Financial Markets and Wiener-Kolmogorov
Prediction Theory: A Study of "Technical Analysis." Journal of Business, 64, 4, pp 549-71

[36]

Nelson, Daniel B., (1991), “Conditional heteroskedasticity in asset returns: A new approach”,
Econometrica, 59, pp 347-370.

[37]

Odean, Terrance, (1998a), “Are investors reluctant to realize their losses?”, Journal of Finance,
53, pp 1775-1798.

[38]

Odean, Terrance, (1998b), “Volume, volatility, price, and profit when all traders are above
average”, Journal of Finance, 53, pp 1887-1934.

[39]

Odean, Terrance, (1999), “Do investors trade too much?”, American Economics Review, 89,5,
pp 1279-1298.

[40]

Park Cheol-Ho and Irwinb Scott H, (2004), “The Profitability of Technical Analysis: A
Review”, AgMas

[41]

Recep Bildik (2001), “Intra-Day Seasonalities on Stock Returns: Evidence from the Turkish
Stock Market”, Emerging Markets Review, Vol 2, No 4, 2001

[42]

Schmidt, A. B. "Why Technical Trading May Be Successful? A Lesson from the Agent-Based
Modeling." Physica A, 303, pp 185-188.

[43]

Shiller, R. J. (2003), "From Efficient Markets Theory to Behavioral Finance" Journal of
Economic Perspectives, Vol 17, pp 83-104.

[44]

Shleifer A., and L. H. Summers (1990), "The Noise Trader Approach to Finance." Journal of
Economic Perspectives, Vol 4, pp 19-33.

[45]

Vasiliou, D. Eriotis, N. and Papathanasiou, S. (2006), “How rewarding is Technical Analysis?
Evidence from Athens Stock Exchange (ASE)”, Operational Research Journal, Vol 3, No 2, pp
85-102.

International Research Journal of Finance and Economics - Issue 14 (2008)

112

[46]

Wang, F. A., (1998), “Strategic trading, asymmetric information and heterogeneous prior
beliefs”, Journal of Financial Markets, Vol 1, pp 321-352.

[47]

Wang, F. A., (2001), “Overconfidence, investor sentiment, and evolution”, Journal of
Financial Intermediation, Vol 10, pp 138-170.

[48]

William Brock, Josef Lakonishok and Blake LeBaron (1992),"Simple Technical Trading Rules
and the Stochastic Properties of Stock Returns", Journal of Finance, Vol 47, 5, pp 1731-1764.

[49]

Wing-Keung Wong, Meher Manzur, Boon-Kiat Chew (2003), “How rewarding is Technical
analysis? Evidence from Singapore stock market”, Applied Financial Economics, Vol 13, No 7,
pp 543 – 551.

[50]

Working, H. (1949), "The Investigation of Economic Expectations." American Economic
Review, Vol 39, pp 150-166.

[51]

Working, H. (1962), "New Concepts Concerning Futures Markets and Prices." American
Economic Review, Vol 52, pp 431-459.