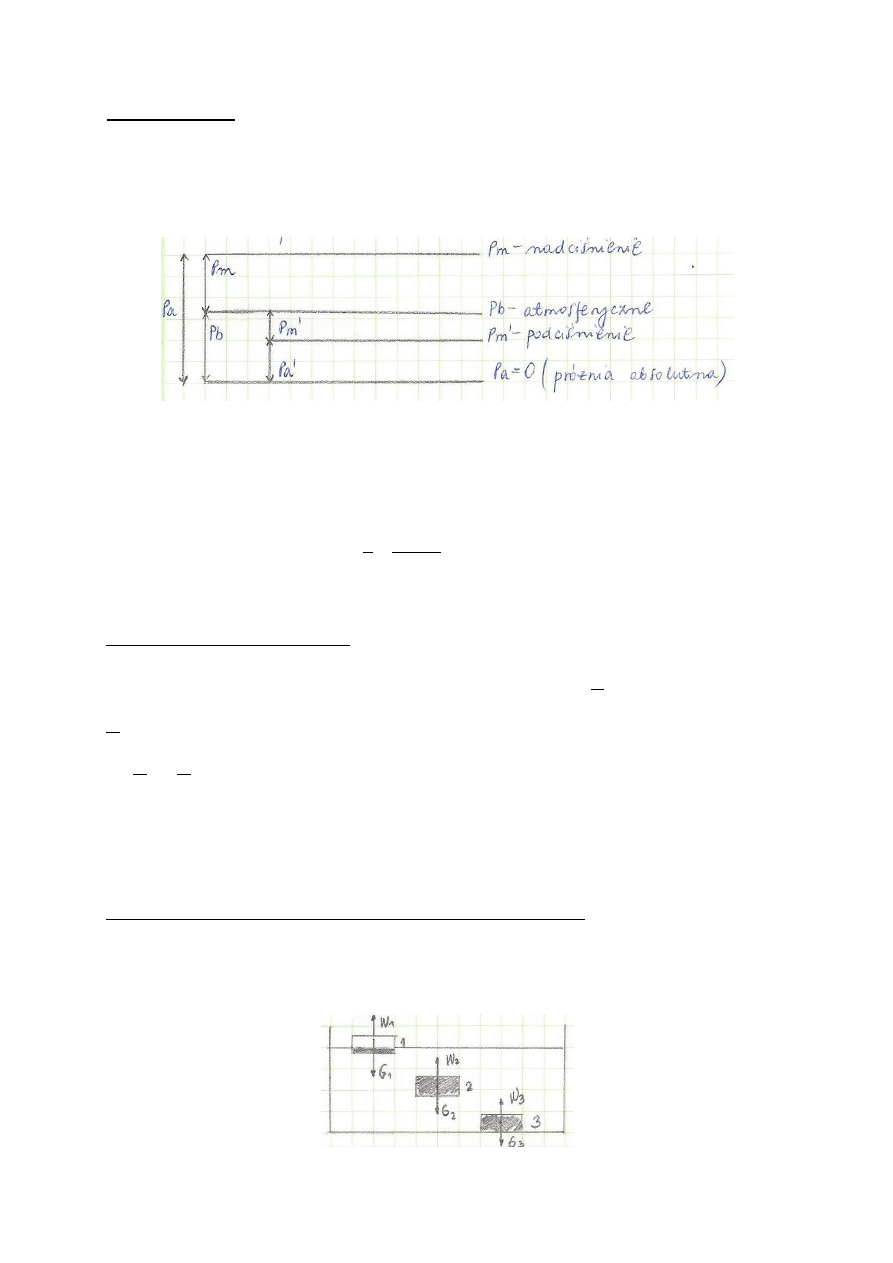
1. Rodzaje ciśnień.
-
absolutne
(
), całkowite ciśnienie, pod którego działaniem znajdują się czynniki
-
atmosferyczne
(barometryczne
) – wywołane ciężarem słupa powietrza atmosfery ziemskiej
-
manometryczne
(nadciśnienie lub podciśnienie
) - stanowiące różnicę pomiędzy ciśnieniem absolutnym i
atmosferycznym,
>
nadciśnienie
<
podciśnienie
W przypadku gdy czynnik porusza się, rozróżniamy:
-
statyczne
(
) – wskazywałby manometr poruszający się z prędkością czynnika
-
dynamiczne
(
) – przyrost ciśnienia jaki by nastąpił gdyby adiabatycznie odwracalnie zahamować czynnik do
prędkości równej zero
-
całkowite
(
) – suma ciśnienia statycznego i dynamicznego
W cieczach mamy do czynienia z ciśnieniem
hydrostatycznym
(
), wywołane ciężarem słupa cieczy.
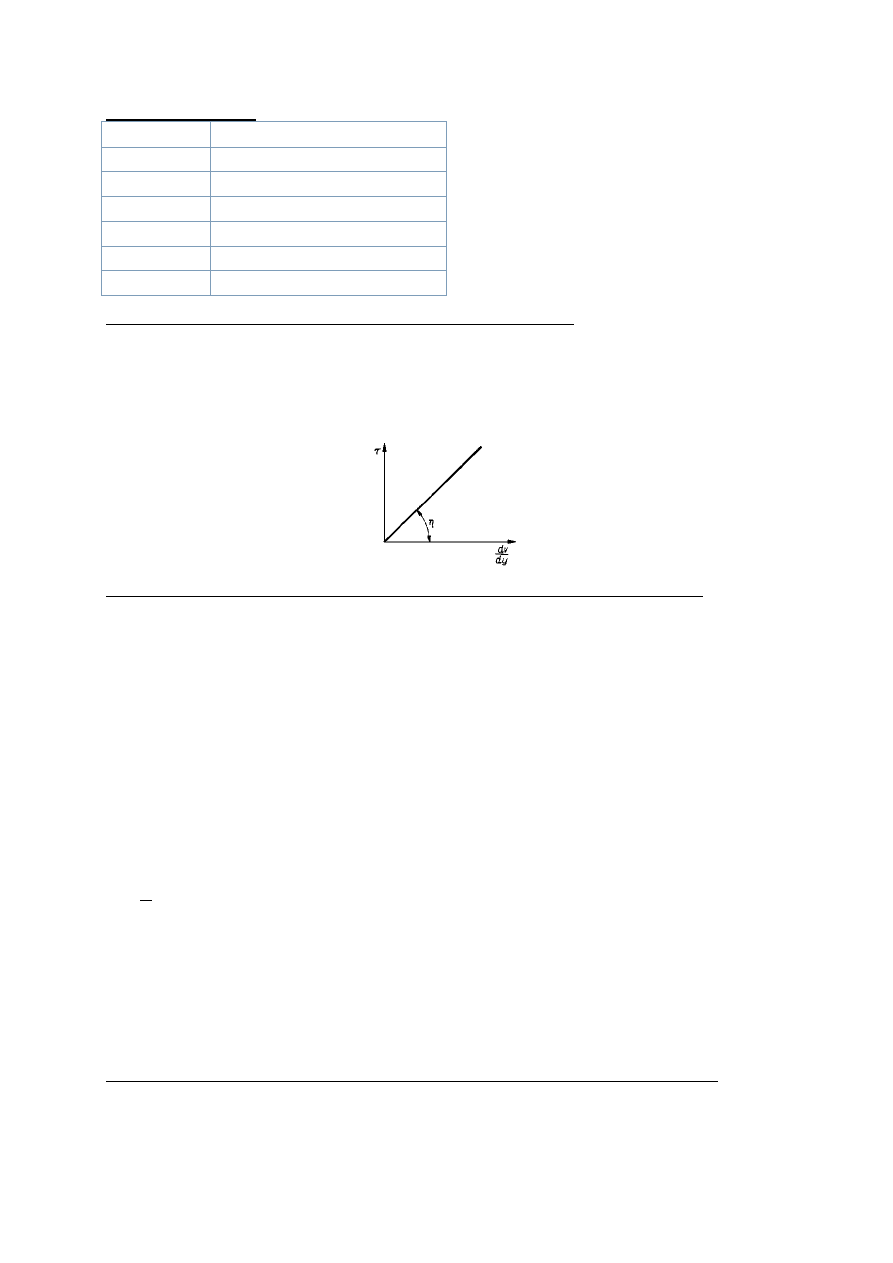
2. Własności cieczy newtonowskich.
Ciecze Newtonowskie to takie, które zachowują sie zgodnie z hipotezą Newtonowska (są to gazy oraz ciecze o
niewielkich gęstościach np. woda). Mówi ona mianowicie. ze "wartość siły stycznej przeciwdziałającej
prostopadłemu odkształceniu elementarnego prostopadłościanu wynosi
";
Gdzie:
-
gradient prędkości
– odległość dwóch sąsiednich warstw o powierzchni
–
naprężenia styczne proporcjonalne do współczynnika lepkości dynamicznej
Dodatkowo:
Płyny, dla których jest słuszny wzór Newtona, nazywają się płynami newtonowskimi. Ze wzrostem ciśnienia
lepkość dynamiczna cieczy i gazów rośnie (wyraźne zmiany występują przy zmianach ciśnienia rzędu
kilkudziesięciu atmosfer), natomiast ze wzrostem temperatury lepkość cieczy maleje, a gazów rośnie
(znajomość lepkości cieczy — np. smarów, olejów — i jej zależność od temperatury ma podstawowe znaczenie
w wielu zagadnieniach techniki). W płynach newtonowskich (np. woda, roztwory org., sole i szkła w stanie
płynnym) µ nie zależy od prędkości przepływu ani od jej gradientu.
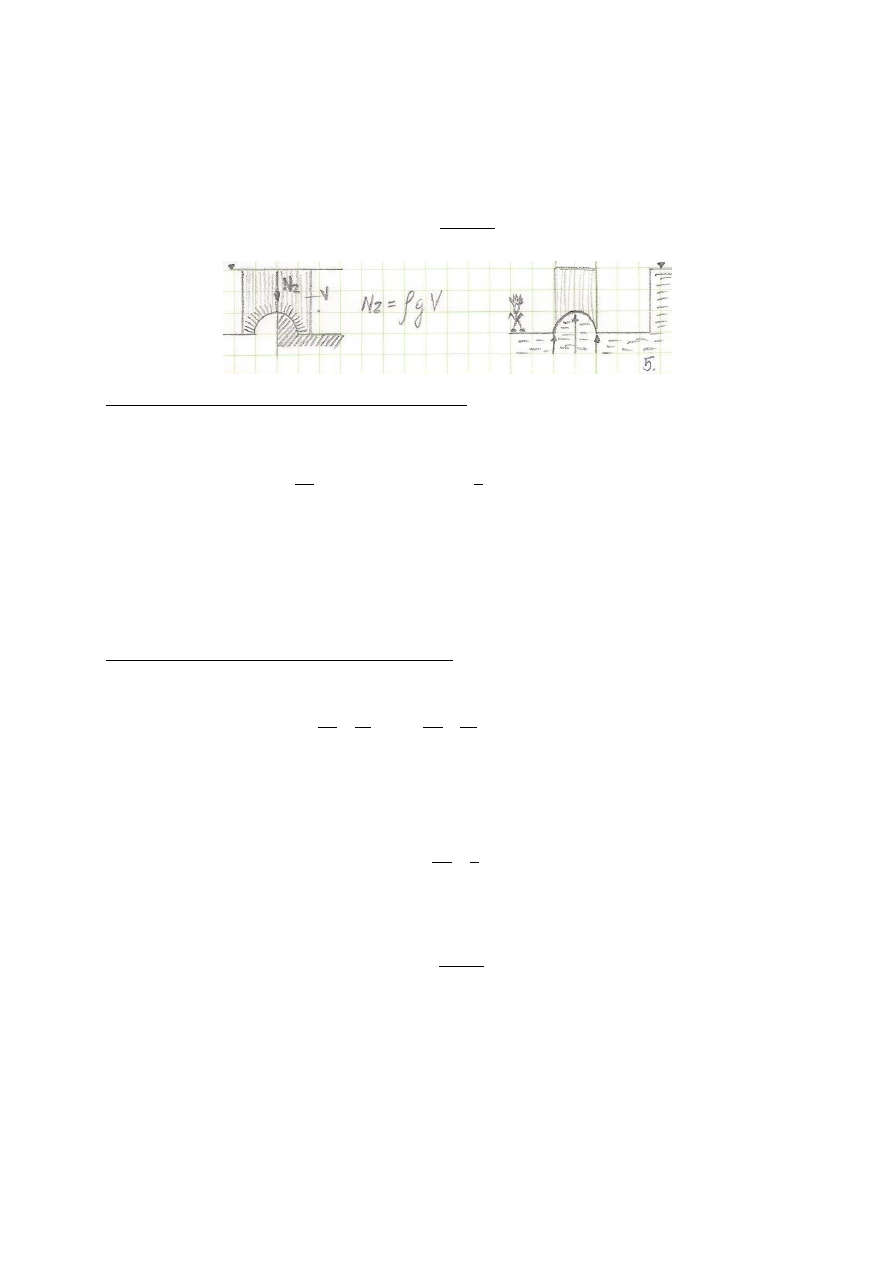
3. Siła wyporu. Kryteria pływalności ciał stałych zanurzonych w cieczy.
Całkowity napór cieczy na zanurzone w niej ciało nazywamy wyporem – W.
Powyższy wzór stanowi treść prawa Archimedesa, które można sformułować następująco: na ciało zanurzone w
cieczy działa pionowo w górę wypór, równy ciężarowi cieczy wypartej przez to ciało.
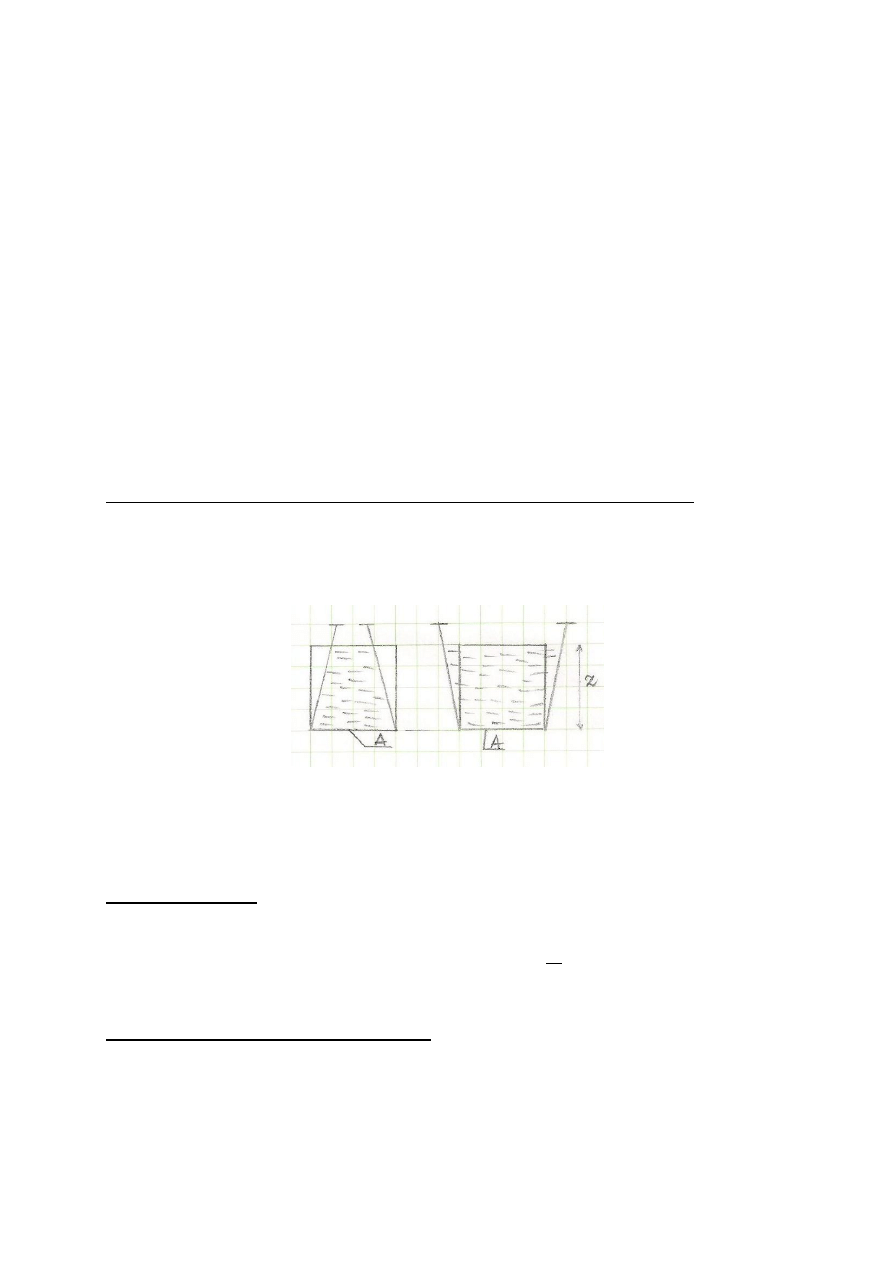
Możemy wyróżnić trzy przypadki pływania ciał:
a) – ciało pływa częściowo zanurzone w cieczy
b) – ciało tonie
c) – ciało jest całkowicie zanurzone i pozostaje w stanie równowagi przy dowolnym zanurzeniu
** Warunek równowagi dla ciał zanurzonych w cieczy ma postać:
Gdzie:
= objętość ciała zanurzonego
= objętość ciała
=gęstość cieczy
= średnia gęstość
Jeśli:
- ciało jest całkowicie zanurzone
- ciało tonie
- ciało unosi się do góry, aż do momentu gdy zajdzie warunek równowagi
, przy czym
,
ciało pływa wówczas częściowo zanurzone.
Powyższy warunek równowagi muszą spełnić wszystkie okręty nawodne. Różnica objętości
nosi nazwę
zaporu wyporności
.
4. Obliczanie sił wyporu hydrostatycznego na ściany płaskie. Paradoks hydrostatyczny.
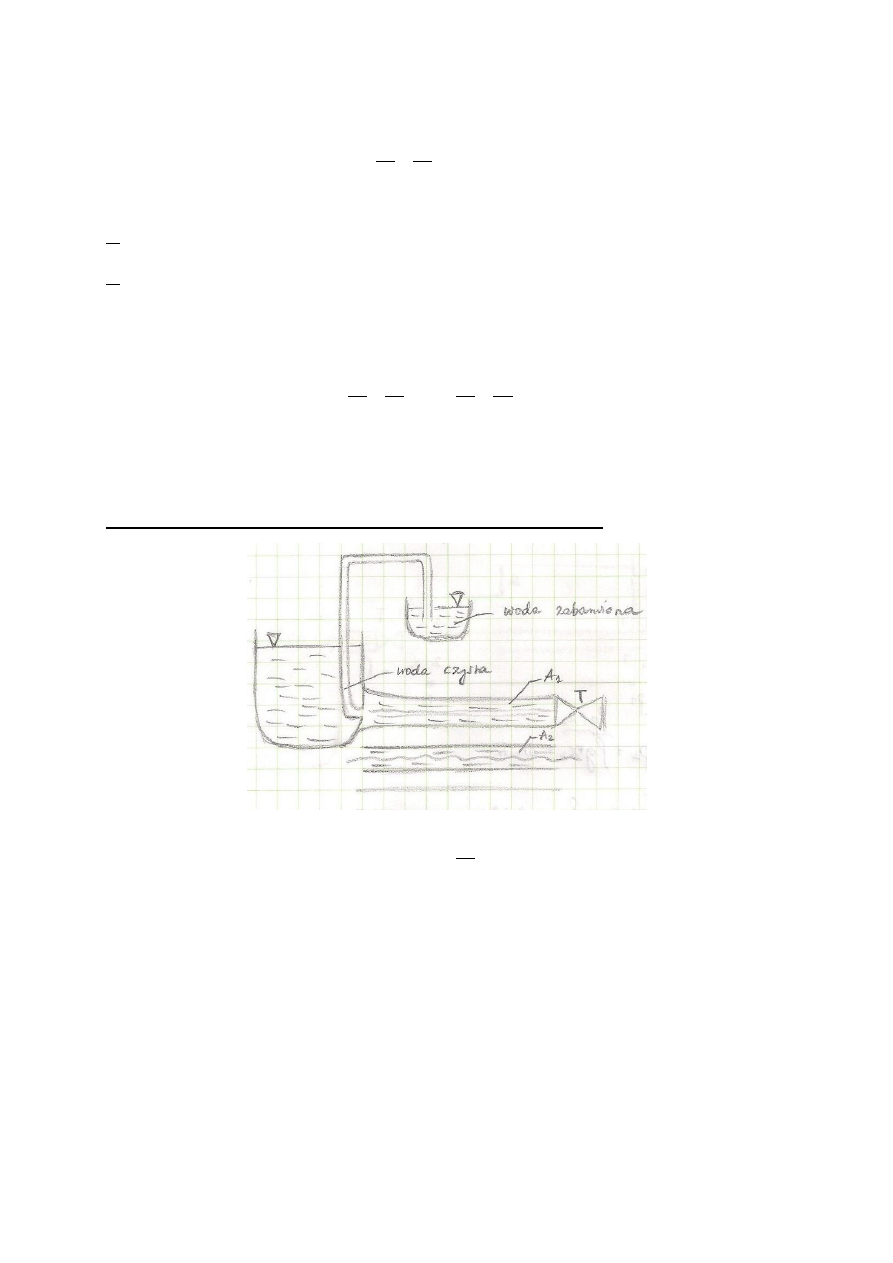
- Napór na ściany płaskie, poziome, np. na dno szklanki.
Napór na płaską ścianę poziomą o polu A, położoną a głębokości z, pod zwierciadłem cieczy wynosi
i równa się ciężarowi słupa cieczy, którego podstawą jest rozpatrywana powierzchnia, a wysokością głębokość
z.
Z tego wynika, że napór na dno naczynia nie zależy od kształtu naczynia, ani od ilości zawartej w nim cieczy,
ale wyłącznie od gęstości cieczy , głębokości dna z i pola powierzchni tego dna A.
Twierdzenie to nazywamy
paradoksem hydrostatycznym. (Twierdzenie Stevina)
- Napór na ściany płaskie dowolnie zorientowane, np. ściany boczne naczyń.
Napór na ścianę płaską dowolnie zorientowaną jest równy ciężarowi słupa cieczy, którego podstawa jest dana
ściana, a wysokością głębokość zanurzenia geometrycznego środka ciężkości tej ściany
.
(ponieważ ciśnienie hydrostatyczne zwiększa się wraz z głębokością, to środek naporu hydrostatycznego
znajduje się zawsze głębiej niż środek ciężkości tej ściany).
5. Równanie ciągłości.
Równanie ciągłości przedstawia równość wydatków objętościowych, masowych lub ciężarowych w obranych
przekrojach. Dla jednowymiarowego przepływu płynu doskonałego równanie to można zapisać w takiej postaci:
;
6. Równanie Bernoulliego dla cieczy doskonałej.
Założenia przy wyprowadzaniu równania Bernoulliego:
- ruch jest ustalony i ciągły
- ciecz jest idealna, tj. lepka i nieściśliwa
- na ciecz nie działają inne siły masowe oprócz siły ciążenia
- przyspieszenie ziemskie jest stałe i wektory przyspieszenia ziemskiego są względem siebie równoległe
- rozpatrujemy tylko jedną strugę
Równanie Bernoulliego:
Gdzie:
= wysokość prędkości
= wysokość ciśnienia
= wysokość położenia
Równanie Bernoulliego zapisane dla dwóch dowolnych przekrojów strumienia ma postać:
Gdzie:
- ciśnienie statyczne w przekrojach 1-1, 2-2,
- prędkości średnie w obu przekrojach,
- odległość środka przekroju od poziomu odniesienia.
7. Reakcje przepływów cieczy rzeczywistych. Krytyczna liczba Reynoldsa.
Doświadczenie Reynoldsa.
Rodzaj przepływu określa się w oparciu o wartość tzw.
Liczby Reynoldsa
Re:
Gdzie:
- prędkość charakterystyczna płynu
- lepkość kinematyczna płynu
d – wymiar charakterystyczny zagadnienia
W przepływie turbulentnym cząsteczka cieczy posiada pulsacje prędkości. W zasadzie jest to zawsze przepływ
3D. Z turbulencją jest tzw. lepkość turbulentu.
Liczba Reynoldsa przy której zachodzi zmiana rodzaju ruchu, nosi nazwę
liczby krytycznej R
. Jest to wartość
absolutna (ścisła).
Szereg czynników ubocznych ma wpływ na jej wartość, np.:
- wlot do przewodu
- chropowatość rury, miejscowe nierówności, drgania, zanieczyszczenia cieczy, itd.
Często mówimy o dolnej i górnej liczbie Reynoldsa:
-wartość poniżej której nie udało się zaobserwować ruchu burzliwego jako trwałego
- wartość powyżej której nie udało się zaobserwować przepływu laminarnego
Generalnie, przejście z przepływu laminarnego w turbulentny odbywa się przy większej liczbie Reynoldsa, z
turbulentnego w laminarny przy mniejszej liczbie Reynoldsa.
Re < 2300 – przepływ laminarny (uporządkowany, warstwowy, stabilny)
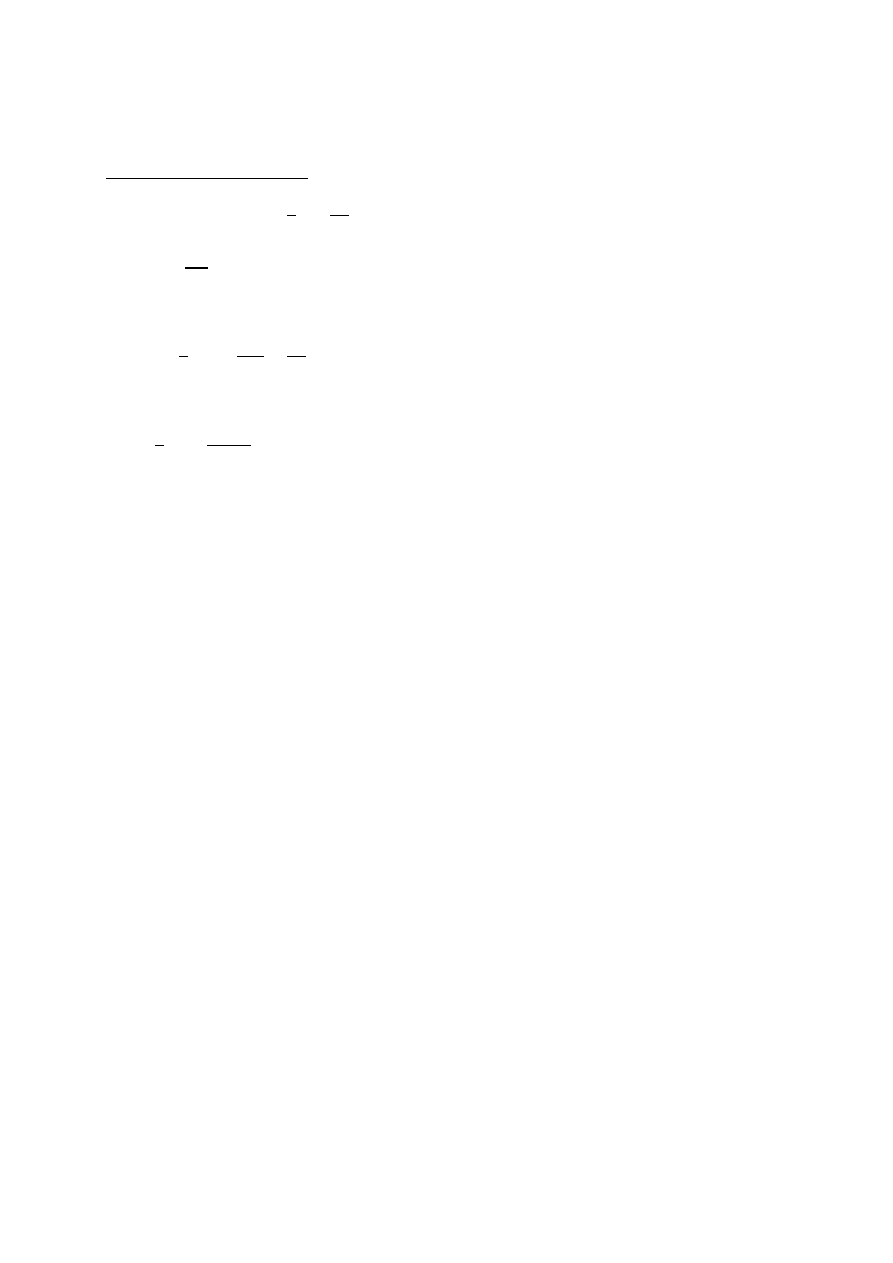
2300 < Re < 10000 – przepływ przejściowy (częściowo turbulentny)
Re > 10000 – przepływ turbulentny (burzliwy)
8. Charakterystyka rurociągu.
Gdzie:
- charakterystyka rurociągu:
- Oporność hydrauliczna rurociągu:
1. Jednostki ciśnienia.
paskal
megapaskal
bar
atmosfera fizyczna
atmosfera techniczna
milimetr słupa rtęci = Tor
milimetr słupa wody
2. Charakterystyka cieczy nienewtonowskich. Współczynnik lepkości.
Ciecze nienewtonowskie są to ciecze, których krzywe płynięcia nie są liniami prostymi. Ich lepkość często jest
nazywana lepkością pozorną lub strukturalną.
Ciecze nienewtonowskie można podzielić na trzy zasadnicze grupy:
- ciecze, których własności reologiczne nie zmieniają się w czasie (prędkość ścinania jest funkcją naprężenia
ścinającego;
- ciecze, których własności reologiczne zmieniają się w czasie (prędkość ścinania jest funkcją naprężenia
ścinającego i czasu);
- ciecze lepko- sprężyste, wykazujące oprócz własności lepkościowych i efekty sprężyste.
3. Prawo Archimedesa. Kryteria stateczności ciał pływających (częściowo zanurzonych).
Ciało pływające (częściowo zanurzone) będzie znajdowało się w stanie równowagi statecznej, jeśli wychylone z
położenia równowagi na skutek działania chwilowego momentu zewnętrznego powróci do położenia
pierwotnego.
Jeśli założy się, że ciężar ciała nie ulega zmianie, to po wychyleniu ciała z położenia równowagi, linia działania
siły wyporu nie pokrywa się z linią działania siły ciężkości. Pojawia się moment, który może przeciwdziałać
dalszemu wychyleniu (ciało stateczne) lub pogłębiać to wychylenie (ciało niestateczne).
Moment ten nosi nazwę momentu prostującego i wynosi:
gdzie:
l
– ramię prostujące
Punkt nazywamy metacentrum, punkt ten, gdy dąży do położenia. Odległość tego punktu od wysokości
położenia środka ciężkości nosi nazwę wysokości metacentrycznej i jest miarą stateczności ciała pływającego.
Wysokość metacentryczną wyraża się zależnością:
gdzie:
promień
metacentryczny
moment bezwładności
objętość ciała zanurzonego
wysokość położenia środka ciężkości
wysokość położenia środka wyporu
Jeśli:
– ciało jest stateczne
-
ciało jest niestateczne
4. Obliczanie sił naporu hydrostatycznego na ściany zakrzywione (powierzchnie dowolne).
- Napór na ściany zakrzywione (pow. dowolne).
Napór na ścianę zakrzywioną wyraża się, obliczając dwie składowe: poziomą i pionową naporu na tę
powierzchnię.
- składowa pozioma naporu
, na zakrzywioną powierzchnię w dowolnym, poziomym kierunku jest równa
naporowi na rzut tej powierzchni na płaszczyznę prostopadłą do rozpatrywanego kierunku (patrz obliczenia sił
naporu na ściany płaskie).
Linia działania naporu poziomego przechodzi przez środek naporu rzutu rozważanej powierzchni .
- składowa pionowa naporu
, jest równa ciężarowi ‘bryły ciekłej’ ograniczonej daną powierzchnią pionowymi
tworzącymi, poprowadzonymi przez jej kontur i zwierciadłem cieczy. Linie działania naporu pionowego
przechodzą przez środek ciężkości ‘bryły ciekłej’.
Napór wypadkowy jest sumą geometryczną naporu poziomego i pionowego.
5. Zasada zachowania pędu. Przykłady zastosowania.
Równanie Naviera – Stokesa
Dla płynów rzeczywistych, przy uwzględnieniu lepkości dynamicznej o współczynniku μ wektora, postać
równania zachowania pędu może być zapisana w formie:
gdzie:
jest tensorem jednostkowym
jest tensorem deformacji
Zasada zachowania pędu wykorzystywana jest dla określenia reakcji ścian przewodu na przepływającą ciecz,
reakcji cieczy wypływającej ze zbiornika, reakcji strumienia przepływającego przez dyszę (np. w silniku
odrzutowym) oraz reakcji cieczy na elementy maszyn przepływowych.
6. Równanie Bernoulliego dla cieczy rzeczywistych.
Równanie Daniela Bernoulliego dla rzeczywistego płynu (newtonowskiego) przy uwzględnieniu strat przepływu
wzdłuż linii prądu ma postać:
gdzie:
jest stratą przepływu, wyróżniając straty liniowe i lokalne.
Energia kinetyczna przepływu zwana wysokością rozporządzalną jest określona zależnością:
gdzie:
- jest współczynnikiem Coriolisa, określonym wzorem:
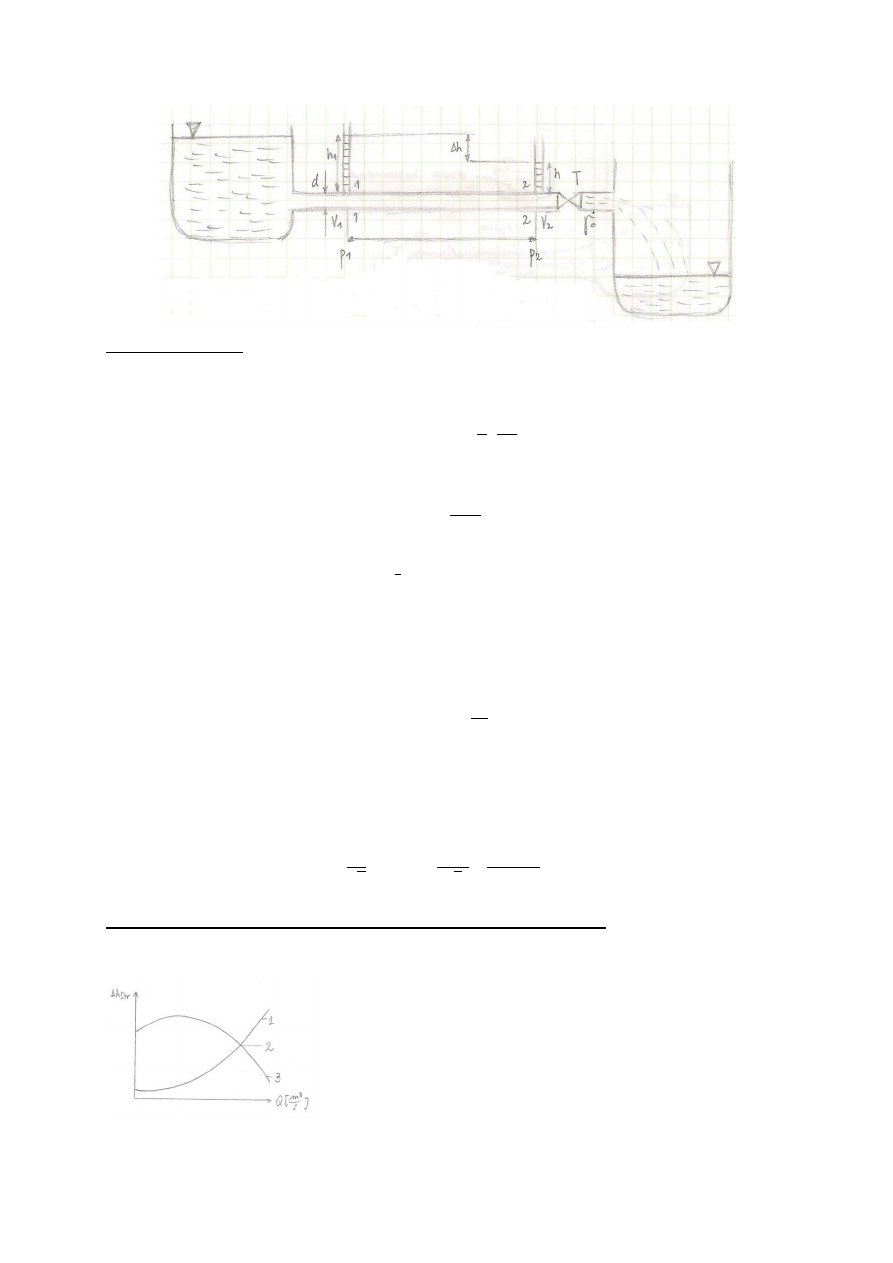
Jeśli ciecz lepka płynie rurociągiem (przewodem) to narastają straty przepływu wynikające z konieczności
pokonania sił stycznych. Występują zatem straty energii, które objawiają się spadkami ciśnienia wzdłuż drogi
przepływu, nie spada natomiast prędkość cieczy w rurociągu (pęd przepływającej cieczy). Potwierdza to
doświadczenie pokazane na rysunku:
7. Straty przepływu.
W przewodzie rurowym występują straty przepływu zwane tarciem hydraulicznym lub stratami ciągłymi oraz
straty w połączeniach przewodów. Straty energii dla rur o przekroju kołowym dla laminarnego przepływu w
rurze są opisane wzorem Darcy’ego:
gdzie jest współczynnikiem strat ciągłych zależnym od liczby Reynoldsa R
e
i od chropowatości wewnętrznych
ścian przewodu. Liczbę Reynoldsa dla przewodu o przekroju kołowym wyznacza się ze wzoru:
gdzie:
gdzie
jest lepkością kinematyczną płynu
, gdzie
lepkość dynamiczna.
Dodatkowo z wykładu:
– dla innych przepływów – turbulentnych wyznacza się doświadczalnie lub zakładając określony model
turbulencji.
, kształtu stanu powierzchni
Straty dzielą się na straty w przewodach (liniowe, lepkości) i straty lokalne. Wielkość strat lokalnych określa
zależność:
Gdzie:
-
współ. Strat lokalnych, miejscowych
Określa się go na podstawie badań lub w oparciu o analizę przepływu nielepkiego. Stary lokalne związane ze
zmianą geometrii przewodu (rozszerzenie, przewężenie), kierunku przepływu, zaburzeniami związanymi z
armaturą (zawory, kryzy, zasuwy), rozgałęzienia przewodów, itp.
Współczynnik start dla przepływu turbulentnego:
8. Charakterystyka układu pompowego. (rura + pompa =układ pompowy)
1.
2. Punkt pracy układu pompowego.
3.