Władysław DYBCZYŃSKI

Politechnika Białostocka, Wydział Elektryczny, Katedra Promieniowania Optycznego

Krzywa światłości diody LED

Streszczenie.

Opisano sposób projektowania kształtu soczewki płasko-wypukłej, współpracującej z diodą świecącą. Zaproponowany układ

świetlno-optyczny może oświetlać ze stałym natężeniem oświetlenia wybrany obszar pola pracy wzrokowej.

Abstrakt.

The designing method of the shape of lens, which is a part of the optical system, is described. This system consists of an LED and flat-

convex lens. It has application in lightening work stand surface with constant value of illuminance. (The LED intensity curve).

Słowa kluczowe: oświetlenie miejscowe, dioda elektroluminescencyjna, natężenie oświetlenia, pole pracy wzrokowej.
Keywords: lighting, LED, illuminance, work stand.

Wprowadzenie

Diody elektroluminescencyjne są nowoczesnymi

źródłami światła. Charakteryzują się niewielką mocą,
ograniczoną skutecznością świetlną i małymi wymiarami.
Łącząc niektóre cechy techniczne tych diod z niezbyt
niskimi cenami dochodzi się do wniosku, że te źródła
światła nie nadają się do oświetlenia wielkich
powierzchni z dużym poziomem natężenia oświetlenia.
Ale do oświetlenia miejscowego i akcentującego
niewielkich powierzchni doskonale się nadają.

Sposób oświetlenia miejscowego, z wykorzystaniem

diod LED został omówiony w czasie trwania Konferencji
Oświetleniowej Lumen V4 (Węgry) [1]. Stwierdzono tam,
że tylko niektóre diody LED, o odpowiednim kształcie
bryły fotometrycznej, można racjonalnie wykorzystywać
do oświetlenia miejscowego. Niektóre, handlowo
dostępne diody, przeznaczone są do oświetlenia
powierzchni płaskich z kierunku normalnego. Uzyskuje
się plamę świetlną o dobrej równomierności natężenia
oświetlenia i o wielkości zależnej od odległości świecenia
i kąta użytecznego wypromieniowanej wiązki świetlnej.
Niestety przy oświetleniu tymi diodami miejsca pracy
wzrokowej, np. w postaci biurka, które realizuje się
zazwyczaj z boku, sprawność takiego urządzenia
oświetleniowego jest ograniczona. Wynika to głównie z
nieodpowiedniego kształtu bryły fotometrycznej samej
diody. Chcąc zaproponować korzystniejszy kształt tej
bryły należy ustalić odpowiednią geometrię usytuowania
oprawy oświetlenia miejscowego.

Rys. 1. Geometria oświetlenia biurka

Geometria oświetlenia biurka

Przyjęto, że miejsce pracy wzrokowej (format A

3

) jest

usytuowane na blacie biurka (rys. 1) o wymiarach
600×900 mm. Środek świetlny oprawy oświetlenia
miejscowego (punkt D) znajduje się na wysokości h =
500 mm ponad blatem biurka. Rzut środka świetlnego
oprawy (punkt S) leży na krawędzi biurka. Najdalszy
punkt (P), który oświetla oprawa, znajduje się w znanej

odległości (SP = 688 mm) od punktu S. Idąc od punktu P
wzdłuż osi x w kierunku punktu S wartość natężenia
oświetlenia powinna być stała i równa E

h

= 200 lx. Zakładając

obrotowo-symetryczny kształt bryły fotometrycznej diody LED,
to w kierunku osi y rozkład natężenia oświetlenia na biurku
będzie zbliżony do funkcji kosinus.

0

10

20

30

40

O

O

O

O

O

0

100

200

300

[cd]

688

650

600

500

400
300

200

[mm]

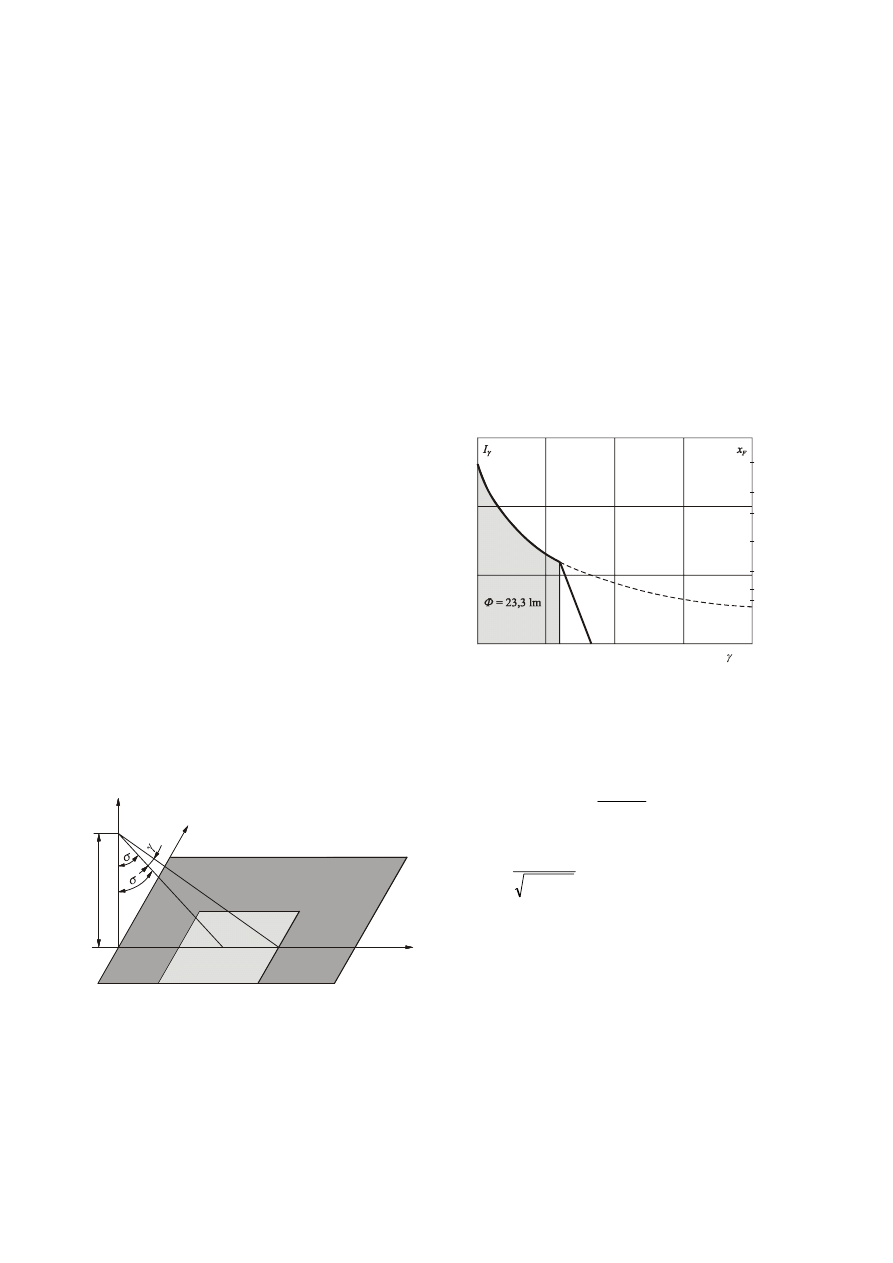
Rys. 2. Wymagana krzywa światłości diody świecącej

W celu wytworzenia w dowolnym punkcie F, leżącym na

osi x, natężenia oświetlenia o wartości E

h

, światłość I

γ

powinna

wynosić

(1)

σ

γ

cos

2

2

h

x

E

I

F

h

+

=

F

G

x

y

z

h

S

D

0

P

przy czym:

2

2

cos

h

x

h

F

+

=

σ

x

F

- współrzędna punktu F.

Wyznaczona w ten sposób krzywa światłości, dająca stałą

wartość natężenia oświetlenia w linii pokrywającej się z osią x
(od punktu P w kierunku S), została przedstawiona na rysunku
2. Wobec usytuowania pola pracy wzrokowej między punktami
P i G, krzywa światłości powinna sięgać też od punktu P do G,
ponieważ strumień świetlny zawarty w kącie między punktami
G i S (rys. 2) trafia już w najbliższe otoczenie wspomnianego
pola, nie jest niezbędny. Ze względu na rzeczywisty wymiar
obszaru świecącego diody, krzywa światłości opada z punktu
G do wartości zerowej w określonym przedziale (niewielkim)
kąta

γ

. Przyjęto, że w rzeczywistych warunkach szybkość

zmian światłości w funkcji kąta

γ

wynosi 25 cd/stopień. Znając

ten wyidealizowany przebieg krzywej światłości można już

PRZEGLĄD ELEKTROTECHNICZNY - KONFERENCJE, ISSN 1731-6106, R. 5 NR 1/2007

14

przystąpić do projektowania układu optycznego
współpracującego z diodą o kosinusowym rozsyle
światłości. Użyteczny strumień

świetlny diody,

wyposażonej w układ optyczny, wyznaczony z krzywej
światłości dla przyjętej powyżej geometrii oświetlenia
stanowiska pracy, powinien wynosić

Φ

u

= 23,3 lm.

Rys. 3. Soczewka współpracująca z diodą świecącą

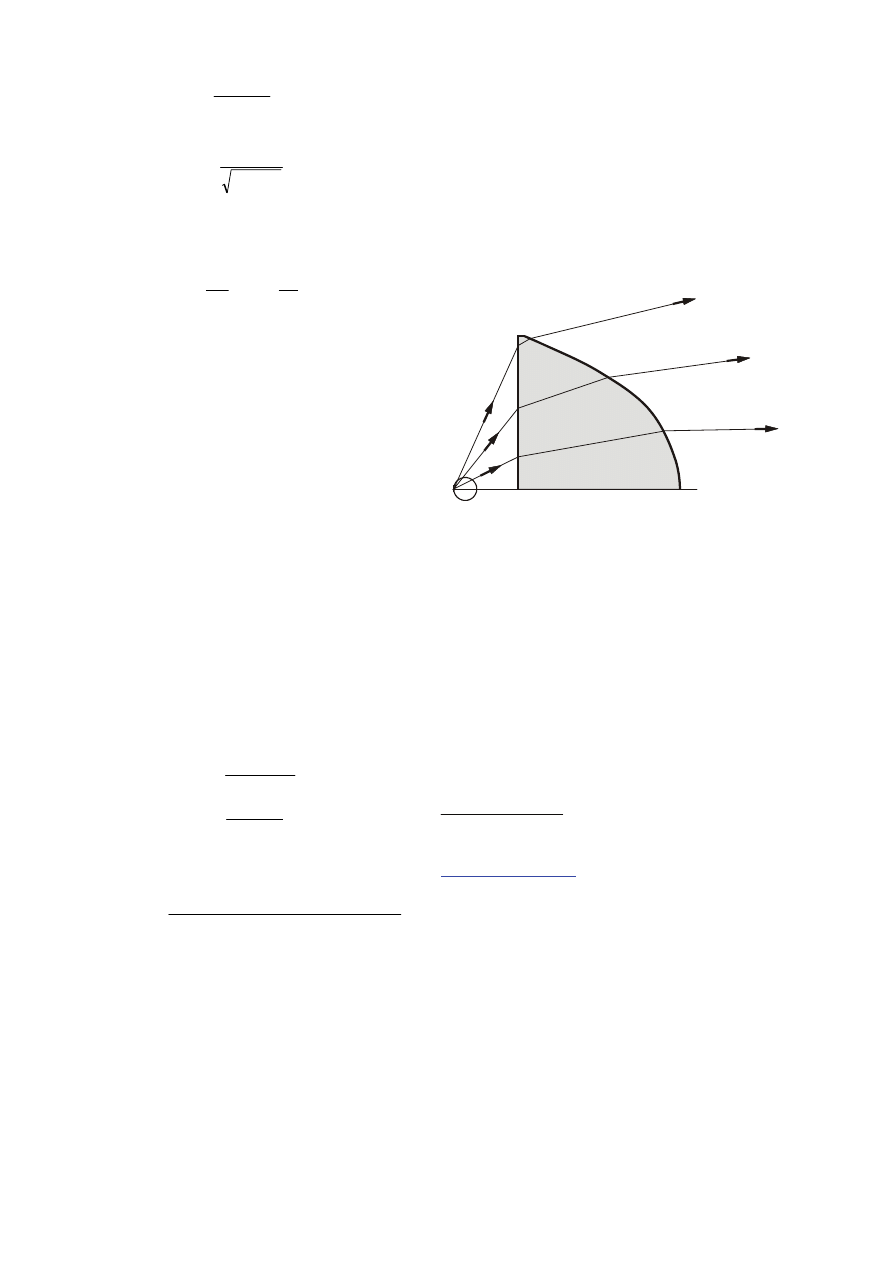
Układ optyczny diody świecącej

Założono, że element świecący diody jest mały, więc

przyjęto punktowe źródło

światła, emitujące

promieniowanie zgodne z funkcją kosinus (rys. 3).
Promienie świetlne trafiają na soczewkę, która powinna
kształtować rozkład przestrzenny strumienia świetlnego
zgodnie z krzywą światłości, przedstawioną na rysunku
2. Przestrzeń przedmiotową podzielono na równe kąty
elementarne

ΔΦ

(rys. 4) i w ten sposób otrzymano

kierunki

β

1

;

β

2 …

β

i

. Reprezentantem elementarnego

strumienia świetlnego jest wektor biegnący pod kątem

ϕ

i

.

Rys. 4. Elementarne strumienie świetlne

Elementarny strumień świetlny

ΔΦ

pi

, padający na

soczewkę, wynosi

(2)

)

cos

(cos

2

1

i

i

pi

pi

I

β

β

π

−

=

ΔΦ

−

przy czym:

(3)

π

ϕ

ϕ

i

u

i

m

pi

I

I

cos

cos

Φ

=

=

I

m

– światłość maksymalna diody,

Φ

u

– strumień

użyteczny diody.

Elementarny strumień świetlny

ΔΦ

wi

wychodzący z

soczewki, można wyznaczyć z zależności

(4)

)

cos

(cos

2

1

i

i

i

wi

I

α

α

π

γ

−

=

ΔΦ

−

przy czym: I

γi

– wymagana wartość światłości skierowana pod

kątem

γ

i

(rys. 2),

α

i-1

,

α

i

– kąty ograniczające rozsył

elementarnego strumienia świetlnego.

i

i

i

i

i

i

i

j

j

‘

‘

Rys. 5. Przebieg promienia świetlnego w soczewce

Elementarny strumień świetlny wychodzący (4) można

porównać z padającym (2) pod warunkiem uwzględnienia
współczynnika przepuszczania

τ

soczewki. Wyznaczenie

kątów

γ

i

w poszczególnych strefach jest dosyć złożone,

ponieważ nie jest znany kąt łamiący

δ

i

w danej strefie

soczewki (rys. 5). Promień padający pod kątem

ϕ

i

, w

rozpatrywanej strefie, ulega załamaniu i biegnie pod kątem

ϕ

i

’.

Kierunek

ϕ

i

’ wyznacza się z zależności Fresnela

(5)

n

i

i

ϕ

ϕ

sin

sin

'

=

.

1

1

1

1

1

1

2

2

2

2

2

2

3

3

3

3

3

3

t

g

D

T

T

T

T

W

W

W

W

0

0

Na drugiej granicy ośrodków

zjawisko przebiega podobnie

(6)

.

'

sin

sin

i

i

j

n

j

=

Jednocześnie wiadomo, że suma

kątów

ϕ

i

’ i j

i

’ jest równa kątowi

łamiącemu

δ

i

w danym miejscu

soczewki

(7)

.

'

'

i

i

i

j

+

=

ϕ

δ

Z rysunku 5 wynika

(8)

.

i

i

i

i

i

i

j

j

j

γ

ϕ

ψ

−

+

=

=

+

'

'

'

Zatem

i

i

i

i

j

sin

)

sin(

'

=

+

ψ

oraz

.

i

i

i

i

i

j

j

j

sin

sin

cos

cos

sin

'

'

=

+

ψ

ψ

Dzieląc powyższe wyrażenie przez

sinj

i

’

oraz po dalszych

przekształceniach otrzymuje się

(9)

)

cos(

)

sin(

'

'

'

i

i

i

i

i

n

arctg

j

γ

ϕ

γ

ϕ

−

−

−

=

.

W praktyce obliczeniowej, przy wyznaczaniu w każdej

strefie kąta

δ

i

zakłada się wstępnie wartość kąta

α

i

(rys. 4),

wylicza się dla niego średni kąt

γ

i

PRZEGLĄD ELEKTROTECHNICZNY - KONFERENCJE, ISSN 1731-6106, R. 5 NR 1/2007

15

(10)

2

1

i

i

i

α

α

γ

+

=

−

,

dla którego wyznacza się światłość I

γi

(11)

2

2

h

x

E

I

F

h

i

+

=

γ

przy czym:

h

x

arctg

DS

SP

arctg

tg

h

x

P

i

F

=

=

−

=

⋅

=

0

0

σ

γ

σ

σ

σ

Następnie porównuje się elementarne strumienie

świetlne: padający

ΔΦ

pi

z przepuszczonym

ΔΦ

wi

z

uwzględnieniem współczynnika przepuszczania

τ

soczewki.

(12)

ε

α

α

π

β

β

ϕ

τ

γ

=

−

−

−

Φ

−

−

)

cos

(cos

)

cos

(cos

cos

1

1

i

i

i

i

i

i

u

I

.

Jeżeli różnica

ε

tych dwóch strumieni świetlnych nie

jest równa zeru, należy przyjąć nową wartość kąta

α

i

.

Obliczenia prowadzi się tak długo, aż różnica

ε

będzie

równa zeru lub będzie mniejsza od dopuszczalnego
błędu (np.

ε

< 0,0001).

Teraz można już wyznaczyć średni kąt łamiący

δ

i

danej strefy soczewki poprzez sumowanie wartości
kątów

ϕ

i

’ oraz j

i

’ (zależności: 7, 9 i 10). Kształt elementu

soczewki jest określony czterema punktami: T

i-1

; W

i-1

; T

i

oraz W

i

(rys. 4). Współrzędne dwóch z tych punktów

zostały wyliczone w poprzedniej strefie. Współrzędna
punktu T

i

z bieżącej strefy (i-tej) wyznacza się z

zależności:

(13)

.

⎭

⎬

⎫

⋅

=

=

i

Ti

Ti

tg

t

y

t

x

β

Współrzędne punktu W

i

są związane zależnościami:

(14)

⎪

⎪
⎭

⎪⎪

⎬

⎫

−

−

=

−

−

=

−

−

t

x

y

y

tg

y

y

x

x

tg

Wi

Ti

Wi

i

Wi

Wi

Wi

Wi

i

'

1

1

β

δ

.

Rozwiązaniem powyższego układu równań są

wyrażenia:

(15)

⎪

⎭

⎪

⎬

⎫

⋅

−

+

=

+

+

⋅

+

−

=

−

−

'

'

'

1

'

1

1

i

i

Wi

Ti

Wi

i

i

i

Wi

i

i

i

Ti

Wi

Wi

tg

t

tg

x

y

y

tg

tg

tg

y

tg

tg

t

tg

y

x

x

β

β

δ

β

δ

δ

β

δ

.

Obliczenia poszczególnych stref prowadzi się tak długo, aż

wartość kąta

β

i

osiągnie założony kąt objęcia źródła światła

przez soczewkę.

Przykładowe wyniki obliczeniowe

Do obliczeń przyjęto następujące dane:

• strumień świetlny użyteczny diody świecącej

Φ

u

= 23,3 lm;

• odległość elementu soczewki od źródła światła t = 10 mm;

• grubość soczewki g = 20 mm;

• kąt objęcia źródła światła przez soczewkę

β

gr

= 60º;

• współczynnik załamania materiału soczewki n = 1,5.

Obliczenia prowadzono z przyrostem kąta

Δϕ

= 2º. Wyniki

obliczeniowe przedstawiono na rysunku 6.

Rys. 6. Kształt soczewki współpracującej z diodą świecącą

Taki układ świetlno-optyczny daje możliwość oświetlenia

powierzchni pracy wzrokowej wzdłuż osi x, od punktu x

F

= 420

mm do x

P

= 688 mm ze stałą wartością natężenia oświetlenia

(rys. 1). W kierunku osi y spadek natężenia oświetlenia będzie
w przybliżeniu przebiegał zgodnie z funkcją kosinus.

Pracę wykonano w Politechnice Białostockiej w ramach zadań
statutowych S/WE/2/06.

LITERATURA

[1] D y b c z y ń s k i W.: Zastosowanie diod elektroluminescencyjnych do

oświetlenia miejscowego. Konferencja Lumen V4. Balatonfüred 28
– 29.9.2006 r.

Autor:

prof. dr hab. inż. Władysław Dybczyński, Politechnika

Białostocka, Wydział Elektryczny, Katedra Promieniowania
Optycznego, ul Wiejska 45D, 15351 Białystok, E-mail:

[e-mail]

PRZEGLĄD ELEKTROTECHNICZNY - KONFERENCJE, ISSN 1731-6106, R. 5 NR 1/2007

16