
Wprowadzenie do fizyki
Mirosław Kozłowski
Mirosław Kozłowski
rok akad. 2002/2003

Część 1a
Dynamika punktu
materialnego w jednym
materialnego w jednym
wymiarze
Dynamika punktu
materialnego w R
1
cz. a
Slajd podsumowania
1.1 Prędkość i przyśpieszenie w R1
1.2 Pochodna funkcji f(t)
1.3 Obliczanie pochodnych funkcji f(t)
Koniec
pokazu
Ruchy w R1
3
1.3 Obliczanie pochodnych funkcji f(t)
1.4 Antypochodna = całka nieoznaczona
1.5 Pochodna funkcji złożonej
1.6 Zasada zachowania energii
1.7 Zasada zachowania pędu

Linki do stron WWW
Hyper Physics
4
Astronomy Picture of the Day
Space Photos and Images

Czas
Chronos
– czas obiektywny,
niezależny od nas, znany ze swej
równomierności. Czas mierzony
przez zegarki, czas eksperymentu
Ruchy w R1
5
przez zegarki, czas eksperymentu
fizycznego.
Od 13 października 1967 roku, jego wzorzec,
sekunda jest zdefiniowana następująco:
Jedna sekunda to trwanie
9 192 631 770 okresów fali
elektromagnetycznej emitowanej lub
absorbowanej przez atom cezu o
Ruchy w R1
6
Tempus
– czas odczuwany subiektywnie,
czas psychologiczny, ten, którego pomiar
odbywa się w naszym mózgu.
absorbowanej przez atom cezu o
liczbie masowej 133.

1 attosekunda
Ultrakrótkie impulsy laserowe – kilka attosekund
1 femtosekunda (procesy biologiczne, chemia)
Czas oddziaływania światła z siatkówką oka
człowieka ~200 fs.
1 pikosekunda
Najszybsze tranzystory pracują w zakresie
Ruchy w R1
7
Najszybsze tranzystory pracują w zakresie
pikosekund.
1 nanosekunda
Mikroprocesor wewnątrz współczesnego
komputera w ciągu kilku nanosekund wykonuje
podstawowe operacje np. dodawania dwóch liczb.

1 sekunda
Czas trwania jednego uderzenia serca człowieka,
oraz 1 sekunda = czas trwania 9 192 631 770
okresów promieniowania elektromagnetycznego
emitowanego przez atom cezu.
1 minuta
Ś
wiatło przebiega odległość Słońce – Ziemia
Ruchy w R1
8
Ś
wiatło przebiega odległość Słońce – Ziemia
w ciągu 8. minut.
1 godzina
Ś
wiatło z Plutona (ostatniej planety w naszym
układzie słonecznym) dociera do Ziemi w ciągu
5 godzin 20 minut.

1 dzień
1 obrót Ziemi trwa: 23 h 56’ 41”.
Ziemia zwalnia ze względu na grawitacyjne
oddziaływanie Księżyca.
1 rok
Ruchy w R1
9
Ziemia wykonuje 1 okres obiegu wokół Słońca
i obraca się wokół osi 365,25 razy.
~10
10
lat
Wiek naszego Wszechświata

1.1 Prędkość i przyśpieszenie w R
1
( ) ( )
,
3
2
pt
ht
bt
d
t
f
t
s
+
+
+
=
=
Rozważmy funkcję
Ruchy w R1
10
( ) ( )
,
pt
ht
bt
d
t
f
t
s
+
+
+
=
=
gdzie t jest czasem mierzonym przez
zegarki. Jest to czas eksperymentu
fizycznego (chronos).
Jak zmieni się funkcja f(t) po upływie
czasu
∆
t?
(
) (
)
(
) (
)
(
)
.
3
2
t
t
p
t
t
h
t
t
b
d
t
t
f
t
t
s
∆
+
+
∆
+
+
∆
+
+
=
=
∆
+
=
∆
+
(
) ( )
t
t
s
t
t
s
t
s
=
∆
−
∆
+
=
∆
∆
A zatem:
Ruchy w R1
11
(
)
( )
(
)
( ) ( )
(
)
.
3
3
2
3
3
2
2
3
2
2
2
t
t
t
t
t
t
t
t
p
t
t
t
t
t
t
h
t
t
t
t
b
d
d
t
t
∆
−
∆
+
∆
+
∆
+
+
+
∆
−
∆
+
∆
+
+
∆
−
∆
+
+
−
=
=
∆
=
∆
(
) ( )
(
)
t
t
s
t
t
s
v
ś
r
=
∆
−
∆
+
=
Definiujemy nowe pojęcie –
prędkość średnia v
ś
r
:
Ruchy w R1
12
(
)
( )
(
)
.
3
3
2
2
2
t
t
t
t
p
t
t
h
b
t
∆
+
∆
+
+
+
∆
+
+
=
∆

Gdy
∆
t
→
0
(
) ( )
.
t
t
s
t
t
s
v
ś
r
∆
−
∆
+
=
.
3
2
2
p
t
th
b
v
ś
r
+
+
=
Ruchy w R1
13
.
3
2
2
p
t
th
b
v
+
+
=
W granicy
∆
t
→
0, v
ś
r
→
v, gdzie v
oznacza prędkość.
ś
r
(
) ( )
(
)
(
)
3
2
3
2
2
2
p
t
ht
b
t
t
p
h
t
t
b
t
t
v
t
t
v
a
ś
r
=
+
+
−
∆
+
+
∆
+
+
=
=
∆
−
∆
+
=
=
Definiujemy nowe pojęcie –
przyśpieszenie średnie a
ś
r
:
Ruchy w R1
14
(
)
(
)
(
)
( )
(
)
,
2
3
2
3
2
3
2
2
2
2
t
t
t
t
t
t
p
t
t
t
h
b
b
t
p
t
ht
b
t
t
t
p
h
t
t
b
∆
−
∆
+
∆
+
+
−
∆
+
+
−
=
=
∆
+
+
−
∆
∆
+
+
∆
+
+
=
(
)
.
2
3
2
t
t
p
h
a
ś
r
∆
+
+
=
W granicy
gdzie a z definicji jest przyśpieszeniem:
,
,
0
a
a
t
ś
r
→
→
∆
Ruchy w R1
15
.
6
2
pt
h
a
+
=
a. Ruch ze stałym przyśpieszeniem
,
6
2
pt
h
g
a
+
=
=
Rozważmy ruchy odbywające się ze
stałym przyśpieszeniem a = stałe
≡
g,
a więc p musi równać się zero, p = 0, stąd
Ruchy w R1
16
.
,
2
,
2
gt
b
v
ht
b
v
h
g
a
+
=
+
=
=
=
a więc p musi równać się zero, p = 0, stąd
(
)
,
0
0
v
b
t
v
=
=
=
+
=
gt
v
v
,
0
Wybieramy chwilę początkową ruchu t = 0,
Stąd:
Ruchy w R1
17
stałe.
=
+
+
=
+
=
g
gt
t
v
d
s
gt
v
v
,
2
,
2
0
0
(
)
.
0
0
d
s
t
s
=
=
=
g
=
stałe,
W chwili t = 0
Ruchy w R1
18
.
2
,
2
0
0
0
gt
t
v
s
s
gt
v
v
+
+
=
+
=
(1)

Zastosowanie wzoru (1)
1. Spadek w polu grawitacyjnym:
Ziemi
g
Z
=9.81 m s
-2
,
Marsa
g
M
=3.7 m s
-2
.
Ruchy w R1
19
2. Ruch w stałym polu elektrycznym o natężeniu E:
g
El
=qE/m,
q = ładunek ciała,
m = masa ciała.

h
tt
p
:/
/p
d
s.
jp
l.
n
as
a.
g
o
v
/p
la
n
et
s/
h
tt
p
:/
/p
d
s.
jp
l.
n
as
a.
g
o
v
/p
la
n
et
s/
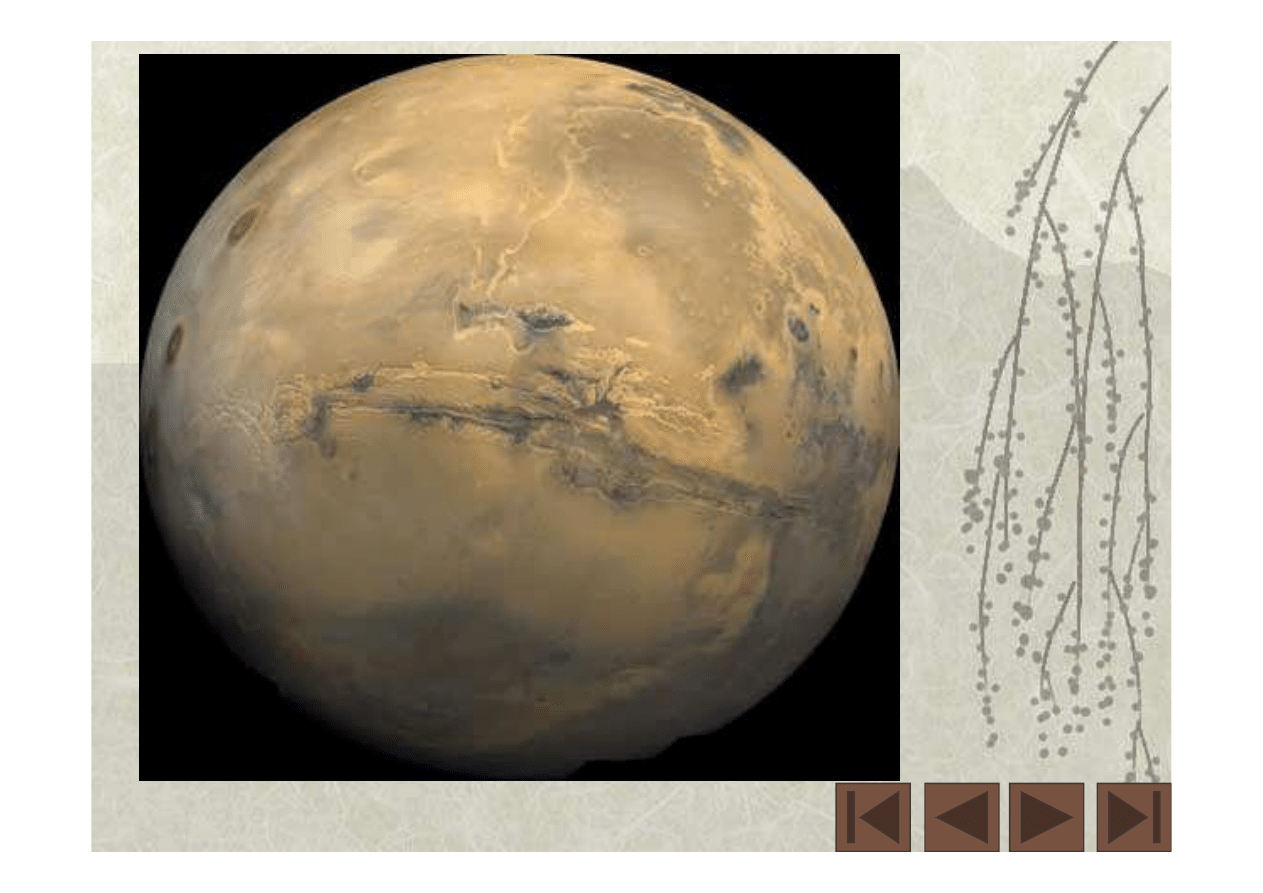
Panorama Marsa. W prawym dolnym rogu widoczna jest część
lądownika (Mars Lander 2).

21
Czy podkarpackie pole nie jest podobne do powierzchni Marsa?
fot. M. Kozłowski

22
Albo bałtycka plaża?
Fot. R. Gauer, Wyd. Kamera
h
tt
p
:/
/p
d
s.
jp
l.
n
as
a.
g
o
v
/p
la
n
et
s/
ci
M
ar
sa
w
id
o
cz
n
a
je
st
„r
an
a”
o
ci
o
k
o
ło
5
0
0
0
k
m
i
g
łę
b
o
k
o
śc
i
7
k
m
.
23
h
tt
p
:/
/p
d
s.
jp
l.
n
as
a.
g
o
v
/p
la
n
et
s/
W
c
en
tr
al
n
ej
c
z
ę
śc
i
M
ar
sa
w
id
o
cz
n
a
je
st
„r
an
a”
o
ca
łk
o
w
it
ej
d
łu
g
o
śc
i
o
k
o
ło
5
0
0
0
k
m
i
g
ł
1.2 Pochodna funkcji f(t)
( )
( )
(
)
( )
,
,
t
t
f
t
t
f
t
s
t
t
f
t
f
s
∆
−
∆
+
=
∆
∆
=
∆
∆
=
Ruchy w R1
24
t
t
t
∆
∆
∆
( )
( )
( )
.
t
f
dt
t
df
dt
t
ds
funkcji
pochodna
≡
=
W granicy
0
→
∆
t
( )
( )
( )
( )
.
.
dt
t
s
d
t
v
dt
t
ds
t
v
r
r
=
=
Ogólnie
s(t) = trajektoria ruchu ciała o masie m.
Definicja prędkości:
Ruchy w R1
25
dt
( )
( )
.
dt
t
v
d
t
a
r
r
=
(2)
Definicja przyśpieszenia:

1.3 Obliczanie pochodnych
funkcji f(t)
,
gt
v
v
+
=
Wykazaliśmy już, że:
Ruchy w R1
26
.
,
g
a
gt
v
v
o
=
+
=
(3)

(
) ( )
(
) (
)
lim
lim
0
0
0
0
t
gt
v
t
t
g
v
t
t
v
t
t
v
dt
dv
a
t
t
=
∆
+
−
∆
+
+
=
=
∆
−
∆
+
=
=
→
∆
→
∆
Teraz, znając definicję pochodnej
sprawdzimy wzór (3).
Ruchy w R1
27
Wszystko w porządku!
.
lim
0
0
g
t
t
g
t
t
t
=
∆
∆
=
∆
→
∆
→
∆
Niech teraz f(t) ma następującą postać:
( )
( )
(
)
.
sin
sin
cos
cos
sin
lim
sin
sin
lim
,
sin
0
0
t
t
t
t
t
t
t
t
t
t
dt
t
df
t
t
f
t
t
∆
−
∆
+
∆
=
=
∆
−
∆
+
=
=
→
∆
→
∆
Ruchy w R1
28
.
lim
0
t
t
∆
=
→
∆
(
)
.
cos
sin
,
cos
sin
cos
sin
lim
sin
0
t
dt
t
d
t
t
t
t
t
t
dt
t
d
t
=
=
∆
−
∆
+
=
→
∆
więc
a

( )
( )
,
t
g
dt
t
df
=
g (t)
≡
pochodna funkcji f(t)
1.4 Antypochodna = całka
nieoznaczona
Ruchy w R1
29
( )
( )
∫
=
dt
t
g
t
F
g (t)
≡
pochodna funkcji f(t)
względem zmiennej niezależnej t
≡
całka
nieoznaczona
funkcji g(t).
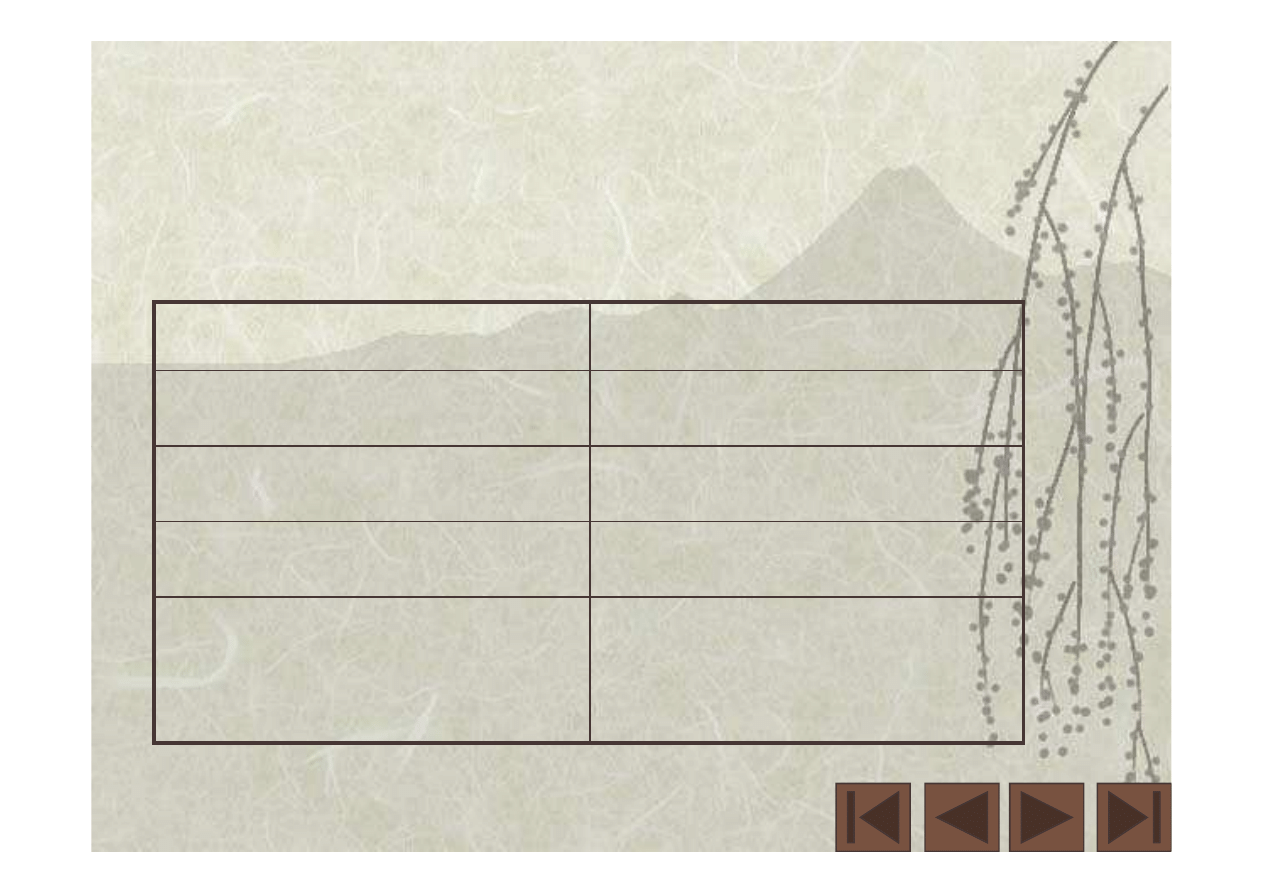
cos t
sin t
Pochodna
Funkcja
Tabela 1
Pożyteczne wzory
(do sprawdzenia)
Ruchy w R1
30
0
Stała, niezależna od t
f(t) = b
n t
n-1
t
n
-sin t
cos t
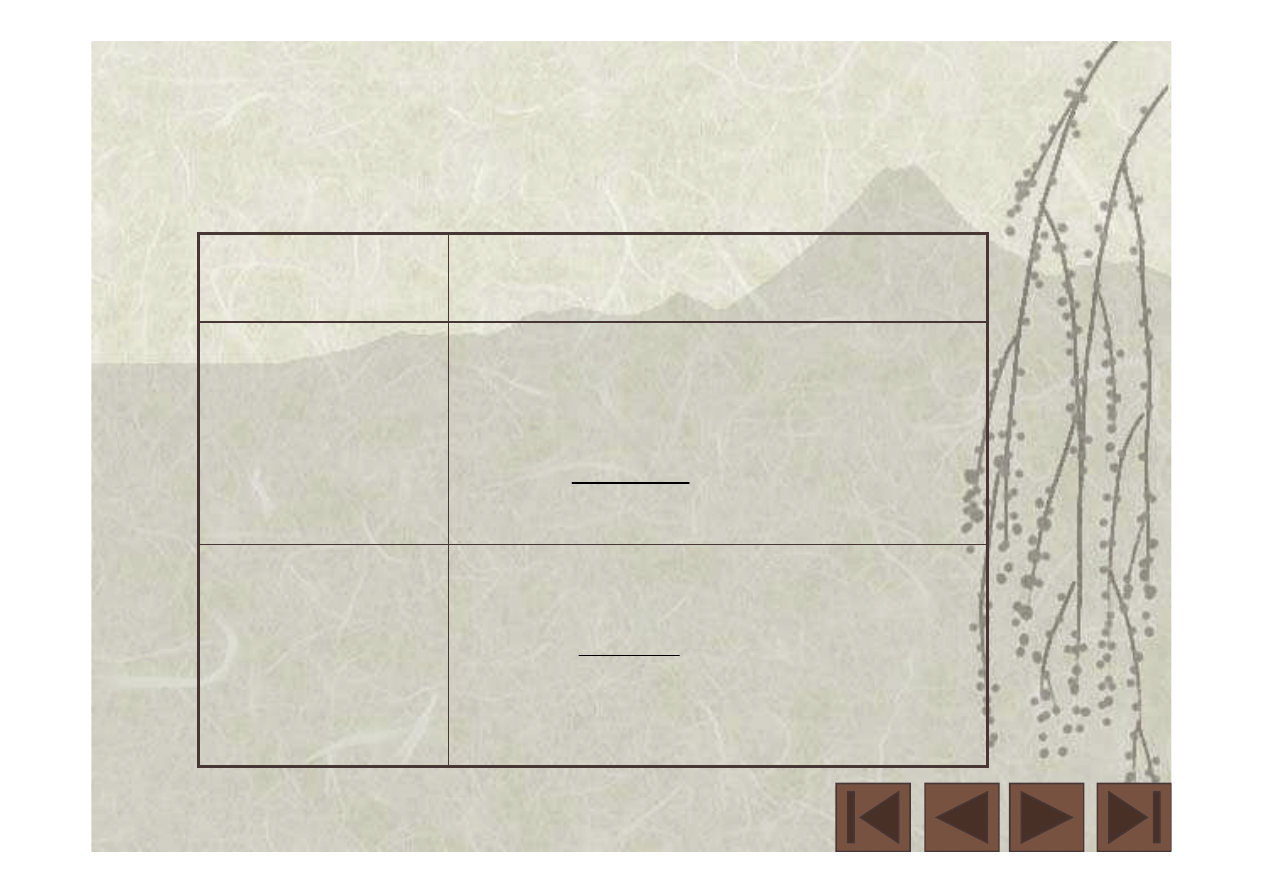
Tabela 2
Całki
a = stała
Całka f (t)
Funkcja g(t)
( )
t
df
at
adt
t
f
=
=
∫
)
(
Ruchy w R1
31
sin t
a = stała
g
a
dt
t
df
=
=
)
(
bo
( )
(
)
( )
t
g
t
t
dt
t
d
t
t
t
f
=
=
=
−
−
=
−
−
=
=
∫
sin
sin
cos
cos
sin
bo

1.5 Pochodna funkcji złożonej
( )
( )
( )
[
]
( )
,
sin
sin
2
t
g
t
t
f
=
=
Niech f(t) ma postać:
Ruchy w R1
32
( )
.
2
t
t
g
=
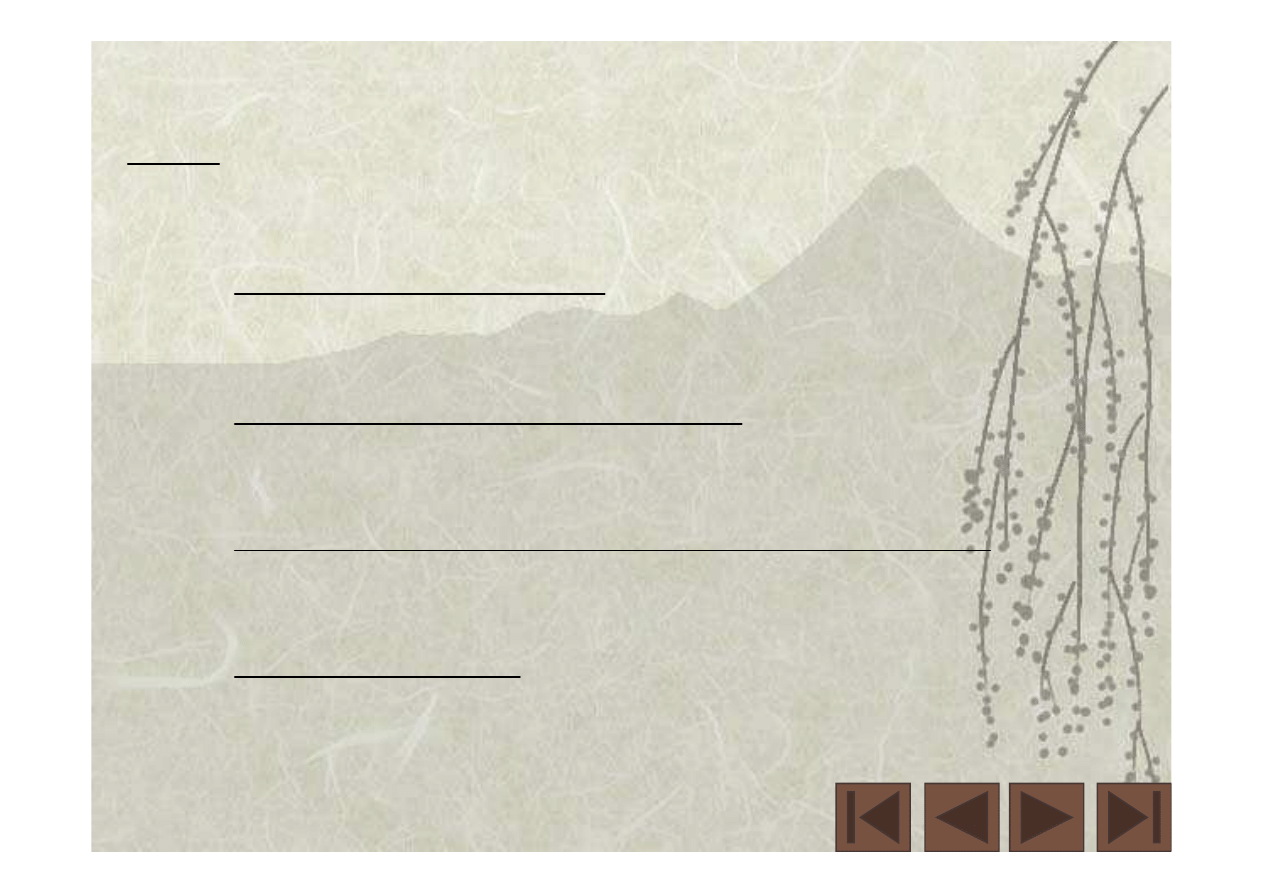
( )
(
)
[
]
( )
( )
[
]
( )
sin
2
sin
lim
sin
sin
lim
2
2
2
0
2
2
0
t
t
t
t
t
t
t
t
t
t
dt
t
df
t
t
=
∆
−
∆
+
∆
+
=
=
∆
−
∆
+
=
=
→
∆
→
∆
Ruchy w R1
33
( )
(
)
( )
(
)
( )
( )
(
)
( )
.
cos
2
2
sin
cos
lim
sin
2
sin
cos
2
cos
sin
lim
2
2
0
2
2
2
0
0
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
t
=
∆
∆
=
=
∆
−
∆
+
∆
=
∆
→
∆
→
∆
→
∆
( )
( )
[
]
( )
( )
( )
[
]
( )
.
2
cos
,
sin
sin
2
2
t
t
dt
t
g
df
dt
t
df
t
t
g
t
f
⋅
=
=
=
=
Ważny wzór (do zapamiętania!)
Ruchy w R1
34
Ważny wzór (do zapamiętania!)
( )
[ ]
( )
.
dt
t
dg
dg
df
dt
t
g
df
=
(4)
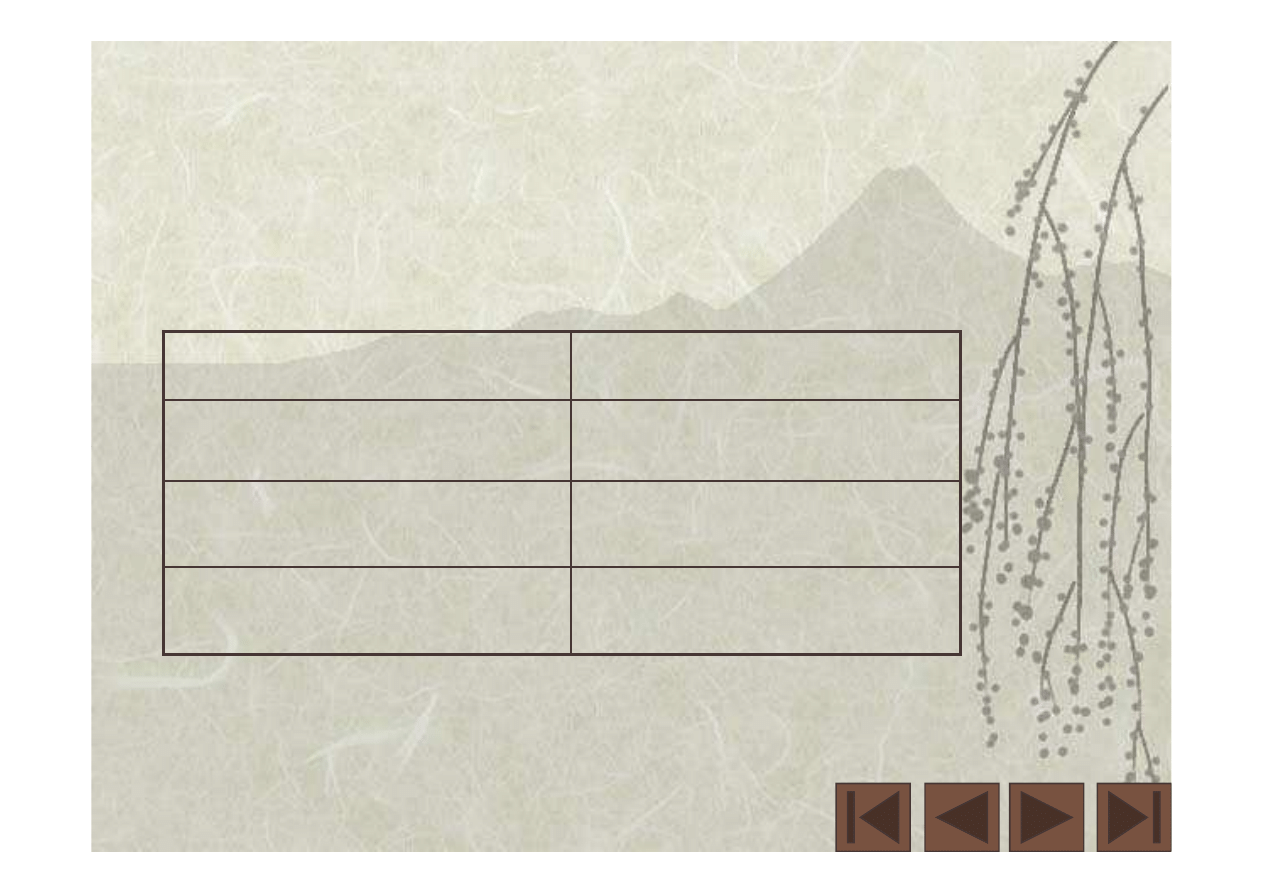
Tabela 3
Sprawdzamy nasze umiejętności
2t cos(t
2
)
sin (t
2
)
pochodna
funkcja
Ruchy w R1
35
a cos at
sin at
-2t sin(t
2
)
cos(t
2
)
2t cos(t
2
)
sin (t
2
)
1.6 Zasada zachowania energii
Fizycy szukają ważnych zasad, których
przestrzeganie ułatwia zrozumienie otaczającego
ś
wiata.
Dla przypomnienia:
( )
( )
x
df
Ruchy w R1
36
( )
( )
( )
( )
∫
=
=
.
,
dx
x
g
x
f
x
g
dx
x
df
Funkcja pierwotna

Druga zasada dynamiki (R
1
)
( )
( )
,
x
ma
x
F
=
( )
( )
dt
dx
dx
dv
dt
x
dv
x
a
=
=
=
Korzystamy ze wzoru (4).
Ruchy w R1
37
( )
( )
,
2
1
2
dx
x
dv
dx
dv
v
dt
dx
dt
x
a
=
=
=
=
=
( )
( )
,
2
2
dx
x
dv
v
dx
x
dv
=
( )
( )
[ ]
,
2
1
2
x
v
dx
d
m
x
F
=
m = stałe,
( )
( )
.
2
dx
x
mv
d
dx
x
F
=
Ruchy w R1
38
( )
( )
.
2
dx
x
mv
dx
d
dx
x
F
=
Praca elementarna na
drodze dx
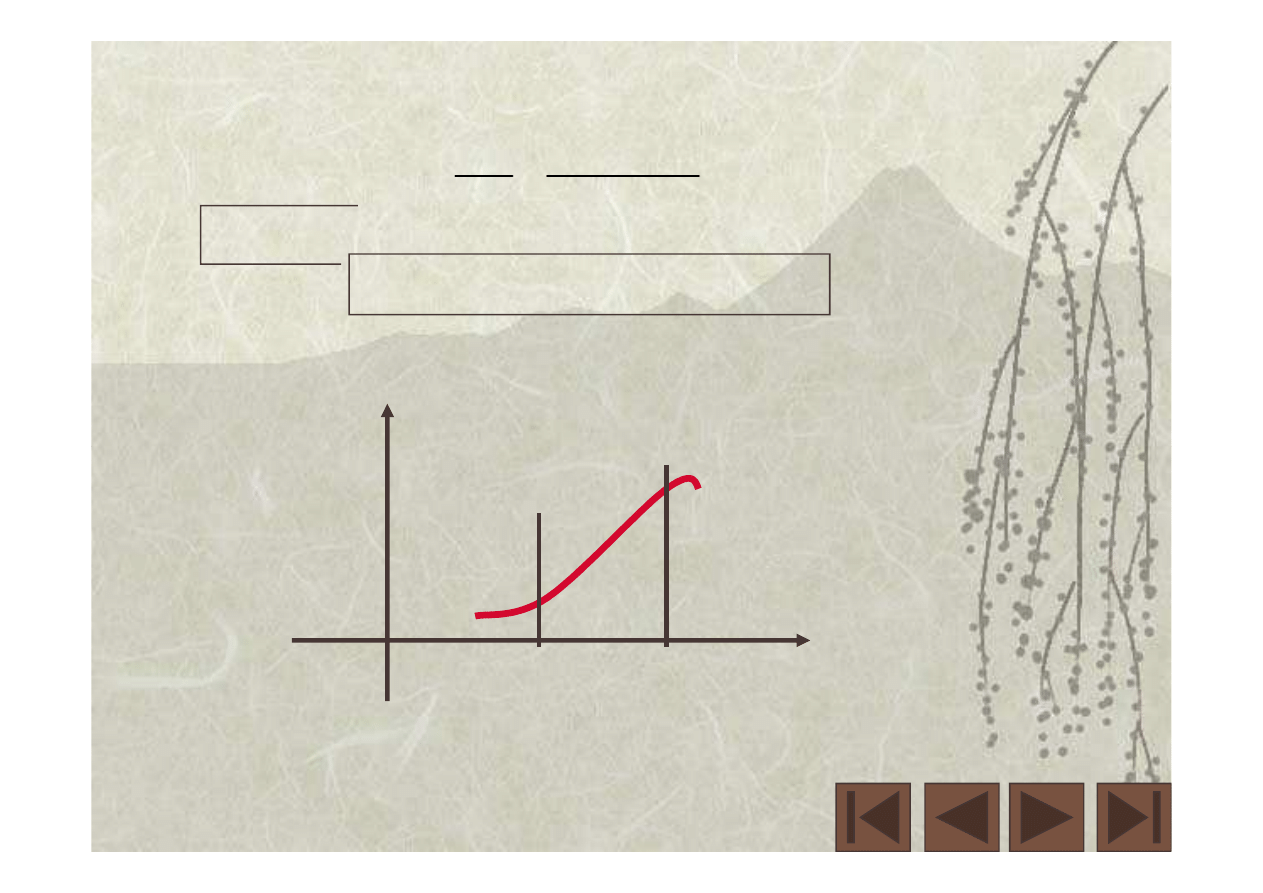
( )
( )
.
2
2
dx
x
mv
dx
d
dx
x
F
∫
∫
=
Suma prac elementarnych
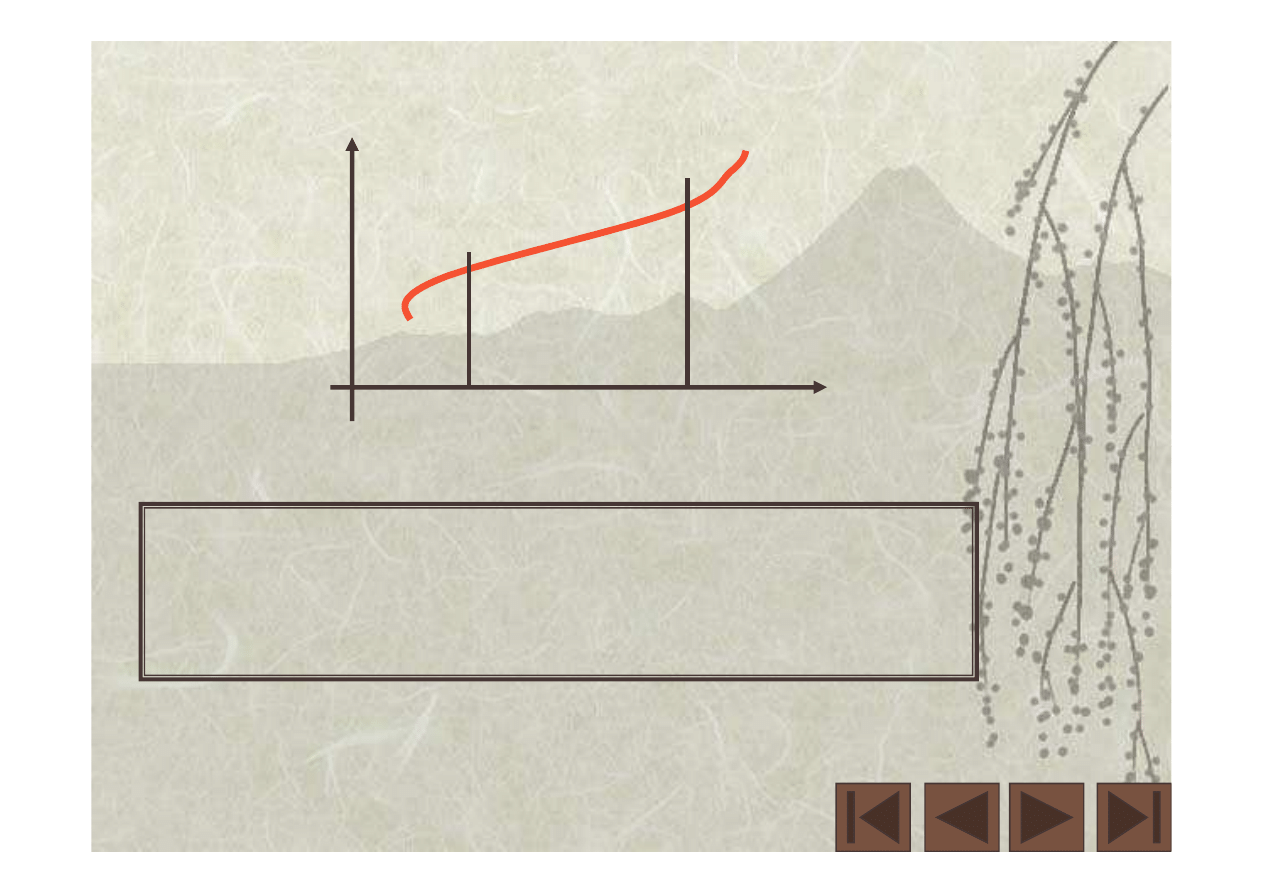
F(x)
Ruchy w R1
39
a
b
x
F(x)
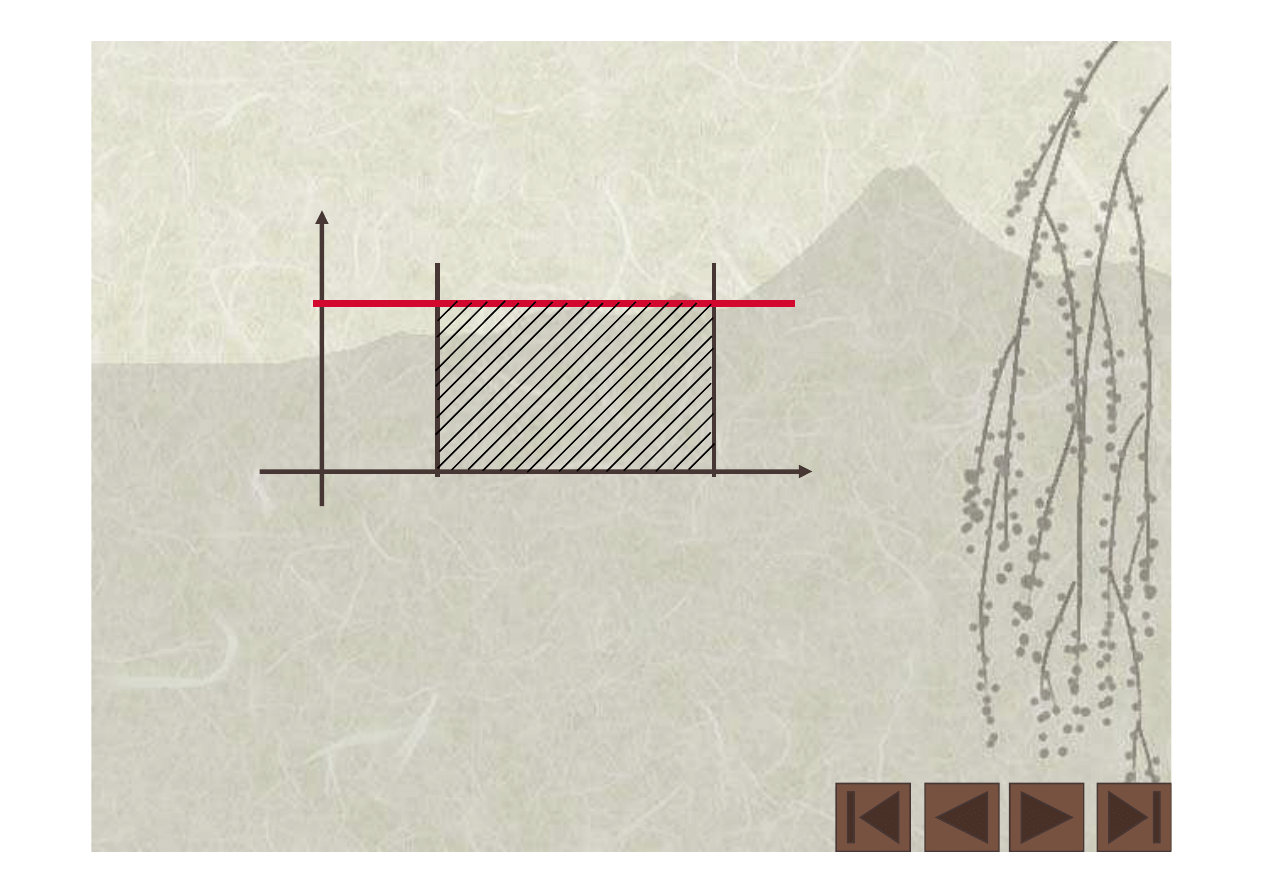
Obliczamy sumę (całkę) prac elementarnych.
Niech F(x) = c = stała.
F(x)
c
c
c
Ruchy w R1
40
[ ]
(
)
.
b-a
c
a
b
c
x
c
cdx
b
a
b
a
i
bokach
o
ta
ą
prostok
pole
=
=
−
=
=
∫
x
a
b
b-a
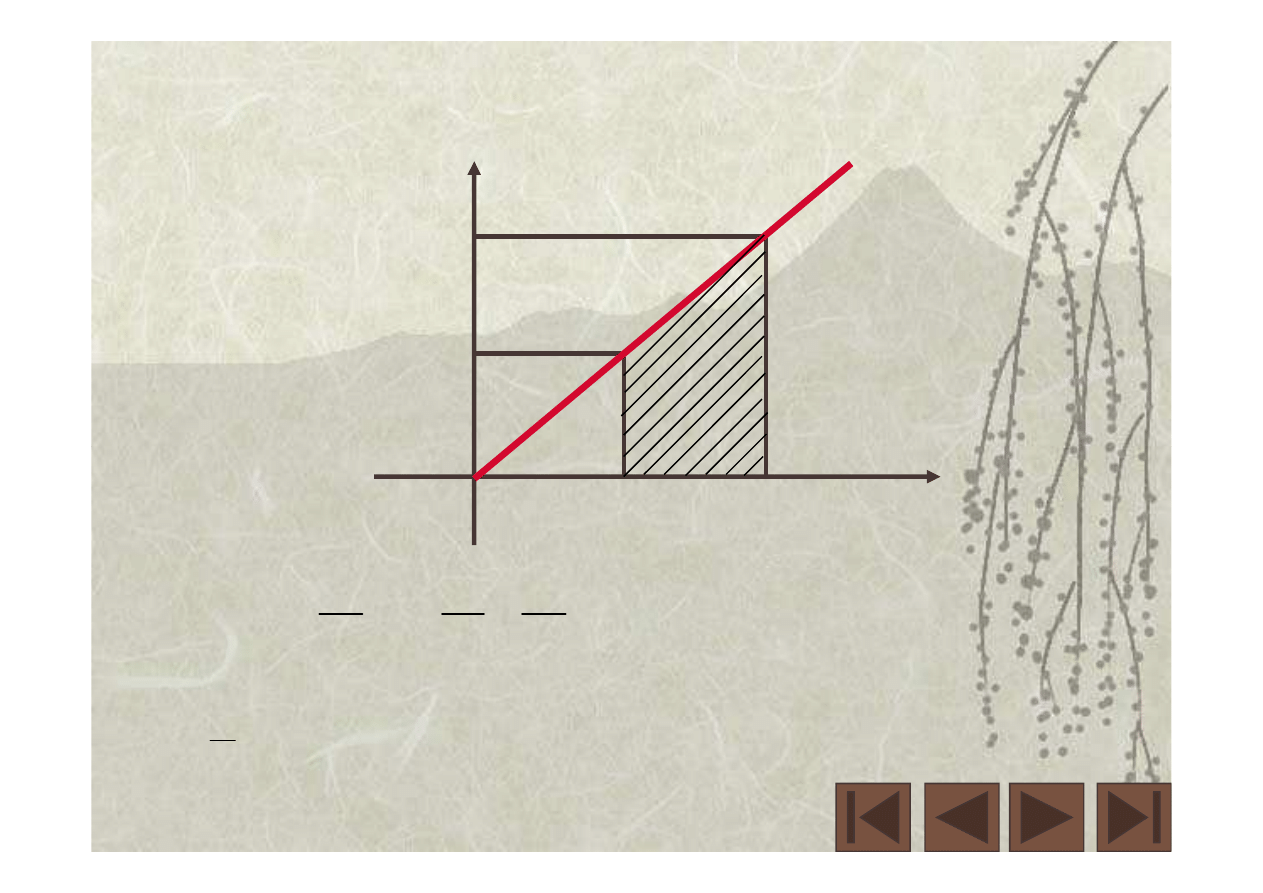
A teraz niech F(x) = x.
F(x)
a
b
F(b)=b
F(a)=a
Ruchy w R1
41
(
)(
)
trapezu.
pole
=
+
−
=
=
−
=
=
∫
a
b
a
b
a
b
x
xdx
b
a
b
a
2
1
2
2
2
2
2
2
x
a
b
a
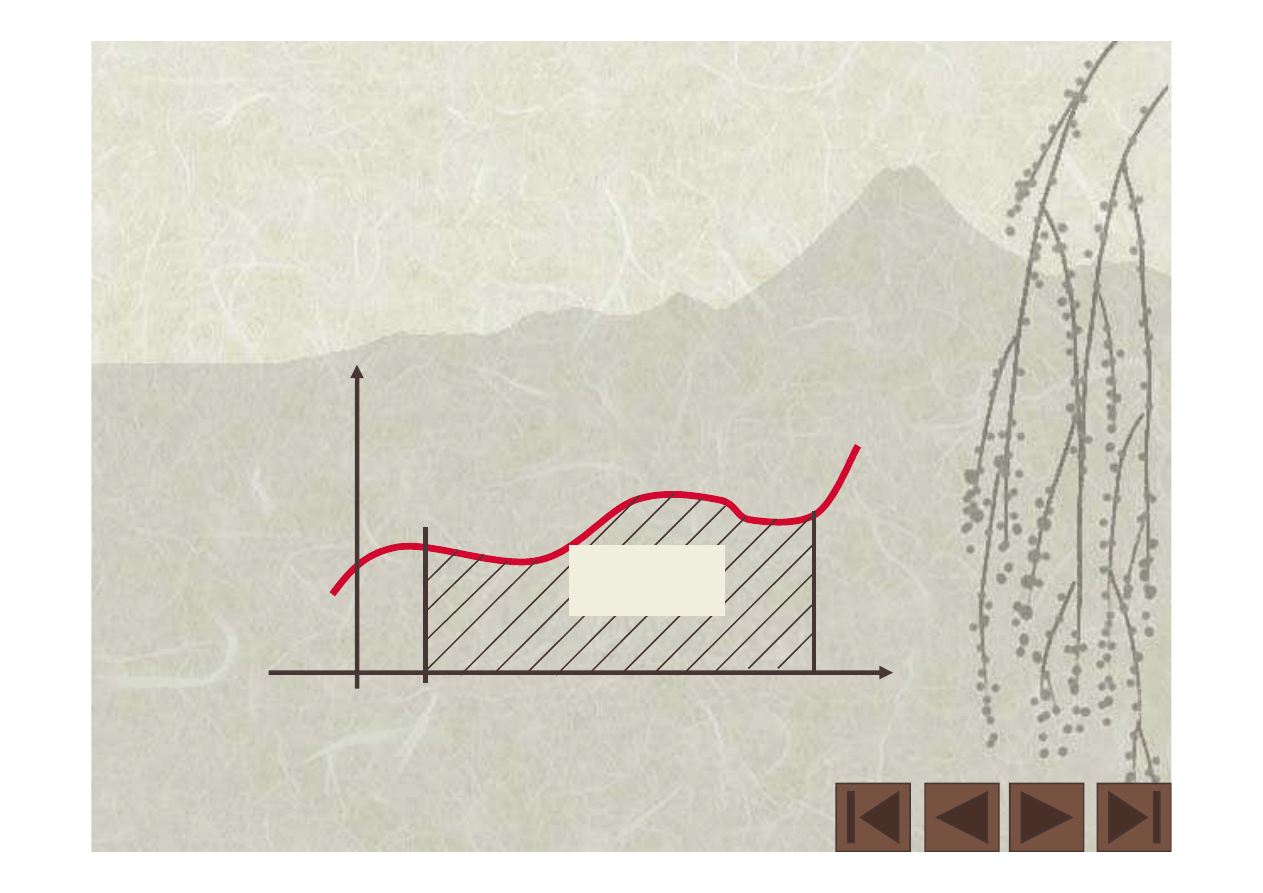
Wniosek
( )
( )
[
]
( )
.
x
F
x
G
dx
x
F
b
a
b
a
krzywą”
„pod
pole
=
=
∫
F(x)
F(x)
Ruchy w R1
42
a
b
F(x)
x
( )
[
]
b
a
x
G
A więc
( )
( )
,
2
2
∫
∫
=
b
a
b
a
dx
x
mv
dx
d
dx
x
F
( )
( )
( )
.
2
2
a
mv
b
mv
dx
x
F
b
−
=
∫
Ruchy w R1
43
( )
( )
( )
.
2
2
a
mv
b
mv
dx
x
F
a
−
=
∫
Jest to prawo zachowania energii w R
1
.
Siły potencjalne
Przypuśćmy, że istnieje taka funkcja
V(x), że spełniony jest wzór:
( )
x
dV
Ruchy w R1
44
( )
( )
.
dx
x
dV
x
F
−
=
Mamy więc:
( )
( )
( )
( )
( )
[
]
( )
( )
,
,
a
T
b
T
a
V
b
V
a
T
b
T
dx
dx
x
dV
b
a
kin
kin
kin
kin
−
=
−
−
−
=
−
∫
Ruchy w R1
45
czyli
( )
( )
( )
( )
.
a
V
a
T
b
V
b
T
+
=
+
kin
kin
F(x)
a
b
x
Ruchy w R1
46
Praca siły potencjalnej na odcinku
drogi (a, b) równa si
ę
zmianie
energii kinetycznej na tym odcinku
.
a
b

( )
( )
,
E
x
T
x
V
=
+
kin
Ruchy w R1
47
gdzie E = suma energii potencjalnej
i kinetycznej jest stała.

1.7 Zasada zachowania pędu
(
)
stała.
dynamiki
Zasada
III
=
+
=
+
=
+
21
12
2
2
1
1
,
0
v
m
v
m
F
F
v
m
v
m
dt
d
r
r
4
3
42
1
r
r
r
r
Ruchy w R1
48
stała.
=
+
2
2
1
1
v
m
v
m
r
r
A więc:
Suma pędów jest wielkością stałą (niezależną
od czasu), gdy działają tylko siły wewnętrzne.
To jest ostatni slajd pierwszej części rozdziału „Ruch
punktu materialnego w przestrzeni jednowymiarowej”.
Możesz:
•przejść do „Spisu treści” i wybrać kolejny rozdział,
•wrócić do materiału tego rozdziału,
•zakończyć pokaz.
Spis treści
49
Spis treści
Koniec
pokazu
Wyszukiwarka
Podobne podstrony:
Dynamika punktu materialnego w jednym wymiarze 1A
DYNAMIKA PUNKTU MATERIALNEGO W JEDNYM WYMIARZE
zestaw 5 dynamika punktu materi Nieznany
05 dynamika punktu materialnego II
04 Dynamika punktu materialnego I
8 Dynamika 1 Dynamika punktu materialnego
04 dynamika punktu materialnego
4 Dynamika punktu materialnego, Fizjoterapia i Rehabilitacja, AWF MGR Fizjoterapia, Biomechanika AWF
8 Dynamika 1, Dynamika punktu materialnego
Dynamika punktu materialnego
3 Dynamika punktu materialnego Nieznany (2)
04 Dynamika punktu materialneg Nieznany (2)
Dynamika punktu materialnego
Mechatronika, Dynamika punktu materialnego w ujęciu Eulera, Euler udowodnił tożsamości Newtona (wzor
kinematyka i dynamika punktu materialnego, Studia 1, I rok, mechanika
więcej podobnych podstron