1

1

Optyka

2

Fotoreceptory na siatkówce oka: pr

ę

ciki i czopki.

Pr

ę

ciki

rejestruj

ą

zmiany

jasno

ś

ci,

a

dzi

ę

ki

czopkom mo

ż

emy rozró

ż

ni

ć

kolory.

W oku znajduj

ą

si

ę

trzy rodzaje czopków, które s

ą

wra

ż

liwe na trzy podstawowe barwy widmowe:

czerwon

ą

,

zielon

ą

i

niebiesk

ą

.

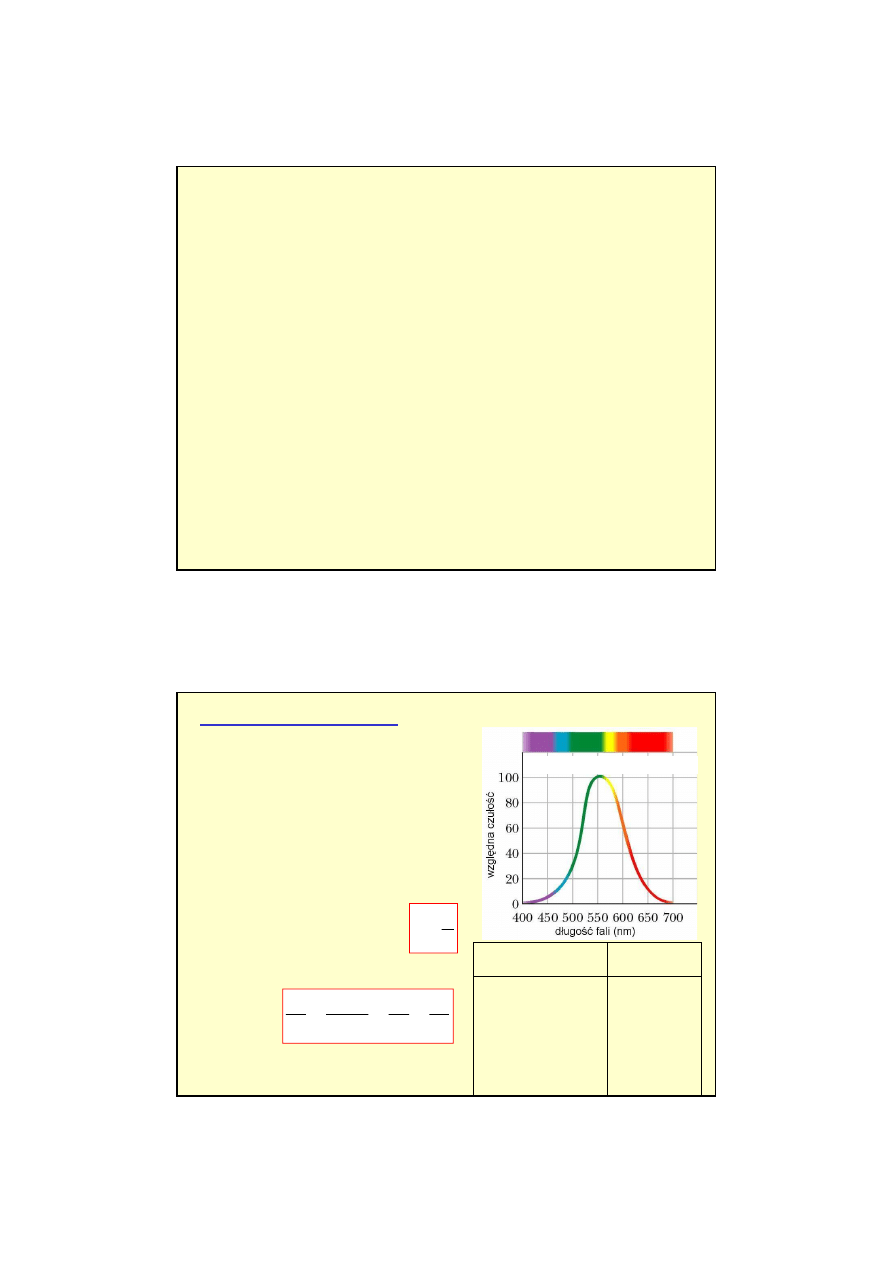
Barwa

ś

wiatła a długo

ść

fali

Względna czułość oka ludzkiego

Ośrodek

Współczynnik

załamania

powietrze

woda

alkohol etylowy

kwarc, topiony

szkło zwykłe

polietylen

szafir

diament

1.003

1.33
1.36
1.46
1.52
1.52
1.77

2.42

Ś

wiatło rozchodzi si

ę

w pró

ż

ni z pr

ę

dko

ś

ci

ą

c.

W o

ś

rodkach materialnych pr

ę

dko

ść

ś

wiatła jest

mniejsza (v) .

Ś

wiatło to fala elektromagnetyczna.

v

c

n

=

Bezwzgl

ę

dny współczynnik

załamania :

2

1

1

2

1

2

1

2

v

v

/

v

/

v

n

n

=

=

=

ν

ν

λ

λ

Stosunek długo

ś

ci fali w dwóch o

ś

rodkach:

Cz

ę

stotliwo

ść

fali

ν

nie zmienia si

ę

na granicy

dwóch o

ś

rodków.

2

3

Je

ż

eli

ś

wiatło pada na granic

ę

dwóch o

ś

rodków to ulega zarówno odbiciu na

powierzchni granicznej jak i załamaniu przy przej

ś

ciu do drugiego o

ś

rodka.

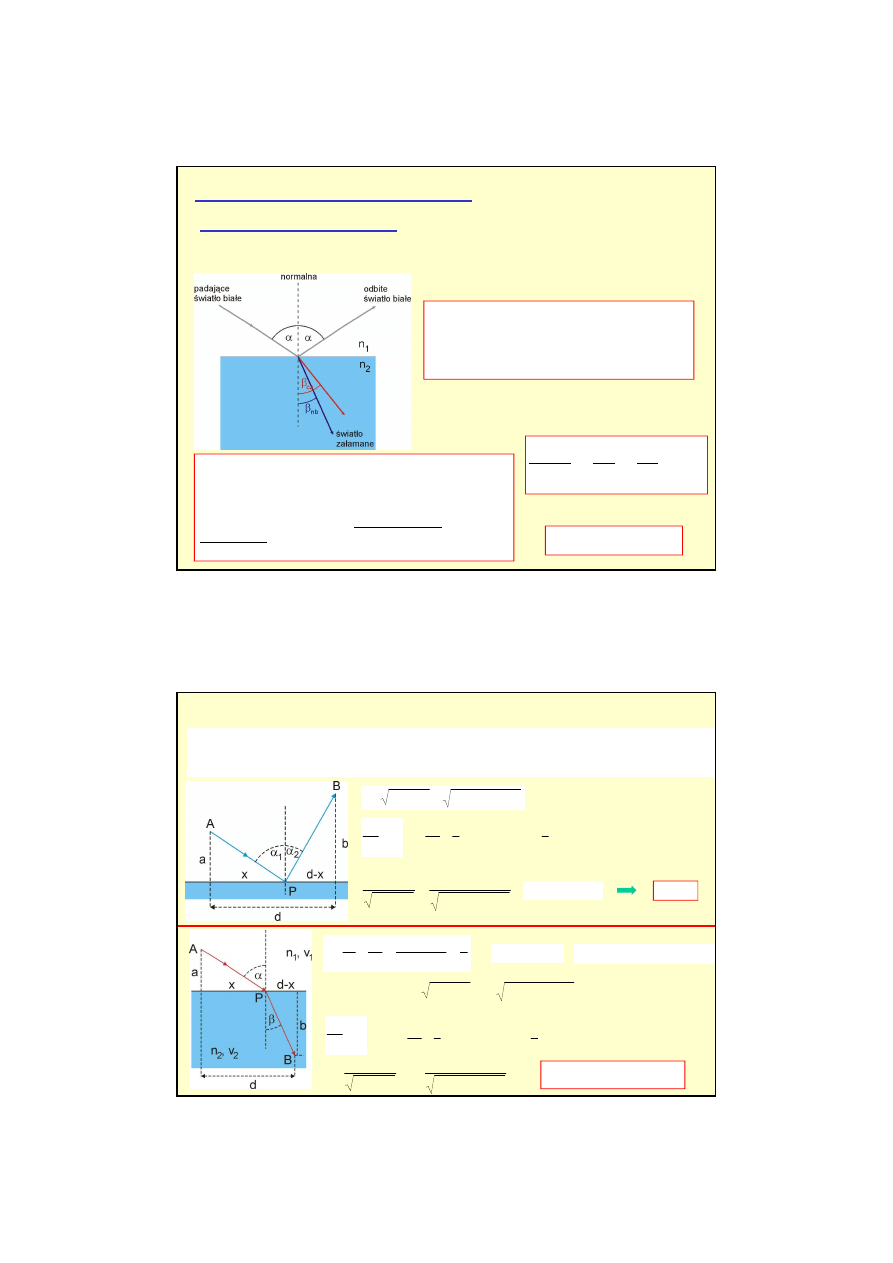
Odbicie i załamanie

ś

wiatła

Prawo odbicia: Promie

ń

padaj

ą

cy, promie

ń

odbity i normalna do powierzchni granicznej
wystawiona w punkcie padania promienia le

żą

w

jednej płaszczy

ź

nie i k

ą

t padania równa si

ę

k

ą

towi odbicia

α

1

=

α

2

.

1

2

1

2

2

1

v

v

sin

sin

,

n

n

n

β

α

=

=

=

Prawo załamania (prawo Snelliusa): Stosunek sinusa kata
padania do sinusa k

ą

ta załamania jest równy stosunkowi

bezwzgl

ę

dnego współczynnika załamania o

ś

rodka

drugiego n

2

do bezwzgl

ę

dnego współczynnika załamania

o

ś

rodka pierwszego n

1

, czyli współczynnikowi

wzgl

ę

dnemu załamania

ś

wiatła o

ś

rodka drugiego

wzgl

ę

dem pierwszego.

.

sin

1

1

const

α

n

=

OPTYKA GEOMETRYCZNA

4

Zasada Fermata:

Ś

wiatło biegn

ą

cy z jednego punktu do drugiego przebywa drog

ę

, na której

przebycie trzeba zu

ż

y

ć

w porównaniu z innymi, s

ą

siednimi drogami, minimum albo maksimum

czasu.

0

d

d

=

x

l

0

)

1

)(

(

2

]

)

(

[

2

1

2

)

(

2

1

d

d

2

/

1

2

2

2

/

1

2

2

=

−

−

−

+

+

+

=

−

−

x

d

x

d

b

x

x

a

x

l

2

2

2

2

)

(

x

d

b

x

d

x

a

x

−

+

−

=

+

2

1

α

α

sin

sin

=

2

1

α

α

=

2

2

2

2

)

(

x

d

b

x

a

l

−

+

+

+

=

długo

ść

drogi promienia

wyprowadzenia:

długość drogi optycznej

c

l

c

l

n

l

n

l

l

t

=

+

=

+

=

2

2

1

1

2

2

1

1

v

v

2

2

1

1

l

n

l

n

l

+

=

2

2

2

2

2

1

2

2

1

1

)

(

x

d

b

n

x

a

n

l

n

l

n

l

−

+

+

+

=

+

=

0

d

d

=

x

l

0

)

1

)(

(

2

]

)

(

[

2

1

2

)

(

2

1

d

d

2

/

1

2

2

2

2

/

1

2

2

1

=

−

−

−

+

+

+

=

−

−

x

d

x

d

b

n

x

x

a

n

x

l

2

2

2

2

2

1

)

(

x

d

b

x

d

n

x

a

x

n

−

+

−

=

+

β

α

sin

sin

2

1

n

n

=

3

5

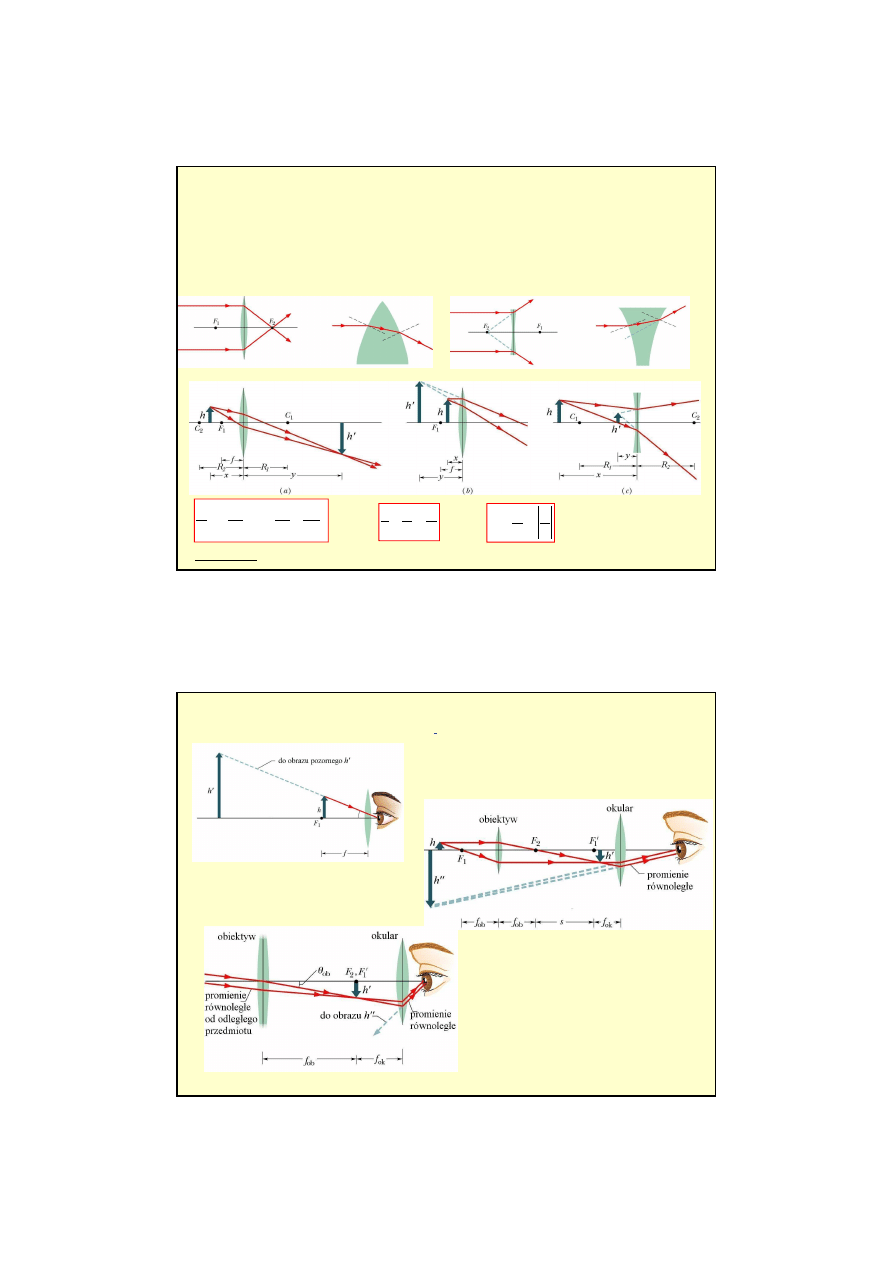
Soczewki i zwierciadła

Prawa odbicia i załamania stosuj

ą

si

ę

równie

ż

do kulistych powierzchni odbijaj

ą

cych (zwierciadeł

kulistych) i kulistych powierzchni załamuj

ą

cych (soczewek).

Soczewkami nazywamy ciała prze

ź

roczyste ograniczone dwoma powierzchniami o promieniach

krzywizn R

1

i R

2

. Soczewki maj

ą

współczynnik załamania n ró

ż

ny od współczynnika załamania

otoczenia n

0

soczewka skupiająca

soczewka rozpraszająca

Zastosowania:













+













−

=

2

1

1

1

1

1

R

R

n

n

f

o

f

y

x

1

1

1

=

+

x

y

h

h

P

=

=

'

- powi

ę

kszenie

ogniskowa : f > 0

soczewka skupiaj

ą

ca, f < 0

soczewka rozpraszaj

ą

ca

6

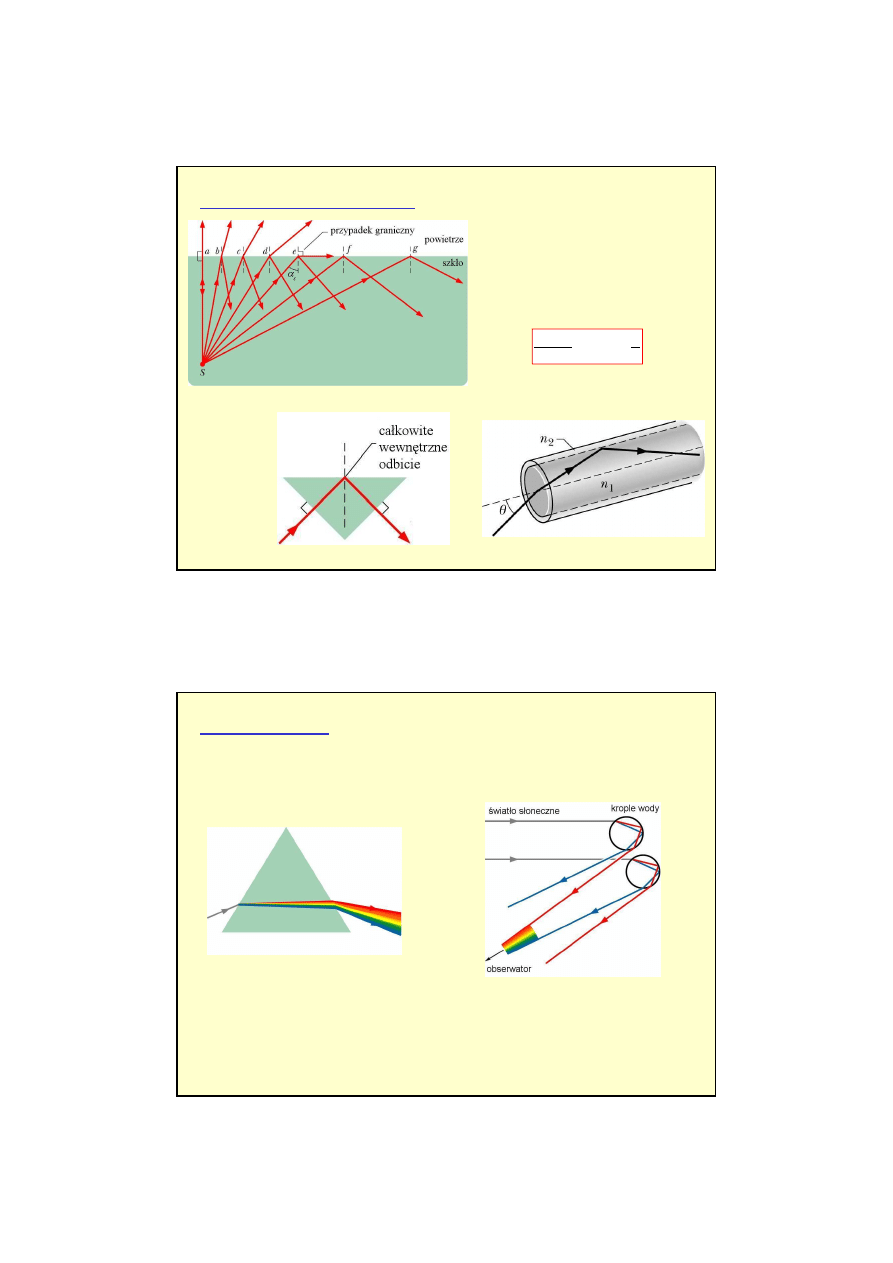
lupa

mikroskop

teleskop

Przyrz

ą

dy optyczne

4

7

Gdy

ś

wiatło przechodzi z o

ś

rodka

optycznie g

ę

stszego do o

ś

rodka

optycznie rzadszego, dla k

ą

ta

krytycznego

α

c

zachodzi całkowite

wewn

ę

trzne odbicie.

n

c

c

1

sin

90

sin

sin

=

=

°

α

α

Zastosowanie:

Urządzenia optyczne
(aparaty foto., lornetki)

Światłowody

Całkowite wewn

ę

trzne odbicie

8

Pr

ę

dko

ść

fali przechodz

ą

cej przez o

ś

rodek zale

ż

y od cz

ę

stotliwo

ś

ci

ś

wiatła.

Zjawisko to nazywamy dyspersj

ą

ś

wiatła.

Dla wi

ę

kszo

ś

ci materiałów obserwujemy,

ż

e wraz ze wzrostem cz

ę

stotliwo

ś

ci fali

ś

wietlnej

maleje jej pr

ę

dko

ść

czyli ro

ś

nie współczynnik załamania

Ś

wiatło białe, zło

ż

one z fal o wszystkich długo

ś

ciach z zakresu widzialnego, ulega

rozszczepieniu

Dyspersja

ś

wiatła

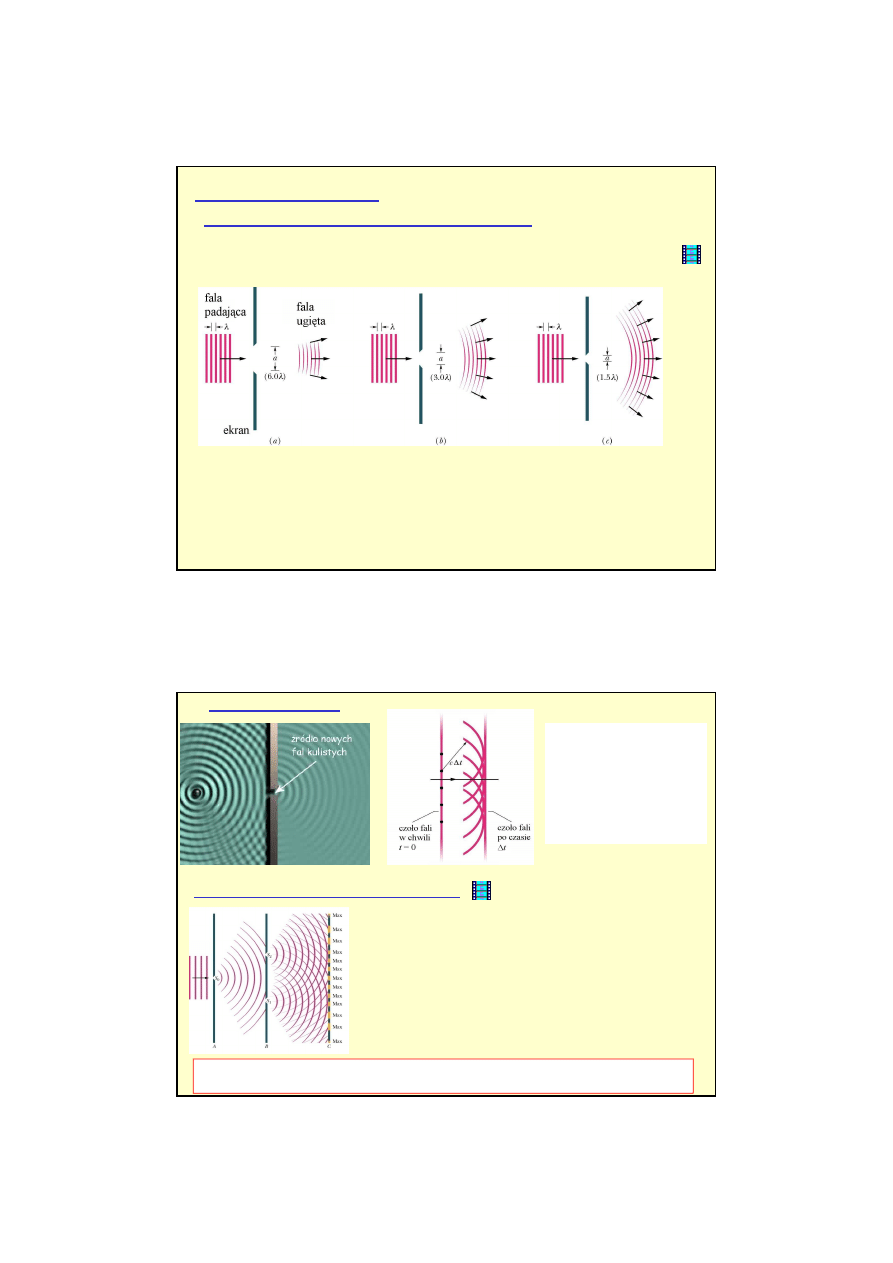
5

9

Poj

ę

ciem promienia

ś

wietlnego (optyka geometryczna) nie mo

ż

emy posłu

ż

y

ć

si

ę

przy

opisie ugi

ę

cia

ś

wiatła.

Ugi

ę

cie staje si

ę

coraz bardziej wyra

ź

ne gdy szczelina staje si

ę

coraz w

ęż

sza

(

a

/

λ

λ

λ

λ

maleje).

W tym zjawisku ujawnia si

ę

falowa natura

ś

wiatła.

Warunkiem stosowalno

ś

ci optyki geometrycznej jest aby wymiary liniowe wszystkich

obiektów (soczewek, pryzmatów, szczelin itp.) były o wiele wi

ę

ksze od długo

ś

ci fali.

OPTYKA FALOWA

Warunki stosowalno

ś

ci optyki geometrycznej

10

Zasada Huygensa mówi,

ż

e

wszystkie punkty czoła fali
mo

ż

na uwa

ż

a

ć

za

ź

ródła

nowych fal kulistych.
Poło

ż

enie czoła fali po

czasie t b

ę

dzie dane przez

powierzchni

ę

styczn

ą

do

tych fal kulistych.

Zasada Huygensa

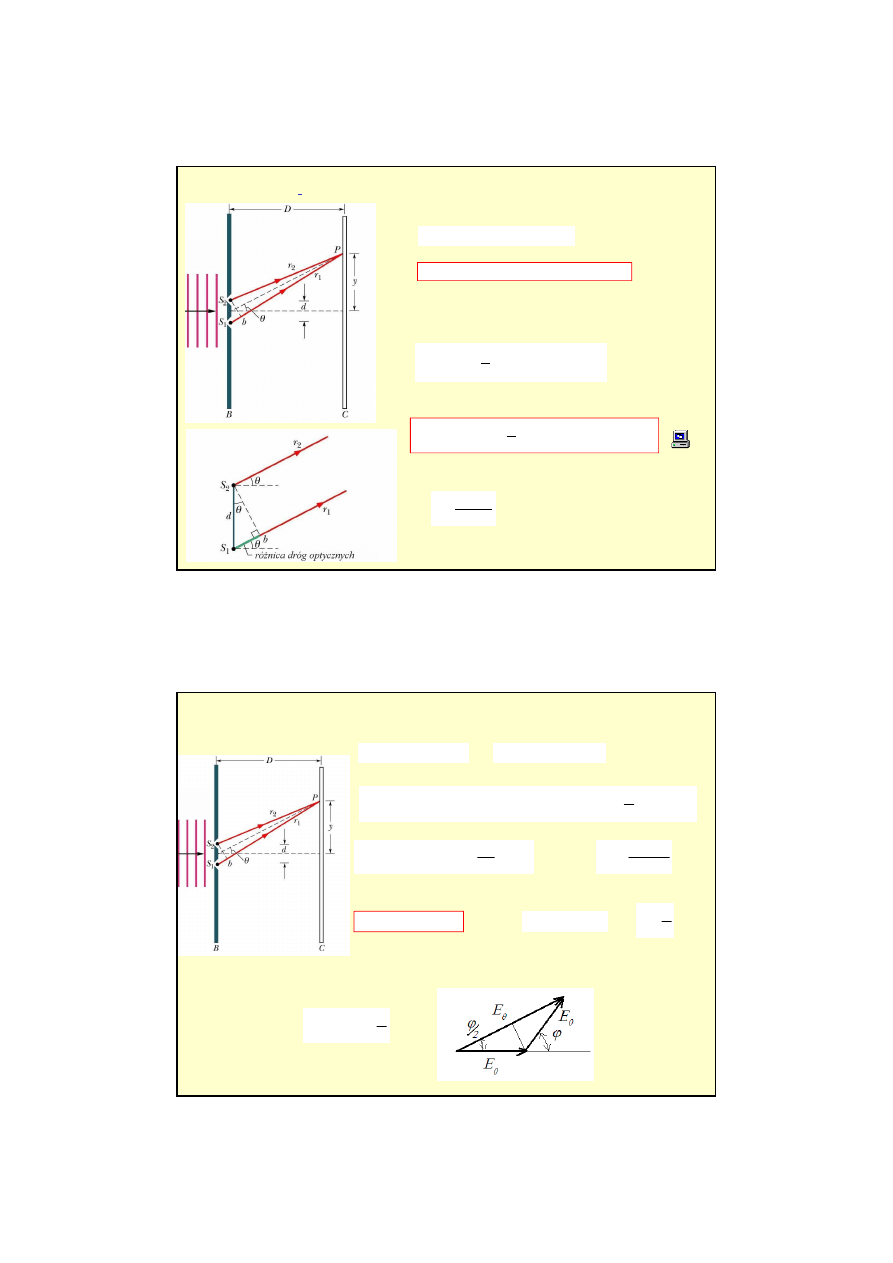
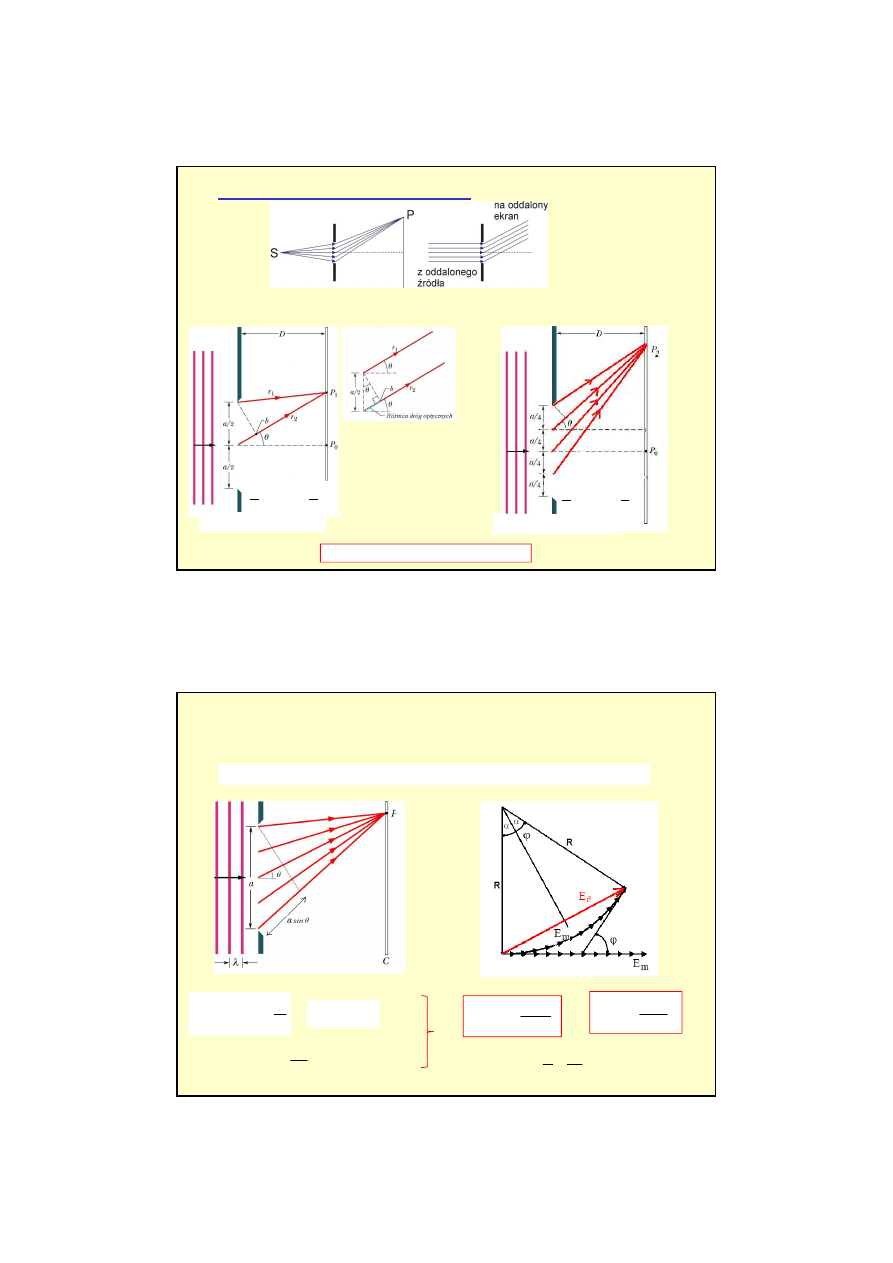
Interferencja, do

ś

wiadczenie Younga

Do

ś

wiadczenie Younga (w 1801 r.)

wykazało istnienie takiej interferencji dla

ś

wiatła. Był to pierwszy eksperyment

wskazuj

ą

cy na falowy charakter

ś

wiatła.

Na ekranie obserwujemy miejsca ciemne
powstaj

ą

ce w wyniku wygaszania si

ę

interferuj

ą

cych fal i jasne powstaj

ą

ce w

wyniku ich wzajemnego wzmocnienia.

Warunkiem stabilno

ś

ci obrazu interferencyjnego jest stało

ść

w czasie ró

ż

nicy faz fal

wychodz

ą

cych ze

ź

ródeł S

1

i S

2

. Mówimy,

ż

e te

ź

ródła s

ą

koherentne czyli spójne

.

6

11

,.....

2

,

1

,

0

,

1

=

=

m

m

b

S

λ

Warunek na maksimum

)

maksima

(

.....

,

2

,

1

,

sin

=

=

m

m

d

λ

θ

θ

sin

1

d

B

S

=

Warunek na minimum

,.....

2

,

1

,

0

,

2

1

1

=













+

=

m

m

B

S

λ

)

minima

(

,.....

2

,

1

,

2

)

1

2

(

sin

=

+

=

m

m

d

λ

θ

m

d

θ

λ

sin

=

Tak Young wyznaczył długo

ś

ci

fal

ś

wiatła widzialnego.

interpretacja

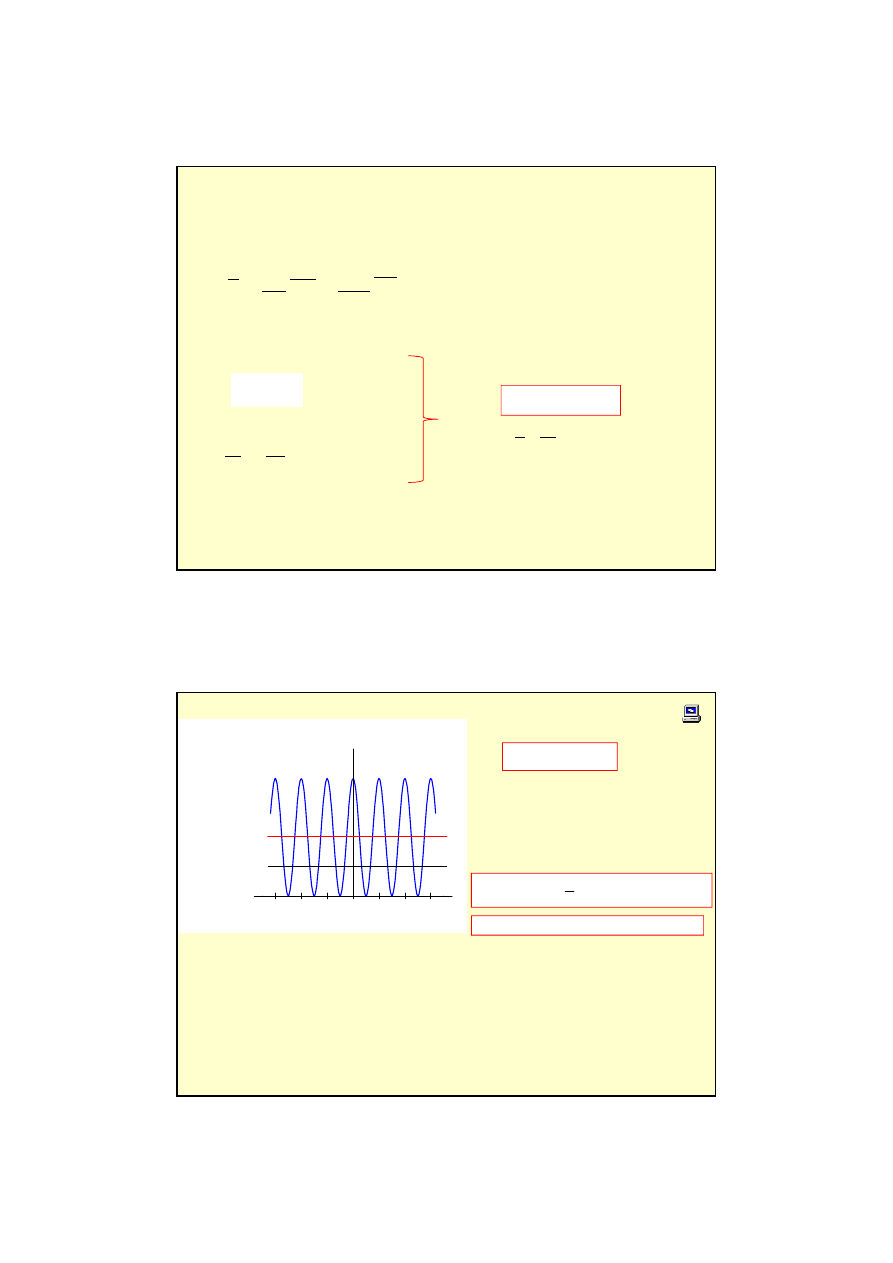
12

)

sin(

1

0

1

t

kr

E

E

ω

−

=

)

sin(

2

0

2

t

kr

E

E

ω

−

=

nat

ęż

enie

ś

wiatła w do

ś

wiadczeniu Younga

Fale wychodz

ą

cych ze

ź

ródeł S

1

i S

2

maj

ą

te same fazy. (

fale koherentne czyli spójne

).

ϕ

to ró

ż

nica faz jaka powstaje na drodze

∆

r

W punkcie P

(

)

t

E

t

kr

E

t

kr

E

E

P

ω

δ

ϕ

ω

ω

−

=

−

+

−

=

sin

2

cos

2

)

sin(

)

sin(

0

2

0

1

0

θ

λ

π

∆

ϕ

sin

2

)

(

2

1

d

r

k

r

r

k

=

=

−

=

gdzie:

2

)

(

2

1

r

r

k

+

=

δ

(

)

t

E

E

P

ω

δ

θ

−

=

sin

β

θ

cos

2

0

E

E

=

gdzie:

i

2

ϕ

β

=

sumowanie fal cz

ą

stkowych:

2

cos

2

0

ϕ

θ

E

E

=

7

13

13

Nat

ęż

enie fali wypadkowej :

2

θ

θ

E

I ~

2

2

0

0

)

cos

2

(

β

θ

θ

=













=

E

E

I

I

β

θ

2

0

cos

4I

I

=

θ

λ

π

ϕ

β

sin

d

=

=

2

2

0

0

1

1

E

c

EB

S

I

µ

µ

=

=

=

Nat

ęż

enie fali to ilo

ść

energii

przechodz

ą

cej przez jednostk

ę

powierzchni w jednostce czasu czyli

ś

rednia warto

ść

wektora Poyntinga.

14

Nat

ęż

enie fali wypadkowej

dwa

ź

ródła niespójne

I = 2I

0

dwa

ź

ródła spójne

I = 4I

0

jedno

ź

ródło

I = I

0

2

λ

/d

λ

/d

2

λ

/d

λ

/d

0

sin

θ

n

a

t

ę

ż

e

n

ie

Dla fal spójnych (np. laser) najpierw dodajemy amplitudy (uwzgl

ę

dniaj

ą

c stał

ą

ró

ż

nic

ę

faz), a

potem celem obliczenia nat

ęż

enia podnosimy otrzyman

ą

amplitud

ę

wypadkow

ą

do

kwadratu.

Dla fal niespójnych (np.

ż

arówki) najpierw podnosimy do kwadratu amplitudy,

ż

eby obliczy

ć

nat

ęż

enia poszczególnych fal, a dopiero potem sumujemy nat

ęż

enia celem otrzymania

nat

ęż

enia wypadkowego.

Energia całkowita taka sama !! (ró

ż

ny jej rozkład)

β

θ

2

0

cos

4I

I

=

)

maksima

(

.....

,

2

,

1

,

sin

=

=

m

m

d

λ

θ

)

minima

(

,.....

2

,

1

,

2

)

1

2

(

sin

=

+

=

m

m

d

λ

θ

Wzór ten potwierdza warunki na maksima i
minima

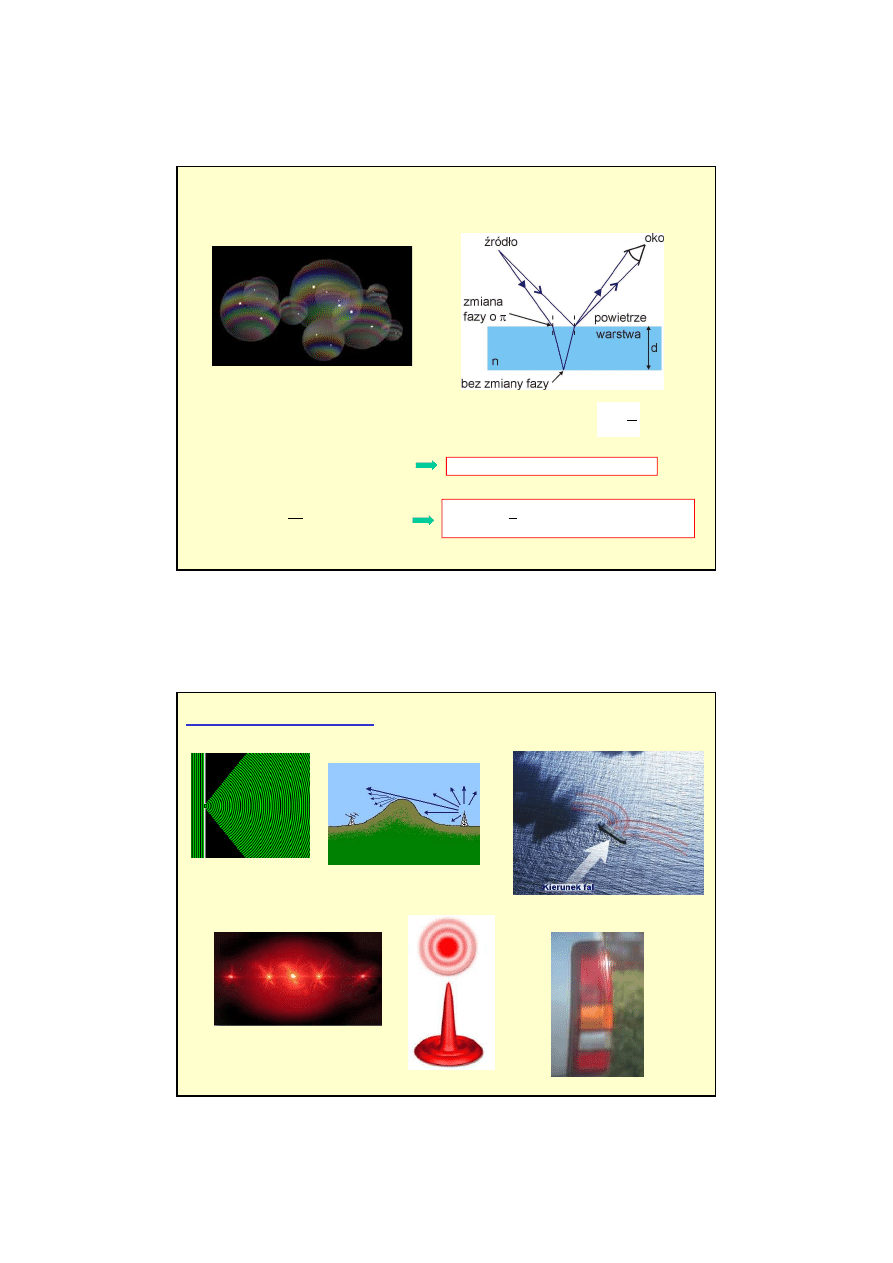
8

15

n

n

λ

λ

=

w warstwie

Warunki interferencyjne (normalne padanie)

ZMIANA FAZY PRZY ODBICIU !!!

,.....

2

,

1

,

0

,

2

2

=

+

=

m

m

d

n

n

λ

λ

)

maksima

.....(

,

2

,

1

,

0

,

2

1

2

=













+

=

m

m

dn

λ

)

minima

....(

,.

2

,

1

,

0

,

2

=

=

m

m

dn

λ

Interferencja w cienkich warstwach

,.....

2

,

1

,

0

,

2

=

=

m

m

d

n

λ

16

Dyfrakcja (ugi

ę

cie)

ś

wiatła

9

17

dyfrakcja
Fresnela
Fraunhofera

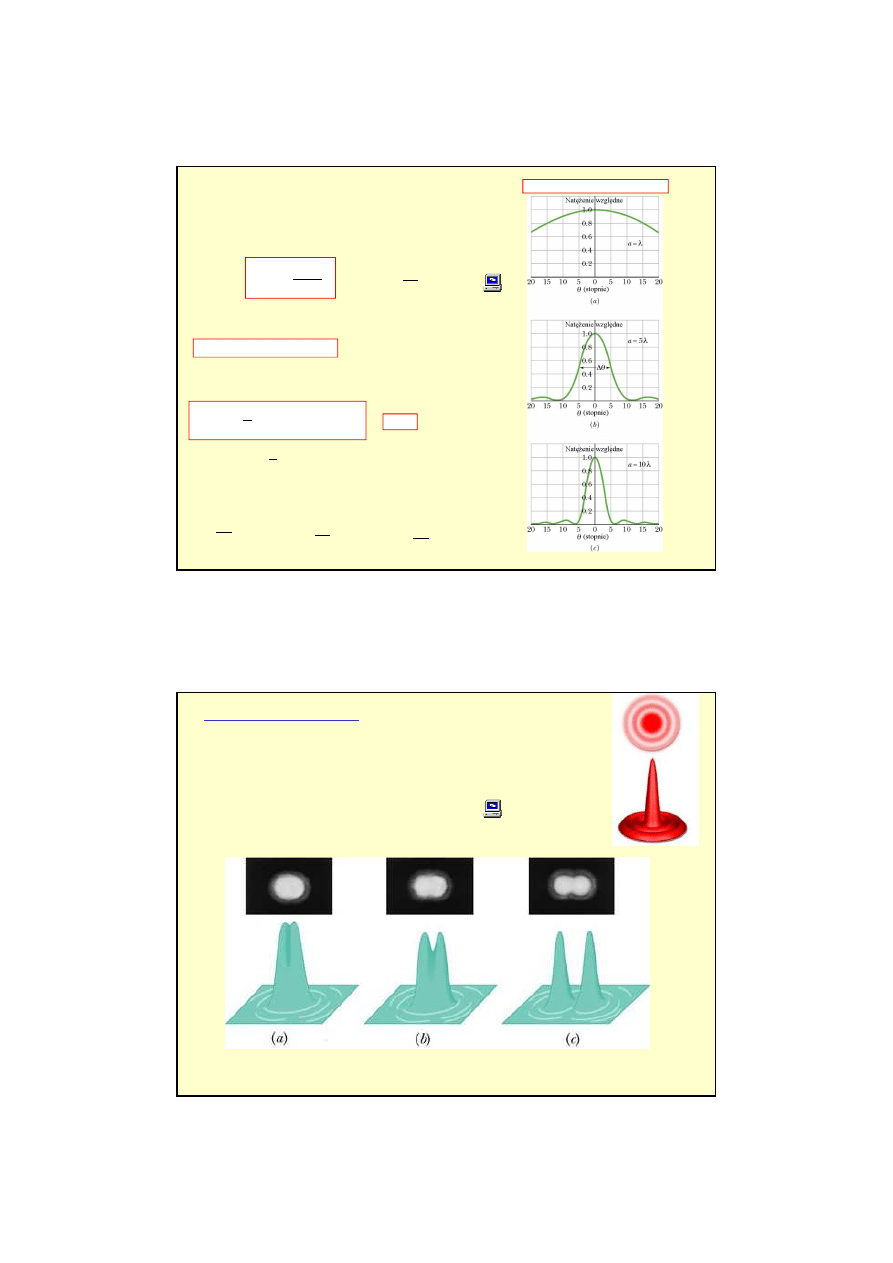
Nat

ęż

enie w punkcie P obliczamy dodaj

ą

c do siebie zaburzenia falowe (wektory

E

) docieraj

ą

ce z

ró

ż

nych punktów szczeliny.

minimum dyfrakcyjne

λ

θ

2

1

2

1

=

sin

a

)

minima

(

,.....

2

,

1

,

sin

=

=

m

m

a

λ

θ

Dyfrakcja na pojedynczej szczelinie

minimum dyfrakcyjne

λ

θ

2

1

sin

4

1

=

a

18

(

)

t

E

t

kr

E

t

kr

E

t

kr

E

E

n

P

ω

δ

ω

ω

ω

θ

−

=

−

+

+

−

+

−

=

sin

)

sin(

...

)

sin(

)

sin(

0

2

0

1

0

Sumowanie niesko

ń

czonej ilo

ś

ci fal cz

ą

stkowych dla jednej szczeliny













=

α

α

θ

sin

m

E

E

2













=

α

α

θ

sin

m

I

I

θ

λ

π

ϕ

α

sin

2

a

=

=

ϕ

R

E

m

=

2

sin

2

ϕ

θ

R

E

=

θ

λ

π

∆

ϕ

sin

2

a

r

k

=

=

10

19

2

sin













=

α

α

θ

m

I

I

θ

λ

π

α

sin

a

=

nat

ęż

enie

ś

wiatła w obrazie dyfrakcyjnym

)

minima

(

,.....

2

,

1

,

sin

=

=

m

m

a

λ

θ

045

0.

=

m

I

I

θ

016

0.

=

m

I

I

θ

008

0.

=

m

I

I

θ

m = 1

m = 2

m = 3

,.....

3

,

2

,

1

,

=

=

m

m

π

α

minimum

λ

θ

m

a

=

sin

,.....

3

,

2

,

1

,

2

1

=













+

=

m

m

π

α

maksimum

0

=

α

i

λ

θ













+

=

2

1

sin

m

a

i

0

=

θ

20

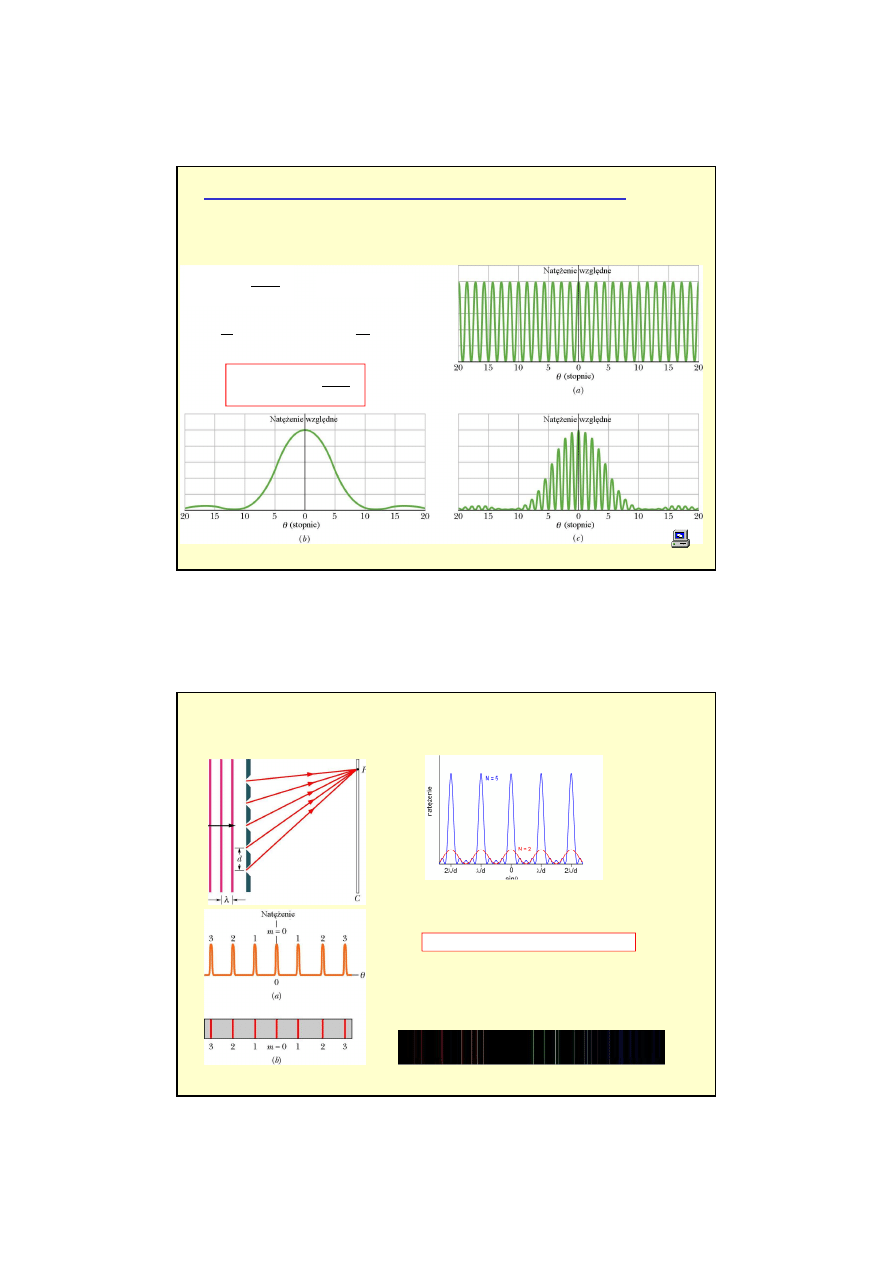
Kryterium Rayleigha

Dwa obiekty s

ą

jeszcze rozró

ż

nialne je

ż

eli maksimum obrazu

dyfrakcyjnego jednego obiektu przypada na pierwsze minimum obrazu
dyfrakcyjnego drugiego obiektu.

Zdolno

ść

rozdzielcza

11

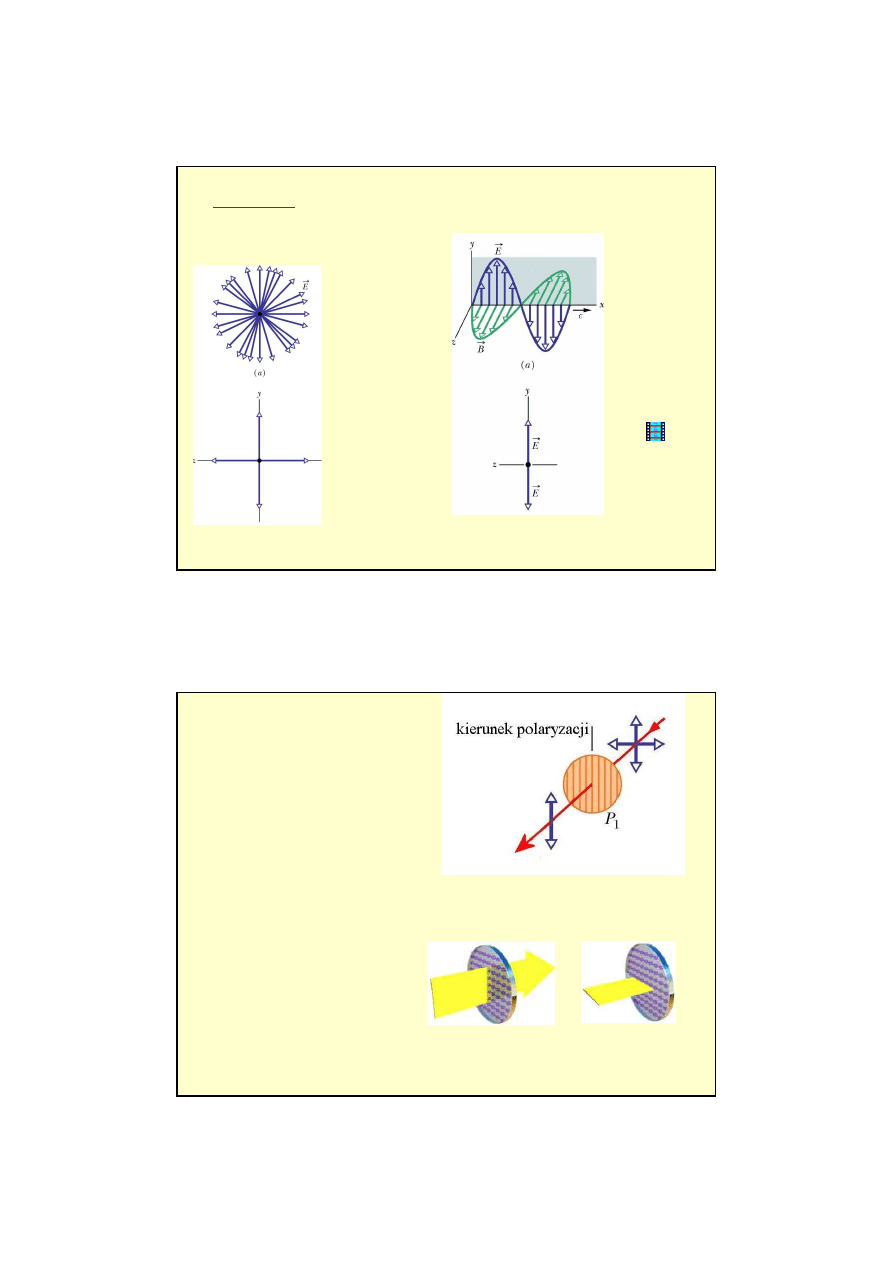
21

Dwie szczeliny

pojedyncza szczelina daje obraz dyfrakcyjny i te obrazy interferuj

ą

.

β

θ

2

0

,

cos

4I

I

Int

=

θ

λ

π

β

sin

d

=

2

,

sin













=

α

α

θ

m

Dyfr

I

I

θ

λ

π

α

sin

a

=

2

2













=

α

α

β

θ

sin

)

(cos

m

I

I

Obraz dyfrakcyjny wielu szczelin – dyfrakcja + interferencja

22

Interferencja fal z wielu

ź

ródeł, siatka dyfrakcyjna

Nie zmienia si

ę

odległo

ś

ci pomi

ę

dzy głównymi maksimami.

Obserwujemy wzrost nat

ęż

enia maksimów głównych.

)

maksima

(

.....

,

2

,

1

,

sin

=

=

m

m

d

λ

θ

d - stała siatki dyfrakcyjnej

w spektrometrii, do pomiaru długo

ś

ci fal

stosuje si

ę

siatki o stałej d = 1

µ

m

tlen

12

23

Fala płasko
spolaryzowana
(spolaryzowana liniowo).

Fala niespolaryzowana

Teoria Maxwella

ś

wiatło jest fal

ą

poprzeczn

ą

Zjawisko polaryzacji jest charakterystyczne dla fal poprzecznych

Polaryzacja

24

Sposoby polaryzacji

ś

wiatła

Niespolaryzowana fala

ś

wietlna pada na

płytk

ę

z materiału polaryzuj

ą

cego

(polaroid)

Płytki polaryzuj

ą

ce

Kierunek polaryzacji polaroidu ustala
si

ę

w procesie produkcji.

Cz

ą

steczki o strukturze ła

ń

cuchowej

uło

ż

one równoległe na elastycznym

podło

ż

u.

13

25

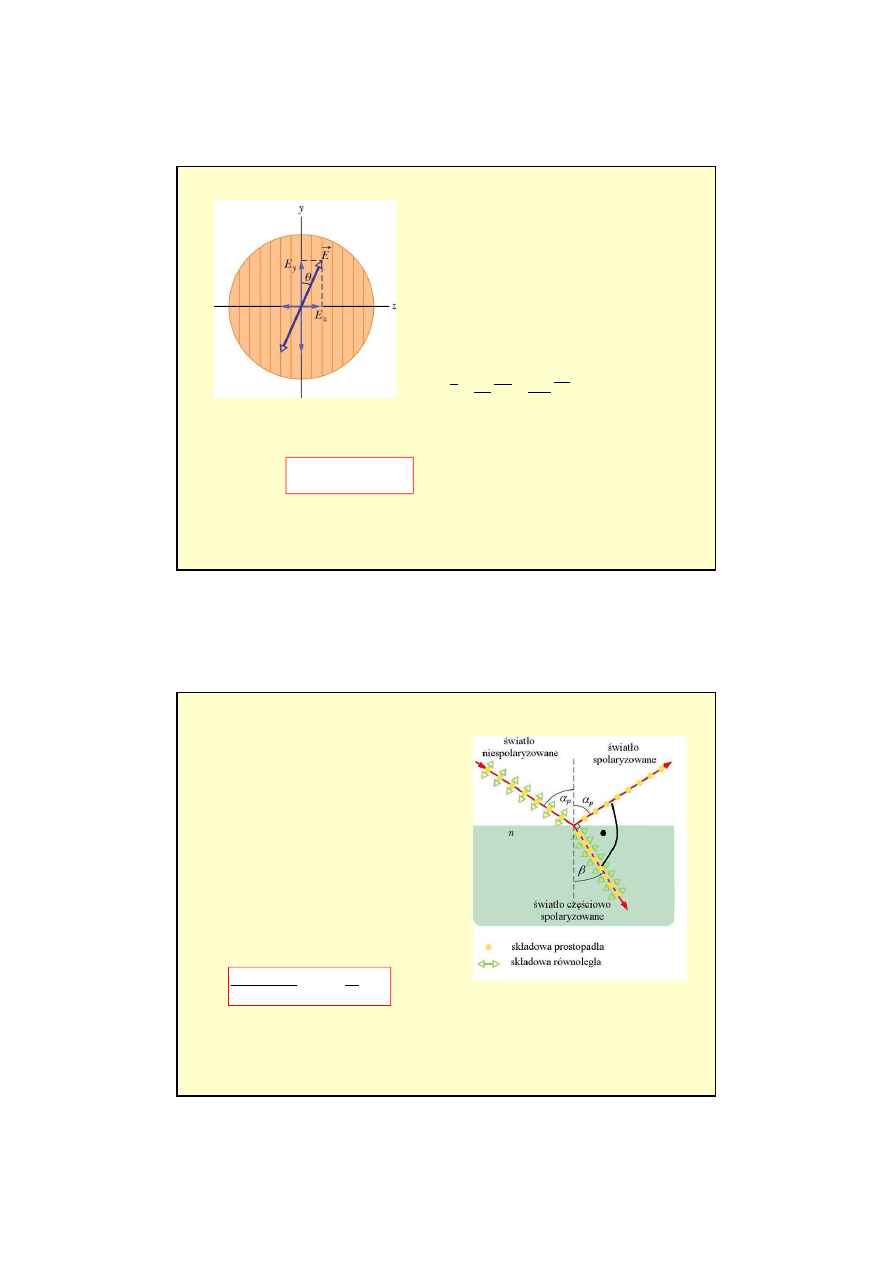
Je

ż

eli wektor

E

wyznaczaj

ą

cy płaszczyzn

ę

drga

ń

tworzy k

ą

t

θ

z kierunkiem polaryzacji

płytki to przepuszczana jest składowa
równoległa

E

y

podczas gdy składowa

prostopadła

E

z

jest pochłaniana.

θ

cos

E

E

y

=

Nat

ęż

enie

ś

wiatła jest proporcjonalne do kwadratu amplitudy nat

ęż

enia pola elektrycznego E

θ

2

0

cos

I

I

=

Prawo Malusa

50% energii wi

ą

zki

ś

wiatła niespolaryzowanego padaj

ą

cego na polaroid jest w nim

pochłaniane, a 50% przepuszczane.

2

0

0

1

1

E

c

EB

S

I

µ

µ

=

=

=

Nat

ęż

enie fali to ilo

ść

energii przechodz

ą

cej przez

jednostk

ę

powierzchni w jednostce czasu czyli

ś

rednia warto

ść

wektora Poyntinga.

26

Polaryzacja przez odbicie

Istnieje pewien k

ą

t padania (k

ą

t całkowitej

polaryzacji

α

p

, dla którego wi

ą

zka odbita jest

całkowicie spolaryzowana liniowo w kierunku
prostopadłym do płaszczyzny padania.

Gdy k

ą

t padania jest równy k

ą

towi całkowitej

polaryzacji to wówczas wi

ą

zka odbita i

załamana tworz

ą

k

ą

t prosty

o

90

=

+

β

α

(k

ą

t Brewstera)

dla n = 1.5 otrzymujemy a

p

= 56

°

1

,

2

1

2

0

)

90

sin(

sin

n

n

n

tg

=

=

=

−

α

α

α

14

27

Dwójłomno

ść

Ś

wiatło spolaryzowane mo

ż

na uzyska

ć

wykorzystuj

ą

c, wyst

ę

puj

ą

c

ą

w pewnych

kryształach, zale

ż

no

ść

współczynnika załamania

ś

wiatła od kierunku polaryzacji.

Promie

ń

zwyczajny (o) i promie

ń

nadzwyczajny

(e) s

ą

spolaryzowane liniowo, przy czym ich

płaszczyzny drga

ń

s

ą

wzajemnie prostopadłe.

Niektóre podwójnie załamuj

ą

ce kryształy wykazuj

ą

ponadto własno

ść

nazywan

ą

dichroizmem. Kryształy te pochłaniaj

ą

jeden z promieni (o lub e) silniej ni

ż

drugi. Na

wykorzystaniu tego zjawiska opiera si

ę

działanie szeroko stosowanych polaroidów.