Materiały dydaktyczne powielane

1

Ćwiczenie 3 i 4

PRÓBKOWANIE I ANALIZA WIDMOWA SYGNAŁÓW

J. Walczak, P. Świszcz

Celem ćwiczenia jest zapoznanie się z podstawowymi ideami i twierdzeniami dotyczącymi

próbkowania sygnałów a także odtwarzania sygnałów na podstawie znanych ciągów próbek.

Innym celem ćwiczenia jest zapoznanie się z metodami analizy widmowej sygnałów, a w

szczególności z zastosowaniem do tej analizy dyskretnego (DFT) i szybkiego (FFT)

przekształcenia Fouriera.

1. Wprowadzenie

Tematyka ćwiczenia dotyczy dwóch ważnych i ściśle ze sobą powiązanych działów teorii

sygnałów: teorii próbkowania i metod analizy widmowej. Niektóre najważniejsze z

problemów dotyczących rozpatrywanych w ramach ćwiczenia zagadnień omówiono poniżej

w sposób skrótowy, dokładna analiza tych zagadnień opisana jest w pracy [1].

1.1. Próbkowanie sygnałów

Polega ono na przekształceniu sygnału ciągłego w równoważny sygnał dyskretny (rys.1) a

następnie w sygnał cyfrowy.

f(t)

t

0

f(h)

h

0

1

2

3

4

5 ...

Rys.1. Próbkowanie sygnału ciągłego

Materiały dydaktyczne powielane

2

Przekształcenie takie powinno umożliwić odtwarzanie sygnału ciągłego f(t) na podstawie

znajomości próbek f[n] sygnału dyskretnego z dowolną dokładnością. Warunki przy których

możliwe jest odtworzenie sygnału wiążą się ściśle z właściwościami szeregu Shannona-

Kotielnikowa i twierdzeniem Shannona-Kotielnikowa.

1.1.1. Szereg Shannona-Kotielnikowa

W teorii próbkowania sygnałów o ograniczonej energii szczególne znaczenie posiada funkcja

S

a

(rys.2)

Sa

t

t

t

dla t

dla t

(

)

sin

,

.

ω

ω

ω

0

0

0

0

1

0

=

≠

=













(1)

Rys.2. Funkcja S

a

Zbiór funkcji S

a

oznaczony przez {e

n

} określony wzorem:

(

)

e

f S

f

t hT) h

h

m

a

m

=

−

= ± ±

2

2

0 1 2

π (

,

, , … (2)

gdzie:

f

m

- częstotliwości Nyquista (por. rozdz.1.1.2)

T=(2f

m

)

-1

jest ortogonalny w przestrzeni sygnałów o ograniczonej energii lecz nie jest zupełny. Szereg

Fouriera (uogólniony) wykorzystujący bazę {e

h

} (2) funkcji S

a

nosi nazwę szeregu Shannona-

Kotielnikowa i jest określony wzorem:

Materiały dydaktyczne powielane

3

(

)

f t

f h S

f t hT

a

m

h

h

( )

[ ]

(

)

=

−

= −∞

=∞

∑

2

π

(3)

Współczynniki f[h] tego szeregu są próbkami sygnału f(t) w chwilach czasu hT

f h

f t

f hT

t hT

[ ]

( )

(

)

=

=

=

, (4)

gdzie

T - okres próbkowania

Poprzez wykorzystanie funkcji e

n

(2) (rys.3) oraz próbek sygnału f[h] możliwe jest

odtworzenie sygnału ciągłego na podstawie próbek

Rys.3. Zmodyfikowane funkcje

S

e

a

n

{ }

=

Warunki przy których możliwe jest odtworzenie sygnału na podstawie próbek określa

fundamentalne twierdzenie Shannona-Kotielnikowa.

1.1.2. Twierdzenie Shannona-Kotielnikowa

Twierdzenie to dla przypadku próbkowania równomiernego (ze stałym odstępem czasu T,

rys.4) wyrazić można w następujący sposób:

Jeżeli f(t) jest sygnałem o ograniczonym widmie F(j

ω):

F j

dla

dla

m

m

(

)

ω

ω ω

ω ω

=

≠

<

=

≥








0

0

(5)

Materiały dydaktyczne powielane

4

to sygnał ten można przedstawić z dowolną dokładnością za pomocą szeregu Shannona-

Kotielnikowa. Próbki sygnału f(t) muszą być równoodległe o stały przedział próbkowania T,

taki że:

T

f

m

m

≤

=

π

ω

1

2

(6)

Częstotliwość

ω

m

nazywamy częstotliwością Nyquista a czas T granicznym czasem

próbkowania. Ilustrację cytowanego twierdzenie przedstawiono na rys.4, natomiast jego

dowód zamieszczone w pracy [1].

f(t)

t

|F(j

ω)|

ω

−ω

m

ω

m

0

0

f(hT)

π

ω

m

T

≤

T 2T

4T

6T

8T

0

hT

T

2T

4T

6T

8T

Rys.4. Ilustracja twierdzenia o próbkowaniu.

W sytuacjach praktycznych rozważa się dwa przypadki próbkowania

f

T

f

m

0

1

2

= >

(7)

f

T

f

m

0

1

2

= <

(8)

Przypadek (7) spełnia założenia twierdzenia Shannona-Kotielnikowa w przeciwieństwie do

przypadku opisanego wzorem (8). Jeżeli częstotliwość próbkowania f

o

spełnia warunek (8), to

występuje efekt nakładania się widma sygnału odtwarzanego nazywany aliasingiem, co

prowadzi w efekcie do błędnego odtwarzania sygnałów. Okresowe powielanie widma sygnału

odtwarzanego jest spowodowane operacja próbkowania sygnału. Ilustrację twierdzenia o

próbkowaniu dla przypadków opisanych wzorami (7), (8) pokazano na rys.5. W sytuacji gdy

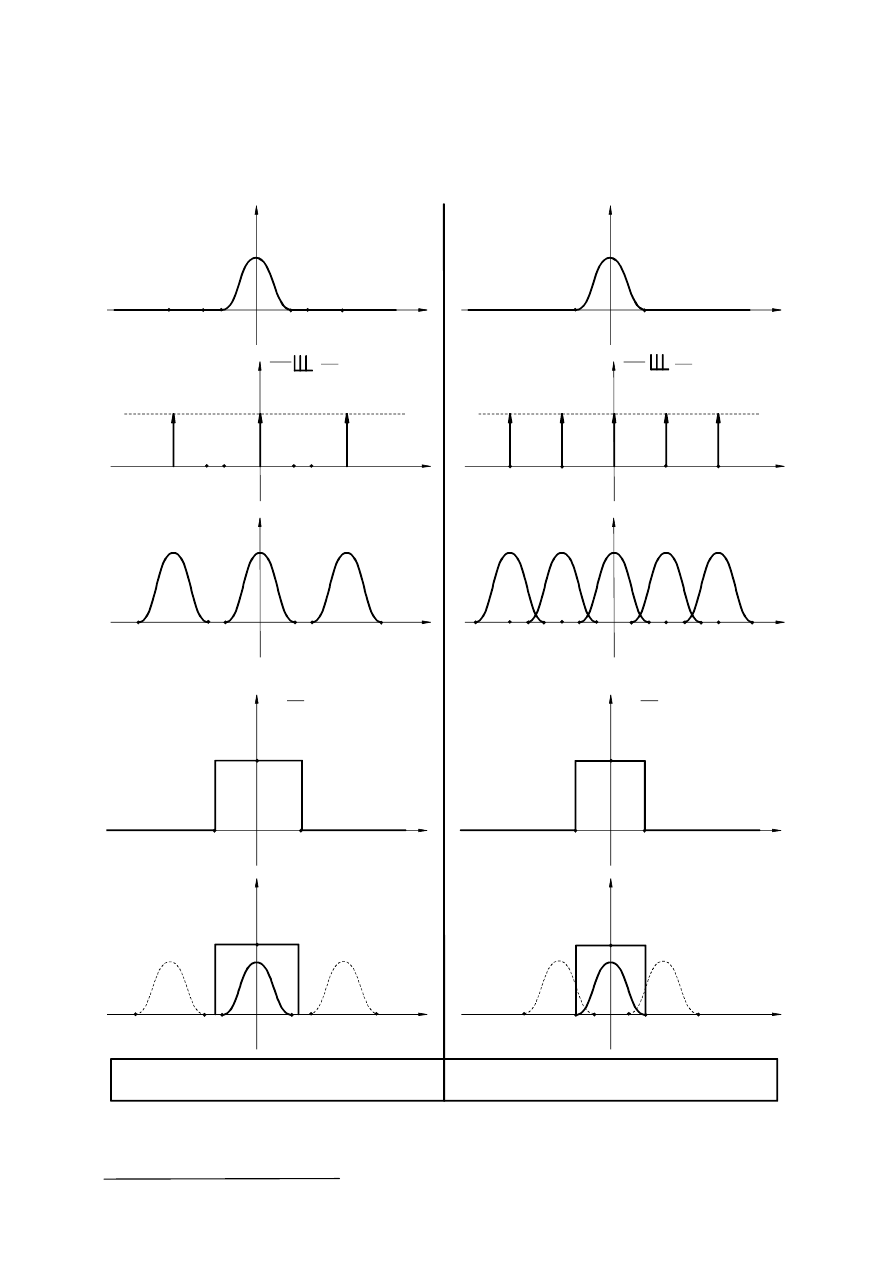
Materiały dydaktyczne powielane

5

niemożliwe jest spełnienie warunku (7) co zachodzi na przykład gdy sygnał f(t) posiada

nieograniczone widmo, konieczne jest zastosowanie filtru dolnoprzepustowego o częstości

odcięcia

ω

g

≥ω

m

, przez co ograniczyć można błędy odtwarzania sygnałów spróbkowanych.

|F(jω)|

ω

−ω

m

ω

m

0

ω

−ω

m

ω

m

0

F'(jω)

ω

0

ω

−ω

1

ω

1

0

|F(jω)|

ω

−ω

m

ω

m

0

( )

ω

ω

m

1

ω

m

ω

m

Π

( )

ω

2ω

1

1

−2ω

m

−3ω

m

2ω

m

3ω

m

−ω

1

−ω

0

ω

1

ω

0

1

ω

1

ω

0

−ω

1

−ω

0

−ω

m

−ω

1

ω

m

−ω

0

−ω

0

−ω

m

ω

0

ω

0

+ω

m

|F(jω)|

ω

−ω

m

ω

m

0

ω

−ω

m

ω

m

0

F'(jω)

ω

0

ω

−ω

1

ω

1

0

|F(jω)|

ω

0

( )

ω

ω

0

1

ω

0

ω

m

Π

( )

ω

2ω

1

1

1

−ω

1

−ω

m

−ω

0

−2ω

0

ω

0

2ω

0

a)

b)

c)

d)

e)

f)

g)

h)

i)

j)

f

0

> 2fm

f

0

< 2fm

1

1

Rys.5. Ilustracja twierdzenia o próbkowaniu - przypadki niekrytyczne.

Materiały dydaktyczne powielane

6

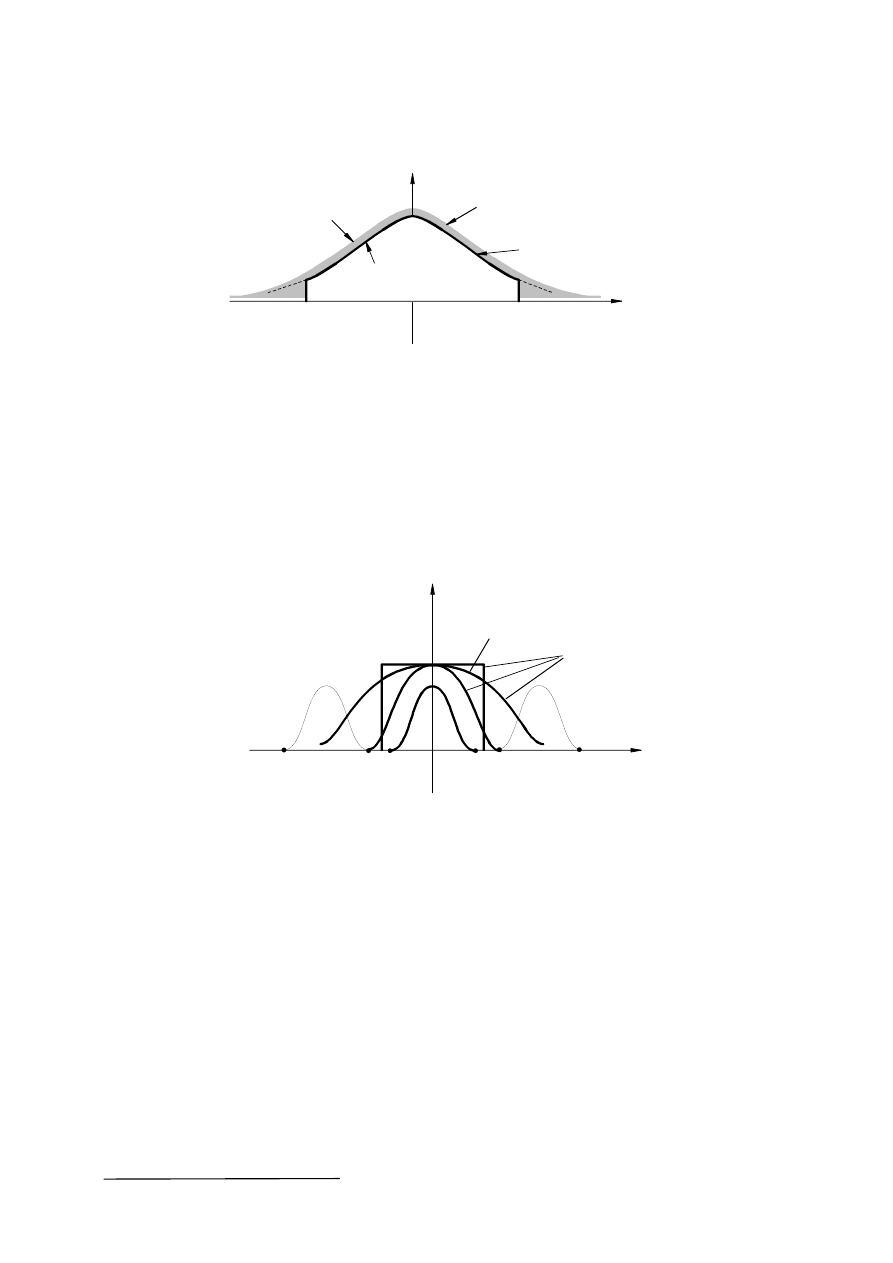
Błędy te są zależne (rys.6) od różnicy powierzchni pod charakterystykami widmowymi

sygnału pierwotnego f(t) i sygnału spróbkowanego

|F(jω)|

ω

−ω

m

ω

m

0

|F(j

ω)|

|F(jω)|

Sygnał pierwotny f(t)

Sygnał próbkowany f(t)

~

~

Rys.6. Widmo sygnału pierwotnego i spróbkowanego

Inne przyczyny błędów odtwarzania sygnałów spróbkowanych to:

• przyjęcie założenia o istnieniu charakterystyki idealnego filtru dolnoprzepustowego,
• charakter impulsów próbkujących, które nie stanowią ciągu idealnych impulsów Diraca

lecz są sygnałem okresowym prostokątnym, rys. 7.

ω

−ω

m

ω

m

0

ω

1

ω

0

|F(jω)|

−ω

1

−ω

0

|K(jω)|

ch-ki filtru

Rys.7. Ilustracja próbkowania nieidealnego

Analizę wymienionych błędów przeprowadza się najczęściej metodami numerycznymi.

1.2. Analiza widmowa sygnałów

Analiza widmowa dotyczy wszystkich występujących w technice sygnałów, do których

zalicza się: sygnały o ograniczonej energii, sygnały o ograniczonej mocy średniej, sygnały

okresowe, prawie okresowe, impulsowe a także stochastyczne. Celem metod widmowych jest

analiza właściwości sygnałów i układów a także ich synteza z wykorzystaniem charakterystyk

częstotliwościowych. Charakterystyki częstotliwościowe sygnałów definiowane są w różny

Materiały dydaktyczne powielane

7

sposób w zależności od klasy przebiegu których one dotyczą. Krótki przykład tych

charakterystyk przedstawiono poniżej.

1

1.2.1. Widmo Fouriera sygnałów okresowych

Każdy sygnał okresowy całkowalny z kwadratem a zatem należący do przestrzeni sygnałowej

L

T

2

można przedstawić w postaci szeregu Fouriera:

f t

F e

F e

h

jh

t

h

h

n

jh

t

h

( )

Re

=

=

= −∞

=∞

=

∞

∑

∑

ω

ω

0

0

0

(9)

gdzie:

ω

π

0

2

=

T

, T - okres przebiegu

(10)

F

T

f t e

dt h

h

jh

t

T

=

= ± ±

−

∫

1

0 1 2

0

0

( )

,

, , ,

ω

… (11)

F

F

F e

h

h

h

j

n

=

=

2

2

ϕ

(12)

Widmem sygnału okresowego f(t) nazywamy zbiory {F

h

, h=0,

±1, ±2...}, { ,

, , ,...}

F h

h

= 0 1 2

.

Podobnie widmem amplitudowym nazywamy zbiory {

,

, , ,...}

F

h

h

= ± ±

0 1 2

,

{

,

, , ,...}

F

h

h

= 0 1 2

natomiast widmem fazowym nazywamy zbiory {arg F

h

, h=0,

±1,±2...},

{arg

,

, , ,...}

F h

h

= 0 1 2

, przy czym:

arg

arg

arg

F

F

F

h

h

h

=

=

−

.

(13)

Przykładowe widma F i F

h

h

sygnału okresowego pokazano na rys.8, 9

1

Bez uwzględnienia charakterystyk dystrybucyjnych sygnałów, por. [1].

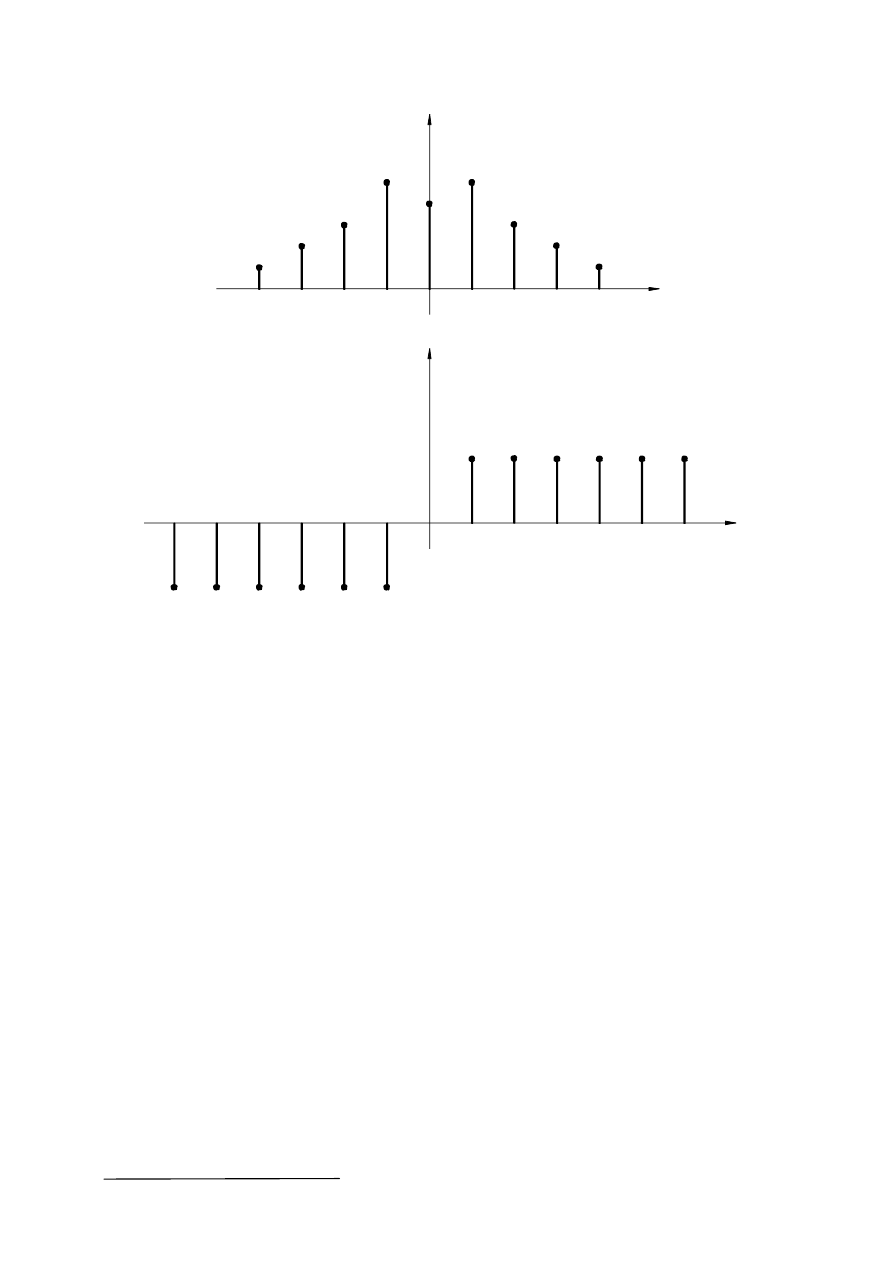
Materiały dydaktyczne powielane

8

|F

h

|

|F

1

|

|F

-4

|

|F

4

|

|F

3

|

|F

2

|

|F

0

|

|F

-3

|

|F

-2

|

|F

-1

|

h

1

2

3

4

-h

-1

-2

-3

-4

0

arg F

h

h

1

2

3

4

-1

-2

-3

-4

0

arg F

1

arg F

6

5

6

-5

-6

arg F

-1

arg F

-6

a)

b)

Rys.8. Widma F

h

sygnału okresowego

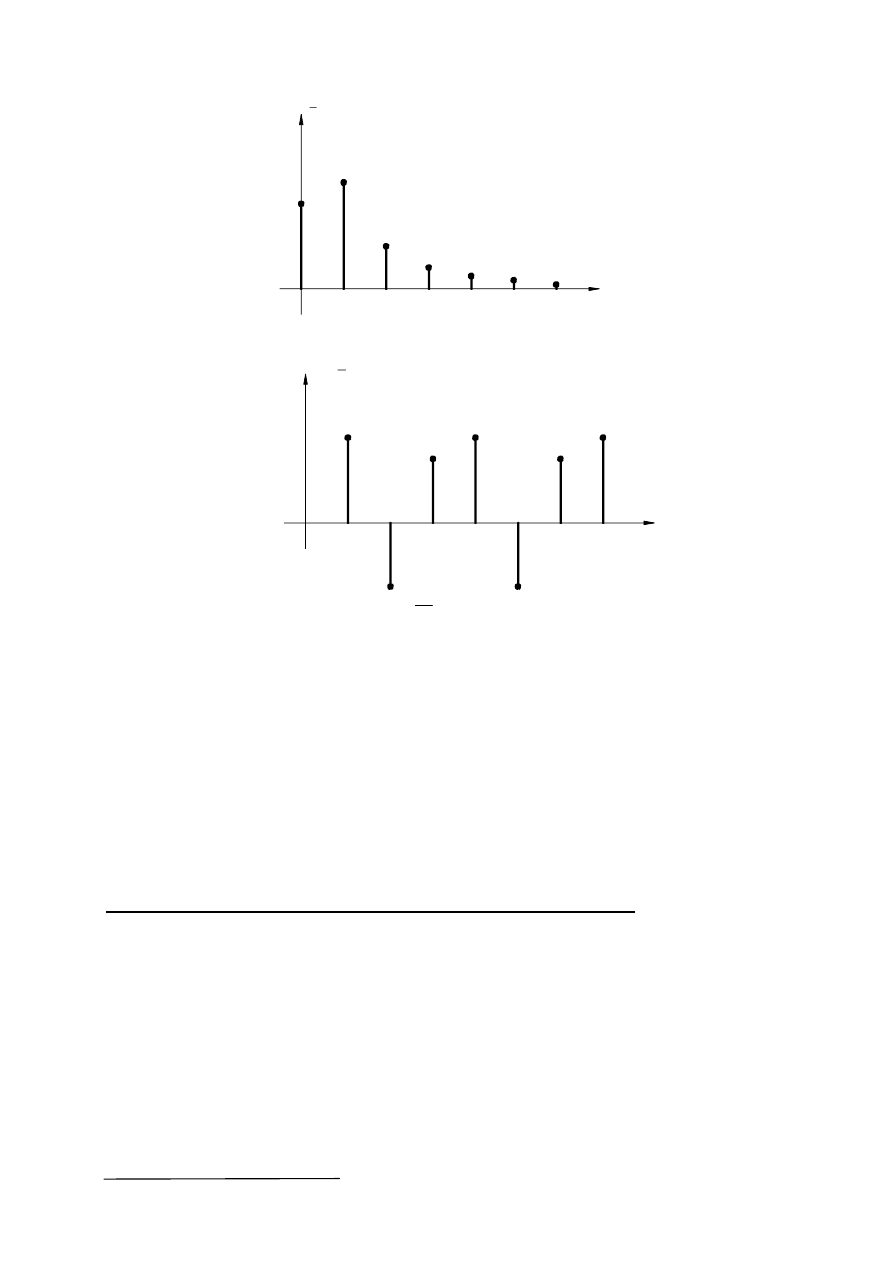
Materiały dydaktyczne powielane

9

h

1

2

3

4

0

5

6

h

1

2

3

4

0

5

6

7

a)

b)

|F

h

|

arg F

h

Rys.9. Widma F

h

sygnału okresowego

Widma sygnałów okresowych mają zawsze charakter dyskretny, przy czym poszczególne

prążki widma są rozmieszczane na osi częstotliwości w jednakowej odległości pomiędzy

sobą.

Szereg Fouriera (9) jest powszechnie wykorzystywany w teorii obwodów elektrycznych do

analizy układów z przebiegami okresowymi i niesinusoidalnymi.

1.2.2. Widmo Fouriera sygnałów nieokresowych o skończonej energii

Widmem Fouriera F(j

ω) sygnału f(t) o skończonej energii nazywamy transformatę Fouriera

tego sygnału:

{ }

F j

f t

f t e

dt

j t

(

)

( )

( )

ω

ω

=

=

−

−∞

∞

∫

F

(14)

gdzie:

F - symbol transformaty Fouriera.

Materiały dydaktyczne powielane

10

Transformata Fouriera F(j

ω) sygnału f(t) jest funkcją zespoloną zmiennej rzeczywistej ω i

może być przedstawiona w postaci wzoru:

F j

F j

e

F j

e

j

F j

j

j

(

)

(

)

(

)

arg (

)

(

)

ω

ω

ω

ω

ϕ ω

=

=

(15)

Funkcje

F j

(

)

ω

i

ϕ(jω) nazywamy widmem amplitudowym i fazowym sygnału f(t).

Wykresy tych funkcji nazywamy charakterystykami Bodego sygnału a wykres funkcji F(j

ω)

na płaszczyźnie zespolonej Gaussa nazywamy charakterystyką Nyquista sygnału.

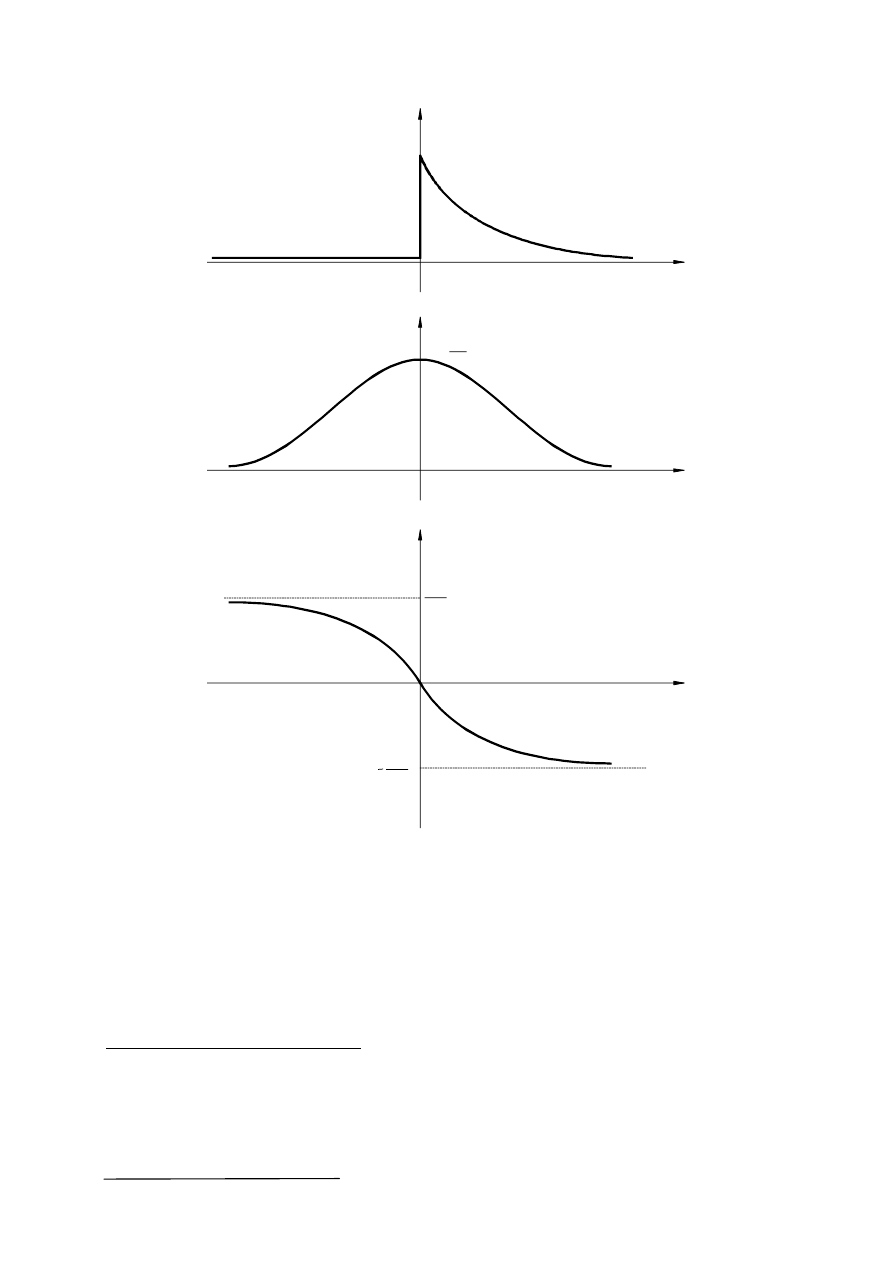
Przykładowo dla sygnału jednostronnie wykładniczego

f t

e

a

dla t

dla t

at

( )

,

=

>

>

<








−

0

0

0

0

(16)

widmo F(j

ω) określa wzór:

F j

a ju

a

e

jarctg

a

(

)

ω

ω

ω

=

+

=

+

−

1

1

2

2

(17)

Sygnał (16) i jego charakterystyki widmowe przedstawiono na rys.10.

Materiały dydaktyczne powielane

11

t

ω

ω

f(t)

|F(jω)|

ϕ(ω)

π
2

π
2

1
2

1

0

0

0

Rys.10. Funkcja jednostronnie wykładnicza i jej charakterystyki widmowe

Widma sygnałów nieokresowych o skończonej energii mają zawsze charakter funkcji

ciągłych. Charakterystyki widmowe wielu częściej występujących sygnałów podano w pracy

[1].

1.2.3. Dyskretny szereg Fouriera

Przy obliczeniach numerycznych szeregu Fouriera (9), (11) należy:

• sumę nieskończoną (9) zastąpić sumą skończoną,

Materiały dydaktyczne powielane

12

• całkę (11) aproksymować sumą skończoną,

• przy obliczeniach uwzględniać tylko skończoną liczbę wartości funkcji f(t),

e

jh

t

ω

0

.

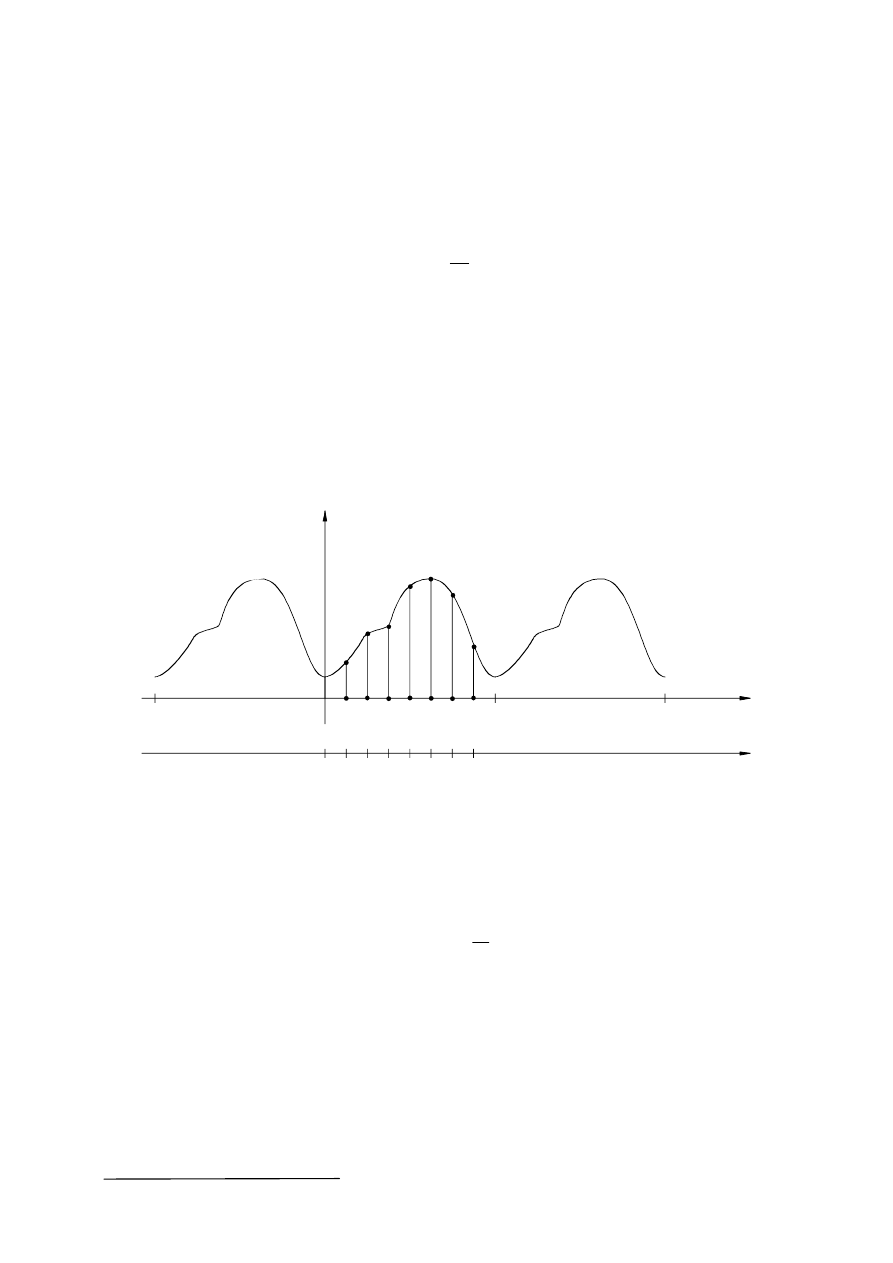
Tak więc przy obliczeniach numerycznych operuje się na ciągach próbek sygnału

f(m)=f(mT

0

), m=0,1,2,.., N-1 równoodległych względem siebie o przedział czasowy T

0

:

T

T

N

0

=

,

(18)

gdzie:

T - okres sygnału,

N - liczba próbek.

Dla ustalonego przedziału czasowego T

o

(okresu próbkowania sygnału) pobór większej liczby

próbek sygnału niż N nie wnosi żadnej dodatkowej informacji o sygnale f(t) z uwagi na jego

okresowość, rys.11.

f(t)

f(h)

t

h

T

0

2T

0

4T

0

(N-1)T

0

N

0

0

1 2

T

2T

-T

N-1

Rys.11. Funkcje f(t), f(m)

Podstawiając we wzorze (9) t=mT

0

uzyskuje się zależność pomiędzy ciągiem próbek sygnału

a ciągiem współczynników F

h

szeregu Fouriera

f mT

f m

F e

F W

h

j

N

hm

h

M

h M

h

hm

h

M

h M

(

)

( )

0

2

=

=

















=

= −

=

=−

=

∑

∑

π

(19)

przy czym:

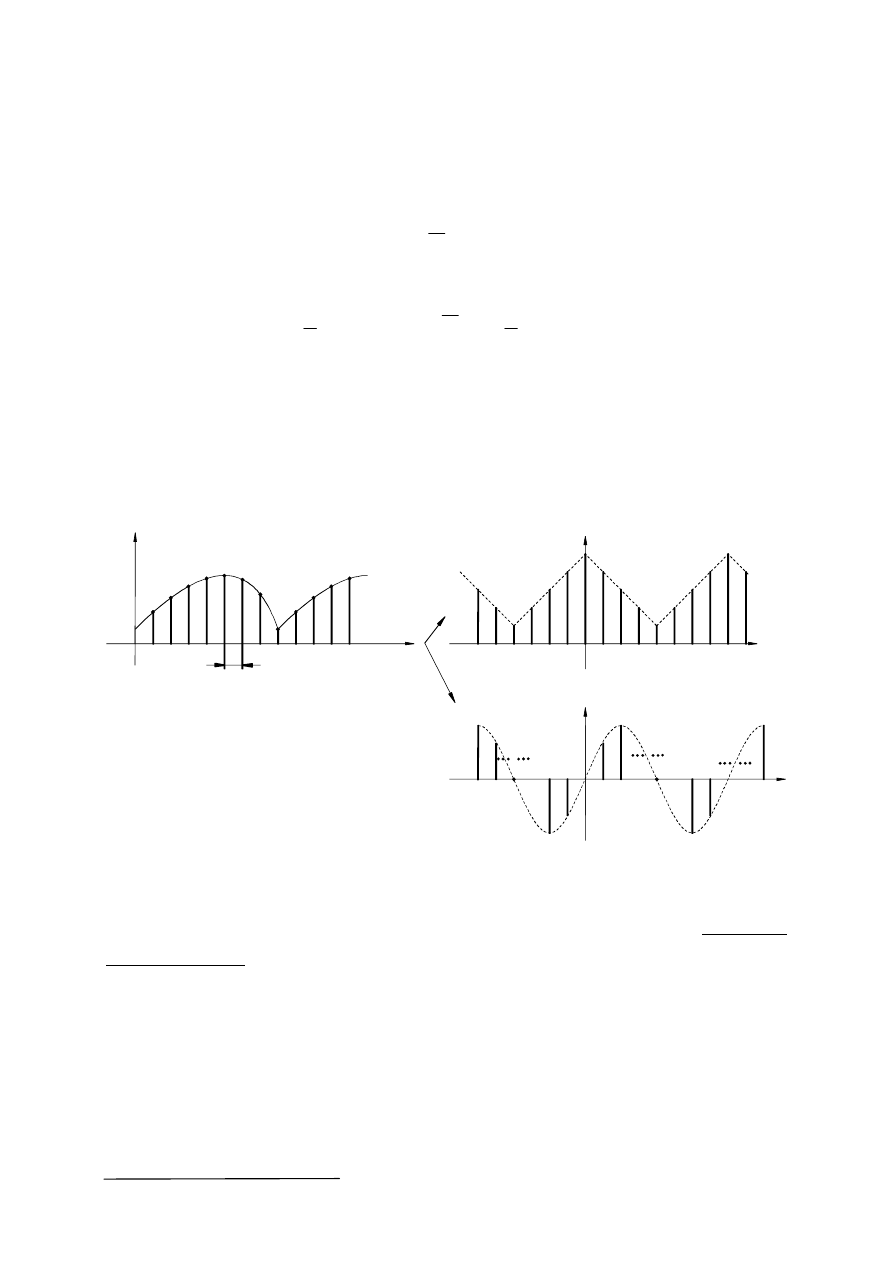
Materiały dydaktyczne powielane

13

h

M

m

N

N

M

w e

j

N

= ± ±

±

=

−

≥

+

=

0 1 2

0 1

1

2

1

2

, , ,..,

, , ,

…

π

(20)

W dalszym ciągu przybliżając (aproksymując) całkę (11) sumą skończoną uzyskujemy:

F

T

T f mT e

T

f m w

h

jh

T

T m

m

N

hm

m

N

=

=

=

−

−

=

−

∑

∑

1

1

0

0

2

0

1

0

1

0

(

)

( )

π

(21)

Wzory (19), (21) wiążą ciągi współczynników Fouriera F

n

sygnału z ciągami próbek tego

sygnału. Można zauważyć, że ciąg współczynników Fouriera F

h

obliczony na podstawie

wzoru (21) jest okresowy (rys.12) i zawiera 2M+1 różniących się wyrazów co wynika z

okresowości funkcji w

hm

(20).

m T

0

0

N

1 2 3

T

T

0

f(m)

0

+M

1 2

|F

h

|

h

-M

-1

-2

0

M

1 2

h

-M

-1

-2

arg F

h

Rys.12. Szereg Fouriera ciągu okresowego f(m)

Odwzorowania (19), którego współczynniki określa wzór (21) nazywamy dyskretnym

szeregiem Fouriera.

Szereg ten wykorzystuje się przy obliczaniu współczynników Fouriera sygnałów okresowych

na podstawie ciągu próbek tych sygnałów.

Na podstawie wzorów (19), (21) można zauważyć, że w przypadku funkcji okresowych

zawierających co najwyżej M harmonicznych dyskretny szereg Fouriera odtwarza te funkcje

z zerowym błędem. Dla funkcji okresowych mających nieskończone widmo harmonicznych

Materiały dydaktyczne powielane

14

w szeregu (19) nie zostają uwzględnione harmoniczne o numerach większych niż M.

Ponieważ (por. (20)):

2

1

2

M

N

M

N

+ ≤

<

(22)

to poprzez zwiększenie liczby próbek w okresie dokładność aproksymacji można dowolnie

zwiększać.

1.2.4. Dyskretna transformata Fouriera

Polega ona na innej interpretacji wzorów (19), (21) opisujących dyskretny szereg Fouriera,

który omówiono w poprzednim punkcie.

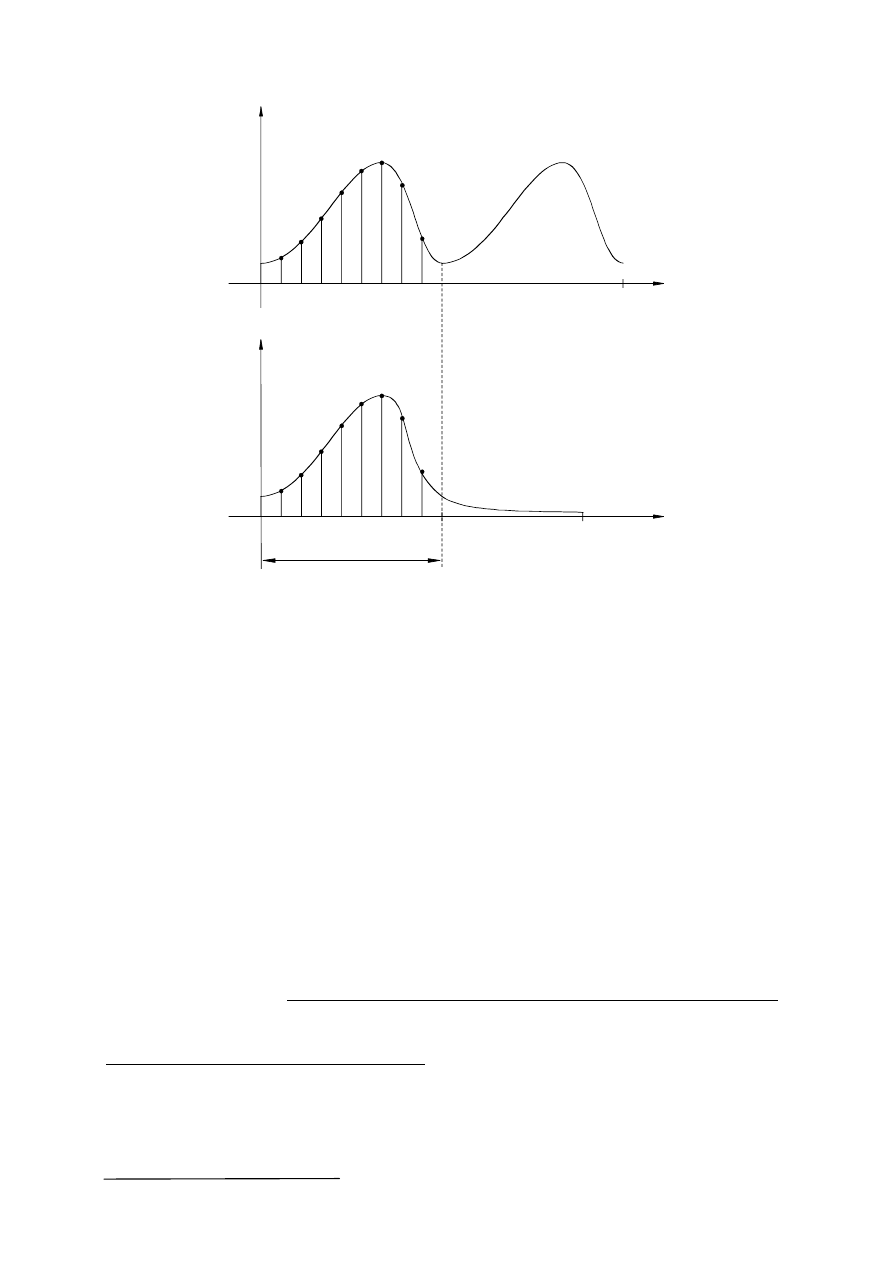
Niech funkcja f(t) w przedziale obserwacji T (rys.13) opisana jest ciągiem próbek f(m),

m=0,1,2,..,N-1. Rozróżnić należy dwa przypadki (rys.13).

1. Funkcja f(t) jest okresowa o okresie T. W tym przypadku funkcja ta opisywana jest

szeregiem dyskretnym Fouriera (19), którego współczynniki określa wzór(21).

2. Funkcja f(t) jest nieokresowa lecz w przedziale obserwacji T (którego nie należy

utożsamiać z okresem, rys.13) jest ona opisana tym samym ciągiem próbek co funkcja

okresowa z punktu 1. Tym samym ciągowi czasowemu f(m) próbek funkcji f(t) zostaje

przyporządkowany ciąg współczynników zespolonych F

n

. Ciąg ten nosi nazwę dyskretnej

transformaty Fouriera sygnału f(t)

Materiały dydaktyczne powielane

15

f(t)

t

m

0

f(t)

t

N

0

1 2 3

N

1 2 3

m

T = NT

0

Rys.13. Interpretacja dyskretnego szeregu Fouriera i dyskretnej transformaty Fouriera

Dyskretną transformatę Fouriera (DFT) można więc zdefiniować w następujący sposób:

Niech będą dane dwa ciągi:

• liczb rzeczywistych (czasowy) a

0

, a

1

,.., a

N-1

• liczb zespolonych A

0

, A

1

, .., A

n-1

o jednakowej liczebności N.

Odwzorowania:

A

a w

h

N

h

m

mh

m

N

=

=

−

−

=

−

∑

0

1

0 1

1

,

, ,...,

(23)

a

A w

m

N

m

h

mh

h

m

=

=

−

=

−

∑

0

1

0 1

1

,

, ,...,

(24)

nazywamy odpowiednio prostym i odwrotnym dyskretnym przekształceniem Fouriera (DFT).

1.2.5. Szybka transformata Fouriera FFT

Obliczenia numeryczne dyskretnej transformaty Fouriera według wzorów (23), (24)

wymagają wykonania N-1 operacji mnożenia oraz jednego dodawania N-1 składników

Materiały dydaktyczne powielane

16

A

a

a w

a w

a

w

h

m

m

N

m N

=

+

+

+ +

−

−

−

−

−

0

1

2

2

1

1

…

(

)

(25)

czyli prawie N

2

operacji mnożenia. Dla ciągów zawierających dużą liczbę wyrazów n oraz

wielokrotnych obliczeń (DFT) wydłuża to znacznie czas obliczeń. Redukcję liczby mnożeń

umożliwiają algorytmy numeryczne noszące nazwę szybkich transformat Fouriera 9FFT).

Omawianie tych algorytmów nie jest celem ćwiczenia. Można wykazać, że dla liczby próbek

N

s

s

=

=

2

3 4

,

, ,...

(26)

całkowita liczba mnożeń może być zredukowania do wartości (N log

2

N)/2.

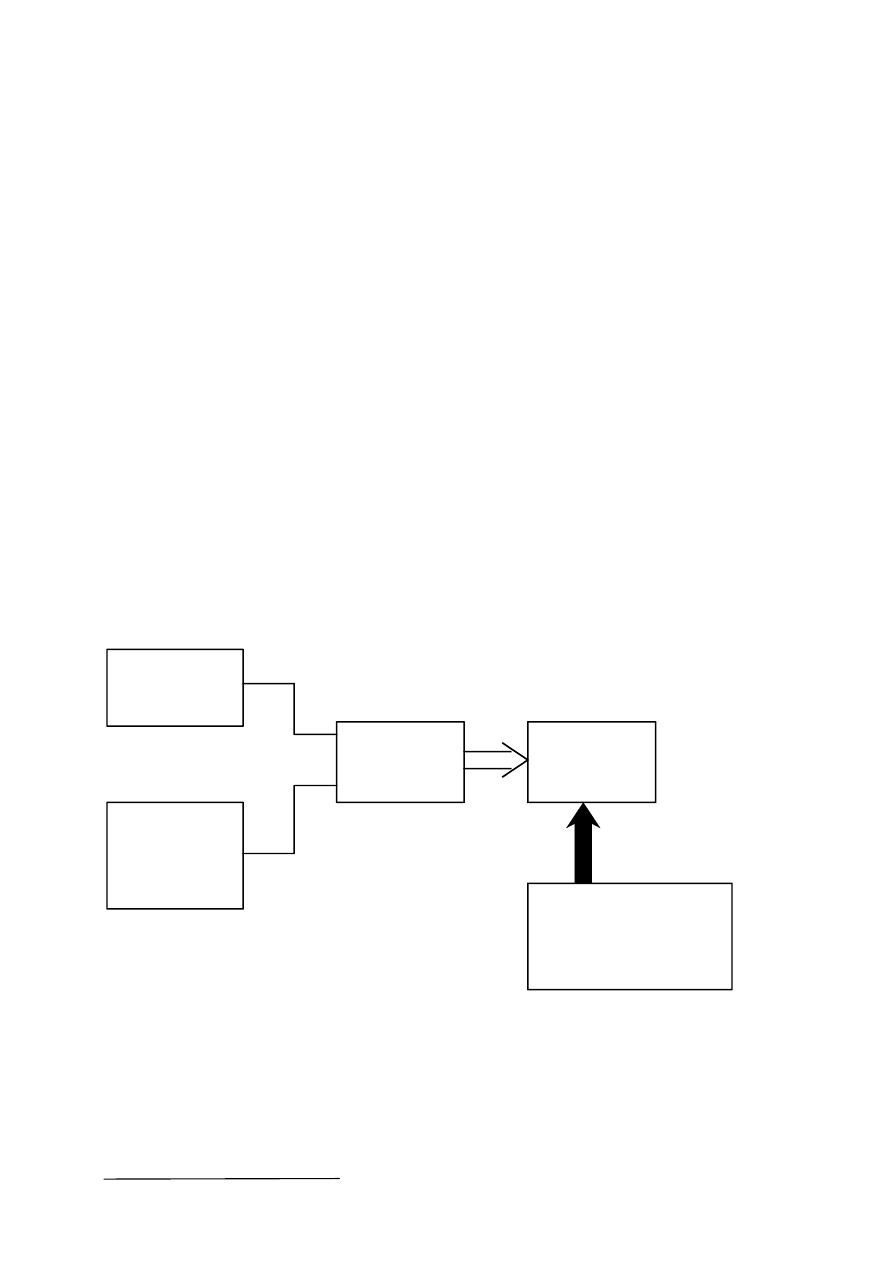
2. Opis układu pomiarowego dla ćwiczenia C3 (Próbkowanie sygnałów)

Schemat ideowy stanowiska pomiarowego przedstawiono na rys.14. Stanowisko to składa się

z następujących bloków funkcyjnych

• generatora sygnałowego napięcia sinusoidalnego, trójkątnego i prostokątnego o

regulowanej amplitudzie i częstotliwości,

• karty pomiarowej PC-LAB sprzężonej z komputerem IBM PC wyposażonym w niezbędne

oprogramowanie.

Generator
sygnałowy

Generator
specjalizowany
przebiegów
odkształconych

Karta
pomiarowa
PC LAB

IBM PC

Oprogramowanie
- karty pomiarowej
- PC DSP
- do odtwarzania sygn.

Rys.14. Schemat ideowy stanowiska.

Sygnały z generatora sygnałowego lub/i generatora przebiegów odkształconych

doprowadzane są do karty pomiarowej skąd w postaci plików ASCII są zapisywane na dysku

komputera. Dalsza obróbka tych plików przeprowadzana jest na drodze programowej z

Materiały dydaktyczne powielane

17

wykorzystaniem pakietu PC DSP oraz specjalnego programu do odtwarzania sygnałów

analogowych z próbek.

3. Opis układu pomiarowego dla ćwiczenia C4 (Analiza widmowa sygnałów)

Stanowisko to składa się z następujących przyrządów:

• generatora sygnałowego napięcia sinusoidalnego, trójkątnego i prostokątnego o

regulowanej amplitudzie i częstotliwości ,

• analizatora widma,
• oscyloskopu.

Literatura

1. Szabatin J.: Podstawy teorii sygnałów. WKŁ, Warszawa 1982.

2. Papoulis A.: Sygnały i układy. WKŁ, Warszawa 1988.