SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ

Katedra Techniki Pożarniczej

Zakład Hydromechaniki i Przeciwpożarowego Zaopatrzenia

Wodnego

LABORATORIUM HYDROMECHANIKI

ĆWICZENIE NR 2

TEMAT: OKREŚLANIE WYDATKU ZA POMOCĄ POMIARU ROZKŁADU

PRĘDKOŚCI DLA PRZEPŁYWU OSIOWO - SYMETRYCZNEGO

WARSZAWA, wrzesień 1999 r.

1. Właściwości fizyczne powietrza

Wykorzystywanym w *wiczeniu czynnikiem roboczym, przepływającym przez układ pomiarowy jest powietrze.

Powietrze jest mieszaniną gazów, głównie dwuatomowych: azotu i tlenu orasz niewielkiej ilości pary wodnej, dwutlenku węgla i gazów szlachetnych. Powietrze może by* traktowane jako gaz dwuatomowy. Gazy wykazują wiele cech wspólnych z cieczami. Podstawowe to brak sprężystości postaciowej czyli brak zdolności zachowania kształtu. Gaz zawsze wypełnia całkowicie naczynie, natomiast ciecz objętoś* równą objętości wprowadzonej do tego naczynia cieczy. Ciecz w naczyniu tworzy zawsze tzw. powierzchnię swobodną. W odróżnieniu od cieczy gazy charakteryzują się bardzo dużą ściśliwością, czyli łatwością zmiany objętości pod wpływem sił zewnętrznych.

Dopóki w gazach nie zachodza zmiany objętości , zachowanie się gazów nie różni się jakościowo od zachowania cieczy, która wypełnia tę sama przestrzeń co gaz i nie ma powierzchni swobodnej. W tym przypadku równania mechaniki płynów rządzące równowagą i ruchem są takie same dla cieczy i gazów. Większa ściśliwoś* gazów wynika z ich budowy. W gazach odległości między cząsteczkami są znacznie większe niż w cieczach. Siły spójności są dlatego bardzo małe. Stąd tez wynika stosunkowo niewielka gęstoś* gazów.

Ponieważ poszczególne gazy różnią się między sobą własnościami fizycznymi zachodziła trudnoś* sformułowania dokładnych praw dla wszystkich rodzajów gazów.

Wobec powyższego, jako podstawowy, przyjęto model gazu doskonałego. Gazem doskonałym nazywamy gaz, w którym nie ma sił przyczepności między cząsteczkami, a same cząsteczki przedstawione są w postaci punktów fizycznych. Pojęcie gazu doskonałego jest pojęciem hipotetycznym, do którego w celu uproszczenia rozważań odnosimy zmiany właściwości fizycznych i chemicznych gazów rzeczywistych.

Przyjmujemy, że gaz doskonały ma następujące właściwości:

• trwałoś* stanu gazowego (nie da się skropli*)

• niezmienną budowę chemiczną i cząsteczkowa

• stałe ciepło właściwe

• nie ma zdolności przeniesienia naprężeń stycznych (jest nielepki)

• stan fizyczny gazu doskonałego można określi* za pomocą trzech parametrów stanu: ciśnienia p., objętości właściwej v, temperatury T

Zależnoś* między tymi trzema parametrami tworzy związek zwany równaniem stanu gazu doskonałego:

p*v = R *T

gdzie: * - ciśnienie gazu,

v - objętoś* właściwa,

T - temperatura gazu,

R - indywidualna stała gazowa.

Gazy doskonałe spełniają prawa Boyle'a - Mariotte'a, Gay - Lussaca, prawa Avogadry i Joule”a - Thompsona. Najbardziej zbliżone do gazów doskonałych pod względem swego zachowania sa gazy jednoatomowe, np. hel, argon, krypton. Stosunkowo nieznaczne odchylenia wykazują gazy dwuatomowe, np. tlen, azot, wodór. Gazy wieloatomowe, takie jak metan, etan wykazują właściwości znacznie odbiegające od właściwości gazów doskonałych.

Każdy gaz występujący w przyrodzie jest gazem rzeczywistym i swymi własnościami mniej lub więcej odbiega od gazu doskonałego. Dlatego też w dokładnych badaniach należy uwzględniac różnice występujące między gazem rzeczywistym a doskonałym.

Powietrze traktowane jako mieszanina gazów dwuatomowych z dostatecznym przybliżeniem, w szerokim zakresie ciśnień i temperatur, spełnia równanie stanu gazu doskonałego.

Gazy rzeczywiste wykazują pewną zdolnoś* do przeniesienia naprężeń stycznych, a więc są lepkie. Związane jest to z ruchem cząsteczek gazu oraz z ich wymianą między sąsiednimi, wyodrębnionymi myślowo elementami gazu składającymi się z nieskończenie wielkiej liczby cząsteczek. Lepkoś* gazu wzrasta ze wzrostem temperatury.

Rys. 1. Wykres zależności współczynnika lepkości kinematycznej ν dla powietrza

w funkcji temperatury.

W warunkach zbliżonych do normalnych można przyjmowa* do obliczeń następujące parametry fizyczne powietrza:

• gęstoś* ρ = 1.23 kg.m³

• stała gazowa R = 287 m²/s²⋅K

• masa cząsteczkowa * = 29

• ciepło właściwe c_p = 1.0227 kJ/kg*K

2. Ciśnienia w poruszającym się płynie

W poruszającym się strumieniu gazu, podobnie jak w cieczy, wyodrębniamy ciśnienie statyczne, ciśnienie dynamiczne i ciśnienie całkowite. Ciśnieniem odniesienia, względem którego mierzymy ciśnienia w gazie przyjmujemy ciśnienie atmosferyczne. Jest to wygodne w praktyce dlatego, że zdecydowana większoś* przyrządów pomiarowych mierzy różnicę ciśnień między danym obszarem a ciśnieniem odniesienia, w tym wypadku atmosferycznym.

Ciśnienie statyczne jest to ciśnienie wskazywane przez przyrząd poruszający się w strumieniu płynu z taką samą prędkością i w tym samym kierunku, w którym porusza się płyn, tak aby prędkoś* względna przyrządu i płynu była równa zeru.

Jeżeli płyn nie porusza się, tj. pozostaje w stanie spoczynku jedynym ciśnieniem, jakie w nim panuje, jest ciśnienie statyczne.

Ciśnienie dynamiczne występuje tylko podczas ruchu płynu. Jest ono nierozerwalnie związane z prędkością przepływu płynu. Ilościowo wielkoś* ciśnienia dynamicznego wyraża zależnoś*:

ρ⋅V²

p_d = ____

2

gdzie: ρ - gęstoś* powietrza,

p_d- ciśnienie dynamiczne,

V - prędkoś* przepływu powietrza.

Ciśnienie całkowite p_c jest suma ciśnienia statycznego p_s i ciśnienia dynamicznego p_d:

p_c = p_s + p_d

W płynie pozostającym w spoczynku ciśnienie całkowite jest równe ciśnieniu statycznemu. Rzeczywiście, jeżeli V = 0, to p_c = p_s.

Ciśnienie całkowite niekiedy jest nazywane ciśnieniem spiętrzenia

Rys. 2. Graficzna ilustracja zależności między ciśnieniami w płynie.

3. Metody pomiaru ciśnień

Do pomiaru ciśnienia statycznego i dynamicznego stosuje się typowe manometry, np. sprężynowy, cieczowy różnicowy itp. O samym pomiarze decyduje sposób podłączenia przyrządu pomiarowego. Podczas pomiarów stosuje się kró*ce lub specjalne rurki pomiarowe podłączone do manometru.

Pomiar ciśnienia statycznego w sposób zgodny z definicją jest bardzo trudny i w praktyce nie jest możliwy do zrealizowania. W celu wyeliminowania wpływu prędkości płynu stosuje się kró*ce pomiarowe, w których powierzchnie otworów impulsowych są styczne do kierunku przepływu płynu. Zasadę pomiaru ciśnienia statycznego przedstawiono na rys. nr 3.

Rys. 3. Zasada pomiaru ciśnienia statycznego

Ciśnienie dynamiczne mierzy się za pomocą tzw. rurek spiętrzeniowych. Pomiar polega w większości przypadków na oddzielnym pomiarze ciśnienia statycznego i ciśnienia całkowitego oraz na wykorzystaniu manometru różnicowego, który wskaże różnicę między ciśnieniem całkowitym i statycznym, a więc ciśnienie dynamiczne. Zasadę pomiaru ciśnienia dynamicznego przedstawiono na rys. nr 4. Do pomiaru ciśnienia statycznego zastosowano piezometr, natomiast do pomiaru ciśnienia całkowitego rurkę spiętrzeniową zwaną rurką Pitota. Rurka ta jest wygięta pod kątem prostym i ustawiona wygiętym, otwartym końcem pod prąd tak, aby powierzchnia otworu impulsowego była prostopadła do kierunku przepływu. Z chwilą gdy rurka wypełni się cieczą do wysokości H, ciecz przestaje do niej napływa* i na powierzchni przekroju wlotowego ciecz zostaje wyhamowana do V = 0. Powierzchnię tę nazywamy powierzchnią spiętrzenia. Na skutek wyhamowania predkości ciśnienie dynamiczne zostaje zamienione na ciśnienie statyczne. Sumuje się ono z ciśnieniem statycznym panującym w przewodzie.

Rurka Pitota mierzy ciśnienie całkowite, a więc sumę ciśnienia statycznego i dynamicznego. Podłączenie do układu rurka Pitota - piezometr manometru różnicowego umożliwia bezpośredni pomiar ciśnienia dynamicznego (Rys. 4).

Rys. 4. Pomiar ciśnienia dynamicznego.

Wykorzystując fakt, że ciśnienie dynamiczne jest zależne od prędkości przepływu płynu można w sposób pośredni zmierzy* prędkoś* przepływu.

Z dotychczasowych rozważań wynika, że słuszne są zależności:

p_d = (ρ⋅V²)/2

p_d = ρ_m⋅g⋅h

z których wynika związek

(ρ⋅V²)/2 = ρ_m⋅g ⋅h

skąd

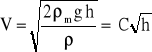
gdzie: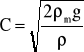

Pomiar ciśnienia dynamicznego umożliwia obliczenie odpowiadającej temu ciśnieniu prędkości przepływu. Możliwe jest również odpowiednie wyskalowanie manometru różnicowego w jednostkach prędkości, np. w m/s.

Do bezpośredniego pomiaru ciśnienia dynamicznego służy tzw. rurka Prandtla. Aby łatwiej zrozumie* zasadę jej działania wystarczy zapozna* się ze zjawiskami występującymi podczas opływu płynu wokół przeszkody.

Rys. 5. Opływ płynu wokół przeszkody.

Jeżeli w jednostajnym przepływie płynu z prędkością W₀ znajdzie się przeszkoda w postaci ciała zanurzonego, to wówczas bezpośrednio przed nią następuje spiętrzenie przepływu oraz opływ rozdzielonych strug wokół tej przeszkody. W punkcie znajdującym się w środku obszaru spiętrzenia zwanym punktem spiętrzenia następuje całkowite zahamowanie przepływu; prędkoś* przepływu w tym punkcie jest równa zeru.

Rozpatrzmy przepływ wzdłuż linii prądu biegnącej do punktu krytycznego. W znacznej odległości przed przeszkodą prędkoś* przepływu jest równa W₀. Ciśnienie panujące w punkcie spiętrzenia oznaczamy przez p₁; ciśnienie panujące w niezakłóconym przepływie, w znacznej odległości od przeszkody i na tej samej wysokości, na której znajduje się punkt spiętrzenia oznaczamy przez p₀. Wówczas dla rozpatrywanej linii prądu równanie Bernouliego przybiera posta*:

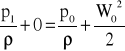
stąd ciśnienie w punkcie spiętrzenia:

p₁ = p₀ + 0.5ρ⋅(W₀)²

zatem przyrost ciśnienia w punkcie spiętrzenia wyniesie:

p₁ -p₀ = 0.5⋅ρ⋅(W₀)²

Obliczona wielkoś* różnicy ciśnień jest więc ciśnieniem dynamicznym.

Jeżeli w punkcie krytycznym rozpatrywanej przeszkody wywiercony zostanie niewielki otwór, to wówczas wewnątrz tego otworu będzie panowało ciśnienie spietrzenia p₁. Ciśnienie to może by* doprowadzone do przyrządu pomiarowego.

Rurka Prandtla zbudowana jest z dwóch współosiowo umieszczonych rurek metalowych. Częś* rurki skierowana pod prąd w stosunku do kierunku przepływu płynu zakończona jest półkulą, w osi której wywiercony jest mały otwór. Na półkuli tej występuje zjawisko spiętrzenia; poprzez otwór i rurkę doprowadzane jest do manometru ciśnienie spiętrzenia.

Pomiar ciśnienia statycznego realizowany jest za pomocą otworków umieszczonych symetrycznie na obwodzie zewnętrznej rurki. Przyjmuje się, że w odległości równej trzem średnicom rurki zewnętrznej (licząc od jej początku) ciśnienie statyczne na powierzchni rurki osiąga wartoś* ciśnienia statycznego odpowiadającego przepływowi niezakłóconemu. Konstrukcja rurki umożliwia oddzielny pomiar ciśnienia całkowitego, ciśnienia statycznego oraz dynamicznego w zależności od sposobu połączenia jej z mikromanometrem cieczowym.

Rozpatrzmy strugę leżącą w osi rurki i obierzmy na niej dwa przekroje, z których jeden wypada w punkcie spiętrzenia, a drugi leży w bardzo dużej odległości od rurki w obszarze przepływu niezakłóconego.

Rys. 6. Zasada pomiaru ciśnień rurką Prandtla.

Zakładając, że przepływający gaz jest nieściśliwy i przepływ jest ustalony napiszemy równanie Bernouliego dla obydwu przekrojów:

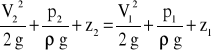
Przy poziomym usytuowaniu rurki z₂ = z₁. Ponadto w punkcie spiętrzenia mamy

V₁ = 0 oraz p₁ = p_c..

W punkcie odpowiadającym przepływowi niezakłóconemu (przekrój 2 oraz otworki w zewnętrznej rurce rurki Prandtla) mamy p₂= p_s oraz V₂ = V.

Po podstawieniu powyzszych wartości do równania Bernouliego otrzymamy:

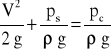
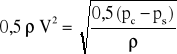
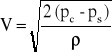
Jeżeli rurkę podłączymy do manometru cieczowego różnicowego, to zmierzymy różnicę ciśnień całkowitego i statycznego. Znając różnicę ciśnień i korzystając z powyższego wzoru możemy obliczy* prędkoś* przepływu. W przypadku, kiedy dokonamy pomiaru prędkości powietrza w warunkach normalnych, w których gęstoś* powietrza wynosi ρ = 1.23 kg/m³, to wyrażenie na prędkoś* będzie miało postac:

V = 4⋅(p_c - p_s)

Do powyższego wzoru należy wstawi* ciśnienie w milimetrach słupa wody. Wówczas otrzymany prędkoś* w m/s.

4. Pomiar wydatku

W przewodzie prostoosiowym o przekroju kołowym w dostatecznej odległości od wlotu przepływ można traktowac jako osiowosymetryczny.

Rys. 7. Rozkład prędkości w przepływie osiowosymetrycznym.

Jeżeli dysponujemy rozkładem prędkości wzdłuż promienia V = V (R) wzdłuż srednicy przewodu, uzyskanym drogą pomiaru za pomoca rurki Prandtla, to możemy obliczy* wydatek objetościowy.

Pole elementarnego pierścienia kołowego o promieniu R i szerokości dR wynosi

dF = 2⋅π⋅R⋅dR

Dla przepływu osiowosymetrycznego prędkoś* w każdym punkcie pierścienia kołowego wynosi V (R), zatem elementarny wydatek objętościowy wyraża się wzorem:

dQ = 2⋅π⋅R⋅V (R)⋅dR

Całkowity wydatek objętościowy będzie wyrażony zależnością:

Dysponując rozkładem predkości V(R) = f(R) można obliczy* wydatek całkowity.

Obliczenia wydatku dokonuje się zazwyczaj metoda graficzna sporzadzając wykres funkcji podcałkowej f(R) = ⋅R⋅V (R), a następnie planimetrując pole ograniczone tym wykresem.

Rys. 8. Przykładowy wykres f(R) = R⋅V (R)

Niech F oznacza pole pod wykresem f(R) = ⋅R⋅V (R), a κ stałą wynikającą z doboru skal na obu osiach. Wtedy

Q = 2⋅π⋅F⋅κ

Obliczając pole wykresu np. w cm², stałą κ wyznaczamy okreslając ilu m³/s wydatku odpowiada 1 cm² na wykresie. Obliczony w ten sposób wydatek objętościowy przyjmujemy w *wiczeniu jako wydatek rzeczywisty.

Rys. 9. Konstrukcja rurki Prandtla.

5. Pomiar wydatku za pomocą kryzy

Wydatek gazu definiowany jest jako iloś* gazu przepływająca w jednostce czasu przez rozpatrywany przekrój rurociągu. Jedną z metod pomiaru wydatku jest pomiar przy użyciu kryzy. Kryza jest to zwężka zainstalowana w rurociągu. Zasadę pomiaru przedstawiono na rys. nr 10. Pomiar ten jest pomiarem pośrednim. Polega na określeniu spadku ciśnienia na kryzie. Spadek ciśnienia na kryzie Δ* = ρ⋅g⋅h jest proporcjonalny do wydatku gazu.

Rys. 10. Pomiar spadku ciśnienia na kryzie.

Zakładając jednorodny rozkład prędkości napiszemy dla przekrojów 1 i 2 równanie ciągłości strugi

V₁⋅F₁ = V₂⋅F₂

oraz równanie Bernoulliego

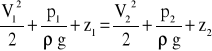
Zakładamy, że spadek ciśnienia na kryzie jest niewielki, wobec czego ρ = const, oraz, że różnica wysokości przekrojów jest bardzo mała, czyli, że z₁ = z₂ = z.

Otrzymamy równanie Bernoulliego w postaci:

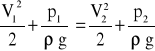
Po wstawieniu wyliczonej z równania ciągłości prędkości V₁ = V₂⋅( F₂/F₁) do równania Bernoulliego otrzymamy:

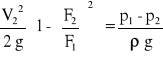
Wielkością charakterystyczną zwężki jest stosunek m pola przekroju zwężki do pola przekroju rurociągu. Możemy napisa*

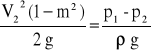
skąd

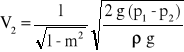
Ponieważ wydatek Q = V₂ ⋅ F₂, otrzymujemy

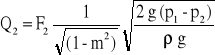
gdzie: p₁ - p₂ = ρ_cm⋅g⋅h (ρ_cm - gęstoś* cieczy manometrycznej).

Po wprowadzeniu stałej

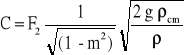
otrzymamy

Ponieważ wprowadzono uproszczenie przez założenie jednorodnego rozkładu prędkości oraz nie uwzględniono strat ciśnienia na kryzie, to obliczony teoretycznie wydatek będzie większy od wydatku rzeczywistego. W celu skorygowania rozbieżności wprowadzamy współczynnik wydatku

α = Q _rz/Q_t

gdzie: Q_rz - wydatek rzeczywisty

Q_t - wydatek teoretyczny.

Po uwzględnieniu korekty otrzymujemy

Współczynnik wydatku w rzeczywistości może byc wyrażony w funkcji liczby Reynoldsa oraz modułu kryzy.

6. Stanowisko pomiarowe

Stanowisko składa się z pomiarowej rury poziomej 1, dyfuzora 2, pionowej rury z kryzą 8. Przepływ powietrza jest wymuszony wentylatorem odśrodkowym 3, napędzanym silnikiem elektrycznym 4. Regulację wydatku uzyskuje się poprzez zmianę napięcia zasilania silnika za pomocą autotransformatora 5.

Ciśnienie dynamiczne jest mierzone rurką Prandtla 6, która jest przesuwana w płaszczyźnie prostopadłej do kierunku przepływu. Do kontroli ustawienia rurki pomiarowej względem ścianki rury służy odpowiednia podziałka. Mikromanometr 7 jest połączony róznicowo z rurką Prandtla. Ciśnienie różnicowe na kryzie jest wskazywane przez mikromanometr 9.

7. Wykonanie *wiczenia

• Wypoziomowa* i wyzerowa* mikromanometry

• Ustawi* żądane napięcie na autotransformatorze

• Dokona* pomiaru rozkładu ciśnienia dynamicznego wzdłuz średnicy w punktach oddalonych od siebie o 2 -5 mm. Zanotowa* położenie rurki Prandtla (promień) i wskazania mikromanometru. Zapisa* ustawienia mikromanometru.

• W czasie sondowania rurką Prandtla zanotowa* trzykrotnie wskazania spadku ciśnienia na kryzie.

7. Wykonanie sprawozdania

• Dla wykonanych pomiarów obliczy* wartoś* ciśnienia dynamicznego ze wzoru

p_d = ρ_cm⋅g ⋅l⋅sin α

gdzie: l - wychylenie cieczy w mikromanometrze,

α - kąt pochylenia ramienia mikromanometru względem poziomu,

ρ_cm - gęstoś* cieczy manometrycznej (ρ_cm = 780 kg/m³)

Rys. 11. Schemat stanowiska pomiarowego.

• Obliczy* prędkoś* powietrza w każdym punkcie pomiarowym

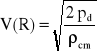
• Narysowa* wykres rozkładu prędkości f(R) = ⋅R⋅V (R)

• Określi* pole F pod wykresem w granicach 0 -R

Obliczy* wydatek objętościowy Q = 2⋅π⋅F⋅κ

• Obliczy* średnie wychylenie cieczy w mikromanometrze kryzy

• Obliczy* ciśnienie różnicowe kryzy p = ρ_cm⋅g ⋅l_śr⋅sin α

• Obliczy* wydatek zmierzony kryzą Q = C
  

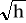
Obliczy* współczynnik wydatku dla kryzy α = Q _rz/Q_t

Literatura

1. J. Bukowski. Mechanika płynów. PWN warszawa, wszystkie wydania.

1. A.T. Troskolański. Hydromechanika. WNT Warszawa, wszystkie wydania.

1. H. Walden, J. Stasiak. Mechanika cieczy i gazów w inżynierii sanitarnej. Arkady, Warszawa.

1. L. Kołodziejczyk. Pomiary w inżynierii sanitarnej. Arkady Warszawa.

Pytania kontrolne

1. Porównac własności cieczy i gazów.

2. Porówna* własności gazów rzeczywistych i gazu doskonałego.

3. Omówic pojęcia ciśnień statycznego, dynamicznego i całkowitego.

4. Omówi* sposoby odbioru ciśnienia przy pomiarach wymienionych w pkt.3 ciśnień.

5. W jaki sposób definiujemy ciśnienie dynamiczne ?

6. Omówi* zasadę pomiaru ciśnienia dynamicznego rurką Prandtla.

7. Czy istnieją warunki, w których zmierzone rurką Prandtla ciśnienie dynamiczne równe jest całkowitemu ?

8. Omówic zasade pomiaru wydatku za pośrednictwem pomiaru rozkładu predkości.

9. W jaki sposób wyznaczamy stała planimetrowania ?

10. Omówic pomiar wydatku za pomocą kryzy.

LABORATORIUM HYDROMECHANIKI Edycja 2

ĆWICZENIE NR 2 Strona 21

Temat: Określanie wydatku za pośrednictwem pomiaru Iloś* stron 21

rozkładu prędkości w przepływie osiowo - symetrycznym Data: 99-11-10

---