SZKOŁA GŁÓWNA SŁUŻBY POŻARNICZEJ

Katedra Techniki Pożarniczej

Zakład Hydromechaniki i Przeciwpożarowego Zaopatrzenia

Wodnego

LABORATORIUM HYDROMECHANIKI

ĆWICZENIE NR 13

TEMAT: BADANIE PROCESU ZASYSANIA WODY

WARSZAWA, sierpień 1998 r.

*WICZENIE 13

BADANIE PROCESU ZASYSANIA WODY

1. Teoretyczne wysokości ssania

Zdolnoś* zasysania wody z określonej głębokości jest jedynym z ważniejszych czynników określających sposób wykorzystania określonego typu pomp w działaniach operacyjnych. Dlatego też istotnego znaczenia nabiera dokładne zapoznanie się z przebiegiem procesu zasysania.

Jeżeli będziemy rozpatrywali zdolnoś* zassania cieczy doskonałej, przy czym założymy, że proces ten przebiega bardzo powoli, to słuszne będzie następujące rozumowanie.

Rys. 1. Ilustracja procesu ssania wody.

Cylinder z tłokiem zanurzono w cieczy, powierzchnia swobodna cieczy jest bardzo duża, co w praktyce odpowiada postulatowi stałości położenia zwierciadła, tak aby między nieważkim tłokiem a powierzchnią swobodną nie było powietrza.

Oznacza to, że w chwili początkowej dolna powierzchnia tłoka znajduje się na wysokości lustra cieczy.

Aby przenieś* tłok w górę niezbędne jest przyłożenie pewnej siły. Siła ta musi by* równa co do modułu ciężarowi słupa cieczy znajdującego się pod tłokiem, zatem

F = ρgh*A /1/

gdzie:

F - siła przyłożona do tłoka

ρ - gęstoś* wody

g - przyspieszenie ziemskie

h - wysokoś* słupa wody pod tłokiem

A - powierzchnia tłoka

O ile w początkowym momencie zasysania ciśnienie bezpośrednio pod tłokiem wynosiło P_a, to po podniesieniu tłoka na wysokoś* h wyniesie ono p= p_a - ρgh. Jednocześnie w cylindrze na wysokości zwierciadła cieczy panuje ciśnienie p= p_a przy czym jest to słuszne w czasie całego procesu zasysania.

Jak łatwo można zauważy* stanem granicznym jest sytuacja kiedy ciśnienie pod tłokiem osiągnie wartoś* p= 0. Otrzymujemy wtedy:

p= 0 = pa - ρgh /2/

stąd

h = pa/ρg

Wielkoś* h jest nazywana największą teoretyczną wysokością ssania dla płynu doskonałego. Jak wida* zależy ona jedynie od ciśnienia atmosferycznego oraz od gęstości cieczy zassanej.

W przypadku gdy ciecz jest cieczą rzeczywistą zachodzi zjawisko parowania. Pod tłokiem będzie pewne ciśnienie pary nasyconej, które zależy od

Aktualnego ciśnienia pod tłokiem i temperatury cieczy. Przebieg tego ciśnienia przedstawiono na rys. 2.

Rys. 2. Prężnoś* pary nasyconej w funkcji ciśnienia i temperatury.

Jeżeli ponadto proces zachodzi powoli, to równanie 2 przyjmie

p* p_a - ρgh - p_par /3/

Jak łatwo można zauważy* w granicy uzyskamy:

0 = p_a - p_par - ρgh

p_a - p_par

h=

ρg

Jak więc wynika z tego równania dodatkowym czynnikiem ograniczającym wysokoś* ssania staje się p_par zależnie od ciśnienia i temperatury.

2. Czynniki zmniejszające w praktyce wysokoś* ssania.

Można założy*, że podczas samego zasysania wody uda się zawsze osiągną* wysokoś* teoretyczną dla płynu rzeczywistego. W praktyce jednak, po zassaniu wody następuje jej przetłoczenie. Ruch wody wywołuje zawsze straty lokalne i liniowe, po stronie ssawnej, a więc pewien spadek ciśnienia. Przy pracy pompy w warunkach ssania zbliżonych do ekstremalnych możliwa jest kawitacja, a więc zjawisko, do którego w zadanym wypadku nie wolno dopuści* z uwagi na możliwoś* zniszczenia pompy.

W praktyce w warunkach pracy pompy równanie 2 przybiera posta*:

0 = p_a - p_par - Δp_str - ρgh /4/

p_a - p_par - Δp_str

h=

ρg

Dochodzi więc dalszy czynnik ograniczający, przy czym należy ograniczy* przedstawioną wyżej wartoś* h do wartości ciśnienia, przy którym w danej temperaturze nie nastąpi kawitacja.

Największe straty po stronie ssawnej występują na smoku, koszu ssawnym oraz przy wejściu na wirnik. Dlatego też przyjmuje się dla motopomp i autopomp jako wysokoś* ssania H_s = 7,5m. przy nominalnym wydatku, przy czym nie określa się max. długości linii ssawnej.

3. Rzeczywisty proces zasysania.

W rzeczywistości proces zasysania realizowany jest przy pomocy urządzenia zasysającego, które spełnia rolę pompy próżniowej. Proces ten polega usunięciu z danego układu, zbudowanego z systemu ssawnego i objętości układu wodno - pianowego, powietrza i zastąpieniu go zasysaną cieczą. W tym rozumieniu proces zasysania możemy uzna* za zakończony, jeżeli układ zostanie całkowicie wypełniony cieczą (w odróżnieniu od definicji normowej wynikającej z definicji czasu zasysania).

Aby umożliwi* w miarę prostą analizę matematyczną przyjmijmy dwa uproszczenia:

• załóżmy, że linia ssawna jest usytuowana pionowo,

• załóżmy, że proces wypełniania układu wodno - pianowego cieczą zachodzi przy stałym ciśnieniu.

Ostatnie uproszczenie daje się uzasadni* prawie poziomym usytuowaniem układu samochodu.

Rozpatrzymy układ przedstawiony schematycznie na rys. 3.

Rys. 3. Ilustracje rzeczywistego procesu zasysania wody.

Podobnie jak poprzednio założymy, że proces zachodzi powoli (w praktyce od kilkunastu do kilkudziesięciu sekund, co całkowicie upoważnia do przyjęcia takiego założenia), pomiędzy kolejnymi stanami równowagi. Założenie takie pozwala na pominięcie ciśnienia pary nasyconej. W rurze ssawnej na wysokości zwierciadła cieczy w zbiorniku uzyskamy:

p_a = ρgh + p_pow /5/

Zakładamy, że charakterystyka urządzenia zasysającego Q = f(p.) jest znana. Cały układ ma objętoś* V_c w momencie rozpoczęcia zasysania. Średnica rury ssawnej oraz geometryczna wysokoś* ssania są znaczne. Po włączeniu pompy próżniowej zmniejsza się ciśnienie w układzie, a tym samym poziom wody w rurze ssawnej się zwiększa, przy czym podciśnienie i wysokoś* słupa wody sobie odpowiadają. Proces wzrostu podciśnienia (wielkości Δp= p_a - p.) zakończy się z chwilą osiągnięcia przez wodę poziomu układu wodno - pianowego; do momentu napełnienia układu będzie przebiegał przy stałym ciśnieniu.

Rozpatrzmy zmiany wysokości słupa cieczy w czasie. Objętoś* bieżąca powietrza w układzie wynosi:

V = V_o - s - h /6/

gdzie:

V - objętoś* bieżąca,

V_o - objętoś* początkowa,

s - przekrój rury ssawnej,

h - bieżąca wysokoś* słupa cieczy.

Podciśnienie odpowiadające wysokości tego słupa jest równe:

Δp= ρgh lub dp= ρgdh /7/

gdzie:

ρ - gęstoś* wody.

Masowy wydatek zasysanego powietrza jest równy:

dm= Q(Δp.)dt /8/

gdzie:

Q(Δp.) - wydatek pompy próżniowej,

t - czas,

dm - ubytek masy.

Uwzględniając powyższe, zgodnie z równaniem stanu można napisa*:

g(10-h)*(Vo-sh) = mRT /9/

ciśnienie objętoś*

lub w postaci równania różniczkowego:

h(2sh-10s-V_o)h = Q(Δp.) RT dt /10/

Skąd czas zasysania rozumiemy jako czas napełniania rury ssawnej /11/:

Równanie to charakteryzuje dynamikę procesu zasysania, przy czym proces

ten jest tym szybszy, im mniejsze V_o, s i h oraz im większe Q/Δp/.

W tym miejscu można łatwo zauważy*, że jeżeli układ wodno - pianowy wraz z układem ssawnym nie będzie hermetyczny, to równolegle z usuwaniem powietrza, przez nieszczelności będzie przenika* do układu powietrze z zewnątrz.

Zatem rzeczywisty efektywny wydatek zasysanego powietrza zmniejszy się i będzie wynosił:

Q_n = Q_p/Δp/ - Q_n/Δp/.

Czas zasysania wydłuży się i wyniesie:

/12/

Działanie nieszczelności na osiągane podciśnienie łatwo można przedstawi* graficznie (rys. 4).

Rys. 4. Wpływ nieszczelności na wysokoś* ssania.

Jak wynika z przedstawionych charakterystyk wydatek zasysanego powietrza spada ze wzrostem podciśnienia, zaś wydatek powietrza wchodzącego do układu na skutek nieszczelności rośnie.

Wpływ nieszczelności może by* znacznie większy niż wymienionych wcześniej czynników, dlatego też zagadnienie sprawdzenia szczelności nabiera kluczowego

znaczenia. Po napełnieniu rury ssawnej zbiornik jest napełniany cieczą przy stałym ciśnieniu.

Zatem czas napełniania zbiornika wyniesie:

V1ρgh 1

tn =

RT Q_p/Δp/ - Q_n/Δp/ /13/

gdzie V1 oznacza objętoś* układu wodno - pianowego (bez objętości linii ssawnych).

Całkowity czas zasysania jest naturalnie sumą wielkości określonych wzorami 12 i 13.

Z przedstawionych zależności wynika, że czynnikami decydującymi o dynamice procesu zasysania, a także wyznaczającymi jego granice są dla rozpatrywanego układu dwie wielkości: charakterystyka pompy próżniowej i stan techniczny układu wodno - pianowego określany charakterystyką Q_n = f/Δp/.

4. Metody wyznaczania charakterystyki pompy próżniowej oraz wydatku powietrza przenikającego do układu na skutek nieszczelności.

Badanie charakterystyki pompy próżniowej możemy przeprowadzi* na stanowisku pomiarowym przedstawionym schematycznie na rysunku 5. W celu dokonania pomiaru należy zamkną* wszystkie zawory odcinające zbiornik od atmosfery oraz zawór do suchej próżni uniemożliwiający zassanie wody. Cały układ pomiarowy powinien by* hermetyczny. Jego objętoś* jest znana. Do przygotowanego w opisany wyżej sposób zbiornika przyłączamy pompę próżniową i rejestrujemy proces spadku ciśnienia w czasie (Δp= f(t)). Ponieważ proces ten zachodzi przy stałej objętości a ponadto przy stałej temperaturze, możemy napisa*, że ciśnienie powietrza w układzie zależy jedynie od ilości /masy/ zawartego w nim powietrza:

p₁V₁ = m₁RT₁

p₂V₂ = m₂RT₂ jeżeli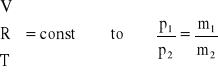
(14)

ponieważ V/RT = const. To prawdziwa jest zależnoś*

m= const p= Cp lub dm = Cdp /15/

Ponieważ jednak dm = Q dt, to

dp

Q = C

dt

Wielkoś* pochodnej dp/dt można określi* drogą aproksymowania wykresu Δp= f(t) a następnie jego zróżniczkowania. Możliwe jest również wykreślenie szeregu stycznych do tego wykresu a następnie określenie tangensa kąta ich nachylenia do osi odciętych, który stanowi wartoś* pochodnej w danym punkcie. Jeżeli do obliczenia wydatku wykorzystamy wartoś* bezwzględną pochodnej, to jest obojętne, czy różniczkujemy funkcję określającą przebieg ciśnienia czy też podciśnienia w zbiorniku w czasie. Przyjmujemy, że powietrze usuwane z układu /wydatek pompy próżniowej Q_p/ będzie oznaczane znakiem „+”, zaś wydatek powietrza przenikającego do układu Q_n będzie oznaczany znakiem „- „.

Charakterystykę nieszczelności Q_n = f (p.) uzyskamy, jeżeli w zbiorniku przygotowanym w sposób opisany wyżej wywołamy podciśnienie, zamkniemy zawór łączący zbiornik z pompą próżniową i zarejestrujemy wzrost ciśnienia w zbiorniku w czasie. Zgodnie z przyjętym założeniem, że zbiornik jest hermetyczny, spadku takiego nie da się zaobserwowa*. Dlatego też należy otworzy* zawór odcinający dyszkę z otworem średnicy kilku milimetrów, która symuluje nieszczelnoś*. Dalsze postępowanie mające na celu uzyskanie charakterystyki Q_n = f(Δp.) jest identyczne z postępowaniem opisanym wyżej, prowadzącym do otrzymania charakterystyki pompy próżniowej Q_p = f(Δp.).

Rys.5. Schemat stanowiska.

5. Prowadzenie pomiarów.

1. Określenie warunków w których dokonywane są pomiary.

• odczyta* z termometru temperaturę powietrza,

• odczyta* z barometru ciśnienie atmosferyczne,

• zmierzy* geometryczną wysokoś* ssania.

1. Określenie charakterystyki pompy próżniowej.

• zamkną* wszystkie zawory łączące zbiornik z atmosferą oraz zawór na rurze ssawnej, uniemożliwiając zassanie wody,

• włączy* rejestrator TZ21s,

• uruchomi* pompę próżniową,

• z chwilą, kiedy ciśnienie w zbiorniku ustabilizuje się /graniczne możliwości pompy próżniowej/, zakręci* zawór łączący zbiornik z pompą próżniową. Po wykonaniu tych czynności należy wyłączy* pompę próżniową i odczyta* wskazanie wakuometru kontrolnego.

3. Określenie charakterystyki nieszczelności.

• w układzie znajdującym się w stanie końcowym z punktu 5.2. otworzy* zawór odcinający dyszkę,

• po zrównaniu się ciśnienia w zbiorniku z ciśnieniem atmosferycznym wyłączy* rejestrator.

4. Określenie czasu zasysania.

• ponownie zakręci* wszystkie zawory odcinające zbiornik od atmosfery,

• włączy* rejestrator,

• włączy* pompę próżniową,

• wyłączy* pompę próżniową w momencie, kiedy woda osiągnie poziom zaznaczony czerwoną kreską na wodowskazie.

UWAGA ! NIEPRZESTRZEGANIE TEGO WYMOGU GROZI USZKODZENIEM POMPY PRÓŻNIOWEJ.

• opróżni* układ /w tym celu należy otworzy* zawór łączący z atmosferą i zawór zrzutu wody/,

• powtórzy* wszystkie czynności przy otwartym zaworze odcinającym dyszkę symulującą nieszczelnoś*.

6. Wykonanie sprawozdania.

Zastosowane w *wiczeniu metody pomiarowe pozwalają na określenie charakterystyki pompy próżniowej, charakterystyki nieszczelności, teoretycznego czasu ssania i rzeczywistego czasu ssania na podstawie zarejestrowanych nieustalonych przebiegów zmian ciśnienia w rozpatrywanym układzie. W celu opracowania wyników najkorzystniej byłoby wykorzysta* możliwości EMC. Ponieważ w chwili obecnej jest to niemożliwe z przyczyn obiektywnych, proponuje się zastosowanie kombinowanej metody obliczeniowo - wykreślnej.

6.1. Określenie charakterystyk Q_p=f/Δp/ i Q_n=f/Δp/.

Naszym celem będzie określenie charakterystyk pompy próżniowej i nieszczelności metodą graficzną. Rezultatem będzie charakterystyka przedstawiona w formie wykresu. Jak zaznaczono wcześniej z pomiarów uzyskujemy wykresy Δp= f/t/. Ponieważ wydatek jest w obydwu przypadkach obliczany ze wzoru 16 w którym nie znamy pochodnej dp/dt, zatem musimy zróżnicowa* graficznie wykresy otrzymane z rejestratora.

Konstrukcja punktów wykresu pochodnej opiera się na fakcie, że pochodna jest równa tangensowi kąta nachylenia stycznej do krzywej /rys. 6/.

Rys. 6. Konstrukcja punktów wykresu pochodnej.

Weźmy pod uwagę rzędną AM rozpatrywanej krzywej. Na osi odciętych od punktu A w lewą stronę odłóżmy odcinek BA=1. Z punktu B wykreślamy prostą BN równoległą do stycznej do krzywej w punkcie M. Punkt N przecięcia tej prostej z prostą AM należy do wykresu pochodnej, gdyż z trójkąta BAN wynika,

że AN / BA = tgα = y'. Powtarzając konstrukcję dla różnych punktów danej krzywej y=f/x/ możemy otrzymywa* dowolnie dużo punktów wykresu pochodnej. Połączenie tych punktów pozwala uzyska* przybliżony wykres pochodnej. Mając dane wartości pochodnej dp/dt możemy obliczy* ze wzoru 16 wartości odpowiadającego im wydatku. Wyniki obliczeń notujemy w tabeli 1 /wg przedstawionego poniżej wzoru/ a następnie sporządzamy na jednym arkuszu wykresy Q_p = f/Δp/ i Q_n = f/Δp/.

Wzór tabeli 1.

L.p.	p	dp/dt	Q
--	pa	pa/s	kg/s

Oczywiście należy sporządzi* oddzielne tabele do określenie Q_p i Q_n.

2. Określenie teoretycznego czasu ssania.

Teoretyczny czas ssania stanowi sumę wielkości określanych wzorami 12 i 13. Ponieważ występujące w tych wzorach charakterystyki pompy próżniowej i nieszczelności są dane wykreślnie, zatem możliwe jest jedynie graficzne określenie całki występującej we wzorze 12. W tym celu niezbędne jest wykreślanie funkcji podcałkowej w granicach od hs = 0 do hs = hgs. Wartości Q_p i Q_n zależą od h, czego nie wolno pominą*. Należy je odczyta* z otrzymanych wcześniej wykresów. Powinno się obliczy* przynajmniej 10 wartości funkcji podcałkowej obejmujących cały przedział zmienności h.

Całkowanie graficzne polega na określeniu pola pod wykresem funkcji podcałkowej. Czas napełniania linii ssawnej wodą określimy ze wzoru:

t=ℵ*F /17/

gdzie:

F- pole między wykresem funkcji podcałkowej a osią odciętych

ℵ - stała planimetrowania

Stałą wyznaczamy jak następuje:

na osi h: 1 cm *X m.

na osi t: 1 cm *Y s/m.

zatem: 1cm² * X*Y *s = ℵ

UWAGA ! Wykres funkcji podcałkowej należy sporządzi* dla tej części przebiegu w której następuje wypełnianie rury ssawnej wodą /odpowiada to momentowi w którym proces wzrostu podciśnienia zostaje zahamowany/.

Drugą składową czasu zasysania, określoną wzorem 13, wyznaczymy przyjmując p., Q_p, Q_n jako stałe, odpowiadające geometrycznej wysokości ssania.

Przedstawiony tok obliczeń pozwala porówna* wartości czasu zasysania określone teoretycznie z czasem określonym doświadczalnie w przypadku układu hermetycznego lub nieszczelnego, a także oceni* wpływ nieszczelności na dynamikę procesu zasysania wody.

Pytania kontrolne.

1. W jaki sposób określamy teoretyczną wysokość ssania ?

2. W jaki sposób temperatura cieczy wpływa na wysokośc ssania ?

3. Przedstawić zależnośc prężności pary nasyconej od temperatury ?

4. Omówić wpływ nieszczelności układu na wysokość ssania ?

5. W jaki sposób wzrost objętości układu wpływa na dynamikę procesu

zasysania wody ?

6. W jaki sposób wzrost wysokości ssania wpływa na dynamikę procesu zasysania wody ?

7. Czy w czasie zasysania wody występują spadki ciśnienia wywołane stratami przepływu ? Uzasadnić odpowiedź.

8. Dlaczego badanie procesu zasysania wymaga użycia rejestratora ?

9. Omówić metodę różniczkowania graficznego.

10. W jaki sposób na podstawie przebiegu zmienności podciśnienia w czasie można określić charakterystykę pompy próżniowej Q = f(Δp) ?
    

LABORATORIUM HYDROMECHANIKI Edycja 2

*WICZENIE NR 13 Strona : 12

Temat: Badanie procesu zasysania wody Iloś* stron: 17

Data: 00-01-23

---