
System Identification and Self-Tuning Pole Placement
Control of the Two-Axes Pneumatic Artificial Muscle
Manipulator Optimized by Genetic Algorithm
Kyoung Kwan Ahn
Ho Pham Huy Anh
School of Mechanical and Automotive Engineering
Graduate School of Mechanical and Automotive Engineering
University of Ulsan
University of Ulsan
San 29, Muger 2dong, Nam-gu, Ulsan, 680-764, Korea
San 29, Muger 2dong, Nam-gu, Ulsan, 680-764, Korea
kkahn@ulsan.ac.kr
hphanh@hcmut.edu.vn
Abstract - In this paper, self-tuning pole placement control of
the 2-axes pneumatic artificial muscle (PAM) manipulator is
proposed as an appropriate strategy which can automatically
accommodate wide changes in operating conditions, such as
payload and time varying parameters of the 2-axes PAM
manipulator. This novel proposed control scheme is initially
applied to the independent control of the PAM manipulator joint
angle position. Proposed pole placement controller utilizes a low
order linear approximation of the PAM manipulator ARX model,
whose parameters are estimated online from past input and
output values by RLS system identification algorithm.
Furthermore, parametric values of ARX model are optimized by
a modified genetic algorithm (MGA). This superb combination
between MGA and self-tuning pole placement controller is
developed for tracking the joint angle position of the prototype 2-
axes PAM manipulator. Simulation and experiment results
demonstrate the excellent performance of the proposed control
scheme. These results can be applied to model, identify and
control other highly nonlinear systems as well.
Index Terms - modified genetic algorithm (MGA), online ARX
model identification, 2-axes pneumatic artificial muscle (PAM)
manipulator, modified self-tuning pole placement control.
I. I
NTRODUCTION
Control of pneumatic artificial muscle (PAM) actuators is
an ongoing area of research due to some challenging
difficulties [1, 2]. Nowadays, research into the control and the
physical and modeling properties of PAM has been
undertaken at the INSA (Toulouse, France) [2], the Bio-
Robotics Lab at the University of Washington, Seattle, [3],
Human Sensory Feedback (HSF) Laboratory at Wright
Patterson Air Force Base [4](Reynolds, Repperger, Phillips
and Bandry 2003), and Fluid Power Machine Intelligence
Laboratory (FPMI Lab) at Ulsan University [5][6] among
others.
This paper addresses the modeling, identification and
control of a two-joint planar PAM manipulator actuated by
two groups of antagonistic PAM pair. Due to their highly
nonlinear and time-varying parameter nature, PAM
manipulator control presents a challenging nonlinear control
problem that has been approached via many methodologies.
Related literature has appeared some of ways for modeling
and control the PAM actuator. In [7], a direct continuous-time
adaptive control technique is applied to control joint angle in a
single-joint arm. The simulation considers PAM individually
in both bicep and tricep positions. In [8], a gain scheduling
controller is designed for a single PAM hanging vertically in
the lab actuating a mass. Both force as well as position control
are considered. Chan and Lilly (2003)[9] suggested a fuzzy
model reference learning controller designed for a single PAM
hanging vertically actuating a mass in the lab. Tracking results
are obtained, and these are shown to agree well with simulated
results. In [10], a fuzzy P+ID controller is designed for the
same previous system. The novel feature is a new method of
identifying fuzzy systems from experimental data using
evolutionary techniques. The experimental results are shown
to be superior to those in [9], i.e., tracking error is less while
using less control effort. All these results prove that up to
now, it is still lack of a simple and quite efficient model for
the PAM manipulator which will be utilized efficiently in
adaptive & self-tuning control such highly nonlinear PAM
manipulator.
The contributions of this paper include ARX model-based
modeling and identification of the 2-axes PAM manipulator
composed two antagonistic groups of PAM actuators;
optimizing PAM manipulator ARX model’s parameters using
a novel proposed modified genetic algorithm (MGA);
formulating a simple but highly efficient ARX model so that it
is suitable for online parameter modified self-tuning pole
placement control the highly nonlinear 2-axes PAM
manipulator. This novel proposed control strategy is initially
applied and obtains from simulation and experiment
outperforming results in comparison with other control
algorithms.
This paper is arranged as follows. Section 2 introduces
modified genetic algorithm (MGA) used in PAM manipulator
modeling and identification. Section 3 presents the
configuration of the 2-axes PAM manipulator with hardware
used in process of modeling, identification and control.
Section 4 presents and analyses the results of MGA-based
PAM manipulator modeling and identification process.
Section 5 introduces the modified pole placement control
algorithm based on online ARX model to control the 2-axes
PAM manipulator. Section 6 presents simulation and
experiment results of the joint angle position control of the
modified pole placement controller. Section 7 contains
discussion and conclusion.
1-4244-0828-8/07/$20.00 © 2007 IEEE.
2604
Proceedings of the 2007 IEEE
International Conference on Mechatronics and Automation
August 5 - 8, 2007, Harbin, China
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
II. M
ODIFIED
G
ENETIC
A
LGORITHM
(MGA)
FOR
O
PTIMIZING
T
HE
2-A
XES
PAM M
ANIPULATOR
ARX M
ODEL
P
ARAMETERS
.
The steps of MGA-based model identification procedure
are summarized as in Fig. 1:
Fig.1 Flow chart of MGA-based optimal Identification Process
III. C
ONFIGURATION OF
T
HE
2-A
XES
PAM M
ANIPULATOR
S
YSTEM
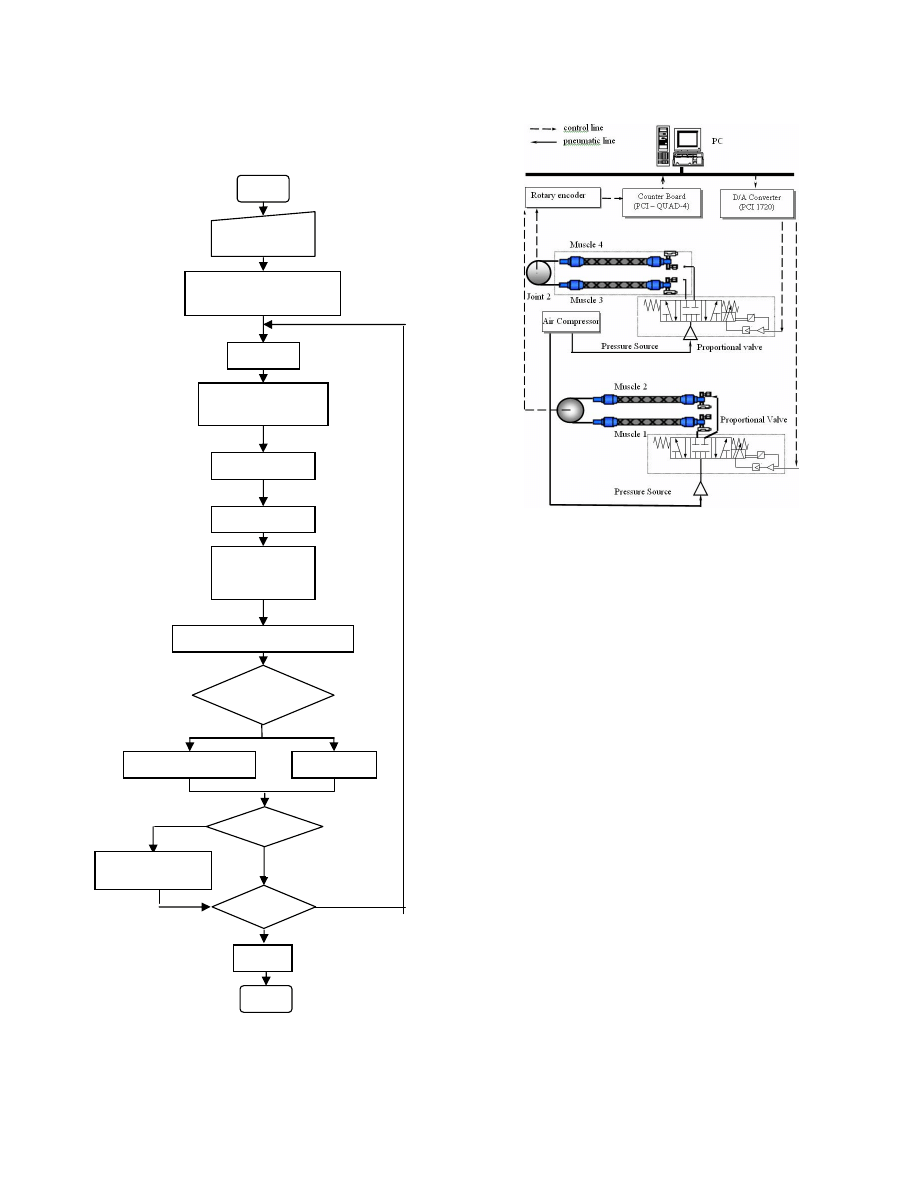
Fig. 2 Schematic diagram of the experimental apparatus
.
Fig. 2 presents the configuration of the hardware set-up
installed from Fig.2 as to model and to identify the 2
nd
order
ARX model of the both of joints of the 2-axes PAM
manipulator by obtaining PRBS training and validating data
from the 2 joints of the 2-axes PAM manipulator. This set-up
is also used to control the 2-axes PAM manipulator based on
adaptive pole placement controller as well.
The hardware includes an IBM compatible PC (Pentium
1.7 GHz) which sends the voltage signals to control the two
proportional valves (FESTO, MPYE-5-1/8HF-710B), through
a D/A board (ADVANTECH, PCI 1720 card). The rotating
torque is generated by the pneumatic pressure difference
supplied from air-compressor between the antagonistic
artificial muscles. Consequently, the both of joints of the 2-
axes PAM manipulator will be rotated to follow the desired
joint angle reference. The joint angles,
θ
1
[deg] and
θ
2
[deg],
are detected by two rotary encoders (METRONIX, H40-8-
3600ZO) and fed back to the computer through a 32-bit
counter board (COMPUTING MEASUREMENT, PCI
QUAD-4 card). The pneumatic line is conducted under the
pressure of 5[bar] and the software control algorithm of the
closed-loop system is coded in C-mex program language run
in Real-Time Windows Target of MATLAB-SIMULINK
environment.
IV. R
ESULTS OF
MGA-B
ASED
I
DENTIFICATION OF
T
HE
2-
AXES
PAM M
ANIPULATOR
.
Considering an ARX model with noisy input which can
be described as
)
(
)
(
)
(
)
(
)
(
)
(
1
1
1
t
e
q
C
T
t
u
q
B
t
y
q
A
−
−
−
+
−
=
(1)
End
Decod
e
no
yes
m=L
t
Extinction strategy
k = 0
no
yes
k=L
e
yes
no
k=k+1, m=m+1
k=0, m=0
1
max
max
−
=
i
i
F
F
Take place the worst
Reproduction
Crossover
Mutation
Fitness Scaling
Elitist strategy
Decode and evaluate
Fitness value
i = i + 1
Randomly generate N set
of Initial population
Set initial value
(i=0, k=0, m=0)
Start
2605
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
with
2
2
1
1
1
1
)
(
−
−
−
+
+
=
q
a
q
a
q
A
1
2
1
1
)
(
−
−
+
=
q
b
b
q
B
2
3
1
2
1
1
)
(
−
−
−
+
+
=
q
c
q
c
c
q
C
with e(t) is the white noise sequence with zero mean and unit
variance.
The purpose here is to apply MGA for optimally
identifying a
1
, a
2
, b
1
and b
2
parameters in present of the noise.
The excitation input u(t) to be used is chosen as pseudo
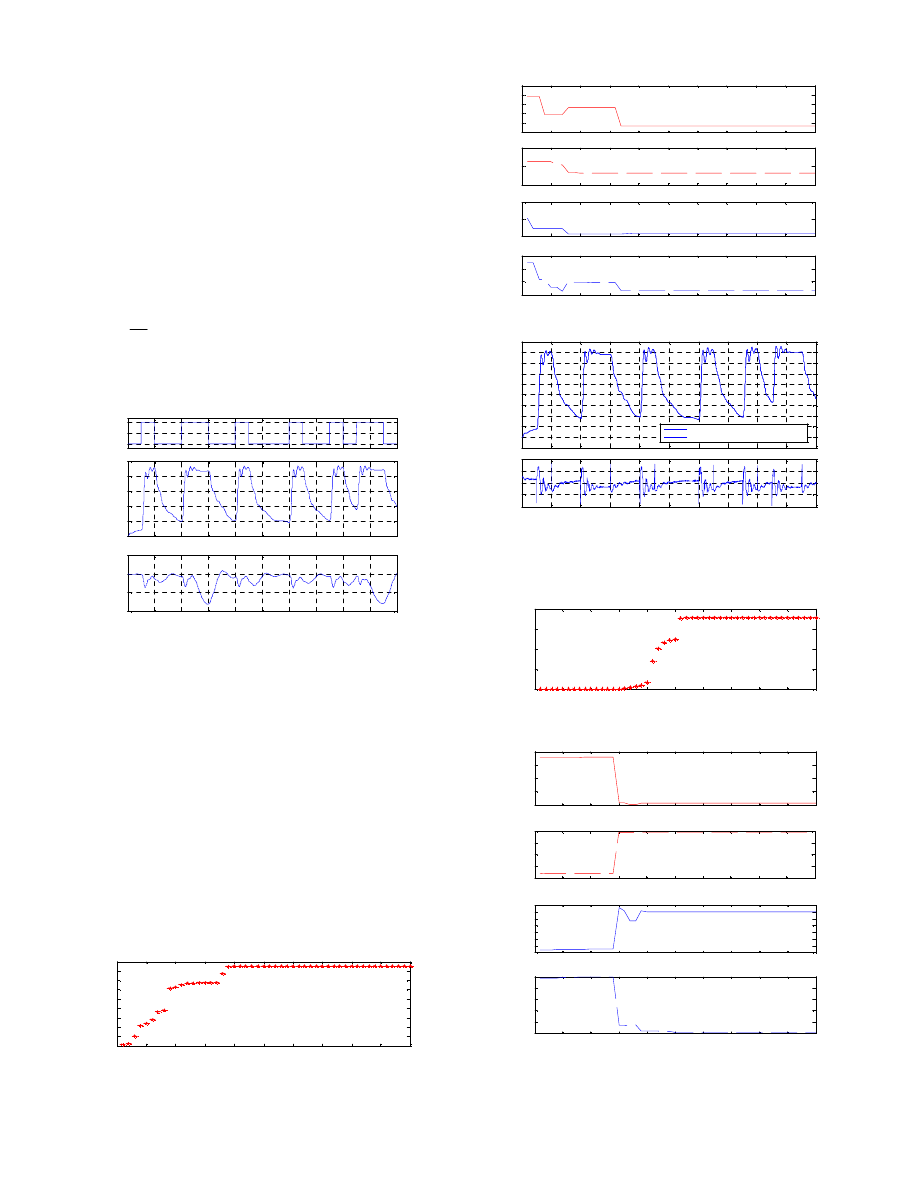
random binary sequence (PRBS). Fig. 3 presents the PRBS
input applied to each joint of the real 2-axes PAM manipulator
and the corresponding output.
The fitness function calculated in this case is given as
¦
−
=
1
2
)]]
(
[
1
[
k
e
M
F
(2)
with e(k) represents the error between the actual PAM
manipulator joint angle output and PAM manipulator ARX
model response.
0
2
4
6
8
10
12
14
16
18
20
4.5
5
5.5
PR
B
S
i
n
put
-
[
v
]
2-AXES PAM MANIPULATOR
(OPEN-LOOP PRBS TEST1)
0
2
4
6
8
10
12
14
16
18
20
0
20
40
60
80
100
T
het
a2 -
[
deg
ree]
0
2
4
6
8
10
12
14
16
18
20
-40
-20
0
20
t - [sec]
T
het
a1 -
[
degr
ee]
Fig. 3 Input PRBS and output response of the 2-axes PAM manipulator
Both fitness values of each Link ARX model converge
rapidly toward the global optimum, as shown in Fig.4a and
Fig.6a. The convergence plot of the estimated parameters by
the MGA is shown in Fig.4b and Fig.6b for 1
st
Link ARX
model’s a
1
, a
2
, b
1
and b
2
and 2
nd
Link ARX model’s
respectively. From these figures, it can note that, even with the
present of noise, the identification parameter value converges
rapidly from a random set of parameters with best obtained
fitness value. The optimized identified parameters of both
Two Link ARX model of the 2-axes PAM manipulator
obtained from MGA at the end of 100
th
generation are
tabulated in Table 1.
Fig.5 and Fig.7 present the output of the MGA-based
identified ARX models against the actual PAM output
response.
ARX-model Link 2 - Max Fitness = 42
[a
1
= -1.9023; a
2
= 0.90625; b
1
= -0.97435; b
2
=1.0156]
.
0
5
10
15
20
25
30
35
40
45
50
0
5
10
15
20
25
30
35
40
45
generat ion
fi
tn
e
s
s
v
a
lu
e
Fig.4a Convergence trace of fitness value (MGA method) – Link2
.
0
5
10
15
20
25
30
35
40
45
50
-1.903
-1.902
-1.901
-1.9
-1.899
-1.898
generat ion
e
s
ti
m
a
te
a
1
0
5
10
15
20
25
30
35
40
45
50
0.9
0.91
0.92
generat ion
e
st
im
a
te
a
2
0
5
10
15
20
25
30
35
40
45
50
-1
-0.8
-0.6
generation
es
ti
m
at
e
b1
0
5
10
15
20
25
30
35
40
45
50
1
1.05
1.1
1.15
generat ion
e
s
ti
m
a
te
b
2
Fig.4b Convergence of the identified parameters (MGA method) – Link2
0
2
4
6
8
10
12
14
16
18
20
-10
0
10
20
30
40
50
60
70
80
90
yy a
nd y
h2 -
[
degr
ee]
2 AXES PAM MANIPULATOR
(COMPARISON OP ENLOOP P RBS TEST - LINK2)
0
2
4
6
8
10
12
14
16
18
20
-1
-0. 5
0
0. 5
1
t - [ sec]
e
rr
2
=
y
y
-y
h2 [
degr
e
e]
2-axes PAM manipulator response
ARX model (a1 a2 b1 b2) response
Fig.5 Output of MGA-based ARX model against actual PAM manipulator
response - (Link2)
ARX-model Link 1 - Max Fitness = 35.97
[a
1
=-1.9374; a
2
=0.9386; b
1
= 1.5; b
2
=-1.4873]
0
5
10
15
20
25
30
35
40
45
50
0
10
20
30
40
generation
fi
tn
e
s
s
v
a
lu
e
Fig.6a Convergence trace of fitness value (MGA method) – Link1
.
0
5
10
15
20
25
30
35
40
45
50
-2
-1. 5
-1
-0. 5
0
generation
e
st
im
a
te
a
1
0
5
10
15
20
25
30
35
40
45
50
-1
-0.5
0
0.5
1
generation
e
st
im
a
te
a
2
0
5
10
15
20
25
30
35
40
45
50
-1. 5
-1
-0. 5
0
0.5
1
1.5
2
generation
e
s
ti
m
a
te
b
1
0
5
10
15
20
25
30
35
40
45
50
-1. 5
-1
-0. 5
0
0.5
1
generation
e
s
ti
m
a
te
b
2
Fig.6b Convergence of the identified parameters (MGA method) – Link1
2606
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
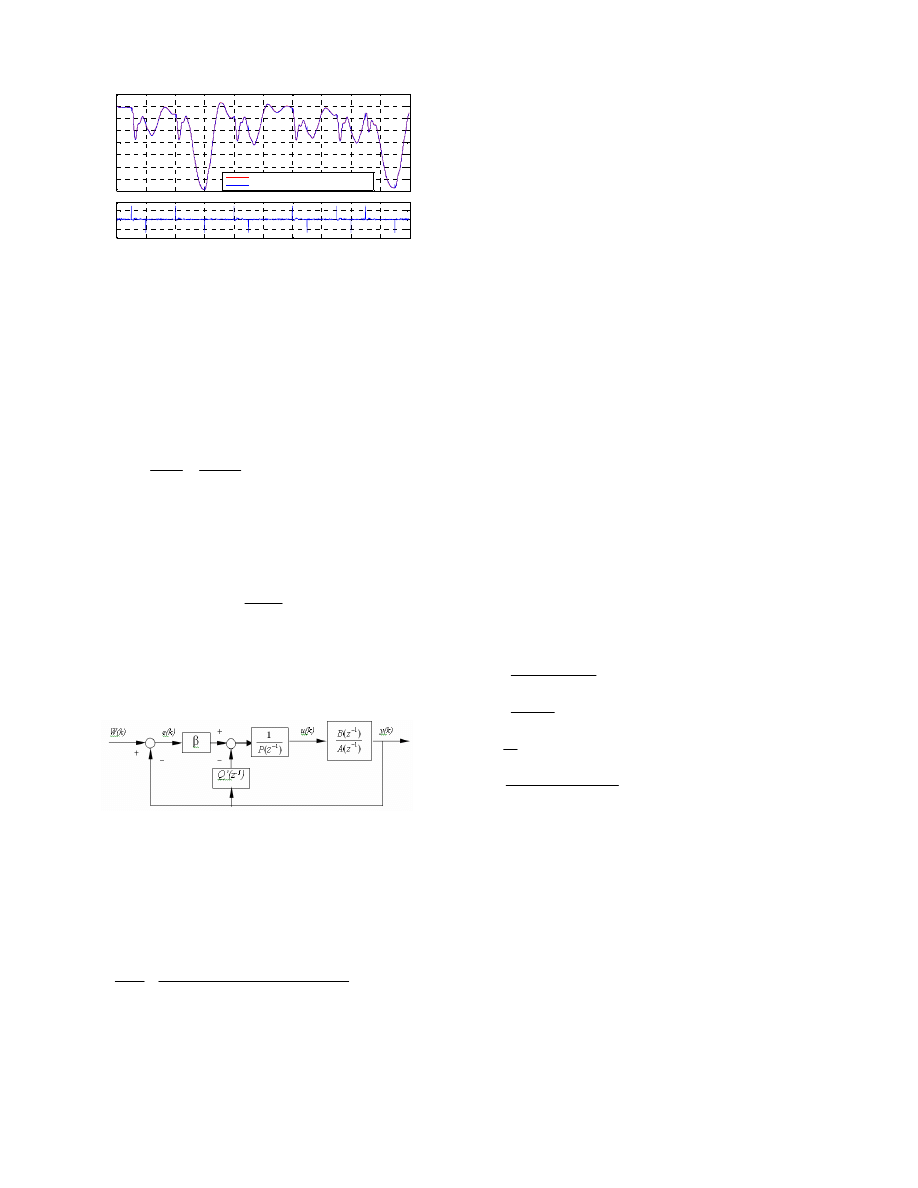
0
2
4
6
8
10
12
14
16
18
20
-35
-30
-25
-20
-15
-10
-5
0
5
yy
a
n
d y
h
1 -
[
d
e
gr
ee
]
2 AXES PAM MANIPULATOR
(COMPARISON OPENLOOP PRBS TEST - LINK1)
0
2
4
6
8
10
12
14
16
18
20
-2
-1
0
1
2
t - [sec]
e
rr1
=
yy
-yh
1
[
d
eg
re
e
]
2-axes PAM manipulator response
ARX model (a1 a2 b1 b2) response
Fig.7 Output of MGA-based ARX model against actual PAM manipulator
response (Link1)
V. A
DAPTIVE
S
ELF
-T
UNING
C
ONTROLLER
B
ASED ON
M
ODIFIED
P
OLE
P
LACEMENT
M
ETHOD
A self-tuning pole placement controller design will ensure
the desired control loop dynamic behavior by choosing the
available characteristic polynomial.
The block diagram of modified Pole placement controller
used in this paper is shown in Fig.8, where
)
(
)
(
)
(
)
(
)
(
1
1
−
−
=
=
z
A
z
B
z
U
z
Y
z
G
P
(3)
is the discrete transfer function of the controlled 2-axes PAM
manipulator with polynomials
2
2
1
1
1
1
)
(
−
−
−
+
+
=
z
a
z
a
z
A
2
2
1
1
1
)
(
−
−
−
+
=
z
b
z
b
z
B
(4)
Pole placement controller equation takes the form
)
(
1
)].
(
).
(
'
)
(
.
[
)
(
1
1
−
−
−
=
z
P
z
Y
z
Q
z
E
z
U
β
(5)
with polynomial P(z
-1
) has the form as
)
.
1
)(
1
(
)
(
1
1
1
−
−
−
+
−
=
z
z
z
P
γ
(6)
and polynomial Q(z
-1
) takes the form
)
.
'
'
)(
1
(
)
(
'
1
2
0
1
1
−
−
−
−
−
=
z
q
q
z
z
Q
(7)
Fig. 8 Block diagram of modified adaptive pole placement controller
.
Substitution (6) and (7) into (5) yields the following
relation for the controller output:
)
(
.
)
2
(
.
)
1
(
).
1
(
)]
2
(
'
)
1
(
).
'
'
(
)
(
).
'
[(
)
(
2
2
0
0
k
k
u
k
u
k
y
q
k
y
q
q
k
y
q
k
u
ω
β
γ
γ
β
+
−
+
−
−
−
−
+
−
+
−
+
−
=
(8)
For the transfer function of the closed loop in Fig.8, it is
obtained the relation:
]
)
(
'
).[
(
)
(
).
(
)
(
.
)
(
)
(
)
(
1
1
1
1
1
β
β
+
+
=
=
−
−
−
−
−
z
Q
z
B
z
P
z
A
z
B
z
W
z
Y
z
G
w
(9)
So the characteristic polynomial takes the form
)
(
]
)
(
'
).[
(
)
(
).
(
1
1
1
1
1
−
−
−
−
−
=
+
+
z
D
z
Q
z
B
z
P
z
A
β
(10)
In the case of a controlled 2-axes PAM manipulator
polynomial in the form of (3), equation (10) will define a
system of 4 linear algebraic equations with 4 unknown
controller parameters
γ
β
,
,
'
,
'
2
0
q
q
:
»
»
»
»
¼
º
«
«
«
«
¬
ª
=
»
»
»
»
¼
º
«
«
«
«
¬
ª
»
»
»
»
¼
º
«
«
«
«
¬
ª
−
−
−
−
−
−
4
3
2
1
2
0
2
2
2
1
1
2
2
1
2
1
1
2
1
1
'
'
0
0
0
1
1
0
x
x
x
x
q
q
a
b
a
a
b
b
b
a
b
b
b
b
b
b
γ
β
(11)
The 1
st
matrix in the left side of (11) depends only on the
parameters of the controlled PAM manipulator ARX model.
The next vector contains the unknown parameters (q
’
0
, q
’
2
,
ȕ
and
Ȗ) of the controller, being the solution of the system (11),
and the vector on the right side depends on the number of
poles of D(z
-1
) and their position in the z complex plane.
Then parameters of adaptive pole placement controller
now are obtained by inserting appropriately modified relation
of D(z
-1
) as
)]
(
)].[
(
.[
)
(
)
(
2
ω
α
ω
α
α
j
z
j
z
z
z
D
−
−
+
−
−
=
(12)
This characteristic polynomial has a pair of complex
conjugated poles
jw
z
±
=
α
2
,
1
placed inside the unit circle at
interval
1
0
<
≤
α
and double real poles
α
=
4
,
3
z
.
The parameter
Į can be used to change the speed of the
control response and the size of the changes in the controller
output. It is also possible to modify parameter
Ȧ to select a
desired overshoot.
Put (12) into (10), where the vector components on the
right side of (11) are determined by
x
1
=c+1- a
1
; x
2
=d + a
1
- a
2
; x
3
= - f - a
2
; x
4
= g
(13)
with
α
4
−
=
c
;
2
2
.
6
ω
α
+
=
d
;
)
2
(
2
2
2
ω
α
α
+
−
=
f
;
)
(
2
2
2
ω
α
α
+
=
g
(14)
By solving equation system (11), it is obtained the
equations for calculating the pole placement controller
parameters as follows:
2
1
4
3
2
1
1
5
1
7
6
2
1
4
3
2
0
'
'
b
b
x
x
x
x
r
r
r
r
r
q
r
r
r
r
q
+
+
−
+
=
=
+
=
+
+
−
=
β
γ
(15)
with
)]
(
)
(
[
)
(
)
(
)]
(
)[
(
)]
(
[
]
)
(
[
4
1
2
2
4
2
2
4
1
1
2
7
4
2
4
1
3
2
2
1
6
1
3
2
2
2
2
3
2
1
4
2
1
1
5
4
3
2
4
1
2
1
4
4
3
2
1
1
2
1
2
3
1
2
4
3
2
1
2
1
2
x
x
a
b
x
x
a
x
a
b
b
r
x
a
x
a
x
a
b
r
x
b
x
b
x
b
b
x
b
b
r
x
x
b
x
b
b
b
r
x
x
x
b
x
b
b
a
r
x
b
x
x
x
b
b
a
r
+
−
−
+
=
−
+
=
−
+
+
=
−
+
+
=
+
−
−
=
−
+
−
=
(16)
VI. S
IMULATION AND
E
XPERIMENT
R
ESULTS
.
Simulation and experimentation will be carried on the 2-
axes PAM manipulator shown in Fig.2. SIMULINK diagram
run in MATLAB for simulating the proposed modified pole
placement control algorithm is presented in Fig. 9 in which the
2607
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
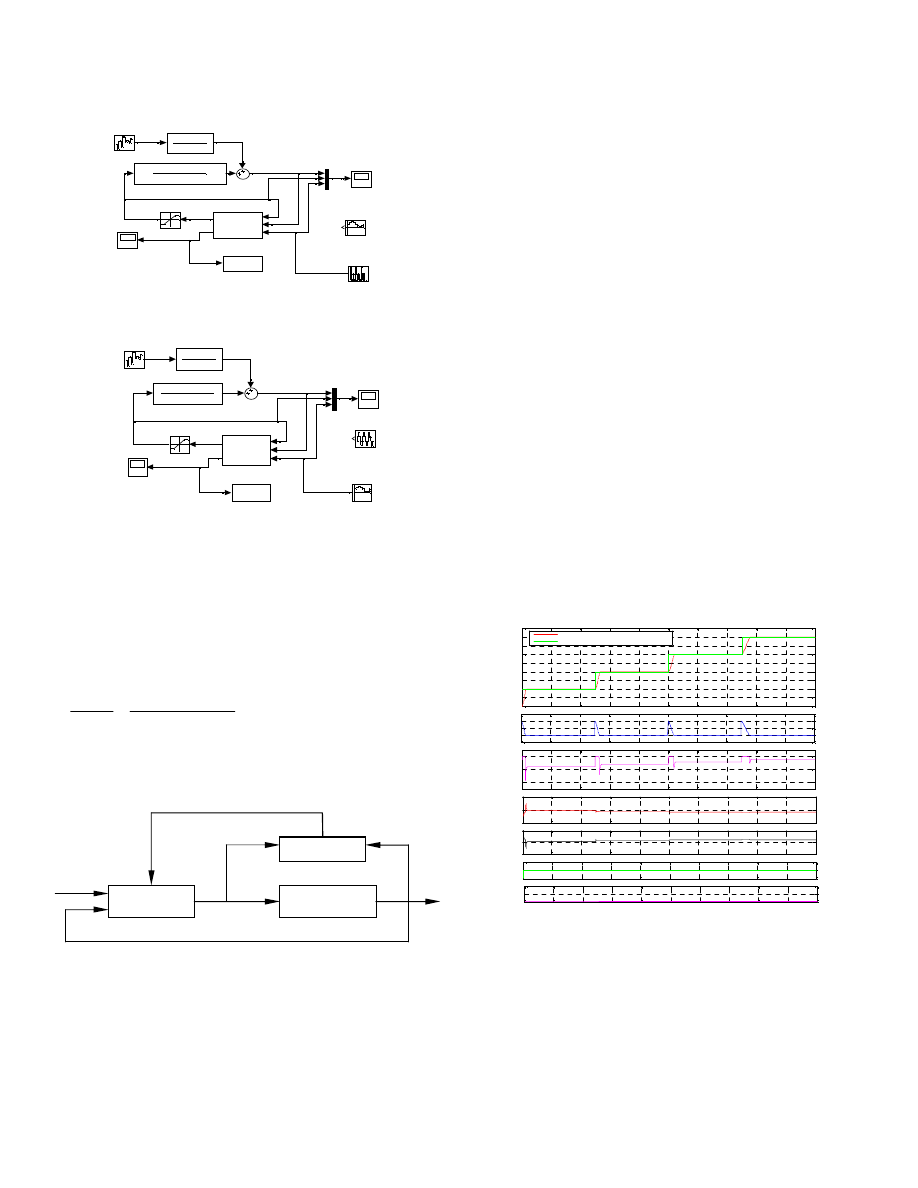
transfer function of each Link of the 2-axes PAM manipulator
is converted from the corresponding ARX model respectively.
u_in(k )
y (k )
w(k )
u(k )
ID params
adapti ve pp2b_1
parameters
To Workspace1
Si ne Wave2
Saturati on1
Reference signal 2
Output1
0.2
5s +10s+1
2
Noi se fi ltration1
ID parameters1
Band-Lim ited
White Noi se1
154.2s+131.1
s +6.337s+12.39
2
2-axes PAM mani pul ator
Link1
a) The first link
.
u_in(k)
y (k)
w(k)
u(k)
ID params
adaptive pp2b_2
parameters
T o Workspace
Sine Wave2
Saturation
Reference signal2
Output
0.2
5s +10s+1
2
Noi se filtration
ID parameters
Band-Lim ited
White Noise
-104.6s+433.2
s +9.846s+41.49
2
2-axes PAM m ani pul ator
Link2
b) The second link
.
Fig.9 The SIMULINK diagram of the 2-axes PAM manipulator joint angle
position control using modified pole placement controller:
The modified pole placement control scheme is shown in
Fig.10 which is in the category of indirect adaptive control.
Referring to Fig.10,
ș
i
is the joint displacement of link i, u
i
is
the corresponding control voltage. To implement modified
pole placement controller strategy, it is required to determine
ARX model the 2-axes PAM manipulator in the form of
2
2
1
1
2
2
1
1
1
1
.
.
1
.
.
)
(
)
(
−
−
−
−
−
−
+
+
+
=
z
a
z
a
z
b
z
b
z
u
z
i
i
θ
(17)
with a
1
, a
2
, b
1
, b
2
parameters of each link’s ARX model of the
2-axes PAM manipulator will be determined from PRBS
input-output testing and be optimized with offline Modified
Genetic Algorithm (MGA).
Fig. 10 Pole placement position control of the 2-axes PAM manipulator
Equation (17) represents a second order system with the
output in discrete time form:
)
2
(
)
1
(
)
2
(
)
1
(
)
(
2
1
2
1
−
+
−
+
−
−
−
−
=
k
u
b
k
u
b
k
a
k
a
k
i
i
i
i
i
i
i
θ
θ
θ
(18)
In order to update the best values for the coefficients of
A(z
-i
) and B(z
-i
), in the sense of minimum square errors, the
RLS is used to perform the online estimation based on the
input-output data pairs ([u
k
,
ș
k
] pairs). The experiment control
voltage is within the range of [4.5v – 5.5v]. The sampling time
T
0
was chosen to be 0.01 [s].
The design parameters of pole placement controller
include pole assignment values
Į, Ȧ and forgetting factor Ȝ.
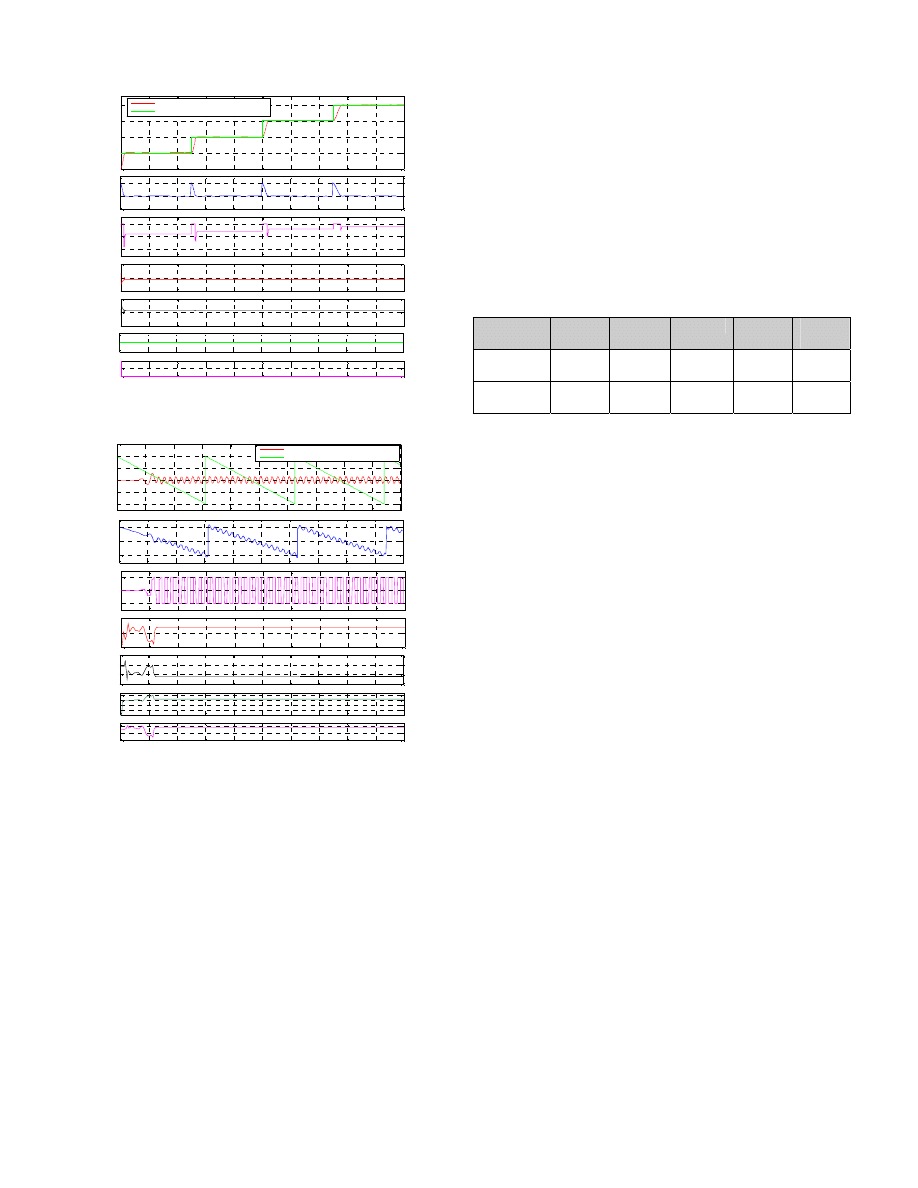
Figure 11 to Figure 13 show the joint displacement and
the control input results. The response of 2-axes PAM
manipulator position control using Modified Pole Placement
controller was fast, overshoot free and offset free despite the
different scales of set-points. Furthermore, these figurative
results demonstrate the performance of the on-line RLS
estimator. The online ARX model parameter values always
converge and roughly remained constant. It is clear that the
estimation was consistent with the initial values obtained from
the offline MGA-based optimization. Before the online ARX
mode1 was correctly established, the response was oscillatory,
which also clearly proved how the on-line estimation helped
the control performance.
Tests were also carried out to study the effects that the
design parameters might have on the pole placement controller
performance. Using (19) as the standard parameter setting, the
tests were carried out in such a way that only one parameter's
value was changed at a time.
In following results, the pole placement controller used in
position control the 2-axes PAM manipulator has the standard
characteristic parameters as follows:
* Forgetting Factor
Ȝ of RLS algorithm = 0.99.
* T
sample
of discrete pole placement control = 0.01 [s]. (19)
* Pole assignment values
Į + j*w = 0.5 +j*0.1.
0
2
4
6
8
10
12
14
16
18
20
0
5
10
15
20
25
30
35
40
45
Jo
in
t A
n
g
le
-
Y
/Y
d
-[
d
e
gr
e
e
]
2-ax es PAM Manipulator - Modified Pole Placement Cont roller
(Forgett ing Fac tor Lambda = 0.999 - Link2)
0
2
4
6
8
10
12
14
16
18
20
-5
0
5
10
15
E
rr
o
r -
[d
eg
re
e
]
0
2
4
6
8
10
12
14
16
18
20
-1
0
1
U
-c
o
n
tr
o
l -
[
v
]
0
2
4
6
8
10
12
14
16
18
20
-2
-1. 9
-1. 8
a1
0
2
4
6
8
10
12
14
16
18
20
0. 8
0. 9
1
a
2
0
2
4
6
8
10
12
14
16
18
20
-1
0
1
b
1
0
2
4
6
8
10
12
14
16
18
20
0
0. 5
1
time - [ second]
b2
Joint Angle Y - [ degree]
Desired Reference Yd - [ degree]
Fig. 11 The 2-axes PAM manipulator Modified Pole Placement Controller
(Online Parameter Self-Tuning– Forgetting Factor
Ȝ = 0.99)
Figure 11 and 12 represent the various results of the 2-
axes PAM manipulator joint angle ramp trajectory tracking
using modified pole placement control algorithm with
forgetting factor
Ȝ chosen equal 0.99 (Fig. 11) and 0.75 (Fig.
12) respectively. These results determine that the best chosen
value of forgetting factor
Ȝ is about 0.99.
RLS
Id
ifi
i
Pole
placement
2-axes PAM
Manipulator
Process parameter
ș
di
u
i
ș
i
2608
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
0
2
4
6
8
10
12
14
16
18
20
0
10
20
30
40
Jo
in
t A
n
gl
e -
Y
&
Y
d
-
[degr
ee]
2-ax es PAM Manipulator - Modified Pole Plac ement Controller
(Forgetting Factor Lambda = 0.75 - Link2)
0
2
4
6
8
10
12
14
16
18
20
-10
0
10
E
rr
o
r -
[
degr
e
e]
0
2
4
6
8
10
12
14
16
18
20
-1
0
1
U
-c
o
nt
ro
l -
[
v
]
0
2
4
6
8
10
12
14
16
18
20
-2
-1.9
-1.8
a1
0
2
4
6
8
10
12
14
16
18
20
0.8
0.9
1
a
2
0
2
4
6
8
10
12
14
16
18
20
-1
0
1
b1
0
2
4
6
8
10
12
14
16
18
20
0
0.5
1
time - [s ec ond]
b2
Joint Angle Y - [degree]
Des ired Reference Yd - [degree]
Fig. 12 The 2-axes PAM Manipulator Modified Pole Placement Controller
(Online Parameter Self-Tuning– Forgetting Factor
Ȝ = 0.75)
0
2
4
6
8
10
12
14
16
18
20
-20
-10
0
10
20
30
J
o
in
t A
n
gl
e
- Y
&
Y
d
-
[d
egr
e
e
]
2-axes PAM Manipulator - Modified Pole Plac ement Controller
(pole ass ignment value: alpha + j*omega = 1 +j*1 - Link 1) - Unstable
0
2
4
6
8
10
12
14
16
18
20
-20
0
20
E
rr
o
r -
[d
e
g
re
e
]
0
2
4
6
8
10
12
14
16
18
20
-1
0
1
U
-c
o
n
tr
o
l -
[v
]
0
2
4
6
8
10
12
14
16
18
20
-2
-1.5
-1
a1
0
2
4
6
8
10
12
14
16
18
20
0
0.5
1
1.5
a2
0
2
4
6
8
10
12
14
16
18
20
-1
0
1
2
3
b1
0
2
4
6
8
10
12
14
16
18
20
-2
0
2
time - [second]
b2
Joint Angle Y - [degree]
Des ired Referenc e Yd - [degree]
Fig. 13 The 2-axes PAM Manipulator Modified Pole Placement Controller
(Online Parameter Self-Tuning– Pole Assignment Value:
Į + j*w = 1 + j*1 ).
Figure 13 shows the attractive results of the 2-axes PAM
manipulator joint angle saw-tooth trajectory tracking using
modified pole placement control algorithm with different pole
assignment values. This figure demonstrates the unstable and
oscillatory result in case chosen pole assignment values
Į +
j*w = 1 +j*1.
All these results prove the superb capacity of proposed
pole placement control algorithm not only in satisfying robust
control requirement but also in modifying specific control
system features (overshoot value, settling time, steady state
error, etc.).
VII. C
ONCLUSIONS
This paper provides a novel and effective method, MGA-
based system identification method, for identifying and
controlling a highly nonlinear 2-axes PAM manipulator.
Through simulation and experimental investigation, the
proposed MGA-based identification algorithm achieves
excellent performance. Although the ARX model obtained is
quite simple, it can be used to describe the dynamics of the
system very well. The proposed control algorithm is applied to
control joint angle position of the 2-axes PAM manipulator.
Simulation and experiment results prove that the novel
proposed Pole Placement controller possesses less settling
time, zero overshoot, small rise time as well as quite accurate
joint angle trajectory tracking
.
These results can be applied to
model, identify and control other highly nonlinear systems as
well.
TABLE 1: MGA-BASED PAM MANIPULATOR ARX MODEL PARAMETERS
Parameter
a
1
a
2
b
1
b
2
Fitness
value
1
st
Link
ARX model
-1.9374
0.9386
1.5
-1.4873
35.97
2
nd
Link
ARX model
-1.9023
0.90625
-0.97435
1.0156
42.98
A
CKNOWLEDGMENT
This research is supported by BK21, Korea.
R
EFERENCES
[1] D. Repperger, and C. Phillips,“Developing intelligent control from a
biological perspective to examine paradigms for activation utilizing
pneumatic muscle actuators," in Proceedings of the 15th IEEE
International Symposium on Intelligent Control, Rio Patras, Greece, 2000,
pp. 205-210.
[2] B.Tondu, and P. Lopez, “Modeling and control of McKibben artificial
muscle robot actuators," IEEE Control Systems Magazine, vol. 20, no. 2,
2000, pp.15-38.
[3] C. Chou, and B.Hannaford, “Dynamic characteristics of McKibben
pneumatic artificial muscles,” in Proceedings IEEE Robotics Automation
Conf., pp. 281–286, 1994.
[4] D. Reynolds, D. Repperger, C. Phillips, and G. Bandry, “Dynamic
characteristics of pneumatic muscle,” Journal of Ann. Biomed. Eng., pp.
310–317, 2003.
[5] K.K. Ahn, and T.D.C. Thanh,
“
Intelligent phase plane switching control
of pneumatic artificial muscle (PAM) manipulators with magneto-
rheological brake”, March 2006, Mechatronics, Vol. 16, Issue 2, pp.85-
95, 2006.
[6] K.K.Ahn, and H.P.H. Anh, “System modeling and identification of the
two-link pneumatic artificial muscle (PAM) manipulator optimized with
genetic algorithm,” in Proceedings 2006 IEEE-ICASE Int. Conf., Busan,
Korea, pp. 356–361, 2006.
[7] J. Lilly, “Adaptive tracking for pneumatic muscle actuators in bicep and
tricep configurations,” IEEE Trans. Neural Syst. Rehab. Eng., pp. 56-63,
2005.
[8] P. Carbonell, Z. Jiang, and D.Repperger, “A fuzzy back-stepping
controller for a pneumatic muscle actuator system,” Proceedings IEEE
Int. Symp. Intelligent Control, Mexico City, Mexico, pp. 353–358, 2001.
[9] S. Chan, J. Lilly, D. Repperger, and J. Berlin, “Fuzzy PD+I learning
control for a pneumatic muscle,” Proceedings 2003 IEEE Int. Conf. Fuzzy
Systems, St. Louis, MO, pp. 278–283, 2003.
[10] X. Chang, and J. Lilly, “Tracking control of a pneumatic muscle by an
evolutionary fuzzy controller,” Journal of Intell. Automat. Soft Comput.,
vol. 9, no. 3, pp. 227–244, 2003.
[11] V. Bobal,“Auto-tuning of digital PID controllers using Recursive
Identification,” Report ESR9409, Ruhr University, Germany, 1994.
[12] V. Bobal, and M. Kubalcik, “Auto-tuning of digital PID controllers using
Recursive Identification”, in Proceedings of the 5
th
IFAC Symposium on
Adaptive Systems in Control and Signal Processing (Budapest), pp. 384-
389, 1995.
2609
Authorized licensed use limited to: Biblioteka Glowna i OINT. Downloaded on May 20, 2009 at 05:48 from IEEE Xplore. Restrictions apply.
Wyszukiwarka
Podobne podstrony:
0415165733 Routledge Personal Identity and Self Consciousness May 1998
Energy Body Manupulation Development and Self Healing Systems Robert Bruce
The gender caste system identity, privacy and heteronormativity
Gerrilyn Smith,?e Cox, Jacqui Saradjian Women and Self harm
SYSTEM OBRONNY RP, Liceum, PO,PP
Identifcation and Simultaneous Determination of Twelve Active
Practical Optical System Layout And Use of Stock Lenses
A systematic review and meta analysis of the effect of an ankle foot orthosis on gait biomechanics a
Luhmann's Progeny Systems Theory and Literary Studies in the Post Wall Era
Embedded Systems Building and Programming Embedded Devices
Am I Who I Say I Am Social Identities and Identification
O'Reilly Programming Embedded Systems in C and C
Measuring power system harmincs and interharmonics by envelope spectrum analysis
Synchronous Generator And Frequency Converter In Wind Turbine Applications System Design And Efficie
Identity and the Young English Language Learner (E M Day)
leadership and self deception
Systems Theory and the System of Theory
wearing ideology state schooling and self presentation in japan
więcej podobnych podstron