Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty sko ´nczone: DAS i NAS

15 listopada 2008 / Wykład

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Literatura

Polskie wydanie:
J.E. Hopcroft, R. Motwani, J.D. Ullman Wprowadzenie do
teorii automatów, j ˛ezyków i oblicze ´n, PWN, Warszawa
2005

Dane oryginału:
J.E. Hopcroft, R. Motwani, J.D. Ullman Introduction to
Automata Theory, Languages and Compuations, Pearson
Education, publishing as Addison-Wesley Higher
Education 2001

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Outline

1

Wprowadzenie

Ogólnie o automatach
Poj ˛ecia podstawowe
Automat sko ´nczony – przedstawienie nieformalnie

2

DAS

Definicja i przykłady
Automat Sko ´nczony (AS) a napisy
Rozszerzona funkcja przej´scia ˆ

δ

3

NAS

Spojrzenie nieformalne, definicja, przykład
Rozszerzona funkcja przej´scia ˆ

δ

4

Równowa˙zno´s´c DAS i NAS

Wst ˛ep
Konstrukcja równowa˙znego DAS
Twierdzenia i dowody
Zły przypadek konstrukcji podzbiorów

5

Zastosowanie

Przeszukiwanie tekstu

6

-NAS

Automaty z pustymi symbolami na wej´sciu

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Ogólnie o automatach

Zastosowanie

Automaty sko ´nczone s ˛

a formalnym modelem matematycznym

dla nast ˛epuj ˛

acych zastosowa ´n

Projektowanie układów cyfrowych (sterowniki)

Analizator leksykalny w kompilatorze

Wyszukiwanie słów w pliku (lub internecie)

Zaawansowane oprogramowanie do weryfikacji systemów
o sko ´nczonej liczbie stanów

Teoria j ˛ezyków i oblicze ´n

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Ogólnie o automatach

Przykłady

Automat sko ´nczony modeluj ˛

acy przeł ˛

acznik on/off

on

off

Naciśnij

Naciśnij

Start

Automat sko ´nczony rozpoznaj ˛

acy ci ˛

ag znaków then

t

Start

the

th

then

t

h

e

n

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Ogólnie o automatach

Reprezentacje strukturalne

Istniej ˛

a dwie wa˙zne notacje, które odgrywaj ˛

a wa˙zn ˛

a rol ˛e w

badaniu automatów i ich zastosowa ´n

Gramatyki to modele po˙zyteczne przy projektowaniu
oprogramowania przetwarzaj ˛

acego dane o strukturze

rekurencyjnej (np. program "parser") np. E => E + E

Wyra˙zenia regularne reprezentuj ˛

a struktur ˛e danych,

szczególnie ła ´ncuchy tekstu, np. wzorzec
’[A-Z][a-z]*[ ][A-Z][A-Z]’
pasuje do
Ithaca NY
Pytanie: jaki wzorzec by´smy utworzyli dla napisu Palo
Alto CA

?

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Poj ˛ecia podstawowe

Alfabety, napisy, napis pusty

Alfabet jest to sko ´nczony niepusty zbiór symboli
Przykład 1:

P = {0, 1} alfabet binarny (zerojedynkowy)

Przykład 2:

P = {a, b, c, . . . , z} alfabet składaj ˛

acy si ˛e z

małych liter
Przykład 3: zbiór znaków kodu ASCII

Ci ˛

ag znaków (napis) to sko ´nczona sekwencja symboli

alfabetu

P, np.: 0011001

Napis pusty to ci ˛

ag znaków z zerowym wyst ˛

apieniem

symboli alfabetu

P

Napis pusty oznaczany jest przez

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Poj ˛ecia podstawowe

Długo´s´c napisu, pot ˛egi alfabetu

Długo ´s ´c napisu to ilo´s´c wyst ˛

apie ´n symboli alfabetu w

ci ˛

agu znaków

|w | oznacza długo´s´c napisu w
|0110| = 4, || = 0

Pot ˛ega alfabetu to zbiór napisów od długo´sci k nad
symbolami alfabetu

P. Oznaczany jest przez P

k

Przykład:

P = {0, 1}

P

1

= {

0, 1}

P

2

= {

00, 01, 11, 10}

P

0

=

Pytanie: ile napisów jest w zbiorze pot ˛egowym

P

3

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Poj ˛ecia podstawowe

Domkni ˛ecie Kleene’go, konkatenacja

Zbiór wszystkich napisów nad alfabetem

P jest oznaczany

jako

P

∗

i jest nazywany

domkni ˛eciem Kleene’go, czyli:

P

∗

=

P

0

∪

P

1

∪

P

2

· · ·

oraz
P

+

=

P

1

∪

P

2

· · ·

P

∗

=

P

+

∪{}

Konkatenacja (ł ˛

aczenie) Je˙zeli x i y s ˛

a napisami,

wówczas xy jest napisem otrzymanym poprzez
umieszczenie kopii napisu y bezpo´srednio za kopi ˛

a napisu

x . Formalnie:
x = a

1

a

2

. . .

a

i

, y = b

1

b

2

. . .

b

j

xy == a

1

a

2

. . .

a

i

b

1

b

2

. . .

b

j

Przykład: x = 01101, y = 110, xy = 01101110

Uwaga: dla ka˙zdego napisu x zachodzi x = x = x

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Poj ˛ecia podstawowe

J ˛ezyki

J ˛ezyk Je˙zeli

P jest alfabetem oraz L ⊆ P

∗

to L jest

j ˛ezykiem. Czyli j ˛ezyk to zbiór napisów
Przykłady j ˛ezyków:

Zbiór słów j ˛ezyka polskiego
Zbiór poprawnych programów w j ˛ezyku C
Zbiór napisów składaj ˛

acych si ˛e z n zer po których

wyst ˛epuj ˛

a n jedynek: {, 01, 0011, 000111, . . .}

Zbiór napisó o równej ilo´sci zer i jedynek:
{, 01, 10, 0011, 0101, 1010 . . .}
L

P

=

zbiór liczb binarnych, których warto´s´c jest liczb ˛

a

pierwsz ˛

a {10, 11, 101, 111, 1011, . . .}

J ˛ezyk pusty ∅
J ˛ezyk {} składaj ˛

acy si ˛e z napisu pustego

Uwaga: ∅ 6= {}
Uwaga 2: alfabet

P nad którym jest okre´slony j ˛ezyk, jest

zawsze zbiorem sko ´nczonym

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Poj ˛ecia podstawowe

Problemy (1)

Problem W teorii automatów problem to kwestia "Czy dany
napis w nale˙zy do j ˛ezyka L?". Wszystko co potocznie
nazywamy "problemem", daje si ˛e wyrazi´c jako nale˙zenie od
pewnego j ˛ezyka
Przykład: pytanie problemowe "Czy dana liczba binarna jest
liczb ˛

a pierwsza?" jest równowa˙zne problemowi "Czy ta dana

liczba jest elementem zbioru L

P

"

Czy 11101 ∈ L

P

? Jakie zasoby obliczeniowe (pami ˛e´c, ilo´s´c

działa ´n czyli czas) s ˛

a potrzebne aby udzieli´c odpowiedzi na to

pytanie?

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Poj ˛ecia podstawowe

Problemy (2)

Nasze obiegowe wyobra˙zenie o problemach ró˙zni si ˛e od
traktowania problemów jako problemów decyzyjnych, których
celem jest udzielenie odpowiedzi tak lub nie. O problemach
my´slimy raczej jak o transformacji, która przetwarza dane
wej´sciowe na dane wyj´sciowe.
Przykład: problem "skompiluj program w j ˛ezyku C" jest
równowa˙zne problemowi "sprawd´z czy program jest poprawny i
je˙zeli tak, to utwórz jego drzewo rozbioru"
Niech L

X

b ˛edzie zbiorem wszystkich poprawnych programów w

j ˛ezyku programowania X . Je˙zeli mo˙zemy pokaza´c, ˙ze
przynale˙zno´s´c do zbioru L

X

jest trudne, wówczas parsowanie

programów napisanych w X nie mo˙ze by´c łatwiejsze
Pytanie: dlaczego?

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automat sko ´nczony – przedstawienie nieformalnie

Przykład protokuł e-biznesowego

Zbiór dopuszczalnych zdarze ´n

Klient mo˙ze zapłaci´

c

sklepowi (czyli wysyła e-pieni ˛

adz

do sklepu)

Klient mo˙ze anulowa´

c

zapłat ˛e (e-pieni ˛

adze zostaj ˛

a

odesłane spowrotem do banku na konto klienta)

Sklep mo˙ze wysła´

c

towar do klienta

Sklep mo˙ze odebra´

c

z banku e-pieni ˛

adz klienta

(spieni ˛e˙zy´c)

Bank mo˙ze dokona´c przelewu e-pieni ˛

adza do sklepu

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

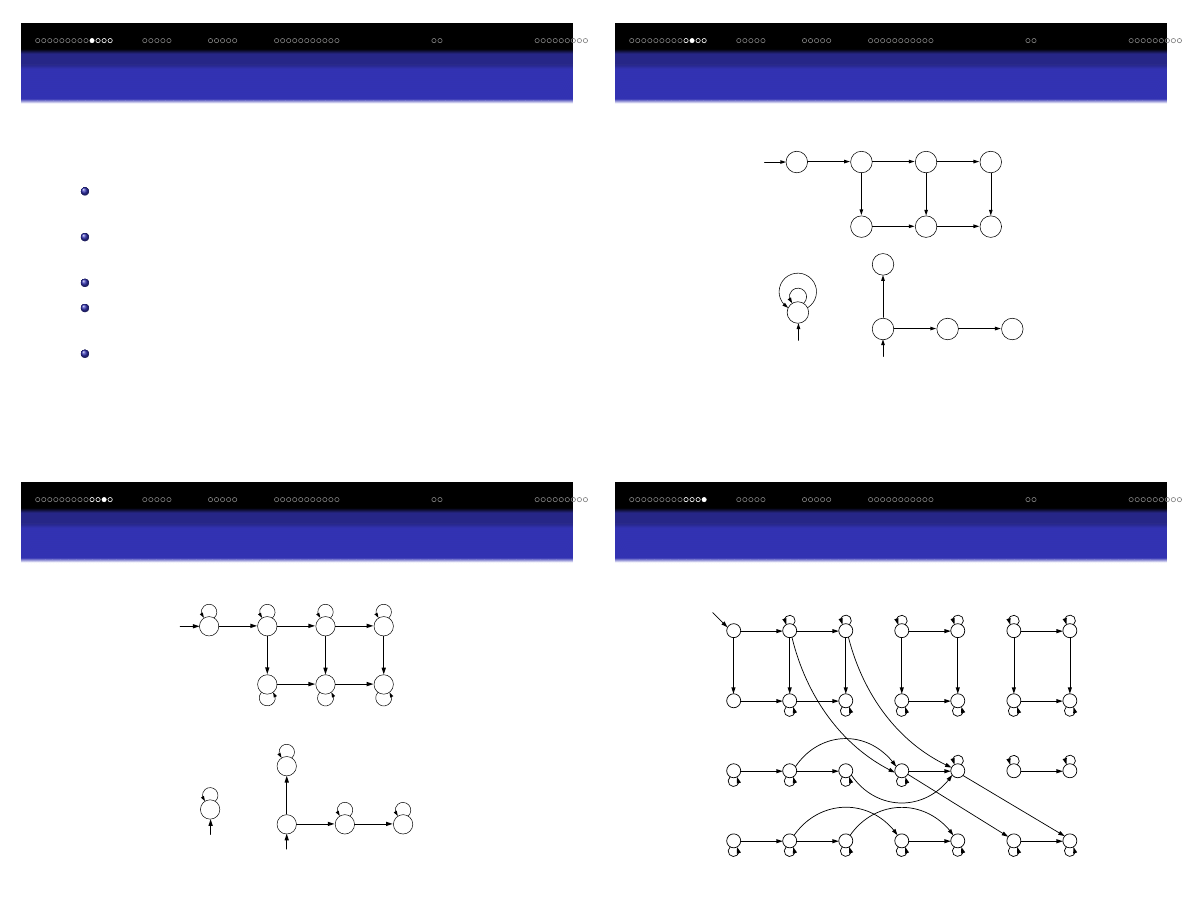
Automat sko ´nczony – przedstawienie nieformalnie

Protokoły uczestników transakcji

a

Start

zapłata

wysyłka

b

odbiór

d

przelew

f

c

odbiór

e

przelew

g

wysyłka

wysyłka

a) Sklep

zapłata

Start

b) Klient

anulowanie

1

odbiór

3

przelew

4

Start

2

c) Bank

anulowanie

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automat sko ´nczony – przedstawienie nieformalnie

Pełny zbiór przej´s´c automatów

a

Start

zapłata

wysyłka

b

odbiór

d

przelew

f

c

odbiór

e

przelew

g

wysyłka

wysyłka

a) Sklep

wysyłka

odbiór

przelew

zapłata

anulowanie

Start

b) Klient

anulowanie

1

odbiór

3

przelew

4

Start

2

c) Bank

zapłata, wysyłka

zapłata

odbiór

anulowanie

wysyłka

zapłata

odbiór

anulowanie

wysyłka

zapłata

anulowanie

zapłata

anulowanie

zapłata

anulowanie

anulowanie

zapłata

anulowanie

zapłata

anulowanie

zapłata

anulowanie

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automat sko ´nczony – przedstawienie nieformalnie

Automat produktowy dla sklepu i banku

Start

A

A

A

Z

W

Z

Z

Z

Z

Z

W

A

A

W

Z

Z

Z

Z

W

A

A

W

Z

Z

Z

Z

W

a

b

c

d

e

f

g

Z

W

Z

O

Z, A

W

W

O

Z, A

Z, A

Z, A

W

W

Z, A

Z, A

Z, A

Z, A

W

Z, A

Z, A

Z, A

Z, A

A

A

1

2

3

4

O

O

O

P

P

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Definicja i przykłady

Deterministyczny Automat sko ´nczony (DAS) – def.

Deterministycznym Automatem Sko ´

nczonym (DAS) jest

nast ˛epuj ˛

aca pi ˛

atka:

A = (Q, Σ, δ, q

0

,

F )

gdzie:

Q jest sko ´nczonym zbiorem stanów

Σ

jest sko ´nczonym alfabetem (zbiorem symboli

wej´sciowych)

δ

jest funkcj ˛

a przej´scia odwzorowuj ˛

ac ˛

a Q × Σ 7→ Q

q

0

∈ Q jest stanem pocz ˛

atkowym

F ⊆ Q jest zbiorem stanów ko ´ncowych (akceptuj ˛

acych)

Dla zadanego symbolu wej´sciowego DAS mo˙ze przej´s´c do co
najwy˙zej jednego stanu nast ˛epnego

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Definicja i przykłady

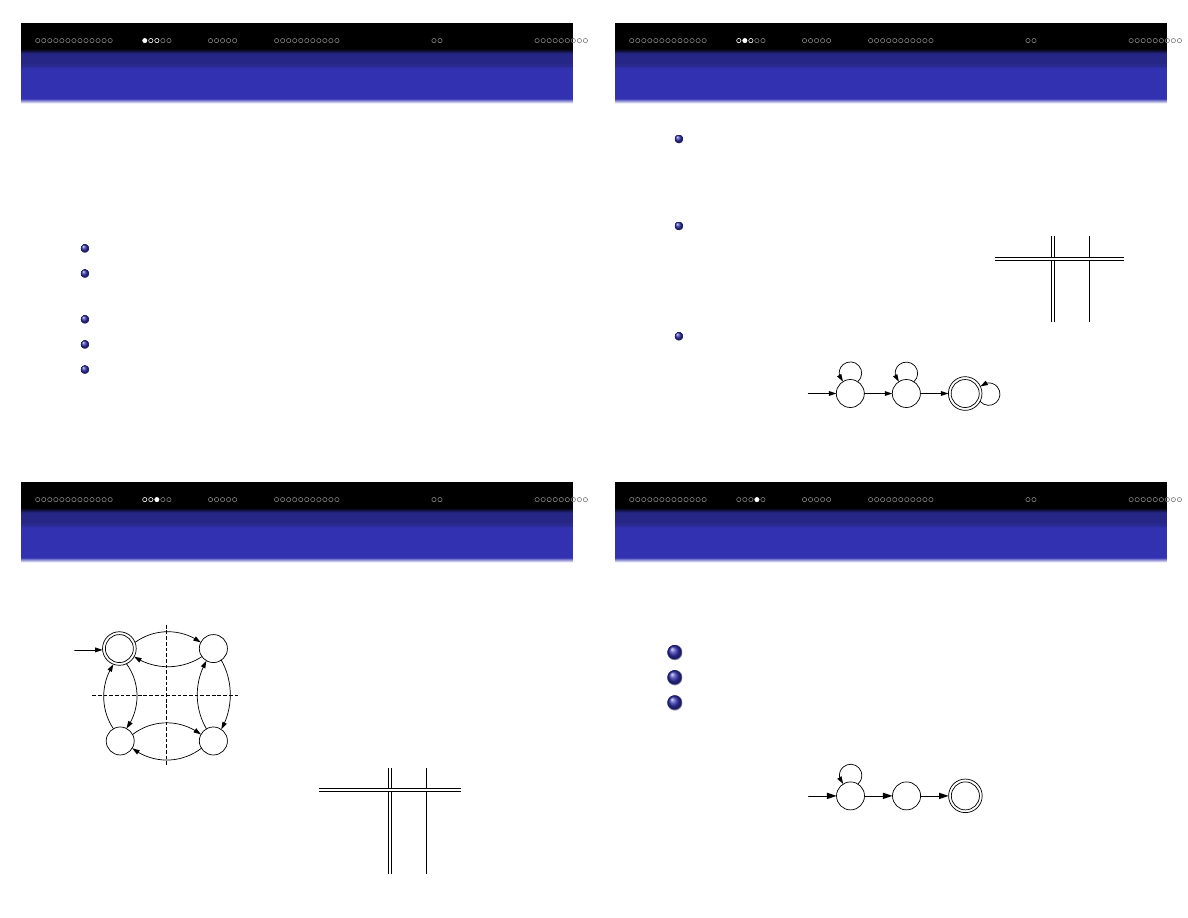
Deterministyczny Automat Sko ´nczony – przykład 1

Opis słowny: Automat A, który akceptuje wszystkie ci ˛

agi

zawieraj ˛

ace w sobie 0 po którym wyst ˛epuje 1. Formalnie

ci ˛

agi te mo˙zna okre´sli´c za pomoc ˛

a

konstruktora zbioru

napisów: L = {x 01y : x , y ∈ {0, 1}

∗

}

Definicja formalna: A = ({q

0

,

q

1

,

q

2

}, {0, 1}, δ, q

0

, {

q

1

})

a δ zadana jest w postaci

tabeli przej ´s ´c:

δ

0

1

→ q

0

q

2

q

0

?

q

1

q

1

q

1

q

2

q

1

q

1

Diagram przej ´s ´c:

Start

q

2

q

0

q

1

1

0

1

0

0,1

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Definicja i przykłady

Deterministyczny Automat Sko ´nczony – przykład 2

DAS akceptuj ˛

acy napisy składaj ˛

ace si ˛e z wył ˛

acznie z parzystej

liczby 0 i parzystej liczby 1

Start

q

1

q

2

q

0

q

3

0

0

0

0

1

1

1

1

Tablicowa reprezentacja automatu

0

1

? →

q

0

q

2

q

1

q

1

q

3

q

0

q

2

q

0

q

3

q

3

q

1

q

2

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automat Sko ´nczony (AS) a napisy

Automat Sko ´nczony (AS) a napisy

O AS mo˙zna powiedzie´c, ˙ze akceptuje ci ˛

ag znaków

w = a

1

a

2

. . .

a

n

, je´sli w diagramie przej´s´c jest ´scie˙zka, taka ˙ze:

1

Rozpoczyna si ˛e w stanie pocz ˛

atkowym

2

Ko ´nczy si ˛e w stanie akceptuj ˛

acym

3

Składa si ˛e z sekwencji etykiet a

1

a

2

. . .

a

n

Przykład: diagram przej´s´c

Start

q

1

q

0

q

2

0,1

0

1

akceptuje przykładowy napis 101101

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Rozszerzona funkcja przej´scia ˆ

δ

Rozszerzona funkcja przej´scia ˆ

δ

Poj ˛ecie funkcji przej´scia δ mo˙ze by´c rozszerzone na
funkcj ˛e ˆ

δ

, która, inaczej ni˙z δ, nie operuje na stanach i

symbolach alfabetu, lecz na stanach i

ci ˛

agach znaków

Podstawa:

ˆ

δ(

q, ) = q

Krok indukcyjny:

ˆ

δ(

q, xa) = δ(ˆ

δ(

q, x ), a)

Z powy˙zszego wi ˛ec wynika, ˙ze j ˛ezyk akceptowany przez
DAS A mo˙zna formalnie okre´sli´c:

L(A) = {w : ˆ

δ(

q

0

,

w ) ∈ F }

J ˛ezyki akceptowane przez automat sko ´nczony, nazywane
s ˛

a j˛

ezykami regularnymi

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Spojrzenie nieformalne, definicja, przykład

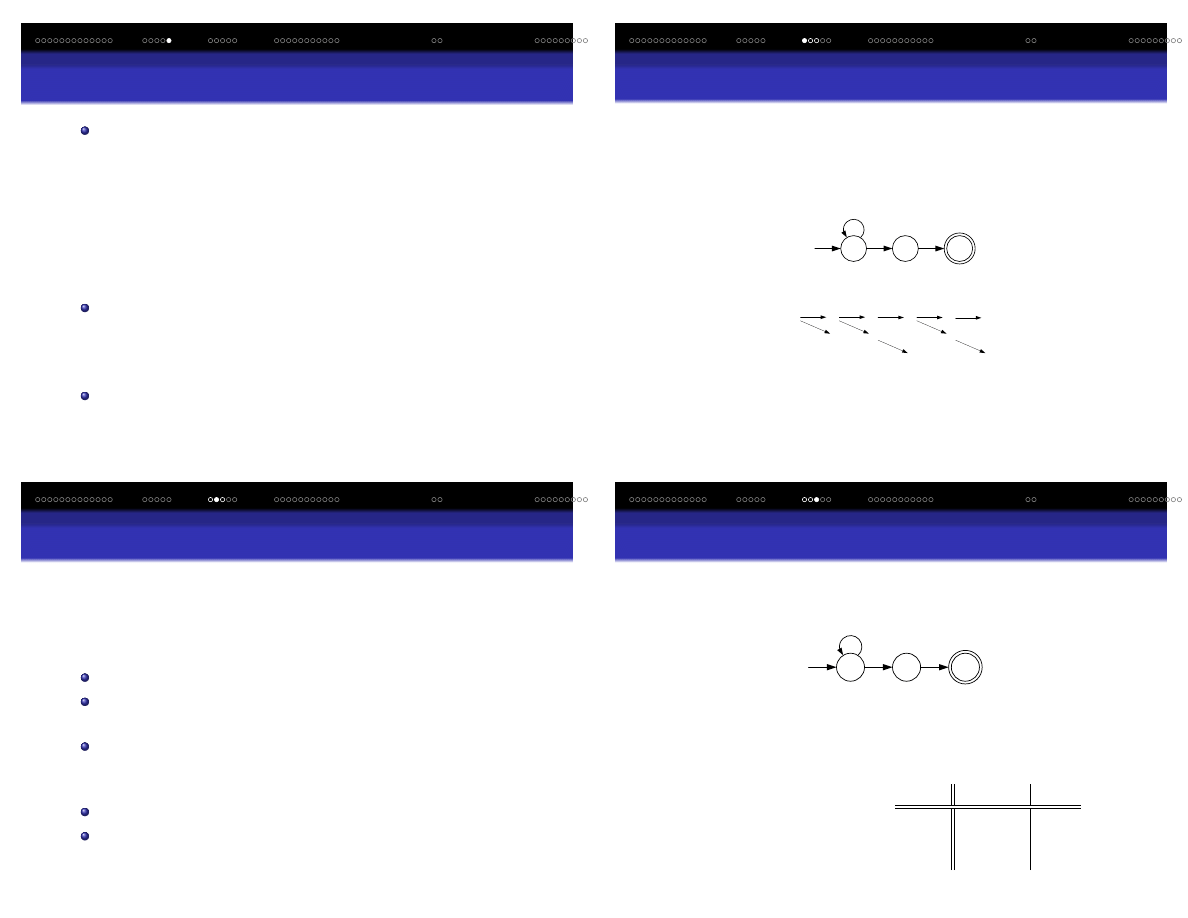
Niedeterministyczny Automat Sko ´nczony (NAS) – opis

NAS ma mo˙zliwo´s´c znajdowania si ˛e w

kilku stanach naraz. W

pewnym sensie NAS ma zdolno´s´c do

zgadywania odno ´snie

wej ´scia, dzi ˛eki czemu mo˙ze wybra´c te stany które je akceptuj ˛

a.

Przykład: Automat, który akceptuje napisy ko ´ncz ˛

ace si ˛e na 01

Start

q

1

q

0

q

2

0,1

0

1

A oto co si ˛e dzieje, gdy powy˙zszy NAS przetwarza napis 00101

0

1

q

0

q

0

q

0

q

0

q

0

q

0

q

1

q

1

q

1

q

2

q

2

brak ruchu

brak ruchu

0

0

1

Dla ka˙zdego mo˙zliwego stanu nast ˛epnego tworzy si ˛e kopia
automatu (proliferacja)

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Spojrzenie nieformalne, definicja, przykład

Niedeterministyczny Automat Sko ´nczony – definicja

NAS jest nast ˛epuj ˛

ac ˛

a pi ˛

atka:

A = (Q, Σ, δ, q

0

,

F )

gdzie:

Q jest sko ´nczonym zbiorem stanów

Σ

jest sko ´nczonym alfabetem (zbiorem symboli

wej´sciowych)

δ

jest funkcj ˛

a przej´scia odwzorowuj ˛

ac ˛

a Q × Σ 7→ 2

Q

w

zbiór pot ˛egowy zbioru stanów, czyli w zbiór wszystkich
mo˙zliwych podzbiorów zbioru Q

q

0

∈ Q jest stanem pocz ˛

atkowym

F ⊆ Q jest zbiorem stanów ko ´ncowych (akceptuj ˛

acych)

Dla zadanego symbolu wej´sciowego NAS mo˙ze przej´s´c do
zera, jednego lub wi ˛ecej stanów nast ˛epnych

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Spojrzenie nieformalne, definicja, przykład

Niedeterministyczny Automat Sko ´nczony – przykład

Przykład: Automat, który akceptuje napisy ko ´ncz ˛

ace si ˛e na 01

Start

q

1

q

0

q

2

0,1

0

1

Definicja formalna:

A = ({q

0

,

q

1

,

q

2

}, {0, 1}, δ, q

0

, {

q

1

})

a δ zadana jest

tabel ˛

a przej ´s ´c:

δ

0

1

→ q

0

{q

0

,

q

1

}

{q

0

}

q

1

∅

{q

2

}

?

q

2

∅

∅

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Rozszerzona funkcja przej´scia ˆ

δ

Rozszerzona funkcja przej´scia ˆ

δ

– definicja

Podstawa:

ˆ

δ(

q, ) = {q}

Krok indukcyjny:

ˆ

δ(

q, xa) =

[

p∈ˆ

δ(

q,x )

δ(

p, a)

Przykład Policzmy ˆ

δ(

q

0

,

00101) na tablicy

Teraz formalnie mo˙zemy okre´sli´c j ˛ezyk akceptowany przez
NAS jako:

L(A) = {w : ˆ

δ(

q

0

,

w ) ∩ F 6= ∅}

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Rozszerzona funkcja przej´scia ˆ

δ

Rozszerzona funkcja przej´scia ˆ

δ

– wykorzystanie

Udowodnijmy formalnie, ˙ze NAS akceptuje j ˛ezyk {x 01 : x ∈ Σ

∗

}

Start

q

1

q

0

q

2

0,1

0

1

Mo˙zna tego dokona´c poprzez zastosowanie indukcji wzajemnej
do trzech poni˙zszych stwierdze ´n:

1

w ∈ Σ

∗

⇒ q

0

∈ ˆ

δ(

q

0

,

w )

2

q

1

∈ ˆ

δ(

q

0

,

w ) ⇔ w = x 0

3

q

2

∈ ˆ

δ(

q

0

,

w ) ⇔ w = x 01

czyli dowodz ˛

ac kolejnych stwierdze ´n mo˙zna skorzysta´c z ju˙z

dowiedzionych stwierdze ´n poprzednich. Dowiedzenie
stwierdzenia 3 ko ´nczy cały dowód. Reszta na tablicy.

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Wst ˛ep

Przedstawienie zagadnienia

NAS s ˛

a zazwyczaj łatwiejsze do zaprogramowania

Zaskakuj ˛

ace jest, ˙ze dla ka˙zdego NAS N istnieje DAS D,

taki ˙ze L(D) = L(N), i odwrotnie
Dowód obejmuje tzw.

konstrukcj ˛e podzbiorów i jest

przykładem na to jak w sposób typowy mo˙zna
skonstruowa´c automat B z automatu A
Maj ˛

ac dany NAS

N = (Q

N

, Σ, δ

N

,

q

0

,

F

N

)

Skonstruujemy DAS

D = (Q

D

, Σ, δ

D

,

q

0

,

F

D

)

taki, ˙ze

L(D) = L(N)

i dowód tego ostatniego przeprowadzimy formalnie

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Konstrukcja równowa˙znego DAS

Tworzenie elementów definicji formalnej

Elementy tworzonego DAS

skonstruowane s ˛

a z podzbiorów

stanów z NAS. A oto szczegóły:

Q

D

= {

S : S ⊆ Q

N

} Q

D

jest zbiorem podzbiorów Q

N

, czyli

jest

zbiorem pot ˛egowym Q

N

, a jego liczno´s´c wynosi

|Q

D

| = 2

|Q

N

|

, lecz nie wszystkie elementy Q

D

musz ˛

a by´c

wykorzystane

F

D

= {

S ⊆ Q

N

:

S ∩ F

N

6= ∅} czyli te podzbiory, które

zawieraj ˛

a chocia˙z jeden stan ko ´ncowy z N

Dla ka˙zdego S ⊆ Q

N

i a ∈ Σ

δ

D

(

S, a) =

[

p∈S

δ

N

(

p, a)

Alfabety wej´sciowe Σ s ˛

a takie same, a stan pocz ˛

atkowy w

D to {q

0

}, gdzie q

0

to stan pocz ˛

atkowy w N

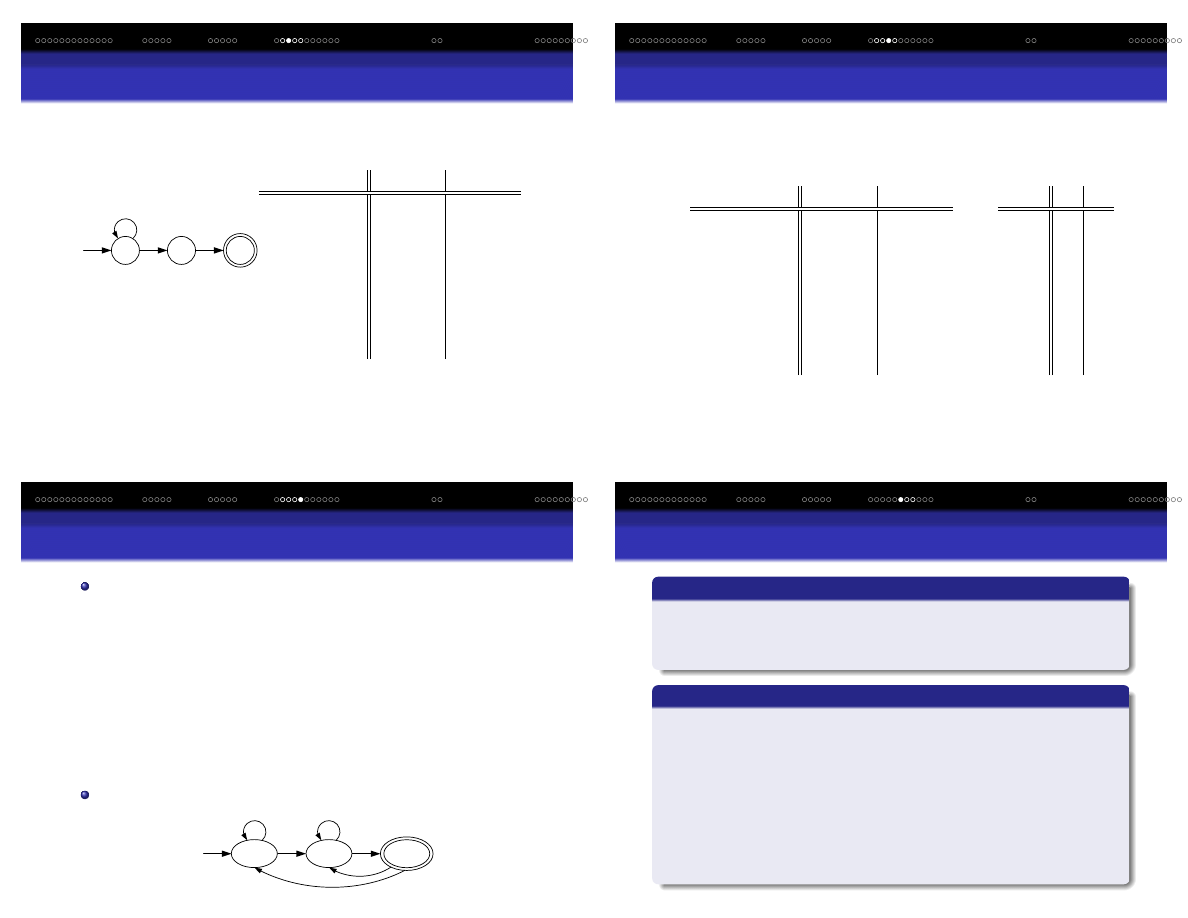
Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Konstrukcja równowa˙znego DAS

Przykład: tablica przej´s´c równowa˙znego DAS

NAS N

Start

q

1

q

0

q

2

0,1

0

1

δ

D

0

1

∅

∅

∅

→ {q

0

}

{q

0

,

q

1

}

{q

0

}

{q

1

}

∅

{q

2

}

?{

q

2

}

∅

∅

{q

0

,

q

1

}

{q

0

,

q

1

}

{q

0

,

q

2

}

?{

q

0

,

q

2

}

{q

0

,

q

1

}

{q

0

}

?{

q

1

,

q

2

}

∅

{q

2

}

?{

q

0

,

q

1

,

q

2

}

{q

0

,

q

1

}

{q

0

,

q

2

}

Automat N składa si ˛e z 3 stanów i 3 przej´s´c

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Konstrukcja równowa˙znego DAS

Zbiory stanów z NAS to stany w DAS

Elementami tablicy dla D s ˛

a zbiory stanów z N. Mo˙zemy nada´c

nowe nazwy tym zbiorom, np. kolejno od A do H i otrzymamy
"normalnie" wygl ˛

adaj ˛

acy automat deterministyczny

δ

D

0

1

∅

∅

∅

→ {q

0

}

{q

0

,

q

1

}

{q

0

}

{q

1

}

∅

{q

2

}

?{

q

2

}

∅

∅

{q

0

,

q

1

}

{q

0

,

q

1

}

{q

0

,

q

2

}

?{

q

0

,

q

2

}

{q

0

,

q

1

}

{q

0

}

?{

q

1

,

q

2

}

∅

{q

2

}

?{

q

0

,

q

1

,

q

2

}

{q

0

,

q

1

}

{q

0

,

q

2

}

δ

D

0

1

A

A

A

→ B

E

B

C

A

D

?

D

A

A

E

E

F

?

F

E

B

?

G

A

D

?

H

E

F

Zaczynaj ˛

ac od stanu pocz ˛

atkowego B osi ˛

agamy tylko stany B,

E i F . Pozostałe 5 stanów s ˛

a nieosi ˛

agalne, i mo˙zna je pomin ˛

a´c.

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Konstrukcja równowa˙znego DAS

"Leniwe" obliczanie podzbiorów

Je˙zeli obliczenia pozycji tablicy przej´s´c dla DAS zaczniemy
od stanu pocz ˛

atkowego i b ˛edziemy je kontynuowa´c tylko

poprzez stany osi ˛

agalne to mo˙zemy unikn ˛

a´c "eksplozji"

stanów, co formalnie:
Podstawa: S = {q

0

} jest osi ˛

agalny w D

Krok indukcyjny: Je˙zeli stan S jest osi ˛

agalny, wtedy dla

ka˙zdego symbolu wej´sciowego a obliczamy zbiór stanów

δ

D

(

S, a) =

[

p∈S

δ

N

(

p, a)

DAS D ze stanami osi ˛

agalnymi (3 stany, 6 przej´s´c):

Start

1

0

1

0

{q

0

, q

2

}

0

1

{q

0

, q

1

}

{q

0

}

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Twierdzenia i dowody

Twierdzenia o równowa˙zno´sci NAS i DAS

Twierdzenie (2.11)

Je˙zeli D = (Q

D

, Σ, δ

D

,

q

0

,

F

D

)

jest DAS skonstruowanym z NAS

N = (Q

N

, Σ, δ

N

,

q

0

,

F

N

)

za pomoc ˛

a konstrukcji podzbiorów, to

L(D) = N(D).

Dowód.

Dowodzimy indukcyjnie po długo´sci |w |, ˙ze

ˆ

δ

D

({

q

0

}, w } = ˆ

δ

N

({

q

0

}, w }

Obie funkcje ˆ

δ

zwracaj ˛

a zbiory, lecz ró˙znie je interpretuj ˛

a.

Podstawa: Niech w = , wówczas z definicji ˆ

δ

ˆ

δ

D

({

q

0

}, ) = ˆ

δ

N

({

q

0

}, ) = {q

0

}

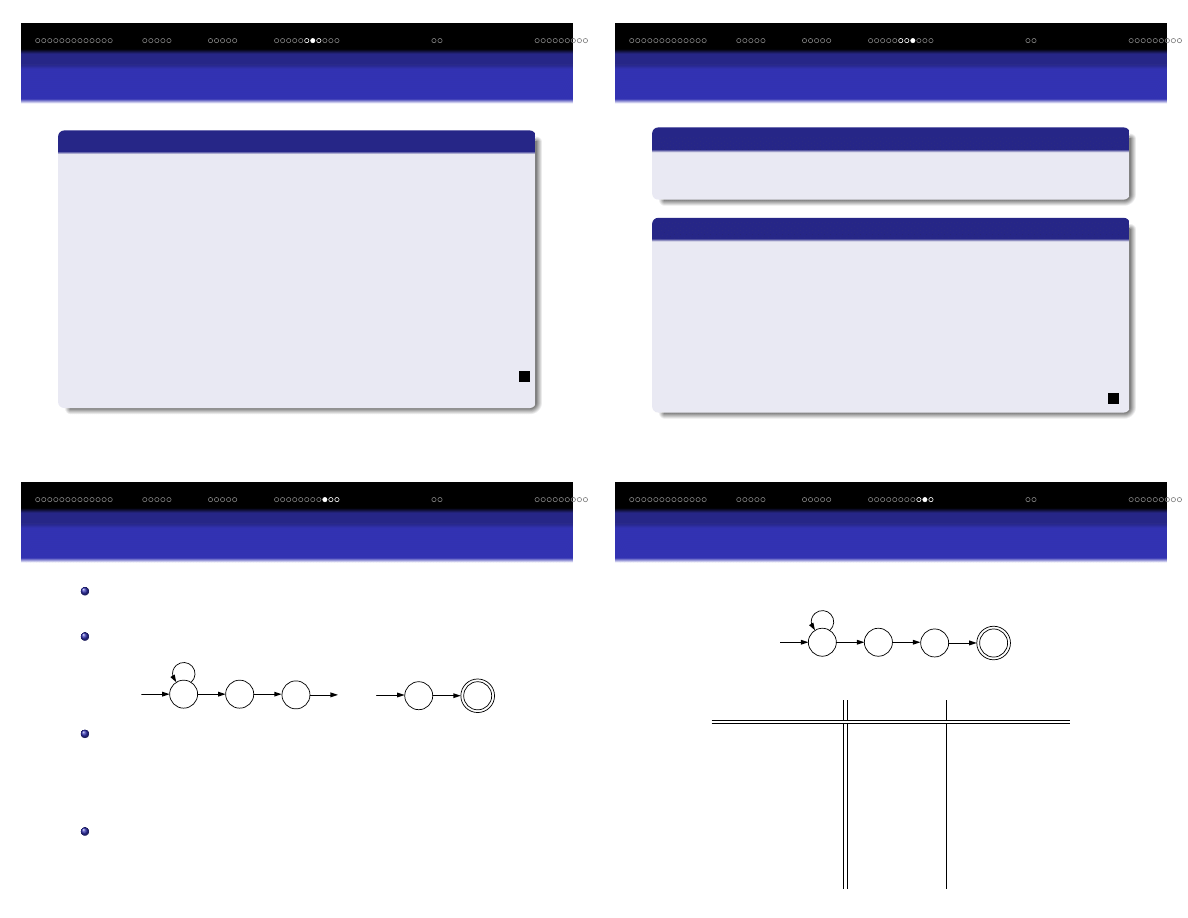
Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Twierdzenia i dowody

Twierdzenie o równowa˙zno´sci NAS i DAS

Dowód c.d.

Krok indukcyjny: Zakładamy, ˙ze ˆ

δ

D

({

q

0

}, x) = ˆ

δ

N

(

q

0

,

x ).

Chcemy dowie´s´c tej równo´sci dla w = xa.

ˆ

δ

D

({

q

0

}, xa)

= δ

D

(ˆ

δ

D

({

q

0

}, x), a)

z definicji ˆ

δ

D

= δ

D

(ˆ

δ

N

(

q

0

,

x ), a)

z zało˙zenia indukcyjnego

=

S

p∈ˆ

δ

N

(

q

0

,

x )

δ

N

(

p, a)

z konstrukcji podzbiorów

= ˆ

δ

N

(

q

0

,

xa)

z definicji ˆ

δ

N

Po wczytaniu w DAS znajduje si ˛e w stanie b ˛ed ˛

acym zbiorem

stanów NAS, w których NAS znajdowałby si ˛e po wczytaniu w .
Je˙zeli NAS znajdowałby si ˛e w stanie akceptuj ˛

acym, to DAS ten

stan równie˙z zawiera, czyli L(D) = L(N).

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Twierdzenia i dowody

Twierdzenia o równowa˙zno´sci NAS i DAS

Twierdzenie (2.12)

J ˛ezyk L jest akceptowany przez jaki´s DAS wtedy i tylko wtedy,
gdy L jest akceptowane przez jaki´s NAS

Dowód.

(<=) Wynikanie <= to konstrukcja podzbiorów z twierdz. 2.11

(=>) Ka˙zdy DAS to NAS, który "przypadkiem" w ka˙zdej sytuacji
ma tylko jedn ˛

a mo˙zliwo´s´c przej´scia. Musimy tylko

zmodyfikowa´c funkcj ˛e przej´scia wg reguły:

Jesli; δ

D

(

q, a) = p, to δ

N

(

q, a) = {p}

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Zły przypadek konstrukcji podzbiorów

Wykładniczy wzrost liczby stanów DAS

Mo˙zna poda´c przykład NAS o n + 1 stanch, dla którego nie
ma równowa˙znego DAS o mniej ni˙z 2

n

.

Ten NAS rozpoznaje napisy z 1 na n-tej pozycji od ko ´nca:

Start

q

1

q

0

0,1

1

0,1

q

2

0,1

• • •

q

n

0,1

0,1

Co formalnie mo˙zna zapisa´c:

L(N) = {x 1c

2

c

3

· · · c

n

:

x ∈ {0, 1}

∗

,

c

i

∈ {0, 1}}

Dowód nieformalny: Intuicyjnie czujemy, ˙ze ka˙zdy stan z
DAS musi pami ˛eta´c kolejno´s´c 1 na n ostatnio wczytanych
pozcyjach, zatem musi by´c 2

n

stanów.

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Zły przypadek konstrukcji podzbiorów

DAS wykrywaj ˛

acy 1 na 3 znaki od ko ´nca

NAS wykrywaj ˛

acy 1 na 3 znaki od ko ´nca (4 stany, 4 przej´scia):

Start

q

1

q

0

q

3

0,1

1

0,1

q

2

0,1

Tabela przej´s´c dla równowa˙znego DAS

δ

D

0

1

→ {q

0

}

{q

0

}

{q

0

,

q

1

}

{q

0

,

q

1

}

{q

0

,

q

2

}

{q

0

,

q

1

,

q

2

}

{q

0

,

q

2

}

{q

0

,

q

3

}

{q

0

,

q

1

,

q

3

}

{q

0

,

q

1

,

q

2

}

{q

0

,

q

2

,

q

3

}

{q

0

,

q

1

,

q

2

,

q

3

}

?{

q

0

,

q

3

}

{q

0

}

{q

0

,

q

1

}

?{

q

0

,

q

1

,

q

3

}

{q

0

,

q

2

}

{q

0

,

q

1

,

q

2

}

?{

q

0

,

q

2

,

q

3

}

{q

0

,

q

3

}

{q

0

,

q

1

,

q

3

}

?{

q

0

,

q

1

,

q

2

,

q

3

}

{q

0

,

q

2

,

q

3

}

{q

0

,

q

1

,

q

2

,

q

3

}

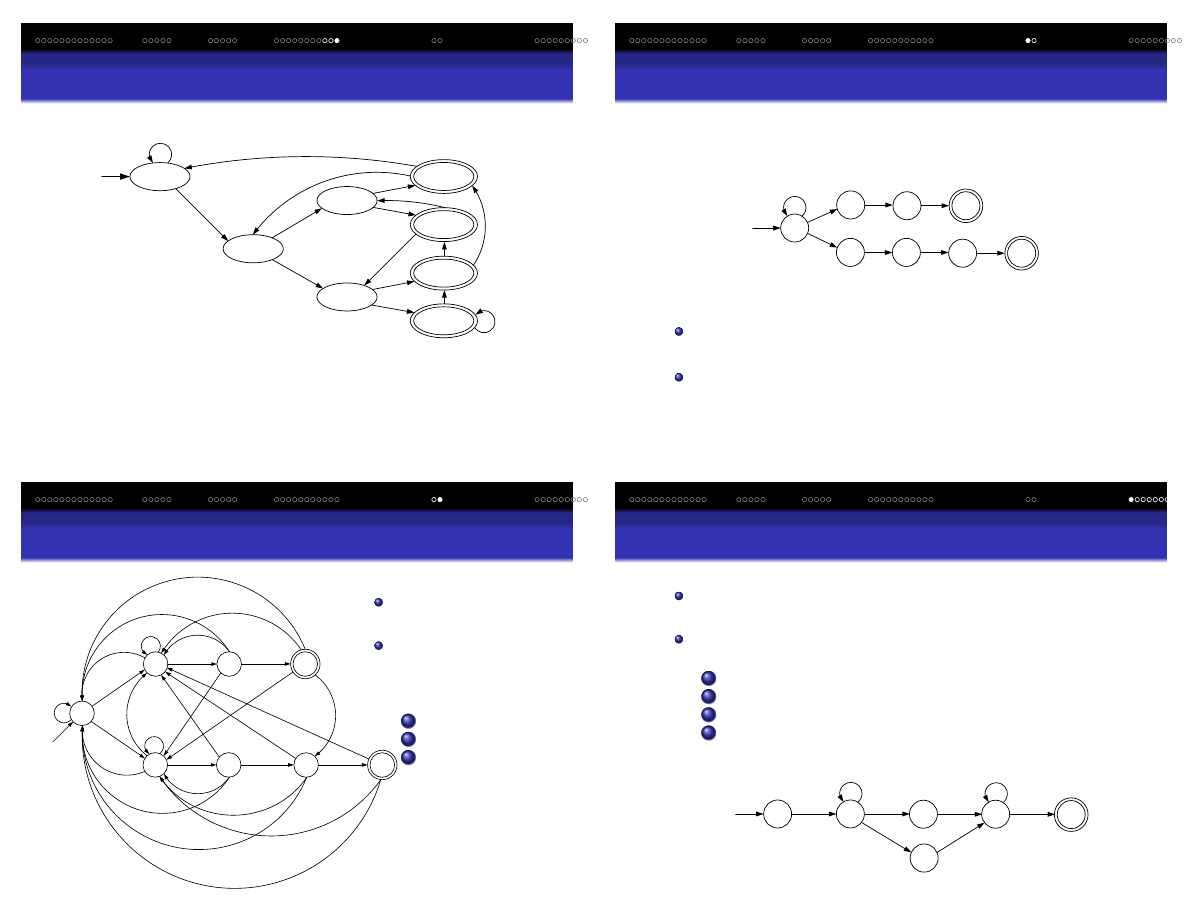
Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Zły przypadek konstrukcji podzbiorów

Diagram stanów dla równowa˙znego DAS

{q

0

,q

1

}

{q

0

}

{q

0

,q

3

}

{q

0

,q

1

,q

3

}

{q

0

,q

2

,q

3

}

{q

0

,q

1

,q

2

,q

3

}

{q

0

,q

1

,q

2

}

{q

0

,q

2

}

0

1

Start

1

1

1

1

1

1

0

0

0

0

0

0

1

0

1

10

11

111

110

101

100

DAS wykrywaj ˛

acy 1 na 3 znaki od ko ´nca (8 stanów, 16 przej´s´c).

W stanach zaznaczono wszystkie wczytane 1 na ostatnich 3
pozycjach.

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Przeszukiwanie tekstu

NAS znajdujacy ła ´ncuchy w tek´scie

NAS rozpoznaj ˛

acy wyst ˛

apienia słów web i ebay. Σ

reprezentuje zbiór znaków ASCI

Start

2

1

4

Σ

w

e

3

b

6

5

8

b

a

7

y

e

Istniej ˛

a dwie opcje implementacyjne:

napisa´c program symuluj ˛

acy ten NAS poprzez ob liczanie

zbioru stanów nast ˛epnych

zamieni´c ten NAS na DAS i nast ˛epnie bezpo´srednio
zasymulowa´c DAS

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Przeszukiwanie tekstu

DAS rozpoznaj ˛

acy zbiór słów kluczowych

Start

12

1

146

Σ-e-w

w

e

135

b

16

15

18

b

a

17

y

e

w

w

w

w

w

w

e

e

e

a

w

e

e

Σ-e-w

Σ-b-e-w

Σ-a-e-w

Σ-b-e-w

Σ-a-e-w

Σ-e-w-y

Σ-e-w

e

q

0

w NAS to {q

0

} w

DAS
je˙zeli p ∈ Q

N

jest

osi ˛

agany z q

0

po ci ˛

agu

a

1

a

2

· · · a

m

to do zbioru

stanów z DAS nale˙z ˛

a:

1

q

0

2

p

3

ka˙zdy stan z NAS
osi ˛

agalny z q

0

,

wzdłu˙z ´scie˙zki, której
etykiety s ˛

a sufiksami

a

1

a

2

· · · a

m

, tzn.

ka˙zdy ci ˛

ag postaci

a

j

a

j+1

· · · a

m

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Automat sko ´nczony z epsilon-przej´sciami

Automat z -przej´sciami to taki automat, który mo˙ze
zmienia´c swój stan bez wczytywania symbolu z wej´scia.

-NAS akceptuj ˛

acy dziesi ˛etne liczby rzeczywiste składa si ˛e

kolejno z:

1

Opcjonalny znak + lub -

2

Ci ˛

ag cyfr

3

Kropka dziesi ˛etna

4

Kolejny ci ˛

ag cyfr

Jeden z ci ˛

agów (2) lub (4) jest opcjonalny

Start

q

1

q

0

q

5

0,1,…,9

ε,+,-

q

2

.

q

4

0,1,…,9

q

3

0,1,…,9

ε

.

0,1,…,9

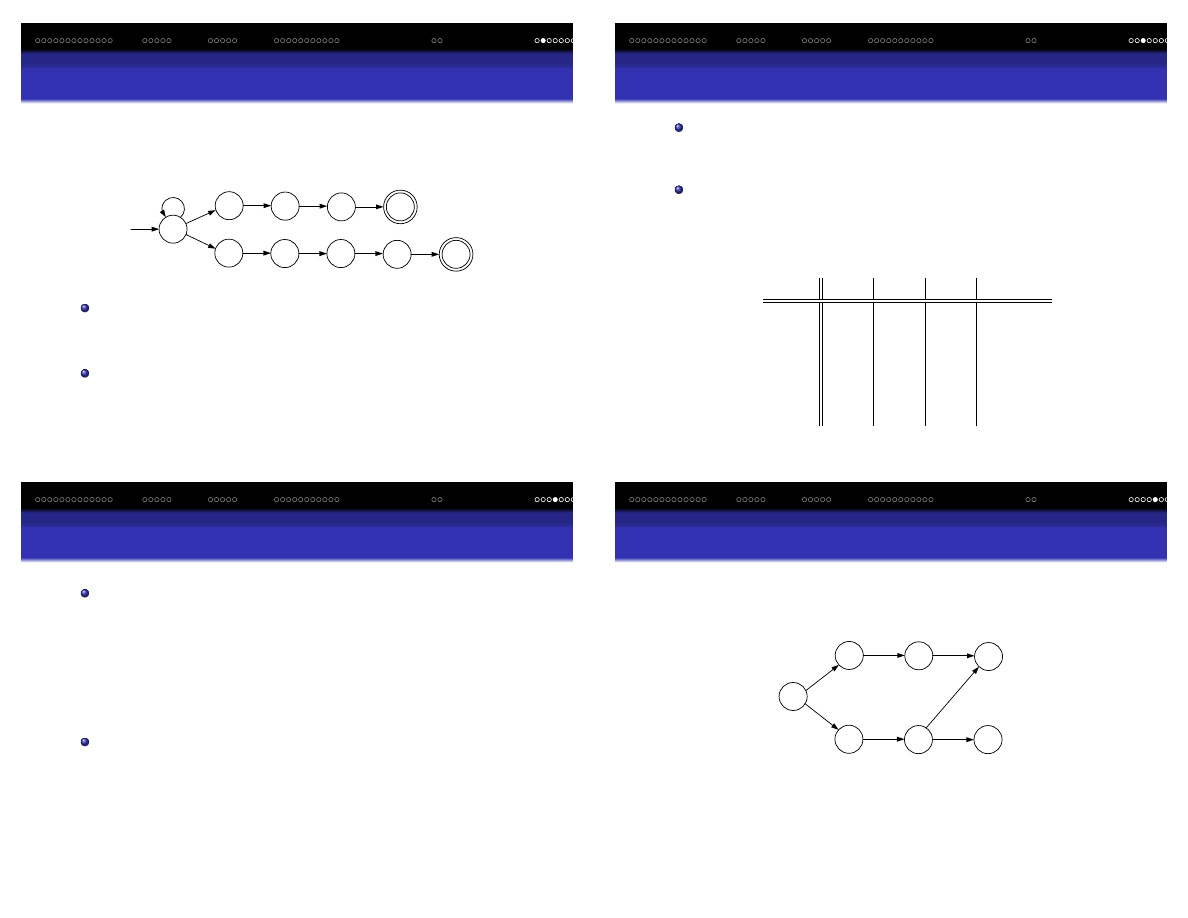
Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Inny przykład -NAS

-przej´scia nie rozszerzaj ˛

a klasy j ˛ezyków akceptowanych przez

AS, lecz nieco zwi ˛ekszaj ˛

a "wygod ˛e programowania".

Uniwersalny -NAS szukaj ˛

acyc słów web i ebay

Start

2

9

4

Σ

ε

e

3

b

6

5

8

b

a

7

y

ε

1

w

0

e

Budujemy pełny ci ˛

ag stanów dla ka˙zdego słowa

kluczowego, jak gdyby było ono jedynym słowem, które
automat rozpoznaje.

Nast ˛epnie dodajemy nowy stan pocz ˛

atkowy (stan nr 9) z

-przej´sciami do stanów automatu dla ka˙zdego ze słów

kluczowych.

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

-NAS definicja formalna

-NAS jest to uporz ˛

adkowana pi ˛

atka (Q, Σ, δ, q

0

,

F ) gdzie δ

jest funkcj ˛

a która odwzorowuje ze zbioru Q × Σ ∪ {} w

zbiór pot ˛egowy Q.

Uwaga: nie nale˙zy do Σ.

Przykład -NAS akceptuj ˛

acego dziesi ˛etne liczby

rzeczywiste.

E = ({q

0

,

q

1

,

q

2

,

q

3

,

q

4

,

q

5

}, {., +, −, 0, 1, . . . , 9}, δ, q

0

, {

q

5

})

gdzie funkcja przej´scia δ jest nast ˛epuj ˛

aca:

δ

+, −

.

0, . . . , 9

→ q

0

{q

1

}

{q

1

}

∅

∅

q

1

∅

∅

{q

2

}

{q

1

,

q

4

}

q

2

∅

∅

∅

{q

3

}

q

3

{q

5

}

∅

∅

{q

3

}

q

4

∅

∅

{q

3

}

∅

?

q

5

∅

∅

∅

∅

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

-domkni ˛ecia

Nieformalnie

-domykamy stan q id ˛

ac po wszystkich przej´sciach ze

stanu q opatrzonych etykiet ˛

a . Gdy dojdziemy do jakiego´s

stanu, dalej pod ˛

a˙zamy z niego po przej´sciach z etykiet ˛

a ,

o ile takie istniej ˛

a. -domkni ˛eciem stanu q jest zbiór tych

wszystkich stanów, do których mo˙zemy doj´s´c z q po
etykietach .

Formalnie
Podstawa: Stan q nale˙zy do EDOMK(q).
Krok indukcyjny: Je˙zeli stan p nale˙zy do EDOMK(q) oraz
istnieje przej´scie ze stanu p do r o etykiecie , to r nale˙zy
do EDOMK(q). Lub bardziej precyzyjnie dla ka˙zdego δ(p, ):

p ∈ EDOMK(q) ⇒ δ(p, ) ∈ EDOMK(q)

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Przykład -domkni ˛ecia

3

1

ε

ε

6

7

5

ε

ε

2

ε

4

a

b

EDOMK

(

1) = {1, 2, 3, 4, 6}

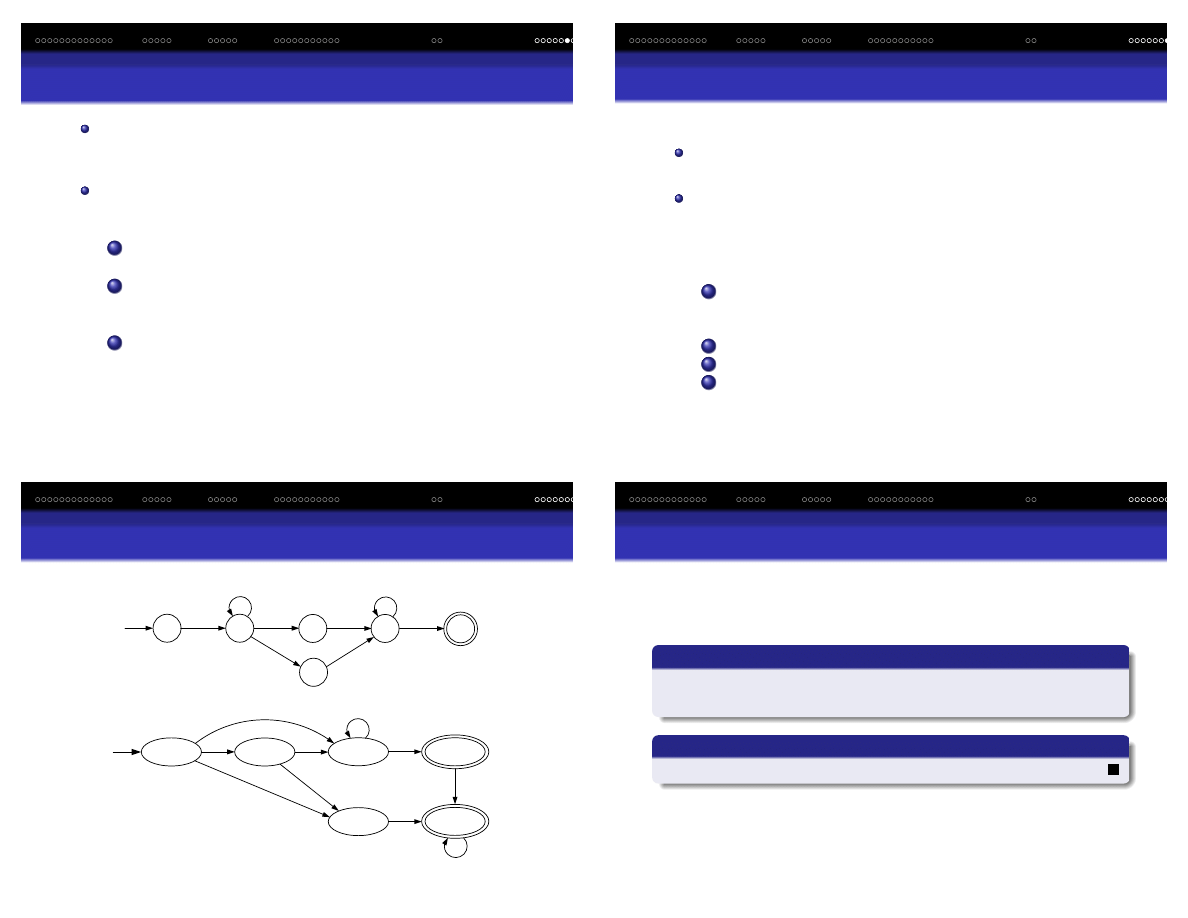
Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Rozszerzona funkcja przej´scia ˆ

δ

dla -NAS

W zamierzeniu ˆ

δ(

q, w ) jest zbiorem stanów osi ˛

agalnych po

´scie˙zce, której etykiety po zło˙zeniu tworz ˛

a ci ˛

ag w . Etykiety

na ´scie˙zce nic nie wnosz ˛

a do w .

Podstawa: ˆ

δ(

q, ) = EDOMK(q).

Krok indukcyjny: Załó˙zmy ˙ze w = xa. Warto´s´c ˆ

δ(

q, w )

obliczamy nast ˛epuj ˛

aco:

1

Niech ˆ

δ(

q, x ) = {p

1

,

p

2

, . . . ,

p

k

}, czyli to s ˛

a te stany do

których mo˙zna doj´s´c z q po etykiecie x .

2

Niech

S

k
i=1

δ(

p

i

,

a) = {r

1

,

r

2

, . . . ,

r

m

}. Stany r

j

to niektóre ze

stanów, do których mo˙zemy doj´s´c z q po etykiecie w .
Brakuje tylko -domkni ˛e´c stanów r

j

.

3

Zatem: ˆ

δ(

q, w ) =

S

m
i=1

EDOMK

(

r

j

)

.

Bardziej formalnie:

ˆ

δ(

q, xa) =

[

p∈δ(ˆ

δ(

q,x ),a)

EDOMK

(

p)

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Eliminacja -przej´s´c

Dla danego -NAS E mo˙zna znle´z´c DAS D, który
akceptuje ten sam j ˛ezyk co E .

Niech E = (Q

E

, Σ, δ

E

,

q

0

,

F

E

)

. Wtedy równowa˙zny DAS:

D = (Q

D

, Σ, δ

D

,

q

D

,

F

D

)

jest zdefiniowany nast ˛epuj ˛

aco:

1

Q

D

jest zbiorem podzbiorów Q

E

, a dokładniej wszystkie

stany D s ˛

a -domkni ˛etymi podzbiorami Q

E

, tj. zbiorami

S ⊆ Q

E

takimi, ˙ze S = EDOMK(S).

2

q

D

= EDOMK(

q

0

)

.

3

F

D

= {

S | S ∈ Q

D

oraz S ∩ F

E

6= ∅}.

4

δ

D

(

S, a) =

S{EDOMK(p) : p ∈ δ(t, a) dla wszystkich t ∈ S}.

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Przykład: -NAS z liczbami rzeczywistymi i jego DAS

Start

q

1

q

0

q

5

0,1,…,9

ε,+,-

q

2

.

q

4

0,1,…,9

q

3

0,1,…,9

ε

.

0,1,…,9

{q

0

,q

1

}

{q

2

,q

3

,q

5

}

{q

3

,q

5

}

{q

1

,q

4

}

0

Start

.

0,1,…,9

{q

1

}

{q

2

}

+,-

.

.

0,1,…,9

0,1,…,9

0,1,…,9

0,1,…,9

Wprowadzenie

DAS

NAS

Równowa˙zno´s´c DAS i NAS

Zastosowanie

-NAS

Automaty z pustymi symbolami na wej´sciu

Twierdzenie o j ˛ezykach -NAS i DAS

Twierdzenie (2.22)

J ˛ezyk L jest akceptowany przez pewien -NAS wtedy i tylko
wtedy, gdy L jest akceptowany przez pewien DAS.

Dowód.