Analiza matematyczna – kol. 1 – przykładowe rozwiązanie
Zadanie 1
Oblicz granice ciągu:
a)
lim
→
= lim
→
1 +
= lim
→
1 +
=
= lim
→
1 +
1
4
5
"
#
= $
#
b)
lim
→
√2 − 5
(
− 4 = lim
→
) 2 −
*
+
−
+
= lim
→
) 2 − −
+
=
= lim
→
, ⋅ ./2 − 5 −
4
0 = lim
→
1 √ 2 ⋅ ./2 −
5
−
4
0 = 1 ⋅ lim
→
√2 = 1
c)
lim
→
⋅
34
(
34
⋅(
54
3*
6
= lim
→
⋅ ⋅ ( ⋅(
⋅( ⋅(
54
⋅
*
6
= lim
→
⋅
(⋅(
(⋅( 7⋅
6
= lim
→
/
(⋅
*
0
(⋅
*
+
7
8
+
=
lim
→
(⋅
*
(⋅
*
+
7 6⋅
4
+
= :+∞ ⋅
(⋅#
(⋅# 7 6⋅#
< = +∞
Zadanie 2
Wykaż, że ciąg
= =
(
+
− 2 nie ma granicy.
//dowód na podstawie rozważań z wykładu (wskazujemy dwa różne podciągi ciągu
= , które mają różne granice i
powołujemy się na odpowiednią własność z wykładu).
Zadanie 3
Oblicz granice funkcji
a)
lim
>→+∞
2arcsin
>
1+>
2
Najpierw liczymy granicę funkcji:
lim
>→+∞
>
1+>
2
= 0 – bo granica w punkcie niewłaściwym funkcji wymiernej, gdzie stopień mianownika wyższy niż stopień
licznika (st(M)>st(L))
Zatem
lim
>→+∞
2arcsin >
1 + >
2
=
2arcsin
0 = 2 ⋅ 0 = 0
b)
lim
>→−∞
3 ⋅
1
2
5>2−4>
3>−2
Najpierw liczymy granicę funkcji z wykładnika:
lim
>→−∞
5>
2
− 4>
3> − 2
= lim
>→−∞
5>
2
> −
4>
>
3>
> −
2
>
= lim
>→−∞
5> − 4
3 − 2>
= F
−∞ − 4
3 − 0 G = −∞
Zatem
lim
>→−∞
3 ⋅ 12
5>
2
−4>
3>−2
= lim
H→−∞
3 ⋅ 12
I
= J3 ⋅ K+∞LM = ∞
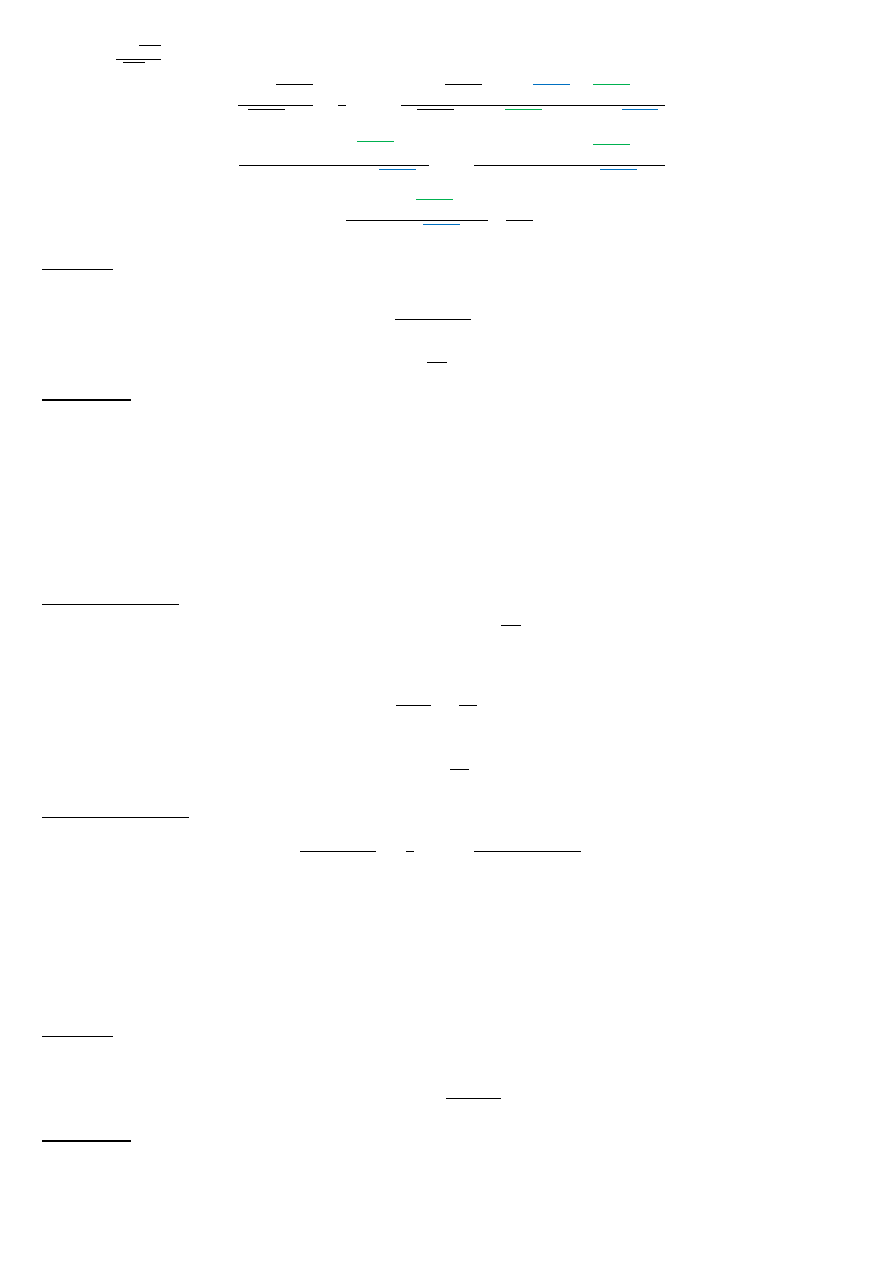
c)
lim
>→1
>−
√
2−>
√
5−>−2
lim
>→1
> −
√
2 − >
√
5 − > − 2
= F
0
0G = lim
>→1
1
> −
√
2 − >
2
1
> +
√
2 − >
2
1√
5 − > + 2
2
1√
5 − > − 2
2
1√
5 − > + 2
2
1
> +
√
2 − >
2
=
lim
>→1
>
2
−
K
2 − >
L
1√
5 − > + 2
2
1K
5 − >
L
− 4
2
1
> +
√
2 − >
2
= lim
>→1
K
> − 1
L
K
> + 2
L
1√
5 − > + 2
2
−K
> − 1
L
1
> +
√
2 − >
2
=
lim
>→1
K
> + 2
L
1√
5 − > + 2
2
−
1
> +
√
2 − >
2
=
3 ⋅ 4
−2 = −6
Zadanie 4
Zbadaj ciągłość funkcji
OK>L =
P
Q
R>
(
− 4> + 3
> − 3
dla > > 3
0
dla > = 3
$
U
U
dla > < 3
Rozwiązanie
Jedyny punkt podejrzany o nieciągłość:
>
#
= 3.
O – ciągła w punkcie >
#
WXY
Z[ lim
U→U
\
OK>L = OK>
#
L
Zastanawiamy się zatem nad granicą funkcji w punkcie podejrzanym o nieciągłość.
lim
U→
OK>L =?
Funkcja
O jest opisana różnymi wzorami zarówno w lewostronnym jak i prawostronnym otoczeniu punktu >
#
= 3.
Liczymy zatem granice jednostronne.
Granica lewostronna
lim
U→
5
OK>L = lim
U→
5
$
>
>−3
Policzmy granicę samego wykładnika:
lim
U→
5
>
> − 3
= F
3
0 G = −∞
Uzyskujemy zatem:
lim
U→
5
OK>L = lim
U→
5
$
>
>−3
= lim
I→
$
H
= 0
Granica prawostronna
lim
U→
3
OK>L = lim
U→
3
>
2
− 4> + 3
> − 3
=
F
0
0
G
=
lim
U→
3
K> − 3LK> − 1L
> − 3
=
lim
U→
3
K> − 1L
=
2
Mamy więc, że:
lim
U→
5
OK>L ≠ lim
U→
3
OK>L ⇒ lim
U→
OK>L – NIE istnieje
W konsekwencji funkcja
O NIE jest ciągła w punkcie >
#
= 3.
Zadanie 5
Wyznacz asymptoty wykresu funkcji
OK>L =
2>
(
− 3
> + 1
Rozwiązanie
Dziedzina:
> + 1 ≠ 0 ⇔ > ≠ −1
a = ℝ\{−1}
•
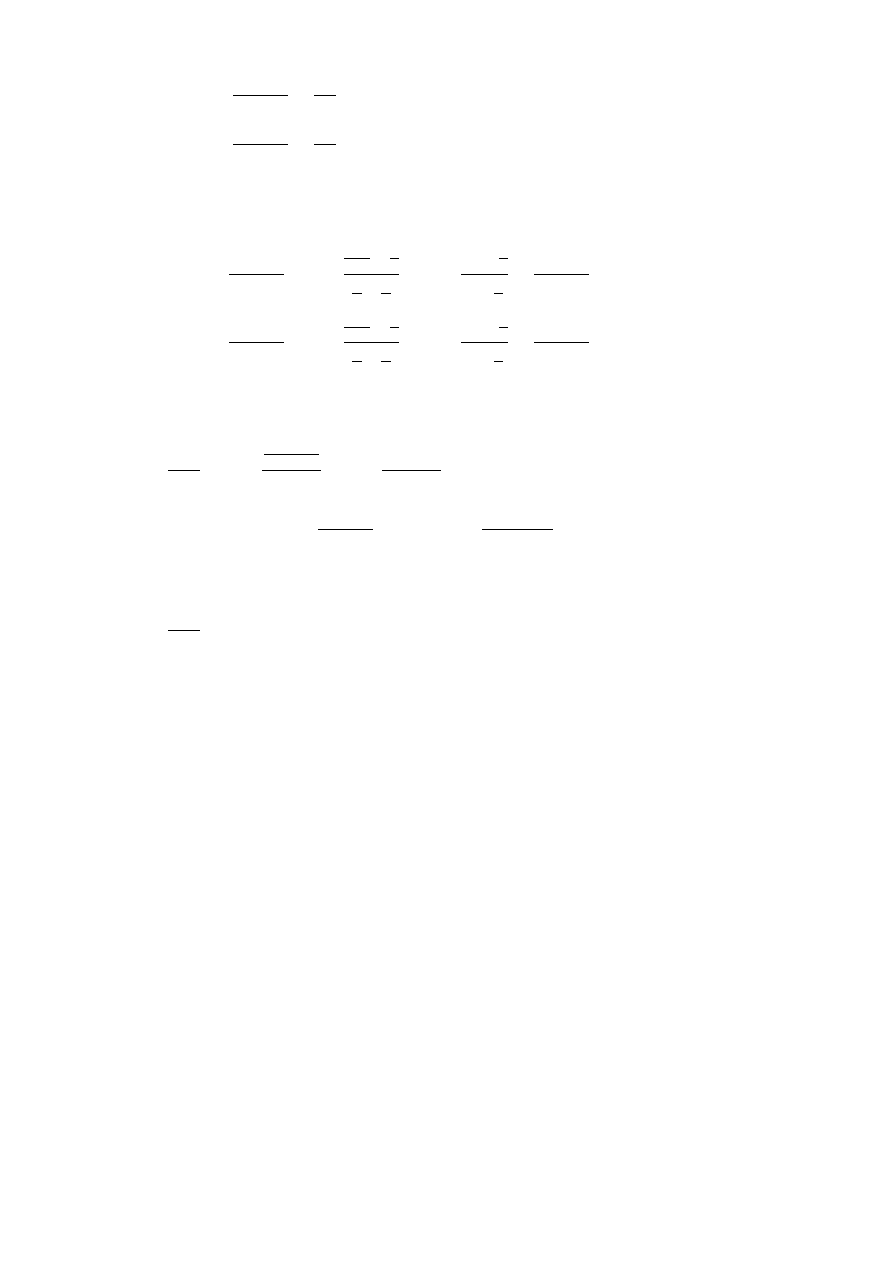
Asymptoty pionowe
lim
U→
5
OK>L = lim
U→
5
2>
(
− 3
> + 1 = F
−1
0 G = +∞
lim
U→
3
OK>L = lim
U→
3
2>
(
− 3
> + 1 = F
−1
0 G = −∞
Obie granice jednostronne w punkcie
>
#
= −1 są niewłaściwe, zatem prosta o równaniu > = −1 jest asymptotą
pionową obustronną.
•
Asymptoty poziome
lim
U→
OK>L = lim
U→
2>
(
− 3
> + 1 = lim
U→
2>
(
> −
3
>
>
> +
1
>
= lim
U→
2> − 3>
1 + 1>
= F
−∞ − 0
1 + 0 G = −∞
lim
U→
OK>L = lim
U→
2>
(
− 3
> + 1 = lim
U→
2>
(
> −
3
>
>
> +
1
>
= lim
U→
2> − 3>
1 + 1>
= F
+∞ − 0
1 + 0 G = +∞
Ż
adna z powyższych granic NIE okazała się być liczbą, w związku z tym brak asymptoty poziomej.
•
Asymptoty ukośne
f = g> + h
g = lim
U→
OK>L
> = lim
U→
2>
(
− 3
> + 1
>
= lim
U→
2>
(
− 3
>
(
+ > = 2
h = lim
U→
KOK>L − g>L = lim
U→
2>
(
− 3
> + 1 − 2> = lim
U→
−2> − 3
> + 1 = −2
Obie powyższe granice istnieją i są liczbami, zatem prosta o równaniu
f = 2> − 2 jest asymptotą ukośną w −∞.
Zauważmy, że w
+∞ mamy również:
g = lim
U→
OK>L
> = 2
h = lim
U→
KOK>L − g>L = − 2
Zatem prosta o równaniu
f = 2> − 2 jest asymptotą ukośną również w +∞.