
SNy: Biotechnologia
Analiza matematyczna II
– kolokwium II
notatki ze studiów na kierunku Biotechnologia
na Wydziale Chemicznym Politechniki Wrocławskiej
Autor:
Mateusz Jędrzejewski
mateusz.jedrzejewski@one.pl
www.jedrzejewski.one.pl
otatka jest częścią projektu SNy Biotechnologia
(Studenckie Notatki Cyfrowe). Udostępniane
są one na stronie internetowej www.sny.one.pl. Każdy
może za darmo korzystać z nich w celach edukacyjnych.
waga na błędy! Mimo staranności jaką włożyli
autorzy w opracowanie tej notatki mogą
zdarzyć się błędy. Więc każdy korzysta z tych
notatek na własną odpowiedzialność. Zauważone błędy
proszę zgłaszać autorowi notatki (najlepiej drogą
elektroniczną).
śyczę wszystkim skutecznego korzystania z notatek.
Mateusz Jędrzejewski
(autor strony www.sny.one.pl)
Szczegółowe informacje o notatce
Nazwa pliku: e-notatka - analiza matematyczna II - kolokwium II.pdf
Nazwa kursu: Analiza matematyczna II (MAP2005w)
Prowadzący kurs: dr Magdalena Rutkowska
Semestr/rok: 07l (rok 1, II semestr)
Kierunek: Biotechnologia
Wydział: Wydział Chemiczny
Uczelnia: Politechnika Wrocławska
Autor notatki: Mateusz Jędrzejewski
Status: Notatka w wersji roboczej
N
U
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 2
Notatka: Analiza matematyczna II (MAP2005w) – kolokwium II.
Utworzona: 11.06.2007 23:05
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 12.06.2007 15:00
Kolokwium II – Zestaw D
16.06.2007 r.
zad. 1.
Zbadać ekstrema funkcji
)
ln(
)
,
(
2
2
y
e
x
y
x
f
+
=
.
Dziedzina funkcji:
2
ℜ
=
D
Bo
0
2
2
>
+
y
e
x
.
(
)
(
)
)
0
,
0
(
)
,
(
0
0
0
2
0
2
0
2
0
2
0
)
,
(
0
)
,
(
2
)
ln(
)
,
(
2
)
ln(
)
,
(
0
0
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
=
=
=
⇒
=
⋅
=
⇒
=
+
⋅
=
+
⇒
=
∂
∂
=
∂
∂
+
⋅
=
+
∂
∂
=
∂
∂
+
=
+
∂
∂
=
∂
∂
y
x
y
x
e
y
x
e
x
e
y
e
x
x
y
x
y
f
y
x
x
f
e
x
e
y
e
x
x
y
x
y
f
e
x
x
e
x
x
y
x
x
f
y
y
y
y
y
y
y
y
y
(
)
(
)
(
)
(
)
(
)
(
)
(
)
0
4
2
0
0
2
)
0
,
0
(
)
0
,
0
(
)
0
,
0
(
)
0
,
0
(
0
)
0
,
0
(
2
)
1
(
)
(
2
)
(
2
2
)
,
(
)
,
(
2
1
0
0
)
1
0
)(
0
1
(
2
)
0
,
0
(
)
2
(
2
)
)(
2
(
2
2
)
,
(
2
1
0
0
4
)
1
0
(
2
0
0
4
)
0
(
2
)
0
,
0
(
4
)
(
2
2
2
)
(
2
2
)
,
(
2
2
2
2
2
2
2
2
2
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
0
2
2
0
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
>
=
=
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
=
∂
∂
∂
⋅
⋅
−
⋅
+
⋅
=
=
+
⋅
∂
∂
=
+
∂
∂
=
∂
∂
∂
=
∂
∂
∂
=
+
−
+
+
⋅
=
∂
∂
+
⋅
⋅
−
+
⋅
⋅
+
=
+
⋅
∂
∂
=
∂
∂
=
+
⋅
−
+
⋅
=
+
⋅
−
+
⋅
=
∂
∂
+
−
+
=
+
⋅
−
+
=
+
∂
∂
=
∂
∂
−
−
y
f
x
y
f
y
x
f
x
f
y
x
f
y
e
e
x
x
e
x
x
y
e
x
x
y
y
x
x
y
f
y
x
y
x
f
y
f
e
x
y
e
e
y
e
x
y
e
y
e
e
x
e
y
y
y
x
y
f
e
e
x
f
e
x
x
e
x
e
x
x
x
e
x
e
x
x
x
y
x
x
f
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
y
Więc
)
,
(
y
x
f
ma ekstremum w
)
0
,
0
(
.
0
2
)
0
,
0
(
2
2
>
=
∂
∂
x
f
Więc
)
,
(
y
x
f
ma minimum w
)
0
,
0
(
.
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 3
Notatka: Analiza matematyczna II (MAP2005w) – kolokwium II.
Utworzona: 11.06.2007 23:05
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 12.06.2007 15:00
zad. 2.
Obliczyć pochodną kierunkową funkcji
)
sin(
)
,
(
2
3
x
y
x
y
x
f
−
=
w punkcie
)
1
,
1
(
−
w kierunku wersora
[
]
5
3
5
4
,
−
.
[?] W kierunku którego wektora, przyrosty funkcji
)
,
(
y
x
f
od punktu
)
1
,
1
(
−
są najmniejsze.
(
)
(
)
(
)
(
)
(
) (
)
5
2
5
6
5
4
5
3
5
4
5
3
5
4
0
0
0
0
0
0
2
3
0
0
2
3
2
3
2
3
2
2
0
0
2
3
2
2
2
3
0
0
5
3
5
4
)
2
(
)
(
1
,
2
,
1
)
,
(
grad
)
,
(
2
,
1
)
,
(
),
,
(
)
,
(
grad
2
))
1
(
2
(
)
1
)
1
cos((
1
)
,
(
)
2
(
)
cos(
)
sin(
)
,
(
1
1
0
3
)
1
(
)
1
)
1
cos((
1
)
1
)
1
sin((
1
3
)
,
(
)
1
(
)
cos(
)
sin(
3
)
sin(
)
,
(
)
1
,
1
(
)
,
(
,
−
=
−
=
⋅
−
+
−
⋅
−
=
−
−
−
=
=
∂
∂
−
−
=
∂
∂
∂
∂
=
−
=
−
⋅
⋅
−
−
=
∂
∂
⋅
−
=
−
∂
∂
=
∂
∂
−
=
−
⋅
=
−
⋅
−
−
+
−
−
⋅
=
∂
∂
−
⋅
−
+
−
=
−
∂
∂
=
∂
∂
−
=
−
=
o
o v
y
x
f
y
x
v
f
y
x
y
f
y
x
x
f
y
x
f
y
x
y
f
y
x
y
x
x
y
x
y
y
x
y
f
y
x
x
f
x
y
x
x
y
x
x
y
x
x
y
x
x
f
y
x
v
zad. 3.
Obliczyć objętość bryły ograniczonej powierzchniami
)
(
3
2
2
y
x
z
+
−
=
oraz
2
2
1
y
x
z
+
+
=
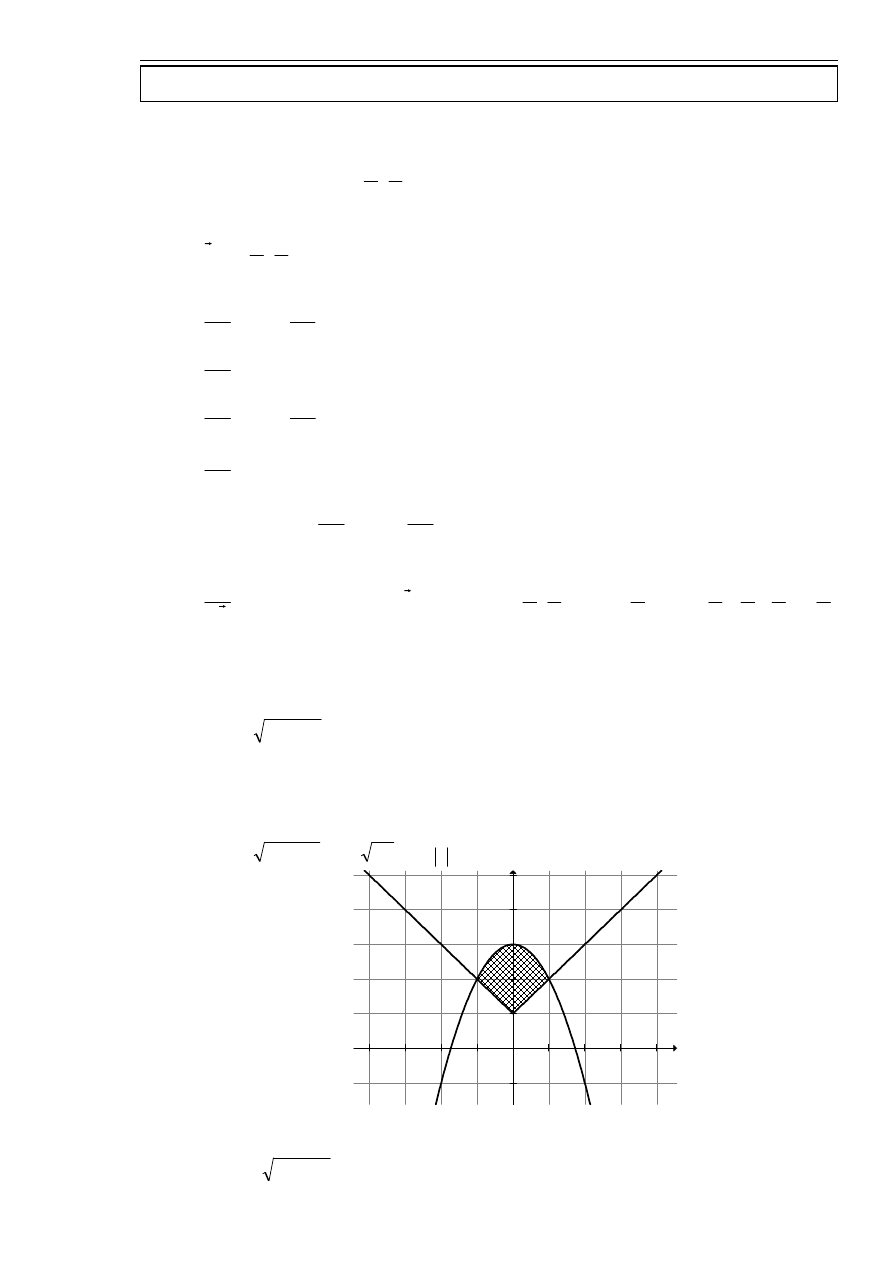
. Sporządzić stosowny rysunek.
Wykres 3D…
Wykres dla
0
=
y
:
2
2
3
)
0
(
3
x
x
z
−
=
+
−
=
x
x
x
z
+
=
+
=
+
+
=
1
1
0
1
2
2
2
-4
-3
-2
-1
1
2
3
4
-1
1
2
3
4
x
y
Szukam obszaru całkowania:
+
+
=
+
−
=
2
2
2
2
1
)
(
3
y
x
z
y
x
z
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 4
Notatka: Analiza matematyczna II (MAP2005w) – kolokwium II.
Utworzona: 11.06.2007 23:05
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 12.06.2007 15:00
2
2
2
2
1
)
(
3
y
x
y
x
+
+
=
+
−
niech:
0
2
2
>
+
=
t
y
x
t
(
)
2
2
3
5
4
2
3
5
3
9
16
25
0
4
5
4
4
2
2
1
3
2
1
2
2
2
2
=
−
=
=
+
=
=
∆
=
−
=
∆
=
+
−
=
+
−
=
−
=
−
+
=
−
t
t
t
t
t
t
t
t
t
t
t
t
t
Rozwiązanie
1
t
odpada bo
2
2
4
4
2
2
≠
−
⇔
≠
−
⇒
=
−
t
t
.
Więc rozwiązanie to:
1
2
2
2
2
=
+
⇒
+
=
y
x
y
x
t
Obszar całkowania:
{
}
2
2
2
1
1
,
1
1
:
)
,
(
x
y
x
x
y
x
D
−
≤
≤
−
−
≤
≤
−
ℜ
∈
=
Powierzchnie ograniczające:
górna:
)
(
3
)
,
(
2
2
y
x
y
x
g
+
−
=
dolna:
2
2
1
)
,
(
y
x
y
x
d
+
+
=
Objętość to:
[
]
∫∫
∫∫
∫∫
−
=
−
=
D
D
D
dxdy
y
x
d
dxdy
y
x
g
dxdy
y
x
d
y
x
g
V
)
,
(
)
,
(
)
,
(
)
,
(
Zmieniam współrzędne na biegunowe:
=
=
ϕ
ϕ
sin
cos
:
r
y
r
x
B
{
}
1
0
,
2
0
:
)
,
(
≤
≤
<
≤
=
∆
∆
→
r
r
D
π
ϕ
ϕ
[
]
[
]
[
]
(
)
(
)
[
]
(
)
(
)
π
π
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
π
π
π
π
π
π
6
5
3
1
4
1
2
0
3
1
4
1
2
0
1
0
3
3
1
4
4
1
2
2
2
2
0
1
0
2
3
2
0
1
0
2
2
0
1
0
2
2
2
2
2
2
2
2
2
0
1
0
1
2
1
2
2
sin
cos
1
)
sin
cos
(
3
)
sin
,
cos
(
)
sin
,
cos
(
)
sin
,
cos
(
)
sin
,
cos
(
=
−
−
⋅
=
−
−
=
−
−
=
=
−
−
=
−
−
=
=
+
−
−
+
−
=
=
−
=
=
−
=
∫
∫
∫ ∫
∫ ∫
∫ ∫
∫ ∫
∫∫
∆
d
d
r
r
r
dr
r
r
r
d
dr
r
r
r
d
dr
r
r
r
r
r
d
dr
r
r
r
d
r
r
g
d
dr
d
r
r
r
d
r
r
g
V
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 5
Notatka: Analiza matematyczna II (MAP2005w) – kolokwium II.
Utworzona: 11.06.2007 23:05
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 12.06.2007 15:00
zad. 4.
Zmienić kolejność całkowania w całce iterowanej
∫
∫
−
−
−
4
2
6
4
2
2
)
,
(
y
y
y
dx
y
x
f
dy
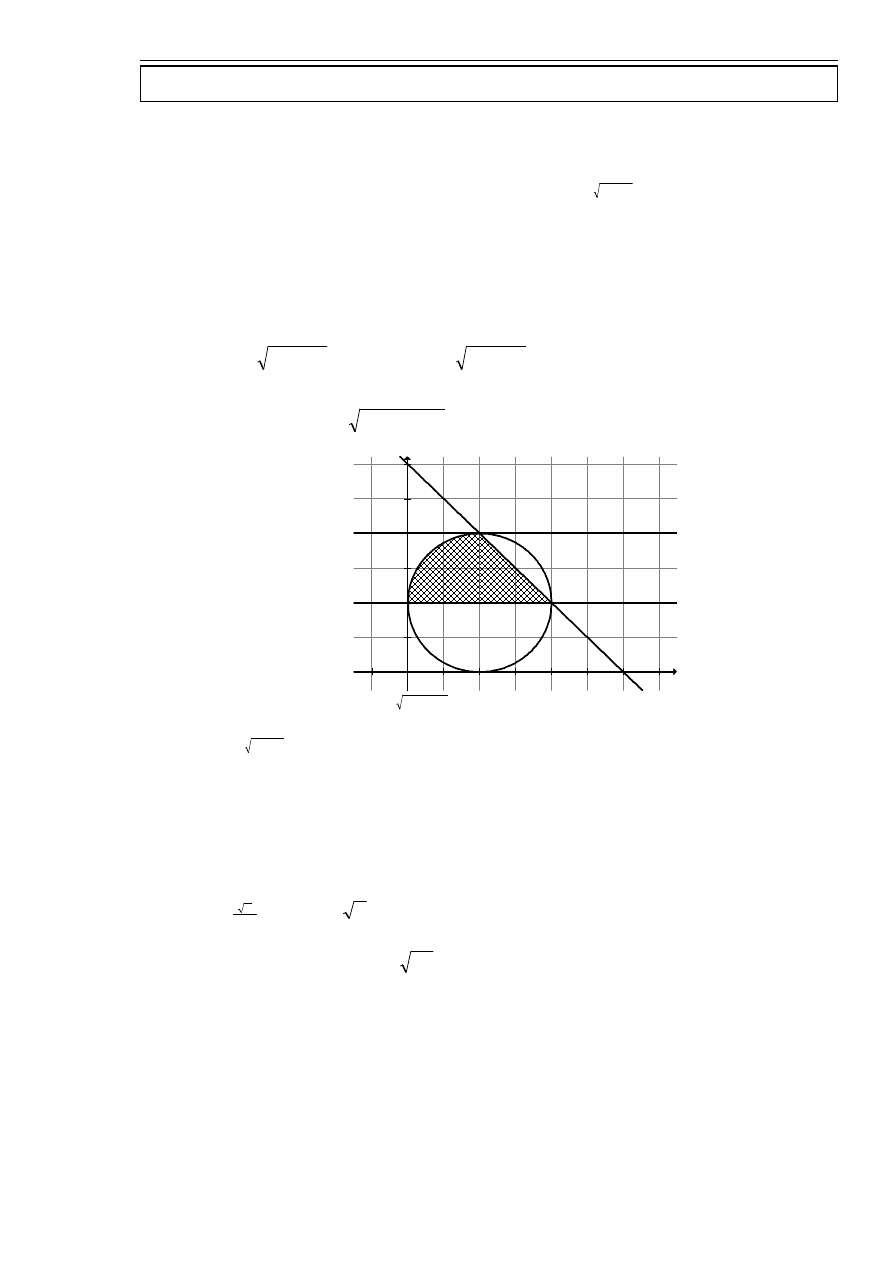
.
Sporządzić stosowny rysunek.
Trzeba odtworzyć obszar całkowania, ograniczenia to:
2
2
2
2
2
2
2
2
2
)
2
(
4
2
4
)
2
(
)
2
(
0
4
)
2
(
4
)
2
(
4
)
2
(
4
2
6
6
4
2
−
−
±
=
⇒
=
−
+
−
⇒
=
−
+
−
⇒
−
=
−
⇒
−
−
=
−
⇒
−
−
=
+
−
=
⇒
−
=
=
=
x
y
y
x
y
y
x
y
y
x
y
y
x
y
y
x
x
y
y
x
y
y
Jest to koło o promieniu 2 i środku (2,2).
-1
1
2
3
4
5
6
7
1
2
3
4
5
6
x
y
∫
∫
∫
∫
∫
∫
+
−
−
−
+
−
−
−
+
=
4
2
6
2
2
0
)
2
(
4
2
2
4
2
6
4
2
)
,
(
)
,
(
)
,
(
2
2
x
x
y
y
y
dy
y
x
f
dx
dy
y
x
f
dx
dx
y
x
f
dy
Zadania z pozostałych grup…
zad. 1.
Obliczyć całkę
∫∫
D
dxdy
x
2
gdzie obszar D ograniczają krzywe:
1
2
2
=
+
y
x
,
4
2
2
=
+
y
x
,
x
y
3
3
=
oraz
x
y
3
=
.
zad. 2.
Dana jest funkcja
)
ln(
)
,
(
2
x
y
xy
y
x
f
+
=
. Znaleźć taki wersor, że pochodna
kierunkowa w punkcie
)
0
,
1
(
równa się zero.
zad. 3.
Znaleźć wartość najmniejszą i największą funkcji
)
4
(
)
,
(
y
x
xy
y
x
f
−
−
=
na obszarze
ograniczonym przez krzywe:
1
=
x
,
1
=
y
oraz
y
x
=
−
4
.
Wyszukiwarka
Podobne podstrony:
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
02 01 11 12 01 56 e notatka analiza matematyczna I kolokwium II
02 01 11 12 01 10 e notatka analiza matematyczna I egzamin
02 01 11 12 01 10 e notatka analiza matematyczna I egzamin
02 01 11 12 01 56 e notatka analiza matematyczna I kolokwium II
ANALIZA MATEMATYCZNA II, Notatki, MATEMATYKA
Analiza matematyczna II cz I
analiza matematyczna II, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semest
ANALIZA MATEMATYCZNA II
Sylabus-WEL-Analiza-matematyczna II Zo, Analiza matematyczna 2 zon ploch
Zad z egz (matma), gik, semestr 3, Analiza Matematyczna II
analiza(1), Politechnika Opolska, Analiza matematyczna II
WEL Analiza Matematyczna II
ANL, Studia, Analiza matematyczna II
WEL Analiza Matematyczna II n
Nawrocki J Matematyka cz 3 Analiza matematyczna II
Analiza matematyczna Rozwiązanie kolokwium
więcej podobnych podstron