
SNy: Biotechnologia
Analiza matematyczna I –
kolokwium II
notatki ze studiów na kierunku Biotechnologia
na Wydziale Chemicznym Politechniki Wrocławskiej
Autor:
Mateusz Jędrzejewski
mateusz.jedrzejewski@one.pl
www.jedrzejewski.one.pl
otatka jest częścią projektu SNy (Studenckie Notatki
Cyfrowe). Notatki są samodzielnie sporządzane
i opracowywane przez studentów Politechniki. Udostępniane
są w Internecie. Każdy możne z nich korzystać dowoli
w celach edukacyjnych.
waga na błędy! Mimo staranności jaką włożyli autorzy
w opracowanie tej notatki mogą zdarzyć się błędy.
Każdy więc korzysta z tych materiałów na własną
odpowiedzialność. Wszelkie zauważone błędy proszę
zgłaszać autorowi notatki (najlepiej drogę elektroniczną).
śyczę wszystkim skutecznego korzystania z notatek.
Mateusz Jędrzejewski
(autor strony www.sny.one.pl)
Szczegółowe informacje o notatce
Nazwa pliku: e-notatka - analiza matematyczna I - kolokwium II.pdf
Nazwa kursu: Analiza matematyczna I (MAP1024c)
Prowadzący kurs: mgr Jerzy Baran
Semestr/rok: 06z (rok 1, I semestr)
Kierunek: Biotechnologia
Wydział: Wydział Chemiczny
Uczelnia: Politechnika Wrocławska
Autor notatki: Mateusz Jędrzejewski
Status: Notatka w wersji roboczej
N
U
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 2
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
Kolokwium II – Grupa A
25.01.2007 r.
zad. 1.
Stosując regułę L’Hospitala obliczyć granicę
)
ln(sin
)
ln(
lim
0
x
x
x
+
→
.
(
)
(
)
1
cos
1
1
cos
1
sin
cos
sin
cos
sin
1
1
)
ln(sin
)
ln(
)
ln(sin
)
ln(
lim
lim
lim
lim
lim
lim
lim
0
0
0
0
0
0
0
=
⋅
=
⋅
=
=
=
=
′
′
=
∞
−
∞
−
+
+
+
+
+
+
+
→
→
→
→
→
→
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
H
x
Wyliczona granica istnieje więc:
1
)
ln(sin
)
ln(
lim
0
=
+
→
x
x
x
.
Skorzystałem z wartości znanej granicy:
1
sin
lim
0
=
+
→
x
x
x
.
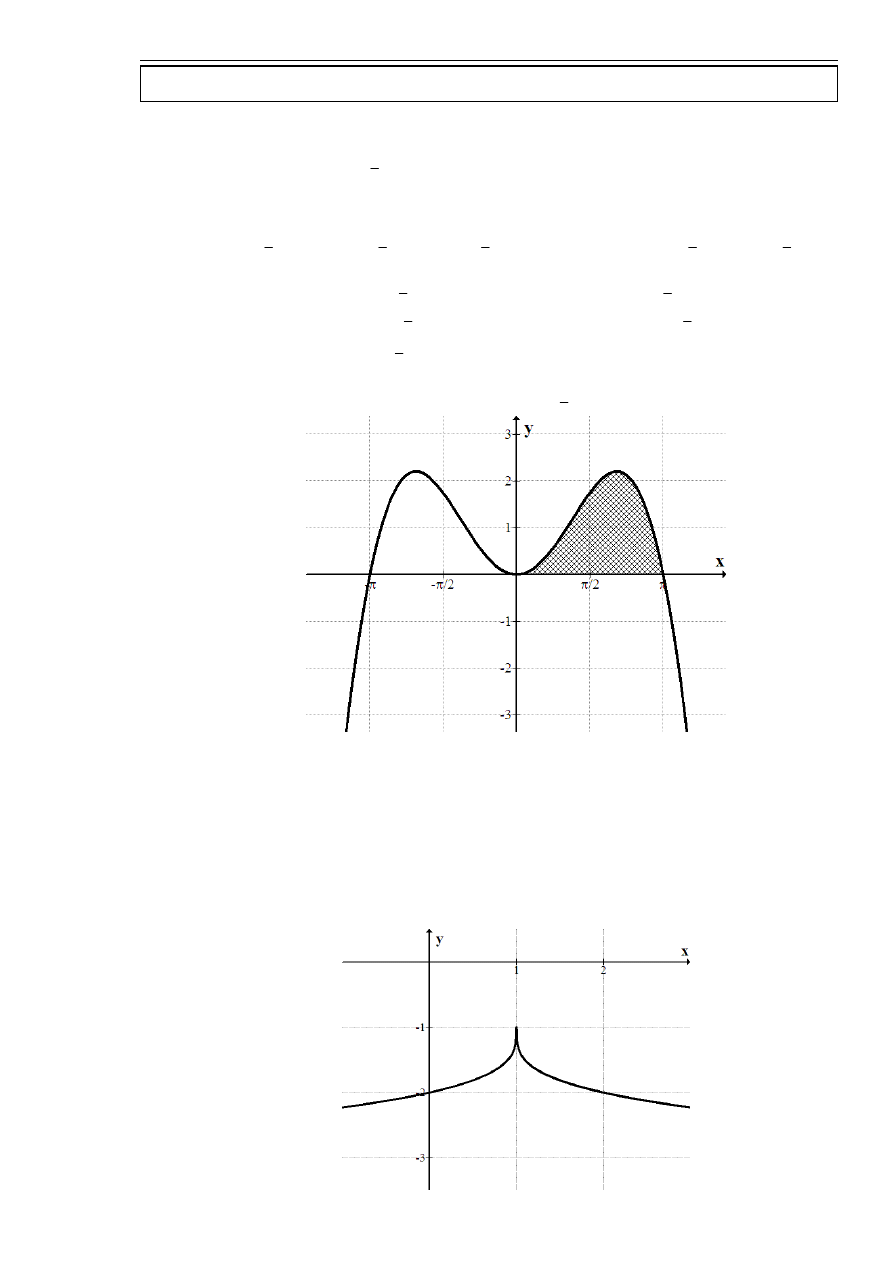
zad. 2.
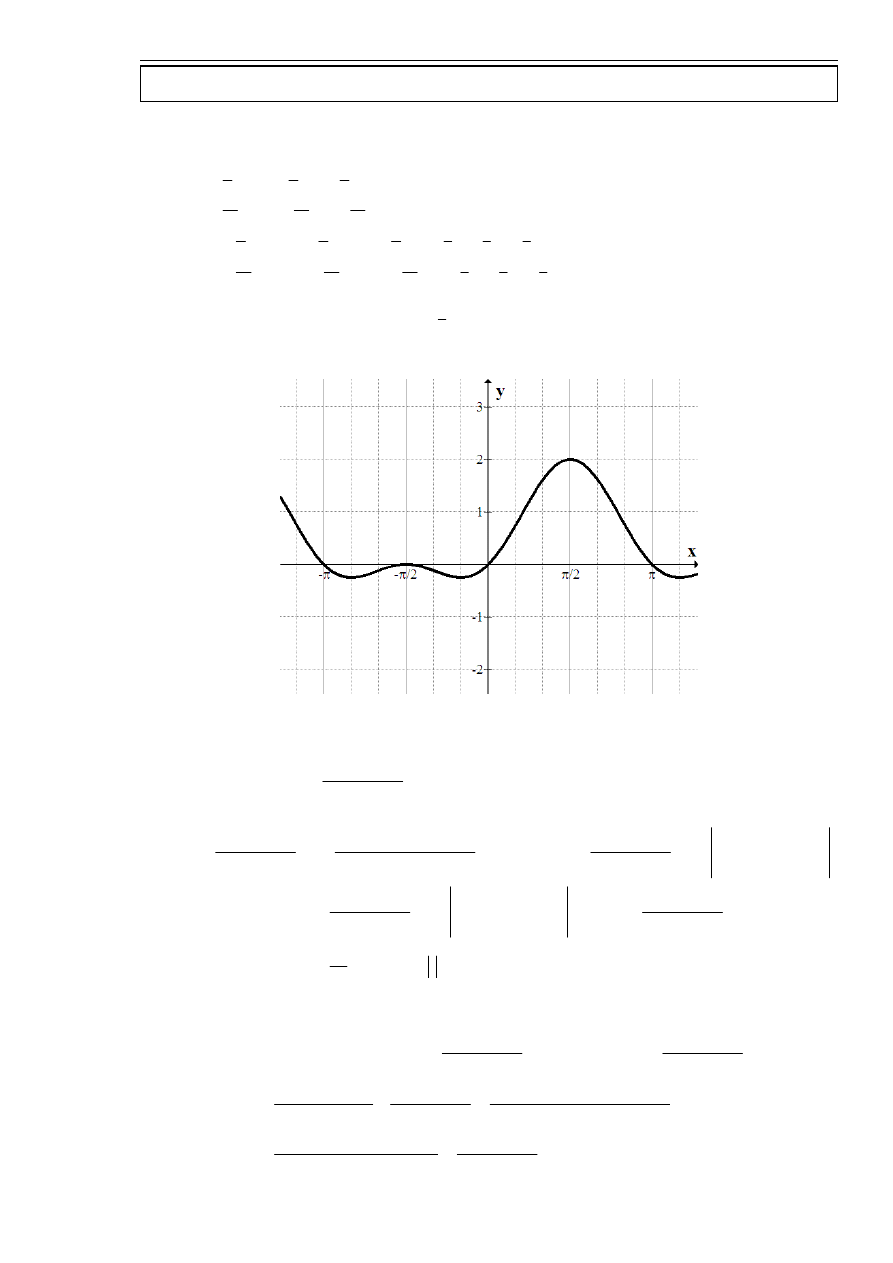
Znaleźć najmniejszą i największą wartość funkcji
x
x
x
f
sin
sin
)
(
2
+
=
na
ℜ
.
(
)
(
)
π
π
π
π
π
π
π
π
π
k
k
x
k
x
k
x
x
x
x
x
x
x
x
f
x
x
x
x
x
x
f
x
x
x
f
2
2
2
sin
0
cos
0
1
sin
2
0
cos
0
1
sin
2
cos
0
)
(
1
sin
2
cos
cos
cos
sin
2
)
(
sin
sin
)
(
6
5
6
6
2
2
1
2
+
−
=
+
+
−
=
∨
+
−
=
∨
+
=
−
=
∨
=
=
+
∨
=
=
+
⇔
=
′
+
=
+
=
′
+
=
Funkcja jest ciągła na
ℜ
, więc jedynymi punktami podejrzanymi o ekstrema są:
Z
k
k
x
k
x
k
k
x
k
x
k
x
∈
+
−
=
∨
+
−
=
+
=
+
+
=
∨
+
=
⇒
+
=
π
π
π
π
π
π
π
π
π
π
π
π
π
2
2
2
2
2
6
5
6
2
3
2
2
2
Sprawdzam warunek dostateczny wystąpienia ekstremum:
(
)
(
)
...
33
32
1
0
2
4
0
2
sin
sin
4
0
)
(
sin
sin
1
cos
1
cos
sin
2
sin
sin
4
sin
2
2
sin
sin
2
cos
2
sin
sin
2
cos
2
cos
1
sin
2
sin
)
(
2
2
2
2
2
2
2
2
2
2
2
2
=
+
=
∆
=
+
−
−
=
+
−
−
⇔
=
′′
=
−
=
⇒
=
+
+
−
−
=
−
+
−
−
=
=
+
−
−
=
+
+
−
=
′′
t
t
x
x
x
f
t
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 3
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
Może jednak wystarczy policzyć wartości funkcji w miejscach gdzie
0
)
(
=
′
x
f
.
Dla
0
=
k
(dla pozostałych będzie to samo, bo korzystam z okresowości funkcji
π
2
=
T
).
( )
( )
( )
( )
( ) ( )
( )
( )
( ) ( )
4
1
2
1
2
2
1
6
5
6
5
2
6
5
4
1
2
1
2
2
1
6
6
2
6
2
2
3
2
3
2
2
3
2
2
2
2
2
sin
sin
sin
sin
0
1
)
1
(
sin
sin
2
1
1
sin
sin
−
=
−
−
=
−
+
−
=
−
−
=
−
−
=
−
+
−
=
−
=
−
−
=
+
=
=
+
=
+
=
π
π
π
π
π
π
π
π
π
π
π
π
f
f
f
f
Najmniejsza wartość funkcji to
4
1
−
, na największa to 2 .
x
x
x
f
sin
sin
)
(
2
+
=
zad. 3.
Obliczyć całkę
∫
+
+
8
4
2
2
2
x
x
dx
x
. Otrzymany rezultat sprawdzić.
(
)
C
x
x
x
t
x
t
dt
x
dx
x
x
x
x
dx
x
dt
x
x
t
dx
x
x
x
x
x
x
dx
x
x
x
dx
dx
x
x
x
x
x
x
x
dx
x
+
+
+
−
=
−
=
−
=
=
+
+
+
−
=
+
=
+
+
=
+
+
+
−
=
=
<
−
=
∆
=
+
+
+
+
+
−
=
+
+
−
−
+
+
=
+
+
∫
∫
∫
∫
∫
∫
∫
8
4
ln
4
2
ln
4
2
4
2
8
4
4
2
4
2
)
4
2
(
8
4
8
4
8
4
2
2
0
32
16
0
8
4
8
4
8
4
2
2
8
4
8
4
8
4
2
8
4
2
2
2
2
2
2
2
2
2
2
2
Sprawdzenie:
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
8
4
2
8
4
16
8
16
8
2
8
4
4
2
4
8
4
2
8
4
4
2
4
8
4
8
4
2
8
4
4
2
4
2
8
4
8
4
4
2
8
4
ln
4
2
2
2
2
2
2
2
2
2
2
2
2
2
2
+
+
=
+
+
−
−
+
+
=
=
+
+
+
−
+
+
=
+
+
+
−
+
+
+
+
=
=
+
+
+
−
=
′
+
+
+
+
−
=
′
+
+
+
−
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
C
x
x
x
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 4
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
zad. 4.
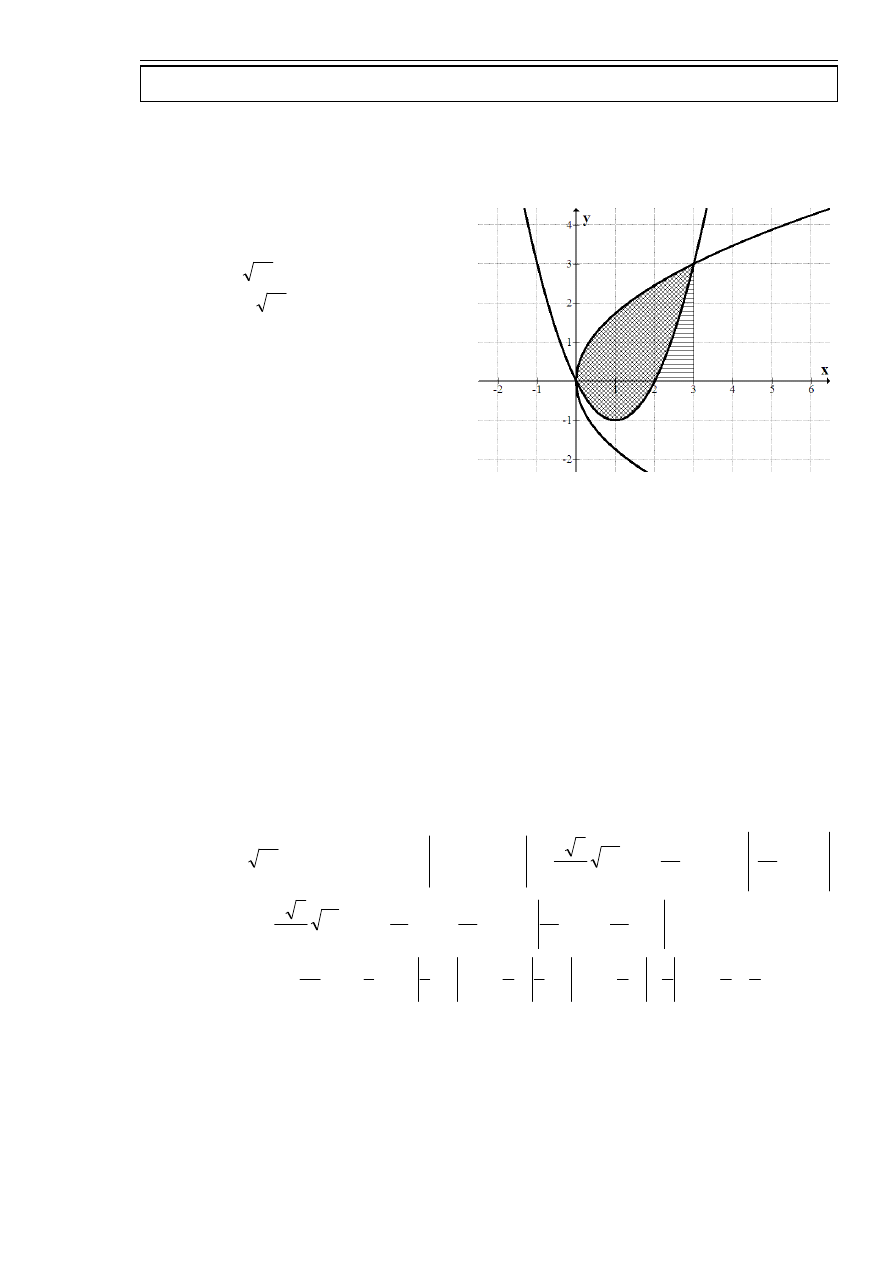
Znaleźć pole obszaru D ograniczonego krzywymi:
x
y
3
2
=
,
x
x
y
2
2
−
=
.
W analizie tych funkcji pomocne będą ich wykresy.
)
2
(
2
0
3
0
3
3
2
2
−
=
−
=
<
−
≥
=
=
x
x
x
x
y
x
x
x
x
y
x
y
Znajduję miejsca przecięcia się wykresów:
0
)
1
)(
3
(
0
)]
3
(
)
3
(
)
3
[(
0
)
3
4
4
(
0
3
4
4
4
4
3
)
2
(
3
)
2
(
3
2
3
2
2
2
3
2
3
4
2
3
4
2
2
2
2
2
2
2
2
=
+
−
−
=
−
+
−
−
−
=
−
+
−
=
−
+
−
+
−
=
−
=
−
=
=
⇒
−
=
=
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
x
y
x
x
y
x
y
Punkty w których wykresy się przecinają to:
dla
0
=
x
0
0
2
0
2
2
2
=
⋅
−
=
−
=
x
x
y
dla
3
=
x
3
6
9
3
2
3
2
2
2
=
−
=
⋅
−
=
−
=
x
x
y
Pole zaznaczonego obszaru wyraża się:
(
)
(
)
6
3
4
3
4
6
3
4
3
4
6
4
3
8
3
4
6
4
3
8
4
3
8
9
3
27
6
0
3
0
2
3
2
2
3
2
3
3
3
0
3
3
3
2
3
3
3
3
2
2
2
3
2
3
2
3
2
3
2
3
3
2
0
2
3
3
2
2
3
3
0
3
2
0
2
3
2
2
3
0
=
+
−
=
−
+
−
=
−
+
−
=
−
+
−
+
+
−
=
=
+
−
−
+
+
−
−
−
−
=
=
−
+
−
−
=
−
+
−
−
=
∫
∫
∫
x
x
x
x
x
dx
x
x
dx
x
x
dx
x
D
Kolokwium II – Grupa B
25.01.2007 r.
…
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 5
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
Kolokwium II – Grupa C
25.01.2007 r.
zad. 1.
Napisać wzór Maclaurina z resztą
3
R
dla funkcji
)
1
ln(
)
(
x
x
f
+
=
, następnie uzasadnić,
że nierówność
2
2
)
1
ln(
x
x
x
−
>
+
jest prawdziwa dla każdego
0
>
x
.
Ogólnie:
3
2
!
3
)
(
!
2
)
0
(
!
1
)
0
(
)
0
(
)
(
x
c
f
x
f
x
f
f
x
f
′′′
+
′′
+
′
+
=
gdzie
)
,
0
(
x
c
∈
.
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
) (
)
(
)
(
)
(
)
3
3
2
3
2
2
3
4
4
2
2
2
1
3
2
2
)
1
ln(
!
3
1
2
!
2
0
1
1
!
1
0
1
1
)
0
1
ln(
)
1
ln(
1
2
1
1
2
1
1
)
1
(
0
)
(
1
1
1
1
1
0
)
(
1
1
)
(
)
1
ln(
)
(
c
x
x
x
x
c
x
x
x
x
x
x
x
x
x
f
x
x
x
x
f
x
x
f
x
x
f
+
+
−
=
+
+
+
+
−
+
+
+
+
=
+
+
=
+
+
=
+
′
+
⋅
−
−
=
′′′
+
−
=
+
′
+
⋅
−
=
′′
+
=
′
+
=
gdzie:
(
)
(
)
0
0
0
1
3
2
1
3
2
3
0
3
3
2
3
3
0
3
3
3
>
>
=
+
>
+
=
>
=
R
x
x
c
x
R
x
c
więc:
2
)
1
ln(
0
2
)
1
ln(
0
2
)
1
ln(
2
)
1
ln(
2
2
3
2
3
2
x
x
x
x
x
x
R
x
x
x
R
x
x
x
−
>
+
>
+
−
+
>
=
+
−
+
+
−
=
+
cbdu.
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 6
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
zad. 2.
Określić przedziały monotoniczności funkcji
3
3
1
)
(
x
x
f
−
=
.
(
)
(
) (
) (
) (
)
(
)
(
)
(
)
(
)
)
,
(
0
0
0
1
0
)
(
0
1
0
1
1
3
1
1
1
)
(
1
1
)
(
2
2
*
3
2
3
2
3
2
3
*
2
3
3
2
3
2
2
3
3
1
3
3
3
1
3
3
3
3
2
3
2
3
1
∞
−∞
∈
⇒
≥
⇒
≤
−
⇒
≤
−
−
⇔
≤
′
>
−
⇒
>
−
−
−
=
−
−
=
′
−
⋅
−
=
′
−
=
−
=
−
−
x
x
x
x
x
x
f
x
x
x
x
x
x
x
x
x
f
x
x
x
f
Funkcja jest malejąca na przedziale
)
,
(
∞
−∞
.
3
3
1
)
(
x
x
f
−
=
zad. 3.
Obliczyć całkę
∫
+
x
dx
sin
1
.
Zależy zastosować podstawienie uniwersalne.
C
C
t
C
k
dk
k
k
dk
dt
dk
t
k
t
dt
t
t
dt
t
t
t
t
t
dt
t
t
t
dt
t
t
x
t
dt
dx
t
t
x
dx
x
x
x
+
+
−
=
+
+
−
=
+
−
=
=
=
=
+
=
+
=
=
+
+
=
+
+
+
+
+
=
+
+
+
=
+
=
+
=
=
=
+
∫
∫
∫
∫
∫
∫
∫
−
−
1
tg
2
1
2
)
(
2
2
2
1
)
1
(
2
1
2
2
1
2
1
1
1
2
1
2
1
1
2
1
2
sin
1
2
tg
arc
tg
sin
1
2
1
2
2
2
2
2
2
2
2
2
2
2
2
2
2
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 7
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
zad. 4.
Obliczyć całkę
( )
dx
x
x
∫
π
0
2
2
cos
.
( )
( )
[
]
( )
( )
[
]
( )
( )
( )
( )
( )
( )
[
]
(
)
16
2
sin
2
2
0
0
4
2
cos
2
)
(
1
)
(
sin
2
)
(
2
)
(
sin
)
(
)
(
cos
)
(
)
(
cos
2
cos
2
4
0
2
sin
4
sin
2
cos
2
0
2
2
2
2
2
2
2
0
2
0
2
2
0
2
0
2
2
0
2
2
−
=
+
+
−
−
=
−
=
=
′
=
=
′
=
′
=
=
′
=
=
+
−
−
−
=
−
=
∫
∫
∫
π
π
π
π
π
π
π
π
π
x
x
x
x
x
x
x
x
x
x
x
v
x
u
x
g
x
x
f
x
v
x
x
u
x
g
x
x
f
dx
x
dx
x
x
dx
x
( )
2
2
cos
)
(
x
x
x
f
=
Kolokwium II – Grupa D
25.01.2007 r.
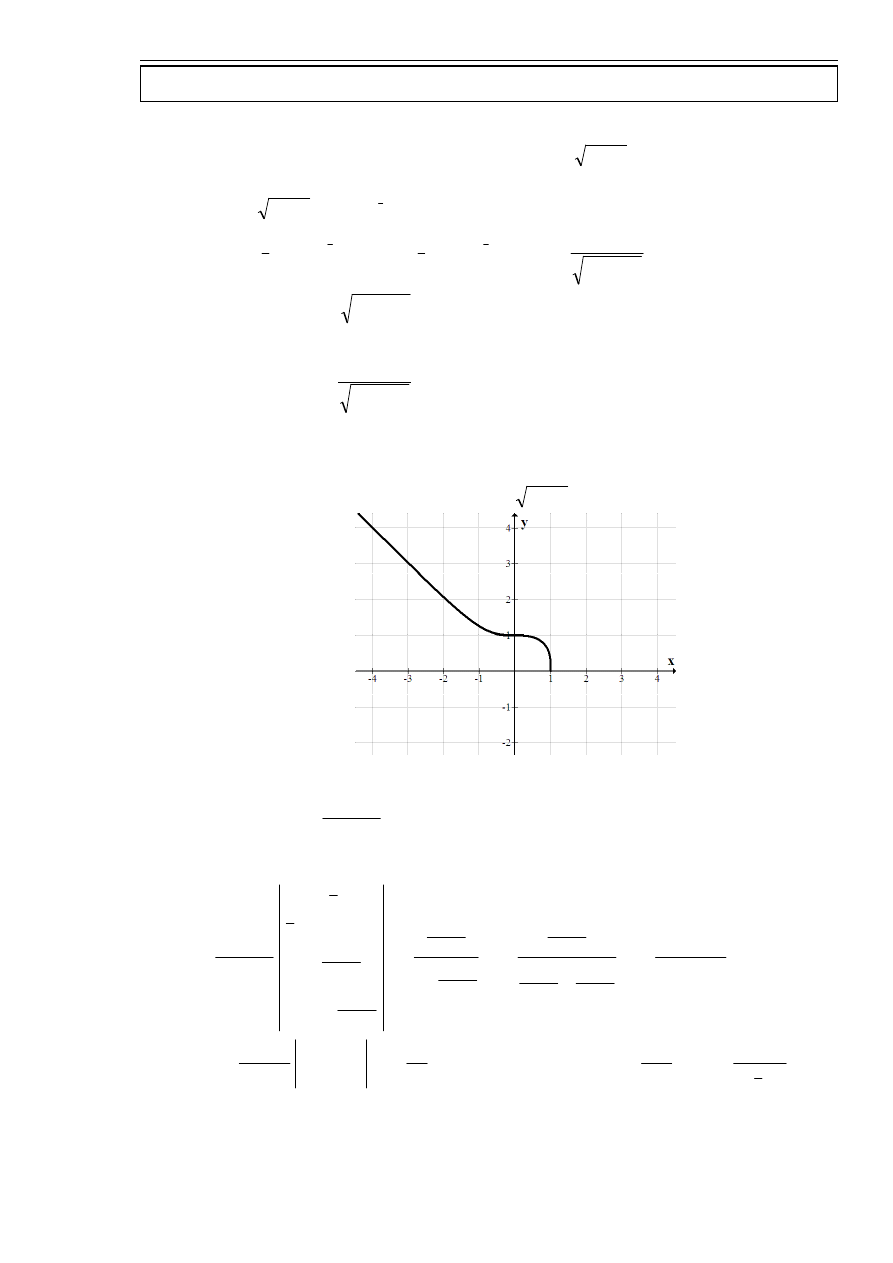
zad. 1.
Naszkicować wykres funkcji ciągłej
ℜ
ℜ
a
:
f
spełniającej warunki:
1
)
1
(
−
=
f
,
∞
=
′
−
)
1
(
f
,
−∞
=
′
+
)
1
(
f
,
0
)
(
>
′′
x
f
dla każdego
0
≠
x
.
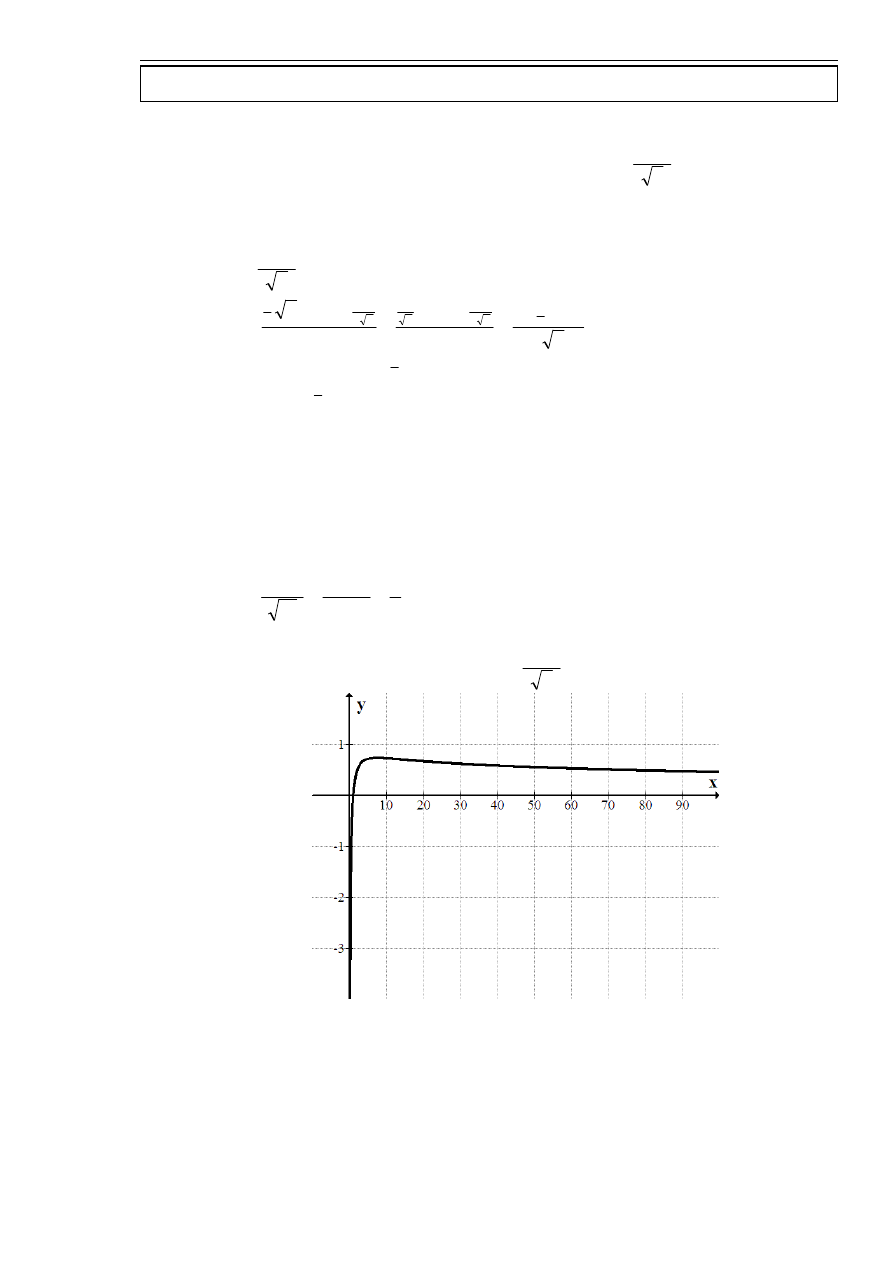
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 8
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
zad. 2.
Znaleźć ekstrema i punkty przegięcia wykresu funkcji
x
x
x
f
)
ln(
)
(
=
.
2
2
2
2
1
2
1
2
1
2
1
1
2
1
1
0
)
(
0
)
(
2
)
ln(
1
)
ln(
0
)
ln(
1
0
)
(
)
ln(
1
)
ln(
)
ln(
)
(
)
ln(
)
(
)
,
0
(
0
e
x
x
f
e
x
x
f
e
x
x
x
x
x
f
x
x
x
x
x
x
x
x
x
f
x
x
x
f
D
x
x
x
x
x
f
>
⇔
<
′
<
⇔
>
′
=
=
=
=
−
⇔
=
′
−
=
−
=
−
=
′
=
∞
=
>
Na lewo od
2
e
x
=
funkcja
)
(x
f
rośnie, a na prawo maleje, więc w
2
e
x
=
ma maksimum.
( ) ( )
e
e
e
e
e
e
f
2
)
ln(
2
ln
2
2
2
=
=
=
x
x
x
f
)
ln(
)
(
=

Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 9
Notatka: Analiza matematyczna I (MAP1024w) – kolokwium II.
Utworzona: 25.01.2007 22:22
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 26.01.2007 2:41
zad. 3.
Obliczyć całkę
dx
x
x
∫
2
)
sin(ln
.
C
x
x
x
dx
x
x
x
x
x
dx
x
x
dx
x
x
x
x
x
x
dx
x
x
x
x
v
x
x
x
u
x
x
g
x
x
x
f
x
x
v
x
x
u
x
x
g
x
x
f
dx
x
x
x
x
x
x
dx
x
x
x
x
dx
x
x
+
+
−
=
+
−
=
−
−
−
=
−
=
−
=
′
−
=
=
′
=
′
=
=
′
=
−
−
−
=
+
−
=
∫
∫
∫
∫
∫
∫
∫
−
−
2
)
cos(ln
)
sin(ln
)
sin(ln
)
cos(ln
)
sin(ln
)
sin(ln
2
)
sin(ln
)
cos(ln
)
sin(ln
)
sin(ln
1
)
(
)
sin(ln
)
(
1
)
(
)
cos(ln
)
(
)
(
)
cos(ln
)
(
)
(
)
sin(ln
)
(
)
sin(ln
)
cos(ln
)
sin(ln
)
cos(ln
)
sin(ln
)
sin(ln
2
2
2
2
2
2
2
2
2
zad. 4.
Obliczyć całkę
∫
π
0
3
sin
dx
x
x
.
(
)
[
]
(
)
[
]
(
)
[
]
[
]
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
π
6
sin
6
0
6
cos
6
cos
6
cos
6
0
3
sin
6
sin
3
sin
3
0
cos
3
cos
cos
sin
3
0
3
0
0
3
0
3
0
0
2
3
0
2
3
0
2
0
3
0
3
0
3
−
=
−
−
−
=
−
+
+
=
′
−
−
⋅
+
=
−
+
=
=
′
+
+
=
+
−
=
′
−
=
∫
∫
∫
∫
∫
∫
∫
x
dx
x
x
x
dx
x
x
dx
x
x
x
x
dx
x
x
dx
x
x
x
x
dx
x
x
dx
x
x
Wyszukiwarka
Podobne podstrony:
02 01 11 12 01 56 e notatka analiza matematyczna I kolokwium II
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
02 01 11 12 01 10 e notatka analiza matematyczna I egzamin
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
02 01 11 12 01 10 e notatka analiza matematyczna I egzamin
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
02-01-11 12 01 41 analiza matematyczna kolokwium 2002-01-16
02 01 11 12 01 41 analiza matematyczna kolokwium 2002 01 16id 3883
Gewert Skoczylas Analiza matematyczna 2 Kolokwia i egzaminy
M Gewert Z Skoczylas Analiza Matematyczna 1 Kolokwia i Egzaminy
Gewert Skoczylas Analiza matematyczna 2 Kolokwia i egzaminy
Kolokwium z analizy, Studia, Informatyka, Semestr II, Analiza Matematyczna cz.II
analiza2poprawa, Informatyka i Ekonometria SGGW, Semestr 2, Analiza matematyczna, kolokwia egzaminy,
analiza matematyczna kolokwia
Analiza matematyczna 1 Kolokwia i egzaminy M Gewert Z Skoczylas
Gewert Skoczylas Analiza matematyczna 2 Kolokwia i egzaminy
Analiza matematyczna 1 Kolokwia,Egzaminy
więcej podobnych podstron