
SNy: Biotechnologia
Analiza matematyczna I – egzamin
notatki ze studiów na kierunku Biotechnologia
na Wydziale Chemicznym Politechniki Wrocławskiej
Autor:
Mateusz Jędrzejewski
mateusz.jedrzejewski@one.pl
www.jedrzejewski.one.pl
otatka jest częścią projektu SNy (Studenckie Notatki
Cyfrowe). Notatki są samodzielnie sporządzane
i opracowywane
przez
studentów
Politechniki.
Udostępniane są w Internecie. Każdy możne z nich korzystać
dowoli w celach edukacyjnych.
Chciałbym podziękować Dorocie Druszkowskiej za pomoc
w stworzeniu notatki oraz zgłoszenie uwag do rozwiązań.
waga na błędy! Mimo staranności jaką włożyli autorzy
w opracowanie tej notatki mogą zdarzyć się błędy.
Każdy więc korzysta z tych materiałów na własną
odpowiedzialność. Wszelkie zauważone błędy proszę
zgłaszać autorowi notatki (najlepiej drogę elektroniczną).
śyczę wszystkim skutecznego korzystania z notatek.
Mateusz Jędrzejewski
(autor strony www.sny.one.pl)
Szczegółowe informacje o notatce
Nazwa pliku: e-notatka - analiza matematyczna I – egzamin.pdf
Nazwa kursu: Analiza matematyczna I (MAP1024c)
Autorzy zadań: dr Jolanta Sulkowska, Andrzej Rehlis (egzamin poprawkowy)
Semestr/rok: 06z (rok 1, I semestr)
Kierunek: Biotechnologia
Wydział: Wydział Chemiczny
Uczelnia: Politechnika Wrocławska
Autor notatki: Mateusz Jędrzejewski
Status: ukończona
N
U
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 2
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 2.02.2007 23:47
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 7.02.2007 18:32
Egzamin – zestaw A
zad. 1.
Obliczyć granicę ciągu o wyrazach:
1
2
9
3
9
+
+
−
+
=
n
n
n
n
n
a
.
Korzystam ze wzoru:
b
a
b
a
b
a
b
a
b
a
b
a
+
−
=
−
⇒
+
−
=
−
2
2
2
2
)
)(
(
( ) ( )
( )
( ) ( )
2
1
1
1
1
1
1
1
9
1
2
9
9
3
9
3
1
2
3
1
2
9
3
9
1
2
3
1
2
9
3
9
1
2
9
3
9
1
2
9
3
9
9
1
9
2
3
1
3
1
3
2
=
+
→
+
+
+
+
−
−
=
+
+
+
+
−
−
=
=
+
+
+
+
−
−
=
+
+
+
+
−
−
−
+
=
+
+
−
+
=
∞
→
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
a
zad. 2.
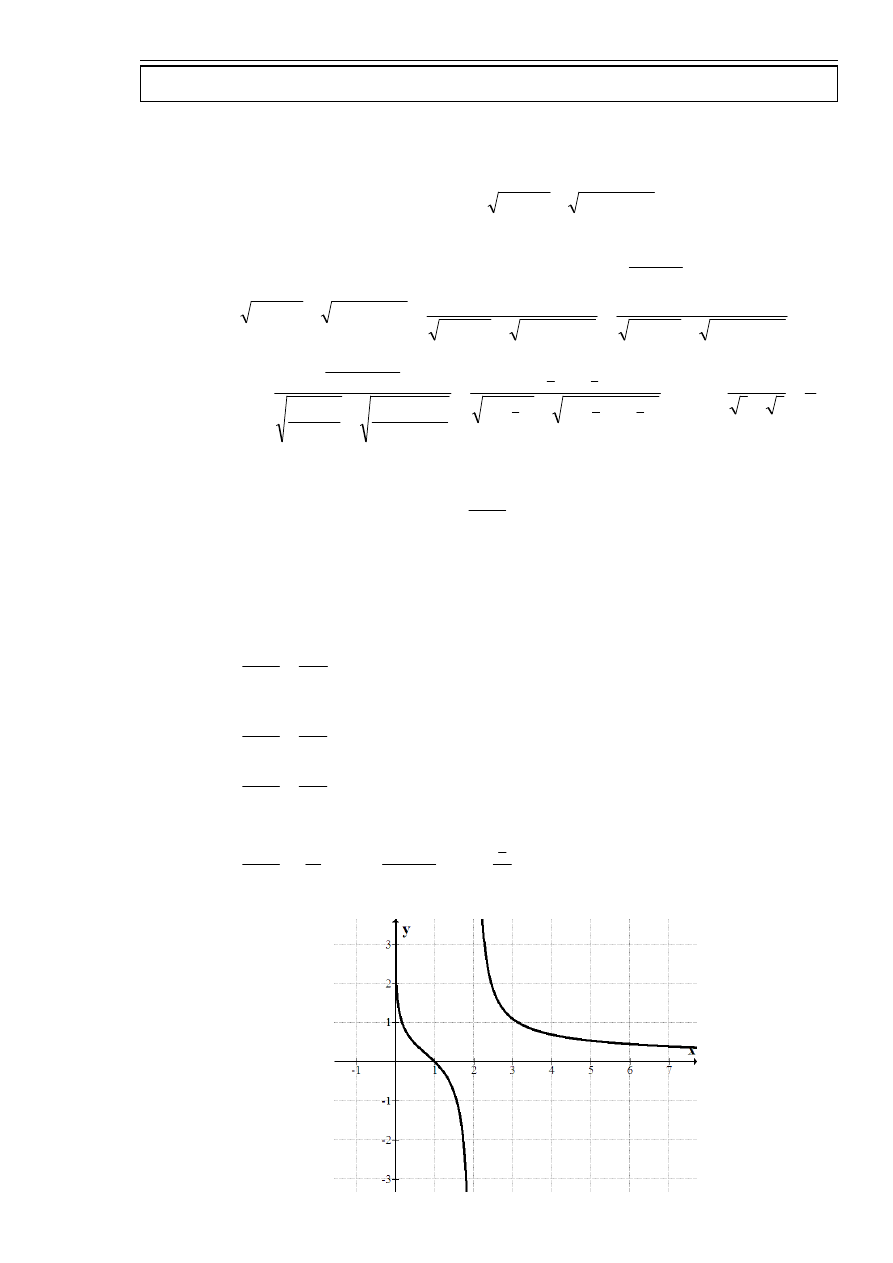
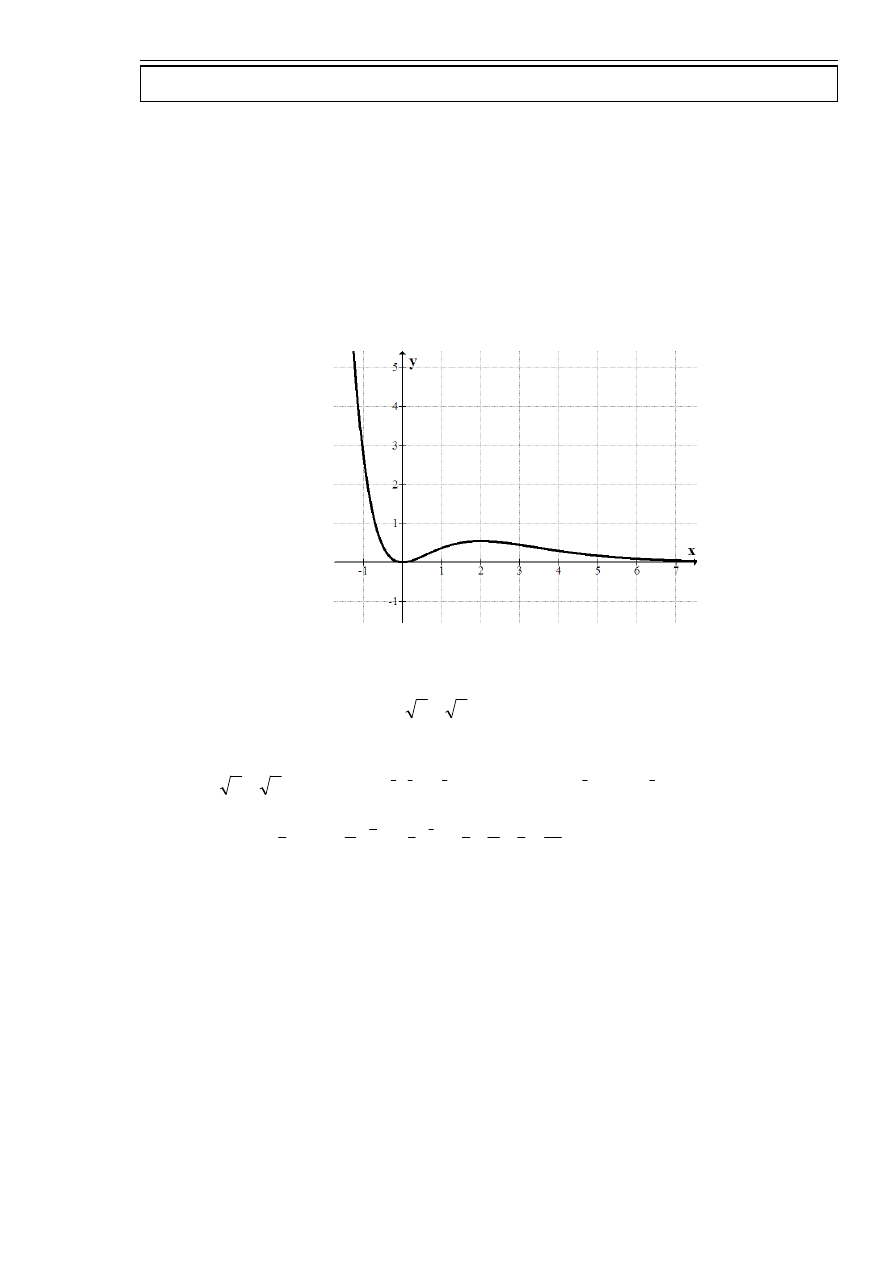
Wyznaczyć asymptoty funkcji
2
ln
)
(
−
=
x
x
x
f
.
Zaczynam od określenia dziedziny funkcji:
)
,
2
(
)
2
,
0
(
+∞
∪
=
f
D
.
Sprawdzam czy jest asymptota prawostronna w „zerze”:
+∞
=
−
∞
−
=
−
+
→
2
2
ln
lim
0
x
x
x
.
Sprawdzam czy jest asymptota w „dwójce”:
−∞
=
=
−
−
→
−
0
2
ln
2
ln
lim
2
x
x
x
,
+∞
=
=
−
+
→
+
0
2
ln
2
ln
lim
2
x
x
x
.
Więc funkcja ma asymptotę prawostronną w
0
=
x
oraz asymptotę obustronną w
2
=
x
.
( )
(
)
0
1
2
ln
2
ln
1
lim
lim
lim
=
=
′
−
′
=
∞
∞
−
∞
→
∞
→
∞
→
x
x
x
H
x
x
x
x
x
– asymptota pozioma
0
=
y
w
∞
+
.
wykres funkcji
)
(x
f
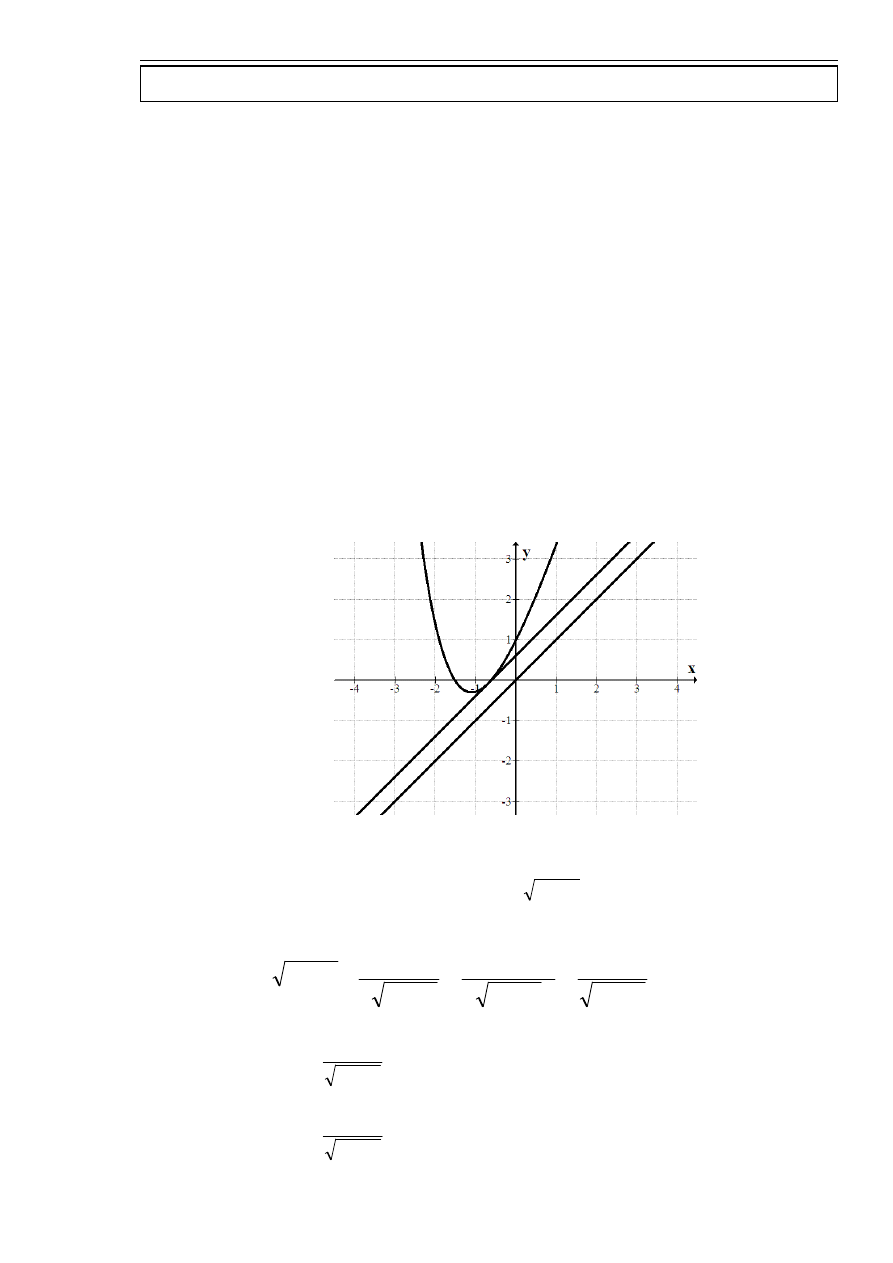
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 3
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 2.02.2007 23:47
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 7.02.2007 18:32
zad. 3.
Napisać równanie stycznej do wykresu funkcji
x
e
x
x
f
−
+
=
3
)
(
, która jest równoległa
do prostej
x
y
=
.
Niech styczną do wykresu będzie funkcja
b
ax
x
g
+
=
)
(
.
Ma być równoległa do prostej
x
y
=
, więc ich współczynniki kierunkowe muszą być
równe, więc
1
=
a
, skądinąd
)
(x
f
a
′
=
.
x
e
x
f
−
−
=
′
3
)
(
Sprawdzam dla jakiego
x
jest tak, że
1
)
(
=
′
x
f
2
ln
2
1
3
−
=
⇒
=
⇒
=
−
−
−
x
e
e
x
x
Liczę wartość funkcji
2
2
ln
3
2
ln
3
)
2
ln
(
2
ln
+
−
=
+
−
=
−
e
f
.
Mam więc punkt przez który ma przechodzić styczna
)
(x
g
.
2
2
ln
2
)
(
2
2
ln
2
2
ln
2
2
ln
3
2
ln
)
2
ln
(
)
(
+
−
=
+
−
=
+
−
=
+
−
+
−
=
−
+
=
x
x
g
b
b
b
g
b
x
x
g
zad. 4.
Wyznaczyć ekstrema lokalne funkcji
2
2
)
(
x
x
x
f
−
=
. Określić ich rodzaj.
Liczę pierwszą pochodną:
2
2
2
2
2
2
2
2
2
2
2
2
2
2
)
2
(
2
)
(
x
x
x
x
x
x
x
x
x
x
f
−
−
=
−
−
−
=
−
−
⋅
+
−
=
′
Sprawdzam kiedy
0
)
(
=
′
x
f
.
1
1
0
2
2
0
2
2
2
0
)
(
2
2
2
−
=
∨
=
⇒
=
−
⇒
=
−
−
⇒
=
′
x
x
x
x
x
x
f
.
Badam zmianę znaku pochodnej:
)
1
,
1
(
0
)
1
)(
1
(
0
2
2
0
2
2
2
0
)
(
2
2
2
−
∈
⇒
>
+
−
⇒
>
−
⇒
>
−
−
⇒
>
′
x
x
x
x
x
x
x
f
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 4
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 2.02.2007 23:47
Temat: Przykładowe szkice rozwiązań do zestawu A.
Zmodyfikowana: 7.02.2007 18:32
)
,
1
(
)
1
,
(
0
)
1
)(
1
(
0
2
2
2
0
)
(
2
2
+∞
∪
−
−∞
∈
⇒
<
+
−
⇒
<
−
−
⇒
<
′
x
x
x
x
x
x
f
Więc w otoczeniu
1
−
=
x
pierwsza pochodna zmienia znak z minusa na plus więc jest
to minimum lokalne.
Natomiast w otoczeniu
1
=
x
pierwsza pochodna zmienia znak z plusa na minus więc jest
to maksimum lokalne.
wykres funkcji
)
(x
f
zad. 5.
Obliczyć całkę nieoznaczoną
dx
x
e
e
e
x
x
x
∫
−
2
.
Korzystam z linowości całki oraz raz całkuję przez części.
C
x
e
x
e
dx
x
dx
x
e
dx
x
e
e
dx
x
e
e
dx
x
e
e
e
x
x
x
x
x
x
x
x
x
x
+
−
−
=
−
=
−
=
−
∫
∫
∫
∫
∫
2
2
1
2
2
.
zad. 6.
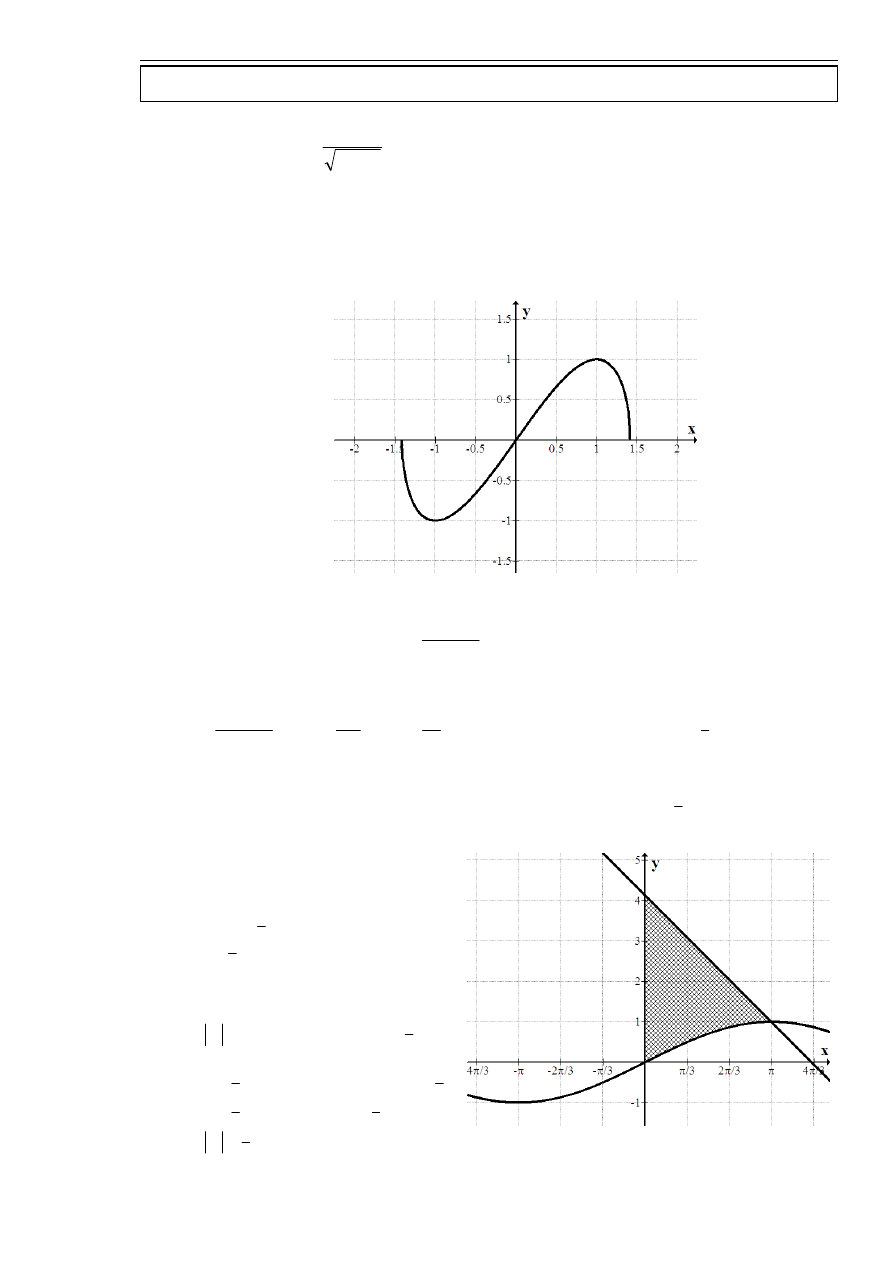
Obliczyć pole obszaru D ograniczonego wykresem funkcji
2
sin
x
y
=
, osią OY i prostą
)
(
1
π
−
−
=
−
x
y
. Rozwiązanie zadania zacząć od wykonania rysunku.
1
)
(
1
+
+
−
=
⇒
−
−
=
−
π
π
x
y
x
y
1
0
+
=
⇒
=
π
y
x
2
sin
x
y
=
π
π
=
⇒
+
+
−
=
x
x
x
1
sin
2
Więc:
[ ]
[ ] [ ]
[
]
=
+
+
+
−
=
=
−
+
+
−
=
∫
∫
π
π
π
π
π
π
π
π
0
2
0
0
0
2
2
1
0
2
0
cos
2
sin
)
1
(
x
x
x
x
x
dx
dx
x
D
2
2
2
2
2
1
2
2
1
2
2
2
1
−
+
=
−
+
=
−
+
+
−
=
π
π
π
π
π
π
π
D
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 5
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 0:57
Temat: Przykładowe szkice rozwiązań do zestawu B.
Zmodyfikowana: 11.02.2007 12:31
Egzamin – zestaw B
zad. 1.
Obliczyć granicę ciągu o wyrazach:
n
n
n
n
n
b
3
2
4
2
5
2
3
1
2
⋅
+
⋅
+
⋅
=
+
.
( )
( )
10
2
1
3
10
3
2
4
2
4
5
2
3
3
2
4
2
5
2
3
4
3
2
1
1
2
→
⋅
+
⋅
+
=
⋅
+
⋅
⋅
+
⋅
=
⋅
+
⋅
+
⋅
=
∞
→
+
n
n
n
n
n
n
n
n
n
n
n
n
b
zad. 2.
Wyznaczyć asymptoty funkcji
1
2
3
5
,
2
)
(
2
+
+
+
=
x
x
x
x
f
.
)
,
(
)
,
(
2
1
2
1
+∞
−
∪
−
−∞
=
f
D
.
Sprawdzam istnienie asymptoty obustronnej
2
1
−
=
x
.
+∞
=
+
⋅
+
=
+
+
+
−∞
=
+
⋅
−
=
+
+
+
+
−
→
−
→
−
−
→
−
→
−
+
−
−
0
3
1
2
3
0
3
1
2
3
2
1
2
5
4
1
2
5
2
2
1
2
5
4
1
2
5
2
lim
lim
lim
lim
2
1
2
1
2
1
2
1
x
x
x
x
x
x
x
x
x
x
Asymptota obustronnej
2
1
−
=
x
istnieje.
Sprawdzam istnienie asymptoty ukośnej:
B
Ax
y
+
=
[
]
1
4
4
4
4
2
4
6
4
2
4
2
6
5
2
1
2
1
2
2
2
2
1
2
3
)
(
2
1
2
1
2
3
)
(
2
6
2
2
2
5
2
1
3
2
5
2
2
5
2
lim
lim
lim
lim
lim
lim
lim
lim
2
=
=
+
+
=
+
+
=
=
+
−
−
+
+
=
+
+
⋅
−
+
+
+
=
−
=
=
+
+
+
=
+
+
+
=
=
∞
→
∞
→
∞
→
∞
→
∞
→
∞
→
∞
→
∞
→
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Ax
x
f
B
x
x
x
x
x
x
f
A
Obydwie granice istnieją, więc istnieje asymptota o równaniu:
1
2
1
+
=
x
y
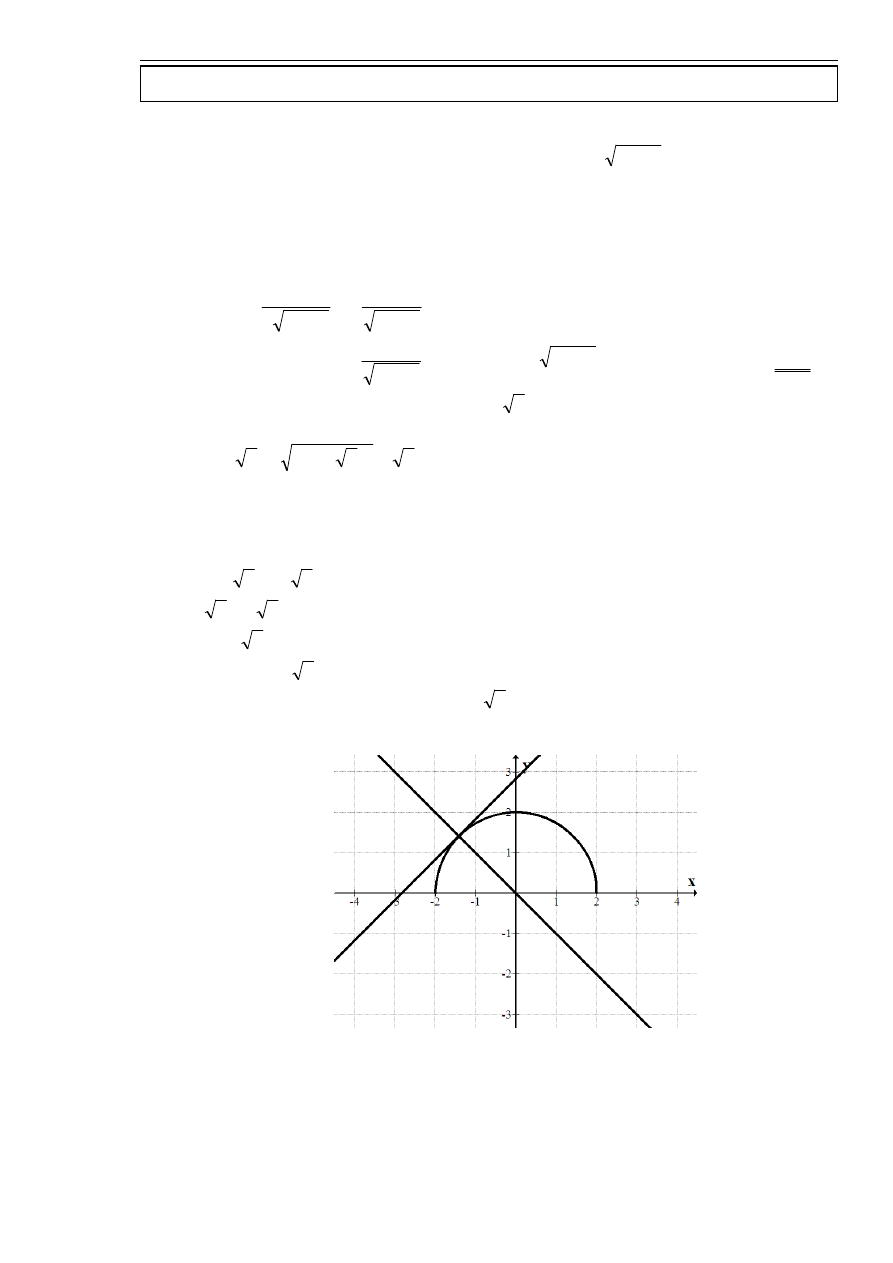
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 6
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 0:57
Temat: Przykładowe szkice rozwiązań do zestawu B.
Zmodyfikowana: 11.02.2007 12:31
zad. 3.
Napisać równanie tej stycznej do wykresu funkcji
2
4
)
(
x
x
f
−
=
, która jest prostopadła
do prostej
x
y
−
=
.
Nie prostą styczną będzie
b
ax
x
g
+
=
)
(
.
Ma być prostopadła do prostej
x
y
−
=
więc:
1
1
)
1
(
=
⇒
−
=
⋅
−
a
a
.
2
2
4
2
0
4
4
1
4
1
)
(
4
4
2
2
)
(
2
2
2
2
2
2
2
2
−
=
⇒
=
⇒
=
<
∧
−
=
⇒
−
=
−
⇒
=
−
−
⇒
=
=
′
−
−
=
−
−
=
′
x
x
x
x
x
x
x
x
x
x
a
x
f
x
x
x
x
x
f
( )
2
)
2
(
4
2
2
=
−
−
=
−
f
W punkcie styczności wartości funkcji są sobie równe:
)
(
)
(
x
g
x
f
=
.
2
2
)
(
2
2
2
2
2
)
2
(
)
(
+
=
=
+
−
=
+
−
=
−
+
=
x
x
g
b
b
b
g
b
x
x
g
więc ostateczne styczna to:
2
2
)
(
+
=
x
x
g
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 7
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 0:57
Temat: Przykładowe szkice rozwiązań do zestawu B.
Zmodyfikowana: 11.02.2007 12:31
zad. 4.
Wyznaczyć przedziały monotoniczności funkcji
x
x
x
f
ln
)
(
2
=
.
)
,
(
0
)
(
1
ln
0
1
ln
2
0
1
ln
2
0
)
1
ln
2
(
0
)
(
)
1
ln
2
(
ln
2
)
(
0
1
2
1
2
2
1
+∞
∈
⇒
>
′
>
>
−
>
>
+
>
+
⇒
>
+
⋅
⇒
>
′
+
⋅
=
+
=
′
>
−
e
x
x
f
e
x
e
x
x
x
x
x
x
x
f
x
x
x
x
x
x
x
f
x
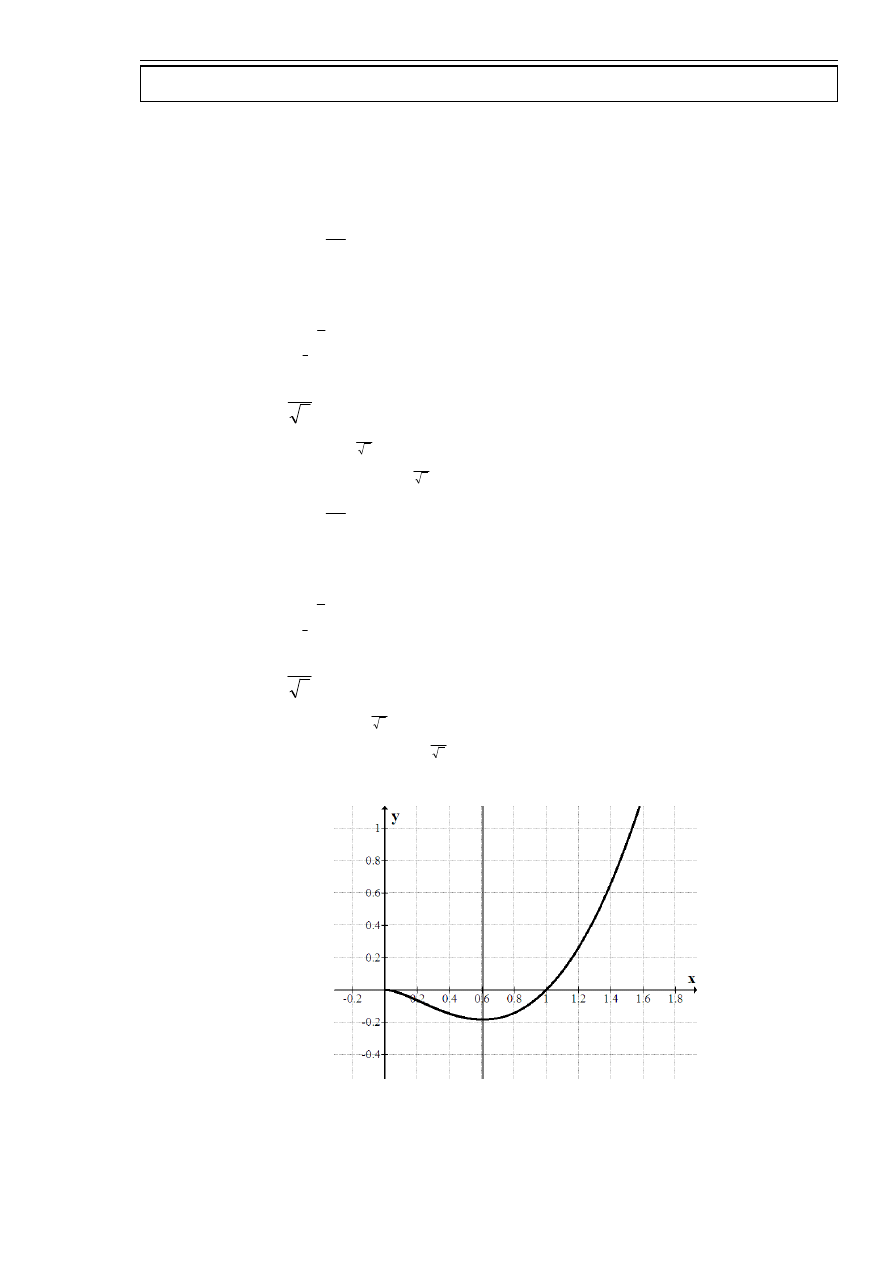
Funkcja rośnie na przedziale
)
,
(
1
+∞
e
.
)
,
0
(
0
)
(
1
ln
0
1
ln
2
0
1
ln
2
0
)
1
ln
2
(
0
)
(
)
1
ln
2
(
ln
2
)
(
1
2
1
2
2
1
e
x
x
f
e
x
e
x
x
x
x
x
x
x
f
x
x
x
x
x
x
x
f
∈
⇒
<
′
<
<
−
<
<
+
<
+
⇒
<
+
⋅
⇒
<
′
+
⋅
=
+
=
′
−
Funkcja maleje na przedziale
)
,
0
(
1
e
.
wykres funkcji
)
(x
f
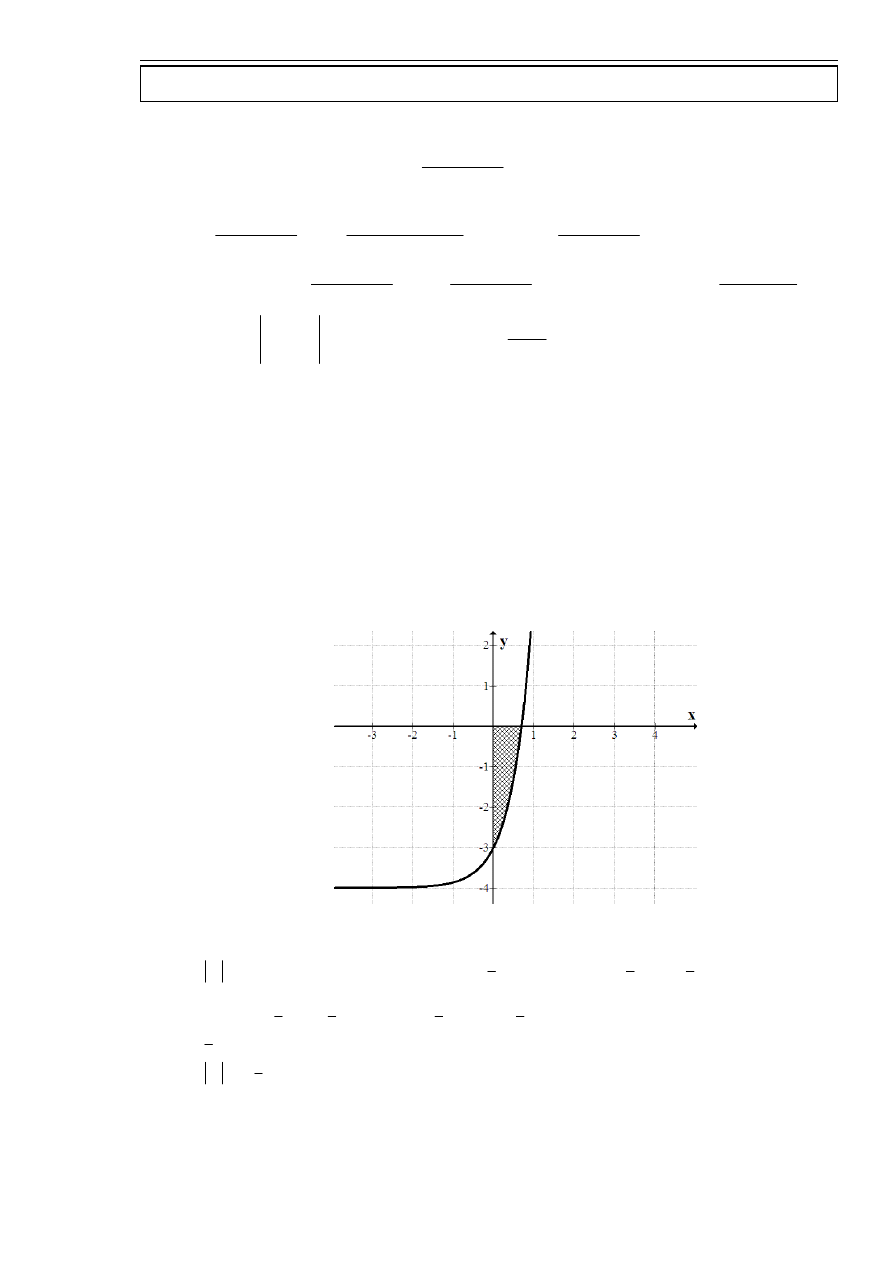
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 8
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 0:57
Temat: Przykładowe szkice rozwiązań do zestawu B.
Zmodyfikowana: 11.02.2007 12:31
zad. 5.
Obliczyć całkę nieoznaczoną
∫
+
+
+
dx
x
x
x
2
2
2
2
2
.
C
x
x
x
x
C
t
x
x
x
t
dx
x
x
x
dx
dt
x
t
x
dx
x
x
x
x
x
dx
dx
x
x
x
x
dx
x
x
x
dx
dx
x
x
x
x
x
dx
x
x
x
+
+
+
+
+
−
=
=
+
+
+
+
−
=
+
+
+
+
−
=
=
+
=
=
+
+
+
+
+
−
=
+
+
+
+
+
+
−
=
=
+
+
−
+
−
=
+
+
−
+
+
=
+
+
+
∫
∫
∫
∫
∫
∫
∫
∫
)
1
(
tg
arc
2
)
2
2
ln(
tg
arc
2
)
2
2
ln(
1
2
)
2
2
ln(
1
1
)
1
(
2
)
2
2
ln(
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
2
zad. 6.
Obliczyć pole obszaru ograniczone wykresem funkcji
4
2
−
=
x
e
y
i osiami układu
współrzędnych.
3
4
1
4
0
2
ln
2
2
ln
2
2
4
ln
4
0
4
0
2
2
−
=
−
=
−
=
⇒
=
=
⇒
=
⇒
=
⇒
=
⇒
=
−
=
e
y
x
x
x
x
e
y
e
y
x
x
Pole wyraża się więc poprzez:
(
)
[ ]
[ ]
2
ln
4
0
2
ln
4
2
ln
4
2
ln
4
2
2
ln
4
2
ln
4
4
4
4
2
3
2
3
2
3
2
1
2
1
4
ln
2
1
0
2
1
2
ln
2
2
1
2
ln
0
2
ln
0
2
2
1
2
ln
0
2
ln
0
2
2
ln
0
2
+
−
=
<
−
−
=
−
−
=
−
−
=
=
−
−
=
−
=
−
=
−
=
∫
∫
∫
D
e
e
e
x
e
dx
dx
e
dx
e
D
x
x
x
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 9
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 2:10
Temat: Przykładowe szkice rozwiązań do zestawu C.
Zmodyfikowana: 3.02.2007 2:10
Egzamin – zestaw C
zad. 1.
Obliczyć granicę ciągu o wyrazach:
4
1
4
4
4
+
−
+
+
=
n
n
n
c
n
.
Korzystam ze wzoru:
b
a
b
a
b
a
b
a
b
a
b
a
+
−
=
−
⇒
+
−
=
−
2
2
2
2
)
)(
(
0
4
4
4
1
4
4
4
1
4
3
4
4
1
4
4
1
4
4
1
4
4
2
1
4
2
3
2
4
2
4
3
4
4
4
4
4
4
4
4
2
=
∞
+
∞
→
+
+
+
+
−
=
+
+
+
+
−
=
=
+
+
+
+
−
=
+
+
+
+
−
−
+
+
=
+
−
+
+
=
∞
→
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
c
zad. 2.
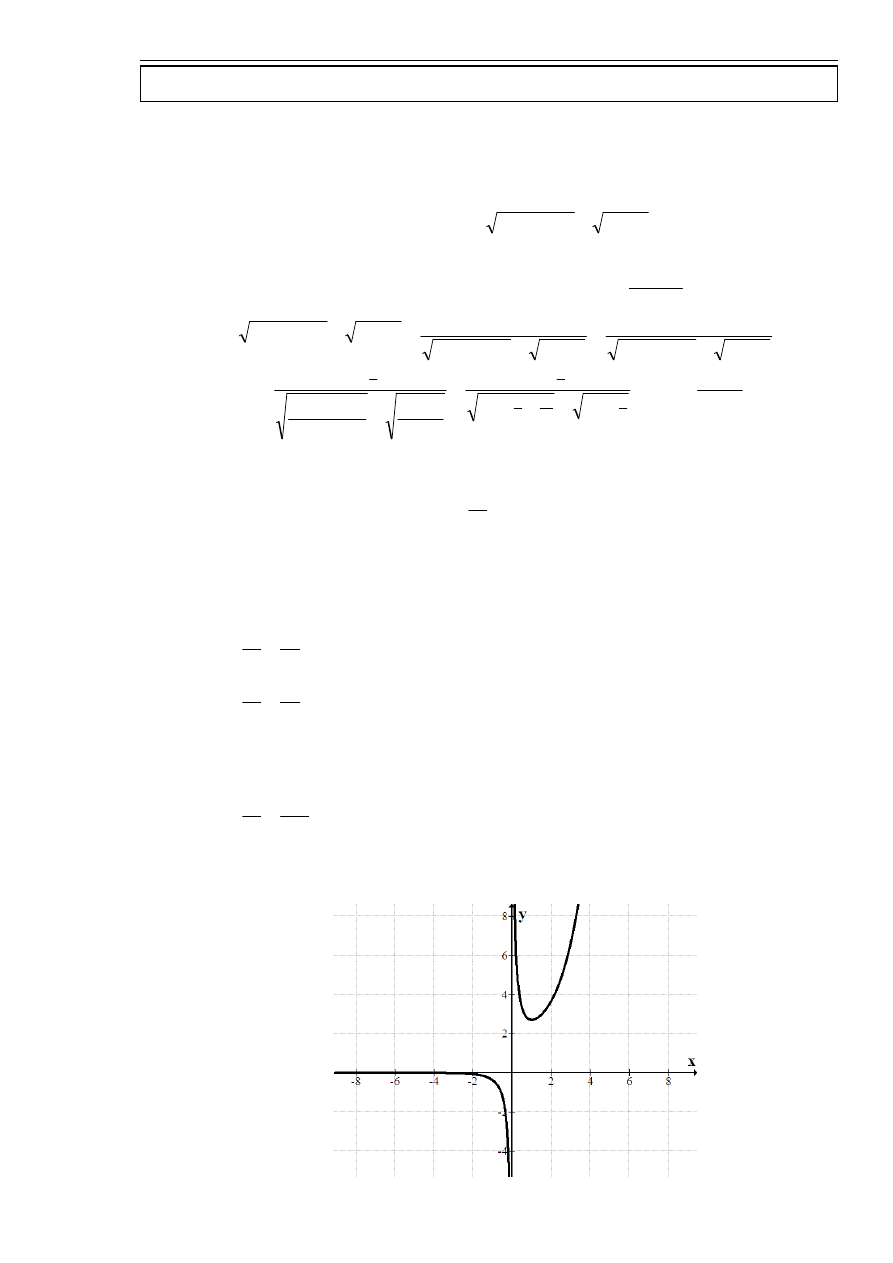
Wyznaczyć asymptoty funkcji
x
e
x
f
x
=
)
(
.
)
,
0
(
)
0
,
(
∞
∪
−∞
=
f
D
Sprawdzam istnienie asymptoty pionowej w
0
=
x
.
+∞
=
=
−∞
=
=
+
→
−
→
+
−
0
1
0
1
lim
lim
0
0
x
e
x
e
x
x
x
x
Istnieje asymptota pionowa obustronna w
0
=
x
.
Sprawdzam istnienie asymptoty poziomej w
∞
−
.
0
0
lim
=
∞
−
=
−∞
→
x
e
x
x
Istnieje asymptota pozioma w
∞
−
.
wykres funkcji
)
(x
f
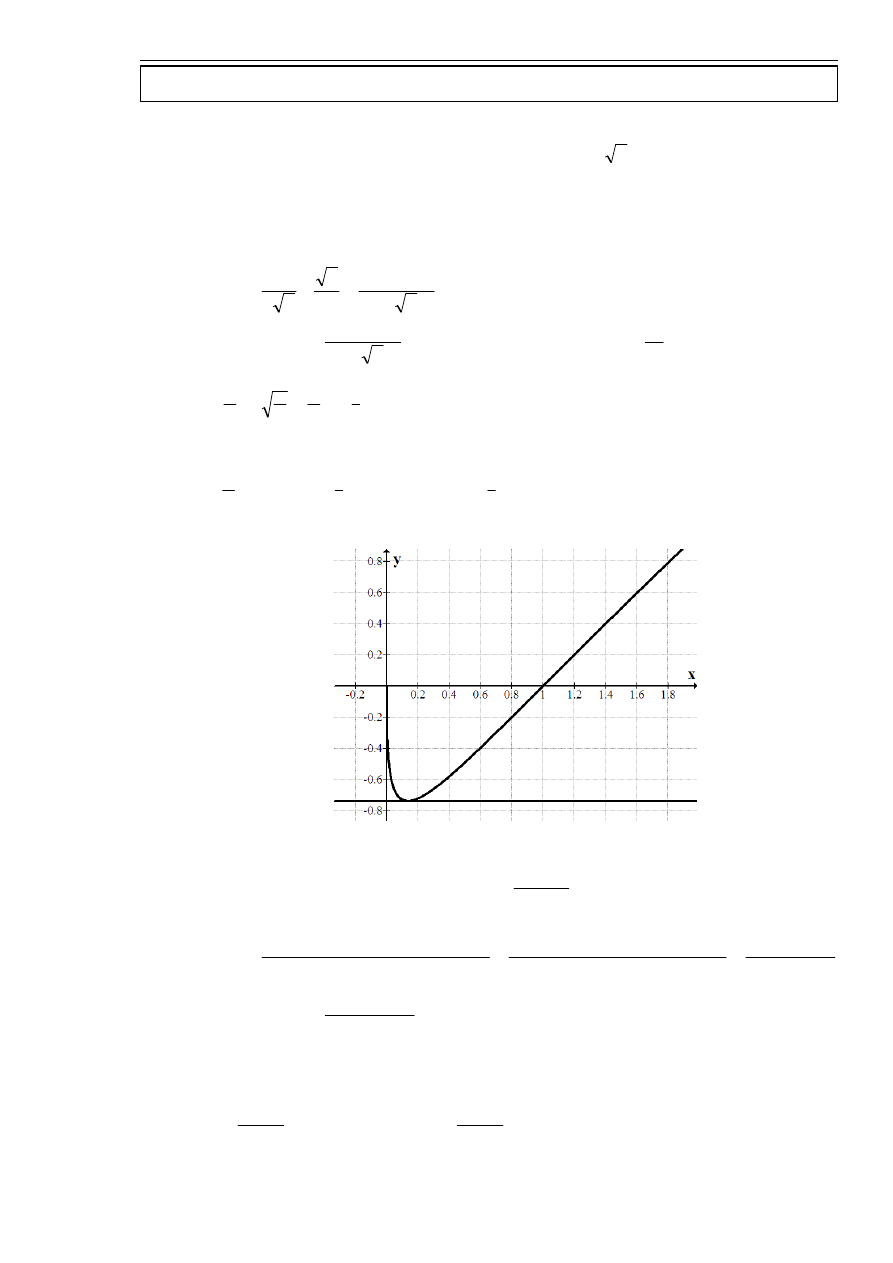
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 10
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 2:10
Temat: Przykładowe szkice rozwiązań do zestawu C.
Zmodyfikowana: 3.02.2007 2:10
zad. 3.
Napisać równanie tej stycznej do wykresu funkcji
x
x
x
f
ln
)
(
=
, która jest pozioma.
Ogólnie równanie stycznej to:
b
ax
x
g
+
=
)
(
.
Styczna ma być pozioma, więc
0
=
a
.
2
1
0
2
ln
0
2
2
ln
0
)
(
2
2
ln
2
ln
)
(
)
,
0
(
)
0
,
(
0
e
x
x
x
x
x
x
x
x
f
x
x
x
x
x
x
x
x
x
x
f
D
x
f
=
⇔
=
+
⇔
=
+
⇔
=
′
+
=
+
=
′
∞
∪
−∞
=
⇒
>
e
e
e
e
e
e
e
x
g
b
b
g
b
x
g
b
ax
x
g
f
2
2
1
2
1
1
1
)
(
)
(
)
(
)
(
ln
)
(
2
2
2
2
−
=
⇒
=
−
⇒
=
=
⇒
+
=
−
=
=
wykres funkcji
)
(x
f
zad. 4.
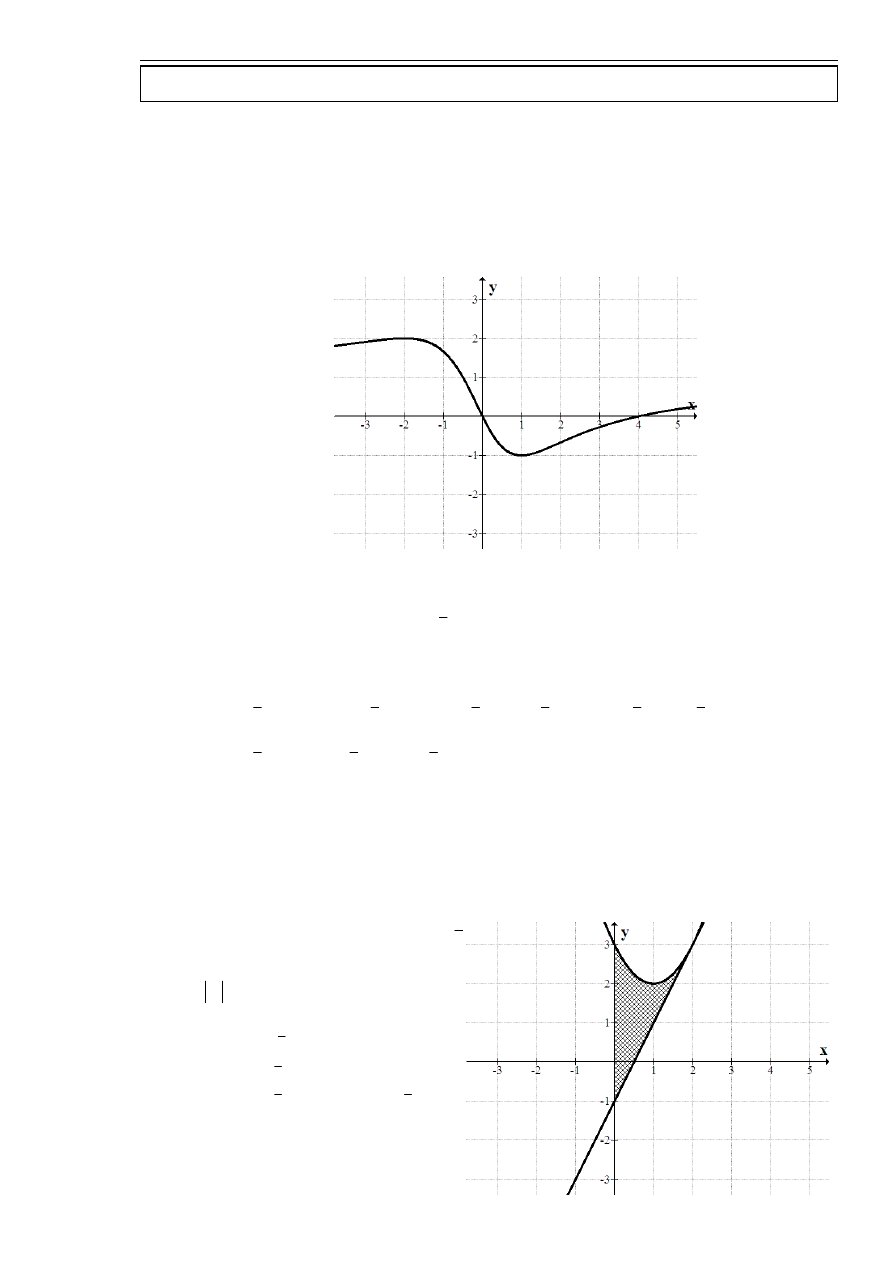
Wyznaczyć ekstrema lokalne funkcji
2
4
)
(
2
2
+
−
=
x
x
x
x
f
. Określić ich rodzaj.
(
)
(
)
(
)
(
)
0
2
0
8
4
4
0
2
8
4
4
0
)
(
2
8
4
4
2
8
2
8
4
4
2
2
)
2
)(
4
(
)
2
)(
4
2
(
)
(
2
2
2
2
2
2
2
2
2
2
2
3
2
3
2
2
2
2
=
−
+
⇔
=
−
+
⇔
=
+
−
+
⇔
=
′
+
−
+
=
+
+
−
−
−
+
=
+
−
−
+
−
=
′
x
x
x
x
x
x
x
x
f
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
f
0
)
2
)(
1
(
2
2
3
1
1
2
3
1
9
8
1
0
2
2
1
2
=
+
−
−
=
−
−
=
=
+
−
=
=
+
=
∆
=
−
+
x
x
x
x
x
x
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 11
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 2:10
Temat: Przykładowe szkice rozwiązań do zestawu C.
Zmodyfikowana: 3.02.2007 2:10
Badam zmianę znaku pochodnej:
)
1
,
2
(
0
)
2
)(
1
(
0
)
(
)
,
1
(
)
2
,
(
0
)
2
)(
1
(
0
)
(
−
∈
⇔
<
+
−
⇔
<
′
∞
∪
−
−∞
∈
⇔
>
+
−
⇔
>
′
x
x
x
x
f
x
x
x
x
f
Funkcja ma maksimum w
2
−
=
x
, a minimum w
1
=
x
.
wykres funkcji
)
(x
f
zad. 5.
Obliczyć całkę oznaczoną
∫
π
0
2
cos dx
x
x
.
Obliczę najpierw całkę nieoznaczoną, całkując przez części:
(
)
C
x
dx
x
dx
x
dx
x
x
x
x
x
x
x
+
+
=
−
=
′
⋅
=
∫
∫
∫
2
2
2
2
2
2
cos
4
sin
2
sin
2
sin
2
sin
2
cos
[
]
[
]
4
2
cos
4
sin
2
cos
0
2
0
2
0
2
−
=
+
=
∫
π
π
π
π
x
x
x
x
dx
x
zad. 6.
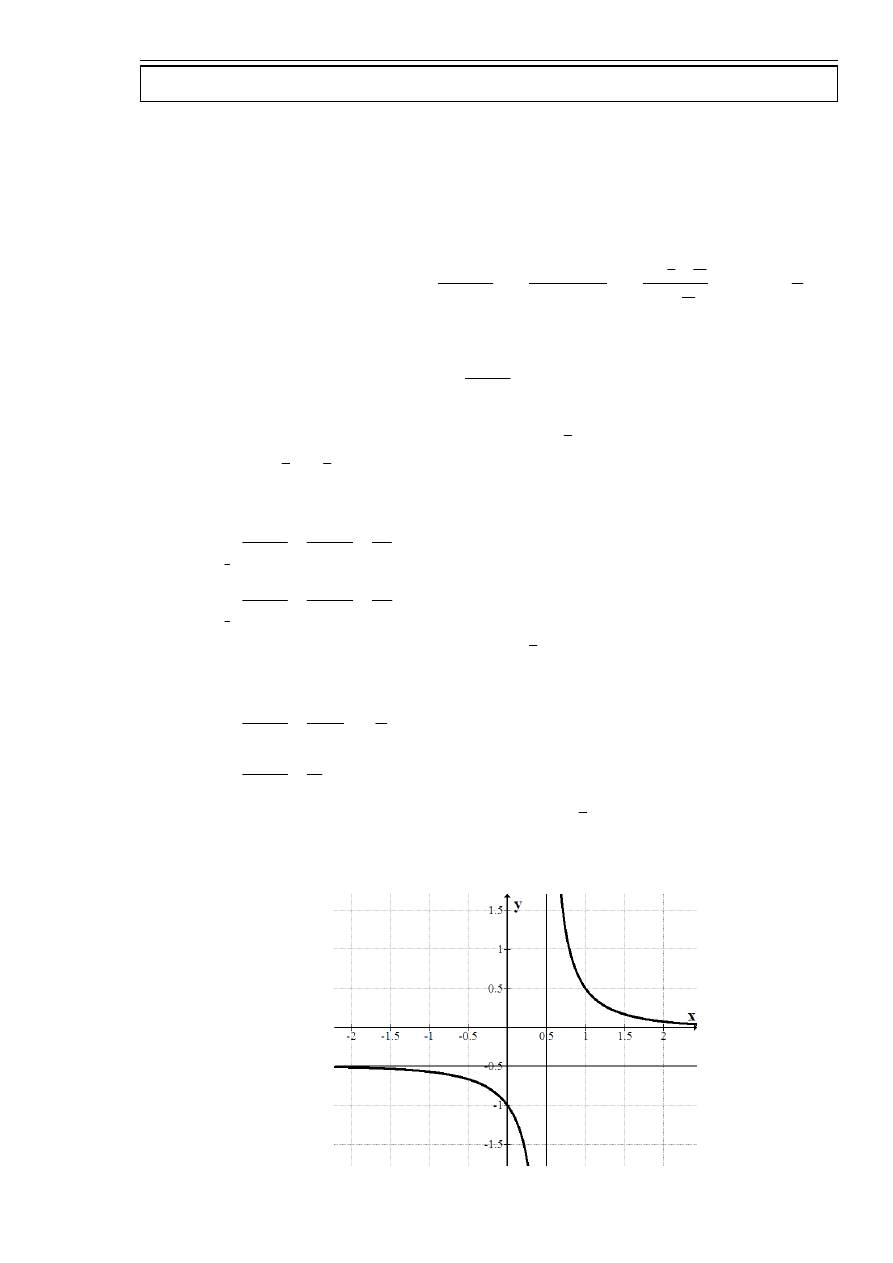
Obliczyć pole obszaru ograniczonego wykresem funkcji
3
2
2
+
−
=
x
x
y
, osią OY
i prostą
1
2
−
=
x
y
. Wykonać rysunek.
Można sprawdzić, że funkcje przecinają się w punkcie
)
3
,
2
(
.
Prosta przecina oś OX w punkcie
)
0
,
(
2
1
.
[
] [
]
3
8
3
8
2
2
3
3
1
2
0
2
2
0
2
3
3
1
2
0
2
0
2
2
4
6
4
2
2
2
3
2
2
3
)
1
2
(
)
3
2
(
=
+
−
+
−
=
=
+
−
⋅
+
−
=
=
−
−
+
−
=
=
−
−
+
−
=
∫
∫
x
x
x
x
x
dx
x
dx
x
x
D
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 12
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 3:19
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 3.02.2007 15:03
Egzamin – zestaw D
zad. 1.
Obliczyć granicę ciągu o wyrazach:
)
1
2
ln(
)
1
ln(
2
2
+
−
+
=
n
n
d
n
.
2
1
ln
2
1
ln
1
2
1
2
ln
1
2
)
1
(
ln
)
1
2
ln(
)
1
ln(
2
2
2
1
1
2
2
2
2
2
2
→
+
+
+
=
+
+
+
=
+
+
=
+
−
+
=
∞
→
n
n
n
n
n
n
n
n
n
n
n
n
d
zad. 2.
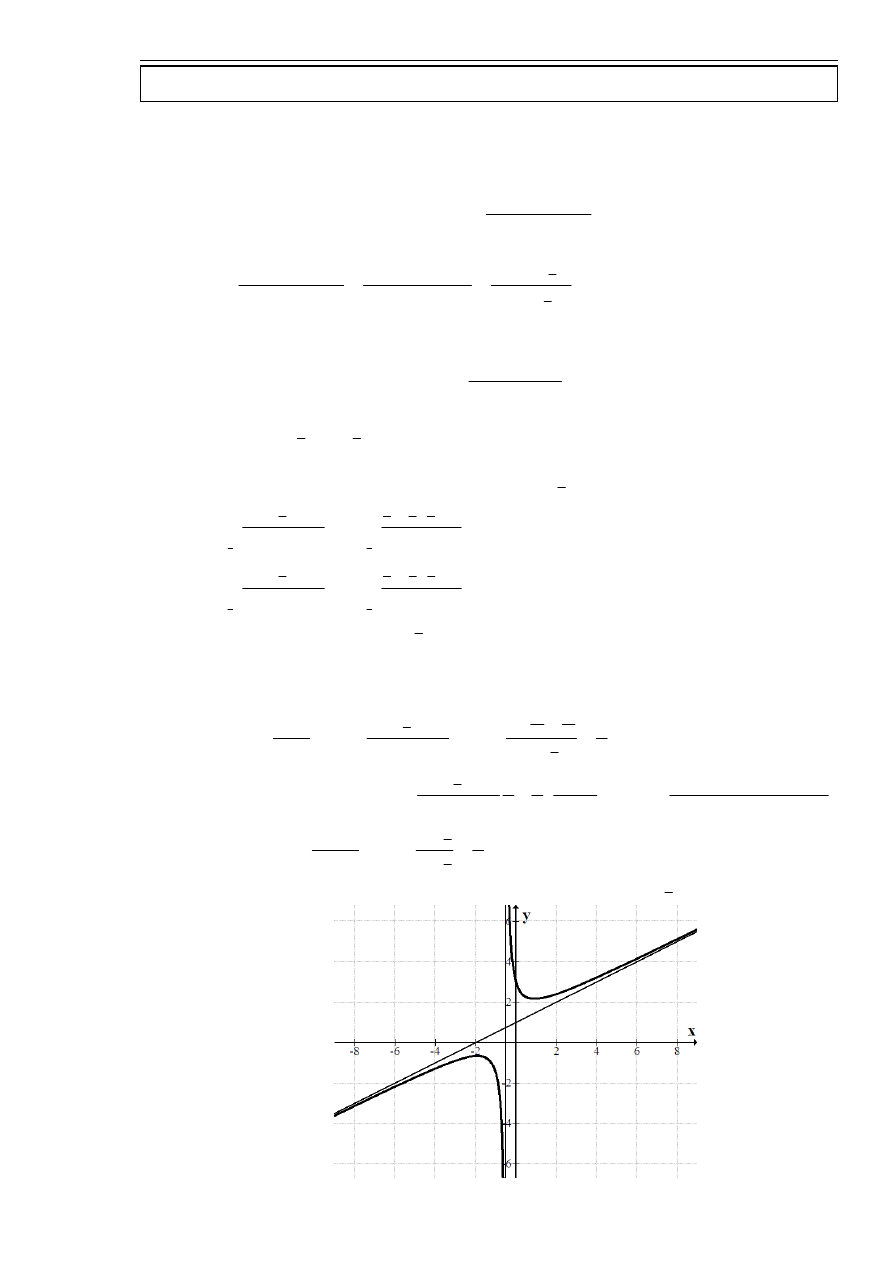
Wyznaczyć asymptoty funkcji
2
4
1
)
(
−
=
x
x
h
.
)
,
(
)
,
(
2
2
2
4
0
2
4
2
1
2
1
2
1
1
2
+∞
∪
−∞
=
≠
⇒
≠
⇒
≠
⇒
≠
−
f
x
x
x
D
x
Sprawdzam istnienie asymptoty pionowej obustronnej.
+∞
=
=
−
=
−
−∞
=
=
−
=
−
+
+
→
−
−
→
+
−
0
1
2
2
1
2
4
1
0
1
2
2
1
2
4
1
lim
lim
2
1
2
1
x
x
x
x
Istnieje asymptota pionowa obustronna w
2
1
=
x
.
Badam istnienie asymptot poziomych.
0
1
2
4
1
2
1
2
0
1
2
4
1
lim
lim
=
∞
=
−
−
=
−
=
−
+∞
→
−∞
→
x
x
x
x
Istnieje asymptota pozioma w
∞
−
o równaniu
2
1
−
=
y
.
Istnieje asymptota pozioma w
∞
+
o równaniu
0
=
y
.
wykres funkcji
)
(x
h
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 13
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 3:19
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 3.02.2007 15:03
zad. 3.
Napisać równanie stycznej do wykres funkcji
2
2
)
(
+
−
=
x
x
x
f
w punkcie przecięcia wykresu
z osią OX .
Nie styczną będzie miała funkcja
b
ax
x
g
+
=
)
(
.
2
0
2
0
2
2
0
)
(
=
⇒
=
−
⇒
=
+
−
⇒
=
x
x
x
x
x
f
(
)
(
)
(
)
4
1
2
2
2
2
2
4
)
2
(
2
4
2
)
2
(
2
)
(
=
+
=
′
+
=
+
−
−
+
=
′
f
x
x
x
x
x
f
2
1
4
1
2
1
4
1
)
(
2
0
)
2
(
0
)
(
)
(
)
(
−
+
=
−
=
⇒
+
⋅
=
′
=
=
=
+
=
x
x
g
b
b
f
a
x
f
x
g
b
ax
x
g
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 14
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 3:19
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 3.02.2007 15:03
zad. 4.
Wyznaczyć przedziały, na których funkcja
x
e
x
x
f
−
=
2
)
(
jest malejąca.
Badam pierwszą pochodną;
)
,
2
(
)
0
,
(
0
)
2
(
0
)
2
(
0
)
(
)
2
(
2
)
(
2
2
2
+∞
∪
−∞
∈
⇒
>
−
⇒
>
−
⇒
<
′
=
−
=
−
=
′
−
−
−
−
x
x
x
x
x
e
x
f
x
x
e
e
x
xe
x
f
x
x
x
x
ponieważ:
0
>
−
∧
x
x
e
.
wykres funkcji
x
e
x
x
f
−
=
2
)
(
zad. 5.
Obliczyć całkę oznaczoną
(
)
∫
−
1
0
2
3
dx
x
x
.
(
)
(
)
[ ]
[ ]
[ ]
110
1
5
3
11
12
2
1
1
0
5
3
1
0
11
6
1
0
2
2
1
1
0
1
0
1
0
1
0
1
0
2
3
3
5
6
11
3
2
6
5
3
2
3
1
2
1
2
2
2
=
+
−
=
+
−
=
=
+
−
=
+
−
=
−
∫
∫
∫
∫
∫
x
x
x
dx
x
dx
x
dx
x
dx
x
x
x
x
dx
x
x
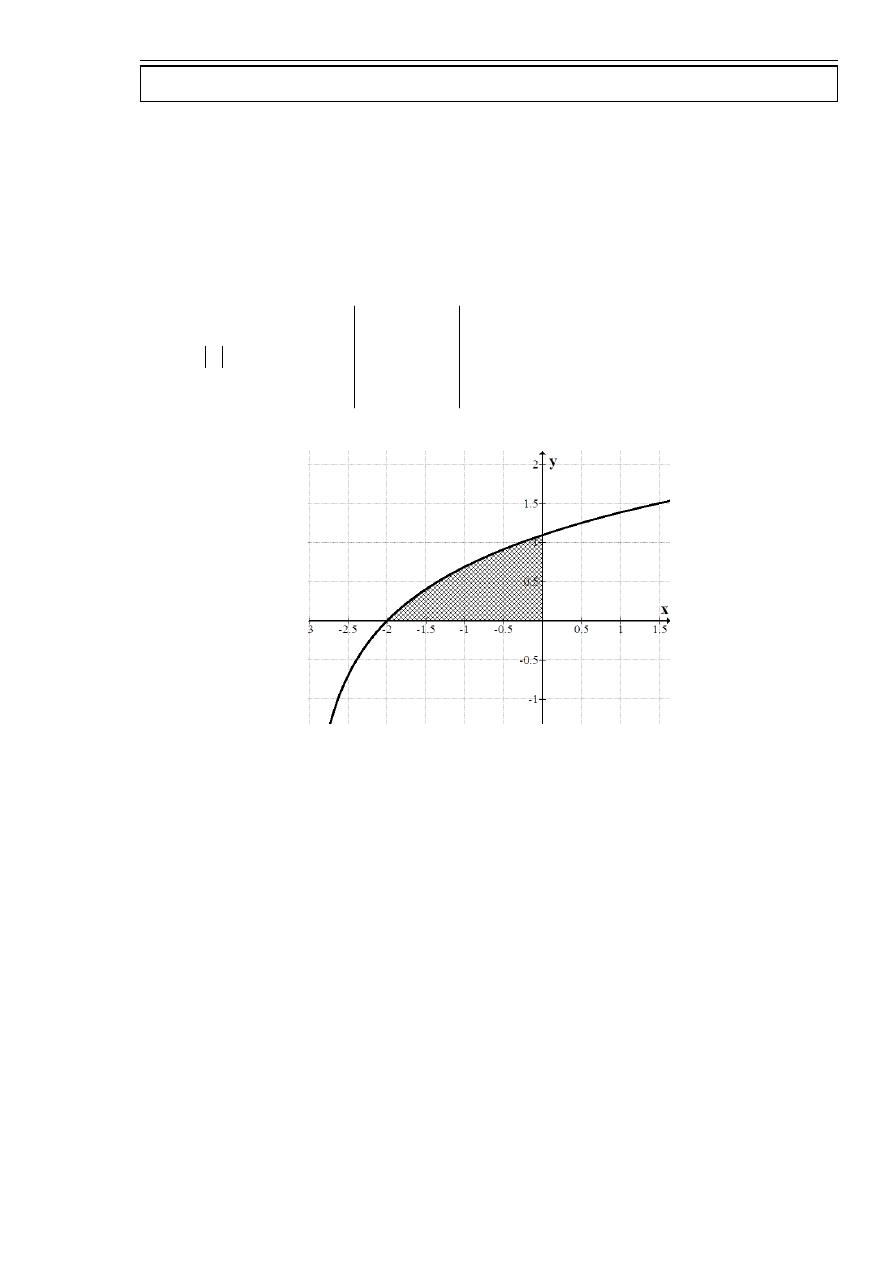
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 15
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 3.02.2007 3:19
Temat: Przykładowe szkice rozwiązań do zestawu D.
Zmodyfikowana: 3.02.2007 15:03
zad. 6.
Obliczyć pole obszaru ograniczonego wykresem funkcji
)
3
ln(
+
=
x
y
i osiami układu
współrzędnych. Wykonać rysunek.
3
ln
)
3
0
ln(
0
2
3
1
)
3
ln(
1
ln
)
3
ln(
0
0
)
3
ln(
=
+
=
⇒
=
−
=
⇒
+
=
⇒
+
=
⇒
+
=
⇒
=
+
=
y
x
x
x
x
x
y
x
y
[ ] [ ]
2
3
ln
3
1
3
3
ln
3
ln
ln
3
0
1
2
3
)
3
ln(
3
1
3
1
3
1
0
2
−
=
+
−
=
−
=
=
=
⇒
=
=
⇒
−
=
=
+
=
+
=
∫
∫
−
t
t
t
dt
t
t
x
t
x
dx
dt
x
t
dx
x
D
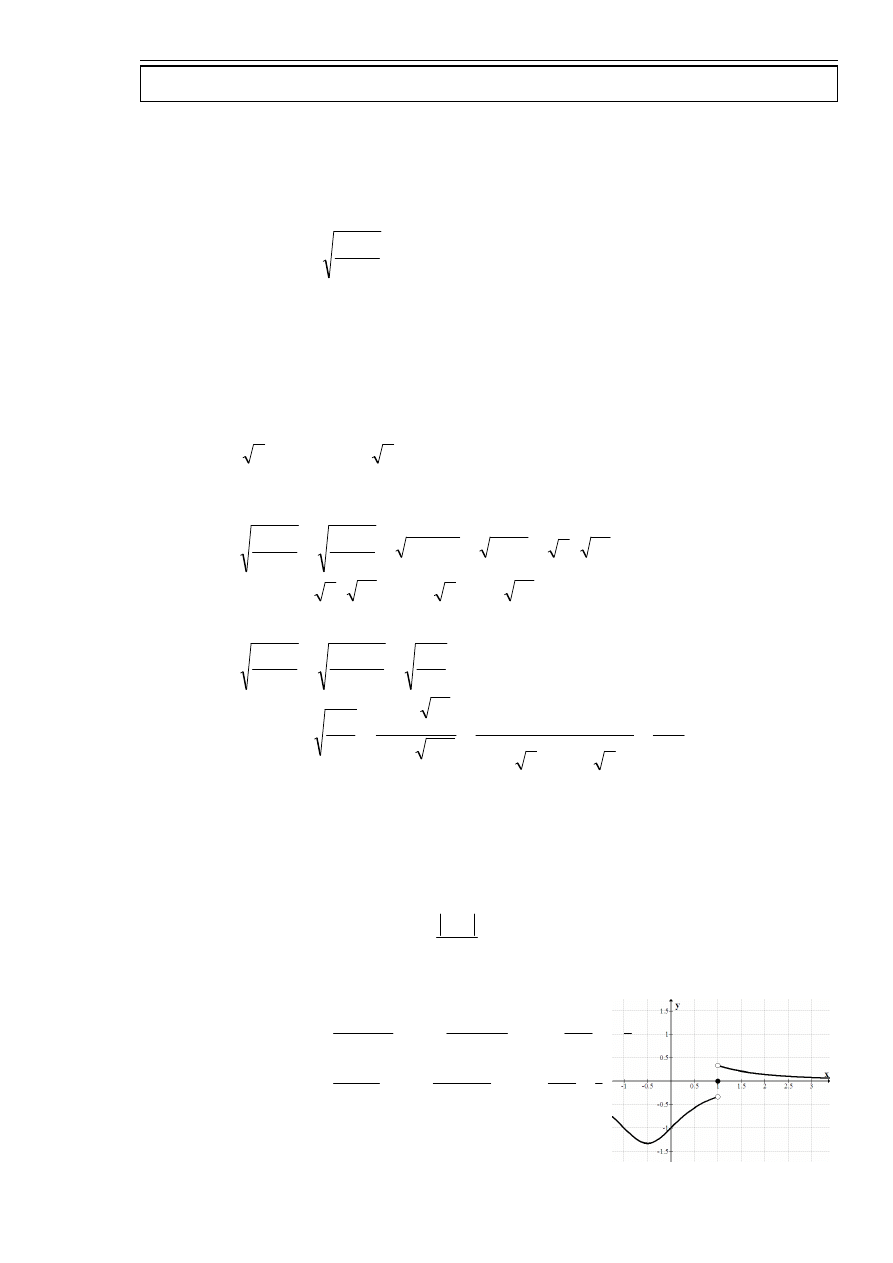
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 16
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 16.02.2007 23:46
Temat: Przykładowe szkice rozwiązań do zestawu A5 (egzamin poprawkowy). Zmodyfikowana: 18.02.2007 0:33
Egzamin poprawkowy – zestaw A5
zad. 1.
Sformułować twierdzenie o trzech ciągach i wykorzystać do obliczenia granicy ciągu
o wyrazach
n
n
n
n
a
3
5
2
2
+
+
=
.
Twierdzenie o trzech ciągach
Jeżeli ciągi
( )
n
a
,
( )
n
b
,
( )
n
c
są takie, że
n
n
n
n
n
c
a
b
≤
≤
∧
≥
0
oraz
a
c
b
n
n
n
n
=
=
∞
→
∞
→
lim
lim
to
a
a
n
n
=
∞
→
lim
.
Wiem, że:
1
lim
=
∞
→
n
n
a
oraz
1
lim
=
∞
→
n
n
n
szacuję ciąg z góry:
n
n
n
n
n
n
n
n
n
n
n
n
n
n
c
n
a
=
⋅
=
⋅
=
+
≤
+
≤
+
+
=
2
2
2
2
2
2
3
5
2
3
5
2
2
2
2
1
2
2
2
2
lim
lim
lim
lim
=
⋅
=
⋅
=
⋅
=
∞
→
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
n
n
c
szacuję ciąg z dołu:
n
n
n
n
n
n
n
n
b
n
n
n
n
a
=
≥
+
≥
+
+
=
2
2
2
2
2
2
2
3
5
2
2
1
1
2
2
2
2
2
2
2
2
2
2
2
lim
lim
lim
lim
lim
lim
=
⋅
=
⋅
=
=
=
∞
→
∞
→
∞
→
∞
→
∞
→
∞
→
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
n
b
więc:
2
2
lim
lim
lim
=
⇒
=
=
∞
→
∞
→
∞
→
n
n
n
n
n
n
a
b
c
zad. 2.
Zbadać ciągłość funkcji
=
≠
−
−
=
1
dla
0
1
dla
1
1
)
(
3
x
x
x
x
x
f
w punkcie
1
0
=
x
.
3
1
2
1
3
1
3
1
1
3
1
)
1
(
)
1
(
1
)
1
(
)
(
lim
lim
lim
lim
−
=
−
=
′
−
′
+
−
=
−
−
−
=
−
−
−
−
→
→
→
→
x
x
x
x
x
x
f
x
x
H
x
x
3
1
2
1
3
1
3
1
1
3
1
)
1
(
)
1
(
1
)
1
(
)
(
lim
lim
lim
lim
=
=
′
−
′
−
=
−
−
=
−
−
−
+
→
→
→
→
x
x
x
x
x
x
f
x
x
H
x
x
Stwierdzam, że:
)
(
)
(
)
(
0
1
1
lim
lim
x
f
x
f
x
f
x
x
≠
≠
+
−
→
→
więc funkcja
)
(x
f
jest nieciągła w punkcie
1
0
=
x
(nieciągłość typu „skok”).
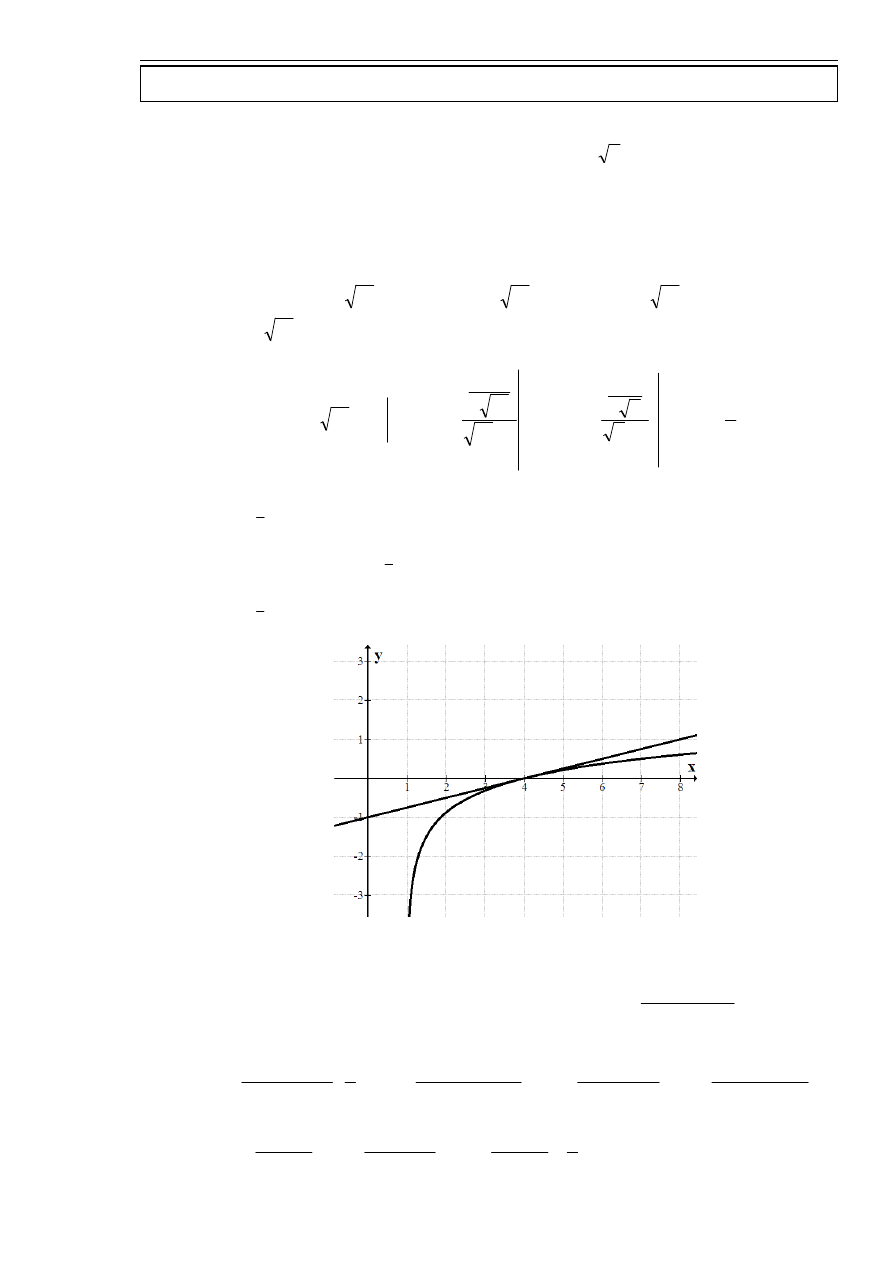
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 17
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 16.02.2007 23:46
Temat: Przykładowe szkice rozwiązań do zestawu A5 (egzamin poprawkowy). Zmodyfikowana: 18.02.2007 0:33
zad. 3.
Napisać równanie styczeń do wykresu funkcji
(
)
1
ln
)
(
−
=
x
x
f
w punkcie jego
przecięcia z osią OX .
Niech styczna będzie opisana równaniem:
b
ax
x
g
+
=
)
(
.
Szukam punktu
0
x
takiego, że
0
)
(
0
=
x
f
ponieważ styczna na przecinać oś OX w tym punkcie.
(
)
(
)
(
)
4
0
2
1
1
1
ln
1
ln
0
1
ln
0
)
(
0
0
0
0
0
0
0
=
⇒
>
∧
=
=
−
⇒
=
−
⇒
=
−
⇒
=
x
x
x
x
x
x
x
f
Wiadomo, że:
(
)
(
)
4
1
4
1
4
4
2
1
4
1
2
1
4
1
ln
)
(
0
0
0
0
0
0
0
=
=
−
=
=
−
=
=
′
−
=
′
=
x
x
x
x
x
x
x
f
a
więc:
b
x
x
g
+
=
4
1
)
(
wiadomo także, że:
1
0
4
0
)
(
)
(
4
1
0
0
−
=
⇒
=
+
⋅
⇒
=
=
b
b
x
f
x
g
ostatecznie:
1
)
(
4
1
−
=
x
x
g
zad. 4.
Korzystając z twierdzenia de l’Hospitala obliczyć granicę
3
0
2
lim
x
x
e
e
x
x
x
−
−
−
→
.
(
)
( )
(
)
( )
(
)
( )
0
6
0
6
6
6
3
2
3
2
2
0
0
2
lim
lim
lim
lim
lim
lim
lim
0
0
0
2
0
2
0
3
0
3
0
=
=
+
=
′
′
−
=
−
=
=
′
′
−
+
=
−
+
=
′
′
−
−
=
−
−
−
→
−
→
−
→
−
→
−
→
−
→
−
→
x
x
x
x
x
x
H
x
x
x
x
x
x
H
x
x
x
x
x
x
H
x
x
x
e
e
x
e
e
x
e
e
x
e
e
x
e
e
x
x
e
e
x
x
e
e
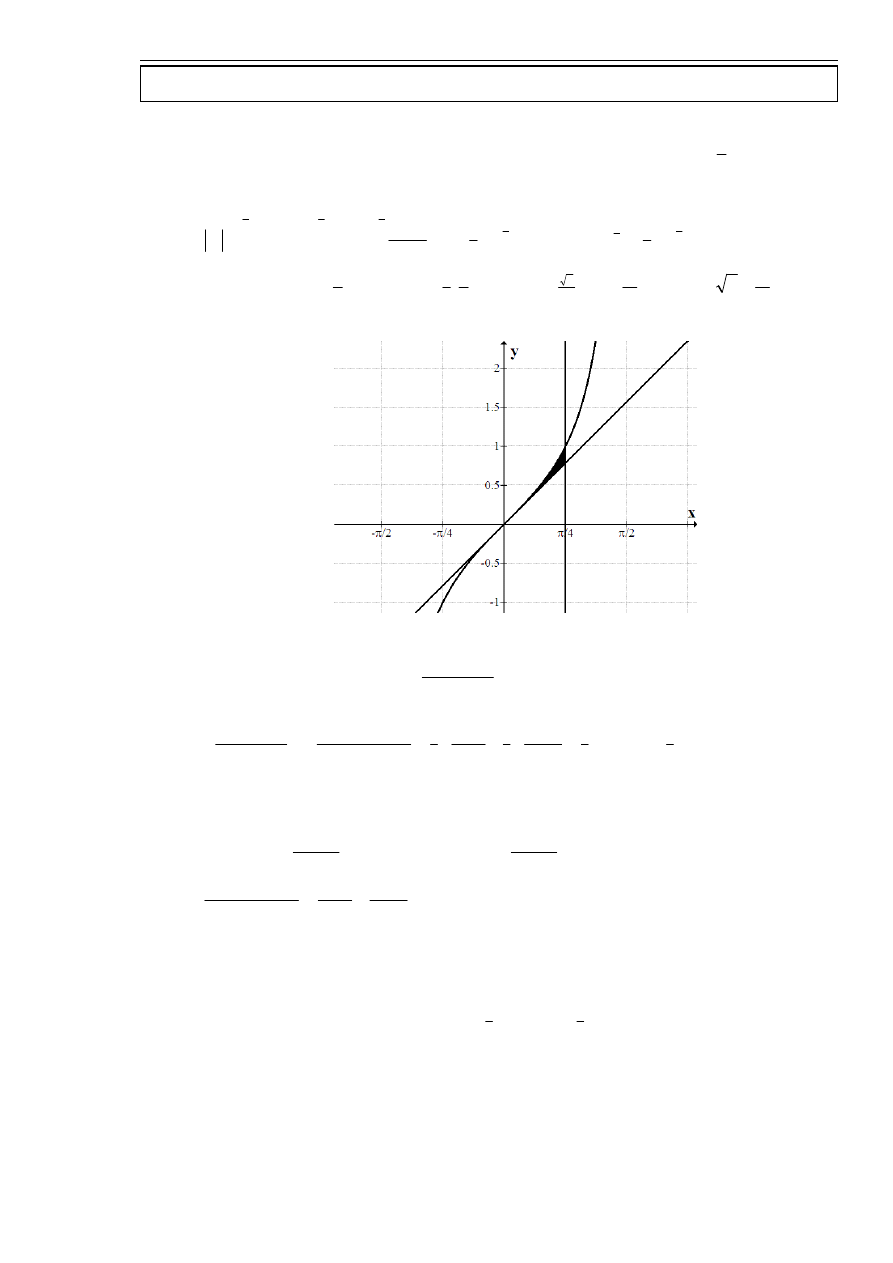
Studenckie Notatki Cyfrowe
SNy: Biotechnologia
www.sny.one.pl sny@sny.one.pl
Strona 18
Notatka: Analiza matematyczna I (MAP1024w) – egzamin.
Utworzona: 16.02.2007 23:46
Temat: Przykładowe szkice rozwiązań do zestawu A5 (egzamin poprawkowy). Zmodyfikowana: 18.02.2007 0:33
zad. 5.
Obliczyć pole obszaru D ograniczonego krzywymi
x
y
tg
=
,
x
y
=
,
4
π
=
x
.
Korzystając poniższego rysunku można zauważyć, że:
[ ]
(
)
[
]
[ ]
(
)
(
)
( )
( )
32
32
2
2
2
4
2
1
4
0
2
2
1
0
0
2
2
1
0
0
0
2
2
4
4
4
4
4
4
2
ln
2
ln
0
ln
0
0
cos
ln
cos
ln
cos
ln
cos
sin
tg
π
π
π
π
π
π
π
π
π
π
−
−
=
−
+
−
=
+
−
+
−
=
=
−
−
=
−
=
−
=
∫
∫
∫
x
x
x
dx
x
x
dx
x
dx
x
D
zad. 6.
Obliczyć całkę nieoznaczoną
∫
−
−
2
2
x
x
dx
.
3
1
3
1
2
1
2
3
1
3
1
3
1
3
1
2
1
3
1
2
0
2
)
(
1
)
1
(
)
2
(
1
2
1
)
2
)(
1
(
1
2
2
3
1
1
2
3
1
9
8
1
0
2
)
2
ln(
)
1
ln(
2
1
)
2
)(
1
(
2
=
⇒
−
=
⇒
=
−
⇒
=
−
−
=
⇒
=
+
−
+
+
=
−
+
+
=
+
+
−
=
+
−
−
=
−
−
=
=
+
−
=
=
+
=
∆
=
−
−
+
+
−
−
=
+
−
−
=
+
−
=
−
−
∫
∫
∫
∫
A
B
B
B
A
B
A
B
A
B
A
B
A
x
x
B
x
A
x
B
x
A
x
x
x
x
x
x
C
x
x
x
dx
x
dx
x
x
dx
x
x
dx
Wyszukiwarka
Podobne podstrony:
02 01 11 12 01 10 e notatka analiza matematyczna I egzamin
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
02 01 11 12 01 56 e notatka analiza matematyczna I kolokwium II
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
02 01 11 12 01 56 e notatka analiza matematyczna I kolokwium II
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
TI 01 02 01 10 T B pl
AiR 11 12 wyklad 10 09 12 2011 MDW
Wyklad-10-AM1, Analiza matematyczna, Analiza matematyczna, Wykłady
11 i 12, ~FARMACJA, I rok, CHEMIA OGÓLNA I NIEORGANICZNA, Egzamin chemia
egzamin analiza 2006, BUDOWNICTWO IL PW, SEMESTR I, Analiza Matematyczna I, Egzaminy
Analiza matematyczna egzamin I (lato) calki teoria, Wykłady - Studia matematyczno-informatyczne
ZAGADNIENIA Z ANALIZY MATEMATYCZNEJ, Fizyka Medyczna, STUDIA, Rok I, Semestr II, Analiza matematyczn
ANALIZA- Gajowski-AE Katowice, Egzamin z analizy matematycznej, Egzamin z analizy matematycznej
Analiza matematyczna egzamin przykładowy
więcej podobnych podstron