
Jan Nawrocki
MATEMATYKA cz. 3
Analiza matematyczna II
Politechnika Warszawska 2010

Politechnika Warszawska
Wydział Samochodów i Maszyn Roboczych
Kierunek "Edukacja techniczno informatyczna"
02-524 Warszawa, ul. Narbutta 84, tel (22) 849 43 07, (22) 234 83 48
ipbmvr.simr.pw.edu.pl/spin/, e-mail:
sto@simr.pw.edu.pl
Opiniodawca: prof. dr hab. Krzysztof CHEŁMIŃSKI
Projekt okładki: Norbert SKUMIAŁ, Stefan TOMASZEK
Projekt układu graficznego tekstu: Grzegorz LINKIEWICZ
Skład tekstu: Janusz BONAROWSKI, Jan NAWROCKI
Publikacja bepłatna, przeznaczona jest dla studentów kierunku
"Edukacja techniczno informatyczna"
Copyright © 2010 Politechnika Warszawska
Utwór w całości ani we fragmentach nie może być powielany ani rozpowszechniany
za pomocą urządzeń elektronicznych, mechanicznych, kopiujących, nagrywających i innych
bez pisemnej zgody posiadacza praw autorskich.
ISBN 83-89703-41-6
Druk i oprawa: Drukarnia Expol P. Rybiński, J. Dąbek Spółka Jawna,
87-800 Włocławek, ul. Brzeska 4

Spis treści
I. Funkcje wielu zmiennych................................................................. 5
Rachunek różniczkowy funkcji wielu zmiennych................................................... 9
II. Różniczkowanie funkcji złożonej................................................... 17
Ekstrema funkcji dwóch zmiennych..................................................................... 22
III. Funkcje uwikłane ........................................................................... 29
Płat regularny i płaszczyzna styczna .................................................................... 33
IV. Elementy teorii pola ....................................................................... 37
Całka podwójna ................................................................................................... 41
V. Zamiana zmiennych w całce podwójnej........................................ 47
Pole płata ............................................................................................................. 52
Całka Gaussa ....................................................................................................... 54
VI. Całka potrójna................................................................................ 57
Całka krzywoliniowa nieskierowana .................................................................... 63
VII. Całka powierzchniowa niezorientowana ....................................... 69
Zastosowania całek w mechanice......................................................................... 72
VIII. Całka krzywoliniowa skierowana .................................................. 77
Niezależność całki od drogi całkowania............................................................... 82
IX. Całka powierzchniowa zorientowana............................................ 87
Literatura ....................................................................................... 97

Przedmowa
Niniejsze materiały zostały opracowane w ramach realizacji Programu Rozwojowego Poli-
techniki Warszawskiej współfinansowanego ze środków PROGRAMU OPERACYJNEGO
KAPITAŁ LUDZKI. Przeznaczone są dla studentów pierwszego roku studiów inżynierskich
kierunku nauczania „Edukacja techniczno-informatyczna” prowadzonych na Wydziale Samo-
chodów i Maszyn Roboczych Politechniki Warszawskiej.
Swoim zakresem obejmują trzecią część tematyki określonej w programie studiów dla przed-
miotu pn. „Matematyka” opisanym w sylabusie opracowanym dla tego przedmiotu. Jest to
przedmiot z grupy przedmiotów podstawowych. W planie studiów przewidziano jego realiza-
cję na pierwszym i drugim roku studiów.
Na pierwszym semestrze są to dwa wykłady 30-godzinne i 15-godzinne ćwiczenia dla każde-
go z nich:
1. Matematyka cz. 1 – Algebra i geometria analityczna,
2. Matematyka cz. 2 – Analiza 1.
Na drugim semestrze 2 wykłady 30-godzinne i 30 -godzinne ćwiczenia dla każdego wykładu:
3. Matematyka cz. 3 – Analiza 2,
4. Matematyka cz. 4 – Szeregi funkcyjne i równania różniczkowe zwyczajne.
Na trzecim semestrze 30 - godzinny wykład:
5. Matematyka cz. 5 – Elementy probabilistyki i statystyki matematycznej.
W materiałach zawarto podstawowe treści z analizy matematycznej funkcji wielu zmiennych
(rachunek różniczkowy i całkowy) potrzebne studentom wydziałów technicznych Politechniki
Warszawskiej.
Postanowiłem pominąć niektóre dowody, starając się jednocześnie ilustrować każde twierdze-
nie przykładem.
Najważniejsze definicje i wszystkie twierdzenia zostały zapisane w ramkach, co pozwala stu-
dentom zwrócić uwagę na te ważne w matematyce zdania.
Skrypt ten został napisany w formie kart do pracy na wykładzie. Student ma napisane
i wyróżnione w tekście definicje i twierdzenia oraz komentarze, może więc skupić się na
objaśnieniach wykładowcy, co pozwala na lepsze zrozumienie pojęć wprowadzanych na
wykładzie. Student na wykładzie uzupełnia samodzielnie tylko dowody twierdzeń i przykłady

I
Funkcje wielu zmiennych

R
OZDZIAŁ
I
Strona 6
6
6
6
Rozpatrywane w części I tego skryptu odwzorowanie f: X
→ℜ, gdzie X⊂ℜ
n
uogólnimy na
przypadek, gdy wartości funkcji leżą w przestrzeni
ℜ
m
.
Odwzorowanie f: X
→
ℜ
m
, gdzie X
⊂ℜ
n
nazywamy funkcją wektorową (n zmiennych).
Funkcję tę zapisujemy krótko: u=f(x), x=(x
1
, ... ,x
n
), u=(u
1
, ..., u
m
) lub w formie pełnej:
).
,...,
(
......
..........
..........
),
,...,
(
1
1
1
n
m
n
x
x
f
u
x
x
f
u
=
=
W przypadku szczególnym, gdy n=m=1 otrzymamy funkcję rzeczywistą jednej zmiennej
W przypadku n=2 i m=1, stosujemy wygodny zapis: z = f(x,y) , jest to funkcja rzeczywista
dwóch zmiennych rzeczywistych.
Zbiór punktów o postaci: {x,y,f(x,y)} nazywamy wykresem funkcji f dwóch zmiennych.
Jeśli funkcja f jest ciągła, to zbiór ten jest powierzchnią.
Gdy n=3 i m=1, będziemy stosować zapis bez indeksów: u=f(x,y,z) – jest to funkcja rzeczy-
wista trzech zmiennych rzeczywistych.
Funkcję f : X
→ℜ, X⊂ℜ
3
nazywamy też polem skalarnym (wynika to z zastosowań fizycz-
nych: temperatura, gęstość, ciśnienie).
Funkcję wektorową f : X
→ℜ
3
, X
⊂ℜ
3
nazywamy polem wektorowym (siła).
Granica i ciągłość funkcjonału rzeczywistego została omówiona w skrypcie I
Przypomnimy teraz podstawowe definicje w przypadku szczególnym, gdy f jest funkcją rze-
czywistą n zmiennych rzeczywistych.
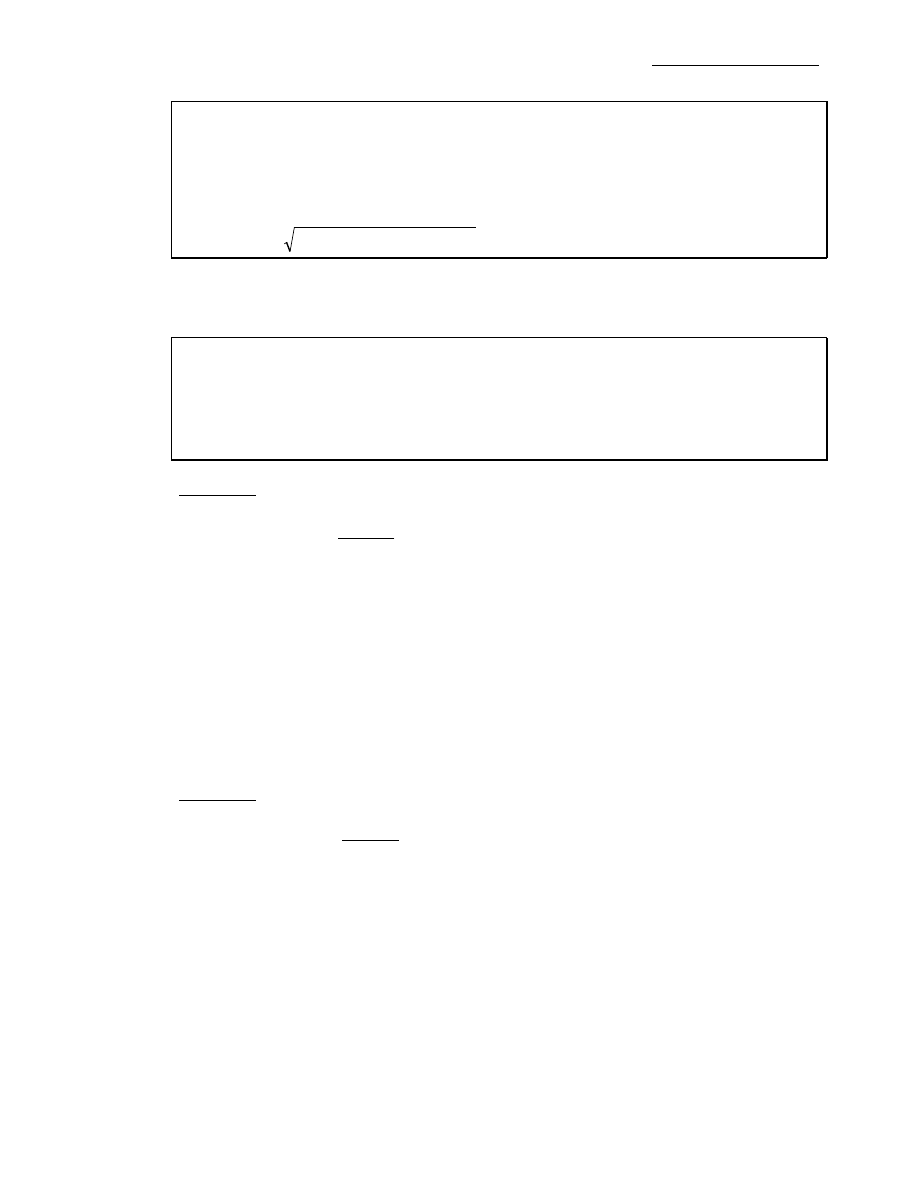
F
UNKCJE WIELU ZMIENNYCH
Strona 7
7
7
7
Definicja Cauchy’ego.
Mówimy, że odwzorowanie f
: X
→
→
→
→
ℜ
ℜ
ℜ
ℜ
, X
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
ma w punkcie p
0
granicę q
∈
∈
∈
∈
B wtedy
i tylko wtedy, gdy
∀
ε
>0
∃
δ
>0
∀
p
∈
X: 0 < d(p,p
0
) <
δ
⇒
|
f(p)
−
q
|
<
ε
,
gdzie d(p,p
0
)=
2
0
2
01
1
)
(
...
)
(
n
n
x
x
x
x
−
+
+
−
Definicja Heinego.
Mówimy, że odwzorowanie f
: X
→
→
→
→
ℜ
ℜ
ℜ
ℜ
, X
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
ma w punkcie p
0
granicę q
∈
∈
∈
∈
B wtedy
i tylko wtedy, gdy dla każdego ciągu (p
n
) o wyrazach ze zbioru X ciąg liczbowy f(p
n
) ma
granicę równą q.
Przykład 1.
Wyznaczyć:
2
2
)
0
,
0
(
)
,
(
lim
y
x
xy
y
x
+
→
.
Przykład 2.
Wyznaczyć:
2
2
2
)
0
,
0
(
)
,
(
lim
y
x
y
x
y
x
+
→
.

R
OZDZIAŁ
I
Strona 8
8
8
8
Dla funkcji wielu zmiennych określa się także tzw. granice iterowane, które można wykorzys-
tać do wykazania, że granica funkcji w punkcie nie istnieje. Funkcja dwóch zmiennych ma
dwie granice iterowane:
→
→
)
,
(
lim
lim
0
0
y
x
f
y
y
x
x
lub
→
→
)
,
(
lim
lim
0
0
y
x
f
x
x
y
y
.
Uwaga 1. Jeżeli funkcja f: X→ℜ, X⊂ℜ
2
ma granicę w punkcie (x
0
,y
0
) oraz istnieją obydwie
granice iterowane, to są one równe tej granicy. Implikacja przeciwna nie jest prawdziwa, co
będzie widoczne w następujących przykładach.
Przykład 3.
Wyznaczyć granicę oraz granice iterowane w punkcie (0,0) funkcji f, gdzie:
a)
f(x,y) =
y
x
y
x
y
x
+
+
+
−
2
2
; b) f(x,y) =
y
x
1
sin
.
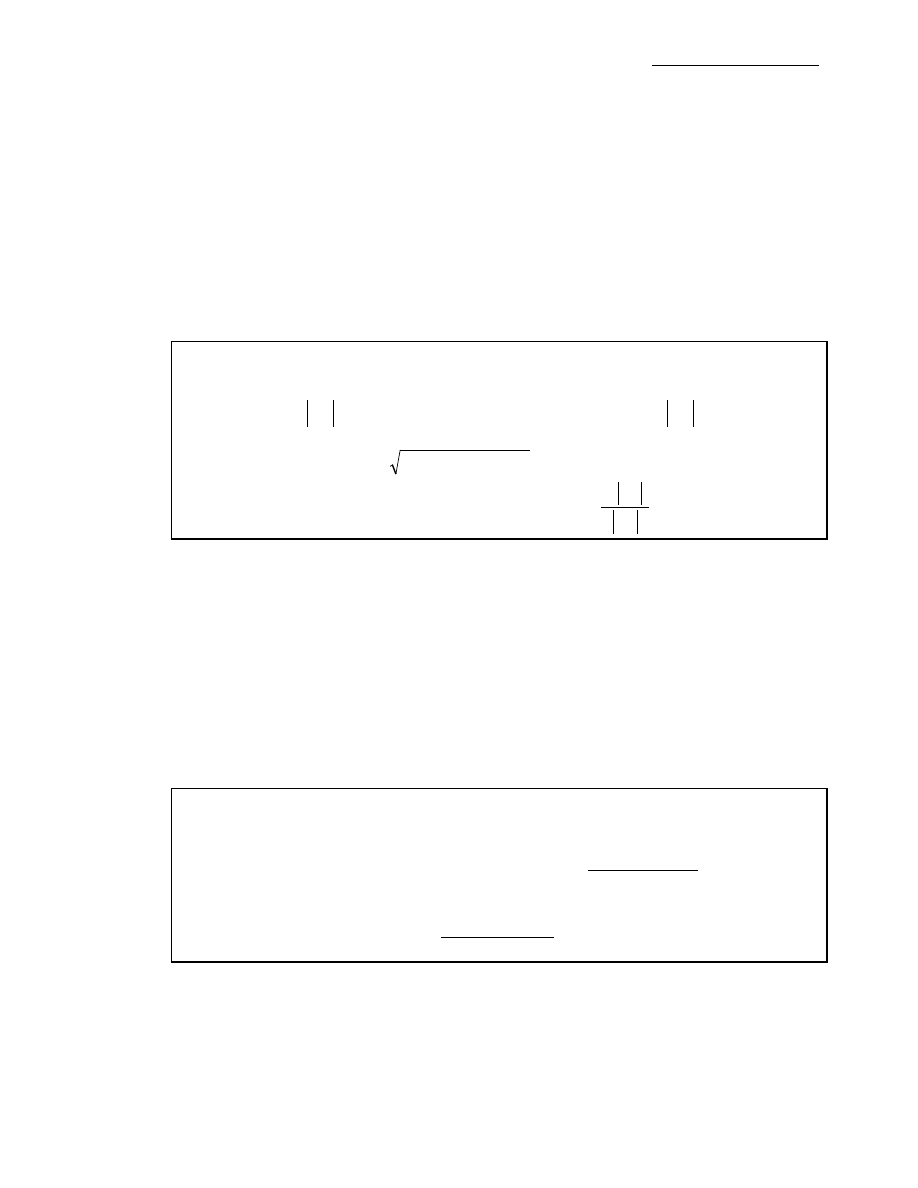
F
UNKCJE WIELU ZMIENNYCH
Strona 9
9
9
9
Granice i ciągłość funkcji została omówiona w skrypcie II. Sformułowano tam także ważne
twierdzenia dla granic ( twierdzenie o zachowaniu nierówności w granicy, twierdzenie
o trzech funkcjonałach oraz twierdzenia dla funkcji ciągłych (twierdzenie o zachowaniu
znaku, twierdzenie Darboux, twierdzenie Weierstrassa).
Rachunek różniczkowy funkcji wielu
zmiennych
Funkcję f określoną w pewnym otoczeniu U(x,
δ
) punktu x=(x
1
, ... ,x
n
) nazywamy
różniczkowalną w tym punkcie , jeżeli istnieją takie stałe a
1
, ... ,a
n
zależne tylko od x , że:
( )
x
o
x
a
x
f
x
x
f
x
n
j
j
j
∆
+
∆
=
−
∆
+
<
∆
∀
∑
=1
)
(
)
(
:
δ
,
gdzie
∆
x=(
∆
x
1
... ,
∆
x
n
),
|∆
x
|
=
2
2
1
)
(
...
)
(
n
x
x
∆
+
+
∆
a o(
|∆
x
|
) jest tzw. nieskończenie małą
rzędu wyższego niż
|∆∆∆∆
x
||||
, tzn. taką funkcją, dla której
( )
∆
x
∆
x
o
lim
0
∆
x
=
→
= 0.
Uwaga2. Suma
∑
=
∆
n
j
j
j
x
a
1
jest iloczynem skalarnym a(x)
∆∆∆∆
x wektora a(x)= (a
1
(x), ... ,a
n
(x))
przez wektor
∆∆∆∆
x=(
∆∆∆∆
x
1
, ... ,
∆∆∆∆
x
n
). Wyrażenie to nazywamy różniczką funkcji f w punkcie x
odpowiadającą przyrostowi
∆∆∆∆
x i oznaczamy df(x,
∆∆∆∆
x) lub krótko df, czyli:
df(x, ∆x):= a(x)∆x =
∑
=
∆
n
j
j
j
x
a
1
.
Twierdzenie 1.
Jeżeli f: X→
→
→
→ℜ
ℜ
ℜ
ℜ, X⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
, jest funkcją różniczkowalną w punkcie x, to istnieje granica
prawostronna w zerze funkcji q:
ℜ
ℜ
ℜ
ℜ
+
→
→
→
→ℜ
ℜ
ℜ
ℜ o postaci q(ττττ):=
ττττ
ττττ
f(x)
e)
f(x
−−−−
++++
, gdzie e jest
ustalonym wersorem przestrzeni
ℜ
ℜ
ℜ
ℜ
n
, granica ta jest równa iloczynowi skalarnemu
wektorów a(x) oraz e, a więc:
e
a(x)
f(x)
e)
f(x
lim
0
⋅⋅⋅⋅
====
−−−−
++++
++++
→
→
→
→
τ
τ
τ
.
Uwaga 3. Wektor a(x) nazywamy pochodną funkcji f w punkcie x i oznaczamy f ′, wtedy
różniczkę funkcji f zapisujemy w postaci: df(x,
∆x)=f ′(x)dx.

R
OZDZIAŁ
I
Strona 10
10
10
10
Uwaga 4. Granicę występującą w tezie twierdzenia 1. nazywamy pochodną kierunkową
funkcji f i oznaczamy symbolem
e
f
∂
∂
, czyli:
e
f
∂
∂
(x)=f
′(x)⋅e.
Uwaga 5. W szczególności, gdy wersor e=e
j
jest wersorem bazy kanonicznej, to pochodną
kierunkową nazywamy pochodną cząstkową funkcji f względem zmiennej x
j
i oznaczamy
symbolem
j
x
f
∂
∂
, tak więc:
j
n
j
n
j
j
x
j
x
x
x
x
f
x
x
x
x
f
x
f
j
∆
−
∆
+
=
∂
∂
→
∆
)
,...,
,...,
(
)
,...,
,...,
(
lim
1
1
0
.
Uwaga 6. Ponieważ
j
x
f
∂
∂
= f ′(x)⋅e
j
, więc f ′(x) =
(
)
n
x
x
x
n
f
f
f
x
f
x
f
′
′
′
=
∂
∂
∂
∂
,...,
,
,
...
,
2
1
1
= grad f
(czytamy: gradient funkcji f) a różniczka funkcji ma postać:
(
)
n
n
dx
x
f
dx
x
f
dx
x
df
∂
∂
+
+
∂
∂
=
...
,
1
1
.
Tak więc funkcja n zmiennych jest różniczkowalna w punkcie x, jeżeli zachodzi równość:
0
)
,
(
)
,
(
lim
0
=
∆
∆
⋅
−
−
∆
+
∆
+
→
∆
x
x
gradf
y
x
f
y
y
x
x
f
x
Uwaga 7. Ponieważ współrzędne wersora w
ℜ
n
to tzw. cosinusy kierunkowe wektora e
(czyli kosinusy kątów jakie tworzy wektor e z osiami układu współrzędnych), więc:
n
n
x
f
x
f
e
f
α
α
cos
...
cos
1
1
∂
∂
+
+
∂
∂
=
∂
∂
.
Uwaga 8. Z różniczkowalności funkcji f w punkcie x wynika istnienie wszystkich
pochodnych cząstkowych w tym punkcie. Implikacja odwrotna nie jest prawdziwa, bo np.
funkcja f, gdzie
( )
=
=
>
+
+
=
,
0
,
0
,
0
,
,
2
2
4
2
2
y
x
gdy
y
x
gdy
y
x
xy
y
x
f
ma pochodne cząstkowe w punkcie (0,0), ale nie jest różniczkowalna w tym punkcie.
Obliczamy pochodne cząstkowe funkcji f w punkcie (0,0):
0
0
0
)
(
0
lim
)
0
,
0
(
)
0
,
0
(
lim
)
0
,
0
(
4
2
2
0
0
=
∆
−
+
∆
⋅
∆
=
∆
−
∆
+
=
∂
∂
→
∆
→
∆
x
x
x
x
f
x
f
x
f
x
x
,
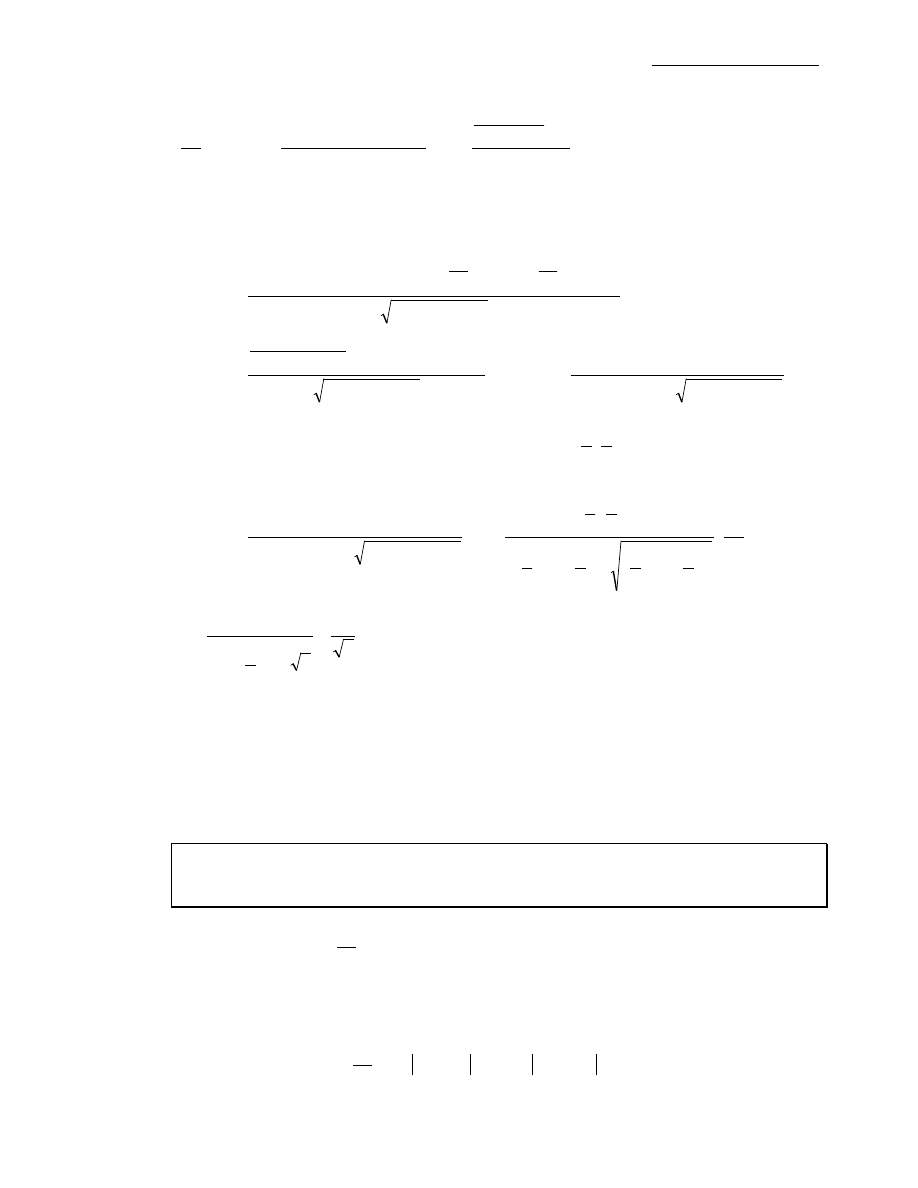
F
UNKCJE WIELU ZMIENNYCH
Strona 11
11
11
11
0
0
)
(
0
)
(
0
lim
)
0
,
0
(
)
,
0
(
lim
)
0
,
0
(
4
2
2
0
0
=
∆
−
∆
+
∆
⋅
=
∆
−
∆
+
=
∂
∂
→
∆
→
∆
y
y
y
y
f
y
y
f
y
f
x
x
.
Zgodnie z definicją funkcji różniczkowalnej, należy wyznaczyć granicę występującą w
uwadze 6:
2
2
)
0
,
0
(
)
,
(
)
(
)
(
)
0
,
0
(
)
0
,
0
(
)
0
,
0
(
)
0
,
0
(
lim
y
x
y
y
f
x
x
f
f
y
x
f
y
x
∆
+
∆
∆
∂
∂
+
∆
∂
∂
−
−
∆
+
∆
+
→
∆
∆
=
[
]
2
2
4
2
2
)
0
,
0
(
)
,
(
2
2
4
2
2
)
0
,
0
(
)
,
(
)
(
)
(
]
)
(
)
[(
)
(
lim
)
(
)
(
0
0
0
)
(
)
(
)
(
lim
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
∆
+
∆
∆
+
∆
∆
∆
=
∆
+
∆
∆
⋅
+
∆
⋅
−
−
∆
+
∆
∆
∆
→
∆
∆
→
∆
∆
.
Granica ta nie może być równa 0, bo dla ciągu
(
)
)
0
,
0
(
1
,
1
,
→
=
∆
∆
∞
→
n
n
n
y
x
mamy:
=
⋅
+
+
=
∆
+
∆
∆
+
∆
∆
∆
∞
→
→
∆
∆
3
3
2
2
4
2
2
2
2
4
2
2
)
0
,
0
(
)
,
(
1
1
1
1
1
1
lim
)
(
)
(
]
)
(
)
[(
)
(
lim
n
n
n
n
n
n
n
n
y
x
y
x
y
x
n
y
x
0
2
1
2
1
1
1
lim
2
≠
=
⋅
+
∞
→
n
n
, czyli funkcja f nie jest różniczkowalna w punkcie (0,0).
Przykład ten pokazuje, że dla funkcji wielu zmiennych nie jest prawdziwe twierdzenie
sformułowane dla funkcji rzeczywistej jednej zmiennej (skrypt I, R4,T1), że
różniczkowalność funkcji jest równoważna istnieniu pochodnej tej funkcji.
Następne twierdzenie określa jak można wzmocnić założenia, aby zagwarantować
różniczkowalność funkcji punkcie, w którym funkcja ma pochodną.
Twierdzenie 2. Jeżeli funkcja f: X→
→
→
→ℜ
ℜ
ℜ
ℜ, X⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
posiada w pewnym otoczeniu punktu x
wszystkie pochodne cząstkowe i pochodne te są ciągłe w tym punkcie, to funkcja ta jest
różniczkowalna w tym punkcie.
Pochodna kierunkowa
e
f
∂
∂
(x)=grad f(x)
⋅e charakteryzuje prędkość zmiany funkcji w punkcie
x w kierunku wektora e.
Oznaczając przez
γ kąt między wersorem e a pochodną gradf mamy:
γ
γ
cos
)
(
cos
)
(
)
(
⋅
=
⋅
=
∂
∂
x
gradf
x
grad
x
e
f
.

R
OZDZIAŁ
I
Strona 12
12
12
12
Wynika stąd, że gdy
γ =0, to:
|gradf(x)|=
[ ]
e
f
∂
∂
−
∈
2
2
,
sup
π
π
γ
,
tak więc gradient funkcji w punkcie wskazuje kierunek największego wzrostu tej funkcji.
Podobnie jak to było dla funkcji jednej zmiennej, wartość funkcji w punkcie możemy
przybliżyć wykorzystując różniczkę tej funkcji w punkcie sąsiednim.
Uwaga 9. Jeżeli funkcja f ma ciągłe pochodne cząstkowe pierwszego rzędu w punkcie x
0
, to:
f(x
0
+
∆x) ≅ f(x
0
) + df(x
0
,
∆x),
przy czym błąd tego przybliżenia dąży szybciej do 0 niż wyrażenie |
∆x|.
Przykład 4.
Obliczyć f
′(x,y), jeżeli f(x,y)=x
y
arctg(xy).
Przykład 5.
Wyznaczyć pochodną kierunkową funkcji f w kierunku wektora s = (1,
−2,1)
w punkcie (2,2,1) jeżeli f(x,y,z) = xy
2
lnz.
Przykład 6.
Obliczyć przybliżoną wartość: (1.03)
2.06
.

F
UNKCJE WIELU ZMIENNYCH
Strona 13
13
13
13
Pochodne wyższych rzędów
Pochodną rzędu drugiego możemy zapisać w postaci macierzy:
∈
∂
∂
∂
=
′′
}
,...,
1
{
,
,
)
(
2
n
j
i
x
x
f
x
f
i
j
- macierz Hessego.
Pochodne cząstkowe wyższych rzędów oznaczamy następująco:
n
k
n
k
k
m
x
x
x
f
∂
∂
∂
∂
...
2
1
2
1
, gdzie m=
∑
=
n
j
j
k
1
, k
j
∈{0,1,...,n}.
Przykład 7.
Wyznaczyć pochodne cząstkowe do rzędu trzeciego włącznie funkcji f, gdzie
f(x,y)=y
2
sin3x + x
2
y. Zapisać pierwszą i drugą pochodną funkcji f.

R
OZDZIAŁ
I
Strona 14
14
14
14
Twierdzenie 3 (Schwarza).
Jeżeli funkcja f: X→
→
→
→ℜ
ℜ
ℜ
ℜ, X⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
ma pochodne mieszane rzędu k i są one ciągłe
w punkcie a
∈
∈
∈
∈X, to te, które różnią się tylko kolejnością różniczkowań, są równe w tym
punkcie.
Różniczkę rzędu drugiego określamy jako różniczkę pierwszej różniczki: d
2
f :=d(df).
Ogólnie:
d
n
f :=d(d
n
−1
f).
Dla funkcji dwóch zmiennych f(x,y) mamy:
d
2
f = ....= f
xx
dx
2
+2f
xy
dxdy+f
yy
dy
2
.
Ogólnie:
d
n
f =
k
k
n
k
k
n
n
n
k
dy
dx
y
x
f
d
k
n
−
−
=
∂
∂
∑
1
, dy
k
:=(dy)
k
.

F
UNKCJE WIELU ZMIENNYCH
Strona 15
15
15
15
Ć
wiczenia
1. Wyznaczyć dziedzinę funkcji f (dla funkcji dwóch zmiennych narysować
dziedzinę), jeżeli:
a)
(
)
2
y
4x
4
ln
y)
f(x,
−
+
=
,
b)
x
1
-
y
arcsin
y)
f(x,
=
,
c)
y
x
−
=
y)
f(x,
,
d)
(
)
[
]
x
-
y
xln
ln
y)
f(x,
=
,
e)
4
x
-
1
z)
y,
f(x,
2
2
2
2
2
2
−
+
+
−
−
=
z
y
x
z
y
.
2. Wyznaczyć granicę funkcji f w punkcie P, jeżeli:
a)
P(0,0)
,
y
x
x
y)
f(x,
+
=
,
b)
P(0,0)
,
xy
1
)sin
y
(
y)
f(x,
2
2
+
= x
,
c)
P(0,0)
,
y
x
y
-
x
y)
f(x,
2
2
+
=
, d)
(
)
P(0,0)
,
1
y)
f(x,
2
2
x
1
2
2
y
y
x
+
+
=
,
e)
P(0,2)
,
)
2
(
1
1
)
2
(
y)
f(x,
2
2
2
2
−
+
−
+
−
+
=
y
x
y
x
,
f)
P(0,3)
,
2x
)
sin(x
y)
f(x,
3
2
3
y
=
,
g)
P(1,1)
,
y
x
x
y)
f(x,
4
4
−
−
=
y
.
3. Wykaza
ć
,
ż
e funkcja f ma obydwie równe granice iterowane, gdy x
→0 i y→0, ale
granica tej funkcji w punkcie P(0,0) nie istnieje, je
ż
eli
.
y)
(
x
x
y)
f(x,
2
2
2
2
2
−
+
=
x
y
y
4. Wyznaczy
ć
pochodne cz
ą
stkowe I rz
ę
du funkcji f, je
ż
eli:
a)
,
y
x
x
y)
f(x,
+
=
b)
,
xy
(sinx)
y)
f(x,
=
c)
zcosy
(xz)
z)
y,
f(x,
=
.
5. Sprawdzi
ć
, czy dana funkcja spełnia podane równanie:
a)
y)
f(x,
xy
f
y
f
x
,
xe
xy
y)
f(x,
y
x
x
y
+
=
′
+
′
+
=
,
b)
(
)
2
1
s
u
s
t
u
t
,
s
t
ln
s)
u(t,
=
∂
∂
+
∂
∂
+
=
.
6. Wyznaczy
ć
f
′ (grad f), je
ż
eli:
a)
4
2
y)
f(x,
xy
=
, b)
)
z
arctg(x
z
y
y
x
z)
y,
f(x,
2
3
3
4
3
2
+
+
=
, c)
3
4
3
2
z)
y,
f(x,
z
y
x
+
+
=
.
7. Zbada
ć
ró
ż
niczkowalno
ść
funkcji f w punkcie P, je
ż
eli:
a)
P(0,0)
,
y)
f(x,
xy
=
; b)
)
P(0,0,
tgz,
y)
f(x,
4
2
π
xy
=
.
8. Wyznaczy
ć
ró
ż
niczk
ę
zupełn
ą
funkcji f, je
ż
eli:
a)
,
y
x
tg
ln
y)
f(x,
=
b)
,
y
x
xy
arcsin
y)
f(x,
−
=
c)
,
z)
y,
f(x,
2
2
2
z
y
x
+
+
=
9. Wykorzystuj
ą
c przybli
ż
enie:
∆f≅df, obliczy
ć
warto
ść
przybli
ż
on
ą
:
a )
01
.
2
003
.
1
, b)
,
03
.
2
98
.
1
97
.
0
2
2
2
+
+
c)
.
3.97
arctg1.02

R
OZDZIAŁ
I
Strona 16
16
16
16
10. Wyznaczy
ć
pochodne kierunkowe funkcji f w punkcie P w kierunku wektora e,
je
ż
eli:
a)
]
1
,
2
[
),
2
,
1
(
,
y
x
ln
y)
f(x,
=
=
e
P
, b)
],
12
,
5
[
),
4
,
3
(
,
y)
f(x,
2
2
=
+
=
e
P
y
x
c)
].
2
,
2
,
1
[
),
2
,
2
,
1
(
,
3
z)
y,
f(x,
3
4
3
2
−
=
+
+
=
e
P
z
y
x
11. Obliczy
ć
pochodne cz
ą
stkowe funkcji f do rz
ę
du trzeciego wł
ą
cznie i porówna
ć
pochodne mieszane,
je
ż
eli
xy
e
=
y)
f(x,
.
12. Wyznaczy
ć
f
′′, je
ż
eli funkcja f dana jest wzorem:
sinxy
y)
f(x,
a)
=
,
2
2
z
e
y
x
z)
y,
f(x,
b)
=
,
xz
y
arctg
z)
y,
f(x,
c)
=
.
13. Wykaza
ć
,
ż
e funkcja u spełnia dane równanie:
a)
Laplace'
równanie
0,
u
u
,
y
x
y
y)
u(x,
a)
yy
xx
2
2
(
=
′′
+
′′
+
=
,
t
-
x
u
u
,
t
-
xt
y)
u(x,
b)
xx
tt
3
6
1
2
=
′′
−
′′
+
+
=
2
1
5
2
xt
x
.
14. Wyznaczy
ć
wskazan
ą
ró
ż
niczk
ę
funkcji f, je
ż
eli:
=
+
+
=
f
d
),
y
xy
ln(x
y)
f(x,
a)
2
2
2
,
=
+
+
=
f
d
,
x
z)
y,
f(x,
b)
2
2
2
2
z
y
=
=
f
d
,
e
y
y)
f(x,
c)
4
3x
2
(wykorzysta
ć
wzór podany na wykładzie).

II
Różniczkowanie funkcji
złożonej
R
OZDZIAŁ
II
Strona 18
18
18
18
Zdefiniujemy teraz funkcje zło
ż
one i sformułujemy twierdzenia o ró
ż
niczkowaniu tych
funkcji.
Niech f: X
→ℜ, X⊂ℜ
n
, u=f (x
1
, ... ,x
n
) i niech g
i
: [a,b]
→ℜ (i=1, ... ,n).Je
ż
eli dla ka
ż
dego
t
∈[a,b] punkt (g
1
(t), ... ,g
n
(t))
∈X,to funkcj
ę
u=f [g
1
(t), ... ,g
n
(t)] nazywamy
funkcją złożoną
zmiennej t okre
ś
lon
ą
w przedziale [a,b].
Twierdzenie 1
Jeżeli funkcja f: X
→
→
→
→ℜ
ℜ
ℜ
ℜ
jest różniczkowalna w obszarze X
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
a funkcje g
i
: (a,b)
→
→
→
→ℜ
ℜ
ℜ
ℜ
(i=1, ... ,n) mają pochodne w przedziale (a,b),to funkcja złożona zmiennej t ma pochodną
w każdym punkcie przedziału (a,b) i:
,
dt
dg
x
f
...
dt
dg
x
f
dt
dg
x
f
dt
df
n
n
2
2
1
1
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
====
lub krócej:
∑
∑
∑
∑
====
∂∂∂∂
∂∂∂∂
====
n
i
i
i
dt
dg
x
f
dt
df
1
.
Przykład 1.
Wyznaczy
ć
dt
df
, gdzie f(x,y,z) = x
(yz)
, je
ż
eli x=cos3t, y=sint
3
, z=arctgt
2
.

R
ÓśNICZKOWANIE FUNKCJI ZŁOśONEJ
Strona 19
19
19
19
Zakładamy teraz,
ż
e x
1
, x
2
, ... , x
n
s
ą
funkcjami k zmiennych t
1
, t
2
, ... ,t
k
, czyli:
x
1
= g
1
(t
1
, ... ,t
k
),
x
2
= g
2
(t
1
, ... ,t
k
),
........................
x
n
= g
n
(t
1
, ... ,t
k
).
Je
ż
eli dla ka
ż
dego (t
1
, ... ,t
k
)
∈T⊂ℜ
k
punkt (g
1
(t
1
, ... ,t
k
), ... , g
n
(t
1
, ... ,t
k
))
∈X, to funkcj
ę
u=f [g
1
(t
1
, ... ,t
k
), ... , g
n
(t
1
, ... ,t
k
)]
nazywamy
funkcją złożoną zmiennych t
1
, ... ,t
k
okre
ś
lon
ą
na T.
Twierdzenie 2.
Jeżeli funkcja f: X
→
→
→
→ℜ
ℜ
ℜ
ℜ
jest różniczkowalna w obszarze X
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
a funkcje
g
i
: T
→
→
→
→ℜ
ℜ
ℜ
ℜ
, T
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
k
, (i=1, ... ,n) mają pochodne względem zmiennych t
1
, ... ,t
k
,
to funkcja złożona zmiennych t
1
, ... ,t
k
ma w obszarze T pochodne cząstkowe względem
tych zmiennych, które wyrażają się wzorami:
1
n
n
1
2
2
1
1
1
1
t
g
x
f
...
t
g
x
f
t
g
x
f
t
f
∂
∂
∂
∂
+
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
,
2
n
n
2
2
2
2
1
1
2
t
g
x
f
...
t
g
x
f
t
g
x
f
t
f
∂
∂
∂
∂
+
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
,
.........................................................
k
n
n
k
2
2
k
1
1
k
t
g
x
f
...
t
g
x
f
t
g
x
f
t
f
∂
∂
∂
∂
+
+
∂
∂
∂
∂
+
∂
∂
∂
∂
=
∂
∂
.
Uwaga 1.
Je
ś
li k=1, to mamy tez
ę
twierdzenia 1.
Macierz pochodnych przekształcenia g=(g
1
,...,g
n
):
(t
1
, ... ,t
k
)
→
g
(g
1
(t
1
, ... ,t
k
), ... , g
n
(t
1
, ... ,t
k
)):
J
g
=
∂
∂
∂
∂
∂
∂
∂
∂
k
n
n
k
t
g
t
g
t
g
t
g
...
...
...
...
...
1
1
1
1
nazywamy
macierzą Jacobiego
.

R
OZDZIAŁ
II
Strona 20
20
20
20
Uwaga 2.
Tez
ę
twierdzenia 2 mo
ż
emy krótko zapisa
ć
:
grad f(t
1
, ... ,t
k
) = grad f(x
1
, ... ,x
n
)
g(t)
⋅J
g
.
Przykład 2.
Wyznaczy
ć
:
2
t
f
∂
∂
oraz J
g
, je
ż
eli: g(t
1
,t
2
) = (t
1
+t
2
, t
2
1
t
e
,
2
1
3
2
t
t
e
+
), f(x,y,z)=e
x
yz
2
. Zapisa
ć
grad
f(t
1
,t
2
) w postaci podanej w uwadze 2.
Uwaga 3.
Je
ś
li n=k, to funkcja wektorowa g=(g
1
,...,g
n
) przekształca przestrze
ń
ℜ
n
w siebie:
x
1
= g
1
(t
1
, ... ,t
n
),
x
2
= g
2
(t
1
, ... ,t
n
),
........................
x
n
= g
n
(t
1
, ... ,t
n
).
Układ ten mo
ż
na interpretowa
ć
jako przej
ś
cie od zmiennych t
1
, ... ,t
n
do zmiennych x
1
, ... ,x
n
,
czyli przej
ś
cie od jednego krzywoliniowego układu współrz
ę
dnych do drugiego.
Przykład 3.
Układ równa
ń
:
=
=
,
sin
,
cos
ϕ
ϕ
r
y
r
x
r∈(0,+∞), ϕ∈[0,2π) okre
ś
la w przestrzeni ℜ
2
przej
ś
cie od
współrzędnych biegunowych
(r,ϕ) do współrz
ę
dnych kartezja
ń
skich (x,y).
Dla unikni
ę
cia niejednoznaczno
ś
ci przyjmuje si
ę
,
ż
e współrz
ę
dne bieguna s
ą
równe (0,0).

R
ÓśNICZKOWANIE FUNKCJI ZŁOśONEJ
Strona 21
21
21
21
Jakobian tego odwzorowania biegunowego ma posta
ć
:
J(r,
ϕ) =
ϕ
ϕ
∂
∂
∂
∂
∂
∂
∂
∂
y
r
y
x
r
x
=
ϕ
ϕ
ϕ
ϕ
cos
sin
sin
cos
r
r
−
= r.
Je
ż
eli
1
)
,
(
>
ϕ
r
J
, to odwzorowanie jest rozciągające, jeśli
1
)
,
(
<
ϕ
r
J
, to – ściągające.
Przykład 4.
Współrzędne walcowe:
=
=
=
,
,
sin
,
cos
z
z
r
y
r
x
ϕ
ϕ
Jakobian J(r,ϕ,z)=r.
Przykład 5.
Współrzędne sferyczne (A)
=
=
=
,
cos
,
sin
sin
,
cos
sin
θ
ϕ
θ
ϕ
θ
r
z
r
x
r
x
],
,
0
[
),
2
,
0
[
),
,
0
[
π
θ
π
ϕ
∈
∈
+∞
∈
r
J(r,
θ,ϕ)=r
2
sin
θ.
Współrzędne sferyczne (B)
=
=
=
,
sin
,
sin
cos
,
cos
cos
θ
ϕ
θ
ϕ
θ
r
z
r
x
r
x
],
,
[
),
2
,
0
[
),
,
0
[
2
2
π
π
θ
π
ϕ
−
∈
∈
+∞
∈
r
J(r,θ,ϕ)=r
2
cosθ.
R
OZDZIAŁ
II
Strona 22
22
22
22
Ekstrema funkcji dwóch zmiennych
Twierdzenie 3 (Taylora).
Jeżeli funkcja f: X→
→
→
→ℜ
ℜ
ℜ
ℜ, X⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
jest klasy C
k
w obszarze X zawierającym odcinek I
łączący punkty a oraz x, to:
(((( )))) (((( ))))
(((( ))))
(((( ))))
k!
ξ
f
d
1)!
(k
f(a)
d
...
2!
f(a)
d
a
df
a
f
x
f
:
I
ξ
k
1
k
2
o
++++
−−−−
++++
++++
++++
++++
====
∈
∈
∈
∈
∃∃∃∃
−−−−
.
Uwaga 4. Dla n=2 i k=3 tezę twierdzenia można zapisać w postaci ( ( x:=(x,y), a=(a
1
,a
2
) ):
f(x,y) = f(a
1
,a
2
)+f
x
′(a
1
,a
2
)
⋅(x-a
1
)+ f
y
′(a
1
,a
2
)
⋅(y-a
2
)+
+
−
⋅
′′
+
−
⋅
′′
+
−
⋅
−
⋅
′′
+
−
⋅
′′
+
]
)
a
(y
)
a
,
(a
f
)
a
(y
)
a
,
(a
f
)
a
(y
)
a
(x
)
a
,
(a
f
2
)
a
(x
)
a
,
(a
f
[
2!
1
2
2
2
1
yy
2
2
2
1
yy
2
1
2
1
xy
2
1
2
1
xx
( )
ξ
f
d
3!
1
3
+
.
Przykład 6.
Napisać wzór Taylora z drugą resztą dla funkcji:
x
xz
e
z
y
x
f
z
y
x
+
+
=
−
+
2
)
,
,
(
w punkcie
(1,0,2)

R
ÓśNICZKOWANIE FUNKCJI ZŁOśONEJ
Strona 23
23
23
23
Twierdzenie 4 (warunek konieczny istnienia ekstremum).
Jeżeli funkcja f : X→
→
→
→ℜ
ℜ
ℜ
ℜ, X⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
jest różniczkowalna w punkcie a∈
∈
∈
∈X
0
i w punkcie tym ma
ekstremum lokalne, to f
′′′′(a)=0 (
0
(a)
f
1
x
=
′
, ... ,
0
(a)
f
n
x
=
′
).
Twierdzenie 5 (warunek wystarczający istnienia ekstremum)
Jeżeli funkcja f : X→
→
→
→ℜ
ℜ
ℜ
ℜ, X⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
n
jest klasy C
2
w otoczeniu U punktu a i f
′′′′(a)=0 oraz dla
każdego a+∆
∆∆
∆a∈
∈
∈
∈U: d
2
f(a,
∆
∆∆
∆a)≠≠≠≠0, to prawdziwe są implikacje:
d
2
f(a,
∆
∆∆
∆a)>0 ⇒
⇒
⇒
⇒ f(a) =
f(x)
min
U
;
d
2
f(a,∆a)<0 ⇒ f(a) =
f(x)
max
U
.
Twierdzenie 6 (warunek wystarczający istnienia ekstremum dla funkcji dwóch
zmiennych).
Jeżeli w pewnym otoczeniu U punktu (x
0
,y
0
) funkcja f: U
→
→
→
→ℜ
ℜ
ℜ
ℜ, U⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
2
spełnia warunki:
1
0
. f
∈
∈
∈
∈C
2
(U);
2
0
.
0;
)
y
,
(x
f
)
y
,
(x
f
0
0
y
0
0
x
====
′′′′
====
′′′′
3
0
. det f
′′′′′′′′(x
0
,y
0
)=
)
y
,
(x
f
0
0
xx
′′
⋅⋅⋅⋅
)
y
,
(x
f
0
0
yy
′′
−−−−(
)
y
,
(x
f
0
0
xy
′′
)
2
> 0,
to funkcja f ma ekstremum w punkcie (x
0
,y
0
), przy czym:
)
y
,
(x
f
0
0
xx
′′
> 0 ⇒
⇒
⇒
⇒ f(x
0
,y
0
)=
y)
f(x,
min
U
;
)
y
,
(x
f
0
0
xx
′′
< 0 ⇒
⇒
⇒
⇒ f(x
0
,y
0
)=
y)
f(x,
max
U
.
Jeżeli det f ′
′′′′′′′(x
0
,y
0
) < 0, to funkcja f nie ma ekstremum.
Dowód.
Wykażemy, że
0
)
(P
f
0
''
xx
≠≠≠≠ .
Do dowodu wykorzystamy wzór Taylora z drugą resztą: (przyjmiemy oznaczenia: P(x,y),
P
0
(x
0
,y
0
), Q(
ξ,η) jest punktem leżącym na odcinku łączącym punkty P i P
0
,
∆x=x – x
0
,
∆y = y – y
0
, ).

R
OZDZIAŁ
II
Strona 24
24
24
24
Ponieważ
0
)
(P
f
0
''
xx
≠ , więc z twierdzenia o zachowaniu znaku przez funkcję ciągłą mamy
także:
0
(Q)
f
''
xx
≠ i wykorzystując założenie 2. przyrost funkcji f: f(P) – f(P
0
) możemy napisać
następująco:
Wykażemy teraz, że jeżeli det f
′′(x
0
,y
0
) < 0, to f nie ma ekstremum w punkcie P
0
.

R
ÓśNICZKOWANIE FUNKCJI ZŁOśONEJ
Strona 25
25
25
25
Uwaga 5. Jeżeli det f
′′(x
0
,y
0
)=0, to f może mieć ekstremum lub nie, np. funkcja
f(x,y) = x
3
− y
3
nie ma ekstremum w punkcie (0,0), a funkcja f(x,y) = x
4
+ y
4
ma minimum
w punkcie (0,0).
Dla obu tych funkcji mamy: det f
′′(0,0)=0.
Przykład 7.
Wyznaczyć ekstrema lokalne funkcji f, gdzie f(x,y) = sinx + siny + sin(x+y),
2
2
,
0
∈
∈
∈
∈
ππππ
x
.

R
OZDZIAŁ
II
Strona 26
26
26
26
Ć
wiczenia
1. Korzystając z twierdzenia o różniczkowaniu funkcji złożonej jednej zmiennej,
obliczyć pochodną F
′(t), jeżeli:
2
2
sint
y
,
cost
x
y),
f(x,
F
a)
=
=
=
,
2
t
2
t
z
arcsint,
y
,
e
x
cosz,
xy
z)
y,
F(x,
b)
=
=
=
=
.
2. Obliczyć
dt
df
, jeżeli
t
costsin
)
t
(sin
f(t)
=
, stosując pochodną funkcji złożonej
jednej zmiennej.
3. Przyjmując: x=r(t)cost, y=r(t)sint wykazać, że zachodzi równość:
r
r
y
y
x
y
y
x
′
=
−
′
′
+
;
wykorzystując tę równość rozwiązać równanie różniczkowe zwyczajne:
1
=
−
′
′
+
y
y
x
y
y
x
.
4. Korzystając z twierdzenia o różniczkowaniu funkcji złożonej wielu zmiennych,
obliczyć:
2
2
2
2
2
v
f
,
v
u
f
,
u
f
2.),
uwaga
(patrz
v)
radf(u,
g
∂
∂
∂
∂
∂
∂
∂
, jeżeli:
ucosv,
y
usinv,
x
gdzie
,
x
y)
f(x,
a)
y
=
=
=
sin(uv)
z
uv,
y
,
v
u
x
gdzie
,
z
xy
y)
f(x,
b)
2
2
3
2
=
=
+
=
=
.
5. Obliczyć
st
z
,
t
s
y
,
e
x
,
z
y
x
arcsin
z)
y,
f(x,
gdy
,
t
f
,
s
f
2
2
st
=
+
=
=
+
=
∂
∂
∂
∂
.
6.
cosθ
r
z
2
=
, gdzie r i θ są współrzędnymi
biegunowymi.
.
z
i
z
pomocą
za
z
i
z
Wyrazić
y
x
θ
r
′
′
′
′
7. Wyznaczyć macierz Jacobiego danego przekształcenia:
)
,
2
xy
y
+
=
ℜ
→
ℜ
2
xy
3
2
x
,
(e
y)
f(x,
,
:
f
a)
,
))
ctg(
),
ln(
2
2
xy
ar
z
y
+
+
=
ℜ
→
ℜ
2
2
3
x
(
z)
y,
f(x,
,
:
f
b)
.
8. Wyznaczyć jacobian przekształcenia F, jeżeli:
)
u
uw,
(uv,
w)
v,
(u,
:
F
a)
2
2
2
w
v
+
+
→
,
ψ
=
ϕ
ψ
=
ϕ
ψ
=
sin
,
cos
cos
,
sin
cos
:
r
z
r
y
r
x
F
b)
,
3
2
3
2
,
:
b)
v
u
y
uv
x
F
=
=
.
9. Wykazać, że funkcja z=f(ax+y)+g(ax−y) (f∈C
2
(ℜ)) spełnia równanie różniczkowe
cząstkowe:
.
0
2
2
2
2
2
=
∂
∂
−
∂
∂
y
z
a
x
z
10. Sprawdzić równość używając współrzędnych biegunowych:
,
rcos
y
,
rsin
x
ϕ
ϕ
=
=
2
2
∂
∂
+
∂
∂
=
ϕ
∂
∂
+
∂
∂
y
u
x
u
u
r
1
r
u
2
2
2
.
11. Napisać wzór Taylora z n-tą resztą dla danej funkcji f i danego punktu P, jeżeli:
4
),
1
,
1
(
)
,
(
,
)
,
(
a)
0
0
=
=
=
+
n
y
x
e
y
x
f
y
x
,
3
),
0
,
0
(
)
,
(
,
sin
)
,
(
b)
0
0
=
=
=
n
y
x
y
e
y
x
f
x
,
3
),
,
2
(
)
,
(
,
2
cos
)
,
(
c)
0
0
=
=
+
=
n
y
x
y
xy
y
x
f
π
.

R
ÓśNICZKOWANIE FUNKCJI ZŁOśONEJ
Strona 27
27
27
27
12. Wyznaczyć ekstrema funkcji f dwóch zmiennych, jeżeli:
xy
xy
3
x
y)
f(x,
a)
2
3
+
+
=
,
5
3
3
x
3
y)
f(x,
b)
2
2
3
2
+
−
−
+
=
y
x
y
y
,
xy
y
x
6
3
2x
-
6
y)
f(x,
c)
2
3
2
+
+
=
,
6
2
x
y)
f(x,
d)
3
3
+
−
−
=
xy
y
,
2
2
)
y
3
(
y)
f(x,
e)
3
y
x
e
x
−
−
+
=
,
y
x
xy
8
1 +
+
=
y)
f(x,
f)
.
13. Wyznaczyć największą i najmniejszą wartość funkcji f na zbiorze D, jeżeli:
2
:
,
x
y)
f(x,
a)
2
2
≤
+
+
=
y
x
D
y
,
9
y
x
:
D
,
y
x
y)
f(x,
b)
2
2
4
4
≤
+
+
=
,
4y,
8x
y
x
y)
f(x,
a)
2
−
−
=
D jest trójkątem o wierzchołkach: A(0,0), B(4,0),
C(0,4).

R
OZDZIAŁ
II
Strona 28
28
28
28

III
Funkcje uwikłane
R
OZDZIAŁ
III
Strona 30
30
30
30
Niech F będzie funkcją rzeczywistą określoną na ustalonym podzbiorze przestrzeni
ℜ
n+1
=ℜ
n
×ℜ.
Równanie F(x,u)=0 (
⇔F(x
1
,...x
n
,u)=0), gdzie x
∈ℜ
n
, u
∈ℜ, określa w przestrzeni ℜ
n+1
pewien podzbiór Q
⊂ℜ
n+1
. Zbiór Q jest relacją (n+1) - argumentową, przy czym niepustą,
jeżeli istnieje taki punkt (x
0
,u
0
), że F(x
0
,u
0
)=0.
Jeżeli w relacji Q
⊂ℜ
n+1
jest zawarty zbiór f będący funkcją określoną na zbiorze X
⊂ℜ
n
,
to f nazywamy funkcją uwikłaną n zmiennych określoną równaniem F(x,u)=0.
Inaczej: jeżeli istnieje taka funkcja f: X
→ℜ
, X
⊂ℜ
n
, że F(x
1
, ... ,x
n
, f(x
1
, ... ,x
n
))
≡
0 w X,
to funkcję f nazywamy funkcją uwikłaną.
Przykład 1.
Dla n=1 równanie F(x,y)=0 może określać funkcje uwikłaną jednej zmiennej.
Równanie: x
2
+y
2
+1=0 określa relacje pustą.
Równanie: x
2
+y
2
−1=0 określa różne funkcje uwikłane dla x∈[ - 1, 1], np.:
f
1
(x) =
2
1
x
−
−
, f
2
(x) =
2
1
x
−
+
, f
3
(x) =
∈
−
+
−
∈
−
−
].
,
[
,
),
,
[
,
1
0
1
0
1
1
2
2
x
dla
x
x
dla
x
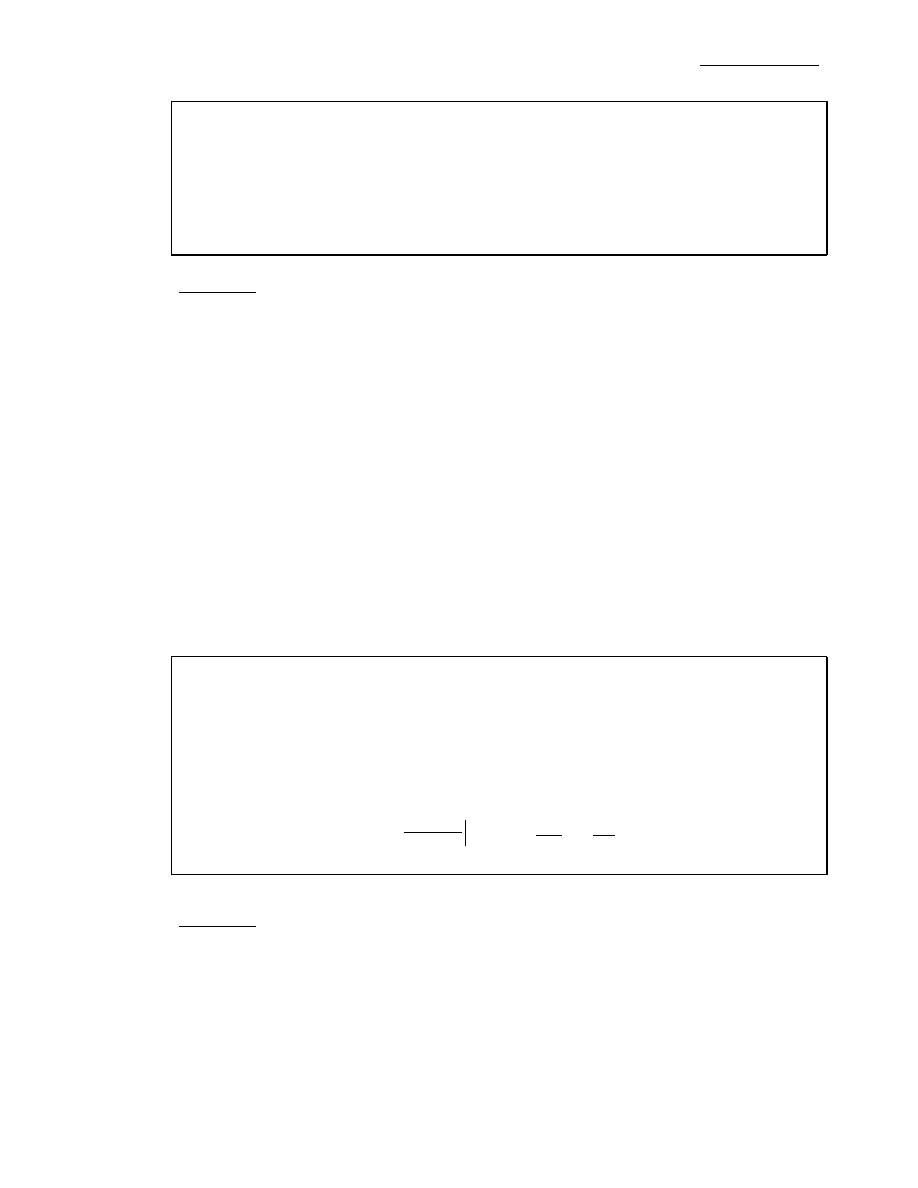
F
UNKCJE UWIKŁANE
Strona 31
31
31
31
Twierdzenie 1 (o istnieniu funkcji uwikłanej).Jeżeli funkcja F jest ciągła w otoczeniu
punktu (x
0
,u
0
)
∈
∈
∈
∈ℜ
ℜ
ℜ
ℜ
n+1
i ma w tym otoczeniu ciągłą pochodną F
u
′′′′
, przy czym F(x
0
,u
0
)=0 i
F
u
′′′′
(x
0
,u
0
)
≠≠≠≠
0, to istnieje takie otoczenie U
0
punktu (x
0
,u
0
), w którym równanie F(x,u)=0
posiada tylko jedno rozwiązanie u=f(x) będące funkcją ciągłą w pewnym otoczeniu
punktu x
0
, przy czym f(x
0
)=u
0
.
Przykład 2.
Omówić istnienie funkcji uwikłanej dwóch zmiennych: x
2
+y
2
+z
2
−1=0.
Twierdzenie 2 (o pochodnej funkcji uwikłanej).
Jeżeli funkcja F jest w otoczeniu punktu (x
0
,u
0
)
∈
∈
∈
∈ℜ
ℜ
ℜ
ℜ
n+1
funkcją klasy C
1
,
przy czym F(x
0
,u
0
)=0 i F
u
′′′′
(x
0
,u
0
)
≠≠≠≠
0, to funkcja uwikłana u=f(x) określona równaniem
F(x,u)=0 jest
w pewnym otoczeniu U punktu x
0
funkcją klasy C
1
i:
∀
∀
∀
∀
x
∈
∈
∈
∈
U:
f(x)
u
u
x
u)
(x,
F
u)
(x,
F
(x)
f
=
′
′
−
=
′
=
′
′
−
=
∂
∂
⇔
n
1,2,...,
i
,
F
F
x
f
u
x
i
i
.
Przykład 3.
Wyznaczyć pochodną funkcji uwikłanej określonej równaniem: xyz+lnxy+e
yz
=0.

R
OZDZIAŁ
III
Strona 32
32
32
32
Przypadek szczególny – funkcja uwikłana jednej zmiennej:
F(x,y(x))=0
Traktując lewą stronę równości jako funkcję jednej zmiennej x i stosując twierdzenie
o różniczkowaniu funkcji złożonej jednej zmiennej otrzymamy:
0
====
⋅⋅⋅⋅
∂∂∂∂
∂∂∂∂
++++
⋅⋅⋅⋅
∂∂∂∂
∂∂∂∂
dx
dy
y
F
dx
dx
x
F
, czyli
)
,
(
)
,
(
)
(
y
x
F
y
x
F
x
y
y
x
′′′′
′′′′
−−−−
====
′′′′
.
Różniczkując powyższą równość stronami po zmiennej x, otrzymamy wzór na drugą
pochodną
funkcji uwikłanej jednej zmiennej:
3
2
2
)
(
)
(
2
)
(
)
(
y
x
yy
y
x
xy
y
xx
F
F
F
F
F
F
F
F
x
y
′′′′
′′′′
⋅⋅⋅⋅
′′′′′′′′
++++
′′′′
⋅⋅⋅⋅
′′′′
⋅⋅⋅⋅
′′′′′′′′
−−−−
′′′′
⋅⋅⋅⋅
′′′′′′′′
−−−−
====
′′′′′′′′
.
Wykorzystując wzór na pierwszą pochodną funkcji uwikłanej oraz twierdzenie Fermata
(warunek konieczny istnienia ekstremum) możemy podać warunki, na podstawie których
możemy wyznaczyć punkty stacjonarne:
≠≠≠≠
′′′′
====
′′′′
====
.
0
)
,
(
,
0
)
,
(
,
0
)
,
(
y
x
F
y
x
F
y
x
F
y
x
Dla funkcji klasy C
2
, stosując wzór na drugą pochodną, możemy sformułować warunek
wystarczający istnienia ekstremum:
Jeżeli w punkcie stacjonarnym (x
0
,y
0
) mamy:
(
)
0
y
,
x
F
0
0
xx
≠
′′
to funkcja uwikłana y(x)
ma ekstremum lokalne w punkcie x
0
, przy czym zachodzą następujące implikacje:
y(x).
min
)
y(x
0
)
y
,
(x
F
)
y
,
(x
F
y(x);
max
)
y(x
0
)
y
,
(x
F
)
y
,
(x
F
U
0
0
0
y
0
0
xx
U
0
0
0
y
0
0
xx
=
⇒
<
′
′′
=
⇒
>
′
′′
Przykład 4.
Wyznaczyć ekstrema lokalne funkcji uwikłanej danej równaniem: (x
2
+ y
2
)
2
– 4(x
2
– y
2
) = 0.
F
UNKCJE UWIKŁANE
Strona 33
33
33
33
Przykład 5.
Wyznaczyć równanie stycznej w punkcie (x
0
,y
0
) do hiperboli o równaniu:
.
1
2
2
2
2
=
−
b
y
a
x
Płat regularny i płaszczyzna styczna
Sposoby przedstawiania powierzchni S:
(a)
postać jawna: z=f(x,y), (x,y)∈
∈
∈
∈D,
np.: paraboloida hiperboliczna: z =
x
2
−
y
2
.
(b)
postać uwikłana: F(x,y,z) = 0 lub F(x,y,z(x,y)) = 0,
np.: stożek: x
2
+ y
2
= z
2
.
(c)
postać parametryczna:
=
=
=
),
,
(
),
,
(
),
,
(
3
2
1
τ
σ
τ
σ
τ
σ
h
z
h
y
h
x
(
σ
σσ
σ,ττττ)∈
∈
∈
∈ΣΣΣΣ××××Τ
ΤΤ
Τ=D,
np.: helikoida:
=
=
=
,
,
sin
,
cos
τ
τ
σ
τ
σ
a
z
y
x
(
⇔
z = a
⋅
arctg
x
y
).

R
OZDZIAŁ
III
Strona 34
34
34
34
Ogólna definicja płata zwykłego S:
Płatem zwykłym nazywamy homeomorficzny obraz obszaru płaskiego D, przy czym brzeg
obszaru
∂
D jest odwzorowany homeomorficznie na brzeg płata S.
Jeżeli funkcje h
i
∈
C
1
(D), (i=1,2,3), to płat zwykły nazywamy płatem gładkim.
Jeżeli ponadto w każdym punkcie obszaru D pochodna funkcji h =(h
1
,h
2
,h
3
) jest różna od
zera (macierz Jakobiego ma rząd 2), to płat gładki nazywamy regularnym.
r(J
g
) = r
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
τ
σ
τ
σ
τ
σ
3
3
2
2
1
1
h
h
h
h
h
h
= 2
⇔
τ
σ
∂
∂
×
∂
∂
h
h
≠
0.
Wektory
τ
σ
∂
∂
∂
∂
h
i
h
są więc niekolinearne, a ponieważ są one styczne do powierzchni,
więc ich iloczyn wektorowy
τ
σ
∂
∂
×
∂
∂
h
h
jest prostopadły do płaszczyzny ściśle stycznej
do powierzchni S.
Używając iloczynu mieszanego wektorów, piszemy równanie płaszczyzny stycznej w postaci:
0
)
(
0
=
∂
∂
∂
∂
−
τ
σ
h
h
p
p
⇔
det
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
∂
−
−
−
τ
τ
τ
σ
σ
σ
3
2
1
3
2
1
0
0
0
h
h
h
h
h
h
z
z
y
y
x
x
= 0.
W przypadku, gdy płat dany jest równaniem jawnym: z = f(x,y),
to uwzględniając przedstawienie parametryczne takiego płata:
====
====
====
),
,
(
,
,
ττττ
σσσσ
ττττ
σσσσ
f
z
y
x
mamy:
σσσσ
ττττ
∂∂∂∂
∂∂∂∂
××××
∂∂∂∂
∂∂∂∂
h
h
=
∂∂∂∂
∂∂∂∂
××××
∂∂∂∂
∂∂∂∂
σσσσ
ττττ
f
f
,
0
,
1
,
1
,
0
=
−−−−
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
1
,
,
ττττ
σσσσ
f
f
−−−−
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
====
1
,
,
y
f
x
f
.
Stąd równanie płaszczyzny stycznej:
0
)
(
)
(
)
(
)
(
)
(
0
0
0
0
0
====
−−−−
−−−−
−−−−
⋅⋅⋅⋅
∂∂∂∂
∂∂∂∂
++++
−−−−
⋅⋅⋅⋅
∂∂∂∂
∂∂∂∂
z
z
y
y
p
y
f
x
x
p
x
f
, ( gdzie p
0
=(x
0
,y
0
,z
0
) )
Jeśli płat jest zadany w postaci uwikłanej: F(x,y,f(x,y))=0, to:
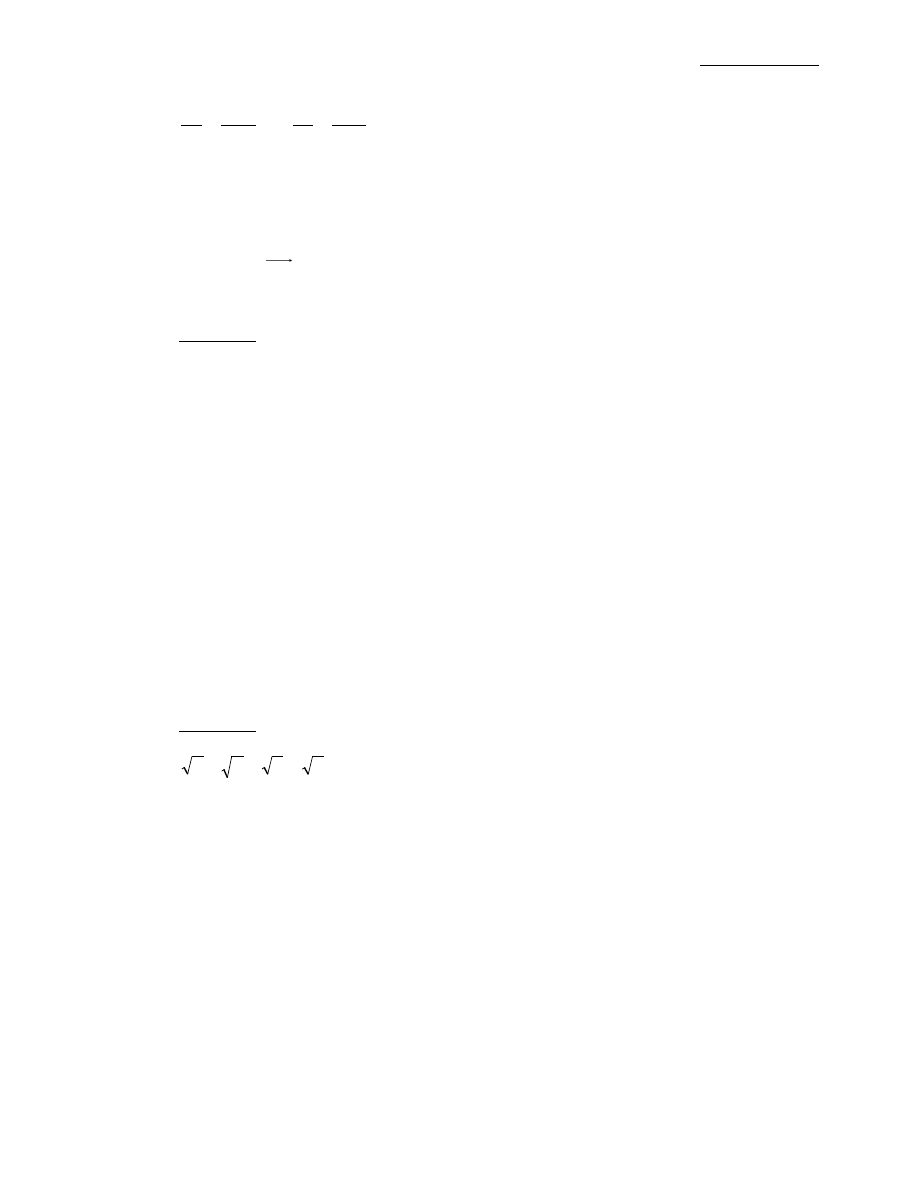
F
UNKCJE UWIKŁANE
Strona 35
35
35
35
z
x
F
F
x
f
′′′′
′′′′
−−−−
====
∂∂∂∂
∂∂∂∂
,
z
y
F
F
y
f
′′′′
′′′′
−−−−
====
∂∂∂∂
∂∂∂∂
,
wtedy równanie płaszczyzny stycznej w punkcie p
0
ma postać:
)
(p
F
0
x
′′′′
(x-x
0
)+
)
(p
F
0
y
′′′′
(y-y
0
)+
)
(p
F
0
z
′′′′
(z-z
0
)=0
( gradF)(p
0
)
⋅ p
p
0
= 0, grad F jest
⊥
do płaszczyzny stycznej).
Przykład 6.
Wykazać, że powierzchnie o równaniach: F(x,y,z)=x + 2y – lnz + 4 = 0,
G(x,y,z)=x
2
– xy – 8x + z + 5 = 0, są styczne do siebie nawzajem w punkcie p
0
(2,
−
3,1).
Napisać równanie prostej normalnej w tym punkcie.
Przykład 7.
Wykazać, że płaszczyzna styczna w dowolnym punkcie powierzchni o równaniu:
,
,
0
>
=
+
+
a
a
z
y
x
odcina na osiach układu współrzędnych odcinki, których
suma długości jest stała.
Ć
wiczenia

R
OZDZIAŁ
III
Strona 36
36
36
36
1. Zbadać istnienie funkcji uwikłanej y = y(x) w otoczeniu punktu P: jeżeli:
P(2,1)
7,
y
xy
x
a)
2
2
=
+
+
,
0
)
cos(
b)
====
xy
x
,
P(1,1)
3,
xy
y
x
c)
5
5
=
+
+
.
2. Wyznaczyć I i II pochodną funkcji uwikłanej jednej zmiennej:
xy
x
y
e
ye
xe
a)
=
+
,
2
2
x
siny
xy
b)
y
+
=
,
x
y
arctg
x
ln
c)
2
2
=
+ y
,
0
x
-
arctgy
y
d)
3
=
+
,
(
)
xy
xy
e
e
−
+
=
+
ln
xy
1
e)
.
3. Wyznaczyć I i II pochodną funkcji uwikłanej dwóch zmiennych:
0,
1
xz
xye
xyz
a)
z
2
=
−
+
+
0
z
xz
2y
3
x
b)
2
2
3
=
+
−
+
.
4. Napisać równanie stycznej do krzywej (danej w postaci uwikłanej) w punkcie P,
jeżeli:
e)
P(0,
,
e
lny
xy
x
a)
x
2
=
+
−
,
P(1,1)
,
y
y
x
x
b)
5
3
3
+
=
+
.
5. Wykazać, że funkcja uwikłana z(x,y) określona równaniem:
),
(
ℜ
∈
=
1
C
F
0,
3z)
-
y
2z,
-
F(x
spełnia równanie:
1
3
2
=
∂
∂
+
∂
∂
y
z
x
z
.
6. Wyznaczyć ekstrema funkcji uwikłanej (jednej lub dwóch zmiennych);
0
2
x
a)
2
4
=
−
+
xy
y
,
0
3
x
b)
3
3
=
−
+
xy
y
,
0
2
4
2
x
c)
2
2
4
4
=
−
+
−
+
y
xy
x
y
,
2
2
4
4
x
d)
y
x
y
+
=
+
,
0
15
3
x
3
e)
3
2
3
=
−
−
+
x
y
y
x
,
0
e
f)
y
x
=
−
+
+
x
y
,
0
2
4
4
x
g)
2
2
2
=
+
+
+
+
+
z
z
xz
y
,
0
1
2
x
h)
2
2
2
=
+
+
+
+
+
z
xz
z
y
.

IV
Elementy teorii pola

R
OZDZIAŁ
IV
Strona 38
38
38
38
Podstawowe pojęcia teorii pola
Oznaczenia:
ϕ
:
ℜ
3
→
ℜ
−
pole skalarne
;
F:
ℜ
3
→
ℜ
3
−
pole wektorowe
, gdzie F=[p(x,y,z),q(x,y,z),r(x,y,z)].
Operatory różniczkowe pierwszego rzędu określamy w układzie ortokartezjańskim
następująco:
operator gradientu:
grad:
ℜ→ℜ
3
,
ϕ
→
grad
ϕ
=
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
z
y
x
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
,
,
;
operator divergencji:
div:
ℜ
3
→ℜ
, F
→
divF =
z
r
y
q
x
p
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
;
operator rotacji:
rot:
ℜ
3
→ℜ
3
, F
→
rotF =
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
y
p
x
q
x
r
z
p
z
q
y
r
,
,
=
r
q
p
z
y
x
k
j
i
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
r
r
r
(
←
zapis
symboliczny).
Te trzy operatory można krócej zapisać za pomocą operatora Hamiltona (operatora nabla):
z
k
y
j
x
i
z
y
x
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
====
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
====
∇
∇
∇
∇
v
r
r
,
,
:
następująco:
grad
ϕ
=
∇ϕ
, divF =
∇⋅
F, rotF =
∇×
F.
Uwaga 1.
Jeżeli pole skalarne
ϕ∈
C
2
(V), V
⊂ℜ
3
, to określone jest wyrażenie:
div(grad
ϕ
)=
2
2
2
2
2
2
z
y
x
∂
∂
+
∂
∂
+
∂
∂
ϕ
ϕ
ϕ
.
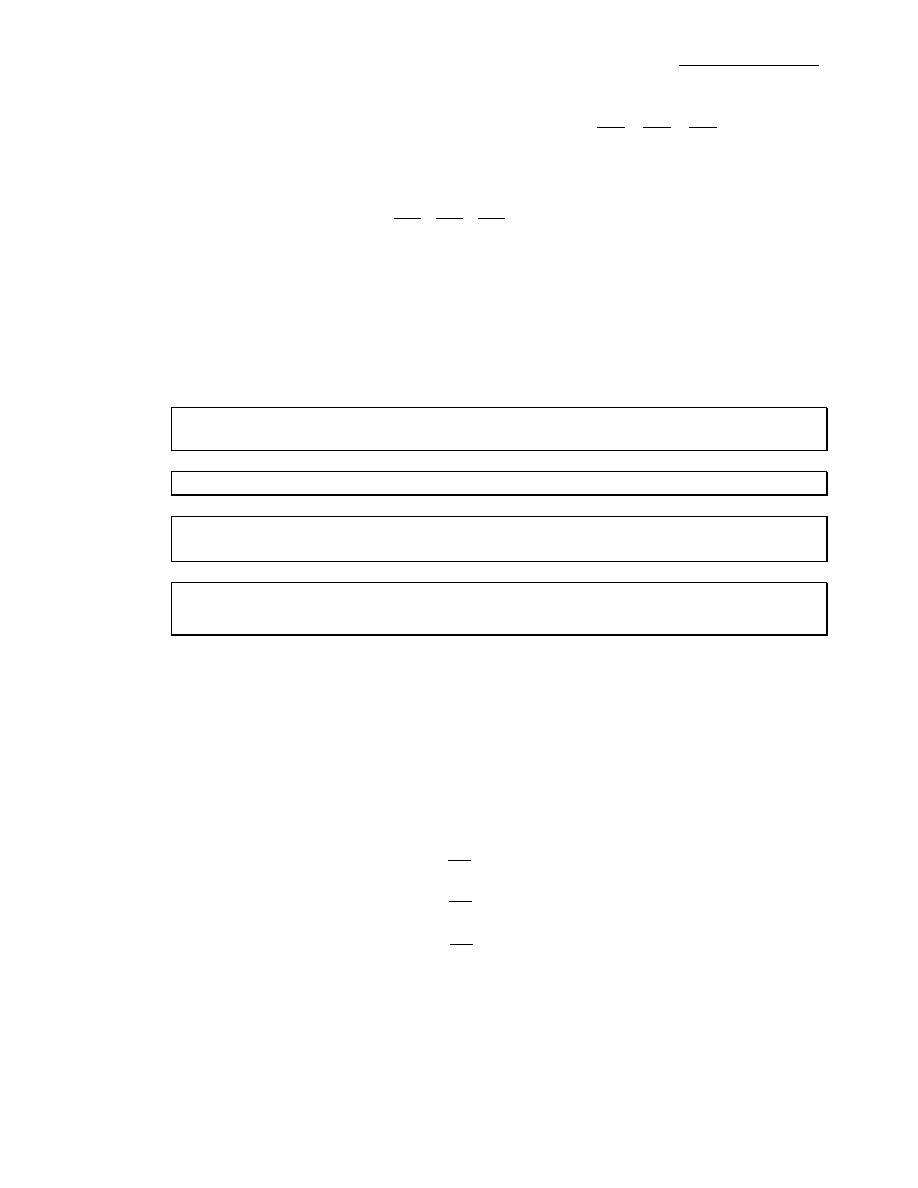
E
LEMENTY TEORII POLA
Strona 39
39
39
39
Operator różniczkowy, który określamy symbolem
∇
2
=
∆
=
2
2
2
2
2
2
z
y
x
∂
∂
+
∂
∂
+
∂
∂
i nazywamy
operatorem Laplace’a (laplasjanem) jest przykładem operatora różniczkowego rzędu
drugiego.
∇
2
ϕ
=
∆
ϕ
=
2
2
2
2
2
2
z
y
x
∂
∂
+
∂
∂
+
∂
∂
ϕ
ϕ
ϕ
= 0 – równanie Laplace’a.
Uwaga 2.
Wszystkie podane operatory są liniowe, co zapisujemy krótko:
∀α
,
β∈ℜ
:
grad(
αϕ
+
βψ
) =
α
grad
ϕ
+
β
grad
ψ
,
div(
α
F+
β
G) =
α
divF+
β
divG,
rot(
α
F+
β
G) =
α
rotF+
β
rotG,
∆
(
αϕ
+
βψ
) =
α∆ϕ
+
β∆ψ
.
Pole wektorowe F, dla którego divF = 0 nazywamy polem bezźródłowym.
Pole wektorowe F, dla którego rotF = 0 nazywamy polem bezwirowym.
Jeżeli istnieje pole skalarne
ϕ
takie, że F = grad
ϕ
, to pole wektorowe F nazywamy polem
potencjalnym (
ϕ
nazywamy wtedy potencjałem).
Twierdzenie 1.
Jeżeli pole wektorowe F jest potencjalne i jest klasy C
1
(V), to jest bezwirowe.
Uwaga 3.
Tezę tego twierdzenia można zapisać krótko: rot(grad
ϕ
) = 0. Twierdzenie
odwrotne jest także prawdziwe przy dodatkowym założeniu, że obszar V jest
jednospójny
,
czyli ma własność: każdy zbiór ograniczony, którego cały brzeg należy do obszaru V jest
zawarty w V (V nie ma dziur).
Uwaga 4.
Jeżeli pole F=[p(x,y,z),q(x,y,z), r(x,y,z)] jest potencjalne, to potencjał
ϕ
wyznaczamy z układu równań:
====
∂∂∂∂
∂∂∂∂
====
∂∂∂∂
∂∂∂∂
====
∂∂∂∂
∂∂∂∂
).
,
,
(
),
,
,
(
),
,
,
(
z
y
x
r
z
z
y
x
q
y
z
y
x
p
x
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
Możemy także skorzystać z gotowego wzoru (który będzie uzasadniony na wykładzie 8.):
∫∫∫∫
∫∫∫∫
∫∫∫∫
++++
++++
====
z
z
y
y
x
x
dt
t
y
x
r
dt
z
t
x
q
dt
z
y
t
p
z
y
x
0
0
0
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
0
0
0
ϕϕϕϕ
gdzie (x
0
,y
0
,z
0
) jest dowolnym punktem, w którym pole wektorowe jest określone.

R
OZDZIAŁ
IV
Strona 40
40
40
40
Przykład 1.
Wykazać, że pole wektorowe F =
+
−
+
z
z
x
xy
z
y
2
,
2
,
1
2
2
jest potencjalne i wyznaczyć jego
potencjał.
Twierdzenie 2.
Jeżeli pole wektorowe klasy C
1
jest rotacją pola wektorowego, to jest to pole
bezźródłowe.
Uwaga 5.
Tezę tego twierdzenia można zapisać krótko: div(rotF) = 0.
Uwaga 6.
Pole wektorowe F w obszarze jednospójnym, które jest jednocześnie bezwirowe
i bezźródłowe nazywamy polem harmonicznym. Potencjał tego pola spełnia równanie:
∆ϕ
=0
(równanie Laplace’a).
Jeśli pola skalarne
ϕ
i
ψ
oraz pola wektorowe F i G są klasy C
1
, to zachodzą następujące
równości:
1.
grad(
ϕψ
) =
ϕ
grad
ψ
+
ψ
grad
ϕ
;
2.
div(
ϕ
F) =
ϕ
divF + F
⋅
grad
ϕ
;
3.
rot(
ϕ
F) =
ϕ
rotF + F
×
grad
ϕ
;
4.
div(F
×
G) = G
⋅
rotF
−
F
⋅
rotG.

E
LEMENTY TEORII POLA
Strona 41
41
41
41
Całka podwójna
Niech funkcja f: D
→ℜ
2
będzie ograniczona, gdzie ograniczony obszar D
⊂ℜ
2
.
Ponieważ obszar D jest ograniczony, więc istnieje prostokąt P=[a,b]
×
[c,d] taki, że D
⊂
P.
Określamy pomocniczą funkcję f
*
będącą rozszerzeniem funkcji f na prostokąt P:
∈
∈
=
.
\
)
,
(
,
0
,
)
,
(
),
,
(
)
,
(
*
D
P
y
x
dla
D
y
x
dla
y
x
f
y
x
f
Dzielimy prostokąt P na n rozłącznych prostokątów P
i
(i=1, ..., n) o średnicach
)
,
(
sup
)
,
(
B
A
d
i
P
B
A
i
∈
=
δ
(długość przekątnej prostokąta) i polach
∆σ
i
.
Zakładamy, że podział prostokąta P jest normalny,
tzn.
0
max
1
→
∞
→
≤
≤
n
i
n
i
δ
.
Z każdego P
i
wybieramy dowolny punkt Q
i
(x
i
,y
i
) i tworzymy sumę całkową:
.
)
(
1
*
i
n
i
i
n
Q
f
s
σ
∆
=
∑
=
Jeżeli przy dowolnym podziale normalnym prostokąta P i przy dowolnym wyborze punktów Q
i
ciąg (s
n
) ma granicę właściwą, to granicę tę nazywamy całką podwójną z funkcji f po
obszarze D
i oznaczamy symbolem:
∫∫
∫∫
D
D
fd
dxdy
y
x
f
σ
krótko
lub
)
,
(
(samą funkcję f nazywamy
całkowalną w sensie Riemanna w obszarze D).
Interpretacja geometryczna.
Jeżeli f
≥
0 w obszarze D, to całka
∫∫
D
fd
σ
jest równa objętości walca o podstawie D,
ograniczonego z góry powierzchnią S
o równaniu: z=f(x,y), którego tworzące
są równoległe do osi OZ.
Jeżeli f=1 w obszarze D,
to
∫∫
D
d
σ
=
|
D
|
(= polu obszaru D).
Twierdzenie 3 (o istnieniu całki podwójnej).
Jeżeli funkcja f: D
→ℜ
jest ciągła w obszarze domkniętym D
⊂ℜ
2
, to f jest całkowalna
w sensie Riemanna w tym obszarze.
Twierdzenie 4.
R
OZDZIAŁ
IV
Strona 42
42
42
42
Jeżeli funkcja f: D→
→
→
→ℜ
ℜ
ℜ
ℜ jest ograniczona i ciągła w obszarze D ⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
2
z wyjątkiem
punktów leżących na skończonej ilości krzywych leżących w tym obszarze, w których
ma nieciągłość I rodzaju, to f jest całkowalna w sensie Riemanna w obszarze D.
Własności całki podwójnej
Twierdzenie 5.
Jeżeli funkcje f i g są całkowalne w sensie Riemanna w obszarze D, to:
1. (liniowość całki)
∫∫
∫∫
∫∫
ℜ
∈
+
=
+
D
D
D
.
µ
λ
,
gdσd
µ
fdσ
λ
µ
g)dσ
(λλ
2. [
∀
∀
∀
∀(x,y)∈
∈
∈
∈D: f(x,y)≥≥≥≥g(x,y)] ⇒
⇒
⇒
⇒
∫∫
∫∫
≥
D
D
σ
gd
σ
fd
.
3.
dσ
f
fdσ
D
D
∫∫
∫∫
≤
4. (addytywność całki względem obszaru całkowania)
(
)
∫∫
∫∫
∫∫
+
=
⇒
∅
=
∩
∧
∪
=
2
1
D
D
D
o
2
o
1
2
1
fdσd
fdσ
fdσ
)
D
D
D
D
D
5. (twierdzenie o wartości średniej)
.
∫∫
=
∈
∃
⇒
∈
D
0
0
D
)
f(P
fdσ
:
D
P
C(D)
f
Obliczanie całki podwójnej
Obszar normalny względem osi OX:
D
x
= {(x,y)
∈ℜ
2
: a
≤
x
≤
b
∧
ϕ
(x)
≤
y
≤
ψ
(x)}.
Obszar normalny względem osi OY:
D
y
= {(x,y)
∈ℜ
2
: c
≤
y
≤
d
∧
f(y)
≤
x
≤
g(y)}.

E
LEMENTY TEORII POLA
Strona 43
43
43
43
Twierdzenie 5(o zamianie całki podwójnej na całki iterowane).
Jeżeli funkcja f: D→
→
→
→ℜ
ℜ
ℜ
ℜ jest ciągła w obszarze D ⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
2
normalnym względem osi OX:
D= {(x,y)
∈
∈
∈
∈ℜ
ℜ
ℜ
ℜ
2
: a
≤≤≤≤ x ≤≤≤≤ b ∧∧∧∧ ϕϕϕϕ(x) ≤≤≤≤ y ≤≤≤≤ ψ
ψ
ψ
ψ(x)}, to
.
)
,
(
)
,
(
)
(
)
(
dx
dy
y
x
f
dxdy
y
x
f
D
b
a
x
x
∫∫
∫∫
∫∫
∫∫
∫∫∫∫ ∫∫∫∫
====
ψ
ψ
ψ
ψ
ϕϕϕϕ
Uwaga 6.
Jeżeli funkcja f: D
→ℜ
jest ciągła w obszarze D
⊂ℜ
2
normalnym względem osi
OY:
D= {(x,y)
∈ℜ
2
: c
≤
y
≤
d
∧
f(y)
≤
x
≤
g(y)}, to
∫
∫
∫∫
∫ ∫
=
=
d
c
y
g
y
f
D
d
c
y
g
y
f
dx
y
x
f
dy
dy
dx
y
x
f
dxdy
y
x
f
)
(
)
(
)
(
)
(
.
)
,
(
)
,
(
)
,
(
Uwaga 7.
Jeżeli obszar D jest prostokątem: D=[a,b]
×
[c,d], to
∫
∫
∫
∫
∫∫
=
=
b
a
d
c
d
c
b
a
D
dx
y
x
f
dy
dy
y
x
f
dx
dxdy
y
x
f
)
,
(
)
,
(
)
,
(
Przykład 2.
Obliczyć całkę:
∫∫
+
D
dxdy
xy
)
2
1
(
,
gdzie D jest obszarem ograniczonym parabolą o równaniu: y = x
2
i prostą o równaniu: y = 1.
Obliczyć tę całkę traktując obszar D:
a) jako normalny względem osi OX;
b) jako normalny względem osi OY.

R
OZDZIAŁ
IV
Strona 44
44
44
44
Przykład 3.
Obliczyć całkę:
∫∫∫∫ ∫∫∫∫
−−−−
1
0
3
3
2
y
x
dx
e
dy
.
Ć
wiczenia
1. Udowodnić następujące równości dla pola skalarnego
ϕ
i pól wektorowych
G
,
F
r
r
:
3
3
ℜ
→
ℜ
:
)
G
rot(
F
)
F
rot(
G
)
G
F
div(
a)
r
o
r
r
o
r
r
r
−
=
×
,
F
grad
)
F
rot(
)
F
rot(
b)
r
r
r
×
+
=
ϕ
ϕ
ϕ
,
ϕ
ϕ
ϕ
grad
F
)
F
div(
)
F
div(
c)
r
r
r
+
=
,
))
F
rot(rot(
))
F
grad(div(
)
F
∆
(
d)
r
r
r
−
=
.
2. Wykaza
ć
,
ż
e dane pole wektorowe jest potencjalne a nast
ę
pnie wyznaczy
ć
potencjał tego
pola:
[
]
3
2
3
3
2
2
4
3
,
3
2
,
z
z
y
z
y
y
x
+
+
+
=
2
2xy
1
F
a)
r
,
[
]
2
z
z
y
x
y
x
3z
ye
,
e
2y
e
2x,
e
F
b)
+
+
+
+
=
+
+
r
.
3. Narysowa
ć
obrazy danych obszarów
∆
(przy wskazanym odwzorowaniu T) płaszczyzny
UOV w płaszczyzn
ę
XOY; o bliczy
ć
jakobian przekształcenia T, je
ż
eli:
{
}
+
−
=
+
=
≤
≤
≤
≤
−
ℜ
∈
=
2v,
u
y
3v,
2u
x
:
T
,
4
v
1
1,
u
1
:
v)
(u,
∆
a)
2

E
LEMENTY TEORII POLA
Strona 45
45
45
45
{
}
=
=
≤
≤
≤
≤
ℜ
∈
=
,
v
-
u
y
uv,
x
:
T
,
2
v
0
2,
u
1
:
v)
(u,
∆
b)
2
2
2
{
}
=
=
≤
≤
≤
≤
ℜ
∈
=
usinv,
y
ucosv,
x
:
T
,
v
4,
u
2
:
v)
(u,
∆
c)
2
4
-
2
π
π
{
}
=
=
≤
≤
≤
≤
ℜ
∈
=
usinv.
3
y
2ucosv,
x
:
T
,
v
2,
u
1
:
v)
(u,
∆
d)
2
2
π
π
4. Obliczy
ć
całk
ę
podwójn
ą
po prostok
ą
tach D, je
ż
eli:
,
[0,1]
[1,2]
D
dxdy,
y
x
x
a)
D
2
2
×
=
+
∫∫
,
]
[0,
]
,
[
D
dxdy,
)
cos(
b)
4
4
4
-
D
π
π
π
×
=
−
∫∫
y
x
.
[0,1]
D
dxdy,
1
x
xy
c)
2
D
2
2
=
+
+
∫∫
y
5. Zamienić całkę podwójną
∫∫
D
y)dxdy
f(x,
na całki iterowane, jeżeli obszar D jest
ograniczony krzywymi:
,
0
,
2
,
0
,
2
1
a)
2
=
=
=
−
+
=
y
x
x
x
x
y
,
,
0
,
1
b)
2
2
x
y
x
y
x
=
=
=
+
,
1
2
,
1
c)
−
−
=
−
=
x
y
x
y
.
,
2
2
x
y
x
y
=
−
=
d)
6. Zmienić porządek całkowania w całce podwójnej:
,
y)dy
f(x,
dx
a)
1
0
2x
x
2
∫ ∫
,
y)dx
f(x,
dy
b)
3
0
y
y
-
∫ ∫
,
y)dx
f(x,
dy
c)
1
0
3
3y
∫ ∫
,
y)dy
f(x,
dx
d)
2
1
-
x
2
x
2
∫ ∫
+
,
y)dx
f(x,
dy
e)
2
1
2
y
y
∫
∫
,
2
y)dy
f(x,
dx
f)
2
0
x
2
x
-
4
∫
∫
,
y)dy
f(x,
dx
g)
e
1
lnx
0
∫
∫
.
y)dx
f(x,
dy
h)
1
0
2
y
-
1
1
y
-
2
∫
∫
+
Obliczyć całki:
{
}
∫∫
≤
≤
≤
≤
ℜ
∈
=
D
2
2
x
y
x
1,
x
0
:
y)
(x,
D
,
xydxdy
a)
,
∫∫
=
=
=
D
1
,
,
2
:
D
,
xydxdy
b)
x
y
x
y
x
,
dx,
dy
c)
1
0
3
3y
2
∫ ∫
x
e
∫∫
=
=
=
D
y
x
D
,
dxdy
e
d)
x
y
y
x
,
1
,
0
:
,
1
:
D
,
}dxdy
y
x
(
e)
D
≤
+
+
∫∫
y
x
.

R
OZDZIAŁ
IV
Strona 46
46
46
46

V
Zamiana zmiennych
w całce podwójnej

R
OZDZIAŁ
V
Strona 48
48
48
48
Obszar płaski D nazywamy obszarem regularnym, jeżeli jest on sumą skończonej ilości
obszarów normalnych (względem osi OX lub osi OY) o rozłącznych wnętrzach.
Twierdzenie 1(o zamianie zmiennych w całce podwójnej).
Jeżeli:
funkcja f: D
→
→
→
→ℜ
ℜ
ℜ
ℜ jest ciągła w obszarze regularnym i domkniętym D ⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
2
,
odwzorowanie bijektywne
ψ
ψ
ψ
ψ: ∆
∆∆
∆
↔
D określone równaniami:
====
====
),
,
(
),
,
(
v
u
y
y
v
u
x
x
jest klasy C
1
(
∆
∆∆
∆
),
jakobian J(u,v) odwzorowania
ψ
ψ
ψ
ψ
jest ograniczony i różny od zera wewnątrz obszaru
∆
∆∆
∆
,
to zachodzi równość:
[[[[
]]]]
.
)
,
(
)
,
(
),
,
(
)
,
(
dudv
v
u
J
v
u
y
v
u
x
f
dxdy
y
x
f
D
⋅⋅⋅⋅
====
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∆
∆∆
∆
Uwaga 1. Po wprowadzeniu współrzędnych biegunowych: x=rcos
ϕ
, y=rsin
ϕ
, otrzymamy
równość:
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∆
∆∆
∆
⋅⋅⋅⋅
====
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
rdrd
r
r
f
dxdy
y
x
f
D
)
sin
,
cos
(
)
,
(
.
Uwaga 2. Jeżeli f(x,y)=1, to
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∆
∆∆
∆
====
====
.
)
,
(
dudv
v
u
J
D
dxdy
D

Z
AMIANA ZMIENNYCH W CAŁCE PODWÓJNEJ
Strona 49
49
49
49
Przykład 1.
Obliczyć całkę:
∫∫
+
+
D
y
x
dxdy
2
2
1
, gdzie D={(x,y)
∈ℜ
2
: x
2
+y
2
≤
1 i y
≥
0}.
Przykład 2.
Obliczyć całkę:
∫∫
D
ydxdy
,
gdzie D={(x,y)
∈ℜ
2
: x
2
+y
2
−
2x
≤
0 i y< 0}.

R
OZDZIAŁ
V
Strona 50
50
50
50
Przykład 3.
Obliczyć całkę:
((((
))))
∫∫
∫∫
∫∫
∫∫
++++
D
2
2
2
3
y
x
dxdy
, gdzie D={(x,y)
∈ℜ
2
: x
2
+y
2
≤
1, y
≥
x, x+y
≥
1}.
Przykład 4.
Obliczyć całkę:
∫∫
D
xydxdy
, gdzie obszar D
jest ograniczony krzywymi o równaniach:
y
2
= x, y
2
= 4x, x
2
=2y, x
2
= 8y.

Z
AMIANA ZMIENNYCH W CAŁCE PODWÓJNEJ
Strona 51
51
51
51
Przykład 5.
Wprowadzając uogólnione współrzędne biegunowe:
====
====
,
brsin
y
,
arcos
x
ϕϕϕϕ
ϕϕϕϕ
obliczyć objętość bryły
ograniczonej powierzchniami o równaniach: z = x2 + y2, z = 16 - x2 - y2 ,
.
1
3
4
2
2
====
++++
y
x
R
OZDZIAŁ
V
Strona 52
52
52
52
Pole płata
Rozważmy płat S o równaniu: z = f(x,y) i wprowadźmy oznaczenia.
Pole S
i
:
∆
S
i
,
pole D
i
:
∆σ
i
.
∆σ
i
=
∆
S
i
⋅
cos
γ
,
∆
S
i
=
γ
σ
cos
i
∆
.
[
]
1
,
,
'
'
y
x
f
f
n
−
−
=
r
[
]
1
0
0
,
,
=
k
r
Ponieważ
2
'
2
'
)
(
)
(
1
1
cos
y
x
f
f
n
k
n
k
++++
++++
====
⋅⋅⋅⋅
====
r
r
r
r
γγγγ
,
więc
i
y
x
i
f
f
S
σσσσ
∆
∆∆
∆
++++
++++
====
∆
∆∆
∆
2
'
2
'
)
(
)
(
1
Jeżeli wyznaczymy sumę pól tych „łusek”, to otrzymamy sumę:
i
n
i
n
i
y
x
i
n
f
f
S
S
σσσσ
∆
∆∆
∆
++++
++++
====
∆
∆∆
∆
====
∑
∑
∑
∑
∑
∑
∑
∑
====
====
1
1
2
'
2
'
)
(
)
(
1
Mamy więc:
Wniosek 1. Jeżeli płat regularny dany jest równaniem: z = f(x,y), gdzie (x,y)∈
∈
∈
∈D, to pole
tego płata wyraża się wzorem:
.
)
(
)
(
1
2
'
2
'
dxdy
f
f
S
D
y
x
∫∫
∫∫
∫∫
∫∫
++++
++++
====
Przykład 6.
Wyznaczyć pole części półsfery o równaniu:
2
2
2
y
x
a
z
−
−
=
wycięte przez walec o równaniu: x
2
+ y
2
=ay.
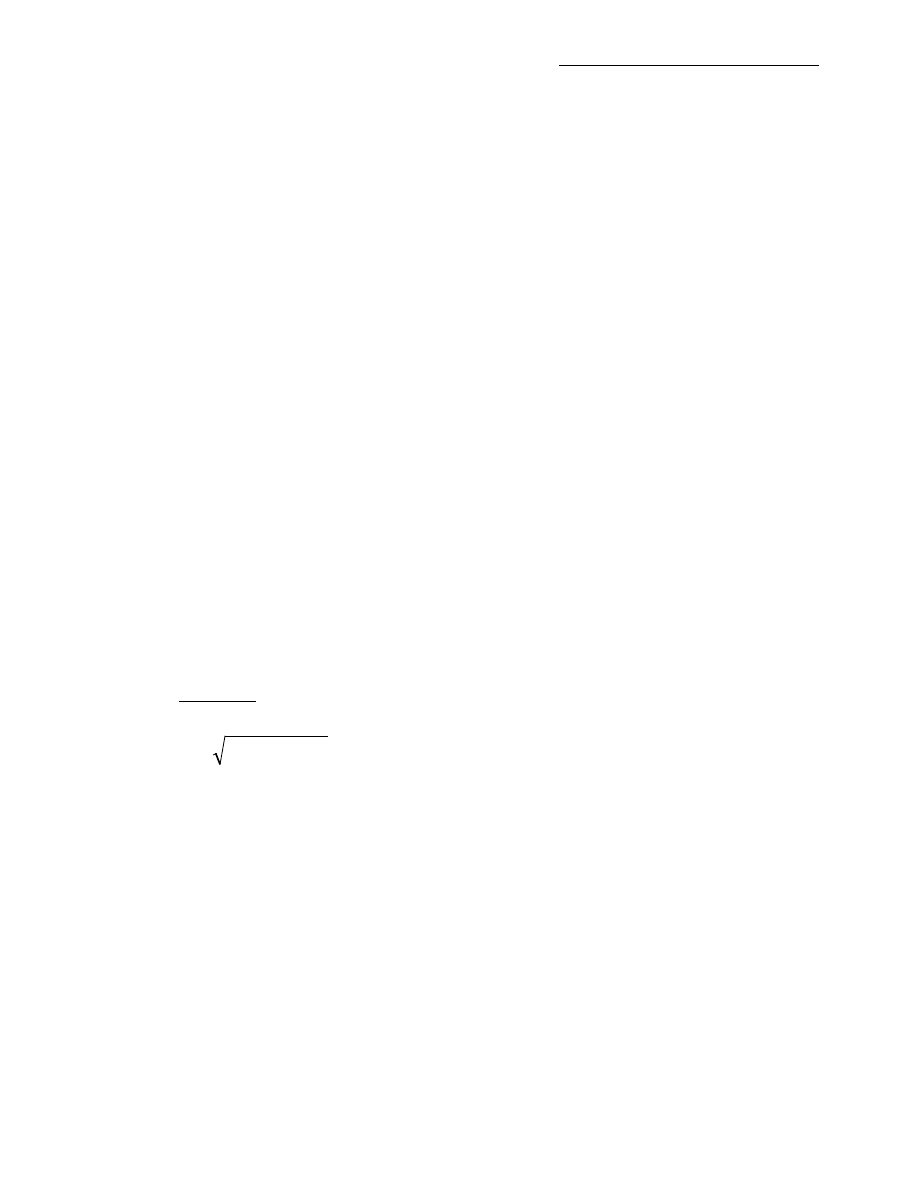
Z
AMIANA ZMIENNYCH W CAŁCE PODWÓJNEJ
Strona 53
53
53
53
Przykład 7.
Wyznaczyć pole części walca o równaniu: x
2
+ y
2
= ay wycięte przez półsferę o równaniu:
2
2
2
y
x
a
z
−
−
=
.

R
OZDZIAŁ
V
Strona 54
54
54
54
Całka Gaussa:
∫∫∫∫
+∞
+∞
+∞
+∞
∞
∞
∞
∞
−−−−
−−−−
dx
e
x
2
Rozważymy całkę podwójną:
∫∫
∫∫
∫∫
∫∫
−−−−
−−−−
D
y
x
dxdy
e
2
2
.
Jeżeli obszar D jest kwadratem [-a,a]
2
, to mamy równości:
2
2
2
2
2
2
2
2
====
====
====
∫∫∫∫
∫∫∫∫
∫∫∫∫
∫∫∫∫ ∫∫∫∫
∫∫
∫∫
∫∫
∫∫
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
a
a
x
a
a
a
a
y
x
a
a
a
a
y
x
D
y
x
dx
e
dy
e
dx
e
dy
e
e
dx
dxdy
e
Jeżeli obszar D jest kołem o promieniu b i o środku (0,0), to wprowadzając współrzędne
biegunowe, otrzymamy: ∆: r∈[0,b), ϕ∈[0,2π),
((((
))))
1
0
2
1
2
2
2
2
2
2
0
2
0
0
++++
−−−−
====
−−−−
====
====
−−−−
−−−−
−−−−
−−−−
−−−−
∫∫∫∫
∫∫∫∫ ∫∫∫∫
∫∫
∫∫
∫∫
∫∫
b
r
b
r
D
y
x
e
d
b
e
dr
r
e
d
dxdy
e
ππππ
ϕϕϕϕ
ϕϕϕϕ
ππππ
ππππ
K
a
- koło o promieniu a
i środku (0,0),
K
R
- koło o promieniu
a
R
2
=
i środku (0,0),

Z
AMIANA ZMIENNYCH W CAŁCE PODWÓJNEJ
Strona 55
55
55
55
Q - kwadrat [-a,a]
2
.
Z własności całki podwójnej mamy:
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
−−−−
−−−−
−−−−
−−−−
−−−−
−−−−
≤≤≤≤
≤≤≤≤
R
a
K
y
x
Q
y
x
K
y
x
dxdy
e
dxdy
e
dxdy
e
2
2
2
2
2
2
Uwzględniając wyżej obliczone całki, mamy:
((((
))))
((((
))))
2
2
2
1
1
2
R
a
a
x
a
e
dx
e
e
−−−−
−−−−
−−−−
−−−−
−−−−
≤≤≤≤
≤≤≤≤
−−−−
∫∫∫∫
ππππ
ππππ
Przechodząc do granicy: a
→+∞ (wtedy R →+∞), otrzymamy na mocy twierdzenia o trzech
funkcjach:
ππππ
ππππ
≤≤≤≤
≤≤≤≤
∫∫∫∫
∞
∞
∞
∞
++++
∞
∞
∞
∞
−−−−
−−−−
2
2
dx
e
x
Ostatecznie:
∫∫∫∫
+∞
+∞
+∞
+∞
∞
∞
∞
∞
−−−−
−−−−
====
ππππ
dx
e
x
2
.
Ć
wiczenia
1. Dokonując odpowiedniej zamiany zmiennych, obliczyć całki, jeżeli D jest obszarem
ograniczonym wskazanymi krzywymi:
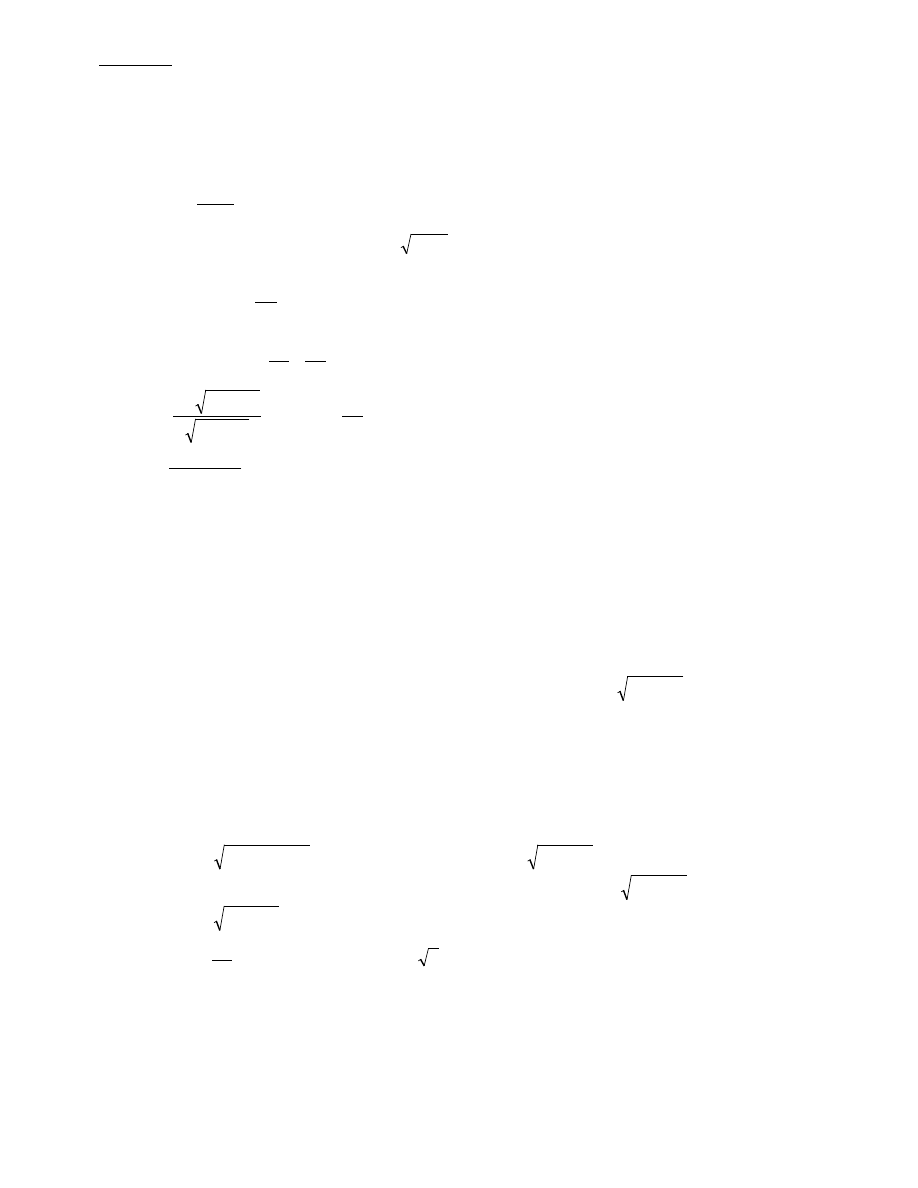
R
OZDZIAŁ
V
Strona 56
56
56
56
2x
y
x,
y
2,
xy
1,
xy
:
D
,
dxdy
xy
a)
D
3
=
=
=
=
∫∫
,
3
y
-
2x
1,
y
-
2x
2,
y
x
1,
y
x
:
D
,
dxdy
)
y
-
(2x
b)
D
=
=
=
+
=
+
∫∫
,
0
y
0,
x
1,
y
x
:
D
,
dxdy
y
x
y
x
cos
c)
D
≥
≥
=
+
+
−
∫∫
,
∫∫
≤
≤
≤
≤
D
2
2
x
-
1
y
0
,
1
0
:
D
,
dxdy
xy
d)
x
,
∫∫
π
≤
+
≤
2
2
1
y
2
dxdy
x
y
-
1
e)
x
2
2
,
(
)
∫∫
≤
+
>
+
ax
y
y
2
2
x
2
2
0
a
dxdy,
x
f)
,
∫∫
≤
+
D
2
2
2
1
4
2
:
D
,
dxdy
x
g)
y
x
,
∫∫
≤
+
≤
+
+
D
2
2
2
2
2
2
2
2
π
y
x
9
π
:
D
,
dxdy
y
x
y
x
sin
h)
,
(
)
2x
y
x,
y
8x,
y
x
4x,
y
x
:
D
,
x
dxdy
i)
D
2
2
2
2
2
2
2
=
=
=
+
=
+
+
∫∫
y
.
2. Obliczy
ć
pole obszaru ograniczonego krzywymi:
4
4x
y
x,
2
y
a)
2
+
=
−
=
,
,
4
x
x),
-
4(1
y
b)
2
2
2
=
+
=
y
na zewn
ą
trz paraboli,
2
r
cost),
-
2(1
r
c)
=
=
, na zewn
ą
trz kardioidy,
2
2
3
,
x
y
,
4
1,
xy
d)
x
y
xy
=
=
=
=
.
3. Obliczy
ć
obj
ę
to
ść
bryły ograniczonej powierzchniami (sporz
ą
dzi
ć
rysunki):
4
z
y
x
0,
z
0,
y
0,
x
8,
y
a)
2
2
=
+
+
=
=
=
=
+
x
,
0
,
1
4y
b)
2
2
=
=
+
+
z
z
x
,
0
2
>
=
+
=
+
a
x
,
a
z
x
,
a
y
c)
2
2
2
2
2
,
2
2
2
y
y
x
+
=
=
+
+
2
2
x
z
0,
y
d)
,
3x
y
,
x
-
9
z
e)
2
2
=
=
=
,
0
z
,
2
2
2
y
x
2
z
,
y
f)
+
+
=
−
−
=
2
4
2
x
z
,
16,
z
4,
z
,
y
g)
2
=
=
+
=
2
x
z
0
a
0,
2ay
-
y
x
,
4a
y
h)
2
2
2
2
>
=
+
=
+
+
2
2
z
x
.
4. Obliczy
ć
pole cz
ęś
ci płata S danego za pomoc
ą
funkcji f i ograniczonego danymi
powierzchniami:
3,
z
1,
z
,
y
x
16
y)
f(x,
a)
2
2
=
=
−
−
=
-2x,
y
x
,
y
x
y)
f(x,
b)
2
2
2
2
≤
+
+
=
1,
z
,
z
-
z)
f(y,
c)
2
2
≤
+
−
=
2
2
4
y
y
,
x
z
,
y
-
y)
f(x,
d)
2
2
2
2
2
y
x
+
=
−
=
0,
p
2px,
z
,
y
x
y)
f(x,
e)
2
2
2
>
=
+
=
2
2
y
2y,
x
2x,
y
,
y)
f(x,
f)
=
=
=
=
2
2
x
.

VI
Całka potrójna

R
OZDZIAŁ
VI
Strona 58
58
58
58
Niech funkcja f: V
→ℜ b
ę
dzie ograniczona, gdzie ograniczony obszar V
⊂ℜ
3
.
Post
ę
puj
ą
c podobnie jak w definicji całki podwójnej, oznaczamy przez P prostopadło
ś
cian
zawieraj
ą
cy obszar V. Definiujemy pomocnicz
ą
funkcj
ę
f
*
b
ę
d
ą
c
ą
rozszerzeniem funkcji f na
prostopadło
ś
cian P:
∈
∈
=
.
\
)
,
,
(
,
0
,
)
,
,
(
),
,
,
(
)
,
,
(
*
V
P
z
y
x
dla
V
z
y
x
dla
z
y
x
f
z
y
x
f
Dzielimy prostopadło
ś
cian P na n rozł
ą
cznych prostopadło
ś
cianów P
i
(i=1, ..., n) o
ś
rednicach
)
,
,
(
sup
)
,
,
(
C
B
A
d
i
V
C
B
A
i
∈
=
δ
(długo
ść
przek
ą
tnej prostopadło
ś
cianu) i obj
ę
to
ś
ciach
∆V
i
.
Zakładamy,
ż
e podział prostopadło
ś
cianu P jest normalny, tzn.
0
max
1
→
∞
→
≤
≤
n
i
n
i
δ
Z ka
ż
dego V
i
wybieramy dowolny punkt Q
i
(x
i
,y
i
,z
i
) i tworzymy sum
ę
całkow
ą
:
.
)
(
1
*
i
n
i
i
n
V
P
f
s
∆
=
∑
=
Je
ż
eli przy dowolnym podziale normalnym prostopadło
ś
cianu P i przy dowolnym wyborze
punktów Q
i
ci
ą
g (s
n
) ma granic
ę
wła
ś
ciw
ą
, to granic
ę
t
ę
nazywamy
całką potrójna z funkcji f
po obszarze V
i oznaczamy symbolem:
∫∫∫
V
dxdydz
z
y
x
f
)
,
,
(
lub krótko
∫∫∫
V
fdV
(sam
ą
funkcj
ę
f nazywamy
całkowalną w sensie Riemanna w obszarze V
).
Interpretacja geometryczna.
Je
ż
eli f =1 w obszarze V,
to całka
∫∫∫
V
dxdydz
jest równa obj
ę
to
ś
ci bryły V.
Twierdzenie 1 (o istnieniu całki potrójnej).
Jeżeli funkcja f: V
→
→
→
→ℜ
ℜ
ℜ
ℜ
jest ciągła w obszarze domkniętym V
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
3
,to f jest całkowalna
w sensie Riemanna w tym obszarze.

C
AŁKA POTRÓJNA
Strona 59
59
59
59
Uwaga 1.
Je
ż
eli funkcja f: V
→ℜ jest ograniczona i ci
ą
gła w obszarze V
⊂ℜ
3
z wyj
ą
tkiem
punktów le
żą
cych na sko
ń
czonej ilo
ś
ci powierzchni (b
ę
d
ą
cych wykresami funkcji ci
ą
głych o
postaci
z=z(x,y), y=y(x,z) lub x=x(y,z) ) le
żą
cych w tym obszarze, w których ma nieci
ą
gło
ść
I
rodzaju,
to f jest całkowalna w sensie Riemanna w obszarze V.
Uwaga 2.
Własno
ś
ci całki potrójnej s
ą
analogiczne do tych przedstawionych dla całki
podwójnej.
Obliczanie całki potrójnej
Obszar normalny wzgl
ę
dem płaszczyzny XOY:
V
xy
= {(x,y,z)∈ℜ
3
:
(x,y) ∈D ∧ ϕ(x,y) ≤ z ≤ ψ(x,y)}.
Obszary normalne wzgl
ę
dem płaszczyzn XOZ i YOZ okre
ś
lamy nast
ę
puj
ą
co:
V
xz
= {(x,y,z)∈ℜ
3
: (x,z) ∈D ∧ f(x,z) ≤ y ≤ g(x,z)}.
V
yz
= {(x,y,z)∈ℜ
3
: (y,z) ∈D ∧ h(y,z) ≤ x ≤ k(y,z)}.
W ka
ż
dym przypadku obszar płaski D jest rzutem
obszaru V na odpowiedni
ą
płaszczyzn
ę
.
Twierdzenie 2 (o zamianie całki potrójnej na całki iterowane).
Jeżeli funkcja f: V
→
→
→
→ℜ
ℜ
ℜ
ℜ
jest ciągła w obszarze V
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
3
normalnym względem płaszczyzny
XOY: V= {(x,y,z)
∈
∈
∈
∈ℜ
ℜ
ℜ
ℜ
3
: (x,y)
∈
∈
∈
∈
D
∧
∧∧
∧
ϕ
ϕϕ
ϕ
(x,y)
≤≤≤≤
z
≤≤≤≤
ψ
ψ
ψ
ψ
(x,y)}, to
.
)
,
,
(
)
,
,
(
)
,
,
(
)
,
,
(
dxdy
dz
z
y
x
f
dxdydz
z
y
x
f
V
D
z
y
x
z
y
x
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫
∫∫
∫∫
∫∫
∫∫∫∫
====
ψ
ψ
ψ
ψ
ϕϕϕϕ
Uwaga 3.
Je
ż
eli zało
ż
ymy dodatkowo,
ż
e obszar D jest normalny np. wzgl
ę
dem osi OX, to
∫∫∫∫
∫∫∫∫
∫∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
====
)
,
(
)
,
(
)
(
)
(
.
)
,
,
(
)
,
,
(
y
x
y
x
b
a
x
d
x
c
V
dz
z
y
x
f
dy
dx
dxdydz
z
y
x
f
ψ
ψ
ψ
ψ
ϕϕϕϕ
Uwaga 4.
Je
ż
eli obszar V jest prostopadło
ś
cianem tzn. V=[a,b]
×[c,d]×[p,q], to:
∫∫∫∫ ∫∫∫∫ ∫∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
====
b
a
d
c
q
p
V
dz
z
y
x
f
dy
dx
dxdydz
z
y
x
f
)
,
,
(
)
,
,
(

R
OZDZIAŁ
VI
Strona 60
60
60
60
Przykład 1.
Obliczy
ć
całk
ę
:
,
)
1
(
3
∫∫∫
∫∫∫
∫∫∫
∫∫∫
++++
++++
++++
V
z
y
x
dxdydz
gdzie V jest czworo
ś
cianem:
V={(x,y,z)
∈ℜ
3
: x
≥0, y≥0, z≥0, x+y+z≤1}.

C
AŁKA POTRÓJNA
Strona 61
61
61
61
Przykład 2.
Obliczy
ć
całk
ę
:
∫∫∫
∫∫∫
∫∫∫
∫∫∫
++++
++++
V
dxdydz
z
y
x
)
2
(
2
2
, gdzie V = {(x,y,z): x
2
+y
2
≤ 1, 0 ≤ z ≤ 2−x
2
−y
2
}.
Zamiana zmiennych w całce potrójnej
Twierdzenie 3 (o zamianie zmiennych w całce potrójnej).
Jeżeli:
1. funkcja f: V
→
→
→
→ℜ
ℜ
ℜ
ℜ
jest ciągła w obszarze regularnym i domkniętym V
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
3
,
2. odwzorowanie bijektywne
V
Ω
:
ψ
↔ określone równaniami:
====
====
====
),
,
,
(
),
,
,
(
),
,
,
(
w
v
u
z
z
w
v
u
y
y
w
v
u
x
x
jest klasy C
1
(
Ω
Ω
Ω
Ω
),
3. jakobian J(u,v,w) odwzorowania
ψ
ψ
ψ
ψ
jest ograniczony i różny od zera wewnątrz
obszaru
Ω
Ω
Ω
Ω
, to zachodzi równość:
[[[[
]]]]
.
)
,
,
(
)
,
,
(
),
,
,
(
),
,
,
(
)
,
,
(
dxdydz
w
v
u
J
w
v
u
z
w
v
u
y
w
v
u
x
f
dxdydz
z
y
x
f
V
⋅⋅⋅⋅
====
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
Ω
Ω
Ω
Ω
Przykład 3.
Obliczy
ć
obj
ę
to
ść
bryły ograniczonej powierzchniami: z
2
= x
2
+ y
2
, z = 2
− x
2
− y
2
, z
≥ 0.
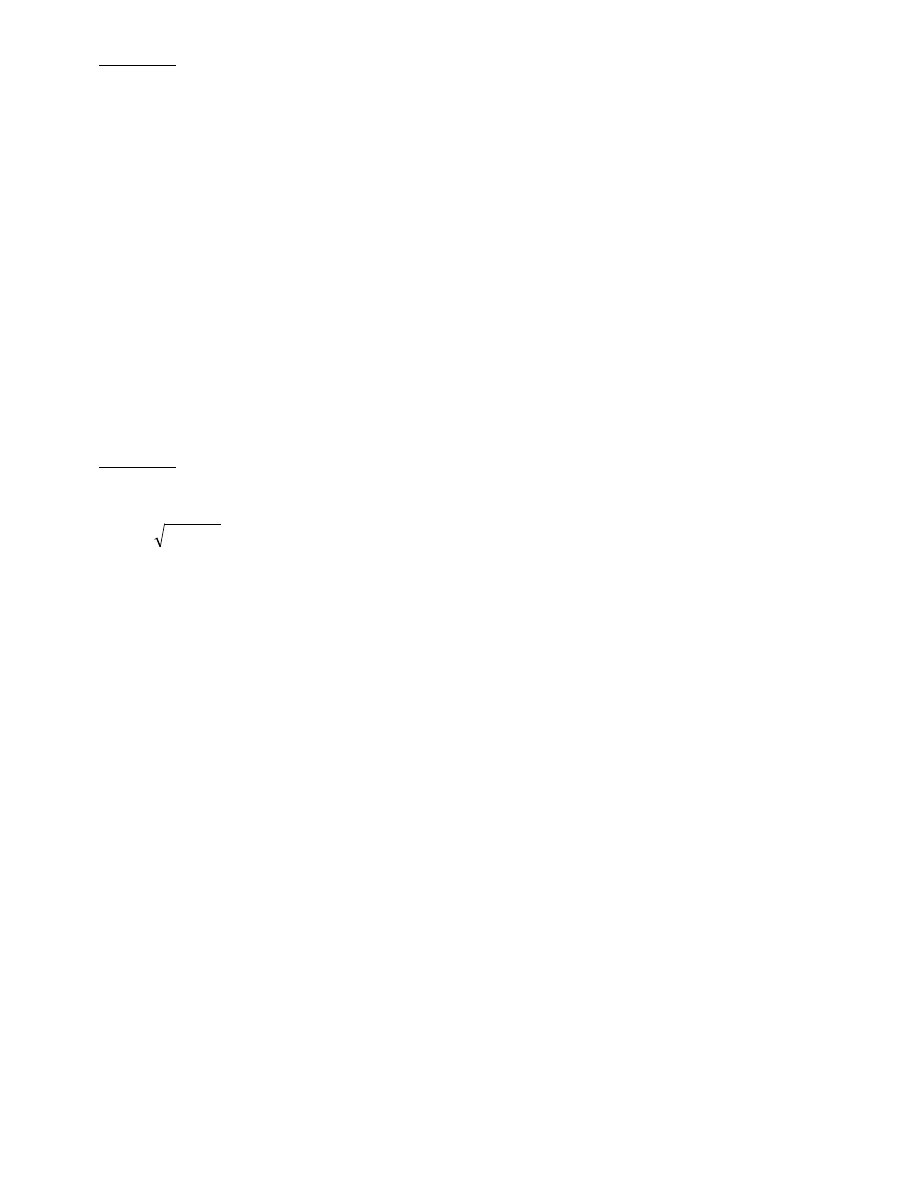
R
OZDZIAŁ
VI
Strona 62
62
62
62
Przykład 4.
Obliczy
ć
całk
ę
:
∫∫∫
V
dxdydz
x
,
2
gdzie V jest cz
ęś
ci
ą
kuli: x
2
+ y
2
+ z
2
≤ 4 le
żą
c
ą
wewn
ą
trz
sto
ż
ka:
z
y
x
≤
+
2
2
.

C
AŁKA POTRÓJNA
Strona 63
63
63
63
Całka krzywoliniowa nieskierowana
Niech
Γ:
=
=
),
(
),
(
t
y
y
t
x
x
t
∈[α,β], b
ę
dzie łukiem gładkim na płaszczy
ź
nie.
Odcinek [
α,β] dzielimy na n cz
ęś
ci:
α=t
0
<t
1
<t
2
< ... <t
n
=
β
i oznaczamy długo
ść
ka
ż
dego k-tego odcinka:
∆t
k
=t
k
− t
k-1
.
Zakładamy,
ż
e podział tego odcinka jest normalny,
tzn.
δ
n
→ 0, gdzie δ
n
=
).
(
max
1
k
n
k
t
∆
≤
≤
Podziałowi odcinka [
α,β] odpowiada podział łuku Γ
na n cz
ęś
ci punktami A
k
= (x(t
k
),y(t
k
)).
Przez P
k
oznaczamy dowolny wybrany punkt łuku A
k-1
A
k
a przez
∆l
k
długo
ść
tego łuku.
Definicja całki krzywoliniowej nieskierowanej:
Niech f b
ę
dzie funkcj
ą
ograniczon
ą
na łuku gładkim
Γ, wtedy całk
ę
krzywoliniow
ą
nieskierowan
ą
z funkcji f po łuku
Γ okre
ś
lamy wzorem:
,
)
(
lim
)
,
(
1
0
∑
∫
=
→
Γ
∆
=
n
k
k
k
l
P
f
dl
y
x
f
n
δ
o ile
granica po prawej stronie równo
ś
ci istnieje i nie zale
ż
y od sposobu podziału odcinka [
α,β]
ani od sposobu wyboru punktów P
k
.
Interpretacja geometryczna
Je
ż
eli f
≥0, to całka krzywoliniowa
nieskierowana po łuku
Γ jest równa
powierzchni bocznej walca o kieruj
ą
cej Γ
i o tworz
ą
cych równoległych do osi OZ
odci
ę
tego z góry przez powierzchni
ę
o równaniu: z=f(x,y).
Je
ż
eli f ≡1 całka krzywoliniowa skierowana po łuku Γ jest równa długo
ś
ci tego łuku.
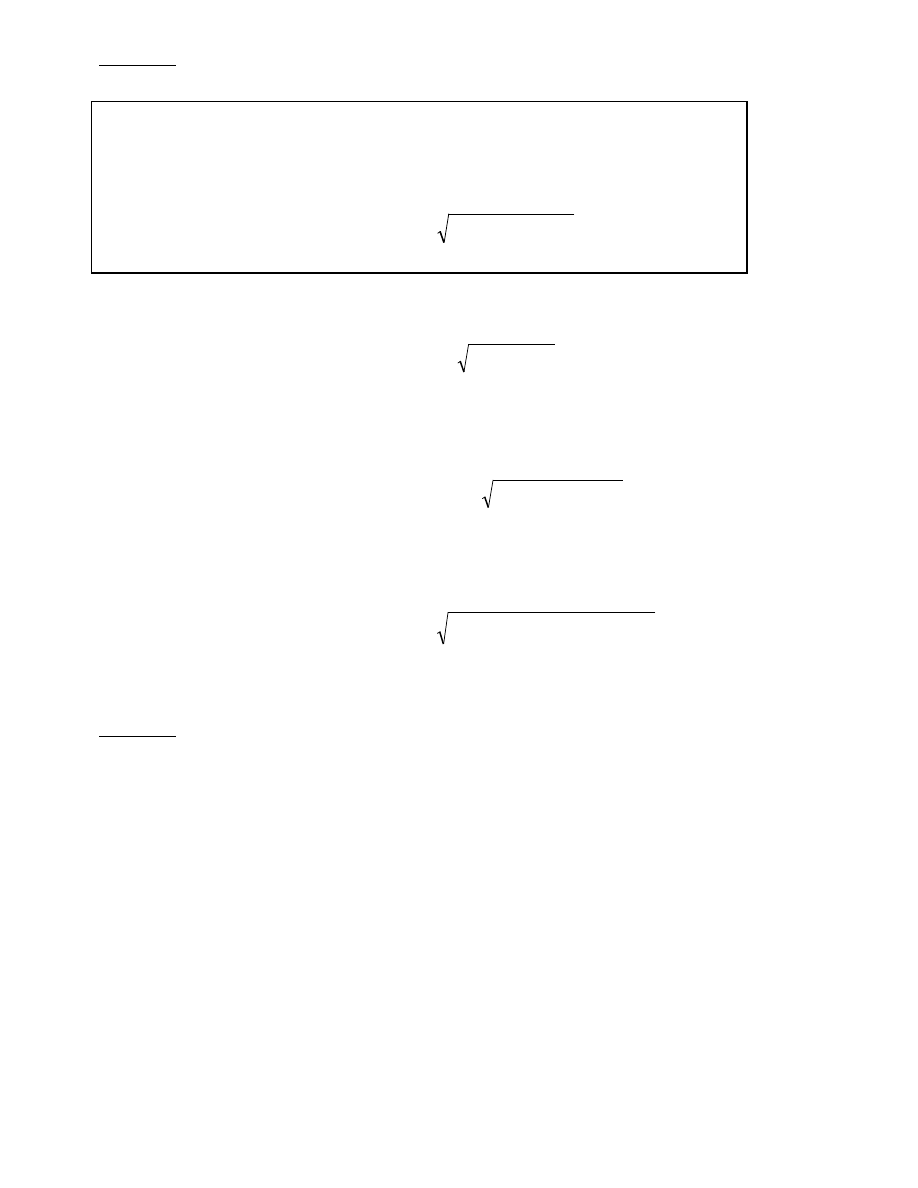
R
OZDZIAŁ
VI
Strona 64
64
64
64
Twierdzenie 3 (o zamianie całki krzywoliniowej nieskierowanej na całkę oznaczoną).
Jeżeli funkcja f jest ciągła na łuku gładkim
Γ
ΓΓ
Γ
={(x(t),y(t)): t
∈
∈
∈
∈
[
α
αα
α
,
ββββ
], to
((((
))))
[[[[ ]]]] [[[[ ]]]]
dt
(t)
y
(t)
x
x(t),y(t)
f
f(x,y)dl
2
2
β
α
Γ
′′′′
++++
′′′′
====
∫∫∫∫
∫∫∫∫
Uwaga 5.
Je
ż
eli łuk dany jest w postaci jawnej:
Γ={(x,y): y=g(x), x∈ [a,b]}, to
((((
))))
[[[[
]]]]
dx
x
g
x
g
x
f
dl
y
x
f
b
a
2
)
(
1
)
(
,
)
,
(
′′′′
++++
====
∫∫∫∫
∫∫∫∫
Γ
ΓΓ
Γ
Uwaga 6. J
e
ż
eli łuk dany jest w postaci biegunowej:
Γ: r=h(ϕ), ϕ∈ [a,b], to
((((
))))
[[[[
]]]] [[[[
]]]]
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
d
h
h
h
h
f
dl
y
x
f
b
a
2
2
)
(
)
(
sin
)
(
,
cos
)
(
)
,
(
′′′′
++++
====
∫∫∫∫
∫∫∫∫
Γ
ΓΓ
Γ
Uwaga 7.
Je
ż
eli łuk
Γ, i Γ = {x=(x
1
,x
2
, ... x
n
): x=
Φ(t)=(ϕ
1
(t),
ϕ
2
(t),...
ϕ
n
(t))}, to
((((
))))
[[[[ ]]]] [[[[ ]]]] [[[[ ]]]]
dt
t
t
t
t
t
t
f
dl
x
f
n
n
2
'
2
'
2
2
'
1
2
1
)
(
)
(
)
(
)
(
),...,
(
),
(
)
(
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ββββ
α
αα
α
++++
++++
====
∫∫∫∫
∫∫∫∫
Γ
ΓΓ
Γ
Przykład 5.
Wyznaczy
ć
pole cz
ęś
ci walca o równaniu x
2
+y
2
=ax wyci
ę
tego sfer
ą
o równaniu: x
2
+y
2
+z
2
=a
2
.

C
AŁKA POTRÓJNA
Strona 65
65
65
65
Przykład 6.
Obliczy
ć
całk
ę
:
∫
Γ
+
+
dl
z
y
x
2
2
2
, gdzie Γ: x=e
t
cost, y=e
t
sint, z=e
t
, t∈[0,1].
R
OZDZIAŁ
VI
Strona 66
66
66
66
Ć
wiczenia
1. Obliczy
ć
całki iterowane:
dz
xyz
1
dx
dy
a)
2
1
3
2
4
2
∫ ∫ ∫
,
dx
cosy
4xz
dy
dz
b)
1
0
0
4
2
∫ ∫ ∫
π
,
dz
xysin
dy
dx
c)
2
1
4
2
0
2
∫ ∫ ∫
π
z
,
dy
x
dz
dx
d)
1
1
-
2
1
-
4
2
∫ ∫ ∫
y
2. Zapisa
ć
dane obszary jako obszary normalne wzgl
ę
dem wszystkich płaszczyzn układu
współrz
ę
dnych:
0
z
,
z
y
x
,
a
z
y
x
a)
2
2
2
2
2
2
2
≥
≤
+
≤
+
+
,
0
z
z,
y
x
,
a
z
y
x
b)
2
2
2
2
2
2
≥
≤
+
≤
+
+
,
h
z
0
,
z
y
x
c)
2
2
2
≤
≤
≤
+
,
h
z
y
x
c)
2
2
≤
≤
+
.
3. Obliczy
ć
całk
ę
potrójn
ą
, je
ż
eli obszar V jest ograniczony danymi powierzchniami:
(
)
∫∫∫
−
+
V
dxdydz
4z
3y
2x
a)
, V: z=0, z=2, x=0, y=0, x+y=1;
∫∫∫
V
dxdydz
xyz
b)
, V: x≥0, y≥0, z≥0, x+y+z≤1,
0
,
0
,
6
cos
≥
≥
∫∫∫
=
=
π
=
π
=
≥
y
x
y
V
0
z
xy,
z
,
6
x
,
x,
y
:
V
dxdydz,
y
x
c)
,
∫∫∫
=
=
−
=
=
V
2
2
2
x
y,
x
:
V
dxdydz,
yz
x
d)
9
,
0
,
3
4
z
z
y
.
4. Wprowadzaj
ą
c współrz
ę
dne walcowe, obliczy
ć
wskazane całki po obszarach
ograniczonych danymi powierzchniami:
∫∫∫
≤
≤
≤
+
V
2
2
3
z
0
1,
y
x
:
V
dxdydz,
x
a)
,
(
)
∫∫∫
=
=
+
+
V
2
2
2
2
2
z
2z,
y
x
:
V
dxdydz,
x
b)
y
,
∫∫∫
=
+
+
=
+
+
V
2
2
2
2
2
0
y
x
,
1
y
x
:
V
dxdydz,
c)
x
z
,
∫∫∫
=
=
+
=
−
V
2
2
2
2
0
,
4
y
x
,
y
x
:
V
dxdydz,
d)
z
z
,
∫∫∫
=
=
≤
=
+
+
V
2
2
2
3
z
0,
z
0,
y
,
y
x
:
V
dxdydz,
x
e)
x
y
z
2
2
.
5. Wprowadzaj
ą
c współrz
ę
dne sferyczne, obliczy
ć
podane całki:
∫∫∫
≥
≥
≥
≤
+
+
+
+
V
2
2
2
2
2
2
0
z
0,
y
0,
x
,
1
y
x
:
V
dxdydz,
x
a)
z
z
y
,
(
)
∫∫∫
≥
≥
≥
≤
+
+
+
V
2
2
2
2
2
0
z
0,
y
0,
x
,
1
y
x
:
V
dxdydz,
b)
z
y
x
,
∫∫∫
≤
+
+
+
+
+
V
2
2
2
2
/
3
2
2
2
4
y
x
:
V
dxdydz,
)
(x
1
c)
z
z
y
,
(
)
∫∫∫
≤
+
+
+
V
2
2
2
2
2
2
y
x
:
V
dxdydz,
d)
z
z
y
x
,

C
AŁKA POTRÓJNA
Strona 67
67
67
67
(
)
∫∫∫
=
=
+
+
=
+
+
V
2
2
2
2
2
2
2
0
z
0,
2y
y
x
,
y
x
:
V
dv,
e)
z
y
x
,
∫∫∫
≤
+
=
+
+
V
2
2
2
2
2
2
z
y
x
,
4
y
x
:
V
dv,
f)
z
.
6. Obliczy
ć
całki:
0
a
ax,
y
x
:
L
dl,
y
x
a)
2
2
L
2
2
>
=
+
+
∫
,
0
4,
y
x
:
L
dl,
b)
2
2
L
2
≥
=
+
∫
y
x
,
[ ]
3
3
L
2
2
,
0
,
2e
r
:
L
dl,
y
x
c)
π
ϕ
ϕ
∈
=
+
∫
,
]
1
,
0
[
,
,
sin
,
cos
:
L
dl,
y
x
d)
L
2
2
2
∈
=
=
=
+
+
∫
t
e
z
t
e
y
t
e
x
z
t
t
t
,
(
)
dl,
e)
L
∫
− x
y
L: łuk krzywej
3
x
y
=
ł
ą
cz
ą
cy punkty A(1,1) i B(2,8),
]
2
,
1
[
2x,
y
:
L
dl,
f)
2
L
∈
=
∫
x
y
x
.
7. Obliczy
ć
pole powierzchni cz
ęś
ci walca S za pomoc
ą
całki krzywoliniowej
nieskierowanej:
1
y
x
:
S
a)
2
2
=
+
zawarte mi
ę
dzy płaszczyznami z = −x, z=5+y,
2
2
2
a
y
x
:
S
b)
=
+
zawarte mi
ę
dzy płaszczyzn
ą
z=0 i powierzchni
ą
0
a
,
a
x
a
z
2
>
+
=
.

R
OZDZIAŁ
VI
Strona 68
68
68
68

VII
Całka powierzchniowa
niezorientowana
R
OZDZIAŁ
VII
Strona 70
70
70
70
Niech g: S
→ℜ b
ę
dzie funkcj
ą
okre
ś
lon
ą
na płacie regularnym S b
ę
d
ą
cym wykresem funkcji f
dla (x,y)∈D.
Dzielimy obszar D na n podobszarów regularnych D
i
i oznaczamy przez S
i
odpowiadaj
ą
ce tym podobszarom cz
ęś
ci płata S, a przez
∆S
i
pola tych płatów cz
ęś
ciowych.
Wybieraj
ą
c z płata cz
ęś
ciowego S
i
dowolny punkt P
i
(x
i
,y
i
,z
i
) tworzymy sum
ę
całkow
ą
:
∑
=
∆
=
n
i
i
i
n
S
P
f
s
1
)
(
Je
ż
eli dla ka
ż
dego normalnego ci
ą
gu podziałów obszaru D ci
ą
g (s
n
) ma granic
ę
niezale
ż
n
ą
od
wyboru punktów P
i
, to granic
ę
t
ę
nazywamy całk
ą
powierzchniow
ą
niezorientowan
ą
z funkcji
g po płacie S i oznaczamy:
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
S
S
S
gdS
dS
g
dS
z
y
x
g
lub
,
lub
)
,
,
(
(w przypadku, gdy powierzchnia S jest zamkni
ę
ta).
Je
ż
eli g=1, to
∫∫
∫∫
∫∫
∫∫
====
S
dS
S
– pole płata S.
Twierdzenie 1 (o zamianie całki powierzchniowej niezorientowanej na całkę
podwójną).
Jeżeli funkcja g jest ciągła na płacie gładkim S={(x,y,z): z=f(x,y), (x,y)
∈
∈
∈
∈
D},
gdzie D
⊂
⊂
⊂
⊂ℜ
ℜ
ℜ
ℜ
2
jest obszarem regularnym, to
[[[[ ]]]] [[[[ ]]]]
dxdy
f
f
1
y))
f(x,
y,
g(x,
dS
z)
y,
g(x,
D
2
'
y
2
'
x
S
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
++++
++++
====
Uwaga 1.
Je
ż
eli płat powierzchniowy S jest obrazem zbioru D le
żą
cego w innej
płaszczy
ź
nie ni
ż
płaszczyzna XOY, to teza twierdzenia b
ę
dzie analogiczna, np. je
ż
eli D le
ż
y
w płaszczy
ź
nie XOZ, to:
[[[[ ]]]] [[[[ ]]]]
dxdz
f
f
z
z
x
f
x
g
dS
z
y
x
g
D
z
x
S
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
++++
++++
====
2
'
2
'
1
)
),
,
(
,
(
)
,
,
(
Przykład 1.
Obliczy
ć
całk
ę
((((
))))
,
2
2
2
dS
z
y
x
S
∫∫
∫∫
∫∫
∫∫
++++
++++
gdzie S jest powierzchni
ą
sto
ż
ka o równaniu:
z
2
= x
2
+ y
2
odci
ę
t
ą
dwiema płaszczyznami: z=1 i z=2.

C
AŁKA POWIERZCHNIOWA NIEZORIENTOWANA
Strona 71
71
71
71
Przykład 2.
Obliczy
ć
całk
ę
:
dS
xyz
S
∫∫
∫∫
∫∫
∫∫
, gdzie S jest powierzchni
ą
walca o równaniu: y
2
=x odci
ę
t
ą
płaszczyznami: z=0, z=4, y=1, y=2.

R
OZDZIAŁ
VII
Strona 72
72
72
72
Zastosowania całek w mechanice
Masa obiektu materialnego
Je
ż
eli ρ jest g
ę
sto
ś
ci
ą
rozkładu masy, to:
∫∫∫∫
L
dl
z
y
x
)
,
,
(
ρρρρ
= M
– masa łuku materialnego L;
∫∫
∫∫
∫∫
∫∫
S
dS
z
y
x
)
,
,
(
ρρρρ
= M – masa płata materialnego S;
dxdy
y
x
D
)
,
(
∫∫
∫∫
∫∫
∫∫
ρρρρ
= M – masa płaskiego obszaru materialnego D;
∫∫∫
∫∫∫
∫∫∫
∫∫∫
V
dxdydz
z
y
x
)
,
,
(
ρρρρ
= M
– masa bryły materialnej V.
Je
ż
eli
ρ
=const., to obiekt materialny nazywamy
jednorodnym
.
Momenty statyczne
Z mechaniki wiadomo,
ż
e moment statyczny układu n punktów materialnych P
1
, P
2
, ... ,P
n
o masach m
1
, m
2
,...,m
n
wzgl
ę
dem płaszczyzny
Π okre
ś
lony jest wzorem:
,
)
,
(
1
*
i
n
i
i
m
P
d
M
⋅⋅⋅⋅
Π
Π
Π
Π
====
∑
∑
∑
∑
====
Π
Π
Π
Π
gdzie d
*
(P
i
,
Π) oznacza tzw. wzgl
ę
dn
ą
(opatrzon
ą
znakiem) odległo
ść
punktu P
i
od
płaszczyzny Π.
Bior
ą
c pod uwag
ę
definicj
ę
odpowiedniej całki Riemanna, mo
ż
emy okre
ś
li
ć
moment
statyczny bryły materialnej V o g
ę
sto
ś
ci rozkładu masy ρ nast
ę
puj
ą
co:
∫∫∫
∫∫∫
∫∫∫
∫∫∫
Π
Π
Π
Π
====
Π
Π
Π
Π
V
dxdydz
z
y
x
z
y
x
P
d
M
.
)
,
,
(
)
),
,
,
(
(
*
ρρρρ
Je
ż
eli w powy
ż
szym wzorze całk
ę
potrójn
ą
zast
ą
pimy całk
ą
powierzchniow
ą
niezorientowan
ą
lub krzywoliniow
ą
nieskierowan
ą
, to otrzymamy odpowiednie momenty wzgl
ę
dem
płaszczyzny, np..:
∫∫∫∫
Π
Π
Π
Π
====
Π
Π
Π
Π
L
dl
z
y
x
z
y
x
P
d
M
,
)
,
,
(
)
),
,
,
(
(
*
ρρρρ
gdzie L jest łukiem materialnym o g
ę
sto
ś
ci masy ρ.
Je
ż
eli w powy
ż
szych wzorach odległo
ść
zast
ą
pimy kwadratem odległo
ś
ci, to otrzymamy
wzór na moment bezwładno
ś
ci, np. wzór
[[[[
]]]]
∫∫
∫∫
∫∫
∫∫
Π
Π
Π
Π
====
Π
Π
Π
Π
S
dS
z
y
x
z
y
x
P
d
B
)
,
,
(
)
),
,
,
(
(
2
ρρρρ
okre
ś
la moment bezwładno
ś
ci płata materialnego S o g
ę
sto
ś
ci rozkładu masy
ρ.
Je
ż
eli zamiast płaszczyzny we
ź
miemy prost
ą
L lub punkt P
0
, to otrzymamy moment
bezwładno
ś
ci obiektu materialnego wzgl
ę
dem prostej lub wzgl
ę
dem punktu.
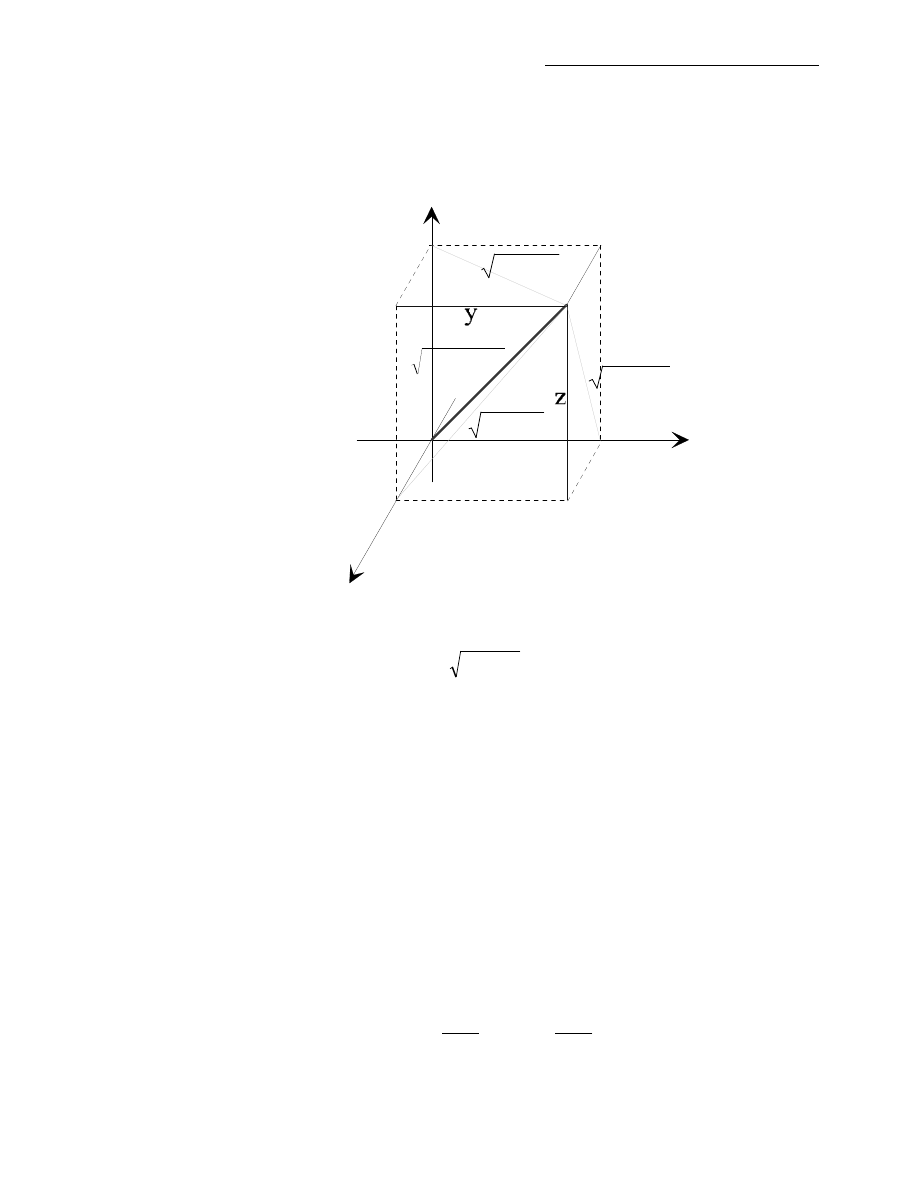
C
AŁKA POWIERZCHNIOWA NIEZORIENTOWANA
Strona 73
73
73
73
W praktyce najcz
ęś
ciej wyznaczamy momenty statyczne lub bezwładno
ś
ci wzgl
ę
dem
płaszczyzn układu, osi układu lub pocz
ą
tku układu współrz
ę
dnych. Poni
ż
szy rysunek
przedstawia odległo
ś
ci dowolnego punktu P(x,y,z) od płaszczyzn, prostych i pocz
ą
tku układu
współrz
ę
dnych.
Moment statyczny wzgl
ę
dem osi OY materialnego płata S o g
ę
sto
ś
ci rozkładu masy
ρ:
.
)
,
,
(
2
2
dS
z
y
x
y
x
M
S
y
ρρρρ
∫∫
∫∫
∫∫
∫∫
++++
====
Moment bezwładno
ś
ci wzgl
ę
dem płaszczyzny XOZ materialnego łuku L o g
ę
sto
ś
ci rozkładu
masy ρ:
.
)
,
,
(
2
∫∫∫∫
====
L
xz
dl
z
y
x
y
B
ρρρρ
Moment statyczny wzgl
ę
dem osi OX materialnego obszaru płaskiego o g
ę
sto
ś
ci rozkładu
masy ρ:
∫∫
∫∫
∫∫
∫∫
====
D
y
dxdy
y
x
x
M
.
)
,
(
ρρρρ
Środek ciężkości obiektu materialnego
Współrz
ę
dne
ś
rodka ci
ęż
ko
ś
ci obiektu płaskiego:
.
,
M
M
y
M
M
x
x
c
y
c
====
====
z
x
y
x
2
2
y
x
+
2
2
z
x
+
2
2
z
y
+
2
2
2
z
y
x
+
+

R
OZDZIAŁ
VII
Strona 74
74
74
74
Np. współrz
ę
dne
ś
rodka ci
ęż
ko
ś
ci łuku materialnego:
,
)
,
(
)
,
(
∫∫∫∫
∫∫∫∫
====
L
L
c
dl
y
x
dl
y
x
x
x
ρρρρ
ρρρρ
.
)
,
(
)
,
(
∫∫∫∫
∫∫∫∫
====
L
L
c
dl
y
x
dl
y
x
y
y
ρρρρ
ρρρρ
Współrz
ę
dne
ś
rodka ci
ęż
ko
ś
ci obiektu przestrzennego:
.
,
M
M
z
M
M
y
M
M
x
xy
c
xz
c
yz
c
====
====
====
Np. współrz
ę
dne
ś
rodka ci
ęż
ko
ś
ci bryły materialnej V:
,
)
,
,
(
)
,
,
(
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
====
V
V
c
dxdydz
z
y
x
dxdydz
z
y
x
x
x
ρρρρ
ρρρρ
,
)
,
,
(
)
,
,
(
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
====
V
V
c
dxdydz
z
y
x
dxdydz
z
y
x
y
y
ρρρρ
ρρρρ
.
)
,
,
(
)
,
,
(
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
====
V
V
c
dxdydz
z
y
x
dxdydz
z
y
x
z
z
ρρρρ
ρρρρ
Przykład 3.
Wyznaczy
ć
współrz
ę
dne
ś
rodka ci
ęż
ko
ś
ci jednorodnego łuku cykloidy L: x=a(t-sint), y=a(1-
cost), a>0, t
∈[0,2π].

C
AŁKA POWIERZCHNIOWA NIEZORIENTOWANA
Strona 75
75
75
75
Ć
wiczenia
1. Obliczy
ć
całki po wskazanych powierzchniach:
∫∫
≥
=
=
=
=
S
2
0
y
2,
x
4,
z
0,
z
x,
y
:
S
dS,
xyz
a)
,
∫∫
≤
+
−
−
=
S
2
2
2
2
1
y
x
,
x
y
1
z
:
S
dS,
b)
,
(
)
0
2
,
x
z
:
S
dS,
x
c)
2
2
2
S
2
2
2
2
≤
−
+
+
+
=
−
∫∫
z
z
y
x
y
y
,
(
)
0
,
0
2
,
x
z
:
S
dS,
x
d)
2
2
S
2
2
2
2
2
2
2
2
>
≤
+
+
+
=
+
+
∫∫
k
x
y
x
y
k
z
y
z
x
y
,
px
z
z
z
y
x
2
,
0
,
2
2
2
2
=
≥
=
+
∫∫
S
:
S
dS,
c)
.
2. Wyznaczy
ć
mas
ę
wskazanego obiektu materialnego o danej g
ę
sto
ś
ci
ρ:
z
x
z)
y,
ρ
(x,
3,
z
0
4,
4y
x
:
V
a)
2
2
2
+
=
≤
≤
=
+
,
[
]
{
}
z
z)
y,
ρ(x,
,
t
t,
z
tsint,
y
tcost,
x
:
z)
y,
(x,
:
L
b)
=
π
∈
=
=
=
2
,
0
,
c) L – pierwsza spirala helisy: x=cost, y=sint, z=t, je
ż
eli g
ę
sto
ść
w ka
ż
dym
punkcie jest równa długo
ś
ci promienia wodz
ą
cego tego punktu,
2
2
2
2
2
2
x
z)
y,
ρ(x,
,
a
y
x
:
S
d)
y
z
+
=
=
+
+
,
2
x
y)
ρ(x,
],
8
,
3
[
lnx,
y
:
L
e)
=
∈
=
x
,
a],
,
0
[
,
a
x
ch
a
y
:
L
f)
∈
=
x
g
ę
sto
ść
jest odwrotnie proporcjonalna do rz
ę
dnej
punktu,
xy
y)
ρ(x,
0,
y
4x,
y
x
:
D
g)
2
2
=
≤
≤
+
.
3. Obliczy
ć
wskazany moment bezwładno
ś
ci danego obiektu materialnego:
const.
a
y)
ρ(x,
Rx,
y
x
:
D
,
B
a)
2
2
0
=
=
≤
+
const.
a
z)
y,
ρ
(x,
0,
z
2x,
x,
y
x
:
V
,
B
b)
2
2
2
z
=
=
=
=
=
+
z
const.
a
z)
y,
ρ
(x,
0,
z
,
0
0,
x
4,
y
x
:
S
,
B
c)
2
2
2
XY
=
=
≥
≥
≥
=
+
+
y
z
4. Wyznaczy
ć
ś
rodek ci
ęż
ko
ś
ci danego jednorodnego obiektu materialnego:
y
x
x,
y
:
D
a)
2
2
=
=
,
0
,
a
y
:
V
b)
2
2
2
2
≥
≤
+
+
z
z
x
,
0
,
0
,
0
,
1
y
:
V
c)
2
2
≥
≥
≥
−
=
+
z
y
x
z
x
,
a
z
0
az,
y
x
:
S
d)
2
2
≤
≤
=
+
,
[
]
π
∈
−
=
−
=
0,2
t
cost),
3(1
y
sint),
3(t
x
:
L
e)
.

R
OZDZIAŁ
VII
Strona 76
76
76
76

VIII
Całka krzywoliniowa
skierowana
(zorientowana)
R
OZDZIAŁ
VIII
Strona 78
78
78
78
Niech
Γ b
ę
dzie łukiem zwykłym w
ℜ
n
okre
ś
lonym równaniem:
x=
Φ(t), t∈[α,β], Φ=(ϕ
1
,
ϕ
2
, ... ,
ϕ
n
).
Punkt A o wektorze wodz
ą
cym Φ(α) nazywamy pocz
ą
tkiem łuku a punkt B o wektorze
wodz
ą
cym Φ(β) ko
ń
cem łuku.
Łuk
Γ b
ę
dziemy oznacza
ć
AB
, wówczas łuk
−Γ = Γ
−
=
BA
okre
ś
lamy równaniem:
x=
Φ(−t), t∈[−β ,−α].
Łuki AB i BA b
ę
dziemy uwa
ż
a
ć
za przeciwnie zorientowane (skierowane).
Na łuku okre
ś
lamy pole wektorowe F:
Γ→ℜ
n
, gdzie F=(f
1
, ... ,f
n
).
Dzielimy przedział na m cz
ęś
ci. Podział ten implikuje podział łuku na m łuków cz
ęś
ciowych.
Oznaczamy wektor
i
i
A
A
1
−
przez
∆x
i
= x
i
- x
i-1
=
Φ(t
i
) -
Φ(t
i-1
) a przez P
i
dowolny punkt łuku
cz
ęś
ciowego i utwórzmy sum
ę
całkow
ą
:
i
m
i
i
x
P
F
∆
∆∆
∆
====
∑
∑
∑
∑
====
)
(
S
1
m
Je
ż
eli ci
ą
g (s
m
) jest zbie
ż
ny do tej samej granicy wła
ś
ciwej przy dowolnym podziale
normalnym odcinka [
α,β] i niezale
ż
nie od wyboru punktów P
i
, to granic
ę
t
ę
nazywamy całk
ą
krzywoliniow
ą
skierowan
ą
z pola wektorowego F (albo z funkcji F) po łuku
Γ
i oznaczamy
symbolem:
.
)
,...,
(
...
)
,...,
(
...
1
1
1
1
1
1
n
n
n
n
n
n
dx
x
x
f
dx
x
x
f
dx
f
dx
f
dx
F
++++
++++
====
++++
++++
====
∫∫∫∫
∫∫∫∫
∫∫∫∫
Γ
ΓΓ
Γ
Γ
ΓΓ
Γ
Γ
ΓΓ
Γ
o
Je
ż
eli łuk jest konturem, to całk
ę
oznaczamy symbolem:
∫
Γ
dx
F
o
i nazywamy
cyrkulacją pola
wektorowego F po łuku zamkniętym zorientowanym
ΓΓΓΓ
.
Gdy n = 2 lub n = 3 to całk
ę
b
ę
dziemy oznacza
ć
symbolami:
,
)
,
(
)
,
(
∫
Γ
+
dy
y
x
q
dx
y
x
p
∫
Γ
+
+
dz
z
y
x
r
dy
z
y
x
q
dx
z
y
x
p
)
,
,
(
)
,
,
(
)
,
,
(

C
AŁKA KRZYWOLINIOWA SKIEROWANA
(
ZORIENTOWANA
)
Strona 79
79
79
79
Uwaga1.
Je
ż
eli f
2
=f
3
= ... =f
n
=0, to
∫
∫
Γ
Γ
=
1
1
dx
f
dx
F o
Wynika st
ą
d równo
ść
:
.
...
...
1
1
1
1
n
n
n
n
dx
f
dx
f
dx
f
dx
f
∫∫∫∫
∫∫∫∫
∫∫∫∫
Γ
ΓΓ
Γ
Γ
ΓΓ
Γ
Γ
ΓΓ
Γ
++++
++++
====
++++
++++
Uwaga 2.
Z definicji całki skierowanej wynika,
ż
e zmienia ona znak, gdy zmienimy
orientacj
ę
łuku na przeciwn
ą
(bo zmieni znak na przeciwny wektor ∆x
i
).
Je
ś
li wi
ę
c istnieje całka po łuku AB to istnieje całka po łuku BA i zachodzi równo
ść
:
∫∫∫∫
∫∫∫∫
−−−−
====
AB
BA
dx
F
dx
F
o
o
Uwaga 3.
Całka krzywoliniowa skierowana jest liniowa a tak
ż
e addytywna wzgl
ę
dem łuku,
tzn. je
ż
eli
AB
C
∈
, to:
.
∫∫∫∫
∫∫∫∫
∫∫∫∫
++++
====
AB
AC
CB
dx
F
dx
F
dx
F
o
o
o
Interpretacja fizyczna
Całka
∫
Γ
dx
F o
wyra
ż
a prac
ę
wykonan
ą
przez sił
ę
F (w polu wektorowym F) na drodze
Γ.
Nast
ę
pne twierdzenie podaje sposób obliczania całki krzywoliniowej skierowanej.
Twierdzenie 1 (o zamianie całki krzywoliniowej skierowanej na całkę oznaczoną)
Jeżeli pole wektorowe F jest ciągłe na łuku regularnym
Γ
ΓΓ
Γ
, to całka krzywoliniowa
skierowana istnieje i zachodzi równość:
[[[[
]]]]
((((
))))
((((
))))
[[[[
]]]]
dt
)
(
(t)
(t),...,
f
...
(t)
(t)
(t),...,
f
)
(
)
(
β
α
'
n
n
1
n
'
1
n
1
1
∫∫∫∫
∫∫∫∫
∫∫∫∫
++++
====
Φ
Φ
Φ
Φ′′′′
Φ
Φ
Φ
Φ
====
Γ
ΓΓ
Γ
t
dt
t
t
F
dx
F
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ϕϕϕϕ
ββββ
α
αα
α
o
Wniosek 1.
Jeżeli łuk dany jest równaniem: y=f(x), x
∈
∈
∈
∈
[a,b], to
[[[[
]]]] [[[[
]]]]
{{{{
}}}}
.
)
(
)
(
,
)
(
,
)
,
(
)
,
(
dx
x
f
x
f
x
q
x
f
x
p
dy
y
x
q
dx
y
x
p
b
a
∫∫∫∫
∫∫∫∫
′′′′
⋅⋅⋅⋅
++++
====
++++
Γ
ΓΓ
Γ
Uwaga 4.
Całk
ę
skierowan
ą
po łuku regularnym mo
ż
na zawsze zamieni
ć
na całk
ę
nieskierowan
ą
po tym łuku wykorzystuj
ą
c kosinusy kierunkowe (I, U7).
((((
))))
.
cos
....
cos
...
1
1
1
1
dl
f
f
dx
f
dx
f
n
n
n
n
∫∫∫∫
∫∫∫∫
Γ
ΓΓ
Γ
Γ
ΓΓ
Γ
++++
====
++++
++++
α
αα
α
α
αα
α

R
OZDZIAŁ
VIII
Strona 80
80
80
80
Przykład 1.
Obliczy
ć
całk
ę
: a)
∫
−
+
i
L
dy
x
y
xydx
,
)
(
b)
∫
+
i
L
dy
x
xydx
,
2
2
1
i=1,2,3, gdzie
L
1
: y=x, x
∈[0,1]; L
2
: y=x
2
, x
∈[0,1]; L
3
: y
2
=x, y
∈[0,1].

C
AŁKA KRZYWOLINIOWA SKIEROWANA
(
ZORIENTOWANA
)
Strona 81
81
81
81
Aby udowodni
ć
zwi
ą
zek mi
ę
dzy całk
ą
krzywoliniow
ą
skierowan
ą
po krzywej zamkni
ę
tej
ograniczaj
ą
cej obszar płaski D, okre
ś
limy krzyw
ą
dodatnio skierowaną (zorientowaną)
wzgl
ę
dem swego wn
ę
trza. Krzywa zamkni
ę
ta jest
dodatnio skierowana
, je
ż
eli poruszaj
ą
c si
ę
w tym kierunku po krzywej mamy po lewej stronie obszar, który ta krzywa ogranicza.
Twierdzenie 2 (Greena)
Jeżeli funkcje p i q są ciągłe wraz z pochodnymi
y
p
i
x
q
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
w domkniętym obszarze
normalnym D, którego brzeg jest skierowany dodatnio, to:
.
)
,
(
)
,
(
dxdy
y
p
x
q
dy
y
x
q
dx
y
x
p
D
D
∫∫∫∫
∫∫
∫∫
∫∫
∫∫
∂∂∂∂
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
====
++++
Uwaga 3.
Przyjmuj
ą
c w tezie twierdzenia Greena kolejno:
1. p=0, q=x mamy:
;
∫∫∫∫
∫∫
∫∫
∫∫
∫∫
∂∂∂∂
====
====
D
D
D
dxdy
xdy
2. p=y, q=0 mamy:
;
∫∫∫∫
∫∫
∫∫
∫∫
∫∫
∂∂∂∂
−−−−
====
−−−−
====
D
D
D
dxdy
ydx
3. p=-y, q=x mamy:
∫∫∫∫
∫∫
∫∫
∫∫
∫∫
∂∂∂∂
====
====
++++
−−−−
D
D
D
dxdy
xdy
ydx
2
2
otrzymamy trzy całki, które wyra
ż
aj
ą
pole obszaru D:
.
2
1
∫∫∫∫
∫∫∫∫
∫∫∫∫
∂∂∂∂
∂∂∂∂
∂∂∂∂
−−−−
====
====
++++
−−−−
====
D
D
D
ydx
xdy
xdy
ydx
D
R
OZDZIAŁ
VIII
Strona 82
82
82
82
Przykład 2.
Wyznaczy
ć
pole p
ę
tli li
ś
cia Kartezjusza: x
3
+ y
3
= 3xy.
Niezależność całki od drogi całkowania
Twierdzenie 3 (o niezależności całki krzywoliniowej skierowanej od drogi całkowania)
Je
ż
eli funkcje p i q s
ą
ci
ą
głe wraz z pochodnymi
y
p
i
x
q
∂∂∂∂
∂∂∂∂
∂∂∂∂
∂∂∂∂
w obszarze jednospójnym
domkni
ę
tym D, to całka
,
)
,
(
)
,
(
∫∫∫∫
Γ
ΓΓ
Γ
++++
dy
y
x
q
dx
y
x
p
po łuku regularnym
D
AB
⊂
⊂
⊂
⊂
jest
niezale
ż
na od drogi całkowania wtedy i tylko wtedy, gdy
.
:
)
,
(
x
q
y
p
D
y
x
∂∂∂∂
∂∂∂∂
====
∂∂∂∂
∂∂∂∂
∈
∈
∈
∈
∀
∀
∀
∀
Uwaga 4.
Warunek z twierdzenia jest tak
ż
e warunkiem koniecznym i wystarczaj
ą
cym
potencjalno
ś
ci pola wektorowego [p,q]. Wyra
ż
enie pdx+qdy jest wtedy ró
ż
niczk
ą
zupełn
ą
pewnej funkcji U, któr
ą
nazywamy funkcj
ą
pierwotn
ą
funkcji wektorowej F=[p,q] (albo
potencjałem tego pola wektorowego);
Wtedy:
∫∫∫∫
−−−−
====
++++
AB
A
U
B
U
qdy
pdx
).
(
)
(
Potencjał U mo
ż
na wyznaczy
ć
z nast
ę
puj
ą
cego wzoru bior
ą
c dowolne (x
0
,y
0
) (w którym pole
F jest okre
ś
lone) nale
żą
ce do D:
.
)
,
(
)
,
(
)
,
(
0
0
0
∫∫∫∫
∫∫∫∫
++++
====
y
y
x
x
dt
t
x
q
dt
y
t
p
y
x
U

C
AŁKA KRZYWOLINIOWA SKIEROWANA
(
ZORIENTOWANA
)
Strona 83
83
83
83
Uwaga 5.
Całka
∫∫∫∫
Γ
ΓΓ
Γ
++++
++++
dz
z
y
x
r
dy
z
y
x
q
dx
z
y
x
p
)
,
,
(
)
,
,
(
)
,
,
(
nie zale
ż
y od drogi całkowania,
je
ż
eli krzywa
Γ
le
ż
y w obszarze jednospójnym i w obszarze tym pole wektorowe F spełnia
warunek:
rotF=rot[p,q,r]=
0
r
.
Potencjał U mo
ż
na wyznaczy
ć
ze wzoru (podobnie jak w uwadze 4.):
.
t)dt
,
y
,
(x
r
z)dt
t,
,
q(x
z)dt
y,
p(t,
z)
y,
U(x,
0
0
x
x
y
y
z
z
0
0
0
0
∫∫∫∫
∫∫∫∫
∫∫∫∫
++++
++++
====
Przykład 3.
Obliczy
ć
całk
ę
:
∫
+
+
+
+
+
+
+
+
(3,2,1)
(1,0,1)
y
2
y
2
2
y
1)dz.
2xz
(2xe
2y)dy
x
z
(xe
y)dx
z
z
(e

R
OZDZIAŁ
VIII
Strona 84
84
84
84
Ć
wiczenia
1. Obliczy
ć
całk
ę
:
∫
+
−
L
ydy
x
dx
xy
2
)
1
(
, je
ż
eli krzywa L ł
ą
czy punkty A(1,0) i B(0,2) i jest:
a) prost
ą
o równaniu: 2x+y=2, b) łukiem paraboli: 4x+y
2
=4, c) łukiem elipsy:
4x
2
+ y
2
= 4.
2. Obliczy
ć
całk
ę
:
∫
+
+
−
L
dy
y
x
dx
y
x
)
(
)
(
2
, gdzie L jest łaman
ą
ł
ą
cz
ą
c
ą
punkty: O(0,0), A(2,0),
B(4,2).
3. Obliczy
ć
całki z danego pola wektorowego F po łuku L, je
ż
eli:
a) F=[xy, y], L: x = t
2
, y = t, t
∈[0,1], b) F=[e
x+y
, xy], L: x = 2+t, y = 3
−t,
t
∈[−1,1],
c) F=[yz, −xz, xy], L: x = e
t
, y =e
2t
, z=e
−t
, t∈[0,1], d) F=[x, y, z], L: x = acost, y =
asint, z=bt, t
∈[0,2π].
4. Obliczy
ć
cyrkulacj
ę
pola wektorowego F=[x+z, x – y, x] wzdłu
ż
elipsy C:
=
=
+
,
1
,
36
4
9
2
2
z
y
x
skierowanej zgodnie z ruchem wskazówek zegara.
5. L jest cz
ęś
ci
ą
prostej :
=
+
−
=
+
+
,
0
1
,
0
y
x
z
y
x
zorientowan
ą
tak,
ż
e y ro
ś
nie i y∈[−1,1]. Wyznaczy
ć
cyrkulacj
ę
F=[y,0,1] wzdłu
ż
L.
6. Wyznaczy
ć
cyrkulacj
ę
pola wektorowego F=[x
−y, x+y] wzdłu
ż
krzywej K. Sprawdzi
ć
wynik korzystaj
ą
c z tw. Greena:
a) K ma orientacj
ę
ujemn
ą
i jest sum
ą
łuku paraboli: x = y
2
– 4 i odcinka prostej: x = 0,
b) K jest okr
ę
giem: x
2
+ 2x + y
2
= 0 zorientowanym dodatnio.
7. Obliczy
ć
całki z podanego pola wektorowego po danej krzywej L:
a) F = [x
2
y, x
3
], gdzie L jest dodatnio zorientowanym brzegiem obszaru ograniczonego
krzywymi: y
2
=x, x
2
= y.
b)
+
+
+
+
=
2
2
2
2
2
ln
,
y
x
x
y
xy
y
x
F
, gdzie L jest dodatnio zorientowanym brzegiem
obszaru ograniczonego krzywymi: y = lnx, x = e, y = 0,
c) F = [ytg
2
x, tgx], gdzie L jest dodatnio zorientowanym okr
ę
giem: x
2
+ 2y + y
2
= 0.
8. Obliczy
ć
całki:
a)
[
] [
]
∫
+
−
−
+
+
+
+
+
)
1
,
1
(
)
0
,
0
(
2
)
cos(
)
cos(
dy
y
x
e
dx
y
x
e
y
x
y
x
,
b)
dy
x
y
x
y
x
y
dx
x
y
x
y
+
+
−
∫
π
cos
sin
cos
1
)
,
2
(
)
0
,
1
(
2
2
,

C
AŁKA KRZYWOLINIOWA SKIEROWANA
(
ZORIENTOWANA
)
Strona 85
85
85
85
c)
(
) (
) (
)
dz
xz
z
xe
dy
y
x
z
xe
dx
y
z
z
e
y
y
y
1
2
2
2
2
)
2
,
1
,
3
(
)
1
,
0
,
1
(
2
2
+
+
+
+
+
+
+
+
∫
.
9. Obliczy
ć
pole obszaru ograniczonego krzywymi:
a) x=cos
3
t, y=sin
3
t, t
∈[0,2π] (asteroida),
b) r =2(1+cos
ϕ), ϕ∈[0,2π] (kardioida),
c) y=x, y=1/x, y=x/4, x>0.
10. Obliczy
ć
całki:
a)
dy
e
ye
x
dx
xe
L
y
y
y
∫
+
+
2
2
2
,
gdzie L jest sum
ą
łuków: L
1
:x+y=
−2 , L
2
: x
2
+y
2
=4, L
3
: x=0, od punktu A(0,-2) przez
punkt B(-2,0) i C(2,0) do punktu D(0,0),
b)
dy
e
x
xy
dx
y
x
L
y
∫
−
+
+
+
2
2
2
3
6
)
3
(
, gdzie L jest półokr
ę
giem: x
2
+y
2
=4, y<0
od punktu A(-2,0) do punktu B(2,0).
11. Obliczy
ć
prac
ę
wykonan
ą
w polu wektorowym F wzdłu
ż
łuku L, je
ż
eli:
a) F=[y
2
, x
2
], L jest łukiem elipsy: x
2
+4y
2
=4 (y>0) ł
ą
cz
ą
cym punkty A(0,1) i B(2,0),
b) F=[y
3
+
2
x
e
, x
3
+tg
2
y], L jest dodatnio zorientowanym okr
ę
giem: x
2
+y
2
+4y=0.

R
OZDZIAŁ
VIII
Strona 86
86
86
86

IX
Całka powierzchniowa
zorientowana
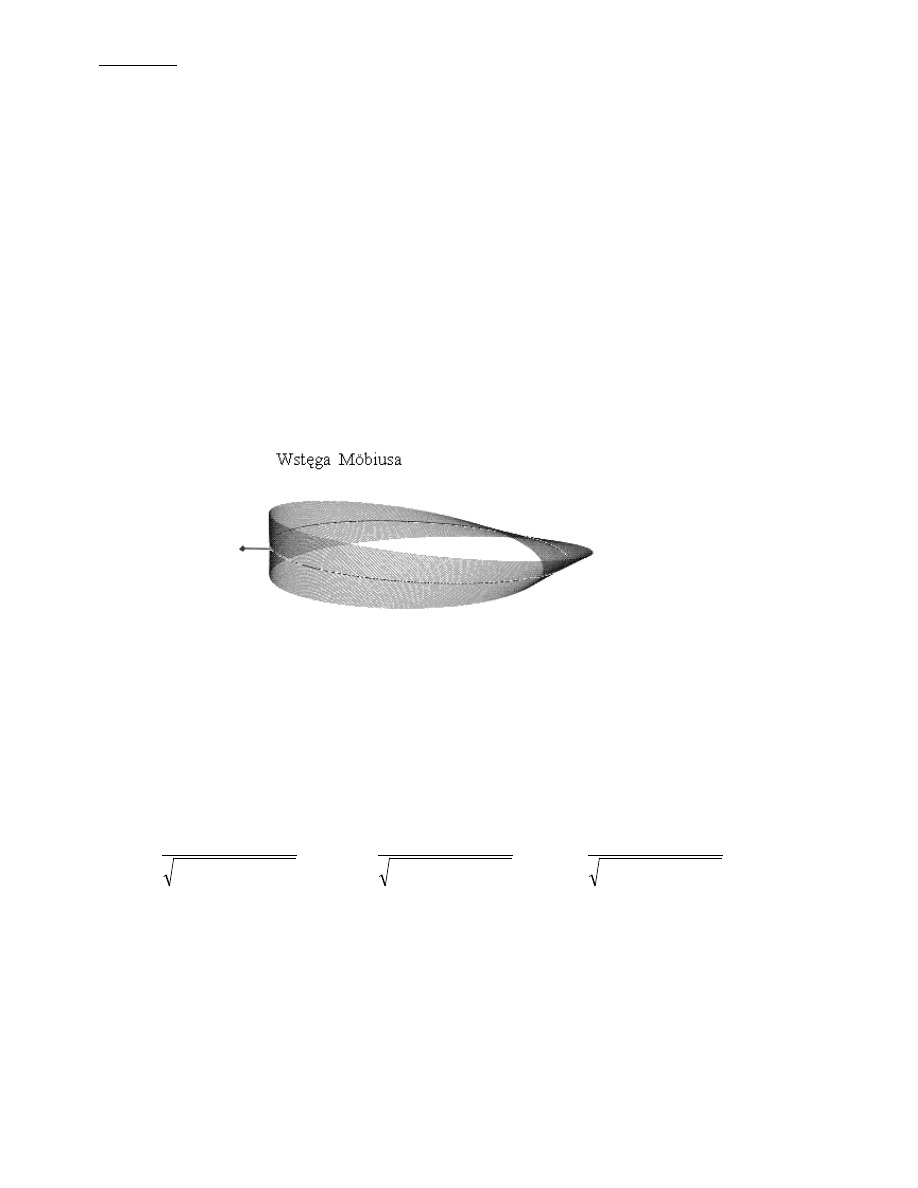
R
OZDZIAŁ
IX
Strona 88
88
88
88
W ka
ż
dym punkcie płata regularnego S o równaniu: z=g(x,y), (x,y)∈D jest okre
ś
lona
płaszczyzna styczna o wektorze normalnym [g
′
x
, g
′
y
,
−1] wzgl
ę
dnie [
−g′
x
,
−g′
y
, 1].
Ze wzgl
ę
du na ci
ą
gło
ść
pochodnych g
′
x
i g
′
y
wektory te poruszaj
ą
c si
ę
po powierzchni nie
mog
ą
przechodzi
ć
wzajemnie na siebie, co oznacza,
ż
e płat S jest powierzchni
ą
dwustronn
ą
.
Przykładem powierzchni jednostronnej jest wst
ę
ga Möbiusa.
We
ź
my pod uwag
ę
jedn
ą
za stron płata S, np. t
ę
, której wektorem normalnym jest wektor (-
g
x
, -g
y
,1). Wektor ten tworzy z osiami współrz
ę
dnych k
ą
ty
α, β i γ o cosinusach:
.
)
(
)
(
1
1
cos
,
)
(
)
(
1
cos
,
)
(
)
(
1
cos
2
2
2
2
2
2
y
x
y
x
y
y
x
x
g
g
g
g
g
g
g
g
′′′′
++++
′′′′
++++
====
′′′′
++++
′′′′
++++
′′′′
−−−−
====
′′′′
++++
′′′′
++++
′′′′
−−−−
====
γγγγ
ββββ
α
αα
α
Wersor n= [cos
α, cosβ, cosγ] jest wersorem normalnym płata S.

C
AŁKA POWIERZCHNIOWA ZORIENTOWANA
Strona 89
89
89
89
Niech b
ę
dzie dane pole wektorowe F=[p,q,r] okre
ś
lone na płacie S.
Całk
ę
postaci:
[[[[
]]]]
dS
z
y
x
r
z
y
x
q
z
y
x
p
ndS
F
S
S
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
++++
++++
====
γγγγ
ββββ
αααα
cos
)
,
,
(
cos
)
,
,
(
cos
)
,
,
(
o
nazywamy
całką powierzchniową zorientowaną z pola wektorowego F po płacie S
, albo
strumieniem pola wektorowego F przez powierzchnię S.
Całk
ę
t
ę
b
ę
dziemy oznacza
ć
tak
ż
e symbolem:
∫∫
∫∫
∫∫
∫∫
++++
++++
S
dxdy
z
y
x
r
dzdx
z
y
x
q
dydz
z
y
x
p
)
,
,
(
)
,
,
(
)
,
,
(
Zastosowanie fizyczne
Je
ż
eli F jest polem pr
ę
dko
ś
ci cieczy przepływaj
ą
cej przez płat S, to
∫∫
∫∫
∫∫
∫∫
S
ndS
F o
wyra
ż
a
obj
ę
to
ść
cieczy, która przepływa przez S w jednostce czasu.
Je
ż
eli zmienimy stron
ę
płata, to zamiast wersora n we
ź
miemy wersor –n i całka zmieni
znak,tzn.
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
−−−−
−−−−
====
S
S
ndS
F
ndS
F
,
o
o
Gdzie
−S oznacza płat przeciwnie zorientowany ni
ż
płat S.
Obliczanie całki powierzchniowej zorientowanej
Niech płat S: z=g(x,y), (x,y)
∈D ma orientacj
ę
tak
ą
,
ż
e cos
γ>0, wtedy:
.
)
(
)
(
1
1
cos
,
)
(
)
(
1
cos
,
)
(
)
(
1
cos
2
2
2
2
2
2
y
x
y
x
y
y
x
x
g
g
g
g
g
g
g
g
′′′′
++++
′′′′
++++
====
′′′′
++++
′′′′
++++
′′′′
−−−−
====
′′′′
++++
′′′′
++++
′′′′
−−−−
====
γγγγ
ββββ
α
αα
α
Uwzgl
ę
dniaj
ą
c twierdzenie o zamianie całki powierzchniowej zorientowanej na całk
ę
podwójn
ą
, wtedy
dxdy
g
g
dS
y
x
2
2
)
(
)
(
1
′′′′
++++
′′′′
++++
====
, otrzymamy:
∫∫
∫∫
∫∫
∫∫
====
++++
++++
S
dxdy
z
y
x
r
dzdx
z
y
x
q
dydz
z
y
x
p
)
,
,
(
)
,
,
(
)
,
,
(
[[[[
]]]]
∫∫∫∫∫∫∫∫
D
y
x
dxdy
y
x
g
y
x
r
g
y
x
g
y
x
q
g
y
x
g
y
x
p
))
,
(
,
,
(
)
(
))
,
(
,
,
(
)
(
))
,
(
,
,
(
++++
′′′′
−−−−
⋅⋅⋅⋅
++++
′′′′
−−−−
⋅⋅⋅⋅
====
R
OZDZIAŁ
IX
Strona 90
90
90
90
Uwaga 2.
Je
ż
eli np. płat S dany jest równaniem: x=h(y,z), (y,z)
∈D, i płat zorientowany jest
tak,
ż
e pierwsza współrz
ę
dna wektora normalnego jest dodatnia, to:
∫∫
∫∫
∫∫
∫∫
====
++++
++++
S
dxdy
z
y
x
r
dzdx
z
y
x
q
dydz
z
y
x
p
)
,
,
(
)
,
,
(
)
,
,
(
[[[[
]]]]
∫∫∫∫∫∫∫∫
D
z
y
dydz
h
z
y
z
y
h
r
h
z
y
z
y
h
q
z
y
z
y
h
p
)
(
))
,
),
,
(
(
)
(
))
,
),
,
(
(
))
,
),
,
(
(
′′′′
−−−−
⋅⋅⋅⋅
++++
′′′′
−−−−
⋅⋅⋅⋅
++++
====
Przykład 1.
Obliczy
ć
całk
ę
:
∫∫
∫∫
∫∫
∫∫
−−−−
S
zdxdy
xdydz
, gdzie S jest cz
ęś
ci
ą
powierzchni o równaniu:
z=
2
2
1
y
x
−−−−
−−−−
dla 0<z<1
−x zorientowan
ą
przez wektor normalny o dodatniej trzeciej współrz
ę
dnej.

C
AŁKA POWIERZCHNIOWA ZORIENTOWANA
Strona 91
91
91
91
Twierdznie 1 (Greena-Gaussa-Ostrogradskiego).
Jeśli pole wektorowe F=[p,q,r] jest klasy C
1
(V), gdzie V jest obszarem normalnym
względem wszystkich trzech płaszczyzn układu, a jego brzeg
∂∂∂∂
V=S jest regularną
powierzchnią zamkniętą zorientowaną tak, że jej wektor normalny n jest skierowany na
zewnątrz obszaru V, to
,
dxdydz
z
r
y
q
x
p
rdxdy
qdzdx
pdydz
S
V
∫∫
∫∫
∫∫
∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
====
++++
++++
albo w zapisie wektorowym:
.
∫∫
∫∫
∫∫
∫∫
∫∫∫
∫∫∫
∫∫∫
∫∫∫
====
S
V
dxdydz
divF
ndS
F o
Dowód.
R
OZDZIAŁ
IX
Strona 92
92
92
92
Uwaga 3.
Twierdzenie to jest uogólnieniem twierdzenia Greena na przestrze
ń
ℜ
3
.
Uwaga 4.
Je
ż
eli krzywa regularna L jest brzegiem płata S
1
i divF=0,
to całka powierzchniowa w polu F po płacie S
1
zale
ż
y tylko od krzywej L i jej orientacji, bo
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
====
⇒
⇒
⇒
⇒
====
2
1
,
0
S
S
S
ndS
F
ndS
F
ndS
F
o
o
o
gdzie S
2
jest drugim płatem rozpi
ę
tym na
krzywej L.
Uwaga 5.
Obj
ę
to
ść
obszaru mo
ż
na obliczy
ć
za pomoc
ą
całki powierzchniowej
zorientowanej:
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
∫∫
++++
++++
====
====
====
====
∂∂∂∂
∂∂∂∂
∂∂∂∂
S
V
V
V
zdxdy
ydzdx
xdydz
zdxdy
ydzdx
xdydz
V
.
3
1
Przykład 2.
Obliczy
ć
całk
ę
:
∫∫
∫∫
∫∫
∫∫
++++
++++
S
zdxdy
y
ydzdx
x
xzdydz
,
2
2
gdzie S jest zewn
ę
trzn
ą
powierzchni
zamkni
ę
tej ograniczonej powierzchniami: x
2
+y
2
=1, z=x
2
+y
2
, x
≥0, y≥0, z≥0.

C
AŁKA POWIERZCHNIOWA ZORIENTOWANA
Strona 93
93
93
93
Twiedzenie 2 (Stokesa).
Jeżeli krzywa L jest brzegiem regularnego płata S zorientowanego tak, że dodatniej
orientacji krzywej L opowiada dodatnia orientacja rzutu tej krzywej na płaszczyznę
XOY a określone na płacie S pole wektorowe F=[p,q,r] jest klasy C
1
, to zachodzi
równość:
dxdy
y
p
x
q
dzdx
x
r
z
p
dydz
z
q
y
r
rdz
qdy
pdx
L
S
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
++++
∂∂∂∂
∂∂∂∂
−−−−
∂∂∂∂
∂∂∂∂
====
++++
++++
∫∫∫∫
∫∫
∫∫
∫∫
∫∫
albo w zapisie wektorowym:
∫∫∫∫
∫∫
∫∫
∫∫
∫∫
====
L
S
ndS
rotF
Fdx
.
)
(
o
Przykład 3.
Stosuj
ą
c twierdzenie Stokesa obliczy
ć
:
∫
+
+
+
+
+
K
x
2
2
sinzdz
arctgy)dy
(xz
sinx)dx
e
)z
y
((x
,
gdzie K jest dodatnio zorientowan
ą
krzyw
ą
b
ę
d
ą
c
ą
cz
ęś
ci
ą
wspóln
ą
paraboloidy o równaniu
z = 4
− x
2
− y
2
i nieujemnych półpłaszczyzn układu współrz
ę
dnych.
R
OZDZIAŁ
IX
Strona 94
94
94
94
Ć
wiczenia
1. S jest cz
ęś
ci
ą
powierzchni bocznej walca o równaniu: x
2
+y
2
=1, gdy 1
≤z≤2 zorientowan
ą
na zewn
ą
trz walca. Obliczy
ć
:
∫∫
−
−
S
zdxdy
ydzdx
xdydz
2
.
2. Powierzchnia S dana jest równaniami: x=u+s, y=u
2
+s
2
, z=u
−s, (u,s)∈[−1,1]
2
. Obliczy
ć
:
∫∫
+
S
dxdy
dzdx
, gdzie S jest zorientowana tak,
ż
e wektor normalny do tej powierzchni
w punkcie (0,0,0) ma kierunek wektora [0,1,0].
3. Obliczy
ć
strumie
ń
pola wektorowego F=[z
2
, 0, 1] przez zewn
ę
trzn
ą
stron
ę
powierzchni
sfery: x
2
+y
2
+z
2
=4.
4. Obliczy
ć
strumie
ń
pola wektorowego F=[x
3
, y
3
, z
3
] przez zewn
ę
trzn
ą
stron
ę
powierzchni:
x
2
+y
2
=z
2
, 1
≤z≤2.
5. Dane jest pole wektorowe F=[1
−x
2
, f(y), z(2x
−y)]. Okre
ś
li
ć
funkcj
ę
f tak, aby divF=0.
Obliczy
ć
strumie
ń
otrzymanego pola wektorowego przez koło:
=
=
+
.
0
,
1
2
2
x
z
y
Wybra
ć
orientacj
ę
tak, aby wektor normalny miał kierunek wektora [1,0,0] w punkcie (0,1,0).
6. Obliczy
ć
:
∫∫
+
+
S
dxdy
z
dzdx
y
dydz
x
3
3
3
, gdzie S zewn
ę
trznie zorientowan
ą
sfer
ą
: x
2
+y
2
+z
2
=9.
7. Obliczy
ć
:
∫∫
−
−
S
z
dzdx
dxdy
e
)
(
2
, gdzie S zewn
ę
trznie zorientowan
ą
powierzchni
ą
sto
ż
ka:
1
,
2
2
≤
+
=
z
y
x
z
.
8. Obliczy
ć
:
∫∫
S
xdydz
, gdzie S jest zewn
ę
trzn
ą
stron
ą
sfery: x
2
+y
2
+z
2
=a
2
.
9. Obliczy
ć
:
[
]
dS
x
y
z
x
y
z
S
∫∫
γ
−
+
β
−
+
β
−
cos
)
(
cos
)
(
cos
)
(
2
2
2
2
2
2
, gdzie S jest zewn
ę
trzn
ą
stron
ą
półsfery: x
2
+y
2
+z
2
=a
2
, z<0.
10. Obliczy
ć
:
∫∫
+
+
S
ydxdy
xzdzdx
dydz
z
2
, gdzie S jest zewn
ę
trzn
ą
stron
ą
paraboloidy:
x
2
+y
2
= 9 – z , z>5.
11. Obliczy
ć
strumie
ń
pola wektorowego F=[y, x, z] przez powierzchni
ę
S zorientowan
ą
zewn
ę
trznie, gdzie S jest brzegiem bryły ograniczonej powierzchniami:
a)
2
2
2
2
1
,
y
x
z
y
x
z
−
−
−
=
+
−
=
, b) x
2
+z
2
=4, y=0, y=4.
12. Stosuj
ą
c twierdzenie Stokesa, obliczy
ć
:
a)
∫
+
+
+
+
+
+
L
dz
x
z
dy
z
y
dx
y
x
)
(
)
(
)
(
, gdzie L:
=
+
+
=
+
+
,
1
,
1
2
2
2
z
y
x
z
y
x

C
AŁKA POWIERZCHNIOWA ZORIENTOWANA
Strona 95
95
95
95
b)
∫
+
+
+
L
zdz
dy
dx
y
x
3
2
, gdzie L jest okr
ę
giem:
=
=
+
,
2
,
1
2
2
z
y
x
c)
∫
+
+
+
−
L
dz
dy
y
x
dx
y
x
)
(
)
(
, gdzie L:
−
+
=
−
+
=
,
1
,
1
2
2
2
2
y
x
z
y
x
z
i L jest zorientowana zgodnie
z wewn
ę
trzn
ą
(ujemn
ą
) orientacj
ą
obu powierzchni.
13. Obliczy
ć
:
∫
+
+
L
dz
z
dy
y
dx
x
2
2
2
, gdzie L jest brzegiem sto
ż
ka
2
2
y
x
z
+
=
odci
ę
tego
płaszczyzn
ą
z=1 o orientacji przeciwnej do ruchu wskazówek zegara.

R
OZDZIAŁ
IX
Strona 96
96
96
96

Strona 97
97
97
97
Literatura
1. Gewart M., Skoczylas Z., Analiza matematyczna 2 (Definicje, twierdzenia, wzory),
OWGiS, Wrocław 2005.
2. Kaczy
ń
ski A. M., Podstawy analizy matematycznej, t.2, OWPW, Warszawa 2000.
3. Karwowski O., Matematyka (cz
ęść
I iII)
, OWPW, Warszawa 1989.
4. Kowalski T. i inni, Zbiór zada
ń
z matematyki, t.2
, WPW, Warszawa 1984.
5. Krysicki W., Włodarski L., Analiza matematyczna w zadaniach, cz. 1, PWN,
Warszawa 1970.
6. Litewska K. i inni, Matematyka, t.1, OWPW, Warszawa 1997.
7. Nawrocki J., Matematyka (30 wykładów z
ć
wiczeniami),
OWPW, Warszawa 2002.
8. Stankiewicz W., Wojtowicz J., Zadania z matematyki dla wy
ż
szych uczelni
technicznych, t.1i 2
, PWN, Warszawa, 1982.

Strona 98
98
98
98
Wyszukiwarka
Podobne podstrony:
Analiza matematyczna II cz I
Pilitowska A Matematyka II IChiP konspekt cz (2)
analiza matematyczna II, Przodki IL PW Inżynieria Lądowa budownictwo Politechnika Warszawska, Semest
ANALIZA MATEMATYCZNA II
Sylabus-WEL-Analiza-matematyczna II Zo, Analiza matematyczna 2 zon ploch
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
Zad z egz (matma), gik, semestr 3, Analiza Matematyczna II
ANALIZA MATEMATYCZNA II, Notatki, MATEMATYKA
analiza(1), Politechnika Opolska, Analiza matematyczna II
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
WEL Analiza Matematyczna II
ANL, Studia, Analiza matematyczna II
Pilitowska A Matematyka II IChiP konspekt cz
WEL Analiza Matematyczna II n
02 01 11 12 01 57 e notatka analiza matematyczna II kolokwium II
Nawrocki J Matematyka cz 4 Szeregi funkcyjne i równania różniczkowe zwyczajne
02 01 11 12 01 16 e notatka analiza matematyczna II kolokwium I
PODSTAWA PROGRAMOWA PRZEDMIOTU MATEMATYKA II etap?ukacyjny
ściąga matematyka II semestr
więcej podobnych podstron