
Jan Nawrocki
MATEMATYKA cz. 4
Szeregi funkcyjne
i równania różniczkowe zwyczajne
Politechnika Warszawska 2010

Politechnika Warszawska
Wydział Samochodów i Maszyn Roboczych
Kierunek "Edukacja techniczno informatyczna"
02-524 Warszawa, ul. Narbutta 84, tel (22) 849 43 07, (22) 234 83 48
ipbmvr.simr.pw.edu.pl/spin/, e-mail:
sto@simr.pw.edu.pl
Opiniodawca: prof. dr hab. Krzysztof CHEŁMIŃSKI
Projekt okładki: Norbert SKUMIAŁ, Stefan TOMASZEK
Projekt układu graficznego tekstu: Grzegorz LINKIEWICZ
Skład tekstu: Janusz BONAROWSKI, Jan NAWROCKI
Publikacja bepłatna, przeznaczona jest dla studentów kierunku
"Edukacja techniczno informatyczna"
Copyright © 2010 Politechnika Warszawska
Utwór w całości ani we fragmentach nie może być powielany ani rozpowszechniany
za pomocą urządzeń elektronicznych, mechanicznych, kopiujących, nagrywających i innych
bez pisemnej zgody posiadacza praw autorskich.
ISBN 83-89703-42-4
Druk i oprawa: Drukarnia Expol P. Rybiński, J. Dąbek Spółka Jawna,
87-800 Włocławek, ul. Brzeska 4

Spis treści
I. Ciągi i szeregi funkcyjne .................................................................. 5
II. Szereg potęgowy ........................................................................... 13
III. Szeregi ortogonalne, szereg Fouriera............................................ 25
IV. Równania różniczkowe zwyczajne ................................................ 33
Równanie różniczkowe I rzędu ............................................................................ 34
V. Przegląd równań różniczkowych I rzędu....................................... 41
VI. Trajektorie ortogonalne, równania różniczkowe rzędu rzędu II
sprowadzalne do równań rzędu I .................................................. 53
VII. Równanie różniczkowe liniowe n-tego rzędu................................ 59
Równanie liniowe jednorodne n-tego rzędu o stałych współczynnikach
rzeczywistych ...................................................................................................... 63
VIII. Równania różniczkowe liniowe niejednorodne ............................. 67
Metoda uzmienniania stałych ............................................................................... 68
Metoda przewidywania rozwiązania szczególnego............................................... 71
Równanie Eulera n-tego rzędu ............................................................................. 75
Literatura ....................................................................................... 79

Przedmowa
Niniejsze materiały zostały opracowane w ramach realizacji Programu Rozwojowego Poli-
techniki Warszawskiej współfinansowanego ze środków PROGRAMU OPERACYJNEGO
KAPITAŁ LUDZKI. Przeznaczone są dla studentów pierwszego roku studiów inżynierskich
kierunku nauczania „Edukacja techniczno-informatyczna” prowadzonych na Wydziale Samo-
chodów i Maszyn Roboczych Politechniki Warszawskiej.
Swoim zakresem obejmują trzecią część tematyki określonej w programie studiów dla przed-
miotu pn. „Matematyka” opisanym w sylabusie opracowanym dla tego przedmiotu. Jest to
przedmiot z grupy przedmiotów podstawowych. W planie studiów przewidziano jego realiza-
cję na pierwszym i drugim roku studiów.
Na pierwszym semestrze są to dwa wykłady 30-godzinne i 15-godzinne ćwiczenia dla każde-
go z nich:
1. Matematyka cz. 1 – Algebra i geometria analityczna,
2. Matematyka cz. 2 – Analiza 1.
Na drugim semestrze 2 wykłady 30-godzinne i 30 -godzinne ćwiczenia dla każdego wykładu:
3. Matematyka cz. 3 – Analiza 2,
4. Matematyka cz. 4 – Szeregi funkcyjne i równania różniczkowe zwyczajne.
Na trzecim semestrze 30 - godzinny wykład:
5. Matematyka cz. 5 – Elementy probabilistyki i statystyki matematycznej.
W materiałach zawarto podstawowe treści z teorii szeregów funkcyjnych i równań
różniczkowych zwyczajnych potrzebne studentom wydziałów technicznych Politechniki
Warszawskiej.
Postanowiłem pominąć niektóre dowody, starając się jednocześnie ilustrować każde twierdze-
nie przykładem.
Najważniejsze definicje i wszystkie twierdzenia zostały zapisane w ramkach, co pozwala stu-
dentom zwrócić uwagę na te ważne w matematyce zdania.
Materiały te zostały napisane w formie kart do pracy na wykładzie. Student ma napisane
i wyróżnione w tekście definicje i twierdzenia oraz komentarze, może więc skupić się na
objaśnieniach wykładowcy, co pozwala na lepsze zrozumienie pojęć wprowadzanych na
wykładzie. Student na wykładzie uzupełnia samodzielnie tylko dowody twierdzeń i przykłady

I
Ciągi i szeregi funkcyjne

R
OZDZIAŁ
I
Strona 6
6
6
6
Ciągi funkcyjne
Oznaczmy przez
ℜ
A
zbiór wszystkich funkcji rzeczywistych określonych na podzbiorze A
przestrzeni metrycznej (Ω,d).
Ciągiem funkcyjnym nazywamy taki ciąg, którego wyrazami są funkcje f
n
∈ℜ
A
(jest to więc
odwzorowanie N
→ℜ
A
), i który oznaczamy (f
n
).
Dla ustalonego a
∈A ciąg (f
n
(a)) jest ciągiem liczbowym, możemy więc zbadać jego
zbieżność.
Ciąg (f
n
) nazywamy punktowo zbieżnym do funkcji f na zbiorze A, jeżeli
∀
x
∈
A: lim f
n
(x) = f(x),
co zapisujemy:
f
f
lim
n
A
=
lub
f
f
A
n
→
.
Uwaga 1. Korzystając z definicji granicy ciągu liczbowego, powyższą definicję możemy
zapisać następująco:
(
f
f
A
n
→
)
⇔
∀
x
∈A
∀
ε>0
∃
δ(x,ε)
∀
n>
δ: |f
n
(x)−f(x)
| < ε .
Przykład 1.
Wyznaczyć granicę ciągu (f
n
), jeżeli f
n
(x) =
1
x
n
1
+
, x
∈ℜ.
Z przykładu wynika, że granica ciągu funkcji ciągłych nie musi być ciągła. Następny przykład
pokazuje, że ciąg funkcji nieciągłych może mieć granicę ciągłą.
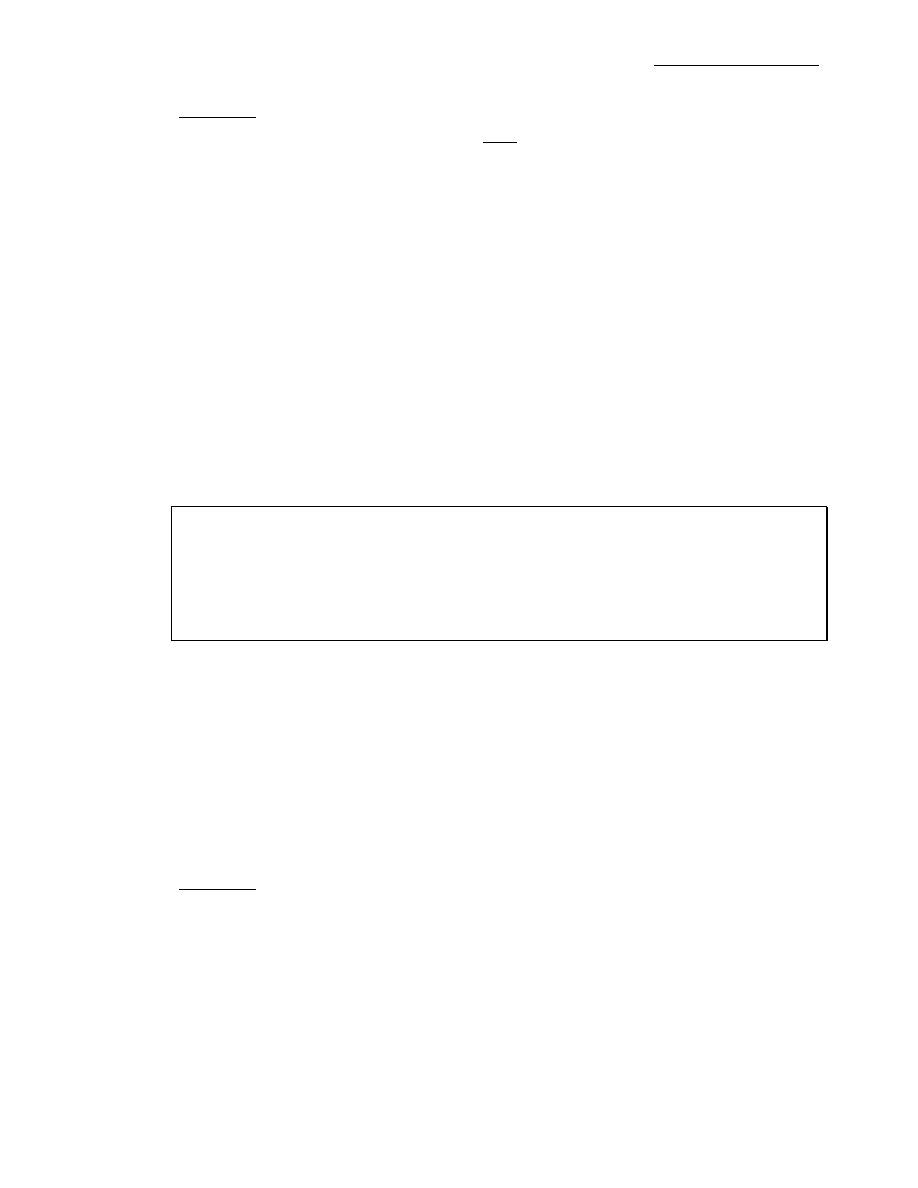
C
IĄGI I SZEREGI FUNKCYJNE
Strona 7
7
7
7
Przykład 2.
Wyznaczyć granicę ciągu (f
n
), jeżeli f
n
(x) =
n
D(x)
, x∈ℜ, gdzie D jest funkcją Dirichleta:
∉
∈
=
Q.
x
gdy
0,
Q,
x
gdy
1,
)
(x
D
Zdefiniujemy teraz inny rodzaj zbieżności, przy którym niemożliwa będzie sytuacja, aby ciąg
funkcji ciągłych miał granicę będącą funkcją nieciągłą.
Ciąg (f
n
) nazywamy jednostajnie zbieżnym do funkcji f na zbiorze A, jeżeli
∀
ε
>0
∃
δ(ε)
∀
x
∈
A
∀
n>
δ
:
|
f
n
(x)−f(x)
|
<
ε
,
co zapisujemy:
f
f
Lim
n
A
=
lub
f
f
A
n
→
→
.
Porównując definicję punktowej i jednostajnej zbieżności widzimy, że w definicji punktowej
zbieżności,
δ jest dobierana dla dowolnego ε i dla każdego x∈A, zaś w definicji jednostajnej
zbieżności, liczba
δ zależy tylko od ε i jest dobra dla każdego x∈A. W zapisie definicji
odpowiada to przestawieniu dwóch kwantyfikatorów ogólnych.
Zbieżność jednostajna ciągu funkcyjnego jest zbieżnością „mocniejszą” niż zbieżność
punktowa.
Wniosek 1. Zbieżność ciągu funkcyjnego jest jednostajna, wtedy i tylko wtedy, gdy dla
dowolnego
εεεε>0 istnieje skończone δ
δδ
δ((((εεεε))))=
A
x
sup
∈
δ
δδ
δ((((εεεε,x)))).
Przykład 3.
Zbadać zbieżność ciągu funkcyjnego (f
n
), gdy f
n
(x) = x
n
, x
∈(0,1).

R
OZDZIAŁ
I
Strona 8
8
8
8
Twierdzenie 1.
Jeżeli wyrazy ciągu funkcyjnego (f
n
) są funkcjami ciągłymi w zbiorze A i ciąg ten jest
jednostajnie zbieżny w A do funkcji f, to f jest funkcją ciągłą w A.
(
∀
∀
∀
∀
n
∈
∈
∈
∈N: f
n
∈
∈
∈
∈C(A) ∧
∧
∧
∧ Lim f
n
= f ) ⇒
⇒
⇒
⇒ ( f∈
∈
∈
∈C(A) ) .
Dowód. Z definicji jednostajnej zbieżności ciągu (f
n
) mamy:
∀
ε>0
∃
δ
1
(ε)
∀
x
∈A
∀
n>
δ
1
:
|f
n
(x)−f(x)
| < ε
Z definicji Cauchy’ego ciągłości funkcji w punkcie x
0
wynika, z uwagi na ciągłość funkcji f
n
,
ż
e:
∀
ε>0
∃
η>0
∀
x∈ A: d
1
(x,x
0
) < η ⇒ | f
n
(x)− f
n
(x
0
) | < ε.
Biorąc pod uwagę dwa powyższe zdania oraz nierówność:
| f(x)− f(x
0
)
| = | f(x)− f
n
(x) + f
n
(x)− f
n
(x
0
) + f
n
(x
0
)− f(x
0
)
| <
<
| f(x)− f
n
(x)
|+ | f
n
(x)− f
n
(x
0
)
| + | f
n
(x
0
)− f(x
0
)
| ,
mamy:
∀
ε>0
∃
η>0
∀
x
∈ A: d
1
(x,x
0
) <
η ⇒ | f(x)− f(x
0
)
| < 3ε,
co oznacza, że funkcja f jest ciągła w punkcie x
0
. Ponieważ x
0
jest dowolnym punktem ze
zbioru A, więc f
∈C(A).
Wniosek 2. Tezę twierdzenia 1 można wyrazić równością:
0
x
lim (
∞
→
n
lim f
n
(x)) =
∞
→
n
lim (
0
x
lim f
n
(x)).
Wniosek 3. Jeżeli ciąg funkcyjny funkcji ciągłych ma granicę, która jest funkcją
nieciągłą, to ciąg ten nie jest jednostajnie zbieżny.
Przykład 4.
Zbadać zbieżność ciągu funkcyjnego (f
n
), gdzie f
n
(x) = e
−nx
, x
∈[0,1].

C
IĄGI I SZEREGI FUNKCYJNE
Strona 9
9
9
9
Szeregi funkcyjne
Analogicznie jak w wykładzie 16 wprowadzamy pojęcie szeregu funkcyjnego.
Szeregiem funkcyjnym o wyrazach f
n
nazywamy parę ciągów funkcyjnych ( (f
n
), (s
n
) ),
gdzie s
n
=
∑
=
n
k
k
f
1
jest wyrazem ogólnym ciągu sum częściowych (s
n
). Szereg funkcyjny
( (f
n
), (s
n
) ) będziemy oznaczać symbolem
∑
∞
=1
n
n
f lub
∑
n
f .
Z uwagi na to, że określiliśmy dwa rodzaje zbieżności ciągu funkcyjnego: punktową
i jednostajną, określimy także dwa rodzaje zbieżności szeregu funkcyjnego.
Szereg
∑
n
f , którego ciąg sum częściowych (s
n
) jest zbieżny punktowo ( jednostajnie )
w zbiorze A, nazywamy szeregiem zbieżnym punktowo ( jednostajnie ) w zbiorze A.
Funkcję s, która jest granicą ciągu (s
n
) nazywamy sumą punktową (jednostajną) szeregu.
Uwaga 2. Jeżeli R
n
=s−s
n
oznacza n-tą resztę szeregu funkcyjnego, to zbieżność szeregu
oznacza zbieżność n-tej reszty do zera, tzn. s
n
→
A
s
⇔ R
n
→
A
0 .
Z twierdzenia 1 dla ciągów funkcyjnych i definicji sumy szeregu wynika:
Wniosek 4. Jeżeli wszystkie wyrazy szeregu
∑
n
f są funkcjami ciągłymi w zbiorze A
i szereg ten jest jednostajnie zbieżny do funkcji s, to funkcja graniczna s jest także ciągła
w zbiorze A.
Udowodnimy teraz twierdzenie, które określa warunek wystarczający zbieżności jednostajnej
szeregu ( takie twierdzenia nazywamy kryteriami).
Twierdzenie 2 (kryterium Weierstrassa).
Jeżeli szereg
∑
n
a jest szeregiem zbieżnym o wyrazach nieujemnych oraz
∀
∀
∀
∀
n
∈
∈
∈
∈N
∀
∀
∀
∀
x
∈
∈
∈
∈A: |||| f
n
(x)
|||| ≤
≤
≤
≤ a
n
,
to szereg funkcyjny
∑
n
f jest jednostajnie zbieżny w zbiorze A.
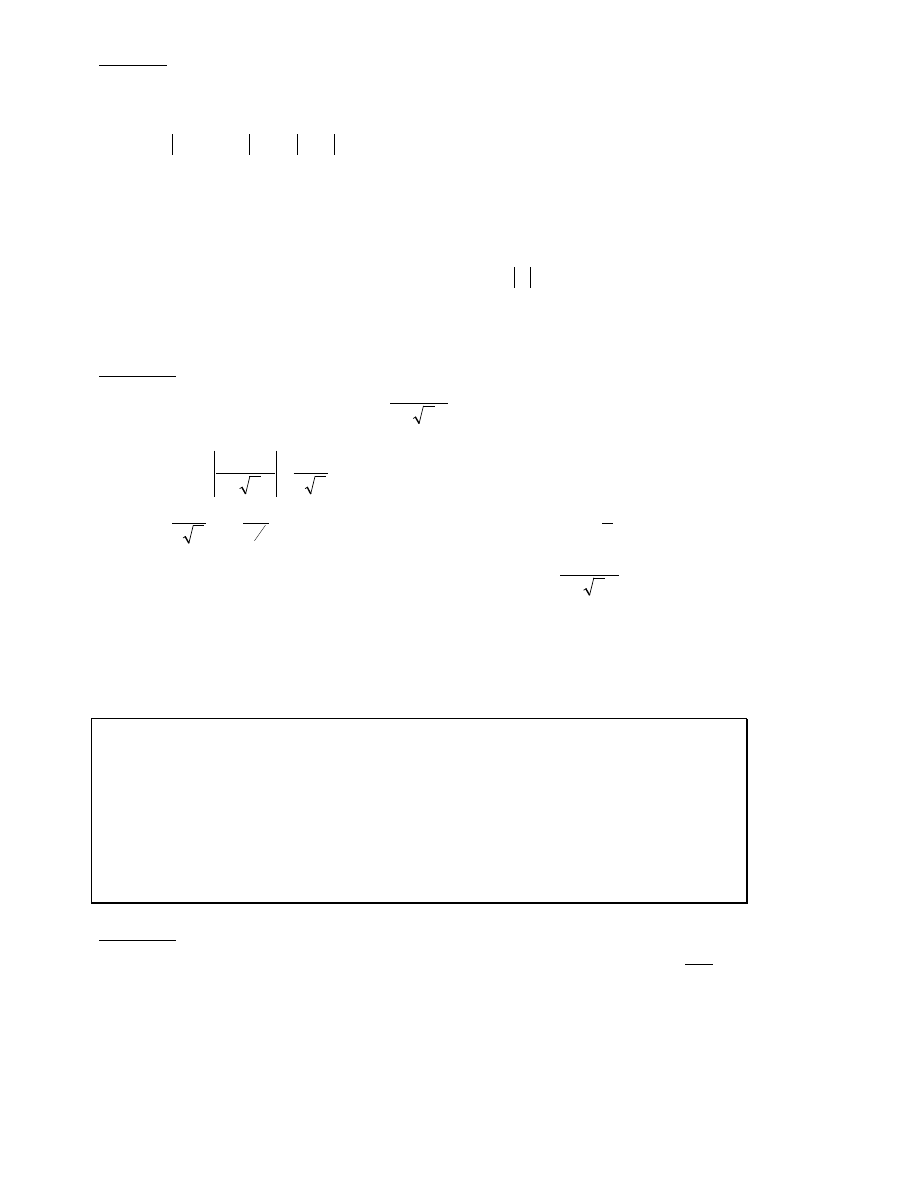
Dowód. Niech r
n
oznacza n-tą resztę szeregu liczbowego
∑
n
a , a ponieważ szereg ten jest
zbieżny, więc lim r
n
= 0, czyli
∀
ε>0
∃
δ>0
∀
n∈N: n>δ ⇒ | r
n
| =
∑
∞
+
=
1
n
k
k
a
< ε.
Uwzględniając uwagę 2, należy wykazać, że ciąg n-tych reszt szeregu funkcyjnego (R
n
) jest
jednostajnie zbieżny do zera na zbiorze A.
R
OZDZIAŁ
I
Strona 10
10
10
10
Dla n >
δ mamy:
| R
n
(x) | =
∑
∞
+
=
1
n
k
k
(x)
f
∑
∞
+
=
≤
1
n
k
n
(x)
f
≤
∑
∞
+
=
1
n
k
k
a
< ε, tak więc prawdziwe jest zdanie:
∀
ε>0
∃
δ(ε)
∀
x∈A
∀
n>δ : |R
n
(x)| < ε.
Zdanie to oznacza, że ciąg (R
n
) jest jednostajnie zbieżny do zera w zbiorze A, czyli szereg
funkcyjny
∑
n
f jest jednostajnie zbieżny w zbiorze A.
Uwaga 3. Jeżeli zamiast szeregu
∑
n
f weźmiemy szereg
∑
n
f , to dowód twierdzenia będzie
identyczny, tzn. jeśli spełnione są założenia twierdzenia Weierstrassa, to szereg funkcyjny
∑
n
f jest także bezwzględnie zbieżny.
Przykład 5.
Zbadać jednostajną zbieżność szeregu
∑
n
n
sin(nx)
n
, dla x∈ℜ .
Ponieważ funkcja sin jest ograniczona, więc
∀
n
∈N
∀
x
∈ℜ:
n
n
1
n
n
sin(nx)
n
≤
.
Szereg
∑
∑
=
2
3
n
1
n
n
1
jest zbieżny jako szereg Dirichleta ze stałą
α =
2
3
> 1.
Spełnione są więc obydwa założenia twierdzenia 2, więc szereg
∑
n
n
sin(nx)
n
jest jednostajnie
i bezwzględnie zbieżny dla x
∈ℜ.
Stwierdzenie jednostajnej zbieżności szeregu pozwala na tzw. „całkowanie wyraz po
wyrazie” i „różniczkowanie wyraz po wyrazie” takiego szeregu, co sprecyzujemy w dwóch
następujących twierdzeniach.
Twierdzenie 3.
Jeżeli spełnione są następujące założenia:
(a) funkcje f
n
: [a,b]
→
→
→
→ℜ
ℜ
ℜ
ℜ są całkowalne w sensie Riemanna w przedziale [a,b]
dla n = 1, 2, 3, ... ;
(b) szereg funkcyjny
∑
n
f jest jednostajnie zbieżny do funkcji s w tym przedziale,
to funkcja s jest całkowalna w sensie Riemanna w przedziale [a,b] i zachodzi równość:
∫
∑∫
=
b
a
b
a
n
(x)dx
f
s(x)dx
(lub inaczej:
(
)
∫
∑∫
∑
=
b
a
b
a
n
n
(x)dx
f
dx
(x)
f
) .
Przykład 6.
Całkując szereg
∑
n
x w przedziale [0,0.5], wyznaczyć sumę szeregu liczbowego
∑
n
n2
1
.

C
IĄGI I SZEREGI FUNKCYJNE
Strona 11
11
11
11
Twierdzenie 4.
Jeżeli spełnione są następujące założenia:
(a) funkcje f
n
:
[a,b]
→
→
→
→ ℜ
ℜ
ℜ
ℜ są różniczkowalne w przedziale [a,b];
(b) szereg funkcyjny
∑
n
f jest zbieżny do funkcji s w tym przedziale;
(c) szereg pochodnych
∑
′
n
f jest jednostajnie zbieżny w przedziale [a,b],
to funkcja s jest różniczkowalna w przedziale [a,b] i jej pochodna jest sumą szeregu
∑
′
n
f , tzn.
∀
∀
∀
∀
x
∈
∈
∈
∈[a,b]:
(
)
∑
∑
′
=
′
(x)
f
(x)
f
n
n
.
Przykład 7.
Wyznaczyć sumę szeregu
∑
−1
n
nx
.

R
OZDZIAŁ
I
Strona 12
12
12
12
Ć
wiczenia
1. Zbadać zbieżność ciągu funkcyjnego (f
n
), jeżeli:
a) f
n
(x) = x
n
, x
∈[0, 0.9]; b) f
n
(x) = e
−nx
, x
∈(0,+∞); c) f
n
(x) =
2
2
x
n
1
x
+
, x
∈ℜ;
d) f
n
(x) =
2
2
x
n
1
nx
+
, x
∈ℜ ; e) f
n
(x) =
n
sinnx
, x
∈ℜ.
2. Określić obszar zbieżności szeregu funkcyjnego:
a)
n
n
1
3x
x
2
n
−
∑
, b)
∑
−nx
2
4
n
, c)
∑
3
n
n
n
x
sin
2
.
3. Zbadać jednostajną zbieżność szeregu:
a)
ℜ
∈
+
∑
x
,
n
x
cosnx
2
2
, b)
∑
+
−
−
n
x
1)
(
1
n
, x
≥ 0, c)
∑
+
n
x
tg
n
x
n
4
4
2
, x
∈[0,1].
4. Wiedząc, że
∑
∞
=
−
0
n
nx
e
=
1
−
x
x
e
e
, gdy x > 0, wyznaczyć sumę szeregów:
∑
∞
=
−
1
n
nx
ne
,
∑
∞
=1
n
-nx
n
e
.

II
Szereg potęgowy
R
OZDZIAŁ
II
Strona 14
14
14
14
Szereg potęgowy
Zbadamy dokładniej szczególny rodzaj szeregów funkcyjnych, które mają rozległe zastoso-
wania w naukach inżynierskich.
Szereg funkcyjny
∑
n
f , którego wyrazy f
n
są funkcjami postaci f
n
(x)
= a
n
(x−x
0
)
n
,
gdzie x, x
0
∈ℜ
, a
n
∈ℜ
, n=0, 1 ,2, 3, ... , nazywamy szeregiem potęgowym o środku x
0
i współczynnikach a
n
.
Ponieważ podstawienie x−x
0
=t sprowadza szereg potęgowy o środku x
0
do szeregu
potęgowego o środku w zerze, więc w dalszym ciągu badać będziemy szereg potęgowy
postaci
∑
∞
=0
n
n
n
x
a
.
Szereg
∑
∞
=0
n
n
n
x
a
jest zbieżny , gdy x = 0 i jego sumą jest a
0
, dla x
≠0 szereg ten może być
zbieżny, albo rozbieżny, ale w tym przypadku można określić cały przedział zbieżności lub
rozbieżności tego szeregu.
Twierdzenie 1 (Abela).
Jeżeli szereg
∑
∞
=0
n
n
n
x
a
jest zbieżny dla x=ρ
ρ
ρ
ρ≠
≠
≠
≠0, to jest bezwzględnie zbieżny w przedziale
(−
||||ρ
ρ
ρ
ρ||||, ||||ρ
ρ
ρ
ρ||||) i jednostajnie zbieżny w każdym przedziale domkniętym zawartym
w przedziale (−
||||ρ
ρ
ρ
ρ||||, ||||ρ
ρ
ρ
ρ||||) .
Dowód.
Wniosek 1. Jeżeli szereg
∑
∞
=0
n
n
n
x
a
jest rozbieżny dla x=ρ
ρ
ρ
ρ≠
≠
≠
≠0, to jest rozbieżny dla
x
∈
∈
∈
∈(−∞
∞
∞
∞, −||||ρ
ρ
ρ
ρ|||| ) ∪
∪
∪
∪ (||||ρ
ρ
ρ
ρ||||, +∞
∞
∞
∞) .

S
ZEREG POTĘGOWY
Strona 15
15
15
15
Jeżeli istnieją takie x
≠0, dla których szereg
∑
∞
=0
n
n
n
x
a
jest zbieżny i szereg ten nie jest zbieżny
dla wszystkich x
∈ℜ, to istnieje kres górny wartości bezwzględnych x, dla których szereg ten
jest zbieżny.
Kres górny wartości bezwzględnych x, dla których szereg
∑
∞
=0
n
n
n
x
a
jest zbieżny nazywamy
promieniem zbieżności tego szeregu i oznaczamy przez r, tak więc
r = sup {
|
x
|
:
∑
∞
=0
n
n
n
x
a
<
∞
}.
Przyjmujemy r = 0, gdy szereg
∑
∞
=0
n
n
n
x
a
jest zbieżny tylko dla x = 0 i r =
∞
, gdy szereg ten jest
zbieżny
dla
każdego
x
∈ℜ
.
Przedział (−r,r) nazywamy przedziałem zbieżności szeregu
∑
∞
=0
n
n
n
x
a
.
Z twierdzenia Abela wynika, że szereg potęgowy o promieniu zbieżności r
≠0 jest zbieżny
w przedziale (−r,r) i rozbieżny w przedziałach (−
∞, −r) ∪ (r,∞). Dla x=r lub x=−r szereg
może być zbieżny lub rozbieżny; zbiór wszystkich x, dla których szereg jest zbieżny
będziemy nazywać obszarem zbieżności szeregu potęgowego.
Przykład 1.
Wyznaczyć obszar zbieżności szeregu
∑
n
x
n
.
Następne twierdzenie poda metodę wyznaczania promienia zbieżności szeregu potęgowego.
Twierdzenie 2 (Cauchy’ego-Hadamarda).
Jeżeli istnieje różna od zera granica właściwa µ
µ
µ
µ = lim
n
n
a , to promień zbieżności r
szeregu potęgowego
∑
∞
=0
n
n
n
x
a
jest równy r =
µ
1
.
R
OZDZIAŁ
II
Strona 16
16
16
16
Dowód.
Uwaga 1. Z dowodu twierdzenia wynika, że jeśli µ= 0, to szereg jest zbieżny dla każdego
x
∈ℜ i wtedy r = ∞, jeżeli zaś µ=∞, to r = 0 i szereg zbieżny jest tylko dla x = 0.
Wniosek 2. Z kryterium D’Alemberta dla szeregów liczbowych o współczynnikach
różnych od zera i twierdzenia Cauchy’ego-Hadamarda wynika, że promień zbieżności
można liczyć ze wzoru
r=lim
1
n
n
a
a
+
.
Wniosek 3. Z twierdzenia 1 (Rozdział I) wynika, że suma szeregu potęgowego jest
funkcją ciągłą w przedziale (−r,r), ponadto można wykazać, że jeśli szereg jest zbieżny
na krańcu przedziału, to suma ta jest funkcją jednostronnie ciągłą.
Przykład 2. Wyznaczyć obszar zbieżności szeregów:
(a)
∑
n
3
n
5
n
x
,
(b)
∑
n
x
!
n
,
(c)
∑
n
2n
3
x
, (d)
(
)
∑
+
n
n
n4
3
x
.

S
ZEREG POTĘGOWY
Strona 17
17
17
17
Rozważymy teraz problem „różniczkowania wyraz po wyrazie” i „całkowania wyraz po
wyrazie” szeregu potęgowego.
Twierdzenie 3 (o różniczkowaniu szeregu potęgowego).
Jeżeli promień zbieżności r szeregu potęgowego
∑
∞
=0
n
n
n
x
a
jest dodatni, to suma s tego
szeregu jest funkcją różniczkowalną i
∀
∀
∀
∀
x
∈
∈
∈
∈(−r,r): s′′′′(x) =
∑
∞
=1
n
1
-
n
n
x
na
,
oraz promień zbieżności szeregu pochodnych
∑
∞
=1
n
1
-
n
n
x
na
jest równy r.
Wniosek 4. Szereg potęgowy
∑
∞
=0
n
n
n
x
a
można „różniczkować wyraz po wyrazie” dowolną
ilość razy i jego suma s jest funkcją klasy C
∞
∞
∞
∞
w przedziale (−r,r).
Analogiczne twierdzenie można udowodnić dla szeregów „całkowanych wyraz po wyrazie”.
Twierdzenie 4 (o całkowaniu szeregu potęgowego)
Jeżeli promień zbieżności r szeregu potęgowego
∑
∞
=0
n
n
n
x
a
jest dodatni, to suma s tego
szeregu jest funkcją całkowalną w sensie Riemanna i
∀
∀
∀
∀
x
∈
∈
∈
∈(−r,r):
∫
x
0
s(t)dt =
∫ ∑
∞
=
x
0
0
n
n
n
dt
t
a
=
1
n
0
n
n
x
1
n
a
+
∞
=
∑
+
,
oraz promień zbieżności szeregu całek
1
n
0
n
n
x
1
n
a
+
∞
=
∑
+
jest równy r.

R
OZDZIAŁ
II
Strona 18
18
18
18
Uwaga 2. Przedział całkowania [0,x] w twierdzeniu 4, można zastąpić dowolnym przedzia-
łem [a,b]
⊂ (−r,r) .
Przykład 3.
Wyznaczyć sumę szeregu potęgowego
( )
∑
∞
=
−
0
n
n
n
x
1
i obliczyć sumę szeregu anharmonicz-
nego
n
1
n
x
n
1)
(
∑
−
−
.
Przykład 4.
Wyznaczyć sumę szeregu
∑
−1
n
nx
, obszar jego zbieżności oraz sumę szeregu liczbowego
∑
n
2
n
.

S
ZEREG POTĘGOWY
Strona 19
19
19
19
Szereg Taylora
Szereg potęgowy o środku w punkcie x
0
i współczynnikach c
n
=
!
)
(
0
)
(
n
x
f
n
(n=0,1,2,3,... ), gdzie
f
∈
C
∞
(U(x
0
,
δ
)), nazywamy szeregiem Taylora funkcji f w tym otoczeniu. Jeżeli x
0
= 0, to taki
szereg nazywamy szeregiem Maclaurina.
Każdej funkcji klasy C
∞
w pewnym otoczeniu U(x
0
,
δ) punktu x
0
odpowiada więc jej szereg
Taylora, ale suma tego szeregu nie musi być równa funkcji f. Wśród funkcji klasy C
∞
wyróżnimy te, dla których zachodzi równość:
∀
x∈U(x
0
,δ): f(x) =
)
x
(x
!
n
)
(x
f
0
0
n
0
(n)
−
∑
∞
=
.
Funkcję spełniającą powyższy warunek nazywamy rozwijalną w szereg Taylora (albo ana-
lityczną w sensie rzeczywistym) w otoczeniu punktu x
0
.
Podamy najpierw przykład funkcji klasy C
∞
, która nie jest rozwijalna w szereg Taylora.
Przykład 5.
Wyznaczyć szereg Maclaurina dla funkcji f, jeżeli f(x) =
=
≠
−
.
0
,
0
,
0
,
2
1
x
gdy
x
gdy
e
x
Sformułujemy teraz twierdzenia, które podadzą warunki wystarczające do tego, aby funkcja
była rozwijalna w szereg Taylora.
Twierdzenie 5 (o rozwijaniu funkcji w szereg Taylora).
Funkcja f
∈
∈
∈
∈C
∞
∞
∞
∞
(U(x
0
,
δ
δδ
δ)) jest sumą swojego szeregu Taylora wtedy i tylko wtedy, gdy
∞
→
n
lim R
n
(x) = 0 w otoczeniu U, gdzie (R
n
) jest ciągiem funkcyjnym postaci:
R
n
(x) =
n
0
0
0
(n)
)
x
(x
!
n
))
x
θ(x
(x
f
−
−
+
.
Dowód.

R
OZDZIAŁ
II
Strona 20
20
20
20
Twierdzenie 6.
Jeżeli funkcja f∈
∈
∈
∈C
∞
∞
∞
∞
(U(x
0
,
δ
δδ
δ)) ma pochodne wspólnie ograniczone, tzn.
∃
∃
∃
∃
M>0
∀
∀
∀
∀
x
∈
∈
∈
∈U(x
0
,
δ
δδ
δ)
∀
∀
∀
∀
n
∈
∈
∈
∈N
0
:
|||| f
(n)
(x)
|||| ≤
≤
≤
≤ M,
to funkcja f jest rozwijalna w szereg Taylora w otoczeniu U.
Dowód.
Rozwijanie funkcji w szereg Taylora nie musi koniecznie odbywać się na podstawie definicji
tego szeregu, ale rozwinięcie w szereg potęgowy otrzymane innymi metodami jest
rozwinięciem w szereg Taylora, co uzasadnia następujące twierdzenie.
Twierdzenie 7 (o jednoznaczności rozwinięcia funkcji w szereg Taylora)
Jeżeli funkcja f jest w pewnym otoczeniu U(x
0
,
δ
δδ
δ) sumą szeregu potęgowego
∑
∞
=
−
0
n
0
n
)
x
(x
a
, to szereg ten jest szeregiem Taylora tej funkcji.
Przykład 6.
Ze znanego wzoru na sumę szeregu geometrycznego:
∑
∞
=0
n
n
aq =
q
1
1
−
, gdy q <1, dla x <1,
podstawiając q = −x
2
, mamy:
∑
∞
=0
n
n
2
)
(-x
=
∑
∞
=0
n
2n
x
=
)
(-x
1
1
2
−
=
2
x
1
1
+
.
Otrzymaliśmy więc w przedziale (−1,1) rozwinięcie funkcji f, gdzie f(x) =
2
x
1
1
+
w szereg
potęgowy, jest to, na mocy twierdzenia 7, szereg Maclaurina tej funkcji.
S
ZEREG POTĘGOWY
Strona 21
21
21
21
Wyprowadzimy teraz kilka rozwinięć w szereg Taylora kilku podstawowych funkcji klasy
C
∞
(
ℜ).
Przykład 7. Rozwinąć w szereg Taylora wokół punktu x
0
=1 funkcję f, jeżeli f(x) = lnx.
Funkcja f jest klasy C
∞
(
ℜ
+
) a jej pochodna n-tego rzędu dana jest wzorem;
∀
x>0
∀
n∈N:
( )
( ) ( ) (
)
n
1
n
n
x
!
1
n
1
x
f
−
−
=
−
,
a stąd mamy:
∀
n∈N: f
(n)
(1) = (−1)
n−1
(n−1)!.
Szereg Taylora tej funkcji ma postać:
ln1 +
(
)
n
1
1
n
1
x
n!
!
1)
(n
1)
(
−
−
−
∑
∞
=
−
n
=
(
)
n
1
1
n
1
x
n
1)
(
−
−
∑
∞
=
−
n
,
przy czym promień zbieżności tego szeregu jest równy 1, a obszar zbieżności to przedział
(0,2], tak więc z uwagi na twierdzenie 7, mamy:
∀
x
∈(0,2]: lnx =
(
)
n
1
1
n
1
x
n
1)
(
−
−
∑
∞
=
−
n
.
Dla x=2 otrzymamy sumę szeregu anharmonicznego: ln2 =
∑
∞
=
−
−
1
n
1
n
n
1)
(
.
Przykład 8. Rozwinąć w szereg Maclaurina funkcję f, jeżeli:
a) f(x) = e
x
, b) f(x) = sinx, c) f(x) = cosx.
a) Funkcja f jest klasy C
∞
(
ℜ) a jej pochodna n-tego rzędu dana jest wzorem:
∀
n
∈N:
( )
( )
x
n
e
x
f
=
, oraz
( )
( )
1
0
f
n
= .
W każdym przedziale ograniczonym [−a,a] (a>0) mamy:
∀
n
∈N: | f
(n)
(x)
| ≤e
a
,
czyli pochodne są wspólnie ograniczone, a więc stosując twierdzenie 6 otrzymamy
rozwinięcie funkcji f w szereg Maclaurina:
∀
x∈ℜ: exp(x) = e
x
=
∑
∞
=0
n
n
!
n
x
.
b) Funkcja f jest klasy C
∞
(ℜ), a jej pochodna n-tego rzędu dana jest wzorem:
∀
x
∈ℜ
∀
n
∈N:
( )
( )
+
=
2
π
n
x
sin
x
f
n
.
Oczywiste jest, że pochodne są wspólnie ograniczone w ℜ, stąd łatwo otrzymujemy
rozwinięcie:
∀
x
∈ℜ: sinx =
1
2n
1
-
n
0
n
x
!
1)
(2n
(-1)
+
∞
=
+
∑
.

R
OZDZIAŁ
II
Strona 22
22
22
22
c) Stosując twierdzenie 3 o różniczkowaniu szeregu „wyraz po wyrazie” oraz biorąc
pod uwagę równość: (sinx)
′ = cosx, mamy:
∀
x∈ℜ: cosx =
2n
1
-
n
0
n
x
!
(2n)
(-1)
∑
∞
=
.
Przykład 9.
Rozwinąć w szereg Maclaurina funkcję f i określić obszar zbieżności otrzymanego szeregu:
a) f(x) = cos
2
x, b)
=
≠
−
=
,
0
x
dla
,
2
1
,
0
x
dla
,
x
x
cos
1
)
x
(
f
2
, c) f(x) = arctg3x.
S
ZEREG POTĘGOWY
Strona 23
23
23
23
Uwaga 3. W dziedzinie zespolonej funkcje exp, sin, cos definiujemy jako sumy szeregów
potęgowych
∑
n
n
z
a
o współczynnikach takich samych, jakie w zbiorze
ℜ mają szeregi
Maclaurina tych funkcji. Tak więc mamy następujące równości:
∀
z∈C: expz = e
z
=
∑
∞
=0
n
n
n!
z
;
∀
z
∈C: sinz =
1
2n
1
-
n
0
n
z
!
1)
(2n
(-1)
+
∞
=
+
∑
;
∀
z
∈ℜ: cosz =
2n
1
-
n
0
n
z
!
(2n)
(-1)
∑
∞
=
.
Rozważmy szczególny przypadek funkcji eksponencjalnej w zbiorze C, gdy z = iy,
gdzie y
∈ℜ. Wykorzystując definicję funkcji exp w dziedzinie zespolonej, mamy:
e
iy
=
∑
∞
=0
n
n
n!
(iy)
=
∑
∞
=0
n
n
n
n!
y
i
=
∑
∞
=0
n
2n
2n
(2n)!
y
i
+
∑
∞
=
+
+
+
0
n
1
2n
1
2n
1)!
(2n
y
i
=
i
2n
= (−1)
n
=
=
∑
∞
=0
n
2n
n
(2n)!
y
(-1)
+ i
∑
∞
=
+
+
0
n
1
2n
n
1)!
(2n
y
(-1)
=
biorąc pod uwagę rozwinięcia z przykładu 8
=
= cosy + isiny.
Z powyższych równości wynika następujący wniosek.
Wniosek 5. Funkcja exponencjalna zmiennej urojonej wyraża się przez funkcje
trygonometryczne zmiennej rzeczywistej i prawdziwe są następujące równości dla
dowolnego y
∈
∈
∈
∈ℜ
ℜ
ℜ
ℜ:
e
iy
= cosy + isiny;
e
−iy
= cosy − isiny;
cosy =
2
e
e
iy
iy
−
+
;
siny =
2i
e
e
iy
iy
−
−
.
Równości przedstawione w powyższym wniosku noszą nazwę wzorów Eulera.
Uwaga 4. Ze wzorów Eulera dla z = x + iy, mamy równość:
e
z
= e
x
(cosy + isiny),
z której wynika, że funkcja exp w dziedzinie zespolonej jest funkcją okresową o okresie
podstawowym 2πi.
R
OZDZIAŁ
II
Strona 24
24
24
24
Tak więc własności funkcji exp w dziedzinie zespolonej i w dziedzinie rzeczywistej nie są
takie same. Podobnie jest z funkcjami sin i cos. Zauważmy, na przykład, że dla a
∈ℜ, ze
wzorów Eulera w dziedzinie zespolonej:
2
e
e
cos
iz
iz
−
+
=
z
, sinz =
2i
e
e
iz
iz
−
−
,
mamy:
cos(ia) =
2
e
e
a
a
+
−
,
a z równości tej wynika, że funkcja cos nie jest funkcją ograniczoną w dziedzinie zespolonej.
Ć
wiczenia
1. Wyznaczyć promień zbieżności szeregu:
a)
∑
n
5
n
3
n
x
, b)
∑
−
+
n
n
n
n
x
n9
3)
(
5
, c)
∑
n
2n
2
x
n
)
(n!
, d)
∑
−
n
nln
x
1)
(
n
n
n
.
2. Wyznaczyć obszar zbieżności szeregu:
a)
∑
+
n
n
3
x
3
n
n
, b)
∑
n
2n
n5
x
, c)
∑
+
+
1)
nln(n
x
2
n
,
d)
∑
+
+
−
3
n
3)
(2n
4)
(x
n
, e)
∑
+
−
n
2n
n
n4
2)
(x
1)
(
, f)
n
n
x
100
(2n)!
∑
.
3. Wyznaczyć sumę i obszar zbieżności szeregu potęgowego:
a)
∑
∞
=
+
0
n
n
1)x
(n
, b)
∑
−
−
3
4n
x
3
4n
, c)
∑
+
−
+
1
3n
x
1)
(
1
3n
n
.
4. Rozwinąć w szereg Maclaurina funkcję f i określić obszar zbieżności otrzymanego
szeregu, jeżeli:
a) f(x) = cos2x, b) f(x) = sin
2
xcos
2
x, c) f(x) = ln(x+3),
d) f(x) =
4
x
4
1
−
, e) f(x) = (1+x)
α
,
α≠0, f) f(x) =
2
1
1
x
−
, g) f(x) =arcsinx.
5. Rozwinąć w szereg Taylora funkcję f i określić obszar zbieżności otrzymanego szeregu,
jeżeli:
a) f(x) =
2
x
1
−
, x
0
= 3, b) f(x) = ln(x+1), x
0
=2, c) f(x) = cos
2
x, x=
2
π
.
6. Obliczyć całkę z dokładnością do 10
−3
, wykorzystując rozwinięcie funkcji podcałkowej w
szereg potęgowy:
a)
dx
x
sinx
1
0
∫
, b)
dx
x
arctgx
1
0
∫
, c)
dx
e
0.5
0
x
-
2
∫
.

III
Szeregi ortogonalne,
szereg Fouriera
R
OZDZIAŁ
III
Strona 26
26
26
26
Szeregi ortogonalne
Drugą po szeregach potęgowych ważną klasą szeregów funkcyjnych są szeregi trygonomet-
ryczne, które są szczególnym przypadkiem szeregów ortogonalnych.
Oznaczmy przez L
2
(a,b) zbiór wszystkich ciągłych funkcji f: (a,b) → ℜ, dla których całka
∫
b
a
2
(x)dx
f
jest zbieżna ( mówimy, że jest to zbiór funkcji ciągłych i całkowalnych z kwadra-
tem w przedziale (a,b)).
Łatwo wykazać, że jest to przestrzeń liniowa nad ciałem
ℜ. W przestrzeni tej wprowadzamy
mnożenie skalarne w następujący sposób:
∀
f,g∈ L
2
(a,b): (f,g) =
∫
b
a
f(x)g(x)dx .
Norma funkcji f
∈ L
2
(a,b) dana jest wtedy następującym wzorem:
||f|| =
f)
(f,
=
∫
b
a
2
(x)dx
f
.
Odległość indukowana przez tę normę ma postać:
d(f,g) =
||f−g|| =
(
)
∫
b
a
2
dx
g(x)
-
f(x)
.
Ciąg funkcyjny (
ϕ
n
) o wyrazach
ϕ
n
∈
L
2
(a,b) nazywamy układem ortogonalnym funkcji, jeżeli
∀
n,k
∈
N: (n
≠
k)
⇒
(
ϕ
n
,
ϕ
k
) =
∫
b
a
k
n
(x)dx
(x)
ϕ
ϕ
= 0.
Jeżeli ciąg (an) jest ciągiem liczbowym, zaś (
ϕ
n
) ciągiem ortogonalnym, to szereg funkcyjny
postaci
∑
n
n
a
ϕ
nazywamy szeregiem ortogonalnym, a wyrazy an− współczynnikami tego
szeregu.
Jeżeli szereg ortogonalny
∑
n
n
c
ϕ
jest zbieżny w przedziale (a,b) jednostajnie i jego sumą
jest funkcja f, to z uwagi na to, że szereg taki można całkować „wyraz po wyrazie” i wtedy
prawdziwe są równości:
(f,
ϕ
n
) =
∑
∞
=0
k
n
k
k
,
c
ϕ
ϕ
=
(
)
∑
∞
=0
k
n
k
k
,
c
ϕ
ϕ
= c
n
(
ϕ
n
,
ϕ
n
) = c
n
||ϕ
n
||
2
.
Wynika stąd, że współczynniki a
n
określone są wzorami:
c
n
=
(
)
2
n
n
f,
ϕ
ϕ
, n 0, 1, 2, ... .

S
ZEREGI ORTOGONALNE
,
SZEREG
F
OURIERA
Strona 27
27
27
27
Udowodnione zostało więc twierdzenie:
Twierdzenie 1.
Jeżeli szereg ortogonalny
∑
n
n
a
ϕ
jest zbieżny w przedziale (a,b) jednostajnie i jego
sumą jest funkcja f, to współczynniki tego szeregu określone są wzorami:
c
n
=
(
)
2
n
n
f,
ϕ
ϕ
, n = 0, 1, 2, ... .
Szereg ortogonalny
∑
n
n
c
ϕ
, którego współczynniki określone są wzorami z twierdzenia 1,
nazywamy szeregiem Fouriera funkcji f.
Przykład 1.
Wykazać, że ciąg funkcji: 1, cos
T
x
π
, sin
T
x
π
, cos
T
x
2
π
, sin
T
x
2
π
, ... ,cos
T
x
n
π
, sin
T
x
n
π
, ... ,
jest ortogonalny w przedziale [−T, T].
Jeżeli n
≠k (n=0,1,2, ... , k=1,2,3, ...), to:
T
x
kπ
cos
,
T
x
nπ
cos
=
T
x
kπ
sin
,
T
x
nπ
sin
=
T
x
kπ
sin
,
T
x
nπ
cos
=
T
x
kπ
sin
,
T
x
kπ
cos
=
R
OZDZIAŁ
III
Strona 28
28
28
28
Uwaga 1. Ponieważ normy kolejnych funkcji z przykładu 1 są równe:
||1|| =
∫
T
T
-
1dx
=
2T
1
,
T
nππ
cos
2
=
∫
−
T
T
2
dx
T
x
nπ
cos
=
T
1
,
T
nππ
sin
2
=
∫
−
T
T
2
dx
T
x
nπ
sin
=
T
1
,
więc współczynniki szeregu Fouriera funkcji f względem ortogonalnego układu funkcji
z przykładu 1, mają postać:
c
0
=
∫
T
T
-
f(x)dx
2
1
T
, c
2n−1
=
∫
−
T
T
dx
T
x
nπ
f(x)cos
1
T
, c
2n
=
∫
−
T
T
dx
T
x
nπ
f(x)sin
1
T
.
Uwaga 2. Funkcji f całkowalnej w przedziale [−T,T] odpowiada następujący szereg
trygonometryczny Fouriera:
f
∼
T
x
nπ
sin
b
T
x
nπ
cos
a
2
a
n
1
n
n
0
+
+
∑
∞
=
,
gdzie: a
0
=
∫
T
T
-
f(x)dx
2
1
T
, a
n
=
∫
−
T
T
dx
T
x
nπ
f(x)cos
1
T
, b
n
=
∫
−
T
T
dx
T
x
nπ
f(x)sin
1
T
, n = 1, 2, 3, ... .
Całkowalność funkcji f w przedziale [−T,T] nie gwarantuje ani zbieżności szeregu Fouriera,
ani tego, że suma tego szeregu jest identyczna z funkcją f. Aby sformułować warunki
dostateczne rozwijalności funkcji f w szereg trygonometryczny Fouriera, zdefiniujemy klasę
funkcji spełniających warunki Dirichleta.
Mówimy, że funkcja f spełnia w przedziale [a,b] warunki Dirichleta, jeżeli:
1. funkcja f jest przedziałami monotoniczna w przedziale [a,b] (tzn. przedział [a,b] da się
podzielić na skończoną liczbę podprzedziałów, w których funkcja f jest monotoniczna),
2. funkcja f jest ciągła w przedziale [a,b], z wyjątkiem co najwyżej skończonej liczby punktów
nieciągłości I rodzaju, przy czym w każdym takim punkcie x
0
mamy:
f(x
0
)=
[
]
)
(
)
(
2
1
0
0
+
+
−
x
f
x
f
,
3. na końcach przedziału spełnione są równości: f(a)=f(b)=
[
]
)
(
)
(
2
1
−
+
+
b
f
a
f
.
Twierdzenie 2 (Dirichleta).
Jeżeli funkcja f spełnia w przedziale [−T,T] warunki Dirichleta, to jest rozwijalna w tym
przedziale w szereg trygonometryczny Fouriera i
∀
∀
∀
∀
x
∈
∈
∈
∈[−l,l]: f(x) =
l
x
nπ
sin
b
l
x
nπ
cos
a
2
a
n
1
n
n
0
+
+
∑
∞
=
.
Jeżeli ponadto funkcja f jest okresowa i ma okres 2T, to równość ta jest prawdziwa dla
każdego x z dziedziny tej funkcji.

S
ZEREGI ORTOGONALNE
,
SZEREG
F
OURIERA
Strona 29
29
29
29
Uwaga 3. Twierdzenie pozostaje prawdziwe, gdy założymy, że funkcja f jest kawałkami
klasy C
1
oraz w każdym punkcie nieciągłości spełnia równość z drugiego warunku
Dirichleta.
Uwaga 4. Wykorzystując własności funkcji parzystej i nieparzystej mamy następujące
implikacje.
1. Jeżeli funkcja f jest parzysta w przedziale [−T,T], to:
∀
n∈N: b
n
=0 ∧ a
n
=
∫
T
0
dx
T
x
nπ
f(x)cos
2
T
.
2. Jeżeli funkcja f jest nieparzysta w przedziale [−T,T], to:
∀
n∈N: a
n
= 0 ∧ b
n
=
∫
T
0
dx
T
x
nπ
f(x)sin
2
T
.
Uwaga 5. Wykorzystując uwagę 4, możemy:
1. funkcję daną na przedziale (0,T] przedłużyć parzyście na przedział [−T,T] otrzymując
wtedy rozwinięcie tej nowej funkcji (a zatem i funkcji f w przedziale (0,T]) w szereg
cosinusów;
2. funkcję daną na przedziale (0,T] przedłużyć nieparzyście na przedział [−T,T] otrzymując
wtedy rozwinięcie tej nowej funkcji (a zatem i funkcji f w przedziale (0,T]) w szereg
sinusów;
Przykład 2.
Funkcję f, gdzie f(x) =
−
∈
∈
−
∈
2,2}.
{
x
gdy
1,
(0,2),
x
gdy
x,
2,0],
(
x
gdy
0,
rozwinąć w szereg trygonometryczny Fouriera.
Wyznaczyć sumę szeregu liczbowego, który otrzymamy dla x=2.

R
OZDZIAŁ
III
Strona 30
30
30
30
Przykład 3.
Rozwinąć w szereg Fouriera funkcję f, jeżeli f(x)=x
2
, x
∈[−π,π]. Wyznaczyć sumy szeregów
liczbowych, jakie otrzymamy dla x = 0 i x = π.

S
ZEREGI ORTOGONALNE
,
SZEREG
F
OURIERA
Strona 31
31
31
31
Przykład 4.
Funkcję f, gdzie f(x) =
1,
x
gdy
,
π
),
(1,
x
gdy
,
(0,1),
x
gdy
,
0
1
2
1
=
∈
∈
rozwinąć w szereg:
a) cosinusów, b) sinusów.
Wykorzystując otrzymane rozwinięcia, wyznaczyć sumy szeregów:
∑
n
sinn
,
∑
n
sin2n
.

R
OZDZIAŁ
III
Strona 32
32
32
32
Ć
wiczenia
1. Wykazać, że ciąg funkcyjny o wyrazie ogólnym f
n
(x) = sinnx, (n = 1, 2, ...) , jest ciągiem
ortogonalnym w przedziale [0,
π].
2. Funkcję f rozwinąć w szereg trygonometryczny Fouriera i wyznaczyć sumę szeregu
dla x = x
0
:
a) f(x) =
∈
−
∈
π
],
[0,
x
gdy
x,
π
,0],
[
x
gdy
0,
x
0
=
π, b) f(x) = |sinx|, x
0
=
π,
c) f(x) =
∈
−
∈
(0,2),
x
gdy
2,
2,0),
(
x
gdy
0,
x
0
=2.
3. Dokonując odpowiedniego przedłużenia, rozwinąć funkcję f w szereg trygonometryczny
sinusów i szereg trygonometryczny cosinusów, jeżeli:
a) f(x) =
∈
−
∈
(1,2),
x
gdy
x,
2
(0,1],
x
gdy
x,
b) f(x) =
2
x
π
−
, x
∈(0,2π), c) f(x) = sinx, x∈(0,π).

IV
Równania różniczkowe
zwyczajne
R
OZDZIAŁ
IV
Strona 34
34
34
34
Równania różniczkowe zwyczajne
Równanie różniczkowe I rzędu
Jeżeli y jest funkcją rzeczywistą klasy D
n
w przedziale I
⊂ℜ
, wtedy związek ( zapisany za
pomocą funkcji ) F o postaci:
((((
))))
,
0
...
,
,
,
,
)
(
=
=
=
=
′′′′′′′′
′′′′
n
y
y
y
y
x
F
który dla każdego x
∈
I jest spełniony przez tę funkcję, nazywamy
równaniem różniczkowym
z niewiadomą funkcją y. Liczbę naturalną n - najwyższy rząd pochodnej funkcji y - nazywamy
rzędem równania różniczkowego.
Funkcję
ϕ
określoną w przedziale I nazywamy
rozwiązaniem równania różniczkowego
(całką równania różniczkowego), jeżeli spełnia ona następujące warunki:
1.
ϕ∈
D
n
(I),
2.
(
)
F
n
D
x
x
x
x
I
x
∈
′
∈
∀
)
(
),...,
(
),
(
,
:
)
(
ϕ
ϕ
ϕ
- dziedzina funkcji F,
3.
((((
))))
.
0
)
(
),...,
(
),
(
,
:
)
(
=
=
=
=
′′′′
∈
∈
∈
∈
∀
∀
∀
∀
x
x
x
x
F
I
x
n
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
ϕ
Jeżeli równanie różniczkowe można rozwiązać względem y
(n)
, to otrzymamy
postać normalną
równania różniczkowego:
(
)
.
,...,
,
,
)
(
)
(
1
−
′
=
n
n
y
y
y
x
f
y
Zagadnienie Cauchy’ego dla równania różniczkowego rzędu n:
wyznaczyć rozwiązanie szczególne równania różniczkowego, które spełnia
warunki początkowe:
y(x
0
)=y
0
, y
′
(x
0
)=y
1
, ... , y
(n-1)
(x
0
) = y
n-1
.
przy czym dowolne liczby rzeczywiste x
0
∈
I, y
0
, y
1
, ... , y
n-1
, zwane
wartościami początkowymi,
są zadane z góry.

R
ÓWNANIA RÓśNICZKOWE ZWYCZAJNE
Strona 35
35
35
35
Przykład 1.
Rozwiązać równanie różniczkowe trzeciego rzędu: y′′′=0.
Całką ogólną lub rozwiązaniem ogólnym równania różniczkowego n-tego rzędu nazywamy
rodzinę funkcji postaci: y=y(x,c
1
, ..., c
n
), która zależna jest od n stałych dowolnych
(tzn. od tylu jaki jest rząd równania), przy czym każda funkcja tej rodziny spełnia równanie.
Poszczególne funkcje tej rodziny przy ustalonych stałych nazywamy
całkami szczególnymi
(rozwiązaniem szczególnym).
Uwaga 1. Równanie różniczkowe może posiadać także rozwiązania osobliwe, których nie
można otrzymać z całki ogólnej.
Interpretacja geometryczna dla n=1.
Równanie y′=f(x,y) określa w każdym punkcie P(x,y(x)) współczynnik stycznej do krzywej
całkowej tego równania. W ten sposób dane równanie różniczkowe określa pole kierunków
stycznych do wykresów rozwiązań.
Przykład 2.
Rozwiązać równanie:
.
y
x
y
=
=
=
=
′′′′

R
OZDZIAŁ
IV
Strona 36
36
36
36
Podamy teraz kilka prostych przykładów pokazujących, w jak różnych zagadnieniach
pojawiają się równania różniczkowe.
Przykład 3.
Okręt zmniejsza swoją prędkość pod wpływem przeciwdziałającej jego ruchowi siły oporu
wody. Siła ta jest proporcjonalna do prędkości okrętu.
Początkowa prędkość okrętu v(0)=10m/s zmalała po 5 s. do wartości v(5)=8m/s.
Po jakim czasie prędkość okrętu zmaleje do 1m/s?
Z drugiej zasady Newtona:
.
10
)
0
(
=
−
=
v
i
kv
dt
dv
m
Rozwiązanie tego zagadnienia:
t
m
k
e
t
v
−
= 10
)
(
Z warunku v(5)=8 otrzymujemy:
.
4
5
ln
5
1
=
m
k
Z równości v(t)=1 mamy: t
≈51.6s.
Przykład 4.
Kultura licząca 500 bakterii po trzech godzinach osiąga stan 8000 bakterii.
Szybkość zmiany liczebności jest w danej chwili proporcjonalna do tej liczebności.
Jaka będzie liczebność bakterii po 15 godzinach.
Równanie opisujące szybkość zmiany populacji:
.
kN
dt
dN
=
Rozwiązaniem tego równania jest:
)
(
0
0
)
(
t
t
k
e
N
t
N
−
=
, gdzie N
0
jest liczebnością populacji
w pewnej chwili t
0
.
Odp. Około 524206107.
Przykład 5.
Ciało o temperaturze 220
°C umieszczono w pomieszczeniu o temperaturze 60°C.
Po 10 minutach jego temperatura obniżyła się do 140
°C.
Jaka będzie temperatura ciała po 20 minutach.
Jeśli T(t) oznacza temperaturę ciała, a T
0
temperaturę otoczenia,
to proces stygnięcia będzie opisany równaniem:
)
(
0
T
T
k
dt
dT
−
−
=
Rozwiązaniem tego równania jest: T(t)= T
0
+(T(0)-T
0
)e
-kt
, gdzie T(0) jest temperaturą
początkową ciała.
Odp. Około 100°C.
Przykład 6.
Wyznaczyć zależność między prędkością v ciała swobodnie spadającego i czasem t
przyjmując,
ż
e opór powietrza jest wprost proporcjonalny do kwadratu prędkości.
Z drugiego prawa dynamiki Newtona mamy:
.
0
)
0
(
,
2
=
−
=
v
kv
mg
dt
dv
m

R
ÓWNANIA RÓśNICZKOWE ZWYCZAJNE
Strona 37
37
37
37
Rozwiązaniem tego zagadnienia jest :
.
1
1
)
(
/
2
/
2
t
m
k
t
m
gk
e
e
k
mg
t
v
−
−
+
−
⋅
=
Zauważmy, że
.
)
(
lim
k
mg
t
v
t
=
∞
→
Twierdzenie 1 (Picarda o istnieniu i jednoznaczności rozwiązania zagadnienia
Cauchy’ego).
Jeżeli funkcja f spełnia warunki:
1. f: [x
0
-a, x
0
+a]
×
×
×
× [y
0
-b,y
0
+b]
→
→
→
→ℜ
ℜ
ℜ
ℜ jest ciągła;
2. f spełnia warunek Lipschitza względem drugiej zmiennej:
∃
∃
∃
∃K>0 ∀
∀
∀
∀x∈
∈
∈
∈ [x
0
-a, x
0
+a]
∀
∀
∀
∀y
1
,y
2
∈
∈
∈
∈
[y
0
-b,y
0
+b]:
2
1
2
1
)
,
(
)
,
(
y
y
K
y
x
f
y
x
f
−
−
−
−
⋅⋅⋅⋅
≤
≤
≤
≤
−
−
−
−
,
to istnieje taka liczba rzeczywista c>0, że w przedziale (x
0
-c,x
0
+c) równanie y
′′′′=f(x,y)
posiada dokładnie jedno rozwiązanie spełniające warunek początkowy y(x
0
) = y
0
.

R
OZDZIAŁ
IV
Strona 38
38
38
38
Uwaga 2. Z dowodu twierdzenia wynika, że ciąg kolejnych przybliżeń:
y
1
(x) = y
0
, y
n
(x)=y
0
+
(
)
du
u
y
u
f
x
x
n
∫
−
0
)
(
,
1
jest zbieżny do rozwiązania równania.

R
ÓWNANIA RÓśNICZKOWE ZWYCZAJNE
Strona 39
39
39
39
Przykład 3.
Zastosować metodę kolejnych przybliżeń do rozwiązania równania: y′=x+y, y(0)=0.
Ć
wiczenia
1. Stosując metodę kolejnych przybliżeń, rozwiązać zagadnienie Cauchy’ego:
=
=
′
.
1
)
0
(
,
2
y
xy
y
2. Wyznaczyć trzy pierwsze wyrazy przybliżonego rozwiązania zagadnienia
Cauchy’ego:
=
−
=
′
.
1
)
0
(
,
2
y
x
y
y

R
OZDZIAŁ
IV
Strona 40
40
40
40

V
Przegląd równań
różniczkowych I rzędu

R
OZDZIAŁ
V
Strona 42
42
42
42
1. Równanie o zmiennych rozdzielonych
Równanie o zmiennych rozdzielonych ma następującą postać: y
′=g(x)h(y) lub ogólniej:
A(x)B(y)dx+C(x)D(y)dy=0.
Piszemy równanie w postaci:
∫
∫
=
⇒
=
⇒
=
.
)
(
)
(
)
(
)
(
)
(
)
(
dx
x
g
y
h
dy
dx
x
g
y
h
dy
y
h
x
g
dx
dy
Przypadek h(y)=0 badamy oddzielnie.
Przykład 4.
Rozwiązać równanie: x(1+y
2
)dx+y(1+x
2
)dy=0.
Przykład 5.
Rozwiązać zagadnienie Cauchy’ego: y
′=y
2
, y(0)=1.

P
RZEGLĄD RÓWNAŃ RÓśNICZKOWYCH
I
RZĘDU
Strona 43
43
43
43
2. Równanie jednorodne:
.
=
=
=
=
′′′′
x
y
f
y
Wprowadzając nową funkcję niewiadomą:
x
x
y
x
u
)
(
)
(
=
sprowadzamy to równanie do równania o zmiennych rozdzielonych.
x
dx
u
u
f
du
u
u
f
dx
du
x
u
f
u
x
u
u
x
u
y
xu
y
x
y
u
=
−
⇒
−
=
⇒
=
′
+
⇒
⇒
′
+
=
′
⇒
=
⇒
=
)
(
)
(
)
(
[
]
?
)
(
u
u
f
=
Przykład 1.
Rozwi
ą
za
ć
równanie:
.
y
x
y
x
y
−
+
=
′

R
OZDZIAŁ
V
Strona 44
44
44
44
3. Równanie postaci: y′′′′=f(ax+by+c), b≠
≠
≠
≠0
Podstawienie: v(x) = ax + by(x) + c sprowadza to równanie do równania o zmiennych
rozdzielonych.
Przykład 2.
Rozwi
ą
za
ć
zagadnienie Cauchy’ego: y
′=x+y+7, y(0)=-3.
4. Równanie liniowe
Równanie ró
ż
niczkowe, które mo
ż
na zapisa
ć
w postaci:
y
′+p(x)y=g(x)
nazywamy
równaniem liniowym pierwszego rzędu
.
Je
ś
li g(x)=0, to równanie nazywamy
równaniem liniowym jednorodnym
(albo uproszczonym).
B
ę
dzie to wtedy równanie o zmiennych rozdzielonych.
Równanie liniowe rozwi
ą
zujemy w dwóch krokach.
1. Wyznaczamy najpierw rozwi
ą
zanie ogólne równania jednorodnego (RORJ):
⇒
−
=
⇒
−
=
⇒
=
+
′
dx
x
p
y
dy
y
x
p
dx
dy
y
x
p
y
)
(
)
(
0
)
(
RORJ
ce
y
c
dx
x
p
y
dx
x
p
−
∫
=
⇒
+
−
=
⇒
−
∫
)
(
ln
)
(
ln
2. Rozwiązanie ogólne równania niejednorodnego (RORNJ) wyznaczymy stosując
M.U.S. (metodę uzmienniania stałej).
P
RZEGLĄD RÓWNAŃ RÓśNICZKOWYCH
I
RZĘDU
Strona 45
45
45
45
Przyjmujemy, że rozwiązanie ogólne ma postać:
∫
=
−
dx
x
p
e
x
c
x
y
)
(
)
(
)
(
Wstawiamy tę funkcję do równania.
⇒
−
∫
+
∫
′
=
′
−
−
))
(
(
)
(
)
(
)
(
)
(
)
(
x
p
e
x
c
e
x
c
x
y
dx
x
p
dx
x
p
⇒
=
∫
+
−
∫
+
∫
′
=
+
′
−
−
−
)
(
)
(
)
(
))
(
(
)
(
)
(
)
(
)
(
)
(
)
(
x
g
e
x
c
x
p
x
p
e
x
c
e
x
c
y
x
p
y
dx
x
p
dx
x
p
dx
x
p
∫
∫
⇒
∫
⋅
+
∫
=
⇒
+
∫
=
⇒
∫
=
′
−
xdx
p
dx
x
p
dx
x
p
dx
x
p
e
C
e
x
g
x
y
C
e
x
g
x
c
e
x
g
x
c
(
)
(
)
(
)
(
]
)
(
[
)
(
)
(
)
(
)
(
)
(
∫
−
∫
⋅
∫
+
∫
=
−
−
RORNJ
e
x
g
e
Ce
x
y
dx
x
p
dx
x
p
dx
x
p
)
(
)
(
)
(
)
(
)
(
Przykład 3.
Rozwiązać zagadnienie Cauchy’ego:
=
=
+
′
.
1
)
1
(
,
3
1
y
x
y
y
x
Przykład 4.
Rozwiązać równanie: 2ydx+(y
2
−2x)dy=0.

R
OZDZIAŁ
V
Strona 46
46
46
46
5. Równanie Bernoullie’ego y′′′′+p(x)y=g(x)y
α
α
α
α
, α
α
α
α≠
≠
≠
≠0, α
α
α
α ≠
≠
≠
≠1
y = 0 jest rozwiązaniem, gdy
α
>0, wyznaczymy więc rozwiązania niezerowe.
Podstawienie nowej funkcji niewiadomej o postaci z=y
1
−α
sprowadza to równanie do
równania liniowego.
(
)
(
)
α
α
α
α
α
−
′
=
′
⇒
′
−
=
′
=
′
−
−
1
1
1
z
y
y
y
y
y
z
.
Jeżeli zapiszemy równanie Bernouli’ego w postaci:
)
(
)
(
1
x
g
y
x
p
y
y
=
+
′
−
α
α
,
to otrzymamy równanie liniowe z funkcją niewiadomą z:
).
(
)
1
(
)
(
)
1
(
)
(
)
(
1
1
x
g
z
x
p
z
x
g
z
x
p
z
α
α
α
−
=
−
+
′
⇔
=
+
′
−
Przykład 5.
Rozwiązać zagadnienie Cauchy’ego:
.
1
)
1
(
,
2
1
1
=
=
−
′
y
y
y
x
y
P
RZEGLĄD RÓWNAŃ RÓśNICZKOWYCH
I
RZĘDU
Strona 47
47
47
47
6. Równanie różniczkowe zupełne
Równanie o postaci: P(x,y)dx+Q(x,y)dy=0
nazywamy równaniem zupełnym, jeżeli P,Q
∈
C
1
(D), gdzie D jest obszarem jednospójnym i
lewa strona jest różniczką zupełną pewnej funkcji U(x,y), czyli gdy zachodzi warunek:
x
Q
y
P
D
y
x
∂
∂
=
∂
∂
∈
∀
:
)
,
(
.
Wtedy równanie można zapisać w postaci: dU=0, a więc rozwiązanie ogólne ma postać:
U(x,y) = C.
Przykład 6.
Rozwiązać równanie:
(
)
(
)
.
0
1
1
2
2
2
2
=
−
−
+
−
−
dy
y
y
x
x
dx
y
x
y
x

R
OZDZIAŁ
V
Strona 48
48
48
48
7. Równanie zupełne – czynnik całkujący
Jeżeli w równaniu: P(x,y)dx+Q(x,y)dy=0, nie jest spełniony warunek:
x
Q
y
P
D
y
x
∂
∂
=
∂
∂
∈
∀
:
)
,
(
,
to szukamy takiej funkcji µ(x,y) klasy C
1
w obszarze D, aby dla równania:
µ(x,y)P(x,y)dx+µ(x,y)Q(x,y)dy=0, spełniony był warunek:
x
Q
y
P
D
y
x
∂
∂
=
∂
∂
∈
∀
)
(
)
(
:
)
,
(
µ
µ
.
Funkcję
µ nazywamy czynnikiem (mnożnikiem) całkującym danego równania.
Przypadki szczególne
1.
µ(x,y) = µ(x),
2.
µ(x,y) = µ(y).

P
RZEGLĄD RÓWNAŃ RÓśNICZKOWYCH
I
RZĘDU
Strona 49
49
49
49
Przykład 7.
Rozwiązać równanie:
(
)
.
0
2
2
2
=
+
−
xydy
dx
y
x
Przykład 8.
Rozwiązać równanie:
(
)
(
)
.
0
2
2
=
−
+
+
dy
tgy
x
x
dx
tgy
x
R
OZDZIAŁ
V
Strona 50
50
50
50
Zbadamy jeszcze równanie rzędu pierwszego, które ma tzw. rozwiązania osobliwe.
8. Równanie Clairauta: y = xy′′′′+ψ
ψ
ψ
ψ(y′′′′),
przy czym ψ(t)≠at+b i ψ∈C
1
(I).
Różniczkujemy stronami równanie Clairauta:
.
0
))
(
(
)
(
1
=
′
′
+
′
′
⇒
′
′
′
′
+
′
′
+
′
⋅
=
′
y
x
y
y
y
y
x
y
y
ψ
ψ
Ostatnie równanie prowadzi do dwóch warunków:
1. y
′′(x) = 0, 2. x+ψ′(y′) = 0.
Warunek 1. prowadzi do funkcji:
y′′(x) = 0 ⇒ y′(x) = A ⇒ y(x) = Ax + B (A i B są stałymi dowolnymi), która nie może
być rozwiązaniem ogólnym równania Clairauta, bo funkcja ta zależy od dwóch stałych
dowolnych
a równanie jest rzędu pierwszego. Wstawiając funkcję y(x) = Ax + B do równania
otrzymamy:
Ax + B = Ax + ψ(A) ⇒ B = ψ(A).
Tak więc rozwiązaniem ogólnym równania Clairauta jest funkcja:
y(x) = Ax +
ψ(A).
Warunek 2. prowadzi do rozwiązania szczególnego równania Clairauta:
x+
ψ′(y′) = 0 ⇒ x = – ψ′(y′),
uwzględniajac równanie Clairauta, stwierdzamy , że także y zależy od y
′:
y = –
ψ′(y′)y′ + ψ(y′).
Przyjmując: y
′ = p (parametr) otrzymamy postać parametryczną rozwiązania szczególnego
równania Clairauta:
+
′
−
=
′
−
=
).
(
)
(
),
(
p
p
p
y
p
x
ψ
ψ
ψ
Rozwiązanie to jest tzw. całką osobliwą tego równania, bo zagadnienie Cauchy’ego dla
równania Claitauta w punktach tego rozwiązania nie ma jednoznacznego rozwiązania.
Geometrycznie rozwiązanie osobliwe jest tzw. obwiednią (lub jej częścią) rodziny prostych z
rozwiązania ogólnego tego równania.
Przykład 1.
Wyznaczyć rozwiązania równania:
.
2
1
y
y
x
y
′
+
′
=
P
RZEGLĄD RÓWNAŃ RÓśNICZKOWYCH
I
RZĘDU
Strona 51
51
51
51
Ć
wiczenia
1. Rozwiązać równania różniczkowe:
a)
y
x
xy
y
2
2
−
=
′
, b)
y
x
y
+
=
′ 10
, c)
y
y
y
x
=
+
′ 1
2
2
d)
0
)
1
(
)
1
(
2
2
=
−
+
−
ydy
x
dx
y
x
, e)
y
y
x
y
ln
sin
=
′
.
2. Rozwiązać zagadnienie Cauchy’ego:
a)
2
)
1
(
,
1
3
2
=
=
+
′
y
y
y
xy
, b)
.
0
)
1
(
,
2
2
=
+
+
+
=
′
y
xy
y
x
y
3. Rozwiązać równanie różniczkowe:
a)
)
1
sin(
+
+
=
′
y
x
y
, b)
xy
y
y
x
2
)
(
2
2
=
′
−
,
c)
2
2
4
4
x
y
x
y
y
+
+
=
′
, d)
0
)
2
(
)
2
(
2
2
2
2
=
−
+
+
−
+
dy
x
xy
y
dx
y
xy
x
, e)
y
x
y
x
y
x
=
+
′
tg
,
f)
=
′
x
y
y
y
x
ln
cos
, g)
(
)
4
2
4
2
)
(
)
(
y
xy
y
x
xy
−
=
′
−
, h)
2
2
y
x
y
y
x
+
−
=
′
.
4. Rozwiązać równanie:
a)
x
x
y
y
cos
tg
+
=
′
, b)
x
y
x
y
3
1
=
+
′
, c)
x
y
y
4
2
=
+
′
, d)
2
2
6
3
x
y
x
y
=
+
′
.
5. Rozwiązać równanie:
a)
2
3
3
2
y
x
xy
y
=
−
′
, b)
y
x
y
x
x
y
=
−
+
′
2
1
, c)
x
xy
y
y
x
ln
2
=
+
′
,
d)
3
3
2
y
xy
y
x
=
−
′
, e)
1
1
8
3
+
−
=
−
′
x
y
y
y
x
, f)
2
3
2
x
y
y
x
y
=
+
′
.
6. Rozwiązać równanie (zupełne lub z czynnikiem całkującym):
a)
0
)
ln
(
3
=
−
+
dy
x
y
dx
x
y
, b)
0
2
)
(
2
=
+
+
xydy
dx
x
y
,
c)
0
cos
3
2
sin
2
1
2
2
=
+
−
xdy
dx
y
x
y
, d)
0
)
2
(
2
2
=
−
+
dy
xy
x
dx
y
,
e)
0
)
ln
cos
(
)
sin
(
2
=
+
+
+
dy
x
x
y
x
dx
y
y
x
, f)
0
)
(
3
2
2
2
3
2
=
+
+
+
+
dy
y
x
dx
y
y
x
xy
.
7. Rozwiązać równanie Clairauta:
a)
2
)
(
2
1
y
y
x
y
′
+
′
=
, b)
2
)
(
1
y
y
x
y
′
+
+
′
=
, c)
2
)
(
1
y
y
y
x
y
′
+
′
+
′
=
.
8. Rozwiązać zagadnienie Cauchy’ego:
a)
0
)
0
(
,
cos
1
tg
=
=
+
′
y
x
x
y
y
,
b)
2
)
1
(
,
1
3
2
=
=
+
′
y
y
y
xy
,

R
OZDZIAŁ
V
Strona 52
52
52
52
c)
1
)
(
,
0
ln
2
=
=
+
−
′
e
y
y
x
y
y
x
,
d)
0
)
1
(
,
0
)
(
)
2
(
2
=
=
+
+
+
y
y
x
ydy
dx
y
x
,
e)
0
)
1
(
,
exp
=
+
=
′
y
x
y
x
y
y
x
,
f)
2
)
0
(
,
sin
)
2
(sin
2
2
=
−
=
y
dy
y
y
x
dx
x
.

VI
Trajektorie ortogonalne,
równania różniczkowe
rzędu II sprowadzalne do
równań rzędu I

R
OZDZIAŁ
VI
Strona 54
54
54
54
Trajektorie ortogonalne
Jeżeli mamy daną rodzinę linii: F(x,y,c)=0, (F
∈C
1
(V)) to można wyznaczyć równanie
różniczkowe, którego rozwiązaniem będzie dana rodzina linii.
Równanie to otrzymamy rugując parametr c z układu równań:
=
=
′
⋅
∂
∂
+
∂
∂
.
0
)
,
,
(
,
0
)
,
,
(
)
,
,
(
c
y
x
F
y
y
c
y
x
F
x
c
y
x
F
Przykład 2.
Wyznaczyć równanie różniczkowe rodziny okręgów: x
2
+y
2
= cx.
Krzywą, która w każdym swoim punkcie tworzy kąt prosty z krzywą rodziny linii przechodzącą
przez ten sam punkt, nazywamy trajektorią ortogonalną danej rodziny linii.
Jeżeli równaniem różniczkowym danej rodziny linii jest równanie:
Φ(x,y,y′)=0,
to równanie różniczkowe trajektorii ortogonalnych będzie miało postać:
.
0
1
,
,
=
′
−
Φ
y
y
x
Przykład 3.
Wyznaczyć trajektorie ortogonalne rodziny parabol: y=cx
2
.

T
RAJEKTORIE ORTOGONALNE
,
RÓWNANIA RÓśNICZKOWE RZĘDU
II
SPROWADZALNE DO RÓWNAŃ RZĘDU
I
Strona 55
55
55
55
Równania różniczkowe rzędu drugiego
sprowadzalne do równań rzędu pierwszego
Ograniczymy się do dwóch typów takich równań.
1. F(x,y
′,y′′)=0 - równanie nie zawiera funkcji niewiadomej
Podstawienie u(x) = y
′ sprowadza to równanie do równania rzędu pierwszego:
F(x,u,u
′)=0.
Przykład 4.
Rozwiązać równanie: y
′=xy′′+(y′′)
2
.

R
OZDZIAŁ
VI
Strona 56
56
56
56
2. F(y,y′′′′,y′′′′′′′′)=0 - równanie nie zawiera zmiennej niezależnej x
Podstawiamy: y
′=v(y), wtedy: y′′=v′(y)y′=v′v i równanie przyjmie postać:
F(y,v,vv
′)=0.
Przykład 5.
Rozwiązać równanie: 2yy
′′ =(y′)
2
+ y
2
.
T
RAJEKTORIE ORTOGONALNE
,
RÓWNANIA RÓśNICZKOWE RZĘDU
II
SPROWADZALNE DO RÓWNAŃ RZĘDU
I
Strona 57
57
57
57
Ć
wiczenia
1. Wyznaczyć trajektorie ortogonalne danej rodziny linii:
a)
cx
y
x
2
2
2
=
+
, b)
2
2
2
c
y
x
=
−
, c) y=kx,
d)
ϕ
=
ρ
2
cos
2
a
, e)
)
(
4
2
a
x
y
−
=
, f)
2
3
ay
x
=
.
2. Rozwiązać równania różniczkowe drugiego rzędu sprowadzając je do rzędu
pierwszego:
a)
x
e
x
y
y
x
2
=
′
−
′′
, b)
x
e
y
y
y
2
)
(
2
′
=
′
+
′
′
, c)
y
y
y
y
′
+
′
=
′′
2
)
(
,
d)
0
)
(
ln
2
2
=
′
−
′
−
′′
y
y
y
y
y
y
, e)
x
tgx
y
y
2
sin
=
′
+
′′
, f)
2
)
(
2 y
tgy
y
′
=
′′
,
g)
1
)
(
2
2
+
′
=
′′
y
y
y
, h)
2
)
(
4
4
y
y
y
x
′′
+
′
=
′′
, i)
y
y
x
y
′′
−
+
′′
=
′
.
3. Rozwiązać zagadnienie Cauchy,ego:
a)
1
)
0
(
,
1
)
0
(
,
1
4
−
=
′
=
=
′′
y
y
y
y
, b)
4
)
2
(
,
0
)
2
(
,
2
=
′
=
′
+
′
=
′′
y
y
y
x
x
y
y
,
c)
1
)
0
(
,
0
)
0
(
,
ln
=
′
=
′
′
=
′′
y
y
y
y
y
, d)
(
)
1
)
2
(
,
2
)
2
(
,
)
(
2
=
′
=
′
+
′′
=
′
y
y
y
y
x
y
,
e)
1
)
0
(
,
1
)
0
(
,
2
3
=
′
=
=
′′
′
y
y
y
y
y
.

R
OZDZIAŁ
VI
Strona 58
58
58
58

VII
Równanie różniczkowe
liniowe n-tego rzędu
R
OZDZIAŁ
VII
Strona 60
60
60
60
Równanie różniczkowe liniowe n-tego rzędu
Równanie różniczkowe o postaci:
(1) y
(n)
+p
n-1
(x)y
(n-1)
+ ... +p
1
(x)y
′′′′ +p
0
(x)y = f(x)
gdzie dane funkcje p
k
(k=0,1,...,n-1) i f są ciągłe w przedziale (a,b)⊂ℜ,
nazywamy równaniem różniczkowym liniowym niejednorodnym n-tego rzędu.
Jeśli f=0, to równanie to nazywamy równaniem liniowym jednorodnym n-tego rzędu:
(2) y
(n)
+p
n-1
(x)y
(n-1)
+ ... +p
1
(x)y
′′′′ +p
0
(x)y = 0.
Zagadnienie Cauchy’ego dla równania liniowego n-tego rzędu:
Wyznaczyć całkę szczególną y spełniającą w przedziale (a,b) równanie (1) (lub (2))
i warunki początkowe:
y(x
0
)=y
0
, y(x
0
)=y
1
, ... y
(n-1)
(x
0
)=y
n-1
, gdzie x
0
∈
(a,b), y
0
, y
1
, ... ,y
n-1
- dowolne dane liczby.
Twierdzenie 1
Jeżeli funkcje p
k
∈
∈
∈
∈C((a,b)), k=0,1,...,n−
−
−
−1, to zagadnienie Cauchy’ego
dla równania liniowego jednorodnego (2) ma dla każdego układu n+1 liczb:
x
0
∈
∈
∈
∈ (a,b), y
0
, y
1
, ... ,y
n-1
, dokładnie jedno rozwiązanie.
Twierdzenie 2
Jeżeli funkcje y
1
, y
2
, ... ,y
m
są rozwiązaniami szczególnymi równania (2),
to kombinacja liniowa tych funkcji:
)
(
)
(
1
x
y
C
x
y
k
m
k
k
∑
∑
∑
∑
=
=
=
=
=
=
=
=
z dowolnymi stałymi C
1
, C
2
, ... ,C
m
jest rozwiązaniem tego równania w rozważanym
przedziale.
Twierdzenie 3
Jeżeli funkcja w(x)=u(x) + iv(x) jest w przedziale (a,b) całką szczególną równania (2)
z rzeczywistymi współczynnikami p
k
(k=0,1,...,n
−
−
−
−1), to jej część rzeczywista u
i część urojona v są także całkami tego równania w tym przedziale.

R
ÓWNANIE RÓśNICZKOWE LINIOWE N
-
TEGO RZĘDU
Strona 61
61
61
61
Układ n rozwiązań szczególnych równania (2) w przedziale (a,b) nazywamy
układem podstawowym rozwiązań (lub fundamentalnym układem rozwiązań)
tego równania, jeżeli wyznacznik Wrońskiego (wrońskian):
)
(
........
)
(
)
(
...
...
...
...
)
(
........
)
(
)
(
)
(
........
)
(
)
(
)
(
)
1
(
)
1
(
2
)
1
(
1
2
1
2
1
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
y
x
W
n
n
n
n
n
n
−
−
−
−
−
−
−
−
−
−
−
−
′′′′
′′′′
′′′′
=
=
=
=
spełnia warunek:
∀
x
∈
(a,b): W(x)
≠
0.
Uwaga 1. Prawdziwe są następujące implikacje:
∃x
0
∈(a,b): W(x
0
)=0 ⇒ ∀ x
∈ (a,b): W(x)=0.
∃x
0
∈(a,b): W(x
0
)
≠ 0 ⇒ ∀ x∈ (a,b): W(x) ≠ 0.
Uwaga 2. Rozwiązania równania (2) są w przedziale (a,b) liniowo niezależne wtedy i tylko
wtedy, gdy dla wszystkich x∈ (a,b) spełniają warunek: W(x) ≠ 0.
Twierdzenie 4 (o rozwiązaniu ogólnym równania liniowego jednorodnego n-tego rzędu).
Jeżeli funkcje y
1
, y
2
, ... ,y
n
tworzą fundamentalny układ rozwiązań równania (2)
w przedziale (a,b), to kombinacja liniowa tych funkcji:
)
(
)
(
1
x
y
C
x
y
k
n
k
k
∑
∑
∑
∑
=
=
=
=
=
=
=
=
z dowolnymi stałymi C
1
, C
2
, ... ,C
n
jest rozwiązaniem ogólnym tego równania
w rozważanym przedziale.
Dowód
R
OZDZIAŁ
VII
Strona 62
62
62
62
Przykład 1.
Wyznaczyć rozwiązanie ogólne równania: x
2
(lnx − 1)y′′ − xy′ + y = 0, wiedząc,że funkcje:
y
1
(x)=x i y
2
(x) = lnx są całkami szczególnymi tego równania w przedziałach: (0,e) i (e,
∞).
Przykład 2.
Wyznaczyć rozwiązanie ogólne równania: x
2
y′′ + xy′ − y=0, wiedząc, że y
1
(x)=x jest
rozwiązaniem tego równania.

R
ÓWNANIE RÓśNICZKOWE LINIOWE N
-
TEGO RZĘDU
Strona 63
63
63
63
Równanie liniowe jednorodne n-tego rzędu
o stałych współczynnikach rzeczywistych.
(3) y
(n)
+a
n-1
y
(n-1)
+ ... +a
1
y
′′′′ +a
0
y = 0,
∀
∀
∀
∀ i=0,1,...,n−
−
−
−1: a
i
=const.
Poszukujemy rozwiązania tego równania w postaci: y(x) = e
rx
.
Podstawiając tę funkcję do równania (3) otrzymamy:
(r
n
+ a
n-1
r
n-1
+ ... + a
1
r + a
0
)e
rx
=0
Funkcja o postaci y(x)=e
rx
jest rozwiązaniem równania (3) jeżeli r spełnia równanie:
r
n
+ a
n-1
r
n-1
+ ... + a
1
r + a
0
= 0,
które nazywamy równaniem charakterystycznym równania (3).
Struktura układu fundamentalnego rozwiązań równania (3) zależy od pierwiastków
wielomianu charakterystycznego.
Rozważymy trzy przypadki:
2. Równanie charakterystyczne ma n różnych pierwiastków rzeczywistych: r
1
, r
2
, ..., r
n
.
3. Równanie charakterystyczne ma n różnych pierwiastków, wśród których mogą być
pierwiastki zespolone.

R
OZDZIAŁ
VII
Strona 64
64
64
64
4. Równanie charakterystyczne ma pierwiastki wielokrotne.
Przykład 3.
Wyznaczyć rozwiązanie ogólne równania:
a) y
′′ + a
2
y = 0,
b) y
′′′ − 5 y′′ + 6 y′ = 0,
c) y
′′′ − 5y′′ + 8 y′ − 4y = 0,
d) y
(4)
+2 y
′′ + y = 0,
e) y
′′′ +3 y′′ + 9 y′ − 13y = 0.

R
ÓWNANIE RÓśNICZKOWE LINIOWE N
-
TEGO RZĘDU
Strona 65
65
65
65
Ć
wiczenia
1. Zbadać liniową zależność następujących układów funkcji:
a) f
1
(x)=4, f
2
(x)=x, b) f
1
(x)=1, f
2
(x)=x, f
3
(x)=4x, f
4
(x)=x
2
,
c) f
1
(x)=3, f
2
(x)=cos
2
x, f
3
(x)=xin
2
x, d) f
1
(x)=e
x
, f
2
(x)=xe
x
, f
3
(x)=x
2
e
x
.
2. Rozwiązać równania liniowe jednorodne:
a)
0
2
=
−
′
+
′
′
y
y
y
, b)
0
2
=
′
+
′
′
+
′
′
′
y
y
y
, c)
0
13
4
)
4
(
=
′
′
+
′
′
′
+
y
y
y
,
d)
0
16
8
)
4
(
=
+
′
′
+
y
y
y
, e)
0
4
3
2
=
+
′
−
′
′
y
y
x
y
x
, f)
0
7
4
2
2
=
+
′
−
′
′
y
y
x
y
x
,
g)
0
2
=
+
′
y
y
x
, h)
0
6
2
3
=
′
+
′
′
+
′
′
′
y
x
y
x
y
x
, j)
0
3
3
3
=
+
′
−
′
′
′
y
y
x
y
x
.
3. Znając układ fundamentalny rozwiązań równania różniczkowego liniowego
jednorodnego o stałych współczynnikach rzeczywistych, napisać odpowiadające mu
równanie różniczkowe:
a) y
1
(x)=e
-x
, y
2
(x)=e
x
,
b) y
1
(x)=1, y
2
(x)=x,
c) y
1
(x)=e
-x
, y
2
(x)=e
x
, y
3
(x)=xe
x
,
d) y
1
(x)=1, y
2
(x)=sinx, y
3
(x)=cosx,
e) y
1
(x)=e
-x
sin2x, y
2
(x)=e
-x
cos2x, y
3
(x)=e
x
.

R
OZDZIAŁ
VII
Strona 66
66
66
66

VIII
Równania różniczkowe
liniowe niejednorodne

R
OZDZIAŁ
VIII
Strona 68
68
68
68
Równania różniczkowe liniowe niejednorodne rzędu n
Rozważamy równanie liniowe niejednorodne n-tego rzędu:
(1) p
n
(x)y
(n)
+ p
n-1
(x)y
(n-1)
+ ... + p
1
(x)y
′′′′ + p
0
(x)y = f(x).Zakładamy, że znane jest
rozwiązanie ogólne równania jednorodnego:
(2) p
n
(x)y
(n)
+ p
n-1
(x)y
(n-1)
+ ... + p
1
(x)y
′′′′ + p
0
(x)y =0.
I Metoda uzmienniania stałych (M.U.S.)
II Metoda przewidywania (tylko dla równania o stałych współczynnikach).
I Metoda uzmienniania stałych
Niech y
1
, y
2
, ... ,y
n
będzie fundamentalnym układem rozwiązań równania (2),
wtedy rozwiązanie ogólne tego równania ma postać:
Y(x) = C
1
y
1
(x) + C
2
y
2
(x) + ... +C
n
y
n
(x).
Zakładamy, że rozwiązanie ogólne równania niejednorodnego (1) ma postać:
y(x) = C
1
(x)y
1
(x) + C
2
(x
)y
2
(x) + ... +C
n
(x)y
n
(x),
gdzie C
1
, C
2
, ... ,C
n
są funkcjami, które należy wyznaczyć.
Aby wstawić funkcje y do równania, wyznaczamy jej pochodną:
y
′(x) = C
1
′(x)y
1
(x)+ C
2
′(x)y
2
(x)+ ... + C
n
′(x)y
n
(x)+ C
1
(x)y
1
′(x)+ C
2
(x)y
2
′(x)+ ... + C
n
(x)y
n
′(x).
Przyjmujemy warunek upraszczający:
U
1
: C
1
′(x)y
1
(x)+ C
2
′(x)y
2
(x)+ ... + C
n
′(x)y
n
(x) = 0.
Wtedy pierwszą pochodną piszemy w postaci:
P
1
: y′(x) = C
1
(x)y
1
′(x)+ C
2
(x)y
2
′(x)+ ... + C
n
(x)y
n
′(x).
Wyznaczamy drugą pochodną funkcji y:
y
′′(x) = C
1
′(x)y
1
′(x)+ C
2
′(x)y
2
′(x)+ ... + C
n
′(x)y
n
′(x)+ C
1
(x)y
1
′′(x)+ C
2
(x)y
2
′′(x)+
...+C
n
(x)y
n
′′(x).
Przyjmujemy warunek upraszczający:
U
2
: C
1
′(x)y
1
′(x)+ C
2
′(x)y
2
′(x)+ ... + C
n
′(x)y
n
′(x) = 0.
Wtedy drugą pochodną piszemy w postaci:
P
2
: y
′′(x) = C
1
(x)y
1
′′(x)+ C
2
(x)y
2
′′(x)+ ... + C
n
(x)y
n
′′(x).
W kroku n-1 tej procedury mamy warunek upraszczający:
U
n-1
: C
1
′(x)y
1
(n-2)
(x)+ C
2
′(x)y
2
(n-2)
(x)+ ... + C
n
′(x)y
n
(n-2)
(x) = 0,
stąd:
R
ÓWNANIA RÓśNICZKOWE LINIOWE NIEJEDNORODNE
Strona 69
69
69
69
P
n-1
: y
(n-1)
(x) = C
1
(x)y
1
(n-1)
(x)+ C
2
(x)y
2
(n-1)
(x)+ ... + C
n
(x)y
n
(n-1)
(x).
Ostatecznie n-ta pochodna przyjmuje postać:
P
n
: y
(n)
(x)=C
1
′(x)y
1
(n-1)
(x)+C
2
′(x)y
2
(n-1)
(x)+...+C
n
′(x)y
n
(n-1)
(x)+C
1
(x)y
1
(n)
(x)+C
2
(x)y
2
(n)
(x)+...
+C
n
(x)y
n
(n)
(x).
Jeśli wstawimy uproszczone pochodne (P
i
) do równania (1), to otrzymamy warunek:
C
1
′(x)y
1
(n-1)
(x)+ C
2
′(x)y
2
(n-1)
(x)+ ... + C
n
′(x)y
n
(n-1)
(x)=
)
(
)
(
x
p
x
f
n
( p
n
(x)≠0 )
Uwzględniając ten ostatni warunek oraz n-1 warunków upraszczających,
otrzymujemy n równań na nieznane funkcje C
1
, C
2
, ... ,C
n
.
C
1
′(x)y
1
(x)+ C
2
′(x)y
2
(x)+ ... + C
n
′(x)y
n
(x) = 0,
C
1
′(x)y
1
′(x)+ C
2
′(x)y
2
′(x)+ ... + C
n
′(x)y
n
′(x) = 0,
...........................................................................
C
1
′(x)y
1
(n-2)
(x)+ C
2
′(x)y
2
(n-2)
(x)+ ... + C
n
′(x)y
n
(n-2)
(x) = 0,
C
1
′(x)y
1
(n-1)
(x)+ C
2
′(x)y
2
(n-1)
(x)+ ... + C
n
′(x)y
n
(n-1)
(x) =
)
(
)
(
x
p
x
f
n
.
Układ ten ma dokładnie jedno rozwiązanie, bo jest to układ cramerowski; jego wyznacznik
główny jest wyznacznikiem Wrońskiego, a ten jest różny od zera (układ rozwiązań jest
fundamentalny).
Stosując wzory Cramera, otrzymamy:
.
,...,
2
,
1
,
)
(
)
(
)
(
n
k
x
W
x
W
x
C
k
k
=
=
′
Stąd otrzymujemy nieznane funkcje:
.
,...,
2
,
1
,
)
(
)
(
)
(
n
k
A
dx
x
W
x
W
x
C
k
k
k
=
+
=
∫
Przykład 1.
Wyznaczyć rozwiązanie ogólne równania: y
′′′ + y ′ =
x
x
2
cos
sin
.
R
OZDZIAŁ
VIII
Strona 70
70
70
70
Następne twierdzenie będzie uzasadniało stosowanie innej metody rozwiązywania równań
liniowych niejednorodnych n-tego rzędu.
Twierdzenie 1
Suma rozwiązania ogólnego równania różniczkowego liniowego jednorodnego
i jakiegokolwiek rozwiązania szczególnego równania niejednorodnego jest rozwiązaniem
ogólnym równania niejednorodnego.
Przykład 1.

R
ÓWNANIA RÓśNICZKOWE LINIOWE NIEJEDNORODNE
Strona 71
71
71
71
Funkcja y(x) = x jest rozwiązaniem szczególnym równania:
x
3
y
′′′+ x
2
y
′′ − 4xy′ = − 4x, wyznaczyć rozwiązanie ogólne tego równania.
II Metoda przewidywania rozwiązania szczególnego
Metodę tę będziemy stosować tylko do równań różniczkowych liniowych n-tego rzędu
o stałych współczynnikach:
y
(n)
+a
n-1
y
(n-1)
+ ... +a
1
y
′ +a
0
y = f(x),
∀ i=0,1,...,n−1: a
i
=const.
i tylko wtedy, gdy funkcja f jest następującej postaci:
(
)
x
x
W
x
x
W
e
x
f
k
l
x
β
β
α
sin
)
(
cos
)
(
)
(
+
=
,
gdzie l oraz k oznaczają stopień wielomianów W
l
oraz W
k
.
Przy takiej prawej stronie równania różniczkowego liniowego, rozwiązanie szczególne będzie
miało postać:
1. y
s
=
(
)
x
x
S
x
x
P
e
m
m
x
β
β
α
sin
)
(
cos
)
(
+
,
gdy α
α
α
α+iβ
β
β
β nie jest pierwiastkiem wielomianu charakterystycznego tego równania.
2. y
s
=
(
)
x
x
S
x
x
P
e
x
m
m
x
p
β
β
α
sin
)
(
cos
)
(
+
,
gdy
α
α
α
α+iβ
β
β
β jest p-krotnym pierwiastkiem wielomianu charakterystycznego tego
równania; m = max(k,l).
Wielomiany P
m
i S
m
wyznaczamy wstawiając y
s
do równania z prawą stroną f.
Przypadki szczególne:
1.
α = 0, β = 0, wtedy f(x) = P
l
(x);
2.
β = 0, wtedy f(x) =
)
(x
P
e
l
x
α
;
3.
α = 0, wtedy f(x) =
(
)
x
x
S
x
x
P
m
m
β
β
sin
)
(
cos
)
(
+
.
Uwaga 1.
Jeżeli funkcja f jest sumą funkcji: f(x) = f
1
(x) + f
2
(x) + ... + f
n
(x), to metodę
przewidywania stosujemy dla każdej funkcji f
i
(i=1,2,…,n) oddzielnie i wtedy rozwiązanie
szczególne dla funkcji f będzie miało postać: y
s
= y
s1
+ y
s2
+ ... + y
sn
.
Przykład 2.

R
OZDZIAŁ
VIII
Strona 72
72
72
72
Wyznaczyć, metodą przewidywania rozwiązania szczególnego, rozwiązanie ogólne równania:
y
′′′ + y′′ − 4y′ = f(x), jeżeli:
a) f(x) =3xe
2x
;
b) f(x) = 5cosx;
c) f(x) = 4x
2
.
Przykład 3.
R
ÓWNANIA RÓśNICZKOWE LINIOWE NIEJEDNORODNE
Strona 73
73
73
73
Rozwiązać równanie: y
′′ + y = 7e
2x
+ 4sinx.
Przykład 4.
Rozwiązać zagadnienie Cauchy’ego: y
′′ − y′ = x + e
x
+e
2x
, y(0)=1, y
′(0)=0.
Przykład 5.

R
OZDZIAŁ
VIII
Strona 74
74
74
74
Wielomian charakterystyczny równania różniczkowego liniowego o stałych współczynnikach
rzeczywistych ma następujące pierwiastki: r
1
= r
2
= 1, r
3
=0, r
4
= r
5
= r
6
= 2+4i, r
7
=3i.
Podać pozostałe pierwiastki i napisać rozwiązanie ogólne równania jednorodnego.
Podać postać rozwiązania szczególnego tego równania,
jeżeli prawa strona tego równania ma postać:
f(x) = x
+ 2 + xsin3x+ e
2x
x
2
cos4x+ e
2x
+3xe
x
+xe
x
cos3x.
Równanie Eulera n-tego rzędu

R
ÓWNANIA RÓśNICZKOWE LINIOWE NIEJEDNORODNE
Strona 75
75
75
75
Równanie Eulera jest równaniem liniowym o zmiennych (ale w bardzo charakterystycznej
postaci) współczynnikach
a
n
x
n
y
(n)
+ a
n-1
x
n-1
y
(n-1)
+ ... + a
1
xy
′ + a
0
y = f(x).
Równanie Eulera jednorodne:
a
n
x
n
y
(n)
+ a
n-1
x
n-1
y
(n-1)
+ ... + a
1
xy
′ + a
0
y= 0,
rozwiązujemy szukając rozwiązań o postaci: y= x
λ
)
(
C
∈
λ
.
Wstawiając takie rozwiązanie do równania Eulera, otrzymamy wielomian
charakterystyczny dla równania Eulera o postaci:
a
n
λ
λ
λ
λ(λ
λ
λ
λ−
−
−
−1)...(λ
λ
λ
λ−
−
−
−n+1) + ... + a
2
(
λ
λ
λ
λ−
−
−
−1)λ
λ
λ
λ + a
1
λ
λ
λ
λ + a
0
= 0.
Rozważymy trzy przypadki:
1. Równanie charakterystyczne ma n różnych pierwiastków rzeczywistych: r
1
, r
2
, ..., r
n
.
2. Równanie charakterystyczne ma n różnych pierwiastków, wśród których mogą być
pierwiastki zespolone.
3. Równanie charakterystyczne ma pierwiastki wielokrotne.

R
OZDZIAŁ
VIII
Strona 76
76
76
76
Przykład 2.
Rozwiązać równanie: x
2
y′′ − xy′ − 2y = 0.
Przykład 3.
Rozwiązać równanie: x
2
y
′′ + xy′ + y = 0.
Przykład 4.
Rozwiązać równanie: x
2
y
′′ − xy′=1.

R
ÓWNANIA RÓśNICZKOWE LINIOWE NIEJEDNORODNE
Strona 77
77
77
77
Ć
wiczenia
1. Rozwiązać równania:
a)
x
y
y
y
sin
6
7
=
+
′
−
′′
, b)
x
xe
y
y
3
9
−
=
+
′′
, c)
)
2
sin
2
(
5
2
x
x
e
y
y
y
x
+
=
+
′
+
′′
−
,
d)
x
y
y
2
sin
=
+
′′
, e)
x
x
y
y
3
cos
sin
=
+
′′
, f)
x
tg
y
y
2
1
1
4
+
=
+
′′
2. Rozwiązać zagadnienie Cauchy’ego:
a)
2
)
0
(
,
1
)
0
(
,
4
=
′
=
=
−
′′
y
y
shx
y
y
,
b)
1
)
(
,
1
)
(
,
2
sin
=
′
=
=
+
′′
π
π
y
y
x
y
y
,
c)
0
)
0
(
,
1
)
0
(
,
sin
10
9
6
=
′
=
=
+
′
+
′′
y
y
x
y
y
y
,
d)
1
)
0
(
,
0
)
0
(
,
0
)
0
(
,
1
4
=
′′
=
′
=
+
=
′
−
′′
′
y
y
y
x
y
y
.
3. Rozwiązać równania:
a)
3
3
9
6
x
e
y
y
y
x
=
+
′
−
′
′
, b)
x
y
y
2
sin
1
4
=
+
′′
,
c)
1
1
2
3
+
=
+
′
+
′′
x
e
y
y
y
.
4. Rozwiązać równania liniowe jednorodne:
a)
0
7
4
2
2
=
+
′
−
′
′
y
y
x
y
x
, b)
0
2
=
+
′
y
y
x
,
c)
0
6
2
3
=
′
+
′
′
+
′
′
′
y
x
y
x
y
x
, d)
0
3
3
3
=
+
′
−
′
′
′
y
y
x
y
x
.
5. Rozwiązać równania:
a)
x
y
y
x
y
x
3
2
=
−
′
+
′′
, b)
x
y
y
x
ln
sin
2
2
=
−
′′
,
c)
.
3
3
2
3
x
y
x
y
x
y
x
=
′
+
′
′
−
′
′
′
.
6. Rozwiązać zagadnienie Cauchy’ego:
a)
4
)
1
(
,
0
)
1
(
,
12
12
2
2
2
−
=
′
=
=
−
′
+
′′
y
y
x
y
y
x
y
x
,
b)
2
)
1
(
,
0
)
1
(
,
ln
12
2
=
′
=
=
′
+
′′
y
y
x
y
x
y
x
.

R
OZDZIAŁ
VIII
Strona 78
78
78
78

Strona 79
79
79
79
Literatura
1. Gewart M., Skoczylas Z., Analiza matematyczna 2 (Definicje, twierdzenia, wzory),
OWGiS, Wrocław 2005.
2. Gewart M., Skoczylas Z., Równania różniczkowe zwyczajne (Teoria, przykłady,
zadania)
, OWGiS, Wrocław 2002.
3. Kaczyński A. M., Podstawy analizy matematycznej, t.2, OWPW, Warszawa 2000.
4. Karwowski O., Matematyka (część I iII), OWPW, Warszawa 1989.
5. Kowalski T. i inni, Zbiór zadań z matematyki, t.2, WPW, Warszawa 1984.
6. Krysicki W., Włodarski L., Analiza matematyczna w zadaniach, cz. I-II, PWN,
Warszawa 1999.
7. Litewska K. i inni, Matematyka, t.1, OWPW, Warszawa 1997.
8. Nawrocki J., Matematyka (30 wykładów z ćwiczeniami), OWPW, Warszawa 2002.
9. Stankiewicz W., Wojtowicz J., Zadania z matematyki dla wyższych uczelni
technicznych, t.1i 2
, PWN, Warszawa, 2002
10. śakowski W., Ćwiczenia problemowe dla politechnik, WNT, Warszawa 1991.

Strona 80
80
80
80
Wyszukiwarka
Podobne podstrony:
chomik Sprawozdanie, matematyczne modelowanie procesów biotechnologicznych, Lista 3 Równania różnicz
chomik mb lab 2, matematyczne modelowanie procesów biotechnologicznych, Lista 3 Równania różniczkowe
raport3 Równania różniczkowe zwyczajne
Metody Komputerowe i Numeryczne, Równania różniczkowe zwyczajne
Kochański P, Kortyka P Sposoby rozwiązywania prostych równań różniczkowych zwyczajnych
12 ELEMENTY RÓWNAŃ RÓŻNICZKOWYCH ZWYCZAJNYCH
chomik Wybrane modele ekologiczne oraz metody rozwiązywania równań różniczkowych zwyczajnych
Rownania rozniczkowe zwyczajne. Zagadnienia poczatkowe
Numeryczne rozwiazywanie zagadnien poczatkowych równan i układów równan rózniczkowych zwyczajnych
Żołądek H Jakościowa teoria równań różniczkowych zwyczajnych
8 Równania rózniczkowe zwyczajne
Definicja i wlasnosci, Matematyka studia, Metody operatorowe w równaniach różniczkowych
4 Równania różniczkowe zwyczajne o stałych współczynnikach
Równania różniczkowe zwyczajne lista zadań
Gewert, Skoczylas Równania różniczkowe zwyczajne , teoria przykłady, zadania
5-RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE, RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE
więcej podobnych podstron