RÓWNANIA RÓŻNICZKOWE ZWYCZAJNE

1)Równania liczbowe: f(x)=0 → rozwiązanie: wszystkie liczby x_i, które są miejscami zerowymi

funkcji f(x)

1.1)równanie funkcyjne → rozwiązaniami są funkcje

1.1.1)równania różniczkowe

• Definicja równania różniczkowego zwyczajnego:

W równaniu funkcyjnym, w którym niewiadomą jest funkcja jednej zmiennej i występuje w tym równaniu pochodna funkcji niewiadomej nazywamy równaniem różniczkowym zwyczajnym.

Przykład: y'+2xy=0

y=y(x) - niewiadoma (funkcja poszukiwana)

x
I

F(x,y,y')=0 - postać ogólna równania różniczkowego

F - funkcja trzech zmiennych

Rozwiązaniem równania F(x,y,y')=0 nazywamy funkcję y=φ(x) w przedziale x
I, posiadającą pochodną φ'(x) w x
I i zamienia ona w/w równanie w tożsamość:

, x
I

Przykład: y'+2xy=0 - równanie pierwszego rzędu

y=y(x) - szukana

- rozwiązanie równania y'+2xy=0, x
R

y'=-2x

-2x
+ 2x
≡ 0, x
(-∞,+∞)

Każda funkcja y=C∙
, C
R jest rozwiązaniem równania y'+2xy=0.

Jest to przykład rozwiązania ogólnego.

• Definicja rzędu równania różniczkowego:

Rzędem równania różniczkowego nazywamy rząd najwyższej pochodnej występującej w tym równaniu.

Przykład: y”+4x²y²+y'=0 - równanie rzędy drugiego

y⁽⁵⁾+lny”=0 - równanie rzędu piątego

(1) F(x,y,y',y”,...,y⁽ⁿ⁾)=0 - równanie n-tego rzędu

F - funkcja n+2 zmiennych

y=y(x) - funkcja szukana

• Definicja zagadnienia Cauchy'ego (początkowego):

Mówimy, że funkcja y=y(x) jest rozwiązaniem zagadnienia Cauchy'ego (zagadnienia początkowego) dla równania (1), jeżeli spełnia ona to równanie i następujące warunki początkowe:

y(x₀)=y₀, y'(x₀)=y₁, ..., y^(n-1)(x₀)=y_n-1

gdzie: x₀
I i y₀,y₁, ...,y_n-1 - dane liczby rzeczywiste zwane wartościami początkowymi

W szczególnym przypadku, gdy n=1 mamy tylko jeden warunek początkowy:

y(x₀)=y₀

Przykład: Jeżeli równanie jest rzędu 3, to mamy 3 warunki początkowe: dla funkcji niewiadomej i dla pierwszej i drugiej pochodnej.

• Definicja rozwiązania ogólnego (całki ogólnej) równania różniczkowego:

Funkcję y=φ(x,C₁,C₂,...,C_n) zależną od n parametrów rzeczywistych C₁,C₂,...,C_n nazywamy rozwiązaniem ogólnym (całką ogólną) równania (1), jeżeli przy każdym wyborze C₁,C₂,...,C_n funkcja ta jest rozwiązaniem tego równania i wszystkie rozwiązania tego równania da się otrzymać przez odpowiedni wybór parametrów.

Gdy n=1, to funkcja zależy tylko od jednego parametru.

§1. RÓWNANIA RÓŻNICZKOWE O ZMIENNYCH ROZDZIELONYCH I RZĘDU

Niech funkcja x→f(x) będzie ciągła w przedziale (a,b), a funkcja y→g(y) będzie ciągła w przedziale (c,d) i g(y)≠0 w (c,d).

Równanie różniczkowe rzędy pierwszego postaci:

(1.1)

lub:

g(y)dy = f(x)dx (1.2)

nazywamy równaniem różniczkowym o zmiennych rozdzielonych.

y=y(x) - funkcja szukana

Scałkujmy teraz równanie (1.2), traktując y jako zmienną niezależną:

Jest to całka ogólna (rozwiązanie ogólne) równania (1.2)

Przykład: Znaleźć całkę ogólną równania: x(y²-1)dx+y(x²-1)dy=0.

x(y²-1)dx + y(x²-1)dy=0 / :(y²-1)(x²-1)

- jest to równanie zmiennych rozdzielonych

Scałkujmy w/w równanie zmiennych rozdzielonych:

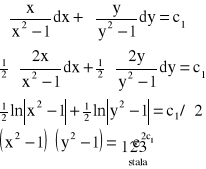
- całka ogólna

Dobierając odpowiednio C otrzymamy rozwiązanie szczególne.

§2. RÓWNANIA JEDNORODNE I RZĘDU

Niech będzie dana funkcja f jednej zmiennej, ciągła w przedziale (a,b) i taka, że f(u)≠u.

• Definicja równania różniczkowego jednorodnego:

Równanie różniczkowe rzędy pierwszego postaci:

(2.1)

nazywamy równaniem różniczkowym jednorodnym.

Aby rozwiązać równanie (2.1) wprowadza się następujące podstawienie:

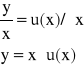
Liczymy pochodną po x:
i wstawiamy ją do równania (2.1):

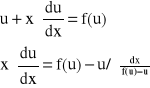
- równanie różniczkowe zmiennych rozdzielonych

- całka ogólna równania (2.1)

Przykład: Rozwiązać równanie:
.

u + xu' = 1+u

§3. RÓWNANIA RÓŻNICZKOWE LINIOWE I RZĘDU

• Definicja równania różniczkowego liniowego:

Równanie różniczkowe pierwszego rzędu postaci:

(3.1)

p i f są to dane funkcje ciągłe w przedziale (a,b)

nazywamy równaniem różniczkowym liniowym

Jeżeli w równaniu tym f(x) ≡ 0 [f(x) jest tożsamościowo równa zero], równanie przyjmuje postać:

(3.2)

i jest równanie różniczkowe liniowe jednorodne.

Jeśli f(x) ≡ 0 to równanie (3.1) jest równaniem różniczkowym liniowym niejednorodnym.

Zauważmy, że równanie (3.2) jest równaniem zmiennych rozdzielonych:

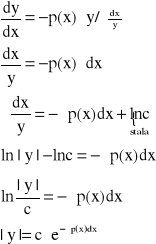
- całka ogólna równania liniowego jednorodnego (3.2)

Całka ogólna równania liniowego jednorodnego = C.O.R.L.J.

Całka szczególna równania liniowego jednorodnego = C.S.R.L.J.

Całka ogólna równania niejednorodnego = C.O.R.N.

Całka szczególna równania niejednorodnego = C.S.R.N.

Przykład: Znaleźć całkę szczególną równania liniowego jednorodnego: y'+sinx∙y=0, spełniającą warunek: y(0)=1

y'+sinx∙y=0

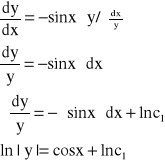
y=C∙e^cosx - C.O.R.L.J.

1=C∙e^cos0

y=e^cosx-1 - C.S.R.L.J.

• Twierdzenie:

Jeżeli y₁(x) jest jakąkolwiek całką szczególną równania niejednorodnego (3.1), a funkcja
jest całką ogólną równania jednorodnego (3.2), to całka ogólna równania niejednorodnego (3.1) jest w następującej postaci:

lub:

C.O.R.N. = C.O.R.J. + C.S.R.N.

• Metoda uzmienniania stałej:

Całki ogólnej równania niejednorodnego (3.1) szukamy w postaci:

Liczymy pochodną:
i wstawiamy do równania (3.1):

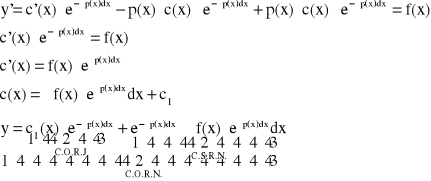
Przykład: Znaleźć całkę szczególną równania
, spełniającą warunek początkowy y(0)=
.

Szukamy całki ogólnej równania jednorodnego:

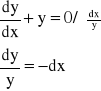
y=C∙e^-x - C.O.R.J.

Następnie uzmienniamy stałą:

y=C(x)∙e^-x

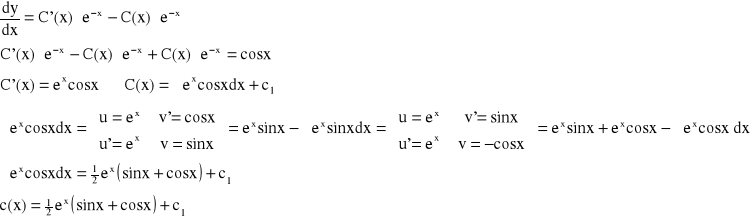
- C.O.R.N.

=c₁+

c₁=0

y=
(sinx+cosx) - całka szczególna równania

§4. RÓWNANIA RÓŻNICZKOWE ZUPEŁNE

Załóżmy, że funkcja (x,y)→P(x,y) i (x,y)→Q(x,y) są klasy C¹ w pewnym obszarze D
R² i Q(x,y)≠0 w obszarze D.

• Definicja równania różniczkowego zupełnego:

Równanie różniczkowe I rzędu postaci:
lub w postaci równoważnej:

P(x,y)dx + Q(x,y)dy = 0 (4.1)

nazywamy równaniem różniczkowym zupełnym, jeżeli istnieje funkcja (x,y)→u(x,y) klasy C² w obszarze D taka, że lewa strona równania (4.1) jest różniczką zupełną tej funkcji, tzn.:

u - funkcja pierwotna różniczki zupełnej Pdx + Qdy

Warunkiem koniecznym i wystarczającym na to, żeby równanie różniczkowe (4.1) było równaniem różniczkowym zupełnym jest:

w obszarze D

• Twierdzenie:

Jeżeli równanie (4.1) jest równaniem różniczkowym zupełnym, a funkcja u jest funkcją pierwotną klasy C² różniczki zupełnej występującej po lewej stronie tego równania, to równość:

jest całką ogólną równania (4.1).

Przykład: Znaleźć całkę ogólną równania:
.

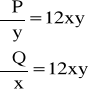
wynika z tego, że jest to równanie różniczkowe zupełne

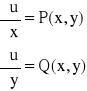
= 3x² + 6xy²

u =

u = x³ + 3x²y² + c(y)

= 6x²y + c'(y)

6x²y + c'(y) = 6x²y + 4y³

c(y) =

c(y) = y⁴ +

u(x,y) = x³ + 3x²y² + y⁴ +

Zgodnie z powyższym twierdzeniem funkcję u(x,y) przyrównujemy do stałej:

x³ + 3x²y² + y⁴ +
= c

x³ + 3x²y² + y⁴ = C - całka ogólna równania różniczkowego zupełnego (C.O.R.R.Z.)

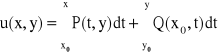
(x₀,y₀)
D

wzór na funkcję pierwotną

§5. TRAJEKTORIE ORTOGONALNE

Niech funkcja (x,y,c)→φ(x,y,c) będzie określona w pewnym obszarze przestrzeni R³ i załóżmy, że będzie ona klasy C¹ w tym obszarze i
.

Załóżmy, że równanie:

φ(x,y,c) = 0 (5.1)

określa nam przy każdym c
R równanie krzywej na płaszczyźnie.

Mówimy wtedy, że równanie (5.1) jest równaniem rodziny linii (krzywych) zależnych od jednego parametru c.

Przykłady rodziny linii:

1. x² + y² = c - rodzina okręgów

2. y - cx = 0 - rodzina prostych

3. y - cx² = 0 - rodzina parabol

itp.

Przypuśćmy, że w równaniu (5.1) y zależy od x [y(x)] i zróżniczkujmy to równanie:

(5.2)

Z układ równań (5.1) i (5.2) wyrugujmy parametr c; wtedy otrzymamy równanie różniczkowe z niewiadomą funkcji y:

F(x,y,y') = 0 (5.3)

Równanie (5.3) nazywamy równaniem różniczkowym rodziny linii (5.1).

Przykład: Znaleźć równanie różniczkowe rodziny parabol: y - cx² = 0.

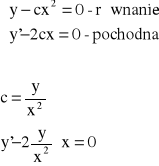
- równanie różniczkowe rodziny parabol

• Definicja trajektorii ortogonalnej rodziny (5.1):

Krzywą, która w każdym swym punkcie tworzy kąt prosty z krzywą rodziny (5.1) przechodzącej przez ten punkt nazywamy trajektorią ortogonalną rodziny (5.1).

Jeżeli w równaniu (5.3) wstawimy w miejsce y' →
, to otrzymamy:

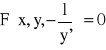
- równanie różniczkowe trajektorii ortogonalnej

Znajdując rozwiązanie ogólne tego równania otrzymamy rodzinę trajektorii ortogonalnej.

Przykład: Znaleźć rodzinę trajektorii ortogonalnych dla rodziny parabol: y - cx² = 0.

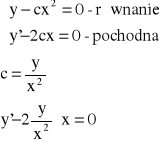
- równanie różniczkowe rodziny parabol

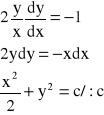
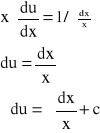
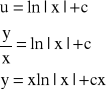
y

x