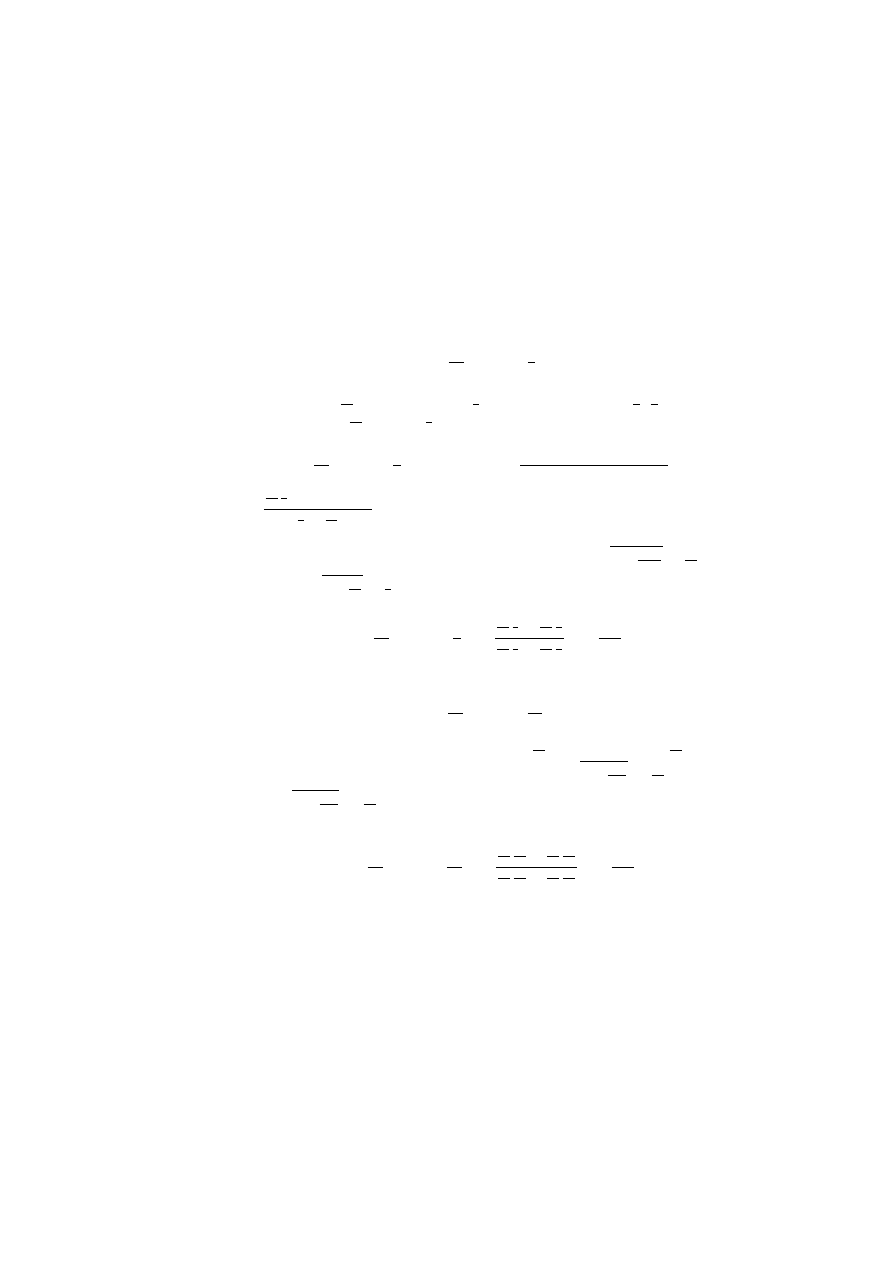
Zadania pogrupowane s¡ tematycznie, aby ka»dy mógª zapozna¢ si¦ z ty-

powymi metodami ich rozwi¡zywania. Oczywi±cie przedstawione rozwi¡zania

nie s¡ jedynymi poprawnymi, mo»na uzyska¢ prawidªowy wynik innymi meto-

dami.

1 Trygonometria

1. Obliczy¢

tg

arcsin

40

41

+ arccos

3

5

Oznaczmy arcsin

40
41

= α

oraz arccos

3
5

= β

. Wtedy α

∗

∈

−

π

2

,

π

2

, β

∗

∈

[0, π]

, oraz sin α =

40
41

, cos β =

3
5

. Mamy po kolei:

tg

arcsin

40

41

+ arccos

3

5

= tg (α + β) =

sin α cos β + cos α sin β

cos α cos β − sin α sin β

=

=

40
41

3
5

+ cos α sin β

cos α

3
5

−

40
41

sin β

Z jedynki trygonometrycznej oraz (*) dostajemy cos α =

q

1 −

1600
1681

=

9

41

,

oraz sin β =

q

1 −

9

25

=

4
5

. Podstawiaj¡c te wyniki obliczamy

tg

arcsin

40

41

+ arccos

3

5

=

40
41

3
5

+

9

41

4
5

9

41

3
5

−

40
41

4
5

= −

156

133

2. Obliczy¢

ctg

arcsin

12

13

+ arccos

7

25

Post¦pujemy analogicznie: Oznaczamy arcsin

12
13

= α

oraz arccos

7

25

=

β

. Z jedynki trygonometrycznej uzyskamy cos α =

q

1 −

144
169

=

5

13

, oraz

sin β =

q

1 −

49

625

=

24
25

. Korzystaj¡c ze wzorów na sinus i cosinus sumy

otrzymamy

ctg

arcsin

12

13

+ arccos

7

25

=

5

13

7

25

−

12
13

24
25

12
13

7

52

+

5

13

24
25

= −

253

204

3. Udowodni¢

sin 3α = 3 sin α − 4 sin

3

α

sin 3α = sin (2α + α) = sin 2α cos α + cos 2α sin α =

= 2 sin α cos

2

α + cos

2

α − sin

2

α

sin α =

= 2 sin α 1 − sin

2

α

+ 1 − 2 sin

2

α

sin α = 3 sin α − 4 sin

3

α

1

4. Udowodni¢

cos 3α = 4 cos

3

α − 3 cos α

Podobnie post¦pujemy tutaj:

cos 3α = cos (2α + α) = cos 2α cos α − sin 2α sin α =

= cos

2

α − sin

2

α

cos α − 2 sin

2

α cos α =

= 2 cos

2

α − 1

cos α − 2 1 − cos

2

α

cos α = 4 cos

3

α − 3 cos α

2 Oblicznie granic

1.

lim

n→∞

n

√

3

n

+ 2

n

+ sin n = lim

n→∞

n

s

3

n

1 +

2

3

n

+

sin n

3

n

=

= 3 lim

n→∞

n

s

1 +

2

3

n

+

sin n

3

n

= 3 · 1 = 3

2.

lim

n→∞

n + 1

n (ln (n + 1) − ln (n))

= lim

n→∞

n + 1

n ln

n+1

n

=

= lim

n→∞

n + 1

ln 1 +

1

n

n

=

∞

ln(e)

= ∞

3.

lim

n→∞

n + 4

n + 3

7−3n

= lim

n→∞

1 +

1

n + 3

−3(n+3)+16

=

= lim

n→∞

1 +

1

n + 3

n+3

!

−3

1 +

1

n + 3

16

= e

−3

· 1 =

1

e

3

4.

lim

n→∞

√

n −

√

n − 1

r

n +

1

n

=

lim

n→∞

√

n −

√

n − 1

√

n +

√

n − 1

√

n +

√

n − 1

r

n

2

+ 1

n

= lim

n→∞

√

n

2

+ 1

√

n +

√

n − 1

√n

=

lim

n→∞

q

n

2

1 +

1

n

2

√

n

2

+

q

n

2

1 −

1

n

= lim

n→∞

q

1 +

1

n

2

1 +

q

1 −

1

n

=

1

1 + 1

=

1

2

3 Twierdzenia o ci¡gach

1. Udowodni¢, »e

lim

n→∞

1

√

1

+

1

√

2

+ . . . +

1

√

n

= ∞

2

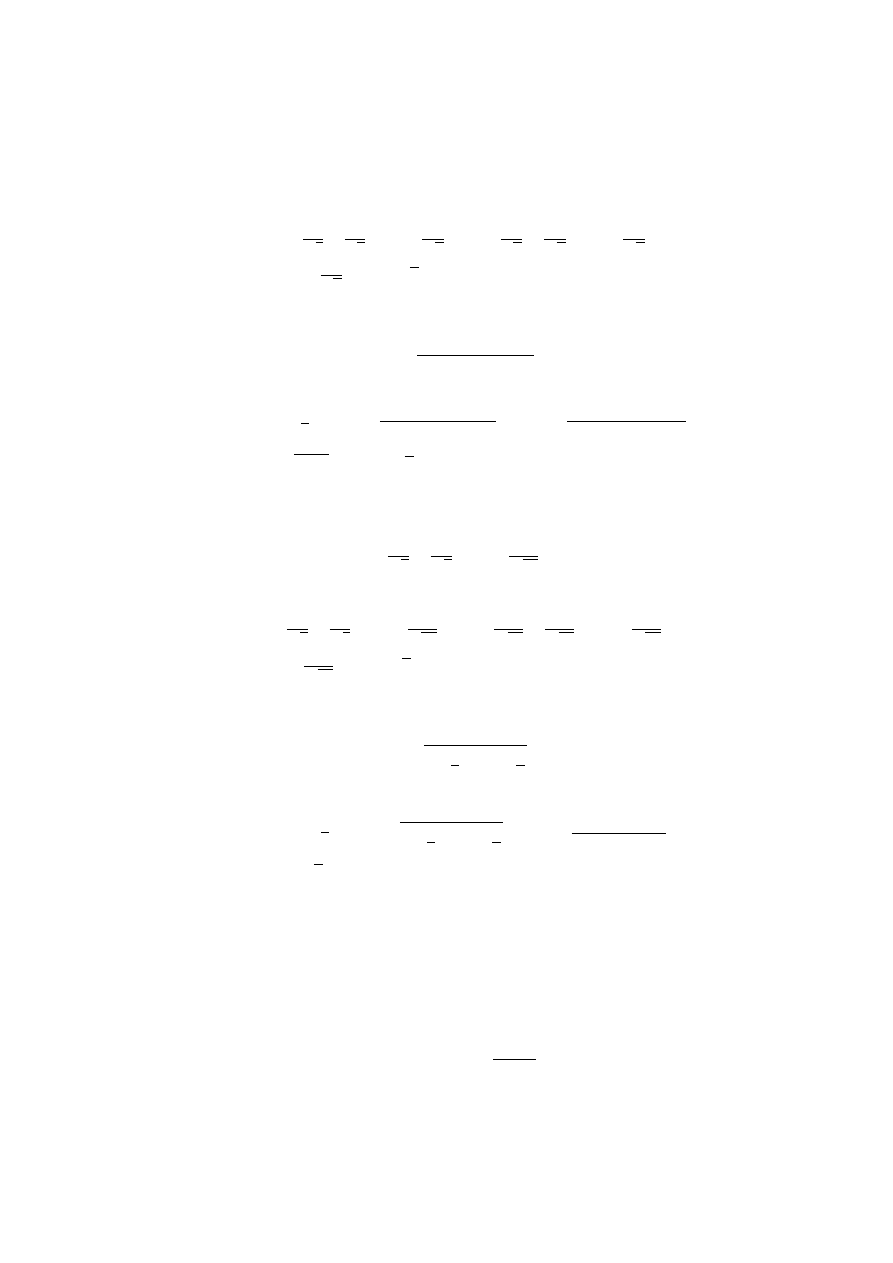
Skorzystamy z twierdzenia o dwóch ci¡gach. Dostajemy

lim

n→∞

1

√

1

+

1

√

2

+ . . . +

1

√

n

> lim

n→∞

1

√

n

+

1

√

n

+ . . . +

1

√

n

=

= lim

n→∞

n

√

n

= lim

n→∞

√

n = ∞

sk¡d otrzymujemy tez¦.

2. Udowodni¢, »e

lim

n→∞

n

p

1

7

+ 2

7

+ . . . + n

7

= 1

Skorzystamy z twierdzenia o 3 ci¡gach. Dostajemy

1 = lim

n→∞

n

√

1 6 lim

n→∞

n

p

1

7

+ 2

7

+ . . . + n

7

6 lim

n→∞

n

p

n

7

+ n

7

+ . . . + n

7

=

= lim

n→∞

n

√

n · n

7

= lim

n→∞

n

√

n

8

= 1

co daje tez¦.

3. Udowodni¢, »e

lim

n→∞

1

3

√

1

+

1

3

√

2

+ . . . +

1

3

√

n

2

= ∞

Skorzystamy z twierdzenia o dwóch ci¡gach. Dostajemy

lim

n→∞

1

3

√

1

+

1

3

√

2

+ . . . +

1

3

√

n

2

> lim

n→∞

1

3

√

n

2

+

1

3

√

n

2

+ . . . +

1

3

√

n

2

=

= lim

n→∞

n

3

√

n

2

= lim

n→∞

3

√

n = ∞

sk¡d otrzymujemy tez¦.

4. Udowodni¢, »e

lim

n→∞

n

r

1 +

1

2

+ . . . +

1

n

= 1

Skorzystamy z twierdzenia o 3 ci¡gach. Dostajemy

1 = lim

n→∞

n

√

1 6 lim

n→∞

n

r

1 +

1

2

+ . . . +

1

n

6 lim

n→∞

n

√

1 + 1 + . . . + 1 =

= lim

n→∞

n

√

n = 1

co daje tez¦.

4 Wyznaczanie dziedziny i zbioru warto±ci funk-

cji

1. Wyznaczy¢ dziedzin¦ naturaln¡ i zbiór warto±ci funkcji

f (x) = 3 arccos

1 − |x|

2

3

Poniewa» dziedzin¡ funkcji arccos(x) jest przedziaª [−1, 1], wi¦c musi za-

chodzi¢

− 1 6

1 − |x|

2

6 1 ⇔

− 2 6 1 − |x| 6 2 ⇔
− 2 6 |x| − 1 6 2 ⇔
− 1 6 |x| 6 3

sk¡d |x| 6 3 i w konsekwencji −3 6 x 6 3. Zatem dziedzin¡ naturaln¡

funkcji f(x) jest zbiór [−3, 3]. Zbiorem warto±ci funkcji arccos(x) jest
[0, π]

, zatem zbiorem warto±ci funkcji 3 arccos(x) jest [3 · 0, 3π]. Jest to

równie» zbiór warto±ci funkcji f(x), gdy» funkcja

1−|x|

2

przyjmuje wszyst-

kie warto±ci ze zbioru [−1, 1].

2. Wyznaczy¢ dziedzin¦ naturaln¡ i zbiór warto±ci funkcji

f (x) = 4 arcsin

1 − x

2

3

Poniewa» dziedzin¡ funkcji arcsin(x) jest przedziaª [−1, 1], wi¦c musi za-

chodzi¢

− 1 6

1 − x

2

3

6 1 ⇔

− 3 6 1 − x

2

6 3 ⇔

− 3 6 x

2

− 1 6 3 ⇔

− 2 6 x

2

6 4

sk¡d x

2

6 4 i w konsekwencji −2 6 x 6 2. Zatem dziedzin¡ naturaln¡

funkcji f(x) jest zbiór [−2, 2]. Zbiorem warto±ci funkcji arcsin(x) jest
[−

π

2

,

π

2

]

, zatem zbiorem warto±ci funkcji 4 arcsin(x) jest [−2π, 2π]. Jest to

równie» zbiór warto±ci funkcji f(x), gdy» funkcja

1−x

2

3

przyjmuje wszyst-

kie warto±ci ze zbioru [−1, 1].

5 Odwracanie funkcji

1. Znale¹¢ funkcj¦ odwrotn¡

f (x) =

ln

2

(x + 1)

dla x > 0,

3x − 2

dla x < 0

Dziedzin¡ funkcji jest zbiór wszystkich liczb rzeczywistych, za± zbiorem

warto±ci (−∞, −2) ∪ [0, ∞). Gdy x > 0, funkcja f(x) przyjmuje warto±ci

ze zbioru [0, ∞). Wyznaczmy funkcj¦ odwrotn¡:

y = ln

2

(x + 1) ⇔

√

y = ln(x + 1) ⇔

e

√

y

= x + 1 ⇔

e

√

y

− 1 = x.

4

Zatem dla x ∈ [0, ∞) dostajemy f

−1

(x) = e

√

x

− 1

. Gdy x < 0, funkcja

f (x)

przyjmuje warto±ci ze zbioru (−∞, −2). Wyznaczmy funkcj¦ od-

wrotn¡:

y = 3x − 2 ⇔

y + 2 = 3x ⇔

y + 2

3

= x.

Zatem dla x ∈ (−∞, −2) dostajemy f

−1

(x) =

x+2

3

. Ostatecznie

f

−1

(x) =

e

√

x

− 1

dla x > 0,

x+2

3

dla x < −2

2. Wyznaczy¢ funkcj¦ odwrotn¡

f (x) = x

2

+ 2

sgn x

Dziedzin¡ funkcji jest zbiór wszystkich liczb rzeczywistych, za± zbiorem

warto±ci (−∞, −2) ∪ {0} ∪ (2, ∞). Gdy x < 0 funkcja przyjmuje warto±ci

ze zbioru (−∞, −2). Wyznaczmy funkcj¦ odwrotn¡ na tym przedziale:

y = −x

2

− 2 ⇔

p−y − 2 = |x|

co w poª¡czeniiu z faktem, »e x < 0 daje x = −

√

−y − 2

. Gdy x = 0, funk-

cja przyjmuje warto±¢ 0. Wreszcie gdy x > 0 funkcja przyjmuje warto±ci

ze zbioru (2, ∞). Wyznaczmy funkcj¦ odwrotn¡ na tym przedziale:

y = x

2

+ 2 ⇔

p

y − 2 = |x|

co w poª¡czeniu z faktem, »e x > 0 daje x =

√

y − 2

. Ostatecznie

f

−1

(x) =







−

√

−x − 2

dla x < −2,

0

dla

x = 0,

√

y − 2

dla

x > 2.

5