
Differential Equations for Reliability,
Maintainability, and Availability
Harry A. Watson, Jr.
September 1, 2005

Abstract
This is an electronic textbook on Differential Equations
for Reliability, Maintainability, and Availability.
It is written to fill the need of an introductory book
which can be accessed on-line, stored in magnetic media
or on CDs (Compact Disks), and cross-referenced electronically.
This entire book was done in
the (public domain) typesetting language L
A
TEX.
The equations, figures, pictures, and tables were
typeset in their respective L
A
TEX environments.
Many thanks are due to those who assisted in the
proofreading and problem sets: Eric Gentile (electrical engineer
and physicist) and Ron Shortt (physicist).
Because computer
software is rapidly replacing rote manipulations and
because modern numerical techniques allow qualitative
real-time graphics, the traditional introductory course
in ordinary differential equations is doomed to oblivion.
However, many textbooks in physics, chemistry, engineering,
medicine, biology, and ecology mention techniques, terms,
and processes covered nowhere else. Advanced courses on
dynamical systems, algebraic topology, and functional analysis
never mention such items as “exact equations,” “integrating
factors,” or the Clairaut
equation. Advanced modern algebra treats differential forms
and tensors in a totally different manner than is done
either in physics or in engineering.
Without a reference in introductory differential equations,
one could never span the disciplines. One
needs practice in modern transform methods in general and
in the Laplace transform in particular.
This practice should be done
at the introductory level and not in
functional analysis, where such topics are introduced
in an abstract manner with much lemmata and with no

correlation to physical reality.
Finally, in this book, we end each proof with the
hypocycloid of four cusps—the diamond symbol (♦).
2

Limit of Liability/Disclaimer of Warranty:
While every effort has been made to ensure the correctness of
this material, the author makes no warranty, expressed or
implied, or assumes any legal liability or responsibility
for the accuracy, completeness, or usefulness of any
information, process, or procedure disclosed herein. In no
event will the author be liable for any loss of profit or any
other commercial damage, including but not limited to
special, incidental, consequential, or other damages.

Copyright c
1997, Harry A.
Watson, Jr. This book may be used by NWAD (Naval Warfare
Assessment Division) and its sponsors freely without
payment of any royalty and any part may be copied freely,
except that no alteration is allowed when the copyright
symbol ( c
) is displayed.

Contents
1
Introduction
5
1.1
First Encounters
. . . . . . . . . . . . . . . . . . . . . . . . .
5
1.2
Basic Terminology
. . . . . . . . . . . . . . . . . . . . . . . .
9
1.3
Solutions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
1.4
Computers and Differential Equations . . . . . . . . . . . . . .
19
1.5
Euler’s Method . . . . . . . . . . . . . . . . . . . . . . . . . .
22
1.6
The equation y
0
= F (x) . . . . . . . . . . . . . . . . . . . . . .
27
1.7
Existence theorems . . . . . . . . . . . . . . . . . . . . . . . .
33
1.8
Systems of Equations . . . . . . . . . . . . . . . . . . . . . . .
42
1.9
The General Solution . . . . . . . . . . . . . . . . . . . . . . .
45
1.10 The Primitive . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
1.11 Summary
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
51
2
First Order, First Degree Equations
61
2.1
Differential Form Versus Standard Form . . . . . . . . . . . .
61
2.2
Exact Equations
. . . . . . . . . . . . . . . . . . . . . . . . .
65
2.3
Separable Variables . . . . . . . . . . . . . . . . . . . . . . . .
71
2.4
First Order Homogeneous Equations
. . . . . . . . . . . . . .
81
2.5
A Theorem on Exactness . . . . . . . . . . . . . . . . . . . . .
88
2.6
About Integrating Factors . . . . . . . . . . . . . . . . . . . .
96
2.7
The First Order Linear Differential Equation . . . . . . . . . . 100
2.8
Other Methods . . . . . . . . . . . . . . . . . . . . . . . . . . 105
2.9
Summary
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
3
The Laplace Transform
110
3.1
Laplace Transform Preliminaries . . . . . . . . . . . . . . . . . 110
3.2
Basic Theorems . . . . . . . . . . . . . . . . . . . . . . . . . . 114
3.3
The Inverse Transform . . . . . . . . . . . . . . . . . . . . . . 123
1

3.4
Transforms and Differential Equations
. . . . . . . . . . . . . 128
3.5
Partial Fractions
. . . . . . . . . . . . . . . . . . . . . . . . . 129
3.6
Sufficient Conditions . . . . . . . . . . . . . . . . . . . . . . . 131
3.7
Convolution . . . . . . . . . . . . . . . . . . . . . . . . . . . . 138
3.8
Useful Functions and Functionals . . . . . . . . . . . . . . . . 140
3.9
Second Order Differential Equations . . . . . . . . . . . . . . . 144
3.10 Systems of Differential Equations . . . . . . . . . . . . . . . . 146
3.11 Heaviside Expansion Formula . . . . . . . . . . . . . . . . . . 148
3.12 Table of Laplace Transform Theorems . . . . . . . . . . . . . . 151
3.13 Table of Laplace Transforms . . . . . . . . . . . . . . . . . . . 152
3.14 Doing Laplace Transforms . . . . . . . . . . . . . . . . . . . . 155
3.15 Summary
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . 157
2

List of Figures
1.1
Inverted Exponential . . . . . . . . . . . . . . . . . . . . . . .
6
1.2
Isoclines . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
20
1.3
Euler’s Method . . . . . . . . . . . . . . . . . . . . . . . . . .
24
1.4
Simple Difference Method . . . . . . . . . . . . . . . . . . . .
29
1.5
Closed Rectangle . . . . . . . . . . . . . . . . . . . . . . . . .
36
2.1
Connected Set . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
2.2
Level Curves . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
2.3
A Closed Path . . . . . . . . . . . . . . . . . . . . . . . . . . .
91
3.1
Transform Pairs . . . . . . . . . . . . . . . . . . . . . . . . . . 115
3.2
The Heaviside Function . . . . . . . . . . . . . . . . . . . . . . 126
3.3
The Dirac Delta Function . . . . . . . . . . . . . . . . . . . . 126
3.4
Heaviside Function . . . . . . . . . . . . . . . . . . . . . . . . 153
3.5
Ramp Function . . . . . . . . . . . . . . . . . . . . . . . . . . 153
3.6
Shifted Heaviside . . . . . . . . . . . . . . . . . . . . . . . . . 153
3.7
Linearly Transformed Heaviside . . . . . . . . . . . . . . . . . 154
3.8
Linearly Transformed Ramp . . . . . . . . . . . . . . . . . . . 154
3.9
Sawtooth Function . . . . . . . . . . . . . . . . . . . . . . . . 154
3

List of Tables
1.1
Euler’s Method Calculations
. . . . . . . . . . . . . . . . .
25
1.2
An Approximation to e
x
. . . . . . . . . . . . . . . . . . . .
26
2.1
Table of Symbols
. . . . . . . . . . . . . . . . . . . . . . . .
64
2.2
Table of Exact Differentials
. . . . . . . . . . . . . . . . 100
2.3
Table of Common Abbreviations
. . . . . . . . . . . . . . . 101
3.1
Named Functions
. . . . . . . . . . . . . . . . . . . . . . . . 118
3.2
Laplace Transform Pairs
. . . . . . . . . . . . . . . . . . . 127
3.3
Theorem Table
. . . . . . . . . . . . . . . . . . . . . . . . . 152
4

Chapter 1
Introduction
1.1
First Encounters
Differential equations are of fundamental importance
in science and engineering because many physical laws
and relations are described mathematically by such
equations.
Roughly speaking, by an ordinary differential equation we mean a relation
between an
independent variable x, a function y of x, and
one or more of the derivatives y
0
, y
00
, . . . ,
y
(n)
of x. For example,
y
0
= 1 − y,
(1.1)
y
00
+ 4y = 3 sin x,
(1.2)
y
00
+ 2x(y
0
)
5
= xy
(1.3)
are ordinary differential equations.
In calculus we learn how to find the successive,
that is higher or higher order, derivatives of a given function y(x). Notice
that we use parentheses to distinguish y
(n)
from y
n
, the nth power of y. If
the function y depends on two or more independent variables, say x
1
, . . .,
x
m
, then the derivatives are partial derivatives and the equation is called a
partial differential equation.
5

-
6
y
x
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
·····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
····
······
········
············
············································
·····················································································································································································
Figure 1.1:
The Curve y = 1 − e
−x
Definition 1 A differential equation is an equation which involves deriva-
tives of a dependent variable with respect to one or more independent vari-
ables.
As an example of a differential equation, if y = 1 − e
−x
, then
y
0
= e
−x
= 1 − y;
(1.4)
thus for this function the relation (1.1) is satisfied. We say that y = 1 − e
−x
is a solution of Equation (1.1). However, this is not the only solution, for
y = 1 − 2e
−x
also satisfies Equation (1.1):
y
0
= 2e
−x
= 1 − y.
We note that the function y = 1 − e
−x
is sometimes called the “inverted
exponential.” Curves of this type are seen in biology where a population is
limited by some factor, e.g., the food supply, and in reliability, where one is
concerned with component failures.
The first fundamental problem is how to determine
6

all possible solutions of a given differential
equation. Even for the simplest example of a
differential equation
dx
dx
= F (x)
or, equivalently
y
0
= F (x),
where F is an explicit function of x
alone, this may not be easy. In fact, entire tables
of integrals and symbolic mathematical software
cannot determine every such solution in closed
form. To solve this equation, one must find a
function y = f (x) whose derivative is the given
function F (x). The solution, y, is the so-called
antiderivative or indefinite integral of F (x).
There is a second fundamental problem.
For many differential equations it is
very difficult to obtain explicit formulas for all the
solutions. However, a general existence theorem guarantees
that there are solutions; in fact, infinitely many. The problem
is to determine properties of the solutions,
or of some of the solutions, from the differential equation
itself. Many properties can be found
without explicit formulas for the solutions;
we can, in fact, obtain numerical values for solutions to any
accuracy desired. Accordingly, we are led to regard a
differential equation itself as a sort of explicit formula
describing a certain collection of functions. For example,
we can show that all solutions of
Equation (1.2) are given by
y = sin x + c
1
cos 2x + c
2
sin 2x
where c
1
and c
2
are arbitrary constants.
Equation (1.2) itself, y
00
+ 4y = 3 sin x, is another
way of describing all these functions.
Historically, differential equations came into existence
at the same time as differential and integral calculus.
It is an artifact of the education system that they are studied
7

in colleges and universities after calculus.
A single differential equation may describe many
of the laws of nature in a unified and concise form,
due to the fact that several different functions can
each be a solution of one differential equation.
Thus, it is not surprising that most laws of physics
are in the form of differential equations.
One noteworthy example is the formulation of
Newton’s second law:
force = mass × acceleration.
Let m denote the mass of a particle constrained to more along
a straight line. The differential equation
m
d
2
x
dt
2
= F
dx
dt
, x, t
!
,
where x is the distance from an origin, t is time, and
and F is force, which depends on velocity dx/dt, x,
and t.
We will be studying the problem of obtaining a solution
as well as the theoretical problems associated with
existence, uniqueness, and the like.
The goal is to obtain explicit
expressions for the solutions wherever possible.
Such solutions are also referred to as
solutions in closed form.
In the course of study, we will observe that solutions
have different appearances, including, but not
limited to, infinite series. We will also try to
make qualitative statements about the
solutions, such as trajectories, graphs, asymptotes,
etc., directly from the differential equations.
It has been observed that, except for a few
special cases, there is no simple way of
solving ordinary differential equations.
If the unknown function and its derivatives
appear linearly in the differential equation,
8

then it is called a linear
differential equation; otherwise, it is said
to be nonlinear. Among the cases for which
simple methods of solution are possible are
the linear equations.
This is fortunate because of the frequency
with which they occur in scientific phenomena.
In fact, many of the fundamental laws of science
are formulated in terms of linear ordinary
differential equations. Consequently, we will
devote a majority of this book to such equations.
1.2
Basic Terminology
An ordinary differential equation of
order n is an equation of the form
F
x, y,
dy
dx
, . . . ,
d
n
y
dx
n
!
= 0.
(1.5)
The above equation involves an unknown function, F ,
and one or more its derivatives, y
(k)
= d
k
y/dx
k
,
where k = 1, 2, . . . , n. Of course, if k = 0, we have
y
(0)
≡ y and equation (1.5)
reduces to an algebraic equation in x and y.
Moreover, y
(1)
≡ y
0
. (Sometimes we
write y
(iv)
instead of y
0000
or y
(4)
.)
For example, observe that
xy
00
+ 3y
0
− 2y + xe
x
= 0,
(1.6)
(y
000
)
2
− 4y
0
y
000
+ (y
00
)
3
= 0
(1.7)
are ordinary differential equations of orders 2
and 3, respectively.
If a differential
equation has the form of an algebraic equation
of degree m in the highest derivative, then we
9

say that the differential equation is of
degree m.
For example, Equation (1.7) is of
degree 2 in its highest
derivative, y
000
, whereas Equation (1.6)
is of degree 1.
In an introductory course, one generally is
restricted to equations of the
first degree.
Moreover, the leading coefficient of the highest
order y
(n)
is generally 1 so that we have
an expression of the form
y
(n)
= ˜
F
x, y, . . . , y
(n−1)
.
A linear ordinary differential
equation is a restriction of Equation (1.5)
to the form
b
0
(x)y
(n)
+ b
1
(x)y
(n−1)
+ · · · + b
n−1
(x)y
0
+ b
n
(x)y = Q(x).
(1.8)
This corresponds to an algebraic equation where the
coefficients are replaced by functions and the powers
are replaced by derivatives, for example:
a
0
t
n
+ a
1
t
n−1
+ · · · + a
n−1
t + a
n
= 0,
where t
0
≡ 1 and the “driving function,”
Q(x), is absorbed into the coefficient a
n
.
This phenomenon will be a recurring theme throughout
all of differential equations, operator theory,
transform calculus, and tensor analysis. Familiar,
common notions will be extended by more general,
complicated concepts. In turn, the more general
concepts will reduce to basic ideas and many of the
theorems and facts can be generalized.
Each of the Equations (1.1), (1.2),
and (1.6) above is linear.
In particular, can write the coefficients
10

for Equation (1.6) as follows:
b
0
(x) := x,
b
1
(x) := 3,
b
2
(x) := −2,
Q(x) := −xe
x
.
It is true that every linear differential equation
is always of degree 1. The converse does not
hold, as one can see from Equation (1.3),
which is of first degree (in its lead coefficient)
and nonlinear (in its first derivative).
The word “ordinary” implies that
there is just one independent
variable. If we have a function of two
or more independent variables, say U (x, y, z),
it is possible to have partial derivatives.
An equation such as
∂
2
U
∂x
2
+
∂
2
U
∂y
2
+
∂
2
U
∂z
2
= 0
is called a partial differential equation.
In this book, with a few notable exceptions, we will be
concerned only with ordinary
differential equations. This being the case,
the word “ordinary” will generally be omitted.
1.3
Solutions
Definition 2 A function y = f (x), defined on some interval
a < x < b (possibly infinite), is said to be a
solution of the differential
equation
F
x, y, y
0
, . . . , y
(n)
= 0
(1.9)
if Equation (1.9) is identically
satisfied whenever y and its derivatives
are replaced by f (x) and its derivatives.
Of course, it is implied in the definition that
if the differential equation defined by
11

Equation (1.9) is of order n
then f (x) has at least n derivatives
throughout the interval (a, b). Moreover,
whatever is valid for a general solution also
holds for a particular solution.
One may observe that the function y = f (x)
is defined on an open interval,
a < x < b, and not on a closed
interval, a ≤ x ≤ b. It is generally true
that derivatives are studied on open sets whereas
continuous functions (and integrals) are studied on
closed sets.
As an example of a solution, suppose that
each of c
1
and c
2
is a constant. The equation,
which is related to Equation (1.2),
y = c
1
cos 2x + c
2
sin 2x
is a solution of the differential equation
y
00
+ 4y = 0
(1.10)
since y
00
= −4c
1
cos 2x − 4c
2
sin 2x, so that
y
00
+ 4y = (−4c
1
cos 2x − 4c
2
sin 2x) + 4 (c
1
cos 2x + c
2
sin 2x) ≡ 0.
Many differential equations have solutions
that can be concisely written as
y = f (x; c
1
, . . . , c
n
) ,
(1.11)
where each of c
1
, . . . , c
n
is an arbitrary constant.
(Two or more of the c’s can assume the same value.)
It is not always possible to let the c’s assume any
real value for unrestricted values of x; however,
for given values of the c’s and an admissible
range of values of the independent variable, x,
Equation (1.11) gives all of the solutions of
Equation (1.9).
12

For example, all of the solutions of
Equation (1.10) are given by
y = c
1
cos 2x + c
2
sin 2x;
(1.12)
the solution y = cos(2x) is obtained when c
1
= 1,
c
2
= 0. When a function (1.11) is
obtained, providing all solutions,
it is called the general solution.
In general, the number of arbitrary constants will
equal the order of n, as will be explained in
Section 1.7. However, there
may be exceptions.
(y
0
)
2
+ y
2
= 0
has exactly one solution, that is y ≡ 0.
In order to gain some experience with the
preceding material, we will preview some of the
material from Section 1.6.
The differential equation
in that section is just
y
0
= F (x),
(1.13)
where F (x) is defined and continuous for
a ≤ x ≤ b. All
possible solutions of Equation (1.13)
come from the integral equation
y =
Z
F (x) dx + c
1
,
a < x < b.
(1.14)
We observe that the arbitrary constant
of the differential equation
is simply the so-called constant of integration
from the indefinite integral. This
generalizes to higher order differential
equations. For example, suppose that
y
00
= 30x.
(1.15)
13

Integrate y
00
twice to obtain
y
0
= 15x
2
+ c
1
,
y = 5x
3
+ c
1
x + c
2
.
(1.16)
Successive integration of
Equation (1.15), which is
or order two, has produced exactly
two arbitrary constants, c
1
, c
2
.
Problems
1. Classify each of the following differential equations
as to order, degree, and linearity:
(a) y
00
+ 3y
0
+ 6y = 0,
(b) y
0
+ P (x)y = Q(x),
(c) (y
0
)
2
= x
3
− y,
(d) y
00
− 2(y
0
)
2
+ xy = 0,
(e) (y
0
)
2
+ 9xy
0
− y
2
= 0,
(f) x
3
y
00
− xy
0
+ 5y = 2x,
(g) y
(vi)
− y
00
= 0,
(h) sin(y
00
) + e
y
0
= 1.
2. Integrate each of the following differential equations
and include constants of integration as arbitrary constants to
give the general solution:
(a) y
0
= xe
x
,
(b) y
000
= 0,
(c) y
00
= x,
(d) y
(n)
= x,
(e) y
0
= log x,
(f) y
0
= 1/x.
14

3. Show that the function y = f (x) is a solution of
the given differential equations:
(a) y = e
x
, for y
00
− y = 0,
(b) y = cos 2x, for y
(iv)
+ 4y
00
= 0,
(c) y = c
1
cos 2x + c
2
sin 2x (each of c
1
and c
2
is a constants), for y
00
+ 4y = 0,
(d) y = sin (e
x
), for y
00
− y
0
+ e
2x
y = 0.
4. Consider the differential equation y
0
= 3x
2
.
(a) Verify that y = x
3
+ c
1
is the general solution;
(b) Determine c
1
such that the solution curve passes through
(1, 3);
(c) Determine c
1
so that the solution
satisfies the integral equation
R
1
0
y(x) dx =
1
2
.
5. Discuss how a differential equation is a
generalization of an algebraic equation.
6. Write a computer program to generate the data points
for Figure 1.1.
Solutions
1. Classify each of the following differential equations
as to order, degree, and linearity:
(a) y
00
+ 3y
0
+ 6y = 0,
2nd order, 1st degree, linear;
15

(b) y
0
+ P (x)y = Q(x),
1st order, 1st degree, linear;
(c) (y
0
)
2
= x
3
− y,
1st order, 2nd degree, nonlinear;
(d) y
00
− 2(y
0
)
2
+ xy = 0,
2st order, 1st degree, nonlinear;
(e) (y
0
)
2
+ 9xy
0
− y
2
= 0,
1st order, 2nd degree, nonlinear;
(f) x
3
y
00
− xy
0
+ 5y = 2x,
2nd order, 1st degree, linear;
(g) y
(vi)
− y
00
= 0,
6th order, 1st degree, linear;
(h) sin(y
00
) + e
y
0
= 1,
2nd order, unknown degree, nonlinear.
2. Integrate each of the following differential equations
and include constants of integration as arbitrary constants to
give the general solution:
(a) y
0
= xe
x
,
for all real x, y = xe
x
− e
x
+ c
1
;
(b) y
000
= 0,
for all real x, y = c
1
x
2
+ c
2
x + c
3
;
(c) y
00
= x,
for all real x, y =
1
6
x
3
+ c
1
x + c
2
;
(d) y
(n)
= x,
for all real x, y =
1
(n+1)!
x
n+1
+c
1
x
n−1
+c
2
x
n−2
+
· · · + c
n
;
(e) y
0
= log x,
for all x > 0, y = x log(x) − x + c
1
;
(f) y
0
= 1/x
for all x 6= 0 and c
1
> 0, y = log (c
1
|x|).
3. Show that the function y = f (x) is a solution of
the given differential equations:
(a) y = e
x
, for y
00
− y = 0,
y
0
= e
x
,
y
00
= e
x
,
16

y
00
− y = e
x
− e
x
= 0,
by substitution.
(b) y = cos 2x, for y
(iv)
+ 4y
00
= 0,
y = cos 2x,
y
0
= −2 sin 2x,
y
00
= −4 cos 2x,
y
000
= 8 sin 2x,
y
(iv)
= 16 cos 2x.
y
(iv)
+ y
00
= 16 cos 2x − 16 cos 2x = 0,
by successive differentiation and substitution.
(c) y = c
1
cos 2x + c
2
sin 2x (each of c
1
and c
2
is a constants), for
y
00
+ 4y = 0,
y
0
= −2c
1
sin 2x + 2c
2
cos 2x,
y
00
= −4c
1
cos 2x − 4c
2
sin 2x.
y
00
+ 4y = −4c
1
cos 2x − 4c
2
sin 2x + 4 (c
1
cos 2x + c
2
sin 2x) = 0
by differentiation and substitution.
(d) y = sin (e
x
), for y
00
− y
0
+ e
2x
y = 0.
y
0
= e
x
cos (e
x
) ,
y
00
= e
x
cos (e
x
) − e
2x
sin (e
x
) .
y
00
− y
0
+ e
2x
y =
e
x
cos (e
x
) − e
2x
sin (e
x
) − [e
x
cos (e
x
)] + e
2x
sin (e
x
) = 0
by direct substitution.
4. Consider the differential equation y
0
= 3x
2
.
17

(a) Verify that y = x
3
+ c
1
is the general solution.
Differentiate.
dy/dx = y
0
= 3x
2
.
(b) Determine c
1
such that the solution curve passes through (1, 3).
Solve the algebraic equation 3 = 1
3
+ c
1
for c
1
.
By inspection, c
1
= 2.
(c) Determine c
1
so that the solution
satisfies the integral equation
R
1
0
y(x) dx =
1
2
.
Integrate y(x) = x
3
+ c
1
from 0 to 1 and require
the definite integral to be equal to
1
2
.
Z
1
0
x
3
+ c
1
dx =
x
4
4
1
0
+ c
1
x
1
0
=
1
2
.
1
4
+ c
1
=
1
2
,
thus
c
1
=
1
4
.
5. Discuss how a differential equation is a
generalization of an algebraic equation.
Starting with an equation
a
0
t
n
+ a
1
t
n−1
+ · · · + a
n−1
t + a
n
= 0,
observe that t
1
= t and t
0
= 1. This gives
a
0
t
n
+ a
1
t
n−1
+ · · · + a
n−1
t
1
+ a
n
t
0
= 0.
Substitute b
k
(x) for a
k
for all k = 0, 1, . . . , n
and substitute y
(k)
for t
k
, with the understanding
that y
(0)
is the function y itself. (Also, y
0
:= y
(1)
.)
b
0
(x)y
(n)
+ b
1
(x)y
(n−1)
+ · · · + b
n−1
(x)y
0
+ b
n
y = 0.
The solution of an algebraic equation is a number
set (either real or complex). On the other hand,
the solutions set of a differential equation is
made up of functions. The last step is to add a
”driving function” Q(x) and the generalization
is complete.
18

6. Write a computer program to generate the data points for Figure 1.1.
The plotting area in the figure is approximately
300 points by 200 points, with 72 points per inch.
With scaling by points, we can write a BASIC (Beginners’
All-purpose Symbolic Instruction Code) program.
100 FOR k = 0 TO 10 STEP .1
110 y = 200 * (1 − EXP( − k / 20) )
120 PRINT k, y
130 NEXT k
140 FOR k = 10 TO 20 STEP .2
150 y = 200 * (1 − EXP( − k / 20) )
160 PRINT k, y
170 NEXT k
180 FOR k = 20 TO 300
190 y = 200 * (1 − EXP( − k / 20) )
200 PRINT k, y
210 NEXT k
220 END
1.4
Computers and Differential Equations
The success that digital computers enjoyed
in solving algebraic equations, both numerically
and symbolically, quickly extended itself to
differential equations. This should not be
surprising because differential equations can
be considered as a generalization, in some
sense, of algebraic equations. For example,
each solution of the algebraic equation
x
2
+ 3x + 1 = 0 is simply a number; each solution
of a differential equation is a function.
Computers have also added plotting and
interactive graphics capabilities to the
19

-
6
x
y
1
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
Figure 1.2:
Isoclines of y
0
= x
2
+ y
2
traditional quantitative numerical tables.
Modern computer software delivers an
approximating function to any differential
equation which cannot be solved explicitly.
This approximating function enables the user
to retrieve output in any desired format:
tables, plots, graphs, etc. The geometric
interpretation of first order differential
equations has been rendered obsolete by this
technology. The process of determining
solutions by isoclines,
once the darling of the numerical analyst,
is now viewed as a fond and vain thing no
longer worth the time to study.
For purely historical reasons, however,
we will touch on the topic of isoclines.
The equation
20

{{−0.0355234}, {0.0749577}, {0.166858},
{0.243498}, {0.30751}, {0.361096}, {0.406214},
{0.444702}, {0.478376}, {0.509112}, {0.53891},
{0.569969}, {0.604761}, {0.646141}, {0.697497},
{0.76299}, {0.847958}, {0.95961}, {1.10828},
{1.30986}, {1.59084}, {2.}, {2.63986}}
y
0
= F (x, y)
(1.17)
has a very simple geometric interpretation.
One can construct from the function F (x, y) above
a very useful graphical method to qualitatively
describe the solutions of Equation (1.17)
without actually obtaining a solution of the
form y = f (x). This is done by letting the
equation F (x, y) be constant and plotting
curves in the xy-plane called
isoclines, or curves of constant slope.
Each isocline is determined by the equation
F (x, y) = m
(1.18)
where m is a fixed constant. For example, consider
the first order differential equation
dy
dx
= x
2
+ y
2
.
(1.19)
The isoclines are concentric circles centered at the origin.
(See the Figure 1.2.) We use some modern
computer software to obtain a solution through the point
(1, 2). The software indicates that a closed form, or
explicit solution, cannot be obtained. We settle for a
numerical solution and get a table of values for y in
terms of x. For this example we let x march from
−1.1 to 1.1 with a step size of 0.1.
The software also produces an outstanding graph, which is
21

available as a computer graphics file.
This method can be helpful in getting a qualitative
knowledge of a solution curve in engineering problems
involving first order differential equations whose
solution set cannot be expressed in terms of known
functions or where finding a solution is mathematically
intractable.
1.5
Euler’s Method
To obtain a numerical solution to a differential
equation, each of the arbitrary constants must have
a definite value. One might view the numerical
techniques as a generalization of the concept of
the definite integral
R
b
a
F (x) dx. On the
other hand, closed form, symbolic solutions
may be considered as a generalization of the
so-called indefinite integral
R
F (x) dx + c
1
.
From an indefinite integral and a particular point
(x
0
, y
0
), with a < x
0
< b, one may compute
the particular solution, f (x).
f (x
0
) := y
0
=
Z
x
0
x
0
F (t) dt + c
1
implies that c
1
= y
0
so that
f (x) = y
0
+
Z
x
x
0
F (t) dt.
Using this construction,
the solution curve { (x, y) | a < x < b, y = f (x)},
passes through the point (x
0
, y
0
) and there
are no arbitrary constants. This is referred to
as an initial value problem
and the subsidiary conditions that determine the
values of the arbitrary constants are known as
initial values. By placing some restrictions
on the function F one may ensure that the initial
22

value problem has a unique solution. The etymology
of the expression “initial value” lies in the
problem of determining the behavior of the motion
of a particle moving along a constrained path and
subject to known forces. Knowing the initial
position and the initial velocity is sufficient to
uniquely determine all future behavior of the
particle.
The simplest, non-trivial initial value problem is
that of determining a particular solution to
y
0
≡
dx
dy
= F (x, y),
(1.20)
where each of F and F
y
≡ ∂F/∂y
is a continuous function in some rectangular region R
having (x
0
, y
0
) in its interior. For a given set
of discrete points x
0
< x
1
< · · · < x
n−1
< x
n
we wish
to compute a table of approximate numerical values
(x
k
, y
k
) to points on the solution curve
(x
k
, f (x
k
)). There are several ways of doing
this, the most elementary being a simple difference
method known as Euler’s method.
The idea is straightforward enough. Starting with
(x
0
, y
0
) and a step of size ∆x := x
1
− x
0
compute
∆y := F (x
0
, y
0
) ∆x
(1.21)
then set x
1
= x
0
+ ∆x and y
1
:= y
0
+ ∆y.
Repeat this procedure, redefining the increment
∆x so that ∆x := x
2
− x
1
and
computing
∆y := F (x
1
, y
1
) ∆x
to obtain
y
2
:= y
1
+ ∆y = y
1
+ F (x
1
, y
1
) · [x
2
− x
1
] .
23

-
6
x
0
x
1
x
2
x
3
y
x
•
•
•
•
∆x
∆y
"
"
"
"
"
a
a
a
a
a
Figure 1.3:
Solution Obtained by Euler’s Method
If we define y
0
k
= F (x
k
, y
k
) and h
k
= x
k
− x
k−1
,
for all appropriate values of the integer k, then
y
k+1
= y
k
+ y
0
k
· h
k
.
(1.22)
This is illustrated in Figure (1.3).
If the points are equally spaced, so that
∆x = x
1
− x
0
= x
2
− x
1
= · · · = x
n
− x
n−1
,
then we simply write h for h
k
, k = 1, 2, . . . , n − 1
and Equation 1.22 becomes
y
k+1
= y
k
+ h y
0
k
k = 0, 1, . . . , n − 1.
One may observe that ∆x is actually an
approximation to the differential dx and
that ∆y := F (x
k
, y
k
) ∆x is
an approximation to dy evaluated at the
point (x
k
, y
k
). From henceforth we will only
24
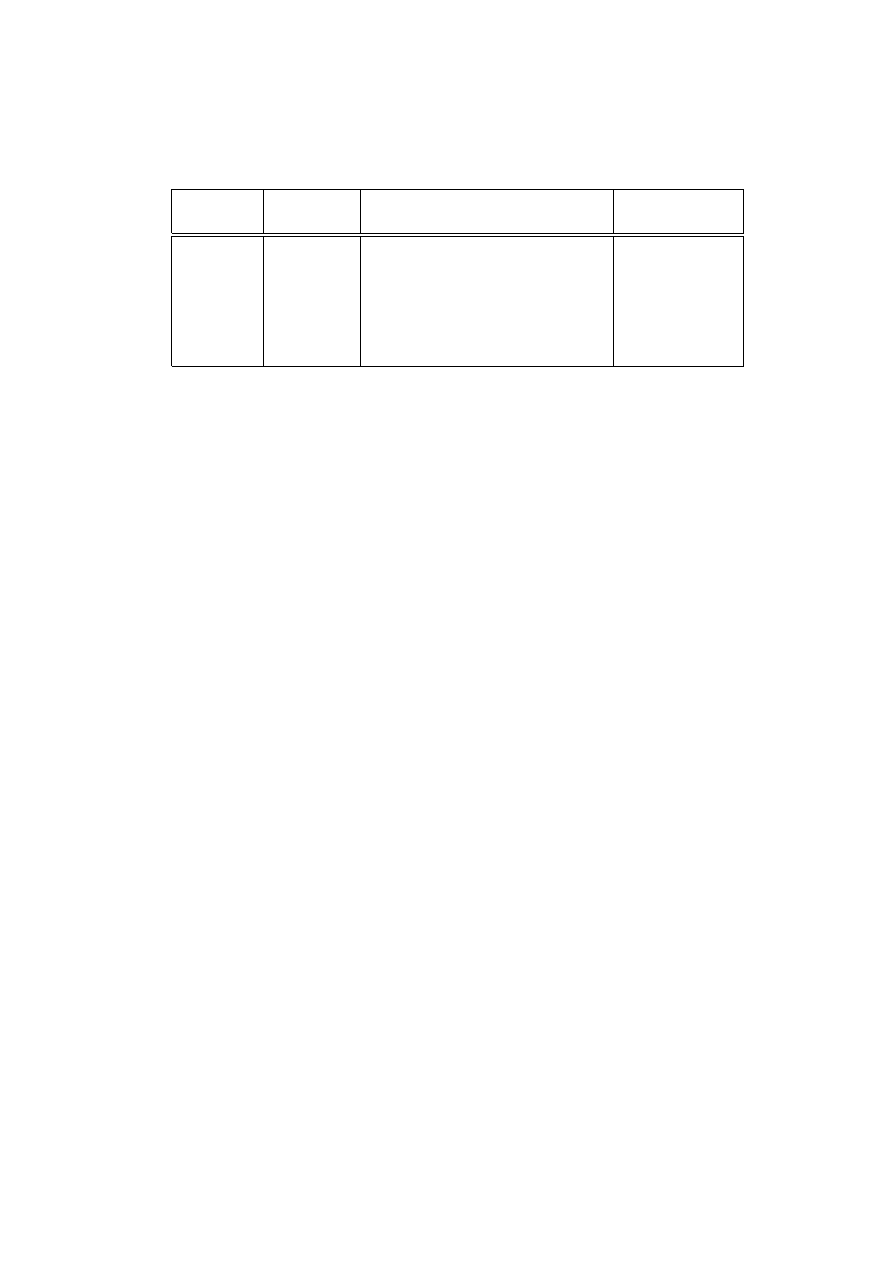
Total
Slope at (x, y)
Increment of y
x
y
F (x, y)
∆y
x
0
y
0
y
0
0
:= F (x
0
, y
0
)
F (x
0
, y
0
) ∆x
x
0
+ ∆x
y
0
+ ∆y
y
0
1
:= F (x
0
+ ∆x, y
0
+ ∆y)
F (x
1
, y
1
) ∆x
x
0
+ 2∆x
y
1
+ ∆y
y
0
2
:= F (x
1
+ ∆x, y
1
+ ∆y)
F (x
2
, y
2
) ∆x
x
0
+ 3∆x
y
2
+ ∆y
y
0
3
:= F (x
2
+ ∆x, y
2
+ ∆y)
· · ·
· · ·
· · ·
· · ·
· · ·
x
0
+ n∆x
y
n−1
+ ∆y
y
0
n
= F (x
n−1
+ ∆x, y
n−1
+ ∆y)
F (x
n
, y
n
) ∆x
Table 1.1:
Euler’s Method Calculations
consider equally spaced points x
k
. Now
look at the table 1.1,
with ∆x kept constant,
for Euler’s method.
The example
y
0
= y
with x
0
= 0, y
0
= 1, ∆x = 0.1, is worked out in
table 1.2.
Of course, the solution to y
0
= y is simply the exponential
function y = e
x
. This function is well behaved and
has is defined for all real numbers. We will compute
the first 5 values (k = 0, . . . , 5) using a BASIC
(Beginners’ All-purpose Symbolic Instruction Code)
program.
25
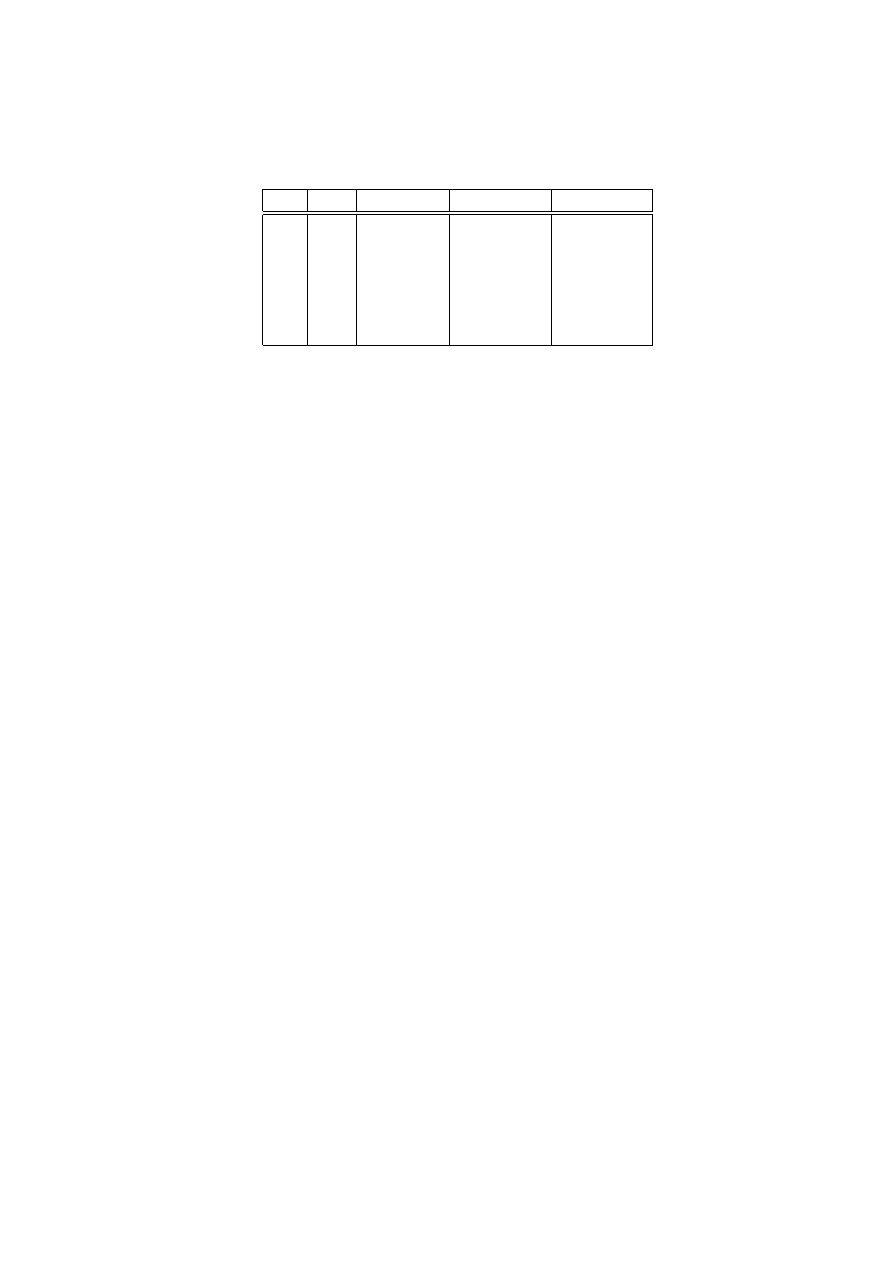
k
x
k
y
k
∆y
e
x
k
0
0
1
0.1
1
1
.1
1.1
0.21
1.105171
2
.2
1.21
0.331
1.221403
3
.3
1.331
0.4641
1.349859
4
.4
1.4641
0.61051
1.491825
5
.5
1.61051
0.771561
1.648721
Table 1.2:
An Approximation to e
x
100 x0 = 0 : y0 = 1
110 h = .1 : n = 5
120 x = x0 : y = y0
130 PRINT x, y, EXP(x)
140 FOR k = 1 TO n
150 yprime = y
160 x = x + h
170 y = y + yprime ∗ h
180 PRINT x,y,EXP(y)
190 NEXT k
200 END
One might observe that the smaller the step
size, that is, the smaller the value of ∆x,
the closer the approximation of Euler’s method is
to the exact solution. We went from x
0
to x
n
by positive increments h := ∆x;
proceeding by negative increments would have
yielded a solution to the left. With modern
computer software, there is little need to
26

apply such techniques as Euler’s method;
however, there is much to be learned about
which technique is best employed for the
computation of a solution to a given differential
equation and which should be avoided. This topic,
the numerical approximation of
solution curves to differential
equations, is part of numerical analysis. The
computer algorithms and techniques found in
commercial software and applied to
various problems require special skills and
knowledge beyond the scope of this introductory
course; however, certain topics in the estimation
of the error in computed versus exact solutions
will be covered in a later chapter. The reader
is encourage to experiment with computer
software which calculates and plots solution
curves to various ordinary differential equations
and systems of ordinary differential equations.
Some of the graphics are truly rad and awesome!
1.6
The equation y
0
= F (x)
The most familiar of all differential equations
are those of the form
y
0
= F (x),
(1.23)
where F (x) is continuous for all x, a ≤ x ≤ b.
Solutions of (1.23) are obtained via
the Fundamental Theorem of Calculus.
Theorem 1 Fundamental Theorem of Calculus
Let F (x) be continuous in the interval a ≤ x ≤ b.
For each real number c
1
, there exists a unique solution
f (x) of (1.23) in the interval [a, b]
such that f (a) := c
1
. The solution is given by the
definite integral
27

f (x) =
Z
x
a
F (t) dt + c
1
.
(1.24)
Letting
R
F (t) dt denote the indefinite integral of F ,
we can denote Equation (1.24) as
y =
Z
F (x) dx + c
1
a ≤ x ≤ b.
Another form of the above is
y =
Z
x
x
0
F (t) dt + c
1
a ≤ x ≤ b,
(1.25)
where a ≤ x
0
≤ b. In the above equation
the indefinite integral
has been replaced by the definite integral with
limits of integration x
0
, x, and with t
as a “dummy” variable
of integration. Again, it is the Fundamental
Theorem of Calculus that says
d
dx
Z
x
x
0
F (t) dt = F (x),
(1.26)
so that the integral on the right of
Equation (1.26) is indeed an
indefinite integral of F (x).
In applications, it is frequently required
that y := y
0
when x = x
0
. The constant c
1
must be chosen in
Equation (1.25) such that
y
0
=
Z
x
0
x
0
F (u) du + c
1
= 0 + c
1
.
Therefore c
1
:= y
0
and the differential equation becomes
y = y
0
+
Z
x
x
0
F (t) dt
a ≤ x ≤ b.
(1.27)
Just because the indefinite integral
R
F (t) dt
cannot be evaluated in closed form does not mean that
28
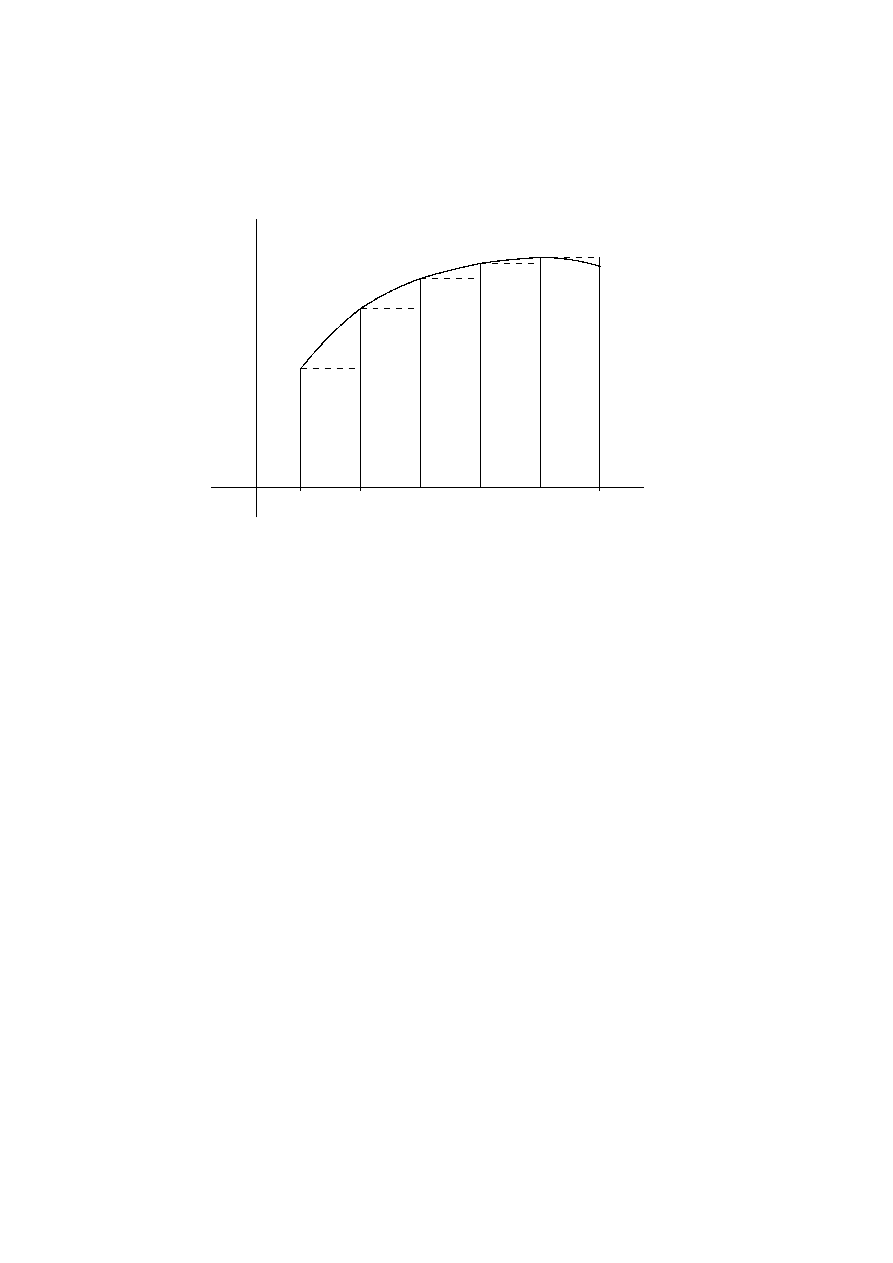
-
6
x
0
x
0
+∆x
x
y
t
∆x
F (x
0
)
Figure 1.4:
Integration by Simple Differences
it does not have a meaning. In fact, several important
functions in statistics (e.g., the normal distribution)
and physics (e.g., the Fresnel integrals) are expressed in
terms of definite integrals. Equation (1.27)
itself can be used to compute the value
of y for each x. Fix x and evaluate the
definite integral by any of the standard
approximation techniques: the
trapezoidal rule, Simpson’s rule, etc.
The most elementary approximation is given by
taking the sums of
“circumscribed rectangles” (also called an
inner sum) as follows.
Divide the closed interval
[x
0
, x] = { t | x
0
≤ t ≤ x } into n equal parts, each
of length ∆x,
so that x = x
0
+ n∆x.
29

y = y
0
+
Z
x
x
0
F (u) du ≈ y
0
+ F (x
0
) ∆x+
F (x
0
+ ∆x) ∆x + . . . + +F (x
0
+ (n − 1)∆x) ∆x,
(1.28)
as suggested in Figure 1.4.
Notice that when F (x, y) ≡ F (x)
Equation (1.28) and the Euler’s method are
precisely the same. We tabulate values for (x
k
, y
k
),
k = 0, 1, . . . , n as follows.
x
0
y
0
y
0
x
1
:= x
0
+ ∆x
y
1
y
0
+ ∆y = y
0
+ F (x
0
) ∆x
x
2
:= x
0
+ 2∆x
y
2
y
0
+ F (x
0
) ∆x + F (x
0
+ ∆x) ∆x,
..
.
..
.
..
.
x
n
:= x
0
+ n∆x y
n
y
0
+ F (x
0
) ∆x + · · · + F (x
0
+ (n − 1)∆x) ∆x.
The Euler’s method is simply a generalization of a first
approximation, the inner sum, to an integral. In fact,
if one defines an outer sum in a manner similar, it is
possible to classify all integrable functions as those
whose inner and outer sums converge in the limit as
∆x → 0 to a number. In some sense, numerical
solution of a differential equation is a generalization
of numerical integration. The earliest attempts at solving
differential equations were via hard wired electrical
circuits and mechanical devices. These “differential
engines” were analog computers and have been made
obsolete by modern digital computers.
The techniques used to solve single equations using Euler’s
method can also be used to solve systems of simultaneous
first order differential equations. Such problems as
reduction of order and solving simultaneous first order
differential equations are a staple in every
elementary book on ordinary differential equations.
30

Problems
1. Use Euler’s method, with ∆x = 0.01,
to find the value of y when x = 1.5 on the solution curve
of y
0
= −y
2
+ x
2
such that y
0
= 1 when x
0
= 1.
Compare with a solution from a software package.
2. Use Euler’s method, with ∆x = 0.01,
to find the value of y when x = 1.5 on the solution curve
of y
0
= −y
2
+ x such that y
0
= 1 when x
0
= 1.
Compare with a solution from a software package.
3. Use Euler’s method, with ∆x = 0.1,
to find the value of y when x = 1.5 on the solution curve
of y
0
= x + y such that y
0
= 1 when x
0
= 0.
Compare with a solution from a software package.
Solutions
1. Use Euler’s method, with ∆x = 0.01,
to find the value of y when x = 1.5 on the solution curve
of y
0
= −y
2
+ x
2
such that y
0
= 1 when x
0
= 1.
Compare with a solution from a software package.
We start with a BASIC program
100 x0 = 1 : y0 = 1
110 h = .01 : n = 50
120 x = x0 : y = y0
130 PRINT x,y
140 yprime = x − y ∗ y
100 x = x + h
31

100 y = y + yprime ∗ h
100 NEXT k
100 END
The BASIC program yields y(1.5) = 1.210649
The Mathematical Software Program yields y(1.5) = 1.2129
2. Use Euler’s method, with ∆x = 0.01,
to find the value of y when x = 1.5 on the solution curve
of y
0
= −y
2
+ x such that y
0
= 1 when x
0
= 1.
Compare with a solution from a mathematical software package.
We start with a BASIC program
100 x0 = 1 : y0 = 1
110 h = .01 : n = 50
120 x = x0 : y = y0
130 PRINT x,y
140 yprime = x ∗ x − y ∗ y
100 x = x + h
100 y = y + yprime ∗ h
100 NEXT k
100 END
The BASIC program yields y(1.5) = 1.09031
The Mathematical Software Program yields y(1.5) = 1.09119
3. Use Euler’s method, with ∆x = 0.1,
to find the value of y when x = 1.5 on the solution curve
of y
0
= x + y such that y
0
= 1 when x
0
= 0.
Compare with a solution from a software package.
We start with a BASIC program
100 x0 = 0 : y0 = 1
110 h = .1 : n = 10
32

120 x = x0 : y = y0
130 PRINT x,y
140 yprime = x + y
100 x = x + h
100 y = y + yprime ∗ h
100 NEXT k
100 END
The BASIC program yields y(1.5) = 3.187485
The Mathematical Software Program yields y(1.5) = 3.43658
From the professional software, we have
{{1.}, {1.11034}, {1.24281}, {1.39972},
{1.58365}, {1.79745}, {2.04424}, {2.32751},
{2.65109}, {3.01922}, {3.43658}}
1.7
Existence theorems
Not every differential equation has a solution.
Look no further than the differential equation
(y
0
)
2
+ y
2
+ 1 = 0.
If there exists a number x for which y(x)
is defined then y
0
(x) cannot be a real number.
However, from what was just done in Section
1.6 one might guess
that the differential equation
dy
dx
= F (x, y)
(1.29)
33

has is a unique solution y = f (x) which passes through a
given initial point (x
0
, y
0
).
Under appropriate assumptions concerning the function
F (x, y), existence of such a solution can indeed be
guaranteed. For the equation of the nth order,
y
(n)
= F
x, y, y
0
, . . . , y
(n−1)
,
(1.30)
we expect that there will be a unique solution satisfying
initial conditions:
y(x
0
) := y
0
,
y
0
(x
0
) := y
0
0
,
. . . ,
y
(n−1)
(x
0
) := y
(n−1)
0
(1.31)
where each of x
0
, y
0
, . . . , y
(n−1)
n
is a real number.
The following fundamental theorem justifies these
expectations.
Theorem 2 Existence Theorem.
Let F
x, y, y
0
, . . . , y
(n−1)
be a
function of the variables x, y, y
0
, . . . , y
(n−1)
,
defined and continuous when
|x − x
0
| < h,
|y − y
0
| < h,
. . . ,
|y
(n−1)
− y
(n−1)
0
| < h,
and having continuous first partial derivatives with
respect to y, y
0
, . . ., y
(n−1)
. Then there
exists a solution y = f (x) of the differential equation
(1.30), defined in some interval |x − x
0
| < h
1
,
and satisfying the initial conditions (1.31).
Furthermore, the solution is unique; that is, if
y = g(x) is a second solution satisfying (1.31),
then f (x) ≡ g(x) whenever both functions are defined.
A proof of this theorem is long and technical. It is
included here because several of the concepts that appear
in the proof are frequently referred to in physics,
engineering, and computer science applications. The student
34

should at least read through the proof to become acquainted
with the terminology and with the thread of the argument.
In a course on advanced calculus, proofs such as this
are common place and require memorization.
Proof:
We will prove this theorem for first order equations,
that is, for n = 1,
y
0
= F (x, y).
Let M denote the maximum of F (x, y) for
|x − x
0
| ≤ h/2 and |y − y
0
| ≤ h/2.
We choose a smaller closed rectangle inside
the original open rectangle to ensure that
F (x, y) attains its maximum there. The closed
rectangle may be denoted as the set
R = { (x, y) | x
0
− h/2 ≤ x ≤ x
0
+ h/2, y
0
− h/2 ≤ y ≤ y
0
+ h/2 }.
(We have to have a closed and bounded set.
A function like g(x) = 1/x is continuous
at every point in the open interval (0, 1)
but it is unbounded!) Let
h
1
=
h
2(M + 1)
.
The fact that F (x, y) has a continuous first
partial derivative with respect to y in R
says that it satisfies a Lipschitz condition
with respect to y in R. This condition is
a technical piece of mathematics; however, it is
found in every advanced textbook in science and
engineering and no course in
differential equations would be complete without
mentioning it. One should be encouraged by
the fact that there are several cases in the
study of shock waves and denotation where the
35
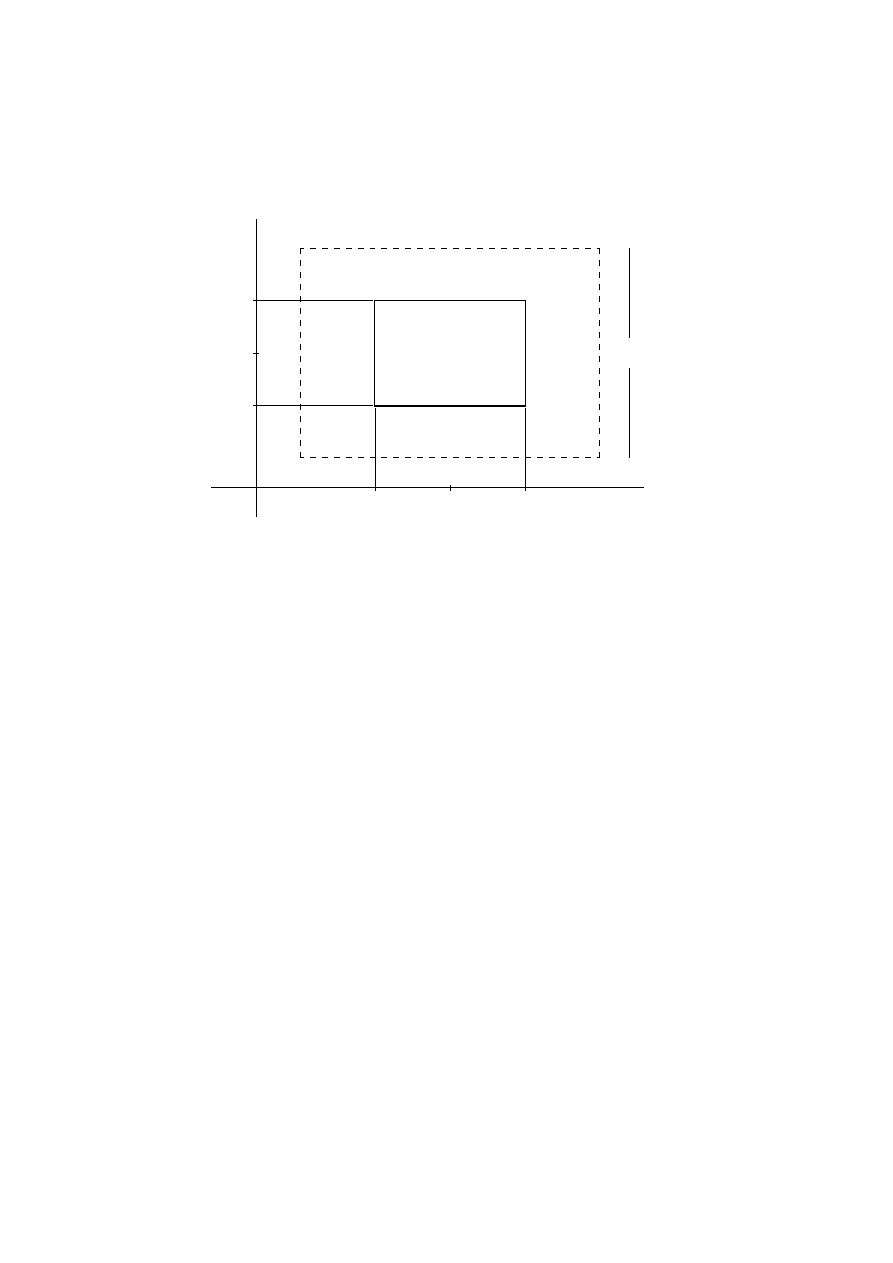
-
6
y
x
y
0
y
0
−h/2
y
0
+h/2
x
0
−h
1
x
0
+h
1
x
0
(x
0
, y
0
)
•
?
6
2h
Figure 1.5:
The Closed Region R
function F (x, y) does not have
a partial derivative with respect to y but
does satisfy the Lipschitz condition. By a Lipschitz
condition, we mean that
there exists a positive number K such that
|y(x) − y
0
| ≤ K |x − x
0
|
for each x ∈ [x
0
− h
1
, x
0
+ h
1
].
We will demonstrate in a solved problem that
if F
y
(x, y) ≡ ∂F (x, y)/∂y
is continuous in R, then F satisfies a Lipschitz
condition in F with respect to y.
Solving an initial value problem is the same as
finding a continuous solution to the integral
equation
y(x) = y
0
+
Z
x
x
0
F (t, y(t)) dt
for
|x − x
0
| ≤ h
1
.
36

The equivalence of the integral equation and the
differential equation follows from the Fundamental
Theorem of Calculus.
For convenience, let x
0
≤ x ≤ x
0
+ h
1
.
A symmetric
proof will hold for the case x
0
− h
1
≤ x ≤ x
0
.
We apply Picard’s method (of successive approximations).
This method is important for historical purposes and also
it is a must for any student who claims
to have completed a course in differential equations.
But it is not something that needs to be dwelt on. Just
remember that prior to the advent of computers, mathematicians
had to rely solely on such methods to solve differential
equations numerically.
y
0
(x) := y
0
y
1
(x) := y
0
+
Z
x
x
0
F (t, y
0
(t)) dt
. . .
y
n
(x) = y
0
+
Z
x
x
0
F (t, y
n−1
(t)) dt
for n = 1, 2, . . .. To prove existence,
we have to show two things: (1)
the sequence of functions {y
n
}
∞
n=0
converges pointwise to a limit function, y(x);
and (2) the pointwise limit, y(x), is continuous on
the interval x
0
− h
1
≤ x ≤ x
0
+ h
1
.
If |y
n−1
(x) − y
0
| ≤ h/2 then
|y
n
(x) − y
0
| ≤
Z
x
x
0
|F (t, y
n−1
(t))| dt ≤ (x − x
0
)M ≤ h
1
M ≤
hM
2(M + 1)
≤
h
2
.
It follows by induction that |y
n
(x) − y
0
| ≤ h/2 for
each positive integer n. From this, we observe that
37
the Lipschitz condition applies to F (x, y
n
(x)).
Going back to the operational definition of F
y
and applying the mean value theorem for derivatives,
we notice that
|F (x, y
n
(x)) − F (x, y
0
(x))| ≤ M · |y − y
0
|
In order to show that the function sequence
{y
n
(x)}
∞
n=0
, x
0
≤ x ≤ x
0
+ h
1
,
converges uniformly to a continuous function y(x) such
that
y(x) = y
0
+
Z
x
x
0
F (t, y(t)) dt
for
|x − x
0
| ≤ h
1
,
we consider the infinite series
y
0
(x) + [y
1
(x) − y
0
(x)] + [y
2
(x) − y
1
(x)] + . . . + [y
n
(x) − y
n−1
(x)] + . . . .
y
n
(x) is the nth partial sum since, it
“telescopes” as a finite series.
|y
1
(x) − y
0
(x)| ≤ M |x − x
0
| .
|y
2
(x) − y
1
(x)| ≤
Z
x
x
0
|F (t, y
1
(t)) − F (t, y
0
(t))| dt,
applying the Lipschitz condition for F (all the y
n
(x)
are in the rectangle R), one gets
|y
2
(x) − y
1
(x)| ≤ M
Z
x
x
0
|y
1
(t) − y
0
(t)| dt ≤ M · M
Z
x
x
0
(t − x
0
) dt
≤
M
2
(x − x
0
)
2
2!
≤
M
2
h
2
1
2!
.
By induction, one obtains
|y
n
− y
n−1
| ≤
M
n
n!
h
n
1
.
The infinite series
38

∞
X
n=1
M
n
n!
h
n
1
converges for all h
1
≥ 0. From the fact that
e
x
=
P
∞
n=0
x
n
/n!, we can even compute
the limit. Now, to define y by passing to the
limit of the infinite series of approximations.
y(x) = lim
n→∞
y
n
(x)
for all
x
0
− h
1
≤ x ≤ x
0
+ h
1
= y
0
+ lim
n→∞
Z
x
x
0
F (t, y
n−1
(t)) dt
= y
0
+
Z
x
x
0
lim
n→∞
F (t, y
n−1
(t)) dt
= y
0
+
Z
x
x
0
F (t, y(t)) dt.
The fact that F (x, y) is continuous and that {y
n
(x)}
is a uniformly convergent sequence justifies interchanging
the limit and integral. This shows that there exists a
solution. (∃ y such that y
0
= F (x, y).)
To prove uniqueness of the solution y(x), we assume that
w(x) is a solution of y
0
= F (x, y) for x
0
≤ x ≤ h
1
.
It must be true that
w(x) = y
0
+
Z
x
x
0
F (t, w(t)) dt
and
|y
n
(x) − w(x)| ≤
Z
x
x
0
|F (t, y
n−1
(t)) − F (t, w(t))| dt
As before, we apply induction to show that
|y
n
(x) − w(x)| ≤
M
n+1
h
n
1
(n + 1)!
x
0
≤ x ≤ x
0
+ h
1
.
39

Passing to the limit as n → +∞,
|y(x) − w(x)| ≤ 0.
Therefore, y(x) ≡ w(x) for each
x ∈ [x
0
, x
0
+ h
1
]. This proves
that the solution is unique.
♦
Example.
Consider the differential equation
y
00
= e
2x
.
(1.32)
Integrate twice to obtain
y
0
=
1
2
e
2x
+ c
1
y =
1
4
e
2x
+ c
1
x + c
2
.
(1.33)
Suppose that each of y
0
, y
0
0
are real
numbers, so that the initial values are
x
0
:= 0
y(0) := y
0
,
and
y
0
(0) := y
0
0
.
From the above initial conditions, it is easy
to compute the definite values for the
arbitrary constants, c
1
, c
2
:
c
1
= y
0
0
−
1
2
,
c
2
= y
0
−
1
4
.
Thus, the solution to the initial value
problem is
y =
1
4
e
2x
+
y
0
0
−
1
2
+
y
0
−
1
4
.
(1.34)
For the initial values problem of
F
x, y
0
, . . . , y
(n)
= 0, we require that
x
0
:= x
0
, y(0) := y
0
, y
0
(0) := y
0
0
,
. . ., y
(n)
(0) := y
(n)
0
,
where each of x
0
, y
0
, y
0
0
, . . .,
40

y
(n)
0
is a real number. This will
determine, in general, definite values for
each of the n arbitrary constants,
c
1
, c
2
, . . ., c
n
. Recall from
algebra that the equation of a straight line,
y = mx + b (m is the slope and b is the
so-called y-intercept), can be determined
in several ways: from two points, (x
0
, y
0
), (x
1
, y
1
), (where x
0
6= x
1
); from
one
point and the slope, (x
0
, y
0
) and the real
number m; by the slope-intercept method;
etc. Likewise the n arbitrary constants
arising from the solution of an nth order
ordinary differential equation can be
determined by other means than by initial
values. One method of determining the constants
relies on data from more than one value of the independent
variable, x. These are called boundary
conditions as opposed to initial conditions.
These are called boundary conditions because they
arose in physical applications of thermodynamics
and vibrating strings where measurements could only
be done on the edges, or boundaries, of the object
being studied.
As an example of the use of boundary conditions,
consider Equation (1.33) and require
that
y(0) = y
0
and
y(1) = y
1
.
(1.35)
Solving for c
1
, c
2
yields
c
2
= y
1
−
1
4
,
c
1
= y
2
− y
1
+
1
4
1 − e
2
.
From the above application of boundary values, one
might be led to assume that for n arbitrary
41

constants one need only apply n boundary values
to solve the problem. This is not true. Take, for
instance, the differential equation
y
00
= −y + 2 cos x,
(1.36)
whose general solution is
y = c
1
cos x + c
2
sin x + x sin x.
If we try to apply the boundary conditions
to Equation (1.36)
y(0) = 0
and
y(π) = 1
we have a problem. The arbitrary constant
c
1
must be equal to 0 and to
1. Clearly additional conditions
must be applied for boundary value problems
to make sense, that is, to be consistent. Indeed,
this is an old problem.
The theorems for boundary value problems
are complicated. Some of the more elementary
boundary value problems will be dealt with in a later
chapter.
1.8
Systems of Equations
There are applications where two or more functions share
a common independent variable. In a typical problem, one might
encounter a system of equations as follows
y
0
(x) = y(x) + z(x)
z
0
(x) = 2y(x),
(1.37)
where each of y and z is a function of x alone.
The solution to the above system of equations is
y(x) = c
1
e
2x
+ c
2
e
−x
z(x) = c
1
e
2x
− 2c
2
e
−x
,
42

as can be verified by differentiation (with respect
to x) and substitution. In later chapters we will
learn routine methods for solving such equations.
This is similar to situations encountered in algebra,
and it won’t be surprising that many of the techniques
from algebra will carry over.
One particularly important feature of systems of differential
equations is its application to a single ordinary
differential equation of order two or higher.
One can reduce the order of a second order equation
y
00
= ˜
F (x, y, y
0
) to two simultaneous equations
by the following substitution:
w :=
dy
dx
,
dw
dx
:= ˜
F (x, y, w).
The above is a special case of a more general concept called
the method of reduction of order. It will
also be considered in more detail in a later chapter.
There is also one instance where an equation of higher
degree can be solved by inspection.
Consider the Clairaut equation
y = xy
0
+ G(y
0
)
where G(·) is an arbitrary function. A solution
is found immediately to be a one-parameter family or
curves
y = c
1
x + G(c
1
).
We will state an analog to the existence theorem in
Section 1.7
for systems of n first order equations.
Let
dy
1
dx
= F
1
(x, y
1
, y
2
, . . . , y
n
),
dy
2
dx
= F
2
(x, y
1
, y
2
, . . . , y
n
),
(1.38)
43

..
.
..
.
dy
n
dx
= F
n
(x, y
1
, y
2
, . . . , y
n
),
be n simultaneous equations in the n
unknown functions y
1
, y
2
, . . . , y
n
of x.
Stating the theorem for two unknowns, y, z,
is sufficient. It is clear how the theorem
will generalize for n unknown functions.
dy
dx
= F (x, y, z),
dz
dx
= G(x, y, z),
(1.39)
Theorem 3 Suppose R is a rectangular region.
If each of functions F and G is a continuous
function in R and if h > 0 such that
each has a continuous first
partial derivative, F
y
, F
z
, G
y
, G
z
,
with respect to y and z for |x − x
0
| < h,
|y − y
0
| < h, |z − z
0
| < h, then
there exists a h
1
> 0 and
there exists a unique solution
y = f (x),
z = g(x),
|x − x
0
| < h
1
,
(1.40)
which contains the point
(x
0
, y
0
, z
0
).
A proof of this theorem can be found
in many advanced textbooks on ordinary
differential equations.
(See [15] in the bibliography.)
The previous theorem, Theorem 2,
for one unknown variable,
is a special case of this theorem,
because Equation (1.30)
is simply Equation (1.38)
44

with n = 1.
Higher order systems are also possible, such as:
d
2
x
dt
2
= F
1
t, x, y,
dx
dt
,
dy
dt
!
,
d
2
y
dt
2
= F
2
t, x, y,
dx
dt
,
dy
dt
!
.
(1.41)
Recall Newton’s law (force = mass × acceleration).
When this formula is written for a system of particles,
second order equations (1.41) occur.
When x, y are each functions of a parameter t (time),
one typically denotes x
0
(t), y
0
(t) as ˙x, ˙
y
and x
00
(t), y
00
(t) as ¨
x, ¨
y.
There exists a unique
solution for (1.41) satisfying
t = t
0
,
x (t
0
) := x
0
,
y (t
0
) := y
0
,
˙x (t
0
) := ˙x
0
,
˙
y (t
0
) := ˙
y
0
,
(1.42)
where each of t
0
, x
0
, ˙x
0
, y
0
,
and ˙
y
0
is a real number.
For a particle moving along a constrained path and
subject to known forces, one can determine the
position and velocity at anytime t ≥ t
0
given
the initial position x
0
, y
0
and the initial
velocity ˙x
0
, ˙
y
0
.
Electrical circuit obey similar laws.
1.9
The General Solution
It is important from both a theoretical and a practical
perspective to derive one formula for a given differential
equation which contains all possible solutions. Such a
formula is called the general solution
of the differential equation. From the existence theorem,
found in Section 1.7, we can be
assured that, under very general conditions, solutions
do exist. Notice that y = c
1
e
3x
+ c
2
e
−3x
is the
45

general solution to y
00
− 9y = 0. The fact that y = c
1
e
3x
+ c
2
e
−3x
is a
solution is readily verified
by successive differentiation. The fact that it is
all the solutions (two, in fact, added together
or superimposed ) can be determined
by calculation. We take the most general set of
initial conditions, namely, for x := x
0
,
we set y(x
0
) := y
0
, t
0
(x
0
) := y
0
0
, for any
real number set { x
0
, y
0
, y
0
0
}. Without
loss of generality, let x
0
:= 0.
c
1
+ c
2
= y
0
,
3c
1
− 3c
2
= y
0
0
,
c
1
= y
0
− c
2
,
3y
0
− 3c
2
− 3c
2
= y
0
0
,
6c
2
= 3y
0
− y
0
0
,
c
2
=
1
2
y
0
−
1
6
y
0
0
,
and c
1
=
1
2
y
0
+
1
6
y
0
0
. c
1
, c
2
are uniquely determined for each choice of real
numbers y
0
, y
0
0
. Therefore,
y = c
1
e
3x
+ c
2
e
−3x
is the general solution of
y
00
− 9y = 0.
To verify that y = f (x; c
1
, c
2
) is a general
solution for the second order differential equation
y
00
= ˜
F (x, y, y
0
),
(1.43)
one has to take successive derivatives and substitute
them into Equation (1.43), ensuring
that it is an identity, and one has to ensure
that for every real number set { x
0
, y
0
, y
0
0
}
for which ˜
F has continuous first partial
derivatives there exist numbers c
1
, c
2
such that
y
0
= f (x
0
, c
1
, c
2
)
and
y
0
0
= f
x
(x
0
, c
1
, c
2
) .
The same procedure applies to systems of equations
46
as well as to higher order differential equations.
The existence theorem cannot be weakened in its
assumption on the continuity of F and its partial
derivatives.
It should be stressed that the existence theorem is
applicable only when the continuity conditions are satisfied.
If 0 < β < 1 then function F in the equation
y
0
= F (x, y) = (1 − β)
−1
y
β
(1.44)
has a partial derivative F
y
(x, y) = β(1 − β)
−1
y
β−1
, −1 < β − 1 < 0, which
has a discontinuity
at y = 0. We refer to the points at which y = 0
as singular points.
Any solution curve containing a singular point
must be dealt with as an exceptional case.
Using the relations
β =
α − 1
α
and
α =
1
1 − β
,
we will observe that
y = (x − c
1
)
α
= (x − c
1
)
1/(1−β)
(1.45)
is a solution to Equation (1.44)
whenever y 6= 0.
This troublesome differential equation has other
properties. Equation (1.45)
does provide a solution through each point
(x, 0); however, the trivial solution (y ≡ 0)
is also a solution passing through the singular
point which does not satisfy Equation
(1.44).
There are other, pathological examples
which will be studied in later chapters.
In physical applications, however, such singular
situations rarely pose a problem. However, it is
important in the setting up of an equation to be
aware that such occurrences bespeak the need for
47

additional investigation of the underlying
assumption in the mathematical model.
1.10
The Primitive
Suppose that each of c
1
, c
2
is a fixed, but arbitrary, constant
and f (x; c
1
, c
2
) is a twice continuously differentiable function
defined on an open interval a < x < b (possibly infinite).
The problem is to construct a differential equation in terms of
x, y, y
0
, and y
00
such that (1) f is a solution of
F (x, y, y
0
, y
00
) = 0 and (2) neither c
1
not c
2
is present in F . In this case, the function f is usually
referred to as the primitive of the
differential equation F (x, y, y
0
, y
00
) = 0. We will
begin with the example
y = c
1
+ c
2
x
2
.
(1.46)
Differentiating twice, we obtain
y
0
= 2c
2
x,
y
00
= 2c
2
.
We eliminate the constants c
1
, c
2
from Equation
(1.46) by substitution
y
0
= 2
1
2
y
00
x,
xy
00
− y
0
= 0.
Now, let’s start with xy
00
− y
0
= 0 and see if we can recover
the original equation. Set v = y
0
and v
0
= y
00
= dv/dx.
The “reduced” equation becomes xv
0
= v.
x
dv
dx
= v
dv
v
=
dx
x
Z
dv
v
=
Z
dx
x
+ c
0
ln v = ln x + c
0
.
48

Now we set c
0
= ln (c
2
/2). Notice that for
each real number c
0
there exists exactly one positive
real number c
2
such that c
0
= ln (c
2
/2).
(The reason for choosing c
2
/2 rather than c
2
will be
clear momentarily.)
ln(v) = ln (c
2
x/2)
v =
dy
dx
=
1
2
c
2
x.
Integrating again, we obtain
y = c
2
x
2
+ c
1
,
the original equation. It would be fortunate if this
procedure could be generalized to a function
f (x; c
1
, c
2
, . . ., c
n
),
where each of
c
1
, . . . , c
n
is an arbitrary constant.
However, a variety of problems may occur.
(Viz., xy
0
= 2y, with a general solution y(x) = c
1
x
2
, x ≥ 0;
y(x) = c
2
x
2
x ≤ 0.)
On the other hand, consider the Clairaut equation
y = xy
0
+ G(y
0
).
Despite its complicated appearance, its primitive contains exactly
one arbitrary constant, c
1
. Elimination of the
c
k
’s by successive differentiation and substitution
may prove to be mathematically intractable. The end
result,
F
x, y, . . . , y
(n)
= 0,
may not be expressible as
y
(n)
= ˜
F
x, y, . . . , y
(n−1)
,
for instance. This leads to the next topic: The function
f (x, y; c
1
, . . . , c
n
) = 0
may define an implicit relationship between x and y.
Frequently, though not always, differentiation and
49

substitution will generate a suitable differential
equation from the implicit relationship between
x, y, and the arbitrary constant set { c
1
, . . . , c
n
}.
One important application of a primitive in which the
function f (x, y; c
1
) = 0 implicitly relates x and y
is that of isotherms (curves of constant temperature)
or isobars (curves of constant pressure). Isotherms
and isobars are examples of the mathematical notion
known as level curves.
These are equations of the form
f (x, y) = c
1
.
(1.47)
If the temperature, θ, is given by the equation
θ = x
2
− y
2
, and it is held constant,
θ = constant, we differentiate to obtain
dθ
dx
= 0 = 2x − 2y
dy
dx
(1.48)
or
yy
0
= x.
Notice that we may express Equation (1.48)
as
x dx = y dy,
where the variables are treated independently.
Here we are taking differentials
rather than derivatives.
The notion of a differential is closely related to
the concept of the Dirac delta function. Both are
linear functionals enjoying certain properties and
obeying certain rules.
This notion
can be generalized into an equation of the form
Q(x, y) dy + P (x, y) dx = 0,
(1.49)
50

a differential equation of first order. Such
expressions as Equation (1.49) are
part of the important topic of exact differential
equations, to be studied later.
1.11
Summary
Differential equations are classified
by type, order, degree, and linearity.
There are two types of differential equations:
ordinary and partial.
The order of a differential equation is
that of the highest
order derivative which occurs in the equation.
The degree of the equation is
the exponent of its highest derivative.
Ordinary differential equations are either
linear or nonlinear in their unknown functions
y
(k)
(x), k = 0, 1, 2, . . . , n.
Many problems in physics and engineering, when
reified mathematically,
give rise to differential equations.
Solutions of differential equations are functions
satisfying (1.9), and are either general
solutions with arbitrary constants
or particular solutions
having initial values or boundary values (or a combination
of both initial conditions and boundary conditions).
Modern software and computing devices permit the explicit
solution of many differential equations and allow
scientists and engineers to generate interpolating functions,
plots, and tabular data for a larger class of
equations F
x, y, y
0
, . . . , y
(n)
.
The existence theorem answers
the vital question about the conditions
under which a solution exists.
Two technical topics of historical interest and
51

theoretical importance, the Lipschitz condition
and Picard’s method of successive approximations,
are introduced. Euler’s method
tells how to manually compute numerical solutions.
Any degree of
accuracy can be obtained by reducing the step size
∆x in Equation (1.21).
At this point, having carefully read this chapter,
one might assume an adequate education
on the subject of differential equations.
There are some good reasons for not
stopping here.
There are certain elementary procedures
which obtain explicit solutions to some
widely used differential equations.
These procedures are central for setting
up physics and engineering models.
Moreover, many books on physics and
engineering assume that the reader has
some exposure to traditional approaches
to solving special kinds of equations.
For a larger class of differential equations,
qualitative information on a solution for
a given differential equation may be
readily available even though explicit
or numerical solutions may be difficult
to obtain. The form of the equation itself
may yield important conclusions as
to the nature of its solution(s). Finally,
for the general equation, (1.5),
there are alternates
to the Euler’s method (the so-called method
of step-by-step integration) which
converge more rapidly, require less
computation, and exhibit greater stability.
Problems
52

1. Solve the following initial value problems (IVPs):
(a) y
0
= e
x
, with the initial condition y(0) = 2;
(b) y
0
= 2y, with the initial condition y(0) = y
0
;
(c) y
00
= cos x, with the initial conditions
y(0) = 0, y
0
(0) = 1.
2. Solve the following boundary value problems (BVPs):
(a) y
00
= e
x
, with the boundary conditions y(0) = 0,
y(1) = e;
(b) y
000
= 0, with the boundary conditions y(0) = 1,
y(1) = 0,
y(2) = 1.
3. Verify that y = c
1
cos 2x + c
2
sin 2x is a solution
of the differential equation
y
00
+ 4y = 0.
Show that it is the general solution.
4. Solve the following BVPs for y
00
+ 4y = 0.
Some may be impossible—if so, explain why.
(a) y(0) = 0, y(π/4) = 1;
(b) y(0) = 1, y(π/2) = 0;
(c) y(0) = 1, y(π/4) = 0.
5. Apply the existence theorem to determine
the domains (of definition) of each of the
following differential equations:
(a) y
0
= y
2
/x;
(b) y
0
= y/(x
2
+ y
2
);
53

(c) y
0
= Arctan(x).
6. Compute differential equations of the
form F
x, y, y
0
, . . . , y
(n)
= 0 for
each of the following primitives:
(a) y = c
1
x + c
3
1
;
(b) y = c
1
x
2
+ c
2
x + c
3
;
Solutions
1. Solve the following initial value problems (IVPs):
(a) y
0
= e
x
, with the initial condition y(0) = 2;
We begin by integrating
R
e
x
dx:
y(x) = e
x
+ c
1
,
where c
1
is an arbitrary constant.
Solve for c
1
when x = 0.
y(0) = 2 = e
0
+ c
1
= 1 + c
1
.
Thus we have c
1
:= 1 and
y(x) = e
x
+ 1.
(b) y
0
= 2y, with the initial condition y(0) = y
0
;
Integrate y
0
to obtain
ln(y(x)) = ln(2x) + c
0
,
Exponentiate both sides of the above to obtain:
y = e
2x+c
0
.
Let c
1
= e
c
0
.
When x = 0, y(0) = y
0
.
y(x) = c
1
e
2x
;
y(x) = y
0
e
2x
.
Since c
1
:= y
0
54

(c) y
00
= cos x, with the initial conditions
y(0) = 0, y
0
(0) = 1.
Again, we integrate y(x), twice this time, to get:
y(x) = − cos(x) + c
1
x + c
2
.
Set x = 0 and we have 0 = −1 + c
2
, so that
c
2
= 1.
Now we determine c
1
.
Differentiate
y to obtain y
0
(x) = sin(x) + c
1
and require
that y
0
(0) = 1.
0 = sin(0) + c
1
and c
1
= 0.
The resulting equation becomes:
y(x) = − cos(x) + 1.
2. Solve the following boundary value problems (BVPs):
(a) y
00
= e
x
, with the boundary conditions y(0) = 0,
y(1) = e;
We integrate to obtain the equation y(x) = e
x
+ c
1
x + c
2
.
When x = 0, e
0
= 1, and 0 = 1 + c
1
· 0 + c
2
.
Thus c
2
:= −1.
We now solve at y(1) = e.
y(1) = e = e
1
+ c
1
· 1 − 1.
Since e
1
= 1, we have c
1
= 1 and the solution is
y(x) = e
x
+ x − 1.
55

(b) y
000
= 0, with the boundary conditions y(0) = 1,
y(1) = 0,
y(2) = 1.
Solving by repeated integration, we have
y(x) = c
1
x
2
+ c
2
x + c
3
.
With the boundary conditions, we have:
1 = c
3
,
0 = c
1
+ c
2
+ c
3
,
1 = 4c
1
+ 2c
2
+ c
3
.
Solving for c
1
, c
2
, c
3
, we have:
c
1
:= 1,
c
2
:= −
3
2
,
c
3
:=
1
2
.
The solution becomes
y(x) =
1
2
x
2
−
3
2
x + 1.
3. Verify that y = c
1
cos 2x + c
2
sin 2x is a solution
of the differential equation
y
00
+ 4y = 0.
Show that it is the general solution.
Differentiating twice yields
y
0
(x) = −2c
1
sin 2x + 2c
2
cos 2x,
y
00
(x) = −4c
1
cos 2x − 4c
2
sin 2x.
Substitution shows that y = c
1
cos 2x + c
2
sin 2x
is a solution to y
00
+ 4y = 0.
56

y
00
+ 4y = −4c
1
cos 2x − 4c
2
sin 2x + 4 (c
1
cos 2x + c
2
sin 2x) ≡ 0.
Consider a number set { y
0
, y
0
0
}
If, for x = 0, y(0) := y
0
and y
0
(0) := y
0
0
, then
c
1
:= y
0
and
c
2
:= y
0
0
/2.
Therefore, from the existence theorem and
the initial value problem, the problem is done.
4. Solve the following BVPs for y
00
+ 4y = 0.
Some may be impossible—if so, explain why.
(a) y(0) = 0, y(π/4) = 1;
The general solution is
y(x) = c
1
cos(2x) + c
2
sin(2x).
Substituting, we have
y(0) = 0 = c
1
cos(2 · 0) + 0,
c
1
= 0.
y
π
4
= 1 = 0 + c
2
sin
π
2
,
c
2
= 1.
(b) y(0) = 1, y(π/2) = 1;
Again, by substitution,
y(0) = 1 = c
1
cos(2 · 0) + 0,
c
1
= 1.
y
π
2
= 0 = c
1
cos(π) + 0,
c
1
= 0.
If c
1
is a real number and c
1
= 1, then
c
1
6= 0.
This boundary value condition is impossible.
57

(c) y(0) = 1, y(π/4) = 0.
Again, we substitute directly
y(0) = 0 = c
1
cos(2 · 0) + 0,
c
1
= 0;
y
π
4
= 0 = 0 + c
2
sin
π
2
.
The only solution here is the trivial solution,
y ≡ 0.
5. Apply the existence theorem to determine
the domains (of definition) of each of the
following differential equations:
(a) y
0
= y
2
/x;
We first have to look at F (x, y) = y
2
/x and take
its partial derivative with respect to y
∂F
∂y
=
2y
x
.
This derivative, ∂F/∂y is continuous
everywhere except when x = 0.
Thus the domain
(of definition) of the differential equation
is (−∞, 0) ∪ (0, ∞).
(b) y
0
= y/(x
2
+ y
2
);
We first have to look at F (x, y) = y
2
/(x
2
+ y
2
)
and take its partial derivative with respect to y
58

∂F
∂y
=
y
2
− 2t + x
2
(x
2
+ y
2
)
2
.
This derivative, ∂F/∂y is continuous
everywhere except when (x, y) = (0, 0).
Thus the
solution curves of this differential equation
exists for all (x, y) not passing
through (0, 0).
(c) y
0
= Arctan(x).
We first have to look at F (x, y) = Arctan(x)
and take its partial derivative with respect to y
∂F
∂y
= 0.
This derivative, ∂F/∂y is continuous
everywhere; moreover, the function F (x, y) is defined
for all x and for y such that
−π/2 < y < π/2.
Thus the solution
curves of this differential equation
exists for all (x, y) where |y| < π/2.
6. Compute differential equations of the
form F
x, y, y
0
, . . . , y
(n)
= 0 for
each of the following primitives:
59

(a) y = c
1
x + c
3
1
;
This equation is the Clairaut’s equation.
Just make the substitution c
1
:= y
0
to get
y = xy
0
+ (y
0
)
3
.
(b) y = c
1
x
2
+ c
2
x + c
3
;
Differentiate successively three times.
The result is
y
000
= 0,
a function F (x, y, y
0
, y
00
, y
000
) = 0 without the
arbitrary constants and also the one of
the lowest order.
60

Chapter 2
First Order, First Degree
Equations
2.1
Differential Form Versus Standard Form
In Section 1.2 we defined a differential
equation of the first order, first degree to be
M (x, y) + N (x, y) y
0
= 0.
(2.1)
If N (x, y) 6= 0, this expression
(that is, Equation (2.1))
is equivalent to
y
0
= F (x, y),
F (x, y) =
M (x, y)
N (x, y)
.
(2.2)
Recall from the existence theorem that if each of
F (x, y) and F
y
(x, y) ≡ ∂F (x, y)/∂y
is continuous in some rectangular region R then Equation
(2.2) has exactly one solution passing through
each interior point, (x
0
, y
0
) of R.
By a region R in the real number plane, we mean a nonempty,
open, connected set. We will introduce some notation from
symbolic logic at this point because the reader is likely to
encounter it elsewhere. The so-called existential quantifier
(∃) stands for “there exists” and the so-called
61

universal quantifier (∀) stands for “for all” or
“for every.” Of course, the symbol (∅) stands
for the empty set, the symbol (∈) stands for “is an
element of” or “belongs to,” and ( /
∈) stands for
“is not in” or “is not an element of.”
Symbolicaly, we write “R is not the empty set” as
“R 6= ∅.” R is an open set means
that ∀ (x, y) ∈ R ∃ r > 0 such that
if B((x, y), r) is a ball having center at
(x, y) and radius r then B((x, y), r) is
contained in R. The statement that B is a ball is
then written, symbolically,
B
(x, y), r
=
n
(s, t)
q
(s − x)
2
+ (t − y)
2
= k(s, t) − (x, y)k < r
o
.
The statement that R is a connected set means that
if (x, y) ∈ R and (x
1
, y
1
) ∈ R then ∃
a broken line of finitely many linear line intervals,
each of which is contained completely
within R, connecting (x, y) and (x
1
, y
1
).
(See Figure 2.1.)
When we say that (x
0
, y
0
) is an
interior point, we mean that there exists a positive
number r such that the open ball centered at
(x
0
, y
0
) and having radius r > 0 is totally
contained in the region R.
The case when N (x, y) = 0
for some (x
1
, y
1
) must be considered separately.
We refer to such points, (x
1
, y
1
), as singular
points of F (x, y). Recall further that in Section
1.10 we discussed the differentials
dx, dy.
M (x, y) dx + N (x, y) dy = 0.
(2.3)
Whenever N (x, y) 6= 0, we can consider Equation
(2.3) to be nothing more than Equation
(2.2). On the other hand, if M (x, y) 6= 0,
then we may form
62
-
6
x
y
(x,y)
•
•
•
H
H
H
H
H
H
H
H
H
H
• (x
1
,y
1
)
Figure 2.1:
A Connected Set
dx
dy
=
N (x, y)
M (x, y)
(2.4)
and consider y as the independent variable and
x(y) as a function of y. If both M (x, y) = 0
and N (x, y) = 0 at some point (x
1
, y
1
), then we
have an indeterminate of the form
0
0
for both of M/N and N/M . In this case, we say
that (x
1
, y
1
) is a singular point of Equation
(2.3).
We will proceed formally throughout this chapter, in
the sense that we will not apply the rigorous theory
of differential forms. All functions are assumed to
be well defined except at singular points.
We will not attempt to deal with jump discontinuities,
these will be handled by integral transform methods
(i.e., the Laplace and the Fourier transform) in a
later chapter.
63

Symbol
Definition
=
Equals
6=
Does not equal
:=
Defines
≡
Is equivalent to
∃
There exists
∀
For each, for every
∈
Is an element of
/
∈
Is not an element of
∅
The empty, or null, set
∞
The infinity symbol, infinitely large
→
Approaches, goes to or towards
⇒
Implies
¬
The negation of, “it is not true that”
<
The real part of, <
x + y
√
−1
= x
=
The imaginary part of, =
x + y
√
−1
= y
Much less than, is greatly exceeded by
Much greater than, greatly exceeds
♦
Diamond symbol, used as “end of proof”
Table 2.1:
Table of Symbols
64
2.2
Exact Equations
In its differential form, the first order, first degree
differential equation becomes
M (x, y) dx + N (x, y) dy = 0.
(2.5)
The above equation, Equation (2.5), is
said to be exact
(in some rectangular region R)
if there exists
a continuously differentiable function U (x, y)
such that
∂U
∂x
= M,
∂U
∂y
= N.
(2.6)
We observe that in this case,
dU = M dx + N dy,
throughout the rectangular region R.
We return to the topic of level
curves and observe that an exact solution
of Equation (2.5) is simply a
level curve of the function U (x, y).
Recall that a level curve for U (x, y) is simply
the locus, or set, of points (x, y) such that
U (x, y) = k, where k is a fixed constant.
Since U (x, y) may be implicitly
defined, that is, it may not be possible to
display y = ˜
U (x) in closed form, singular
points may occur on certain level curves.
In the Figure 2.2, we observe
two such singular points, P and Q.
If we are able to express y as a function of x,
then dy/dx makes sense and we may apply
a classic calculus computation:
∂U
∂x
·
∂x
∂x
+
∂U
∂y
dy
dx
=
∂U
∂x
· 1 +
∂U
∂y
dy
dx
= M (x, y) + N (x, y)
dy
dx
= 0.
65

•
•
P
Q
U (x,y)=
√
2
U (x,y)=1
U (x,y)=
√
2/2
U (x,y)=3/π
Figure 2.2:
Level Curves
Examples are essential in understanding exact differential
equations.
Example 1.
Solve the differential expression.
x
2
+ y
2
dx + 2xy dy = 0.
Here M (x, y) = x
2
+ y
2
and N (x, y) = 2xy. What is required
is to determine a function U (x, y) such that
∂U
∂x
= M (x, y)
and
∂U
∂y
= N (x, y).
We integrate with respect to x and with respect to
y and combine the two results to obtain,
U (x, y) =
1
3
x
3
+ xy
2
= c
1
.
The function is implicitly defined.
The result can be verified by differentiation.
66

Example 2.
Show that the equation
(y
2
− 1) dx + (2xy + sin y) dy = 0
is exact. We require that
∂U
∂x
= y
2
− 1
and
∂U
∂y
= 2xy + sin y.
Integrating and combining results,
we obtain U (x, y) = xy
2
− x − cos y = c
1
.
Again, the result can be verified by differentiation.
Example 3.
Solve y dx + x dy = 0.
Proceeding formally, we write
dx
x
+
dy
y
= 0,
whenever x 6= 0 and y 6= 0. Integrating, we obtain
e
y
= e
−x
+ c
0
,
where c
0
> 0. (If c
0
< 0 we would have an imaginary
argument.) But, for any c
0
> 0 there exists a real
number c
1
such that c
0
= e
c
1
. On the other hand,
for each real number c
1
there exists exactly one
positive number c
0
such that c
1
= ln(c
0
). So
we solve and obtain
y =
c
1
x
as the solution. We observe that the lines
y = 0 and x = 0 are both solutions of the
the differential expression. The point
(0, 0) is a singular point—it lies on two
different solution curves.
There is a simple test for determining whether or not
a given differential expression is exact. If each of
M (x, y) and N (x, y) is a continuously differentiable
67

function in some region in the xy-plane, then
M (x, y) dx + N (x, y) dy = 0 is exact if and
only if
∂M (x, y)
∂y
=
∂N (x, y)
∂x
.
This test for exactness will be stated later as
a theorem and an outline for a proof will be given.
Problems
1. Show that the differential expression
(sin y − 2x) dx + (x cos y − 2y) dy = 0
is exact by finding its general solution.
2. Show that the differential expression
(ye
xy
+ 2x) dx + (xe
xy
+ 2y) dy = 0
is exact by finding its general solution.
3. The differential expression
x dy − y dx = 0
fails the test for exactness. However, by
dividing through by x
2
, one can obtain
x dy − y dx
x
2
= 0,
and observe that ∂M (x, y)/∂x = −x
−2
and that ∂N (x, y)/∂y = −x
−2
.
Determine the general solution.
68

4. Level curves are called contour plots
by certain mathematical software. Apply some
mathematical software to plot level curves for
each of the following functions U (x, y)
of x and y:
(a) U (x, y) = sin(x, y);
(b) U (x, y) = ye
−x
;
(c) U (x, y) = y − e
x
;
(d) U (x, y) = arctan(x/y).
Solutions
1. Show that the differential expression
(sin y − 2x) dx + (x cos y − 2y) dy = 0
is exact by finding its general solution.
We integrate and write the two functions
x sin y − x
2
= c + f (y)
x sin y − y
2
= c
0
+ g(x).
Clearly f (y) = y
2
and g(x) = x
2
so that the
general solution becomes
x sin y − x
2
− y
2
= c
1
,
where c
1
is an arbitrary constant.
69

2. Show that the differential expression
(ye
xy
+ 2x) dx + (xe
xy
+ 2y) dy = 0
is exact by finding its general solution.
We integrate and write the two functions
ye
xy
y
+ x
2
= c + f (y)
xe
xy
x
− y
2
= c
0
+ g(x).
Clearly f (y) = y
2
and g(x) = −x
2
so that the
general solution becomes
e
xy
+ x
2
− y
2
= c
1
,
where c
1
is an arbitrary constant.
3. The differential expression
x dy − y dx = 0
fails the test for exactness. However, by
dividing through by x
2
, one can obtain
x dy − y dx
x
2
= 0,
and observe that ∂M (x, y)/∂x = −x
−2
and that ∂N (x, y)/∂y = −x
−2
.
Determine the general solution.
70

Clearly there is a problem when x = 0.
Setting x 6= 0 for the moment, we compute
d
y
x
= −
y
x
2
dx +
1
x
dy = 0,
from
y
x
= c
1
, with c
1
a constant.
Therefore, from the elementary differential expression,
we write a general solution
y
x
= c
1
or
y = c
1
x
for x 6= 0.
When x = 0 the y-axis is a solution.
2.3
Separable Variables
There is a distinct difference between the concept
of a function and the notion of an equation.
Historically, equations are much older than
functions. At one time, however, the two
were synonymous. An equation is generally
defined to be an algebraic relation (implicit
or explicit) between two or more variables. A function
f may be defined as consisting of three things:
(1) an initial set, called the domain; (2) a final set,
called the range or codomain; and (3) a rule which
assigns to each member of the initial set exactly
one member of the final set. The rule itself may
take the form of an algebraic equation, and it
traditionally does. Certainly y = |x| is the same
as y =
√
x
2
. On the other hand, the
equation
71

f (x) =
x
|x|
has a problem at the point x = 0 whereas
f (x) =
1
whenever x > 0
0
at
x = 0
−1 whenever x < 0
defines a function for each real number x.
While we are avoiding many pathological mathematical
constructions and we are pursuing a formal rather
than a rigorous development, some care must be
taken in approaching the topic of separable
variable to avoid troublesome anomalies.
For instance, in the previous section we noticed
that
−y dx + x dy = 0
and
−y dx + x dy
x
2
= 0
both represent the same equivalence class of
solutions to the differential expression.
Both are different. In particular,
the first expression is well defined everywhere
whereas the second has a singularity
at the point x = 0 that requires additional
investigation. To go from
M (x, y) dx + N (x, y) dy = 0
to
˜
M (x) dx + ˜
N (y) dy = 0
via some suitable manipulation of M and N
by a function G(x, y) so that
˜
M (x) :=
M (x, y)
G(x, y)
and
˜
N (x) :=
N (x, y)
G(x, y)
72

may introduce singularities, discontinuities,
or extraneous solutions. Some of the singularities
may be “removable” and pose no problem; some of
the discontinuities may be gotten around by carefully
choosing the region in the xy-plane for the family
of solution curves; and, some extraneous solutions
may be eliminated by inspection or from initial
conditions. In each case, one must investigate
additional conditions imposed by the function
G(x, y).
When an equation
M (x, y) dx + N (x, y) dy = 0
can be converted into the form
˜
M (x) dx + ˜
N (y) dy = 0,
(2.7)
then the equation is said to have separable
variables. As an example, consider
the equation
dy
dx
= −
x
y
!
2
.
(2.8)
We “multiply through by ” y
2
dx to obtain the differential
expression
x
2
dx + y
2
dy = 0,
(2.9)
an exact differential expression.
The general
solution as
x
3
+ y
3
= c
1
(c
1
real) .
(2.10)
Every differential expression of the form (2.7)
is exact (except at discontinuous) because
U (x, y) =
Z
˜
M (x) dx +
Z
˜
N (y) dy,
(2.11)
73

taking indefinite integrals.
Writing in the notation of a total differential:
dU =
∂U
∂x
dx +
∂U
∂y
dy = ˜
M dx + ˜
N dy.
(2.12)
Therefore, the level curves of Equation(2.11)
the level curves
Z
˜
M (x) dx +
Z
˜
N (y) dy = c
1
.
(2.13)
The differential equation y
0
= ˜
F (x, y)
will have separable variables
whenever ˜
F is a product of the form
y
0
= F
1
(x)F
2
(y).
(2.14)
In this case, we may re-write Equation
(2.14) as a differential expression
F
1
(x) dx −
dy
F
2
(y)
= 0.
(2.15)
Example 1.
Solve the differential equation
yy
0
+ 4x = 0.
We re-write the differential equation as a differential
expression of the form
y dy + 4x dx = 0
and integrate
Z
y dy +
Z
4x dx = c
1
1
2
y
2
+
4
2
x
2
= c
1
74

1
2
y
2
+ 2x
2
= c
1
where
c
1
≥ 0.
The set of solution curves is a family of ellipses.
There is one degenerate solution curve, that is
{(0, 0)}, when c
1
= 0.
Example 2.
Solve the differential equation
y
0
= −xy.
As suggested, we convert the differential equation into
a differential expression and integrate term by term.
dy
y
= −x dx.
Z
dy
y
=
Z
−x dx + c
0
.
ln(|y|) = −
1
2
x
2
+ c
0
.
Now, we immediately notice the above equation is well
defined for each real number c
0
and for all values
of y except y = 0. We “exponentiate” both side
of the above equation to obtain.
e
ln(|y|)
= e
−x
2
/2+c
0
= ˜
c
1
e
x
2
/2
where
˜
c
1
= e
c
0
.
If y > 0, then we choose c
1
= ˜
c
1
> 0; if
y < 0, then we choose c
1
= −˜
c
1
< 0. The
equation becomes
y = c
1
e
−x
2
/2
where
c
1
6= 0.
If we allow c
1
to vanish, that is, to equal 0,
then the line y = 0 is also allowed as a solution.
75

If we have (0, y
0
) as an initial condition, then
the solution curve becomes
y = y
0
e
−x
2
/2
,
the Gaussian distribution from
elementary statistics, also known as the
bell-shaped curve.
Example 3.
Solve the differential equation
dy
dx
=
y
2
x + x
x
2
y + y
.
In the usual manner, create a differential expression
y dy
1 + y
2
=
x dx
1 + x
2
from the facts that y
2
x + x = x(y
2
+ 1) and
x
2
y + y = y(x
2
+ 1). Now integrate term by term.
Z
2y dy
1 + y
2
=
Z
2x dx
1 + x
2
+ c
0
,
with c
0
the arbitrary constant of integration.
ln |1 + y
2
| = ln |1 + x
2
| + c
0
.
Let c
0
= ln(|c
1
|) and obtain, exponentiating
both sides of the above equation:
1 + y
2
= c
1
(1 + x
2
).
We have observed that to solve separable variables differential
equations one must really know how to do integrals and some
algebra. We have also observed that problems can arise in
the domain of definition of the solution function and that,
in putting the differential equation into the correct format,
76

some solutions may be lost. This same concept is central in
the solution of partial differential equations. One will try
to separate the function F (x, y) by writing it as a product
of two functions F
1
(x), F
2
(y).
One final item of interest is that in some (older) books,
differential equations which we have referred to as
“separable variables” are also called variables
separable.
Problems
1. How can one determine the solution of
a first-order separable variables differential
equations y
0
= ˜
F (x, y)?
2. Solve the separable variables differential
equation
dy
dx
− k
1
= 0,
where k
1
is a nonzero constant.
3. Solve the differential expression
dx +
√
x dy = 0,
using the techniques of separable variables.
4. Solve the differential equation
(x cos y)
dy
dx
= 1 − y.
Solutions
77

1. How can one determine the solution of
a first-order separable variables differential
equations y
0
= ˜
F (x, y)?
The above will have separable variables
whenever ˜
F is a product of the form
y
0
= F
1
(x)F
2
(y).
In this case, we may re-write the above Equation
as a differential expression
F
1
(x) dx −
dy
F
2
(y)
= 0.
Provided, of course, that F
2
(y) 6= 0.
Then integrate to obtain
Z
F
1
(x) dx −
Z
dy
F
2
(y)
= c
1
,
where c
1
is a constant of integration.
2. Solve the separable variables differential
equation
dy
dx
− k
1
y = 0,
where k
1
is a nonzero constant.
Manipulate the above expression into the form
78

dy
y
− k
1
dx = 0,
assuming that y 6= 0.
Later we’ll deal with
case as a separate issue.
Integrate.
ln |y| − k
1
x = c
0
,
where c
0
is the constant of integration.
Exponentiate, or take the antilogarithm, of
both sides of the above equation to get
y = c
1
e−k
1
x
(c
1
= ±e
c
0
) ,
where c
1
= e
c
0
for y > 0 and c
1
= −c
c
0
for y < 0.
Notice that the x-axis, y = 0 is also a solution.
3. Solve the differential expression
dx +
√
x dy = 0,
using the techniques of separable variables.
The equation is not in the correct form.
Multiply
through by x
−1/2
(x 6= 0) to obtain
dx
√
x
+ dy = 0.
79
Now we can integrate term by term.
Z
dx
√
x
+
Z
dy + c
0
= 0.
−
1
2
x
−3/2
+ y + c
0
= 0,
where c
0
is the constant of integration.
Set c
1
= −c
0
to obtain y as a function of x.
y =
1
2
x
−3/2
+ c
1
.
4. Solve the differential equation
(x cos y)
dy
dx
= 1 − y.
This equation becomes separable variables
cos y dy
1 − y
=
dx
x
when y 6= 1, x 6= 0.
Integrating yields
Z
cos y dy
1 − y
= ln(x) + c
0
,
where c
0
is a constant of integration.
By the indefinite integral
R
cos y dy/(1 − y)
isn’t in any tables book.
Using definite integrals
and assuming that (x
0
, y
0
) is on a solution
80

curve (x 6= 0, y 6= 1), we obtain
Z
y
y
0
cos t dt
1 − t
= ln(x) − ln(x
0
) = ln (x/x
0
) .
The function defined by the integral
R
y
y
0
cos t dt/(1 − t) has to be evaluated
numerically.
Try some quality software to plot
several solution curves.
2.4
First Order Homogeneous Equations
If the function F (x, y) of a first order
differential equation
y
0
= F (x, y)
(2.16)
can be written in the form
y
0
=
dy
dx
= ˜
F
x
y
!
(2.17)
then we call the Equation (2.16)
a first order homogeneous differential equation
or simply a homogeneous
first order equation. Problems of this type can
always be reduced to exact differential equations,
a topic which was covered in Section 2.2,
by the substitution
u =
y
x
.
We can compute
y = xu,
y
0
= xu
0
+ u
81

so that
xu
0
+ u = ˜
F (u).
The variables can be separated at this point to yield
du
˜
F (u) − u
=
dx
x
.
(Of course, ˜
F (u) − u 6= 0.)
Integrate term
by term to get
Z
du
˜
F (u) − u
=
Z
dx
x
+ c
0
= ln (c
1
|x|) ,
(c
1
= e
c
0
)
where the number c
0
is the constant of integration.
This can be best illustrated by the following examples:
Example 1.
Solve the differential equation
x
2
dy
dx
−
x
2
4
− y
2
= 0.
The first thing we do is to observe that a substitution
y = xu, dy = u dx + x du will change the equation to
x
2
u + x
du
dx
!
−
x
2
4
− x
2
u
2
= 0,
u + x
du
dx
−
1
4
− u
2
= 0,
du
u
2
− u +
1
4
=
dx
x
,
du
u −
1
2
2
=
dx
x
.
82

Integrate term by term to obtain
Z
du
u −
1
2
2
=
Z
dx
x
+ c
0
,
−1
u −
1
2
= ln |x| + c
0
.
We can substitute c
0
= ln c
1
, where c
0
is any real number
and c
1
> 0 and u = y/x to obtain
y
x
−
1
2
=
−1
ln(c
1
|x|)
.
Further simplification yields
y =
x
2
−
x
ln(c
1
|x|)
.
That the above equation is a solution of the original
differential equation (2.16) can be
determined from differentiation and substitution.
Example 2.
Solve the differential equation
xy
0
− x − y = 0.
Substitute y = ux, y
0
= xu
0
+ u.
x(xu
0
+ u) − x − xu = 0.
Assume that x 6= 0 and obtain
xu
0
+ u − 1 − u = 0
xu
0
= 1.
Integrate
u =
Z
dx
x
+ c
0
= ln |x| + c
0
= ln (c
1
|x|) ,
83

where c
0
= ln c
1
, c
1
> 0.
Verify the solution by integration.
Example 3.
Solve the differential equation
x
2
y
0
= y
2
+ xy + x
2
.
Substitute y = ux, y
0
= xu
0
+ u.
x
2
(xu
0
+ u) = x
2
u
2
+ x
2
u + x
2
.
Again, suppose that x 6= 0, we divide out x
2
.
xu
0
+ u = u
2
+ u + 1.
xu
0
= u
2
+ 1,
du
u
2
+ 1
=
dx
x
.
arctan
y
x
= ln (c
1
|x|)
y = x tan (ln(c
1
|x|)) .
84

Problems
1. Solve the following differential equation:
y
2
+ (xy + y
2
)
dy
dx
= 0.
2. Solve the following differential equation:
y
x
+
cos
y
x
dy
dx
= 0.
3. Solve the following differential equation:
y
0
− 2 = e
y/x
85

Solutions
1. Solve the following differential equation:
y
2
+ (xy + y
2
)
dy
dx
= 0.
The above differential is homogeneous.
We make the substitution y = ux.
x
2
u
2
+
x
2
u + x
2
u
2
(xu
0
+ u) = 0.
Factor out x
2
u to get
u + (1 + u)(xu
0
+ u) = 0.
Collect terms and write as a differential expression.
u(u + 2) + (1 + u)u
0
= 0;
(1 + u) du
u(u + 2)
= −
dx
x
.
We have to rationalize the denominator.
1 + u
u(u + 2)
=
A
u
+
B
u + 2
1 + u = Au + 2A + Bu,
A =
1
2
,
B =
1
2
.
Group and integrate, to obtain
1
2
du
u
+
du
u + 2
!
= −
dx
x
;
1
2
ln [u(u + 2)] = − ln x + c
0
.
86

Which is equivalent to
u(u + 2) =
c
1
x
2
,
c
1
= e
2c
0
.
Substituting u = y/x, we have
y
x
y
x
+ 2
=
c
1
x
2
.
The solution is
y(y + x) = c
1
.
We verify by differentiating.
2. Solve the following differential equation:
y
x
+
cos
y
x
dy
dx
= 0.
The above differential is homogeneous.
We make the substitution y = ux.
3. Solve the following differential equation:
y
0
− 2 = e
y/x
The above differential is homogeneous.
We make the substitution y = ux.
87

2.5
A Theorem on Exactness
We mentioned in Section 2.2 that the test
for exactness in the first order equations,
∂M
∂y
=
∂N
∂x
was necessary and sufficient to ensure the solution of the
differential equation M (x, y) + N (x, y)y
0
= 0, where the partial
derivatives are assumed to be continuous in some region R
in the xy-plane. On the other hand, if there exists a
function U (x, y) such that
∂U
∂x
= M (x, y),
∂U
∂y
= N (x, y),
under suitable regularity conditions, namely that the second
partial derivatives of all orders are continuous, then there
is a theorem in advanced calculus which states that
∂
2
U
∂x∂y
≡
∂
2
U
∂y∂x
.
How can we prove the converse? Here we will have to construct
a function U (x, y), having second partial derivatives, from
the functions M (x, y) and N (x, y). This is actually a special
case of a much more general theorem which is found in vector
analysis concerning independence of path and exactness. For this
case, however, we will be content to prove the following theorem.
Theorem 4 Let R be a rectangular region in the xy-plane,
each of M (x, y) and N (x, y) have continuous first partial
derivatives at each point (x, y) ∈ R, and
M (x, y) dx + N (x, y) dy = 0
(2.18)
in R. The following equality
∂M
∂y
=
∂N
∂x
(∀ (x, y) ∈ R)
(2.19)
88

is true if and only if
there exists a function U (x, y) such that
∂U
∂x
= M (x, y),
∂U
∂y
= N (x, y)
(∀ (x, y) ∈ R) .
(2.20)
Proof:
We have already seen
that the existence of such a function U (x, y) is sufficient.
To show necessity, we first need to form an initial value
problem. Let c
0
be a fixed but arbitrary constant and define
U (0, 0) := c
0
. We will define a function, ˜
U which will
later be proven to be U itself, as follows:
˜
U (x, y) = U (0, 0) +
Z
(x,0)
(0,0)
M (r, 0) dr +
Z
(x,y)
(x,0)
N (x, s) ds
(2.21)
≡ c
0
+
Z
x
0
M (r, 0) dr +
Z
y
0
N (x, s) ds.
We can re-write Equation (2.21) as follows
˜
U (x, y) = U (0, 0) +
Z
(0,y)
(0,0)
N (0, s) ds +
Z
(x,y)
(0,y)
M (r, y) dr
(2.22)
≡ c
0
+
Z
y
0
N (0, s) ds +
Z
x
0
M (r, y) dr.
So, ˜
U has been defined in Equation (2.21)
and in Equation (2.22). Are the two the same,
that is, is ˜
U well defined? At this point we apply the
hypothesis, namely Equation (2.19), and observe
that Γ = [(0, 0), (x, 0)] ∪ [(x, 0), (x, y)] ∪ [(x, y), (0, y)] ∪ [(0, y), (0, 0)] is a
closed path.
The notation [(x
1
, y
1
), (x
2
, y
2
)] stands for the closed line
interval from the point (x
1
, y
1
) to the point (x
2
, y
2
) in
the xy-plane. Γ starts
at the origin (0, 0) and transverses counter-clockwise through
89

the points (x, 0), (x, y), and (0, y), respectively,
returning to the origin. See Figure 2.3.
Stokes’ theorem (actually Green’s Lemma in the plane)
ensures that the
line integral about the path Γ is zero and so the function
˜
U is well defined. If S is the surface enclosed by
the path Γ, then
Z
Γ
M (x, y) dx + N (x, y) dy =
Z Z
S
∂N
∂x
−
∂M
∂y
!
dx dy = 0.
Now, writing out
R
Γ
M dx + N dy, we have
Z
x
0
M (r, 0) dr +
Z
y
0
N (x, s) ds +
Z
0
y
N (0, s) ds +
Z
0
x
M (r, y) dr = 0.
The above equation is exactly the same as
Z
x
0
M (r, 0) dr +
Z
y
0
N (x, s) ds −
Z
y
0
N (0, s) ds −
Z
x
0
M (r, y) dr = 0
which is also
c
0
+
Z
x
0
M (r, 0) dr +
Z
y
0
N (x, s) ds = c
0
+
Z
y
0
N (0, s) ds +
Z
x
0
M (r, y) dr.
Substitute back for ˜
U (x, y) on both the
right-hand side and the left-hand side to ensure
that ˜
U (x, y) is, in fact, well defined.
Having shown that the function ˜
U (x, y) is well defined,
we next must show that it satisfies
∂ ˜
U
∂x
= M (x, y),
∂ ˜
U
∂y
= N (x, y).
This can be done directly from Equations (2.21)
and (2.22) directly.
∂ ˜
U (x, y)
∂y
=
∂
∂x
U (0, 0) +
Z
(x,0)
(0,0)
M (r, 0) dr +
Z
(x,y)
(x,0)
N (x, s) ds
!
=
∂
∂y
Z
(x,y)
(x,0)
N (x, s) ds = N (x, y).
90
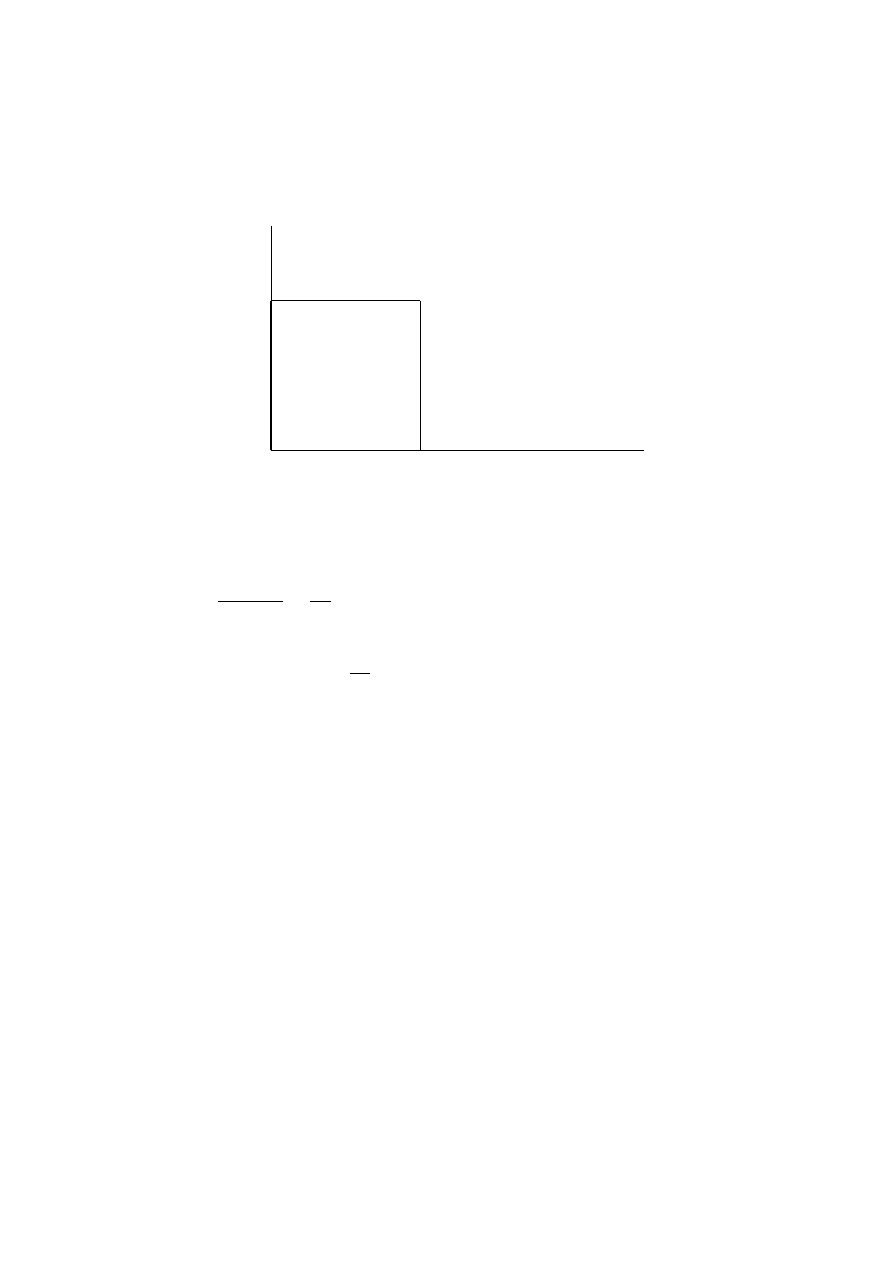
•
Γ
y
x
(x,y)
(x,0)
(0,y)
(0,0)
-
6
?
Figure 2.3:
A Closed Path Γ
∂ ˜
U (x, y)
∂x
=
∂
∂x
U (0, 0) +
Z
(0,y)
(0,0)
N (0, s) ds +
Z
(x,y)
(0,y)
M (r, y) dr
!
=
∂
∂x
Z
(x,y)
(0,y)
M (r, y) dr = M (x, y).
This completes the proof of the theorem.
♦
One might observe in the proof of the theorem that we
made use of the fact that U (0, 0) := c
0
. The arbitrary
constant c
0
can be determined if U (0, 0) is known.
In general, if U (x, y) = c
1
, an arbitrary constant,
then if one knows a single value of U at a point, say
(x
0
, y
0
), then c
1
:= U (x
0
, y
0
). This can also be
written in an integral form, when the equation is
separated variables.
Z
x
x
0
˜
M (x) dx +
Z
y
y
0
˜
N (y) dy = 0.
(2.23)
The above integral equation, Equation (2.23),
is frequently found in physics. Finally, a word of caution:
91

There exist equations which satisfy ∂M/∂y = ∂N/∂x everywhere except
at isolated points
and whose integral
R
Γ
M dx + N dy is
not independent of the choice of path, Γ.
−
y
x
2
+ y
2
dx +
x
x
2
+ y
2
dy = 0.
92

Problems
1. Test the following equation, if it is exact, then find
the function U such that U (x, y) = c
1
is its solution.
e
x
cos y dx − e
x
sin y dy = 0.
2. Test the following equation, if exact find
the function U such that U (x, y) = c
1
is its solution.
e
x
sin y dx − e
x
cos y dy = 0.
3. Test the following equation, if exact find
the function U such that U (x, y) = c
1
is its solution.
x
3
− 3xy
2
+ sin(y)
dy +
3x
2
y − y
3
dx = 0.
4. If R is any rectangular region not containing the
origin, show that following differential expression
is exact and find its solution U (x, y) = c
1
.
2xy
(x
2
+ y
2
)
2
dx +
y
2
− x
2
(x
2
+ y
2
)
2
dy = 0.
Solutions
1. Test the following equation, if it is exact, then find
the function U such that U (x, y) = c
1
is its solution.
e
x
cos y dx − e
x
sin y dy = 0.
93

Apply the test ∂M/∂y = ∂N/∂x:
∂M
∂y
= −e
x
sin y,
∂N
∂x
= −e
x
sin y.
The equation is exact.
By inspection, we find
U (x, y) = e
x
cos(y) = c
1
.
2. Test the following equation, if exact find
the function U such that U (x, y) = c
1
is its solution.
e
x
sin y dx − e
x
cos y dy = 0.
Apply the test ∂M/∂y = ∂N/∂x:
∂M
∂y
= −e
x
sin y,
∂N
∂x
= +e
x
sin y.
The equation is not exact.
No such U exists.
3. Test the following equation, if exact find
the function U such that U (x, y) = c
1
is its solution.
x
3
− 3xy
2
+ sin(y)
dy +
3x
2
y − y
3
dx = 0.
94

Apply the test ∂M/∂y = ∂N/∂x:
∂M
∂y
= 3x
2
− 3y
2
,
∂N
∂x
= 3x
2
− 3y
2
.
The equation is exact.
We compute U (x, y):
Z
y
x
3
− 3xs
2
+ sin s
ds = yx
3
− xy
3
− cos y + F
1
(x);
Z
x
3t
2
y − y
3
dt = x
3
y − xy
3
+ F
2
(y).
Therefore,
U (x, y) = yx
3
− xy
3
− cos y = c
1
,
where c
1
is an arbitrary constant.
4. If R is any rectangular region not containing the
origin, show that following differential expression
is exact and find its solution U (x, y) = c
1
.
2xy
(x
2
+ y
2
)
2
dx +
y
2
− x
2
(x
2
+ y
2
)
2
dy = 0.
Apply the test ∂M/∂y = ∂N/∂x:
∂M
∂y
=
2x
(x
2
+ y
2
)
2
− 2
4xy
2
(x
2
+ y
2
)
3
95

=
2x
3
− 6xy
2
(x
2
+ y
2
)
3
.
∂N
∂x
=
−2x
(x
2
+ y
2
)
2
− 2
(y
2
− x
2
)(2x)
(x
2
+ y
2
)
3
=
2x
3
− 6xy
2
(x
2
+ y
2
)
3
.
The equation is exact.
We compute U (x, y):
U (x, y) =
Z
x
2ty
(t
2
+ y
2
)
2
dt
=
−y
x
2
+ y
2
= c
1
,
where c
1
is an arbitrary constant.
2.6
About Integrating Factors
If the differential expression
M (x, y) dx + N (x, y) dy = 0
(2.24)
is not exact and there exists a function
G(x, y) such that
G(x, y) [M (x, y) dx + N (x, y) dy] = 0
is exact, we call such a function G an
integrating factor. An integrating factor
is abbreviated IF.
Otherwise stated, an integrating factor is a function of x
96

and y, G(x, y), such that
∂M
∂y
6=
∂N
∂x
and
∂(GM )
∂y
=
∂(GN )
∂x
.
The original equation, Equation (2.24),
is modified when it is multiplied by an integrating
factor. Particular attention has to be given to two
special cases: (1) points (x
0
, y
0
) at which the
IF vanishes (G(x
0
, y
0
) = 0), and (2)
points (x
1
, y
1
) of singularity of the IF, that is
lim
(x,y)→(x
1
,y
1
)
G(x, y) = ∞.
When the IF vanishes, one encounters extraneous solutions.
A singularity in the IF may alter the domain of definition
of the solution.
Once an appropriate IF has been applied, the resulting
exact equation
˜
M (x, y) dx + ˜
N (x, y) dy = 0,
where
˜
M (x, y) := G(x, y) · M (x, y)
and
˜
N (x, y) := G(x, y) · N (x, y),
can be solved by techniques from Section
2.2, Section 2.3,
or Section 2.4.
For a given first order differential equation, Equation
(2.24), there can be several possible
integrating factors, each of which could make Equation
(2.24) exact. In general, there is no
one unique IF for a given DE (differential equation).
Three questions remain to be answered:
(1) “Do IFs always exist?”
(2) “Are there conditions which guarantee the existence
of an IF?” and (3) “How can one find an IF for a given
DE?”
97

Example 1.
Examine the differential equation
3xy + 2y
2
+ (x
2
+ 6xy)y
0
= 0 and determine whether
it is exact or not. If it is not exact, then locate
a suitable integrating factor to make it exact and
solve it.
Taking partials ∂M/∂y and
∂N/∂x, we get
∂M
∂y
=
∂
∂y
3xy + 2y
2
= 3x + 4y.
∂N
∂x
=
∂
∂x
x
2
+ 6xy
= 2x + 6y.
The equation is not exact. But, if we multiply through
by the integrating factor (x + 2y) we obtain
(x + 2y)(3xy + 2y
2
) + (x + 2y)(x
2
+ 6xy)y
0
= 0.
And, taking partial derivatives again,
∂M
∂y
=
∂
∂y
h
(x + 2y)(3xy + 2y
2
)
i
= 3x
2
+ 16xy + 12y
2
,
∂N
∂x
=
∂
∂x
h
(x + 2y)(x
2
+ 6xy)
i
= (x
2
+ 6xy) + (x = 2y)(2x + 6y) = 3x
2
+ 16xy + 12y
2
.
The equation is now exact and can be solved.
(3x
2
y + 8xy
2
+ 4y
3
) + (x
3
+ 8yx
2
+ 12y
2
)y
0
= 0.
The solution is
U (x, y) = x
3
y + 4x
2
y
2
+ 4xy
3
= c
1
.
And we may simplify this by factoring into
98

U (x, y) = (x
2
+ 4xy + 4y
2
)(xy) = (x + 2y)
2
xy = c
1
.
Example 2.
Examine the differential equation
y − xy
0
= 0 and determine whether
it is exact or not. If it is not exact, then locate
a suitable integrating factor to make it exact and
solve it.
Taking partials ∂M/∂y and
∂N/∂x, we get
∂M
∂y
=
∂y
∂y
= 1.
∂N
∂x
=
∂(−x)
∂x
= −1.
The equation is not exact. But, if we multiply through
by the integrating factor y
−2
we obtain
1
y
−
x
y
2
y
0
= 0,
which is exact. And we solve immediately,
U (x, y) =
x
y
= c
1
,
where c
1
is an arbitrary constant.
These example illustrate the principle of integrating
factor. How to determine such an integrating factor
is another matter. One can best learn by doing plenty
of examples and gaining an insight into just which
functions work best.
99
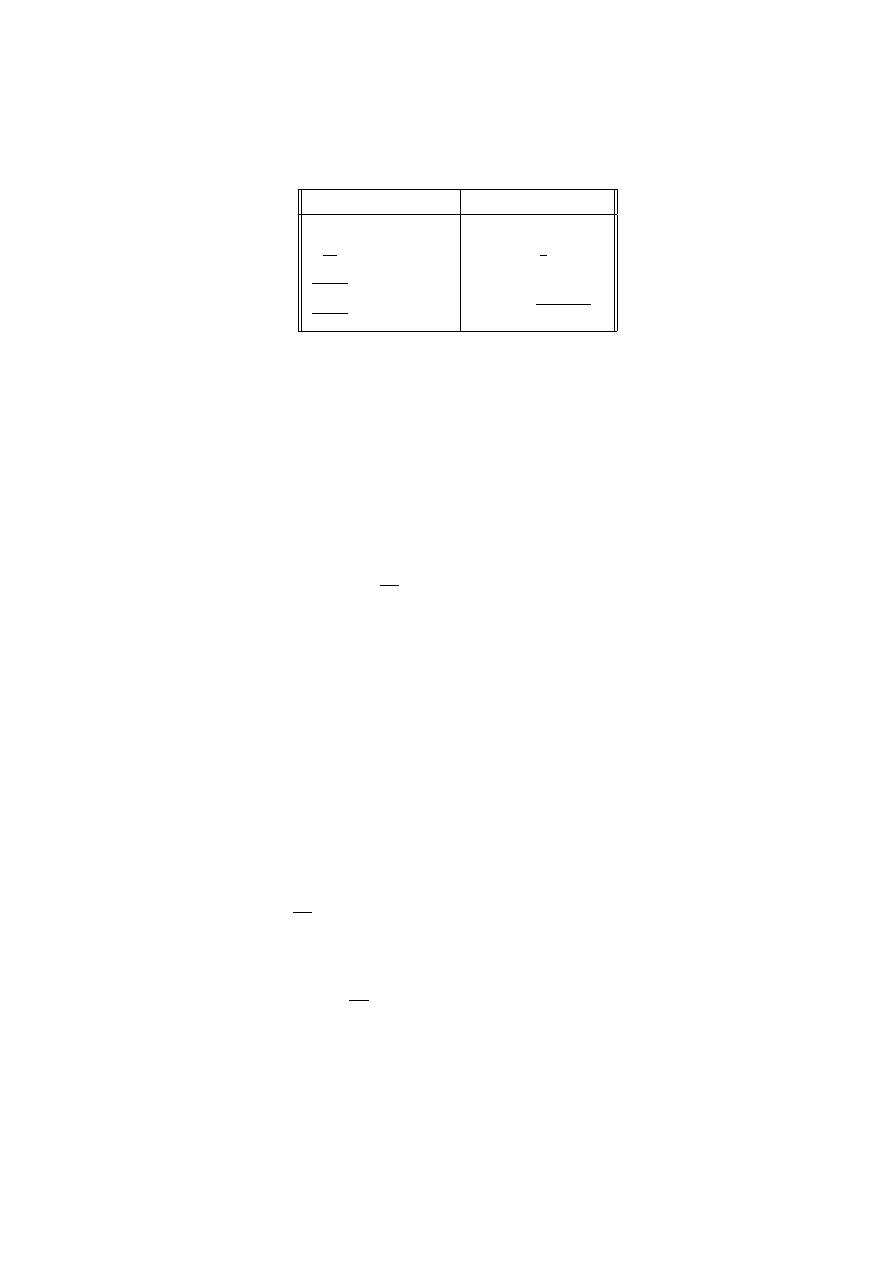
Differential
Exact Differential
y dx + x dy
d (xy)
1
x
2
(x dy − y dx)
d
y
x
1
x
2
+y
2
(x dy − y dx)
d [arctan (y/x)]
1
x
2
+y
2
(x dx + y dy)
d
log
√
x
2
+ y
2
Table 2.2:
Table of Exact Differentials
2.7
The First Order Linear Differential Equa-
tion
A first order differential equation is said to be
linear whenever it can be
written in the form
dy
dx
+ P (x) y = Q(x).
(2.25)
The differential expression for Equation (2.25)
is
[P (x) y − Q(x)] dx + dy = 0.
We observe that the above expression is not exact; however,
one can apply an integrating factor, namely
IF := e
R
P dx
.
If set set M (x, y) := e
R
P dx
[P (x) y − Q(x)]
and N (x, y) := e
R
P dx
, then taking partial derivatives
yields
∂
∂y
e
R
P dx
[P (x)y − Q(x)]
= P (x)e
R
P (x) dx
and
∂
∂x
e
R
P dx
= P (x)e
R
P (x) dx
.
100

Abbreviation
Definition
BC
Boundary Condition(s)
BVP
Boundary Value Problem
DE
Differential Equation
FTOC
Fundamental Theorem Of Calculus
IC
Initial Condition(s)
IF
Integrating Factor
IVP
Initial Value Problem
LC
Life Cycle
MDT
Mean Down Time
MTBF
Mean Time Between Failure
OA
Operational Availability
ODE
Ordinary Differential Equation
PDE
Partial Differential Equation
RM&A
Reliability, Maintaintability, and Availability
WLOG
Without Loss Of Generality
Table 2.3:
Table of Common Abbreviations
The above equation is exact, so we apply techniques from the
previous sections.
This can be summarized in the following theorem.
Theorem 5 Suppose that [a, b] is a number interval and
that each of P (x) and Q(x) is a continuous function on
[a, b]. If c
1
is an arbitrary constant then
y(x) = e
−
R
P dx
Z
e
R
P dx
Q(x) dx + c
1
e
−
R
P dx
(2.26)
is a solution of Equation (2.25). For
each real number y
0
and for each x
0
such that
a < x
0
< b, there exists a unique value for c
1
such that Equation (2.26) passes
through the point (x
0
, y
0
).
Proof:
Let [a, b] be a number
interval. Define a function u(x) from [a, b] such that
101

u(x) := exp
Z
x
P (t) dt
,
where
R
x
P (t) dt is one function representing the
indefinite integral
R
P (x) dx. Observe that u(x),
∀ x ∈ [a, b], is continuous. It is the composition
of two continuous functions. Furthermore, u
0
exists
and is also continuous.
u
0
(x) = P (x) · exp
Z
x
P (t) dt
= P (x) u(x).
If u(x) is an IF for Equation (2.25), then
d
dx
(u(x)y(x)) = Q(x) · u(x).
d
dx
(u(x)y(x)) = u
0
(x)y(x) + u(x)y
0
(x)
= u(x) [y
0
(x) + P (x) y(x)] ;
and,
d
dx
Z
x
u(t)Q(t) dt = u(x) Q(x);
Therefore,
u(x) [y
0
(x) + P (x) y(x)] = u(x) Q(x)
and u(x) is an integrating factor for Equation
(2.25).
We have
u(x) y(x) =
Z
x
Q(t)u(t) dt + c
1
,
where c
1
is a constant of integration. Whenever
u(x) 6= 0, we may divide it out to get
102

y(x) =
1
u(x)
Z
x
Q(t)u(t) dt +
c
1
u(x)
.
Observe that we have Equation (2.26)
y(x) = exp
−
Z
x
P (t) dt
Z
x
exp
Z
x
P (s) ds
Q(t) dt
+ c
1
exp
−
Z
x
P (t) dt
.
Since u is continuous, each of the above steps
can be reversed. u(x) 6= 0 for each x ∈ [a, b]
because e
w
> 0 for each real number w.
From an inital condition, (x
0
, y
0
), we wish to
determine c
1
u(x
0
)y(x
0
) = exp
−
Z
x
0
P (t) dt
Z
x
0
exp
−
Z
t
P (s) dx
Q(t) dt
+c
1
exp
−
Z
x
0
P (t) dt
.
Set
R(x) = e
−
R
x
P (t) dt
Z
x
e
−
R
t
P (s) ds
Q(t) dt
for convenience.
u(x
0
)y
0
≡ u(x
0
) y(x
0
) = R(x
0
) + c
1
u(x
0
),
c
1
=
u(x
0
) y
0
− R(x
0
)
u(x
0
)
,
u(x
0
) > 0,
c
1
= y
0
− R(x
0
)/u(x
0
).
This solves the IVP and completes the proof.
♦
103

Example 1.
Solve the first order
linear differential equation
y
0
− y = e
x
.
P (x) = −1,
Q(x) = e
x
,
and
u(x) = exp
Z
x
P (t) dt
.
We compute
R(x) = exp
−
Z
x
(−1) dx
Z
x
exp
Z
t
(−1) ds
e
t
dt
,
y(x) = R(x) + c
1
/u(x)
= e
+x
Z
x
e
−t
e
t
dt + c
1
e
−
R
x
(−1) dt
= xe
x
+ c
1
e
x
.
Example 2.
Solve the first order
differential equation
xy
0
+ y + 1 = 0.
We make it into a linear first order
differential equation by dividing by x:
y
0
+
y
x
= −
1
x
.
P (x) =
1
x
,
Q(x) = −
1
x
,
and
u(x) = exp
Z
x
dt/t
= e
ln x
= x.
R(x) = exp
−
Z
x
dt/t
Z
t
exp
Z
t
ds/s
−
1
t
dt
104

= e
− ln x
Z
x
e
ln t
−
1
t
dt
=
1
x
Z
x
(−1) dt =
1
x
(−x) = −1.
Therefore,
y(x) = R(x) + c
1
/u(x),
y(x) = −1 + c
1
/x,
is the solution.
2.8
Other Methods
Not every first order differential equation can be
solved by the methods previously discussed in this
chapter. In this section some substitutions, artifacts,
and special techniques are considered. In technical references,
one may find many more methods, some of which are equation
specific or computational in nature.
Substitution, or transformation of variables, is the
most common and useful of the alternate methods. An
unknown equation may be converted into an equation of
a known type by a suitable transform.
One could try to alter the form of the equation
M (x, y) + N (x, y)y
0
= 0 by a suitable substitution
x = x(u, v),
x = y(u, v).
Proceeding formally, we look at the total
differentials
dx =
∂x
∂u
du +
∂x
∂v
dv,
dy =
∂y
∂u
du +
∂y
∂v
dv.
105

Each of x, y, dx, dy is now expressed in terms of
u, v, du, dv and M (x, y) dx + N (x, y) dy = 0 is
transformed into
˜
M (u, v)
∂x
∂u
du
!
+ ˜
N (u, v)
∂y
∂u
du +
∂y
∂v
dv
!
.
(2.27)
and
˜
M (u, v) := M (x(u, v), y(u, v)) ,
˜
N (u, v) := N (x(u, v), y(u, v)) .
Collecting terms, we have Equation (2.27) as
ˆ
M (u, v) du + ˆ
N (u, v) dv = 0.
(2.28)
If Equation (2.28) can be solved, we have
U (u, v) = c
1
.
(2.29)
Substitute back to get
U [u(x, y), v(x, y)] = c
1
,
(2.30)
the desired solution.
2.9
Summary
We have examined a variety of techniques, methods,
and procedures to solve first order, first degree
equations. We have learned to recognize certain
particular cases and know immediately which method
to apply. It is also true that computer software
can recognize certain types of first order, first
degree equations and produce amazing results. But
human manipulation is often better than even the
cleverest algorithms, as will be seen in the following
problem section.
We proved that every differential expression of
the form M dx + N dy = 0 always has a unique
solution if it is exact. We next examined separable
106

variables, the most elementary form of exact
expressions, and extended our knowledge of integral
calculus. The first order homogeneous differential
equations were our first encounter with substitution
and with the pitfalls that accompany it. Integrating
factors, in general, and the special integrating
factors for the first order linear differential
equations, in particular, rounded out our classification
of first order differential equations and their
standard solution methods. We then mentioned some
exotic means of obtaining solutions.
Problems
Classify each of the following problems as
separable variables, homogeneous first order,
exact, or linear first order. Use mathematical
software to obtain a solution whenever possible.
If the software fails to obtain a solution, then
solve the problem manually. One will observe that
the computer is not infallible and that a human
touch is sometimes necessary. Try to guess at
reasons as to why the computer software might
fail in each given case.
1. Classify and solve y
0
= − ((y/x) + x(xy + 1)).
2. Classify and solve (y
2
+ 1)y
0
= (x
2
− 1).
3. Classify and solve (x
2
− x)y
0
= −(2xy − y + 2x).
4. Classify and solve y
0
= −y + 2x + 1.
5. Classify and solve yy
0
= (x + 1).
Solutions
107

1. Classify and solve y
0
= − ((y/x) + x(xy + 1)).
The above equation is first order linear
y
0
+ P (x) y = Q(x),
where P (x) = (1/x + x
2
) and Q(x) = −x.
The computer gives a solution.
{{y(x) →
x
2
(−1 − xy)
2
+ C(1) − y log(x)}}.
2. Classify and solve (y
2
+ 1)y
0
= (x
2
− 1).
The above equation can be written in the form
˜
M (x) dx + ˜
N dy = 0.
Thus it is separable variables.
The computer generated the following solution:
{{y(x) → −
x
1 + y
2
+
x
3
3 (1 + y
2
)
+ C(1)}}
3. Classify and solve (x
2
− x)y
0
= −(2xy − y + 2x).
The above equation is exact.
∂M
∂y
= (2x − 1) =
∂N
∂x
The computer gives a solution
{{y(x) → (1 − x) x C(1)
+
2 e
log(1−x)+log(x)
(1 + log(x/(1 − x)) + x log((1 − x)/x) )
−1 + x
}}.
108

4. Classify and solve y
0
= −y + 2x + 1.
The above equation is first order linear.
The computer gives a solution
{{y(x) → −1 + 2 x +
C(1)
e
x
}}.
5. Classify and solve yy
0
= (x + 1).
The above equation is clearly exact since
∂y
∂x
= 1 =
∂(x + 1)
∂y
The computer gives the solution
{{y(x) → −
q
2 x + x
2
+ C(1)}, {y(x) →
q
2 x + x
2
+ C(1)}}.
109

Chapter 3
The Laplace Transform
3.1
Laplace Transform Preliminaries
Suppose that f is a real-valued function
from [0, ∞) = { x | 0 ≤ x < +∞ }.
The Laplace transform of f (x)
is defined as the function F (s) such that
F (s) :=
Z
∞
0
f (x)e
−sx
dx,
(3.1)
wherever it exists. It is important to note
that the improper integral in the definition
of F (s) above usually means
Z
∞
0
f (x)e
−sx
dx = lim
r→0
+
Z
1
r
f (x)e
−sx
dx + lim
R→+∞
Z
R
1
f (x)e
−sx
dx,
where 0 < r 1 R < +∞.
The function F (s), defined above
is a complex-valued function of one
complex variable, s.
Throughout this chapter, we will let lower case italic
letters, f , g, h, etc., denote the real-valued
functions and upper case italic letters, F , G, H,
etc., denote their respective Laplace transforms. Moreover, we
will always denote f as f (x), F as F (s),
etc., to ensure that there is no misunderstanding
110
as to whether a given function is a function of a real
variable, x, or of a complex variable, s.
The operator L (calligraphic “L”)
is defined as F (s) = L[f (x)]; F (s)
results from the application
of the integral operator L
to f (x). One has to place certain restrictions
on the function f (x) to guarantee that the integral
in Equation (3.1) exists and is finite;
moreover, the function F (s) may not exist for all values
of the complex variable s. For a given function
F (s), one must specify its domain of definition.
In particular, if the integral in Equation (3.1)
exists for some real number s
0
, then F (s) exists for
all complex numbers s whose real part exceeds s
0
. In
some textbooks f (x) is called the original
function and F (s) is called the image
function.
To work effectively with Laplace transforms,
one needs to establish some elementary transform
pairs, that is, definite functions f (x) and their corresponding
Laplace transform F (s). These function pairs and the
elementary theorems on the Laplace transform give powerful
tools for solving ordinary differential equations, especially
those frequently encountered in RM&A.
(Laplace
transforms are also used in solving partial differential
equations.) Some pairs will be presented
in the following illustrative examples.
Example 1.
If x ∈ [0, ∞) and f (x) = 1, then
F (s) = L[1] =
Z
∞
0
e
−sx
dx =
1
s
.
(3.2)
Z
∞
0
e
−sx
dx =
e
−sx
−s
∞
0
= lim
R→∞
e
−sR
−s
+
e
0
s
=
1
s
.
Let <(s) denote the real part of the complex number s.
111

As long as <(s) > 0, the above integral exists.
If <(s) < 0 then lim
R→∞
e
−sR
−s
fails to exist.
So the strip of convergence of
the function f (x) ≡ 1 is 0 < <(s).
Otherwise stated, this improper integral exists
and is finite
whenever s is real and positive or whenever
s is complex with a positive real part.
Example 2.
If x ∈ [0, ∞) and f (x) = x, then
F (s) = L[x] =
Z
∞
0
xe
−sx
dx
= lim
R→∞
"
xe
−sx
−s
#
R
0
+ lim
R→∞
1
s
Z
R
0
e
−sx
dx
= lim
R→∞
"
Re
−Rs
−s
−
e
−Rs
s
2
+
1
s
2
#
=
1
s
2
,
where <(s) > 0.
Example 3.
If x ∈ [0, ∞), α > −1,
and f (x) = x
α
, then
F (s) = L[x
α
] =
Z
∞
0
x
α
e
−sx
dx
=
1
s
α+s
lim
R→∞
"
Z
R
0
y
α
e
−y
dy
#
R
0
,
where −1 < α and <(s) > 0. We made
a change of variable in the integrand using
y = sx. Restricting s to be a positive,
real number and α to be a real number,
112

α > −1 defines the improper integral
Z
∞
0
x
α
e
−x
dx
as the well-known Gamma function Γ(α + 1).
Therefore,
L [x
α
] =
Γ(α + 1)
s
α+1
(x > 0, α > −1) .
There is one special case of interest, namely
α = −
1
2
.
L
h
x
−1/2
i
=
Z
∞
0
x
−1/2
e
−sx
dx =
r
π
s
.
Example 4.
If x ∈ [0, ∞) and f (x) = x
n
,
where n is a positive integer, then
F (s) = L [x
n
] =
Z
∞
0
x
n
e
−sx
dx =
x
n
e
−sx
−s
∞
0
+
n
s
Z
∞
0
x
n−1
e
−sx
dx,
and hence, for <(x) > 0
L[x
n
] =
n
s
L
h
x
n−1
i
.
Using recursion and Equation (3.2),
we have
F (s) = L [x
n
] =
n!
s
n+1
(n = 0, 1, 2, . . .).
One important property of the Laplace transform, which it shares
with other operators, is that it is linear, in the
sense that if each of f
1
and f
2
is a real-valued function
from [0, ∞) and if each of c
1
and c
2
is a real
number then
L [c
1
f
1
(x) + c
2
f
2
(x)] = c
1
L [f
1
(x)] + c
2
L [f
2
(x)] .
Under suitable assumptions on f (x),
113

(lim
R→∞
|f (R)|e
−sR
= 0)
one can define the Laplace transform of f
0
(x) as
L [f
0
(x)] =
Z
∞
0
f
0
(x)e
−sx
dx
= lim
R→∞
f (x)e
−sx
R
0
+ lim
R→∞
Z
R
0
s f (x)e
−sx
dx
= −f (0) + sL [f (x)] .
Recursively applying the above yields
L [f
0
(x)]
= sL [f (x)] − f (0)
L [f
00
(x)]
= s
2
L [f (x)] − (sf (0) + f
0
(0))
..
.
..
.
..
.
L
h
f
(n)
(x)
i
= s
n
L [f (x)] −
s
n−1
f (0) + · · · + sf
(n−2)
(0) + f
(n−1)
Whenever L [f (x)] = L [g(x)],
we say that f, g belong to the same equivalence class with
respect to the operator L and we write f ≡ g.
If, in addition, each of f and g is continuous, then
f = g. Later we will prove a theorem on the uniqueness of the
Laplace transform.
3.2
Basic Theorems
Theorem 6 Suppose that s
0
is a real number.
If F (s) = L [f (x)] exists for
<(s) > s
0
, then for any real number a
L [e
ax
f (x)] = F (s − a),
(<(s) > s
0
+ a) .
Proof:
Starting with the operational definition of the
Laplace transform
114

-
6
1/s
1
·
·
·
·
·
·
·
·
·
·
·
··
··
··
···
····
·····
······
········
············
··················
······························
··································································
··························································································
Figure 3.1:
f (x) = 1 and F (s) = 1/s
F (s) =
Z
∞
0
e
−sx
f (x) dx.
Replace s with s − a (that is, s := s − a) to obtain
F (s − a) =
Z
∞
0
e
−(s−a)x
f (x) dx
=
Z
∞
0
e
−sx
(e
ax
f (x)) dx = L [e
ax
f (x)] .
This ends the proof of the so-called “translation theorem.”
♦
Corollary 1 Let z be a complex number.
L [e
zx
f (x)] = F (s − z), ∀ <(s) > <(z).
Proof:
Make a change of variables and observe that the
theorem implies that L [e
zx
f (x)] = F (s − z) whenever <(s − z) > s
0
.
Therefore, <(s) > s
0
+ <(z).
♦
115

Theorem 7 Suppose that s
0
is a real number.
If F (s) = L [f (x)] exists for
<(s) > s
0
, then for any real number a > 0
L [f (ax)] =
1
a
F
s
a
,
(<(s) > as
0
) .
Proof:
Starting with the operational definition of the
Laplace transform
F (s) =
Z
∞
0
e
−sx
f (x) dx.
Replace s with s/a (that is, s := s/a) to obtain
F
s
a
=
Z
∞
0
e
−sx/a
f (x) dx
Performing a change of variable by
redefining x := ax yields
F
s
a
= a
Z
∞
0
e
−sx
f (ax) dx.
Finally, divide both sides by the constant a > 0 to get
1
a
F
s
a
=
Z
∞
0
e
−sx
f (ax) dx = L [f (ax)] .
This ends the proof of the so-called “change of scale theorem.”
♦
Theorem 8 Suppose that each of f (x) and f
0
(x) is a
continuous function from the number set [0, ∞).
Let s
0
be a positive real number.
If each of L [f (x)] (s) ≡ L [f (x)]
and L [f
0
(x)] (s) ≡ L [f
0
(x)] exists for
<(s) > s
0
, then
L [f
0
(x)] = sL [f (x)] − f (0),
(<(s) > s
0
) .
116

Proof:
Starting with the operational definition of the
Laplace transform
L [f
0
(x)] = lim
R→∞
Z
R
0
e
−sx
f
0
(x) dx.
Perform integration by parts to obtain
Z
R
0
e
−sx
f
0
(x) dx = e
−sx
f (x)
R
0
+ s
Z
R
0
e
−sx
f (x) dx.
Therefore,
Z
R
0
e
−sx
f
0
(x) dx = s
Z
R
0
e
−sx
f (x) dx − f (0) + e
−sR
f (R).
(3.3)
To complete the proof of this theorem, it remains to show that
lim
R→∞
e
−sR
f (R) = 0.
The existence of L [f (x)],
L [f
0
(x)], and the fact that
f (0) is finite imply that
lim sup
R→∞
e
−s
0
R
f (R) = M < +∞.
Suppose that <(s) > s
0
is fixed, but arbitrary.
lim
R→∞
e
−sR
=
lim
R→∞
e
−s
0
R
f (R)
lim
R→∞
e
−(s−s
0
)R
≤ M ·
lim
R→∞
e
−(s−s
0
)R
= M · 0 = 0.
Let R → +∞ in Equation (3.3). Then
Equation (3.3) becomes
L [f
0
(x)] =
Z
∞
0
e
−sx
f
0
(x) dx = s
Z
∞
0
e
−sx
f (x) dx − f (0) = sL [f (x)] − f (0).
Also written as
L [f
0
(x)] = sF (s) − f (0).
This ends the proof of the so-called “derivative theorem.”
♦
117

Name
Symbol
Definition
Bessel’s
J
0
(x)
:=
∞
X
n=0
(−1)
n
x
2n
2
2n
(n!)
2
.
Beta
B(x, y)
:=
Z
1
0
u
x−1
(1 − u)
y−1
du
0 < x, y.
Dirac delta
δ(x)
:= L
−1
[1].
Z
∞
−∞
f (x)δ(x) dx = f (0).
δ(x − x
0
)
:= L
−1
[e
−sx
0
], <(s) > 0, x
0
real.
Delta prime
δ
0
(x − x
0
)
:= L
−1
[se
−sx
0
], <(s) > 0.
Gamma
Γ(x)
:=
Z
∞
0
e
−u
u
x−1
du.
Γ(n)
= (n − 1)!, n a positive integer.
Γ(1/2)
=
√
π.
Gamma prime
Γ
0
(x)
:=
Z
∞
0
u
x−1
e
−u
ln(u) du, x ∈ (0, ∞).
Γ
0
(1)
= 0.577215 . . ., the Euler constant.
Heaviside
H(x − x
0
)
:=
(
1,
x ≥ x
0
;
0,
x < x
0
.
Sine integral
Si(x)
:=
Z
∞
x
sin u
u
du.
Table 3.1:
Named Functions
118
Problems
1. Use the translation theorem to show that
L [x
n
e
ax
] =
n!
(s − a)
n+1
2. Prove that
L [sin(kx)] =
k
s
2
+ k
2
.
(Hint:
Use integration by parts.)
3. Use the derivative theorem to show that if
L [1] =
1
s
then
L [x] =
1
s
2
.
4. Use the derivative theorem to show that if
L [sin(kx)] =
k
s
2
+k
2
then
L [cos(kx)] =
s
s
2
+k
2
.
5. Use the derivative theorem to show that if
L [cos(kx)] =
s
s
2
+k
2
and
L [sin(kx)] =
k
s
2
+k
2
then
L [x cos(kx)] =
s
2
−k
2
s
2
+k
2
.
6. Use the derivative theorem to show that if
L [cos(kx)] =
s
s
2
+k
2
and
L [sin(kx)] =
k
s
2
+k
2
then
L [x sin(kx)] =
2ks
s
2
+k
2
.
Solutions
119

1. Use the translation theorem to show that
L [x
n
e
ax
] =
n!
(s − a)
n+1
Recall that L [x
n
] = n!/s
n+1
.
The translation theorem states that
L [e
ax
f (x)] = F (s − a)
∀ a ∈ (−∞, ∞).
Therefore,
L [e
ax
x
n
] =
n!
(s − a)
n+1
∀ <(s) > a.
2. Prove that
L [sin(kx)] =
k
s
2
+ k
2
.
(Hint:
Use integration by parts.)
Starting from the operational definition of F (s),
L [sin(kx)] =
Z
∞
0
e
−sx
sin(kx) dx
=
− cos(kx)
k
e
−sx
∞
0
−
s
k
Z
∞
0
e
−sx
cos(kx) dx
=
1
k
−
s
k
Z
∞
0
e
−sx
cos(kx) dx
=
1
k
−
s sin(kx)
k
2
e
−sx
∞
0
−
s
2
k
2
Z
∞
0
e
−sx
sin(kx) dx
120

=
1
k
2
−
s
2
k
2
F (s).
Therefore,
F (s)
1 +
s
2
k
2
!
=
1
k
,
F (s) =
1
k
k
2
s
2
+ k
2
=
k
s
2
+ k
2
.
3. Use the derivative theorem to show that if
L [1] =
1
s
then
L [x] =
1
s
2
.
Recall the derivative theorem
L [f
0
(x)] = sL [f (x)] − f (0
+
).
Require that f (x) = x, f
0
(x) = 1, L [1] = 1/s,
∀ x ≥ 0, <(s) > 0.
Then write
1
s
= L [f
0
(x)] = sL [f (x)] − f (0).
Therefore,
L [f (x)] = L [x] =
1
s
1
s
− 0
=
1
s
2
.
4. Use the derivative theorem to show that if
L [sin(kx)] =
k
s
2
+k
2
then
L [cos(kx)] =
s
s
2
+k
2
.
121

Immediately we write f (x) = sin(kx) and obtain
L [k cos(kx)] = sL [sin(kx)] − sin(k · 0) = sL [sin(kx)] .
From the fact that L is linear,
L [cos(kx)] =
s
k
k
s
2
+ k
2
!
=
k
s
2
+ k
2
.
5. Use the derivative theorem to show that if
L [cos(kx)] =
s
s
2
+k
2
and
L [sin(kx)] =
k
s
2
+k
2
then
L [x cos(kx)] =
s
2
−k
2
s
2
+k
2
.
Set f (x) = x cos(kx) and use
L [f
00
(x)] = s
2
L [f (x)] − sf (0) − f
0
(0).
Doing the calculations,
f (x) = x cos(kx),
f (0) = 0;
f
0
(x) = cos(kx) − kx sin(kx),
f
0
(0) = 1;
f
00
(x) = −2k sin(kx) − k
2
x cos(kx).
Plug in the functions and compute.
L
h
−2k sin(kx) − k
2
x cos(kx)
i
= s
2
L [x cos(kx)] − s · 0 − 1.
Therefore,
L [x cos(kx)] =
1
s
2
+ k
2
−2k
2
s
2
+ k
2
+ 1
!
=
s
2
− k
2
(s
2
+ k
2
)
2
122

6. Use the derivative theorem to show that if
L [cos(kx)] =
s
s
2
+k
2
and
L [sin(kx)] =
k
s
2
+k
2
then
L [x sin(kx)] =
2ks
s
2
+k
2
.
Set f (x) = x sin(kx) and use
L [f
00
(x)] = s
2
L [f (x)] − sf (0) − f
0
(0).
Doing the calculations,
f (x) = x sin(kx),
f (0) = 0;
f
0
(x) = sin(kx) + kx cos(kx),
f
0
(0) = 0;
f
00
(x) = 2k cos(kx) − k
2
x sin(kx).
Plug in the functions and compute.
L
h
2k cos(kx) − k
2
x sin(kx)
i
= s
2
L [x sin(kx)] − s · 0 − 0.
Therefore,
L [x sin(kx)] =
1
s
2
+ k
2
2ks
s
2
+ k
2
!
=
2ks
(s
2
+ k
2
)
2
3.3
The Inverse Transform
Instead of starting from a function f (x) defined
for x ∈ [0, ∞), one might have a function
F (s) defined for a complex variable s on
a strip s
0
≤ <(s) ≤ s
1
, where s
0
is a real number
and s
1
is either a real number or the symbol
123

+∞. The inverse problem is to determined
a function f (x), given the function F (s),
such that F (s) = L [f (x)].
We are tempted to write
f (x) = L
−1
[F (s)] ,
(3.4)
but we have to ask if the operator L
−1
is well defined.
If F (s) is analytic on some nonempty open set, then
it is clear from the definition
of the integral that L
−1
exists and is linear.
Assuming for the moment that such a function f (x)
can be uniquely determined, we say that f (x) is
the inverse transform of F (s).
The problems are resolved by the following theorem
on the uniqueness of the inverse Laplace transform.
Theorem 9 Let s
0
be a real number.
Suppose that each of f (x) and g(x)
is continuous on [0, ∞) and that each of
F (s) and G(s) is a continuous function of the
complex variable s such that
<(s) ≥ s
0
. If F (s) = G(s) ∀ s,
such that <(s) ≥ s
0
, then f (x) = g(x) for
all x ∈ [0, ∞).
The above theorem is justification for the use of
tables of inverse Laplace transforms. Such tables
are invaluable in the solution of problems in physics,
engineering, biology, statistics, and reliability.
However, there are certain discontinuous functions,
the prime examples being the so-called Dirac delta
function and the unit step function, which also have
Laplace transforms. Their uniqueness will be assumed
until sufficient lemmata is developed to prove it
rigorously. In Table 3.2,
H(x) is the Heaviside function which is 1 whenever
x ≥ 0 and 0 whenever x < 0, δ(x) is the
124

Dirac delta function, and a is a real number.
The Dirac delta function is also known as the
impulse function. It is actually
a linear functional rather than a function; however,
the name is now in common usage. The Heaviside function
and the Dirac delta function are plotted in Figures
3.2 and 3.3, respectively.
We can resort to methods of complex analysis to
recover an original function f (x) from an image
function F (s). If the defining improper integral
for F (s) exists for some real number s
0
then
the image function F (s) is a single-valued
analytic function of the complex variable s
for all s such that <(s) > s
0
. The inverse
Laplace transform of F (s) can be found directly
by complex analysis from the improper integral
f (x) =
1
2πi
Z
c+i∞
c−i∞
e
sx
F (s) ds,
where c is a real number such that every
singularity of F (s) lies in the half plane
<(s) < c. Recall that
Z
c+i∞
c−i∞
e
sx
F (s) ds := lim
R→∞
Z
c+iR
c−iR
e
sx
F (s) ds.
Finally, the above theorem can be generalized.
If we simply allow each of f (x) and g(x) to have
Laplace transforms F (s) and G(s), respectively,
without regard to their continuity, then whenever
F (s) = G(s) ∀ <(s) > s
0
then f (x) ≡ g(x) in the sense that
Z
∞
0
e
−sx
[f (x) − g(x)] dx = 0.
(Otherwise stated, f (x) = g(x) almost everywhere.)
125

-
6
x
0
1
2
x
y
Figure 3.2: The Heaviside Function H(x − x
0
)
(x
0
> 0)
-
6
x
0
1
2
x
y
6
Figure 3.3: The Dirac Delta Function δ(x − x
0
) = H
0
(x − x
0
)
(x
0
> 0)
126

f (x)
L [f (x)]
Strip of convergence
e
−ax
H(x)
1
a + s
−a < <(s)
H(x)
1
s
0 < <(s)
xH(x)
1
s
2
0 < <(s)
δ(x)
1
all s
δ
0
(x)
s
all s
sin(kx)
k
s
2
+ k
2
0 < <(s)
cos(kx)
s
s
2
+ k
2
0 < <(s)
xe
−ax
H(x)
1
(s + a)
2
−a < <(s)
Table 3.2:
Laplace Transform Pairs
127

3.4
Transforms and Differential Equations
Ordinary differential equations with constant
coefficients can easily be solved with Laplace
transform methods. One simply takes the transform
of the function and its derivatives, performs
algebraic manipulation of the complex variable
s, and computes the inverse transform. The
only troublesome portion is that of the computation
of the inverse Laplace transform. Modern symbolic
mathematical software has been a boon in solving
such problems.
Example 1.
Solve the differential equation using Laplace
transform techniques
y
0
+ 2y = e
−2x
,
subject to the initial condition y(0) = 1.
Take the Laplace transform of both sides
of the above equation and apply the derivative
theorem.
sY (s) − 1 + 2Y (s) =
1
s + 2
,
where
Y (s) = L [y(x)] .
Solve the above algebraic equation for Y (s).
Y (s) =
1
(s + 2)
2
+
1
s + 2
.
Therefore, we have
y(x) = L
−1
"
1
(s + 2)
2
+
1
s + 2
#
= xe
−2x
+ e
−2x
= e
−2x
(x + 1).
Of course, this is a first order linear
differential equation and we could have used the integrating
factor e
−2x
from Section 2.6.
128

3.5
Partial Fractions
Let each of N (s) and D(s) be a polynomial in the
complex variable s having real coefficients. If the
the degree of N (s) is less than that of D(s) then
the inverse transform of N (s)/D(s), that is
L
−1
"
N (s)
D(s)
#
,
exists. It is customary to evaluate this rational polynomial
by means of a partial fraction decomposition.
From the Fundamental Theorem of Algebra it follows that
D(s) can be factored into a product of two types of factors,
each with real coefficients: (1) (s − s
j
)
n
and (2)
(s
2
+ t
k
s + s
k
)
m
, where each of m and n is a nonnegative
integer. The first can be rationalized into terms of the
form
a
1
(s − s
j
)
+
a
2
(s − s
j
)
2
+ · · · +
a
n
(s − s
j
)
n
;
the second can also be rationalized into
b
1
s + c
1
(s
2
+ t
k
s + s
k
)
+
b
2
s + c
2
(s
2
+ t
k
s + s
k
)
2
+ · · · +
b
m
s + c
m
(s
2
+ t
k
s + s
k
)
m
.
The most elementary partial fraction decomposition occurs
when each of the roots of D(s) is real and distinct.
In this case, we have the following
N (s)
D(s)
=
a
1
(s − s
1
)
+
a
2
(s − s
2
)
+ · · · +
a
n
(s − s
n
)
.
Example 1.
Given F (s) find f (x) = L
−1
[F (s)].
F (s) =
s
s
2
− 1
=
s
(s + 1)(s − 1)
.
We rationalize the denominator.
129

s
(s + 1)(s − 1)
=
A
s + 1
+
B
s − 1
,
s = As − A + Bs + B,
A + B = 1
B − A = 0
)
2B = 1, B =
1
2
,
A =
1
2
.
L
−1
s
s
2
− 1
=
1
2
L
−1
1
s + 1
+
1
2
L
−1
1
s − 1
=
1
2
e
−x
+
1
2
e
x
= cosh(x),
for
x ≥ 0.
We notice that for F (s) =
1
(s+1)(s−1)
=
1
2
1
s−1
−
1
2
1
s+1
that
L
−1
"
s
(s + 1)(s − 1)
#
=
1
2
e
x
−
1
2
e
−x
= sinh(x).
Example 2.
Given F (s) find f (x) = L
−1
[F (s)].
F (x) =
1
s
2
(s + 1)
.
We rationalize the denominator.
1
s
2
(s + 1)
=
A
s
+
B
s
2
+
C
s + 1
,
1 = As(s + 1) + B(s + 1) + Cs
2
= (A + C)s
2
+ (A + B)s + B,
giving
B = 1,
A + B = 0,
A = −1,
C = −A = 1.
Therefore,
L
−1
[F (s)] = L
−1
−
1
s
+
1
s
2
+
1
s + 1
= −1 + x + e
−x
.
130

3.6
Sufficient Conditions
The following theorem expresses some conditions on the function
f (x), x ∈ [0, ∞), sufficient to ensure that
L [f (x)] = F (s) exists. These are not the
weakest conditions possible; there are functions which
possess Laplace transforms and fail to meet each of the
conditions. However, the theorem covers real phenomena
for most engineering work. Before stating and proving
the theorem, we need to introduce some new concepts.
Definition 3 The statement
that the function f (x) is little-o of
g(x) as x → x
0
means that
lim
x→x
0
|f (x)|
|g(x)|
= 0.
The statement that the function f (x) is Big-O
of g(x) as x → x
0
means that
lim sup
x→x
0
|f (x)|
|g(x)|
= M < ∞,
where the notation M < ∞ means “M is finite.”
The above definitions are written f (x) = o (g(x))
and f (x) = O (g(x)), respectively.
If one simply says that f (x) is O (g(x)), then
it is assumed that f (x) is O (g(x)) for all
x in the domain of definition of f . A similar statement
applies to o (g(x)). Let a be a real number,
we say that f (x) is of exponential order if
there exists some number x
0
such that
f (x) = O (e
ax
)
for all x ∈ [x
0
, ∞)
Clearly, if f (x) is defined on [0, ∞) and
f (x) = O (e
ax
), then f (x) = O (e
ax
)
131

as x → ∞. All bounded functions are
O (e
ax
) ∀ a ≥ 0. The exponential
function e
kx
, k ≥ 0 is O (e
ax
) for
all a > k.
We now proceed to the important theorem. While the proof is
somewhat technical, it is important because it presents
techniques that can be used with functions which fail to
satisfy the hypotheses yet still possess Laplace transforms.
Theorem 10 Let a be a real number and let f (x) be
defined for all x ∈ [0, ∞). If
f (x) = O (e
ax
) and f (x) is sectionally
continuous, then
F (x) = L [f (x)] =
Z
∞
0
e
−sx
f (x) dx
exists for <(s) > a. Moreover,
Z
∞
0
e
−sx
f (x) dx is absolutely convergent
∀ <(s) > a.
Proof:
Let {x
1
, x
2
, . . . , x
n
} be an increasing sequence
of positive numbers such that
lim
n→∞
x
n
= +∞
and let each point of discontinuity, x
k
, of f (x)
belong to {x
1
, x
2
, . . . , x
n
}. (We may consider
{x
k
}
∞
k=1
to be the set of
discontinuities of f (x) WLOG.) Let 0 < r x
1
Consider
Z
∞
0
e
−sx
f (x) dx = lim
r→0
+
Z
x
1
r
e
−sx
f (x) dx
+
Z
x
2
x
1
e
−sx
f (x) dx + · · · +
Z
x
n
x
n−1
e
−sx
f (x) dx + lim
R→∞
Z
R
x
n
e
−sx
f (x) dx
=
Z
x
1
0
e
−sx
f (x) dx + · · · +
Z
x
n
x
n−1
e
−sx
f (x) dx + · · ·
132
because f (x) is continuous from the right at 0,
i.e., f (0
+
) = lim
r→0
+
f (r) = lim
h→0
f (|h|) exists and is finite.
lim
R→∞
Z
R
x
n
e
−sx
f (x) dx ≤ lim
R→∞
Z
R
x
n
e
−sx
M e
ax
dx
= lim
R→∞
−
M
a − s
e
−(s−a)x
R
x
n
=
M
s − a
e
−(s−a)x
n
→ 0
as
n → ∞.
Therefore, let x
0
:= 0 so that
Z
∞
0
e
−sx
f (x) dx =
∞
X
k=1
Z
x
k
x
k−1
e
−sx
f (x) dx;
Z
∞
0
e
−sx
f (x) dx ≤
∞
X
k=1
Z
x
k
x
k−1
e
−sx
M e
ax
dx.
For each positive integer k, we have
Z
x
k
x
k−1
e
−sx
|f (x)| dx ≤
M e
−(s−a)x
−(s − a)
x
k
x
k−1
=
M
s − a
h
e
−(s−a)x
k−1
− e
−(s−a)x
k
i
,
(s > a).
The series
∞
X
k=1
M
s − a
h
e
−(s−a)x
k−1
− e
−(s−a)x
k
i
telescopes to give (∀ n)
Z
x
n
0
e
−sx
|f (x)| dx ≤
M
s − a
h
e
−(s−a)0
− e
−(s−a)x
n
i
→
M
s − a
as
n → ∞.
Z
∞
0
e
−sx
|f (s)| dx ≤
M
s − a
< ∞.
Therefore,
Z
∞
0
e
−sx
f (x) dx
exists for all <(s) > a. Therefore F (s) = L [f (x)] exists.
♦
133

Problems
1. Show that the function f (x) = e
x
2
is continuous
on [0, ∞) and that it does not possess a Laplace
transform. Deduce that sectional continuity is not a
sufficient condition to ensure that the Laplace transform
exists.
2. Show that the function f (x) = 1/x
2
is
O (e
x
) on [1, ∞) (in fact, f (x) = 1/x
2
is O (e
x
) on [, ∞) for
any positive number ). Prove that this function
does not have a Laplace transform. This shows that
there exist functions of exponential order which fail to
possess a Laplace transform.
3. Find the Laplace transform of the real-valued function
f (x) = 2x cos(e
x
2
)e
x
2
defined on the interval [0, ∞). Prove that this function
is not of exponential order, that is, that this function is not
O (e
ax
) for any real number a and as
x → x
0
for any x
0
∈ [0, ∞).
4. Prove that if f
0
(x) is continuous on [0, ∞)
and that if each of L [f (x)] and
L [f
0
(x)] exists for some real value
of s, say s = a, then f (x) is of exponential order
e
ax
.
134

Solutions
1. Show that the function f (x) = e
x
2
is continuous
on [0, ∞) and that it does not possess a Laplace
transform. Deduce that sectional continuity is not a
sufficient condition to ensure that the Laplace transform
exists.
A continuous function of a continuous function
is a continuous function, that is, the composition
of two (or more) continuous functions is continuous.
f ◦ g (x) = f (g(x))
is continuous whenever each of f and g are.
The function f (x) = e
x
2
does not possess
a Laplace transform because for any complex
number s we find
lim
R→∞
Z
R
0
e
−sx
e
x
2
dx = e
s
2
/4
lim
R→∞
Z
R
0
e
(x−s/2)
2
dx
≥ e
s
2
/4
lim
R→∞
Z
R
0
1 · dx = +∞.
Thus the improper integral
Z
∞
0
e
−sx
e
x
2
dx
fails to exist for any complex number s.
135

2. Show that the function f (x) = 1/x
2
is
O (e
x
) on [1, ∞) (in fact, f (x) = 1/x
2
is O (e
x
) on [, ∞) for
any positive number ). Prove that this function
does not have a Laplace transform. This shows that
there exist functions of exponential order which fail to
possess a Laplace transform.
We observe that h(x) = f (x)/e
x
= e
−x
/x
2
is a strictly
decreasing function on [, ∞) since
h
0
(x) = −
e
−x
x
3
(x + 1) < 0
∀ x ≥ > 0.
Therefore, on the interval [, ∞), h(x)
has an absolute maximum at .
max{|h(x)| | x ∈ [, ∞} = e
/
2
⇒ f (x) = O (e
x
)
on
[, ∞).
Now we argue by contradiction that f (x) does not have a
Laplace transform.
If it did then the improper integral
Z
1
0
f (x)e
−sx
dx = lim
r→0
+
Z
1
r
f (x)e
−sx
dx
would exist (and be finite).
However, for s > 0,
lim
r→0
+
Z
1
r
e
−sx
dx
x
2
≥ e
−s
lim
r→0
Z
1
r
x
−2
dx = lim
r→0
+
−r
−1
1
r
= lim
r→0
+
1
r
− 1
= +∞.
The improper integral fails to exist.
136

3. Find the Laplace transform of the real-valued function
f (x) = 2x cos(e
x
2
)e
x
2
defined on the interval [0, ∞). Prove that this function
is not of exponential order, that is, that this function is not
O (e
ax
) for any real number a and as
x → x
0
for any x
0
∈ [0, ∞).
From the operational definition of L [f (x)], compute
L [f (x)] =
Z
∞
0
e
−sx
f (x) dx
=
Z
∞
0
e
−sx
2xe
x
2
cos(e
x
2
) dx.
Integrate by parts.
u(x) = e
−sx
du(x) = −se
−sx
dx;
dv(x) = 2xe
x
2
cos(e
x
2
)
v(x) = sin(e
x
2
).
L [f (x)] = e
−sx
sin(e
x
2
)
∞
0
+ s
Z
∞
0
e
−sx
sin(e
x
2
) dx
= − sin(1) + s
Z
∞
0
e
−sx
sin(e
x
2
) dx,
(<(s) > 0) .
The integral
Z
∞
0
e
−sx
sin(e
x
2
) dx
can be shown to exist for all <(s) > 0 from a
theorem in advanced calculus.
137

4. Prove that if f
0
(x) is continuous on [0, ∞)
and that if each of L [f (x)] and
L [f
0
(x)] exists for some real value
of s, say s = a, then f (x) is of exponential order
e
ax
.
From the operational definition of F (s) = L [f (x)],
Z
∞
0
f
0
(x)e
−ax
dx ≤ M < +∞
and
Z
∞
0
f (x)e
−ax
dx ≤ ˜
M < +∞.
Integrate by parts.
lim
R→∞
f (R)e
−aR
− lim
r→0
+
f (r)e
−ar
−
Z
∞
0
f (x)e
−ax
dx ≤ M
⇒
lim
R→∞
f (R)e
−aR
≤ M + f (0) + ˜
M .
From the above and the continuity of f
0
(x),
lim sup
x∈[0,∞)
|f (x)| exists and
is finite on bounded intervals.
Therefore,
f (0) is finite and f (x) = O (e
ax
).
3.7
Convolution
If each of f and g is a sectionally
continuous function of exponential order, then
(f ∗ g) (x) :=
Z
x
0
f (u)g(x − u) du
138
is a sectionally continuous function of
exponential order. We refer to f ∗ g
as the convolution of f and g.
Moreover,
L [f ∗ g] = F (s) G(s),
(<(s) > max{a
1
, a
2
}) ,
where
f (x) = O(e
a
1
x
)
and
g(x) = O(e
a
2
x
).
For unbounded regions, multiple integrals can sometimes be
separated into iterated integrals and further separated into
a product of two (or more) usual Riemann integrals:
F (s) G(s) =
Z
∞
0
e
−sx
f (x) dx
Z
∞
0
e
−sx
g(x) dx
= lim
R→∞
Z
2R
0
e
−sx
Z
x
0
f (u)g(x − u) du
dx,
(<(s) > a) .
The convolution property, L
−1
[F (s)G(s)] = (f ∗ g) (x), can be used to
prove a number of
corollaries and determine a number of useful Laplace transforms.
Let f (x) = O (e
ax
), then
L
Z
x
0
f (u) du
=
1
s
f (s),
<(x) >
1
2
(a + |a|)
.
We can compute the inverse transform of F (s)/s
2
, for
example.
1
s
2
F (s) = L [f (x) ∗ 1 ∗ 1]
= L
Z
x
0
f (u) du ∗ 1
= L
Z
x
0
du
Z
u
0
f (v) dv
.
139

3.8
Useful Functions and Functionals
The most basic building block in Laplace
transform theory and the principal, prime paradigm
of functions with jump discontinuities is the
so-called Heaviside function (also known as the
unit step function). Its operational definition is
H(x − x
0
) =
(
1,
∀ x ≥ x
0
;
0,
∀ x < x
0
.
The graph is shown in Figure 3.2.
In the definition, it is assumed that x
0
> 0.
Although this function is discontinuous, it is
O (e
as
) for each a > 0 and possesses
a Laplace transform
L [H(x − x
0
)] =
Z
∞
0
H(x − x
0
)e
−sx
dx
=
Z
x
0
0
0 · e
−sx
dx +
Z
∞
x
0
1 · e
−sx
dx =
e
−sx
0
s
,
(<(s) > 0) .
The function f (x) = 1 ∀ x ∈ [0, ∞) is a
special case when x
0
= 0. In this case,
L [1] = L [H(x − 0)] =
1
s
e
−s·0
=
1
s
.
Many functions can conveniently be written using
the Heaviside function notation.
One of the most frequently encountered and
useful properties that a real-valued function
can possess is that of being periodic. A function
f (x) is periodic (of period τ ) if
f (x) = f (x + τ ) ∀ x ∈ (−∞, ∞).
The Laplace transform of a periodic functions has a
special characterization.
F (s) =
Z
∞
0
e
−sx
f (x) dx
140

=
Z
τ
0
e
−sx
f (x) dx +
Z
∞
τ
e
−sx
f (x) dx.
We will make a substitution, or change of variable,
so that when x = τ , y = 0. y = x − τ and
x = y + τ , dy = dx, and dx = d(y + τ ).
Z
∞
τ
e
−sx
f (x) dx =
Z
∞
0
e
−s(y+τ )
f (y + τ ) d(y + τ )
=
Z
∞
0
e
−s(y+τ )
f (y) dy,
because f (y) = f (y + τ ). The variable of
integration, y, is a “dummy” so we may define
x := y.
Z
∞
0
e
−s(y+τ )
f (y) dy =
Z
∞
0
e
−s(x+τ )
f (y) dx
= e
−sτ
Z
∞
0
e
−sx)
f (x) dx = e
−sτ
F (s).
Therefore,
Z
∞
0
e
−sx
f (x) dx =
Z
τ
0
e
−sx
f (x) dx + e
−sx
Z
∞
0
e
−sx
f (x) dx.
It follows that
F (s) =
1 − e
−sτ
−1
Z
τ
0
e
−sx
f (x) dx.
We may employ the Heaviside function, H(x),
under certain circumstances to characterize a
periodic function. If f (x) is a periodic
function, then
f
p
(x) := H(x)f (x) − H(x − τ )f (x − τ ),
where f
p
is f on [0, τ ] and zero elsewhere.
141

For other functions f (x), we may also construct
such a function f
p
f
p
(x) =
(
f (x),
0 ≤ x < τ
0,
otherwise.
by a variety of artifacts.
Example 1.
The so-called square wave function of period τ = 2a:
f
p
(x) = H(x) − 2H(x − a) + H(x − 2a).
Example 2.
The so-called sawtooth function of period τ = 1:
f
p
(x) = H(x)x − H(x − 1)(x − 1) − H(x − 1).
Example 3.
The so-called triangular wave function of period τ = 2a:
f
p
(x) =
1
a
[H(x)x − 2H(x − a)(x − a) + H(x − 2a)(x − 2a)] .
Example 4.
The so-called half-wave rectified sine wave
function of period τ = 2π/k:
f
p
(x) = H(x) sin(kx) + H(x − π/k) sin [k(x − aπ/k)] .
Example 5.
The so-called full-wave rectified sine wave
function of period τ = π/k:
f
p
(x) = H(x) sin(kx) + H(x − π/k) sin [k(x − aπ/k)] .
In reliability engineering (see [10, page 274]),
one frequently has need of the age distribution function,
g. It is customary to use t instead of x as the
independent variable and write
142

g(x; t
0
) :=
ψ(t
0
− t)[1 − φ(t)],
t < t
0
;
δ(t − t
0
)[1 − φ(t)],
t = t
0
;
0,
t > t
0
;
where δ(t − t
0
) is the so-called Dirac delta
function and each of ψ and φ are probability
functions with φ(t) continuous in an open
interval containing t
0
. We need an operational
definition for the Dirac delta function (also known
as the impulse function). One could say that
δ(x − x
0
) := L
−1
h
e
−sx
0
i
,
where <(s) > 0. Could this definition suffice?
Suppose we let 0 < 1 and
δ
(x − x
0
) =
1
H(x − x
0
) − H(x − [x
0
+ ])
,
L [δ
(x − x
0
)] = e
−sx
0
1 − e
−s
s
!
,
lim
→0
L [δ
(x − x
0
)] = e
−sx
0
.
Thus we have a function δ(x) = 0 for all x 6= 0
and δ(0) is undefined whereas
Z
+∞
−∞
δ(x − x
0
)f (x) dx = f (x
0
),
whenever f (x) is continuous in some open neighborhood
containing x
0
.
143

3.9
Second Order Differential Equations
The most common second order, ordinary differential
equation encountered anywhere—engineering, physics,
biology, ecology, etc.—is the initial value problem
with constant coefficients
y
00
+ 2ay
0
+ c
2
y = q(x),
where a ≥ 0 and c > 0. This is a linear ODE subject to the initial
conditions
y
0
:= y(x
0
),
y
0
0
:= y
0
(x
0
),
and, usually
x
0
:= 0
so that
y
0
:= y(0)
and
y
0
0
= y
0
(0).
Taking the Laplace transform, we obtain
s
2
Y (x) − sy(0) − y
0
(0) + 2asY (s) − 2ay(0) + c
2
Y (s) = Q(s).
Collecting terms yields
Y (s) =
Q(s) + (s + 2a)y
0
+ y
0
0
s
2
+ 2as + c
2
.
(3.5)
Case 1.
c > a. In this case the denominator
−2a ±
√
4a
2
− 4c
2
2
has a solution set
n
−a +
√
a
2
− c
2
, −a −
√
a
2
− c
2
o
.
Set b = c
2
− a
2
> 0 to obtain a solution set
{−a + ib, −a − ib}
i =
√
−1
.
Re-write Equation (3.5) as
144

Y (s) =
Q(s) + (s + 2a)y
0
+ y
0
0
(s + a)
2
+ b
2
.
At this point we simplify, by writing
Y (s) =
Q(s)
(s + a)
2
+ b
2
+
ay
0
+ y
0
0
(s + a)
2
+ b
2
+
y
0
(s + a)
(s + a)
2
+ b
2
.
(3.6)
The three terms on the right-hand side of the above
equation (Equation (3.6))
can be solved with the standard processes
for taking an inverse Laplace transform:
L
−1
"
Q(s)
(s + a)
2
+ b
2
#
= q(t) ∗
e
−ax
sin bt
b
!
;
L
−1
"
ay
0
+ y
0
0
(s + a)
2
+ b
2
#
= (ay
0
+ y
0
0
)
e
−ax
sin bt
b
!
;
L
−1
"
(s + 1)y
0
(s + a)
2
+ b
2
#
= y
0
e
−ax
cos(bt).
The general solution to
Case 1
, with
initial conditions, is given by the equation
y(x) = (ay
0
+ y
0
0
)e
−ax
sin bt
b
+ y
0
e
−ax
cos(bt) +
Z
x
0
q(x − τ )e
−aτ
sin(bτ )
τ
dτ.
(3.7)
The term e
−ax
is the damping
factor. It is present whenever a > 0 and represented
friction or energy loss of the system from the
driving function q(x).
Case 2.
c = a. In this case the differential equation may be
factored as follows
145

(D + a) (D + a) y = (D + a) (y
0
+ ay) = y
00
+ 2ay
0
+ a
2
y
and the denominator in Equation (3.5)
has a double root {−a, −a}. The equation becomes
Y (s) =
Q(s) + (s + 2a)y
0
+ y
0
0
(s + a)
2
and is readily solved by applying the inverse Laplace transform
L
−1
"
n!
(s + a)
n
#
= e
−ax
x
n
.
Case 3.
c < a. In this case the denominator in Equations
(3.5) has two distinct real roots,
a +
√
a
2
− c
2
and a −
√
a
2
− c
2
. Denote
these two roots by r
1
and r
2
, respectively,
and apply the method of partial fractions to obtain
solutions in terms of exponential functions.
001 002 003
3.10
Systems of Differential Equations
004 005 006 007 Laplace transforms are useful in solving 008 009 systems of
ordinary differential equations. 010 011 In particular, the Laplace transform
can 012 013 readily convert a system of linear differential 014 015 equations
with constant coefficients into a system 016 017 of simulteneous linear alge-
braic equations. 018 019 Recall the system of equations in Section 020 021
1.8, Equation (1.37): 022 023
024y
0
(x) = y(x) + z(x)
025z
0
(x) = 2y(x).026
027 028 We will now solve this system of equations using 029 030 Laplace
transforms. The transformed system becomes 031 032
033sY (x) − y
0
= Y (s) + Z(s), 034
146

035 036
037sZ(s) − z
0
= 2Y (s), 038
039 040 where Y (s) = L[y(x)], Z(s) = L[z(x)]. 041 042 We define y
0
:=
y(x
0
), z
0
:= z(x
0
), for a real 043 044 number x
0
in the domain of each of
y(x) and z(x). 045 046 We re-write the above transformed system 047 048
049Y (x)(s − 1) = y
0
+ Z(s), 050
051 052
053sZ(s) = z
0
+ 2Y (s).054
055 056 First solve for Z(s). 057 058
059sZ(s) = z
0
+ 2
y
0
+ Z(s)
s − 1
!
, 060
061 062
063Z(s)
s
2
− s − 2
= z
0
(s − 1) + 2y
0
, 064
065 066
067Z(s) (s − 2) (s + 1) = 068z
0
(s − 1) + 2y
0
, 069
070 071
072073Z(s) =
z
0
(s − 1) + 2y
0
(s − 2)(s + 1)
074075
076 077
078 =
1
3
z
0
+ 2y
0
s − 2
079 +
2
3
z
0
− y
0
s + 1
.080
081 082 Then solve for Y (s). 083 084
085086Y (s)(s − 1) = y
0
+
z
0
+ 2Y (s)
s
, 087088
089 090
091092s(s − 1)Y (s) = sy
0
+ z
0
+ 2Y (s), 093094
095 096
097098Y (s)
s
2
− s − 2
= sy
0
+ z
0
, 099100
101 102
103104Y (s) =
sy
0
+ z
0
(s − 2)(s + 1)
105106
147

107 108
109110 =
1
3
2y
0
+ z
0
s − 2
111112 +
1
3
y
0
− z
0
s + 1
.113114
115 116 Applying the elementary inverse Laplace transform 117 118 pairs,
we obtain at once. 119 120
121122y(x) =
1
3
(2y
0
+ z
0
)e
2x
123124 +
1
3
(y
0
− z
0
)e
−x
125126
127 128 and 129 130
131132z(x) =
1
3
(z
0
+ 2y
0
)e
2x
133134 +
2
3
(z
0
− y
0
)e
−x
.135136
137 138 If we define c
1
, c
2
such that c
1
:=
1
3
(2y
0
+ z
0
) 139 140 and c
2
:=
1
3
(y
0
− z
0
), then the solution to the 141 142 system of equations becomes 143
144
145146y(x) = c
1
e
2x
+ c
2
e
−x
147148z(x) = c
1
e
2x
− 2c
2
e
−x
.149150
151 152 The last equation is precisely the same as the one in 153 154 Section
1.8.
3.11
Heaviside Expansion Formula
One particularly important transform pair,
which finds frequent use in reliability
engineering, is the Heaviside expansion
formula
f (x) =
n
X
k=1
P (a
k
)
Q
0
(z
k
)
e
a
k
x
F (s) =
P (s)
Q(s)
,
(3.8)
where each of P and Q is a polynomial.
The degree of P is less than the degree
of Q and Q has exactly n distinct
real roots {a
1
, a
2
, . . . , a
n
}.
(deg(P ) < deg(Q).)
Also significant is the transform pair
f (x) = e
ax
n
X
k=1
P
(n−k)
(a)
(n − k)!
x
k−1
(k − 1)!
F (s) =
P (s)
(s − a)
n
.
(3.9)
148

We will derive the Heaviside expansion formula
of Equation (3.8). Since
{a
1
, a
2
, . . ., a
n
} are the real, distinct
roots of Q, we may write
Q(s) = (s − a
1
)(s − a
2
) · · · (s − a
n
).
Using the partial fractions expression, we write
P (s)
Q(s)
=
b
1
s − a
1
+
b
2
s − a
2
+ · · · +
b
n
s − a
n
.
(3.10)
Let k be a positive integer such that 1 ≤ k ≤ n.
Multiply both sides by s − a
k
and let s → a
k
.
This will yield.
b
k
=
P (s)
Q(s)
(1 − s
k
) −
b
1
(s − a
k
)
s − a
1
−
b
2
(s − a
k
)
s − a
2
− · · ·
−
b
k−1
(s − a
k
)
s − a
k−1
−
b
k+1
(s − a
k
)
s − a
k+1
− · · · −
b
n
(s − a
k
)
s − a
n
.
We see at once that, in the limit as s → a
k
,
b
k
= lim
s→a
k
P (s)
Q(s)
(s − a
k
) =
0
0
,
since all the terms b
j
(s − a
k
)/(s − a
j
), j 6= k,
vanish. This indeterminate,
0
0
, indicates
that we may apply l’Hˆ
ospital’s rule.
b
k
= lim
s→a
k
P (s)
Q(s)
(s − a
k
) = P (a
k
) lim
s→a
k
s − a
k
Q(s)
= P (a
k
)
1
Q
0
(a
k
)
,
since Q
0
(a
k
) 6= 0. Q
0
(s) consists of a sum of n terms,
one of which must be
Y
j6=k
(s − a
j
)
and is nonzero, and (n − 1) other terms,
each of which is zero and vanishes.
Thus Equation (3.10) can be written
149

P (s)
Q(s)
=
P (a
1
)
Q(a
1
)
1
s − a
1
+
P (a
2
)
Q(a
2
)
1
s − a
2
+ · · · +
P (a
n
)
Q(a
n
)
1
s − a
n
.
Taking the inverse Laplace transform of both sides of
the above equation, we have
L
−1
"
P (s)
Q(s)
#
=
P (a
1
)
Q
0
(a
1
)
e
a
1
x
+
P (a
2
)
Q
0
(a
2
)
e
a
2
x
+ · · · +
P (a
n
)
Q
0
(a
n
)
e
a
n
x
.
Equations (3.8) and (3.9) are
preferred by reliability engineers over the convolution integrals.
Convolution is somewhat more general; however, the majority
of reliability differential equations consist of rational
polynomials and yield immediate solution by the Heaviside
expansion techniques. Nevertheless, all specialized Laplace
transform techniques are
primarily of theoretical interest due
to the availability and reliability of modern scientific
mathematical software. The following examples illustrate
computer generated solutions to problems previously described
in the Heaviside calculus.
In[1]:=
InverseLaplaceTransform[(2s
2
− 9s + 19)/
((s − 1)
2
(s + 3)), s, x]
Out[1]=
4/e
(3∗x)
− 2 ∗ e
x
+ 3 ∗ e
x
∗ x
In[2]:=
InverseLaplaceTransform[(3s + 5)/((s + 1)(s + 2)), s, x]
Out[2]=
e
(−2∗x)
+ 2/e
x
In[3]:=
InverseLaplaceTransform[(2s
2
− 6s + 5)/
(s
3
− 6s
2
+ 11s − 6), s, x]
Out[3]=
e
x
/2 − e
(2∗x)
+ (5 ∗ e
(3∗x)
)/2
In[4]:=
InverseLaplaceTransform[(s + 5)/((s + 1)(s
2
+ 1)), s, x]
Out[4]=
2/e
x
− 2 ∗ cos[x] + 3 ∗ sin[x]
150

In[5]:=
InverseLaplaceTransform[(2s
2
− 9s + 19)/
((s − 1)
2
(s + 3)), s, x]
Out[5]=
4/e
(3∗x)
− 2 ∗ e
x
+ 3 ∗ e
x
∗ x
In[6]:=
InverseLaplaceTransform[(2s + 3)/((s + 1)
2
(s + 2)
2
), s, x]
Out[6]=
−(x/e
(2∗x)
) + x/e
x
3.12
Table of Laplace Transform Theorems
Let each of f and g be a real-valued
function from [0, ∞). We assume that f (x), g(x) each
have a Laplace transform on some (non-trivial) strip of
convergence. The domain of
definition of each of the complex-valued
Laplace transforms, F (s) and G(s), of
f (x) and g(x), respectively is
s
0
< <(s) < s
1
and t
0
< <(s) < t
1
,
where each of s
0
, t
0
is a real number and
each of s
1
, t
1
is either a real number
or the symbol ∞. Let each of a, b, and τ
be a real number, s be a complex number,
and H(x) denote the Heaviside
function from (−∞, ∞).
(See Figure 3.2.)
The above table is simply an outline. The hypotheses are
lacking. Probably one of the most difficult parts of
applying mathematics is reading the hypothesis of a given
theorem and ensuring that the function conforms to them.
Proofs are important for situations in which a given function
fails to meet one or more conditions in the hypothesis.
By examining the argument in the proof, one can sometimes
determine if the theorem can be “extended” to cover the
exceptional function or will the function fail altogether.
151

real-valued function
Laplace transform
Strip of Convergence
af (x) + bg(x)
aF (s) + bG(s)
max{s
0
, t
0
} < <(s)
< min{s
1
, t
1
}
e
ax
f (x)
F (s − a)
a + s
0
< <(s) < a + s
1
f (ax)
(1/a)F (s/a)
s
0
/a < <(s) < s
1
/a
f
0
(x)
sF (s) − f (0)
s
0
< <(s) < s
1
f (x − a)H(x − a)
e
−as
F (s)
s
0
< <(s) < s
1
f (x + τ ) = f (x)
1
1 − e
−sτ
Z
τ
s
e
−sx
f (x) dx
<(s) > 0
f (x)/x
Z
∞
s
F (u) du
s
0
< <(s) < s
1
f ∗ g (x)
F (s) G(s)
max{s
0
, t
0
} < <(s)
< min{s
1
, t
1
}
Table 3.3:
Table of Theorems
3.13
Table of Laplace Transforms
Throughout this entire section, f (x)
will denote a real-valued function of
the real variable x, F (s) will denote
a function of the complex variable s,
<(s) will denote the real part of
s, =(s) will denote the purely
imaginary part of s, and the graph of
F (s) will simply be the function F (s)
plotted against <(s), for simplicity.
152
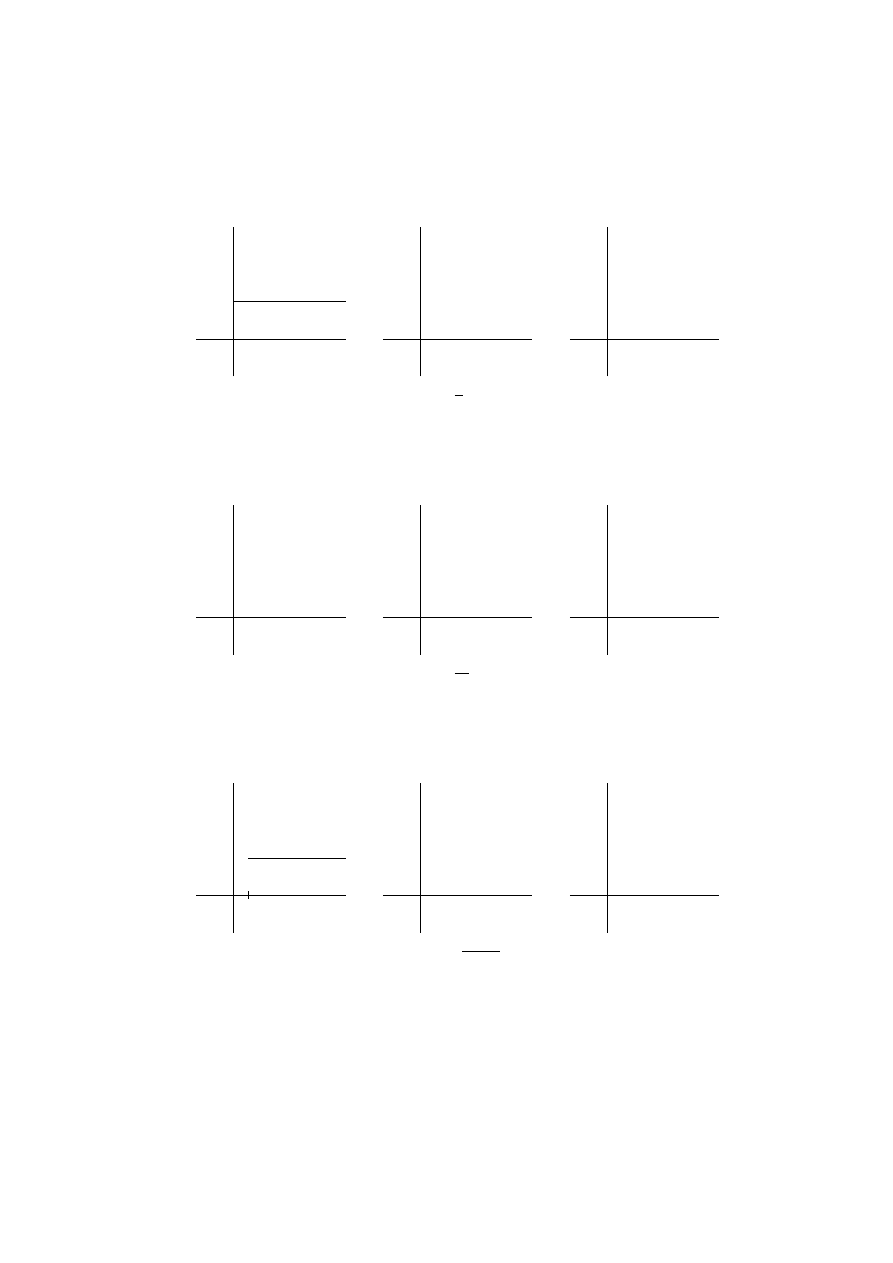
-
6
-
6
-
6
H(x) =
(
1,
x ≥ 0
0,
x < 0
F (s) =
1
s
<(s) > 0
<(s)
=(s)
−→
−→
−→
−→
−→
−→
···········
················
················
···················
·························
···································································
·························
Figure 3.4:
Heaviside Function
-
6
-
6
-
6
f (x) =
(
x,
x ≥ 0
0,
x < 0
F (s) =
1
s
2
<(s) > 0
<(s)
=(s)
−→
−→
−→
−→
−→
−→
·········
············
················
················
···················
····························
·········································································
Figure 3.5:
Ramp Function
-
6
-
6
-
6
x
0
H(x − x
0
) =
(
1,
x ≥ x
0
0,
x < x
0
F (s) =
e
−sx
0
s
<(s) > 0
<(s)
=(s)
−→
−→
−→
−→
−→
−→
·········
············
··················
···············
·····················
····································
··········································································
Figure 3.6:
Shifted Heaviside Function
153
-
6
-
6
-
6
a
a
f (x) = e
ax
H(x)
F (s) =
1
s − a
<(s) > a
<(s)
=(s)
−→
−→
−→
−→
−→
−→
··························
······················
··················
················
··············
················
················
··············
···········
···········
················
················
···················
·························
···································································
·····
Figure 3.7:
Linearly Transformed Heaviside Function
-
6
-
6
-
6
a
a
f (x) = xe
ax
H(x)
F (s) =
1
(s − a)
2
<(s) > a
<(s)
=(s)
−→
−→
−→
−→
−→
−→
··············
············
···········
··········
············
············
···········
···········
··········
·········
·········
········
·······
·········
············
················
················
···················
····························
·····················································
Figure 3.8:
Linearly Transformed Ramp Function
-
6
-
6
-
6
a
2a
3a
§ 3.8 Example 2.
F (s) =
1
as
2
−
e
−as
s(1 − e
−as
)
<(s) > 0
<(s)
=(s)
−→
−→
−→
−→
−→
−→
−→
·············
·················
················
·················
······················
·····································
········································
Figure 3.9:
The Sawtooth Function
154
3.14
Doing Laplace Transforms
Most textbooks devote time and energy to explaining
how to use the shift theorem, the linearly translated
transform theorem, and the derivative theorem to do
transforms. They spend time developing various artifacts
and clever ploys to manually compute Laplace transforms.
This book is concerned with the application of the
Laplace transform to RM&A engineering, particularly to
Reliability Engineering. One is expected
to use modern mathematical software to verify each
Laplace transform, even if it comes from a table book.
With that in mind, we present here some sample values from
symbolic software versus values from tables.
In[1]:=
LaplaceTransform[1,x,s]
Out[1]:=
1
s
Reference Table
f (x) = 1,
F (s) =
1
s
.
In[2]:=
LaplaceTransform[x,x,s]
Out[2]:=
s
−2
Reference Table
f (x) = x,
F (s) =
1
s
2
.
In[3]:=
LaplaceTransform[Exp[a x],x,s]
Out[3]:=
1
−a+s
Reference Table
f (x) = e
ax
,
F (s) =
1
s−a
.
In[4]:=
LaplaceTransform[x Exp[a x],x,s]
Out[4]:=
(−a + s)
−2
Reference Table
f (x) = xe
ax
F (s) =
1
(s−a)
2
In[5]:=
LaplaceTransform[x^(-1/2),x,s]
Out[5]:=
√
π
√
s
Reference Table
f (x) = x
−1/2
,
q
π
s
.
In[6]:=
LaplaceTransform[x^a,x,s]
155
Out[6]:=
s
−1−a
Gamma(1 + a)
Reference Table
f (x) = x
a
,
Γ(a+1)
s
a+1
(a > −1).
In[7]:=
LaplaceTransform[Cos[k x],x,s]
Out[7]:=
s
k
2
+s
2
Reference Table
f (x) = cos(kx),
s
s
2
+k
2
.
In[8]:=
LaplaceTransform[Sin[k x],x,s]
Out[8]:=
k
k
2
+s
2
Reference Table
f (x) = sin(kx),
k
s
2
+k
2
.
In[9]:=
LaplaceTransform[Cosh[k x],x,s]
Out[9]:=
s
−k
2
+s
2
Reference Table
f (x) = cosh(kx),
s
s
2
−k
2
.
In[10]:=
LaplaceTransform[Sinh[k x],x,s]
Out[10]:=
k
−k
2
+s
2
Reference Table
f (x) = sinh(kx),
k
s
2
−k
2
.
In[11]:=
LaplaceTransform[Exp[a x] Cos[k x],x,s]
Out[11]:=
−a+s
k
2
+(−a+s)
2
Reference Table
f (x) = e
ax
cos(kx),
s−a
(s−a)
2
+k
2
.
In[12]:=
LaplaceTransform[x^n Exp[a x],x,s]
Out[12]:=
(−a + s)
−1−n
Gamma(1 + n)
Reference Table
f (x) = x
n
e
ax
,
n!
(s−a)
n+1
.
In[13]:=
LaplaceTransform[x Cos[k x],x,s]
Out[13]:=
2 s
2
(k
2
+s
2
)
2
−
1
k
2
+s
2
Reference Table
f (x) = x cos(kx),
s
2
−k
2
(s
2
+k
2
)
2
.
In[14]:=
LaplaceTransform[BesselJ[0,a x],x,s]
Out[14]:=
1
√
a
2
+s
2
Reference Table
f (x) = J
0
(x),
1
√
s
2
+a
2
.
In a like manner we may compute inverse
Laplace transform.
156

In[15]:=
InverseLaplaceTransform[(s-a)^(-2),s,x]
Out[15]:=
e
a x
x
Reference Table
F (s) = 1/(s − a)
2
,
f (s) = xe
ax
3.15
Summary
In this chapter we investigated the powerful
and extremely useful Laplace transform.
We developed an operational definition for
the Laplace transform, computed certain
elementary transforms, stated and proved
some basic theorems, and demonstrated how
to apply the transform technique to problems
in RM&A.
Although we presented and proved many theorems
and illustrated techniques with examples, we have only
scratched the surface of this procedure. The
Laplace transform procedure is particularly well-suited
to engineering problems, especially initial value
problems, because the entire IVP can be solved
directly rather than by first finding a general
solution and then using the initial conditions
to determine the values of the arbitrary constants.
Laplace transforms are also useful in problems
where the so-called driving function, q(x) in
the equation
y
0
(x) + ay(x) = q(x),
has discontinuities or is periodic.
Despite the time and effort in solving application
problems this transform saves, it does not
enlarge the class of problems solvable from previously
explored techniques. The Laplace transform
does replace a differential equation
with an algebraic equation. This is a simplification
and a reduction since differential equations are a
generalization of algebraic equations.
157

The generalized derivative theorem
L
h
f
(n)
(x)
i
= s
n
F (s) −
n−1
X
k=0
s
n−1−k
f
(k)
0
+
= s
n
F (s) − s
n−1
f (0
+
) − s
n−1
f
0
(0
+
) − · · · − sf
(n−2)
(0
+
) − f
(n−1)
(0
+
),
where f
k
(0
+
) := lim
h→0
f
(k)
(|h|), k = 0, 1, . . . , n − 1,
makes the Laplace transform ideal for solving
IVPs involving linear DEs with constant coefficients.
In addition to the Laplace transform, we defined an
inverse transform. The function f (x), whose Laplace
transform is F (s), is called the inverse transform
of F (s). The operator L
−1
[F (s)]
was then shown to be a well-defined linear integral operator.
We asked the question: “If one knows
that F (s) is the Laplace transform of some
function f (x), how can one compute the inverse
transform f (x) from the information given
about F (s)?” We stated (without proof) theorems which
ensured the uniqueness of the inverse Laplace transform,
under suitable conditions, and discussed methods of
obtaining an inverse transform f (x) solely from
information about the Laplace transform F (s).
In particular, any two continuous
functions having the same Laplace transform are
identical.
We mentioned that there exist certain tools from
complex variable theory that permit a direct
calculation of the inverse Laplace transform from
an analytic function F (s) in the half plane
<(s) > s
0
, where all the singularities of F (s)
lie to the right of the line <(s) = s
0
.
Finally, we presented tables of transform pairs,
of transform theorems, and of named functions.
One attractive feature of the Laplace transform
is that it can be computed in a routine fashion
158

solely from transform tables and algebraic considerations.
It is necessary, however, that the user of Laplace
transforms be aware of the correct way to apply shifting,
convolution, and composition of functions to obtain
the solution of ordinary differential equations.
Graphical illustrations help, and a number have been
included. A table of Laplace transforms has the
same relation to ordinary, linear differential equations
as an integral table does to the integrand functions.
From a relatively small table of Laplace transforms
and the elementary Laplace transform theorems,
nearly every differential equation in Reliability,
Maintainability, and Availability can be successfully solved.
Some references refer to the definition in Equation
(3.1) as a one-dimensional Laplace transform
while others defined the Laplace transform as
Z
∞
−∞
e
−sx
f (x) dx
and restrict the function f (x) to a subinterval
of (−∞, ∞).
159

Glossary
Absolute convergence A function series
∞
X
n=1
f
n
(x) is said to
be absolutely convergent for some number set S if
the function series
∞
X
n=1
|f
n
(x)|
converges for each x ∈ S.
Autonomous differential equation A differential equation
that does not contain the independent variable explicitly.
Autonomous system A system of first-order differential
equations of the form
dy
j
dx
= F
j
(y
1
, . . . , y
n
)
j = 1, . . . , n
is said to be autonomous. The system is characterized by the
fact that each function, F
j
, does not depend on the
independent variable x.
Bessel function The Bessel function is defined as
the (improper) integral
J
n
(x) =
x
n
2
n
Γ(n + 1)
"
1 −
x
2
2(2n + 2)
+
x
4
2 · 4(2n + 2)(2n + 4)
− · · ·
#
.
Beta function The Beta function is defined as the (improper) integral
B(x, y) =
Z
1
0
u
x−1
(1 − u)
y−1
du, where x, y > 0.
160
Big-O The statement that f (x) is Big-O of g(x) at x
0
means that ∃ M > 0
such that lim sup
x→x
0
|f (x)|/|g(x)| ≤ M .
It is written as f (x) = O (g(x)).
Boundary value problem The problem of finding a solution to a differ-
ential equation (or system of differential equations) satisfying certain
requirements for a point set of the independent variable, the so-called
boundary conditions.
Complementary Error function The complementary error function is
defined as
the integral
erfc(x) = 1−erf(x) =
2
√
π
Z
∞
x
e
−t
2
dt.
Cosine integral The cosine integral is
defined as the (improper) integral
Ci(x) =
Z
∞
x
cos(t)
t
dt.
Error function The error function is defined as
the integral
erf(x) =
2
√
π
Z
x
0
e
−t
2
dt.
Exponential integral The exponential integral is defined as the (improper)
integral
Ei(x) =
Z
∞
x
e
−t
t
dt.
Exponential order A function f (x) is said to be of exponential order α if
there exists a constant x
0
such that f (x) = O (e
αx
), for all x > x
0
.
Fresnel integrals The Fresnel (cosine and sine) integrals are defined as
C(z) :=
q
2
π
Z
z
0
cos x
2
dx, S(z) :=
q
2
π
Z
z
0
sin x
2
dx.
161

Fundamental theorem of algebra Every polynomial equation with com-
plex coefficients of degree n ≥ 1 has at least at least one root. The root
may be real or complex.
Fundamental theorem of calculus If f (x) is
continuous on [a, b] and
F (x) =
Z
x
a
f (u) du,
then F (x) has a derivative in (a, b) such that
dF (x)
dx
= f (x).
Gamma function The Gamma function is defined
as the (improper)
integral Γ(x) =
Z
∞
0
e
−u
u
x−1
du, where x ∈ (0, ∞).
General solution A formula y = f (x; c
1
, . . . , c
n
)
which provides each solution of a given differential equation
F
x, y, y
0
, . . . , y
(m)
= 0.
Improper integral The statement that
Z
b
a
f (x) dx is an improper integral
means that one
or more of the following is true:
1. a = −∞,
2. b = +∞,
3. f (x) is undefined at x = a > −∞, x = b < +∞ or x = c for some
c ∈ (a, b).
Indeterminate form Let each of f (x) and g(x) be
defined in a neighborhood of x
0
and
lim
x→x
0
f (x) = lim
x→x
0
g(x) = 0.
Then
f (x
0
)
g(x
0
)
≡
0
0
162

is an indeterminate form. Other indeterminate forms include
∞
∞
,
0 · ∞, 1
∞
,
∞
0
, and ∞ − ∞.
Evaluation of the first two cases, when they exist, sometimes
results from an application of l’Hˆ
ospital’s rule.
Iteration method A method that yields a sequence of
approximating functions {y
0
, y
1
, . . . , y
n
, . . .}
to an unknown function y, where the nth approximation
(n is a positive integer) is obtained from the set
{y
0
, y
1
, . . . , y
n−1
} by some well-defined operation,
is known as an iteration method. One example is Picard’s
method.
l’Hˆ
ospital’s rule Let each of f (x) and g(x) be
defined (and subject to certain regularity conditions)
in a neighborhood of x
0
. If lim
x→x
0
f (x)
g(x)
is of the indeterminate form
0
0
or
∞
∞
and if lim
x→x
0
f
0
(x)
g
0
(x)
exists, then
lim
x→x
0
f (x)
g(x)
= lim
x→x
0
f
0
(x)
g
0
(x)
.
Lipschitz condition The statement that a function f (x) satisfies a Lips-
chitz condition at a point x
0
means that ∃ K > 0 and ∃ δ > 0 such that
if |x − x
0
| < δ
then |f (x) − f (x
0
)| ≤ K|x − x + 0|.
Little-o The statement that f (x) is Little-o
of g(x) at x
0
means that
163
lim
x→x
0
|f (x)|/|g(x)| = 0.
It is written as f (x) = o (g(x)).
Modified Bessel function The Modified Bessel function
is defined as the (improper) integral
I
n
(x) = i
−n
J
n
(x)
=
x
n
2
n
Γ(n + 1)
"
1 +
x
2
2(2n + 2)
+
x
4
2 · 4(2n + 2)(2n + 4)
+ · · ·
#
.
Picard’s method An iteration technique for solving
ordinary differential equations of the type
y
0
= F (x, y) with an initial condition of (x
0
, y
0
)
such that y
1
(x) =
Z
x
x
0
F (t, y
0
) dt and y
n
(x) =
Z
x
x
0
F (x, y
n−1
(t)) dt.
Sine integral The sine integral is
defined as the (improper) integral
Si(x) =
Z
x
0
sin(t)
t
dt.
Singular solution A solution to a differential equation
which cannot be obtained from any solution formula containing
an arbitrary constant. (Viz., the Clairaux equation
(y
0
)
2
− xy
0
+ y = 0 and its corresponding singular solution
y = x
2
/4. The general solution is y = cx − c
2
.)
Taylor series Let f (x) be defined on
(a, b) = { x | a < x < b } and x
0
∈ (a, b).
If f
(n)
(x
0
) exists for each n ≥ 0 then
the series
f (x
0
) + f
0
(x
0
)(x − x
0
) +
1
2
f
00
(x
0
)(x − x
0
)
2
+ . . .
164

+
f
(n)
(x
0
)
n!
(x − x
0
)
n
+ . . .
≡
∞
X
n=0
f
(n)
(x
0
)
n!
(x − x
0
)
n
,
where
f
(0)
(x) := f (x)
∀ x ∈ (a, b)
is called the Taylor series of f (x) at x
0
. Convergence
of the series to f (x) depends on regularity conditions.
Uniform continuity The statement that f (x)
is uniformly continuous on the finite number interval
[a, b] means that if > 0 there exists a
δ = δ() > 0 such that if x, y ∈ [a, b]
and |x − y| < δ then |f (x) − f (y)| < .
Uniform convergence A convergent function series
∞
X
n=1
f
n
(x) is said to converge
uniformly on a number set S if ∀ > 0
∃ N = N (), a positive integer, such that
if n ≥ N then
∞
X
j=1
f
j
(x) −
n
X
j=1
f
j
(x)
< for each x ∈ S.
165

Bibliography
[1] Birkhoff, Garrett and Gian-Carla
Rota, Ordinary Differential Equations.
Boston: Ginn and Company, 1962.
[2] Boyce, William E., and Richard C. DiPrima,
Elementary Differential Equations and Boundary
Value Problems—Third Edition. New York: John
Wiley & Sons, 1977.
[3] Bracewell, Ron,
The Fourier Transform and Its Applications.
New York: McGraw-Hill, Inc., 1965.
[4] Brauer, Fred and John A. Nohel,
Introduction to Differential Equations with
Applications. New York: Harper & Row,
Publishers, 1986.
[5] Bronson, Richard, Schaum’s
Outline Series Theory and Problems of Modern Introductory
Differential Equations with Laplace Transforms, Matrix
Methods, Numerical Methods, Eigenvalue Problems.
New York: McGraw-Hill Book Company, 1973.
166

[6] Copi, Irving M.,
Introduction to Logic.
New York: MacMillan Publishing Co., Inc., 1978.
[7] Hall, Dio L., et al.,
Introduction to the Laplace Transform.
New York: Appleton-Century Crofts, Inc., 1959.
[8] Kaplan, Wilfred,
Elements of Ordinary Differential Equations.
Reading, Massachusetts: Addison-Wesley Publishing Company, Inc.,
1964.
[9] Kreyszig, Erwin,
Advanced Engineering Mathematics—5th ed.
New York: John Wiley & Sons, 1983.
[10] Lloyd, David K. and Myron Lipow,
Reliability: Management, Methods, and
Mathematics. Englewood Cliffs, NJ: Prentice-Hall,
Inc., 1962.
[11] Olmsted, John M. H.,
Advanced Calculus.
New York: Appleton-Century-Crofts, Inc., 1956.
[12] Quinney, Douglas,
An Introduction to the
Numerical Solution of Differential Equations.
Letchworth, Hertfordshire, England:
Research Studies Press, Ltd,
1985.
167

[13] Rabenstein, Albert L.,
Elementary Differential Equations with Linear
Algebra—Second Edition.
New York: Academic Press, 1975.
[14] Rainville, Earl D., and Phillip
E. Bedient, Elementary Differential Equations–Fourth
Edition. New York: The Macmillan Company, 1969.
[15] Ritger, Paul D., and Rose, Nicholas J.,
Differential Equations with Applications.
New York: McGraw-Hill Book Company, 1968.
[16] Sagan, Hans,
Advanced Calculus. Boston: Houghton Mifflin
Company, 1974.
[17] Scheid, Francis, Schaum’s
Outline Series Theory and Problems of Numerical Analysis,
Second Edition.
New York: McGraw-Hill Book Company, 1973.
[18] Spiegel, Murray R.,
Applied Differential Equations—Second Edition.
Englewood Cliffs, N.J.:
Prentice-Hall, Inc., 1967.
[19] Spiegel, Murray R., Schaum’s
Outline Series Theory and Problems of Laplace Transforms.
New York: Schaum Publishing Co., 1965.
[20] Stark, Peter A., Introduction
to Numerical Methods. New York: Macmillan Publishing
Co., Inc., 1970.
168

[21] Thomas, George B., Calculus
and Analytic Geometry—Third Edition.
Reading, Massachusetts:
Addison-Wesley Publishing Company, Inc., 1966
169
Wyszukiwarka
Podobne podstrony:
Complex Numbers and Ordinary Differential Equations 36 pp
Mathematics HL paper 3 series and differential equations 001
Mathematics HL paper 3 series and differential equations
Using Matlab for Solving Differential Equations (jnl article) (1999) WW
Schmitt K , Thompson R C Nonlinear analysis and differential equations and introduction (LN, 1998)(
EARQ Energy Aware Routing for Real Time and Reliable Communication in Wireless Industrial Sensor Net
Complex Numbers and Ordinary Differential Equations 36 pp
Contrasting Clients in Dialectical Behavior Therapy for BPD Marie and Dean , Two Caseswith Diffe
Pinchover Y , Rubinstein J An introduction to partial differential equations Extended solutions for
Prentice Hall Carlson & Johnson Multivariable Mathematics with Maple Linear Algebra, Vector Calcul
CALC1 L 11 12 Differenial Equations
G B Folland Lectures on Partial Differential Equations
Evans L C Introduction To Stochastic Differential Equations
2 grammar and vocabulary for cambridge advanced and proficiency QBWN766O56WP232YJRJWVCMXBEH2RFEASQ2H
Flash on English for Mechanics, Electronics and Technical Assistance
06 User Guide for Artlantis Studio and Artlantis Render Export Add ons
BRAUN recipes for your baby and toddler
więcej podobnych podstron