1

1. WYZACZAIE CIEPŁA WŁAŚCIWEGO c

p

i c

v

DLA POWIETRZA

1.1 Wprowadzenie

Zgodnie z definicją ciepła właściwe c

v

i c

p

dane są wzorami:

)

-

(

1

2

2

1

T

T

m

Q

c

v

v

−

=

(1)

)

-

(

1

2

2

1

T

T

m

Q

c

p

p

−

=

(2)

gdzie : Q

v1-2

, Q

p1-2

– ciepło doprowadzone do układu przy stałej, odpowiednio objętości,

ciśnieniu,

m – masa czynnika termodynamicznego,

T

1

, T

2

– temperatury bezwzględne w stanie 1 i 2.

Wyznaczenie c

v

i c

p

wymaga więc zmierzenia wszystkich wielkości występujących we

wzorach. Metody korzystające z definicji to metody kalorymetryczne. Dają one dokładne

wyniki dla cieczy i ciał stałych.

Dla gazów, tak w zakresie niskich jak i wysokich ciśnień, prowadzą do dużych błędów.

Dlatego do pomiaru c

v

i c

p

gazu o niskim ciśnieniu używa się metody dynamicznej,

wykorzystującej proces ekspansji adiabatycznej.

Równanie adiabaty powietrza o własnościach zbliżonych do gazu doskonałego ma postać:

const

p

k

=

υ

(3)

gdzie wykładnik adiabaty k:

v

p

c

c

k =

(3.1)

Ponadto c

v

i c

p

powiązane są zależnością:

c

p

– c

v

= R

(4)

gdzie R – indywidualna stała gazowa.

Z indywidualną stałą gazową jest związane pojęcie uniwersalnej stałej gazowej, przedsta-
wianej jako iloczyn (MR) = 8, 314 kJ / kmol K, gdzie M – masa molowa badanego gazu.

Ze skojarzenia wzorów (3.1) i (4) wynika:

1

-

k

R

c

v

=

(5.1)

1

-

k

k

R

c

p

=

(5.2)

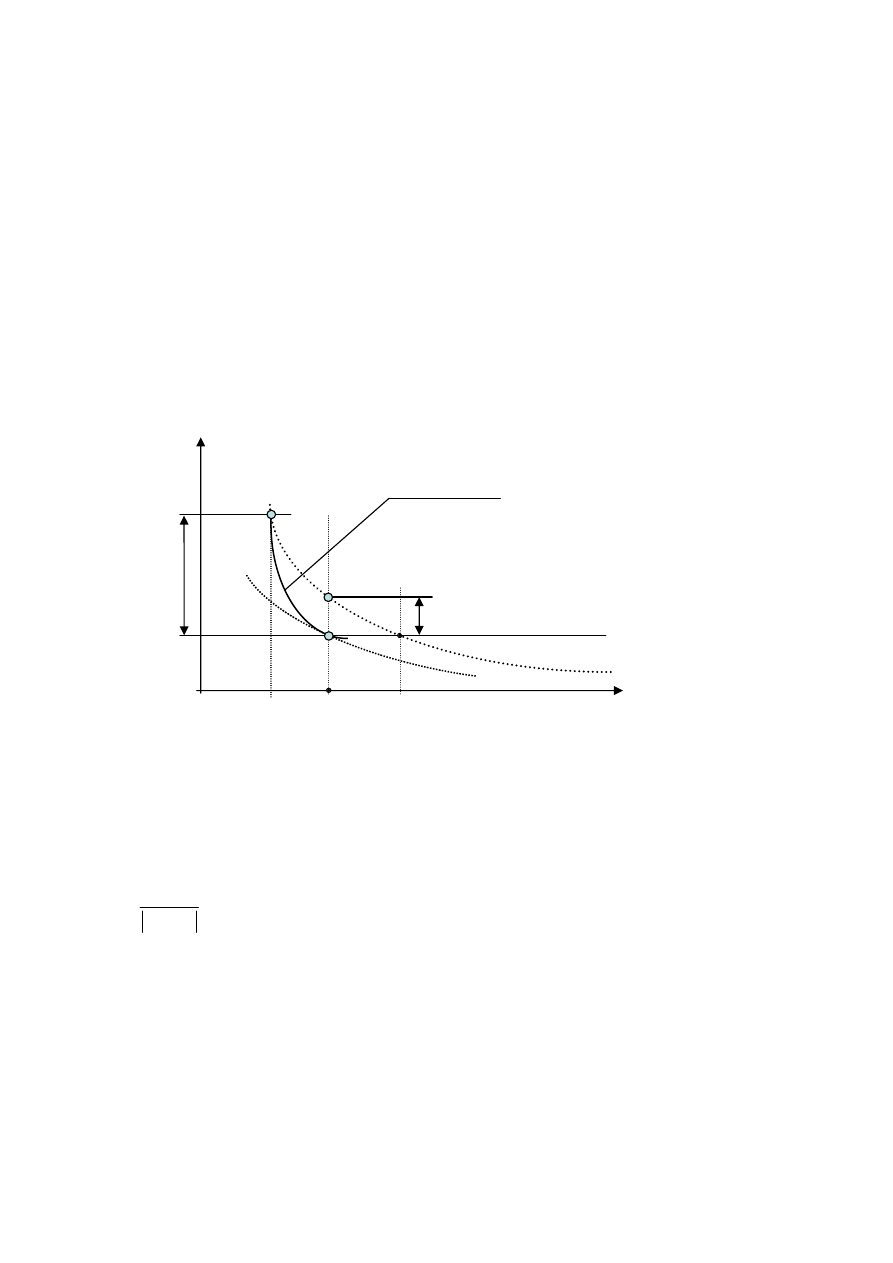
2

1.2 Opis doświadczenia

Zbiornik o stałej objętości napełnia się powietrzem do ciśnienia p

1

> p

o

(p

o

–

ciśnienie otoczenia; p

1

=p

o

+∆p

1

). Temperatura początkowa powietrza t

1

= t

ot

= t

0

. Otwierając

"na moment" zawór łączy się zbiornik z otoczeniem. Następuje szybki wypływ powietrza do

otoczenia. Ciśnienie w zbiorniku spada do wartości p

2

= p

o

, a temperatura osiąga wartość

t

2

< t

0

. Po zamknięciu zaworu należy odczekać, aż temperatura powietrza t

3

zrówna się

z temperaturą otoczenia t

0

, tzn. t

3

= t

0

(a ∆p

3

ustabilizuje się). Wówczas odczytuje się

ciśnienie p

3

> p

o

(p

3

=p

o

+∆p

3

).

Podczas wypływu gazu ze zbiornika z oczywistych względów nieuniknione są dopływy

ciepła, ale można wykazać, że w rozpatrywanym przedziale zmian temperatury i ciśnienia ich

wielkość jest taka, że wskaźnik Y jest mały:

1

2

2

-

1

- U

U

Q

Y

z

=

(6)

gdzie:

• Q

z

l-2

- całkowita ilość ciepła (dodatnia lub ujemna) dostarczona do gazu w czasie ∆τ,

• U

2

– U

1

 - całkowita zmiana energii wewnętrznej gazu przy przejściu od stanu 1 do

stanu 2.

p

1

2

3

υ = V/m

p

o

p

1

p

2

= p

o

T

o

T

2

<T

o

p

3

>p

o

; T

3

=T

o

∆p

1

T

1

=T

0

υ

= const

υ

o

υ

1

p

υ

w

= const

∆p

3

3

Rzeczywista adiabata występuje w przypadku Y = 0. W przeciwnym, wypadku w zależności od

konkretnej wartości tego wskaźnika, mówi się o adiabacie zrealizowanej z dokładnością do

1% , 0,1% itd.

Przyjmując wstępnie Q

z

≠ 0, sugeruje się, że realizowana jest przemiana politropowa

o wykładniku w ≠ k . Znając wartość wykładnika „w” możnaby oszacować wielkość Q

z

.

Opisane doświadczenie daję tę możliwość, albowiem „w” można wyliczyć ze wzoru, w

którym po prawej stronie znaku równości występują tylko wielkości mierzone. Poszukiwaną

wartość wykładnika „w” oblicza się ze wzoru:

)

/

ln(

)

/

ln(

3

1

0

1

i

i

i

i

p

p

p

p

w =

(7)

Doświadczenie należy wykonać dla kilku wartości ciśnienia początkowego:

i

i

p

p

p

1

0

1

∆

+

=

gdzie:

• i – numer pomiaru; przyjmuje wartości od 1 do 5,
• ∆p - nadwyżka ciśnienia z przedziału (0 – 1000 mmH

2

O), np. 800, 650, 500, 350, 200.

1.3 Opracowanie wyników

1.3.1 Dla każdego pomiaru „i” obliczyć wartość „w

i

” a następnie wartość średnią

arytmetyczną:

i

w

w

i

i

sr

∑

=

(8)

1.3.2 Obliczyć c

v

i c

p

z zależności:

1

-

sr

vm

w

R

c

=

(9.1)

1

-

sr

sr

pm

w

w

R

c

=

(9.2)

Te wartości należy porównać z wartościami obliczonymi z wzorów (5.1) i (5.2) dla k=1,4
i wyznaczyć błąd względny pomiaru.

4

Wzór tabel:

Ćw. 1. Wyznaczanie ciepła właściwego c

p

i c

v

dla powietrza

data: ....................................godz.: ................................
Układ pomiarowy 1

lp

wielkość \ i

1

2

3

4

5

1

p

o,

Pa /p

o

, mm H

2

O

2

∆p

1i

, mm H

2

O

800

650

500

350

200

3

p

1i

4

∆p

3i

, mm H

2

O

5

p

3i

6

w

i

7

w

sr

8

c

vm

9

c

pm

10

c

v

11

c

p

12

c

vm

/c

v

13

c

pm

/c

p

Układ pomiarowy 2

lp

wielkość \ i

1

2

3

4

5

1

p

o,

Pa /p

o

, mm H

2

O

2

∆p

1i

, mm H

2

O

800

650

500

350

200

3

p

1i

4

∆p

3i

, mm H

2

O

5

p

3i

6

w

i

7

w

sr

8

c

vm

9

c

pm

10

c

v

11

c

p

12

c

vm

/c

v

13

c

pm

/c

p