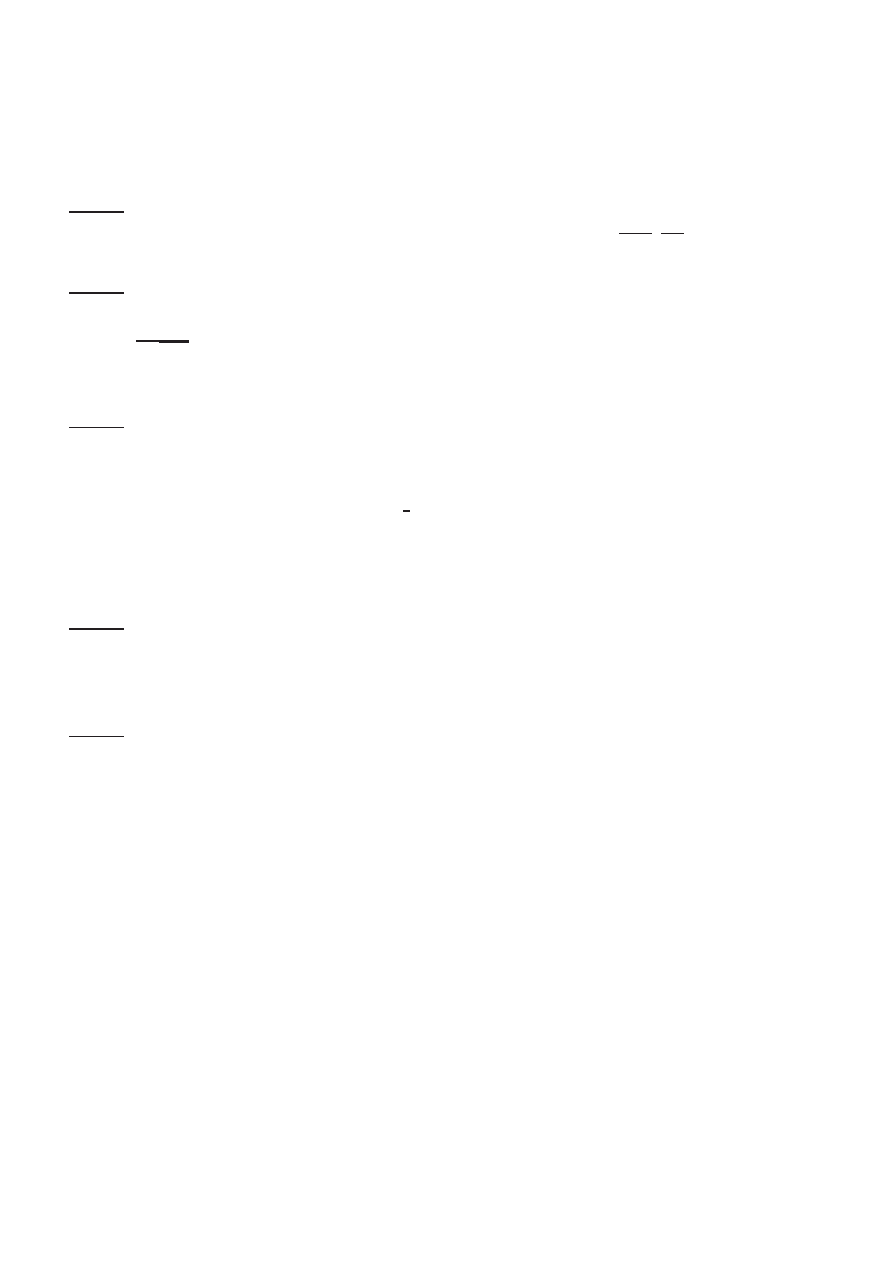
Egzamin pisemny z matematyki

Wydzia l WILi´

S, Budownictwo, sem. 3, r.ak. 2008/2009

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [4p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c kryterium Cauchy’ego zbie˙zno´sci szeregu liczbowego. Zbada´c, czy szereg

∞

P

n

=1

(−1)

n

9

n

+1

(

n

+2
n

)

n

2

jest zbie˙zny.

Zad.T2. [5p — rozwi¸

azanie piszemy na stronie 2 ]

Poda´c twierdzenie Cauchy’ego-Hadamarda o promieniu zbie˙zno´sci szeregu pot¸egowego. Promie´

n zbie˙zno´sci sz-

eregu

∞

P

n

=1

(2x+8)

n

8

n

√

2n+8

jest r´owny R = 4. Narysowa´c przedzia l zbie˙zno´sci tego szeregu, zbada´c zbie˙zno´s´c (i okre´sli´c

jej rodzaj) szeregu w lewym kra´

ncu przedzia lu zbie˙zno´sci.

Zad.T3. [4p — rozwi¸

azanie piszemy na stronie 3 ]

Poda´c w lasno´sci dystrybuanty rozk ladu zmiennej losowej typu ci¸ag lego. Dla jakich warto´sci parametru A

F

(x) =



















0

x

∈ (−∞, 0]

1
2

x

2

x

∈ (0, A]

1

x

∈ (A, +∞)

jest dystrybuant¸a zmiennej losowej typu ci¸ag lego?

Zad.T4. [4p — rozwi¸

azanie piszemy na stronie 3 ]

Zmienna losowa X ma rozk lad N (1, 4). Za pomoc¸a tablic obliczy´c P (−1 < X < 7). Poda´c warto´s´c oczekiwan¸a

i wariancj¸e zmiennej losowej Y = 3X − 4. Jaki rozk lad ma zmienna losowa Y ?

Zad.T5. [3p — rozwi¸

azanie piszemy na stronie 4 ]

Poda´c za lo˙zenia i tez¸e twierdzenia Greena.

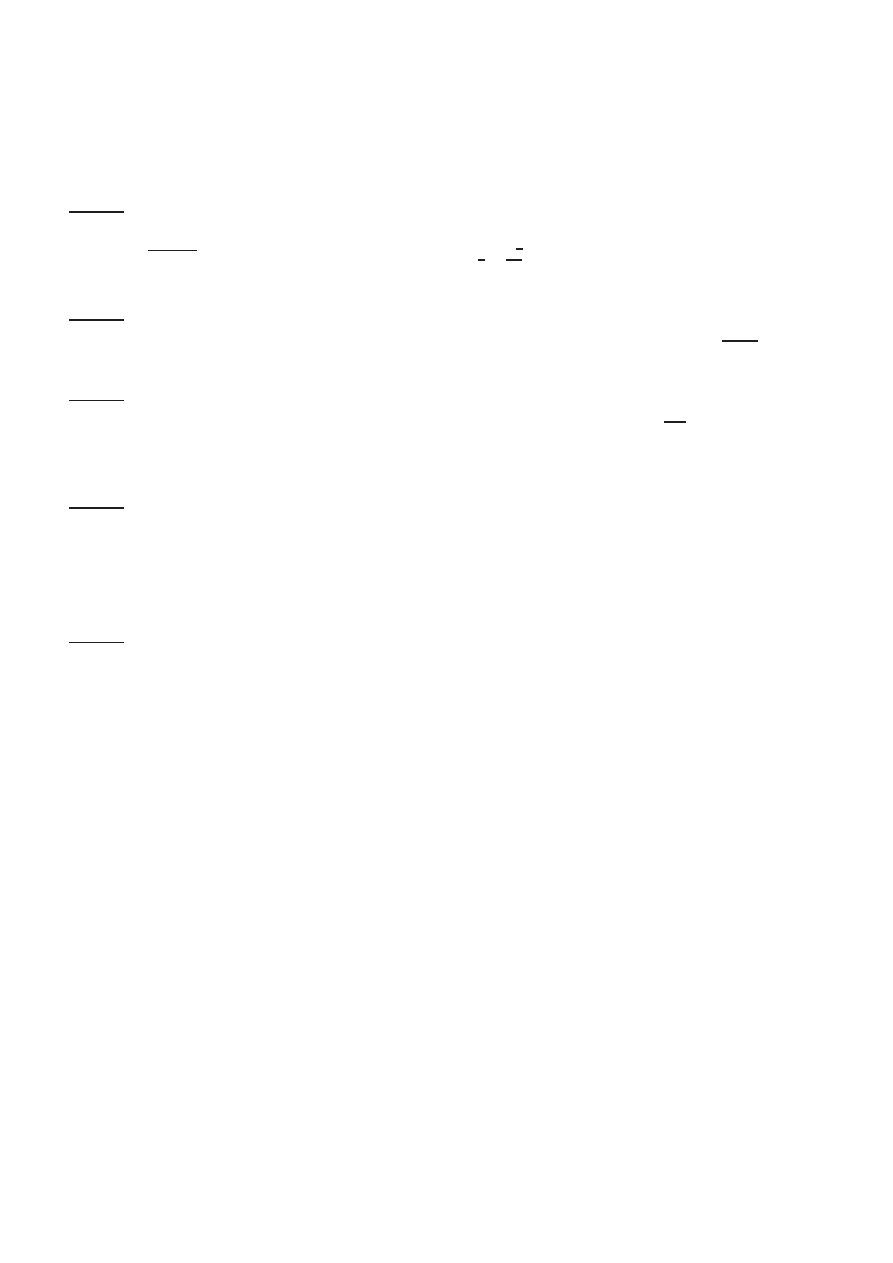
Egzamin pisemny z matematyki

Wydzia l WILi´

S, Budownictwo, sem. 3, r.ak. 2009/2010

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [4p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c definicj¸e pochodnej kierunkowej funkcji, a nast¸epnie korzystaj¸ac z tej definicji obliczy´c pochodn¸a funkcji

f

(x, y) =

px

2

+ y

2

w punkcie (0, 0) w kierunku wektora ~a = [

1
2

,

−

√

3

2

].

Zad.T2. [4p — rozwi¸

azanie piszemy na stronie 2 ]

Korzystaj¸ac z warunku koniecznego zbie˙zno´sci odpowiedniego szeregu liczbowego wykaza´c, ˙ze lim

n→∞

(n−1)!

3n

n

+1

= 0.

Zad.T3. [4p — rozwi¸

azanie piszemy na stronie 3 ]

Poda´c twierdzenie o r´o˙zniczkowaniu szeregu pot¸egowego. Dana jest funkcja f (x) =

∞

P

n

=1

x

n

2

n

n

. Funkcj¸e f

′

(x)

przedstawi´c w postaci szeregu i obliczy´c jego sum¸e.

Zad.T4. [5p — rozwi¸

azanie piszemy na stronie 3 ]

Poda´c trzy w lasno´sci warto´sci oczekiwanej zmiennej losowej. Zmienna losowa X ma rozk lad Bernoulliego z

parametrami n = 10 i p = 0.5. Obliczy´c EX i D

2

X

. Poda´c warto´s´c oczekiwan¸a i wariancj¸e zmiennej losowej

Y

= 1 − 2X.

Zad.T5. [3p — rozwi¸

azanie piszemy na stronie 4 ]

Zmienna losowa X ma rozk lad N (15, 2). Za pomoc¸a tablic obliczy´c P (|X − 13| < 5).

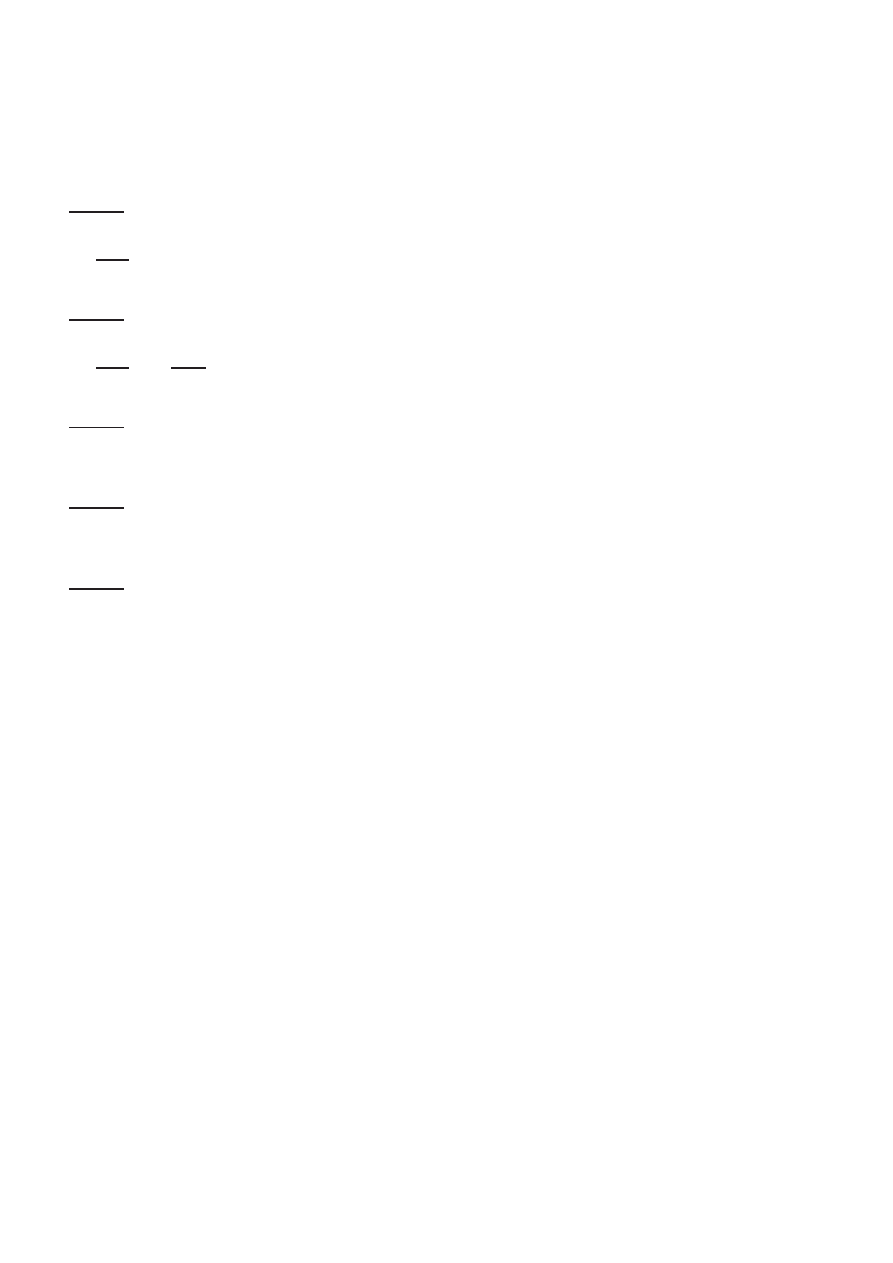
Egzamin pisemny z matematyki

Wydzia l WILi´

S, Budownictwo, sem. 3, r.ak. 2010/2011

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [4p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c twierdzenie Cauchy’ego-Hadamarda o promieniu zbie˙zno´sci. Obliczy´c promie´

n zbie˙zno´sci szeregu

∞

P

n

=1

(−1)

n

n

3

n

(x − 3)

n

.

Zad.T2. [6p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c definicj¸e zbie˙zno´sci bezwzgl¸ednej i warunkowej szeregu liczbowego. Okre´sli´c rodzaj zbie˙zno´sci szereg´ow

∞

P

n

=1

(−1)

n

2n+5

i

∞

P

n

=1

(−1)

n

2n

2

+5

.

Zad.T3. [3p — rozwi¸

azanie piszemy na stronie 2 ]

Poda´c podstawowe w lasno´sci dystrybuanty zmiennej losowej X.

Zad.T4. [3p — rozwi¸

azanie piszemy na stronie 2 ]

Zmienna losowa X ma warto´s´c oczekiwan¸a EX = 2 i wariancj¸e D

2

X

= 1. Obliczy´c EY i σ

Y

, je˙zeli Y = 3X −2.

Zad.T5. [4p — rozwi¸

azanie piszemy na stronie 3 ]

Zmienna losowa X ma rozk lad normalny N (1, 2). Dokona´c standaryzacji zmiennej losowej X. Za pomoc¸a tablic

obliczy´c P (X ≥ 0.5) oraz P (|X| < 2.4).

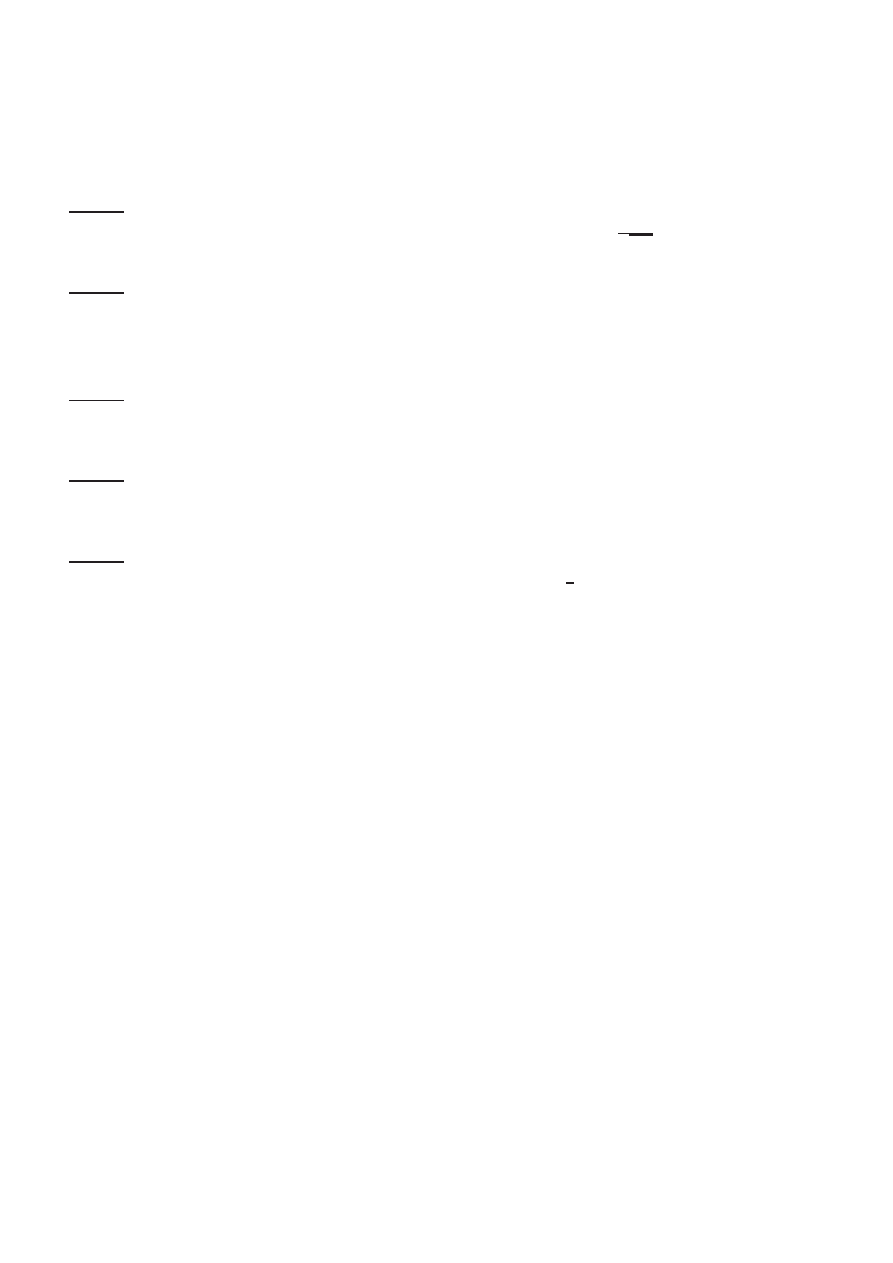
Egzamin poprawkowy z matematyki

Wydzia l WILi´

S, Budownictwo, sem. 3, r.ak. 2010/2011

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [6p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c kryterium Leibnitza. Zbada´c zbie˙zno´s´c (oraz okre´sli´c jej rodzaj) szeregu

∞

P

n

=1

(−1)

n

3

√

n

+1

.

Zad.T2. [4p — rozwi¸

azanie piszemy na stronie 2 ]

Poda´c twierdzenie o r´o˙zniczkowaniu szeregu pot¸egowego. Napisa´c rozwini¸ecie funkcji f

′

(x) w szereg Maclaurina,

je˙zeli f (x) =

∞

P

n

=1

2x

n

.

Zad.T3. [3p — rozwi¸

azanie piszemy na stronie 3 ]

Poda´c definicj¸e potencja lu pola wektorowego.

Zad.T4. [3p — rozwi¸

azanie piszemy na stronie 3 ]

Zmienna losowa X ma rozk lad N (−1, 3). Za pomoc¸a tablic obliczy´c P (−3 < X < 0).

Zad.T5. [4p — rozwi¸

azanie piszemy na stronie 4 ]

Zmienna losowa X ma rozk lad Bernoulliego z parametrami n = 12, p =

1
3

. Obliczy´c warto´s´c oczekiwan¸a i

wariancj¸e zmiennej losowej Y = 2X − 1.

Egzamin poprawkowy z matematyki

Wydzia l WILi´

S, Geodezja i Kartografia, sem. 3, r.ak. 2010/2011

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [4p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c twierdzenie Cauchy’ego-Hadamarda o promieniu zbie˙zno´sci. Obliczy´c promie´

n zbie˙zno´sci szeregu

∞

P

n

=1

(−1)

n

n

3

n

(x − 3)

n

.

Zad.T2. [6p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c definicj¸e zbie˙zno´sci bezwzgl¸ednej i warunkowej szeregu liczbowego. Okre´sli´c rodzaj zbie˙zno´sci szereg´ow

∞

P

n

=1

(−1)

n

2n+5

i

∞

P

n

=1

(−1)

n

2n

2

+5

.

Zad.T3. [3p — rozwi¸

azanie piszemy na stronie 2 ]

Poda´c podstawowe w lasno´sci dystrybuanty zmiennej losowej X.

Zad.T4. [3p — rozwi¸

azanie piszemy na stronie 2 ]

Zmienna losowa X ma rozk lad Poissona z parametrem λ = 3. Za pomoc¸a tablic obliczy´c warto´s´c dystrybuanty

F

(2).

Zad.T5. [4p — rozwi¸

azanie piszemy na stronie 3 ]

Zmienna losowa X ma rozk lad normalny N (0,

√

2). Dokona´c standaryzacji zmiennej losowej X. Za pomoc¸a

tablic obliczy´c P (X ≥

√

2).

Egzamin pisemny z matematyki

Wydzia l WILi´

S, Budownictwo, sem. 3, r.ak. 2011/2012

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [4p — rozwi¸

azanie piszemy na stronie 1 ]

Napisa´c definicj¸e zbie˙zno´sci szeregu liczbowego. Korzystaj¸ac z definicji znale´z´c sum¸e szeregu

∞

P

n

=1

1

n

(n+1)

.

Zad.T2. [3p — rozwi¸

azanie piszemy na stronie 1 ]

Sformu lowa´c kryterium ca lkowe zbie˙zno´sci szeregu. Czy mo˙zna zastosowa´c kryterium ca lkowe do badania

zbie˙zno´sci szeregu

∞

P

n

=1

(−1)

n

n

2

?

Zad.T3. [6p — rozwi¸

azanie piszemy na stronie 2 ]

Poda´c twierdzenie o rozwijaniu funkcji f (x) w szereg Taylora. Rozwin¸a´c f (x) i f

′

(x) w szereg Taylora w otocze-

niu punktu x

0

= 1, je˙zeli f (x) =

1

x

.

Zad.T4. [4p — rozwi¸

azanie piszemy na stronie 2 ]

Zmienna losowa skokowa X ma rozk lad Bernoulliego z parametrami n = 300 i p = 0.01. Obliczy´c EX i D

2

X

.

Za pomoc¸a tablic obliczy´c warto´sc prawdopodobie´

nstwa P (X < 2).

Zad.T5. [3p — rozwi¸

azanie piszemy na stronie 3 ]

Zmienna losowa X ma rozk lad normalny N (3, 1). Dokona´c standaryzacji zmiennej losowej X. Za pomoc¸a tablic

obliczy´c P (−1 ≤ X ≤ 7).

Egzamin pisemny z matematyki

Wydzia l WILi´

S, Budownictwo, sem. 3, r.ak. 2012/2013

Cz¸

e´

s´

c Teoretyczna

Zad.T1. [5p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c kryterium ca lkowe zbie˙zno´sci szeregu. Korzystaj¸ac z tego kryterium wykaza´c zbie˙zno´s´c szeregu

∞

P

n

=1

1

n

2

.

Zad.T2. [4p — rozwi¸

azanie piszemy na stronie 1 ]

Poda´c twierdzenie Greena. Korzystaj¸ac z tego twierdzenia obliczy´c

R

L

(2x + y)dx − (x + 2y)dy,

gdzie luk L jest okr¸egiem zorientowanym ujemnie o r´ownaniu (x − 1)

2

+ (y + 1)

2

= 4.

Zad.T3. [4p — rozwi¸

azanie piszemy na stronie 2 ]

Poda´c definicj¸e punktu wyprostowania krzywej. Czy krzywa, dla kt´

orej dla dowolnego t: ℵ(t) =

e

t

e

t

+1

ma punkty

wyprostowania?

Zad.T4. [3p — rozwi¸

azanie piszemy na stronie 2 ]

Zmienna losowa X ma rozk lad Bernoulliego, gdzie n = 20, p = 0.2. Obliczy´c EX, D

2

X

. Poda´c wz´

or (nie

oblicza´c) na P (X = 2).

Zad.T5. [3p — rozwi¸

azanie piszemy na stronie 3 ]

Zmienna losowa X ma rozk lad N (2, 2). Za pomoc¸a tablic obliczy´c P (−1 < X < 3).