Egzamin z Algebry, 30 I 2009 godz. 12.00

1. Zadanie wstępne

Nr

Zadanie

Odp.

1

Zapisać w postaci kanonicznej (algebraicznej) liczbę zespoloną z = w + u
jeżeli
w = 1 + i

u = cos

π

2

+ i sin

π

2

Rozwiązanie:
u = i
z = 1 + i + i = 1 + 2i

1 + 2i

2

Obliczyć wyznacznik macierzy D

D =











0 1 3 1
1 1 0 0
0 2 2 0
0 1 2 0











Rozwiązanie:

|D| =

0 1 3 1
1 1 0 0
0 2 2 0
0 1 2 0

= 1·(−1)

2+1

1 3 1
2 2 0
1 2 0

= −1·1·(−1)

1+3

2 2
1 2

= −2

Stosujemy rozwinięcia Laplace’a najpierw względem pierwszej kolumny, po-
tem względem trzeciej kolumny.

−2

3

Obliczyć sinus kąta między wektorami ~u i ~v jeżeli
~u = [1, 0, 1] , ~v = [2, 1, 2]
Rozwiązanie:

cos α =

~u · ~v

|~u| · |~u|

=

4

√

2 ·

√

9

=

4

3

√

2

sin α =

√

1 − cos

2

α =

s

1 −

16
18

=

1
3

Uwaga: kąt między dowolnymi wektorami α ∈< 0, π > więc sin α ­ 0

1
3

4

Wyznaczyć wersor normalny płaszczyzny 2x + y + 2z − 3 = 0
Rozwiązanie:
Wektor normalny ~n = [2, 1, 2]

Wersor normalny:

~n

|~n|

=

1

√

9

· [2, 1, 2] =

2
3

,

1
3

,

2
3

Uwaga: Jest jeszcze drugi wersor normalny:

h

−

2
3

, −

1
3

, −

2
3

i

h

2
3

,

1
3

,

2
3

i

5

Obliczyć odległość środka sfery S od płaszczyzny xOy jeżeli
S : x

2

+ y

2

+ z

2

+ 4x − 2z − 10 = 0

Rozwiązanie:
Przekształcamy równanie sfery:
(x + 2)

2

− 4 + y

2

+ (z − 1)

2

− 1 − 10 = 0

(x + 2)

2

+ y

2

+ (z − 1)

2

= 15

Środek sfery jest w punkcie A(−2, 0, 1)
Odległość punktu A od płaszczyzny xOy jest równa d = |z

A

| = 1

1

1

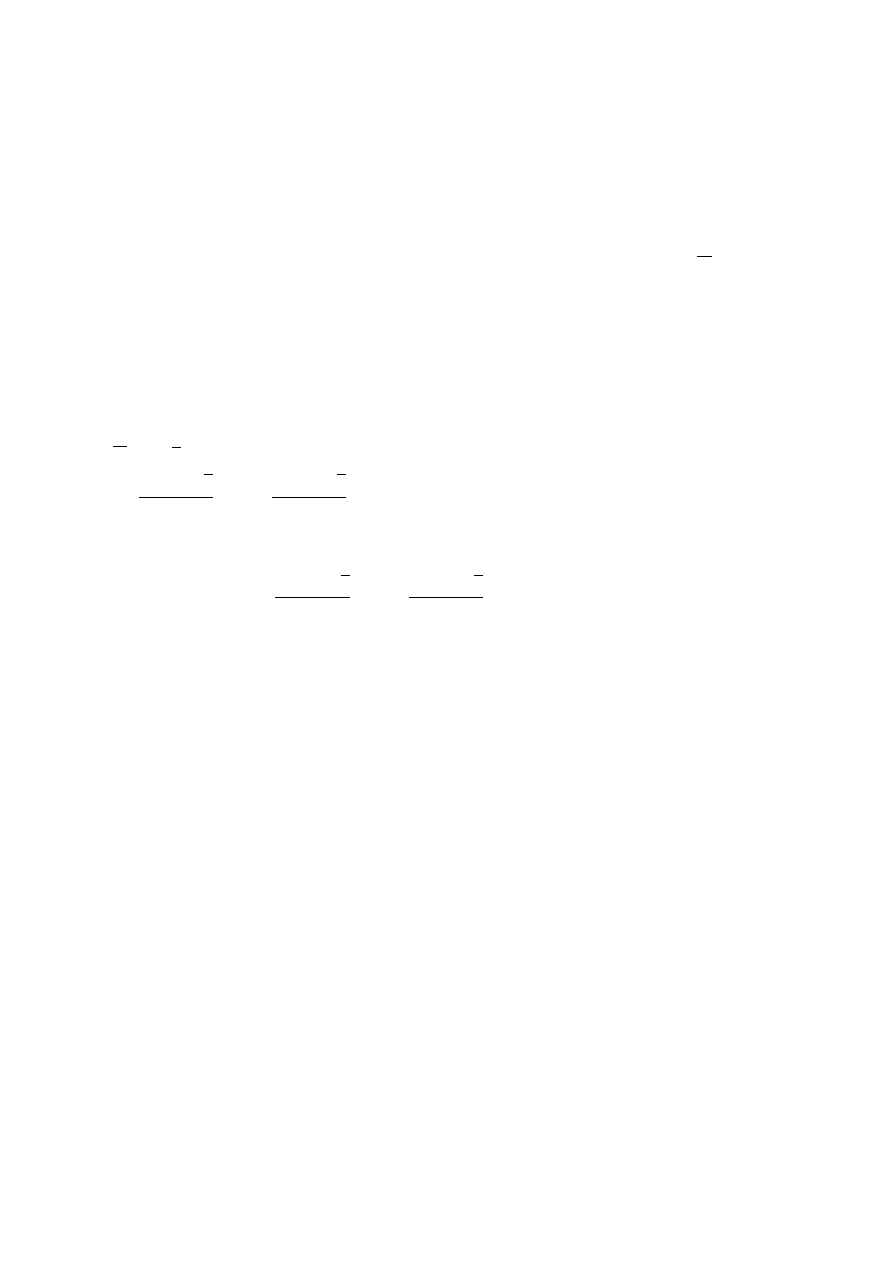
2. Obliczyć W (−i) i następnie znaleźć wszystkie pierwiastki wielomianu:

W (z) = z

4

+ z

3

+ 2z

2

+ z + 1 , z ∈ C

Rozwiązanie:

W (−i) = (−i)

4

+ (−i)

3

+ 2(−i)

2

− i + 1 = 1 + i − 2 − i + 1 = 0

Wynika stąd, że z

1

= −i jest pierwiastkiem W (z) . Ponieważ wielomian ten ma współ-

czynniki rzeczywiste, więc pierwiastkiem tego wielomianu musi też być z

2

= z

1

= i .

Wielomian W dzieli się więc prze: (z + i)(z − i) = z

2

+ 1.

Dzielimy:

z

4

+ z

3

+ 2z

2

+ z + 1 = (z

2

+ 1)(z

2

+ z + 1)

Rozwiązujemy równanie:

z

2

+ z + 1 = 0

∆ = 1 − 4 = −3

√

∆ = i

√

3

z

3

=

−1 − i

√

3

2

, z

4

=

−1 + i

√

3

2

Odpowiedż:

Pierwiastki wielomianu:

z

1

= −i , z

2

= i , z

3

=

−1 − i

√

3

2

, z

4

=

−1 + i

√

3

2

2

3. Znaleźć macierz A spełniającą równanie:







1 2 1
0 1 2
1 0 1







−1

· A = A +







1
0
1







Rozwiązanie:

Oznaczmy

B =







1 2 1
0 1 2
1 0 1







, C =







1
0
1







Wyznacznik |B| = 1 + 4 − 1 = 4 6= 0 wuęc macierz odwrotna B ∗ −1 istnieje. Prze-
kształcamy równanie macierzowe:

B

−1

· A = A + C

mnożymy lewostronnie przez B

B · B

−1

· A = B · A + B · C

B · B

−1

= I

A = B · A + B · C

odejmujemy B · A

A − B · A = B · C

wstawiamy macierz jednostkową I

I · A − B · A = B · C

(I − B) · A = B · C

Obliczamy:

I − B =







0 −2 −1
0

0 −2

−1

0

0







, B · C =







4
2
2







Wiadać, że macierz A ma 3 wiersze i 1 kolumnę:

A =







x

y
z







Powstałe równanie macierzowe możemy traktować jak układ równań. Układ ten roz-
wiązujemy stosując wzory Crammera.

|M| =

0 −2 −1
0

0 −2

−1

0

0

= −4 6= 0

, |M

1

| =

4 −2 −1
4

0 −2

2

0

0

= 8

|M

2

| =

0 4 −1
0 2 −2

−1 2

0

= 4 − 2 = 2

, |M

3

| =

0 −2 4
0

0 2

−1

0 2

= 4

Stąd: z =

|M

1

|

|M|

= −2

, y =

|M

2

|

|M|

= −

1
2

, z =

|M

3

|

|M|

= −1

Odpowiedż:

A =







−2

−

1
2

−1







3

4. Wyznaczyć rozwiązania układu równań w zależności od parametru m ∈ R











mx +

y =

1

x + my =

1

x +

y = m

Rozwiązanie:

Badamy rząd macierzy

A =







m

1

1 m
1

1







i

A

R

=







m

1

1

1 m

1

1

1 m







Zaczynamy od rzędu A

R

W tym celu rozwiązujemy równanie: |A

r

| = 0

|A

R

| = m

3

+ 1 + 1 − m − m − m = m

3

− 3m + 2

m

3

− 3m + 2 = 0

Widać, że wielomian ma pierwiastek wymierny m

1

= 1 . Dzielimy wielomian przez

(m − 1)

m

3

− 3m + 2 = (m − 1)(m

2

+ m − 2)

Rozwiązujemy równanie:

m

2

+ m − 2 = 0

∆ = 9

m

2

= −2 , m

3

= 1

Wniosek:

Dla m 6= −2 ∧ m 6= 1 rząd A

R

jest równy 3. Rząd macierzy A ¬ 2 więc układ jest

sprzeczny.

Dla m = −2 rząd rzA

R

¬ 2

rzA

R

= rz







−2

1

1

1 −2

1

1

1 −2







= 2 , ponieważ

−2

1

1 −2

= 3 6= 0

rzA = rz







−2

1

1 −2
1

1







= 2 , ponieważ

−2

1

1 −2

= 3 6= 0

Układ ma więc jedno rozwiązanie. Szukamy w macierzy A macierzy 2×2 o wyznaczniku
różnym od zera np. pierwsze dwa wiersze. Z układu usuwamy trzecie równanie:

(

−2x +

y = 1

x − 2y = 1

Stosujemy wzory Cramera:

|M| = 3 , |M

1

| =

1

1

1 −2

= −2 − 1 = −3 . |M

2

| =

−2 1

1 1

= −2 − 1 = −3

z =

|M

1

|

|M|

= −1

, y =

|M

2

|

|M|

= −1

Dla m = 1 rząd rzA

R

¬ 2

4

rzA

R

= rz







1 1 1
1 1 1
1 1 1







= rz

h

1 1 1

i

= 1 , ponieważ wiersze są proporcjonalne

rzA = rz







1 1
1 1
1 1







= rz

h

1 1

i

= 1

Układ ma więc nieskończenie wiele rozwiązań zależnych od jednego parametru. Szu-
kamy w macierzy A macierzy 1 × 1 o wyznaczniku różnym od zera. Np. element A

11

.

Usuwamy równania 2 i 3; zmienna y będzie parametrem: y = t. Wtedy układ redukuje
się do jednego równania:

x = 1 − t

Odpowiedź:

Dla m 6= −2 ∧ m 6= 1 układ jest przeczny

Dla m = −2 układ ma jedno rozwiązanie: x = −1 , y = −1

Dla m = 1 układ ma nieskończenie wiele rozwiązań zleżnych od jednego parametru:
x = 1 − t , y = t , t ∈ R

5

5. Znaleźć równanie prostej przechodzącej przez punkt A(1, 0, −1) , równoległej do płasz-

czyzny π : 3x − 2y − 3z + 3 = 0 i przecinającej prostą l :

x − 2

1

=

y − 1

−2

=

z + 2

2

Rozwiązanie:

Konstuujemy płaszczyznę π

1

równoleglą do π i przchodzącą przez punkt A. Szukamy

punktu przecięcia B płaszczyzny π

1

i prostej l. Szukana prosta to prosta AB

π

1

: 3x − 2y − 3z + D = 0

ponieważ π

1

jest równoległa do π

3 + 3 + D = 0

A ∈ π

1

D = −6

π

1

: 3x − 2y − 3z − 6 = 0

Współrzędne punktu B(x, y, z) spełniają układ równań:











3x − 2y − 3z − 6 = 0
y − 1 = −2(x − 2)
y − 1 = −z − 2

B ∈ π

1

∩ l

y = −2x + 5

z = −y − 1 = 2x − 6

3x + 4x − 10 − 6x + 18 − 6 = 0

x = −2 , y = 9 , z = −10

Mamy więc punkt B(−2, 9, −10)

Wektor kierunkowy szukanej prostej:
−→

AB = [−3, 9, −9] k [1, −3, 3]

Odpowiedź:

x − 1

1

=

y

−3

=

z + 1

3

6

6. Znaleźć równanie płaszczyzny przechodzącej przez początek układu współrzędnych i

przez prostą powstałą z przecięcia płaszczyzn x + 3y − z + 1 = 0 oraz 2x + 3z − 10 = 0

Rozwiązanie:

Szukna płaszczyzna π ma równanie:

α(x + 3y − z + 1) + β(2x + 3z − 10) = 0

pęk płaszczyzn

α − 10β = 0

punkt (0, 0, 0) ∈ π

α = 10β

β = 1

możemy wybrać dowolną wartość 6= 0

α = 10

10x + 30y − 10z + 10 + 2x + 3z − 10 = 0

Odpowiedź:

Szukana płaszczyzna:

12x + 30y − 7z = 0

7