Egzamin z ALgebry, 8 IX 2009
1. Zadanie wstępne
Zadanie
Odp.
1. Zapisać w postaci kanonicznej (algebraicznej)
√
2
2
+ i
√
2
2
3
Rozwiązanie:
z =
√
2
2
+ i
√
2
2
,
|z| =
q
1
2
+
1
2
= 1 , arg z =
π
4
z = 1 ·
cos
π
4
+ i sin
π
4
postać trygonometryczna
z
3
= cos
3π
4
+ i sin
3π
4
= −
√
2
2
+ i
√
2
2
−
√
2
2
+ i
√
2
2
2. Obliczyć wyznacznik macierzy C , jeżeli C = A · B , zaś
A =
1 0 0
0 2 0
0 0 3
,
B =
1 2 3
0 1 0
0 0 1
Rozwiązanie:
|C| = |A| · |B|
|A| = 1 · 2 · 3 = 6
,
|B| = 1 · 1 · 1 = 1
macierze trójkątne
|C| = 6
6
3. Dla jakiej wartości parametru p wektor ~v = [p, 2, 3] jest prostopadły do
wektora normalnego płaszczyzny o równaniu: x + y + z + 1 = 0
Rozwiązanie:
~n = [1, 1, 1]
wektor normalny płaszczyzny
~v · ~n = 0
p + 2 + 3 = 0
p = −5
−5
4. Wyznaczyć wersor kierunkowy prostej
l :
(
x − y = 0
x − z + 1 = 0
Rozwiązanie:
x = t =⇒ y = t , z = t + 1
równanie parametryczne
~v = [1, 1, 1]
wektor kierunkowy
±
~v
|~v|
= ±
[1, 1, 1]
√
3
= ±
h
1
√
3
,
1
√
3
,
1
√
3
i
wersor kierunkowy
±
h
1
√
3
,
1
√
3
,
1
√
3
i
5. Wyznaczyć punkt P symetryczny względem początku układu współrzęd-
nych do środka sfery o równaniu: x
2
+ y
2
+ z
2
− 2x − 2y − 2z − 4 = 0
Rozwiązanie:
(x − 1)
2
+ (y − 1)
2
+ (z − 1)
2
= 7
równanie sfery
S(1, 1, 1)
środek sfery
P (−1, −1, −1)
punkt symetryczny do S
(−1, −1, −1)
1
2. Wiedząc, że z
1
= i jest jednym z pierwiastków wielomianu W (z) = z
3
− iz
2
− 2iz − 2
wyznaczyć pozostałe pierwiastki w dziedzinie zespolonej.
Rozwiązanie:
Ponieważ z
1
= i jest peierwiastkiem więc W (z) dzieli się przez wielomian (z − i)
W (z) = (z − i) · (z
2
− 2i)
Uwaga: Współczynniki welomianu W (z) nie są rzeczywiste, więc z
2
= z
1
nie musi być
pierwiastkiem W (z)
z
2
− 2i = 0
z
2
= 2i
z =
√
2i
2i = 2 · (cos
π
2
+ i cos
π
2
)
postać trygonometryczna
z
2
=
√
2 · (cos
π
4
+ i cos
π
4
) =
√
2 · (
√
2
2
+ i
√
2
2
) = 1 + i
z
3
=
√
2 · (cos
5π
4
+ i cos
5π
4
) =
√
2 · (−
√
2
2
− i
√
2
2
) = −1 − i
Odpowiedź:
z
2
= 1 + i , z
3
= −1 − i
2
3. Wyznaczyć wartości parametru p ∈ R , dla których spełniona jest równość
"
1 0
0 1
#
· p +
"
1 2
0 1
#
2
=
"
1 4
0 1
#
Rozwiązanie:
"
1 0
0 1
#
· p +
"
1 2
0 1
#
2
=
"
p + 1
2
0
p + 1
#
2
=
"
p + 1
2
0
p + 1
#
·
"
p + 1
2
0
p + 1
#
=
"
(p + 1)
2
4p + 4
0
(p + 1)
2
#
Rozwiązujemy układ równań:
(p + 1)
2
= 1
4p + 4 = 4
(p + 1)
2
= 1
0 = 0
Z drugiego równania mamy p = 0 . Sprawdzamy, że dla p = 0 spełnione są pozostałe
3 równania.
Odpowiedź:
p = 0
3
4. Obliczyć pole trójkąta wyciętego przez płaszczyzny układu współrzędnych z płaszczy-
zny π , 3x + 2y + 6z − 18 = 0
Rozwiązanie:
Znajdujemy wierzchołki trójkąta.
3x + 2y + 6z − 18 = 0 ,
x = 0 ,
y = 0 =⇒ A(0, 0, 3)
3x + 2y + 6z − 18 = 0 ,
x = 0 ,
z = 0 =⇒ B(0, 9, 0)
3x + 2y + 6z − 18 = 0 ,
y = 0 ,
z = 0 =⇒ C(6, 0, 0)
−→
AB = [0, 9, −3]
,
−→
AC = [6, 0, −3]
wektory rozpinające trójkąt
S =
1
2
|
−→
AB ×
−→
AC|
pole trójkąta
−→
AB ×
−→
AC =
i j
k
0 9 −3
6 0 −3
= −27i − 18j − 54k = [−27, −18, −54]
S =
1
2
[−27, −18, −54]
=
9
2
[3, 2, 6]
=
9
2
√
49 =
63
2
Odpowiedź:
S =
63
2
4
5. Obliczyć kąt między płaszczyzną π
1
: 2x + y + 3z − 2 = 0 oraz płaszczyzną π
2
prze-
chodzącą przez punkt P (1, 0, −2) i rozpiętą na wektorach ~u = [1, 1, −1] i ~v = [0, −2, 3]
Rozwiązanie:
−
→
n
1
= [2, 1, 3]
wektor normalny płaszczyzny π
1
−
→
n
2
= ~u × ~v
wektor normalny płaszczyzny π
2
−
→
n
2
=
i
j
k
1
1 −1
0 −2
3
= 3i − 2k − 2i − 3j = [1, −3, −2]
Kąt między płaszczyznami jest równy kątowi mięczy wektorami normalnymi ( w przy-
padku kąta rozwartego π minus kąt między wketorami)
cos α =
|−
→
n
1
· −
→
n
2
|
|−
→
n
1
| · |−
→
n
2
|
=
|2 − 3 − 6|
√
14 ·
√
14
=
1
2
α =
π
3
Odpowiedź:
α =
π
3
5
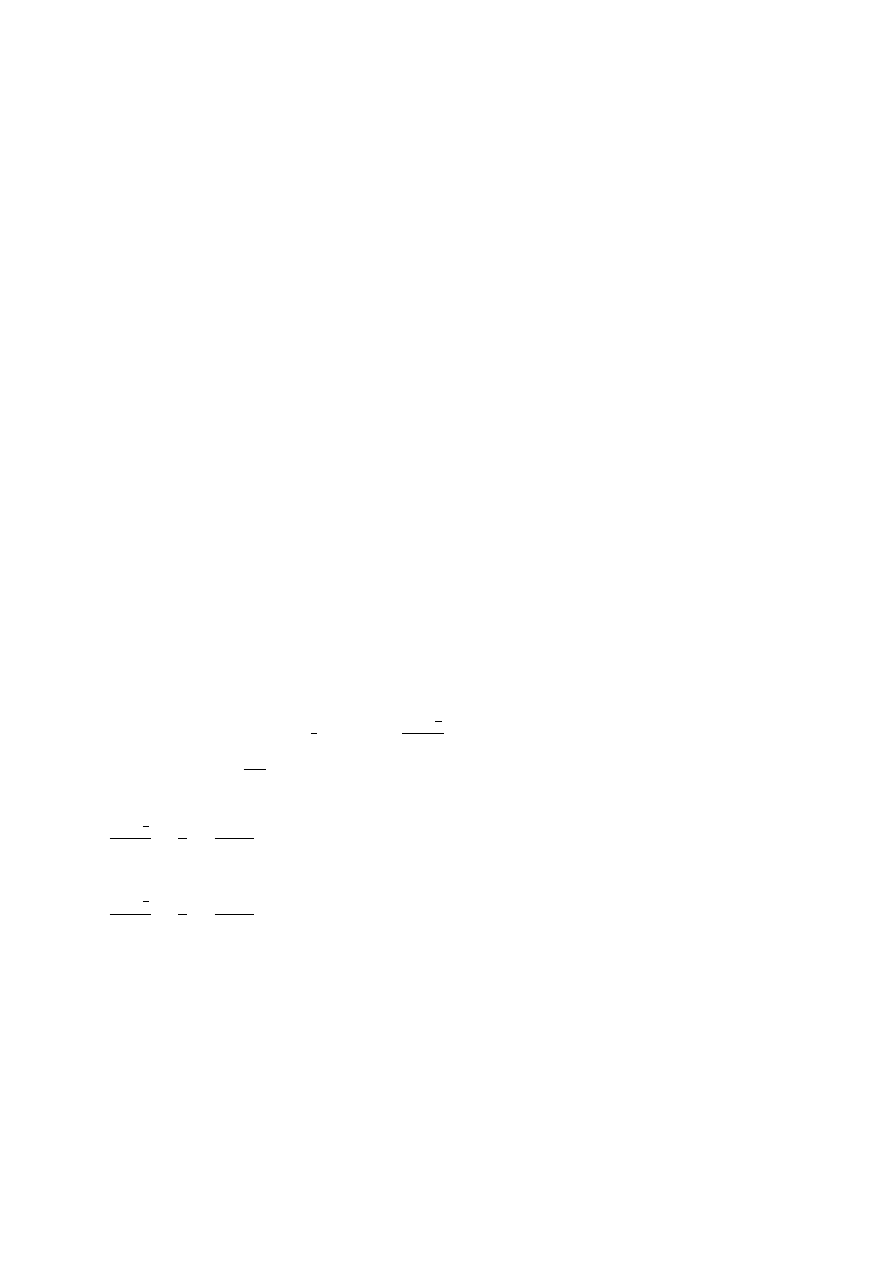
6. Zapisać w postaci kierunkowej równanie rzutu prostej l :
(
x − 4y + 2z − 5 = 0
3x + y − z + 2 = 0
na
płaszczyznę π : 2x + 3y + z − 6 = 0
Rozwiązanie:
Szukamy płasczyzny rzutującej π
1
. Płaszczyzna ta jest wyznaczoma przez warunki:
π
1
⊥ π , l ⊂ π
1
Warunek l ⊂ π
1
oznacza, że π
1
jest jedną z pęku płaszczyzn przechodzących przez
prostą l .
π
1
:
α(x − 4y + 2z − 5) + β(3x + y − z + 2) = 0
równanie pęku płaszczyzn
π
1
:
(α + 3β)x + (−4α + β)y + (2α − β)z − 5α + 2β = 0
−
→
n
1
= [α + 3β , −4α + β , 2α − β]
wektor normalny płaszczyzny π
1
−
→
n = [2, 3, 1]
wektor normalny płaszczyzny π
−
→
n
1
· −
→
n = 0
ponieważ π
1
⊥ π
−8α + 8β = 0
Podstawiamy za β = 1 ( możemy wybrać dowolną wartość β 6= 0 i tak dostaniemy tę
samą płaszczyznę)
wtedy α = 1
π
1
:
4x − 3y + z − 3 = 0
Szukana prosta l
0
jest przecięciem płaszczyzn π i π
1
.
l
0
:
(
2x + 3y + z − 6 = 0
4x − 3y + z − 3 = 0
równanie krawędziowe
Odejmujemy równania. Wtedy
2x − 6y + 3 = 0 =⇒ x = 3y −
3
2
=⇒ y =
x +
3
2
3
z = −9y + 9 =⇒ y =
z−9
−9
Stąd:
l
0
:
x +
3
2
3
=
y
1
=
z − 9
−9
równanie kierunkowe
Odpowiedź:
l
0
:
x +
3
2
3
=
y
1
=
z − 9
−9
6