
7.1
Dane:
Szukane:
Wzory:
20
0, 2
l
cm
m
=
=
10
0,1
D
cm
m
=
=
'
314
/ (
3000
/ min)
rad s n
obr
ω
=
=
0, 4
3
7
0;
;
;
;
;
;
6 4 3 2 4
4
B
T
π π π π
α
π π
=
=
(
)
1
liczba par biegunów p
=
1...7
T
f
e
ω
=
=
=
=
2
1
sin
m
m
f
T
f
E
Blv
e
E
ω
π
α
=
=
=
=
'
1 314
50
2
2
1
1
0, 02
50
'
3 314
314
/
2
2
2
2
2
2
2
2
2
2
0,1
2 0, 4 0, 2 314
2, 51
2
m
m
p
f
Hz
T
s
f
p
rad s
r
D
D
E
Blv
B l
B l
fr
B l
f
B l
T
E
V
ω
π
π
ω
ω
π
π
π
ω
⋅
=
=
=
=
=
=
=
= ⋅
=
= ⋅
= ⋅ ⋅ ⋅
= ⋅ ⋅ ⋅
= ⋅ ⋅ ⋅
⋅ = ⋅ ⋅ ⋅ ⋅
= ⋅
⋅
⋅
⋅
≈
1
2
3
4
5
6
sin
2, 51 sin 0
0
sin
2, 51 sin 30
2, 51 0, 5 1, 26
6
sin
2, 51 sin 45
2, 51 0, 707
1, 77
4
sin
2, 51 sin 60
2, 51 0,866
2,17
3
sin
2, 51 sin 90
2, 51 1
2, 51
2
3
sin
2, 51 sin135
2,
4
o
m
o
m
o
m
o
m
o
m
o
m
e
E
V
e
E
V
e
E
V
e
E
V
e
E
V
e
E
α
π
π
π
π
π
=
=
⋅
=
=
=
⋅
=
⋅
=
=
=
⋅
=
⋅
=
=
=
⋅
=
⋅
=
=
=
⋅
=
⋅ =
=
=
⋅
=
7
51 sin(180
45 )
2, 51 sin 45
2, 51 0, 707
1, 77
7
sin
2, 51 sin 315
2, 51 sin(360
45 )
2, 51 ( sin 45 )
2, 51 0, 707
1, 77
4
o
o
o
o
o
o
o
m
V
e
E
V
π
⋅
−
=
⋅
=
⋅
=
=
=
⋅
=
⋅
−
=
⋅ −
= −
⋅
= −
______________________________________________________________________
7.2
Dane:
Szukane:
Wzory:
500
f
Hz
=
T
=
1
T
f
=
1
1
0, 002
500
T
s
f
=
=
=

______________________________________________________________________
7.3
Dane:
Szukane:
Wzory:
0, 004
T
s
=
f
=
1
T
f
=
2 f
ω
π
=
1
1
250
0, 004
f
Hz
T
= =
=
2
6, 28 250 1570
/
f
rad s
ω
π
=
=
⋅
=
______________________________________________________________________
7.4
Dane:
Szukane:
Wzory:
50
f
Hz
=
T
ω
λ
=
=
=
1
T
f
=
2 f
c
f
ω
π
λ
=
=
1
1
250
0, 004
f
Hz
T
= =
=
2
6, 28 250 1570
/
f
rad s
ω
π
=
=
⋅
=
8
6
3 10
6 10
6000
50
c
m
km
f
λ
⋅
=
=
= ⋅
=
______________________________________________________________________
7.5
Dane:
Szukane:
Wzory:
3
1
3
2
6
3
227
227 10
818
227 10
67, 94
67, 94 10
f
kHz
Hz
f
kHz
Hz
f
MHz
Hz
=
=
⋅
=
=
⋅
=
=
⋅
T
λ
=
=
1
T
f
=
c
f
λ
=

6
1
3
1
8
1
3
1
6
2
3
2
8
2
3
2
9
3
6
3
8
3
6
3
1
1
4, 4 10
4, 4
227 10
3 10
1322
227 10
1
1
1, 222 10
1, 222
818 10
3 10
367
818 10
1
1
14, 72 10
14, 72
67, 94 10
3 10
4, 42
67, 94 10
T
s
s
f
c
m
f
T
s
s
f
c
m
f
T
s
ns
f
c
m
f
µ
λ
µ
λ
λ
−
−
−
=
=
=
⋅
=
⋅
⋅
=
=
=
⋅
=
=
=
⋅
=
⋅
⋅
=
=
=
⋅
=
=
=
⋅
=
⋅
⋅
=
=
=
⋅
______________________________________________________________________
7.6
Dane:
Szukane:
Wzory:
1 m
λ
=
f
=
c
f
λ
=
8
8
3 10
3 10
300
1
c
f
Hz
MHz
λ
⋅
= =
= ⋅
=
______________________________________________________________________
7.7
Dane:
Szukane:
Wzory:
50
f
Hz
=
ω
=
2 f
ω
π
=
2
6, 28 50
314
/
f
rad s
ω
π
=
=
⋅
=
______________________________________________________________________
7.8
Dane:
Szukane:
Wzory:
50
'
20, 9
/ (
200
/ min)
f
Hz
rad s n
obr
ω
=
=
=
p
=
'
2
p
f
ω
π
=

2
6, 28 50
15
'
20, 9
f
p
π
ω
⋅
=
=
=
______________________________________________________________________
7.9
Dane:
Szukane:
Wzory:
2
'
52, 3
/ (
500
/ min)
p
rad s n
obr
ω
=
=
=
f
=
'
2
p
f
ω
π
=
'
2 52, 3
16, 66
2
6, 28
p
f
Hz
ω
π
⋅
=
=
=
______________________________________________________________________
7.10
Dane:
Szukane:
Wzory:
1
2
3
4
2
3
4
5
50
p
p
p
p
f
Hz
=
=
=
=
=
1...4
'
ω
=
'
2
p
f
ω
π
=
1
1
2
2
3
3
4
3
2
6, 28 50
'
157
/
2
2
6, 28 50
'
104, 7
/
3
2
6, 28 50
'
78, 5
/
4
2
6, 28 50
'
62,8
/
5
f
rad s
p
f
rad s
p
f
rad s
p
f
rad s
p
π
ω
π
ω
π
ω
π
ω
⋅
=
=
=
⋅
=
=
=
⋅
=
=
=
⋅
=
=
=
______________________________________________________________________
7.11
Dane:
Szukane:
Wzory:
t
t
e
i
=
=
2
f
ω
π
=

310 sin
2 sin(
)
4
0, 005
50
u
t
i
t
t
s
f
Hz
ω
π
ω
=
=
−
=
=
(
)
2
360
360
50 0, 005 360
90
2
2
310 sin
310 sin
310 sin 90
310
8 50 0, 005 1
4
4 2
4 360
360
360
360
0,125 360
45
2
4 2
4 2
8
2 sin
2 sin
2 sin 45
1, 41
4
lub
o
o
o
o
o
t
o
o
o
o
o
o
o
t
t
ft
u
t
V
t
t
ft
i
t
A
i
ω
π
α
π
π
ω
α
π
ω
π
ω π
π
π
α
π
π
π
π
π
ω
α
=
⋅
=
⋅
=
⋅
⋅
=
=
=
=
=
−
⋅ ⋅
−
−
⋅
−
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
=
⋅
⋅
=
−
=
=
=
2 sin
2 cos
2 cos 45
1, 41
4
4
o
t
t
A
π
π
ω
=
−
=
=
=
______________________________________________________________________
7.12
Dane:
Szukane:
Wzory:
6
500
f
Hz
π
ϕ
=
=
t
=
2
f
ω
π
=
4
2
2
1
6
1, 667 10
166, 7
2
2
12 500
t
T
tf
t
s
s
f
f
ϕ
π
ϕ
π
π
ϕ
µ
π
π
−
=
=
=
=
=
=
⋅
=
⋅
______________________________________________________________________
7.13
Dane:
Szukane:
Wzory:

5
300
3 10
50
l
km
m
f
Hz
=
= ⋅
=
t
T
ϕ
=
=
2
f
ω
π
=
c
f
λ
=
8
6
3 10
6 10
50
c
m
f
λ
⋅
=
=
= ⋅
W ten sposób
lub troszkę inaczej
5
6
360
3 10
360
360
18
6 10
18
1
360
360
20
o
o
o
o
o
o
o
l
l
t
T
ϕ
λ
ϕ
λ
ϕ
=
⋅
=
=
=
⋅
=
=
=
5
6
2
3 10
2
2
6 10
10
2
360
360
360
10
18
2
2
1
1
2
10
1
2
10 2
20
o
o
o
o
l
l
t
f
T
f
ϕ
π λ
π
ϕ
π
π
λ
ϕ
α
π
π
ϕ
α
π
π
ϕ
π
π
π
=
⋅
=
=
=
⋅
=
⋅
⋅
=
=
=
=
=
=
=
⋅
______________________________________________________________________
7.14
Dane:
Szukane:
Wzory:
1
2
3
10 sin(
) [ ]
4
10 sin(
) [ ]
2
5sin
[ ]
i
t
A
i
t
A
i
t A
π
ω
π
ω
ω
=
+
=
+
=
i
=
sin(
)
i
I
t
ω ϕ
=
+
c
f
λ
=
1
2
3
4 360
45
2
2 360
90
2
0
360
0
2
o
o
o
o
o
o
π
ϕ
π
π
ϕ
π
ϕ
π
=
⋅
=
=
⋅
=
=
⋅
=
1
2
3
i
i
i
i
= + +
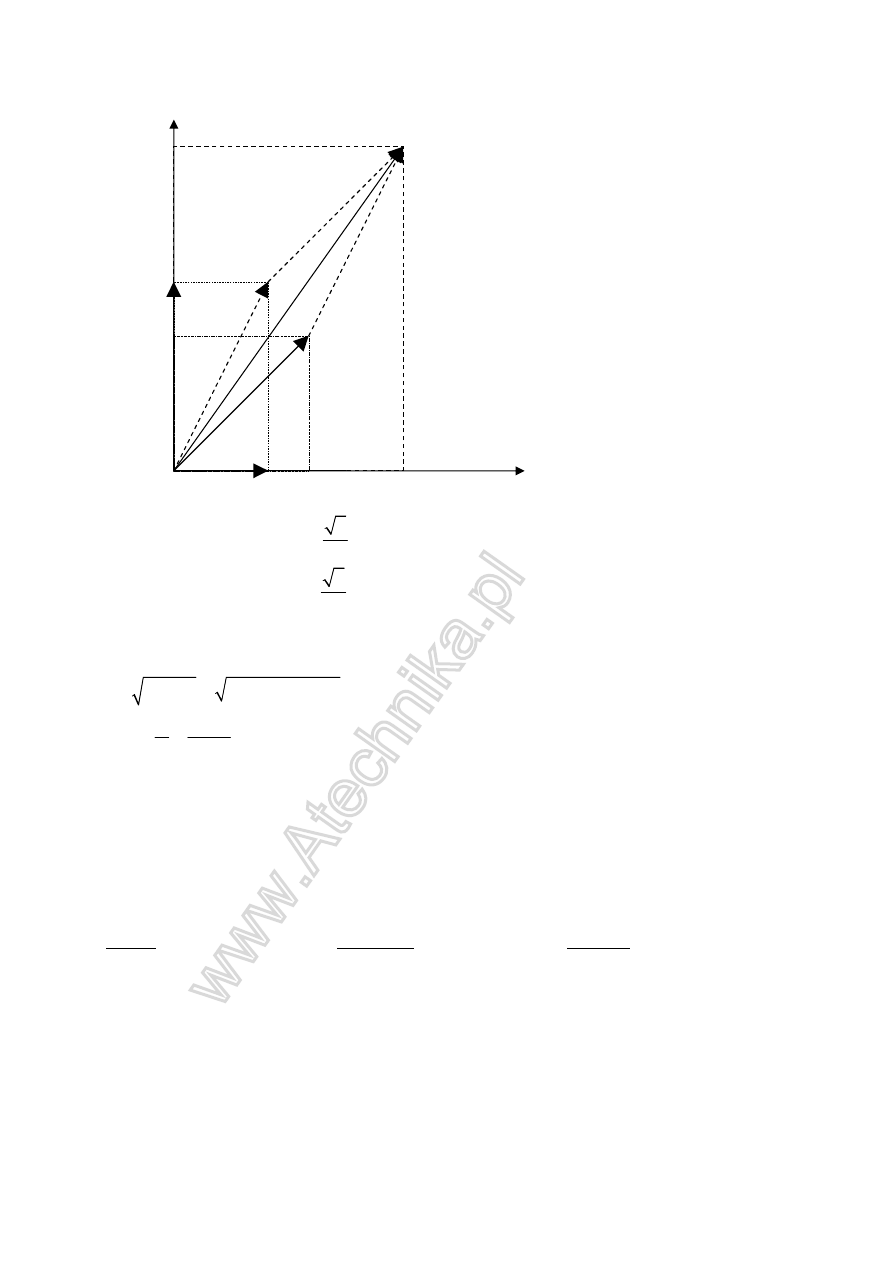
1
1
1
1
1
1
1
2
3
1
2
2
2
2
2
2
cos
10 cos 45
10
10 0, 707
7, 07
2
2
sin
10 cos 45
10
10 0, 707
7, 07
2
7, 07 0 5 12, 07
7, 07 10 0 17, 07
12, 07
17, 07
20, 91
17, 07
tg
1, 4142
12, 07
5
o
x
o
y
x
x
x
x
y
y
y
xy
x
y
y
x
i
I
A
i
I
A
i
i
i
i
A
i
i
i
i
A
i
i
i
A
i
i
ϕ
ϕ
α
α
=
=
=
= ⋅
=
=
=
=
= ⋅
=
= + +
=
+ + =
= +
+ =
+ + =
=
+
=
+
=
= =
=
=
4 44 '
20, 91sin(
54 44 ')
o
o
i
t
ω
=
+
______________________________________________________________________
7.15
Dane:
Szukane:
Wzory:
1
2
0
0
0
0
0
200
50
0
2
0 ; 60 ; 90 ; 120 ; 180
m
m
U
U
V
f
Hz
od
do
π
α
=
=
=
=
m
U
=
sin(
)
m
u
U
t
ω ϕ
=
+
Odświeżyć wzory
trygonometryczne i związki
pomiędzy kątami
1sposób
y
x
i
1
i
2
i
3
i
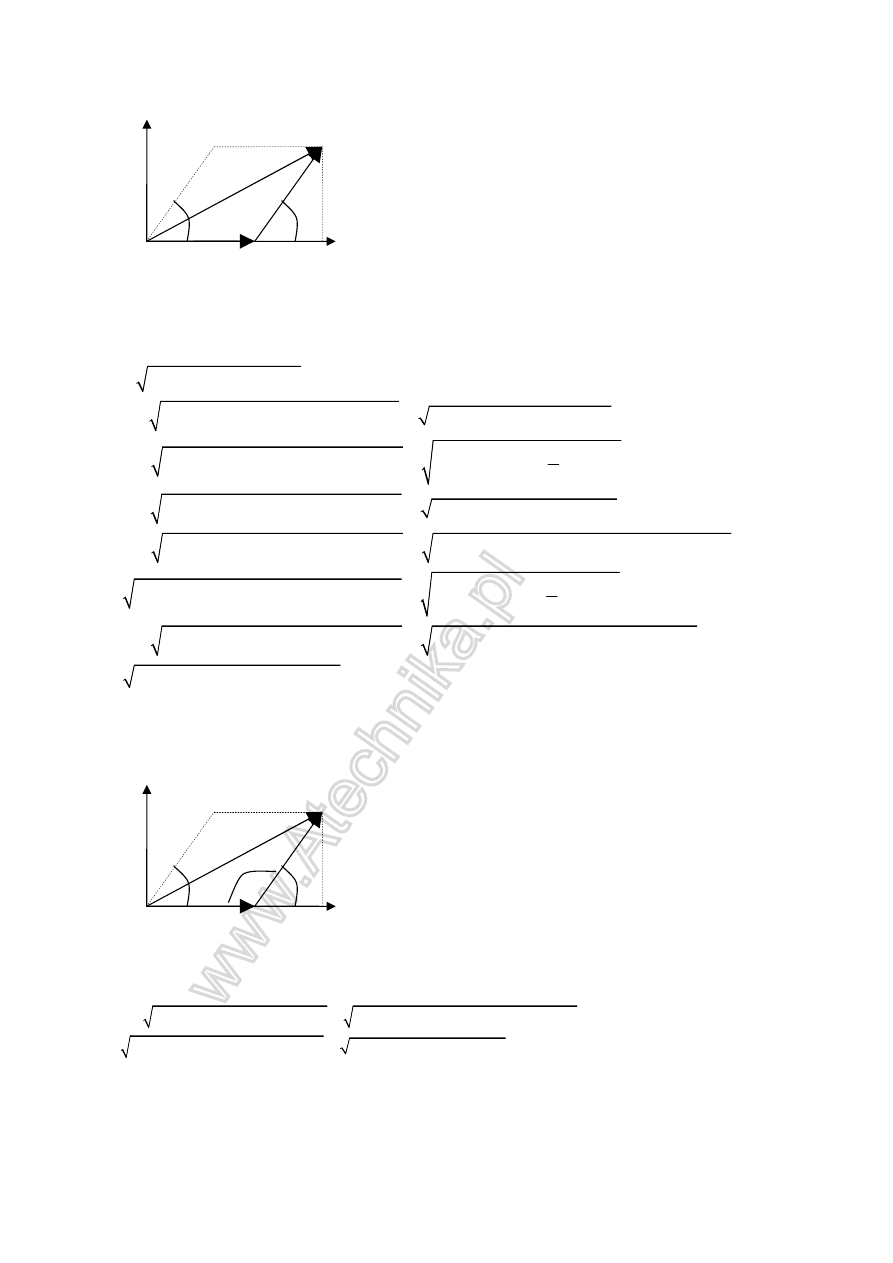
Teraz dodawanie wektorów jak na geometrii.
( )
(
)
( )
2
2
2
2
2
2
2
2
1
2
2
1
1 2
2
2
2
2
2
2
2
2
1
1 2
2
1
1 2
2
2
2
1
1 2
2
2
2
1
1
1
2
1
2
2
2
1
1
2
2
(
cos )
(
sin )
2
cos
cos
sin
2
cos
(cos
sin
)
2
cos
1
2
cos
2
cos
40000 80000 1 40000
400
2
cos
m
m
m
m
m
m
m
m
m
u
u
u
u
u
u u
u
u
u
u u
u
u
u u
u
u
u
u u
u
u
U
U U
U
V
u
U
U U
α
α
α
α
α
α
α
α
α
α
α
α
=
+
+
=
+
+
+
=
=
+
+
+
=
+
+
⋅
=
+
+
=
+
+
=
+
⋅ +
=
=
+
(
)
( )
(
)
( )
(
)
( )
(
)
( )
(
)
2
2
2
2
3
1
1
2
3
2
2
2
2
2
0
0
4
1
1
2
4
2
1
1
2
2
2
2
0
1
1
2
2
5
1
40000 80000
40000
346, 4
2
2
cos
40000 80000 0 40000
282,8
2
cos
2
cos(90
30 )
1
2
( sin 30 )
40000 80000
40000
200
2
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
U
V
u
U
U U
U
V
u
U
U U
U
U
U U
U
U
U U
U
V
u
α
α
+
=
+
⋅ +
=
=
+
+
=
+
⋅ +
=
=
+
+
=
+
+
+
=
=
+
−
+
=
−
⋅ +
=
=
( )
(
)
( )
( )
2
2
2
2
0
1
1
2
5
2
1
1
2
2
2
cos
2
cos(180 )
40000 80000 ( 1) 40000
0
m
m
m
m
m
m
m
m
U
U U
U
U
U U
U
V
α
+
+
=
+
+
=
=
+
⋅ − +
=
2sposób
Dodawanie wektorów z wykorzystaniem Twierdzenia Cosinusów
2
2
2
2
cos
a
b
c
bc
α
= + −
0
180
β
α
=
−
2
2
2
1
1 2
2
cos
u
u
u
u u
β
=
+ −
2
2
2
2
0
1
1
2
1
2
1
2
1
2
2
2
1
2
1
2
2
cos
2
cos(180
)
2
( cos )
40000 40000 80000 1
400
m
m
m
m
m
m
m
m
m
m
m
m
m
u
U
U
U U
U
U
U U
U
U
U U
V
β
α
α
=
+
−
=
+
−
−
=
=
+
−
−
=
+
+
⋅ =
y
x
u
2
u
1
u
α
α
β
y
x
u
2
u
1
u
α
α
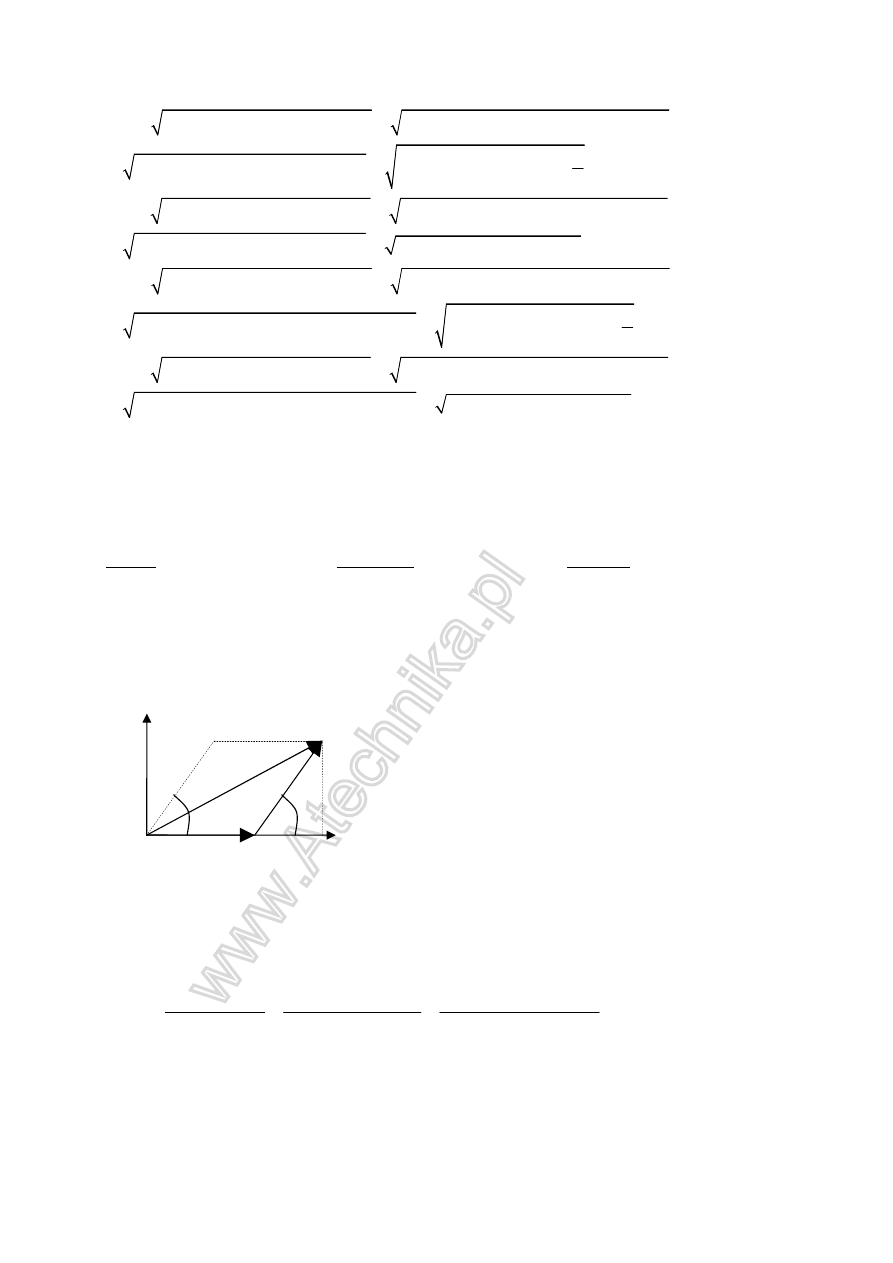
2
2
2
2
0
2
1
2
1
2
2
1
2
1
2
2
2
2
1
2
1
2
2
2
2
2
2
0
3
1
2
1
2
3
1
2
1
2
3
2
2
1
2
1
2
3
2
cos
2
cos(180
)
1
2
( cos
)
40000 40000 80000
346, 4
2
2
cos
2
cos(180
)
2
( cos
)
40000
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
u
U
U
U U
U
U
U U
U
U
U U
V
u
U
U
U U
U
U
U U
U
U
U U
β
α
α
β
α
α
=
+
−
=
+
−
−
=
=
+
−
−
=
+
+
⋅ =
=
+
−
=
+
−
−
=
=
+
−
−
=
2
2
2
2
0
4
1
2
1
2
4
1
2
1
2
4
2
2
0
0
1
2
1
2
2
2
2
2
0
5
1
2
1
2
5
1
2
1
2
5
2
1
40000 80000 0
282,8
2
cos
2
cos(180
)
1
2
cos(180
120 )
40000 40000 80000
200
2
2
cos
2
cos(180
)
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
m
V
u
U
U
U U
U
U
U U
U
U
U U
V
u
U
U
U U
U
U
U U
U
U
β
α
β
α
+
+
⋅ =
=
+
−
=
+
−
−
=
=
+
−
−
=
+
−
⋅ =
=
+
−
=
+
−
−
=
=
+
2
0
0
2
1
2
2
cos(180
180 )
40000 40000 80000 0
0
m
m
m
U U
V
−
−
=
+
−
⋅ =
______________________________________________________________________
7.16
Dane:
Szukane:
Wzory:
1
2
200
50
220
m
m
m
U
U
V
f
Hz
u
V
=
=
=
=
α
=
sin(
)
m
u
U
t
ω ϕ
=
+
Odświeżyć wzory
trygonometryczne i związki
pomiędzy kątami
1sposób
Teraz dodawanie wektorów jak na geometrii.
2
2
2
2
2
2
2
2
1
2
2
1
1 2
2
2
2
2
2
2
2
2
1
1 2
2
1
1 2
2
2
2
2
1
1 2
2
2
2
2
2
2
2
1
2
1 2
(
cos )
(
sin )
2
cos
cos
sin
2
cos
(cos
sin
)
2
cos
1
2
cos
220
200
200
48400 40000 4000
cos
0
2
2 200 200
80000
m
m
u
u
u
u
u
u u
u
u
u
u u
u
u
u u
u
u
u
u u
u
u
u
u
u u
α
α
α
α
α
α
α
α
α
α
α
=
+
+
=
+
+
+
=
=
+
+
+
=
+
+
⋅
=
+
+
−
−
−
−
−
−
=
=
=
= −
⋅
⋅
, 395
Cosinus przyjmuje wartość ujemną w II i III ćwiartce
0
0
0
0
cos
cos(180
)
66 14 '
180
113 46 '
α
ϕ
α
ϕ
α
−
=
−
=
=
− =
lub
y
x
u
2
u
1
u
α
α
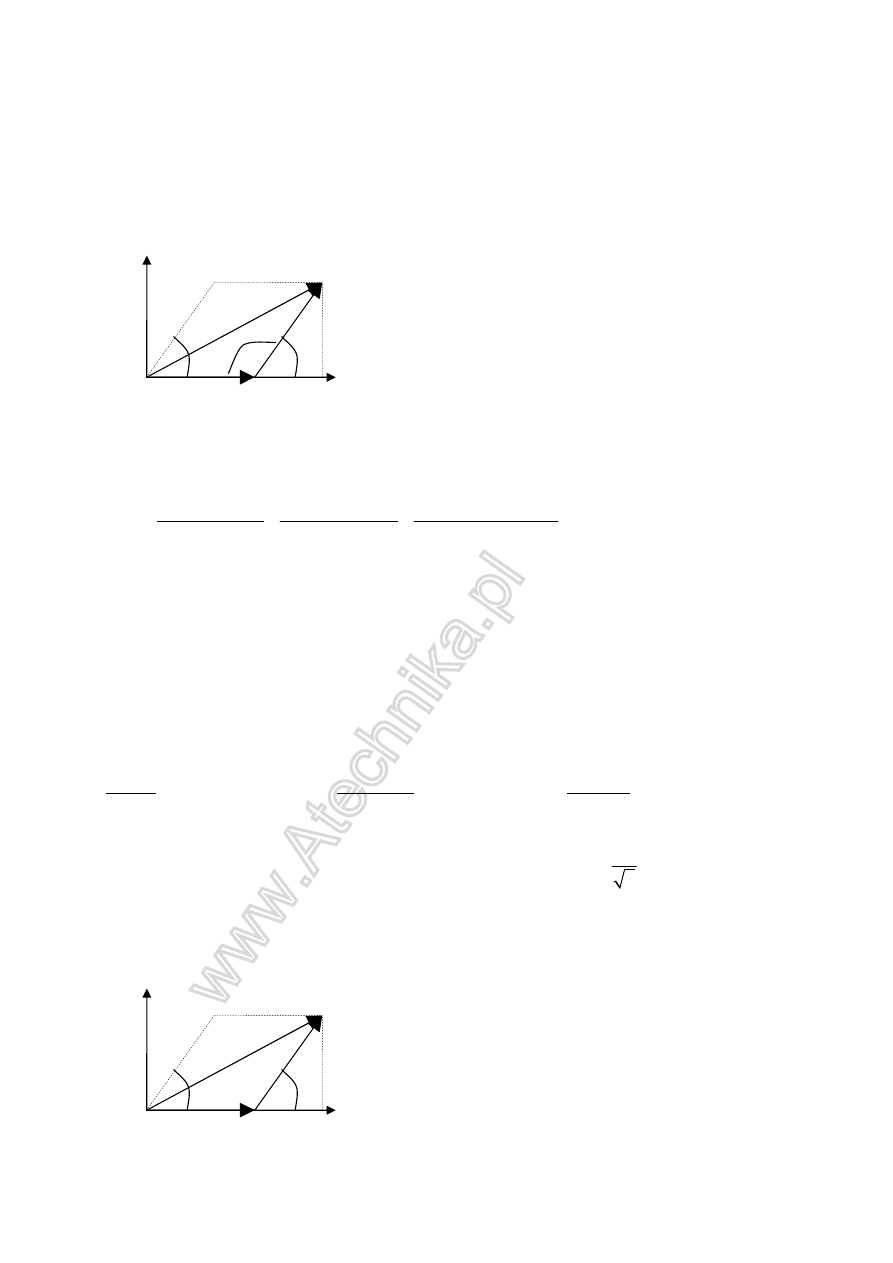
0
0
0
0
cos
cos(180
)
66 14 '
180
226 14 '
α
ϕ
α
ϕ
α
−
=
+
=
=
+ =
2sposób
Dodawanie wektorów z wykorzystaniem Twierdzenia Cosinusów
2
2
2
2
cos
a
b
c
bc
α
= + −
0
180
β
α
=
−
2
2
2
1
1 2
2
cos
u
u
u
u u
β
=
+ −
2
2
2
1
2
1
2
2
2
2
2
2
2
1
2
1
2
2
cos
220
200
200
48400 40000 40000
cos
0,395
2
2 200 200
80000
m
m
m
m
m
m
m
m
m
m
u
U
U
U U
u
U
U
U U
β
β
=
+
−
−
−
−
−
−
−
=
=
=
=
−
− ⋅
⋅
−
Cosinus przyjmuje wartość dodatnia w I i IV ćwiartce
0
0
0
66 14 '
180
113 46 '
α
β
α
=
=
− =
lub
0
0
0
0
0
cos
cos(
)
66 14 '
180
180
66 14 '
246 14 '
α
ϕ
α
ϕ
α
=
−
= −
=
− =
+
=
______________________________________________________________________
7.17
Dane:
Szukane:
Wzory:
1
2
200
50
220
m
m
sk
U
U
V
f
Hz
U
V
=
=
=
=
α
=
sin(
)
m
u
U
t
ω ϕ
=
+
2
m
sk
U
U
=
Odświeżyć wzory
trygonometryczne i związki
pomiędzy kątami
1sposób
y
x
u
2
u
1
u
α
α
y
x
u
2
u
1
u
α
α
β
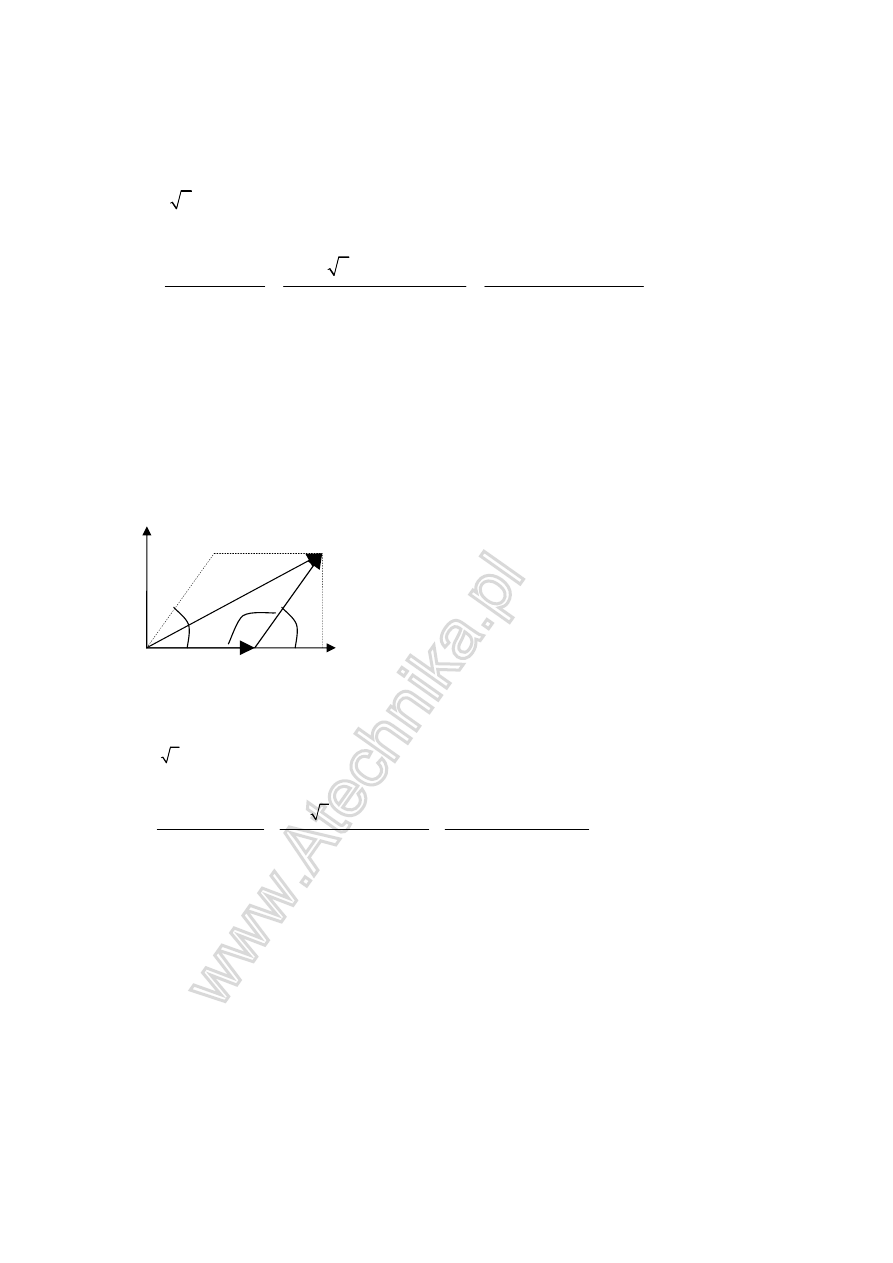
Teraz dodawanie wektorów jak na geometrii.
(
)
2
2
2
2
2
2
2
2
1
2
2
1
1 2
2
2
2
2
2
2
2
2
1
1 2
2
1
1 2
2
2
2
2
1
1 2
2
2
2
2
2
2
2
1
2
1 2
(
cos )
(
sin )
2
cos
cos
sin
2
cos
(cos
sin
)
2
cos
1
2
2
cos
220
2
200
200
96800 40000 400
cos
2
2 200 200
m
sk
m
m
u
u
u
u
u
u u
u
u
u
u u
u
u
u u
u
u
U
u
u
u u
u
u
u
u
u u
α
α
α
α
α
α
α
α
α
α
α
=
+
+
=
+
+
+
=
=
+
+
+
=
+
+
⋅
=
=
+
+
⋅
−
−
−
−
−
−
=
=
=
⋅
⋅
0
0, 21
80000
=
Cosinus przyjmuje wartość dodatnią w I i IV ćwiartce
0
78 54 '
α
=
lub
0
0
cos
cos(
)
78 58 '
78 58 '
α
ϕ
α
ϕ
=
−
=
= −
2sposób
Dodawanie wektorów z wykorzystaniem Twierdzenia Cosinusów
2
2
2
2
cos
a
b
c
bc
α
= + −
0
180
β
α
=
−
2
2
2
1
1 2
2
cos
u
u
u
u u
β
=
+ −
(
)
2
2
2
1
2
1
2
2
2
2
2
2
2
1
2
1
2
2
2
cos
220 2
200
200
96800 40000 40000
cos
0, 21
2
2 200 200
80000
m
sk
m
m
m
m
m
m
m
m
m
m
u
U
u
U
U
U U
u
U
U
U U
β
β
=
=
+
−
−
−
−
−
−
−
=
=
=
= −
−
− ⋅
⋅
−
Cosinus przyjmuje wartość ujemną w II i III ćwiartce
0
0
0
0
0
cos
cos(180
)
180
78 54 '
180
78 54 '
ϕ
β
β
α
β
−
=
−
=
−
=
− =
lub
0
0
cos
cos(
)
78 54 '
78 54 '
ϕ
β
β
α
β
−
=
−
=
= − = −
______________________________________________________________________
7.18
y
x
u
2
u
1
u
α
α
β

Dane:
Szukane:
Wzory:
5, 55
sk
I
A
=
( )
m
sr
I
I
π
=
=
( )
2
sr
m
I
I
π
π
=
2
m
sk
I
I
=
( )
2
5, 55 2
7,82
2
2
2 2
2
5, 55
4, 98
m
sk
sr
m
sk
I
I
A
I
I
I
A
π
π
π
π
=
=
=
=
=
=
=
______________________________________________________________________
7.19
Dane:
Szukane:
Wzory:
230
sk
U
V
=
m
U
=
2
m
sk
U
U
=
2
230 2
324,3
m
sk
U
U
V
=
=
≈
______________________________________________________________________
7.20
Dane:
Szukane:
Wzory:
2
sin(
)
6
m
i
I
t
π
ω
=
+
1, 3
0
i
A
t
=
=
sk
I
=
2
m
sk
I
I
=
0
0
2
2
sin(
)
sin(
)
sin(60 )
6
6
1, 3
1, 5
sin(60 )
3
2
1, 06
2
m
m
m
m
m
sk
i
I
t
I
I
i
I
A
I
I
A
π
π
ω
=
+
=
=
=
=
≈
=
=
______________________________________________________________________
7.21
Dane:
Szukane:
Wzory:
1
2
1,8
m
m
U
U
V
=
=
0
90
2
π
α
=
=
sk
U
=
2
m
sk
U
U
=
1
2
1
2
sin(
)
sin(
)
2
m
m
u
u
u
U
t
U
t
π
ω
ω
= + =
+
+
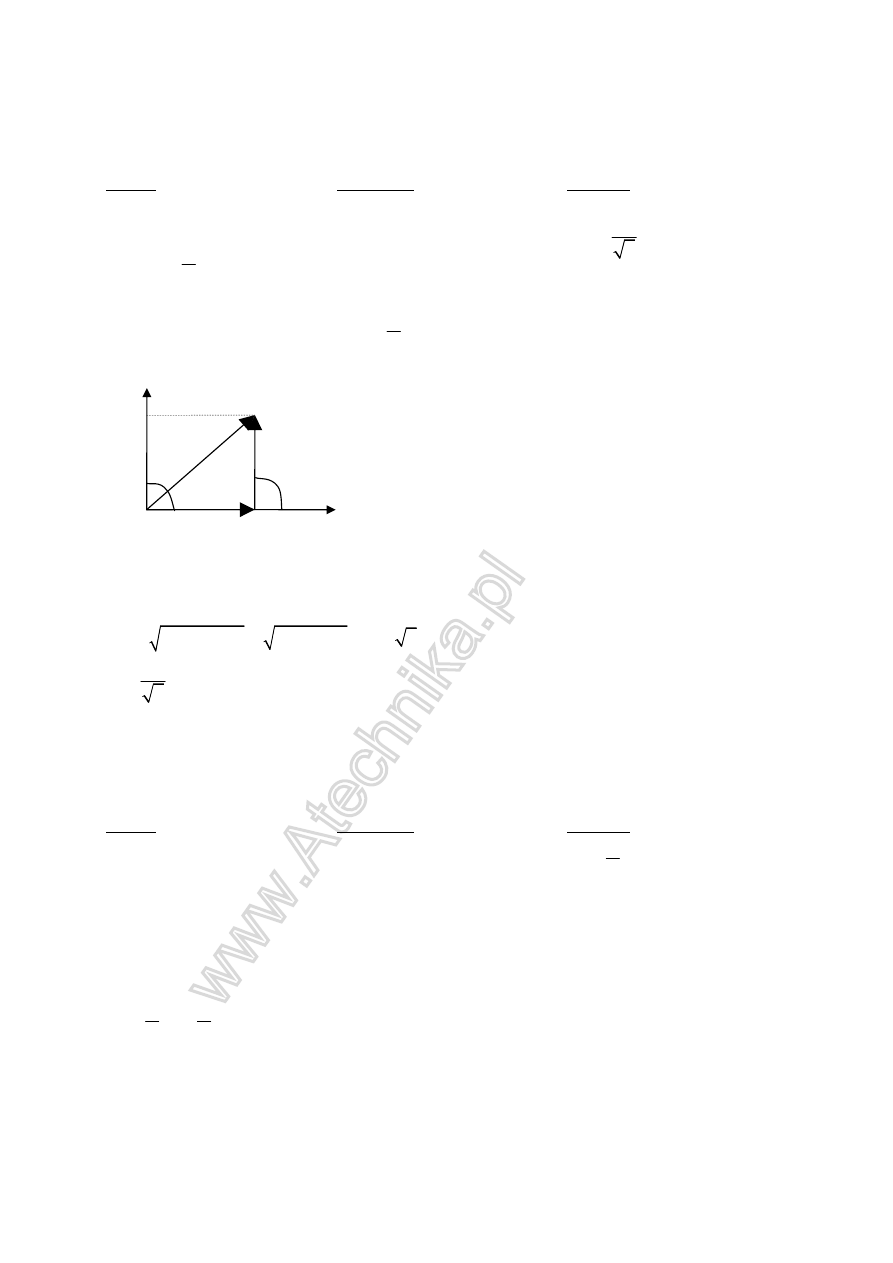
1sposób
Teraz dodawanie wektorów jak na geometrii.
Przy tym kącie najlepiej od razu z Pitagorasa
2
2
2
1
2
2
2
2
2
1
2
1,8
1,8
1,8
2
2, 55
1,8
2
m
m
m
m
m
m
m
U
U
U
U
U
U
V
U
U
V
=
+
=
+
=
+
=
⋅
=
=
=
______________________________________________________________________
7.22
Dane:
Szukane:
Wzory:
5sin
i
t
ω
=
( )
sr
I
π
=
2
sr
m
I
I
π
=
sin
5
m
m
i
I
t
I
A
ω
=
=
2
2
5
3,18
sr
m
I
I
A
π
π
=
=
≈
______________________________________________________________________
7.23
y
x
u
2
u
1
u
α
α

Dane:
Szukane:
Wzory:
5 2
8
m
I
A
t
h
=
=
1
Q
=
2
Q
=
Q
I
t
=
2
sr
m
I
I
π
=
Do obliczeń bierzemy prąd średni. (patrz definicja wartości średniej)
Przy prostowanie dwupołówkowym, wartość średnia prądu dla każdego półokresu jest taka
sama.
2
2
2
5 2 8 3600 129711
sr
m
Q
I t
I t
C
π
π
=
=
=
⋅ ⋅
=
lub
2
2
2
5 2 8
36
sr
m
Q
I t
I t
Ah
π
π
=
=
=
⋅ =
Przy prostowanie jednopołówkowym, w każdym okresie jeden półokres prądu jest blokowany
czyli wartość średnia w okresie jest o połowę mniejsza.
1
2
1
5 2 8 3600
64855
2
2
sr
m
I
Q
t
I t
C
π
π
=
=
=
⋅ ⋅
=
lub
1
2
1
5 2 8 18
2
2
sr
m
I
Q
t
I t
Ah
π
π
=
=
=
⋅ =
______________________________________________________________________
7.24
Dane:
Szukane:
Wzory:
2
0, 222
I
A
=
1
1
a
b
I
I
=
=
2
sr
m
I
I
π
=
2
m
sk
I
I
=
Miernik elektromagnetyczne wyskalowane są w wartości skutecznej.
Miernik magnetoelektryczne reagują na wartość średnią.
2
2
2
0, 222 2
0, 314
a
b
m
sk
I
I
I
I
A
=
=
=
=
=
Prostowanie dwópołówkowe
1
2
2
2
2 0, 222 2
0, 2
3,14
m
sk
a
sr
I
I
I
I
A
π
π
⋅
=
=
=
=
=
Prostowanie jednopołówkowe

1
2
2
2
0, 222 2
0,1
2
2
2
3,14
sr
m
sk
b
I
I
I
I
A
π
π
=
=
=
=
=
______________________________________________________________________
7.25
Dane:
Szukane:
Wzory:
180
m
U
V
=
sr
U
=
1
1
2
2
3
3
1
2
3
0
2
2
2
2
2
2
2
0
2
2
2
2
4
4
2
2
180 120
3
3
6
6
m
m
m
m
sr
sr
m
m
m
m
sr
sr
m
m
m
m
m
m
sr
sr
m
m
m
sr
sr
sr
sr
m
U
I
I
U
R
U
I R
R
R
R
I
I
I
U
U
I
R
R
R
I R
R
U
R
U
I
I
U
R
U
I
R
R
R
R
U
U
U
U
U
U
U
U
V
+
=
=
=
=
=
+
=
=
=
=
=
=
+
=
=
=
=
=
+
+
+
+
=
=
=
=
=
______________________________________________________________________
7.26
Dane:
Szukane:
Wzory:
10
Cu
m
g
=
3
3
10800
12
0, 3294
/
0, 3294 10
/
t
h
s
R
k
mg C
g C
−
=
=
=
Ω
=
=
⋅
R
W
=
m
kIt
=
3
2
6
10
10
2,8109
0, 3294 10
10800
3, 55752
2
2,8109 3,14
2
3,1298
2
2
2 2
2 2
1269570
1, 26 10
sr
sr
m
sr
m
sr
sk
sk
m
I
A
kt
I
I
I
I
I
I
A
W
Pt
I
Rt
J
J
π
π
π
−
=
=
=
=
⋅
⋅
=
⋅
=
=
=
=
=
=
=
=
≈
⋅

______________________________________________________________________
7.27
Dane:
Szukane:
Wzory:
2
2
j
+
; I ćwiartka
3
j
−
; IV
1
3
j
− +
; II
1
j
− −
; III
______________________________________________________________________
7.28
Dane:
Szukane:
Wzory:
j
z
a
jb
z
re
ϕ
= +
=
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
2
2
j
+
;I ćwiartka;
0
2
arctg
2
2
45
2
2
2
2 2
j
j
e
e
+ ⋅
=
⋅
1
j
−
;IV ćwiartka;
0
0
0
0
1
arctg
2
2
45
( 45
360 )
315
1
1
1
2
2
2
j
j
j
j
e
e
e
e
−
−
−
+
+ ⋅
=
⋅
=
⋅
=
⋅
1
3
j
− −
;III ćwiartka;
(
)
0
0
0
0
0
0
3
arctg
arctg 3
2
2
(60
180 )
( 120 )
( 120
360 )
240
1
( 1)
(
3)
2
2
2
2
2
j
j
j
j
j
j
e
e
e
e
e
e
π
−
−
−
−
−
+
−
−
+ −
=
=
=
=
=
______________________________________________________________________
7.29

Dane:
Szukane:
Wzory:
j
z
a
jb
z
re
ϕ
= +
=
2
2
r
a
b
=
+
arctg
b
a
ϕ
=
cos
sin
a
r
b
r
ϕ
ϕ
=
=
cos
sin
j
re
r
j
ϕ
ϕ
ϕ
=
+
0
30
0
0
3
1
10
10 cos 30
10 sin 30
10
10
8, 65
5
2
2
j
e
j
j
j
=
+
=
+
=
+
0
45
0
0
0
0
2
2
2
2 cos( 45 )
2 sin( 45 )
2 cos 45
2( sin 45 )
2
2
2
2
2
2
j
e
j
j
j
j
−
=
−
+
−
=
+
−
= ⋅
−
⋅
=
−
0
90
0
0
3
3cos 90
3sin 90
3 0
3 1
3
j
e
j
j
j
=
+
= ⋅ + ⋅ =
0
0
3
1
3
18
18 cos 60
18sin 60
18
18
9
9 3
2
2
j
e
j
j
j
π
=
+
= ⋅ +
⋅
= +
2
0
0
0
0
0
0
3
0
0
4
4 cos120
4 sin120
4 cos(180
60 )
4 sin(180
60 )
1
3
4( cos 60 )
4sin 60
4
4
2
2 3
2
2
j
e
j
j
j
j
j
π
=
+
=
−
+
−
=
= −
+
= − ⋅ +
⋅
= − +
0
135
0
0
0
0
0
0
0
0
16
16 cos135
16 sin135
16 cos(180
45 )
16 sin(180
45 )
2
2
16 ( cos 45 )
16 sin 45
16
16
8 2
8 2
2
2
j
e
j
j
j
j
j
=
+
= ⋅
−
+
−
=
= ⋅ −
+
= − ⋅
+
⋅
= −
+
______________________________________________________________________
7.30
Dane:
Szukane:
Wzory:
j
z
a
jb
z
re
ϕ
= +
=
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<

cos
sin
a
r
b
r
ϕ
ϕ
=
=
(
)
0
0
6
10 cos
sin
[ ]
6
6
3
1
10 cos
sin
10 cos 30
sin 30
10
10
5 3
5
6
6
2
2
10
10
j
I
j
A
I
j
j
j
j
r
I
e
π
π
π
π
π
=
+
=
+
=
+
=
+
=
+
=
=
______________________________________________________________________
7.31
Dane:
Szukane:
Wzory:
(
)
(
)
1
2
2
3 [ ]
2, 5
2, 5 [ ]
I
j
A
I
j
A
= +
=
−
I
=
j
z
a
jb
z
re
ϕ
= +
=
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=

(
)
(
)
1
2
1
2
2
2
1
2
2
2
1
2
2
3 [ ]
2, 5
2, 5 [ ]
2
3 2, 5
2, 5
4, 5
0, 5 [ ]
2
3
13
2, 5
( 2, 5)
6, 25 6, 25
12, 5 [ ]
I
j
A
I
j
A
I
I
I
j
j
j
A
r
r
A
r
r
= +
=
−
= + = +
+
−
=
+
=
+
=
=
+ −
=
+
=
>
______________________________________________________________________
7.32
Dane:
Szukane:
Wzory:
0
120
230
230
A
j
B
V
V
V
e
V
−
=
=
AB
U
=
j
z
a
jb
z
re
ϕ
= +
=
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
0
120
0
0
0
0
0
0
0
0
0
230
230
230(cos( 120 )
sin( 120 ))
230(cos120
( sin120 ))
230(cos(180
60 )
( sin(180 60 )))
1
3
230( cos 60 )
( sin 60 ))
230(
)
230(
))
115
115 3 [ ]
2
2
A
j
B
V
V
V
e
j
j
j
j
j
j
V
−
=
=
=
−
+
−
=
=
+ −
=
−
+ −
−
=
=
−
+ −
=
− +
−
= −
−

(
)
2
2
230 ( 115
115 3)
345
115 3 [ ]
345
115 3
119025 39675
398, 4
AB
A
B
AB
U
V
V
j
j
V
r
=
−
=
− −
−
=
+
=
+
=
+
≈
______________________________________________________________________
7.33
Dane:
Szukane:
Wzory:
j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
(
)(
)
( )
(
) (
)
(
)(
) (
)(
)
(
)(
)
( )
(
)
( )
(
)
(
)
( )
( )
2
2
2
2
2
2
2
1
1
1
1
1
2
1
1
1
1
1
1
1
1
1
2
1
1
2
1
2
2
4
1 4
4
(1
)
1
1
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
+
− = − + −
= − − =
+
−
=
+
+
−
−
= + + +
− − +
=
= +
+ −
−
+ −
=
−
= −
= − −
=
− = −
= − − = +
______________________________________________________________________
7.34
Dane:
Szukane:
Wzory:

j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
(
)
(
)
2
2
2
2
2
2
2
1
1
1
1
1
2 1
1
1
1
1
2
1
1
1
1
1
2 1
1
1
1
1
2
1
1 1
1
1
1
1
1
1
1
1
2
2
1
1 1
1
1
1
1
1
1
1
1
2
2
1
1
2
2
2
6
2
6
2
6
2
6
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
j
+
+
+
+ + +
+
−
=
=
=
=
−
−
+
−
−
−
−
− − +
−
−
=
=
=
= −
+
+
−
−
−
−
−
=
=
=
=
−
+
+
−
−
+
+
+
=
=
=
=
+
−
−
+
−
−
−
= ⋅
=
= −
−
−
−
−
− −
=
⋅
− +
− +
− −
(
)
2
2
4
12
2
6
10
10
1
1
4
36
40
4
j
j
j
j
j
j
− −
+
+
− −
=
=
= −
+
−
______________________________________________________________________
7.35

Dane:
Szukane:
Wzory:
3
4
2
4
I
j
Z
j
= +
= −
j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
(
)(
)
( )
2
3
4 2
4
6
12
8
16
6
4
1 16
22
4
I Z
j
j
j
j
j
j
j
⋅ = +
−
= −
+
−
= −
− −
=
−
IV ćwiartka
( )
2
2
0
0
0
22
4
500
10 5
22, 36
4
sin
0,1789
22, 36
10 18 '
22
cos
0, 9839
22, 36
10 18 '
lub
arctg
0
0
4
arctg
10 18 '
22
r
b
r
a
r
b
dla
a
i b
a
ϕ
α
ϕ
ϕ
α
ϕ
α
α
=
+ −
=
=
≈
= =
≈
= − = −
= =
≈
= − = −
= −
>
<
= −
= −
0
10 18'
22, 36
j
I Z
e
−
⋅ =
______________________________________________________________________
7.36

Dane:
Szukane:
Wzory:
0
15
75
5
30
j
j
I
e
Z
e
−
=
=
j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
0
0
0
0
15
75
(15
( 75 ))
60
0
0
0
0
5
30
5 30
150
150(cos( 60 )
sin( 60 ))
150(cos 60
( sin 60 ))
1
3
150
75
75 3
2
2
j
j
j
j
I Z
e
e
e
e
I Z
j
j
j
j
−
+ −
−
⋅ =
= ⋅
=
⋅ =
−
+
−
=
+ −
=
=
−
=
−
______________________________________________________________________
7.37
Dane:
Szukane:
Wzory:
j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+

arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
5
5
j
−
; sprzężona to 5
5
j
+
j
−
; sprzężona to j
2
; sprzężona to 2
10
j
+
; sprzężona to 10
j
−
0
20
3
j
e
; sprzężona to
0
20
3
j
e
−
0
30
1,5
j
e
−
; sprzężona to
0
30
1,5
j
e
______________________________________________________________________
7.38
Dane:
Szukane:
Wzory:
0
0
90
30
380
76
j
j
U
e
Z
e
=
=
j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+

arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=
0
0
0
0
0
90
(90
30 )
60
30
380
380
5
76
76
j
j
j
j
U
e
e
e
Z
e
−
=
=
=
______________________________________________________________________
7.39
Dane:
Szukane:
Wzory:
1
2
2
4
2
6
Z
j
Z
j
= +
= −
j
z
a
jb
z
re
ϕ
= +
=
2
1
j
= −
2
2
r
a
b
=
+
arctg
0
0
arctg
0
0
arctg
0
0
arctg
0
0
0
0
2
0
0
2
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
b
dla
a
i b
a
dla
a
i b
dla
a
i b
ϕ
ϕ
ϕ
π
ϕ
π
π
ϕ
π
ϕ
=
>
≥
= −
>
<
=
+
<
≥
=
−
<
<
= +
=
>
= −
=
<
cos
sin
a
r
b
r
ϕ
ϕ
=
=

(
) (
)
( )
2
1
2
1
2
2
2
2
2
4
2
6
4
4
1 24
4
12
8
24
2
4 2
6
4
2
4
2
28
4 4
2
112
16
56
8
120
40
6
2
4
2 4
2
4
2
20
Z Z
j
j
j
j
j
j
Z
Z
j
j
j
j
j
j
j
j
j
j
j
j
j
⋅
+
⋅ −
−
− −
−
+
−
=
=
=
=
+
+
+ −
−
−
−
+
−
+
−
+
=
=
=
= +
−
+
+
______________________________________________________________________
7.40
Dane:
Szukane:
Wzory:
200
311sin 314
R
u
t
=
Ω
=
sk
i
i
=
=
u
i
R
=
311sin 314
311
sin 314
1, 555sin 314 [ ]
200
200
1, 555 [ ]
1, 555
1,1[ ]
1, 41
2
m
m
sk
u
t
i
t
t A
R
I
A
I
i
A
= =
=
=
=
=
=
≈
______________________________________________________________________
7.41
Dane:
Szukane:
Wzory:
40
2, 5
R
I
A
=
Ω
=
m
P
=
u
i
R
P
ui
=
=
( )
2
2
2
6, 25 2 40
500
m
m
P
I R
I
R
W
=
=
=
⋅ ⋅
=
______________________________________________________________________
7.42
Dane:
Szukane:
Wzory:
0, 6
220
50
L
H
U
V
f
Hz
=
=
=
L
x
I
=
=
2
L
x
L
fL
ω
π
=
=

2
2 3,14 50 0, 6 188, 4
220
1,168
188, 4
L
L
x
L
fL
U
I
A
x
ω
π
=
=
= ⋅
⋅ ⋅
=
Ω
=
=
≈
______________________________________________________________________
7.43
Dane:
Szukane:
Wzory:
0
0, 23
150
50
R
I
A
U
V
f
Hz
≈ Ω
=
=
=
L
=
2
L
x
L
fL
ω
π
=
=
L
U
I x
= ⋅
150
652
0, 23
652
652
2, 08
2
2 3,14 50
314
L
L
L
U
x
I
x
x
L
s
H
f
ω
π
=
=
=
Ω
=
=
=
=
Ω ≈
⋅
⋅
______________________________________________________________________
7.44
Dane:
Szukane:
Wzory:
1
2
12
1000
20
L
mH
f
Hz
f
kHz
=
=
=
x
B
=
=
2
L
x
L
fL
ω
π
=
=
L
U
I x
= ⋅
1
L
B
x
=
I
U
φ
=
π
/2

1
1
1
1
2
2
2
2
2
75, 36
1
1
0, 01226
12, 26
75, 36
2
1507, 2
1
1
0, 00066
0, 66
2
1507, 2
L
L
L
x
f L
B
S
mS
x
x
f L
B
S
mS
f L
π
π
π
=
=
Ω
=
=
≈
=
=
=
Ω
=
=
=
=
______________________________________________________________________
7.45
Dane:
Szukane:
Wzory:
22 sin 6280 [ ]
0, 25
i
t A
L
H
=
=
2
L
x
L
fL
ω
π
=
=
L
U
I x
= ⋅
(
)
0
0, 22 sin 6280
sin
6280 0, 25 1570
0, 22 sin 6280 1570
345, 4 sin 6280
90
m
L
L
i
t
i
I
t
x
L
u
ix
t
t
V
ω
ω
=
=
=
=
⋅
=
Ω
=
=
⋅
=
+
Ponieważ napięcie na elemencie indukcyjnym jest przyspieszone o
0
90 w stosunku do prądu.
czyli
345, 4 sin 6280
2
u
t
V
π
=
+
______________________________________________________________________
7.46
Dane:
Szukane:
Wzory:
10
50
C
F
f
Hz
µ
=
=
C
C
x
B
=
=
1
1
2
C
x
C
fC
ω
π
=
=
1
C
C
B
x
=
I
U
φ
=
π
/2

6
6
6
3
1
1
1
10
318, 47
2
2 3,14 50 10 10
3140
1
1
3140 10
3,14 10
318, 47
C
C
C
x
C
fC
B
S
S
x
ω
π
−
−
−
=
=
=
=
≈
Ω
⋅
⋅ ⋅ ⋅
=
=
=
⋅
=
⋅
______________________________________________________________________
7.47
Dane:
Szukane:
Wzory:
5
400 sin 314 [ ]
C
F
u
t V
µ
=
=
m
i
W
=
=
1
1
2
C
x
C
fC
ω
π
=
=
1
C
C
B
x
=
2
2
CU
W
=
400 sin 314 [ ]
sin
m
u
t V
U
U
t
ω
=
=
6
6
6
3
1
1
10
636, 94
314 5 10
1570
1
1
1570 10
1, 57 10
636, 94
C
C
C
x
C
B
S
S
x
ω
−
−
−
=
=
=
≈
Ω
⋅ ⋅
=
=
=
⋅
=
⋅
2
6
2
2
5 10
400
5 16 10
0, 4
2
2
2
m
m
CU
W
J
−
−
⋅
⋅
⋅ ⋅
=
=
=
=
Ponieważ w idealnym kondensatorze prąd jest przyspieszony w stosunku do napięcia o
0
90
(
)
0
400 sin 314
0, 628sin 314
90
[ ]
636, 94
C
u
t
i
t
A
x
=
=
=
+
I
U
φ
=
π
/2

______________________________________________________________________
7.48
Dane:
Szukane:
Wzory:
0, 35
135
50
I
A
U
V
f
Hz
=
=
=
C
=
1
1
2
C
x
C
fC
ω
π
=
=
C
U
I
x
=
6
1
0, 3
0, 3
7, 08 10
7, 08
2
2 3,14 50 135
42390
C
U
x
I
U
C
I
I
I
C
F
F
U
fU
ω
µ
ω
π
−
=
=
=
=
=
=
≈
⋅
=
⋅
⋅ ⋅
______________________________________________________________________
7.49
Dane:
Szukane:
Wzory:
0,1
0,1
1000 : 5000
L
H
C
F
f
Hz
µ
=
=
=
C
=
1
1
2
C
x
C
fC
ω
π
=
=
2
L
x
L
fL
ω
π
=
=
3
6
1
1
1
10
796, 2
2
2 3,14 2000 0,1 10
1, 256
2
2 3,14 2000 0,1 1256
C
L
x
C
fC
x
L
fL
ω
π
ω
π
−
=
=
=
=
=
Ω
⋅
⋅
⋅
⋅
=
=
= ⋅
⋅
⋅
=
Ω
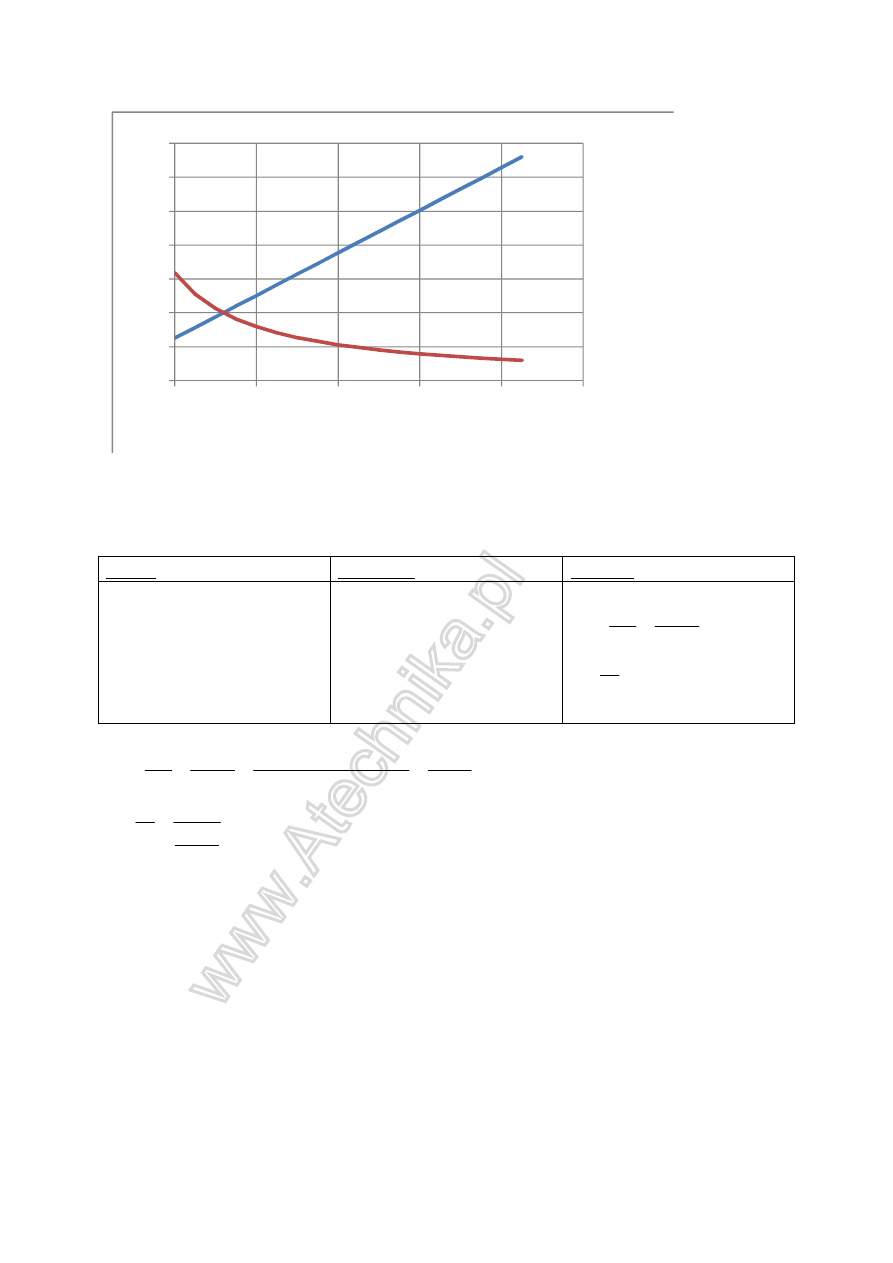
0
500
1000
1500
2000
2500
3000
3500
1000
2000
3000
4000
5000
6000
f [Hz]
______________________________________________________________________
7.50
Dane:
Szukane:
Wzory:
6
3
0, 75
0, 75 10
15
15 10
50
C
F
F
U
kV
V
f
Hz
µ
−
=
=
⋅
=
= ⋅
=
I
=
1
1
2
C
x
C
fC
ω
π
=
=
L
U
I
x
=
6
6
1
1
1
10
4246
2
2 3,14 50 0, 75 10
235, 5
2
3, 53
1
2
C
L
x
C
fC
U
U
I
U
fC
A
x
fC
ω
π
π
π
−
=
=
=
=
=
Ω
⋅
⋅ ⋅
⋅
=
=
=
=
______________________________________________________________________
Wyszukiwarka
Podobne podstrony:
1a Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 1 1 do 1 64
1b Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 1 65 do 1 137
7b Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 7 51 do 7 88
2 Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 2 1do2 16
3 Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 3 1do3 71
5 Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 5 1do5 44
7c Zbiór zadań z elektrotechniki Aleksy Markiewicz rozwiązania od 7 89 do 7 121
mity od 1 do 50, ODK, Ikonografia Brus, Mity
mity od 1 do 50, ODK, Ikonografia Brus, Mity
8. Indukcja elektromagnetyczna. Prad przemienny, budownictwo PG, fizyka, zadania, zbior zadan
02 zbiór zadan rozwiązania
więcej podobnych podstron