POLITECHNIKA LUBELSKA

INSTYTUT PODSTAW ELEKTROTECHNIKI I ELEKTROTECHNOLOGII

Laboratorium Teorii Pola Elektromagnetycznego

Nazwisko, imię wykonujących:

Wojtal Mateusz
Wojtiuk Michał

Wójcicki Kamil

Zdunek Maksymilian

Grupa dziekańska:

EIST 4.5b

Rok akademicki

2012/2013

Data wykonania:

15.05.2013

Podpis:

Ćwiczenie nr 7

Temat ćwiczenia: Modelowanie pól płaskich na papierze

elektroprzewodzącym.

1. Badanie rozkładu natężenia pola elektrycznego dla kabla
koncentycznego.

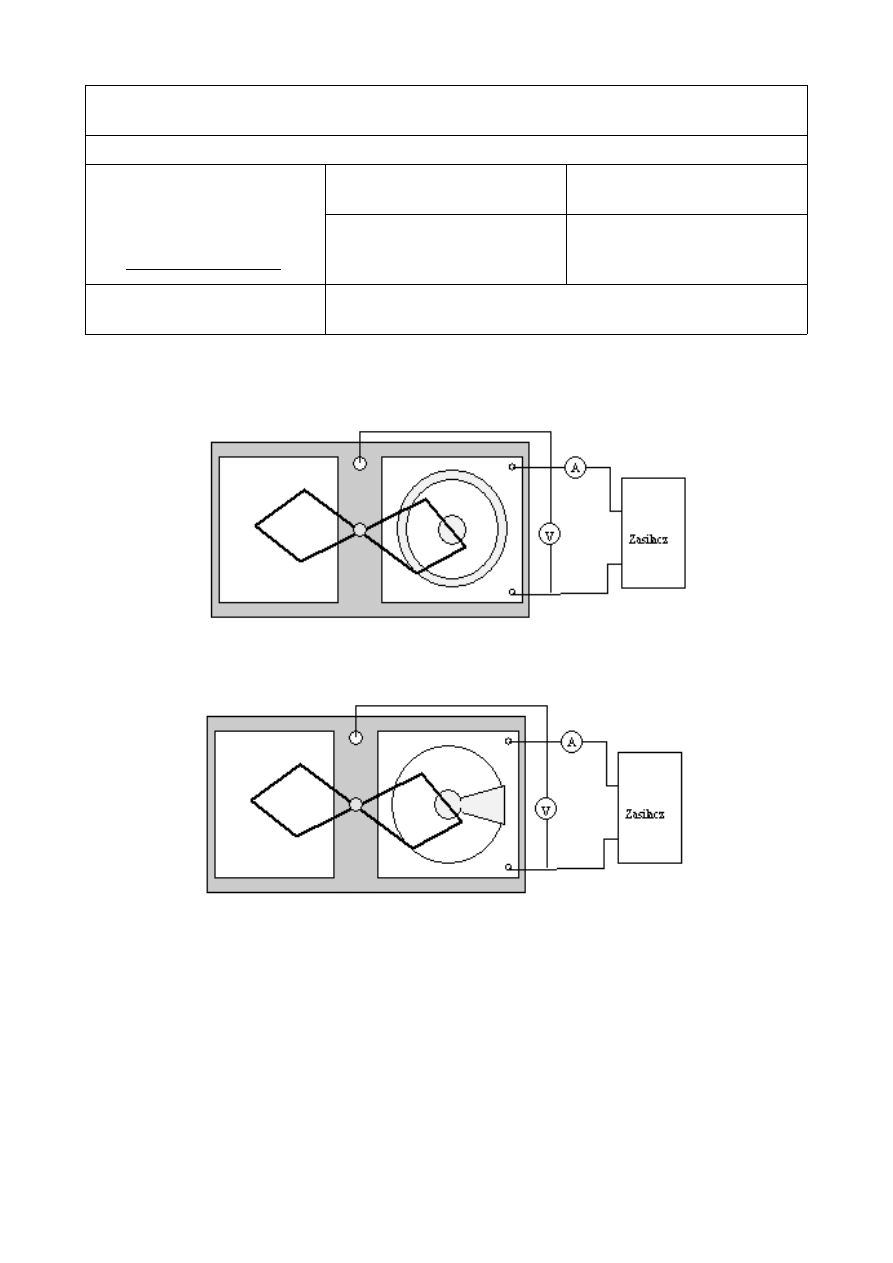
Rys. 1. Schemat pomiarowy do badania rozkładu natężenia pola.Układ walców współosiowych
(model prosty).

Rys. 2. Schemat pomiarowy do badania rozkładu natężenia pola.Układ walcowy (model odwrotny).

Pomiary wykonano dla wartości napięcia U =10 V.

Uzyskane wykresy linii ekwipotencjalnych są narysowane na załączonych kartkach papieru
kancelaryjnego. Wyznaczenie pola przeprowadziliśmy rysując wspólny obraz linii
ekwipotencjalnych modelu prostego i odwrotnego.

a) Wykres nateżenia pola elektrycznego oraz potencjalu w funkcji odleglości od
środka układu

r

Δr

V

ΔV

E

m

m

V

V

V/m

0,11

0

0

0

0

0,09

-0,03

1

1

33,3

0,07

-0,02

2

1

50

0,06

-0,01

3

1

100

0,045

-0,015

4

1

66,7

0,037

-0,008

5

1

125

0,03

-0,007

6

1

142,9

0,022

-0,008

8

2

250

0,016

-0,006

10

2

333,3

Tab. 1. Tabela pomiarowa i obliczeniowa dla kabla koncentrycznego – natężenie pola.

Przykładowe obliczenia:

E=

−

ΔV

Δr

E=

−

ΔV

Δr

=

−

1

−

0,03

=

33,3

V

m

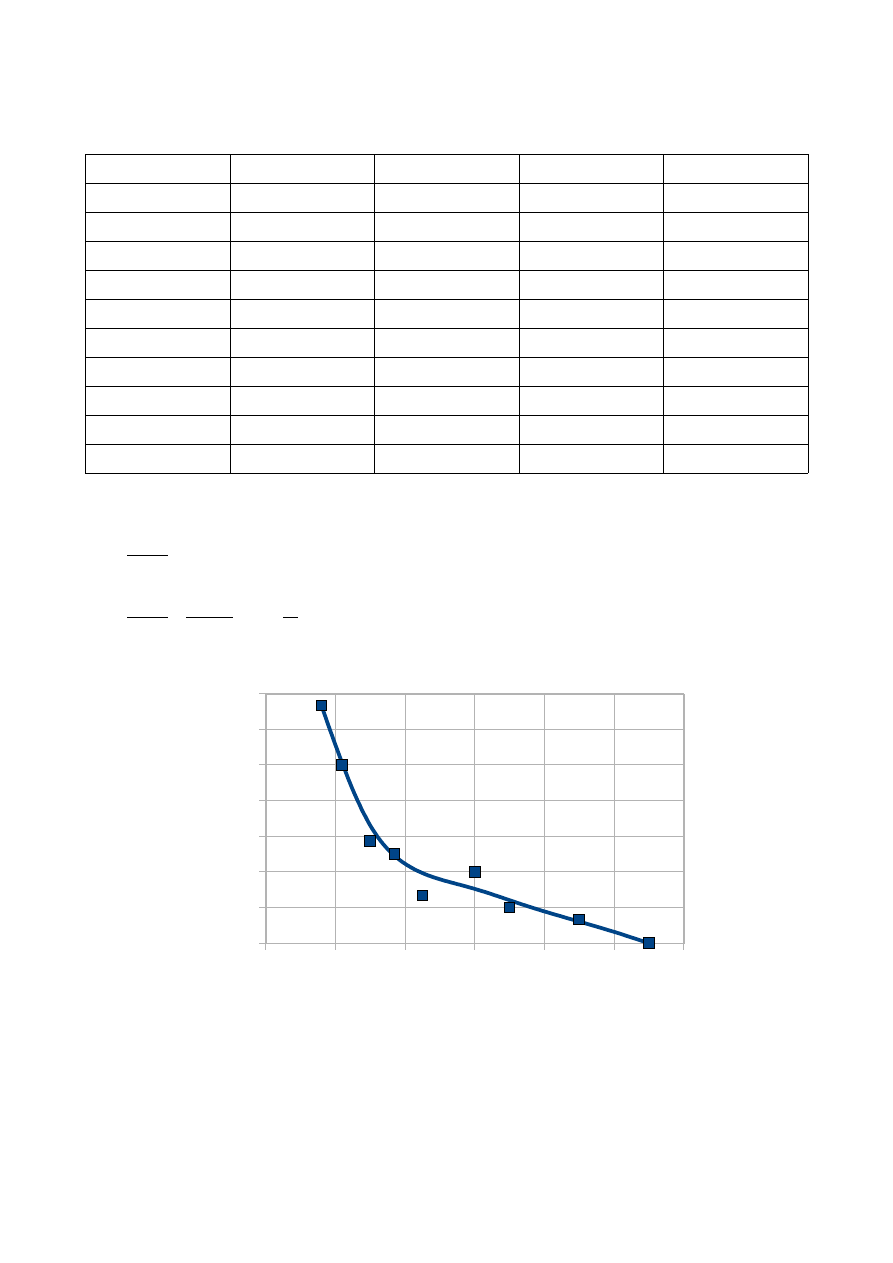
Wyk. 1. Wykres nateżenia pola elektrycznego w funkcji odleglości od środka układu.

0

0,02

0,04

0,06

0,08

0,1

0,12

0,0

50,0

100,0

150,0

200,0

250,0

300,0

350,0

r [m]

E

[V

/m

]

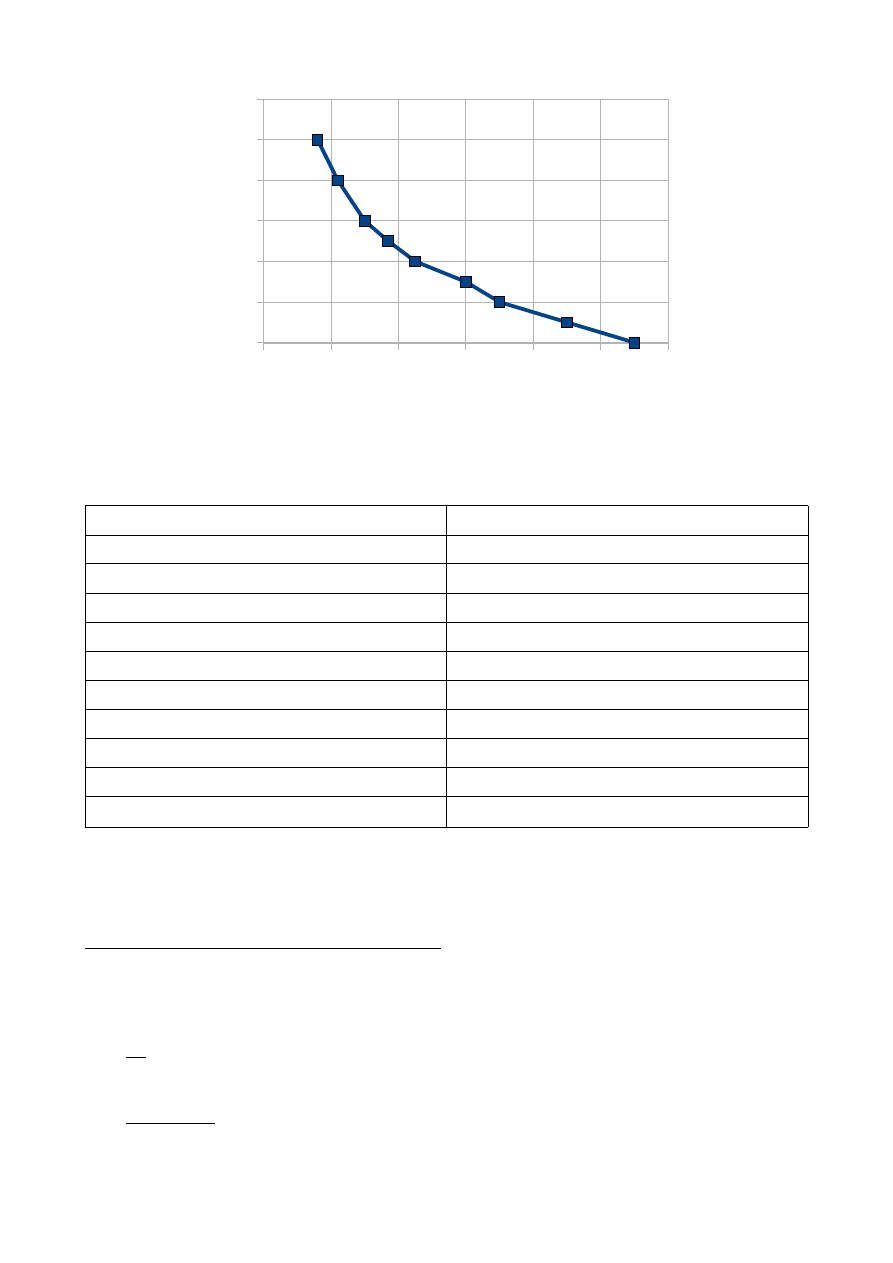
Wyk. 2. Wykres potencjału w funkcji odleglości od środka układu.

b) Wykres gęstości prądu w funkcji odleglości od środka układu

r

k

J

m

A/m

2

0,11

274,17

0,09

335,09

0,07

430,83

0,06

505,64

0,045

670,18

0,037

815,09

0,03

1005,28

0,022

1370,83

0,016

1884,89

Tab. 2. Tabela obliczeniowa dla kabla koncentrycznego – gęstość prądu.

Przykładowe obliczenia:
I = 25 mA = 25*10

-3

A

Dane papieru elektroprzewodzącego do obliczeń:
R=1190

Ω

h=0,132 mm=1,32*10

-4

m (grubość papieru)

ρ

=Rh=1190*1,32*10

-4

=0,157

J =

I

S

k

,

S

k

=

2∗ pi∗r

k

∗

h

J =

I

2∗pi∗r

k

∗

h

0

0,02

0,04

0,06

0,08

0,1

0,12

0

2

4

6

8

10

12

r [m]

V

[V

]

J =

I

2∗pi∗r

k

∗

h

=

25∗10

−

3

2∗3,14∗0,11∗1,32∗10

−

4

=

274,17

A

m

2

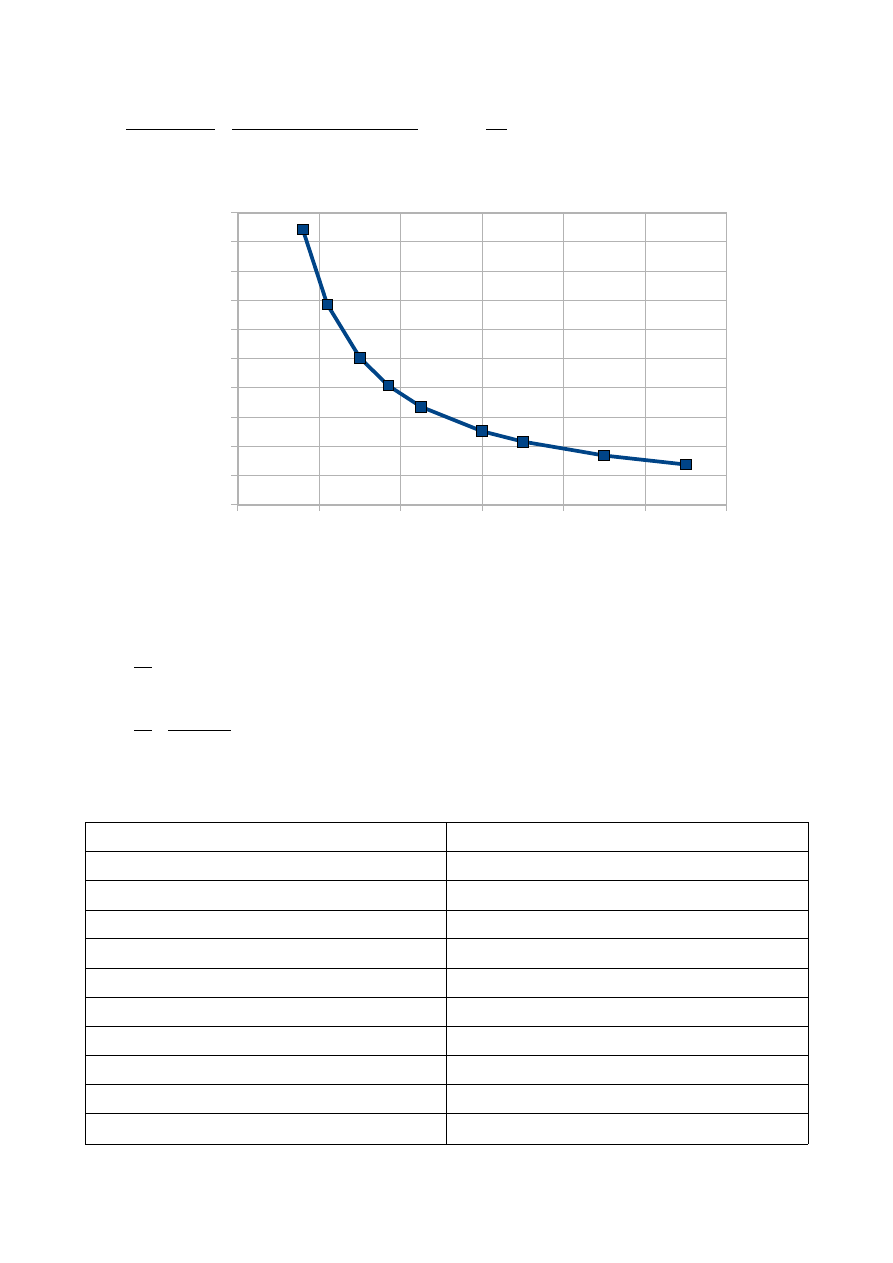
Wyk. 3. Wykres gęstości prądu w funkcji odleglości od środka układu.

c) Rezystancja przejścia

R

p

=

U

I

R

p

=

U

I

=

10

25∗10

−

3

=

400 Ω

d) Obliczenia gęstości prądu i rezystancji przejścia dla

h=l=1 m

r

k

J

m

A/m

2

0,11

0,036

0,09

0,044

0,07

0,057

0,06

0,066

0,045

0,088

0,037

0,108

0,03

0,133

0,022

0,181

0,016

0,249

Tab. 3. Tabela obliczeniowa dla kabla koncentrycznego – gęstość prądu (dla h=1m).

0

0,02

0,04

0,06

0,08

0,1

0,12

0

200

400

600

800

1000

1200

1400

1600

1800

2000

r [m]

J

[A

/m

2

]

J =

I

2∗pi∗r

k

∗

h

=

25∗10

−

3

2∗3,14∗0,11∗1

=

0,036

A

m

2

R

p

=

U

I

=

10

25∗10

−

3

=

400 Ω

e) Obliczanie pojemności kondensatora elementarnego C' oraz pojemności
całego układu C (dla h=1 m).

C '=

εah

d

C=

n

m1

C '

ε = 8,85 * 10

-12

a = 0,022 m
h = 1 m
d = 0,011 m
ρ = 0,157

n=7
m=10

C '=

εah

d

=

8,85∗10

−

12

∗

0,022∗1

0,011

=

1,77∗10

−

11

F

C=

n

m1

C ' =

7

101

∗

1,77∗10

−

11

=

1,126∗10

−

11

F

f) Sprawdzanie zależności

R

p

∗

C=ε∗ρ

C=

2∗ pi∗ε∗l

ln

r

2

r

1

=

2∗3,14∗8,85∗10

−

12

∗

1,32∗10

−

4

ln

0,11

0,016

=

3,805∗10

−

15

F

R

p

∗

C=400∗3,805∗10

−

15

=

1,522∗10

−

12

ε∗ρ=0,157∗8,85∗10

−

12

=

1,389∗10

−

12

R

p

∗

C≈ε∗ρ

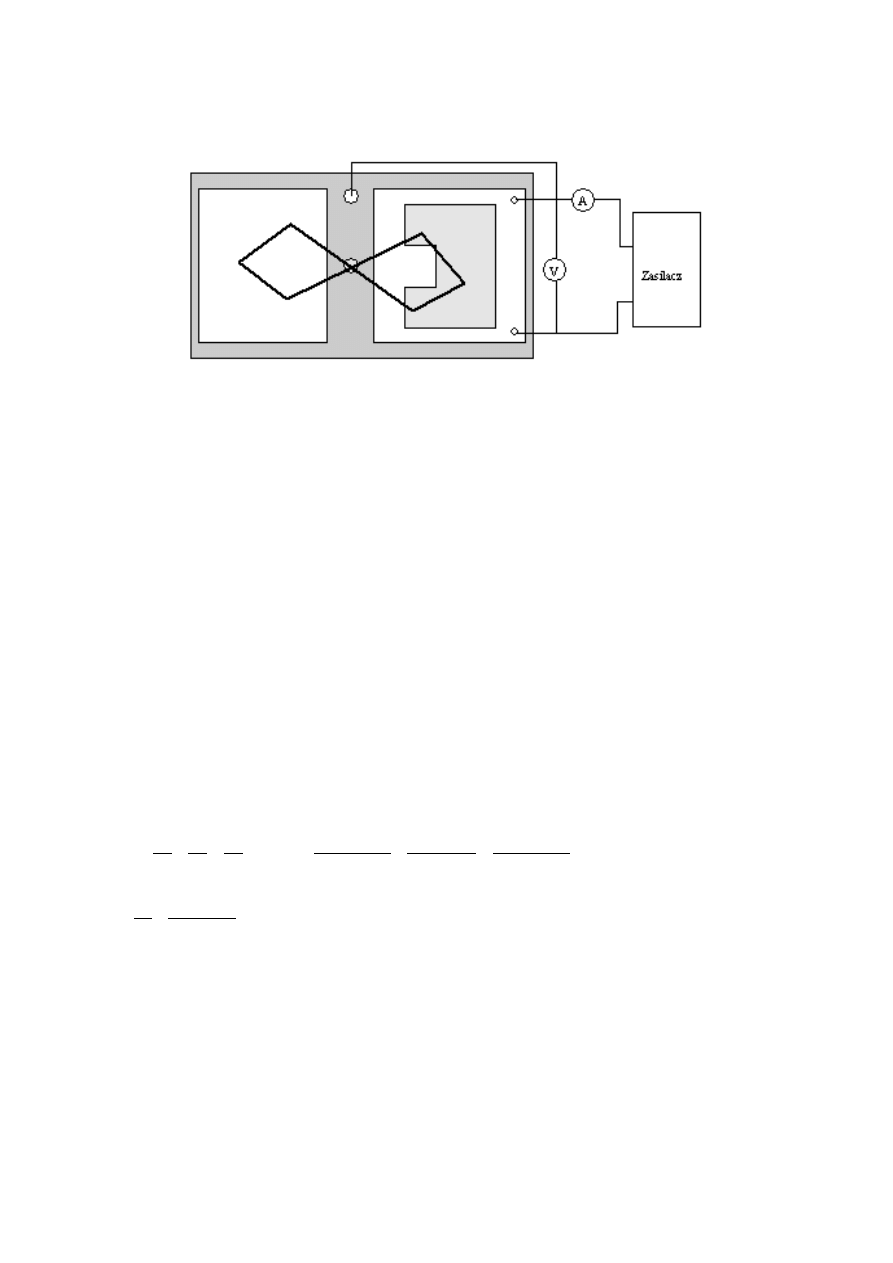
2. Badanie rozkładu natężenia pola dla przewodnika o zmiennym
przekroju.

Rys. 3. Schemat pomiarowy do badania rozkładu natężenia pola przewodnika o zmiennym
przekroju.

Wykresy linii ekwipotencjalnych dla przewodnika o zmiennym przekroju są narysowane na
załączonej kartce papieru kancelaryjnego.

a) Obliczanie rezystancji przejścia dla przewodnika o zmiennym kształcie.

l

1

= 0,12 m

l

2

= 0,05 m

l

3

= 0,12 m

h = 0,132*10

-3

m

R=1190 Ω
h=0,132 mm=1,32*10

-4

m (grubość papieru)

ρ=Rh=1190*1,32*10

-4

=0,157

I=2,5 mA=2,5*10

-3

A

S

1

=

0,12∗0,132∗10

−

3

=

1,58∗10

−

5

m

2

S

2

=

0,05∗0,132∗10

−

3

=

6,6∗10

−

6

m

2

S

3

=

0,12∗0,132∗10

−

3

=

1,58∗10

−

5

m

2

R

p

=

ρ

l

1

S

1



l

2

S

2



l

3

S

3

=

0,157 

0,12

1,58∗10

−

5



0,05

6,6∗10

−

6



0,12

1,58∗10

−

5

=

3574,2 Ω

R

p

=

U

I

=

10

2,5∗10

−

3

=

4000 Ω

3. Wnioski

Naszym celem podczas tego ćwiczenia było modelowanie pól płaskich kabla koncentrycznego oraz
przewodnika o zmiennym przekroju na papierze elektroprzewodzącym. Na podstawie pomiarów
potencjałów oraz lini ekwipotencjalnych sporządzonych na papierze kancelaryjnym możliwe było
polieczenie natężenia pola elektrycznego, a także gęstości prądu w danych punktach. Wyniki
uzyskane z rozkładu pola z wynikami otrzymanymi z zależności analitycznej są do siebie podobne
co świadczy o skuteczności metody graficznej.