International Round Robin on Room Acoustical

Impulse Response Analysis Software 2004

Brian F. G. Katz

Perception Situe´e, LIMSI-CNRS, BP 133, F91403 Orsay, France

Abstract:

The intent of this study is to examine the variations between cur-

rent implementations of standard room acoustic measures for impulse re-
sponse measurements. An international round robin has been conducted using
a single real measured impulse response, rather than a synthesized response.
This offers a more rigorous test of analysis procedures. While there is good
agreement at higher frequencies, large variations are found at lower frequen-
cies in which the noise level within the measurement is greater. Some errors
are attributed to the existence or robustness of noise-floor detection.

© 2004 Acoustical Society of America
PACS numbers: 43.55.Mc, 43.58.−e [DQ]
Date Received: November 21, 2003

Date Accepted: August 17, 2004

1. Introduction

The art of room acoustics involves the control of room geometry and materials to achieve a
desired goal. The science of room acoustics involves the knowledge and correlations between a
physical space and its acoustic response. As the sole objective means of evaluation,
measurement is the fundamental key to quantifying an acoustic and to comparing one acoustic
to another, for which various standard measures have been created.

1

The implementation of

these standards, though explicitly stated, is still open to variations which can affect the results.
The purpose of this study is to investigate the variations between implementations of the
standard measures through an international round robin. Round-robin studies have become
more frequent of late, with the recent third-phase round robin on room acoustical simulations
and the round robin on room acoustical measurement systems.

2,3

The goal of a round-robin

study is to limit the number of unknowns and challenge the community at large to solve a
common problem. In the case of standard measurement techniques and analysis, the ideal result
is that all answers are identical. If variances exist, and they are greater than the subjective
threshold of detection, then this is an indication that additional efforts must be made in standard
specifications or implementations in order to justify the measurement parameter. Otherwise, the
concept of a standard measure becomes trivial.

This study involves the comparison of current implementations of the measurement of

room acoustic parameters. Smaller studies of a similar nature, using either real or synthetic
impulse responses, have been performed. The study by Lundeby

4

examined the variations

between systems due to the entire measurement chain by providing a single room to participants.
Bradley

5

examined variations between entries of the measurement of an artificial reverberation

unit, thereby eliminating the variations of the physical response while allowing participants to
use measurement and analysis procedures of their choosing. Finally, Ikegame

6

provided a small

group of subjects with the measured room impulse response directly. Results of these studies, in
addition to those found here, are summarized at the end of the end of this work in Table 3. In
particular, this study examines the calculation phase of the measurement (post data acquisition)
in an attempt to separate data acquisition from analysis variances, which have often been studied
collectively. In keeping with the common practice of blind round-robin studies, the details of the
entries have not been disclosed. As such, the round-robin study is able to indicate when
variances occur, and to what degree, but not necessarily the exact cause.

While it is desirable to obtain measurements in good conditions, it is not always

possible, especially over all frequency ranges (i.e., due to background noise issues, transducer
limitations, etc.). For this reason, this study has used a real impulse response which contains,

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/158/7/$19.00

158

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

158

among other real-world conditions, a level of background noise which can corrupt certain
measures if not accounted for by the software.

2. Source impulse response

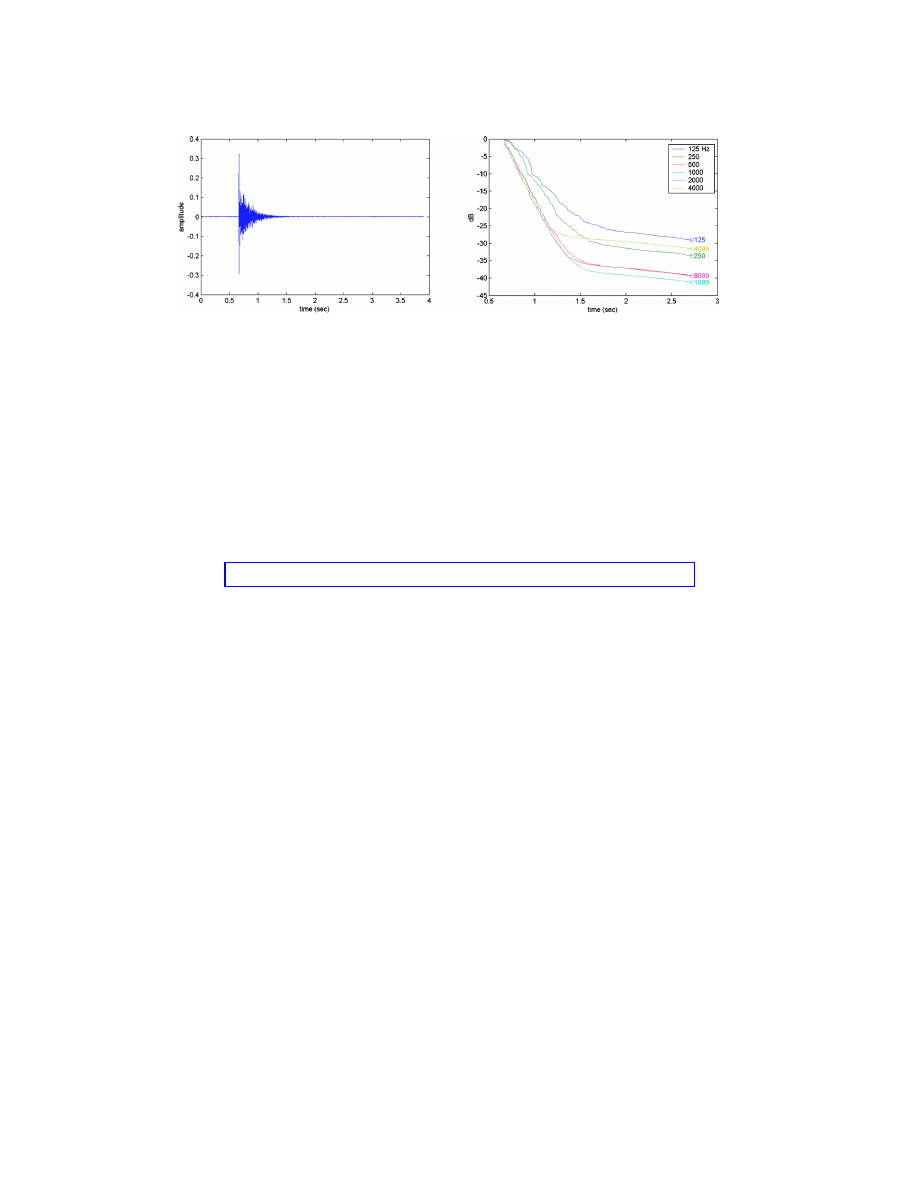
The source material for this study was a single monochannel impulse response, available as Mm
1 and shown in Fig. 1. The impulse response was measured in a lecture theater using a balloon
burst and an omnidirectional microphone, recorded directly onto a PC as a 16-bit ‘‘wav’’ file
with a sampling rate of 44.1 kHz. Aside from cropping the signal, no additional processing or
filtering was performed on the original signal recording.

Mm 1. Impulse response test signal (337 Mb). This is a file of type ‘‘wav’’ and should be available to authorized
reviewers and editors of ARLO.

The two key factors that separate a typical real impulse response from a synthetic re-

sponse are the presence of background noise and the nonideal decay behavior at lower frequen-
cies. To better understand the behavior of the test impulse response with regard to these issues,
the reverse Schroeder integration curves for the octave band-filtered signal, including back-
ground noise, are provided in Fig. 1. This analysis was not provided to the participants, as fil-
tering and analysis were part of the task to be performed (see Sec. 3). Note the nonideal linear
decay in the 125- and 250-Hz bands in addition to the various levels of background noise in each
octave band, identified by the horizontal tail at the end of the curve.

1

3. Parameters

Participants were invited to provide the following acoustical parameters based on the analysis of
the given test signal (Mm 1) in octave bands from 125–4000 Hz: reverberation time (T20, T30,
and/or other delimitations which are noted here as RTXX); early decay time (EDT-10 and/or
EDT-15); clarity (C50 and/or C80); and any other pertinent parameters that the user felt were
useful (contributed entries consisted of center time, Ts, and clarity, D50). The parameters and
their calculation details are all present in standard ISO 3382.

1

According to the standard, the

level of the noise floor should be at least 10 dB below the last used data point in any calculation
made from the decay curve. The calculation of all these parameters involves three basic tasks:
filtering the signal into various frequency bands, identification of the start of the impulse
response t

0

, and detection of the noise-floor level. Subsequent identifications are then needed

depending on the parameter in question, such as the 5-dB down point (for T20 and T30) and t

0

⫹80 ms (for C80). It is the execution of these tasks which is being evaluated in this study.
Compared to previous works using synthesized impulse responses, this study focuses on the
tasks which are affected by the use of real measured impulse responses. As such, the filtering
task should not be affected by the use of a real versus synthesized response and therefore is not
considered to be a contributing factor to any new variances found. The results of Bradley,

5

which

Fig. 1. (Left) Linear amplitude plot of source impulse response used in study. (Right) Reverse
Schroeder integration curves of octave band-filtered test signal. Curves are truncated and normal-
ized to 0-dB peak levels.

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/159/7/$19.00

159

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

159

used a synthesized response, can be taken as a best-case scenario for comparison with a real
impulse response.

Entries were also to be classified according to their level of human intervention

required (manual, semiautomated, fully automated) as pertaining to the selection of the
calculation points such as the start of the impulse response, the start and stop points for
interpolations, etc. As the source signal is a true measurement and not a synthetically generated
response, there are no ‘‘true’’ solutions to the response analysis. It is only expected that a
consensus would be arrived at from the various entries.

An important comparison to be made is that between the degree of variance in the

results and the just-noticeable difference (JND), or subjective limens, of the parameters. A
summary of pertinent studies and JND values is presented in Table 1.

4. Entries

Solicitation for participants in this study was done via several requests over email to numerous
persons involved in the research, development, and use of room acoustics analysis software. In
total, there were 19 different institution entries, from nine different countries, using 25 different
software packages, for a total of 37 different entries. Institution entries consisted of 57%
consultants, 38% research, and 5% software development. The software used was 40%
commercially available and 60% experimental. One clear sign from the summary is that many
research institutions and private consultants create their own developmental software for
impulse response analysis, rather than using commercial programs. For reasons of anonymity,
identifications of any specific entry are not made public. Commercial programs which have been
used by participants (submitted by developers and/or users) include the following:

AURORA

,

DBBATI32

,

DIRAC

,

SMAART

,

TEF

, and

WINMLS

. Additional participants who have consented to be

named include the following, in alphabetical order: Aercoustics Engineering Limited; Arup
Acoustics; Chiba Institute of Technology; Commins Acoustic Workshop; Centre Scientifique et
Technique du Ba`timent (CSTB); Dipartimento di Fisica Tecnica—Politecnico di Bari;
Dipartimento di Ingegneria—Universita` di Ferrara; Institute of Technical Acoustics—Aachen
University; Kahle Acoustics; Kirkegaard Associates; Laboratoire d’Informatique pour la
Me´canique et les Sciences de l’Inge´nieur (LIMSI)—CNRS; Peutz & Associates; Sound Space
Design, University of British Columbia; and Yamaha.

Not all parameters were reported by all entries. In addition, 44% of the entries for EDT

did not provide their calculation details (notation of EDT10 or EDT15). These results have
therefore been reported here simply as EDT. Analysis of EDT15 has been omitted due to the
limited number of entries.

Table. 1. Summary of subjective limens studies for relevant room acoustics parameters.

7–9

Percentage of correct

answers needed in the definition of the limen is stated. Individual octave band data was not available.

Reference

General details

JND

Ref. 7-Seraphim

共1958兲

共see Cremer-Ref. 10兲

75% detection difference
using decay noise bursts.
Values increase when
using nonexpert subjects.

RT

⬍0.6 s;

0.6

⬍RT⬍4.9;

jnd

⫽0.024 s

3%

⬍jnd⬍4%

Ref. 8-Cox et al. (1993)

50% detection difference
using simulated impulse

response (RT

⬃1.8 s)

compared results with
two music motifs.

Ts
C80

Handel

5.7

⫾0.9

0.44

⫾0.07

Mendelssohn

11.4

⫾2.7 ms

0.92

⫾0.22 dB

Ref. 9-Vo¨rlander

共1995兲

Rounded summary and
interpretation of
Cox

共1993兲 共Ref. 8兲.

T30
D50
Ts

5%
5%

10 ms

EDT

5%

C80

0.5 dB

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/160/7/$19.00

160

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

160

5. Results

The median values for the various parameters reported from the entries are summarized in Table
2. These values represent a general consensus on the acoustic parameters of the given test
impulse response. The degree to which this consensus is unanimous, and to what precision the
consensus adheres to the reliability of such a decision, is the key element in evaluating the
results.

Calculation of the reverberation time is generally the first and most basic calculation

made in impulse response analysis. Idealized as the time for the energy to decay by 60 dB (T60),
the standard measures are defined using the decay rate from

⫺5 to ⫺25 dB (T20) or to ⫺35 dB

(T30) with respect to the level at the start of the response. Results were collected for these
measures, as well as RTXX. The RTXX parameter allows for the user to freely define (or
intelligently define using human or automated techniques) the end limits of the RT calculation,
rather than using the precise definitions of T20 and T30. This action is common in most analysis
software so that users can correct by eye for the presence of background noise or other
anomalies and chose the ‘‘best’’ start/stop points for the analyses. The approach is the same for
all entries, though the choice of points may be different. A statistical summary of the
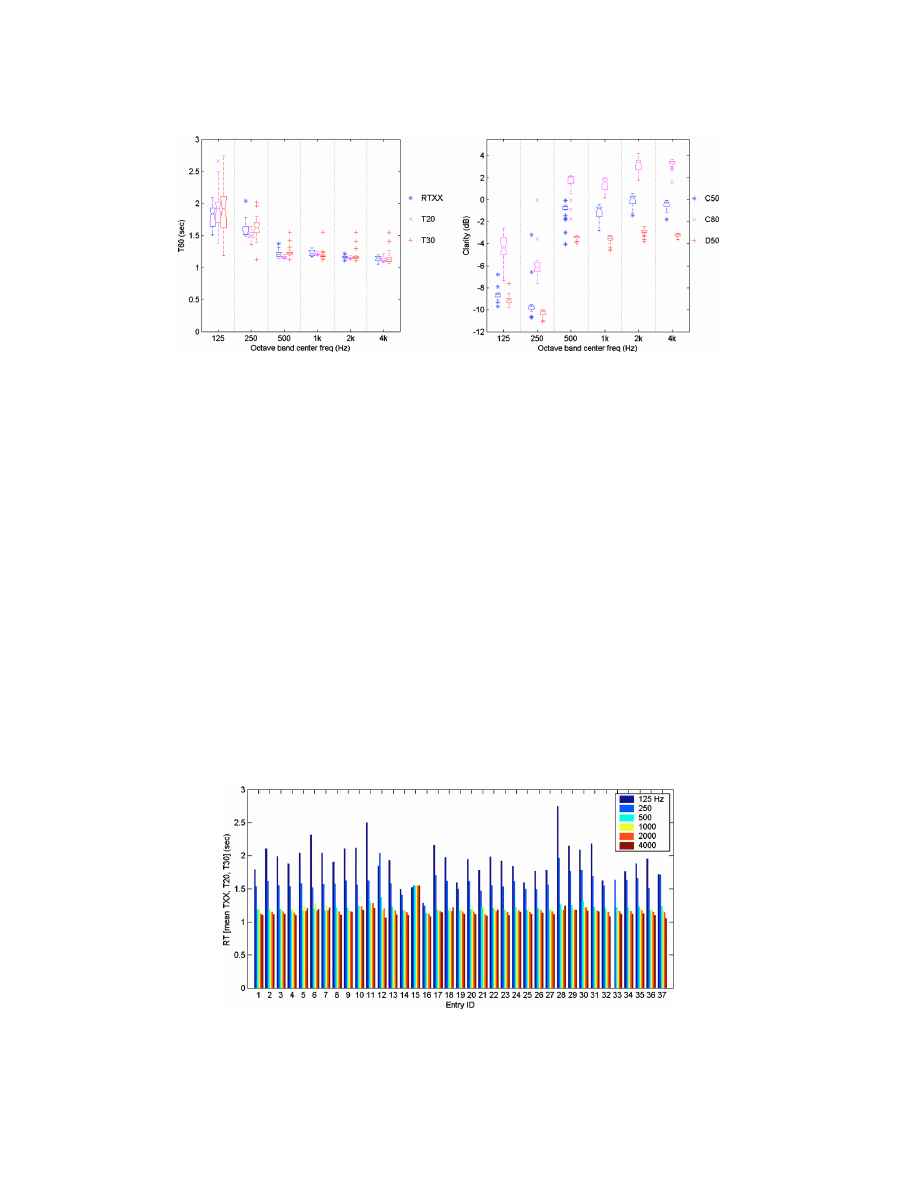
reverberation time entries (using notched whisker plots to show the median, confidence interval,
spread, main data extent, and outliers) is shown in Fig. 2. It was expected that the results for
RTXX would be better, with less variation, as they indicate some sort of intelligence behind the
calculation. This, interestingly, was not the case.

While generally consistent above 250 Hz, there are large variations between and within

the measured parameters at 125 and 250 Hz. The extremely large variations for T30 at 125 Hz
are a strong indicator of an inherent problem. In noting the level of background noise in the data
(as shown in Fig. 1), it is clear that there is not sufficient signal level to correctly calculate T30
(requiring 35 dB of clean signal above the noise floor). Using the standard rule of only including
data at least 10 dB above the noise floor, such that there is no corruption of the data by the noise,
then T30 would require 45 dB and T20 would require 35 dB of signal above the noise floor.
Accordingly, there is no suitable data for a T30 calculation, and only data in the 500–2K octave
bands is suitable for T20. Of all the entries, only five eliminated some data from the T30
calculation as being corrupted by noise, and only one entry eliminated all T30 and some T20
results as corrupt due to noise. It is possible that noise reduction or interpolation procedures
could be put into place to attempt to improve the apparent signal-to-noise ratio, but only one
entry stated that this was done. The individual entries for reverberation time are summarized in
Fig. 3 by showing individually the average reverberation time calculation, RTmean (the mean of
RTXX, T20, and T30) as provided by each entry.

One means of categorizing entries is to consider the level of human interaction

Table. 2. Median, standard deviation, and interquartile range value results for acoustic parameters in octave bands.
The interquartile range is formed by subtracting the 25th percentile of the data from the 75th percentile of the data,
providing an estimate of the spread of the main data while ignoring outliers. RTmean is the mean of

关RTXX, T20,

T30

兴 for each entry. Values for 4-kHz octave band result vary little from the 2-kHz octave band results.

Param

Median values

STD

IQR

125

250

500

1k

2k

4k

125

250

500

1k

2k

125

250

500

1k

2k

EDT

2.10

1.66

1.25

1.12

1.11

1.08

0.51 0.27 0.05 0.16 0.06 0.10 0.05 0.02 0.05 0.02

EDT10

2.18

1.69

1.25

1.12

1.11

1.07

0.19 0.12 0.13 0.16 0.17 0.13 0.06 0.03 0.02 0.02

RTXX

1.84

1.52

1.21

1.22

1.17

1.15

0.19 0.16 0.06 0.04 0.03 0.28 0.13 0.06 0.08 0.02

T20

1.92

1.51

1.16

1.21

1.14

1.11

0.33 0.07 0.02 0.01 0.02 0.32 0.09 0.02 0.02 0.02

T30

1.92

1.62

1.22

1.18

1.16

1.12

0.35 0.17 0.08 0.07 0.09 0.49 0.16 0.03 0.02 0.02

RTmean

1.93

1.57

1.21

1.19

1.16

1.12

0.28 0.14 0.07 0.06 0.07 0.33 0.10 0.05 0.03 0.02

C50

⫺8.6 ⫺9.7 ⫺0.6 ⫺0.8 0.2 ⫺0.3 0.5

1.6

0.9

0.8

0.6

0.3

0.3

0.3

0.9

0.7

C80

⫺4.4 ⫺6.1

2.1

1.7

3.4

3.5

1.1

1.3

0.9

0.6

0.7

1.5

0.8

0.7

1.0

0.8

Ts

179

161

80

82

70

73

11

14

9

10

8

6

4

4

3

4

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/161/7/$19.00

161

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

161

necessary. Considering RTmean, the mean values across frequencies are very similar with
respect to the mode of interaction, with the maximum variation between means being 0.1 s. In
contrast, the standard deviations show an interesting result. Variances for ‘‘manual’’ (17% of
entries) and ‘‘semiautomatic’’ (13% of entries) systems are quite similar across all frequency
bands. In contrast, ‘‘automatic’’ (70% of entries) systems had variances more than twice that of
the other systems for all but the 250-Hz band (where they were manual:0.18s, semiauto:0.10s,
and automatic:0.13 s). Standard deviation values in the 125-Hz band were approximately 0.15 s
for manual and semiautomatic and 0.32 s for automatic. These results clearly indicate
deficiencies in current automated routines.

In addition to reverberation time, the measures of clarity show a similar tendency, good

agreement at higher frequencies and less at lower frequencies. A statistical summary for clarity
measures, being C50, C80, and D50, is shown in Fig. 2.

An overall comparison of the distribution of entry results with regard to the subjective

limens is essential. Two methods of comparison are used to judge the spread of the data,
presented in Table 2. The first uses a measure of the standard deviation calculated from all
entries. As there are a number of entries that have results outside the general population
(outliers, indicated by individual markers in the various figures) a second calculation of the
spread is used instead of the standard deviation. The interquartile range, which is calculated by

Fig. 2. (Left) Reverberation time calculation results summary showing RTXX (left), T20 (cen-
ter), and T30 (right). (Right) Clarity calculation results showing C50 (left), C80 (center), and D50
(right). Values for D50 submitted as % have been converted to D50 dB using: 10
⫻log10(D50%/100).

Fig. 3. Mean reverberation calculation (RTXX, T20, and T30) for each entry in octave bands.

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/162/7/$19.00

162

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

162

subtracting the 25th percentile of the data from the 75th percentile of the data, is a robust
estimation. These results better represent the general consensus of the entries. If larger than the
STD results, this indicates the lack of outliers and the STD should be used.

The similarities between the results shown and the subjective limens in Table 1 are

disturbing. Regarding measurements of reverberation time (including EDT) and center time, Ts,
the variations between analysis systems is comparable to perceivable differences. In the case of
clarity measures, the analysis systems present a variance which is greater by a factor of 2,
illustrating that measured C80 values are only reliable within two subjective limens. A summary
of results and the results from similar studies for the 1-kHz octave band are presented in Table 3.

6. Conclusion

This study has presented the results of a room acoustic analysis software round robin using a real
measured impulse response, with 37 entries. The test signal included a non-negligible level of
background noise in the lower frequency bands. While it is clear that a test example with a
strong reflection, as used by Ikegame,

6

or double-slope decay would present different challenges

to the analyses software entries, the purpose of this study is not to find all the shortcomings
possible, but to highlight a rather fundamental problem in the systems. This limitation is the
handling of background noise, an issue in all real measurements. There are other variations

Table. 3. Summary of measurement error studies for relevant room acoustic parameters in the 1-kHz octave
band

共Refs. 4–6兲.

Reference

Type of test results

1-kHz octave bands data

Ref. 4-Lundeby
共1995兲

Standard deviation of room
acoustic parameter
measurement results for a

real room

共RT ⬃1.2 s).

This study included
the entire measurement system.

T30

6%

EDT

6%

D50

8%

C80

0.6 dB

Ts

7%

Ref. 5-Bradley
共1996兲

Standard deviation of ‘‘better’’
room acoustic parameter
measurement results for a
reverberation unit

共three settings.

RT

⬃1.3,⬃2, & ⬃1.4 s).

⬃1.3

⬃2

⬃1.4

RT

0.025
共⬃2%兲

0.025
共⬃1%兲

0.012 sec
共⬃1%兲

EDT

0.163

0.034

0.011 sec

C50

0.097

0.069

0.238 dB

C80

0.090

0.166

0.121 dB

Ts

1.6

1.7

2.8 msec

Ref. 6-Ikegame
共2001兲

Difference between minimum
and maximum value of room
acoustic parameter measurement
results for a real room impulse

response

共RT ⬃1.4 s).

RT

0.1 s (

⬃7%) EDT

0.3 sec

C50

1 dB

D50

7%

Ts

10 ms

Katz
共present
study

兲

Standard deviation of room
acoustic parameter measurement
results for a real room impulse

response (RT

⬃1.2s) with

background noise.

T20

1%

RTmean

5%

EDT/EDT10

14%

Ts

10 ms

C50

0.8 dB

C80

0.6 dB

Interquartile range representing the
variance of ‘‘better’’ room acoustic
parameter measurement results for
a real room impulse response

(RT

⬃1.2 s) with background noise.

T20

EDT
C50
Ts

2%

4%
0.9 dB
3 ms

RTmean

EDT10
C80

3%

2%
1.0 dB

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/163/7/$19.00

163

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

163

between systems, as seen in the summary graph and tables, but the problems regarding
background noise are overwhelmingly apparent and show a strong divergence from previous
works which have utilized synthesized responses.

The results of this study indicate that there is a substantial degree of variation between

current impulse response analysis software, even when isolated from the measurement system.
The variances in the 1-kHz octave band (where noise corruption was not a serious issue) are
comparable to or greater than subjective difference limens, with the degree of variance greatly
increasing for the lower octave bands. For the general collection of results (ignoring aberrant
entries) variances of 1-kHz values of reverberation times (and related indices) are slightly
smaller than difference limens: 2%–4% as compared to a limen of 5%, with the full spread of
data containing standard deviations of up to 14%. Variances of clarity values exceed the
difference limens: 0.6–1.0 dB as compared to a limen of 0.5 dB. These variances are not due to
treatment of noise-floor level. Determination of t

0

is more difficult in the lower frequency bands

where filtering broadens the response. In addition, various notions exist for the definition and
determination of t

0

, including the maximum of the response, using an onset threshold, and using

a drop threshold in the decay curve. The procedure for start time is not defined and some
variations, as found in clarity where the establishment of t

0

is crucial, could very likely cause

such errors. Center time results are within the difference limen.

In light of the attention shown toward comparisons of measurement systems and room

acoustic prediction software, the lack of coherence in the analysis of the resulting impulse
response is disturbing to this author. While essentially calibrated well for idealized synthesized
impulse responses, the addition of real-world conditions has resulted in further discrepancies
and disagreement between competing software. Furthermore, it appears that the current
standard is insufficient (either in theory or due to generally poor implementations) to be
considered as both an implemented and working standard, when considered in respect to the
results found here. Further investigation is needed to determine the cause and determine
potential modifications to the standard necessary to alleviate these variations. While the
introduction of software certification is not expected, issues of software falsely claiming to be
performing measures in accordance with the standard need to be addressed in some manner.

Acknowledgment

The author would like to thank all those who participated in this study.

References and links

1

ISO 3382:1997 Acoustics—Measurement of the reverberation time of rooms with reference to other acoustical
parameters.

2

I. Bork, ‘‘Simulation and measurement of auditorium acoustics—The round robins on room acoustical simula-
tion,’’ Proceedings of the Institute of Acoustics v.24, Part 4, 2002.

3

NPL workshop on ‘‘Acoustic Measurements in Auditoria and Listening Rooms,’’ July 2002, http://
www.npl.co.uk/acoustics/publications/acnews/11/, results not published to date.

4

A. Lundeby, T. E. Vigran, H. Bietz, and M. Vo¨rlander, ‘‘Uncertainties of measurements in room acoustics,’’ Acus-
tica 81, 344–355 (1995).

5

J. S. Bradley, ‘‘An international comparison of room acoustic measurement systems.’’ Institute for Research in
Construction, IRC Internal Report IRC-IR-714, Jan. 1996.

6

M. Ikegame and K. Uchida, ‘‘Comparison of various types of acoustic indexes calculated from the same impulse
response,’’ (in Japanese), Proceedings of the Symposium on Impulse Response Measurements and Evaluation of
Acoustic Indexes, Architectural Institute of Japan, April 2001, pp. 7–13.

7

H. P. Seraphim, ‘‘Untersuchungen u¨ber die Unterschiedsschwelle exponentiellen Abklingens von Rauschbandim-
pulsen’’ (Investigations on the difference limen of exponentially decaying bandlimited noise pulses) (in German)
Acustica 8, 280–284 (1958).

8

T. J. Cox, W. J. Davies, and Y. W. Lam, ‘‘The sensitivity of listeners to early sound field changes in auditoria,’’
Acustica 79, 27–41 (1993).

9

M. Vo¨rlander, ‘‘International round robin on room acoustical computer simulations,’’ Proceedings 15th ICA
Trondheim, June 1995, pp. 689–692.

10

L. Cremer, and H. A. Mu¨ller, Principles and Applications of Room Acoustics, translated by T. Schultz (Applied
Science Publishers, London/New York, 1982), Vol. 1.

Brian F. G. Katz: Acoustics Research Letters Online

[DOI: 10.1121/1.1758239]

Published Online 23 August 2004

1529-7853/04/5(4)/164/7/$19.00

164

ARLO 5(4), October 2004

© 2004 Acoustical Society of America

164