IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

27

Step Construction of Visual Cryptography Schemes

Feng Liu, Chuankun Wu, Senior Member, IEEE, and Xijun Lin

Abstract—Two common drawbacks of the visual cryptography

scheme (VCS) are the large pixel expansion of each share image
and the small contrast of the recovered secret image. In this paper,
we propose a step construction to construct VCS

OR

and VCS

XOR

for general access structure by applying (2,2)-VCS recursively,
where a participant may receive multiple share images. The pro-
posed step construction generates VCS

OR

and VCS

XOR

which

have optimal pixel expansion and contrast for each qualified set
in the general access structure in most cases. Our scheme applies
a technique to simplify the access structure, which can reduce the
average pixel expansion (APE) in most cases compared with many
of the results in the literature. Finally, we give some experimental
results and comparisons to show the effectiveness of the proposed
scheme.

Index Terms—Secret sharing, step construction, visual cryptog-

raphy.

I. I

NTRODUCTION

T

HE basic principle of visual cryptography scheme (VCS)
was first introduced by Naor and Shamir. The idea of the

visual cryptography model proposed in [1] is to split a secret
image into two random share images (printed on transparencies)
which separately reveal no information about the original secret
image. The secret image is composed of black and white pixels.
The original secret image can be recovered by superimposing
the two share images together. The underlying operation of such
a scheme is the logical operation

OR

. Generally, a

-VCS

takes a secret image as input, and outputs

share images that

satisfy two conditions: First, any

out of

share images can

recover the secret image; second, any less than

share images

cannot get any information about the secret image.

Similar models of visual cryptography with different under-

lying operations have been proposed, such as the

XOR

operation

introduced in [2]–[6], and the

NOT

operation introduced in [7],

which uses the reversing function of the copy machines. Denote

as the

XOR

operation,

as the

OR

operation,

as

the

AND

operation, and

as

NOT

operation; then, we have the

following relation between the operations

XOR

and

OR

:

Manuscript received June 03, 2009; accepted October 09, 2009. First pub-

lished December 01, 2009; current version published February 12, 2010. This
work was supported by China national 973 Project 2007CB807902 and Project
2007CB311202, by NSFC Grant 60873260 and Grant 60903210, and by China
National 863 Project 2009AA01Z414. The associate editor coordinating the re-
view of this manuscript and approving it for publication was Prof. Ton Kalker.

F. Liu and C. Wu are with The State Key Laboratory of Information Security,

Institute of Software, Chinese Academy of Sciences, Beijing 100190, China
(e-mail: [e-mail]; [e-mail]).

X. Lin is with the Department of Computer Science and Technology, Ocean

University of China, Qingdao 266100, China (e-mail: [e-mail]).

Digital Object Identifier 10.1109/TIFS.2009.2037660

i.e., the

XOR

operation can also be achieved by the operation

OR

and

NOT

, which is implemented by using a copy machine with

the reversing function.

In the following, we will consider the VCS both under the op-

erations

XOR

and

OR

. To simplify the discussion, the notion VCS

means a visual cryptography scheme regardless of the under-
lying operation, and we use the notations VCS

and VCS

to denote the visual cryptography scheme with particular under-
lying operations

XOR

and

OR

respectively.

Traditionally, visual cryptography schemes are evaluated by

two parameters: the pixel expansion, which is the number of
subpixels that each pixel of the original secret image is encoded
into, and the contrast, which reflects the visual quality of the re-
covered secret image. From the point of view of the participants,
the pixel expansion is expected to be as small as possible, and
the contrast is expected to be as large as possible. Many studies
focused on improving the properties of pixel expansion and con-
trast [8]–[11], [7], [12]. Also studies have tried to trade the pixel
expansion for the contrast [13].

In this paper, we propose a step construction which generates

VCS

and VCS

that, in most cases, have optimal pixel

expansion and contrast for each qualified set in the general ac-
cess structure. Because each participant in the proposed scheme
may have multiple share images with different pixel expansions,
so we introduce the notion average pixel expansion (APE, for-
mally defined in Section III). The proposed scheme can also re-
duce APE in many cases compared with the known results in the
literature. With our step construction, the VCS with general ac-
cess structure can be constructed only by applying a (2,2)-VCS
recursively, for both the

OR

and

XOR

operations. This result is

important for the reason that the construction of VCS

for

the general access structure was once thought as impossible be-
fore. Finally, we give the experimental results and comparisons
to show the effectiveness of our scheme compared to the known
results in [14], [2].

The rest of this paper is organized as follows. In Section II, we

give some definitions about the VCS. In Section III, we propose
the step construction of VCS for the general access structure.
In Section IV, we give some experimental results and compar-
isons to show the effectiveness of our scheme, and the paper is
concluded in Section V.

II. P

RELIMINARIES

Suppose all the participants of an access structure form a set

. The specification of all qualified and for-

bidden subsets of participants constitutes an access structure

. Denote

as the set of qualified sets (the par-

ticipants in a qualified set can collaboratively recover the secret
image), and

as the set of forbidden sets (the participants in

a forbidden set cannot recover the secret image). Obviously, we
have

. In this paper, we only consider access

1556-6013/$26.00 © 2010 IEEE

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

28

IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

structures with

, where

is the power set

of

, i.e., the set of all the possible subsets of

. The set

is monotone because of that, if part of the participants in a set

can recover the secret image, then obviously all the

participants in

can recover the secret image as well. We de-

fine

and

We call

the minimal qualified access structure, and a subset

is called the minimal qualified set. We call

the

maximal forbidden access structure, and a subset
is called the maximal forbidden set. For any

, define

. We call

the

closure

of . Since

is monotone, then

.

This means that the qualified access structure

and the min-

imal qualified access structure

are determined by each other.

Similarly,

and

can be determined by each other as

well. Furthermore, because

, we have that

and

can be determined by each other. So when we dis-

cuss a general access structure, we only need to give discussions
based on its minimal qualified access structure

in the fol-

lowing of this paper.

Particularly, we call a qualified set

that has the

largest cardinality the maximum qualified set of

. Formally,

the maximum qualified set

satisfies

. Note that, the maximum qualified set of

may not be

, and there may be several maximum qualified sets in

.

It should be pointed out that, the threshold access structure is a

special case of the general access structure, because a threshold

access structure is a general access structure with the fol-

lowing constraints:

and

In a VCS, there is a secret image which is encrypted into

some share images. The secret image is called the original secret
image

for clarity, and the share images are the encrypted images

(and are called the transparencies if they are printed out). When
a qualified set of share images (transparencies) are stacked to-
gether properly, it gives a visual image which is almost the same
as the original secret image; we call this the recovered secret
image

. In the case of black and white images, the original se-

cret image is represented as a pattern of black and white pixels.
Each of these pixels is divided into subpixels which themselves
are encoded as black and white to produce the share images. The
recovered secret image is also a pattern of black and white sub-
pixels which should visually reveal the original secret image if
a qualified set of share images is stacked.

In this paper, we will focus on the black and white images,

where a white pixel is denoted by the number 0 and a black pixel

is denoted by the number 1. We notice that the definitions of
VCS under

OR

and

XOR

operation are quite similar. We will give

some definitions about visual cryptography under the operation
“ ”, which can either be the

OR

operation such as in [1] or the

XOR

operation such as in [2]. In this paper, we use the subscripts

and

for emphasizing different underlying operations

when necessary.

Because the proposed constructions in this paper are all based

on the traditional

-VCS, we first give the definition of the

traditional

-VCS.

For a vector

, denote

as the Hamming

weight of the vector , i.e., the number of nonzero coordinates
in . A

-VCS, denoted by

, consists of two col-

lections of

binary matrices

and

. To share a white

(respectively, black) pixel, a dealer (the one who sets up the
system) randomly chooses one of the matrices, called a share
matrix

, in

(respectively,

) and distributes its rows (rep-

resenting a pattern of subpixels in the share image) to the
participants of the scheme, i.e., giving row

to participant

. More precisely, we give a formal definition of

-VCS as follows.

Definition 1:

Let

and

be nonnegative integers satis-

fying

. The two collections of

binary matrices

constitute a visual cryptography scheme

-VCS

if there exist a value

and satisfies:

1) (Contrast) Any

participants can recover the secret image

by stacking (the “ ” operation) their share images. More
precisely, for any

, the stacking (the “ ” operation)

of any out of

rows of is a vector that satisfies

, whereas for any

, we have

.

2) (Security) Any less than participants have no information

about the secret image. More precisely, for any

in

with

, the two collections

of

matrices

,

, obtained by restricting

each

matrix in

, to rows

, are

indistinguishable in the sense that they contain the same
matrices with the same frequencies.

In the above definition,

is called the pixel expansion of the

scheme, and each secret pixel is represented by

subpixels in

the recovered secret image. We denote

and

as the

pixel expansions under the operation

OR

and

XOR

, respectively.

The

defined above is called the contrast and is related to

the visual quality of the recovered secret image. For different
operations

OR

and

XOR

, we use the notations

and

,

respectively. In fact, there are several definitions about contrast
in the literature; we use the simple one to simplify the discus-
sion, and this definition of contrast has also been used in [1],
[14], etc.

The implementation of VCS has two phases: the distribution

phase and the reconstruction phase. In the distribution phase,
the dealer generates all the share images and distributes them
to the participants; in the reconstruction phase, the participants
reconstruct the secret image by stacking a qualified set of share
images.

The (2,2)-VCS, for

OR

and

XOR

operations, respectively, is as

follows:

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

LIU et al.: STEP CONSTRUCTION OF VISUAL CRYPTOGRAPHY SCHEMES

29

Example 1:

The

-VCS

:

and

The (2,2)-VCS

:

and

In Example 1, for the (2,2)-VCS

, the pixel expansion and

contrast are

and

, respectively, i.e.,

the size of the recovered secret image and share images will
be twice the size of the original secret image. The contrast of
the recovered secret image will be half of that of the original
secret image. For the (2,2)-VCS

, we have that,

and

, i.e., the recovered secret image is identical to

the original secret image and the share images have no pixel
expansion.

III. S

TEP

C

ONSTRUCTION OF

VCS

FOR

G

ENERAL

A

CCESS

S

TRUCTURE

In this section, we give a formal definition of step construc-

tion VCS. We propose the step construction of general access
structure VCS in Construction 3, which is based on two sim-
pler step constructions: Construction 1 and Construction 2 in
Section III-A and Section III-C, respectively.

A. Definition of Step Construction and Step Construction of

-VCS

In this section, we first show the formal definition of step con-

struction VCS, and then give a step construction of

-VCS

in Construction 1.

Recall that

and

are the minimal qualified access

structure and the maximal forbidden access structure of

, respectively. The formal definition of step

construction VCS is as follows.

Definition 2:

Denote

as an access structure on the par-

ticipant set

. The step construction

-VCS

exists if there exist values

and

satisfying:

1) (Contrast) Any qualified set of participants can recover the

secret image by stacking (the “ ” operation) their share
images. More precisely, for any share images in a quali-
fied set

with pixel expansion

, respectively, let

,

then the adjusting stacking (the “ ” operation) of the share
images

can recover the secret image.

If the secret pixel is black, the adjusting stacking (the
“ ” operation) of

is a vector

that satisfies

, whereas for a white secret pixel, we have

.

2) (Security) Any forbidden set of participants has no infor-

mation about the secret image. More precisely, for any for-
bidden set

, there exist a participant , then the

share images of set

, after being adjusted, form a

VCS under the Definition 1, where

is a forbidden set of

the VCS under the Definition 1.

In the above definition, because a qualified set of share im-

ages may have different pixel expansion when they are stacked,
they should first be adjusted to the same size, i.e., the share im-
ages

should be expanded by replicating their sub-

pixels for

times, respectively. The ad-

justing stacking makes sense because the share images need to
be stored, and only need to be expanded when used to recover
the secret image. Apparently a smaller share image is more con-
venient to preserve. Furthermore, the VCS often carries impor-
tant secret information, however, it does not provide authenti-
cation ability. Hence, the participants should authenticate other
participants by other authentication means. Therefore, it is rea-
sonable to assume that the participants have authenticated each
other before stacking their share images, i.e., they can know,
in advance, the exact set of participants who are going to stack
their shares. According to the step constructions proposed in this
paper (Construction 1, Construction 2, and Construction 3), any
participant can know, in advance, the size of other participants
share images. This also implies the reasonableness of the adjust
stacking.

According to the security condition of Definition 2, a for-

bidden set of share images of VCS under Definition 2 is also
a forbidden set of share images under Definition 1, hence the
security condition of Definition 2 is no weaker than that of Def-
inition 1.

Note that, for the security condition of Definition 2, we only

need to guarantee that any set in

cannot recover the secret

image, because, for any forbidden set

, there exists

a set in

, denoted by

, satisfying

. It is clear that

if

cannot get any information about the secret image, then

cannot either.

In a traditional VCS, each participant takes one share image

and all the share images have the same pixel expansion. How-
ever, in the proposed construction of this paper, each of the par-
ticipants may take multiple share images with different pixel
expansions. So, in the following part, we list the pixel expan-
sions of all the share images for each participant. We compute
the average pixel expansion (APE) as well, where the APE is
defined as the average value of the total pixel expansions of the
share images that each participant holds.

Particularly, for a set of participants

, we define the pixel

expansion of

as the largest pixel expansion of the share images

of

. If

is a qualified set, then define the contrast of

as the

contrast of the recovered secret image after adjusting stacking.

The participants may have multiple share images, and dif-

ferent qualified sets of share images may result in different con-
trasts. So, in the following part of this paper, we will list all the
possible contrasts of the proposed VCS.

To make things clearer, we give the following example for the

step construction of (3,3)-VCS.

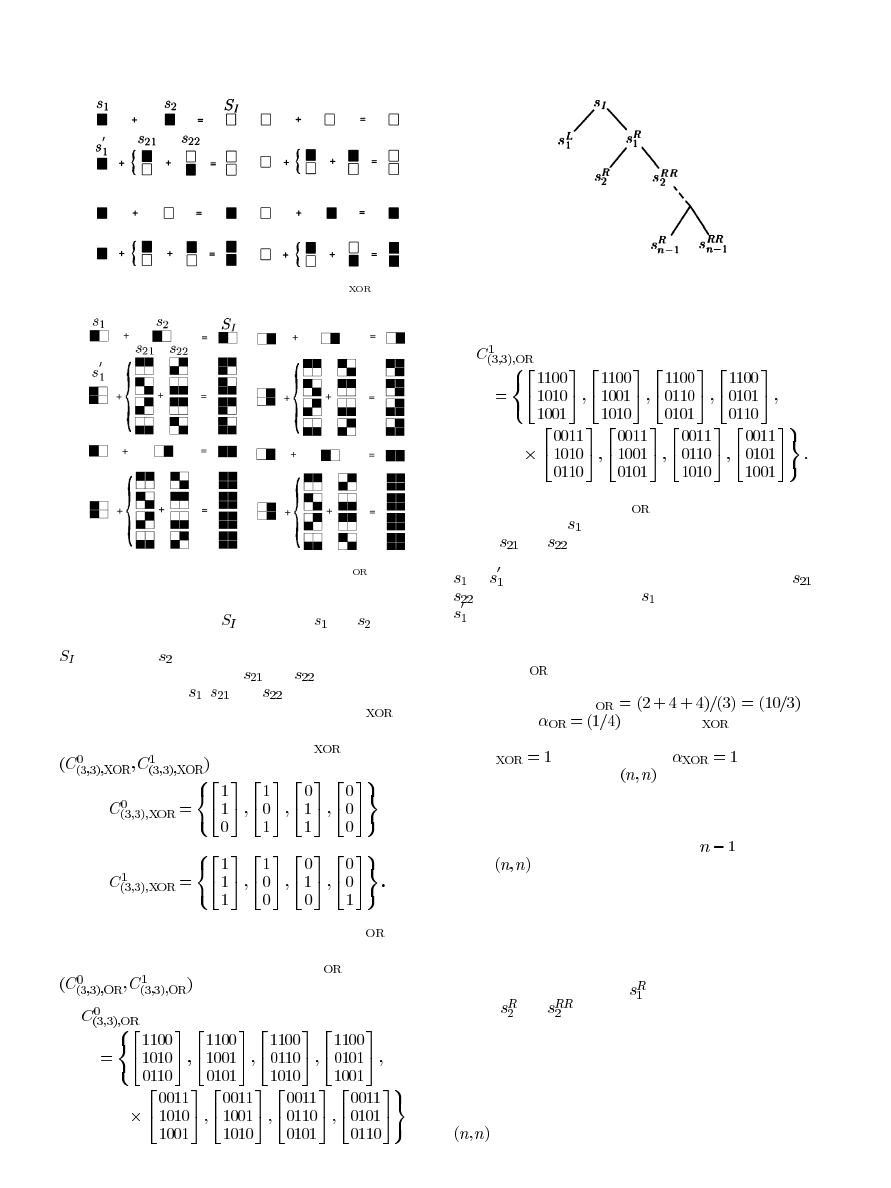
Example 2:

The step construction of (3,3)-VCS can be real-

ized by applying traditional (2,2)-VCS twice. Denote the secret

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

30

IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

Fig. 1. The step construction of the (3,3)-VCS

.

Fig. 2. The step construction of the (3,3)-VCS

.

image of the (3,3)-VCS as

, and denote

and

as the two

share images of the (2,2)-VCS by encrypting the secret image

. Then taking

as the secret image of a new (2,2)-VCS, we

get another two share images

and

. It is easy to verify

that the share images

,

, and

constitute a (3,3)-VCS.

Fig. 1 depicts the step construction of (3,3)-VCS

.

According to Fig. 1, the corresponding collections

of

share

matrix

of

the

(3,3)-VCS

,

denoted

as

, are as follows:

and

Fig. 2 depicts the step construction of (3,3)-VCS

.

According to Fig. 2, the corresponding collections

of

share

matrices

of

the

(3,3)-VCS

,

denoted

as

, can be as follows:

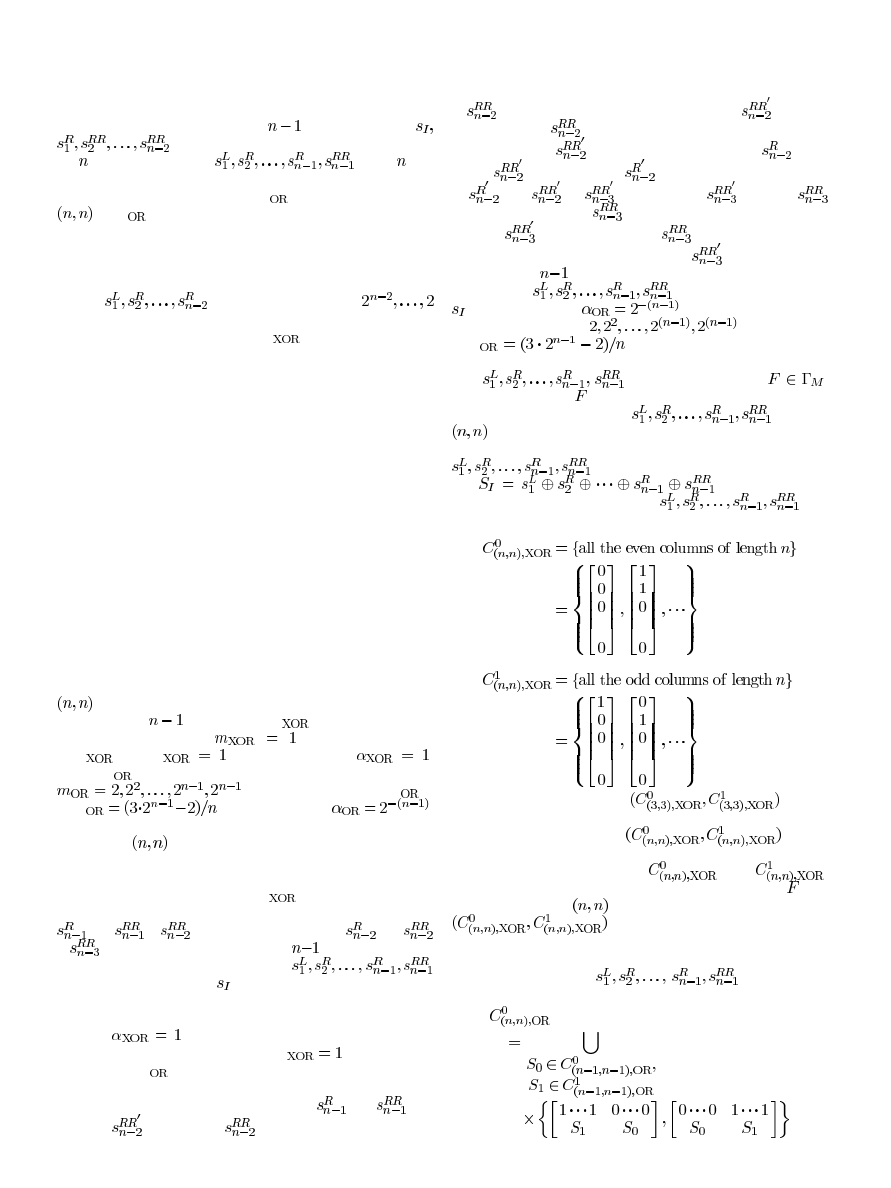
Fig. 3. The construction tree for the

(n; n)-VCS.

and

In Example 2, for the VCS

in Fig. 2, the pixel expansion

of the share image

is 2, and the pixel expansion of the share

images

and

is 4. So in the reconstruction phase, the par-

ticipants should first adjust (enlarge) the smaller share image

to

which is of the same size as the other share (

or

). We call the share image

the primary share image of

. The dealer only needs to distribute the primary share im-

ages to the participants, because the participants can expand
their share images easily in the reconstruction phase. Hence,
for the VCS

, the pixel expansions for the share images of

the three participants are 2, 4, and 4, respectively, the average
pixel expansion is APE

, and

the contrast is

. For the VCS

, the pixel expan-

sions are 1, 1, and 1, respectively, the average pixel expansion
is APE

, and the contrast is

.

For step construction of

-VCS, we start with a (2,2)-

VCS, and by taking one of its share images as the secret image
of another (2,2)-VCS, we get a (3,3)-VCS; then we take one of
the newly generated share images as the secret image of another
(2,2)-VCS, and so on, repeat the process

times, and then

get an

-VCS (Construction 1). The procedure can be de-

scribed by using the binary tree (Fig. 3). We call such a binary
tree the construction tree, and we call this kind of construction
the step construction.

In a construction tree, once a (2,2)-VCS is applied, we gen-

erate two new share images out of a “secret image;” we call
such a generation of share images the dividing generation. For
example, the “secret image”

is divided into two new share

images

and

.

Because the construction tree depicts how to generate the

share images precisely, hence in the proposed Constructions 1,
2, and 3 of this paper, we only provide the construction trees in-
stead of the detailed text descriptions for explicit access struc-
tures.

Formally, we give the following step construction of

-VCS.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

LIU et al.: STEP CONSTRUCTION OF VISUAL CRYPTOGRAPHY SCHEMES

31

Construction 1:

As the construction tree of Fig. 3 depicts, we

apply the traditional (2,2)-VCS for

times which takes

as the secret images in turn, and distributes

the

share image images

to the

par-

ticipants, respectively.

For the step construction of VCS

, the share images of the

-VCS

may not have the same pixel expansions. So, in

the distribution phase, the dealer distributes the primary share
images to the participants, and in the reconstruction phase, the
participants adjust the smaller share images to the size of the
largest share image before stacking. More precisely, the share
images

should be expanded by

times, respectively.

For the step construction of VCS

, because all the share

images have the same pixel expansion, the participants do not
need to adjust their share images.

It should be pointed out that the construction trees of this

paper all satisfy that at most one of the two share images of a
dividing generation is divided by other dividing generation, i.e.,
there does not exist the case that both the two share images of a
dividing generation are divided by another dividing generation.

The reason that we do not divide both the share images of

a dividing generation is to avoid the bad visual quality of the
recovered secret image. In fact, if both the share images of a di-
viding generation are divided, then the newly generated share
images will not satisfy the contrast condition of Definition 2 (or
equivalently that of Definition 1) any more, and the newly gener-
ated share images will form a probabilistic visual cryptography
scheme (PVCS), which was introduced in [15] and [16]. How-
ever, the PVCS has bad visual quality of the recovered secret
image, and Yang et al. has pointed out the phenomenon in [15]
and given some simulations about the visual quality of PVCS.

We conclude the above discussion as the following theorem.
Theorem 1:

Construction 1 is a step construction of

-VCS which is realized by applying traditional (2,2)-VCS

recursively for

times. For VCS

, the pixel expansion

for each share image is

, and the APE of the

VCS

is APE

, and the contrast is

.

For VCS

, the pixel expansions for the share images are

, and the APE of the VCS

is

APE

, and the contrast is

.

Proof:

In order to prove that Construction 1 is a step con-

struction of

-VCS, we need to prove that it satisfies the

contrast and security conditions of Definition 2.

First, we prove the contrast condition. According to the con-

struction tree of Fig. 3, for the VCS

, the adjusting stacking

procedure is as follows: The stacking result of the share images

and

is

, and the stacking result of

and

is

. When we repeat the process for

times, we have that

the stacking result of the share images
recovers the secret image

, which means that, a black pixel

in the secret image is represented by a black pixel and a white
pixel in the secret image is represented by a white pixel. Hence,
we have

and the pixel expansions of all the share

images equal to 1, which implies APE

.

For the VCS

, the adjusting stacking procedure is as fol-

lows: According to the share matrices in Example 1, we have
that the stacking result of the share images

and

, de-

noted by

, recovers the

. More precisely, a black pixel

in

is represented by two black subpixels in

, whereas

a white pixel in

is represented by a black subpixel and a

white subpixel in

. Then adjust the share image

to the

size of

, and denote it as

. Denoting the stacking result

of

and

as

, we have that

recovers

where a black pixel in

is represented by four black sub-

pixels in

, and a white pixel in

is represented by three

black subpixels and a white subpixel in

. When we repeat

the process for

times, we have that the adjusting stacking of

share images

recovers the secret image

, and the contrast is

and the pixel expansions

of the share images are

, which implies

APE

.

Then we prove the security condition. Consider the share im-

ages

. For any forbidden set

,

the participants of

lack one of these share images. We

prove that the share images

form an

-VCS under the security condition of Definition 1.

For

the

XOR

operation,

the

stacking

of

recovers

the

secret

image,

i.e.,

. We have that the

share matrices corresponding to

can

be as follows:

..

.

..

.

and

..

.

..

.

where a simple example of

can be

found in Example 2.

It is easy to verify that

satisfy

the security condition of Definition 1, where by deleting one
row of the share matrices in

and

,

we will get the same collection of submatrices; i.e.,

is a

forbidden set of the

-VCS under the Definition 1. Hence,

also satisfy the security condition of

Definition 2.

For the

OR

operation, similarly, we have that the share ma-

trices corresponding to

can be as fol-

lows:

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

32

IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

and

where a simple example of

can be found

in Example 2.

It is easy to verify that

satisfy the

security condition of Definition 1 via simple inductive proof,
where by deleting one row of the share matrices in
and

, we will get the same collection of submatrices,

i.e.,

is a forbidden set of the

-VCS under the Definition

1. Hence,

also satisfy the security con-

dition of Definition 2.

From Theorem 1, for the

-VCS

, it is easy to see that,

the largest pixel expansion of the share images is

.

The pixel expansion grows exponentially on the number of the
participants . However, it is still the optimal value. This is seen
in [1, Theorem 4.3]. (Another study [11] about the contrast of

-VCS confirms this bound).

Theorem 2 ([1]):

In any

-VCS

and

.

Note that the study in [1] did not consider the technique of ad-

justing stacking. Theorem 1 confirms Theorem 2 after adjusting
the size of the share images of Construction 1.

For the

-VCS

, according to Definition 1, it is ob-

vious that,

and

. Hence, the step

construction for the

-VCS also generates the VCS

with optimal pixel expansion

and optimal contrast

.

The above discussions can be summarized as the following

theorem.

Theorem 3:

The step construction of Constriction 1 gener-

ates the

-VCS

and

-VCS

with optimal pixel

expansion and contrast.

B. Simplifying the Access Structure by Using Equivalent
Participants

Now, we introduce the concept of equivalent participants

(equivalent participants can be viewed as the participants who
have the same rights). Participant is equivalent to

in a secret

sharing scheme means that they can be assigned to identical
shares without affecting the access structure of the secret
sharing scheme. Formally, we define the equivalent participants
as follows.

Definition 3 [17, Definition 2.1]:

Denote

as an access

structure on participant set

. If participants

and

satisfy that, for

hold iff

hold,

then participants and are called to be equivalent participants
on

, denoted by

.

It is easy to verify that

is an equivalence relation on

. Then

we can simplify the access structure

based on the equivalent

participants as follows:

Definition 4 [17, Definition 2.2]:

Denote

as an access

structure on participant set

. Let

be the

quotient set of

on the equivalence relation

. We call

the simplified access structure

on

, where is the equivalence class of (simply we call the

corresponding participant of , and the set

is called the corresponding set of

). When

, we

call

the most simplified access structure.

At this point, we can construct VCS for the most simpli-

fied access structure instead of the original access structure. To
demonstrate how to simplify an access structure, we give the
following example.

Example

3:

For

the

access

structure

on

, we

have that,

, hence, we have

4 and

3. Then

. We can distribute the

identical share images to participants 1 and 4 (respectively, 2
and 3). Hence, we only need to construct a (2,2)-VCS for the
access structure

. Then distribute the first share image to

participants 1 and 4, and the second share image to participants
2 and 3. Hence, we constructed a VCS for the access structure

by constructing VCS for its simplified access structure

.

According to Definitions 3 and 4, the following Theorem 4

becomes obvious.

Theorem 4:

Let

be an access structure with equivalent

participants on the participant set

, denote

as the quotient

set of

on the equivalent relation

. Let

, we have that by distributing the share images

of corresponding participants to the equivalent participants, a
construction of VCS for the

is also a construction of VCS

for

.

Definition 4 and Theorem 4 provide a technique to simplify

the access structure

.

C. Step Construction of VCS for Access Structure

Such that

In this section, we give Construction 2 for the particular ac-

cess structure

such that

, and then discuss its contrast and pixel expan-

sion properties.

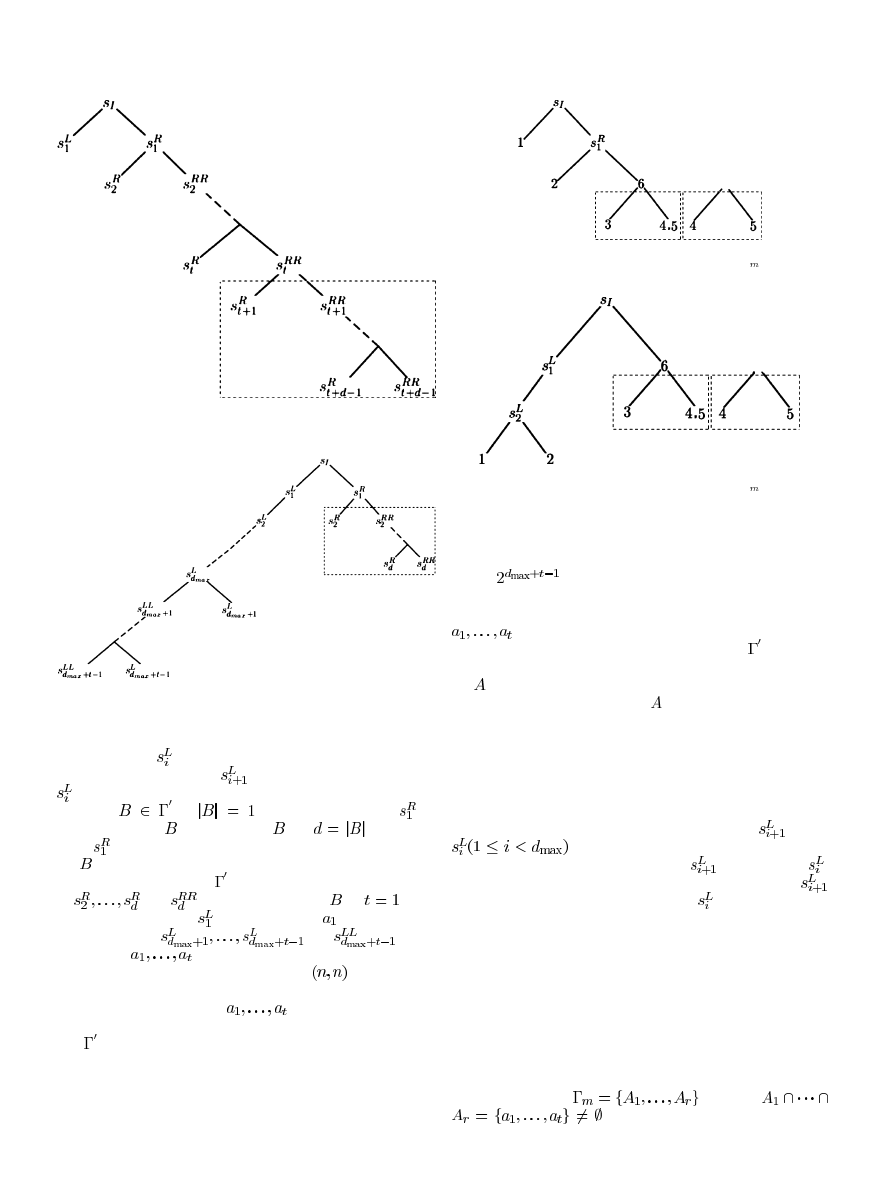
Construction

2:

For

the

access

structure

, where

,

let

and denote

as the maximum value of

for all

, i.e.,

. Two methods (Method 1 and

Method 2) of step construction for the

are depicted by the

construction trees of Figs. 4 and 5, respectively.

Method 1:

In the construction tree of Fig. 4, the dealer

distributes the share images

to the participants

. For all

, if

, distributes

to the

participant in

, else for every

, let

, takes

as

the secret image and generates the share images for

as Fig. 4

depicts (i.e., the subtree in the dashed box is changeable for the
sets in

), and distributes the share images of

and

to the participants in

.

Method 2:

In the construction tree of Fig. 5, for the step con-

struction

based on the

OR

operation, in the left branch of the

construction tree, the share image

is obtained by expanding

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

LIU et al.: STEP CONSTRUCTION OF VISUAL CRYPTOGRAPHY SCHEMES

33

Fig. 4. The construction tree of Method 1.

Fig. 5. The construction tree of Method 2.

the share image

to its double pixel expansion. For the

XOR

operation, the share image

is identical to the share image

.

For all

, if

, the dealer distributes

to

the participant in

, else for every

, let

, the dealer

takes

as the secret image and generates the share images

for

as Fig. 5 depicts (i.e., the subtree in the dashed box is

changeable for the sets in

), and distributes the share images

of

and

to the participants in

. If

, then

distributes share image

to the participant

, else distributes

the share images

and

to the

participants

.

It is clear that, the step construction of

-VCS is just a

special case of Construction 2.

Note that, the participants

are distributed with only

one share image, and the participants that appear in access struc-
ture

may be distributed with more than one share images. In

the rest of this paper, we will use the indexes of the participants,
directly, in the construction trees. In such a case, it is easy to
obtain the number of share images that are distributed to each
participant by counting the number of times that each partici-
pant appears in the construction trees.

Fig. 6. The construction tree of Method 1 for

0 .

Fig. 7. The construction tree of Method 2 for

0 .

According to the two methods of step construction of Figs. 4

and 5, we know that the pixel expansion of each share image is
at most

. The difference between the two construction

trees of Method 1 and Method 2 is that, the construction tree
of Method 1 first generates the share images for participants

, whereas the construction tree of the Method 2 first

generates the share images for the participants in

.

Generally, in this paper, a construction tree for a qualified

set

is a binary tree that contains all the share images that

distributed to the participants in

. A construction tree for an

access structure is a binary tree with several changeable subtrees
(see examples in Figs. 4, 5, 6, and 7).

According to the construction tree of Method 2 (Fig. 5), we

define another way of generating share images, called the trans-
mitting generation

, where the information of a share image is

duplicated to another share image with or without pixel ex-
pansion. In Fig. 5, the generation of share image

out of

is of this kind. Precisely, if the underlying

operation is

XOR

, then the share image

is identical to

,

and if the underlying operation is

OR

, then the share image

is generated by duplicating each pixel in

twice.

Together

with

the

dividing

generation

defined

in

Section III-A, we have two ways of generating share images
in the construction trees of this paper. Note that, the dividing
generation of this paper generates at least one share image
that will be distributed to the participants, and the transmitting
generation does not generate share images that will be
distributed to the participants.

In light of the above discussions, we have the following the-

orem.

Theorem 5:

Construction 2 is a step construction of VCS for

the access structure

such that

, which is realized by applying tradi-

tional (2,2)-VCS recursively.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

34

IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

Proof:

In order to prove that Construction 2 is a step con-

struction of VCS for access structure

such

that

, we need to prove that it

satisfies the contrast and security conditions of Definition 2.

First, we prove the contrast condition. For both Method 1 and

Method 2, according to Figs. 4 and 5, the step construction of the
sets

are processed independently, i.e., for each

,

let

, then the step construction of the set

forms a step construction of

-VCS. Then

according to Theorem 1, the contrast property of Definition 2 is
satisfied.

Second, we prove the security condition. For a forbidden set

of participants

, there exist a participant

, by

similar discussion of Theorem 1; i.e., when we list all the share
matrices, we have that the share images of

form a VCS

under Definition 1, where

is a forbidden set of the VCS under

the Definition 1. Hence, the security condition of Definition 2 is
satisfied.

We then discuss the pixel expansion and contrast properties

of the VCS

and VCS

that constructed by the step con-

struction of Method 1 and Method 2.

For the VCS

as Figs. 4 and 5 depict, for any qualified set

, there is a corresponding construction tree. Note that,

the share images that are distributed to the participants of

are

all the leaves of the construction tree. Because both the transmit-
ting generation and dividing generation expand the share image
to twice its original size, denote

as the height of the construc-

tion tree, then the pixel expansion of

is

. Be-

cause the dividing generation applies the (2,2)-VCS which re-
duces the contrast of the recovered image to the half of its orig-
inal value, and the transmitting generation does not affect the
contrast of the recovered image, when we denote the number of
dividing generations in the construction tree of

as

, we have

that the value of contrast of the recovered secret image by ad-
justing stacking the share images of

is

. For the

VCS

, similar to the above discussion, the pixel expansion

of all the share images is equal to

, and the contrast

is

.

In light of the above discussion, we get the following theorem.
Theorem 6:

The step construction of Construction 2 gener-

ates VCS with the following pixel expansion and contrast.

For the step construction of Method 1, the values of pixel

expansion and contrast are optimal for each qualified set of
both for the VCS

and VCS

; i.e., for any qualified set

, the pixel expansion and contrast of

satisfy that

and

.

For the step construction of Method 2, we have the following:

a) The values of pixel expansion and contrast are optimal

for each qualified set in

for the VCS

, i.e., for any

qualified set

, the pixel expansion and contrast of

satisfy

;

b) The value of contrast is optimal for each qualified set in

for the VCS

, i.e., for any qualified set

, the

contrast of

satisfies

;

c) The value of pixel expansion is optimal for the maximum

qualified set of

for the VCS

, i.e., let

be a max-

imum qualified set of

, the pixel expansion of

satis-

fies

.

Proof:

First, consider the step construction of Method 1.

For the VCS

, because the pixel expansion and contrast

for each qualified set in

are

and

, this

means that they reach their optimal values.

For the VCS

, according to the construction tree in Fig. 4,

for any

, the height of the construction tree is

,

and there exist

dividing generations in the construction

tree. We have that, the pixel expansion of the qualified set

is

, and the contrast of

is

.

According to Theorem 2, they reach their optimal values.

Second, consider the step construction of Method 2.
For the VCS

, because the pixel expansion and contrast

for each qualified set in

are

and

, this

means that they reach their optimal values.

For the VCS

, because the number of dividing generations

in the construction tree of

is

, we have that the con-

trast of

is

, which reaches its optimal value

according to Theorem 2.

Recall that in Construction 2, for any maximum qualified

set

, we have

, and

, i.e.,

. Because the height of the

construction tree in Fig. 5 is

, we have that, the pixel

expansion of

is

, which reaches

its optimal value according to Theorem 2.

From Theorem 6 it is noted that, Method 2 may not al-

ways generate optimal pixel expansion for each qualified set
in

-VCS

. However, Method 2 is still useful, because

Method 2 can generated VCS

with smaller average pixel

expansion

(APE) in some cases.

Recall that the average pixel expansion (APE) of VCS

is

defined as the average value of the total pixel expansions of
the share images each participants holds. Define the multiset

; denoting APE and APE as the APE of

Method 1 and 2 in Figs. 4 and 5 respectively, we have

and

The above values of APE and APE can easily be verified since
they are the sum of the pixel expansion of the leaves in the con-
struction trees.

Hence, for different

and

, the dealer can choose the

method with APE

APE APE

according to dif-

ferent requirements.

D. Step Construction of VCS for General Access Structure

In this section, we give the step construction of VCS for gen-

eral access structure based on the assess structure simplifying
technique and Construction 2.

Note that, a general access structure

can be divided into

several parts where each part has the form

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

LIU et al.: STEP CONSTRUCTION OF VISUAL CRYPTOGRAPHY SCHEMES

35

TABLE I

E

XPERIMENTAL

R

ESULTS AND

C

OMPARISONS

such that

; i.e., each part

satisfies the condition of Construction 2. Hence, each part can
be constructed by applying Construction 2. However, in order
to construct a step construction of VCS with smaller APE, we
also need to apply the access structure simplifying technique
introduced in Section III-B.

Construction 3:

For a general access structure

, the

dealer generates the construction trees of the step construction
of

-VCS by executing the following steps:

Step 1) Simplify

to

according to Theorem 4;

Step 2) Divide

into several parts with each part being in

the form

such that

;

Step 3) For each part, let

and

. If

,

then apply Construction 2 directly on

, and the

construction is done. Else treat

as a participant

in

, by applying Construction 2, we have two

cases:

1) If Method 1 of Construction 2 is used, denote the

share image that distributed to

as

, goto Step

1 for a new step construction of VCS, which
takes

as the secret image, for the access struc-

ture

.

2) If Method 2 of Construction 2 is used, denote

the share image that distributed to

as

, and

denote

as the cardinality of the maximum

set of

, i.e.,

.

We insert

transmitting generations be-

tween the secret image and the subtree corre-
sponding to the participant set

, and

goto Step 1 for a new step construction of VCS,
which takes

as the secret image, for the access

structure

.

Step 4) Repeat Steps 1, 2, and 3 until all the participants

receive their share images for all the qualified sets
in

.

Remark:

In the above Construction 3, we call the participant

and the share image

the virtual participant and virtual share

image

, respectively.

To show how Construction 3 works, we give the following

example.

Example 4:

Let

. Be-

cause

is already the most simplified access structure and it

satisfies the condition of Construction 2, we have

, treat

as a virtual participant

, then

can be represented by

. Apply Construction 2 for

, i.e., apply the (2,2)-VCS, and denote the share image

distributed to

as

. Take

as the secret image, and construct

a step construction of VCS for

. We divide

into two parts

and

. For the first part, because

4,

we apply a (2,2)-VCS and distribute the first share image to par-
ticipants 3 and 4 and the second share image to the participant
2. For the second part, we apply a (2,2)-VCS and distribute the
two share images to participant 3 and 4, respectively.

The pixel expansions and contrasts of the above construction

can be found in Table I.

Because Theorem 4 simplifies the access structure

, Step

1 reduces the number of qualified sets in

, and hence reduces

the number of dividing generations in the construction trees of
Construction 3.

In Step 2, since each part of

satisfies the condition of Con-

struction 2, Construction 3 seems to terminate at Step 2. How-
ever, in order to obtain a smaller APE, the dealer needs to further
divide each

, i.e., Construction 3 needs to be recursively ap-

plied until all the participants receive their share images for all
the qualified sets in

.

We claim that there always exist partitions for a general ac-

cess structure where each part satisfies the condition of Con-
struction 2. In order to show the feasibility of Construction 3,
we give, for example, a simple partition method for a general
access structure

. Suppose

. Let

be the collection of all the sets

which are chosen from

and contain the participant 1, i.e.,

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

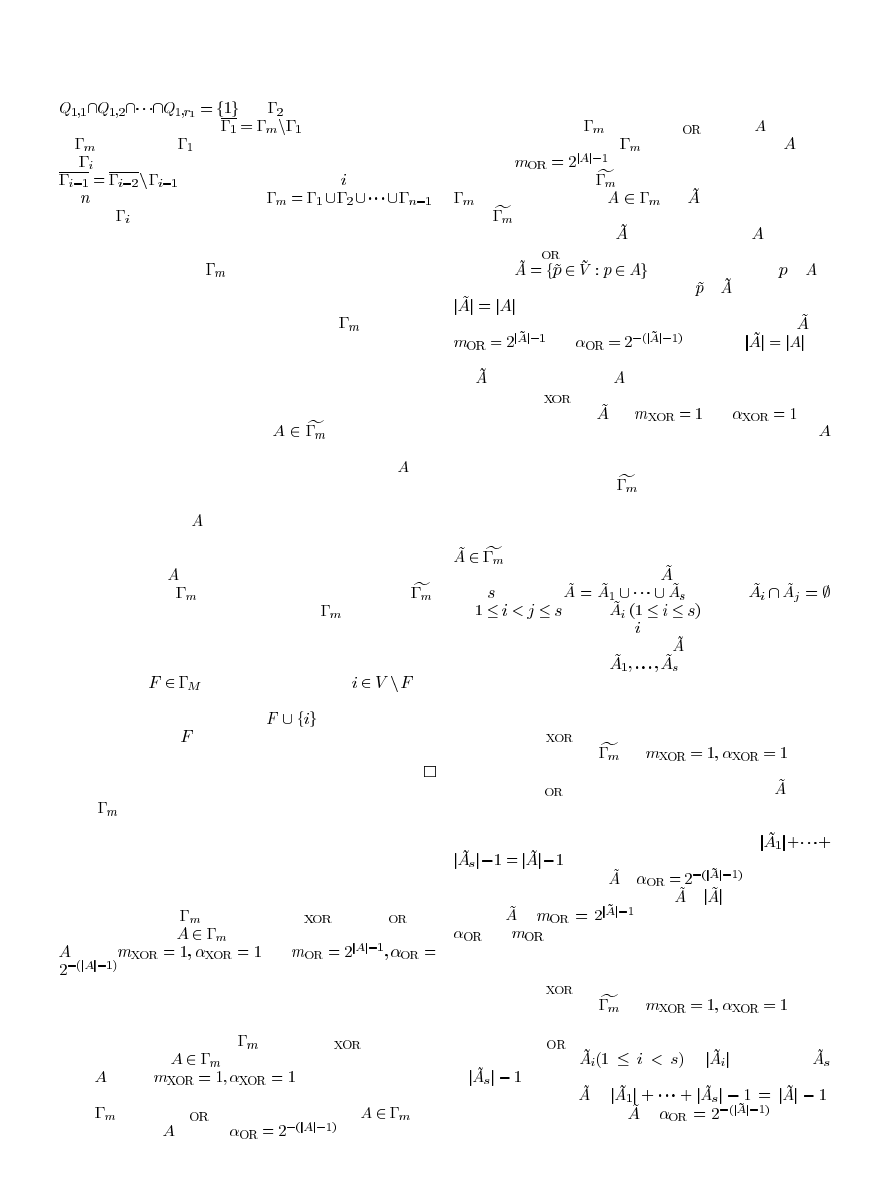
36

IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

. Let

be the collection of all the

sets which are chosen from

(i.e., the remaining set

of

by removing

) and contain the participant 2. Similarly,

let

be the collection of all the sets which are chosen from

and contain the participant . Because there

are

participants in total, we have

,

and each

satisfies the condition of Construction 2.

As a summary, we give the following theorem.
Theorem 7:

Construction 3 is a step construction of VCS for

general access structure

, which is realized by applying tra-

ditional (2,2)-VCS recursively.

Proof:

In order to prove that Construction 3 is a step con-

struction of VCS for general access structure

, we need to

prove that it satisfies the contrast and security conditions of Def-
inition 2.

First, we prove the contrast condition. Note that in Construc-

tion 3, the access structure is divided into several parts. Con-
struction 2 is applied recursively to generate the share images
for each part. For any qualified set

, it belongs to one

part. When applying Construction 2, the share images and vir-
tual share images are distributed to the participants of

and

the virtual participants, respectively. The virtual share images
are further divided in the next execution of Construction 2 until
all the participants of

receive their share images. Hence, ac-

cording to Theorem 5, the secret image and all the virtual share
images can be recovered by adjusting stacking the share images
that distributed to

. Furthermore, according to Theorem 4, for

any qualified set in

, there exists a corresponding set in

,

i.e., the share images of any qualified set in

can recover the

secret image. Hence, the contrast condition of Definition 2 is
satisfied.

Second, we prove the security condition. For a forbidden set

of participants

, there exist a participant

; by

similar discussion of Theorem 1, i.e., list all the share matrices,
we have that the share images of

form a VCS under

Definition 1, where

is a forbidden set of the VCS under the

Definition 1. Hence, the security condition of Definition 2 is
satisfied.

Then we consider the pixel expansion and contrast properties

of the

-VCS generated by applying Construction 3; we give

the following theorem.

Theorem 8:

The step construction of Construction 3 gener-

ates VCS with pixel expansion and contrast as follows.

If only Method 1 of Construction 2 is used in Construction 3,

then the values of pixel expansion and contrast are optimal for
each qualified set of

both for the VCS

and VCS

, i.e.,

for any qualified set

, the pixel expansion and contrast of

satisfy

and

.

Once Method 2 of Construction 2 is used in Construction 3,

then:

a) The values of pixel expansion and contrast are optimal

for each qualified set in

for the VCS

, i.e., for any

qualified set

, the pixel expansion and contrast of

satisfy

.

b) The value of contrast is optimal for each qualified set in

for the VCS

, i.e., for any qualified set

, the

contrast of

satisfies

.

c) The value of pixel expansion is optimal for the maximum

qualified set of

for the VCS

, i.e., let

be a max-

imum qualified set of

, the pixel expansion of

satis-

fies

.

Proof:

Recall that

is the simplified access structure of

, for any qualified set

, let

be the corresponding

set in

. We first prove that the optimal values of the pixel

expansion and contrast for

are also optimal for

.

For the VCS

, according to Definition 4 in Section III-B, we

have that,

, i.e., each participant

in

is

replaced by its corresponding participant in . Hence, we have

. According to Theorem 2 in Section III-A, we have

that the optimal values of pixel expansion and contrast of

are

and

. Because

, we

have that the optimal values of the pixel expansion and contrast
for

are also optimal for

.

For the VCS

, because the optimal values of the pixel ex-

pansion and contrast of

are

and

, they

are the optimal values of the pixel expansion and contrast of
as well.

Given the above, we only need to prove the theorem for the

simplified access structure

.

Construction 3 applies Construction 2 recursively, and each

time when Construction 2 is applied, it generates several share
images and a virtual share image (if it exists). For a qualified set

, without loss of generality, assume that Construction 3

generates all the share images for

by applying Construction

2 for

times. Let

such that

for

, where

is the the set of share

images that generated by the th execution of Construction 2.
We have that the construction tree of

is formed by connecting

the corresponding trees of

, one by one, at the virtual

share images.

Particularly, if only Method 1 is used when applying Con-

struction 2, we have:

For the VCS

, because the pixel expansion and contrast

for each qualified set in

are

, hence

they reach their optimal values.

For the VCS

, note that, the construction tree of

is gen-

erated only by dividing generations. Each dividing generation
generates one share image except the last dividing generation
which generates two share images. Hence, there are

dividing generations in the construction tree.

Hence, the contrast of the

is

. We have that,

the height of the construction tree of

is

, i.e., the pixel ex-

pansion

is

. According to Theorem 2, both

and

reach their optimal values.

Once Method 2 is used when applying Construction 2, we

have:

For the VCS

, because the pixel expansion and contrast

for each qualified set in

are

, hence

they reach their optimal values.

For the VCS

, the number of dividing generations in the

construction tree of

is

, and that of

is

. Hence, the number of dividing generations in the

construction tree of

is

,

we have that the contrast of

is

, which is

optimal according to Theorem 2.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

LIU et al.: STEP CONSTRUCTION OF VISUAL CRYPTOGRAPHY SCHEMES

37

For the VCS

, and for any maximum qualified set

,

assume that

is the first set of share images gen-

erated by using Method 2 of Construction 2, i.e., the share im-
ages of

are all generated by using Method 1

of Construction 2. At the point when Method 2 is used, denoting

as the access structure when using Method 2 of Construction

2, we have

. Then

is the maximum set of

, the reason is as follows.

For any set

, we have

.

Because

is the maximum

qualified set of

, by deleting the same number of elements

from each set in

, then

has the largest

cardinality, i.e.,

is the maximum set of

.

According to the second case of Step 3, we have that the height
of the construction tree that corresponds to
is

. Hence, the height of the construction

tree that corresponds to

is

, i.e., the pixel expansion of

is

, which reaches its optimal value according to

Theorem 2.

The following example demonstrates how Construction 3

works.

Example

5:

Let

. For the step construction of Construc-

tion 3 which only uses Method 1, the construction trees are
shown in Fig. 6.

For the VCS

, the APE

, note that participants 4 and 5 are distributed with

the same share image since they are equivalent participants for
the access structure

. The pixel expansion for

the qualified sets

is 8, and

the contrast is

, which are optimal for a qualified set with

four participants according to Theorem 2. The pixel expansion
for qualified set

is 4, and the contrast is

which are

also optimal for a qualified set with three participants according
to Theorem 2.

For the VCS

, the pixel expansion and contrast for each

qualified set are 1 and 1, respectively, which are optimal.

Once Method 2 is used when applying Construction 2 in the

step construction of Construction 3, the construction trees are
shown in Fig. 7.

For the VCS

, we have the APE

, which is smaller than that of

Method 1; note that participants 4 and 5 are distributed with
the same share image since they are equivalent participants
for the access structure

. The contrast of the

set

is

which is optimal for a qualified set with

three participants according to Theorem 2. The contrast of the
maximum qualified sets

is

, which is optimal for a qualified set with four participants

according to Theorem 2. However, the pixel expansion of
the qualified set

is 8 which is larger than its optimal

value 4. The pixel expansion for the maximum qualified sets

is 8, which is optimal for a

qualified set with 4 participants according to Theorem 2.

For the VCS

, the pixel expansion and the contrast for

each qualified set are 1 and 1, respectively, which are optimal.

IV. E

XPERIMENTAL

R

ESULTS AND

C

OMPARISONS FOR UP TO

F

OUR

P

ARTICIPANTS

Note that, different partition methods of the access structure

will result in different values of APE. However, it is quite

complicated to find a general partition method to obtain the min-
imal average pixel expansion APE

of the step construction of

the

-VCS. Here we only give the APE

of the VCS for the

access structures with up to four participants (Table I) by com-
puting search. We also compare these results to the well-known
results in the literature [14], [2].

In Table I, the total pixel expansion and pixel expansion of

each share of each participant are listed in sequence. For ex-
ample, the pixel expansion

for the access structure

means that the third participant re-

ceives two share images with pixel expansions 2 and 4, respec-
tively, and the total pixel expansion is obtained by

.

For the VCS

, the values in brackets in the column APE

and

of Table I are from the paper [14]. It is obvious that,

our construction improves the properties with regard to the APE,
pixel expansion, and contrast in most cases. For VCS

, the

values in brackets in the column APE

and

of Table I

are from the paper [2]; we only compare the threshold access
structure, because there is no known construction of VCS
for the general access structure.

We also provide the partition method of the access structures

by using a semicolon between different parts of the qualified
sets, where each part satisfies the condition of Construction 2.

V. C

ONCLUSION

In this paper, we proposed the step construction of VCS for

general access structure which improves the pixel expansion and
contrast properties compared with many of the known results in
the literature. According to the step construction proposed in
this paper, the VCS with general access structure can be con-
structed by only applying (2,2)-VCS recursively, regardless of
whether the underlying operation is

OR

or

XOR

, where a par-

ticipant may receive multiple share images. This result is most
interesting, because the construction of VCS

for general

access structure has never been claimed to be possible before.
The proposed construction can generate optimal VCS

and

VCS

for each qualified set in

, and our schemes can also

reduce the APE in most cases compared with the known results
in the literature. However, how to efficiently partition the access
structure to reduce the APE to the minimum remains as an open
problem.

Note that it is easy to adjust the pixel expansion of the shares

for every participant to the same. However, this will likely to
sacrifice the low APE of the proposed VCS.

A

CKNOWLEDGMENT

The authors would like to thank the anonymous reviewers for

their valuable comments.

R

EFERENCES

[1] M. Naor and A. Shamir, “Visual cryptography,” in EUROCRYPT’94,

Berlin, 1995, vol. LNCS 950, pp. 1–12, Springer-Verlag.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.

38

IEEE TRANSACTIONS ON INFORMATION FORENSICS AND SECURITY, VOL. 5, NO. 1, MARCH 2010

[2] P. Tuyls, H. D. L. Hollmann, J. H. van Lint, and L. Tolhuizen,

“Xor-based visual cryptography schemes,” Designs Codes and Cryp-
tography

, vol. 37, pp. 169–186, 2005.

[3] E. Biham and A. Itzkovitz, “Visual cryptography with polarization,” in

The Dagstuhl Seminar on Cryptography

, Sep. 1997.

[4] E. Biham and A. Itzkovitz, “Visual cryptography with polarization,” in

RUMP Session of CRYPTO’98

, 1997.

[5] P. Tuyls, T. Kevenaar, G. J. Schrijen, T. Staring, and M. V. Dijk, “Secu-

rity displays enabling secure communications,” in First Int. Conf. Per-
vasive Computing

, Boppard, Germany, 2004, vol. 2802, pp. 271–284,

Berlin Springer LNCS.

[6] S. S. Lee, J. C. Na, S. W. Sohn, C. Park, D. H. Seo, and S. J. Kim, “Vi-

sual cryptography based on an interferometric encryption technique,”
ETRI Journal

, vol. 24, no. 5, pp. 373–380, 2002.

[7] D. Q. Viet and K. Kurosawa, “Almost ideal contrast visual cryptog-

raphy with reversing,” Topics in Cryptology—CT-RSA, pp. 353–365,
2004.

[8] S. Droste, “New results on visual cryptography,” in CRYPTO’96, 1996,

vol. 1109, pp. 401–415, Springer-Verlag LNCS.

[9] C. Blundo, A. De Santis, and D. R. Stinson, “On the contrast in vi-

sual cryptography schemes,” J. Cryptology, vol. 12, no. 4, pp. 261–289,
1999.

[10] S. Cimato, R. De Prisco, and A. De Santis, “Optimal colored threshold

visual cryptography schemes,” Designs, Codes and Cryptography, vol.
35, pp. 311–335, 2005.

[11] M. Krause and H. U. Simon, “Determining the optimal contrast for

secret sharing schemes in visual cryptography,” Combinatorics, Prob-
ability Comput.

, vol. 12, no. 3, pp. 285–299, 2003.

[12] H. Koga, “A general formula of the (t,n)-threshold visual secret

sharing scheme,” in ASIACRYPT’2002, 2002, vol. 2501, pp. 328–345,
Springer-Verlag LNCS.

[13] C. N. Yang and T. S. Chen, “Size-adjustable visual secret sharing

schemes,” IEICE Trans. Fundamentals, vol. E88-A.NO.9, pp.
2471–2474, 2005.

[14] G. Ateniese, C. Blundo, A. De Santis, and D. R. Stinson, “Visual cryp-

tography for general access structures,” Inf. Computation, vol. 129, pp.
86–106, 1996.

[15] C. N. Yang, “New visual secret sharing schemes using probabilistic

method,” Pattern Recognit. Lett., vol. 25, pp. 481–494, 2004.

[16] S. Cimato, R. De Prisco, and A. De Santis, “Probabilistic visual cryp-

tography schemes,” Computer J., vol. 49, no. 1, pp. 97–107, 2006.

[17] X. M. Chen, “On the simplification of the access structure secret

sharing schemes (in chinese),” China Sci. Bulletin, vol. 15, pp.
1599–1603, 1999.

Feng Liu

received the bachelor degree in computer

science from Shandong University, in 2003, and the
Ph.D. degree in information security from the Insti-
tute of Software, Chinese Academy of Sciences, in
2009.

He is now an Assistant Professor with the Institute

of Software, Chinese Academy of Sciences. His re-
search interests include visual cryptography and de-
sign and analysis of security protocols.

Chuankun Wu

(M’99–SM’00) received the B.Sc.

degree, the M.Sc. degree, and the Ph.D. degree in en-
gineering in 1985, 1988, and 1994, respectively.

Since January 1988, he has been teaching at

Xidian University, China. He was promoted by
Xidian University to Lecturer in 1990, Associate
Professor in 1992, and Full Professor in 1995. In
September 1995, he became a postdoctoral fellow
at Queensland University of Technology, then in
1997 a research fellow at the University of Western
Sydney, and in 2000 a Lecturer in the Department

of Computer Science, Australian National University. In 2003, he joined the
Institute of Software, Chinese Academy of Sciences, as a Research Professor in
the State Key Laboratory of Information Security. His current research interests
include Boolean functions, wireless network security, and group-oriented
cryptography.

As a cofounder, Dr. Wu has served as a program chair for the 2001, 2002,

and 2003 International Workshop on Cryptology and Network Security (CANS)
which has become a regular annual conference since 2005. He has served as
an Associate Editor of IEEE C

OMMUNICATIONS

L

ETTERS

since 2001. He is a

member of the editorial board of the International Journal of Network Security,
and was invited to be a guest editor for a number of special journal issues, in-
cluding the 2008 and 2009 issues of IEICE-Special Section on Information and
Communication System Security

.

Xijun Lin

received the Masters degree in computer

science from Ocean University of China, in 2004, and
the Ph.D. degree from the Institute of Software, Chi-
nese Academy of Sciences, in 2008.

His research interests include cryptography and in-

formation security.

Authorized licensed use limited to: IEEE Xplore. Downloaded on May 13,2010 at 11:48:23 UTC from IEEE Xplore. Restrictions apply.