1

INNOWACJA PEDAGOGICZNA

KLASA MATEMATYCZNO-PRZYRODNICZA

Z PODZIAŁEM NA DWIE GRUPY

ZE ZINDYWIDUALIZOWANYM PROGRAMEM

NAUCZANIA

GIMNAZJUM Z ODDZIAŁAMI INTEGRACYJNYMI NR 4 W SŁUPSKU

2

I. Informacje wprowadzające

1.

Nazwa innowacji:

Klasa matematyczno-przyrodnicza z podziałem na dwie grupy ze

zindywidualizowanym programem nauczania.

2.

Podstawa prawna:

Rozporządzenie Ministra Edukacji Narodowej i Sportu z dnia 9 kwietnia

2002r. w sprawie warunków prowadzenia działalności innowacyjnej i

eksperymentalnej przez publiczne szkoły i placówki (Dz. U. Nr 56 z dnia 15

maja 2002r., poz. 506).

3.

Miejsce realizacji:

Gimnazjum z Oddziałami Integracyjnymi nr 4 w Słupsku

4.

Autorzy innowacji:

mgr Joanna Kaszowska – matematyka,

mgr Jolanta Mól – chemia,

mgr Joanna Sikorska – biologia,

mgr Michał Derra – fizyka,

mgr Piotr Sikorski – geografia

5.

Realizatorzy innowacji:

jak wyżej

6.

Czas realizacji innowacji:

Rok szkolny 2011/1012, 2012/2013, 2013/2014

7.

Klasa objęta innowacją:

Klasa I matematyczno – przyrodnicza od roku szkolnego 2011/2012

3

8.

Idea wiodąca:

Z raportu Ministerstwa Pracy i Polityki Społecznej Departamentu Analiz

Ekonomicznych i Prognoz „ O zatrudnieniu w Polsce” można wywnioskować,

ż

e będzie coraz większe zapotrzebowanie na osoby z wykształceniem ścisłym.

Poprawa stanu zatrudnienia ma polegać na „ podniesieniu jakości edukacji w

szkolnictwie powszechnym zwłaszcza w obszarze formowania umiejętności

matematycznych polskich uczniów oraz na zmianach dotyczących struktury

kształcenia wyższego poprzez zwiększanie liczby studentów kierunków

przyrodniczych i inżynieryjnych”.

Ponadto według ustawy z dnia 7 września 1991r. o systemie oświaty (Dz .

U. z 2004 r., Nr 256, poz 2572, z późn. zmianami, stan na dzień 31 sierpnia

2010r. ) przewiduje się prowadzenie placówek o charakterze eksperymentalnym

lub prowadzącymi działalność innowacyjną, w których to, wychodzi się

naprzeciw uczniom mającym szczególne potrzeby edukacyjne. Uczniom o

wysokim poziomie zdolności ogólnych lub kierunkowych wskazuje się różne

formy opieki poprzez umożliwienie im kształcenia według indywidualnych

programów nauczania.

Kolejnymi przesłankami do powstania tej innowacji są dwa raporty:

1). MEN z dnia 14 grudnia 2010r. z konferencji pt.: „Rozwijanie kompetencji

matematycznych i podstawowych kompetencji naukowych i technicznych w

projektach współpracy europejskiej”,

4

2). Zespołu PISA Instytutu Filozofii i Socjologii PAN z dnia 7 grudnia 2010r.,

w których to raportach podano dane dotyczące poziomu umiejętności polskich

uczniów na tle krajów europejskich. W tej chwili w Polsce odsetek uczniów

osiągających najsłabsze wyniki w naukach przyrodniczych w Europie wynosi

13,1%, zaś w przypadku matematyki aż 20%, co klasyfikuje nas odpowiednio na

7 miejscu w naukach przyrodniczych, i na 11 w matematyce.

Ważnym czynnikiem jest także fakt, że od 2010r. matematyka jest

przedmiotem obowiązkowym egzaminu dojrzałości.

Wychodząc, naprzód tym oczekiwaniom postanowiliśmy utworzyć w

naszej szkole klasę matematyczno – przyrodniczą. Chodzi nie tyle o wiedzę

matematyczną, lecz o kształtowanie umiejętności poszukiwania, samodzielnego

myślenia i podejmowania samodzielnych wyborów przy rozwiązywaniu

problemów natury matematycznej w praktyce. Unikając jednostronności,

chcielibyśmy, żeby uczniowie mieli dobre warunki do rozwijania zainteresowań

również w obrębie przedmiotów przyrodniczych: fizyki, biologii, chemii,

geografii. Chcielibyśmy, aby ta innowacja pozwoliła uczniom z sukcesami

startować w konkursach i olimpiadach, a po zakończonej edukacji w gimnazjum

wszystkie najlepsze licea stały dla nich otworem.

9.

Założenia programowe

Innowacja została opracowana na podstawie podstawy programowej

gimnazjum i programów nauczania:

5

Kryteriami naboru do klasy matematyczno – przyrodniczej są:

1.

wyniki sprawdzianu kompetencji po szóstej klasie,

2.

ocena z matematyki z klasy V i I semestru klasy VI,

3.

ocena z przyrody z klasy V i I semestru klasy VI,

4.

zainteresowania ucznia,

5.

udział w konkursach i kołach zainteresowań w szkole podstawowej.

Uczniowie klasy matematyczno – przyrodniczej podzieleni zostaną w

pierwszych dwóch tygodniach nauki roku szk. 2011/2012 na podstawie testu

opracowanego przez nauczycieli prowadzących innowację. Test ten będzie

składał się z zagadnień matematycznych i przyrodniczych obejmujących

materiał klasy VI.

Zakwalifikowanie do grupy podstawowej lub rozszerzonej nie jest ostateczne.

Jeżeli uczeń z grupy podstawowej wykaże się umiejętnościami wyższymi z

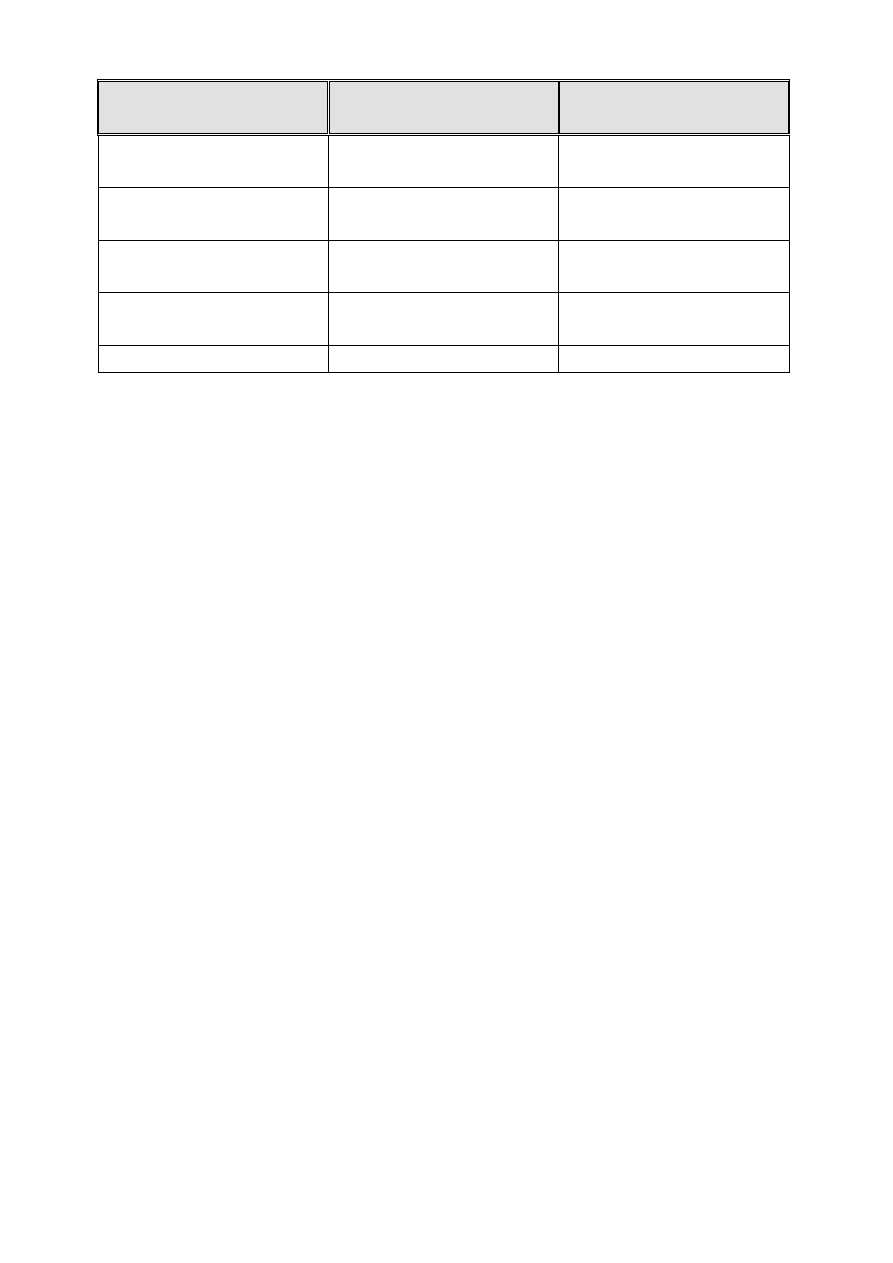
PROGRAM NAUCZANIA

AUTOR

NUMER

MATEMATYKA

„MATEMATYKA Z PLUSEM”

M.Jucewicz, M.Karpiński, J.Lech

168/1/2009

FIZYKA

„SPOTKANIE Z FIZYKĄ”

G. Francuz -Ornat, T. Kulawik

93/1/2009

CHEMIA

„CHEMIA NOWEJ ERY”

T. Kulawik, M. Litwin

49/1/2009

BIOLOGIA

„PULS ŻYCIA”

A. Zdziennicka

58/1/2009

GEOGRAFIA

E. Tuz

5/1/2009

6

co najmniej dwóch przedmiotów zostanie przeniesiony do grupy rozszerzonej

wraz z początkiem następnego semestru. Zasada ta działać będzie również w

drugą stronę. Jeżeli uczeń nie będzie wykazywał postępów w nauce z co

najmniej dwóch przedmiotów będzie przeniesiony do grupy podstawowej.

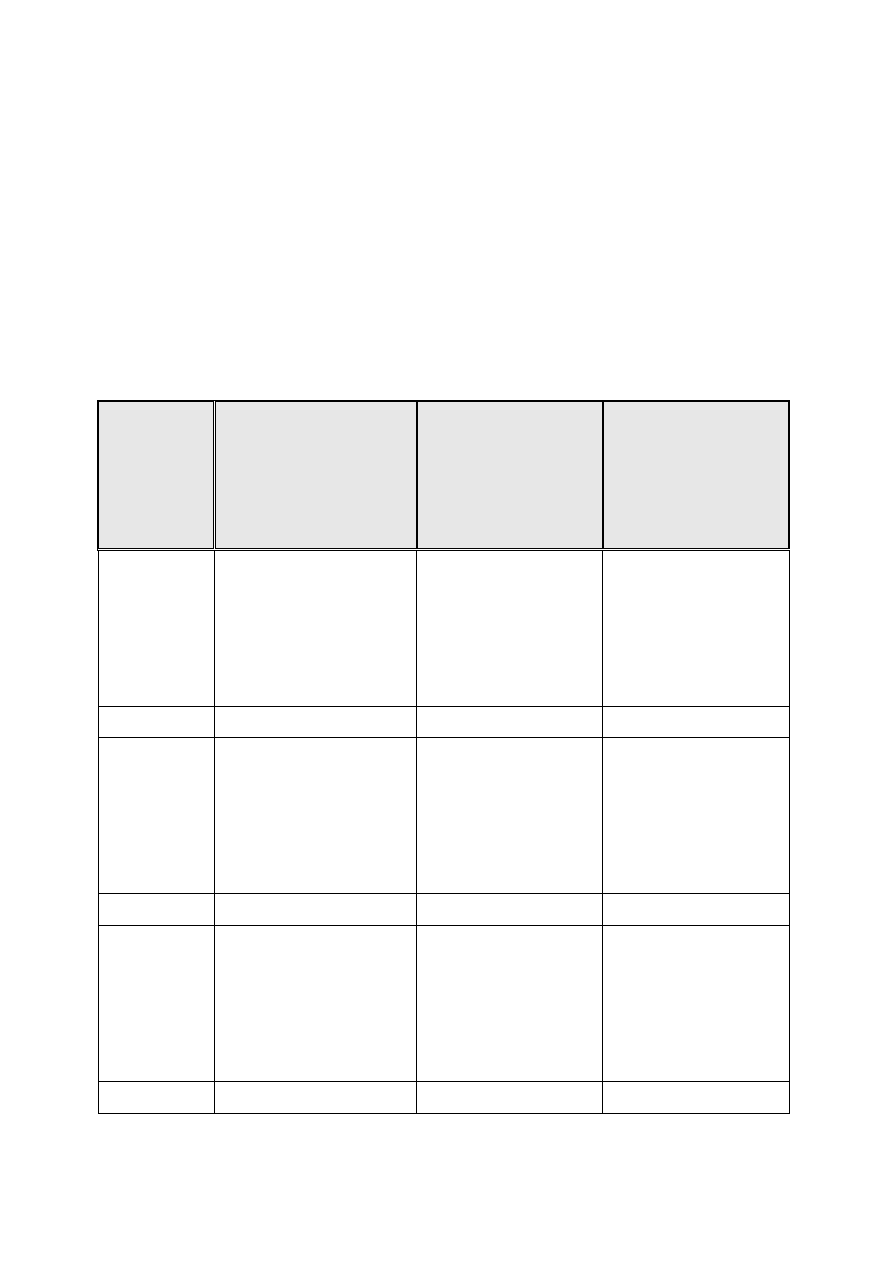
Proponowany przydział godzin:

KLASA

BLOK

PRZEDMIOTÓW

MATEMATYCZNO -

PRZYRODNICZYCH

GODZINY

Z RAMOWEGO PLANU

NAUCZANIA

REALIZOWANE W

CIĄGU TYGODNIA

grupa I

GODZINY

Z URZĘDU

MIASTA

grupa II

KLASA I

MATEMATYKA

CHEMIA

BIOLOGIA

FIZYKA

GEOGRAFIA

4

1

2

1

1

4

1

2

1

0

RAZEM

9

8

KLASA II

MATEMATYKA

CHEMIA

BIOLOGIA

FIZYKA

GEOGRAFIA

4

2

1

2

1

4

2

0

2

0

RAZEM

10

8

KLASA III

MATEMATYKA

CHEMIA

BIOLOGIA

FIZYKA

GEOGRAFIA

4

1

1

1

1

4

1

1

1

1

RAZEM

8

8

7

II. Ogólne cele edukacyjne innowacji

Przygotowanie uczniów do wykorzystania wiedzy matematycznej

i przyrodniczej

do rozwiązywania problemów.

Przygotowanie do uczestnictwa w konkursach.

Przygotowanie do sprostania wymaganiom w szkole

ponadgimnazjalnej.

Rozwijanie zainteresowań i uzdolnień matematyczno - przyrodniczych

uczniów.

Wykazanie przydatności wiedzy matematyczno - przyrodniczej w życiu

codziennym.

Stosowanie technologii informacyjnej.

Pobudzanie do twórczego myślenia.

Wdrażanie do ścisłego rozumowania.

Rozwijanie logicznego myślenia.

Przygotowanie do pracy metodą projektu.

Realizowanie ciekawych projektów.

Rozwijanie wrażliwości na problemy środowiska.

Dostrzeganie zależności między rozwojem cywilizacji a występującymi

zagrożeniami środowiska.

Rozpoznawanie środowisk zagrożonych degradacją.

8

III. Realizowane treści kształcenia i wychowania

Wszystkie treści programowe są zgodne z podstawą programową.

Nauczyciele rozszerzają wiedzę i umiejętności indywidualizując proces

nauczania,

przygotowują

do

egzaminu

gimnazjalnego

i

konkursów

przedmiotowych.

IV. Treści programowe zawarte w innowacji

dodano jako załącznik nr 1

V. Planowane osiągnięcia ucznia po zakończeniu cyklu:

Przygotowywanie uczniów do wykorzystania wiedzy matematyczno -

przyrodniczej do rozwiązywania problemów z zakresu różnych dziedzin

kształcenia szkolnego oraz życia codziennego.

Kształtowanie umiejętności myślenia i jasnego formułowania

wypowiedzi.

Ułatwianie dostrzegania problemów i badania ich w konkretnych

przypadkach, przez prowadzenie prostych rozumowań matematycznych.

Sukcesy uczniów w konkursach matematycznych, przyrodniczych.

Przyzwyczajenie uczniów do projektowania i organizowania pracy

własnej oraz w grupach lub zespołach.

9

VI. Kontrola i ocena osiągnięć ucznia

Ocenianie uczniów będzie zgodne z zasadami zawartymi w

Wewnątrzszkolnym Systemie Oceniania Gimnazjum z Oddziałami

Integracyjnymi nr 4 w Słupsku. Szczególna uwaga będzie zwrócona na

zaangażowanie oraz aktywność i twórczość uczniów.

Sprawdzanie osiągnięć będzie przyjmowało różne formy w zależności

między innymi od omawianych zagadnień. Podstawową formą będą

sprawdziany, pisemne i ustne. Uczniowie po każdej lekcji będą oceniani za:

aktywność na zajęciach

omawianie określonych treści, które zostały wcześniej samodzielnie

przygotowane

ć

wiczenia

prace domowe

prace dodatkowe

udział w konkursach przedmiotowych

udział w projektach

udział w testach diagnozujących matematyczno- przyrodniczych na

początku, po I, II i III roku nauki

VII. Procedury osiągania celów

Realizując tę innowację każdy z nauczycieli będzie stosował system ocen

tak, jak na każdym przedmiocie. Ponadto po przeprowadzeniu testów

10

diagnozujących dokonana będzie analiza postępów w nauce uczniów, na

podstawie, której wyciągane będą wnioski do dalszej pracy. Planowane jest

również, dołączenie kółek przedmiotowych do grupy rozszerzonej, w celu

realizacji zagadnień wykraczających poza program nauczania, zaś dla grupy

podstawowej zespołów wyrównawczych.

VIII. Ewaluacja programu

Aby otrzymać informacje zwrotne dotyczące realizacji innowacji planujemy

co pewien czas przeprowadzać ankiety ewaluacyjne. Po zakończonym cyklu

zajęć lub jednostce lekcyjnej uczniowie wypełnią karty samooceny. Zarówno

w ankietach, jak i w/w kartach zamieszczone będą między innymi

następujące pytania:

Co podobało się Ci na zajęciach, a stanowiło trudność?

Czy sposób przekazania informacji był dla Ciebie zrozumiały?

Które metody i formy pracy na lekcji odpowiadają ci najbardziej?

Jak oceniam swoją pracę na lekcji?

Czy sposób prowadzenia lekcji umożliwił Ci aktywny w niej udział?

Ponadto, aby uzyskać również informacje zwrotne od rodziców

konieczne jest i tu przeprowadzenie ankiet ewaluacyjnych. Z ankiet tych

zamierzamy dowiedzieć się czy przygotowanie do zajęć nie pochłania zbyt

dużo czasu i czy nie obciąża zbyt mocno uczniów, ale także czy zajęcia

11

spełniają oczekiwania rodziców i uczniów. Jesteśmy otwarci na sugestie

dotyczące pracy na tych zajęciach, zarówno ze strony uczniów, jak i

rodziców.

Należy pamiętać, że nieodzowną informacją zwrotną jest analiza

osiąganych wyników nauczania i opanowania umiejętności przez uczniów.

IX. Bibliografia

1.

Ś

liwerski B. „ Edukacja autorska.”, Kraków 1996

2.

Brodnik E., Moszyńska A., Owczarska R. „ Ja i mój uczeń pracujemy aktywnie.

Przewodnik po metodach aktywizujących”, Zakład Wydawniczy SFS Kielce 2000

3.

Kruszewski K. „ Sztuka nauczania”, PWN, Warszawa 1992

4.

Mentrak A. „Zarządzanie projektami edukacyjnymi. Nowa Szkoła. Skuteczne

zarządzanie w praktyce”, Warszawa 1994

5.

Dobrowolska M. „Matematyka z plusem. Klasa 1-3”, GWO 2009

6.

Biernat B., Biernat S. „Zbiór zadań z matematyki dla gimnazjum”, NOWIK 2008

7.

Janowicz J. „Zbiór zadań konkursowych w gimnazjum”, GWO 2008

8.

Praca zbiorowa „ Matematyka. Kalendarz gimnazjalisty. Przygotowanie do egzaminu

gimnazjalnego”, GWO 2008

9.

Praca zbiorowa „Vademecum gimnazjalne – Matematyka”, OPERON 2009

10.

Kleiner A. „Zadania konkursowe dla uczniów gimnazjum z rozwiązaniami”, Zamkor

2009

11.

Machowina R. „Fizyka dla gimnazjalistów. To proste”, Eremis 2006

12.

Jefimow M., Sęktas M. „Puls życia 1”, Nowa Era

13.

Sągin B., Sęktas M. „Puls życia 3”, Nowa Era

14.

Sędecka Z., Szedzianis E., Wierbiłowicz E. „Vademecum. Egzamin gimnazjalny

Biologia”, OPERON

15.

Szafirowa J. „Poznaj 100 roślin”

16.

Durrell G. „Poradnik przyrodnika”

17.

Chmielewska G., Chmielewski W. „Geografia dla gimnazjum 3”,

OPERON

12

18.

Dąbrowska B., Zaniewicz Z. „Egzamin gimnazjalny Geografia”,

OPERON

19.

Licińska D., Słownik szkolny „Geografia-Człowiek i jego działalność”, WSiP

20.

Skinder N. W. „Chemia a ochrona środowiska”, WSiP

21.

Gobis E. „Chemia z ochroną środowiska”, OPERON

22.

Gulińska M. ,Multimedialny podręcznik dla gimnazjum „Chemia z elementami ekologii”

WSiP