
Akademia Górniczo-Hutnicza
im. Stanisława Staszica w Krakowie
Budowa i eksploatacja pojazdów
Sprawozdanie
Obliczanie sprzęgła suchego
Wykonał:
Damian Kaproń
gr. P2, rok I mgr., IMiR
1. Obliczanie sprzęgła suchego
Typ samochodu : Toyota Corolla 1.3 86KM, (120Nm)
𝛽 = 1,3
𝛿 = 0,68
Mmax= 120Nm – moment maksymalny
i=2 – liczba powierzchni ciernych
p
dop
=0,2MPa – naprężenie dopuszczalne na nacisk dla materiału okładziny
µ=0,4 – współczynnik tarcia okładziny o stal
Dz – średnica zewnętrzna tarczy sprzęgła
Dw – średnica wewnętrzna tarczy sprzęgła
𝐷𝑧 = 20
3 ∙ 𝛽 ∙ 𝑀𝑚𝑎𝑥
2 ∙ 𝑝
𝑑𝑜𝑝
∙ 𝜋 ∙ 𝜇 ∙ 𝑖 ∙ 1 − 𝛿
3
3
= 20
3 ∙ 1,3 ∙ 120
2 ∙ 0,2 ∙ 𝜋 ∙ 0,4 ∙ 2 ∙ 1 − 0,68
3
3
= 175,79𝑚𝑚
Dz=180mm, Dw=125mm – wartości dobrane z tabeli
F
doc
− siła docisku tarcz
𝐅
𝐝𝐨𝐜
= 𝒑
𝒅𝒐𝒑
∙ 𝑨
𝒐𝒌ł𝒂𝒅𝒛𝒊𝒏𝒚
= 𝟎, 𝟐 ∙ 𝟏𝟎
𝟔
∙
𝝅
𝟒
∙ 𝑫𝒛
𝟐
− 𝑫𝒘
𝟐
= 𝟎, 𝟐 ∙ 𝟏𝟎
𝟔
∙
𝝅
𝟒
∙ 𝟎, 𝟏𝟖
𝟐
− 𝟎, 𝟏𝟐𝟓
𝟐
= 𝟐𝟔𝟑𝟓, 𝟎𝟏𝑵
Obliczona siła docisku sprężyny talerzowej Fdocisku:
Fdocisku=
2635
[N]
Obliczenia dla sprężyny talerzowej:
Sprawdzenie, czy wytworzy siłę Fspr.
Grubośd blachy sprężyny talerzowej:
t=
1,88
[mm]
Wymiar sprężyny De (przyjąd taki sam jak obliczone D
z
):
De=
180
[mm]
Stosunek D
i
/D
e
:
Di/De=
35
[%]
Wymiar sprężyny Di:
Di=
63
[mm]
Stosunek Df/De:
Df/De=
84
[%]
Wymiar sprężyny Df:
Df=
151,2
[mm]
Wratośd hi:
hi=
16
[mm]
Wartośd hf:
hf=
3,9
[mm]
Obliczenie współczynników do modelu G. Schremmera:
Wartośd współczynnika K:
K=
14,2
Moduł Younga dla stali:
E=
2,05E+11
[MPa]
Współczynnika Poissona dla stali:
ni=
0,3
Liczba listków w sprężynie:
n=
14
Stosunek szerokości listka do przerwy:
stos=
5
Szerokośd listka wi:
wi=
11,8
Szerokośd listka wf:
wf=
28,3
Wartośd współczynnika c:
c=
1,19
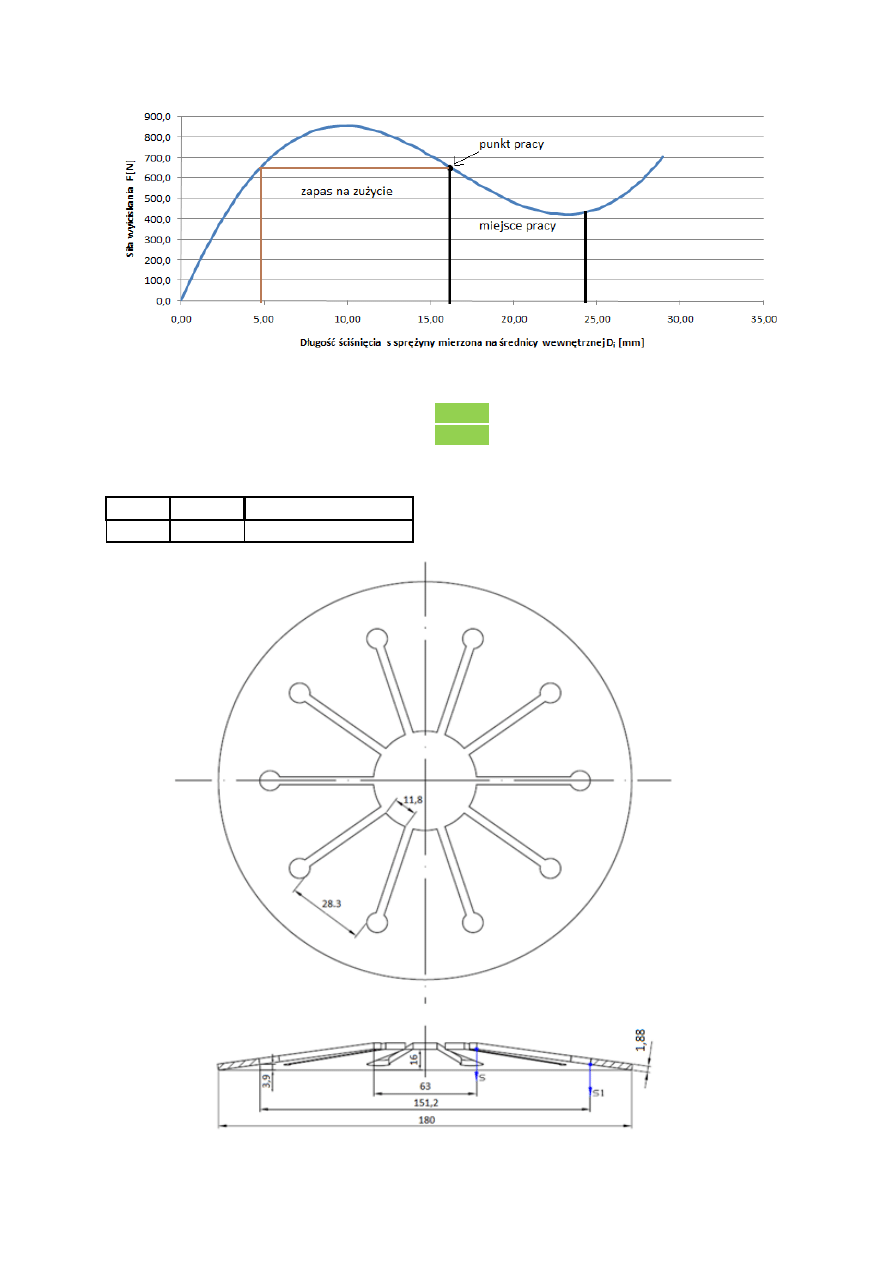
Siła sprężyny w punkcie pracy:
F
wycisk
= 648,6 [N]
"Przełożenie" siły F
docisk
na siłę F:
4,1
Obliczenia wartości siły wyciskania F jako
funkcji s
1
i s:
s
1
[mm] s [mm]:
F [N]:
3,8
15,9
664,9
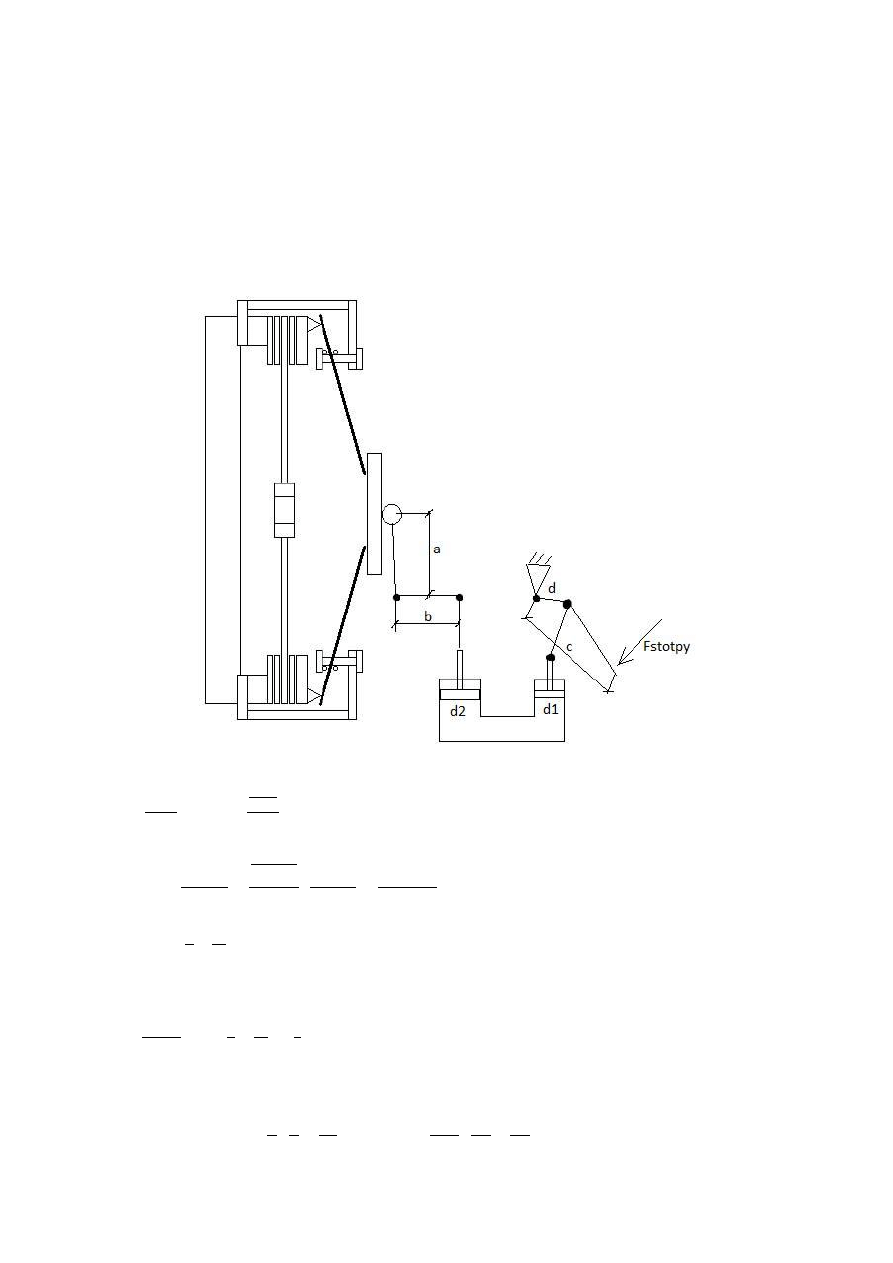
2. Obliczanie siły stopy (F
S
) oraz drogi pedała stopy (S
ped
)
Dane do obliczeo:
d
1
=10mm c=160mm s=8mm
d
2
=12mm a=40mm 𝐹
𝑤𝑦𝑐𝑖𝑠𝑘
= 648,6𝑁
d=30mm b=80mm
𝐹
𝑠
∙ 𝑐 = 𝐹
𝑆𝑖ł
∙ 𝑑
𝐹
𝑠
=
𝐹
𝑆𝑖 ł
∙𝑑
𝑐
𝑝 =
𝐹𝑆𝑖ł
𝜋 ∙𝑑 1
2
4
𝐹
𝑤𝑦𝑝
= 𝑝 ∙
𝜋 ∙ 𝑑
2
2
4
=
𝐹
𝑆𝑖ł
𝜋 ∙ 𝑑
1
2
4
∙
𝜋 ∙ 𝑑
2
2
4
=
𝐹
𝑆𝑖ł
∙ 𝑑
2
2
𝑑
1
2
𝐹
𝑤𝑦𝑝
= 𝐹
𝑠
∙
𝑐
𝑑
∙ (
𝑑
1
𝑑
2
)
2
𝐹 ∙ 𝑎 = 𝐹
𝑤𝑦𝑝
∙ 𝑏
𝐹 =
𝐹
𝑤𝑦𝑝
∙𝑏
𝑎
= 𝐹
𝑠
∙
𝑐
𝑑
∙ (
𝑑
1
𝑑
2
)
2
∙
𝑏
𝑎
𝑭
𝒔
=
𝒅
𝒄
∙
𝒂
𝒃
∙
𝒅
𝟏
𝒅
𝟐
∙ 𝑭
𝒘𝒚𝒄𝒊𝒔𝒌
=
𝟑𝟎
𝟏𝟔𝟎
∙
𝟒𝟎
𝟖𝟎
∙
𝟏𝟎
𝟏𝟐
∙ 𝟔𝟒𝟖, 𝟔 = 𝟒𝟐, 𝟐𝑵

𝑠
𝑝𝑒𝑑
𝑐
=
𝑠
𝑠𝑖ł
𝑑
𝑠
𝑠𝑖ł
= 𝑠
𝑝𝑒𝑑
∙
𝑑
𝑐
𝐴
1
∙ 𝑠
𝑠𝑖ł
= 𝐴
2
∙ 𝑠
𝑤𝑦𝑝
𝑠
𝑤𝑦𝑝
= 𝑠
𝑠𝑖ł
𝐴
1
𝐴
2
= 𝑠
𝑝𝑒𝑑
𝑑
𝑐
∙
𝜋 ∙𝑑 1
2
4
𝜋 ∙𝑑 2
2
4
= 𝑠
𝑝𝑒𝑑
𝑑
𝑐
∙ (
𝑑
1
𝑑
2
)
2
𝑠
𝑎
=
𝑠
𝑤𝑦𝑝
𝑏
𝑠 = 𝑠
𝑤𝑦𝑝
∙
𝑎
𝑏
= 𝑠
𝑝𝑒𝑑
∙
𝑑
𝑐
∙ (
𝑑
2
𝑑
1
)
2
∙
𝑎
𝑏
𝑺
𝒑𝒆𝒅
=
𝒃
𝒂
∙
𝒄
𝒅
∙
𝒅
𝟐
𝒅
𝟏
∙ 𝒔 =
𝟖𝟎
𝟒𝟎
∙
𝟏𝟔𝟎
𝟑𝟎
∙
𝟏𝟐
𝟏𝟎
∙ 𝟖 = 𝟓𝟗, 𝟑𝒎𝒎
Wyszukiwarka
Podobne podstrony:
Projekt 1 obliczanie sprzęgla suchego
Projekt 1 obliczanie sprzęgla suchego
PN B 03002 2007 Konstrukcje murowe Projektowanie i obliczanie
obliczenia7, inżynieria ochrony środowiska kalisz, Rok 1 IOS, Mechanika budowli, Mechanika budowli -
projekt obliczenia
Projekt1 obliczenia od m dyrki nie ropowszechniać
projekt obliczenia moje początek
projekt 2 obliczenia, PKM projekty, PROJEKTY - Oceloot, Projekt II kratownica PKM, Inne, Obliczenia
projekt 1 K&K, obliczenia2, h=750[m] , 150C, 1013hPa
Projekt obliczenia?rek
projek i oblicznia wysypisak śmieci w Mielcu
Projekt Obliczenia
obliczenia5, inżynieria ochrony środowiska kalisz, Rok 1 IOS, Mechanika budowli, Mechanika budowli -
gazy Zuza projekt obliczenia
Projekt obliczenia
obliczenia1, inżynieria ochrony środowiska kalisz, Rok 1 IOS, Mechanika budowli, Mechanika budowli -
więcej podobnych podstron