Powodzenia!
KWIECIEŃ 2005
Czas pracy:
120 minut
Liczba punktów
do uzyskania: 50
EGZAMIN
W TRZECIEJ KLASIE GIMNAZJUM
Z ZAKRESU PRZEDMIOTÓW
MATEMATYCZNO-PRZYRODNICZYCH
Instrukcja dla ucznia
1. Sprawdź, czy zestaw egzaminacyjny zawiera 14 stron.
Ewentualny brak stron lub inne usterki zgłoś nauczycielowi.
2. Na tej stronie i na karcie odpowiedzi wpisz swój kod i datę urodzenia.
3. Czytaj uważnie wszystkie teksty i zadania.
4. Rozwiązania zapisuj długopisem lub piórem z czarnym tuszem/atramentem.
Nie używaj korektora.
5. W zadaniach od 1. do 25. są podane cztery odpowiedzi: A, B, C, D.
Odpowiada im następujący układ na karcie odpowiedzi:
A
B
C
D
Wybierz tylko jedną odpowiedź i zamaluj kratkę z odpowiadającą jej literą -
np. gdy wybrałeś odpowiedź "A":
6. Staraj się nie popełniać błędów przy zaznaczaniu odpowiedzi, ale jeśli
się pomylisz,
błędne zaznaczenie otocz kółkiem i zamaluj inną odpowiedź.
7. Rozwiązania zadań od 26. do 35. zapisz czytelnie i starannie
w wyznaczonych miejscach. Pomyłki przekreślaj.
8. Redagując odpowiedzi do zadań, możesz wykorzystać miejsce
opatrzone napisem Brudnopis. Zapisy w brudnopisie nie będą sprawdzane
i oceniane.
DATA URODZENIA UCZNIA
WPISUJE UCZEŃ
KOD UCZNIA
dzień miesiąc
rok
UZUPEŁNIA ZESPÓŁ
NADZORUJĄCY
dysleksja
miejsce
na naklejkę
z kodem
GM-A1-052
Strona 2 z 14
Poniższy diagram wykorzystaj do rozwiązania zadań od 1. do 4.
Przyjmij, że lądy na Ziemi zajmują łącznie 150 mln km
2
.
Diagram przedstawia procentowy udział powierzchni poszczególnych kontynentów
w całkowitej powierzchni lądów.
B. Dobosik, A. Hibszer, J. Soja, Tablice geograficzne, Katowice 2002.
Zadanie 1. (0-1)
Które zdanie jest prawdziwe?
A. Ameryka Północna i Azja zajmują łącznie więcej niż połowę lądów Ziemi.
B. Europa ma najmniejszą powierzchnię spośród wszystkich kontynentów.
C. Afryka i Azja mają łącznie większą powierzchnię niż pozostałe lądy Ziemi.
D. Powierzchnia Azji stanowi mniej niż jedną trzecią powierzchni lądów Ziemi.
Zadanie 2. (0-1)
Jaką część powierzchni lądów na Ziemi zajmuje Afryka?
A.
4
1
B.
5
1
C.
20
1
D.
50
1
Zadanie 3. (0-1)
Jaką powierzchnię ma Australia?
A. 0,9 mln km
2
B. 6 mln km
2
C. 9 mln km
2
D. 90 mln km
2
Zadanie 4. (0-1)
Powierzchnia Antarktydy jest większa od powierzchni Europy o
A. 3 mln km
2
B. 7,5 mln km
2
C. 30 mln km
2
D. 34,5 mln km
2
7%
30%
20%
16%
12%
6%
9%
Europa
Azja
Afryka
Ameryka Północna
Ameryka Południowa
Australia
Antarktyda
Strona 3 z 14
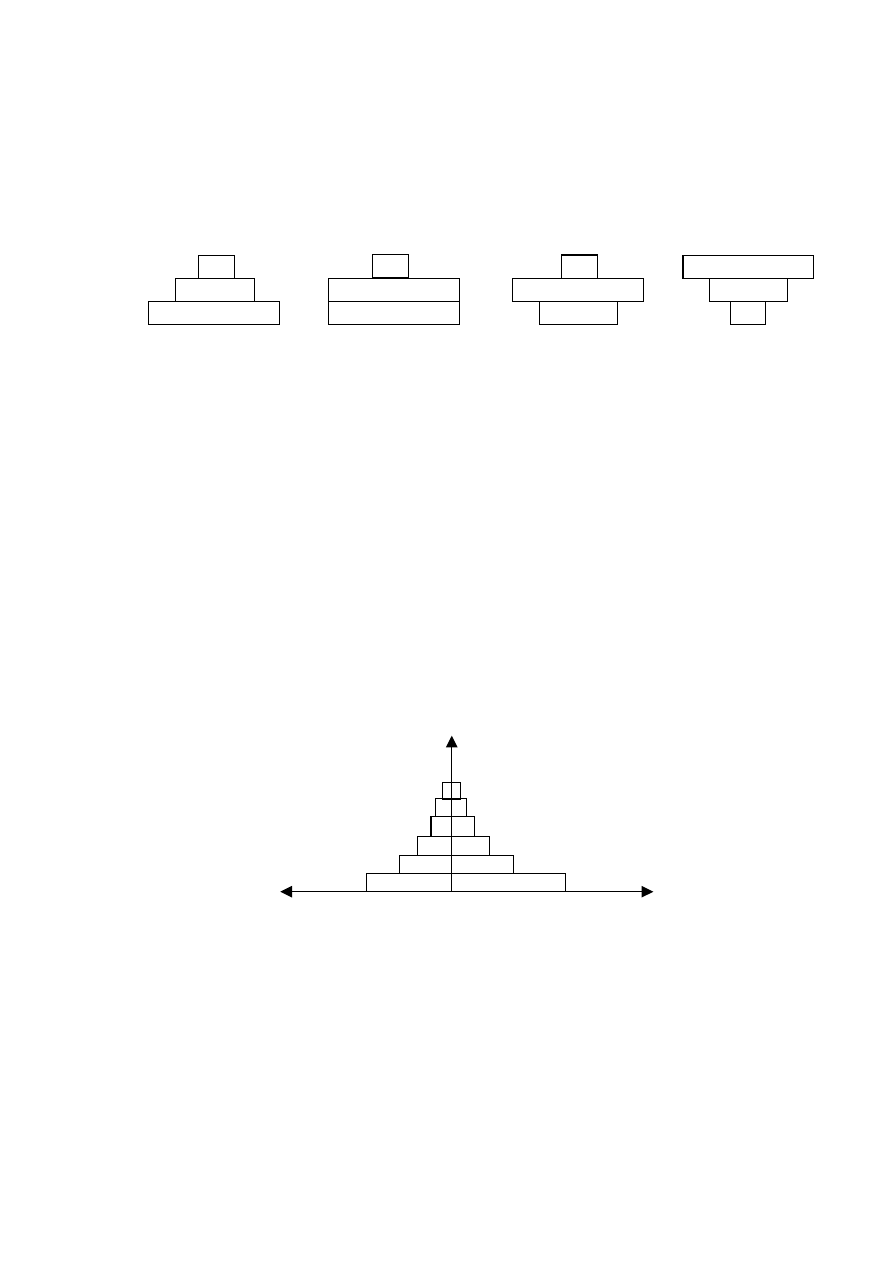
Zadanie 5. (0-1)
Drzewa tworzą największą biomasę w lesie. Która piramida przedstawia ten stan?
Zadanie 6. (0-1)
Określ oddziaływania między populacją mszycy a populacją brzozy.
A. Rywalizują o zasoby środowiska.
B. Obie odnoszą wzajemne korzyści.
C. Nie są zdolne do życia jedna bez drugiej.
D. Jedna z populacji osiąga korzyści, a druga ponosi straty.
Zadanie 7. (0-1)
Między którymi organizmami zachodzą oddziaływania nieantagonistyczne?
A. Pająk – mucha.
B. Sosna – dąb.
C. Kleszcz – człowiek. D.
Pszczoła – lipa.
Schemat do zadania 8.
Zadanie 8. (0-1)
Analizując piramidę przedstawiającą strukturę wiekową i płciową populacji, można
stwierdzić, że
A. rodzi się więcej samic niż samców.
B. liczebność najstarszych samic i samców jest taka sama.
C. liczebność samic i samców jest w każdej grupie wiekowej różna.
D. różnica między liczebnością samców i samic w każdej grupie wiekowej jest taka sama.
P
– producenci
K I
– konsumenci I rzędu
K II
– konsumenci II rzędu
P
K I
K II
K II
P
K I
K I
P
K II
A .
P
K I
K II
B .
C .
D .
wiek osobnika
liczebność samce
samice
58%
42%
50%
50%
Strona 4 z 14
Rozwiązując zadania od 9. do 12., wykorzystaj poniższą informację i mapę.
Azymut geograficzny to kąt między kierunkiem północnym a kierunkiem marszu, mierzony
od kierunku północnego do kierunku marszu zgodnie z ruchem wskazówek zegara.
Zadanie 9. (0-1)
Turysta, który wyruszył z punktu P na azymut 135º, dojdzie do
A. kładki. B.
ostańca.
C. gajówki.
D. wieży obserwacyjnej.
Zadanie 10. (0-1)
Przybliżona odległość w linii prostej od gajówki do ostańca wynosi
A. 390 m
B. 550 m
C. 780 m
D. 3900 m
Zadanie 11. (0-1)
Turysta, który chce przejść od ostańca przez punkt P do kładki, powinien pójść
w kierunku
A. północno-zachodnim, a następnie zachodnim.
B. północno-wschodnim, a następnie wschodnim.
C. południowo-zachodnim, a następnie zachodnim.
D. południowo-wschodnim, a następnie wschodnim.
N
azymut
0
0,2 km
P
Jez. Leśne
– gajówka
– skała, ostaniec
– wieża obserwacyjna
Legenda
– las mieszany
– łąka
– kładka
N
Strona 5 z 14
Zadanie 12. (0-1)
Który zestaw nazw roślin pozwala wnioskować, że dotyczy on lasu przedstawionego na
mapie?
A. Graby, dęby,
leszczyny.
B.
Świerki, sosny, jodły.
C. Sosny, dęby, leszczyny.
D. Lipy, jarzębiny, akacje.
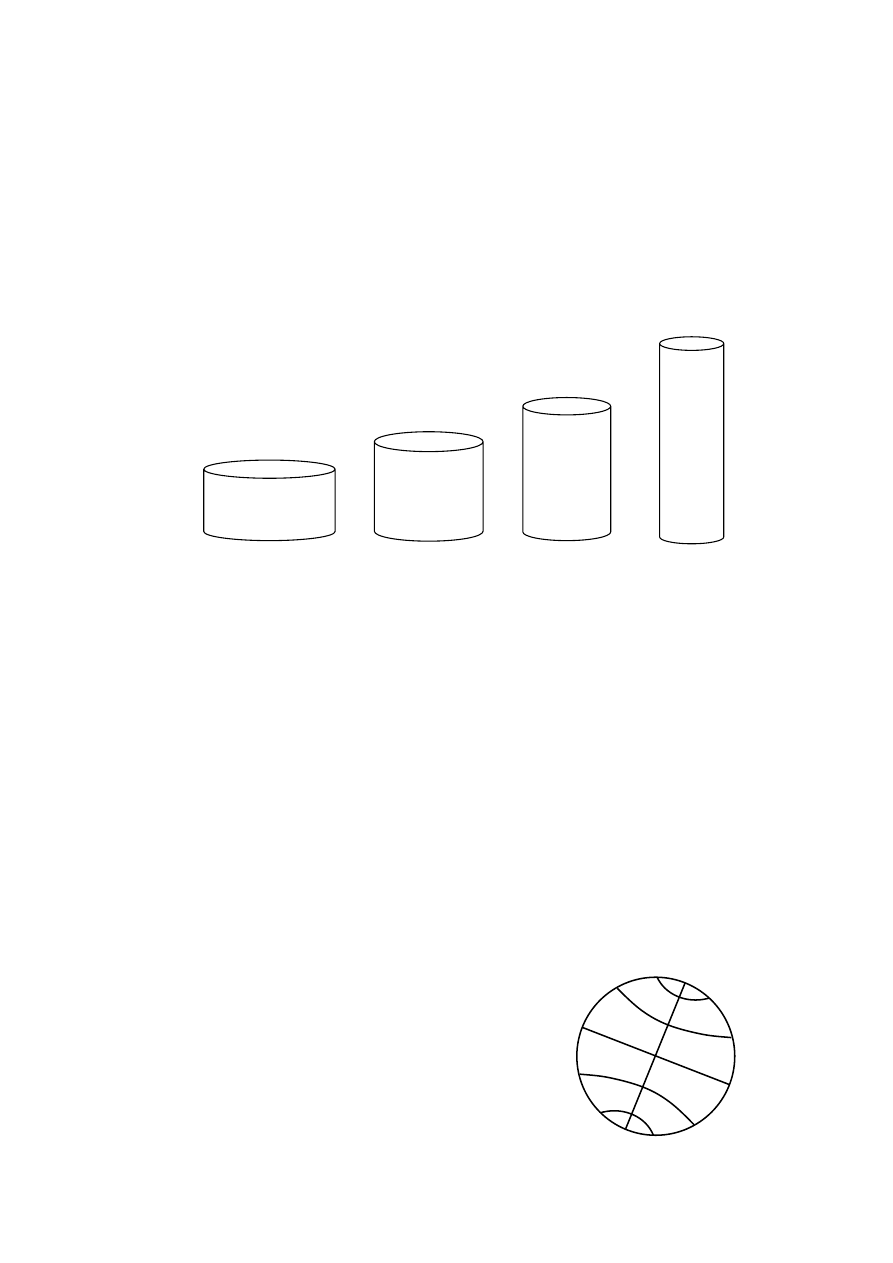
Zadanie 13. (0-1)
Które z naczyń w kształcie walca, o wymiarach przedstawionych na rysunku, ma
największą objętość?
h
– wysokość walca
r
– promień podstawy walca
A.
I
B.
II
C.
III
D.
IV
Zadanie 14. (0-1)
Do naczynia o objętości V = 0,75 l wlano 0,45 l wody. Jaki procent objętości tego
naczynia stanowi objętość wody?
A. 6
B. 16,(6)
C. 33,75
D. 60
Zadanie 15. (0-1)
Na południe od pewnego równoleżnika Słońce codziennie wschodzi i zachodzi, zaś na
północ od tego równoleżnika występuje zjawisko dni i nocy polarnych. Powyższy opis
dotyczy równoleżnika
A. 66º33′N
B.
66º33′S
C. 23º27′N
D.
23º27′S
N
S
66º33′
66º33′
23º27′
23º27′
0º
r
= 6 cm
h
= 6 cm
r
= 5 cm
h
= 9 cm
r
= 3 cm
h
= 18 cm
r
= 4 cm
h
= 12 cm
I
II
III
IV
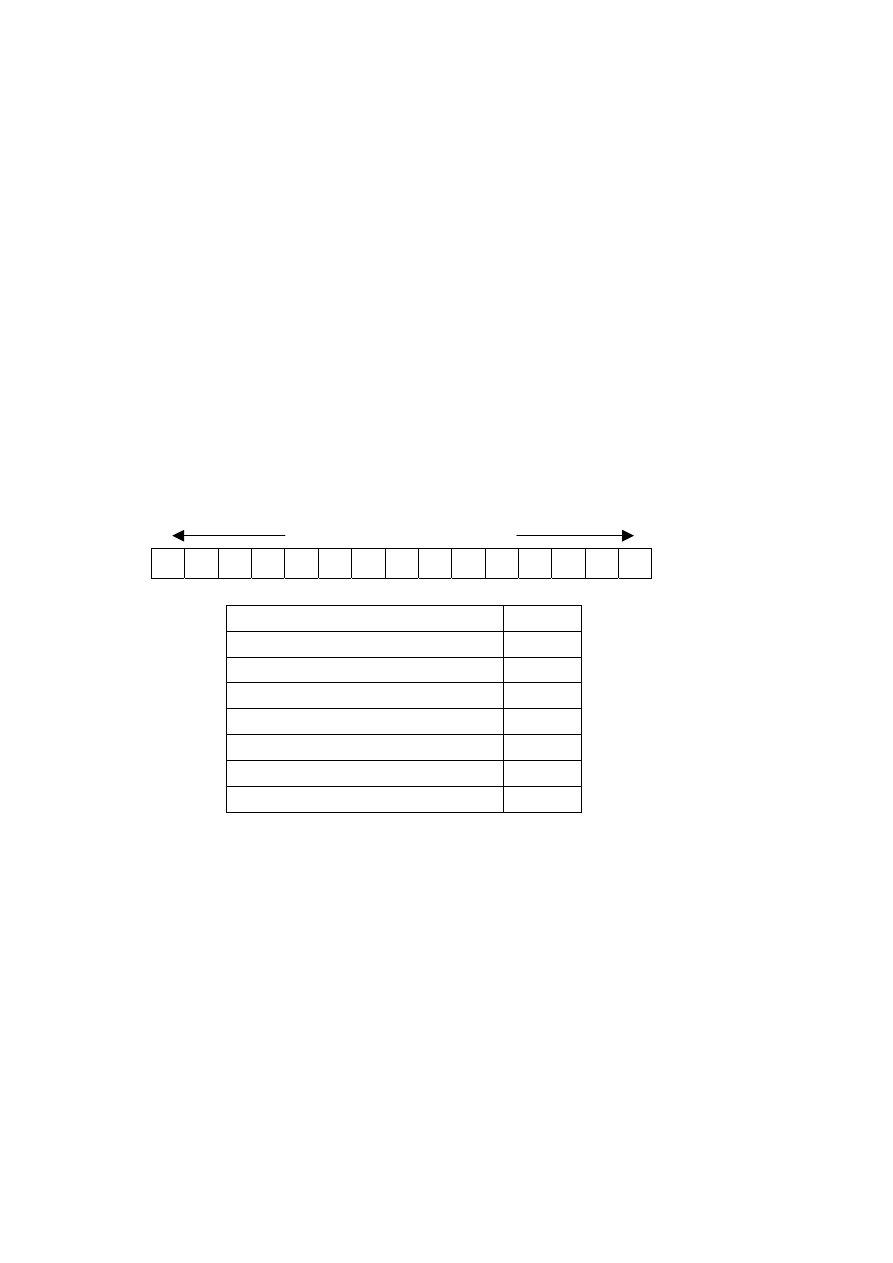
Strona 6 z 14
Zadanie 16. (0-1)
Która cecha dotyczy południków?
A. Są różnej długości. B.
Mają kształt okręgów.
C. Łączą dwa bieguny Ziemi.
D. Wyznaczają kierunek wschód-zachód.
Zadanie 17. (0-1)
Średnia odległość Marsa od Słońca wynosi
8
10
2,28
⋅
km. Odległość ta zapisana bez
użycia potęgi jest równa
A. 22 800 000 km
B. 228 000 000 km
C. 2 280 000 000 km
D. 22 800 000 000 km
Schemat i tabela do zadań 18. i 19.
Skala pH służy do określania odczynu badanej substancji.
Roztwór pH
woda sodowa
5,5
sok pomarańczowy 3,5
coca-cola 3,0
mleko 6,5
woda destylowana
7,0
amoniak
11,5
preparat do udrażniania rur
14,0
Na podstawie: Witold Mizerski, Tablice chemiczne, Warszawa 1997.
Zadanie 18. (0-1)
Który z podanych napojów ma najbardziej kwasowy odczyn?
A. Mleko.
B. Coca-cola.
C. Woda sodowa.
D. Sok pomarańczowy.
Zadanie 19. (0-1)
Wybierz zdanie prawdziwe.
A. Woda sodowa ma odczyn zasadowy.
B. Woda destylowana ma odczyn obojętny.
C. Roztwór amoniaku ma odczyn kwasowy.
D. Preparat do udrażniania rur ma właściwości silnego kwasu.
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
odczyn kwasowy
odczyn zasadowy
Strona 7 z 14
Zadanie 20. (0-1)
Tlenki azotu o ogólnym wzorze N
x
O
y
mogą reagować z parą wodną znajdującą się
w chmurach, tworząc kwaśne deszcze. Wówczas może zajść reakcja
N
x
O
y
+ H
2
O → 2HNO
3
Wartości indeksów stechiometrycznych
x i y są rozwiązaniem układu równań
A.
=
+
=
3
y
2
:
1
y
x
x :
B.
=
+
=
5
y
3
:
2
y
x
x :
C.
=
+
=
3
y
1
:
2
y
x
x :
D.
=
+
=
7
y
5
:
2
y
x
x :
Schemat do zadań 21. i 22.
Obwód elektryczny składa się z 9 V baterii, amperomierza i trzech identycznych żarówek.
Zadanie 21. (0-1)
Na podstawie przedstawionego schematu można wnioskować, że
A. żarówka 1 świeci jaśniej niż żarówka 3.
B. żarówka 3 świeci jaśniej niż żarówka 1.
C. żarówka 2 świeci jaśniej niż żarówki 1 i 3.
D. wszystkie żarówki świecą tak samo jasno.
Zadanie 22. (0-1)
Całkowity opór obwodu wynosi
A. 2,7
Ω B.
8,1
Ω C.
10
Ω D.
30
Ω
A
0,9 A
9 V
2
3
1
Strona 8 z 14
Metale aktywniejsze od wodoru,
wypierające go z zimnej wody i kwasów
(reagują z zimną wodą).
Metale aktywniejsze od wodoru,
wypierające go z gorącej wody i kwasów
(reagują z gorącą wodą i kwasem).
Metale mniej aktywne od wodoru,
nie wypierające go z wody i kwasów.
Wzrost aktywno
ści chemicznej
K
Na
Ca
Mg
Al
Zn
Fe
Sn
Pb
Bi
Cu
Hg
Ag
Pt
Au
H
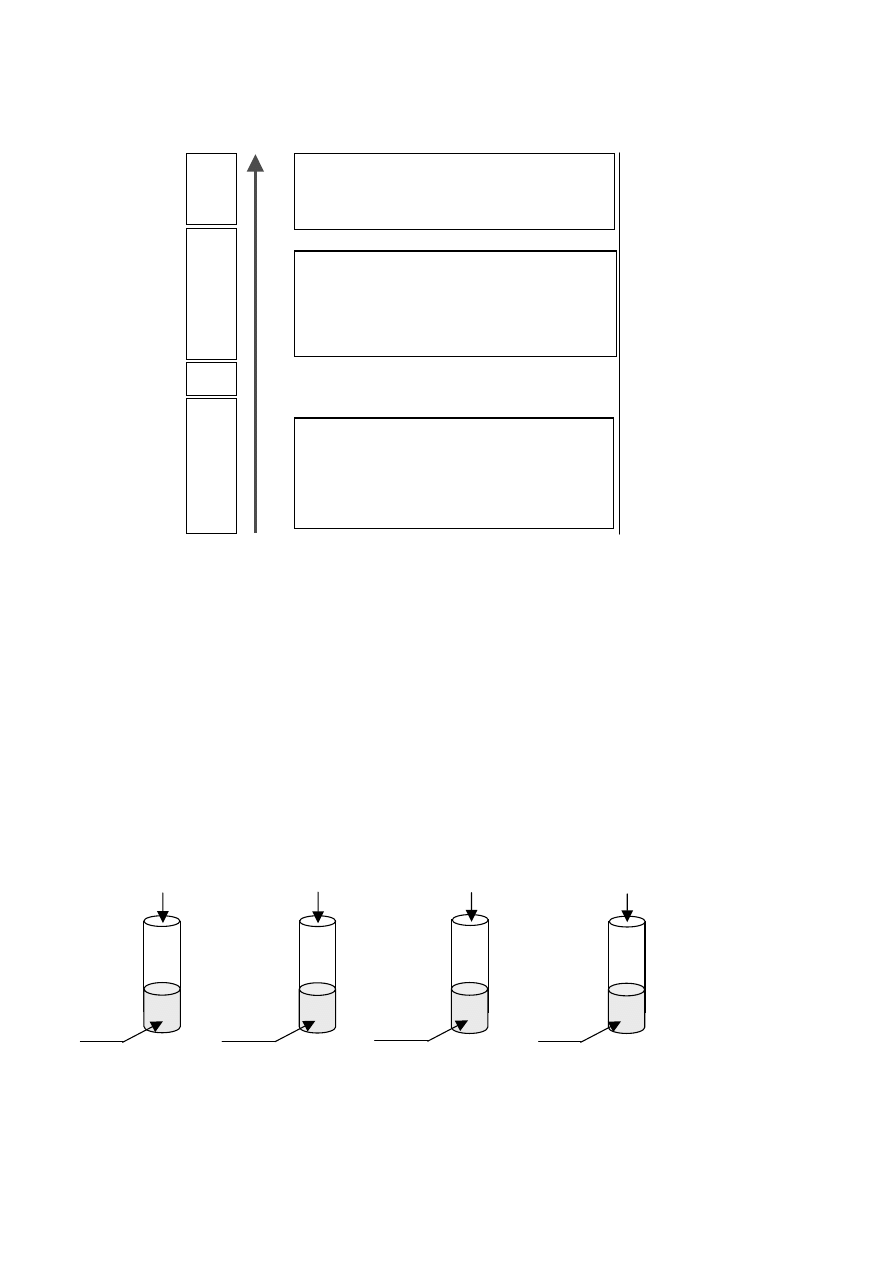
Schemat do zadań 23. i 24.
Zadanie 23. (0-1)
Wybierz zdanie prawdziwe.
A. Sód (Na) reaguje z wodą.
B. W reakcji srebra (Ag) z ZnCl
2
wydzieli się cynk (Zn).
C. Złoto (Au) jest bardziej aktywne chemicznie niż potas (K).
D. W reakcji złota (Au) z kwasem siarkowym(VI) wydzieli się wodór.
Zadanie 24. (0-1)
Przeprowadzono doświadczenia przedstawione na poniższym rysunku. W której
probówce jednym z produktów reakcji jest wodór?
A
.
I
B.
II
C.
III
D.
IV
II
Ag
H
2
SO
4
Bi
HCl
I
Mg
H
2
SO
4
III
Cu
HCl
IV
Strona 9 z 14
Przedstawiony poniżej fragment układu okresowego pierwiastków wykorzystaj do
rozwiązania zadań 25. i 26.
1
1
1
H
Wodór
1,008
2
13 14 15 16
2
3
Li
Lit
6,94
4
Be
Beryl
9,01
5
B
Bor
10,81
6
C
Węgiel
12,01
7
N
Azot
14,01
8
O
Tlen
15,99
3
11
Na
Sód
22,99
12
Mg
Magnez
24,31
3 4
...
9 10 11 12
13
Al
Glin
26,98
14
Si
Krzem
28,09
15
P
Fosfor
30,97
16
S
Siarka
32,07
4
19
K
Potas
39,09
20
Ca
Wapń
40,08
21
Sc
Skand
44,96
22
Ti
Tytan
47,90
...
27
Co
Kobalt
58,93
28
Ni
Nikiel
58,71
29
Cu
Miedź
63,55
30
Zn
Cynk
65,39
31
Ga
Gal
69,72
32
Ge
German
72,59
33
As
Arsen
74,92
34
Se
Selen
78,96
Zadanie 25. (0-1)
Na podstawie zamieszczonego fragmentu układu okresowego wybierz zdanie prawdziwe
dotyczące sodu (
Na
23
11
).
A. W jądrze atomu sodu jest 11 neutronów.
B. Liczba atomowa sodu jest równa 12.
C. Atom sodu ma konfigurację elektronową: 2, 8, 1.
D. Sód leży w trzecim okresie i drugiej grupie układu okresowego.
Zadanie 26. (0-2)
Pewien pierwiastek, umownie oznaczony literą E, tworzy tlenek o ogólnym wzorze EO
3
.
Jaki to pierwiastek, jeżeli masa cząsteczkowa jego tlenku wynosi 80,04 u? Zapisz
obliczenia.
Odpowiedź: .............................................................................................................................
SYMBOL
PIERWIASTKA
8
O
Tlen
15,99
NAZWA
LICZBA ATOMOWA
MASA ATOMOWA (u)
Strona 10 z 14
Zadanie 27. (0-2)
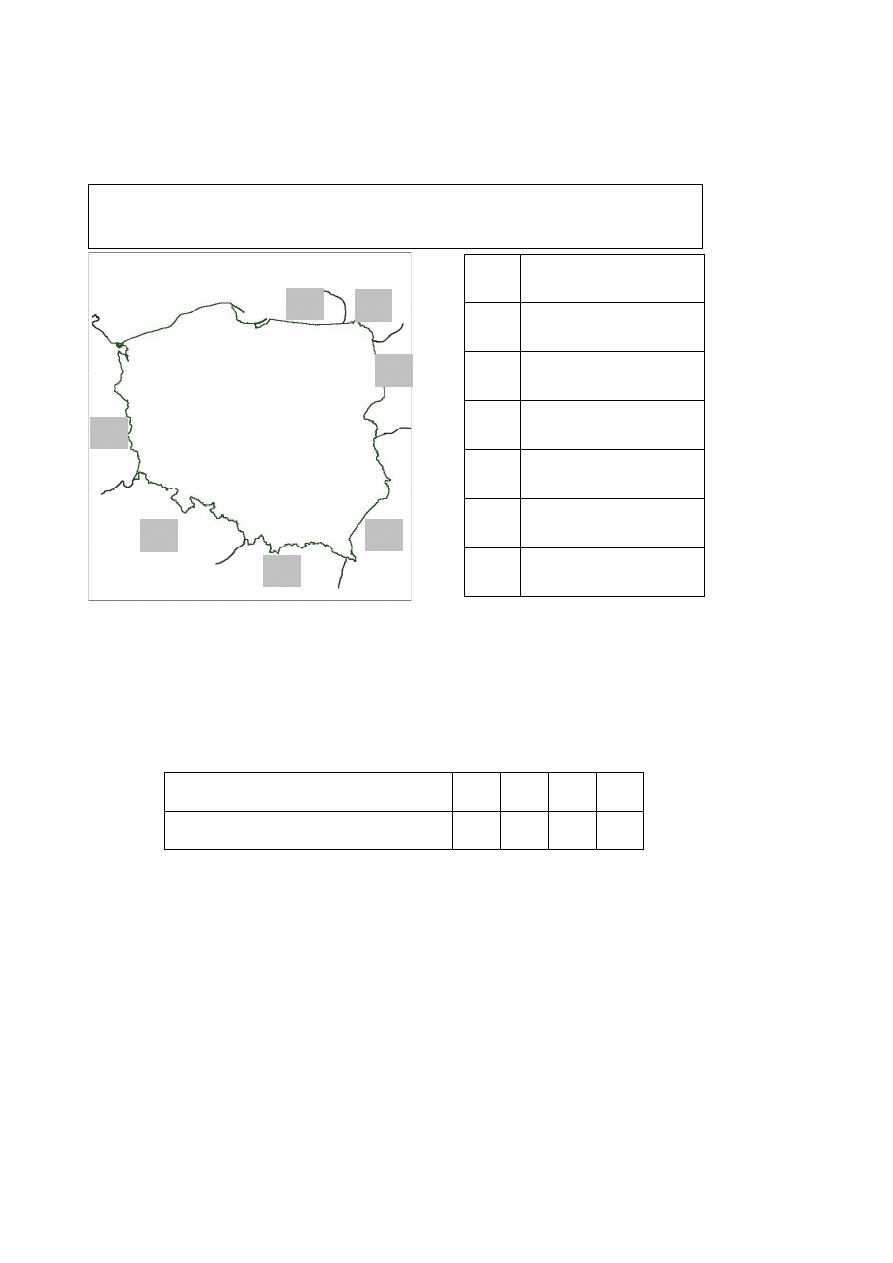
Korzystając z mapy i podanych w ramce nazw państw, wpisz do odpowiedniego wiersza
tabeli nazwy państw sąsiadujących z Polską.
Informacje i tabela do zadań 28. i 29.
Most zbudowany jest z przęseł o długości 10 m każde. Przęsło pod wpływem wzrostu
temperatury wydłuża się. Przyrost tego wydłużenia jest wprost proporcjonalny do przyrostu
temperatury. Wartość przyrostu długości przęsła dla wybranych wartości przyrostu
temperatury przedstawia poniższa tabela.
przyrost temperatury ∆t (°C)
0
10
30
45
przyrost długości przęsła ∆l (mm)
0
1
4,5
Zadanie 28. (0-1)
Wpisz do tabeli brakującą wartość przyrostu długości przęsła.
Zadanie
29.
(0-2)
Zapisz zależność przyrostu długości przęsła (∆l) od przyrostu temperatury (∆t) za
pomocą wzoru. Podaj współczynnik proporcjonalności ∆l do ∆t z odpowiednią
jednostką.
wzór
…………………………….…………
współczynnik proporcjonalności
……..……………...............................
1
2
3
4
5
6
7
1
........................................
2
........................................
3
........................................
4
........................................
5
........................................
6
........................................
7
........................................
Białoruś, Czechy, Litwa, Łotwa, Niemcy,
Rosja (Federacja Rosyjska), Słowacja, Ukraina
Strona 11 z 14
Schemat i informacje do zadania 30.
Fragment siatki kartograficznej przedstawia południk 180º
oraz południki, na których leżą
Nowy Orlean i Makasar.
Zadanie 30. (0-2)
Podaj dzień tygodnia i godzinę, która jest w Nowym Orleanie.
dzień tygodnia
..................................................
godzina
..................................................
Zadanie 31. (0-3)
Teleskop Hubble’a znajduje się na orbicie okołoziemskiej na wysokości około 600 km
nad Ziemią. Oblicz wartość prędkości, z jaką porusza się on wokół Ziemi, jeżeli czas
jednego okrążenia Ziemi wynosi około 100 minut. Zapisz obliczenia.
(Przyjmij R
Z
= 6400 km,
7
22
=
π
)
Odpowiedź: .............................................................................................................................
Ziemia
R
Z
orbita
teleskop Hubble’a
Ś
r
o
d
a
A Z J A
A M E R Y K A P N.
linia zmiany daty
120º
180º
90º
Nowy Orlean
Makasar
7:00 rano
E
W
Strona 12 z 14
Zadanie 32. (0-2)
Oblicz czas swobodnego spadku metalowej kulki z wysokości 20 m. Przyjmij wartość
przyspieszenia ziemskiego g = 10
2
s
m
i pomiń opór powietrza. Zapisz obliczenia.
Odpowiedź: ............................................................................................................................
Zadanie 33. (0-2)
Wieża Eiffla znajduje się na obszarze w kształcie kwadratu o boku długości 125 m.
Ile
hektarów powierzchni ma ten obszar? Zapisz obliczenia. Wynik podaj
z dokładnością do 0,1 ha.
Odpowiedź: ...........................................................................................................................
Strona 13 z 14
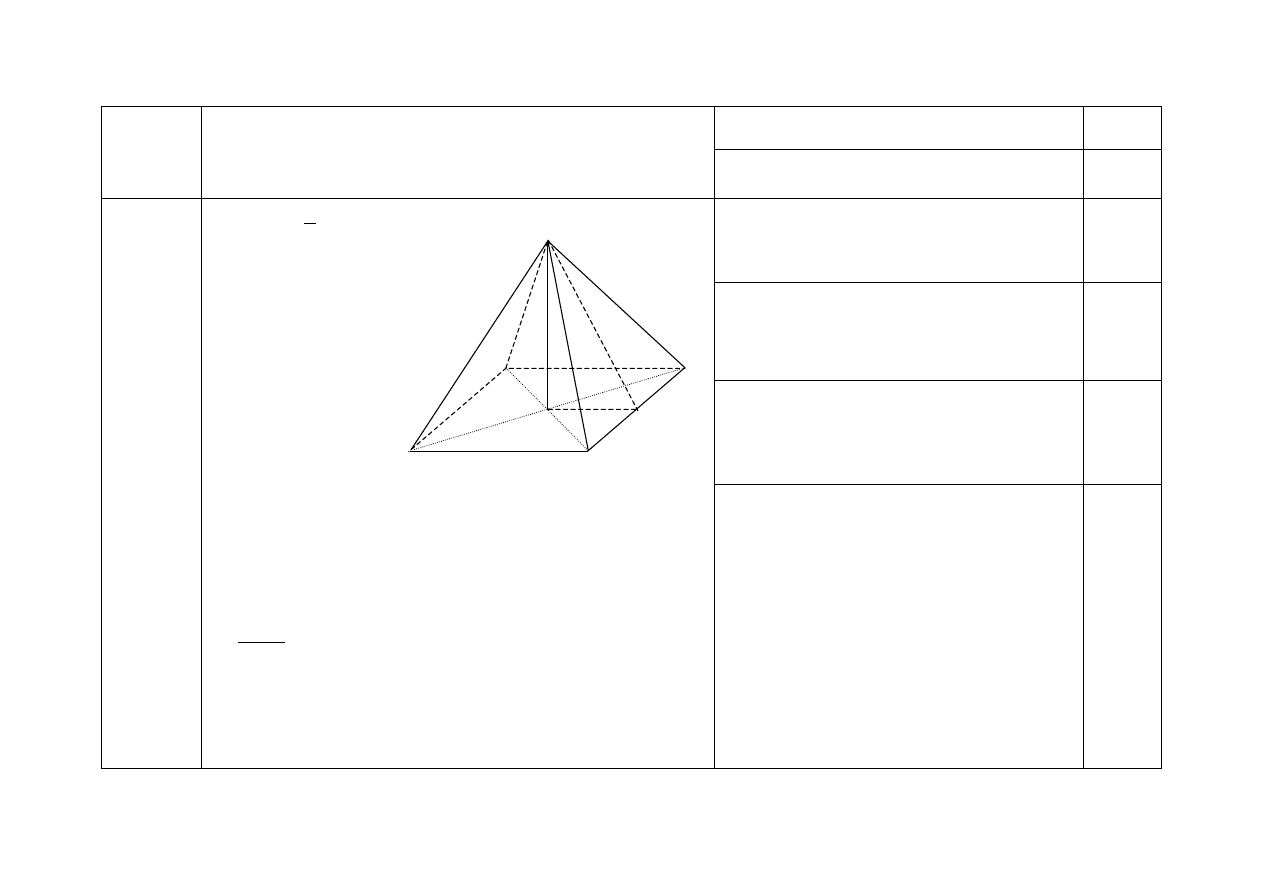
Zadanie 34. (0-4)
Piramida ma kształt ostrosłupa prawidłowego czworokątnego. Ile cm
2
papieru potrzeba
na wykonanie modelu tej piramidy (wraz z podstawą), w którym krawędzie podstawy
mają długość 10 cm a wysokość 12 cm? Ze względu na zakładki zużycie papieru jest
większe o 5%. Zapisz obliczenia.
Odpowiedź: ..............................................................................................................................
Tabela do zadania 35. zawiera ceny paliw.
Cena benzyny
Cena gazu
3,80 zł/l 1,60
zł/l
Zadanie 35. (0-5)
Montaż instalacji gazowej w samochodzie kosztuje 2208 zł. Samochód spala średnio
7 litrów benzyny lub 8 litrów gazu na każde 100 km drogi. Oblicz, po ilu miesiącach
zwrócą się koszty instalacji, jeśli w ciągu miesiąca samochód przejeżdża średnio
2000 km. Zapisz obliczenia.
Odpowiedź: .............................................................................................................................
C
B
A
D
S
O
Strona 14 z 14
Brudnopis
ODPOWIEDZI I PUNKTACJA ZADAŃ ZESTAWU EGZAMINACYJNEGO DLA UCZNIÓW BEZ DYSFUNKCJI
ORAZ UCZNIÓW Z DYSLEKSJĄ ROZWOJOWĄ (GM-A1-052)
Klucz odpowiedzi do zadań zamkniętych
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
D B C A A D D B D A C C B D A C B B B D D C A C C
Schemat punktowania do zadań otwartych
Uwagi ogólne:
Punkty za wykonanie (obliczenia) przyznajemy tylko wtedy, gdy uczeń stosuje poprawną metodę. Obliczenia nie muszą być szczegółowe,
powinny jednak ilustrować metodę rozwiązania.
Jeśli uczeń mimo polecenia „zapisz obliczenia” nie przedstawił żadnych obliczeń, a napisał poprawną odpowiedź, to nie otrzymuje punktów.
Za każde inne poprawne i pełne rozwiązanie przyznaje się maksymalną liczbę punktów należnych za zadanie.
Numer
zadania
(liczba
punktów
)
Przykład poprawnej odpowiedzi
Zasady przyznawania punktów
poprawna metoda obliczenia masy atomowej
pierwiastka E
1p.
26.
(2 p.)
M
EO
3
= 80,04 u
M
O
= 15,99 u
M
E
+ 3 · M
O
= 80,04 u
M
E
+ 3 · 15,99 u = 80,04 u
M
E
+ 47,97 u = 80,04 u
M
E
= 32,07 u
E oznacza siarkę
odczytanie nazwy pierwiastka (siarka)
1p.
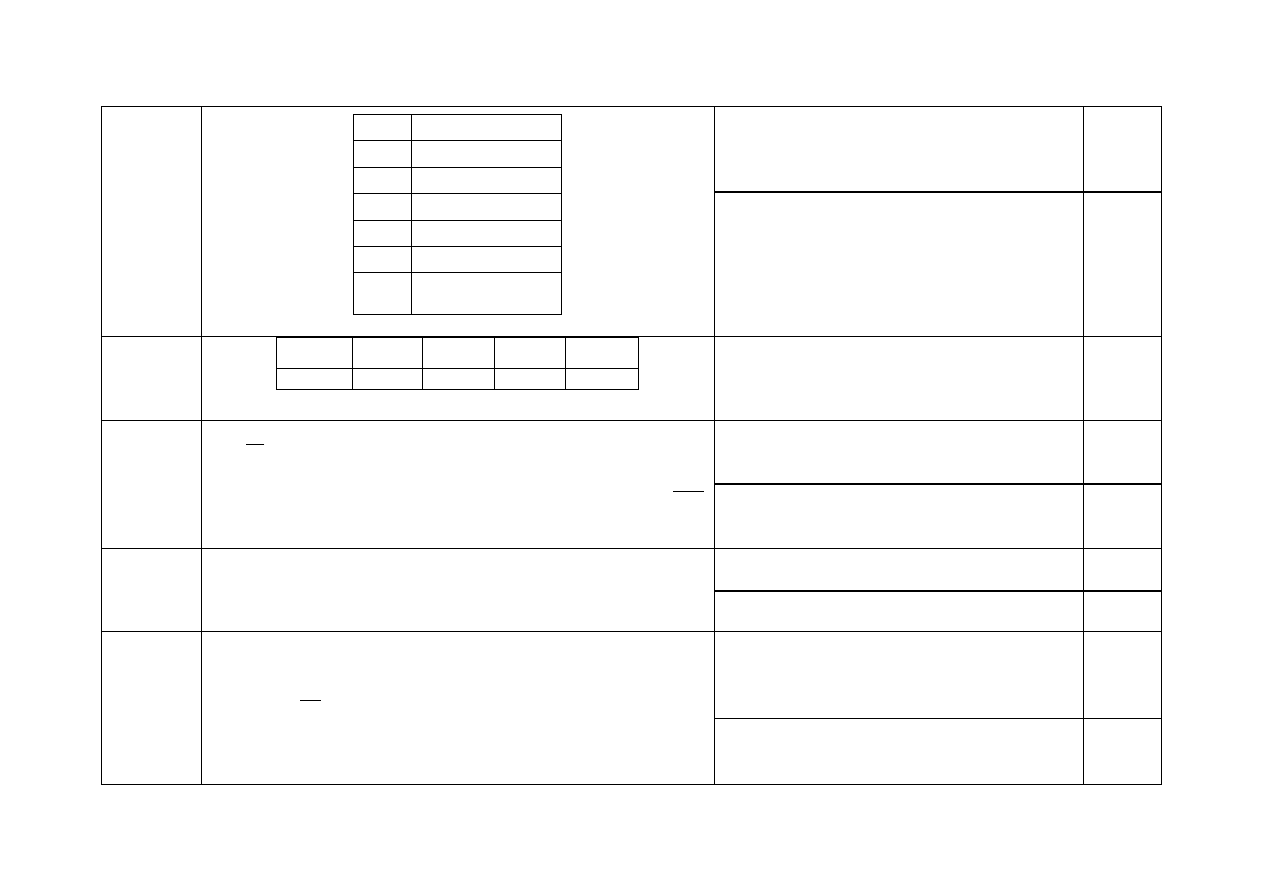
7 poprawnych odpowiedzi
2p.
27.
(2 p.)
1 Niemcy
2 Czechy
3 Słowacja
4 Ukraina
5 Białoruś
6 Litwa
7
Rosja (Federacja
Rosyjska)
5-6 poprawnych odpowiedzi
1 p.
28.
(1 p.)
∆t (°C)
0 10 30 45
∆l (mm)
0 1 3
4,5
poprawnie uzupełniona tabela
1p.
poprawnie zapisany wzór
1 p.
29.
(2 p.)
t
l
∆
=
∆
10
1
Wartość współczynnika proporcjonalności wraz z jednostką 0,1
C
º
mm
poprawnie określony współczynnik wraz
z jednostką
1 p.
poprawne określenie dnia tygodnia
1 p.
30.
(2 p.)
wtorek
17:00
poprawnie określona godzina
1 p.
poprawna metoda obliczania drogi w czasie
jednego okrążenia - długość okręgu o promieniu
7000
=
r
km
1p.
31.
(3 p.)
7000
600
6400
=
+
=
r
(km)
7000
7
22
2
2
⋅
⋅
=
=
r
s
π
44000
=
s
(km)
poprawna metoda obliczania wartości prędkości
satelity
1p.
t
s
v
=
100
60
44000
60
100
44000
⋅
=
=
v
60
440
⋅
=
v
h
km
26400
=
v
h
km
Odp: Wartość prędkości, z jaką porusza się teleskop Hubble’a wokół
Ziemi jest równa 26400
h
km
.
poprawne obliczenia i poprawny wynik
z jednostką
1p.
poprawna metoda obliczania czasu spadku kulki
(poprawnie podstawione dane)
1p.
32.
(2 p.)
2
2
t
g
h
⋅
=
g
h
t
2
2
=
g
h
t
2
=
4
10
20
2
=
⋅
=
t
2
=
t
(s)
s
=
m
•
m
=
s
m
m
2
2
s
poprawne obliczenia i poprawny wynik
z jednostką
1p.
poprawne obliczenie pola kwadratu
bez jednostki lub z poprawną jednostką
1p.
33.
(2 p.)
125
125
⋅
=
P
(m
2
)
15625
=
P
m
2
5625
,
1
=
P
ha
6
,
1
≈
P
ha
zamiana na hektary i podanie wyniku
z dokładnością do 0,1 ha
1p.
poprawna metoda obliczania wysokości ściany
bocznej
1p.
poprawna metoda obliczania pola powierzchni
całkowitej ostrosłupa
1p.
poprawna metoda obliczania pięciu procent pola
powierzchni całkowitej (5% P
C
)
1p.
34.
(4 p.)
h
a
a
P
C
⋅
⋅
⋅
+
=
2
1
4
2
h - wysokość ściany bocznej
ah
a
P
C
2
2
+
=
W
OES
∆
:
2
2
2
5
12
+
=
h
169
2
=
h
13
=
h
(cm)
360
13
10
2
100
=
⋅
⋅
+
=
C
P
(cm
2
)
360 cm
2
– 100%
x cm
2
– 5%
100
360
5
⋅
=
x
(cm
2
)
18
=
x
cm
2
360 cm
2
+ 18 cm
2
= 378 cm
2
Odp: Na wykonanie modelu potrzeba 378 cm
2
papieru.
poprawne obliczenia i poprawny wynik z
jednostką
1p.
12
10
B
D
S
h
5
O
E
poprawna metoda obliczania kosztu benzyny
potrzebnej do przejechania 100 km
1p.
poprawna metoda obliczania kosztu gazu
potrzebnego do przejechania 100 km
1p.
poprawna metoda obliczania kwoty
zaoszczędzonej w ciągu miesiąca (oszczędność
na 100 km, oszczędność na 2000 km)
1p.
poprawna metoda obliczania czasu amortyzacji
inwestycji
1p.
35.
(5 p.)
Obliczenie oszczędności miesięcznej
60
,
26
80
,
3
7
=
⋅
(zł) – koszt benzyny na 100 km
80
,
12
60
,
1
8
=
⋅
(zł) koszt gazu na 100 km
oszczędność na 100 km
80
,
13
80
,
12
60
,
26
=
−
(zł)
oszczędność miesięczna
276
80
,
13
20
=
⋅
(zł)
Obliczenie czasu t amortyzacji inwestycji
8
276
2208 =
=
t
(miesięcy)
Odp: Koszty instalacji zwrócą się po 8 miesiącach.
poprawne obliczenia i poprawny wynik
1p.