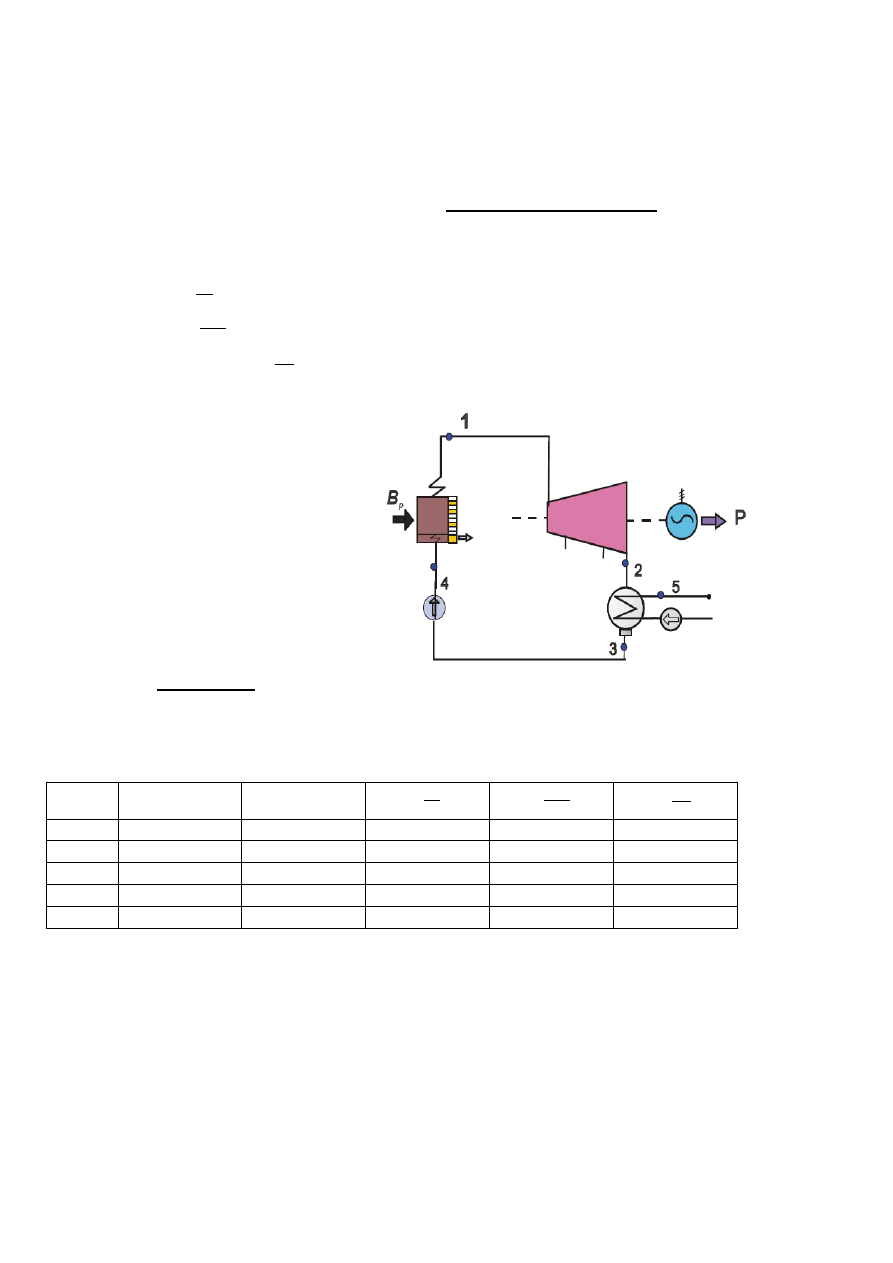
Marcin Grabarczyk

Nr Albumu 221720

Zadanie 1

Naszym zadaniem jest, dla prostego układu cieplnego elektrowni kondensacyjnej, określić następujące,
brakujące parametry termodynamiczne:



p - ciśnienie [bar]



T - temperatura [

℃]



i - entalpia

𝑘𝐽

𝑘𝑔



s - entropia

𝑘𝐽

𝑘𝑔𝐾



v - objętość właściwa

𝑚

3

𝑘𝑔

Dane:

PES = 10
p

1

= 132 [bar]

T

1

= 580 [

℃]

p

2

= 0,036 [bar]

p

3

= p

2

= 0,036 [bar]

p

4

= 171,6 [bar]

T

4

= 200 [

℃]

p

5

= 2 [bar]

T

5

= 28 [

℃]

Dla pkt. 3

→ x = 1

𝜂

𝑖𝑇

= 0,86 ≜

∆𝑖

𝑟𝑧𝑒𝑐𝑧𝑦𝑤𝑖𝑠𝑡𝑦

∆𝑖

𝑖𝑧𝑒𝑛𝑡𝑟𝑜𝑝𝑜𝑤𝑦

Rozwiązanie:

p [bar]

T [

℃]

i

𝑘𝐽

𝑘𝑔

s

𝑘𝐽

𝑘𝑔𝐾

v

𝑚

3

𝑘𝑔

1

132

580

3540,02

6,685

0,027697

2

0,036

27,1733

2217,4088

7,40171

33,1780

3

0,036

27,16

113.79

0,397175

0,001003

4

171,6

200

859,12

2,307

0,001141

5

2

28

117,49

0,408792

0,001004

Kolorem niebieskim

zaznaczone są parametry podane w treści zadania,

kolorem czerwonym

parametry

obliczone na drodze przedstawionego poniżej rozumowania.

Wykonane czynności

a) Dla punktu 1 wyznaczam pozostałe parametry pary w funkcji ciśnienia (p

1

) oraz temperatury (T

1

).

Czynnik traktuję, jako parę przegrzaną.

𝑠

1

= 𝑓 𝑝

1

, 𝑇

1

= 6,685

𝑘𝐽

𝑘𝑔𝐾

𝑖

1

= 𝑓 𝑝

1

, 𝑇

1

= 3540,02

𝑘𝐽

𝑘𝑔

𝑣

1

= 𝑓 𝑝

1

, 𝑇

1

= 0,027697

𝑚

3

𝑘𝑔

b) Wyznaczam entalpię w punkcie 2. Dla potrzeb dalszych rozważań traktuję przemianę, jako

izentropową. To znaczy: na wykresie i-s schodzę po linii stałej entropii z izobary p

1

do izobary p

2

.

Czynnik wchodzi, więc w obszar pary wilgotnej. W tym miejscu wykresu wyznaczam teoretyczną
entalpię właściwą

𝑖

2𝑇

. Następnie korzystając z definicji sprawności wewnętrznej turbiny (𝜂

𝑖𝑇

)

wyznaczam rzeczywistą entalpię właściwą

𝑖

2𝑅

w punkcie 2.

𝑖

2𝑇

= 𝑓 𝑝

2

, 𝑠

1

= 2002,10

𝑘𝐽

𝑘𝑔

∆𝑖

𝑖𝑧𝑒𝑛𝑡𝑟𝑜𝑝𝑜𝑤𝑦

= 𝑖

1

− 𝑖

2𝑇

= 3540,02 − 2002,10 = 1537,92

𝑘𝐽

𝑘𝑔

∆𝑖

𝑟𝑧𝑒𝑐𝑧𝑦𝑤𝑖𝑠𝑡𝑦

= 𝜂

𝑖𝑇

∙ Δ𝑖

𝑖𝑧𝑒𝑛𝑡𝑟𝑜𝑝𝑜𝑤𝑦

= 0,86 ∙ 1537,92 = 1322,6112

𝑘𝐽

𝑘𝑔

𝑖

2𝑅

= 𝑖

1

− Δ𝑖

𝑟𝑧𝑒𝑐𝑧𝑦𝑤𝑖𝑠𝑡𝑦

= 3540,02 − 1322,6112 = 2217,4088

𝑘𝐽

𝑘𝑔

c) Znając entalpię oraz ciśnienie w punkcie 2 wyznaczam brakujące parametry w ów punkcie, mając na

uwadze, że czynnik znajduje się w obszarze pary wilgotnej.

𝑠

2

= 𝑓 𝑖

2

, 𝑝

2

= 7,40171

𝑘𝐽

𝑘𝑔𝐾

𝑣

2

= 𝑓 𝑖

2

, 𝑝

2

= 33,1780

𝑚

3

𝑘𝑔

𝑇

2

= 𝑓 𝑖

2

, 𝑝

2

= 27,1733[℃]

d) W tym momencie należy się zastanowić nad sensem otrzymanych wyników. T

2

, czyli temperatura za

turbiną, jest mniejsza od T

5

, czyli temperatury wody chłodzącej. Oznacza to, że w skraplaczu woda

zamiast odzyskiwać ciepło, chłodząc parę, będzie ją ogrzewać. W tym przypadku, użycie skraplacza

traci sens.

Nasuwa się wniosek, że źle zostały dobrane parametry termodynamiczne dla tego układu.

Aby ostatecznie utwierdzić się w wyżej wymienionym przekonaniu wyliczę stopień suchości pary w

punkcie 2 w funkcji ciśnienia

(𝑝

2

) i entalpii właściwej (𝑖

2

).

Dla pkt. 2

→ 𝑥 = 𝑓 𝑝

2

, 𝑖

2

= 0,862898

Obliczony stopień suchości pary wynosi x=0,862898. Jest to dużo za dużo. Każdy 1%

wilgotności powoduje obniżenie sprawności turbiny o 1%. Jest to niedopuszczalne w pracy turbin

wysokoprężnych.

Moja teoria źle dobranych parametrów termodynamicznych układu broni się sama.

e) Nie przejmując się otrzymanymi wynikami kontynuuje rozwiązywanie układu cieplnego.

Wyznaczam parametry w punkcie 3. Z danych zadania wiadomo, że dla pkt. 3

→ x = 1. Woda w

skraplaczu jest, więc w stanie nasycenia, pozwala to na odczytanie temperatury w punkcie, 3 czyli

temperatury nasycenia dla p

3

. Czynnik roboczy traktuję, jako wodę.

𝑇

3

= 𝑓 𝑝

3

= 27,16 ℃

f) Odczytałem z linii nasycenia temperaturę T

3

dla ciśnienia p

3

. Widać, że temperatura przed

skraplaczem jest większą od tej za skraplaczem – jest to sensowny wynik. Problem leży, zatem w

doborze temperatury wody chłodzącej T

5

. W danych zadania jest ona zbyt wysoka. Sensowną

temperaturą dla tych danych była by temperatura równa 27

℃, ponieważ spadek temperatur ∆𝑇 =

𝑇

2

− 𝑇

3

jest niewielki, rzędu setnych części 1℃.

g) Następnie wyznaczę pozostałe parametry w funkcji ciśnienia (p

3

) oraz temperatury (T

3

).

𝑠

3

= 𝑓 𝑝

3

, 𝑇

3

= 0,397175

𝑘𝐽

𝑘𝑔𝐾

𝑖

3

= 𝑓 𝑝

3

, 𝑇

3

= 113,79

𝑘𝐽

𝑘𝑔

𝑣

3

= 𝑓 𝑝

3

, 𝑇

3

= 0,001003

𝑚

3

𝑘𝑔

h) Dla punktu 4 oraz 5 procedura jest analogiczna. Znamy odpowiednie ciśnienia oraz temperatury. W

tym wypadku za czynnik roboczy przyjmujemy wodę.

Dla pkt. 4

𝑠

4

= 𝑓 𝑝

4

, 𝑇

4

= 2,307

𝑘𝐽

𝑘𝑔𝐾

𝑖

4

= 𝑓 𝑝

4

, 𝑇

4

= 859,12

𝑘𝐽

𝑘𝑔

𝑣

4

= 𝑓 𝑝

4

, 𝑇

4

= 0,001141

𝑚

3

𝑘𝑔

Dla pkt. 5

𝑠

5

= 𝑓 𝑝

5

, 𝑇

5

= 0,408792

𝑘𝐽

𝑘𝑔𝐾

𝑖

5

= 𝑓 𝑝

5

, 𝑇

5

= 117,49

𝑘𝐽

𝑘𝑔

𝑣

5

= 𝑓 𝑝

5

, 𝑇

5

= 0,001004

𝑚

3

𝑘𝑔

i) Zastrzeżenie budzi jeszcze temperatura w punkcie 4. Jest to temperatura za pompą. Różnica między

temperaturą w punkcie 4 a punkcie 3 jest zbyt duża. Proces pompowania wody nie powoduje tak

dużego przyrostu temperatury. Można by było domyślać się czy w turbinie zastosowane są jakieś

upusty, gdyby w treści zadania nie zostało powiedziane, że jest to układ cieplny elektrowni

kondensacyjnej. Ta informacja definiuje nam brak upustów.

j) Dokonując analizy poprawności obliczeń (podpunkt 2 zadania domowego dla przypadku n równego

PES=16) użyłem tablic parowych Wukałowicza otrzymując następujące rezultaty:

Dla pary wilgotnej

𝑖 = 𝑓 𝑇, 𝑝 ≈ 2216

𝑘𝐽

𝑘𝑔

𝑇 = 𝑓 𝑖, 𝑠 ≈ 27 [℃]

Wyniki są bliskie tym, otrzymanym w programie FT_2010_SC.exe.

Dokładność odczytu z wykresu Wukałowicza zależy jedynie od chęci i zaangażowania zainteresowanego

oraz jakości druku wykresu.

Zadanie 2

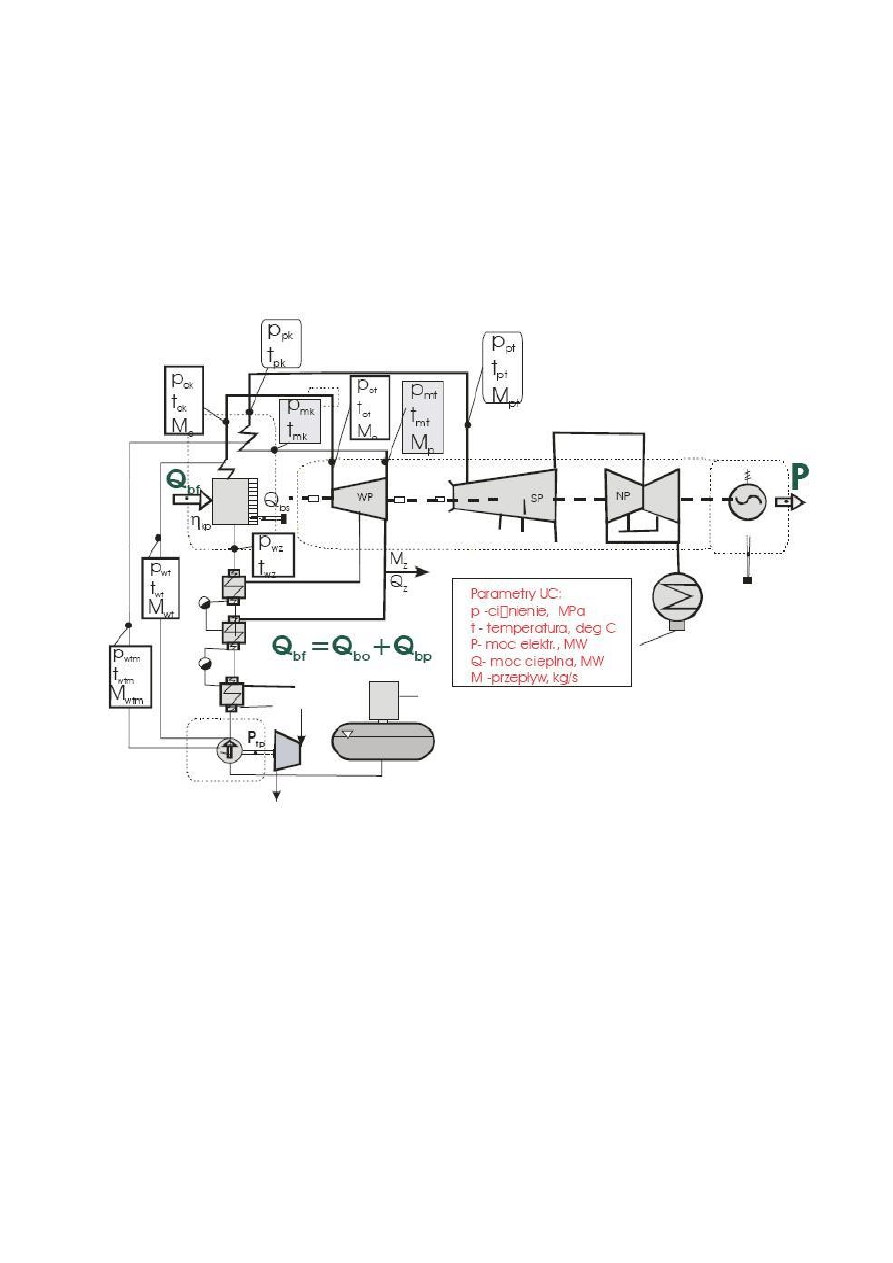
Naszym zadaniem jest określić zmianę sprawności i jednostkowego zużycia ciepła w bloku w

wyniku wtrysku wody zza pompy zasilającej do pary świeżej oraz wyjaśnić główne przyczyny zmniejszenia

sprawności i wzrostu zużycia ciepła w wyniku wtrysku wody do kotła.

Układ:

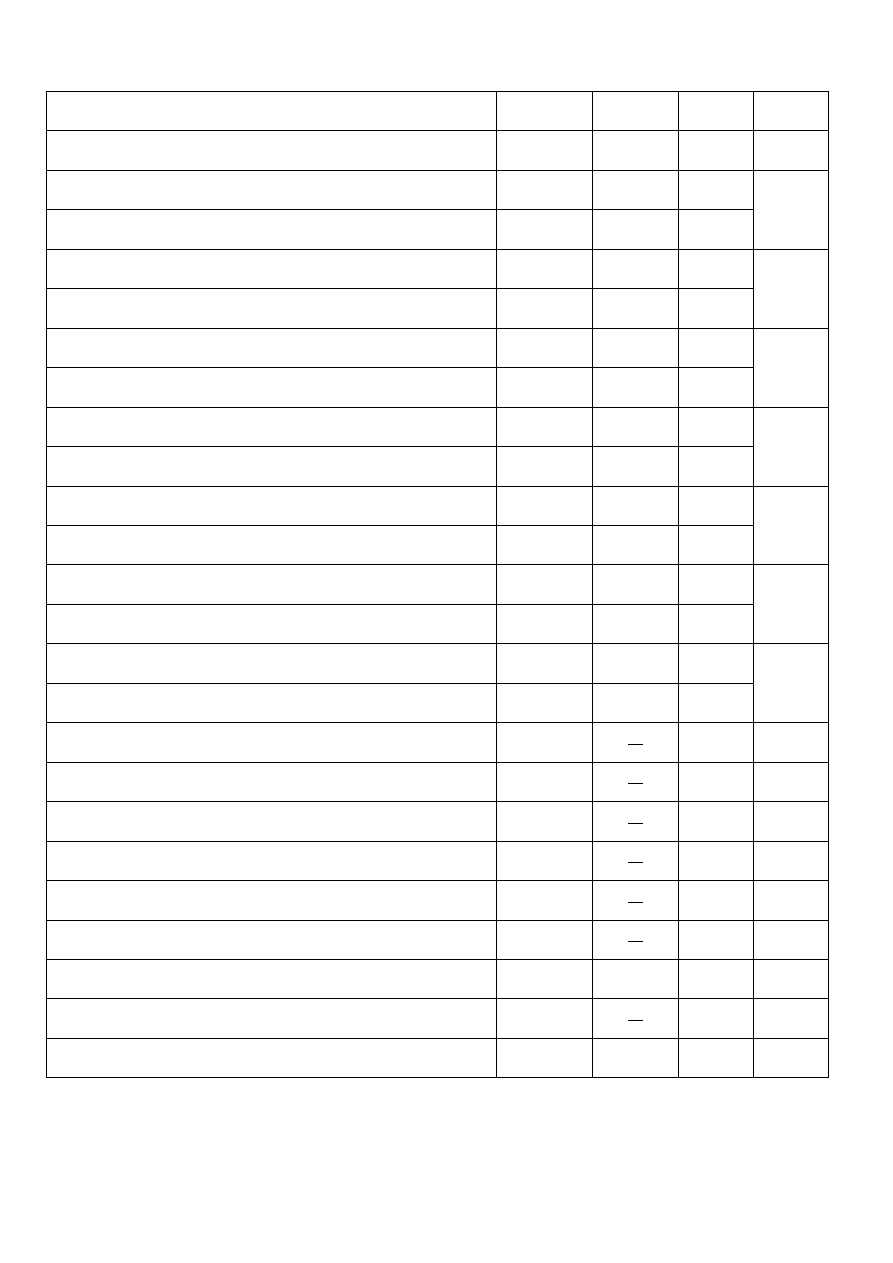
Dane:

Oznaczenie Jednostka Wartość Entalpia

Moc elektryczna bloku

P

MW

480

Ciśnienie pary świeżej za kotłem

P

ok

bar

266

3298,29

Temperatura pary świeżej za kotłem

T

ok

℃

544

Ciśnienie pary świeżej przed turbiną

P

ot

bar

258

3294,79

Temperatura pary świeżej przed turbiną

T

ot

℃

540

Ciśnienie pary za częścią wysokoprężną turbiny

P

mt

bar

54,86

2943,05

Temperatura pary za częścią wysokoprężną za turbiną

T

mt

℃

311

Ciśnienie pary za częścią wysokoprężną turbiny przed kotłem

P

mk

bar

53,7

2939,49

Temperatura pary za częścią wysokoprężną przed kotłem

T

mk

℃

308

Ciśnienie pary przegrzanej za kotłem

P

pk

bar

42,8

3589,6

Temperatura pary przegrzanej za kotłem

T

pk

℃

570

Ciśnienie pary przegrzanej przed turbiną średnioprężną

P

pt

bar

39,97

3583,53

Temperatura pary przegrzanej przed turbiną średnioprężną

T

pt

℃

565

Ciśnienie wody zasilającej przed kotłem

P

wz

bar

310

1201,76

Temperatura wody zasilającej przez kotłem

T

wz

℃

273

Ilość wody wtryskiwanej do przegrzewacza pierwotnego *

M

wt

𝑘𝑔

𝑠

0

805,777

Ilość wody wtryskiwanej do przegrzewacza wtórnego *

M

wtm

𝑘𝑔

𝑠

3,61

781,316

Wtrysk wody do pary świeżej **

M

wt

𝑘𝑔

𝑠

3,65

805,777

Wtrysk wody do pary przegrzanej **

M

wtm

𝑘𝑔

𝑠

3,65

781,316

Przepływ pary świeżej

M

o

𝑘𝑔

𝑠

365,3

Przepływ pary przegrzanej ***

M

p

𝑘𝑔

𝑠

330,6

Sprawność całkowita kotła

η

k

%

0,9

Ilość pary oddawanej na zewnątrz z turbiny wysokoprężnej

M

z

𝑘𝑔

𝑠

3,61

Moc turbiny pomocniczej

P

tp

kW

8,35

* dane do przypadku a)

** dla parametrów:

t = 184,5[℃] oraz p = 21[MPa], dane do przypadku b)

*** wlot do kotła

Rozwiązanie:

Przypadek a)

M

wt

= 0 oraz M

wtm

= 3,61

𝑘𝑔

𝑠

Ciepło Q

bf

dostarczone do kotła wynosi:

𝑄

𝑏𝑓

= 𝑀

𝑜

⋅ 𝑖

𝑜𝑘

+ 𝑀

𝑝

+ 𝑀

𝑤𝑡𝑚

⋅ 𝑖

𝑝𝑘

− 𝑀

𝑤𝑧

⋅ 𝑖

𝑤𝑧

− 𝑀

𝑤𝑡

⋅ 𝑖

𝑤𝑡

− 𝑀

𝑤𝑡𝑚

⋅ 𝑖

𝑤𝑡𝑚

− 𝑀

𝑝

⋅ 𝑖

𝑚𝑘

𝑄

𝑏𝑓

= 990,9266802 𝑀𝑊

Energia zawarta w paliwie:

𝑄

𝑏

=

𝑄

𝑏𝑓

𝜂

𝑘

𝑄

𝑏

= 1101,029645 𝑀𝑊

Jednostkowe zużycie ciepła bloku:

𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

=

𝑄

𝑏

𝑃

𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

= 8257,722335

𝑘𝐽

𝑘𝑊𝑕

Sprawność bloku:

𝜂

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

=

3600

𝑞

𝑛𝑒𝑡𝑡𝑜

𝜂

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

= 0,435955564

Ciepło dostarczone do turbiny:

𝑄

𝑡

= 𝑀

𝑜

− 𝑀

𝑤𝑡

⋅ 𝑖

𝑜𝑡

− 𝑖

𝑤𝑧

+ 𝑀

𝑝

⋅ 𝑖

𝑝𝑡

− 𝑖

𝑚𝑡

+ 𝑀

𝑤𝑡𝑚

⋅ 𝑖

𝑝𝑡

− 𝑖

𝑤𝑡𝑚

+ 𝑀

𝑤𝑡

⋅ 𝑖

𝑜𝑡

− 𝑖

𝑤𝑡

− 𝑖

𝑤𝑧

⋅ 𝑀

𝑜

− 𝑀

𝑝

𝑄

𝑡

= 944,7414675

𝑘𝐽

𝑘𝑊𝑕

Jednostkowe zużycie ciepła przez turbinę:

𝑞

𝑛𝑒𝑡𝑡𝑜 𝑡𝑢𝑟𝑏𝑖𝑛𝑦

=

𝑄

𝑡

𝑃

= 7085,561007

𝑘𝐽

𝑘𝑊𝑕

Przypadek b)

M

wt

= 3,65

𝑘𝑔

𝑠

oraz M

wtm

= 3,65

𝑘𝑔

𝑠

Ciepło Q

bf

dostarczone do kotła wynosi:

𝑄

𝑏𝑓

= 𝑀

𝑜

⋅ 𝑖

𝑜𝑘

+ 𝑀

𝑝

+ 𝑀

𝑤𝑡𝑚

⋅ 𝑖

𝑝𝑘

− 𝑀

𝑤𝑧

⋅ 𝑖

𝑤𝑧

− 𝑀

𝑤𝑡

⋅ 𝑖

𝑤𝑡

− 𝑀

𝑤𝑡𝑚

⋅ 𝑖

𝑤𝑡𝑚

− 𝑀

𝑝

⋅ 𝑖

𝑚𝑘

𝑄

𝑏𝑓

= 992,4843496 𝑀𝑊

Energia zawarta w paliwie:

𝑄

𝑏

=

𝑄

𝑏𝑓

𝜂

𝑘

𝑄

𝑏

= 1102,760388 𝑀𝑊

Jednostkowe zużycie ciepła bloku:

𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

=

𝑄

𝑏

𝑃

𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

= 8270,702913

𝑘𝐽

𝑘𝑊𝑕

Sprawność bloku:

𝜂

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

=

3600

𝑞

𝑛𝑒𝑡𝑡𝑜

𝜂

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

= 0,435271347

Ciepło dostarczone do turbiny:

𝑄

𝑡

= 𝑀

𝑜

− 𝑀

𝑤𝑡

⋅ 𝑖

𝑜𝑡

− 𝑖

𝑤𝑧

+ 𝑀

𝑝

⋅ 𝑖

𝑝𝑡

− 𝑖

𝑚𝑡

+ 𝑀

𝑤𝑡𝑚

⋅ 𝑖

𝑝𝑡

− 𝑖

𝑤𝑡𝑚

+ 𝑀

𝑤𝑡

⋅ 𝑖

𝑜𝑡

− 𝑖

𝑤𝑡

− 𝑖

𝑤𝑧

⋅ 𝑀

𝑜

− 𝑀

𝑝

𝑄

𝑡

= 946,2988941

𝑘𝐽

𝑘𝑊𝑕

Jednostkowe zużycie ciepła przez turbinę:

𝑞

𝑛𝑒𝑡𝑡𝑜 𝑡𝑢𝑟𝑏𝑖𝑛𝑦

=

𝑄

𝑡

𝑃

= 7097,241705

𝑘𝐽

𝑘𝑊𝑕

Rozwiązanie końcowe oraz komentarz do zadania:

a) Określić zmianę sprawności i jednostkowego zużycia ciepła w bloku w wyniku wtrysku wody zza

pompy zasilającej do pary świeżej

∆𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

= 𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢 𝑏)

− 𝑞

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢 𝑎)

= 12,98058 𝑘𝐽 𝑘𝑊𝑕

∆𝜂

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢

= 𝜂

𝑛𝑒𝑡𝑡𝑜 𝑏𝑙𝑜𝑘𝑢 𝑎)

− 𝜂

𝑛𝑒𝑡 𝑡𝑜 𝑏𝑙𝑜𝑘𝑢 𝑏)

= 0,000684

b) Wyjaśnić główne przyczyny zmniejszenia sprawności i wzrostu zużycia ciepła w wyniku wtrysku

wody do kotła

Jeżeli do pary wtryskujemy wodę efektem jest obniżenie wartości entalpii. Efektem tego zabiegu jest wzrost

jednostkowego zużycia ciepła, a jego następstwem spadek sprawności.