ĐHĐN Giáo Trình Cấu Trúc Dữ Liệu Và Giải Thuật (NXB Đà Nẵng 2003) Phạm Anh Tuấn, 72 Trang

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 1

Män hoüc Cáúu truïc dæî liãûu vaì Giaíi thuáût coï mäüt vai troì quan troüng âäúi våïi caïc hoüc viãn

vaì sinh viãn chuyãn ngaình Tin hoüc, cung cáúp cho hoüc viãn vaì sinh viãn caïc cáúu truïc dæî liãûu
vaì caïc giaíi thuáût thêch håüp âãø giaíi quyãút caïc baìi toaïn trong thæûc tãú bàòng maïy tênh. Giaïo trçnh
naìy coìn coï thãø duìng laìm taìi liãûu tham khaío bäø êch cho nhæîng ngæåìi muäún tçm hiãøu vãö män
hoüc naìy.

Giaïo trçnh âæåüc biãn soaûn nhàòm phuûc vuû cho caïc âäúi tæåüng hoüc viãn Trung cáúp Tin hoüc

vaì Kyî thuáût viãn Tin hoüc. Näüi dung cuía Giaïo trçnh âæåüc biãn soaûn phuì håüp våïi caïc âäúi
tæåüng hoüc viãn vaì cå cáúu män hoüc hiãûn nay âang âæåüc giaíng daûy taûi Trung tám Phaït triãøn
pháön mãöm - Âaûi hoüc Âaì Nàông. Caïc giaíi thuáût trong Giaïo trçnh naìy âæåüc trçnh baìy theo cáúu
truïc âiãöu khiãøn chuáøn vaì âæåüc minh hoüa bàòng ngän ngæî láûp trçnh Pascal.

Giaïo trçnh naìy âæåüc chia laìm 6 Chæång:
Chæång 1: Giåïi thiãûu caïc kiãún thæïc cå baín vãö ngän ngæî láûp trçnh Pascal nhàòm muûc âêch

tråü giuïp cho viãûc âoüc, hiãøu caïc giaíi thuáût âæåüc trçnh baìy åí caïc chæång sau. Pháön naìy ráút hæîu
êch âäúi våïi caïc hoüc viãn chæa biãút hoàûc chæa thaình thaûo vãö ngän ngæî láûp trçnh Pascal maì
muäúc âoüc, hiãøu caïc giaíi thuáût âæåüc trçnh baìy trong giaïo trçnh naìy.

Chæång 2: Trçnh baìy caïc cáúu truïc dæî liãûu vaì giaíi thuáût thæåìng duìng trãn danh saïch.
Chæång 3: Trçnh baìy caïc giaíi thuáût tçm kiãúm trãn daîy.
Chæång 4: Trçnh baìy caïc giaíi thuáût sàõp xãúp thæï tæû daîy.
Chæång 5: Trçnh baìy cáúu truïc dæî liãûu vaì giaíi thuáût trãn cáy, âàûc biãût laì cáy nhë phán.
Chæång 6: Giåïi thiãûu mäüt säú æïng duûng cuía caïc cáúu truïc dæî liãûu vaì giaíi thuáût âãø giaíi

quyãút caïc baìi toaïn trãn âäö thë nhæ tçm kiãúm theo chiãöu räüng, tçm kiãúm theo chiãöu sáu, tçm
âæåìng âi ngàõn nháút.

Do thåìi gian chuáøn bë khäng nhiãöu, khäúi læåüng kiãún thæïc laûi låïn. Vç váûy âãø giuïp hoüc

viãn nàõm âæåüc kiãún thæïc cå baín män hoüc, chuïng täi âaî ráút kyî caìng trong quaï trçnh biãn
soaûn, tham khaío nhiãöu taìi liãûu cuîng nhæ thæûc tãú giaíng daûy män hoüc Cáúu truïc dæî liãûu vaì Giaíi
thuáût taûi Trung tám phaït triãøn pháön mãöm - Âaûi hoüc Âaì Nàông trong thåìi gian qua. Màûc duì
váûy, Giaïo trçnh naìy chàõc chàõn seî khäng traïnh khoíi thiãúu soït. Chuïng täi ráút mong nháûn âæåüc
sæû goïp yï chán tçnh cuía baûn âoüc cuîng nhæ baûn beì âäöng nghiãûp gáön xa.

Âaì Nàông, ngaìy 10/02/2003

TT. Phaït triãøn Pháön mãöm - ÂHÂN

Âëa chè: 41 Lã Duáøn - Tp. Âaì Nàông

Email: sdc@ud.edu.vn

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 2

Chæång naìy giåïi thiãûu nhæîng thaình pháön cå baín cuía ngän ngæî láûp trçnh Pascal âæåüc sæí

duûng cho viãûc mä taí giaíi thuáût trong caïc chæång sau cuía giaïo trçnh naìy. Caïc thaình pháön cå
baín cuía ngän ngæî láûp trçnh Pascal bao gäöm caïc kiãøu dæî liãûu chuáøn, caïc kiãøu dæî liãûu coï cáúu
truïc, âënh nghéa kiãøu, caïc cáúu truïc âiãöu khiãøn.

I. CAÏC KIÃØU DÆÎ LIÃÛU CÅ BAÍN

Trong Pascal moüi hàòng, trë, biãún, biãøu thæïc hoàûc haìm phaíi thuäüc mäüt kiãøu nháút âënh. Caïc

kiãøu phaíi âæåüc âënh nghéa tæåìng minh khi khai baïo caïc hàòng, trë, biãún hoàûc haìm vaì sæû khai
baïo naìy phaíi coï træåïc khi sæí duûng hàòng, trë biãún hoàûc biãøu thæïc âoï.

I.1. Caïc kiãøu dæî liãûu cå baín

Caïc kiãøu dæî liãûu cå baín laì nhæîng kiãøu dæî liãûu âaî âæåüc âënh nghéa båíi Pascal. Caïc kiãøu

naìy bao gäöm kiãøu säú nguyãn, kiãøu säú thæûc, kiãøu luáûn lyï (lägic) vaì kiãøu xáu kyï tæû.

a) Kiãøu Integer (nguyãn)
Coï 5 kiãøu säú nguyãn âæåüc täøng kãút trong baíng sau:

Tãn

Miãön giaï trë

Dung læåüng

Shortint

Integer

Longint

Byte

Word

-128

127

-32768

32767

-2147483648

2147483647

255

65535

1 bytes
2 bytes
4 bytes
1 bytes
2 bytes

b) Kiãøu Real (thæûc)
Coï 5 kiãøu säú thæûc âæåüc täøng kãút trong baíng sau:

Tãn

Miãön giaï trë

Dung læåüng

Single

Real

Double

Extended

Comp

1.5*10

-45

3.4*10

2.9*10

-39

1.7*10

5.0*10

-324

1.7*10

308

3.4*10

-4932

1.1*10

4932

-9.2*10

9.2*10

4 bytes
6 bytes
8 bytes

10 bytes

8 bytes

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 3

c) Kiãøu Boolean (luáûn lyï)
Kiãøu Boolean chè nháûn hai giaï trë luáûn lyï laì True (âuïng) vaì False (sai). Caïc pheïp toaïn cå

baín gäöm Not (phuí âënh), And (vaì), Or (hoàûc). Baíng chán trë cuía 3 pheïp toaïn naìy nhæ sau:

a And b a Or b

Not a

False

True

False

True

False

True

False

True

False

True

d) Kiãøu Char (kyï tæû)
Kiãøu kyï tæû gäöm mäüt táûp håüp caïc kyï tæû in âæåüc. Caïc kyï tæû thæåìng duìng laì 26 chæî caïi

Latin, 10 chæî säú vaì mäüt säú kyï tæû âàûc biãût. Mäùi kyï tæû âæåüc gaïn tæång âæång våïi mäüt maî cho
trong baíng maî ASCII.

Vê duû: ‘A’

≈

65 , ‘B’

≈

66 , ... , ‘a’

≈

97 , ‘b’

≈

98 , ..., ‘0’

≈

48 , ‘1’

≈

49 , ‘’2’

≈

50 , ...

Hai haìm chuáøn chuyãøn âäøi giæîa kyï tæû vaì maî cuía noï laì: Ord vaì Chr: Ord(Chr(i)) = i vaì

Chr(Ord(c)) = c.

I.2. Kiãøu liãût kã (enumerated types)

Kiãøu liãût kã bao gäöm mäüt táûp håüp caïc giaï trë bàòng caïch liãût kã caïc danh hiãûu (identifier)

chè âënh caïc giaï trë naìy. Thæï tæû cuía caïc giaï trë laì thæï tæû liãût kã caïc danh hiãûu. Kiãøu liãût kã
âæåüc âënh nghéa nhæ sau:

Type T = (c

, c

, ..., c

)

, trong âoï c

, c

, ..., c

laì caïc danh hiãûu chè âënh caïc giaï trë

cuía kiãøu liãût kã.

Vê duû:

Type weekday = (Monday, Tuesday, Wednesday, Thursday, Friday, Saturday, Sunday) ;

Caïc haìm trãn kiãøu liãût kã gäöm coï:
-

Pred(x) traí vãö giaï trë âi ngay træåïc cuía x. Vê duû: Pred(Thursday) laì Wednessday

Succ(x) traí vãö giaï trë âi ngay sau x. Vê duû: Succ(Thursday) cho Friday

I.3. Kiãøu miãön con (subrange types)

Cho pheïp âënh nghéa biãún maì giaï trë cuía noï bë giåïi haûn trong mäüt miãön con theo daûng:

Type T = min .. max

, trong âoï min vaì max laì giåïi haûn cuía kiãøu miãön con.

Vê duû :

Type year = 1990 .. 1999;
Type Letter = ‘A’ .. ‘Z’;

I.4. Kiãøu chuäùi kyï tæû (string types)

Duìng âãø biãøu diãùn mäüt chuäùi kyï tæû, chuäùi kyï tæû âæåüc bao boüc båíi 2 dáúu nhaïy âån (‘) vaì

coï täúi âa 255 kyï tæû. Säú kyï tæû trong chuäùi goüi laì chiãöu daìi cuía chuäùi. Mäüt chuäùi coï chiãöu daìi
bàòng 0 goüi laì chuäùi räùng.

Vê duû: Khai baïo vaì sæí duûng biãún

Var s: string[10]; (* Khai baïo chuäùi coï täúi âa laì 10 kyï tæû *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 4

s := ‘Tuanpa‘;

Âãø truy xuáút kyï tæû thæï i trong chuäùi s ta duìng cuï phaïp: s[i], Vê duû: s[i] = ’T’. Âãø gheïp 2

chuäùi ta duìng pheïp toaïn +, Vê duû:

s1 := ‘Dai hoc ’; s2 := ‘Da Nang’;

thç

s3 := s1 + s2;

I.5. Kiãøu maíng (array types)

Maíng laì mäüt táûp håüp caïc biãún coï cuìng kiãøu dæî liãûu âæåüc bäú trê caûnh nhau trong bäü nhåï.

Âãø truy xuáút tåïi mäüt pháön tæí cuía maíng ta duìng tãn maíng keìm theo chè säú. Trong Pascal chè
säú maíng phaíi laì kiãøu dæî liãûu âãúm âæåüc. Maíng coï thãø laì maíng mäüt chiãöu hoàûc nhiãöu chiãöu.

Vê duû:

Type mang1c = array [1..5] of Real; (* Maíng mäüt chiãöu *)
Type mang2c = array [‘A’ .. ‘Z’ , True .. False] of Byte; (* Maíng hai chiãöu *)
Var m: mang1c; mm: mang2c;

(* Khai baïo caïc biãún maíng *)

m[2] := 3.14; mm[‘B’ , True] := 100; (* Truy xuáút caïc pháön tæí cuía maíng *)

I.6. Kiãøu baín ghi (record types)

Tæång tæû nhæ kiãøu maíng nhæng caïc pháön tæí coï thãø coï kiãøu dæî liãûu khaïc nhau. Kiãøu dæî

liãûu baín ghi âæåüc âënh nghéa nhæ sau:

Type T = Record

: T

;

: T

;

...

: T

;

End;

Âãø truy xuáút âãún mäüt thaình pháön S

cuía mäüt biãún baín ghi x ta duìng cuï phaïp:

x.Si

I.7. Kiãøu táûp håüp (set types)

Chè âënh táûp håüp gäöm caïc pháön tæí thuäüc kiãøu cå såí. Kiãøu táûp håüp âæåüc âënh nghéa theo

cuï phaïp:

Type T = Set of Kiãøu_cå_såí;

Vê duû:

Type Color = (Red , Green , Blue , Yellow); (* Kiãøu liãût kã *)
Type Pen = Set of Color;

(* Kiãøu táûp håüp *)

Type byteset = Set of 0..100;

(* Kiãøu táûp håüp *)

Type intset = Set of Integer;

(* Kiãøu táûp håüp *)

Caïc pheïp toaïn cå baín trãn táûp håüp gäöm: * (giao 2 táûp håüp); + (håüp 2 táûp håüp); - (hiãûu 2

táûp håüp); in (thuäüc vãö táûp håüp).

Vê duû:

Type IntSet = Set of Integer;
Var clr: Color; s1, s2, s3: intset;
s1 := [1, 4, 2]; s2 := [4, 8, 5];
clr := [Red, Green];
s3 := [];

(* táûp håüp räùng *)

s3 := s3+ [9];

(* thãm pháön tæí 9 vaìo s3 *)

s3 := s1 * s2;

(* s3 laì giao cuía s1 vaì s2, s3=[4] *)

Trong âoï:
S

, S

, ..., S

laì caïc thaình pháön vaì T

, T

, ..., T

laì kiãøu dæî liãûu cuía caïc thaình pháön tæång æïng.

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 5

I.8. Kiãøu con troí (pointer types)

Kiãøu con troí duìng âãø chè âãún caïc biãún âäüng (dynamic variable) thuäüc kiãøu dæî liãûu cå såí.

Mäüt biãún thuäüc kiãøu con troí seî chæïa âëa chè cuía mäüt biãún âäüng coï kiãøu tæång æïng. Coï bao
nhiãu kiãøu dæî liãûu thç coï báúy nhiãu kiãøu con troí, âãø coï thãø chæïa âæåüc âëa chè thç kiãøu cuía
biãún âäüng vaì kiãøu cuía con troí phaíi giäúng nhau. Kiãøu con troí âæåüc âënh nghéa nhæ sau:

Type Kiãøu_con_troí = ^ Kiãøu_dæî_ liãûu;

Vê duû:

Type person = Record

(* âënh nghéa kiãøu dæî liãûu cáúu truïc person *)

Name: String[25];

Age: Integer;

Male: Boolean;

End;
Type Pperson = ^person; (* âënh nghéa kiãøu con troí Pperson kiãøu person*)
Type Pint = ^Integer;

(* âënh nghéa kiãøu con troí Pint kiãøu Integer *)

Var p: Pperson; x: Pperson; (* khai baïo caïc biãún con troí *)

Khi con troí p chæïa âëa chè cuía biãún x coï cuìng kiãøu thç ta noïi p troí tåïi x, khi âoï hai caïch

viãút sau laì tæång âæång: x vaì p^ vaì, âãø chè ra thaình pháön Name cuía x ta viãút: p^.Name

Âãø cáúp phaït âäüng mäüt vuìng nhåï räöi cho con troí p troí tåïi vuìng nhåï âoï ta duìng thuí tuûc:

New(p). Âãø giaíi phoïng (thu häöi) laûi vuìng nhåï hiãûn con troí p âang troí tåïi ta duìng thuí tuûc:
Dispose(p).

II. CAÏC CÁÚU TRUÏC ÂIÃØU KHIÃØN

II.1. Khäúi lãûnh

Khäúi lãûnh laì mäüt táûp håüp caïc cáu lãûnh âæåüc bao boüc båíi càûp tæì khoïa Begin vaì End, caïc

cáu lãûnh trong mäüt khäúi lãûnh thæåìng âæåüc thæûc hiãûn theo tuáön tæû tæì trãn xuäúng dæåïi. Khi
khäúi lãûnh chè coï mäüt cáu lãûnh ta coï thãø khäng sæí duûng Begin vaì End. Vê duû:

Begin (* bàõt âáöu khäúi lãûnh 1 *)

d := b*b - 4*a*c;
If d > 0 Then
Begin (* bàõt âáöu khäúi lãûnh 2 *)

x1 := (-b - sqrt(d))/(2 * a);
x2 := (-b + sqrt(d))/(2 * a);

End; (* kãút thuïc khäúi lãûnh 2 *)

II.2. Cáúu truïc âiãöu kiãûn (conditional statements)

a) Cáúu truïc If
Cáúu truïc If coï hai daûng:
Daûng 1:

If <âiãöu kiãûn> Then <khäúi lãûnh>

(nãúu <âiãöu kiãûn> âuïng thç thæûc hiãûn <khäúi lãûnh>, ngæåüc laûi thç boí qua)
Daûng 2:

If <âiãöu kiãûn> Then <khäúi lãûnh 1> Else <khäúi lãûnh 2>

(nãúu âiãöu kiãûn âuïng thç thæûc hiãûn <khäúi lãûnh 1>, ngæåüc laûi thç thæûc hiãûn <khäúi lãûnh 2>)
Vê duû:

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 6

If (a = b) And (b = c) Then

Writeln (‘Tam giác âãöu’)

Else

If (a = b) Or (b = c) Or (a = c) Then

Writeln (‘Tam giaïc cán’)

Else writeln(‘Khäng biãút !’)

End

b) Cáúu truïc Case
Âãø giaím båït sæû phæïc taûp cuía cáu lãûnh If khi coï nhiãöu âiãöu kiãûn cáön kiãøm tra ta sæí duûng

cáúu truïc Case. Cuï phaïp nhæ sau:

Case <biãøu thæïc> Of

Value 1: <khäúi lãûnh 1>
Value 2: <khäúi lãûnh 2>
...
Value n: <khäúi lãûnh n>
[Else: <khäúi lãûnh n+1>] (* trong càûp ngoàûc naìy laì pháön tuìy choün *)

End

Khi thæûc hiãûn maïy seî so khåïp giaï trë cuía <biãøu thæïc> våïi giaï trë cuía Value1, Value2, ..

räöi thæûc hiãûn caïc khäúi lãûnh tæång æïng, trong træåìng håüp khäng coï giaï trë naìo truìng khåïp maïy
seî thæûc hiãûn khäúi lãûnh n+1 (nãúu coï), khi thæûc hiãûn mäüt khäúi lãûnh thç maïy boí qua caïc khäúi
lãûnh coìn laûi.

II.3. Caïc cáúu truïc làûp (repetitive statements)

a) Cáúu truïc While
Laì cáúu truïc làûp coï säú láön làûp khäng xaïc âënh. Cuï phaïp nhæ sau:

While <âiãöu kiãûn> do <khäúi lãûnh>

<âiãöu kiãûn> laì mäüt biãøu thæïc traí vãö kãút quaí laì True hoàûc False. Khi gàûp cáu lãûnh While

maïy seî kiãøm tra <âiãöu kiãûn>, nãúu <âiãöu kiãûn> âuïng maïy thæûc hiãûn <khäúi lãûnh> räöi quay laûi
kiãøm tra <âiãöu kiãûn>, cæï tiãúp tuûc làûp cho âãún khi <âiãöu kiãûn> sai, maïy thoaït khoíi voìng làûp.

b) Cáúu truïc Repeat
Laì cáúu truïc làûp coï säú láön làûp khäng xaïc âënh. Khaïc våïi While kiãøm tra âiãöu kiãûn træåïc

khi thæûc hiãûn khäúi lãûnh, Repeat thæûc hiãûn khäúi lãûnh räöi måïi kiãøm tra âiãöu kiãûn do váûy voìng
làûp Repeat thæûc hiãûn êt nháút laì mäüt láön. Cuï phaïp nhæ sau:

Repeat <khäúi lãûnh> Until <âiãöu kiãûn>

Âáöu tiãn maïy thæûc hiãûn <khäúi lãûnh> räöi måïi kiãøm tra <âiãöu kiãûn>, nãúu <âiãöu kiãûn> sai

thç quay laûi thæûc hiãûn <khäúi lãûnh> räöi tiãúp tuûc kiãøm tra <âiãöu kiãûn>, cæï tiãúp tuûc nhæ váûy cho
âãún khi <âiãöu kiãûn> âuïng, maïy thoaït khoíi voìng làûp.

c) Cáúu truïc For
Laì cáúu truïc làûp våïi säú láön làûp âãúm âæåüc. Cáúu truïc voìng làûp For coï hai daûng:
Daûng 1:

For <biãún âãúm> := <giaï trë âáöu> To <giaï trë cuäúi> do <khäúi lãûnh>

Daûng 2:

For <biãún âãúm> := <giaï trë âáöu> DownTo <giaï trë cuäúi> do <khäúi lãûnh>

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 7

Våïi cáúu truïc For <khäúi lãûnh> âæåüc thæûc hiãûn nhiãöu láön tæång æïng våïi <biãún âãúm> chaûy

tæì <giaï trë âáöu> âãún <giaï trë cuäúi>. Våïi Daûng 1 sau mäùi láön làûp <biãún âãúm> tæû âäüng tàng
lãn 1 âån vë, våïi Daûng 2 sau mäùi láön làûp <biãún âãúm> tæû âäüng giaím âi 1 âån vë.

d) Cáúu truïc With
Cáúu truïc With duìng âãø tham khaío âãún caïc thaình pháön cuía kiãøu dæî liãûu baín ghi (Record)

mäüt caïch ngàõn goün. Vê duû:

Var hs: person; (* Kiãøu baín ghi *)
With hs do

hs.Name := “Phaûm Vàn Khoaït”;
hs.Age := 80;
hs.Male := True;

End

III. CHÆÅNG TRÇNH CON VAÌ CHÆÅNG TRÇNH CHÊNH

Âãø giaím båït sæû làûp laûi cuía caïc âoaûn chæång trçnh giäúng nhau cuîng nhæ laìm cho chæång

trçnh saïng suía vaì dãù hiãøu hån ngæåìi ta sæí duûng chæång trçnh con. Chæång trçnh con trong
Pascal âæåüc chia laìm hai loaûi: Thuí tuûc con (Procedure) vaì Haìm con (Function). Sæí duûng
chæång trçnh con bao gäöm hai giai âoaûn: âënh nghéa chæång trçnh con vaì goüi chæång trçnh
con thæûc hiãûn.

III.1. Haìm con (function)

a) Âënh nghéa haìm
Haìm con laì chæång trçnh con coï traí vãö giaï trë, cuï phaïp âënh nghéa cuía haìm con nhæ sau:

Funtion <tãn haìm> [(<danh saïch âäúi säú>)] : Kiãøu traí vãö;
Khai baïo cuûc bäü trong haìm: Type, Const, Var, Label, ...
Begin

<Khäúi lãûnh cuía thán haìm>
<tãn haìm> := <giaï trë traí vãö>;

End;

Vê duû:

Function Giaithua(n: Byte): LongInt;
Var gt: LongInt; i: Byte; (* khai baïo trong haìm *)
Begin (* thán haìm *)

gt := 1;
For i := 1 To n do gt := gt * i;
Giaithua := gt; (* gaïn giaï trë traí vãö cho tãn haìm *)

End;

b) Goüi haìm
Haìm coï kãút quaí traí vãö båíi váûy låìi goüi haìm coï thãø tham gia vaìo tênh toaïn trong biãøu thæïc.

Trong låìi goüi haìm ta truyãön caïc tham säú thæûc vaìo cho caïc tham säú hçnh thæïc tæång æïng. Säú
tham säú thæûc vaì kiãøu cuía tham säú thæûc phaíi truìng våïi säú vaì kiãøu cuía tham säú hçnh thæïc.

Vê duû:

x := (Sin(x) + x)/(Giaithua(6) - 12); (* goüi haìm Giaithua våïi ts thæûc laì 6 *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 8

III.2. Thuí tuûc con (procedure)

a) Âënh nghéa thuí tuûc
Thuí tuûc laì chæång trçnh con khäng coï giaï trë traí vãö, cuï phaïp âënh nghéa nhæ sau:

Procedure <tãn thuí tuûc> [(<danh saïch âäúi säú>)];
Khai baïo cuûc bäü trong haìm: Type, Const, Var, Label, ...
Begin

<Khäúi lãûnh cuía thán thuí tuûc>

End;

b) Goüi thuí tuûc
Thuí tuûc khäng coï giaï trë traí vãö nãn khäng thãø tham gia vaìo trong biãøu thæïc, âãø goüi thuí

tuûc ta duìng cuï phaïp:

Tãn_thuí_tuûc (danh saïch tham säú thæûc);

Vê duû:

DrawBox(100, 200, 50, 50);

(* thuí tuûc veî mäüt hçnh chæî nháût lã maìn hçnh *)

III.3. Truyãön tham säú cho chæång trçnh con

a) Tham trë (value parameters)
Tham säú hçnh thæïc trë (tham trë) âæåüc sæí duûng nhæ caïc biãún cuûc bäü trong thuí tuûc hoàûc

haìm, chuïng nháûn giaï trë ban âáöu tæì caïc tham säú thæûc tæång æïng khi goüi thæûc hiãûn thuí tuûc
hoàûc haìm. Moüi sæû thay âäøi cuía tham säú hçnh thæïc trë khäng laìm thay âäøi giaï trë cuía caïc tham
säú thæûc tæång æïng.

Tham säú thæûc tæång æïng våïi tham säú hçnh thæïc trë phaíi laì mäüt biãøu thæïc, chuïng âæåüc ghi

trong låìi goüi thuí tuûc hoàûc goüi haìm vaì phaíi phuì håüp våïi thæï tæû xuáút hiãûn cuîng nhæ kiãøu dæî
liãûu cuía caïc tham säú hçnh thæïc tæång æïng. Caïc tham säú hçnh thæïc trë âæåüc khai baïo trong
danh saïch tham säú khäng coï tæì khoïa Var âæïng træåïc.

b) Tham biãún (variable parameters)
Tham säú biãún (tham biãún) âæåüc sæí duûng khi cáön mäüt hoàûc nhiãöu giaï trë traí vãö tæì haìm

hoàûc thuí tuûc cho chæång trçnh goüi. Tham säú thæûc âæåüc truyãön cho tham säú hçnh thæïc trong
låìi goüi haìm hoàûc thuí tuûc phaíi laì mäüt biãún. Tham säú hçnh thæïc biãún biãøu diãùn tham säú thæûc
trong khi thæûc hiãûn thuí tuûc hoàûc haìm vç thãú moüi sæû thay âäøi giaï trë cuía tham säú hçnh thæïc seî
aính hæåíng âãún giaï trë cuía tham säú thæûc tæång æïng. Trong thuí tuûc hoàûc haìm moüi tham khaío
âãún tham säú hçnh thæïc biãún seî truy xuáút âãún tham säú thæûc.

Kiãøu File coï thãø âæåüc duìng cho tham säú hçnh thæïc biãún, khai baïo tham säú hçnh thæïc biãún

trong danh saïch tham säú coï tæì khoïa Var âæïng træåïc.

III.4. Sæû âãû quy (rcursion)

Trong thán cuía mäüt thuí tuûc coï thãø chæïa caïc låìi goüi tåïi chênh thuí tuûc naìy âæåüc goüi laì thuí

tuûc âãû quy. Tæång tæû ta coï caïc haìm âãû quy.

Vê duû: Chæång trçnh tênh n! viãút theo kiãøu duìng âãû quy

Function Giaithua(n: integer): LongInt;
Begin

If n < 1 Then Giaithua := 1
Else Giaithua := n * Giaithua (n - 1)

End;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 9

I. DANH SAÏCH VAÌ CAÏC PHEÏP TOAÏN TRÃN DANH SAÏCH

I.1. Âënh nghéa danh saïch

Danh saïch laì mäüt táûp håüp gäöm nhiãöu pháön tæí: a

, a

, ... , a

coï cáúu truïc tæång tæû nhau vaì

coï mäúi liãn hãû våïi nhau thãø hiãûn åí chäù nãúu biãút âæåüc pháön tæí a

thç seî biãút âæåüc vë trê cuía

pháön tæí âæïng sau noï a

i+1

Säú caïc pháön tæí n goüi laì chiãöu daìi (length) cuía danh saïch. Nãúu n = 0 ta noïi danh saïch naìy

räùng (empty list). Danh saïch laì mäüt cáúu truïc thæåìng gàûp nháút, vê duû: danh saïch caïn bäü cäng
nhán viãn, danh saïch sinh viãn, ...

I.2. Caïc pheïp toaïn trãn danh saïch

Coï nhiãöu pheïp toaïn âæåüc thæûc hiãûn trãn cáúu truïc danh saïch, Vê duû:

Khåíi taûo danh saïch træåïc khi sæí duûng.

Thãm mäüt pháön tæí vaìo danh saïch.

Loaûi mäüt pháön tæí khoíi danh saïch.

Gheïp nhiãöu danh saïch laûi thaình mäüt danh saïch.

Sàõp thæï tæû trong danh saïch.

Tçm kiãúm mäüt pháön tæí trong danh saïch.

II. DANH SAÏCH ÂÀÛC

II.1. Âënh nghéa vaì caïch biãøu diãùn

Danh saïch âàûc laì danh saïch maì caïc pháön tæí âæåüc sàõp xãúp kãú tiãúp nhau trong bäü nhåï,

âæïng ngay sau pháön tæí a

laì pháön tæí a

i+1

. Trong Pascal vaì âa säú caïc ngän ngæî láûp trçnh khaïc,

danh saïch âàûc thæåìng âæåüc biãøu diãùn dæåïi daûng maíng (Array) mäüt chiãöu.

Vê duû:
- Khai baïo danh saïch âàûc laì mäüt maíng säú nguyãn a[1], a[2], ..., a[n] nhæ sau:

Const Max = 100;
Var a : Array [1 .. Max] of Integer; (* khai baïo danh saïch caïc säú nguyãn *)

- Danh saïch hoüc sinh trong mäüt låïp coï täúi âa 50 hoüc sinh âæåüc biãøu diãùn nhæ sau:

Type person = Record (* âënh nghéa kiãøu pháön tæí *)

Name : String [25];
Age : Integer;
Male : Boolean;

End;
Var myclass : Array [1 .. 50] of person; (* khai baïo danh saïch låïp hoüc *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 10

II.2. Caïc pheïp toaïn trãn danh saïch âàûc

a) Khåíi taûo danh saïch
Træåïc khi sæí duûng danh saïch yãu cáöu phaíi khåíi taûo, âäúi våïi danh saïch räùng ta cho säú

pháön tæí cuía noï bàòng 0.

Procedure Initialize; (* Thuí tuûc khäng coï tham säú hçnh thæïc *)
Begin

n := 0;

End;

b) Thãm mäüt pháön tæí vaìo danh saïch
Giaí sæí ta thãm mäüt pháön tæí coï näüi dung laì NewInfo vaìo vë trê thæï i, khi âoï caïc pháön tæí tæì

a[i] âãún a[n] dëch ra phêa sau mäüt vë trê.

Procedure Insert_Element (i : Integer ; NewInfo : Integer);
Var j : Integer;
Begin

For j := i To n Do a[j+1] := a[j]; (* Di chuyãøn caïc pháön tæí phêa sau *)
a[i] := NewInfo;

(* Thãm vaìo giaï trë pháön tæí måïi *)

n := n + 1;

(* Tàng säú pháön tæí cuía danh saïch *)

End

c) Loaûi boí mäüt pháön tæí khoíi danh saïch
Khi loaûi boí pháön tæí a[i] khoíi danh saïch, khi âoï caïc pháön tæí tæì a[i+1] âãún a[n] âæåüc di

chuyãøn lãn phêa træåïc mäüt vë trê. Chuï yï kiãøm tra säú pháön tæí cuía danh saïch træåïc khi loaûi boí.

Procedure Delete_element (i : Integer);
Var j : Integer;
Begin

If n > 0 Then
Begin

For j := i+1 to n do a[j-1] := a[j]; (* Di chuyãøn caïc pháön tæí lãn phêa træåïc *)
n := n - 1;

(* Giaím säú pháön tæí sau khi âaî loaûi boí *)

End;

d) Tçm kiãúm mäüt pháön tæí trong danh saïch
Âãø tçm kiãúm mäüt pháön tæí coï giaï trë laì Info trong danh saïch ta seî tçm láön læåüt tæì âáöu âãún

cuäúi danh saïch, nãúu tçm tháúy haìm traí vãö giaï trë True, coìn khäng haìm traí vãö giaï trë False.

Function Find_Element (Info : Integer) : Boolean;
Var j : Integer;
Begin

Find_Element := False;
For j := 1 to n do
Begin

If a[j] = Info Then (* nãúu tçm tháúy thç *)
Begin

Find_Element := True; (* traí vãö giaï trë True *)
Break; (* kãút thuïc tçm kiãúm *)

End;

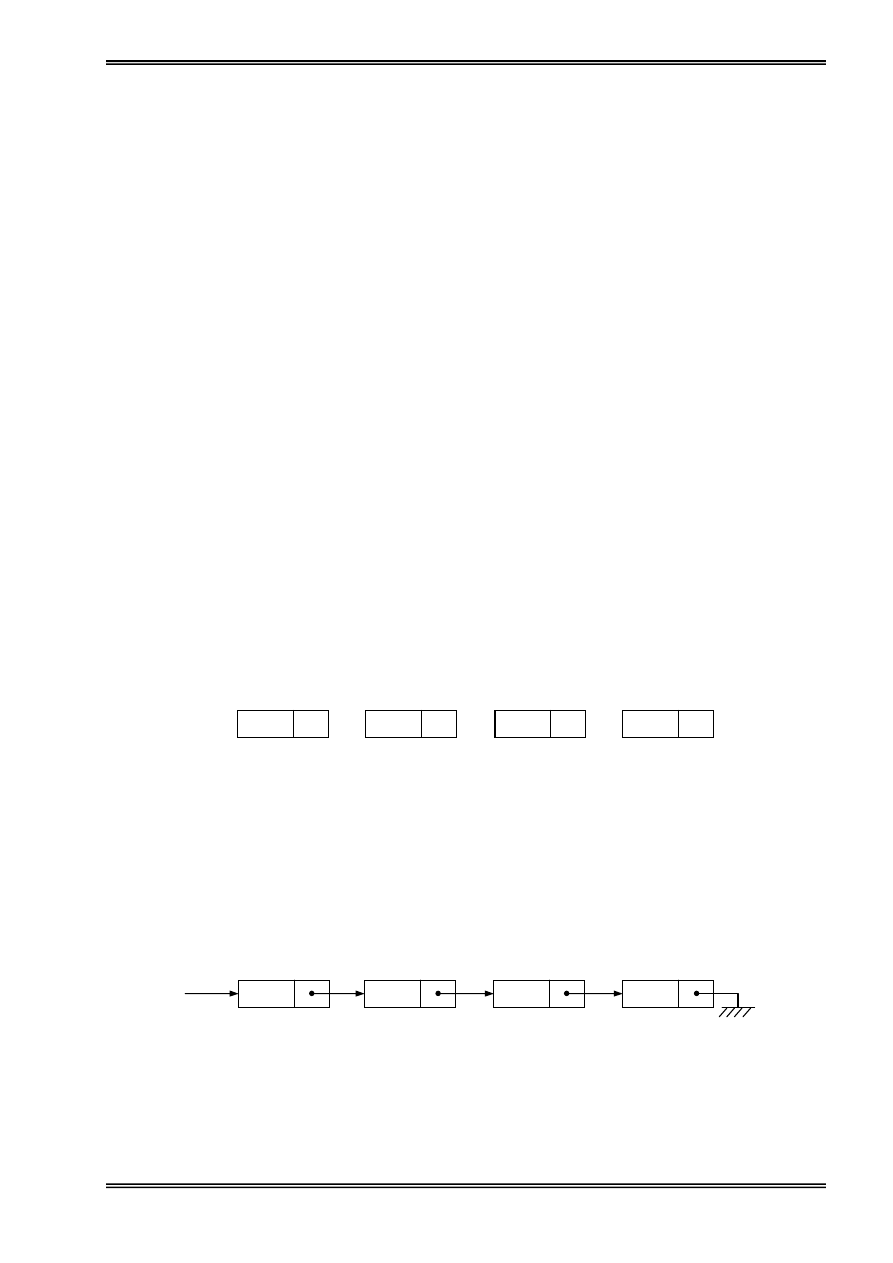
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 11

End;

II.3. Æu vaì nhæåüc âiãøm cuía danh saïch âàûc

a) Æu âiãøm
-

Máût âäü sæí duûng bäü nhåï cuía danh saïch âàûc laì 100%, âoï laì tè säú giæîa säú Byte duìng âãø
ghi nhåï thäng tin chia cho täøng säú Byte cuía danh saïch .

Nhanh choïng vaì dãù daìng truy xuáút pháön tæí a[i] bàòng cäng thæïc tênh âëa chè.

Dãù daìng tçm kiãúm mäüt pháön tæí trong danh saïch trong træåìng håüp danh saïch âaî coï thæï
tæû bàòng phæång phaïp tçm kiãúm nhë phán.

b) Nhæåüc âiãøm
-

Danh saïch âàûc khäng phuì håüp cho pheïp thãm vaìo vaì pheïp loaûi boí do caïc pháön tæí sau
pháön tæí thãm vaìo hoàûc loaûi boí seî phaíi thay âäøi vë trê.

Säú pháön tæí cuía danh saïch bë cäú âënh vaì phaíi xaïc âënh træåïc khi chæång trçnh âæåüc
biãn dëch. Do váûy nãúu khai baïo låïn thç bë dæ thæìa, khai baïo êt thç bë thiãúu.

III. DANH SAÏCH LIÃN KÃÚT

III.1. Danh saïch liãn kãút

a) Khaïi niãûm
Danh saïch liãn kãút laì mäüt danh saïch maì caïc pháön tæí âæåüc näúi kãút våïi nhau nhåì vaìo vuìng

liãn kãút cuía chuïng. Pháön tæí âæïng træåïc seî chæïa âëa chè cuía pháön tæí âæïng ngay sau noï.

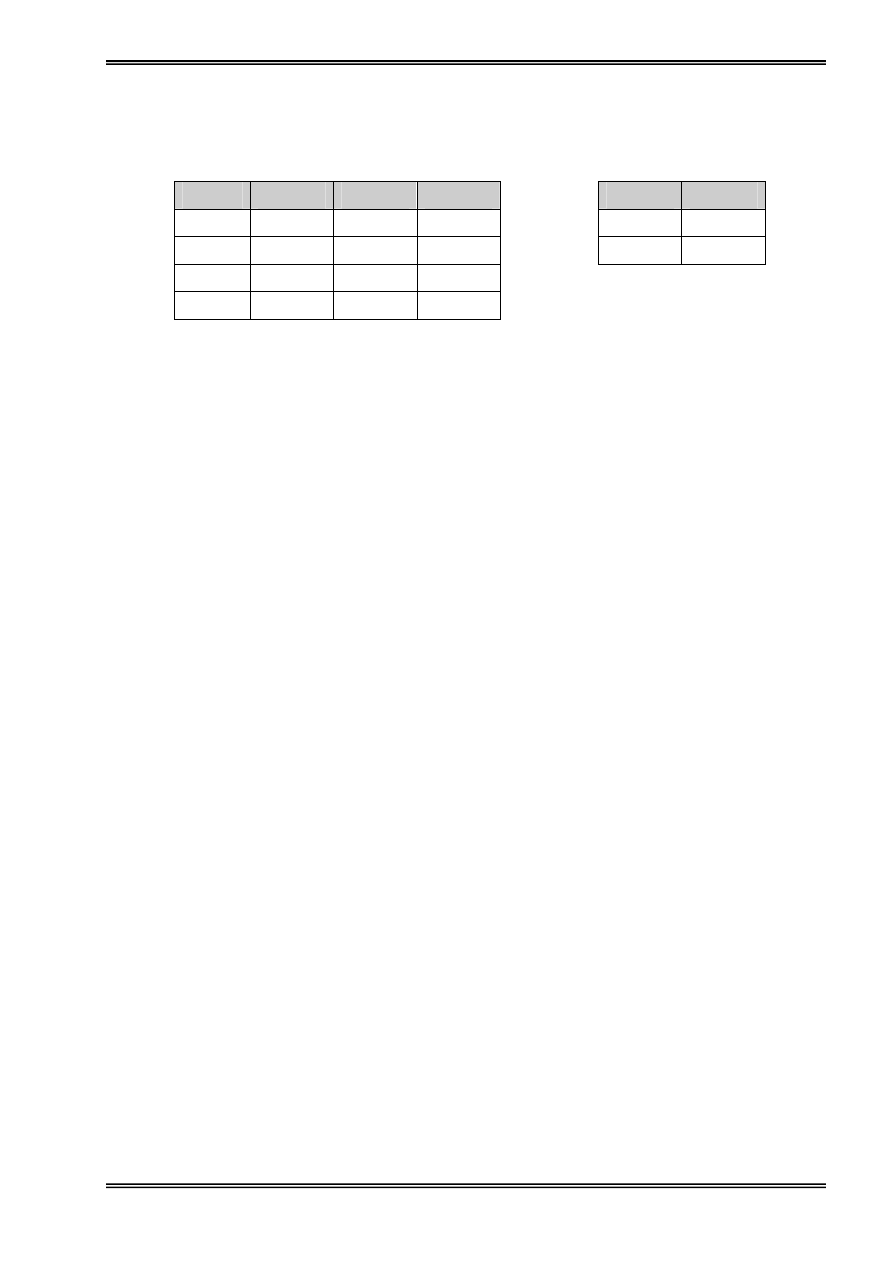
Vê duû: Giaí sæí trong bäü nhåï coï 4 pháön tæí thuäüc kiãøu baín ghi (Record), mäùi pháön tæí coï 2

thaình pháön láön læåüt chæïa tãn vaì âëa chè. Âëa chè mäùi pháön tæí trong bäü nhåï âæåüc ghi åí dæåïi:

Hçnh 1: Näüi dung caïc pháön tæí cuía danh saïch liãn kãút.

Ta tháúy pháön tæí thæï nháút chæïa âëa chè cuía pháön tæí thæï 3, ta noïi pháön tæí thæï nháút âæïng

træåïc pháön tæí thæï 3 trong danh saïch liãn kãút. Tæång tæû pháön tæí thæï 3 chæïa âëa chè cuía pháön tæí
thæï 4, pháön tæí thæï tæ chæïa âëa chè cuía pháön tæí thæï 2. Pháön tæí thæï 2 coï âëa chè khäng xaïc âënh
(Nil) ta noïi 2 laì pháön tæí cuäúi cuìng cuía danh saïch. Nhæ váûy khi biãút âëa chè cuía pháön tæí âáöu
tiãn ta hoaìn toaìn coï thãø truy xuáút âæåüc caïc pháön tæí coìn laûi trong danh saïch. Våïi danh saïch
trãn ta biãøu diãùn nhæ sau:

Hçnh 2: Biãøu diãùn danh saïch liãn kãút

Con troí First troí tåïi pháön tæí âáöu tiãn, noï âaûi diãûn cho mäüt danh saïch liãn kãút. Danh saïch

liãn kãút coï thãø coï nhiãöu loaûi nhæ: danh saïch liãn kãút âån, danh saïch âa liãn kãút, danh saïch
liãn kãút keïp.

Mäùi pháön tæí cuía danh saïch liãn kãút thæåìng âæåüc biãøu diãùn dæåïi daûng kiãøu dæî liãûu baín

ghi (Record), trong âoï bãn caûnh caïc thaình pháön chæïa thäng tin ta coìn phaíi khai baïo thãm

Tuán

Thoü

Duîng

Haíi

First

Tuán

914

Haíi NIL

Thoü 039

Duîng 666

914

039

666

000

Âëa chè:

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 12

caïc thaình pháön khaïc âoïng vai troì nhæ con troí troí tåïi caïc pháön tæí kãú tiãúp trong danh saïch, ta
goüi laì thaình pháön liãn kãút. Säú caïc thaình pháön liãn kãút phuû thuäüc vaìo tæìng loaûi danh saïch.

b) Æu vaì nhæåüc âiãøm cuía danh saïch liãn kãút
Æu âiãøm:
-

Danh saïch liãn kãút laì loaûi cáúu truïc âån giaín vaì thêch kåüp våïi pheïp thãm vaìo, pheïp
loaûi boí, pheïp gheïp nhiãöu danh saïch maì caïc pheïp toaïn naìy laûi khäng thêch håüp trong
danh saïch âàûc.

Danh saïch liãn kãút khäng haûn chãú säú læåüng pháön tæí, noï chè phuû thuäüc vaìo dung læåüng
bäü nhåï cho pheïp.

Sæí duûng âæåüc caïc vuìng coï kêch thæåïc nhoí trong bäü nhåï.

Nhæåüc âiãøm:
-

Danh saïch liãn kãút khoï sæí duûng, khoï truy xuáút hoàûc tçm kiãúm giaï trë cuía mäüt pháön tæí
báút kyì trong danh saïch do phaíi láön tæì âáöu danh saïch, thåìi gian truy xuáút láu.

Do âàûc âiãøm cuía danh saïch liãn kãút nãn phaíi täún thãm caïc vuìng nhåï daình cho caïc
biãún con troí.

III.2. Danh saïch liãn kãút âån (DSLK)

a) Biãøu diãùn danh saïch liãn kãút âån
Âãø biãøu diãùn mäüt daîy caïc säú nguyãn sæí duûng danh saïch liãn kãút, ta âënh nghéa cáúu truïc

cuía mäüt pháön tæí gäöm hai pháön: pháön chæïa säú nguyãn cáön biãøu diãùn vaì pháön chæïa con troí chè
âãún pháön tæí tiãúp theo trong danh saïch liãn kãút:

Type

Infor = Integer;

(* Âënh nghéa kiãøu *)

PointInt = ^ Element; (* PointInt laì kiãøu con troí chè âãún mäüt pháön tæí cuía danh saïch *)
Element = Record

(* Khai baïo kiãøi pháön tæí *)

Info : Infor;

(* Thaình pháön chæïa dæî liãûu *)

Next : PointInt;

(* Thaình pháön liãn kãút coï kiãøu con troí PointInt *)

End;

Var First : PointInt

(* Biãún con troí duìng âãø chè âãún âáöu danh saïch liãn kãút *)

Danh saïch sinh viãn bao gäöm nhæîng sinh viãn maì mäùi sinh viãn coï kiãøu dæî liãûu Record:

Type

PointSV = ^ Sinhvien; (* PointInt laì kiãøu con troí chè âãún mäüt pháön tæí cuía ds *)
Sinhvien = Record

(* Khai baïo kiãøu pháön tæí *)

Maso : Integer;

(* Thaình pháön chæïa dæî liãûu – Maî sä SV *)

Hoten : String[30]; (* Thaình pháön chæïa dæî liãûu – Hoü tãn SV*)
Lop : String[3];

(* Thaình pháön chæïa dæî liãûu - Tãn låïp hoüc *)

Têep : PointSV;

(* Thaình pháön liãn kãút chè âãún sinh viãn kãú tiãúp *)

End;

b) Caïc pheïp toaïn trãn danh saïch liãn kãút âån
•

Khåíi taûo danh saïch:

Khi khåíi taûo danh saïch liãn kãút, danh saïch âang räùng ta gaïn con troí First chè âãún âáöu

danh saïch bàòng NIL.

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 13

Procedure Initialize; (* Thuí tuûc khäng coï tham säú hçnh thæïc *)

Begin

First := Nil;

End;

‚

Tçm kiãúm mäüt pháön tæí trong danh saïch:

Giaí sæí ta cáön tçm kiãúm mäüt pháön tæí coï thaình pháön Info laì x trong danh saïch liãn kãút.

Pheïp tçm kiãúm âæåüc bàõt âáöu tæì pháön tæí âáöu tiãn räöi tuáön tæû theo thaình pháön liãn kãút âãø âãún
pháön tæí kãú tiãúp. Giaíi thuáût kãút thuïc khi tçm tháúy pháön tæí coï thaình pháön Info laì x (thaình cäng)
hoàûc khi hãút danh saïch (khäng thaình cäng).

Haìm Search traí vãö âëa chè cuía pháön tæí tçm tháúy âáöu tiãn nãúu tçm tháúy hoàûc traí vãö Nil nãúu

khäng tçm tháúy. ÅÍ âáy ta xeït hai træåìng håüp khi danh saïch chæa coï thæï tæû vaì khi danh saïch
âaî coï thæï tæû.

Træåìng håüp danh saïch chæa coï thæï tæû

Haìm Search traí vãö âëa chè cuía pháön tæí âáöu tiãn trong danh saïch nãúu tçm tháúy hoàûc traí vãö

Nil nãúu khäng tçm tháúy.

Function Search (x: Integer) : PointInt;
Var p: PointInt; Found: Boolean;
Begin

Found := False; p := First; (* âáöu tiãn cho con troí p troí tåïi âáöu danh saïch *)
While (p <> Nil) and (Found = False) do
Begin

If (p^.Info = x) Then Found := True (* nãúu tçm tháúy *)

Else p := p^.Next; (* âi âãún pháön tæí tiãúp theo trong danh saïch âãø tçm tiãúp *)

End;
Search := p;

(* traí vãö con troí *)

End;

Træåìng håüp danh saïch âaî coï thæï tæû (tàng dáön)

Vç danh saïch âaî coï thæï tæû nãn ta chè cáön tçm kiãúm khoïa x cho âãún khi tçm tháúy khoïa naìy

trong danh saïch hoàûc cho âãún khi khoïa cuía pháön tæí hiãûn taûi låïn hån x nãúu khäng tçm tháúy.

Haìm Search traí vãö âëa chè cuía pháön tæí âáöu tiãn trong danh saïch nãúu tçm tháúy hoàûc traí vãö

NIL nãúu khäng tçm tháúy.

Function Search (x : Integer) : PointInt;
Var p : PointInt;
Begin

p := First;

(* cho p troí tåïi pháön tæí âáöu tiãn trong danh saïch *)

While (p <> Nil) And (p^.Info < x) do p := p^.Next; (* Boí qua caïc pháön tæí < x *)
If (p <> Nil) And (p^.Info = x) Then Search := p

(* Tçm tháúy *)

Else Search := Nil; (* khäng tçm tháúy *)

End;

Thãm mäüt pháön tæí vaìo danh saïch:

Coï hai træåìng håüp khi thãm mäüt pháön tæí måïi coï näüi dung laì x vaì do con troí p âang troí

tåïi vaìo danh saïch:

Thãm vaìo âáöu danh saïch: Ta cho thaình pháön liãn kãút cuía p chè vaìo First, sau âoï First
chè vaìo pháön tæí p.

First

Nil

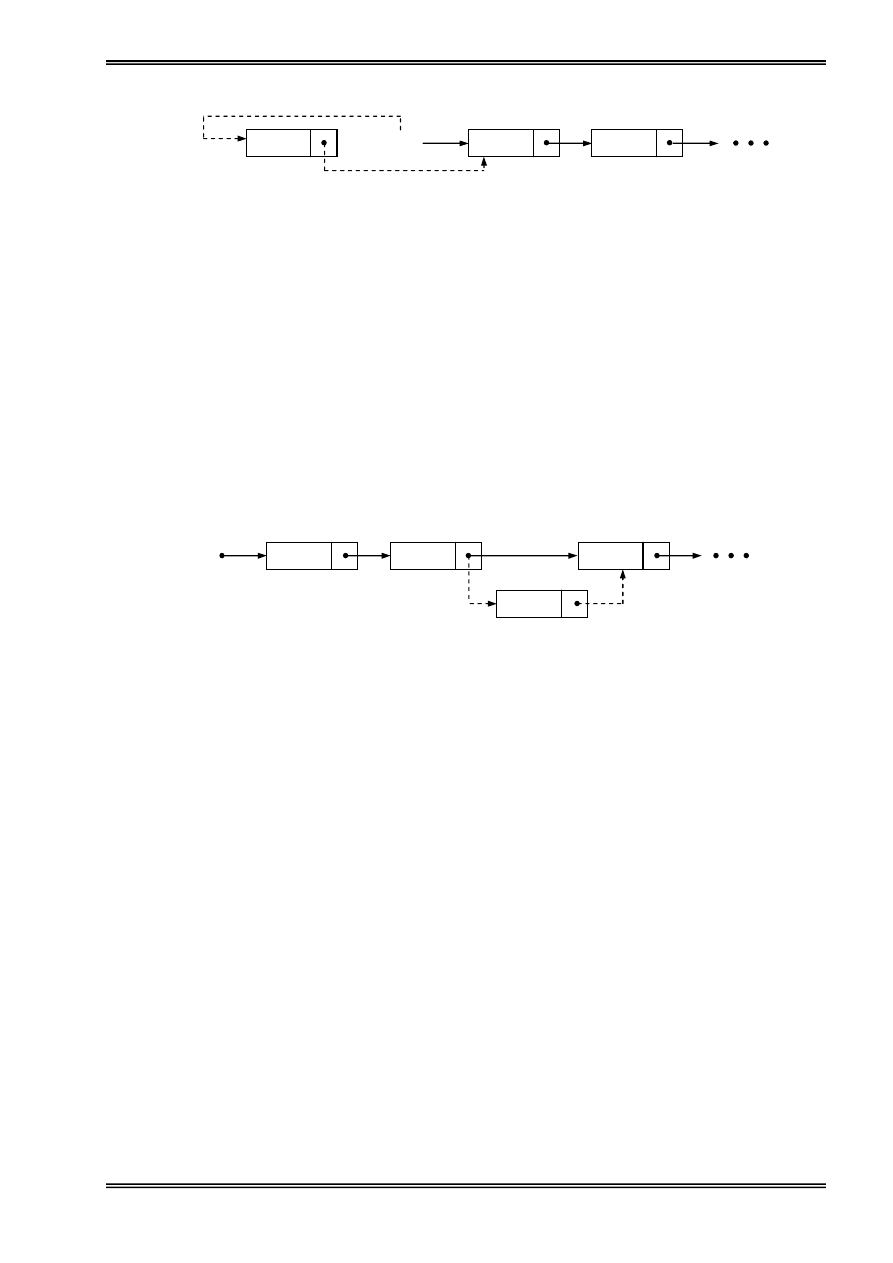
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 14

Hçnh 3: Thãm mäüt pháön tæí vaìo âáöu danh saïch liãn kãút

Function Insert_First (NewInfo : Integer) : PointInt;
Var p : PointInt;
Begin

New(p);

(* cáúp phaït vuìng nhåï vaì cho con troí p troí tåïi vuìng nhåï âoï *)

p^.Info := NewInfo; (* gaïn giaï trë cho thaình pháön Info *)
p^.Next := First;

(* Cho thaình pháön liãn kãút cuía p troí tåïi First *)

First := p;

(* thay âäøi con troí âáöu cuía danh saïch *)

Insert_First := p;

(* haìm traí vãö con troí chè tåïi pháön tæí væìa thãm *)

End;

Thãm vaìo giæîa hoàûc cuäúi danh saïch: Goüi q laì pháön tæí âæïng ngay træåïc pháön tæí p cáön
thãm, ta cho thaình pháön liãn kãút cuía p chè vaìo thaình pháön liãn kãút cuía q vaì thaình
pháön liãn kãút cuía q chè vaìo p.

Hçnh 4: Thãm mäüt pháön tæí vaìo giæîa hoàûc cuäúi danh saïch

Function Insert_Element (q : PoiniInt ; NewInfo : Integer) : PointInt;
Var p : PointInt;
Begin

New(p);

(* cáúp phaït vuìng nhåï vaì cho p troí tåïi *)

p^.Info := NewInfo; (* gaïn giaï trë *)
p^.Next := q^.Next; (* Thao taïc (1) trãn hçnh veî *)
q^.Next := p;

(* Thao taïc (2) trãn hçnh veî *)

Insert_Element := p; (* Traí vãö con troí chè tåïi pháön tæí væìa âæåüc thãm vaìo *)

End

Haìm thãm vaìo täøng quaït: Haìm sau cho pheïp thãm mäüt pháön tæí vaìo danh saïch âaî coï
thæï tæû sao cho váùn âaím baío thæï tæû, haìm xeït âãún caí hai træåìng håüp noïi trãn. Trong
haìm coï sæí duûng con troí before âãø troí tåïi pháön tæí âæïng ngay træåïc p theo liãn kãút.

Function Insert_List (NewInfo : Integer) : PointInt;
Var p, q, before : PoinInt;
Begin

New(p);
p^.Info := NewInfo;
q := First; (* cho q troí tåïi âáöu danh saïch *)
While (q <> Nil) And (q^.Info < NewInfo) Do (* làûp qua caïc pháön tæí nhoí hån *)
Begin

before := q; (* gaïn con troí q cho con troí before *)
q := q^.Next; (* cho q troí tåïi pháön tæí tiãúp theo *)

NewInfo

First

(1)

(2)

NewInfo

First

(1)

(2)

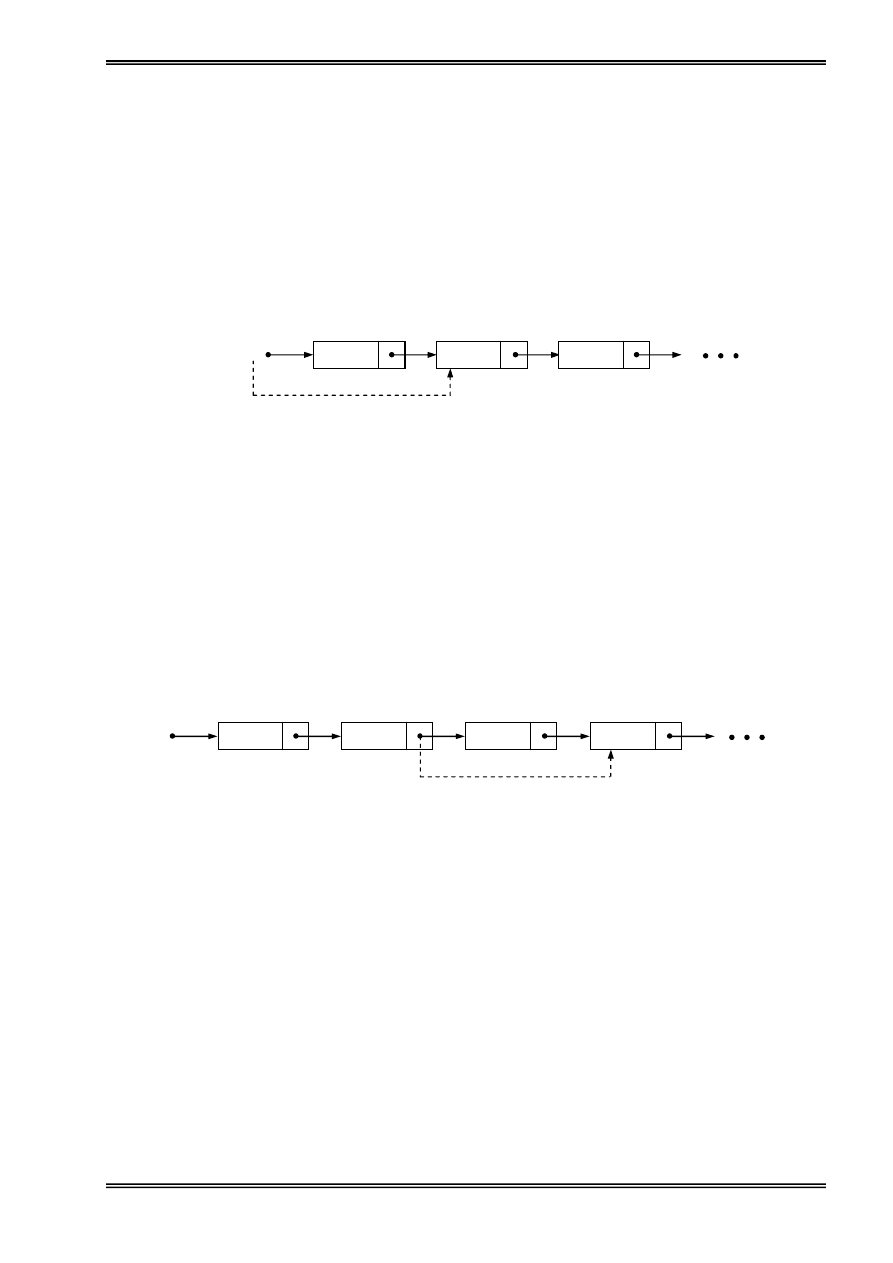
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 15

End;
(* q hiãûn âang troí tåïi pháön tæí âæïng sau pháön tæí cáön thãm, before âæïng træåïc q *)
If q = First Then First := p; (* Thãm vaìo âáöu danh saïch *)
Else before^.Next := p; (* Thãm vaìo giæîa hoàûc cuäúi danh saïch *)
p^.Next := q;
Insert_List := p;

End;

„

Loaûi boí mäüt pháön tæí khoíi danh saïch:

Coï hai træåìng håüp khi loaûi boí mäüt pháön tæí p khoíi danh saïch:
-

Loaûi boí pháön tæí âáöu danh saïch:

Hçnh 5: Loaûi boí mäüt pháön tæí âáöu danh saïch

Procedure Delete_First;
Var p : PointInt;
Begin

If (First <> Nil) Then (* Nãúu danh saïch khaïc räùng *)
Begin

p := First;

(* Gaïn con troí First cho p *)

First := p^.Next; (* Cho First troí âãún pháön tæí thæï hai *)
Dispose(p);

(* Giaíi phoïng vuìng nhåï do con troí p troí tåïi *)

End;

Loaûi boí pháön tæí giæîa hoàûc cuäúi danh saïch:

Ta giaí sæí loaûi boí mäüt pháön tæí âæïng ngay sau pháön tæí q trong danh saïch:

Hçnh 6: Loaûi boí mäüt pháön tæí åí giæîa hoàûc cuäúi danh saïch

Procedure Delete_Element (q : PointInt);
Var p : PointInt;
Begin

p := q^.Next;
If p <> Nil Then
Begin

q^.Next := p^.Next;
Dispose(p); (* giaíi phoïng vuìng nhåï do con troí p troí tåïi *)

End;

Loaûi boí mäüt pháön tæí coï näüi dung laì x cuía danh saïch liãn kãút âaî coï thæï tæû tàng dáön thç
thuí tuûc âæåüc viãút nhæ sau:

Procedure Delete_Element (x : Integer);
Var p, before : PointInt;
Begin

First

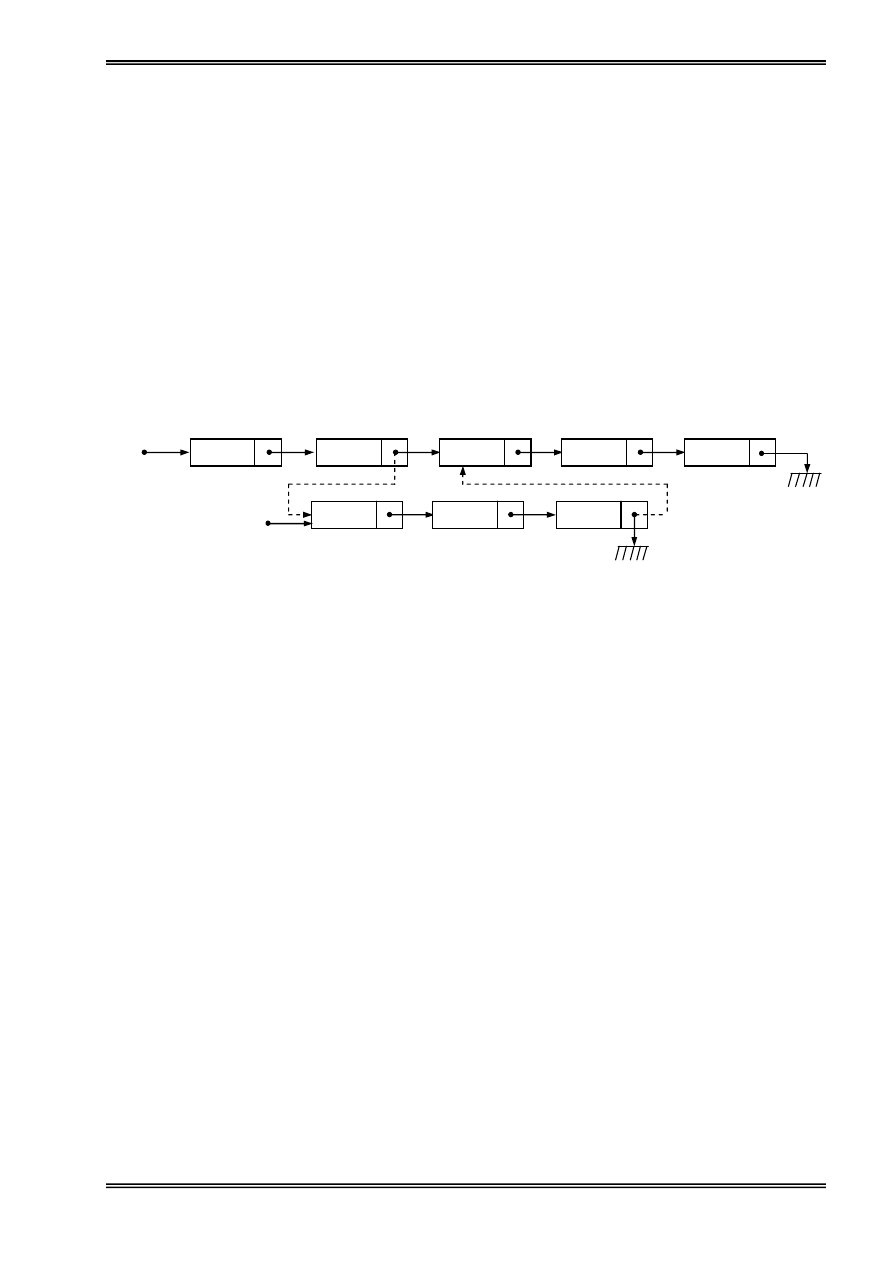
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 16

p := First;

(* Gaïn p cho con troí âáöu tiãn *)

While (p <> Nil) And (p^.Info < x) do (* Duyãût qua caïc pháön tæí coï khoïa nhoí hån x *)
Begin

before := p; (* before luän troí tåïi pháön tæí træåïc p *)
p := p^.Next; (* Cho p troí âãún pháön tæí tiãúp theo *)

End;
If (p <> Nil) And (p^.Info = x) Then (* Nãúu tçm tháúy *)
Begin

If (p = First) Then First := p^.Next (* Xoïa pháön tæí âáöu tiãn *)
Else before^.Next := p^.Next;

(* Khäng phaíi xoïa pháön tæí âáöu tiãn *)

Dispose(p); (* Giaíi phoïng vuìng nhåï do con troí p troí tåïi *)

End;

…

Gheïp mäüt danh saïch vaìo mäüt danh saïch khaïc:

Hçnh 7: Gheïp mäüt danh saïch vaìo mäüt danh saïch khaïc

Procedure Insert (q : PointInt);
Var p : PointInt;
Begin

If (First2 <> Nil) Then

(* Chè thæûc hiãûn khi danh saïch First2 khaïc räùng *)

Begin

p := First2;

(* Ban âáöu cho p troí tåïi âáöu First2 *)

While (p^.Next <> Nil) do p := p^.Next; (* cho p di chuyãøn tåïi cuäúi First2 *)
p^.Next := q^.Next; (* Thao taïc (2) trãn hçnh veî *)
q^.Next := First2;

(* Thao taïc (1) trãn hçnh veî *)

End;

III.3. Danh saïch liãn kãút keïp (doubly link list)

Ta nháûn tháúy khi loaûi boí mäüt pháön tæí p trong danh saïch liãn kãút âån, ta phaíi biãút pháön tæí

âæïng ngay træåïc noï (before). Âãø coï âæåüc pháön tæí naìy ta phaíi tçm kiãúm noï tæì âáöu danh saïch,
båíi trong danh saïch liãn kãút âån pháön tæí âæïng træåïc chæïa âëa chè cuía pháön tæí âæïng ngay sau
noï nhæng ngæåüc laûi pháön tæí âæïng sau khäng chæïa âëa chè cuía pháön tæí âæïng ngay træåïc. Âãø
khàõc phuûc nhæåüc âiãøm naìy ngæåìi ta âæa ra cáúu truïc danh saïch liãn kãút keïp.

a) Âënh nghéa
Danh saïch liãn kãút keïp laì danh saïch liãn kãút maì mäùi pháön tæí cuía noï coï hai thaình pháön

liãn kãút: mäüt thaình pháön liãn kãút chè âãún pháön tæí âæïng ngay træåïc noï, goüi laì liãn kãút ngæåüc
(previous) vaì mäüt thaình pháön liãn kãút chè âãún pháön tæí âæïng ngay sau noï, goüi laì liãn kãút
thuáûn (next).

First1

First2

(1)

(2)

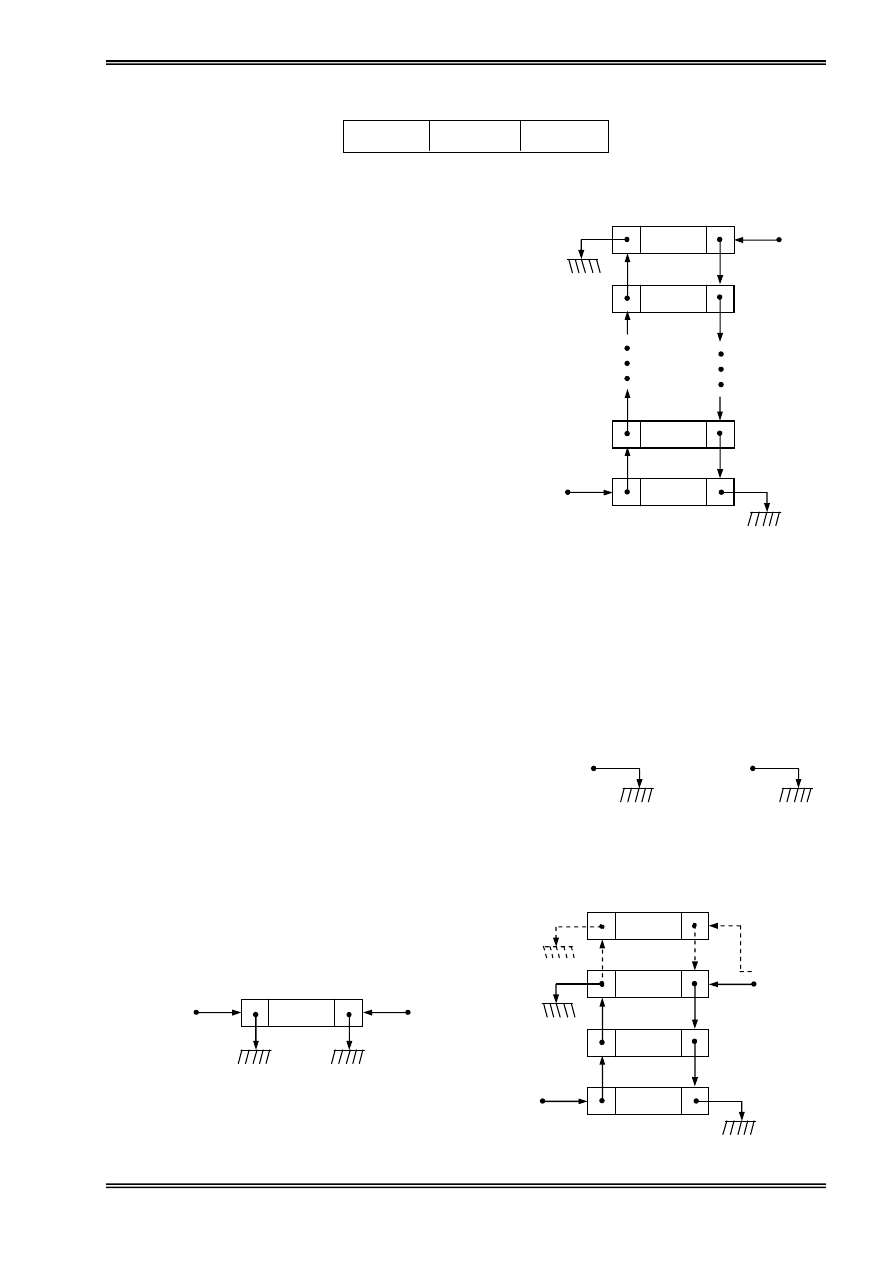
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 17

Mäùi pháön tæí cuía danh saïch liãn kãút keïp coï daûng:

Hçnh 8: Cáúu truïc mäüt pháön tæí cuía danh saïch liãn kãút keïp

b) Täø chæïc danh saïch liãn kãút keïp
Khaïc våïi danh saïch liãn kãút âån âæåüc âaûi diãûn

båíi mäüt con troí First chè âãún pháön tæí âáöu tiãn, danh
saïch liãn kãút keïp âæåüc âaûi diãûn båíi hai con troí: mäüt
chè vaìo pháön tæí âáöu tiãn theo liãn kãút thuáûn, goüi laì
First vaì mäüt chè vaìo pháön tæí âáöu tiãn theo liãn kãút
nghëch, goüi laì Last. Täø chæïc cuía danh saïch liãn kãút
kãút keïp âæåüc thãø hiãûn nhæ hçnh bãn:

Ta khai baïo cáúu truïc cáúu truïc dæî liãûu nhæ sau:

Type PointDbl = ^Element; (* Kiãøu con troí *)
Element = Record

Info : Integer;

(* Tp chæïa thäng tin *)

Previous : PointDbl; (* Tp liãn kãút nghëch *)
Next : PointDbl;

(* Tp liãn kãút thuáûn *)

End;
Var First, Last: PointDbl; (* Khai baïo 2 con troí *)

c) Caïc pheïp toaïn trãn danh saïch liãn kãút keïp
Caïc pheïp toaïn trãn danh saïch liãn kãút keïp tæång tæû nhæ trãn danh saïch liãn kãút âån:
•

Khåíi taûo danh saïch

Khi khåíi taûo, danh saïch liãn kãút keïp laì räùng, ta cho 2 con troí First vaì Last âãöu bàòng Nil.

Procudure Initialize;
Begin

First := Nil;
Last := Nil;

End;

‚

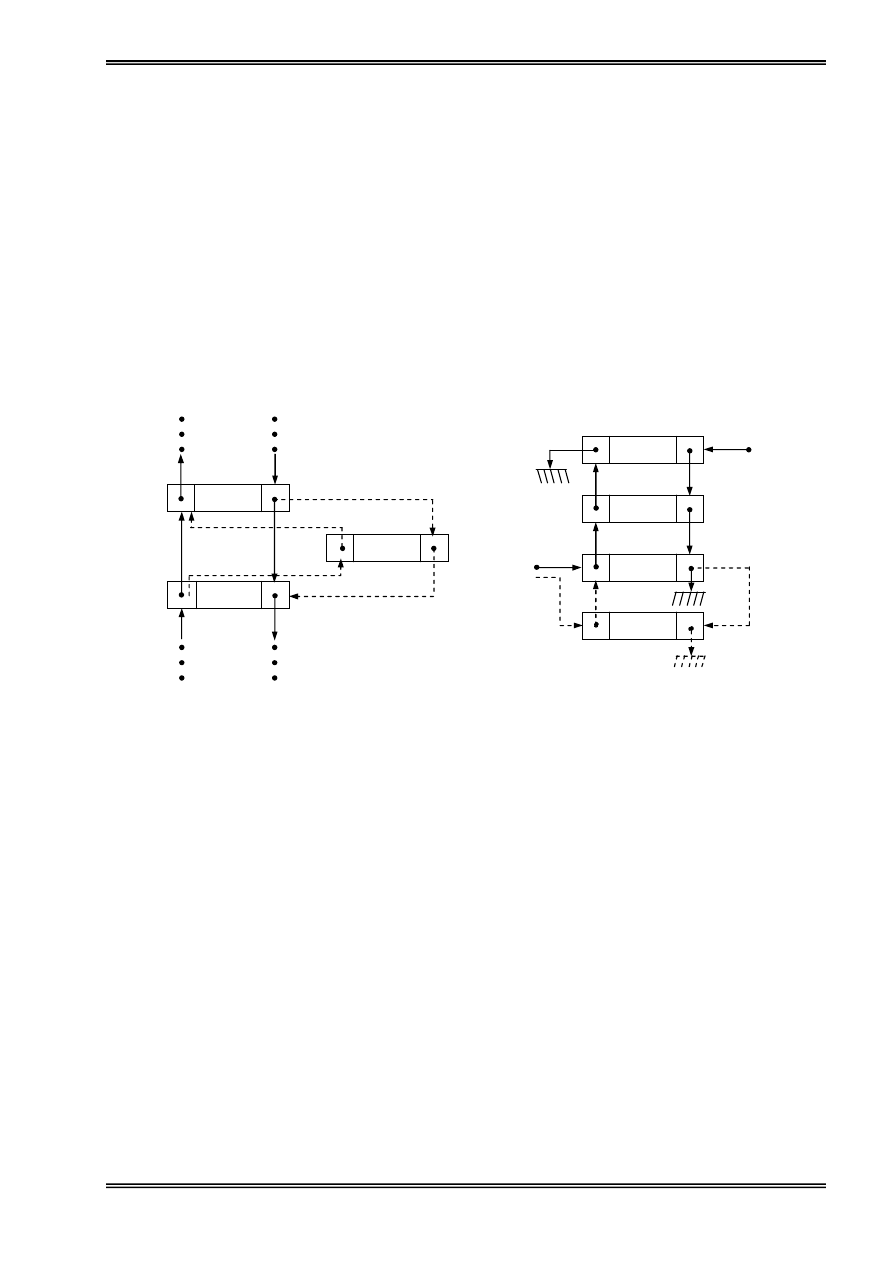
Thãm mäüt pháön tæí vaìo danh saïch

Coï hai træåìng håüp khi thãm mäüt pháön tæí måïi p vaìo danh saïch âoï laì thãm vaìo âáöu danh

saïch vaì thãm vaìo giæîa hoàûc cuäúi danh saïch.

Thãm vaìo âáöu danh saïch:

Info

First

Last

Hçnh 9: Täø chæïc cuía danh

saïch liãn kãút keïp.

First

Last

Hçnh 10: Thãm mäüt pháön tæí vaìo danh saïch liãn kãút keïp

(a): khi danh saïch räùng (b): khi danh saïch khaïc räùng

First

Last

NewInfo

(1)

(3)

(2)

(4)

NewInfo

(2)

(5)

(4) First

Last

(1)

(a)

(b)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 18

Haìm Insert_First sau traí vãö âëa chè cuía pháön tæí måïi thãm vaìo danh saïch.

Function Insert_First (NewInfo : Integer) : PointDbl;
Var p : PointDbl;
Begin

New(p);

(* cáúp phaït vuìng nhåï do p troí tåïi *)

p^.Info := NewInfo; (* gaïn giaï trë læu træî *)
p^.Next := First;

(* ngay sau p laì First - thao taïc 1 *)

p^.Previous := Nil; (* gaïn con troí ngæåüc bàòng Nil – thao taïc 2 *)
If First <> Nil Then First^.Previous := p; (* nãúu hiãûn danh saïch khaïc räùng – thao taïc 3 *)
First := p;

(* thay âäøi First – thao taïc 4 *)

If Last = Nil Then Last := p; (* nãúu danh saïch âang räùng thç thay âäøi Last – thao taïc 5 *)
Insert_Element := p; (* gaïn giaï trë traí vãö *)

End;

Thãm vaìo giæîa hoàûc cuäúi danh saïch:

Haìm Insert_Element sau seî thãm vaìo mäüt pháön tæí vaìo ngay sau pháön tæí q, haìm traí vãö

âëa chè cuía pháön tæí måïi thãm vaìo danh saïch.

Function Insert_Element (q : PointDbl ; NewInfo : Integer) : PointDbl;
Var p , r : PointDbl;
Begin

New(p);

(* Cáúp phaït vuìng nhåï *)

p^.Info := NewInfo; (* Gaïn giaï trë cáön læu træî *)
p^.Next := q^.Next; (* Cho liãn kãút thuáûn cuía p troí tåïi pháön tæí sau q – thao taïc 1 *)
p^.Previous := q;

(* Cho liãn kãút nghëch cuía p troí tåïi q – thao taïc 3 *)

r := q^.Next;

(* Goüi r laì pháön tæí âæïng ngay sau q *)

q^.Next := p;

(* Cho liãn kãút thuáûn cuía q troí tåïi p – thao taïc 2 *)

If r <> Nil Then r^.Previous := p; (* thãm vaìo giæîa danh saïch – thao taïc 4 *)
Else Last := p; (* thãm vaìo cuäúi danh saïch thç thay âäøi Last – thao taïc 5 *)
Insert_Element := p; (* Giaï trë traí vãö cuía haìm *)

End;

NewInfo

(2)

(1)

(4)

(3)

(a)

(b)

Hçnh 11: Thãm mäüt pháön tæí vaìo danh saïch liãn kãút keïp

(a): Thãm vaìo giæîa danh saïch (b): thãm vaìo cuäúi danh saïch

First

Last

(2)

(3)

(5)

(1)

NewInfo

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 19

Nãúu ta thãm pháön tæí p coï näüi dung laì NewInfo vaìo danh saïch liãn kãút keïp âaî coï thæï tæû

(tàng dáön) sao cho váùn âaím baío thæï tæû cuía danh saïch thç giaíi thuáût âæåüc viãút nhæ sau:

Function Insert_Element (NewInfo : Integer) : PointDbl;
Var p , q , before : PointDbl;
Begin

New(p);
p^.Info := NewInfo;
q := First;

While (q <> Nil) And (q^.Info < NewInfo) do (* Duyãût qua caïc pháön tæí nhoí hån *)
Begin

before := q;

(* before luän troí tåïi træåïc q *)

q := q^.Next;

(* Cho q troí tåïi pháön tæí tiãúp theo *)

End;
If (q = First) Then

Begin (* Thãm vaìo âáöu danh saïch *)

p^.Next := First;

(* Cho liãn kãút thuáûn cuía p troí tåïi First *)

p^.Previous := Nil; (* Cho liãn kãút nghëch cuía p bàòng Nil *)
If q <> Nil Then q^.Previous := p;
First := p;

(* Thay âäøi First *)

If Last = Nil Then Last := p; (* Nãúu danh saïch âang räùng thç âàût laûi Last *)

End
Else
Begin (* Thãm vaìo sau pháön tæí before *)

p^.Next := before^.Next;
p^.Previous := before;
before^.Next := p;
If q <> Nil Then q^.Previous := p (* Thãm vaìo giæîa danh saïch *)
Else Last := p; (* Thãm vaìo cuäúi danh saïch *)

End;

Loaûi boí mäüt pháön tæí khoíi danh saïch

Giaí sæí cáön loaûi boí mäüt pháön tæí p khoíi danh saïch, caïc træåìng håüp coï thãø xaíy ra âæåüc mä

taí trong hçnh veî sau:

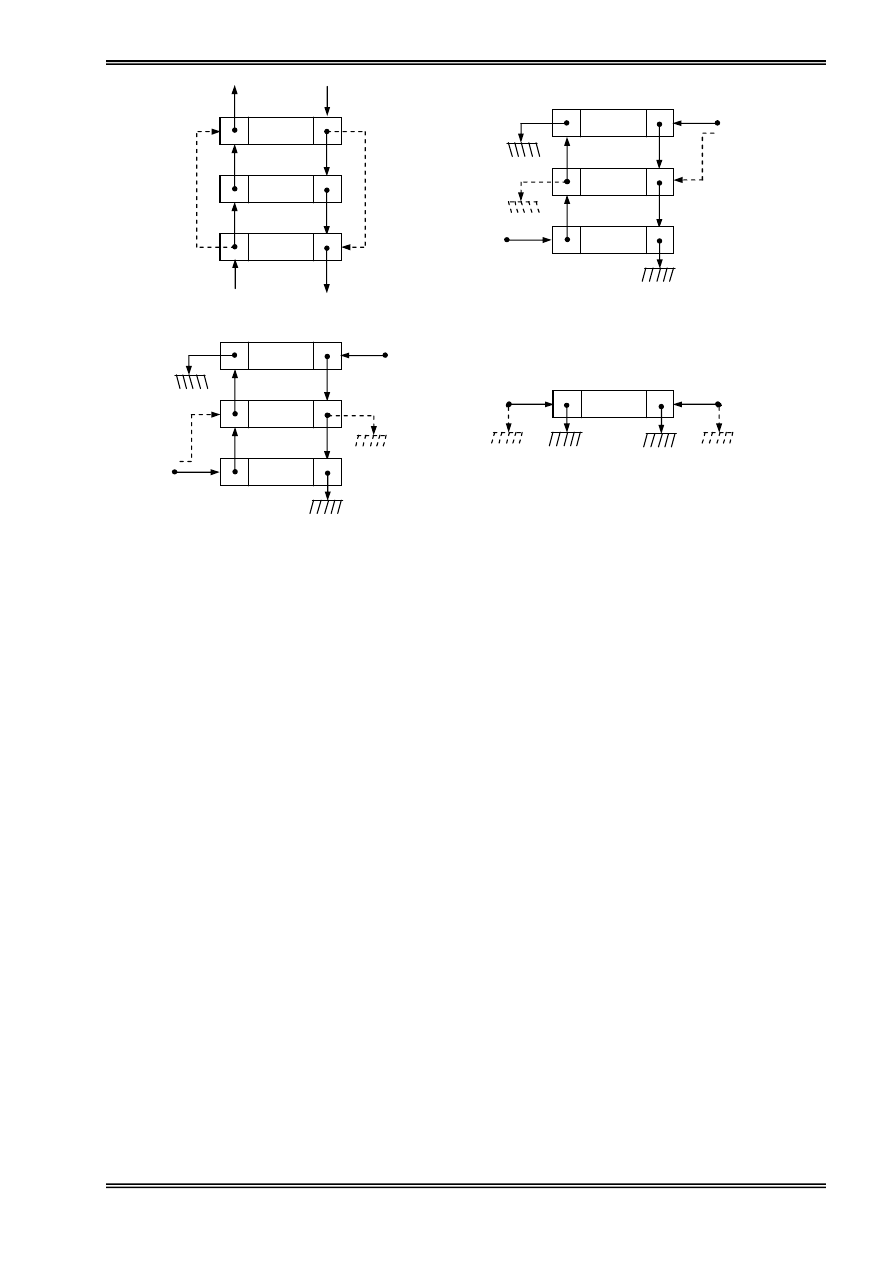
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 20

„

Tçm kiãúm mäüt pháön tæí trong danh saïch

Âãø tçm kiãúm trong danh saïch liãn kãút keïp ta coï thãø theo thaình pháön Next xuáút phaït tæì

con troí First (thæï tæû tàng dáön) hoàûc theo thaình pháön Previous xuáút phaït tæì con troí Last (thæï
tæû giaím dáön). Giaíi thuáût tçm kiãúm giäúng nhæ giaíi thuáût tçm kiãúm cuía danh saïch liãn kãút âån.

IV. CAÏC DANH SAÏCH HAÛN CHÃÚ

Trong pháön trãn ta âaî xeït caïc loaûi danh saïch maì caïc pheïp thãm vaìo vaì caïc pheïp loaûi boí

âæåüc thæûc hiãûn åí mäüt vë trê báút kyì trãn danh saïch. Trong thæûc tãú täön taûi caïc danh saïch maì
pheïp thãm vaìo vaì pheïp loaûi boí chè âæåüc thæûc hiãûn åí mäüt vë trê nháút âënh trãn danh saïch (âáöu
hoàûc cuäúi) ngæåìi ta goüi chuïng laì danh saïch haûn chãú. Caïc danh saïch haûn chãú thæåìng gàûp laì:

Haìng âåüi (Queue): Pheïp thãm vaìo âæåüc thæûc hiãûn mäüt âáöu vaì pheïp loaûi boí âæåüc thæûc
hiãûn âáöu kia.

Ngàn xãúp (Stack): Pheïp thãm vaìo vaì pheïp loaûi boí chè âæåüc thæûc hiãûn åí cuìng mäüt âáöu.
Caïc danh saïch haûn chãú coï thãø âæåüc täø chæïc theo danh saïch âàûc hoàûc danh saïch liãn kãút.

IV.1. Cáúu truïc dæî liãûu haìng (queue)

a) Âënh nghéa vaì caïch biãøu diãùn haìng
Cáúu truïc haìng âåüi tæång tæû nhæ mäüt haìng ngæåìi xãúp haìng vaìo raûp mua veï, ngæåìi âãún

træåïc mua træåïc, ngæåìi âãún sau mua sau. Âiãöu âoï coï nghéa pháön tæí naìo vaìo træåïc thç ra træåïc
pháön tæí naìo vaìo sau thç ra sau, do váûy noï coìn coï tãn goüi laì FIFO (First in First out).

before

after

(2)

(4)

First

Last

(1)

(4)

First

Last

(1)

(3)

First

Last

(1)

(3)

(a)

(b)

(c)

(d)

Hinh 12: Loaûi boí mäüt pháön tæí trong danh saïch liãn kãút keïp

(a): pháön tæí cáön loaûi boí åí giæîa ds ; (b): pháön tæí cáön loaûi boí âáöu danh saïch

(c): pháön tæí cáön loaûi boí cuäúi ds ; (d): pháön tæí cáön loaûi boí laì duy nháút trong ds

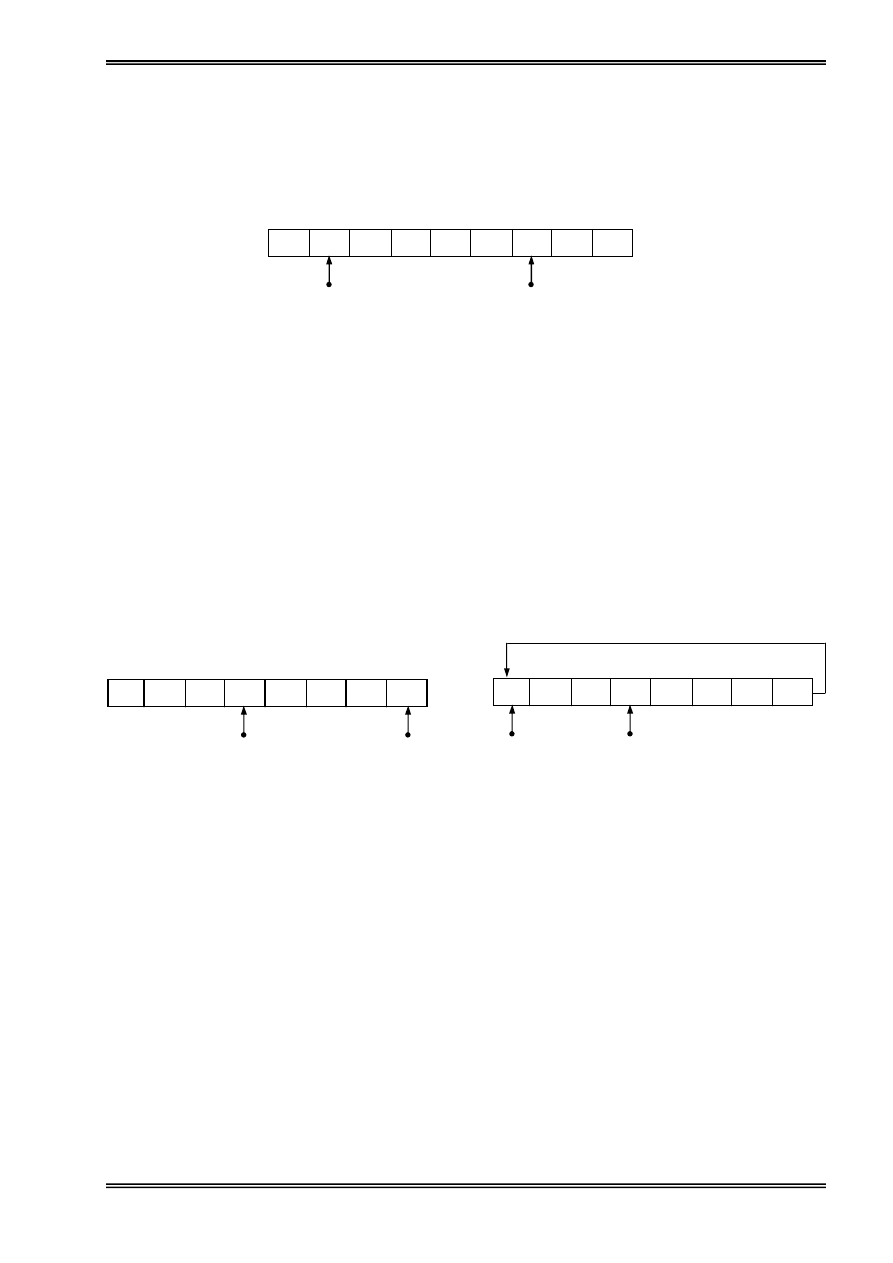
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 21

Haìng âåüi coï thãø biãøu diãùn bàòng mäüt danh saïch âàûc hoàûc danh saïch liãn kãút, mäüt haìng

âæåüc âaûi diãûn båíi hai con troí: con troí Front chè vë trê thæûc hiãûn pheïp loaûi boí vaì con troí Rear
âãø chè vë trê thæûc hiãûn pheïp thãm vaìo.

b) Haìng âæåüc biãøu diãùn bàòng danh saïch âàûc

Ta khai baïo:

Const n = 100;
Var Queue : array [1 .. n] of Integer; Front, Rear : Integer;

Âäúi våïi maíng laì mäüt danh saïch âàûc, thç khi thãm åí Rear vaì loaûi boí åí Front seî laìm cho

pháön tæí sæí duûng cuía haìng coï khuynh hæåïng di chuyãøn vãö phêa dæåïi vaì seî âãún mäüt luïc haìng
bë traìn. Ta coï thãø khàõc phuûc bàòng caïch cho kêch thæåïc cuía haìng âuí låïn, nhæng våïi caïch naìy
thç ráút laîng phê bäü nhåï vaì hãû säú sæí duûng bäü nhåï tháúp. Nhæ váûy ta phaíi coï giaíi thuáût âãø khàõc
phuûc haìng bë traìn âoï laì: phæång phaïp di chuyãøn voìng.

Goüi n laì säú pháön tæí täúi âa cuía haìng, thç khi thãm vaìo haìng träúng hoàûc haìng âang coï Rear

bàòng n thç ta seî thãm vaìo pháön tæí thæï nháút cuía haìng.

Vê duû: Thãm pháön tæí 7 vaìo danh saïch

•

Pheïp toaïn khåíi taûo haìng

Khi khåíi taûo haìng, haìng laì räùng ta cho Front vaì Rear bàòng 0:

Procedure Initialize;
Begin

Front := 0; Rear := 0;

End;

‚

Thãm mäüt pháön tæí vaìo haìng

Khi thãm mäüt pháön tæí måïi vaìo haìng thç ta coï thãø gàûp træåìng håüp haìng bë âáöy hoàûc haìng

bë traìn. Khi haìng bë âáöy nghéa laì táút caí caïc pháön tæí cuía haìng âãöu âæåüc sæí duûng, nãn ta khäng
coìn pháön tæí naìo träúng âãø âæa vaìo haìng âæåüc. Khi haìng bë traìn nghéa laì khäng thãø thãm vaìo
haìng màûc duì haìng váùn coìn caïc pháön tæí träúng, ta phaíi khàõc phuûc bàòng phæång phaïp di
chuyãøn voìng.

Front (=2)

Pear (=7)

Hçnh 13: Biãøu diãùn haìng âåüi bàòng danh saïch âàûc

Hçnh 14: Khàõc phuûc haìng bë traìn bàòng Phæång phaïp di chuyãøn voìng

(a): Træåïc khi thãm ; (b): Sau khi thãm

Front (=4)

Rear (=8)

Front (=4)

Rear (=1)

(a)

(b)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 22

Âäúi våïi phæång phaïp naìy, ta coï Front coï thãø nhoí hån, låïn hån hoàûc bàòng Rear. Haìng bë

âáöy khi (Rear - Front + 1 = 0) hoàûc (Rear - Front + 1 = n). Haìm Insert_Queue sau traí vãö vë
trê cuía pháön tæí måïi thãm vaìo hoàûc traí vãö 0 nãúu haìng bë âáöy:

Function Insert_Queue (NewInfo : Integer) : Integer;
Begin

If (Rear - Front + 1 = 0) Or (Rear - Front + 1 = n) Then Insert_Queue := 0
Else
Begin

If Front = 0 Then
Begin

Front := 1; Rear := 0;

End;
If Rear = n Then Rear := 0;
Rear := Rear + 1;
Queue[Rear] := NewInfo;
Insert_Queue := Rear;

End;

Loaûi boí mäüt pháön tæí cuía haìng

Thuí tuûc loaûi boí sau coï hai tham biãún, tham biãún Succ traí vãö giaï trë laì True nãúu haìng khaïc

räùng vaì ngæåüc laûi, näüi dung cuía pháön tæí láúy ra laì Infox.

Procedure Delete_Queue (Var Succ : Integer ; Var Empty : Boolean);
Begin

Succ := False;
Infox := Queue[Front];
If Front = Rear Then
Begin

Succ := 0;
Rear := 0;

End
Else
Begin

Front := Front + 1;
If Front > n Then Front := 1;

End;

c) Haìng âæåüc täø chæïc theo danh saïch liãn kãút
•

Biãøu diãùn haìng theo danh saïch liãn kãút

Front

Rear

Hçnh 15: Täø chæïc haìng theo danh saïch liãn kãút

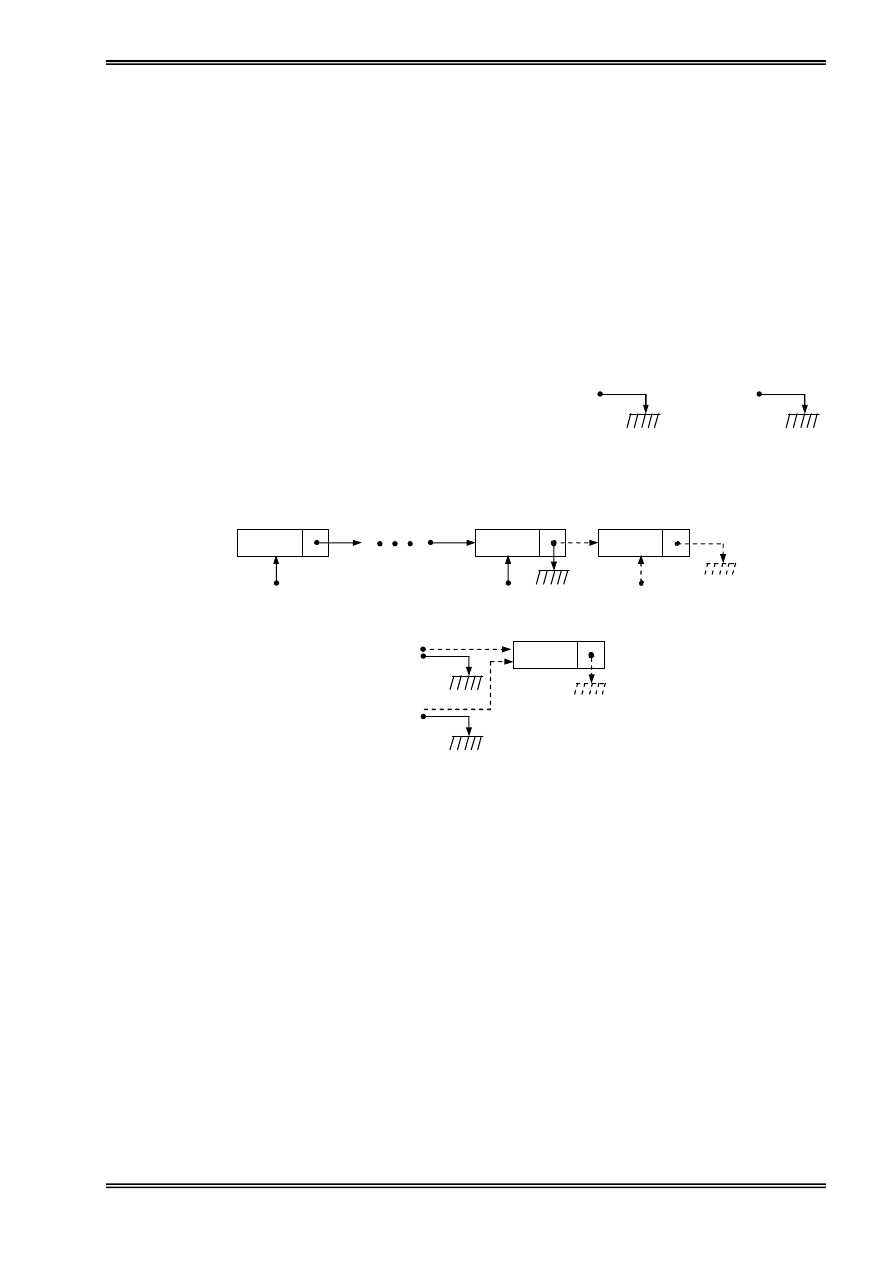
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 23

Ta khai baïo:

Type PointLst = ^Element;
Element = Record

Info : Integer;
Next : PointLst;

End;
Var Front , Rear : PointLst;

Caïc pheïp toaïn trãn haìng âæåüc täø chæïc theo danh saïch liãn kãút cuîng tæång tæû nhæ caïc

pheïp toaïn trãn haìng âæåüc täø chæïc theo danh saïch âàûc.

‚

Khåíi taûo haìng

Khi khåíi taûo haìng, haìng laì räùng, ta cho Front vaì Rear coï giaï trë laì Nil.

Frocedure Initialize;
Begin

Front := Nil; Rear := Nil;

End;

Thãm mäüt pháön tæí vaìo haìng

Giaí sæí ta cáön thãm mäüt pháön tæí måïi p coï näüi dung laì NewInfo vaìo haìng.

Haìm Insert_Queue traí vãö âëa chè cuía pháön tæí måïi thãm vaìo haìng.

Function Insert_Queue (NewInfo : Integer) : PointLst;
Var p , q : PointLst;
Begin

New(p);

(* Cáúp phaït vuìng nhåï *)

p^.Info := NewInfo;

(* Gaïn giaï trë *)

p^.Next := Nil;

(* Thao taïc 1 *)

If Rear = Nil Then Front := p (* Nãúu danh saïch âang räùng – thao taïc 2 *)
Else Rear^.Next := p; (* Nãúu danh saïch khaïc räùng – thao taïc 3 *)
Rear := p;

(* Thay âäøi con troí cuäúi – thao taïc 4 *)

Insert_Queue := p;

End;

Front

Rear

Hçnh 16: Thãm mäüt pháön tæí vaìo haìng

(a): khi haìng khäng räùng ; (b): khi haìng âang räùng

Rear

Front

(1)

(4)

(2)

Front

Rear

NewInfo

(4)

(3)

(1)

(a)

(b)

NewInfo

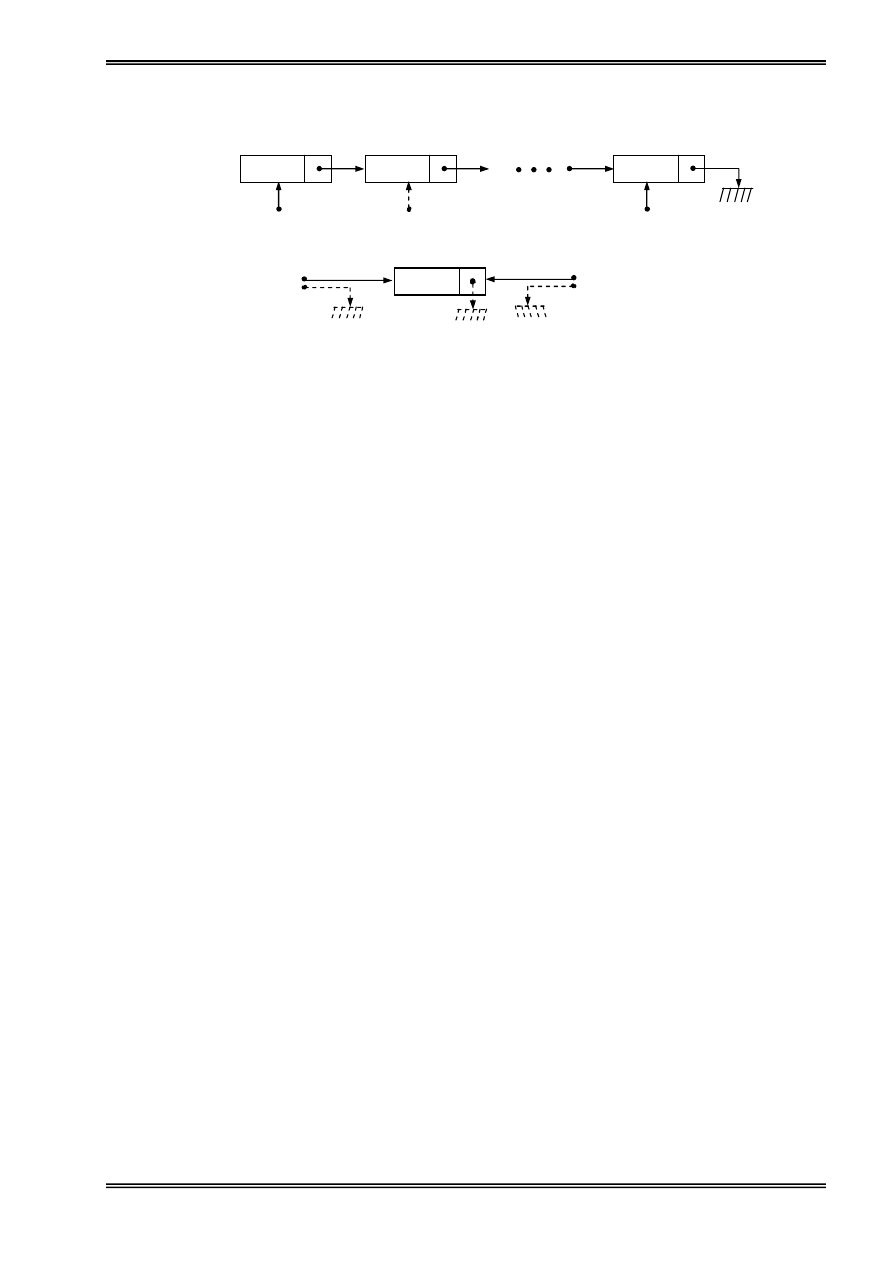
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 24

„

Loaûi boí mäüt pháön tæí khoíi haìng

Thuí tuûc sau coï hai tham biãún, tham biãún Succ traí vãö giaï trë laì True nãúu haìng khaïc räùng

vaì ngæåüc laûi, tham biãún Infox traí vãö näüi dung cuía pháön tæí âæåüc láúy ra.

Procedure Delete_Queue (Var Infox : Integer ; Var Succ : Boolean);
Var p : PointLst;
Begin

Succ := False;
If Front <> Nil Then
Begin

Succ := True;
p := Front;
Front := p^.Next; (* Thao taïc 1 *)
Infox := p^.Info;
If Front = Nil Then Rear := Nil; (* Khi haìng chè coï mäüt pháön tæí – thao taïc 2 *)
Dispose(p);

(* Giaíi phoïng vuìng nhåï cuía pháön tæí âaî bë loaûi boí *)

End;

d) ÆÏng duûng cuía haìng âåüi
Haìng âåüi thæåìng âæåüc æïng duûng âãø giaíi quyãút caïc baìi toaïn maì caïc pháön tæí âæåüc xæí lyï coï

tênh cháút vaìo træåïc ra træåïc.

IV.2. Cáúu truïc dæî liãûu ngàn xãúp (stack)

a) Âënh nghéa ngàn xãúp
Ngàn xãúp laì mäüt danh saïch maì caí pheïp thãm vaìo vaì pheïp loaûi boí âãöu âæåüc thæûc hiãûn åí

trãn mäüt âáöu tæång tæû nhæ mäüt chäöng âéa. Nhæ váûy pháön tæí naìo thãm vaìo sau seî bë láúy ra
træåïc nãn ngàn xãúp coìn âæåüc goüi laì LIFO (Last in First out).

Ngàn xãúp âæåüc æïng duûng ráút nhiãöu trong thæûc tãú, vê duû: chæång trçnh A goüi chæång trçnh

B, chæång trçnh B goüi chæång trçnh C. Khi chæång trçnh C thæûc hiãûn xong thç âiãöu khiãøn
quay laûi vaì tiãúp tuûc thæûc hiãûn chæång trçnh B, khi chæång trçnh B thæûc hiãûn xong thç âiãöu

Hçnh 17: Loaûi boí mäüt pháön tæí khoíi haìng

(a): khi haìng coï hån 1 pháön tæí ; (b): khi haìng chè coï 1 pháön tæí

(a)

Front

Rear

Front

(1)

Front

Rear

(2)

(1)

(b)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 25

khiãøn quay laûi chæång trçnh A. Nhæ váûy chæång trçnh naìo goüi sau seî âæåüc thæûc hiãûn xong
træåïc.

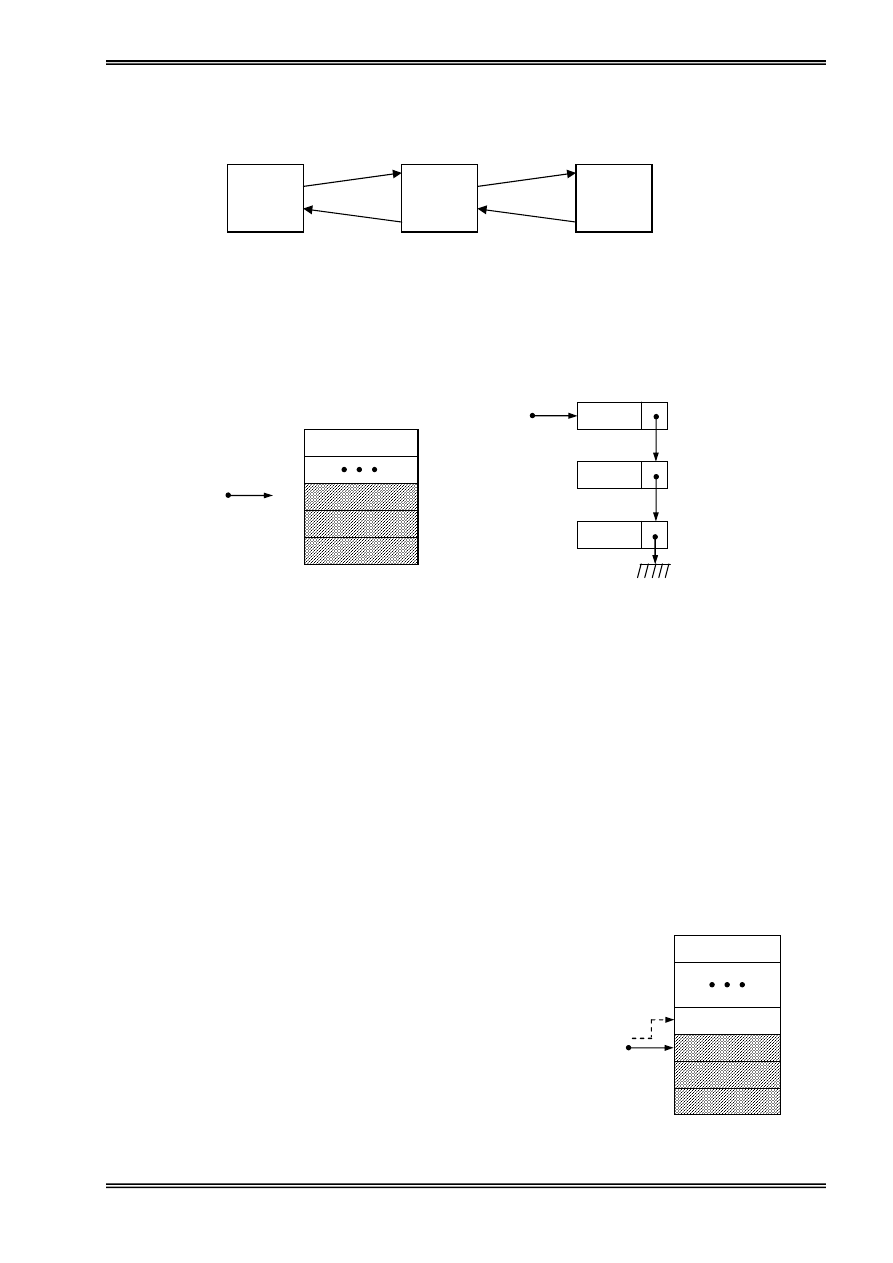
b) Täø chæïc cuía ngàn xãúp
Ngàn xãúp coï thãø âæåüc täø chæïc theo danh saïch âàûc hoàûc theo danh saïch liãn kãút. Vç pheïp

thãm vaìo vaì pheïp loaûi boí chè âæåüc thæûc hiãûn mäüt âáöu nãn mäüt ngàn xãúp chè âæåüc âaûi diãûn
båíi mäüt con troí chè vaìo âènh ngàn xãúp, kyï hiãûu laì Top.

c) Caïc pheïp toaïn trãn ngàn xãúp täø chæïc theo danh saïch âàûc
Khai baïo:

Var Stack : Array[1..100] of Integer; (* Ngàn xãúp *)
Var Top : Integer;

(* Con troí ngàn xãúp *)

•

Khåíi taûo ngàn xãúp

Khi khåíi taûo ngàn xãúp laì räùng ta cho Top bàòng 0:

Procedure Initialize;
Begin

Top := 0;

End;

‚

Thãm mäüt pháön tæí vaìo ngàn xãúp

Giaí sæí ta thãm mäüt pháön tæí coï näüi dung laì NewInfo

vaìo ngàn xãúp, haìm sau traí vãö giaï trë 0 nãúu ngàn xãúp bë âáöy
hoàûc traí vãö vë trê cuía pháön tæí måïi thãm vaìo ngàn xãúp.

Function Inssert_Stack(NewInfo : Integer) : Integer;
Begin

If Top = n Then (* traí vãö 0 nãúu ngàn xãúp âáöy *)

Inssert_Stack := 0

Else

Goüi

Tråí vãö

Goüi

Tråí vãö

Hçnh 18: Quaï trçnh goüi chæång trçnh con

3
2
1

Top

Hçnh 19: Täø chæïc ngàn xãúp

(a): Sæí duûng danh saïch âàûc ; (b): Sæí duûng danh saïch liãn kãút

Top

(a)

(b)

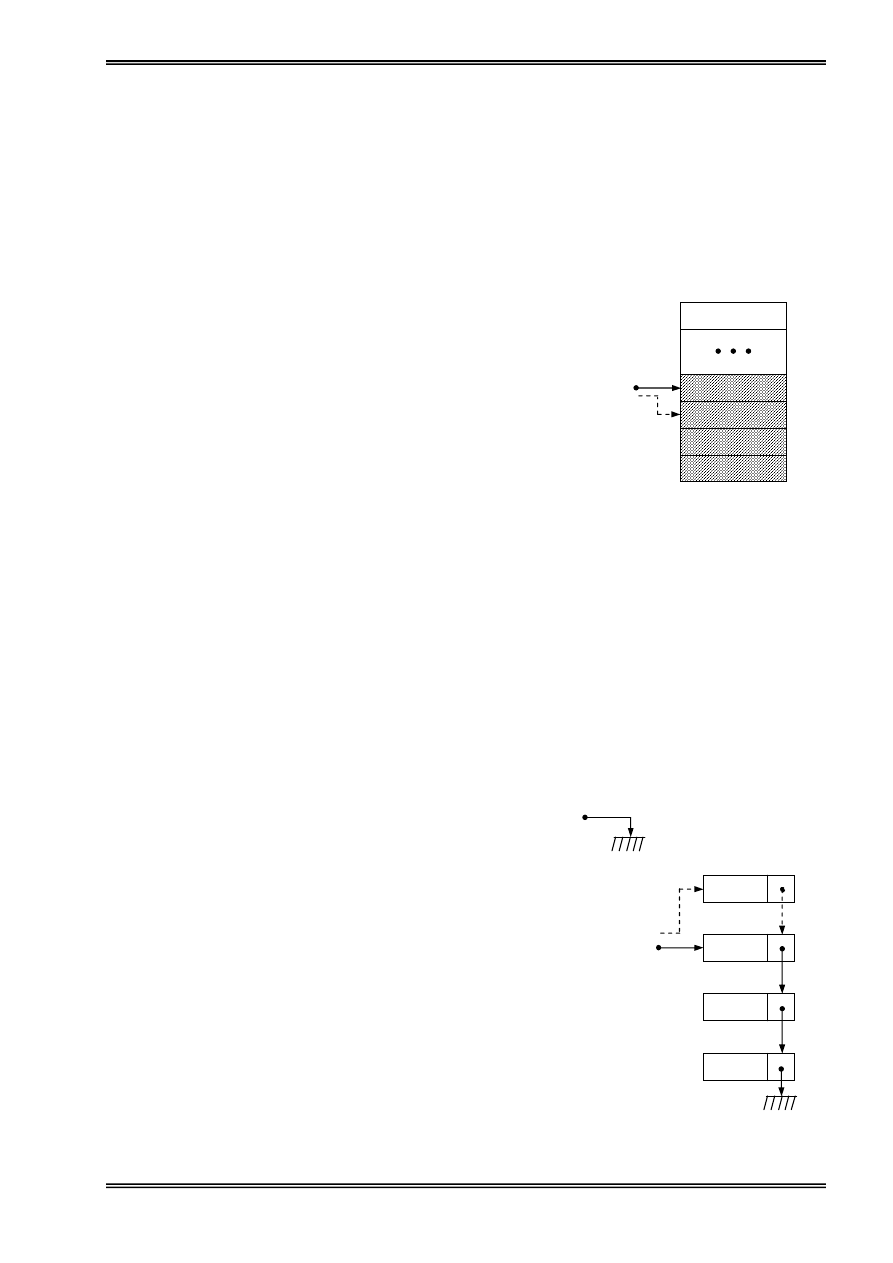
Hçnh 20: Thãm mäüt pháön

tæí vaìo âènh ngàn xãúp

NewInfo

4
3
2
1

Top

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 26

Begin

Top := Top + 1;

(* Tàng âènh ngàn xãúp )

Stack[Top] := NewInfo; (* Ghi nháûn giaï trë *)
Inssert_Stack := Top; (* Traí vãö giaï trë *)

End;

Láúy ra mäüt pháön tæí cuía ngàn xãúp

Thuí tuûc sau coï 2 tham biãún, tham biãún Succ traí vãö laì True nãúu ngàn xãúp khaïc räùng,

ngæåüc laûi nãúu ngàn xãúp räùng. Näüi dung láúy ra laì Infox.

Procedure Delete_Stack (Var Infox : Integer ; Var Succ :

Boolean);

Begin

Succ := False;
If Top <> 0 Then

(* Nãúu ngàn xãúp khäng räùng *)

Begin

Succ := True;

(* Thaình cäng *)

Infox := Stack[Top]; (* Láúy giaï trë *)
Top := Top - 1;

(* Giaím âènh ngàn xãúp *)

End;

d) Caïc pheïp toaïn trãn ngàn xãúp täø chæïc theo danh saïch liãn kãút
Khai baïo:

Type PointStack = ^Element;
Element = Record

(* Kiãøu baín ghi *)

Info : Integer;

(* Thaình pháön chæïa thäng tin *)

Next : PointStack; (* Thaình pháön liãn kãút *)

End;
Var Top : PointStack; (* Con troí chè tåïi âènh ngàn xãúp *)

•

Khåíi taûo ngàn xãúp

Khi khåíi taûo ngàn xãúp, ngàn xãúp laì räùng, ta cho Top nháûn giaï trë laì Nil.

Frocedure Initialize;
Begin

Top := Nil;

End;

‚

Thãm mäüt pháön tæí vaìo ngàn xãúp

Haìm Insert_Stack traí vãö âëa chè cuía pháön tæí måïi coï näüi

dung laì NewInfo væìa âæåüc thãm vaìo ngàn xãúp.

Function Insert_Stack (NewInfo : Integer) : PointStack;
Var p : PointStack;
Begin

New(p);

(* Cáúp phaït vuìng nhåï *)

p^.Info := NewInfo; (* Ghi nháûn näüi dung *)
p^.Next := Top;

(* Thao taïc 1 *)

Top := p;

(* Thao taïc 2 *)

Insert_Stack := p; (* Traí vãö giaï trë *)

End;

Hçnh 21: Loaûi boí mäüt

pháön tæí khoíi ngàn xãúp

4
3
2
1

Top

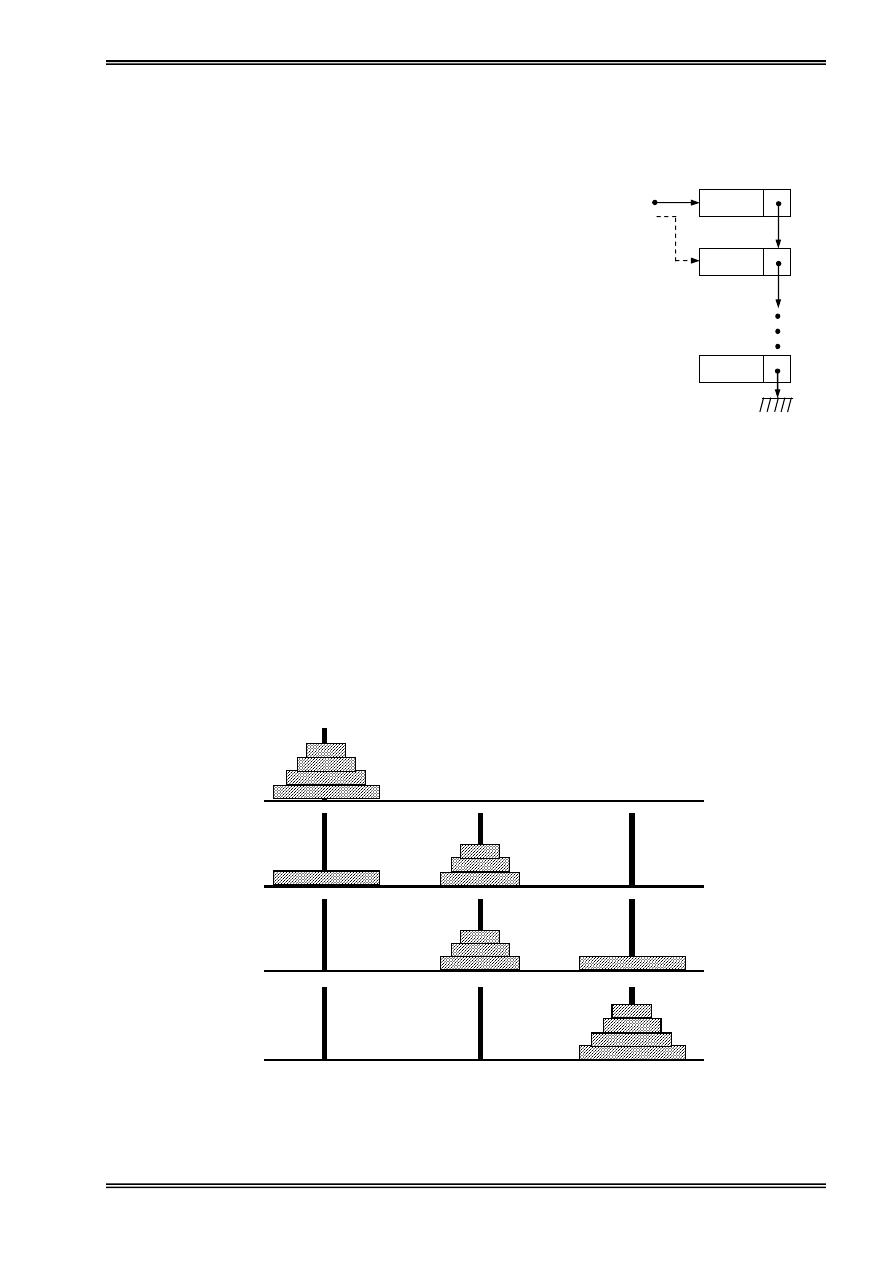
Hçnh 22: Thãm mäüt pháön

tæí vaìo ngàn xãúp

Top

NewInfo

(1)

(2)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 27

Láúy ra mäüt pháön tæí cuía ngàn xãúp

Thuí tuûc sau coï 2 tham biãún, tham biãún Succ traí vãö laì True nãúu ngàn xãúp khaïc räùng,

ngæåüc laûi nãúu ngàn xãúp räùng. Näüi dung láúy ra laì Infox.

Procedure Delete_Stack (Var Infox : Integer ; Var Succ : Boolean);
Var p : PointStack;
Begin

Succ := False;
If Top <> Nil Then

(* Nãúu ngàn xãúp khaïc räùng *)

Begin

Succ := True;
P := Top;
Top := Top^.Next; (* Thao taïc 1 *)
Infox := p^.Info; (* Traí vãö giaï trë *)
Dispose(p);

(* Giaíi phoïng vuìng nhåï *)

End;

d) ÆÏng duûng cuía ngàn xãúp
Do âàûc âiãøm cuía ngàn xãúp laì pháön tæí vaìo sau âæåüc láúy ra træåïc nãn ngàn xãúp thæåìng

âæåüc sæí duûng âãø biãún âäøi mäüt giaíi thuáût âãû quy thaình mäüt giaíi thuáût khäng âãû quy.

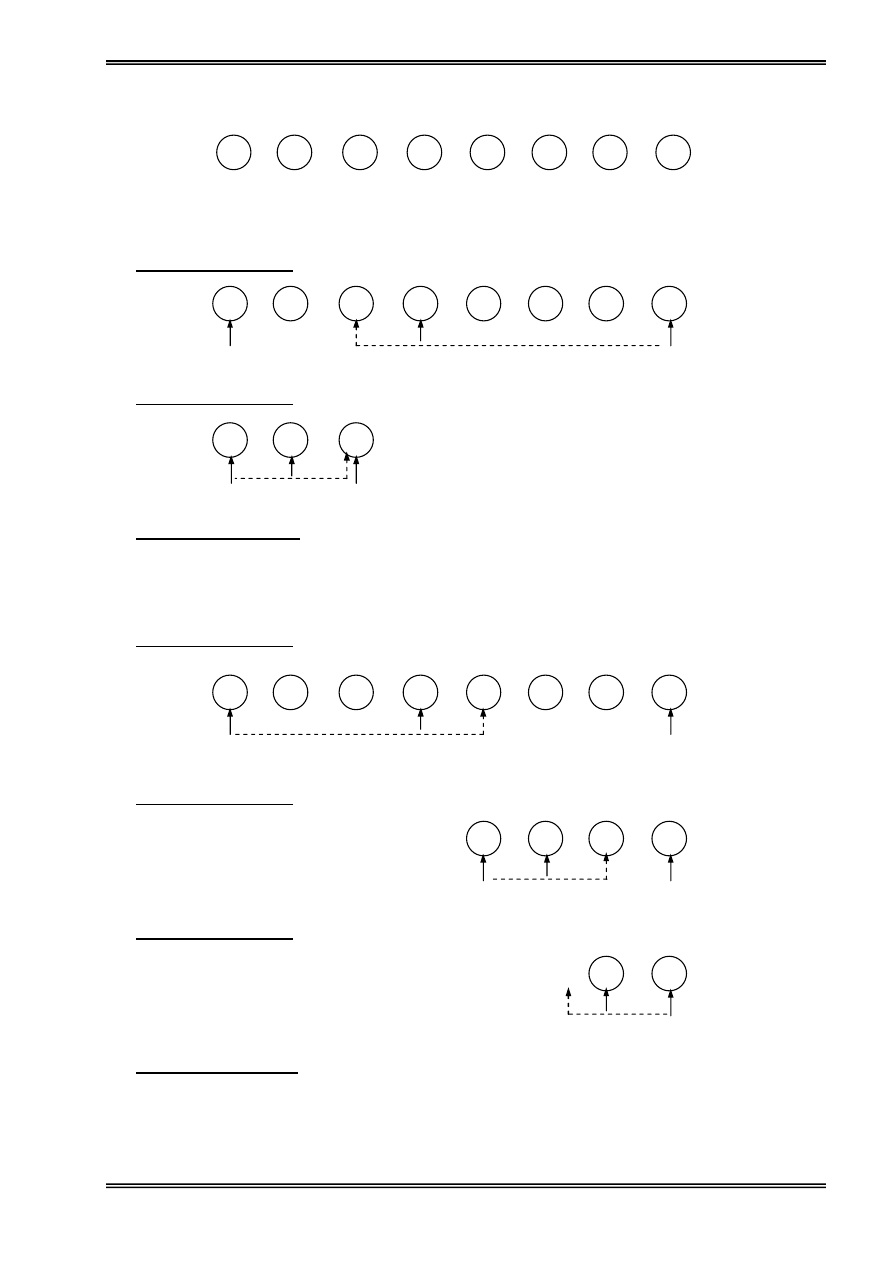
Vê duû giaíi baìi toaïn thaïp Haì Näüi: Coï 3 cäüt, ban âáöu åí cäüt 1 coï n táöng âæåüc xãúp theo thæï

tæû tæì låïn tåïi nhoí, haîy tçm caïch di chuyãøn n táöng tæì cäüt 1 sang cäüt 3 sæí duûng cäüt 2 laìm trung
gian sao cho taûi mäùi thåìi âiãøm caïc táöng trãn mäùi cäüt phaíi âaím baío thæï tæû tæì låïn tåïi nhoí vaì
mäùi láön chè di chuyãøn âæåüc mäüt táöng.

•

Giaíi thuáût âãû quy

Giaíi thuáût âãû quy coï thãø âæåüc hiãøu nhæ sau:

Hçnh 23: Loaûi boí mäüt

pháön tæí khoíi ngàn xãúp

Top

(1)

(c)

(1)

(2)

(3)

(d)

(b)

n = 4

(a)

Hçnh 24: Giaíi baìi toaïn thaïp Haì Näüi bàòng âãû quy

(a): Ban âáöu ; (b): di chuyãøn n-1 âéa trãn cuìng sang cäüt 2 ; (3): di
chuyãøn âéa coìn laûi tæì 1 sang 3 ; (d): di chuyãøn n-1 âéa åí 2 sang 3

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 28

Baìi toaïn trãn âæåüc giaíi quyãút theo phæång phaïp âãû quy nhæ sau:
-

Giai âoaûn 1: Âæa n -1 âéa trãn cuìng tæì cäüt 1 sang cäüt 3 sæí duûng cäüt 2 laìm trung gian.

Giai âoaûn 2: Âæa âéa låïn nháút coìn laûi åí cäüt 1 sang cäüt 3.

Giai âoaûn 3: Âæa n -1 âéa åí trãn cäüt 2 sang cäüt 3 sæí duûng cäüt 1 laìm trung gian.

Ta tháúy giai âoaûn 1 vaì giai âoaûn 3 chênh laì hçnh aính âãû quy cuía chæång trçnh khi säú thaïp

bàòng n-1 do váûy ta dãù daìng thæûc hiãûn chuïng âæåüc bàòng caïch goüi âãû quy. Chæång trçnh âæåüc
viãút nhæ sau:

Program HaNoi;
Var n , Step : Integer;
Procedure ThapHN(So_tang , Cot_nguon , Cot_dich, Cot_trung_gian : Integer);
Begin

If So_tang = 1 Then
Begin

Step := Step + 1; (* tàng säú bæåïclãn *)
Write(‘Bæåïc ’, Step:2, ‘:’, ‘Chuyãøn 1 âéa tæì cäüt: ’, Cot_nguon:2, ‘ -> ’, Cot_dich:2);

End
Else
Begin

ThapHN(So_tang -1 , Cot_nguon , Cot_trung_gian , Cot_dich); (* giai âoaûn 1 *)
ThapHN(1, Cot_nguon , Cot_dich , Cot_trung_gian);

(* giai âoaûn 2 *)

ThapHN(So_tang -1, Cot_trung_gian , Cot_dich, Cot_nguon); (* giai âoaûn 3 *)

End;

End;
Begin (* Chæång trçnh chênh *)

Step := 0;
Write(‘Nháûp säú táöng cuía thaïp:’); Readln(n);
Tours(n,1,3); Readln;

End.

‚

Giaíi thuáût khäng âãû quy

Âãø biãún âäøi giaíi thuáût âãû quy thaình giaíi thuáût khäng âãû quy ta sæí duûng mäüt ngàn xãúp.

Mäüt pháön tæí cuía ngàn xãúp chæïa mäüt bäü dæî liãûu gäöm (säú táöng cáön di chuyãøn, cäüt xuáút phaït,
cäüt âãún, cäüt trung gian). Thay vç goüi âãû quy nhæ trong giaíi thuáût trãn ta âæa bäü dæî liãûu vaìo
ngàn xãúp. Ban âáöu ta khåíi taûo ngàn xãúp våïi (n, 1, 3). Sau âoï làûp laûi nhiãöu láön caïc cäng viãûc
sau cho âãún khi ngàn xãúp räùng:

“Láúy ra tæì ngàn xãúp bäü (So_tang , Nguon , Dich , Trung_gian) “
Nãúu So_thap = 0 Thç

“Thæûc hiãûn di chuyãøn mäüt táöng tæì cäüt Nguon âãún cäüt Dich“

Nãúu khäng thç
Begin

“Âæa vaìo ngàn xãúp bäü (So_tang -1 , Nguon , Trung_gian , Dich);”
“Âæa vaìo ngàn xãúp bäü (1 , Nguon , Dich , Trung_gian);”
“Âæa vaìo ngàn xãúp bäü (So_tang -1, Trung_gian , Dich , Nguon);”

End;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 29

Chæång trçnh âáöy âuí âæåüc viãút nhæ sau:

Program Thap_HaNoi;
Type Item = Record

(* Kiãøu cuía mäüt pháön tæí trong ngàn xãúp *)

So_tang , Nguon , Dich, Trung_gian : Integer;

End;
Var Stack : Array [1..50] Of Item; (* Ngàn xãúp *)
Var n, Top, kNguon, kDich, kSo_tang, kTrung_gian: Integer; (* Caïc biãún trung gian *)
Begin (* Chæång trçnh chênh *)

Write(‘Nháûp vaìo säú táöng:’); Readln(n); (* Nháûp säú táöng cuía thaïp *)
Top := 1;

(* Khåíi taûo ngàn xãúp *)

Step := 0;

(* Chæïa säú bæåïc dëch chuyãøn *)

(* Âæa mäüt pháön tæí vaìo ngàn xãúp *)
Stack[1].So_tang := n ; Stack[1].Nguon := 1 ; Stack[1].Dich := 3;
Repeat (* Làûp laûi caïc bæåïc sau cho âãún khi ngàn xãúp räùng *)

(* Láúy mäüt pháön tæí tæì ngàn xãúp âãø xæí lyï chæïa vaìo caïc biãún trung gian *)
kNguon := Stack[Top].Nguon; kSo_tang := Stack[Top].So_tang;
kDich := Stack[Top].Dich;

kTrung_gian := Stack[Top].Trung_gian;

Top := Top -1;
If kSo_tang = 1 Then
Begin

Step := Step + 1;
Write(‘Bæåïc ’, Step:2, ‘:’, ‘Chuyãøn 1 âéa tæì cäüt: ’, kNguon:2, ‘ -> ’, kDich:2);

End
Else
Begin

(* Thay vç goüi âãû quy ta âæa caïc bäü giaï trë sau vaìo ngàn xãúp âãø xæí lyï *)
Stack[Top+1].So_tang := kSo_tang -1; Stack[Top+1].Nguon := kNguon;
Stack[Top+1].Dich := kTrung_gian;

Stack[Top+1].Trung_gian := kDich;

(* Pháön tæí thæï 2 *)
Stack[Top+2].So_tang := 1; Stack[Top+2].Nguon := kNguon;
Stack[Top+2].Dich := kDich; Stack[Top+2].Trung_gian := kTrung_gian;
(* Pháön tæí thæï 3 *)
Stack[Top+3].So_tang := kSo_tang -1; Stack[Top+3].Nguon := kTrung_gian;
Stack[Top+3].Dich := kDich;

Stack[Top+3].Trung_gian := kNguon;

(* Âaî âæa vaìo ngàn xãúp 3 pháön tæí *)
Top := Top + 3;

End;

Until Top = 0;
Readln;

End; (* Kãút thuïc chæång trçnh chênh *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 30

Chæång naìy giaíi quyãút mäüt váún âãö ráút quan troüng laì laìm sao coï thãø tçm kiãúm dæî liãûu âaî

âæåüc læu træî våïi mäüt khoïa (key) cho træåïc. Thäng thæåìng dæî liãûu âæåüc phán chia thaình caïc
máùu tin (Record), mäùi máùu tin coï mäüt khoïa âæåüc sæí duûng trong viãûc tçm kiãúm.

Sau khi tçm kiãúm coï thãø hai træåìng håüp xaíy ra: Tçm kiãúm thaình cäng vaì khäng thaình

cäng. Nãúu khäng tçm tháúy máùu tin coï khoïa k, âäi khi ta muäún thãm mäüt máùu tin måïi coï
khoïa laì k vaìo danh saïch. Phæång phaïp âoï goüi laì: “Tçm kiãúm vaì thãm vaìo”.

I. TÇM KIÃÚM TUÁÖN TÆÛ (SEQUENTIAL SEARCHING)

Våïi phæåg phaïp tçm kiãúm tuáön tæû, ta bàõt âáöu tçm kiãúm tæì pháön tæí âáöu tiãn. Nãúu khoïa cuía

pháön tæí naìy khäng phaíi laì khoïa cáön tçm thç ta âi âãún pháön tæí kãú tiãúp vaì cæï nhæ thãú ta âi âãún
pháön tæí coï khoïa cáön tçm hoàûc âãún khi naìo âi hãút danh saïch.

I.1. Tçm kiãúm trãn danh saïch âàûc

Goüi n laì säú pháön tæí cuía danh saïch, ta khai baïo danh saïch nhæ sau:

Type Element = Record;

Key : Integer; (* Khoïa âãø tçm kiãúm *)
Info : Integer; (* Chæïa thäng tin læu træî *)

End;
Var a : Array[1 .. n] of Integer; (* Danh saïch cáön tçm kiãúm *)

Haìm Search traí vãö chè säú cuía pháön tæí tçm tháúy âáöu tiãn trong danh saïch hoàûc traí vãö 0

nãúu khäng tçm tháúy.

a) Træåìng håüp danh saïch chæa coï thæï tæû
Haìm sau tçm kiãúm khoïa x trong danh saïch bàõt âáöu tæì pháön tæí âáöu tiãn cho âãún khi tçm

tháúy khoïa naìy hoàûc cho âãún khi âi hãút danh saïch.

Function Search (x : Integer) : Integer;
Var found : Boolean; i : Integer;
Begin

found := False;
i := 1;

(* Khåíi taûo biãún âãúm *)

While (i <= n) And (Not found) Do (* Chæìng naìo chæa hãút danh saïch vaì khäng tçm tháúy *)
Begin

If a[i].Key = x Then found := True (* Nãúu tçm tháúy *)
Else i := i + 1; (* Nãúu khäng thç tiãúp tuûc tçm kiãúm åí pháön tæí tiãúp theo *)

End;
If found Then Search := i Else Search := 0;

End;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 31

b) Træåìng håüp danh saïch âaî coï thæï tæû
Vç danh saïch âaî coï thæï tæû (tàng dáön) nãn ta chè cáön tçm kiãúm khoïa x cho âãún khi tçm

tháúy khoïa naìy trong danh saïch hoàûc cho âãún khi khoïa cuía pháön tæí hiãûn taûi låïn hån x (khäng
tçm tháúy) hoàûc cho âãún khi âi hãút danh saïch.

Function Search (x : Integer) : Integer;
Var i : Integer; (* Biãún âãúm *)
Begin

i := 1; (* Khåíi taûo biãún âãúm *)
While (a[i].Key < x) And (i <= n) Do i := i + 1; (* Boí qua caïc pháön tæí nhoí hån x *)
If (a[i].Key = x) And (i <= n) Then Search := i (* Tçm tháúy *)
Else Search := 0; (* Khäng tçm tháúy *)

End;

I.2. Tçm kiãúm trãn danh saïch liãn kãút

Ta khai baïo cáúu truïc danh saïch nhæ sau:

Type PointLst = ^Element;
Element = Record

Key : Integer; (* Khoïa tçm kiãúm *)
Info : Integer; (* Chæïa thäng tin *)
Next : PointLst; (* Thaình pháön liãn kãút *)

End;
Var First : PointLst; (* Con troí âáöu danh saïch *)

Haìm Search traí vãö âëa chè cuía pháön tæí âáöu tiãn nãúu tçm tháúy hoàûc traí vãö giaï trë Nil nãúu

khäng tçm tháúy.

a) Træåìng håüp danh saïch chæa coï thæï tæû

Function Search (x: Integer) : PointLst;
Var p: PointLst; Found: Boolean;
Begin

Found := False; p := First; (* Cho con troí p troí tåïi âáöu danh saïch *)
While (p <> Nil) and (Not Found) do
Begin

If (p^.Key = x) Then Found := True (* Nãúu tçm tháúy *)

Else p := p^.Next; (* Tçm pháön tæí tiãúp theo trong danh saïch *)

End;
Search := p;

(* Traí vãö con troí *)

End;

b) Træåìng håüp danh saïch âaî coï thæï tæû

Function Search (x : Integer) : PointLst;
Var p : PointLst;
Begin

p := First;

(* Cho p troí tåïi pháön tæí âáöu tiãn trong danh saïch *)

While (p <> nil) And (p^.Key < x) do p := p^.Next;

(* Boí qua caïc pháön tæí < x *)

If (p <> Nil) And (p^.Key = x) Then Search := p;

(* Tçm tháúy *)

Else Search := Nil;

(* Khäng tçm tháúy *)

End;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 32

II. TÇM KIÃÚM NHË PHÁN (BINARY SEARCH)

Giaíi thuáût tçm kiãúm nhë phán chè âæåüc aïp duûng âäúi våïi danh saïch âàûc âaî coï thæï tæû (tàng

dáön). Näüi dung cuía phæång phaïp naìy laì tçm kiãúm bàòng caïch liãn tuûc phán âäi danh saïch räöi
loaûi boí âi mäüt næía chàõc chàõn khäng chæïa pháön tæí cáön tçm cho âãún khi danh saïch chè coìm
mäüt pháön tæí coï khoïa bàòng x (thaình cäng) hoàûc khäng thãø phán âäi tiãúp (khäng thaình cäng).
Caïc bæåïc nhæ sau:

•

Ban âáöu: Phaûm vi tçm kiãúm ban âáöu laì toaìn bäü danh saïch vaì giaí sæí danh saïch coï thæï tæû

tàng dáön.

‚

Bæåïc 1: Láúy khoïa pháön tæí åí giæîa cuía phaûm vi tçm kiãúm (goüi laì y) so saïnh våïi x

Nãúu

x = y

thç ta tçm tháúy khoïa naìy, giaíi thuáût kãút thuïc thaình cäng.

Nãúu

x < y

thç loaûi boí pháön danh saïch bãn phaíi cuía y, phaûm vi tçm kiãúm måïi laì caïc

pháön tæí nàòm bãn traïi cuía y.

Nãúu

x > y

thç loaûi boí pháön danh saïch bãn traïi cuía y, phaûm vi tçm kiãúm måïi laì caïc

pháön tæí nàòm bãn phaíi cuía y.

Bæåïc 2: Nãúu täön taûi phaûm vi tçm kiãúm thç làûp laûi Bæåïc 1, ngæåüc laûi giaíi thuáût kãút thuïc

khäng thaình cäng.

Haìm Binary_Search traí vãö chè säú cuía pháön tæí tçm tháúy hoàûc traí vãö giaï trë 0 nãúu khäng

tçm tháúy.

Function Binary_Search (x : Integer) : Integer;
Var j, k, m : Integer; found : Boolean;
Begin

found := False;
k := 1; m := n; (* k vaì m laì chè säú âáöu vaì cuäúi cuía phaûm vi tçm kiãúm *)
While (k <= m) And (Not found) do
Begin

j := (k + m) Div 2;

(* Láúy chè säú cuía pháön tæí giæîa danh saïch *)

If a[j] = x Then found := True

(* Nãúu tçm tháúy, træåìng håüp x = y *)

Else
Begin

If a[j].Key < x Then k := j +1 (* Træåìng håüp x > y, thay âäøi chè säú âáöu *)
Else m := j - 1;

(* Træåìng håüp x < y, thay âäøi chè säú cuäúi *)

End;

End;
If found Then Binary_Search := j

(* Traí vãö giaï trë *)

Else Binary_Search := 0;

End;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 33

Vê duû: Ta cáön tçm kiãúm trãn danh saïch:

Ban âáöu: k = 1 vaì m = 8
•

Træåìng håüp khoïa cáön tçm laì x = 4 (tçm tháúy):

Láön 1 (k=1 vaì m=8)

: j = (k + m) Div 2 = 4, do a[j] = 5 > x nãn k = 1 vaì m = j - 1 = 3:

Láön 2 (k=1 vaì m=3):

j = (k + m) Div 2 = 2, do a[j] = 3 < x nãn k = j + 1 = 3 vaì m = 3:

Láön 3 (k=3 vaì m= 3):

j = (k + m) Div 2 = 3, do a[j] = 4 = x nãn thuáût toaïn kãút thuïc, haìm

traí vãö giaï trë cuía j (tçm tháúy x åí vë trê thæï 3).

•

Træåìng håüp khoïa cáön tçm laì x = 11 (khäng tçm tháúy):

Láön 1 (k=1 vaì m=8)

: j = (k + m) Div 2 = 4, do a[j] = 5 < x nãn k = j + 1 = 5 vaì m = 8:

Láön 2 (k=5 vaì m=8):

j = (k + m) Div 2 = 6, do a[j] = 10 < x nãn k = j + 1 = 7 vaì m = 8:

Láön 3 (k=7 vaì m=8):

j = (k + m) Div 2 = 7, do a[j] = 12 > x nãn k = 7 vaì m = j -1= 6:

Láön 4 (k=7 vaì m= 6):

Do k > m nãn giaíi thuáût kãút thuïc khäng thaình cäng, haìm traí vãö giaï

trë 0 (khäng tçm tháúy)

j=4

m=j –1=3

k=1

m=8

m=3

k=1

j=2

j=4

k=j+1=5

k=1

m=8

j=6

k=5

m=8

k,j =7 m=8

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 34

Sàõp thæï tæû laì caïc pheïp toaïn thæåìng gàûp trong cäng viãûc hàòng ngaìy cuîng nhæ trong caïc

baìi toaïn quaín lyï kinh tãú nhàòm âãø tçm kiãúm dæî liãûu dãù daìng vaì nhanh choïng. Coï ráút nhiãöu
giaíi thuáût sàõp xãúp khaïc nhau, mäùi giaíi thuáût coï nhæîng æu âiãøm vaì nhæåüc âiãøm riãng. Thäng
thæåìng ngæåìi ta phán chia thaình hai nhoïm chênh:

- Sàõp thæï tæû näüi (hay sàõp thæï tæû maíng): Toaìn bäü dæî liãûu cáön sàõp xãúp thæï tæû phaíi âæåüc âæa

vaìo trong bäü nhåï chênh. Do âoï dæî liãûu cáön sàõp thæï tæû khäng nhiãöu làõm do dung læåüng cuía bäü
nhåï chênh bë giåïi haûn trãn tæìng maïy tênh cuû thãø, nhæng thåìi gian sàõp thæï tæû näüi tæång âäúi
nhanh.

- Sàõp thæï tæû ngoaûi (hay sàõp thæï tæû táûp tin): mäüt pháön caïc dæî liãûu cáön sàõp thæï tæû âæåüc âæa

vaìo trong bäü nhåï chênh, pháön dæî liãûu coìn laûi âæåüc læu træî åí bäü nhåï ngoaìi (bàng tæì, âéa tæì).
Do âoï dæî liãûu cáön sàõp thæï tæû tæång âäúi låïn (phuû thuäüc vaìo dung læåüng cuía bàng tæì, âéa tæì),
nhæng thåìi gian sàõp xãúp thæï tæû tæång âäúi cháûm.

Do âiãöu kiãûn thåìi gian nãn trong chæång naìy chuí yãúu âi sáu vaìo caïc giaíi thuáût sàõp thæï tæû

näüi theo chiãöu tàng dáön, Phæång phaïp sàõp thæï tæû ngoaûi chuí yãúu laì giåïi thiãûu laìm quen trong
muûc V åí cuäúi chæång.

Khai baïo daîy cáön sàõp thæï tæû laì mäüt maíng caïc baín ghi (Record), mäùi baín ghi bao gäöm hai

thaình pháön: mäüt thaình pháön chæïa khoïa âãø sàõp xãúp vaì mäüt thaình pháön chæïa dæî liãûu.

Type Item = Record

key : Integer;

(* Chæïa khoïa, khoïa cuía pháön tæí coï thãø laì chæî, säú hoàûc caí chæî vaì säú *)

Info : Integer; (* Thaình pháön chæïa dæî liãûu *)

End;
Var a : Array[1..n] of Item; (* Daîy cáön sàõp thæï tæû *)

I. SÀÕP THÆÏ TÆÛ BÀÒNG PHÆÅNG PHAÏP ÂÃÚM

Näüi dung cuía phæång phaïp naìy laì âãúm säú pháön tæí coï khoïa nhoí hån hay bàòng khoïa cuía

pháön tæí a[i]. Nãúu coï j pháön tæí coï khoïa nhoí hån khoïa cuía pháön tæí a[i] thç pháön tæí a[i] seî coï vë
trê thæï j+1 trong daîy âaî coï thæï tæû.

Trong giaíi thuáût ta duìng maíng count, våïi count[i] cho biãút säú pháön tæí coï khoïa nhoí hån

khoïa cuía pháön tæí a[i]. Nhæ váûy count[i]+1 laì vë trê cuía pháön tæí a[i] trong daîy âaî coï thæï tæû.

Âãø biãút âæåüc säú caïc pháön tæí coï khoïa nhoí hån khoïa cuía pháön tæí a[i], vãö nguyãn tàõc ta

phaíi so saïnh khoïa cuía pháön tæí a[i] våïi khoïa cuía táút caí caïc pháön tæí coìn laûi trong danh saïch.
Nhæng âãø traïnh sæû làûp laûi so saïnh nhæ (giæîa a[1] våïi a[8]) vaì (giæîa a[8] våïi a[1]) ta thiãút kãú
hai voìng làûp läöng nhau:

For i := 2 To n do

(* Cho i chaûy tæì 2 âãún n *)

For j := 1 To i-1 do (* So saïnh a[i] våïi caïc pháön tæí âæïng træåïc noï räöi tàng biãún âãúm *)

Thuí tuûc sàõp xãúp âáöy âuí:

Procudure Counting_Sort;

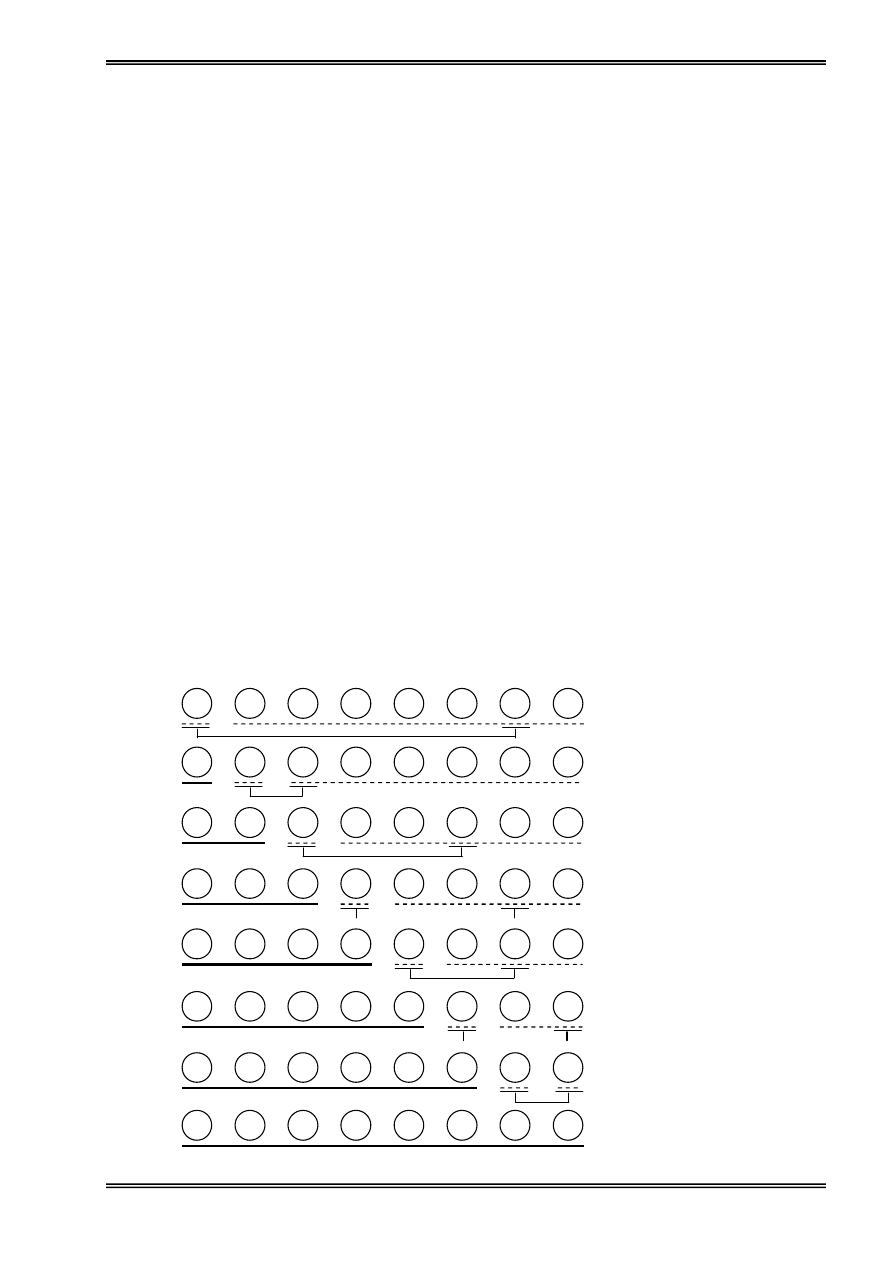
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 35

Var count : Array [1..n] of Integer; s : Array [1..n] of Item;
Var i, j : Integer;
Begin

For i := 1 To n do count[i] := 0; (* Khåíi taûo maíng âãúm *)
For i := 2 To n do
Begin

For j := 1 To i-1 do (* Làûp âãø kiãøm tra caïc pháön tæí âæïng træåïc i *)
Begin

If a[i].key < a[j].key Then count[j] := count[j] + 1 (* Thãm mäüt pháön tæí < a[j] *)
Else count[i] := count[i] + 1; (* Thãm mäüt pháön tæí nhoí hån a[i] *)

End;

End;
(* Chuyãøn caïc pháön tæí vaìo âuïng vë trê cuía noï trong maíng taûm thåìi s *)
For i := 1 To n do s[count[i]+1] := a[i];
For i := 1 To n do a[i] := s[i]; (* Chuyãøn caïc pháön tæí tæì s vaìo maíng a *)

End;

II. SÀÕP THÆÏ TÆÛ BÀÒNG PHÆÅNG PHAÏP CHOÜN LÆÛA

Näüi dung cuía phæång phaïp naìy laì åí bæåïc thæï i (i = 1, 2, ..., n-1) ta choün pháön tæí nhoí nháút

trong daîy a[i+1]...a[n] räöi âäùi chäù pháön tæí naìy våïi pháön tæí a[i] nãúu noï nhoí hån a[i]. Sau n-1
bæåïc daîy a[1]...a[n] seî coï thæï tæû. Chuï yï ràòng våïi giaíi thuáût trãn, taûi bæåïc thæï i thç i-1 pháön tæí
âáöu tiãn âaî coï thæï tæû.

Vê duû: Âãø minh hoüa giaíi thuáût, trong hçnh veî sau ta quy æåïc: âæåìng gaûch liãön âáûm laì caïc

pháön âaî coï thæï tæû; caïc âæåìng neït âæït daìi laì caïc pháön tæí âang xeït âãø tçm giaï trë nhoí nháút trong
âoï, âæåìng näúi biãøu hiãûn sæû hoaïn âäøi giaï trë cuía hai pháön tæí cho nhau:

Max(a[2],..,a[8]) = 06<44

Max(a[3],..,a[8]) =12<55

Max(a[4],..,a[8]) =18<55

Max(a[5],..,a[8]) =44>42

Max(a[6],..,a[8]) =44<94

Max(a[7],..,a[8]) =67>55

Max(a[8],..,a[8]) =67<94

Daîy âaî coï thæï tæû !

Hçnh 25: Minh hoüa sàõp thæï tæû bàòng phæång phaïp choün læûa

i=1

i=2

i=3

i=4

i=5

i=6

i=7

i=8

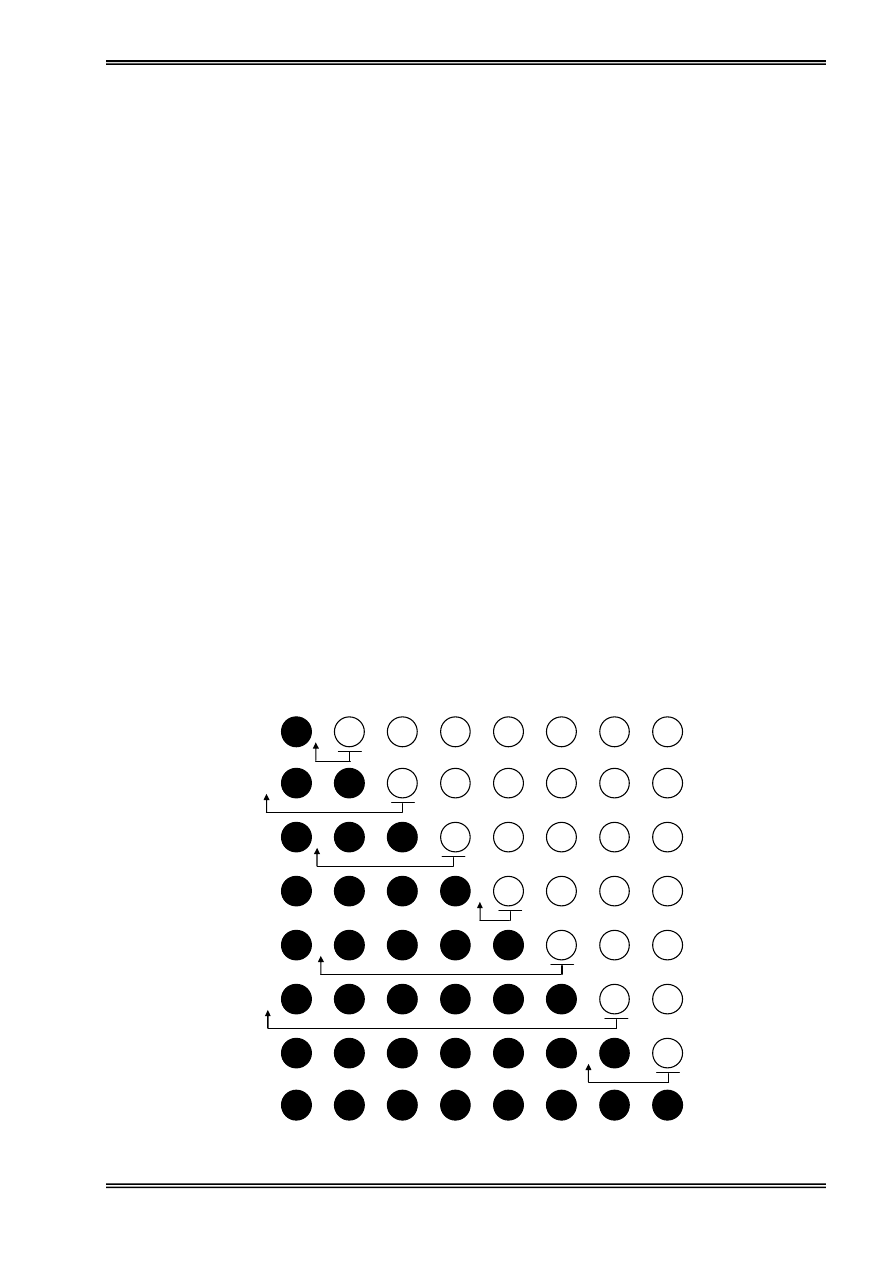
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 36

Procedure Selection_Sort;
Var i, j, k, min : Integer;
Begin

For i := 1 To n-1 do
Begin

(* Choün a[k] coï khoïa nhoí nháút trong daîy a[i]..a[n] *)
min := a[i].key; k := i;

(* min vaì k chæïa giaï trë min vaì chè säú cuía pháön tæí naìy *)

For j := i+1 To n do

(* Làûp âãø tçm pháön tæí låïn nháút *)

If a[j].key < min Then
Begin

min := a[j].key; k := j; (* Thay âäøi min vaì ghi nháûn vë trê *)

End;

If min < a[i].key Then

(* Chè hoaïn âäøi khi min < a[i].key *)

Begin

x := a[k]; a[k] := a[i]; a[i] := x; (* hoaïn âäøi giaï trë giæîa a[k] vaì a[i] thäng qua x *)

End;

III. SÀÕP XÃÚP BÀÒNG PHÆÅNG PHAÏP XEN VAÌO (INSERTION)

III.1. Phæång phaïp xen vaìo træûc tiãúp

Näüi dung cuía phæång phaïp naìy laì giaí sæí ta coï daîy a[1] ... a[i-1] âaî coï thæï tæû, ta phaíi xaïc

âënh vë trê thêch håüp cuía pháön tæí a[i] trong daîy a[1] ... a[i-1] bàòng phæång phaïp tçm kiãúm
tuáön tæû tæì a[i-1] tråí vãö a[1] âãø tçm ra vë trê thêch håüp cuía a[i]. Ta xen a[i] vaìo vë trê naìy âãø
âæåüc daîy a[i] ... a[i] coï thæï tæû. Ta làûp laûi thao taïc trãn våïi i = 2, 3, ..., n.

Vê duû: Ta cáön sàõp thæï tæû daîy: 44, 55, 12, 42, 94, 18, 06, 67

i =1

i =2

i =3

i =4

i =5

i =6

i =7

i =8

Hçnh 26: Minh hoüa giaíi thuáût sàõp thæï tæû bàòng phæång phaïp xen vaìo træûc tiãúp.

(Caïc pháön tæí maìu xaïm laì caïc pháön âaî coï thæï tæû)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 37

Procedure Selection_Sort;
Var i, j : Integer; x : Item;
Begin

For i := 2 To n Do
Begin

x := a[i]; j := i - 1;
a[0] := x; (* Pháön tæí cáöm canh *)
While (x.key < a[j].key) Do
Begin

a[j+1] := a[j]; (* Luìi caïc pháön tæí ra sau mäüt vë trê *)
j := j - 1;

(* Giaím j âãø làûp tiãúp *)

End;
a[j+1] := x;

End;

III.2. Phæång phaïp xen vaìo nhë phán

Näüi dung cuía phæång phaïp naìy cuîng tæång tæû nhæ phæång phaïp xen vaìo træûc tiãúp. Trong

phæång phaïp xen vaìo træûc tiãúp, ta xaïc âënh vë trê thêch håüp cuía a[i] trong daîy a[1]...a[i-1]
bàòng giaíi thuáût tçm kiãúm tuáön tæû thç trong phæång phaïp xen vaìo nhë phán ta duìng giaíi thuáût
tçm kiãúm nhë phán: chia âäi daîy a[1]...a[i-1] âãø tçm ra vë trê thêch håüp cuía a[i].

Procedure Selection_Sort;
Var x : Item; i, j, k, m, w : Integer;
Begin

For i := 2 To n Do
Begin

x := a[i]; (* Chæïa taûm giaï trë *)
k := 1; m := i – 1; (* Chè säú âáöu vaì cuäúi âãø tçm kiãúm nhë phán *)
While k <= m Do (* Liãn tiãúp chia âäi daîy *)
Begin

w := (k + m) Div 2; (* Láúy pháön tæí åí giæîa *)
If x.key < a[w].key Then m := w – 1 (* Thay âäøi chè säú âáöu vaì cuäúi *)
Else k := w + 1;

End;
(* Xen a[i] vaìo daîy a[i]...a[i-1] *)
For j := i – 1 Downto k Do a[j+1] := a[j]; (* Däön caïc giaï trë ra sau âãø xen x vaìo *)
a[k] := x;

End;

IV. SÀÕP THÆÏ TÆÛ BÀÒNG PHÆÅNG PHAÏP ÂÄØI CHÄÙ

IV.1. Phæång phaïp näøi boüt (bubbleSort)

Näüi dung cuía phæång phaïp naìy laì duyãût daîy a[1]...a[n]: nãúu a[i].key > a[i+1].key (i = 1,

2, ..., n-1) thç ta âäøi chäù pháön tæí a[i] våïi pháön tæí a[i+1]. Làûp laûi quaï trçnh duyãût daîy naìy cho
âãún khi khäng xaíy ra viãûc âäøi chäù giæîa hai pháön tæí.

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 38

Våïi phæång phaïp naìy caïc pháön tæí “nheû” cuía daîy láön læåüt âæåüc näøi lãn trãn khi so saïnh

våïi giaï trë cuía pháön tæí âæïng ngay trãn noï, cho âãún khi pháön tæí âæïng ngay trãn noï coï giaï trë
nhoí hån.

Vê duû: Ta cáön sàõp thæï tæû daîy 44, 55, 12, 42, 94, 18, 06, 76

Thuí tuûc sàõp thæï tæû theo phæång phaïp Näøi boüt âáöy âuí:

Procedure Bubble_Sort;
Var i, j : Integer; x : Item;
Begin

For i := 2 To n Do
Begin

For j := n Downto i Do

If a[j-1].key > a[j].key Then
Begin

x := a[j-1]; a[j-1] := a[j]; a[j] := x; (* Hoaïn âäøi giaï trë cuía a[j]-1 vaì a[j] *)

End;

Theo giaíi thuáût trãn, khi khäng xaíy ra sæû âäøi chäù giæîa hai pháön tæí (do daîy âaî coï thæï tæû)

thç giaíi thuáût váùn âæåüc tiãúp tuûc nhæ caïc Bæåïc 5, 6, 7, 8, 9. Âãø caíi tiãún ta duìng mäüt cåì hiãûu âãø
ghi nháûn thåìi âiãøm xaíy ra træåìng håüp naìy. Giaíi thuáût nhæ sau:

Procedure Bubble_Sort;
Var i : Integer; x : Item; flag : Boolean;
Begin

flag := False;
While flag Do
Begin

flag := False;
For i := 1 To n - 1 Do

If a[i].key > a[i+1].key Then

i =2

i =3

i =4

i =5

i =6

i =7

i =8

i =9

Hçnh 27: Minh hoüa sàõp thæï tæû bàòng phæång phaïp näøi boüt (BubbleSort)

(Dáúu muîi tãn thãø hiãûn caïc pháön tæí hoaïn âäøi giaï trë cho nhau)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 39

Begin

x := a[i]; a[i] := a[i+1]; a[i+1] := x; (* Hoaïn âäøi giaï trë *)
flag := True;

End;

IV.2. Phæång phaïp ShakerSort

Phæång phaïp Näøi boüt (BubbleSort) coï thãø âæåüc tiãúp tuûc caíi tiãún. Ta khäng chè ghi nhåï coï

mäüt sæû âäøi chäù giæîa hai pháön tæí (duìng cåì hiãûu) maì coìn ghi nhåï vë trê k cuía láön âäøi chäù cuäúi
cuìng, båíi vç caïc pháön tæí coï chè säú låïn hån k âãöu âaî coï thæï tæû, nãn láön duyãût thæï i seî dæìng khi
âãún chè säú k maì khäng cáön âãún chè säú i. Ngoaìi ra ta coìn nháûn tháúy tênh khäng âäúi xæïng cuía
phæång phaïp: âäúi våïi caïc pháön tæí coï khoïa nhoí nàòm åí cuäúi daîy thç chè cáön mäüt láön duyãût
ngæåüc pháön tæí naìy seî åí ngay âuïng vë trê thæï tæû cuía noï, trong khi âoï âäúi våïi caïc pháön tæí coï
khoïa låïn hån nàòm åí âáöu daîy thç chè tiãún âi mäüt vë trê âuïng cuía noï qua mäüt láön duyãût.

Vê duû: Ta xeït daîy: 12, 18, 42, 44, 55, 67, 94, 06 seî âæåüc sàõp thæï tæû sau mäüt láön duyãût,

trong khi daîy: 94, 06, 12, 18, 42, 44, 55, 67 phaíi cáön âãún baíy láön duyãût måïi coï thæï tæû.

Phæång phaïp caíi tiãún naìy âæåüc goüi laì ShakerSort, giaíi thuáût nhæ sau:

Procedure ShakerSort;
Var j, k, q, r : Integer; x : Item;
Begin

q := 2; r := n; k := n;
Repeat

For j := r Downto q Do

If a[j-1].key > a[j].key Then
Begin (* Âoíi chäù a[j-1] våïi a[j] *)

x := a[j-1]; a[j-1] := a[j]; a[j] := x; (* Hoaïn âäøi giaï trë hai pháön tæí *)
k := j; (* Ghi nháûn laûi vë trê naìy *)

End;

q := k + 1;
For j := q To r Do

If a[j-1].key > a[j].key Then
Begin (* Âoíi chäù a[j-1] våïi a[j] *)

x := a[j-1]; a[j-1] := a[j]; a[j] := x; (* Hoaïn âäøi giaï trë hai pháön tæí *)
k := j; (* Ghi nháûn laûi vë trê naìy *)

End;

r := k - 1;

Until q>r ; (* Làûp laûi cho âãún khi q>r *)

End;

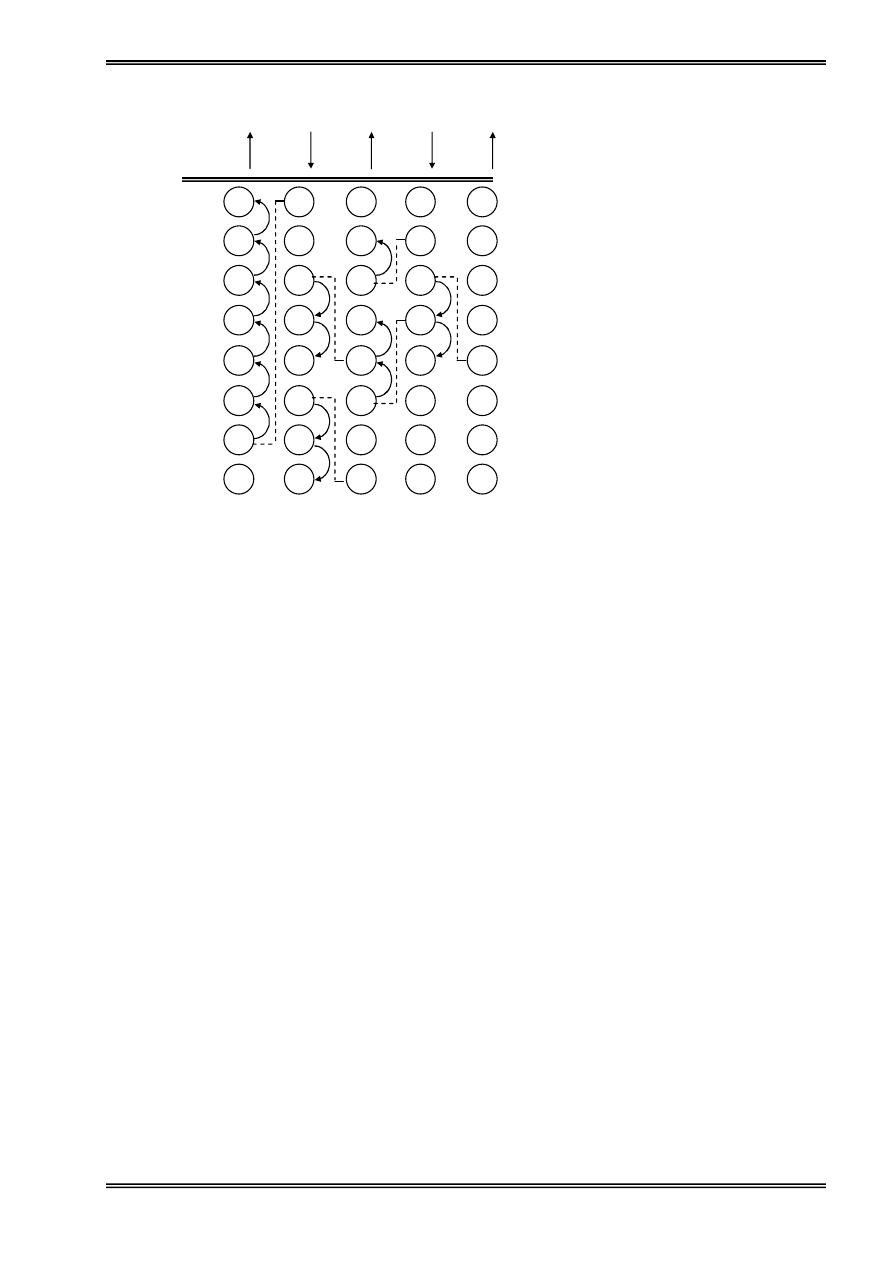
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 40

Vê duû: Ta cáön sàõp thæï tæû daîy: 44, 55, 12, 42, 94, 18, 06, 67

IV.3. Phæång phaïp Phán hoaûch (quickSort)

Näüi dung cuía phæång phaïp naìy laì ta choün ngáùu nhiãn mäüt pháön tæí x cuía daîy, x âæåüc goüi

laì pháön tæí biãn. Ta phán hoaûch daîy naìy thaình ba daîy con liãn tiãúp nhau:

- Daîy con thæï nháút gäöm caïc pháön tæí coï khoïa nhoí hån khoïa cuía x.
- Daîy con thæï hai gäöm caïc pháön tæí coï khoïa bàòng khoïa cuía x.
- Daîy con thæï ba gäöm caïc pháön tæí coï khoïa låïn hån khoïa cuía x.
Sau âoï ta tiãúp tuûc aïp duûng giaíi thuáût phán hoaûch naìy cho daîy con thæï nháút vaì daîy con

thæï ba nãúu caïc daîy con naìy coï nhiãöu hån mäüt pháön tæí. Giaíi thuáût phán hoaûch mäüt daîy gäöm n
pháön tæí nhæ sau:

i := 1; j := n; “Ban âáöu cho i vaì j troí tåïi âáöu vaì cuäúi daîy”
“Choün tuìy yï pháön tæí x thuäüc daîy”
Repeat

While a[i].key < x.key Do i := i + 1; “Âi qua caïc pháön tæí nhoí hån x bãn traïi”
While a[j].key > x.key Do j := j - 1; “Âi qua caïc pháön tæí låïn hån x bãn phaíi”
If i <= j Then “Kiãøm tra âiãöu kiãûn âãø hoaïn âäøi giaï trë”
Begin

y := a[i]; a[i] := a[j]; a[j] := y;
i := i + 1; j := j - 1;

End;

Until i>j; “Cho âãún khi daîy âæåüc chia laìm 3 pháön”
Làûp laûi caïc thao taïc trãn cho pháön 1 vaì pháön 3.

Hçnh 28:

Minh hoüa sàõp thæï tæû bàòng

phæång phaïp ShakerSort. (Dáúu

muîi tãn thãø hiãûn caïc pháön tæí

hoaïn âäøi giaï trë cho nhau).

q =

r =

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 41

Vê duû: Ta cáön sàõp thæï tæû daîy 44, 55, 12, 42, 94, 18, 06, 67. Choün pháön tæí giæîa laì 42

Ta tháúy giaíi thuáût naìy coï mäüt láön âäøi chäù khäng cáön thiãút, âoï laì khi i=j (phaït biãøu

If i=j

Then ...

), nhæng nãúu ta âäøi laûi thaình

If i<j Then ...

thç khi âoï phaït biãøu

i:=i+1

vaì

j:=j+1

seî

khäng âæåüc thæûc hiãûn trong træåìng håüp i=j vaì âiãöu naìy seî dáùn âãún træåìng håüp âäøi chäù sai
cho láön doì tçm kãú tiãúp.

Vê duû: Xeït daîy cáön sàõp thæï tæû laì: 1, 1, 1, 2, 1, 1, 1 vaì choün x laì 2. Bæåïc doì tçm vaì âäøi chäù

láön âáöu tiãn seî cho daîy: 1, 1, 1, 1, 1, 1, 2 våïi i=5 vaì j=6. Trong láön doì tçm kãú tiãúp thç i=7,
j=6. Nhæ váûy nãúu khäng coï âiãöu kiãûn i<=j thç gáy ra viãûc âäøi chäù sai láöm giæîa a[6] vaì a[7],
keït quaí laì daîy: 1, 1, 1, 1, 1, 2, 1.

Ta coï giaíi thuáût QuickSort sæí duûng âãû quy vaì chæång trçnh con läöng nhau:

Procedure QuickSort;

Procedure Sort (q, r : Integer); (* Sort nàòm trong thuí tuûc QuickSort *)
Var i, j : Integer; x, y : Item;
Begin (* Bàõt âáöu Sort *)

i := q; j := r;

(* Chè tåïi âáöu vaì cuäúi daîy cáön sàõp thæï tæû *)

x := a[(q+r) Div 2]; (* Choün pháön tæí åí giæîa *)
Repeat

While a[i].key < x.key Do i := i+1; (* Boí qua caïc pháön tæí nhoí hån x âáöu daîy *)
While a[j].key > x.key Do j := j-1; (* Boí qua caïc pháön tæí låïn hån x cuäúi daîy *)
If i <= j Then
Begin

y := a[i]; a[i] := a[j]; a[j] := y; (* Hoaïn âäøi giaï trë *)
i := i+1; j := j-1;

End;

Until i>j;
If q<r Then Sort(q, j); (* Goüi âãû quy cho daîy con thæï nháút *)
If i<r Then Sort(i, r); (* Goüi âãû quy cho daîy con thæï ba *)

End; (* Kãút thuïc Sort *)

Begin (* Bàõt âáöu QuickSort *)

Sort(1, n);

End; (* Kãút thuïc QuickSort *)

44 55 12

18 06 67

i = 1

j = 8

x = 4

44 55 12

18 06 67

x = 4

06 55 12

18 44 67

j=j-1

i=i+1

j=j-1

06 18 12

55 44 67

j=j-1

i=i+1

06 18 12

55 44 67

i=j=x

à Do i > j nãn giaíi thuáût keït thuïc. Daîy âæåüc chia laìm ba pháön

Hçnh 29: Minh hoüa sàõp thæï tæû daîy bàòng phæång phaïp QuickSort.

06 18 12

55 44 67

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 42

V. SÀÕP THÆÏ TÆÛ NGOAÛI (SÀÕP THÆÏ TÆÛ TÁÛP TIN)

Trong pháön trãn, ta âaî xeït caïc phæång phaïp sàõp thæï tæû näüi. Caïc phæång phaïp naìy âoìi hoíi

toaìn bäü dæî liãûu cáön sàõp thæï tæû phaíi âæåüc âæa vaìo bäü nhåï chênh, nãn caïc phæång phaïp naìy chè
âæåüc aïp duûng cho viãûc sàõp thæï tæû daîy (maíng) båíi vç dæî liãûu cuía chuïng khäng nhiãöu làõm. Tuy
nhiãn ta khäng thãø aïp duûng phæång phaïp naìy cho viãûc sàõp thæï tæû táûp tin båíi vç thäng thæåìng
táûp tin chæïa nhiãöu máùu tin (Record) vaì mäùi máùu tin coï chiãöu daìi tæång âäúi låïn vaì do âoï ta
khäng thãø naûp toaìn bäü táûp tin vaìo bäü nhåï chênh âãø sàõp thæï tæû. Vç váûy ta phaíi coï nhæîng
phæång phaïp thêch håüp cho viãûc sàõp thæï tæû táûp tin.

Phæång phaïp thæåìng duìng laì phán chia táûp tin cáön sàõp thæï tæû thaình caïc táûp tin nhoí hån

coï säú læåüng máùu tin maì bäü nhåï coï khaí nàng chæïa chuïng. Ta naûp chuïng vaìo bäü nhåï chênh räöi
duìng phæång phaïp sàõp thæï tæû daîy âãø sàõp xãúp chuïng laûi thaình caïc run, sau âoï träün caïc run
naìy laûi vaì âæa vaìo táûp tin. Cuäúi cuìng ta seî coï táûp tin âaî sàõp thæï tæû.

Nhæ váûy âãø sàõp thæï tæû mäüt táûp tin ta phaíi giaíi quyãút hai váún âãö sau:
- Taûo caïc run ban âáöu
- Träün caïc run laûi våïi nhau

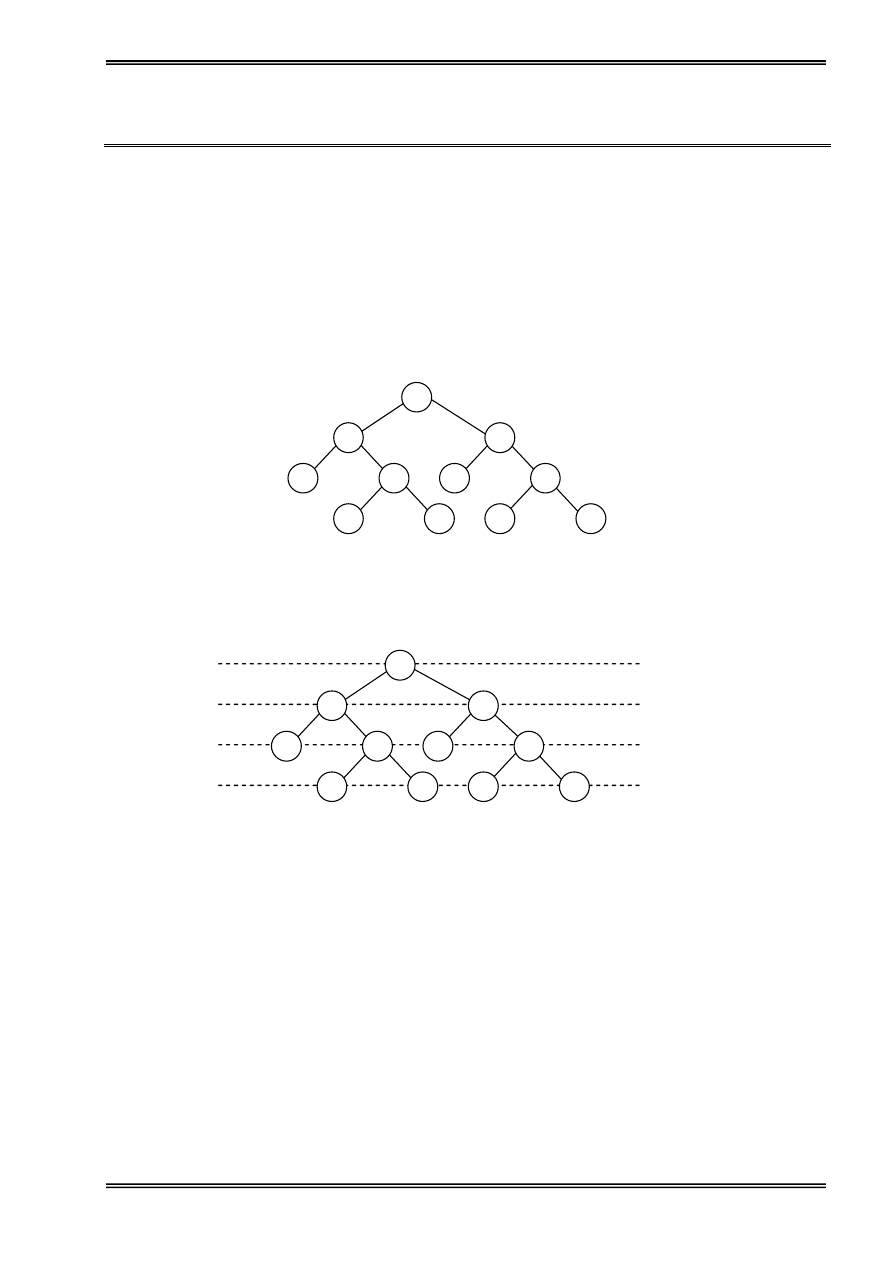
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 43

Cáy (Tree) laì mäüt cáúu truïc Dæî liãûu ráút quan troüng vaì âæåüc duìng ráút nhiãöu trong caïc giaíi

thuáût. Trong chæång naìy ta seî tçm hiãøu caïc khaïi niãûm cå baín vãö cáy, caïch biãøu diãùn cáy
trong maïy tênh, caïc pheïp toaïn quan troüng trãn cáy. Cuäúi chæång ta seî tçm hiãøu vãö cáy nhë
phán tçm kiãúm. Cáy cuîng coï nhiãöu æïng duûng trong âåìi säúng hàòng ngaìy, chàóng haûn täø chæïc
caïc quan hãû hoü haìng trong mäüt gia phaí, muûc luûc cuía mäüt quyãøn saïch, ...

Vê duû: Duìng cáy âãø biãøu diãùn biãøu thæïc

(a + b / c) * (d – e * f)

I. MÄÜT SÄÚ KHAÏI NIÃÛM

•

Cáy laì mäüt táûp håüp gäöm nhiãöu nuït (Node), trong âoï:

- Mäüt nuït âæåüc goüi laì nuït gäúc (Root)
- Caïc nuït coìn laûi âæåüc chia laìm m nhoïm (m>=0), mäùi nhoïm laì mäüt cáy vaì âæåüc goüi laì

cáy con (SubTree). Cáy khäng coï nuït naìo caí goüi laì cáy räùng (null tree).

‚

Báûc cuía nuït laì säú cáy con cuía nuït âoï, vê duû: B coï báûc laì 2, báûc cuía cáy laì báûc låïn nháút

cuía caïc nuït cuía cáy. Nãúu cáy coï báûc laì n thç ta goüi laì cáy n-phán. Hçnh 30 biãøu diãùn mäüt
cáy nhë phán.

Nuït laï (Leaf) hay nuït kãút thuïc laì nuït coï báûc bàòng 0, vê duû: C, E, F, J, K laì caïc nuït laï.

Nuït trung gian (interior node) laì nuït coï báûc khaïc 0 vaì khäng phaíi laì nuït gäúc, vê duû: B,
D, G, I laì caïc nuït trung gian.

„

Mæïc (Level) cuía nuït gäúc laì 1, mæïc cuía nuït khaïc gäúc bàòng mæïc cuía nuït gäúc cuía cáy con

nhoí nháút chæïa noï cäüng våïi 1. Chiãöu cao cuía cáy laì mæïc låïn nháút cuía caïc nuït laï.

Hçnh 30: ÆÏng duûng cuía cáy âãø biãøu diãùn biãøu thæïc

Hçnh 31: Caïc mæïc cuía Cáy

Mæïc 1

Mæïc 2

Mæïc 3

Mæïc 4

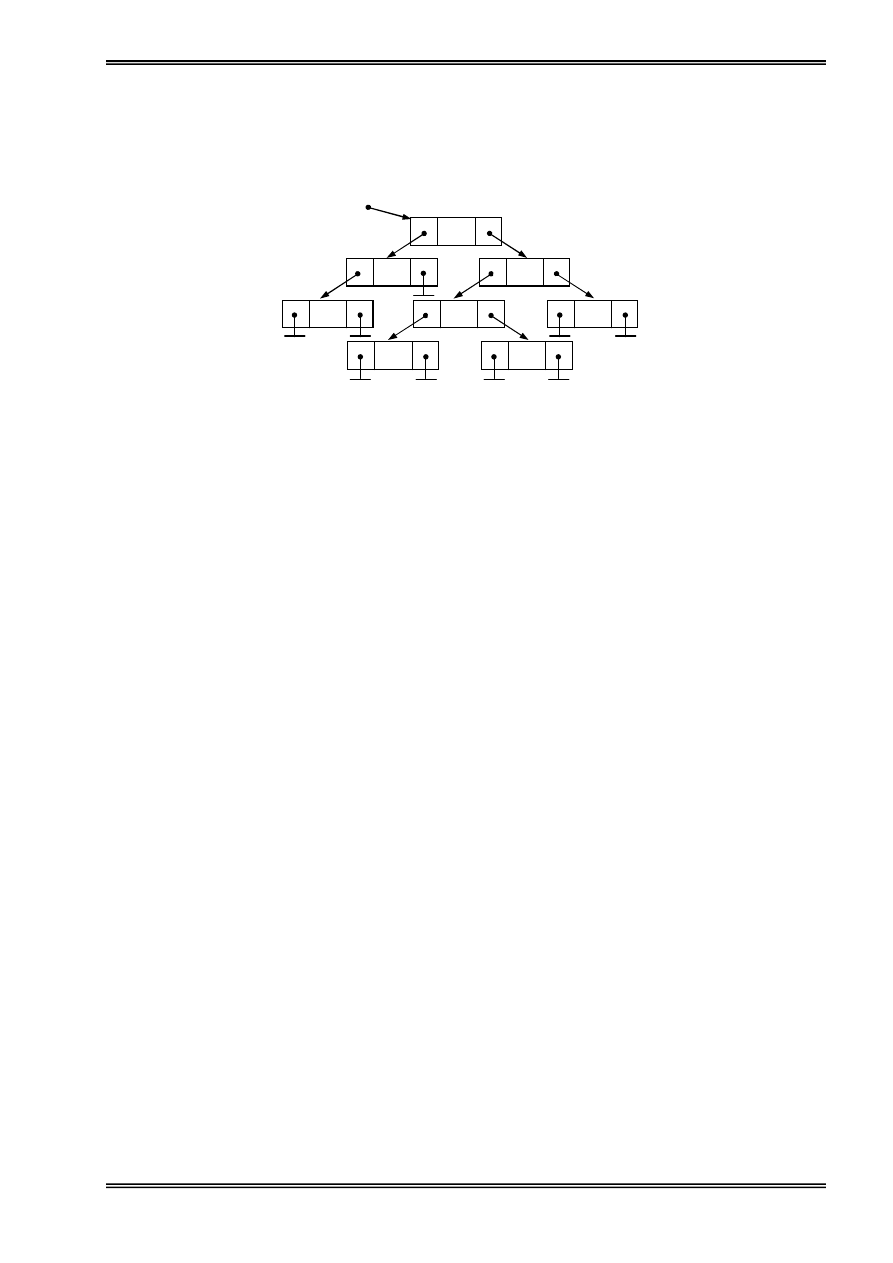
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 44

…

Nãúu nuït y laì nuït træåïc cuía nuït x vaì mæïc cuía nuït x bàòng mæïc cuía nuït y cäüng våïi 1 thç nuït

y âæåüc goüi laì nuït cha cuía nuït x vaì nuït x âæåüc goüi laì nuït con cuía nuït y.

II. CAÏCH CHÆÏA CÁY TRONG BÄÜ NHÅÏ MAÏY TÊNH

Ta coï thãø chæïa cáy trong bäü nhåï bàòng caïch sæí duûng danh saïch liãn kãút. Âãø biãøu diãùn cáy

nhë phán ta duìng danh saïch gäöm coï hai thaình pháön liãn kãút, mäüt thaình pháön chè âãún nuït gäúc
cuía cáy con bãn traïi (goüi laì Left), mäüt thaình pháön chè âãún nuït gäúc cuía cáy con bãn phaíi (goüi
laì Right). Trong træåìng håüp täøng quaït ta duìng danh saïch n-liãn kãút âãø chæïa cáy n-phán. Mäüt
cáy âæåüc âaûi diãûn båíi mäüt con troí chè âãún nuït gäúc cuía noï, thæåìng âàût laì Root.

Cáy nhë phán laì cáy cå baín âæåüc æïng duûng nhiãöu nháút nãn trong chæång naìy seî táûp trung

nghiãn cæïu caïc pheïp toaïn trãn cáy nhë phán.

Ta khai baïo:

Type PointTree = ^Node;
Node = Record

Info: Integer;

(* Chæïa thäng tin cuía nuït *)

Left, Right : PointTree; (* Hai thaình pháön liãn kãút *)

End;
Var Root : PointTree;

(* Con troí chè âãún pháön tæí gäúc cuía cáy *)

Nhæ váûy pheïp khåíi taûo cáy laì:

Procedure Initialize;
Begin

Root := Nil;

End;

III. CAÏC PHEÏP TOAÏN TRÃN CÁY NHË PHÁN

III.1. Caïc pheïp duyãût cáy nhë phán

Pheïp duyãût cáy laì láön læåüt âi qua caïc nuït cuía cáy, vaì mäùi nuït chè âæåüc duyãût mäüt láön. Coï

saïu pheïp duyãût cáy dæûa vaìo thæï tæû duyãût cuía caïc nuït bãn traïi (L), nuït gäúc (N), caïc nuït bãn
phaíi (R) laì:

Thæï tæû nuït gäúc æu tiãn træåïc: NLR, NRL.

Thæï tæû nuït gäúc åí giæîa: LNR, RNL.

Thæï tæû nuït gäúc cuäúi cuìng: LRN, RLN.

Root

Hçnh 32: Biãøu diãùn cáy nhë phán bàòng danh saïch liãn kãút.

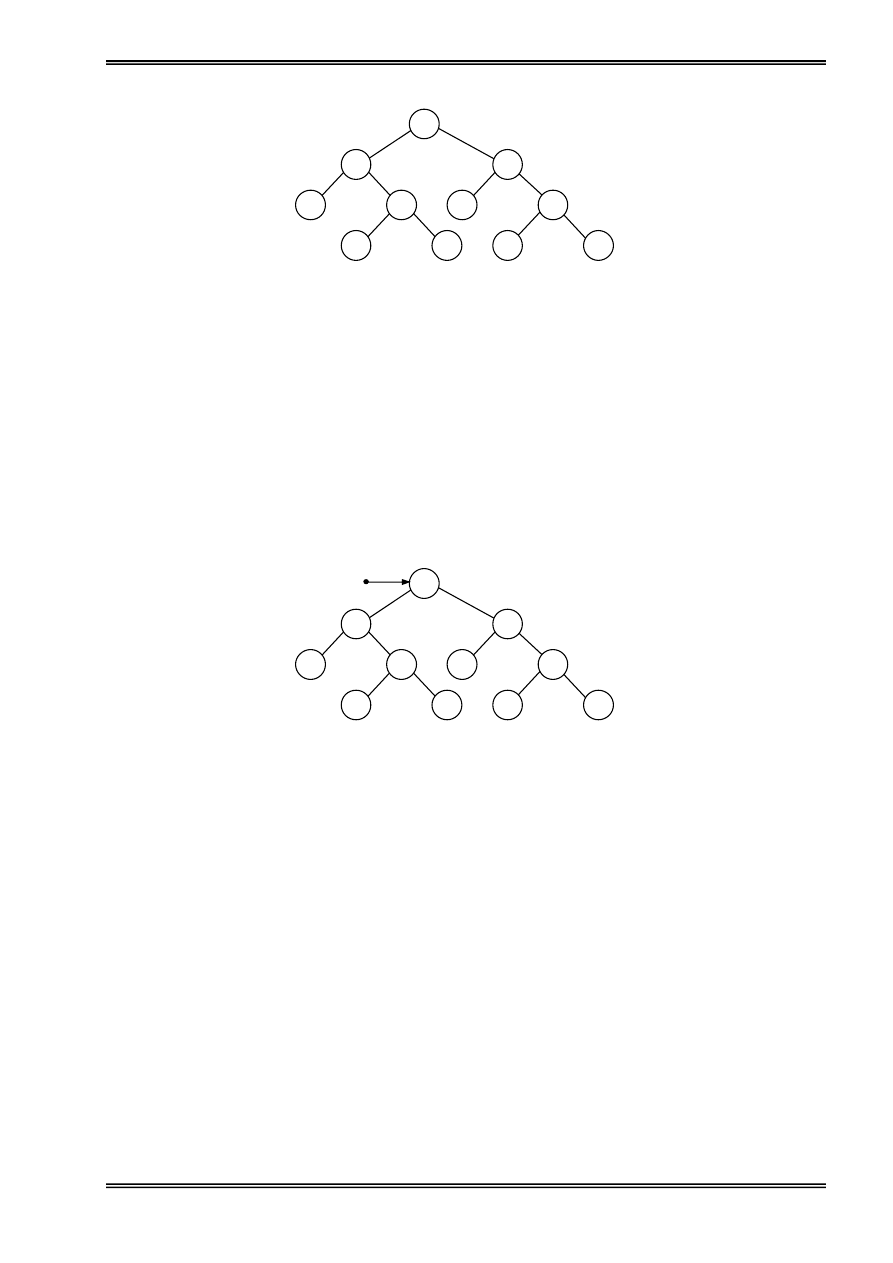
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 45

Vê duû: Duyãût cáy nhë phán sau âáy

Thæï tæû duyãût caïc nuït cuía 6 pheïp duyãût laì:
NLR : ABCDEFGHIJK

RLN

: KJIHGFEDCBA

LNR : CBEDFAHGJIK

RNL

: KIJGHAFDEBC

LRN : CEFDBHJKIGA

NRL

: AGIKJHBDFEC

Ta nháûn tháúy thæï tæû cuía NLR ngæåüc våïi RLN, LNR ngæåüc våïi RNL, LRN ngæåüc våïi

NRL. Do âoï trong chæång naìy ta chè xeït ba pheïp duyãût cå baín laì NLR (thæï tæû træåïc), LNR
(thæï tæû giæîa) vaì LRN (thæï tæû sau).

III.2. Duyãût cáy theo thæï tæû NLR (gäúc-traïi-phaíi)

a) Duìng giaíi thuáût âãû quy

Procedure Traverse_NLR (p : PointTree);
Begin

If p <> Nil Then
Begin

Write(p^.Info);

(* Xuáút giaï trë cuía nuït gäúc cuía cáy p *)

Traverse_NLR(p^.Left); (* Duyãût cáy con bãn traïi cuía p *)
Traverse_NLR(p^.Right); (* Duyãût cáy con bãn phaíi cuía p *)

End;

Trong chæång trçnh chênh ta goüi:

Traverse_NLR(Root);

b) Duìng Ngàn xãúp
Ta coï thãø duìng ngàn xãúp âãø duyãût cáy thay cho viãûc goüi âãû quy, khi âi theo nhaïnh traïi ta

phaíi læu giæî caïc nuït con bãn phaíi vaìo ngàn xãúp âãø sau naìy coï thãø tråí laûi caïc nuït naìy:

Procedure Traverse_NLR;
Var Stack : Array [1..100] of PointTree; (* Ngàn xãúp *)
p : PointTree; Cont : Boolean; Top : Integer; (* Top Chè âãún âènh ngàn xãúp *)

Hçnh 33: Minh hoüa caïc pheïp duyãût cáy

Root

Hçnh 34: Minh hoüa duyãût cáy theo thæï

NLR, kãút quaí: ABCDEFGHIJK

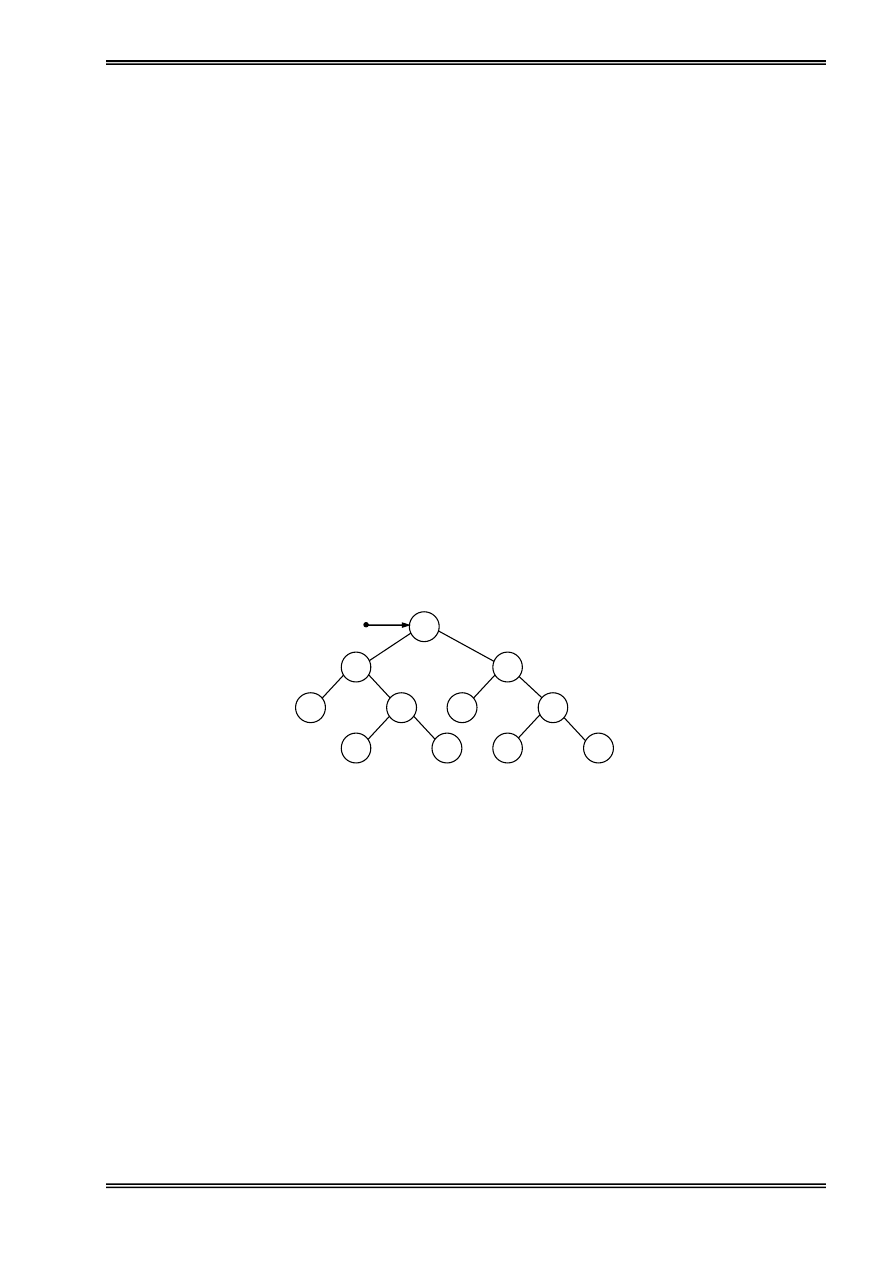
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 46

Begin

p := Root; Top := 0; cont := True; (* Khåíi taûo caïc giaï trë *)
While (p <> Nil) And Cont Do
Begin

Write(p^.Info); (* In giaï trë cuía nuït gäúc *)
If p^.Right <> Nil Then (* Nãúu p coï nuït bãn phaíi thç âæa noï vaìo ngàn xãúp *)
Begin

Top := Top + 1;

(* Tàng âènh ngàn xãúp *)

Stack[Top] := p^.Right; (* Âæa p^.Right vaìo ngàn xãúp *)

End;
If p^.Left <> Nil Then p := p^.Left (* Âi qua bãn traïi nãúu coï thãø *)
Else (* Nãúu khäng thç kiãøm tra ngàn xãúp *)

If Top = 0 Then Cont := False (* Nãúu ngàn xãúp räùng thç kãút thuïc *)
Else
Begin (* Nãúu khäng thç láúy pháön tæí åí âènh ngàn xãúp âãø xæí lyï *)

p := Stack[Top];
Top := Top -1;

End;

End; (* Cuía While *)

End;

III.3. Duyãût cáy theo thæï tæû LNR (traïi-gäúc-phaíi)

a) Duìng giaíi thuáût âãû quy

Procedure Traverse_LNR (p : PointTree);
Begin

If p <> Nil Then
Begin

Traverse_LNR(p^.Left); (* Duyãût cáy con bãn traïi cuía p *)
Write(p^.Info);

(* Xuáút giaï trë cuía nuït gäúc cuía cáy p *)

Traverse_LNR(p^.Right); (* Duyãût cáy con bãn phaíi cuía p *)

End;

Trong chæång trçnh chênh ta goüi:

Traverse_LNR(Root);

b) Duìng Ngàn xãúp
Do biãút nuït gäúc ta hoaìn toaìn coï thãø biãút âæåüc nuït con bãn phaíi, do váûy ta chè cáön læu giæî

nuït gäúc vaìo ngàn xãúp træåïc khi âi qua nuït con bãn traïi.

Procedure Traverse_LNR;

Root

Hçnh 35: Minh hoüa duyãût cáy theo thæï

LNR, kãút quaí: CBEDFAHGJIK

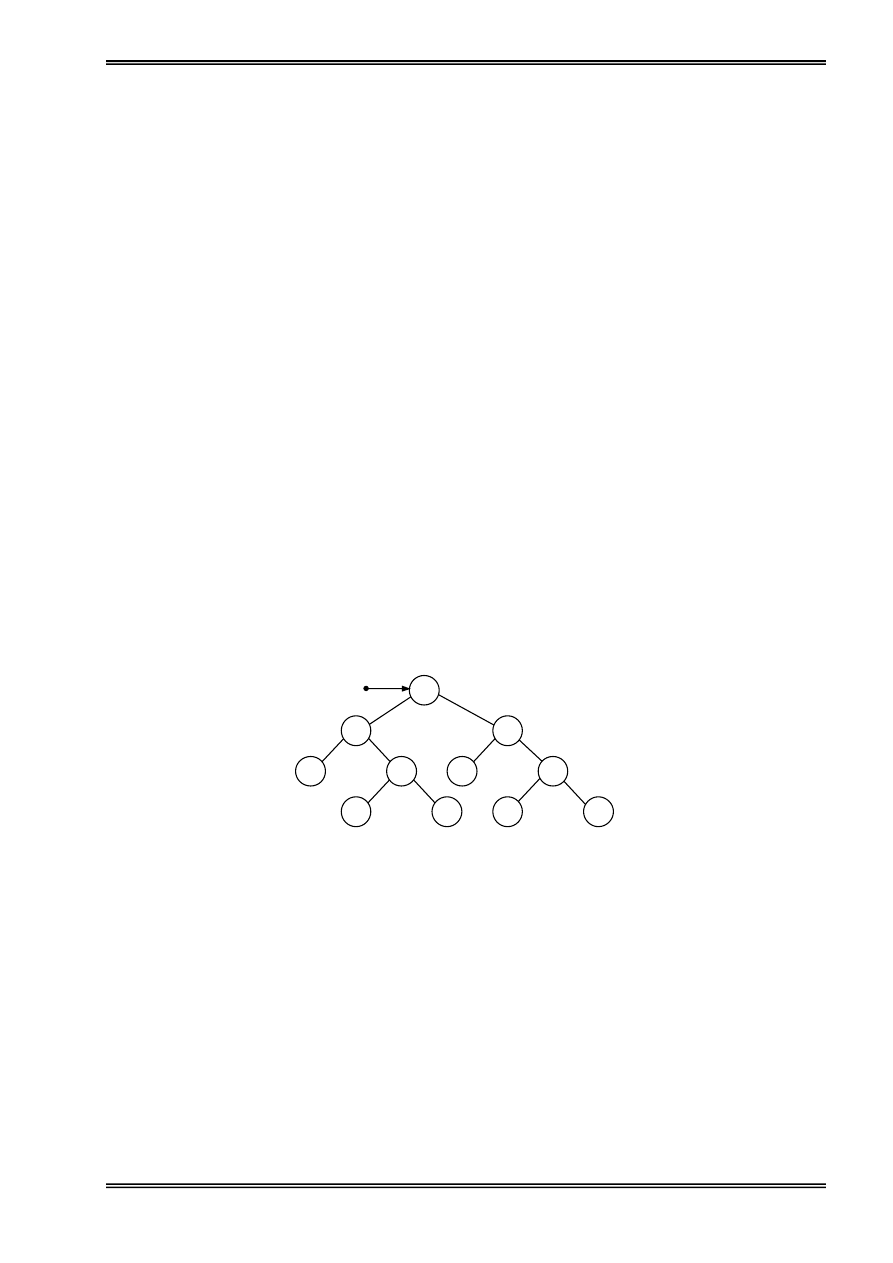
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 47

Var Stack : Array [1..100] of PointTree; (* Ngàn xãúp *)
p : PointTree; Cont : Boolean; Top : Integer; (* Top Chè âãún âènh ngàn xãúp *)
Begin

p := Root; Top := 0; (* Khåíi taûo caïc giaï trë *)
Repeat

While p <> Nil Do

(* Âáøy p vaìo ngàn xãúp vaì âi qua bãn traïi *)

Begin

Top := Top + 1;
Stack[Top] := p; (* Âáøy p vaìo ngàn xãúp *)
p := p^.Left;

(* Âi qua bãn traïi *)

End;
If Top <> 0 Then (* Kiãøm tra ngàn xãúp khi khäng thãø qua traïi âæåüc næîa *)
Begin

p := Stack[Top]; (* Láúy ra mäüt nuït gäúc tæì ngàn xãúp *)
Top := Top – 1;
Writeln(p^.Info); (* Hiãøn thë giaï trë giaï trë cuía p *)
p := p^.Right;

(* Âi qua nhaïnh bãn phaíi *)

Cont := True;

End
Else

Cont := False; (* Kãút thuïc nãúu ngàn xãúp räùng *)

Until Not Cont;

End;

III.4. Duyãût cáy theo thæï tæû LRN (traïi-phaíi-gäúc)

a) Duìng giaíi thuáût âãû quy

Procedure Traverse_LRN (p : PointTree);
Begin

If p <> Nil Then
Begin

Traverse_LNR(p^.Left); (* Duyãût cáy con bãn traïi cuía p *)
Traverse_LNR(p^.Right); (* Duyãût cáy con bãn phaíi cuía p *)
Write(p^.Info);

(* Xuáút giaï trë cuía nuït gäúc cuía cáy p *)

End;

Trong chæång trçnh chênh ta goüi:

Traverse_LRN(Root);

Root

Hçnh 36: Minh hoüa duyãût cáy theo thæï

LRN, kãút quaí: CEFDBHJKIGA

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 48

b) Duìng Ngàn xãúp
Duyãût cáy theo thæï tæû LRN tæång âäúi khoï hån hai pheïp duyãût âaî trçnh baìy åí trãn. Trong

pheïp duyãût naìy ta phaíi âæa caí nuït gäúc vaì nuït con bãn phaíi vaìo ngàn xãúp. Nuït gäúc âæåüc âæa
vaìo træåïc vaì nuït con bãn phaíi âæåüc âæa vaìo sau (âãø âæåüc láúy ra træåïc). Âãø phán biãût giæîa nuït
gäúc vaì nuït con bãn phaíi trong ngàn xãúp thç mäüt pháön tæí cuía ngàn xãúp phaíi coï hai thaình
pháön: thaình pháön chæïa âëa chè cuía nuït vaì thaình pháön coï kiãøu Boolean âãø phán biãût nuït gäúc
(False) vaì nuït con bãn phaíi (True).

Procedure Traverse_LRN;
Type Element = Record

addr: PointTree; (* Chæïa âëa chè cuía nuït *)
typ: Boolean;

(* =False: nuït gäúc ; =True :nuït con bãn phaíi *)

End;
Var ps : PointTree; Stack : Array[1..100] of Element; (* Ngàn xãúp *)
Top : Integer; (* Âènh cuía ngàn xãúp *)
Begin

sp := 0; p := Root; ps := True;
Stack[0].addr := Nil; (* Âæa Nil vaìo Stack âãø kãút thuïc giaíi thuáût *)
Repeat

While (p <> Nil) And ps Do
Begin

Top := Top + 1; (* Âæa nuït gäúc p vaìo ngàn xãúp *)
Stack[Top].addr := p;
Stack[Top].typ := False;
If p^.Right <> Nil Then (* Nãúu p coï nuït gäúc bãn phaíi *)
Begin

(* Âæa nuït con bãn phaíi cuía p vaìo ngàn xãúp *)
Top := Top + 1;
Stack[Top].addr := p^.Right;
Stack[Top].typ := True;

End;
p := p^.Left; (* Âi âãún nuït con bãn traïi cuía nuït p *)

End;
If p <> Nil Then Write(p^.Info);
P := Stack[Top].addr; (* Láúy nuït gäúc tæì ngàn xãúp *)
Ps := Stack[Top].typ;
Top := Top – 1;

Until p=Nil;

End;

III.5. Duyãût cáy theo mæïc

Ngoaìi caïc pheïp duyãût cáy âaî trçnh baìy åí trãn, cáy coìn coï thãø dæåüc duyãût theo mäüt caïch

khaïc nhæ sau: ta láön læåüt duyãût caïc nuït trãn cuìng mäüt mæïc tæì traïi qua phaíi, bàõt âáöu tæì mæïc
âáöu tiãn (mæïc 1) cho âãún mæïc cuäúi cuìng (mæïc låïn nháút).

Ta sæí duûng mäüt haìng âåüi seî chæïa caïc nuït seî âæåüc duyãût, giaíi thuáût duyãût cáy theo mæïc

nhæ sau:

“Âæa nuït gäúc vaìo haìng”

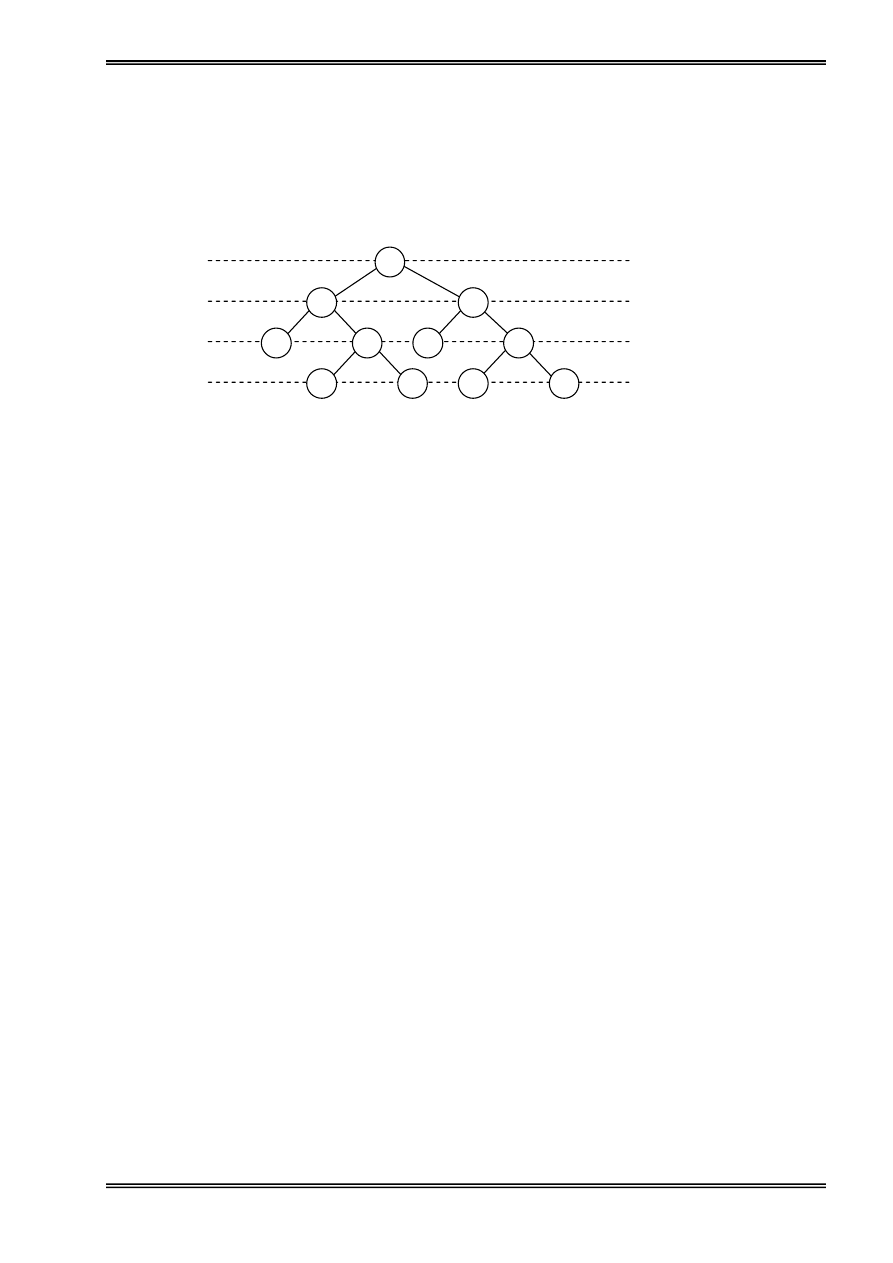
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 49

While haìng <> Räùng do
Begin

“Láúy mäüt nuït T ra khoíi haìng”
“Duyãût nuït T”
“Âæa caïc nuït con cuía T vaìo haìng nãúu coï”

End;

Vç säú nuït cuía cáy chæa biãút træåïc nãn ta täø chæïc haìng laì mäüt danh saïch liãn kãút maì mäùi

pháön tæí cuía haìng coï thaình pháön addr âãø chæïa âëa chè cuía nuït vaì thaình pháön Next âãø chè âãún
pháön tæí kãú tiãúp trong haìng. Ta khai baïo:

Type

Point = ^Node;

(* Kiãøu con troí chè âãún mäüt nuït *)

PointLst = ^Item;

(* Kiãøu con troí chè âãún mäüt pháön tæí trong haìng *)

Node = Record

(* Cáúu truïc mäùi nuït cuía cáy *)

Info : Integer;

(* Thaình pháön chæïa dæî liãûu *)

Left, Right : Point; (* Troí tåïi cáy con bãn traïi vaì bãn phaíi *)

End;
Item = Record

(* Cáúu truïc mäüt pháön tæí cuía haìng âåüi *)

Addr : Point;

(* Troí âãún mäüt nuït cuía cáy *)

Next : PointLst; (* Troí tåïi pháön tæí tiãúp theo trong haìng *)

End;

Giaíi thuáût âáöy âuí nhæ sau:

Procedure Traverse_Level;
Var Front, Rear, q : PointLst; (* Con troí chè tåïi Âáöu vaì Cuäúi cuía haìng âåüi *)

p : Point;
(* === Âënh nghéa caïc chæång trçnh con cuía Traverse_Level === *)
Procedure Init_Queue; (* Thuí tuûc khåíi taûo haìng âåüi *)
Begin

Front := Nil; Rear := Nil;

End;
Procedure Insert_Queue (r : Point); (* Thuí tuûc cheìn mäüt pháön tæí vaìo haìng âåüi *)
Begin

New(q); q^.addr := r; q^.Next := Nil;
If Rear <> Nil Then Rear^.Next := q;
Rear := q;
If Front = Nil Then Front := q;

End;
Procedure Delete_Queue (Var r : Point); (* Thuí tuûc láúy ra mäüt pháön tæí khoíi haìng âåüi *)

Hçnh 37: Minh hoüa duyãût cáy theo mæïc. Kãút quaí: ABGCDHIEFJK

Mæïc 1

Mæïc 2

Mæïc 3

Mæïc 4

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 50

Begin

r := Front.^addr; q := Front;
Front := Front^.Next;
If Front = Nil Then Rear := Nil;
Dispose(q); (* Giaíi phoïng vuìng nhåï *)

End;

Begin (* ===Bàõt âáöu Traverse_Level === *)

Init_Queue; (* Khåíi taûo haìng *)
If Root <> Nil Then Insert_Queue(Root); (* Âæa nuït gäúc vaìo haìng *)
While Front <> Nil do (* Thæûc hiãûn cho âãún khi haìng räùng *)
Begin

Delete_Queue(p); (* Láúy nuït p ra khoíi haìng *)
Write(p^.Info);

(* Hiãøn thë thäng tin cuía nuït p *)

If p^.Left <> Nil Then Insert_Queue(p^.Left);

(* Âáøy nuït bãn traïi cuía p vaìo haìng *)

If p^.Right <> Nil Then Insert_Queue(p^.Right); (* Âáøy nuït bãn phaíi cuía p vaìo haìng *)

End;

End; (* Kãút thuïc Traverse_Level *)

IV. CÁY NHË PHÁN TÇM KIÃÚM

IV.1. Âàûc âiãøm cuía cáy nhë phán tçm kiãúm

Cáy nhë phán tçm kiãúm (binary search tree) laì cáy nhë pháön maì taûi mäùi nuït báút kyì cuía

cáy thç khoïa cuía nuït naìy låïn hån khoïa caïc nuït cuía cáy con bãn traïi vaì nhoí hån khoïa caïc nuït
cuía cáy con bãn phaíi noï.

Nhæ váûy, theo tênh cháút trãn thç khi duyãût cáy nhë phán tçm kiãúm theo thæï tæû LNR ta seî

âæåüc mäüt daîy coï thæï tæû tàng dáön.

Vê duû: Ta coï cáy nhë phán tçm kiãúm:

Khi duyãût cáy theo thæï tæû LNR ta âæåüc daîy coï thæï tæû: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12,

13, 14, 15, 16, 17, 18.

Dæî liãûu cuía cáy nhë phán tçm kiãúm âæåüc khai baïo nhæ sau:

Type PointTree = ^Node;
Node = Record

Key : Integer;

(* Khoïa cuía nuït *)

Left, Right : PointTree; (* Chè âãún thaình pháön bãn traïi vaì bãn phaíi *)

End;

Root

Hçnh 38: Minh hoüa duyãût cáy nhë phán tçm kiãúm

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 51

IV.2. Tçm kiãúm

Âãø tçm kiãúm mäüt nuït coï näüi dung laì x trãn cáy nhë phán tçm kiãúm ta aïp duûng giaíi thuáût

sau âáy:

Bæåïc 1: Bàõt âáöu tæì nuït p laì nuït gäúc
Bæåïc 2: Taûi nuït p naìy ta xeït:
- Nãúu p^.key = x thç nuït cáön tçm laì nuït p, giaíi thuáût kãút thuïc thaình cäng.
- Nãúu p^.key > x thç ta âãún nuït con bãn traïi cuía p, goüi laì nuït q.
- Nãúu p^.key < x thç âi âãún nuït con bãn phaíi cuía p, goüi laì nuït q.
Bæåïc 3: Nãúu q=Nil thç giaíi thuáût kãút thuïc khäng thaình cäng (khäng tçm tháúy), ngæåüc laûi

thç gaïn p := q vaì làûp laûi Bæåïc 2.

Haìm Search traí vãö âëa chè cuía nuït tçm tháúy hoàûc traí vãö giaï trë Nil nãúu khäng tçm tháúy:

Function Search(x: Integer): PointTree;
Var found : Boolean; p : PointTree;
Begin

found := False;
p := Root; (* Cho p chè vaìo gäúc cuía cáy *)
While (p <> Nil) And (Not found) Do
Begin

If p^.key = x Then found := True (* Tçm tháúy *)
Else
If p^.key > x Then p := p^.Left (* Âi qua nhaïnh bãn traïi *)
Else p := p^.Right; (* Âi qua nhaïnh bãn phaíi *)

End;
Search := p;

End;

IV.3. Tçm kiãúm vaì thãm vaìo cáy

Bàõt âáöu tæì cáy räùng, ta láön læåüt xeït tæìng pháön tæí cuía mäüt daîy (hoàûc maíng). Nãúu tçm tháúy

pháön tæí naìy trong cáy thç tàng säú láön xuáút hiãûn lãn 1, nãúu khäng tçm tháúy thç ta thãm pháön tæí
naìy vaìo trong cáy vaì cho säú láön xuáút hiãûn bàòng 1. Sau âoï ta xeït âãún pháön tæí kãú tiãúp cuía daîy.
Ta khai baïo cáúu truïc cuía mäüt nuït nhæ sau:

Type PointTree = ^Node;
Node = Record

Key : Integer;

(* Khoïa cuía nuït *)

Count : Integer;

(* Âãúm säú láön xuáút hiãûn *)

Left, Right : PointTree; (* Chè âãún thaình pháön bãn traïi vaì bãn phaíi *)

End;

a) Duìng giaíi thuáût âãû quy
Nãúu ta thãm nuït måïi coï âëa chè laì p vaì coï khoïa laì x vaìo bãn traïi (hoàûc phaíi) cuía nuït N

thç liãn kãút Left (hoàûc liãn kãút Right) cuía nuït N phaíi chè vaìo p. Do âoï tham säú p trong giaíi
thuáût âãû quy phaíi laì tham biãún.

Procedure Tree_Insert(x : Integer; Var p : PointTree);
Begin

If p = Nil Then

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 52

Begin

New(p); (* x chæa coï trong cáy, thãm x vaìo cáy *)
With p^ Do
Begin

Key := x; Count := 1; (* Gaïn giaï trë vaì cho säú láön xuáút hiãûn bàòng 1 *)
Left := Nil; Right := Nil; (* Cho con troí traïi vaì phaíi âãöu Nil *)

End;

End
Else (* Tçm tiãúp taûi caïc vë trê khaïc trong cáy *)
Begin

If x < p^.key Then Tree_Insert(x, p^.Left)

(* Tçm tiãúp trong cáy con bãn traïi *)

Else

If x > p^.key Then Tree_Insert(x, p^.Right) (* Tçm tiãúp trong cáy con bãn phaíi *)
Else p^.Count := p^.Count + 1;

(* Tàng biãún âãúm nãúu tçm tháúy *)

End;

Trong chæång trçnh chênh ta goüi:

Tree_Insert(x, Root);

b) Duìng giaíi thuáût khäng âãû quy
Âãø giaíi thuáût âæåüc âån giaín, ta duìng thãm mäüt nuït phuû goüi laì Head. Ta cho liãn kãút phaíi

(Right) cuía Head chè âãún nuït gäúc (Root) cuía cáy:

New(Head); Head^.Right := Root;

Trong giaí thuáût sau, ta goüi p1 laì nuït âang xeït, p2 laì nuït cha cuía nuït p1 vaì biãún d coï thãø

nháûn mäüt trong caïc giaï trë:

- Nãúu d = 0: tçm tháúy nuït coï näüi dung laì x taûi nuït p1.
- Nãúu d = -1: Thãm nuït måïi p1 vaìo bãn traïi cuía nuït p2.
- Nãúu d = +1: Thãm nuït måïi p1 vaìo bãn phaíi cuía nuït p2.
Giaíi thuáût khäng âãû quy âáöy âuí nhæ sau:

Procedure Tree_Insert (x : Integer);
Var p1, p2: PointTree; d : Integer;
Begin

p2 := Head; p1 := p2^.Right; d := 1; (* Khåíi taûo caïc biãún *)
(* Tçm kiãúm nuït coï khoïa laì x trãn cáy *)
While (p1 <> Nil) And (d <> 0) Do (* Chæìng naìo p1<>Nil vaì khäng tçm tháúy *)
Begin

p2 := p1; (* p2 nháûn giaï trë cuía p1 træåïc khi p1 troí tåïi caïc nhaïnh con *)
If x < p1^.key Then (* Âi qua bãn traïi âeí tçm *)
Begin

p1 := p1^.Left; d := -1;

(* Ghi nháûn âi qua bãn traïi bàòng caïch âàût d=-1 *)

End
Else

If x > p1^.key Then

(* Âi qua bãn phaíi *)

Begin

p1 := p1^.Right; d := 1; (* Ghi nháûn âi qua bãn phaíi bàòng caïch âàût d=1 *)

End
Else d := 0; (* Tçm tháúy x taûi nuït p1 *)

End; (* cuía While *)

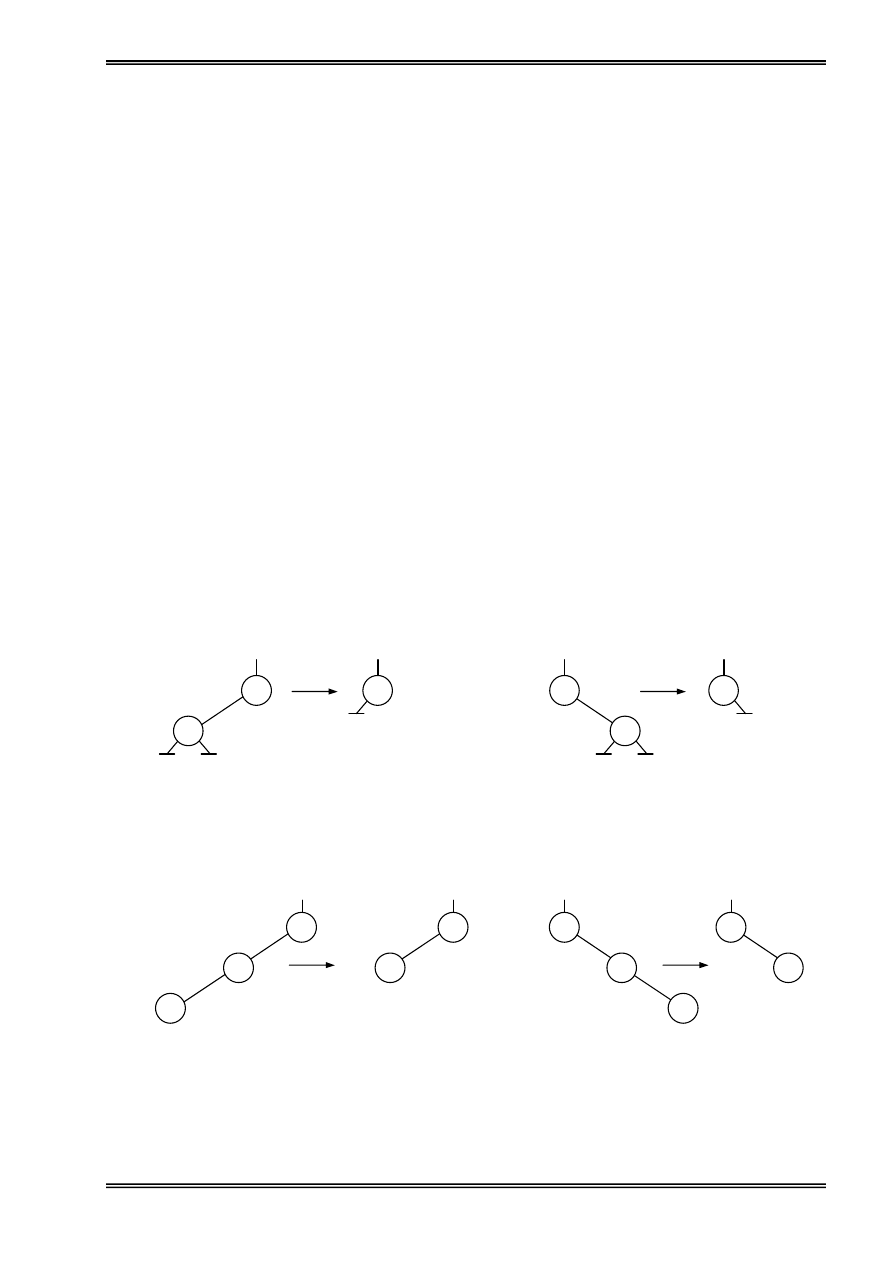
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 53

(* Voìng làûp While kãút thuïc khi p1 = Nil hoàûc d = 0 *)
If d = 0 Then p1^.Count := p1^.Count+1 (* Nãúu d=0, tçm tháúy x, tàng biãún âãúm lãn 1 *)
Else (* Tæïc p1=Nil, thãm nuït måïi vaìo cáy *)
Begin

New(p1);

(* Cáúp phaït vuìng nhåï do p1 troí tåïi *)

With p1^ Do
Begin

Key := x; Count := 1; (* Gaïn caïc giaï trë *)
Left := Nil; Right := Nil; (* p1 hiãûn khäng coï cáy con *)

End;
If d < 0 Then p2^.Left := p1 (* Do d<0 nãn thãm p1 vaìo bãn traïi cuía nuït p2 *)
Else p2^.Right := p1;

(* Do d>0 nãn thãm p1 vaìo bãn phaíi cuía nuït p2 *)

End;

Nháûn xeït: Ta coï thãø duìng giaíi thuáût tçm kiãúm vaì thãm vaìo cáy âãø sàõp thæï tæû mäüt daîy

bàòng caïch: tæì daîy ban âáöu ta taûo ra cáy nhë phán tçm kiãúm theo giaíi thuáût trãn, räöi sau âoï
duyãût cáy theo thæï tæû LNR.

IV.4. Tçm kiãúm vaì loaûi boí trãn cáy

Viãûc loaûi boí trãn cáy nhë phán tçm kiãúm khäng âån giaín nhæ viãûc thãm vaìo, khi loaûi boí

nuït p phaíi âaím baío cáy coìn laûi cuîng laì mäüt cáy nhë phán tçm kiãúm. Ta xeït caïc træåìng håüp
loaûi boí sau:

Træåìng håüp 1: Nuït p cáön loaûi boí laì nuït laï. Ta cho liãn kãút Left (nãúu p laì nuït con bãn traïi)

hoàûc liãn kãút Right (nãúu p laì nuït con bãn phaíi) cuía nuït cha cuía p chè vaìo Nil:

Træåìng håüp 2: Nuït p chè coï cáy con bãn traïi hoàûc cáy con bãn phaíi. Ta cho liãn kãút Left

(nãúu p laì nuït con bãn traïi) hoàûc liãn kãút Right (nãúu p laì nuït con bãn phaíi) cuía nuït cha cuía p
chè vaìo gäúc cuía cáy con naìy:

Hçnh 39: Loaûi boí p laì nuït laï

(a): p laì nuït con bãn traïi ; (b): p laì nuït con bãn phaíi

(a)

(b)

Hçnh 40: Loaûi boí p laì nuït coï cáy con bãn traïi hoàûc bãn phaíi

(a): p laì nuït coï cáy con bãn traïi ; (b): p laì nuït coï cáy con bãn phaíi

(a)

(b)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 54

Træåìng håüp 3: Nuït p coï caí cáy con bãn traïi vaì cáy con bãn phaíi. Ta thay nuït p båíi nuït

cæûc phaíi cuía cáy con bãn traïi cuía nuït p. Pháön tæí cæûc phaíi naìy coï thãø laì nuït laï hoàûc chè coï cáy
con bãn traïi:

Giaíi thuáût âáöy âuí nhæ sau:

Procedure Tree_Delete (x : Integer; Var p : PointTree)
Var q : PointTree;

(* === Âënh nghéa thuí tuûc con cuía Tree_Delete === *)
Procedure Del (Var r : PointTree); (* Thæûc hiãûn Træåìng håüp 3 *)
Begin

If r^.Right <> Nil Then Del(r^.Right)
Else
Begin

q^.key := r^.key;
q^.Count := r^.Count;
q := r; r := r^.Left;

End;

Begin (* Bàõt âáöu Tree_Delete *)

If p = Nil Then Write(‘Khäng tçm tháúy khoïa naìy !’)
Else

If x < p^.key Then Tree_Delete(x, p^.Left) (* Tçm tiãúp bãn nhaïnh traïi *)
Else

If x > p^.key Then Tree_Delete(x, p^.Right) (* Tim tiãúp bãn nhaïnh phaíi *)
Else (* Nãúu tçm tháúy x trãn cáy *)
Begin

q := p; (* Gaïn taûm p cho con troí q *)
If q^.Right = Nil Then p := q^.Left (* Âi qua traïi nãúu q khäng coï nhaïnh phaíi *)
Else (* Nãúu q coï nhaïnh phaíi *)

If q^.Left = Nil Then p := q^.Right (* coï nhaïnh phaíi maì khäng coï nhaïnh traïi *)
Else Del(q^.Left);

Dispose(q);

End;

End; (* Kãút thuïc Tree_Delete *)

Thuí tuûc goüi laì:

Tree_Delete(x, Root);

Hçnh 41:

Loaûi boí p laì nuït coï caí cáy con bãn

traïi vaì cáy con bãn phaíi.

(q laì nuït cæûc phaíi cuía cáy con bãn

traïi nhæng khäng phaíi laì nuït laï)

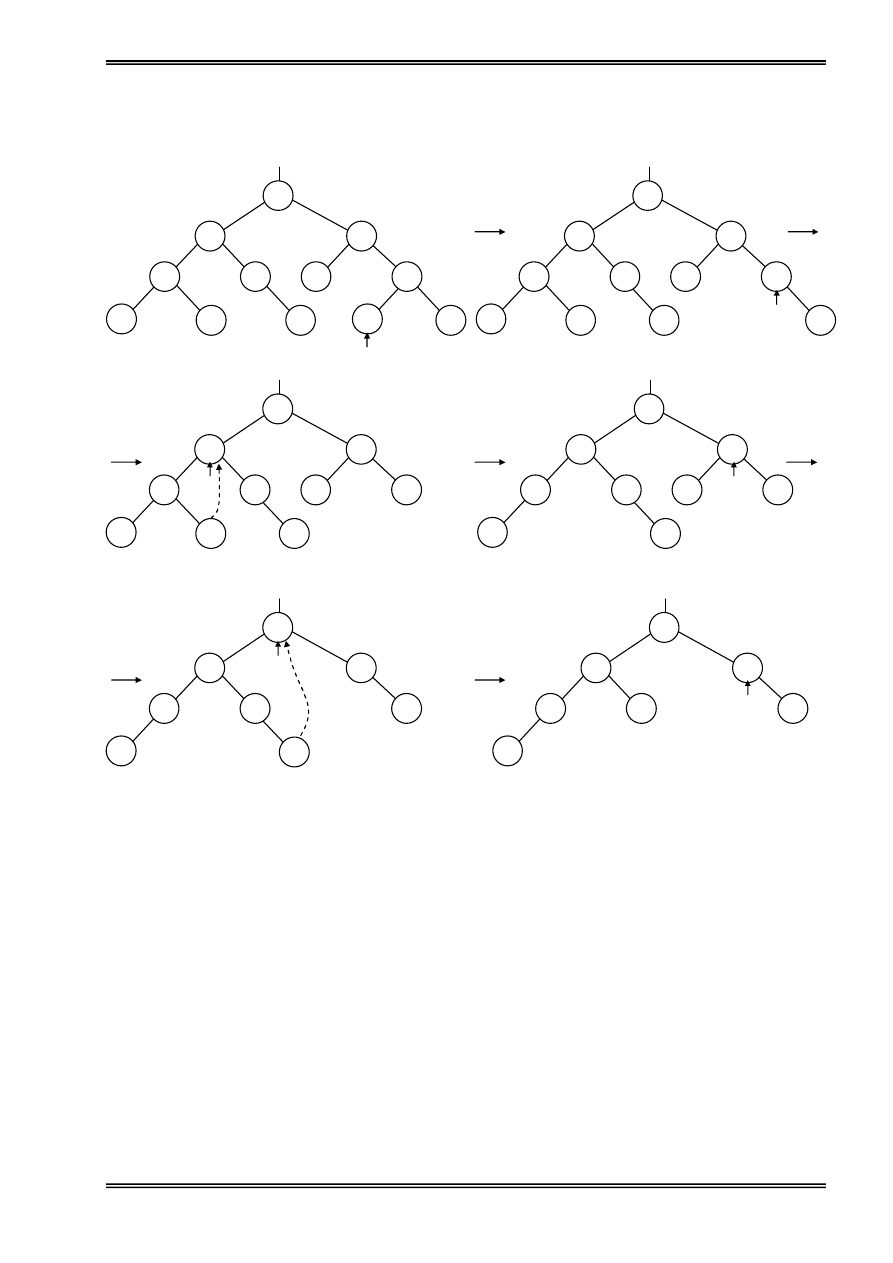
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 55

Vê duû: Xoïa boí mäüt säú pháön tæí trong cáy nhë phán tçm kiãúm

Hçnh 42: Minh hoüa caïc pheïp loaûi boí nuït trãn Cáy tçm kiãúm

(a): Cáy ban âáöu ; (b): Cáy sau khi loaûi boí nuït 10 ; (c): Cáy sau khi

loaûi boí nuït 11 ; (d): Cáy sau khi loaûi boí nuït 4 ; (e): Cáy sau khi loaûi

boí nuït 9 ; (f): Cáy khi loaûi boí nuït 7.

(a)

(b)

(c)

(d)

(e)

(f)

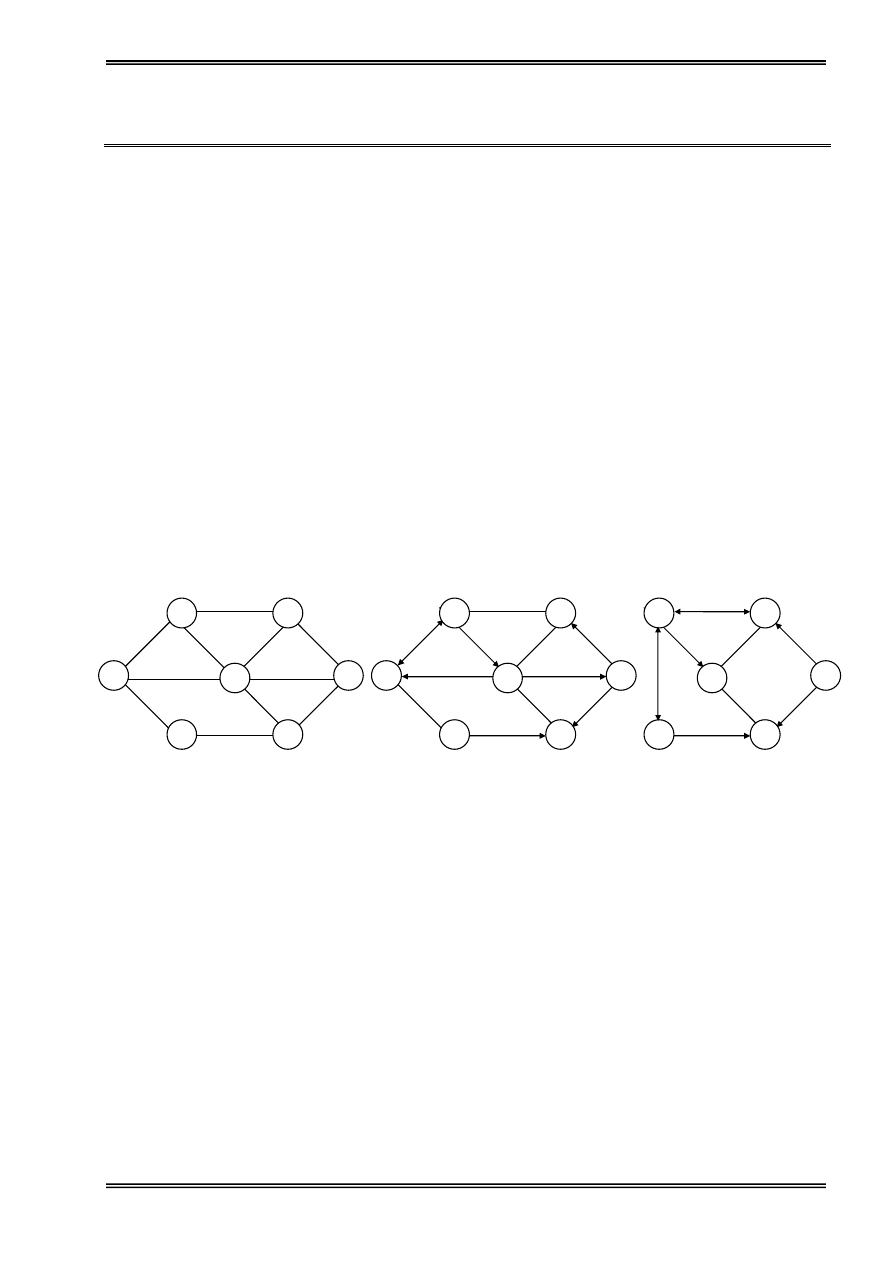
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 56

Âäö thë laì mäüt ngaình cuía Toaïn hoüc, ngaìy nay lyï thuyãút vãö Âäö thë âæåüc æïng duûng ráút nhiãöu

âãø giaíi quyãút caïc baìi toaïn trong thæûc tãú trãn táút caí caïc lénh væûc. Trong chæång naìy ta seî
nghiãn cæïu vãö phæång phaïp biãøu diãùn âäö thë trãn maïy tênh vaì aïp duûng âãø giaíi quyãút mäüt säú
baìi toaïn nhæ: duyãût âäö thë, tçm âæåìng âi ngàõn nháút, kiãøm tra tênh liãn thäng cuía âäö thë .

I. MÄÜT SÄÚ ÂËNH NGHÉA VAÌ KHAÏI NIÃÛM

Âäö thë G laì mäüt táûp håüp gäöm caïc âènh (kyï hiãûu laì V) vaì táûp håüp caïc cung näúi caïc âènh

laûi våïi nhau (kyï hiãûu laì U). Kyï hiãûu: G = (V, U).

Mäüt cung u

∈

U âæåüc kyï hiãûu båíi càûp (x, y) ta noïi cung u näúi tæì âènh x tåïi âènh y, x laì

âènh gäúc, y laì âènh ngoün vaì x, y kãö nhau.

Nãúu âènh laì ngoün cuía mäüt cung duy nháút vaì khäng laì gäúc cuía mäüt cung naìo caí thç âènh

naìy âæåüc goüi laì âènh treo, cung tæång æïng goüi laì cung treo.

Coï hai loaûi âäö thë: âäö thë vä hæåïng vaì âäö thë hæîu hæåïng. Âäö thë vä hæåïng khäng xaïc âënh

hæåïng âi giæîa hai âènh báút kyì coìn âäö thë hæîu hæåïng thç ngæåüc laûi.

Âæåìng âi laì mäüt daîy caïc âènh hoàûc caïc caûnh liãn tiãúp, ta thæåìng kyï hiãûu: D = (x

, x

, ...,

) hoàûc D = (u

, u

, ..., u

). Nãúu âæåìng âi coï âènh âáöu vaì âènh cuäúi truìng nhau goüi laì mäüt

âæåìng âi kheïp kên. Âäü daìi cuía mäüt âæåìng âi laì säú caûnh (hay cung) taûo thaình noï.

Mäüt âäö thë hæîu hæåïng G âæåüc goüi laì liãn thäng nãúu våïi moüi càûp âènh phán biãût bao giåì

cuîng täön taûi mäüt âæåìng âi tæì âènh naìy âãún âènh kia.

Hai âènh âæåüc goüi laì liãn thäng nãúu chuïng âæåüc näúi liãön våïi nhau båíi êt nháút mäüt âæåìng

âi, ngæåüc laûi thç chuïng âæåüc goüi laì khäng liãn thäng.

Âäö thë hæîu hæåïng laì mäüt træåìng håüp âàûc biãût cuía âäö thë vä hæåïng, mäüt caûnh cuía âäö thë

vä hæåïng âæåüc biãøu diãùn thaình hai cung ngæåüc chiãöu nhau trong âäö thë hæîu hæåïng. Do âoï
caïc giaíi thuáût trãn âäö thë vä hæåïng cuîng coï thãø aïp duûng âæåüc trãn âäö thë hæîu hæåïng.

Hçnh 43: Biãøu diãùn Âäö thë.

(a): Âäö thë vä hæåïng ; (b): Âäö thë hæîu hæåïng ; (c): Âäö thë coï troüng säú.

(a)

(c)

(b)

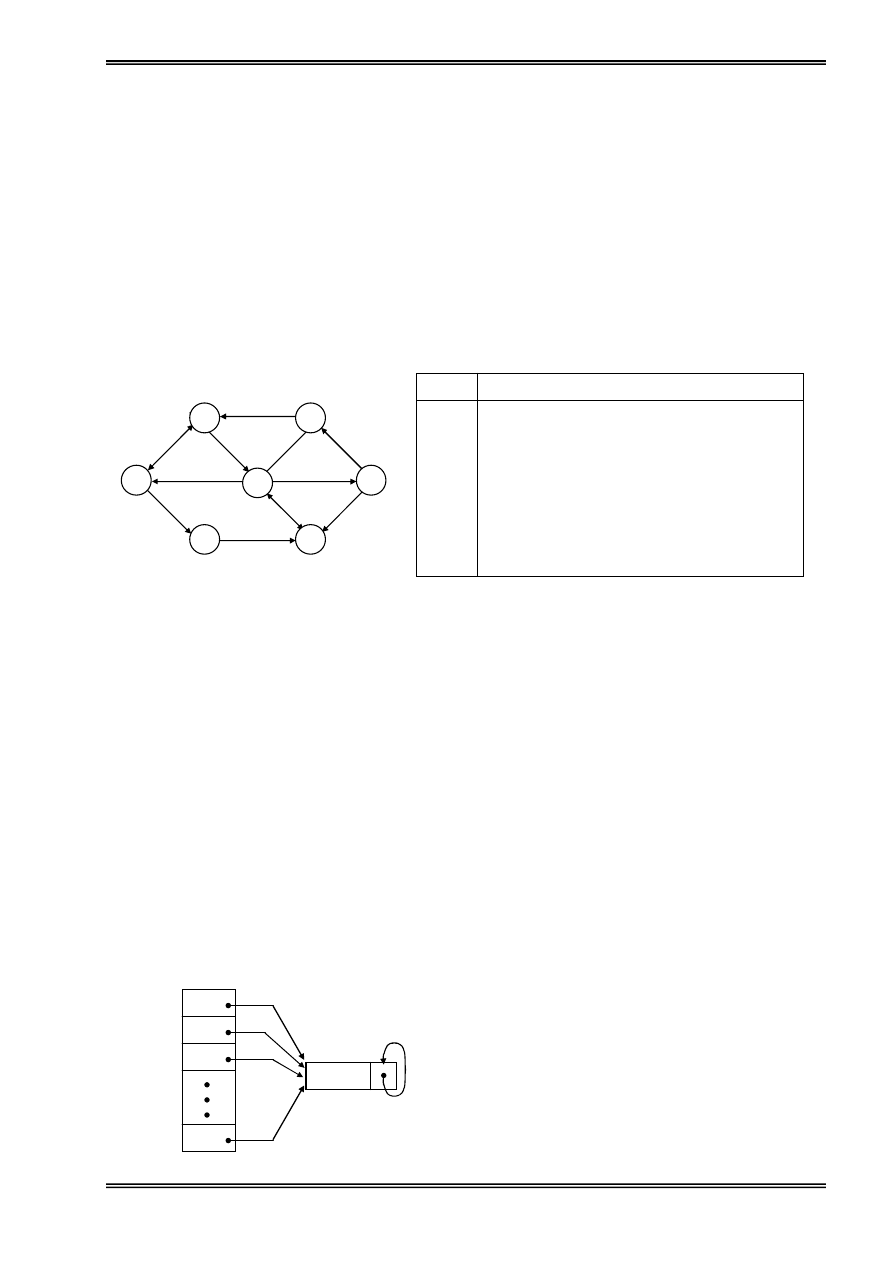
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 57

II. CAÏC CAÏCH BIÃØU DIÃÙN ÂÄÖ THË

II.1. Biãøu diãùn âäö thë bàòng ma tráûn kãö

Våïi phæång phaïp naìy, âãø biãøu diãùn mäüt âäö thë gäöm coï n âènh ta duìng mäüt maíng hai

chiãöu a cáúp n * n mäùi pháön tæí coï giaï trë Boolean våïi a[x,y] âæåüc gaïn giaï trë True nãúu coï mäüt
caûnh tæì âènh x tåïi âènh y vaì ngæåüc laûi thç gaïn giaï trë False.

Ma tráûn kãö coìn coï thãø âæåüc æïng duûng âãø biãøu diãùn Âäö thë coï troüng säú våïi yï nghéa a[x,y]

laì troüng säú cuía caûnh (cung) xy nãúu a[x,y]>0, coìn nãúu a[x,y]=0 thç khäng täön taûi âæåìng âi näúi
tæì âènh x tåïi âènh y.

Vê duû: Xeït âäö thë sau âáy:

II.2. Biãøu diãùn âäö thë bàòng danh saïch kãö

Danh saïch kãö laì mäüt danh saïch liãn kãút, mäùi pháön tæí trong danh saïch kãö naìy bao gäöm

hai thaình pháön: mäüt thaình pháön id âãø chæïa tãn âènh âæåüc näúi âãún (y âæåüc näúi âãún tæì x) vaì
mäüt thaình pháön liãn kãút Next âãø chè âãún pháön tæí kãú tiãúp trong danh saïch. Táút caí caïc danh
saïch kãö âãöu coï pháön tæí cuäúi cuìng laì z (goüi laì pháön tæí cáöm canh). Thaình pháön liãn kãút cuía z
chè vaìo chênh noï.

Træåïc tiãn cho caïc danh saïch kãö chè coï mäüt pháön tæí laì z (hçnh dæåïi). Sau âoï khi thãm

vaìo mäüt caûnh näúi tæì âènh x tåïi âènh y thç ta thãm x vaìo danh saïch kãö cuía y vaì ta thãm y vaìo
danh saïch kãö cuía x. Pheïp thãm vaìo âæåüc thæûc hiãûn åí âáöu danh saïch. Cáúu truïc danh saïch kãö
cuía mäüt âäö thë nhæ sau:

Hçnh 44: Biãøu diãùn Âäö thë bàòng ma tráûn kãö

(a): Âäö thë ; (b): Biãøu diãùn âäö thë bàòng ma tráûn kãö

A B C

(a)

(b)

Hçnh 45: Hçnh aính cuía danh saïch kãö ban

âáöu (khi chæa thãm vaìo caïc caûnh).

(A)
(B)
(C)

(D)

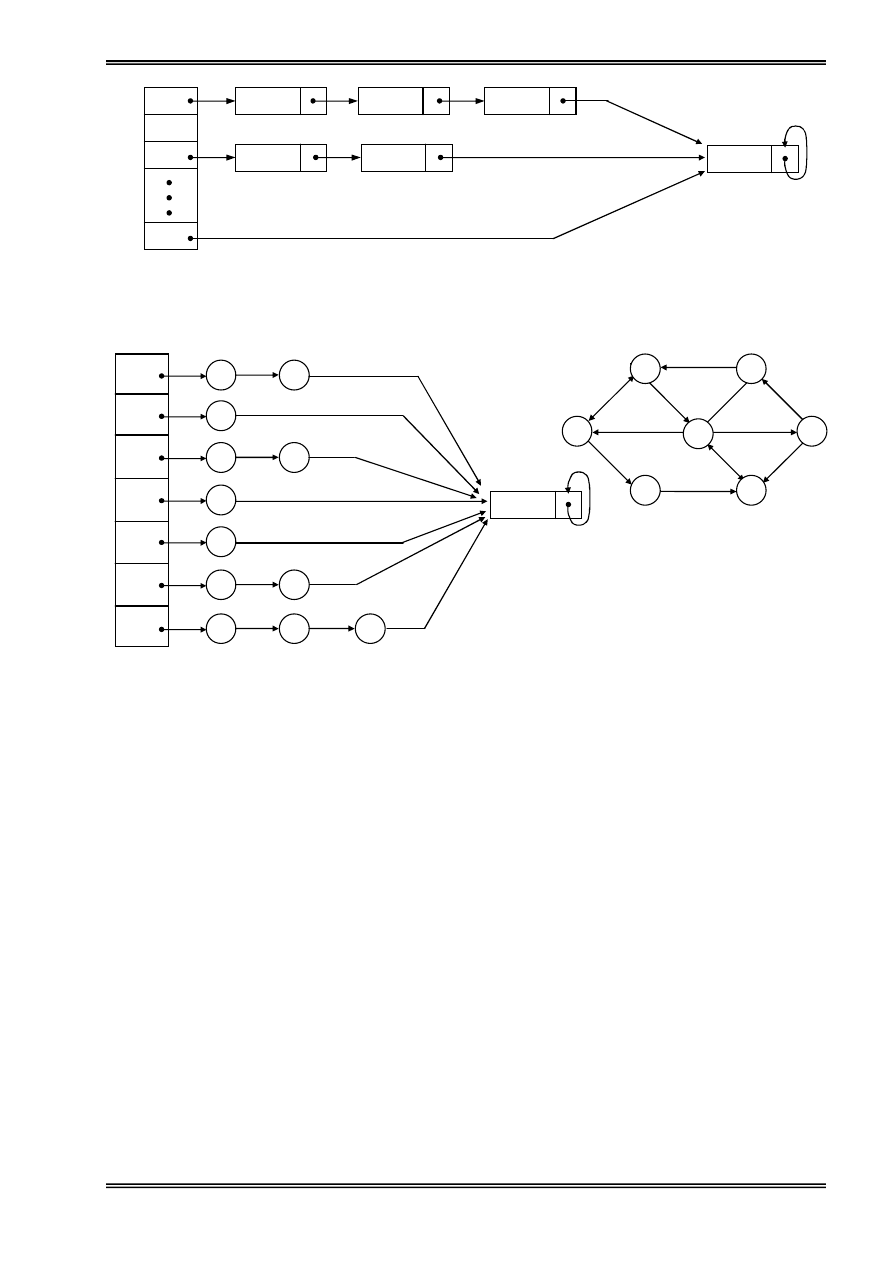
GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 58

Vê duû: Biãøu diãùn ma tráûn kãö:

Ta khai baïo cáúu truïc dæî liãûu nhæ sau:

Type PointGrp = ^Node;
Node = Record (* Cáúu truïc mäüt pháön tæí cuía danh saïch kãö *)

Id : Integer;
Next : PointGrp;

End;
Var n, U : Integer; adj : Array[1..100] of PointGrp; (* Maíng caïc âènh cuía âäö thë *)

Giaíi thuáût taûo cáúu truïc danh saïch kãö cuía mäüt âäö thë nhæ sau:

Procedure AdjList;
Var j, x, y : Integer; t, z : PointGrp;
Begin

Readln(n, U); (* Nháûp vaìo säú âènh vaì säú caûnh cuía âäö thë *)
New(z);

(* Pháön tæí cáöm canh *)

For j := 1 To n Do adj[j] := z; (* Khåíi taûo caïc danh saïch kãö *)
For j := 1 To E Do

(* Nháûp vaìo tæìng caûnh cuía âäö thë *)

Begin

Read(v1, v2);

(* v1 laì âènh âáöu, v2 laì âènh âêch *)

x := Index(v1); y := Index(v2); (* Traí vãö thæï tæû cuía caïc âènh v1 vaì v2 *)
New(t);

(A)
(B)
(C)

(D)

Hçnh 46: Hçnh aính cuía danh saïch kãö khi âaî

thãm vaìo caïc caûnh cuía âäö thë.

Hçnh 47: Biãøu diãùn âäö thë (a) bàòng ma tráûn kãö (b).

(A)

(B)

(C)

(D)

(E)

(F)

(G)

(a)

(b)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 59

t^.id := x; t^.Next := adj[y]; adj[y] := t; (* Thãm x vaìo danh saïch kãö cuía y *)
New(t);
t^.id := y; t^.Next := adj[x]; adj[x] := t; (* Thãm y vaìo danh saïch kãö cuía x *)

End;

Chuï yï ràòng mäùi caûnh âæåüc biãøu diãùn hai láön: mäüt caûnh näúi âènh x våïi âènh y âæåüc biãøu

diãùn båíi pháön tæí khoïa x trong danh saïch kãö cuía y vaì båíi pháön tæí khoïa y trong danh saïch kãö
cuía x. Âäúi våïi caïch biãøu diãùn naìy, thæï tæû cuía caïc caûnh khi nháûp vaìo tæång âäúi quan troüng,
do váûy cuìng mäüt âäö thë coï thãø âæåüc biãøu diãùn theo nhiãöu caïch khaïc nhau trong mäüt cáúu truïc
danh saïch kãö.

Danh saïch kãö cuîng coï thãø biãøu diãùn âæåüc âäö thë coï troüng säú bàòng caïch thãm vaìo thaình

pháön chæïa troüng säú cho mäùi pháön tæí cuía danh saïch kãö trong cáúu truïc danh saïch kãö.

III. BAÌI TOAÏN TÇM KIÃÚM THEO CHIÃÖU SÁU

Âäúi våïi mäüt âäö thë cho træåïc, ta coï thãø coï nhiãöu cáu hoíi khaïc nhau. Chàóng haûn âäö thë coï

liãn thäng hay khäng? Nãúu khäng thç âäö thë coï bao nhiãu thaình pháön liãn thäng? Âäö thë coï
chu trçnh hay khäng?,...Táút caí caïc cáu hoíi naìy âãöu coï thãø traí låìi mäüt caïch dãù daìng båíi mäüt
kyî thuáût goüi laì: “Tçm kiãúm theo chiãu sáu”.

Våïi kyî thuáût naìy thç taûi mäüt âènh v báút kyì cuía âäö thë, ta duyãût âènh v räöi sau âoï xeït táûp

caïc âènh âãún âæåüc tæì âènh v. Khi xeït âènh w thuäüc táûp naìy ta laûi aïp duûng caïch duyãût naìy cho
âènh w.

Procedure Depth;

Procedure Visit(v);
Begin

Mark[v] := “âaî duyãût”;
For “mäùi âènh w näúi tæì v” Do

If mark[w] = “chæa duyãût” Then Visit(w);

End;

Begin

For “mäùi âènh v thuäüc U” Do mark[v] := “chæa duyãût”;
For “mäùi âènh v thuäüc U” Do

If mark[v] = “chæa duyãût” Then Visit(v);

End;

III.1. Giaíi thuáût âãû quy

Procedure Depth;
Var i, k : Integer; mark : Array[1..100] of Integer; (* Duìng maíng âãø âaïnh dáúu caïc âènh *)

Procedure Visit(k : Integert); (* Thuí tuûc con vuía Depth *)
Var t : PointGrp;
Begin

i := i + 1; mark[k] := i; (* Gaïn âènh k âaî duyãût láön thæï i *)
(* Duyãût caïc âènh trong danh saïch kãö cuía k – caïc âènh kãö våïi âènh k *)
t := adj[k] ; (* Duyãût caïc âènh trong danh saïch kãö cuía âènh k *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 60

While t <> z Do (* Duyãût caïc âènh kãö cuía âènh k *)
Begin

If mark[t^.id] = 0 Then Visit(t^.id); (* Duyãût nãúu chæï duyãût *)
t := t^.Next; (* Duyãût tiãúp *)

End;

Begin (* Bàõt âáöu Depth *)

i := 0;
For k := 1 To n Do mark := 0; (* Táút caí caïc âènh âãöu chæa duyãût *)
For k := 1 To n Do If mark[k] = 0 Then Visit(k);

End; (* Kãút thuïc *)

Ta duìng maíng mark âãø nháûn biãút caïc âènh âaî âæåüc duyãût hay chæa, nãúu âènh k chæa

duyãût thç mark[k]=0, ngæåüc laûi nãúu âènh k âaî duyãût thç mark[k] cho biãút säú thæï tæû cuía âènh k
âaî duyãût. Thuí tuûc Visit(k) duyãût táút caí caïc âènh trong cuìng mäüt thaình pháön liãn thäng våïi
âènh k.

Vê duû: Minh hoüa duyãût âäö thë sau:
Våïi caïch duyãût naìy ta liãn tuûc âi theo chiãöu sáu nãúu coìn

coï thãø âi âæåüc sau âoï quay laûi vaì duyãût caïc âènh chæa duyãût:
Âáöu tiãn duyãût A, sau âoï duyãût F (laì âènh con âáöu tiãn cuía
A), tæång tæû våïi F ta duyãût E, våïi E ta duyãût G, våïi G ta
duyãût A, nhæng do A âaî duyãût nãn luìi laûi âènh E duyãût âènh
D. Våïi âènh D caïc âènh con laì E vaì F âaî duyãût, våïi F caïc
âènh con cuía F cuîng âaî duyãût ta luìi laûi âènh A. Våïi A caïc
âènh con F vaì G âaî âæåüc duyãût nãn ta duyãût B vaì C. Giaíi
thuáût kãút thuïc, thæï tæû caïc âènh âæåüc duyãût caïc âènh nhæ sau: AFEGDBC.

III.2. Giaíi thuáût khäng âãû quy

Ta tháúy våïi giaíi thuáût trãn, caïc âènh con cuía A laì B, C âæåüc duyãût sau caïc âènh khaïc,

hay noïi caïch khaïc laì chuïng chè âæåüc duyãût khi giaíi thuáût duyãût xong caïc âènh khaïc räöi quay
lui. Nhæ váûy âènh naìo “nhçn tháúy” træåïc seî âæåüc duyãût sau, âoï laì lyï do maì ta coï thãø thay giaíi
thuáût âãû quy bàòng mäüt giaíi thuáût khäng âãû quy sæí duûng ngàn xãúp.

Caïc âènh maì chuïng ta âaî “nhçn tháúy” nhæng chæa âæåüc duyãût seî âæåüc âæa vaìo mäüt ngàn

xãúp. Khi duyãût mäüt âènh, ta âi qua caïc caûnh cuía noï vaì âæa caïc âènh maì caïc caûnh naìy näúi âãún
vaìo ngàn xãúp våïi âiãöu kiãûn caïc âènh naìy chæa coï trong ngàn xãúp. Âãø nháûn biãút mäüt âènh naìo
âoï âaî coï trong ngàn xãúp hay chæa ta phaíi quy âënh laûi giaï trë cuía caïc pháön tæí trong maíng
mark nhæ sau:

- mark[k]=0. âènh k chæa âæåüc gàûp
- mark[k]>0, âènh k âaî âæåüc duyãût
- mark[k]=-1, âènh k âaî âæåüc gàûp vaì âang åí trong ngàn xãúp

Procedure Depth;
Var i, k, Top: Integer; (* Top chè tåïi âènh ngàn xãúp *)

mark : Array[1..100] of Integer; (* Biãún âaïnh dáúu caïc âènh âaî âæåüc duyãût *)
Stack : Array[1..100] of Integer; (* Chæïa ngàn xãúp *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 61

Procedure Visit(k : Integer)

(* Thuí tuûc con cuía thuí tuûc Depth *)

Var t : PointGrp;
Begin

Top := Top + 1; Stack[Top] := k; (* Âæa âènh k vaìo ngàn xãúp *)
Repeat (* Thæûc hiãûn làûp laûi *)

k := Stack[Top]; Top := Top -1 ; (* Láúy ra mäüt âènh tæì Stack *)
i := i + 1; mark[k] := i;

(* Âaïnh dáúu âènh naìy âaî duyãût *)

t := adj[k];

While t <> z Do

(* Duyãût danh saïch caïc âènh kãö cuía k *)

Begin

If mark[t^.id]=0 Then

(* Âæa âènh kãö cuía k vaìo ngàn xãúp nãúu chæa duyãût *)

Begin

Top := Top + 1; Stack[Top] := t^.id;
mark[t^.id] := -1;

(* Baïo hiãûu âènh âang nàòm trong ngàn xãúp *)

End;
t := t^.Next;

End;

Until Top =0; (* Cho âãún khi ngàn xãúp räùng *)

End; (* Kãút thuïc Visit *)

Begin (* Bàõt âáöu thuí tuûc Depth *)

i := 0; Top := 0;
For k := 1 To n Do mark[k] := 0;

(* Khåíi taûo caïc giaï trë *)

For k := 1 To n Do If mark[k] =0 Then Visit(k);

End; (* Kãút thuïc Depth *)

Trãn âáy ta chè xeït giaíi thuáût tçm kiãúm trãn âäö thë vä hæåïng, nhæng do âäö thë hæîu hæåïng

laì mäüt træåìng håüp âàûc biãût cuía âäö thë hæîu hæåïng, mäüt caûnh cuía âäö thë vä hæåïng âæåüc biãøu
diãùn thaình hai cung ngæåüc chiãöu nhau trong âäö thë hæîu hæåïng. Do âoï caïc giaíi thuáût trãn
cuîng âæåüc aïp duûng cho âäö thë hæîu hæåïng.

IV. BAÌI TOAÏN TÇM KIÃÚM THEO CHIÃÖU RÄÜNG

Âäúi våïi mäüt âäö thë cho træåïc, ngoaìi caïch duyãût âäö thë theo chiãu sáu nhæ âaî trçnh baìy

trãn, ta coìn mäüt caïch duyãût khaïc laì duyãût theo chiãöu räüng.

Våïi giaíi thuáût naìy thç taûi mäüt âènh báút kyì v cuía âäö thë ta duyãût âènh v räöi duyãût caïc âènh

âãún âæåüc tæì âènh v. Sau âoï ta xeït táút caí caïc âènh w thuäüc táûp naìy vaì aïp duûng laûi caïch duyãût
naìy cho âènh w.

Mäüt æïng duûng cuía giaíi thuáût tçm kiãúm theo chiãöu sáu laì duyãût cáy theo mæïc nhæ âaî trçnh

baìy åí chæång “Cáy”

IV.1. Âäö thë âæåüc biãøu diãùn bàòng cáúu truïc danh saïch kãö

Procedure Width;

Procedure Visit(v);
Begin

“Âæa âènh v vaìo haìng Q”
While “Q khaïc räùng” Do
Begin

“Láúy mäüt âènh tæì haìng Q vaì gaïn cho v”

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 62

mark[v] := “âaî duyãût”;
For “mäùi âènh w näúi tæì v” do

If mark[w] = “chæa duyãût” Then
Begin

“Âæa âènh w vaìo haìng Q”
mark[w] := “âaî duyãût”;

End;

Begin

“Haìng Q räùng”
For “mäùi âènh v thuäüc V” Do mark[v] := “chæa duyãût”;
For “mäùi âènh v thuäüc V” Do

If mark[v] = “chæa duyãût” Then Visit(v);

End;

Nhæ váûy âãø thæûc hiãû tçm kiãúm theo chiãö räüng, ta chè âån giaín thay thãú caïc thao taïc cuía

ngàn xãúp (Stack) båíi caïc thao taïc cuía haìng (Queue) trãn cå såí cuía chæång trçnh tçm kiãúm
theo chiãöu sáu duìng ngàn xãúp.

Ta khai baïo:

Type

ref = ^Node;

(* Pháön tæí cuía danh saïch kãö *)

pt = ^Item;

(* Pháön tæí cuía haìng âåüi *)

Node = Record

(* Mäüt pháön tæí cuía Danh sach kãö *)

id : Integer;

(* Säú hiãûu cuía nuït *)

Next : ref;

(* Chè âãún pháön tæí tiãúp theo trong danh saïch kãö *)

End;
Item = Record

(* Mäüt pháön tæí cuía Haìng âåüi*)

Info : Integer;

(* Pháön tæí *)

Link : pt;

(* Chè âãún pháön tæí tiãúp theo *)

End;

Var adj : Array[1..100] of ref; z : ref; (* Chæïa danh saïch kãö vaì pháön tæí cáöm canh *)

Giaíi thuáût âáöy âuí nhæ sau:

Procedure Width;
Var Front, Rear, q : pt; (* Con troí chè tåïi Âáöu vaì Cuäúi cuía haìng âåüi *)

mark : Array[1..100] of Integer;
i, k : Integer;
(* === Âënh nghéa caïc chæång trçnh con cuía Width === *)
Procedure Init_Queue; (* Thuí tuûc khåíi taûo haìng âåüi *)
Begin

Front := Nil; Rear := Nil;

End;
Procedure Insert_Queue (r : Integer); (* Thuí tuûc cheìn mäüt pháön tæí vaìo haìng âåüi *)
Begin

New(q); q^.info := r; q^.Link := Nil;
If Rear <> Nil Then Rear^.Link := q;
Rear := q;
If Front = Nil Then Front := q;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 63

End;
Procedure Delete_Queue (Var r : Integer); (* Thuí tuûc láúy ra mäüt pháön tæí khoíi haìng âåüi *)
Begin

r := Front.^info; q := Front;
Front := Front^.Link;
If Front = Nil Then Rear := Nil;
Dispose(q); (* Giaíi phoïng vuìng nhåï *)

End;
Procedure Visit(k : Integer); (* Thuí tuûc duyãût âènh k *)
Var t : ref;
Begin

Insert_Queue(k); (* Âæa k vaìo haìng *)
Repeat (* Làûp laûi cho âãún khi haìng räùng *)

Delete_Queue(k); (* Láúy ra mäüt pháön tæí *)
i := i + 1; mark[k] := i; (* Âaïnh dáúu âaî duyãût *)
t := adj[k];
While t <> z Do (* Làûp caïc âènh trong danh saïch kãö cuía k *)
Begin

If mark[t^.id] = 0 Then (* Âæa vaìo haìng nãúu chæa duyãût *)
Begin

Insert_Queue(t^.id);
mark[t^.id] := -1;

End;
t := t^.Next;

End;

Until Front = Nil

End;

Begin (* ===Bàõt âáöu Width === *)

i := 0;
Init_Queue; (* Khåíi taûo haìng *)
For k := 1 To n Do mark[k] := 0;
For k := 1 To n Do

If mark[k] = 0 Then Visit(k);

End; (* Kãút thuïc Width *)

IV.2. Âäö thë âæåüc biãøu diãùn bàòng ma tráûn kãö

Caïc thuí tuûc cuía giaíi thuáût tçm kiãúm theo chiãöu räüng trãn âäö thë âæåüc biãøu diãùn bàòng ma

tráûn kãö cuîng tæång tæû nhæ trãn. Cuû thãø ta giæî nguyãn caïc thuí tuûc Init_Queue, Insert_Queue,
Delete_Queue vaì ta chè cáön sæía laûi thuí tuûc Visit. Goüi A laì ma tráûn kãö cuía âäö thë ta coï giaíi
thuáût sau:

Procedure Visit(k : Integer); (* Thuí tuûc duyãût âènh k *)
Var t : Integer;
Begin

Insert_Queue(k); (* Âæa k vaìo haìng *)
Repeat (* Làûp laûi cho âãún khi haìng räùng *)

Delete_Queue(k); (* Láúy ra mäüt pháön tæí *)
i := i + 1; mark[k] := i; (* Âaïnh dáúu âaî duyãût *)
For t := 1 To N (* Làûp caïc âènh trong danh saïch kãö cuía k *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 64

Begin

If a[k,t] Then

If mark[t] = 0 Then (* Âæa vaìo haìng nãúu chæa duyãût *)
Begin

Insert_Queue(t);
mark[t] := -1;

End;

Until Front = Nil

End;

V. BAÌI TOAÏN TÇM ÂÆÅÌNG ÂI NGÀÕN NHÁÚT

Baìi toaïn tçm âæåìng âi ngàõn nháút laì tçm âæåìng âi trong mäüt âäö thë coï troüng säú näúi hai

âènh x, y âaî cho træåïc sao cho täøng caïc troüng säú cuía táút caí caïc caûnh laì nhoí nháút trong táút caí
caïc âæåìng âi tæì âènh x âãún âènh y. Pháön naìy seî trçnh baìy caïc giaíi thuáût tçm âæåìng âi ngàõn
nháút trãn mäüt âäö thë hæîu hæåïng.

Goüi L laì ma tráûn chiãöu daìi, chiãöu daìi cuía cung laì mäüt säú khäng ám. Ta coï:
L[i,i] = 0, våïi moüi i=1,2,...,n.
L[i,j] > 0, nãúu täön taûi mäüt cung tæì âènh i âãún âènh j.
L[i,j] = vä cæûc nãúu khäng täön taûi cung tæì âènh i âãún âènh j.

V.1. Giaíi thuáût Dijkstra

Goüi C laì táûp håüp caïc âiãøm chæa âæåüc choün vaì S laì mäüt táûp håüp caïc âènh âaî âæåüc choün.

Taûi mäùi thåìi âiãøm, táûp håüp S chæïa caïc âènh maì âæåìng âi ngàõn nháút tæì âènh nguäön âãún chuïng
âaî âæåüc xaïc âënh, trong khi âoï táûp håüp C chæïa caïc âènh coìn laûi.

Bàõt âáöu giaíi thuáût våïi táûp håüp S chè chæïa mäüt âènh nguäön. Khi giaíi thuáût kãút thuïc thç táûp

håüp S chæïa táút caí caïc âènh cuía âäö thë vaì baìi toaïn âaî âæåüc giaíi quyãút xong. Taûi mäùi bæåïc, ta
choün mäüt âènh cuía táûp håüp C maì khoaíng caïch tæì âènh nguäön âãún âènh naìy laì nhoí nháút vaì
âæa âènh naìy vaìo táûp håüp S.

Âãø chæïa âäü daìi âæåìng âi ngàõn nháút, ta duìng mäüt maíng mäüt chiãöu D (n pháön tæí) våïi D[i]

laì âäü daìi âæåìng âi ngàõn nháút tæì âènh nguäön âãún âènh i tênh âãún thåìi âiãøm hiãûn taûi. Giaï trë cuía
D liãn tuûc âæåüc thay âäøi trong khi thæûc hiãûn giaíi thuáût. Khi giaíi thuáût kãút thuïc D[âêch] chênh
laì âäü daìi cuía âæåìng âi ngàõn nháút tæì âènh nguäön âãún âêch.

Giaí sæí caïc âènh âæåüc âaïnh säú tæì 1 âãún n, âènh 1 laì âènh nguäön vaì ma tráûn chiãöu daìi laì L

chæïa chiãöu daìi cuía caïc cung. Giaíi thuáût nhæ sau:

Procedure Dijkstra;
Begin

“Cho C laì táûp håüp gäöm caïc âènh 2,3,.., n”
For i := 2 To n Do D[i] := L[1,i];
For i := 1 To n-2 Do
Begin

“Choün âènh v thuäüc táûp håüp C våïi D[v] nhoí nháút”
“Loaûi boí âènh v thuäüc táûp håüp C” vaì “Âæa âènh v vaìo táûp håüp S”
For “mäùi âènh w kãö våïi dènh v” do

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 65

D[w] := Min(D[w], D[v]+L[v,w])

End;

Âãø xaïc âënh âæåìng âi ngàõn nháút âi qua nhæîng âènh naìo, ta duìng thãm mäüt maíng mäüt

chiãöu P gäöm n pháön tæí våïi P[v] chæïa säú hiãûu cuía âènh maì âènh naìy nàòm ngay træåïc âènh v
trong âæåìng âi ngàõn nháút. Do âoï âæåìng âi ngàõn nháút âæåüc xaïc âënh bàòng caïch xem caïc giaï
trë cuía P bàõt âáöu tæì âènh âêch ngæåüc tråí vãö âènh nguäön. Luïc bàõt âáöu giaíi thuáût ta cho caïc giaï
trë cuía P âãöu bàòng 1. Giaíi thuáût Dijkstra âæåüc viãút laûi nhæ sau:

Procedure Dijkstra;

Begin

“Cho C laì táûp håüp caïc âènh tæì 2 âãún n”
For i := 2 To n Do
Begin

D[i] := L[1, i]; P[i] := 1;

End;
For i := 1 To n-1 Do
Begin

“Choün âènh v thuäüc táûp håüp C våïi D[v] nhoí nháút”
“Loaûi boí âènh v thuäüc táûp håüp C” vaì “Âæa âènh v vaìo táûp håüp S”
For “mäùi âènh w thuäüc táûp håüp C” do

If D[w] > D[v] + L[v,w] Then
Begin

D[w] := D[v]+L[v,w];
P[w] := v; (* Âènh træåïc âènh w laì âènh v *)

End;

Sau âáy laì thuí tuûc Dijkstra tçm âæåìng âi ngàõn nháút:

Procedure Dijkstra;
Var D, P, C : Array[1..n] of Integer;
i, j, k, mk, mx, min, x : Integer;
Begin

k := n-1; (* Säú pháön tæí cuía táûp håüp C *)
(* Xáy dæûng táûp håüp C, maíng D vaì P *)
For i := 2 To n Do
Begin

C[i-1] := i; D[i] := L[1,i]; P[i] := 1;

End;
For j := 1 To n-2 Do
Begin

(* Tçm giaï trë nhoí nháút cuía maíng D *)
min := D[C[1]]; mx := 1;
For i := 2 To k Do

If D[C[i]] < min Then
Begin

Min := D[C[i]]; mx := i;

End;

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 66

(* Loaûi boí âènh C[mx] ra khoíi táûp håüp C *)
mk := C[mx]; C[mx] := C[k];
k := k-1;
For i :=1 To k Do
Begin

x := C[i];
If D[x] > D[mk] + L[mk,x] Then
Begin

D[x] := D[mk]+L[mk,x];
P[x] := mk;

End;

Vê duû: Xeït âäö thë sau

Quaï trçnh thæûc hiãûn giaíi thuáût Dijkstra nhæ sau:

Bæåïc

Âènh choün v

Táûp håüp C

Maíng D

Maíng P

Ban âáöu

{2, 3, 4, 5}

[50, 30, 100, 10]

[1, 1, 1, 1]

{2, 3, 4}

[50, 30, 20, 10]

[1, 1, 5, 1]

{2, 3}

[40, 30, 20, 10]

[4, 1, 5, 1]

{2}

[35, 30, 20, 10]

[3, 1, 5, 1]

Nhæ váûy, khi giaíi thuáût kãút thuïc D[i] chênh laì âæåìng âi ngàõn nháút tæì âènh nguäön âãún âènh

i. Vê duû: âæåìng âi ngàõn nháút tæì âènh 1 âãún âènh 2 laì 35, âènh 3 laì 30, âènh 4 laì 20 vaì âènh 5
laì 10. Sau âáy laì thuí tuûc Path âãø in ra âæåìng âi ngàõn nháút tæì âènh nguäön (source) âãún âènh j:

Procedure Path(x : Integer);
Begin

If x <> Source Then
Begin

Path(P[x]); Write(x:3);

End;

Thuí tuûc goüi laì:

Path(j);

Vê duû: Âãø xaïc âënh âæåìng âi ngàõn nháút tæì âènh 1 âãún âènh 4: Ta tháúy P[4]=5, nghéa laì

âènh 5 laì âènh træåïc âènh 4, P[5]=1, nghéa laì âènh 1 laì âènh træåïc âènh 5. Váûy âæåìng âi ngàõn
nháút tæì âènh 1 âãún âènh 4 laì 1, 5, 4 våïi chiãöu daìi laì D[4]=20.

30 100 10

∝

0 50

∝

100

L =

(a)

(b)

Hçnh 48: Minh hoüa giaíi thuáût Dijkstra

(a): Ma tráûn chiãöu daìi âæåìng âi ; (b): Âäö thë coï troüng säú

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 67

V.2. Giaíi thuáût Floyd

Goüi L laì ma tráûn chiãöu daìi, giaï trë cuía L coï thãø laì 0, >0, vä cæûc nhæ âaî trçnh baìy caïc muûc

trãn. Âáöu tiãn ta gaïn ma tráûn L cho ma tráûn D räöi thæûc hiãûn n bæåïc làûp. Sau bæåïc làûp thæï k,
ma tráûn D cho biãút chiãöu daìi cuía âæåìng âi ngàõn nháút âi qua caïc âènh trung gian thuäüc táûp
âènh {1, 2, ..., k}. Sau láön làûp thæï n ta tçm âæåüc âæåìng âi ngàõn nháút.

Taûi láön làûp thæï k, giaíi thuáût kiãøm tra âäúi våïi mäùi càûp âènh i vaì j coï hay khäng täön taûi mäüt

âæåìng âi qua trung gian âènh k maì coï chiãöu daìi nhoí hån chiãöu daìi cuía âæåìng âi ngàõn nháút
hiãûn taûi qua táûp âènh trung gian {1, 2, ..., k-1}. Goüi D

laì ma tráûn D sau láön làûp thæï k, ta coï:

[i,j] = min(D

k-1

[i,j], D

k-1

[i,k]+D

k-1

[k,j])

Giaíi thuáût Floyd nhæ sau:

Procedure Floyd;
Begin

“Gaïn ma tráûn L cho ma tráûn D”
For k := 1 To n Do

For i := 1 To n Do

For j := 1 To n Do

D[i,j] := min(D[i,j], D[i,k]+D[k,j])

End;

Tuy nhiãn, D[i,j] chè cho ta biãút chiãöu daìi cuía âæåìng âi ngàn nháút tæì âènh i âãún âènh j maì

khäng cho biãút âæåìng âi naìy âi qua nhæîng âènh naìo. Âãø coï thãø xaïc âënh âæåìng âi ngàõn nháút
naìy, ta duìng thãm mäüt ma tráûn thæï hai goüi laì P. Ban âáöu ma tráûn P bàòng 0. Trong caïc bæåïc
làûp, ma tráûn D vaì ma tráûn P âæåüc tênh nhæ sau:

If D[i,k] + D[k,j] < D[i,j] Then
Begin

D[i,j] := D[i,k] + D[k,j];
P[i,j] := k;

End;

Khi giaíi thuáût kãút thuïc, P[i,j] chæïa säú thæï tæû cuía bæåïc làûp cuäúi cuìng maì D[i,j] bë thay âäøi

giaï trë. Âãø coï âæåüc âæåìng âi ngàõn nháút tæì âènh i âãún âènh j, ta xeït:

Nãúu P[i,j] = 0 thç âæåìng âi ngàõn nháút træûc tiãúp tæì âènh i âãún âènh j
Nãúu P[i,j] = k thç âæåìng âi ngàõn nháút tæì âènh i âãún âènh j âi qua trung gian âènh k. Ta

tiãúp tuûc xeït âãû quy âäúi våïi P[i,k] vaì P[k,j] âãø tçm nhæîng âènh trung gian coìn laûi åí trãn âæåìng
âi ngàõn nháút naìy.

Var L, D, P: Array[1..100 , 1..100] of Integer;
Procedure Floyd;
Var k, i, j: Integer;
Begin

(* Khåíi taûo ma tráûn D vaì P *)
For i := 1 To n Do

For j := 1 To n Do
Begin

D[i,j] := L[i,j]; P[i,j] := 0;

End;

(* Tênh ma tráûn D vaì P åí bæåïc làûp thæï k *)

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 68

For k := 1 To n Do

For i := 1 To n Do

For j := 1 To n Do

If D[i,k] + D[k,j] < D[i,j] Then
Begin

D[i,j] := D[i,k] + D[k,j]; P[i,j] := k;

End;

Vê duû: Xeït âäö thë sau:

∝

15 5

∝

0 15

∝

= L =

∝

15 5

0 15

20 10

15 5

0 15

20 10

15 5

0 15

15 10

10 5

0 15

Hçnh 49: Minh hoüa giaíi thuáût Floyd tçm âæåìng

âi ngàõn nháút

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 69

Vç P[1,3]=4 nãn âæåìng âi ngàõn nháút tæì âènh 1 âãún âènh 3 âi qua âènh 4. Ta xem P[1,4]=2

vaì P[4,3]=0, âæåìng âi tæì âènh 1 âãún âènh 4 âi qua âènh 2, nhæng tæì âènh 4 træûc tiãúp âãún âènh
3. Cuäúi cuìng ta xem P[1,2]=0 vaì P[2,4]=0, tæì âènh 1 træûc tiãúp âãún âènh 2 vaì tæì âènh 2 træûc
tiãúp âãún âènh 4. Nhæ váût âæåìng âi ngàõn nháút tæì âènh 1 âãún âènh 3 laì: 1, 2, 4, 3 våïi chiãöu daìi
âæåìng âi laì D[1,3]=15.

Thuí tuûc Path chè ra âæåìng âi ngàõn nháút tæì âènh i âãún âènh j sau khi âaî xáy dæûng xong ma

tráûn D vaì P.

Procedure Path(x, y : Integer)
Var r : Integer;
Begin

If P[x,y]=0 Then Writeln(x:3,’->’,y:3)
Else
Begin

r := P[x,y]; (* r nàòm trãn âæåìng âi tæì x âãún y *)
Path(x, r); (* Goüi âãû quy cho âæåìng âi tæì x tåïi r *)
Path(r, y); (* Goüi âãû quy cho âæåìng âi tæì r tåïi y *)

End;

Thuí tuûc goüi laì:

Path(i,j);

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 70

MUÛC LUÛC

MÅÍ ÂÁÖU ..................................................................................................... 1

NGÄN NGÆÎ LÁÛP TRÇNH PASCAL ................................................................ 2

I. CAÏC KIÃØU DÆÎ LIÃÛU CÅ BAÍN .................................................................................2

I.1. Caïc kiãøu dæî liãûu cå baín ................................................................................2
I.2. Kiãøu liãût kã (enumerated types) ..................................................................3
I.3. Kiãøu miãön con (subrange types)..................................................................3
I.4. Kiãøu chuäùi kyï tæû (string types) ...................................................................3
I.5. Kiãøu maíng (array types).............................................................................4
I.6. Kiãøu baín ghi (record types).........................................................................4
I.7. Kiãøu táûp håüp (set types) .............................................................................4
I.8. Kiãøu con troí (pointer types) ........................................................................5

II. CAÏC CÁÚU TRUÏC ÂIÃØU KHIÃØN..............................................................................5

II.1. Khäúi lãûnh ....................................................................................................5
II.2. Cáúu truïc âiãöu kiãûn (conditional statements) .............................................5
II.3. Caïc cáúu truïc làûp (repetitive statements) ...................................................6

III. CHÆÅNG TRÇNH CON VAÌ CHÆÅNG TRÇNH CHÊNH .....................................7

III.1. Haìm con (function)..................................................................................7
III.2. Thuí tuûc con (procedure) ...........................................................................8
III.3. Truyãön tham säú cho chæång trçnh con .......................................................8
III.4. Sæû âãû quy (rcursion).................................................................................8

CÁÚU TRUÏC DANH SAÏCH.............................................................................. 9

I. DANH SAÏCH VAÌ CAÏC PHEÏP TOAÏN TRÃN DANH SAÏCH ...................................9

I.1. Âënh nghéa danh saïch..................................................................................9
I.2. Caïc pheïp toaïn trãn danh saïch......................................................................9

II. DANH SAÏCH ÂÀÛC....................................................................................................9

II.1. Âënh nghéa vaì caïch biãøu diãùn .....................................................................9
II.2. Caïc pheïp toaïn trãn danh saïch âàûc ...........................................................10
II.3. Æu vaì nhæåüc âiãøm cuía danh saïch âàûc ......................................................11

III. DANH SAÏCH LIÃN KÃÚT......................................................................................11

III.1. Danh saïch liãn kãút ..................................................................................11
III.2. Danh saïch liãn kãút âån (DSLK) ............................................................12
III.3. Danh saïch liãn kãút keïp (doubly link list) ...............................................16

IV. CAÏC DANH SAÏCH HAÛN CHÃÚ .............................................................................20

IV.1. Cáúu truïc dæî liãûu haìng (queue)................................................................20

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 71

IV.2. Cáúu truïc dæî liãûu ngàn xãúp (stack).........................................................24

CAÏC GIAÍI THUÁÛT TÇM KIÃÚM ...................................................................... 30

I. TÇM KIÃÚM TUÁÖN TÆÛ (SEQUENTIAL SEARCHING) ........................................30

I.1. Tçm kiãúm trãn danh saïch âàûc .....................................................................30
I.2. Tçm kiãúm trãn danh saïch liãn kãút ...............................................................31

II. TÇM KIÃÚM NHË PHÁN (BINARY SEARCH).......................................................32

CAÏC GIAÍI THUÁÛT SÀÕP THÆÏ TÆÛ .................................................................. 34

I. SÀÕP THÆÏ TÆÛ BÀÒNG PHÆÅNG PHAÏP ÂÃÚM.........................................................34

II. SÀÕP THÆÏ TÆÛ BÀÒNG PHÆÅNG PHAÏP CHOÜN LÆÛA............................................35

III. SÀÕP XÃÚP BÀÒNG PHÆÅNG PHAÏP XEN VAÌO (INSERTION) ...........................36

III.1. Phæång phaïp xen vaìo træûc tiãúp................................................................36
III.2. Phæång phaïp xen vaìo nhë phán...............................................................37

IV. SÀÕP THÆÏ TÆÛ BÀÒNG PHÆÅNG PHAÏP ÂÄØI CHÄÙ ..............................................37

IV.1. Phæång phaïp näøi boüt (bubbleSort)..........................................................37
IV.2. Phæång phaïp ShakerSort.........................................................................39
IV.3. Phæång phaïp Phán hoaûch (quickSort) ...................................................40

V. SÀÕP THÆÏ TÆÛ NGOAÛI (SÀÕP THÆÏ TÆÛ TÁÛP TIN) ..................................................42

CÁÚU TRUÏC CÁY - CÁY NHË PHÁN TÇM KIÃÚM ............................................. 43

I. MÄÜT SÄÚ KHAÏI NIÃÛM .............................................................................................43

II. CAÏCH CHÆÏA CÁY TRONG BÄÜ NHÅÏ MAÏY TÊNH ............................................44

III. CAÏC PHEÏP TOAÏN TRÃN CÁY NHË PHÁN .......................................................44

III.1. Caïc pheïp duyãût cáy nhë phán ..................................................................44
III.2. Duyãût cáy theo thæï tæû NLR (gäúc-traïi-phaíi)............................................45
III.3. Duyãût cáy theo thæï tæû LNR (traïi-gäúc-phaíi)............................................46
III.4. Duyãût cáy theo thæï tæû LRN (traïi-phaíi-gäúc)............................................47
III.5. Duyãût cáy theo mæïc ................................................................................48

IV. CÁY NHË PHÁN TÇM KIÃÚM................................................................................50

IV.1. Âàûc âiãøm cuía cáy nhë phán tçm kiãúm ......................................................50
IV.2. Tçm kiãúm..................................................................................................51
IV.3. Tçm kiãúm vaì thãm vaìo cáy.......................................................................51
IV.4. Tçm kiãúm vaì loaûi boí trãn cáy ...................................................................53

BIÃØU DIÃÙN ÂÄÖ THË .................................................................................... 56

I. MÄÜT SÄÚ ÂËNH NGHÉA VAÌ KHAÏI NIÃÛM..............................................................56

II. CAÏC CAÏCH BIÃØU DIÃÙN ÂÄÖ THË .........................................................................57

II.1. Biãøu diãùn âäö thë bàòng ma tráûn kãö .............................................................57
II.2. Biãøu diãùn âäö thë bàòng danh saïch kãö..........................................................57

III. BAÌI TOAÏN TÇM KIÃÚM THEO CHIÃÖU SÁU.......................................................59

GIAÏO TRÇNH CÁÚU TRUÏC DÆÎ LIÃÛU VAÌ GIAÍI THUÁÛT

TRUNG TÁM PHAÏT TRIÃØN PHÁÖN MÃÖM - ÂAÛI HOÜC ÂAÌ NÀÔNG

Trang: 72

III.1. Giaíi thuáût âãû quy ....................................................................................59
III.2. Giaíi thuáût khäng âãû quy .........................................................................60

IV. BAÌI TOAÏN TÇM KIÃÚM THEO CHIÃÖU RÄÜNG...................................................61

IV.1. Âäö thë âæåüc biãøu diãùn bàòng cáúu truïc danh saïch kãö ..................................61
IV.2. Âäö thë âæåüc biãøu diãùn bàòng ma tráûn kãö ...................................................63

V. BAÌI TOAÏN TÇM ÂÆÅÌNG ÂI NGÀÕN NHÁÚT .........................................................64

V.1. Giaíi thuáût Dijkstra ...................................................................................64
V.2. Giaíi thuáût Floyd .......................................................................................67

Wyszukiwarka

Podobne podstrony:
Cấu Trúc Dữ Liệu Và Giải Thuật Phan Chí Tùng, 80 Trang
Nhập Môn Hệ Điều Hành Linux (NXB Hồ Chí Minh 2001) Trịnh Ngọc Minh, 38 Trang
ĐHTN Giáo Trình Môn Học Xử Lý Ảnh Ts Đỗ Năng Toàn & Ts Phạm Việt Bình, 76 Trang
ĐHĐN Giáo Trình Môn Học Thí Nghiệm Động Cơ Ts Dương Việt Dũng, 43 Trang
ĐHĐN Bài Giảng Môi Trường Trong Xây Dựng Pgs Ts Trần Cát, 145 Trang
ĐHQG Nhập Môn Hệ Điều Hành Linux (NXB Hồ Chí Minh 2001) Trịnh Ngọc Minh, 38 Trang
Giám Sát Thi Công Và Nghiệm Thu Lắp Đặt Thiết Bị Trong Công Trình Dân Dụng (NXB Hà Nội 2002) Lê Kiề
LVDA Các Phương Pháp Bão Mật Thông Tin (NXB Hà Nội 1999) Đăng Văn Hạnh, 74 Trang
ĐHĐN Giáo Trình Quy Hoạch Đô Thị 2 Ths Tô Văn Hùng & Phan Hữu Bách, 28 Trang
ĐHSP Giáo Trình Trí Tuệ Nhân Tạo (NXB Hà Nội 2011) Phạm Thọ Hoàn, 58 Trang
ĐHĐN Giáo Trình Thủy Khí Kỹ Thuật Ứng Dụng Huỳnh Văn Hoàng, 96 Trang
ĐHĐN Giáo Trình Cơ Khí Đại Cương Nhiều Tác Giả, 124 Trang
KC 01 01 Công Nghệ Cứng Hóa Các Thuật Toán Mật Mã (NXB Hà Nội 2004) Nguyễn Hồng Quang, 71 Trang
ĐHĐN Giáo Trình Quy Hoạch Đô Thị 1 Ths Tô Văn Hùng & Phan Hữu Bách, 71 Trang
Giáo Trình Khai Thác, Kiểm Định, Sửa Chữa, Tăng Cường Cầu Gs Ts Nguyễn Viết Trung, 72 Trang
Hướng Dẫn Cấu Hình Các Chức Năng Cơ Bản Của Cisco Router Nhiều Tác Giả, 94 Trang
ĐHBK Trí Tuệ Nhân Tạo Và Hệ Chuyên Gia (NXB Đại Học Quốc Gia 2006) Nguyễn Thiện Thành, 118 Trang
ĐTKH Thực Trạng Quản Lý Vốn ODA Phát Triển Cơ Sở Hạ Tầng Ở Việt Nam Pgs Ts Nguyễn Hồng Thái, 6 Tran
Hỏi Đáp Đề Cương Môn Học Kỹ Thuật Truyền Số Liệu

więcej podobnych podstron