Contrib. Plasma Phys., 1 – 10 (2012) / DOI 10.1002/ctpp.201200002

Thermal Conductivity of Three-Dimensional Yukawa Liquids
(Dusty Plasmas)

A. Shahzad

1,2

∗

and M.-G. He

1

∗∗

1

Key Laboratory of Thermo-Fluid Science and Engineering of Ministry of Education (MOE), Xi’an Jiaotong
University, Xi’an 710049, P. R. China

2

Department of Physics, Government College University Faisalabad (GCUF), Allama Iqbal Road, Faisalabad
38000, Pakistan

Received 18 January 2012, revised 23 February 2012, accepted 07 March 2012
Published online 27 April 2012

Key words Thermal conductivity, dusty plasmas, non-equilibrium molecular dynamics, Yukawa liquids, field
strengths.

An improved method is proposed to investigate the behavior of a Yukawa liquid under the action of an external
field strength using computer simulated nonequilibrium molecular dynamics. The thermal conductivity cal-
culations with appropriate normalizations, in the limit of low value field strengths, are estimated over a wide
range of the Coulomb coupling and screening strengths. The new simulations provide more reliable data for
the thermal conductivity than the previously known results for the Yukawa liquids. The calculations show that
the thermal conductivity is dependent on both the Coulomb coupling and screening parameters in the three-
dimensional (3D) Yukawa liquids. The low value field strength simulation data are found to obey the universal
and quasiuniversal scaling. It is shown that the homogenous nonequilibrium method can be used to predict
the thermal conductivity in Yukawa systems and to understand the fundamental features of 3D dusty plasma
liquids.

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

1

Introduction

Thermophysical properties have played a fundamental role in system design and optimization, and have diverse
applications in many process industries. The major outcome is to minimize operating and developmental cost
in designing new systems in terms of shortening the time and reducing the uncertainty in going from process
innovation at the small scale to industrial scale commercialization. The thermal conductivity is one of the most
important and difficult property of the dusty plasma liquids (DPLs), and it is sensitive to the internal energy of
the molecules. It determines the amount of energy transport of the DPLs and its tendency with an applied flow
field. Recent advances in heat designing processes and heat flow technologies require the detailed understandings
of the thermal conductivity in many systems of interest industrially. Consequently, the suitable development,
widely applicable, predictive method for the thermal conductivity estimation is an enduring goal of much of the
thermophysical property research in both engineering and science applications.

The most practical characteristics of heat transport in materials have moved into the group of engineering

problems [1], but there are some areas such as phonon thermal conductivity in semiconductor systems which
have attracted attention recently because of the applications in thermoelectronic devices. The recent nanotech-
nology demands the prediction of heat transport characteristics of nanometer scale materials [2]. Molecular
level computations and observations have been recognized to be more important and practical for microscale and
nanoscale heat transport solutions. The molecular scale phenomena of heat transfer in phase transition demand
the understanding of the microscopic studies, and the heat transport through three-phase boundary becomes the
singular problem in the macroscopic treatment. Moreover, the current developments in microscale and nanoscale
heat transport and in nanotechnology need the detailed observations of phase transition and the heat and mass
transport in nanometer and micrometer scale regimes. It is a new challenge to extend the method to the spatial

∗

E-mail:

aamirshahzad [e-mail]

∗∗

Corresponding author. E-mail:

[e-mail], Phone: [phone], Fax: [phone]

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

2

A. Shahzad and M.-G. He: Thermal conductivity of three-dimensional Yukawa liquids

and temporal scale of the macroscopic heat transport phenomena [3]. The microscopic dynamical origin of heat
transport is a fundamental issue in statistical mechanics [4] with the derivation of modified equations of motion
for fully homogenous systems as the ultimate goal. The subject of a complex multicomponent plasma containing
grains of solid matter (dust particles) typically of a micrometer size is now attracting much attention [5-7].

With the increasing computational power, the last two decades have witnessed a considerable increase in the

number of researchers using nonequilibrium molecular dynamics (NEMD) techniques to study liquids under the
influence of various types of flow field strengths [8,9]. The determination of transport coefficients using the
equilibrium molecular dynamics (EMD) simulations through the Green-Kubo relations is generally much more
computationally expensive, in terms of time, than by direct NEMD techniques [10]. There have generally been
used three inhomogenous NEMD (InH-NEMD) approaches [11-13] to investigate the thermal conductivity of the
simple and Yukawa liquids. These approaches have disadvantage of spatially inhomogenous systems, in which
the boundaries play an important role. The very large temperature gradients are used in these inhomogenous
approaches. Inhomogenous systems must allow for perturbations (temperature gradients) to the structure and
dynamics due to the presence of the walls, for the determination of thermal conductivity. The thermal conductivity
obtained with the variation of the walls temperature is clearly supported by the non linear temperature profiles
observed in these techniques [11,13]. Furthermore, inhomogenous systems may not exist at a uniquely defined
temperature or density, essential if any comparison with experiment is to be made, and as a consequence of
the relatively large force is required to drive the mass or heat flow combined with the small system size [14].
As a result, the development of a nonequilibrium method to obtain the thermal conductivity (

λ) for Yukawa

liquids without above mentioned difficulties and weaknesses remains an open problem. The homogenous NEMD
(HNEMD) offers an alternative choice to determine thermal properties of liquids without all above problems, and
the more familiar transport coefficients can indeed be studied in this way. One of the promising computational
techniques, the homogenous NEMD algorithm [15-20] is overviewed with a special emphasis on the application
to heat transport problems of fluids. The reason for preferring HNEMD method is that if physical walls can
be eliminated (and replaced by PBC’s) all atoms perceive a similar environment. This method is therefore best
considered as a computational technique whose results are applicable in the limit of zero applied heat force.

The homogenous NEMD schemes have been used and are well developed as very powerful tools in statistical

mechanics [4,21]. This is motivated by the rapid increase in the use of NEMD techniques for homogeneous
molecular fluids such as one component Coulomb plasma (OCCP) [22], simple and ionic liquids [16, 17] under
the action of external field flow for the thermal conductivity. The HNEMD techniques are also used for two
and three-dimensional (3D) Yukawa liquids [23,24] and LJ fluids [10,21] under different shear rates. Recently,
the HNEMD method has been employed for the semiconductor systems [19,20] in order to estimate the linear
regime for the heat flux averages with a decreasing sequence of the external field. The present work is particularly
motivated by the first time to extend the Evans [16] algorithm for the computation of thermal conductivity of the
Yukawa dusty plasma liquids (YDPLs).

This paper summarizes the outcomes of investigations carried out in the last decade, which facilitate us to

present a picture of the variation in the thermal conductivity over the whole range of plasma parameters of
the YDPLs. The dust systems combine the physics of nonideal plasmas and condensed matter. There have
been studied numerous measurements of the dynamical properties [23-29] for the behavior of strongly-coupled
complex (dusty) plasmas (SCCDPs). This area of interest has rapidly grown over the past 15-20 years to become
a major area of study in the field of plasma physics. The results of SCCDPs for

λ by Salin and Caillol [25],

Faussurier and Murillo [26] and lastly Donko and Hartmann [13] indicate current interest in the subject.

The aim of this paper is to implement a homogenous NEMD algorithm and to delve the understanding of

thermal conductivity behaviors in Yukawa liquids, and this numerical method is different from those used in
the earlier studies. Outside the linear regime but close to equilibrium, homogenous conductivity algorithm has
no known physical meaning for the field dependent nonlinear effective thermal conductivity [4,15-20]. The
computations are carried out over a wide range of plasma parameters (

Γ, κ) than those used previously for the

YDPLs.

This paper is organized as follows: In Section 2, the estimate of the thermal conductivity coefficient for

Yukawa liquids is analyzed through the homogenous NEMD method, and this section also describes the simula-
tion technique. Next, the results are presented and discussed with simulation data published by other authors in
Section 3. The work is summarized in Section 4.

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

www.cpp-journal.org

Contrib. Plasma Phys. (2012) / www.cpp-journal.org

3

2

Model and method of numerical simulation

In 3D Yukawa liquid simulation, a novel homogenous NEMD method proposed by the Evans [4,16] is used
for the thermal conductivity. Yukawa system consists of charged particles interact with each other through the
Yukawa (screened Coulomb) potential given by

φ(|r|) =

Q

2

4πε

0

e

−|r|/λ

D

|r|

.

(1)

Here,

Q is the charge on a dust particle, r is the interparticle distance and λ

D

is the Debye screening length. Such

a Yukawa system can fully be described by three reduced (dimensionless) parameters [16,22-24]: the Coulomb
coupling parameter

Γ = (Q

2

/4πε

0

)(1/a

ws

k

B

T ), the external field strength F

∗

= F

z

a

ws

and the inverse screen-

ing length

κ ≡ a

ws

/λ

D

. Here,

T is particle kinetic temperature (in energy units), a

ws

= (3/4nπ)

1/3

is the

Wigner-Seitz (WS) radius [27] and

n is the dust number density. Time scale of interest is characterized by

inverse of the plasma frequency

ω

p

= (nQ

2

/ε

0

m)

1/2

, where

m is the dust particle mass.

The Green-Kubo relations (GKRs) for the hydrodynamic transport coefficients of uncharged particles are well

known [30]. It has been shown that the standard GKRs of fluids apply to the OCCP [22] and YDPLs [25,27,28].
The thermal conductivity for dust particles interacting through a Yukawa pair potential is

λ =

V

3k

B

T

2

∞

0

J

Q

(t)J

Q

(0) dt,

(2)

where J

Q

is the heat flux vector. The microscopic expression for the heat flux vector is

J

Q

V =

N

i=1

E

i

p

i

m

−

1
2

i=j

r

ij

(

p

i

m

.F

ij

),

(3)

where,

E

i

is the energy of particle

i, and it is given by

E

i

=

p

2

i

2m

+

1
2

i=j

φ

ij

.

(4)

In the above expressions, r

ij

=r

i

-r

j

and p

i

are the coordinates and momenta, respectively, of particle

i, φ

ij

is the

Yukawa pair potential given in Eq. (1) and F

ij

is the force on particle

i due to j. The detailed microscopic

expression for heat flux vector J

Q

of the YDPLs is reported in Ref. [25].

The Evans [4] has proposed the generalization of linear response theory to a system moving according to the

(non-Hamiltonian) dynamics represented by the equations of motion

˙r

i

=

p

i

m

,

(5)

and

˙p

i

=

N

j=1

F

i

+ E

i

F

e

(t) −

1
2

N

j=1

F

ij

(r

ij

.F

e

(t)) +

1

2N

N

j,k

F

jk

(r

jk

.F

e

(t)) − αp

i

.

(6)

In these equations,

F

i

= −

∂φ

ij

∂r

i

,

(7)

and

F

i

= E

i

F

e

(t) −

1
2

N

j=1

F

ij

(r

ij

.F

e

(t)) +

1

2N

N

j,k

F

jk

(r

jk

.F

e

(t)),

(8)

also

α =

N

i=1

[p

i

/m

i

.(F

i

+ F

i

)]

N

i=1

p

2

i

/m

i

.

(9)

www.cpp-journal.org

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

4

A. Shahzad and M.-G. He: Thermal conductivity of three-dimensional Yukawa liquids

Here,

F

i

is an additional force on each particle whereas F

e

(t) is an external field, F

i

is the total internal force

acting on particle

i and α is the Gaussian thermostat [15,17] multiplier. In the framework of non-Hamiltonian

dynamics, a linear response theory [16] can be applied in a straightforward fashion. It is clear from the term
E

i

F

e

(t) in Eq. (6) that the above equations of motion will drive a heat current. The external field has the result of

driving particles with a higher than average energy in the direction of F

e

(t), while those with a lower energy are

driven in the opposite direction. In other words, the hotter particles are driven with the field and colder particles
are driven against the field which generates a heat flux J

Q

.

The force conserves total momentum because

F

i

= 0. Assuming the force is sufficiently weak that the

system remains homogenous and compatible with the usual periodic boundary conditions (PBCs). Then the
dissipation is:

˙H

0

≡ F

e

(t).

⎡
⎣

N

i=1

E

i

p

i

m

−

1
2

i=j

r

ij

(

p

i

m

.F

ij

)

⎤
⎦ = F

e

(t).J

Q

V.

(10)

Using the linear response theory we have

J

Q

(t) = −βV

t

0

dt

J

Q

(t

)J

Q

(0).F

e

(t

).

(11)

When F

e

(t) = (0,0,

F

z

) is chosen parallel to the z-axis, then in the limit

t → ∞, the thermal conductivity is the

ratio of the induced heat flux to the product of the temperature and the external field strength

F

z

:

λ =

V

3k

B

T

2

∞

0

J

Q

z

(t)J

Q

z

(0) dt = lim

F

z

→0

lim

t→∞

− J

Q

z

(t)

T F

z

,

(12)

where J

Qz

, is the z-component of the heat flux vector.

In our simulation, the number of particles is to be chosen

N =2000-32000, which allows a study of the effects

of system size. There is no significant effect of the system size found on the thermal conductivity and all the
numerical calculations are within limited statistical uncertainties. A predictor-corrector algorithm [14] is used to
integrate the normalized equations of motion of

N Yukawa dust particles. The force acting on the ith particle F

i

[Eq. (7)] is numerically computed by the Yukawa interaction potential given in Eq. (1) between particle

i (at r

i

)

and the particle

j (at r

j

) and its periodic images. The particle number is placed in a cubic computational cell, and

in order to simulate the infinite system, PBCs are imposed to the computational cell of the Yukawa system with
the size of

L/a. The Ewald sums method is used to take care of the long range interaction between the Yukawa

dust particles. In the Ewald summation method, the interaction potential is divided into two parts, one converges
rapidly in real space sum and the other converges rapidly in the reciprocal space sum. For higher screening values
of

κ, the real space sum part alone exhibits enough performance and precision. Pair wise Yukawa interparticle

forces are summed over a

κ-dependent cutoff radius. Further details of the Ewald sums method for Yukawa

liquids are reported in [25,31]. A thermostat is used to control the particle kinetic temperature. Once the system
reaches thermodynamical equilibrium, the thermostat continues and allows the system progress under the constant
kinetic energy conditions. The simulation time step 0.001

Δt 0.003 ω

−1

p

takes the plasma frequency of the

Yukawa systems into account. In such a HNEMD simulation, the system total energy slightly fluctuates but
remains within statistical uncertainties. The statistical average

< > of dynamical quantities is then achieved

by taking the time average over an adequately long time period in the constant temperature simulation. All runs
are evolved betwee 3

×10

5

ω

−1

p

and 2

×10

5

ω

−1

p

time units in the series of the data recording of

λ. To further

reduce statistical noise, the three independent HNEMD simulation runs are carried out with arbitrarily chosen
configurations of the particle positions for each target temperature

T and then average these measurements to

improve the statistics.

In this paper, it is reported that the simulation data of the thermal conductivity of 3D Yukawa systems are in

a wide domain of the Coulomb coupling (1

Γ 800) and screening (1 κ 5) parameters. It is shown that

the Yukawa conductivity follows a simple temperature functional form proposed by Faussurier and Murillo [26].

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

www.cpp-journal.org

Contrib. Plasma Phys. (2012) / www.cpp-journal.org

5

The 3D thermal conductivity

λ is normalized by the plasma frequency λ

0

= λ/nk

B

ω

p

a

2

ws

or by the Einstein

frequency

λ

∗

= λ/

√

3nk

B

ω

E

a

2

ws

. It has been shown that the Einstein frequency decreases with increase of

κ,

ω

E

→ ω

p

/

√

3 as κ → 0 and λ

0

= λ

∗

(

√

3ω

E

/ω

p

) [27].

3

Simulation results and discussion

In this section, the simulation measurements for the lattice correlation in 3D Yukawa systems with applied exter-
nal field strength (

F

∗

= F

z

a

ws

) are presented. The calculations of thermal conductivity with appropriate nor-

malizations through the HNEMD method are discussed. The universal and quasiuniversal behaviors are tested to
the present numerical results normalized by the Einstein frequency.

3.1

Lattice correlation

The long range order provides the presence and information of lattice structure in the liquid systems. It describes
the quantity underlying x-ray scattering calculations from crystalline materials. If the local density at a point r
can be given as a sum over atoms:

ρ(r) =

N

j=1

δ(r − r

j

),

(13)

then its Fourier transform simply provides the lattice correlation [14] as

Ψ =

1

N

N

j=1

exp(−ik.r

j

).

(14)

The computation of

|Ψ| implemented to test the presence of long range order in the Yukawa systems. The k is a

reciprocal lattice vector of the ordered state and its values can be chosen as 2

π/l (1,-1,1), 2π/l (1,0,1) and 2π/l

(1,0,0) for face-centered cubic (FCC), body-centered cubic (BCC) and simple cubic (SC) lattices, respectively,
and

l is the unit cell edge. If value of |Ψ| ∼

= 1, the system is near fully ordered state but in the disorder liquid

state the system should follow

|Ψ| ∼

= O(N

−1/2

).

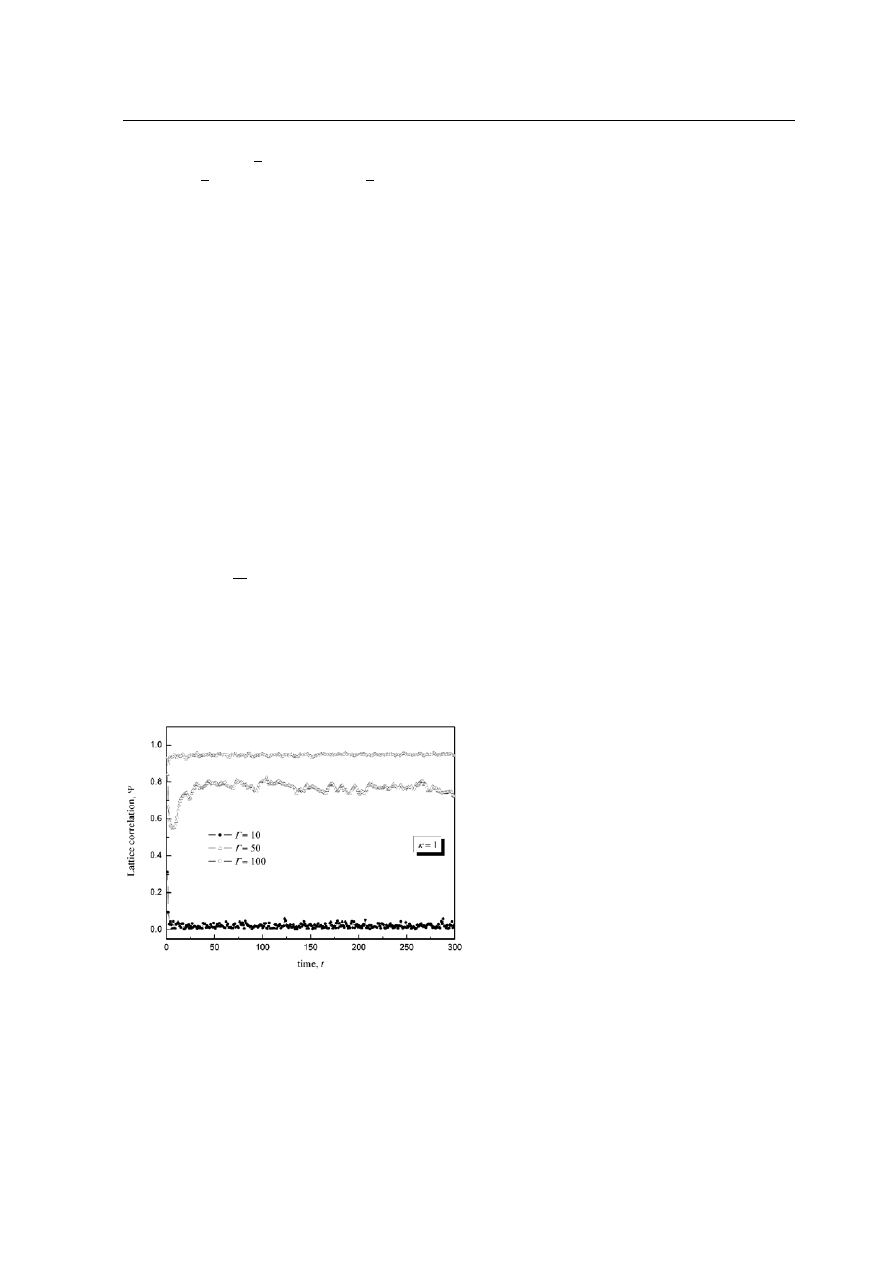
Fig. 1 Lattice correlation (

|Ψ|): time dependence of long-

range order in Yukawa liquids with an applied external field
F

∗

=0.005 and k=2

π/l(1,-1,1), for three values of cou-

pling

Γ=10, 50 and 100, and the screening is κ=1 (with

N=13500 particles).

Figure 1 illustrates the lattice correlation varies with time in the order and disorder states with the application

of a reduced external field strength

F

∗

=

F

z

a

ws

. Here, the value of lattice vector is taken as k =

2π/l (1,-1,1) in

our HNEMD simulations. The computer simulations are carried out for the three values of coupling

Γ = 10, 50

and 100, and the screening parameter is

κ = 1, at F

∗

= 0.005. At the higher Coulomb couplings a moderate to

high degree of order persists throughout the observation period, whereas at the lowest coupling the long-range
order rapidly vanishes. For the lowest coupling (

Γ = 10) a system is near disordered liquid state.

www.cpp-journal.org

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

6

A. Shahzad and M.-G. He: Thermal conductivity of three-dimensional Yukawa liquids

3.2

Normalized thermal conductivity

The HNEMD method is applied to estimate the thermal conductivity normalized by the plasma frequency (

λ

0

)

of YDPLs, at the reduced external field strength

F

∗

=

F

z

a

ws

. In order to implement the homogenous NEMD

technique, possible low value of the field strength

F

∗

is used to determine the near equilibrium thermal con-

ductivity. The higher and lower values of

F

∗

are also tested in order to establish the equilibrium conditions for

the homogenous conductivity of Yukawa liquids. The previous study of YDPLs thermal conductivities has been
restricted to the lower Coulomb coupling and high screening values [13]. The present homogenous conductivity
algorithm makes it possible to study all the domains (

Γ, κ) of state points.

The chief results of HNEMD simulations are shown in Figs. 2-6 for

κ = 1, 2, 3, 4 and 5, respectively. The

present simulation trends obtained at a reduced field strength of

F

∗

= 0.005 have a generally good agreement

with the earlier InH-NEMD simulations of Donko and Hartmann [13] and EMD simulations of Salin and Caillol
[25]. This value

F

∗

= 0.005 is reasonable field strength for the determination of the near-equilibrium values of the

thermal conductivity, and the signal-to-noise ratio at this value is acceptable for all the plasma parameters (

κ, Γ).

The field strengths lower than the value of

F

∗

< 0.005 give noisy calculations particularly for the lower Coulomb

coupling. In addition to the present HNEMD data, Figs. 2-6 also include the simulation results reported in Refs.
[13,25,26] for the YDPLs comparison.

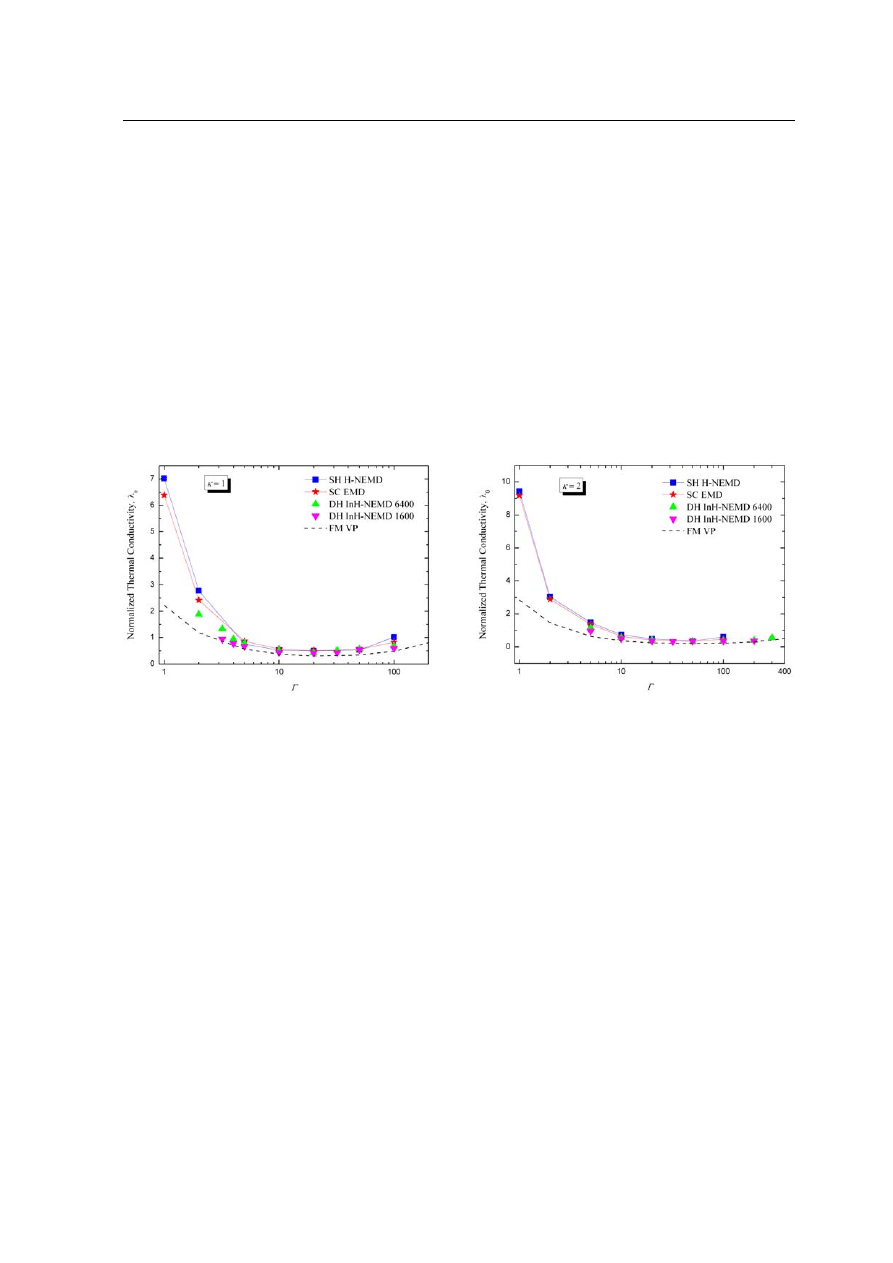
Fig. 2

Reduced thermal conductivity normalized by

plasma frequency

λ

0

as a function of

Γ for κ= 1. EMD of

Salin and Caillol (SC EMD) [25], Inhomogenous NEMD of
Donk´o and Hartmann (DH InH-NEMD) [13], Variational
Procedure of Faussurier and Murillo (FM VP) [26] and
Homogenous NEMD of Shahzad and He (SH H-NEMD):
present calculations (with

N=13500 particles).

Fig. 3

Reduced thermal conductivity normalized by

plasma frequency

λ

0

as a function of

Γ for κ= 2: present

calculations (with

N=32000 particles). For details, see the

caption of Fig. 2.

First systematically consider the results computed for the cases

κ= 1 and 2, and the HNEMD simulation data

for these cases are shown in figures 2 and 3, respectively. The simulations are carried out with

N = 13500 for κ= 1

and the particles number extended up to

N = 32000 for κ= 2. It is significant that the homogenous NEMD method

provides calculations for

λ

0

within the limited statistical uncertainties over the wide range of system sizes. It is

observed that the present results of

λ

0

are slightly higher than and lie more close to the earlier EMD work of

Salin and Caillol [25] but these are slightly lower (within

∼3% - 13%) at region between 5 Γ 50 for the κ=

1 case. These results are important because the calculations happen at the same values of

Γ where the λ

0

∼

= 0.5

at

κ= 1 and λ

0

∼

= 0.4 at κ = 2 were earlier shown to have the minimum values of λ

0

. For

κ = 1, at the lowest

values of

Γ at which the HNEMD simulations give a definitely higher λ

0

, compared to the InH-NEMD results of

Donko and Hartmann [13] and variational procedure of Faussurier and Murillo [26].

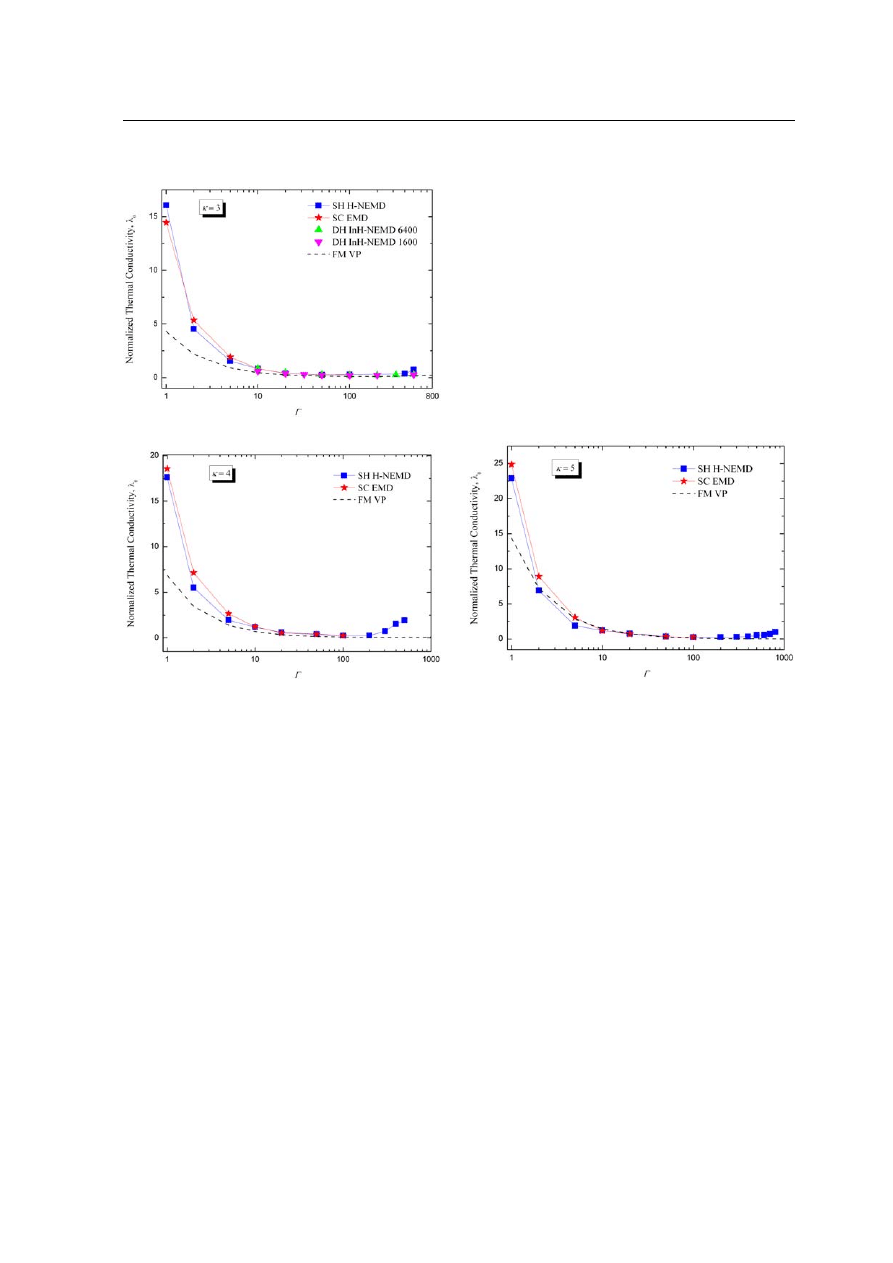
The computer simulation results for

λ

0

as a function of

Γ for κ = 3 are plotted in Fig. 4. For this case, simula-

tions are carried out with

N = 13500 particles. The results obtained from the present HNEMD computations well

agree with the earlier results computed for the Yukawa liquids [13,25], especially at the intermediate and higher
Γ values. At the lowest Γ = 1, the present simulations give a slightly higher but at Γ = 2 and 5 offer slightly lower

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

www.cpp-journal.org

Contrib. Plasma Phys. (2012) / www.cpp-journal.org

7

(

∼15% - 19%) λ

0

as compared to the data of Ref. [25]. This tendency also shows the position of minimum of

λ

0

∼

= 0.3 at Γ = 50.

Fig. 4 Reduced thermal conductivity normalized by plasma
frequency

λ

0

as a function of

Γ for κ= 3. For details, see the

caption of Fig. 2.

Fig. 5

Reduced thermal conductivity normalized by

plasma frequency

λ

0

as a function of

Γ for κ= 4. For details,

see the caption of Fig. 2.

Fig. 6 Reduced thermal conductivity normalized by plasma
frequency

λ

0

as a function of

Γ for κ= 5. For details, see the

caption of Fig. 2.

Figures 5 and 6 display the more succinct analysis of the thermal conductivity obtained from the HNEMD

simulations with

N = 13500 for κ = 4 and 5, respectively. The curves establish overall the same trends as in

the earlier 3D YDPLs [13,25,26] and these are exposed in the figures. The present data for 1

Γ 10 are

significantly lower (within

∼4% - 23%) than that reported in the EMD simulations of Ref. [25] and these are

clearly well matched at the intermediate and higher coupling strengths. The calculations of Faussuurier and
Murillo [26] for 1

Γ 100 at κ = 5 lie between the present data and the results of Salin and Caillol [25]. At

higher screening and coupling (

Γ > 100) strengths, the λ

0

reveals a growing behavior with an increase in

Γ same

as in OCCP [22] and its references therein.

It is concluded from Figs. 2-6 that the thermal conductivity with appropriate normalizations is dependent on

both the degree of correlation and screening strength in the 3D YDPLs. The HNEMD technique is found to have
more comparable performance with the EMD than that of InH-NEMD. It is also examined from figures that the
position of the minimum of

λ

0

shifts towards higher

Γ with an increase in κ, as expected. The minimum value of

λ

0

decreases with increasing

κ, as λ

0

∼

= 0.5 at κ =1 and λ

0

∼

= 0.2 at κ= 5, for the YDPLs. The present HNEMD

calculations are significantly lie above the results calculated by the variational approach proposed in Ref. [26]
except at

κ= 5. Comparison of the data obtained with the homogenous NEMD method showed that the results

of

λ

0

are within (

∼3% - 10% at the lowest Γ and ∼3% - 22% at the highest Γ) the results of the EMD [25]

and significantly higher (

∼23% - 33% at the lowest Γ and ∼33% - 39% at the highest Γ corresponding to κ= 1,

2) than the data reported in InH-NEMD [13]. We can suggest two possible reasons for these differences in the
values of

λ

0

, both arising from homogeneity and Gaussian thermostat in the HNEMD simulation that are lacking

www.cpp-journal.org

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

8

A. Shahzad and M.-G. He: Thermal conductivity of three-dimensional Yukawa liquids

in the InH-NEMD and EMD simulations, respectively. First, the homogenous simulation was nonequilibrium,
with an applied external force that had a minimum specific scale length and was in a specific direction that all
atoms have a similar environment. In contrast, the inhomogenous simulation was also in nonequilibrium but with
varying large perturbation and relatively large momenta was required to drive the heat flux in the system. The
values reported for

λ

0

over different values of

Γ and κ in the InH-NEMD [13] were computed as spatial and

temporal averages of the temperature gradient that had a specific spatial temperature profile; this probably had
its most significant effect on the values of

Γ for λ

0

. Second, the HNEMD had a Gaussian thermostat (constant

temperature condition); therefore, it had uniform values of

Γ and λ

0

whereas the EMD simulation was also

uniform with constant energy (NVE simulation). In the EMD simulation, this difference might have caused by
the limited and smaller system size. In contrast, our simulation was in nonequilibrium with sufficient observation
time scale for significant system sizes. This suggests that the previous values have indeed larger statistical errors.

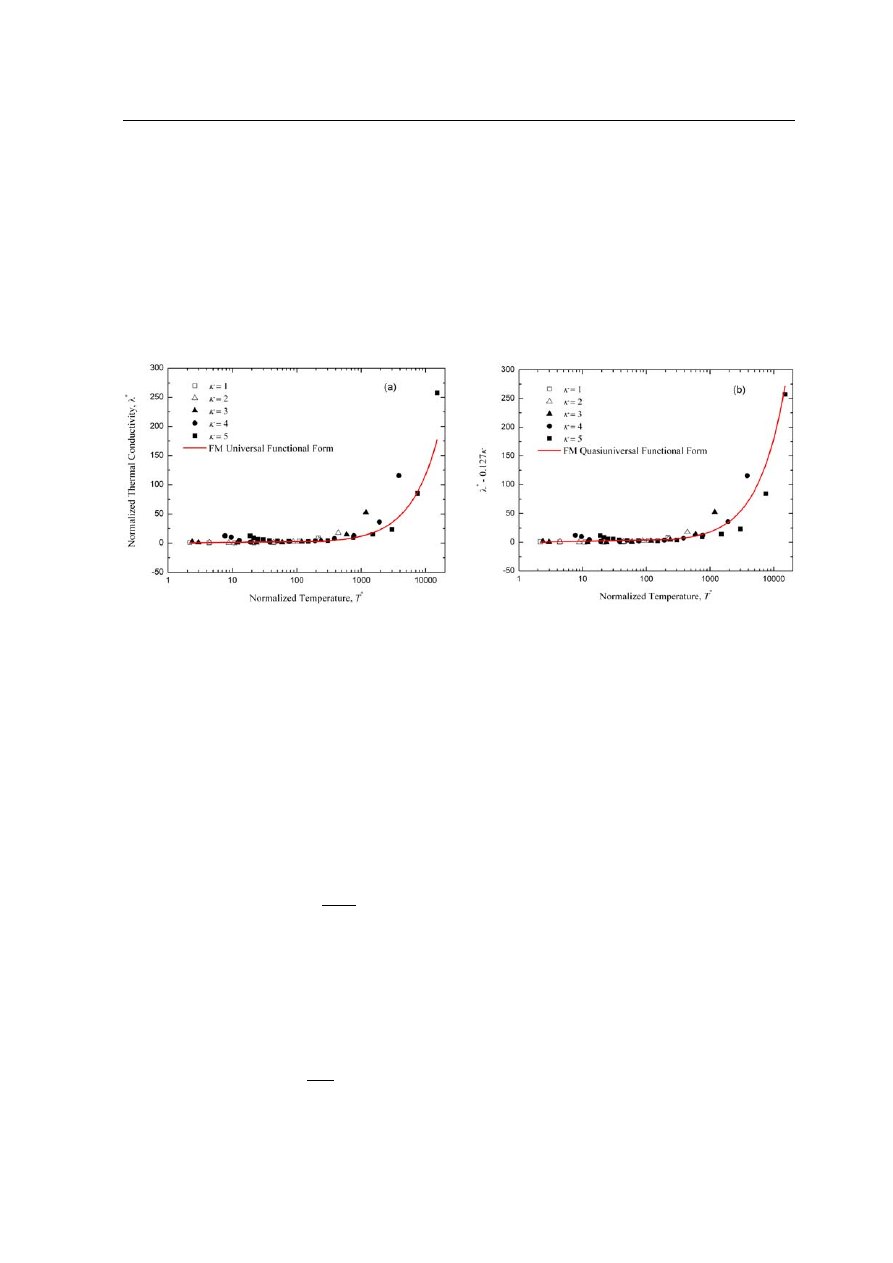
Fig. 7 Reduced thermal conductivity normalized by Einstein frequency

λ

∗

as a function of reduced temperature

T

∗

, for

different

κ= 1, 2, 3, 4 and 5 (a) Universal behavior is established for all κ and Γ values. The solid line is the result of the fit

of the functional form given by Faussurier and Murillo [26] (b) A quasi-universal scaling is demonstrated for the normalized
thermal conductivity with an additional

κ dependent term added to Eq. (15). The heavy line is a functional fit of form given

by Donko and Hartmann [13].

Figure 7 exhibits the variation of thermal conductivity normalized by the Einstein frequency (

λ

∗

) for

κ=

1, 2, 3, 4 and 5 but for different

T

∗

. Where

T

∗

≡ T/T

m

= Γ

m

/Γ is normalized temperature, with Γ

m

is

the Coulomb coupling corresponding to melting [27]. The homogenous normalized conductivity

λ

∗

gives the

acceptable tendency at all

κ and Γ values. It is observed that the λ

∗

shows an increasing behavior with increasing

κ and normalized temperature T

∗

, and the present data signify that the thermal conductivity normalized by the

Einstein frequency

λ

∗

is dependent on both the

κ and T

∗

(ratio of the temperature to melting temperature) in the

Yukawa systems. Since the thermal conductivity of Yukawa system is measured in the fluid phase, therefore the
whole simulation data are taken for

T

∗

> 1. The solid line in Fig. 7(a) is a fitting curve based on the simple

universal functional form given by Faussurier and Murillo [26]

λ

∗

= 0.01176T

∗

+

0.881

T

∗

+ 0.1655.

(15)

The normalizations indicate that the functional form offers nearly fitting for the 1

κ 5 range of screening

strength and for all

Γ range. It can clearly be seen from Fig. 7(a) that the universal functional form gives

accurate fit for all

κ, and it is unlike the earlier InH-NEMD simulations [13] where this functional could not

generate accurate fitting. This functional provides the correct universal tendency with the minimum of curves
shift towards higher

T

∗

corresponds to each

κ. A quasi-universal functional form for the thermal conductivity

is introduced by Donko and Hartmann [13], and this functional has an additional

κ-dependent term added to Eq.

(15)

λ

∗

= 0.018T

∗

+

1.05

T

∗

+ 0.115 + 0.127κ.

(16)

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

www.cpp-journal.org

Contrib. Plasma Phys. (2012) / www.cpp-journal.org

9

The results of the present simulation of

λ

∗

are presented in Fig. 7(b) for all

κ and Γ values, and the heavy line

is a quasiuniversal functional fit form given in Eq. (16). This functional exhibits more accurate relationship
between

λ

∗

and

T

∗

for the whole plasma parameters. The present HNEMD method is applicable over the whole

domain of plasma parameters (

Γ, κ) and the simulation results provide more reliable calculations of the thermal

conductivity than those obtained previously, based on different numerical methods [13,25], for the YDPLs.

4

Summary

A novel HNEMD method has employed to compute the thermal conductivity of strongly coupled 3D Yukawa
liquids. The conductivity values have been obtained for a wide domain of the plasma parameters of

Γ and κ.

The thermal conductivity obtained through the homogenous NEMD simulations is found to be in fair agreement
with that obtained through the earlier EMD and InH-NEMD simulations for the Yukawa systems. The HNEMD
method has an advantage that it can be used to explore the behavior of conductivity over the whole range of plasma
parameters than those used earlier. This HNEMD method yields results of reasonable accuracy for relatively
higher system size and the signal-to-noise ratio is acceptable due to the action of the finite nonzero external field
strength

F

∗

. It seems that the normalized thermal conductivities (

λ

∗

) follow the simple functional formulas with

respect to system temperature, which are consistent with the universal and quasiuniversal scaling. The lattice
correlation has shown the presence of exact lattice structure in the Yukawa systems. Finally, it is concluded
that the homogenous NEMD algorithm is the best alternative choice to study the overall effect of the thermal
conductivity behavior for Yukawa liquids. We suggest that the homogenous NEMD method described here can be
employed to explore both linear and nonlinear phenomena in the other Coulomb systems, and it may nonetheless
provide vitally important information for the theoretical understanding of both phenomena of the complex dusty
plasmas. Our simulation results look forward to new developments in this field over the next few years and to a
wide spread range of applications in both material and biological sciences.

Acknowledgements

The authors thank Z. Donk´o (Hungarian Academy of Sciences) for providing his thermal conductivity

data of Yukawa Liquids for the comparisons of our simulation results, and useful discussions. This work was supported by
the National Nature Science Fund Committee (NSFC No. 50836004).

References

[1] H. Carslaw and J. Jaege, ”Conduction of Heat in Solids“ (Clarendon, Oxford, 1959).
[2] A. Majumdar, Micro. Thermophys. Eng. 4, 77 (2000).
[3] W.J. Minkowycz and E. M. Sparrow, ”Advances in Numerical Heat Transfer“ (Taylor & Francis, New York, 2000).
[4] D.J. Evans and G.P. Morriss, ”Statistical Mechanics of Non-equilibrium Liquids“ (Academic, London, 1990).
[5] S. Khrapak and G. Morfill, Contrib. Plasma Phys. 49, 148 (2009).
[6] H.M. Thomas and G. E. Morfill, Nature (London) 379, 806 (1996).
[7] S. Bardin, J.-L. Briancon,F. Brochard, V. Martin, Y. Zayachuk, R. Hugon and J. Bougdira, Contrib. Plasma Phys. 51,

246 (2011).

[8] M. Kr¨oger, Phys. Rep. 390, 453 (2004).
[9] S. Sarman, D.J. Evans, and P.T. Cummings, Phys. Rep. 305, 1 (1998).

[10] D.J. Evans, Phys. Rev. A 23, 1988 (1981).
[11] W.G. Hoover and W.T. Ashurst, Theor. Chem. Adv. Perspectives 1, 2 (1975).
[12] G. Ciccotti, G. Jacucci and I.R. McDonald, J. Phys. C 11, L509 (1978).
[13] Z. Donko and P. Hartmann, Phys. Rev. E 69, 016405 (2004).
[14] D.C. Rapaport, ”The Art of Molecular dynamics Simulation“ (Cambridge University Press, New York, 2004).
[15] D.J. Evans and G.P. Morriss, Comp. Phys. Rep. 1, 297 (1984).
[16] D.J. Evans, J. Phys. Lett. A 91, 457 (1982).
[17] N. Galamba and C.A. Nieto de Castro, J. Chem. Phys. 126, 204511 (2007).
[18] K.K. Mandadapu, R.E. Jones, and P. Papadopoulos, J. Chem. Phys. 130, 204106 (2009).
[19] Z. Wang, X. Zu, F. Gao, W.J. Weber, and J.-P. Crocombette, Appl. Phys. Lett. 90, 161923 (2007).
[20] K.K. Mandadapu, R.E. Jones, and P. Papadopoulos, J. Chem. Phys. 133, 034122 (2010).
[21] B.D. Todd and P.J. Daivis, Mol. Sim. 33, 189 (2007).
[22] C. Pierleoni, G. Ciccotti and B. Bernu, Europhys. Lett. 4, 1115 (1987).
[23] Z. Donko, J. Goree, P. Hartmann and K. Kutasi, Phys. Rev. Lett. 96, 145003 (2006).
[24] Z. Donko and P. Hartmann, Phys. Rev. E 78, 026408 (2008).

www.cpp-journal.org

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

10

A. Shahzad and M.-G. He: Thermal conductivity of three-dimensional Yukawa liquids

[25] G. Salin and J.-M. Caillol, Phys. Plasmas 10, 1220 (2003).
[26] G. Faussurier and M.S. Murillo, Phys. Rev. E 67, 046404, (2003).
[27] H. Ohta and S. Hamaguchi, Phys. Plasmas 7, 4506 (2000).
[28] T.S. Ramazanov, K.N. Dzhumagulova, Contrib. Plasma Phys. 48, 357 (2008).
[29] T. Ohde, M. Bonitz, T. Bornath and M. Schlange, Contrib. Plasma Phys. 37, 229 (1997).
[30] J.-P. Hansen and I.R. McDonald, ”Theory of Simple Liquids“ (Academic, London, 1986).
[31] A. Shahzad and M.-G. He, ”Thermodynamic Characteristics of Dusty Plasma by Molecular Dynamics Simulation“ in

Plasma Sci. Technol., in press.

c

2012 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim

www.cpp-journal.org