Przedstawiany materiał pochodzi z książki:

Biomedical Engineering Principles

Autorzy:
Arthur B. Ritter
Stevens Institute of Technology
Hoboken, New Jersey, U.S.A.
Stanley Reisman
New Jersey Institute of Technology
Newark, New Jersey, U.S.A.
Bozena B. Michniak
University of Medicine and Dentistry of New Jersey-
New Jersey Medical School, Newark
and New Jersey Center for Biomaterials
Piscataway, New Jersey,. U.S.A

2005, CRC Press Taylor & Francis Group

Tłumaczenie fragmentów i wykład: Prof. dr hab. Antoni Grzanka

Zasady i biomedyczne zastosowania hemodynamiki

1. Wstęp
2. Analogie elektryczne przepływu ustalonego: prawo Ohma
3. Prawo lepkości Newtona
4. Przepływ laminarny i lepkość krwi
5. Przepływ w rurze
6. (...)
7. Powszechnie spotykane tony serca
8. Efekty grawitacyjne
9. (...)

Wstęp

Krew krąży w naczyniach i narządach w zamkniętej pętli zwanej układem krążenia. Układ składa
się z dwóch oddzielnych, szeregowo ułożonych obwodów, krążenia systemowego (krwiobieg duży),
krążenia płucnego (krwiobieg mały). Utlenowana krew opuszcza krążenie płucne do lewej części
serca. Utlenowana krew po wstrzyknięciu przez lewą komorę (rzut minutowy) przemieszcza się w
układzie tętniczym przez krążenie systemowe do głowy i wszystkich dużych narządów, gdzie
następuje wymiana tlenu na dwutlenek węgla w mikrokrążeniu.

(Mikrokrążenie składa się ze wszystkich

naczyń krwionośnych o średnicy mniejszej od 200 μm. W to wlicza się arteriole, prawdziwe kapilary i wenule.
Większość wymiany krew-tkanka oraz regulacja przypływu ma miejsce na poziomie mikrokrążenia)

. Odtlenowana

krew wraca do prawej strony serca poprzez naczynia żylne (powrót żylny) zamykając obwód.
Krążenie płucne dostarcza krew do tkanki płucnej i zapewnia wymianę dwutlenku węhla na tlen.
Szereg czterech zastawek, po dwie po każdej ze stron serca (

zastawkami po prawej stronie serca są

przedsionkowo-komorowa AV i pnia płucnego. Zastawki lewej strony serca to przedsionkowo-komorowa i aortalna.

)

zapewnia przepływ jednokierunkowy w układzie krążenia. Przepływ (rzut minutowy serca) w

układzie krążenia jest równy 4-6 l/min i jest wymuszany prze lewą komorę. Przepływ w obwodzie
płucnym jest zasilany przez prawą komorę. Lewa i prawa komory kurczą się i pompują krew
równolegle tak więc rzut minutowy serca i powrót żylny są sobie równe.
Krążenie płucne jest obwodem o stosunkowo małym ciśnieniu. Normalne maksymalne ciśnienie w
tętnicy płucnej waha się między 25-28 mm Hg. Z kolei, normalne maksymalne ciśnienie w aorcie
waha się między 100-120 mm Hg. Ciśnieni jakie musi wytworzyć lewa komora aby otworzyć
zastawkę aortalną jest 4-5 razy większe od ciśnienia, które musi wytworzyć prawa komora, aby
otworzyć zastawkę pnia płucnego. W związku z tym, ściana prawej komory jest mniej umięśniona i
znacznie cieńsza od ściany lewej komory.
Ściany komór i ściany tętniczych naczyń krwionośnych są rozciągliwe. Oznacza to, że ich średnica
w równowadze w każdej chwili zależy od ich (materiałowych) właściwości sprężystych i różnicy
między siłami ciśnienia wewnętrznego i zewnętrznego oddziałującymi na ściany. Różnica między
siłami ciśnienia wewnętrznego i zewnętrznego jest nazywana ciśnieniem transmuralnym. Naczynie
napinają się kiedy są poddane narastającemu ciśnieniu transmuralnemu.
W stanach chorobowych, takich jak niewydolność aortalna, niesprawna zastawka aortalna zwiększa
objętość roboczą lewej komory (przeciążenie objętościowe). To rozciągnięcie prowadzi do
zgrubienia ściany komory (hipertrofia), usztywnienie i wzrost ciśnień zarówno szczytowego
skurczowego jak końcowo-rozkurczowego. Serce powiększa się w ten sposób, aby utrzymać
stosunek grubości ściany do promienia komorowego (h/R) tak jak w normalnym sercu.
Niekontrolowane nadciśnienie (przeciążenie ciśnieniowe) także powoduje, że ściana lewej komory
grubieje (hipertrofia). Lecz w tym przypadku stosunek h/R rośnie, prowadząc do zmniejszonej
objętości komory, zwiększonej sztywności, zwiększonych ciśnień szczytu skurczowego i końcowo-
rozkurczowego i zmniejszonego wypełnienia komorowego. W każdym z tych przypadków,
końcowem wynikiem jet niewydolność serca ( zmniejszona możliowość utrzymania rzutu
minutowego serca).
W normalnym procesie starzenia, jak i w stanach chorobowych takich jak miażdżyca
(atherosclerosis) przemodelowanie ścian tętnic prowadzi do zwiększonej sztywności z wynikowym
zwiększeniem oporu przepływu i ciśnienia krwi tętniczej. Miażdżyca także powoduje odkładanie
się płytki w ścianach pewnych tętnic (w szczególności tętnic wieńcowych). To zmniejsza przekrój
poprzeczny, który jest dostępny dla przepływu (stenosis), powodując lokalny wzrost oporu
przepływu i prowadząc do obniżenia przepływu poniżej poziomu normalnego lub brak przepływu
(ischemia). Jeśli tak się zdarzy w jednej lub więcej tętnicach wieńcowych, nazywa się to chorobą
tętnic wieńcowych. Gdy przepływ w tętnicach wieńcowych staje się zbyt mały, niewydolność serca
staje się groźna, pacjent jest kandydatem bądź do angioplastyki lub operacji bypassów tętnicy
wieńcowej.
Zastawki serca (w szczególności zastawka aortalna) może także podlegać zwapnieniu i stenozie.
To prowadzi do zwiększenia ciśnienia w komorze i słabe wstrzykiwanie. Gdy stenoza przekracza
pewną granicę, pacjent staje się kandydatem do wymiany zastawki.
Zarówno w stanie zdrowia (n.p. podczas ćwiczeń) jak i choroby, związek pomiędzy ciśnieniem,
przepływem oraz oporem (impedancja) w naczyniach tętniczych jest procesem dynamicznym.
Takie procesy zależą od czynników takich jak pulsacyjny charakter wstrzykiwania, lepkość krwi,
własności mechaniczne ściany naczynia, zredukowanie i rozdwojenie naczyń, sposób połączenia
naczyń obwodowych w sieć (połączenia szeregowe i równoległe) oraz odruchy oraz mechanizmy
miejscowej regulacji, które oddziałują dla utrzymania stabilnego ciśnienia tętniczego krwi i
objętości krwi.
W tym rozdziale rozważamy związek między ciśnieniem, przepływem oraz oporem przepływu
zarówno w dużych naczyniach takich jak tętnice, gdzie można korzystać z matematyki kontinuum,
jak i z mikrokrążenia, gdzie matematyka kontinuum może nie wystarczać.

Analogie elektryczne przepływu ustalonego: prawo Ohma

Hemodynamika jest tą gałęzią dynamiki płynów, w której krew jest jedynym rozważanym płynem.
Przepływ krwi w dużych naczyniach jest, ze swej istoty, pulsacyjny. Oznacza to, że ciśnienie,
prędkość i szybkość przepływu wolumetrycznego w dużych tętnicach i komorach zmienia się w
czasie w ramach pojedynczego cyklu serca. Tym niemniej. W normalnych warunkach
spoczynkowych, te zmiany są w przybliżeniu okresowe, tak więc cykl się powtarza przynajmniej
raz w krótkim okresie czasu. Z pewnych powodów, zostało uznano za użyteczne podejście, w
którym rozważa się uśrednione w czasie wartości ciśnienia, prędkości oraz przepływu jako
parametry stanu ustalonego.
W stanie ustalonym możemy napisać prawo Ohma dla szybkości transportu materii
przemieszczającej się między dwoma punktami następująco:

Szybkość=

siła napędowa
równoważny opór

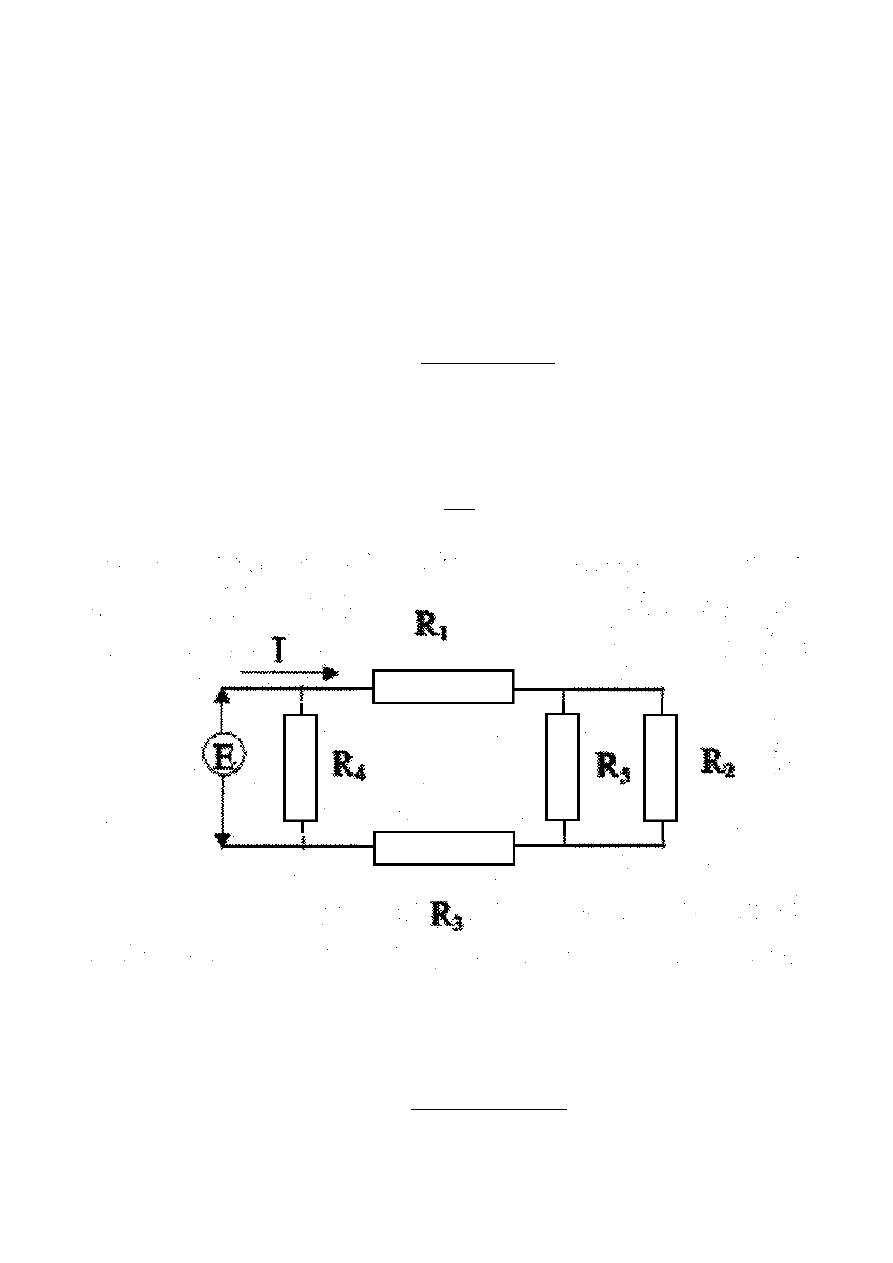
Rozważmy obwód oporowy prądu stałego pokazany na Rys 3.1. W tym obwodzie, przepływem jest
przepływ elektronów (lub inaczej prąd I), siłą napędową jest różnica potencjałów na obwodzie (ΔE)
i zastępcza rezystancja (opór R

eq

), którym jest połączenie szeregowo-równoległe oporników. Dla

tego obwodu na Rys 3.1, można napisać prawo Ohma następująco:

I =



E

R

eq

Analogicznie możemy zapisać prawo Ohma dla ustalonego laminarnego objętościowego przepływu
krwi między dwoma punktami w układzie krążenia jako

Q[l/ min]=



P [mm Hg]

R

eq

[

mm Hg/l/min]

Przepływ wolumetryczny (Q) między dwoma punktami jest równy sile napędowej tego przepływu

Rysunek 3.1: Szeregowo-równoległy obwód elektryczny. Oporniki R

1

, R

2

tworzą połączenie szeregowe wraz z

równolegle połączonymi opornikami R

5

i R

2

, natomiast opornik R

4

jest równoległą ścieżką dla przepływu prądu

(różnica ciśnień między dwoma punktami,  P ) podzielonej przez równoważny opór
hemodynamiczy naczyń i narządów na drodze przepływu ( R

eq

), gdzie



P=P

1

−

P

2

, a

jednostki równoważnego oporu są tak dobrane, że aby zapewnić zgodność jednostek po obu
stronach równania (3.1).
Jakie są te czynniki, które określają równoważną oporność hemodynamiczną? Są one analogicznie
do tych czynników, które określają równoważną oporność elektryczną.

1. Właściwości fizyczna płynu, w szczególności lepkość płynu
2. Długość drogi między punktami 1 i 2
3. Średnica naczynia lub naczyń na tej drodze
4. Szczegóły układu połączeń szeregowo-równoległych naczyń w sieci
5. Podatny (rozciągliwy) charakter ścian naczyń

Znajdujemy, że równanie (3.1) jest jedynie przybliżeniem. Zarówno przepływ jak i ciśnienie są
zmienne w czasie (pulsujące), a modele naczyń składają się z elementów oporowych,
pojemnościowych i (być może) indukcyjnych. Bardziej realistyczne podejście może polegać na
potraktowaniu przepływu między dwoma punktami jako analogowego obwodu prądu zmiennego
(ac) i napisanie prawa Ohma w sensie impedancji obwodu

Z =



P 

Q 

(3.2)

gdzie  jest pewną częstotliwością charakterystyczną fali ciśnienia.
Ponieważ impedancja jest pojęciem związanym z częstotliwością, może ona być zdefiniowana na
wiele sposobów. Powrócimy do równ. (3.2) w dalszej części, gdy będziemy pulsacyjny przepływ w
rurze.

Przykład 3.1 Całkowity opór obwodowy

Opór równoważny wszystkich naczyń w sieci szeregowo-równoległej między lewą a prawą stroną
serca nazywany jest całkowitym oporem obwodowym ( R

TP

). Dla naszego wzorca osobniczego,

przepływ między tymi dwoma punktami jest rzutem minutowym serca (CO). Średnie (uśrednione w
czasie) ciśnienie w aorcie jest równe 100 mm Hg. Ciśnienie w prawym przedsionku jest, umownie,
równe 0 mm Hg (ciśnienie atmosferyczne). Zadaniem jest obliczenie R

TP

.

Rozwiązanie. Korzystając z równ. (3.1),

R

TP

=



P

Q

=

100−0

5

=

20

mm Hg

l /min

Całkowity opór obwodowy rośnie z wiekiem i w pewnych stanach chorobowych, gdzie tętnice są
sztywne, R

TP

maleje z wysiłkiem. Wtedy miejscowe procesy regulacyjne sprawiają, że

rozszerzają się arteriole (główne naczynia oporowe) w mięśniach szkieletowych.

Prawo lepkości Newtona

Krew jest płynem złożonym o składzie wielofazowym. Zawiera on fazę uwodnioną (osocze) z
rozpuszczonymi białkami (albuminy, globuliny, fibrynogen) oraz elektrolitami a także zawieszone
cząstki (krwinki czerwone, leukocyty, płytki). Własności mechaniczne krwi w całości zależą od
frakcji objętościowej krwinek czerwonych (hematokryt) jak i od ilości i rozkładu zawartości białek
w osoczu. W dużych naczyniach, pulsacyjny charakter przepływu utrzymuje komórki w zawiesinie
i możemy w przybliżeniu uważać krew za płyn jednorodny. W mikrokrążeniu, w szczególności w
małych naczyniach, czerwone krwinki i osocze w oczywisty sposób tworzą oddzielne fazę.
W następnych częściach wprowadzimy równania ruchu jednorodnego lepkiego płynu i zastosujemy
je do przepływu w dużych naczyniach.

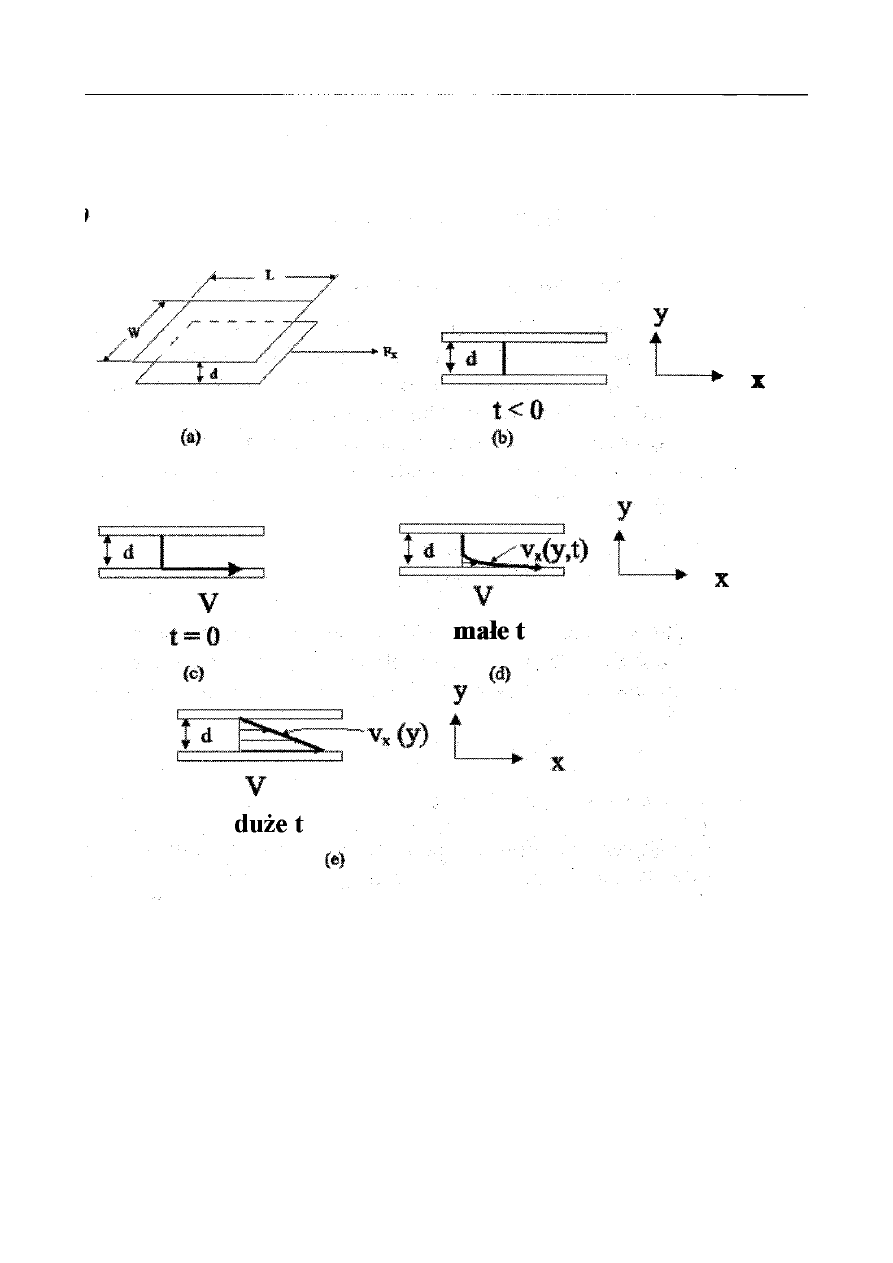
Rysunek 3.2a pokazuje parę dużych równoległych płyt o długości L a szerokości W ustawionych w
niewielkim odstępie d. Górna płyta jest unieruchomiona, a dolna płyta może być przesuwana w
kierunku x. Przestrzeń między płytami jest wypełniona lepkim płynem. W chwili t=0, prędkość
płynu jest zerowa wszędzie w przestrzeni między płytami (Rys. 3.2b). W chwili t=0 pociągamy
dolną płytę w kierunku x ze stałą siłą F

x

(Rys. 3.2c), która wywołuje ruch dolnej płyty z prędkością

V. Zakładamy, że płyn w pobliżu ścianki płyty przylega do niej i przesuwa się z tą samą prędkością
jak ściana. Nazywamy to warunkiem brzegowym „braku poślizgu na ściance”. W chwilach
początkowych zachodzą zjawiska przejściowe i pokazuje się profil prędkości taki jak na Rys. 3.2d.
Po znacznym upływie czasu, profil prędkości stanu ustalonego wygląda pewnie tak jak na Rys. 3.2.
Zostało potwierdzone doświadczalnie, że w stanie ustalonym przyłożona siła na jednostkę
powierzchni F

x

/A jest proporcjonalna do prędkości V i odwrotnie proporcjonalna do odległości d.

Rysunek 3.2: Laminarny przepływ między równoległymi płytami

Możemy to zapisać jako

F / A∝V /d

gdzie A=LW (pole powierzchni równoległe do płynącej cieczy).
Siła na jednostkową powierzchnię nazywa się naprężeniem. W tym wypadku siła jest przyłożona
równolegle do powierzchni płyt, tak że naprężenia są naprężeniami ścinającymi i są oznaczane
symbolem 

yx

. W tej notacji, drugi indeks odnosi się do orientacji siły (kierunek x), a pierwszy

indeks odnosi się do kierunku prostopadłego (normalnego) do powierzchni, na którą oddziałuje siła
ścinająca. W tym przepadku, siła ścinająca działa na powierzchnię zorientowaną w kierunku xz.
Odnotujmy, że górna płyta purusza się z zerową prędkością, tak więc różnica prędkości między
górną i dolną płytą wynosi (góra - dół) = 0 - V. Jeśli wybierzemy jako początek osi y na górnej
płycie, różnica między górą i dolną płytą jest równa d-0. Związek (3.3) może teraz być zapisany
jako



yx

∝−

0−V / d −0

(3.4)

Znak „-” został wstawiony tak, aby były spełnione równania opisane związkami (3.3) i (3.4). Aby
uczynić związek (3.4) równaniem, musimy pomnożyć prawą stronę przez czynnik
proporcjonalności. Oznaczymy tej czynnik proporcjonalności przez  . Związek (3.4) przyjmuje
taką postać



yx

=−



0−V 



d −0

(3.5)

Przechodzimy teraz do granicy d 0 i znajdujemy, że wyrażenia w nawiasach prawej strony
równania (3.5) są definicją pochodnej składowej x prędkości wzdłuż y.



yx

=−

dy

x

dy

(3.6)

Równanie (3.6) jest jednowymiarową postacią bardziej ogólnego, zasadniczego równania zwanego
prawem lepkości Newtona. Płyny, które podlegają trójwymiarowemu uogólnieniu tego równania w
całym obszarze przepływu nazywane są płynami newtonowskimi. Inne zasadnicze równania są
stosowane dla płynów, które nie spełniają prawa lepkości Newtona (płyny nie-newtonowskie).
Przedyskutujemy kilka z nich (płyt prawa potęgowego, płyn Casson, płyn Bingham) w następnej
części.
Równanie (3.6) może być interpretowane na różnych poziomach. Na jednym z poziomów, można
użyć tego równania jako definicji lepkości. W ten sposób lepkość płynu newtonowskiego jest
współczynnikiem fenomenologicznym, który po wymnożeniu ze znakiem przeciwnym przez
obserwowany gradient swojej prędkości równa się przyłożonym naprężeniom ścinającym. Na
innym poziomie, możemy spojrzeć na Równ. (3.6) jako na przykład prawa liniowej szybkości
[patrz równanie (1.1)]. W tym przypadku, lepkość jest interpretowana jako parametr materiałowy,
to jest, fizyczną właściwość płynu. Taka interpretacja lepkości jest najbardziej użyteczna.

Jednostki lepkości

Równanie (3.6) wymaga, aby jednostki po prawej stronie równe były jednostkom po lewej stronie.
Jednostki po prawej stronie odpowiadają naprężeniom (siła/powierzchnię), gdy z kolei jednostki po
lewej stronie odpowiadają gradientowi prędkości (prędkość/długość). Jednostki lepkości muszą być
tego rodzaju, że jednostki po obu stronach są równe. W systemie cgs, siła/powierzchnię może być
wyrażona jako dyna/cm

2

. Gradient prędkości ma jednostki cm/(s·cm). Z równania (3.6) lepkość (



) misi mieć następujący wymiar:

dyna·s/cm

2

=(dyna/cm

2

)/(cm/(s·cm))

Ponieważ dyna jest siłą g·cm/s

2

jednostki lepkości są często zapisywane jako g/(s·cm). Jeden gram

na centymetr na sekundę nazywany jest pauzem (poise) ku czci Jean L.M. Poiseuille (1790-1869),
francuskiego lekarza (i fizyka), który był jednym z pionierów badań ilościowych przypływu krwi w

rurkach. Ponieważ pauz (w skrócie P) jest raczej dużą wartością dla zwykłych płynów, więc
lepkości są zazwyczaj wyrażane w centypauzach. Jeden centypauz (cps) = 10

-2

pauza. Aby mieć

jakieś porównanie, lepkość wody dla 25°C i 1 atm jest równa około 1 cps. Lepkość osocza krwi w
37°C jest równa około 1,2-1,5 cps, a całkowita lepkość krwi dla 45% hematokrytu (w normie) i
37°C jest 3,5-4,5 cps.

Przepływ laminarny i lepkość krwi

Reologia zajmuje się badaniem własności mechanicznych płynów. Płyny, w tym krew, są
sklasyfikowane ze względu na ich zachowanie przepływu, inaczej zachowanie reologiczne pod
wpływem ciągłej siły przyłożonej do tego płynu.
W doświadczeniu pokazanym na Rys 3.2, płyn między płytami porusza jako przepływ laminarny.
Oznacza to, że płyn porusza się w cienkich jak kartki warstwach (zwanych lamellae), tak że
wzajemne ślizganie się warstw jedna po drugiej ma miejsce w uporządkowany sposób. Warstwy
laminarne płynu poruszające się z większymi prędkościami wywierają siły ścinające na
najbliższych sąsiadów poruszających się z mniejszą prędkością i z kolei, są pociągane do przodu
przez siły ścinające wywierane przez swojego sąsiada poruszającego się z jeszcze większą
prędkością. Ponieważ każda taka siła ścinająca wytwarza równą i przeciwną siłę, warstwy płynu
poruszające się z większą prędkością doświadczają siły reakcji ze strony przylegających warstw ze
strony niższych prędkości. Ta siła reakcji działa hamująco ruch do przodu warstwy o większej
prędkości. Wielkość tej siły hamującej zależy od wzajemnej międzycząsteczkowej siły przyciągania
cząstek płynu. Gdy mierzymy siłę wymaganą dla uzyskania danego gradientu prędkości dla danego
płynu przy ustalonej geometrii, stosunek tych dwóch pomiarów jest miarą sił przeciągania
międzycząsteczkowego w płynie. Definiujemy to jako lepkość. W ten sposób lepkość odgrywa tę
samą rolę dla płynów jak współczynnik tarcia ślizgowego w ciałach stałych. Ponieważ lepkość
płynu zależy od międzycząsteczkowych sił przeciągania jest to fizyczna własność płynu.
Jeżeli płyn spełnia równ. (3.6) możemy nakreślić przyłożone naprężenia ścinające na osi y, a
zmierzony gradient prędkości ze znakiem przeciwnym (szybkość ścinania) na osi x i otrzymujemy
linię prostą, której nachylenie jest (newtonowską) lepkością.

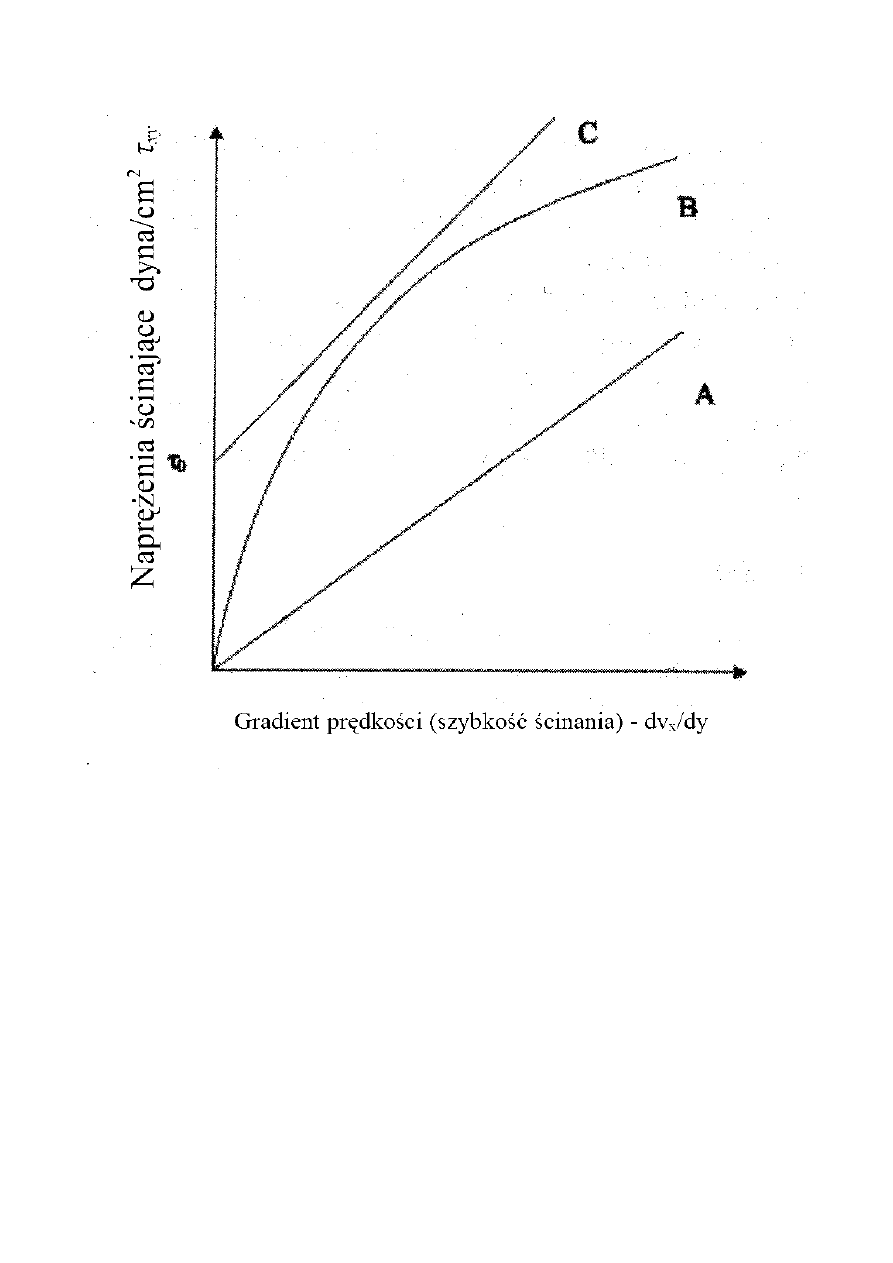
Różne płyny wykazują różne typy zachowania reologicznego. Rysunek 3.3 pokazuje pewne
możliwe związki. Płyn A przedstawia płyn newtonowski. Płyny B i C przedstawiają różne płyny
zachowujące się nie-newtonowsko. W płynie B, lepkość (określona jako nachylenie krzywej w
dowolnym punkcie) maleje z rosnącym naprężeniem ścinającym. To zachodzi w płynach
zawierających rozpuszczone polimery, które mogą tworzyć mikrostruktury dla małych szybkości
ścinania (n.p. białka osocza i fibrogeny), które są rozbijane przy większych szybkościach
ścinających. Krzywa C dotyczy płynu nie-newtonowskiego z naprężeniem początkowym τ

0

.

Naprężenie początkowe często występuje w płynach niejednorodnych, które zawierają fazę
cząsteczkową zespoloną w pewną mechaniczną strukturę dla małych szybkości ścinania. Przy
pewnym skończonym naprężeniu ścinającym τ

0

, agregaty rozsypują się i płyn zaczyna płynąć.

Zwykła krew w całości jest płynem niejednorodnym, a czerwone krwinki mają zdolność do
agregacji przy małych szybkościach ścinających. Jeżeli zachowanie płynu jest podobne do
newtonowskiego powyżej pewnego naprężenia ścinającego, nazywa się plastikiem Binghama
(płynem plastyczno-lepkim Binghama).
Choć krew jako całość wykazuje naprężenie początkowe dla małych szybkości ścinania, ta wartość
jest zupełnie mała (~0,05 dyn/cm

2

) Oznacza to, że do utrzymania przepływu w kapilarze o średnicy

Rysunek 3.3: Zachowanie reologiczne płynów

50 μm i długości 0,5 cm wystarczy ciśnienie mniejsze od 0,02 mm Hg. Jednakże, w łożu
kapilarnym odpowiadającym 500 takich naczyń w szeregu, jeżeli przypływ zatrzymałby się w
sposób nagły na wskutek skurczu naczyniowego tętniczego naczynia końcowego zaopatrującego to
łoże, skok ciśnienia rzędu 10 mm Hg będzie potrzebne aby wznowić przepływ. Naprężenie
początkowe krwi jest bardzo trudno mierzalne, ponieważ wpływają na nie takie czynniki jak
stężenie antykoagulantów, stężenie pewnych dużych białek (fibrogeny, albuminy), hematokryt i
zmieniające się w szerokim zakresie właściwości z próbki na próbkę.
Z powodu złożonego charakteru krwi, używa się różnych związków definiujących (modele
reologiczne) do opisu zachowania relacji naprężenie-ścinanie. Każdy z tych modeli ma swoje
zalety i wady, gdy używa się go w różnych zakresach naprężeń ścinających i stężeniach
czerwonych krwinek. Najbardziej popularnymi modelami są model Casson'a, model prawa
potęgowego i model plastyczny Binghama.
Model Casson'a
Równanie Cassona jest najbardziej popularnym modelem stosowanym dla przedstawienia
zachowania się nie-newtonowskiego krwi z szerokim zakresie stężenia czerwonych krwinek i
szybkości ścinania 1-100000 s

-1

. Jest to szczególnie korzystne w regionie małych szybkości

ścinania dla modelowania naprężenia ścinającego.



1 /2

=

1/ 2

˙

1 / 2



y

1 /2

(3.7)

gdzie  = jest naprężeniem ścinającym, 

y

= naprężenie początkowe, ˙ szybkość ścinania i



lepkość Casson'a (lepkość pozorna).

(...)
Model przepływu z prawem potęgowym
Model zgodny z prawem potęgowym jest związkiem empirycznym między naprężeniami
ścinającymi i szybkością ścinania, który symuluje reologiczne zachowanie krwi w szerokim
zakresie wartości hematokrytu. Nie stosuje się dla małych szybkości ścinania.



rz

=−

m

∣

dv

z

dr

∣

n−1

dv

z

dr

(3.8)

Równanie prawa potęgowego redukuje się do prawa lepkości Newtona gdy n = 1 i m = μ.
Odchylenie n od jedności jest w ten sposób miarą odchylenia zachowania się płynu
newtonowskiego. Dla wartości n<1, lepkość maleje ze wzrostem szybkości ścinania i to
zachowanie określa się jako pseudoplastyczność. Krew zachowuje się jako płyn pseudoplastyczny
w szerokim zakresie naprężeń ścinających.
(...)

Przepływ w rurze

(...)
Szybkość przepływu objętościowego Q [l/min] jest iloczynem średniej prędkości i pola przekroju
poprzecznego, gdzie ten przepływ się odbywa. Dla rury, pole przekroju poprzecznego jest równe po
prostu πR

2

, więc

Q=



R

4



P

0

−

P

L



8 L

(3.23)

Ten wynik jest nazywany równaniem Hagena-Poiseulle lub prawem Poiseulle'a od dwóch
naukowców, którzy wyprowadzili je niezależnie niemalże w tym samym czasie (1839-1841).
Ten wynik jest ważny fizjologicznie z dwóch powodów.

1. Jeśli porównamy Równ. (3.23) z prawem ohma [równ. (3.1)] możemy znaleźć określone

czynniki, które mają wkład w opór przepływu w sztywnej rurze. Porównując (3.1) z (3.23)
otrzymujemy

R

eq

=

8  L



R

4

(3.24)

To równanie mówi nam, że opór dla przepływu laminarnego pojedynczego, sztywnego
naczynia jest wprost proporcjonalny do długości naczynia i lepkości płynu i odwrotnie
proporcjonalny do promienia rurki podniesionego do czwartej potęgi. (...) Zależność typu
czwartej potęgi oznacza, że małe zmiany promienia naczynia mają duży wpływ na opór
przepływu. W rzeczywistości, wazokonstrykcja i wazodilatacja arterioli są głównymi
mechanizmami, poprzez które rzut minutowy serca jest rozdzielany na tkanek i narządów w
odpowiedzi na zmienne zapotrzebowanie metaboliczne (jak w wysiłku).

2. Mimo, że Równ. (3.23) zostało wyprowadzone dla przepływu laminarnego w sztywnej

rurce, pokazano doświadczalnie, że związek zawierający odwrotność czwartej potęgi
między oporem naczynia i promieniem jest zachowany także in vivo, to znaczy w
naczyniach elastycznych. In vivo nie stosuje się jednak czynnik 8/π.

(...)

Powszechnie spotykane tony serca

U większości normalnych osobników można wykryć dwa tony serca, gdy stetoskop lub mikrofon
jest umieszczony po lewej stronie mostka (sternum, breastbone) na trzecim lub czwartym
międzyżebrzu (nad koniuszkiem serca). Pierwszy ton serca, nazywany S

1

, pojawia się na początku

skurczu z powodu gwałtownego zamykania się zastawek przedsionkowo-komorowych (AV). To
zjawisko wytwarza wibracje struktur sercowych i gwałtowne zablokowanie krwi w objętości
komór. Jest to podobne do „uderzenia wodny”, jakie jest wytwarzane w wężu wodnym, gdy
zamknie się gwałtownie zawór. Drugi dźwięk serca, nazywany S

2

, bierze się z zamykania zastawek

aortalnej i pnia płucnego na początku okresu relaksacji izowolumetrycznej. Te dwa dźwięki są
opisywane przez wielu ludzi jako sercowe dźwięki „lab-dab”, gdy słucha ich się stetoskopem.
Trzeci ton serca, S

3

, nie jest normalnie słyszalny stetoskopem u dorosłych. S

3

może być słyszalny u

dzieci i występuje krótko po S

2

, w czasie okresu szybkiego, intensywnego, pasywnego wypełniania

lewej komory. Gdy S

3

jest słyszalne u dorosłych, jest na ogół związane z uszkodzeniem lewej

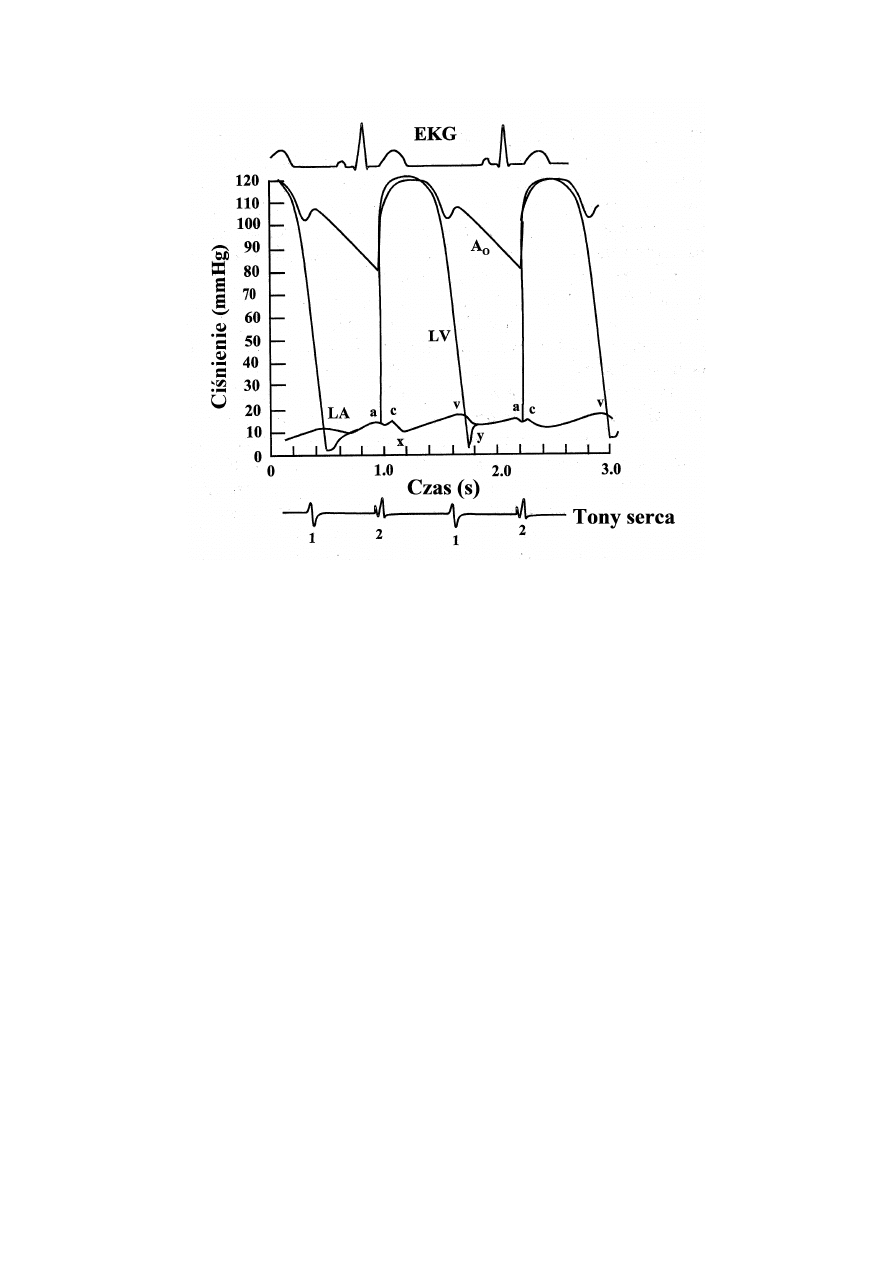
komory. Rysunek 3.11 pokazuje normalne ciśnienia w lewej komorze, lewym przedsionku, aorcie
jak i pozycję czasową dwóch normalnych tonów serca. (...)

Efekty grawitacyjne

Efekty grawitacyjne stają się ważne w przepływie krwi płucnej. Krążenie płucne i obwodem nisko-
oporowym. Dlatego, prawa komora musi wytworzyć tylko około 20 procent ciśnienia
wytwarzanego w lewej komorze w celu wstrzyknięcia objętości wyrzutowej do tętnicy płucnej.
Anatomicznie, tętnica płucna leży u podstawy płuc. W normalnych, spoczynkowych warunkach
ciśnienia skurczowe/rozkurczowe w tętnicy płucnej są 25 mm Hg/8 mm Hg, ze średnim ciśnieniem
równym 15 mm Hg. Porównajmy te wartości z 120 mm Hg/80 mm Hg (skurczowe/rozkurczowe) i i
średnią 100 mm Hg dla krwiobiegu dużego. U normalnego dorosłego w pozycji stojącej, koniuszek
płuc (najwyższy punkt) jest około 30 cm powyżej podstawy (najniższy punkt). Ponieważ 1 mm Hg
= 1,36 cm H

2

O, kolumna krwi o wysokości 30 cm może wytworzyć nadwyżkę ciśnienia

hydrostatycznego z powodu grawitacji (ρgΔh) równą około 22 mm Hg, które przeciwstawia się
ciśnieniu w tętnicy płucnej (zauważmy, że krew jest nieco bardziej gęsta od wody, około 1,04-
1,08 g/ml w 37°C). Ta nadwyżka ciśnienia jest nierówno rozdzielona, około 8 mm Hg poniżej serca
i około 15 mm Hg powyżej serca. Skutkiem tego jest to, że tętnicze ciśnienia w najwyższej części
stojącej dorosłej osoby są 15 mm Hg poniżej tych w tętnicy płucnej, a ciśnienia w najniższej części
płuc są 8 mm Hg powyżej tych jakie są w pniu płucnym. Skutki tego gradientu ciśnienia
spowodowanego grawitacją dla przepływu krwi w płucach są takie, że w normalnych,
spoczynkowych warunkach nie ma przepływu w najwyżej położonej (w przybliżeniu jedna trzecia)
części płuc podczas wszystkich części cyklu serca (strefa I), ponieważ ciśnienie w tętnicy płucnej w
tym regionie jest mniejsze od ciśnienia pęcherzykowego i naczynia tętnicze są zamknięte. W
przybliżeniu trzeciej środkowej części płuc (strefa II), przepływ krwi ma miejsce podczas
skurczowej fazy cyklu sercowego, gdy ciśnienie tętnicze jest większe od ciśnienia pęcherzykowego
i naczynia tętnicze są otwarte. W około trzeciej, najniższej części płuc (strefa III) ma miejsce ciągły
przepływ krwi, ponieważ ciśnienie tętnicze tutaj jest zawsze wyższe od ciśnienia pęcherzykowego.

Rysunek 3.11: Ciśnienia w normie w lewym przedsionku, lewej komorze i aorcie.
EKG jest pokazane dla odniesienia w czasie. Normalne tony serca są pokazane jako 1
i 2 na dole rysunku. Oznaczenia a, c i v na fali ciśnienia przedsionkowego pokazują
odpowiednio wzrost ciśnienia przy skurczu przedsionkowym, zwiększenie ciśnienia w
wyniku skurczu komór i maksymalne ciśnienie przedsionkowe przy zamknięciu
zastawki aortalnej.

Dobrą wiadomością jest to, że prawie dwie trzecie płuc jest łatwo dostępna jako rezerwa dla
wymiany gazowej krew-tkanka, gdy wymagany jest wysiłek lub pojawią się inne czynniki
zwiększające zapotrzebowanie metaboliczne. Wówczas podnosi się ciśnienie krwi w tętnicy płucnej
i więcej z normalnie zamkniętych naczyń tętniczych bierze udział w perfuzji w górnej części płuc.
(...)