Próbny egzamin maturalny z matematyki
Poziom rozszerzony
1
Kujawsko-Pomorskie Centrum Edukacji Nauczycieli
w Bydgoszczy
PLACÓWKA AKREDYTOWANA
KOD
PESEL
PRÓBNY EGZAMIN MATURALNY
Z MATEMATYKI
POZIOM ROZSZERZONY
1. Sprawdź, czy arkusz egzaminacyjny zawiera 16 stron
(zadania 1-12). Ewentualny brak zgłoś przewodniczącemu
zespołu nadzorującego próbny egzamin.
2. Rozwiązania zadań i odpowiedzi wpisuj w miejscu na
to przeznaczonym.
3. Pamiętaj, że pominięcie argumentacji lub istotnych obliczeń
w rozwiązaniu zadania otwartego może spowodować, że za to
rozwiązanie nie będziesz mógł dostać pełnej liczby punktów.
4. Pisz czytelnie i używaj tylko długopisu lub pióra z czarnym
tuszem lub atramentem.
5. Nie używaj korektora, a błędne zapisy wyraźnie przekreśl.
6. Pamiętaj, że zapisy w brudnopisie nie będą oceniane.
7. Możesz korzystać z zestawu wzorów matematycznych, cyrkla
i linijki oraz kalkulatora.
8. Na karcie odpowiedzi wpisz swój numer PESEL.
9. Nie wpisuj żadnych znaków w części przeznaczonej
dla egzaminatora.
We współpracy
Luty 2013
Czas pracy:
180 minut
Liczba punktów
do uzyskania: 50

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
2
Zadanie 1. (4 pkt)
Rozwiąż równanie:
w przedziale 〈 〉.

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
3
Zadanie 2. (4 pkt)
Dany jest czworokąt
Niech będzie punktem przecięcia jego przekątnych.
Udowodnij, że czworokąt
można wpisać w okrąg wtedy i tylko wtedy,
gdy
| |
| |
| |
| |
.

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
4
Zadanie 3. (4 pkt)
Dane są funkcje
( )
oraz
( )
, o których wiadomo, że ich wykresy mają
punkt wspólny
(
) a miejscem zerowym funkcji jest liczba:-
. Wyznacz wartości
parametrów
Próbny egzamin maturalny z matematyki
Poziom rozszerzony
5
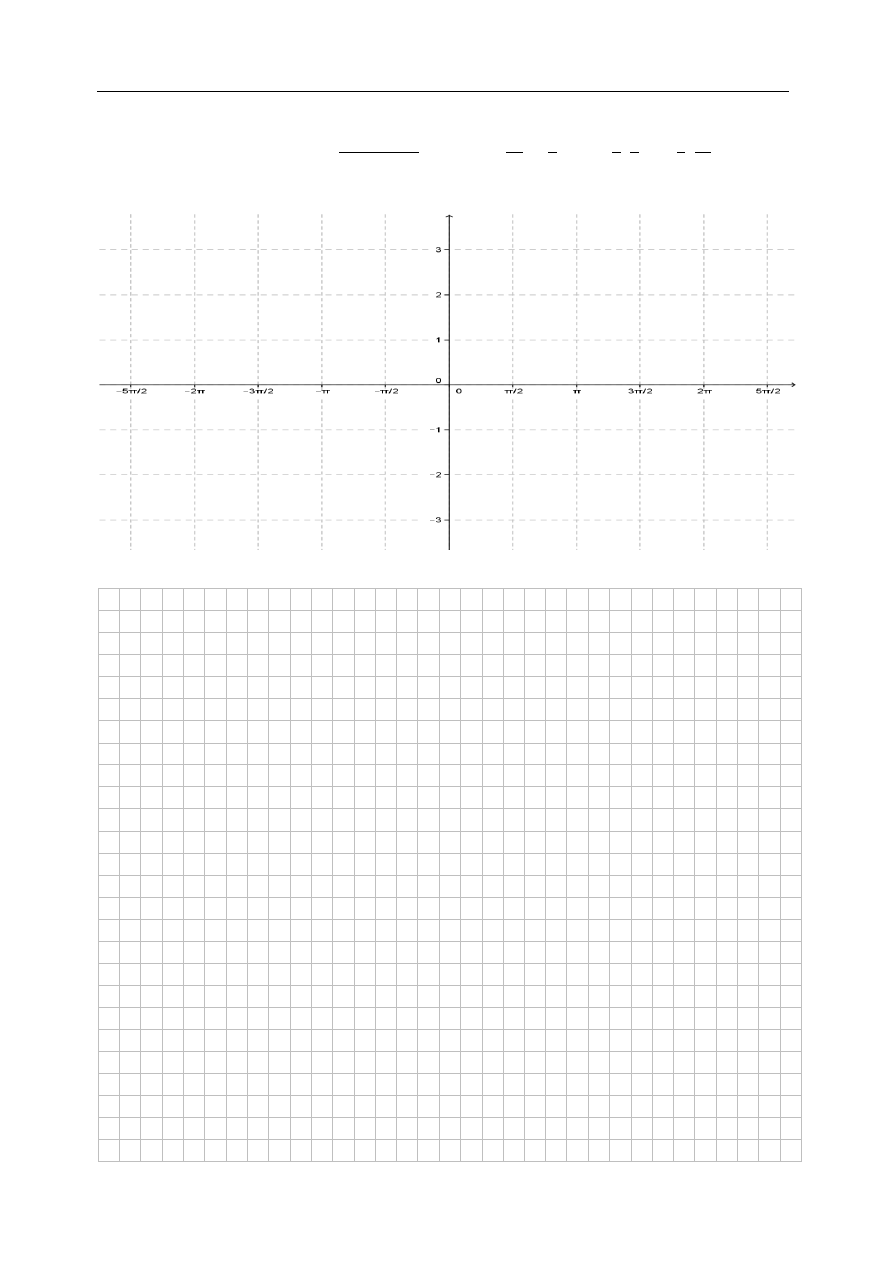
Zadanie 4. (4 pkt)
Narysuj wykres funkcji
( )
| |
dla
(
) (
) (
)
Podaj zbiór rozwiązań nierówności
( )
Próbny egzamin maturalny z matematyki
Poziom rozszerzony
6
Zadanie 5. (4 pkt)
Suma trzech liczb będących kolejnymi wyrazami rosnącego ciągu geometrycznego jest równa
. Jeżeli do pierwszej liczby dodamy do drugiej a do trzeciej to otrzymamy trzy
kolejne wyrazy ciągu arytmetycznego. Wyznacz ten ciąg.
Próbny egzamin maturalny z matematyki
Poziom rozszerzony
7
Zadanie 6. (5 pkt)
Podstawą ostrosłupa jest trójkąt, którego jeden z boków ma długość 6, a kąty do niego
przyległe mają miary
i
. Wysokość ostrosłupa ma długość równą długości promienia
okręgu opisanego na podstawie. Oblicz objętość ostrosłupa. Wynik podaj w postaci
√ ,
gdzie
są liczbami wymiernymi.

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
8
Zadanie 7. (4 pkt)
Dany jest wielomian
( ) stopnia , którego suma wszystkich współczynników jest
równa 4, a suma współczynników przy potęgach o wykładnikach nieparzystych jest równa
sumie współczynników przy potęgach o wykładnikach parzystych. Wykaż, że reszta
( ) z dzielenia tego wielomianu przez wielomian ( ) ( )( ) jest równa
( ) .
Próbny egzamin maturalny z matematyki
Poziom rozszerzony
9
Zadanie 8. (5 pkt)
Narysuj wykres funkcji
( )
(
)
(
)

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
10
Zadanie 9. (4 pkt)
Ze zbioru liczb {
} wybieramy losowo jednocześnie cztery liczby. Oblicz
prawdopodobieństwo zdarzenia
polegającego na tym, że najmniejszą wylosowaną liczbą
będzie
lub największą wylosowaną liczbą będzie .

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
11
Zadanie 10. (5 pkt)
Punkty
( ) i ( ) są wierzchołkami trapezu równoramiennego , którego
podstawy
i są prostopadłe do prostej o równaniu
Oblicz współrzędne
pozostałych wierzchołków trapezu, wiedząc, że punkt
należy do prostej .

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
12
Zadanie 11. (3 pkt)
Wykaż, że dla dowolnych liczb rzeczywistych
zachodzi nierówność
.

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
13
Zadanie 12. (4 pkt)
W trapezie opisanym na okręgu boki nierównoległe mają długości
i , zaś odcinek łączący
środki tych boków dzieli trapez na dwie części, których pola są w stosunku
. Oblicz
długości podstaw trapezu.

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
14
Brudnopis

Próbny egzamin maturalny z matematyki
Poziom rozszerzony
15
Brudnopis
Próbny egzamin maturalny z matematyki
Poziom rozszerzony
16
PESEL
WYPEŁNIA SPRAWDZAJĄCY
Punkty
0
1
2
3
4
5
1
2
3
4
5
6
7
8
9
10
11
12
SUMA
PUNKTÓW
Wyszukiwarka
Podobne podstrony:
Matematyka arkusz2012 2013
Matematyka arkusz
MATEMATYKA ARKUSZ ZESTAW M2
Kuratoryjny konkurs matematyczny 2012 2013(mathluk website pl)
MATEMATYKA ARKUSZ ZESTAW M1
2012 01 16 probna matura matematyka arkusz poziom podstawowy
Egzamin gimnazjalny 2015 Matematyka arkusz
Arkusz obserwacji - Umiejętności matematyczne, Arkusze obserwacji, dojrzałość szkolna
matematyka arkusz
MATURA ROZSZERZONA MATEMATYKA ARKUSZ
matematyka arkusz 2 id 765903 Nieznany
matematyka arkusz zr
Kuratoryjny konkurs matematyczny 2012 2013(mathluk website pl)
Matematyka arkusz
więcej podobnych podstron