11/2009

66

Warsztaty

Komputery kwantowe – przyszłość informatyki?

www.sdjournal.org

67

W

1947 roku, jeden z amerykań-
skich pionierów informatyki,
Howard Aiken, przewidywał,

że sześć standardowych komputerów cyfro-
wych powinno zaspokoić potrzeby oblicze-
niowe całych Stanów Zjednoczonych. Oczy-
wiście, z naszego punktu widzenia prognoza
ta jest rażąco nierealistyczna, musimy jednak
brać pod uwagę zastosowanie komputerów w
tamtych czasach – były one bowiem budo-
wane głównie na użytek wojskowy oraz aka-
demicki. Howard Aiken, podobnie jak inni
twórcy komputerów z tego okresu, nie mógł
przewidzieć, że ich pomysły, chociaż w nie-
znacznie zmodyfikowanej formie, zrewolu-
cjonizują oblicze świata.

Wraz z postępem technologii budowy

komputerów, następował rozwój informa-
tyki teoretycznej, a w szczególności algoryt-
miki. Bardzo szybko okazało się, że sama me-
todologia przetwarzania danych wykorzy-
stywana w klasycznych komputerach cyfro-
wych, budowanych w oparciu o podzespo-
ły elektroniczne, powoduje duże trudności
w rozwiązywaniu pewnych klas problemów.
Chodzi tu nie tylko o zagadnienia, w których
nie udaje się skonstruować algorytmu, jak np.

w problemie komiwojażera, lecz o problemy,
których rozwiązanie wymaga ogromnej mocy
obliczeniowej. Rozwiązanie dużej liczby po-
zornie banalnych zadań na standardowych
komputerach jest praktycznie niemożliwe.

Część genialnych naukowców, zajmują-

cych się budową pierwszych komputerów,
pracowało również nad powstałą w XX wie-
ku nową dziedziną fizyki – fizyką kwanto-
wą. Jednym z nich był John von Neumann,
znany głównie jako twórca architektury von
Neumanna – komputera mogącego wykony-
wać wiele różnych programów, bez potrzeby
zmiany jego budowy. W architekturze von
Neumanna, dane i instrukcje, przechowywa-
ne w jednym typie pamięci, przetwarzane są
przez jednostkę arytmetyczno-logiczną, zaś
wyniki operacji i polecenia operatora prze-
kazywane są przy użyciu urządzeń wejścia/
wyjścia. Pomimo faktu, że John von Neu-
mann sformalizował cały aparat matema-
tyczny wykorzystywany w fizyce kwantowej
oraz był zaangażowany w rozwój wczesnych
technologii komputerowych, nie wpadł na
pomysł połączenia ze sobą tych dwóch dzie-
dzin. Dokonali tego inni naukowcy niemal
30 lat później.

Wróćmy jednak do czasów współczesnych.

Obecnie nad rozwojem teorii informaty-
ki kwantowej oraz praktycznej realizacji za-
dań obliczeniowych na komputerach kwanto-
wych zajmują się duże grupy naukowców. Roz-
wojem tej dziedziny zainteresowane są nie tyl-
ko wielkie firmy, takie jak IBM, lecz również

agencje wojskowe oraz uniwersytety. Pomimo
dość znacznych postępów, jakich udało się do-
konać na przestrzeni ostatnich kilkunastu lat,
wciąż jesteśmy daleko od zbudowania kompu-
tera kwantowego, który mógłby zostać efek-
tywnie zastosowany do rozwiązywania kon-
kretnych problemów.

Pewnie zadajesz sobie teraz pytanie: dlacze-

go zbudowanie komputera kwantowego jest ta-
kie trudne? Otóż okazuje się, że problemy nie
wynikają w głównej mierze z niedoskonałości
technologii. Te same zjawiska, które powodu-
ją, że wizja kwantowego przetwarzania infor-
macji wydaje się tak atrakcyjna, są również
odpowiedzialne za problemy przy budowie
urządzeń je realizujących. Aby zrozumieć tę
poniekąd paradoksalną sytuację, musimy po-
znać podstawy fizyki kwantowej. Nie martw
się jednak – pomimo iż zachęcam Cię, abyś
zapoznał się z aparatem matematycznym wy-
korzystywanym w tej dziedzinie, zrozumie-
nie tego artykułu nie będzie wymagało jego
znajomości.

Naszą podróż do świata komputerów

kwantowych rozpoczniemy od zapoznania
się z podstawami fizyki kwantowej. Omó-
wimy najważniejsze zjawiska, których od-
krycie na zawsze zmieniło myślenie o bu-
dowie materii, a które znajdują ogrom-
ne zastosowanie w dziedzinie kwantowe-
go przetwarzania informacji. Następnie
przyjrzymy się klasycznej architekturze
komputerów oraz algorytmom determini-
stycznym – poznamy również sposób ich
realizacji we współczesnych urządzeniach.
Po zapoznaniu się z tymi informacjami bę-
dziemy już mogli skupić się na właściwym
temacie artykułu – komputerach kwanto-
wych.

Fizyka kwantowa

Fizyka kwantowa to dwa słowa, na których
dźwięk cierpnie skóra każdego, komu fizy-

Komputery kwantowe

Każdy z nas z pewnością słyszał o komputerach kwantowych, próbach

ich zbudowania oraz niemalże nieograniczonych możliwościach, jakie

miałoby dać ich wykorzystanie. W tym artykule zapoznasz się z podstawami

technologii przetwarzania informacji przy użyciu komputerów kwantowych.

Zapraszam do lektury!

Dowiesz się:

• Czym są komputery kwantowe;
• W jaki sposób przebiegał rozwój tej dziedziny;
• Czym różni się budowa komputera kwanto-

wego od komputera klasycznego;

• Czym są i jak działają algorytmy kwantowe

Poziom

trudności

przyszłość informatyki?

oraz poznasz najważniejsze z nich;

• Dlaczego zbudowanie komputera kwanto-

wego jest tak trudne.

11/2009

66

Warsztaty

Komputery kwantowe – przyszłość informatyki?

www.sdjournal.org

67

ka kojarzy się jedynie ze spadającymi jabłka-
mi oraz rzędami niezrozumiałych równań,
służących do opisu bardzo prostych zjawisk.
Na fizyce kwantowej opiera się jednak cała
współczesna chemia, elektronika oraz bar-
dzo wiele innych dziedzin. Co ciekawe, jest
to bardzo młoda gałąź wiedzy – jej początki
datujemy na początek wieku XX.

Krótka historia fizyki kwantowej
Pod koniec XIX wieku fizycy byli bardzo
dumni ze stopnia rozwoju tejże dziedziny na-
uki. Większość problemów, które frapowały
już starożytnych filozofów przyrody, została
dawno rozwiązana i potwierdzona odpowied-
nimi eksperymentami. Nikt nie przejmował
się kilkoma doświadczeniami, które dawa-
ły zaskakujące, niezgodne z przewidywania-
mi wyniki – prawdopodobnie uważano, że z
pewnością znajdzie się ktoś, kto zinterpretu-
je je w odpowiedni sposób na gruncie istnieją-
cej teorii. Paradoksalnie, wyjaśnienie tych zja-
wisk stało się przyczyną obalenia większości
ówczesnych poglądów na temat funkcjono-
wania przyrody.

Za pioniera fizyki kwantowej uznaje się

Maxa Plancka – to on pierwszy zapostulo-
wał, że energia fali elektromagnetycznej (kon-
kretnie światła) jest skwantowana, tzn. może
przyjmować lub zmieniać się jedynie o cał-
kowite wielokrotności pewnej elementarnej
porcji, zwanej kwantem.

Badania Plancka zostały następnie wyko-

rzystane przez Alberta Einsteina w celu wyja-
śnienia zjawiska fotoelektrycznego, polegają-
cego na emisji elektronów z powierzchni me-
talu pod wpływem padającego światła. Ein-
stein wytłumaczył je w następujący sposób:
wiązka światła niesie ze sobą dyskretne war-
tości energii w postaci cząstek zwanych fo-
tonami, które przy zderzeniu z elektronami
sieci krystalicznej danej substancji powodu-
ją ich wybicie. Należy mieć na uwadze, że je-
den foton przekazuje całą swą energię jedne-
mu elektronowi, a następnie znika. Elektro-
ny uzyskują przy tym energię równą różnicy
energii fotonu i pracy wyjścia elektronu z me-
talu. Zjawisko fotoelektryczne nie zachodzi
dla częstości fali elektromagnetycznej niższej
od pewnej granicy, niezależnie od natężenia
promieniowania padającego na płytkę. Dowo-
dzi to jednoznacznie, że energia przenoszona
przez falę elektromagnetyczną jest skwanto-
wana i zależy jedynie od długości fali.

W 1913 roku Niels Bohr ogłosił swoje po-

stulaty dotyczące budowy atomu wodoru.
Oprócz wyjaśnienia paradoksu związane-
go ze stabilnością jądra atomowego (według
praw mechaniki klasycznej, elektrony krą-
żące wokół jądra powinny wypromieniowy-
wać energię, wskutek czego po krótkim cza-
sie musiałyby spaść na jądro), model Bohra
zakładał, że elektrony poruszają się po ści-

śle określonych orbitach, a przejścia pomię-
dzy nimi mogą zachodzić jedynie wskutek
absorbcji lub emisji odpowiednich kwantów
energii (równych różnicy energii pomiędzy
powłokami).

Skoro fala elektromagnetyczna może

być interpretowana jako strumień cząstek
o określonym pędzie, to strumień cząstek
powinien posiadać właściwości falowe – do
takiego wniosku doszedł Louis de Broglie
w swojej pracy opublikowanej w 1924 ro-
ku. Jego hipoteza została potwierdzona do-
świadczalnie przez Davissona i Germera w
1927 roku, gdy po skierowaniu wiązki elek-
tronów na strukturę krystaliczną (działają-
cą jako trójwymiarowa siatka dyfrakcyjna)
zaobserwowali oni zjawisko dyfrakcji, cha-
rakterystyczne dla fal elektromagnetycz-
nych. Cechę fal elektromagnetycznych, po-
legającą na jednoczesnej obecności własno-
ści korpuskularnych (cząsteczkowych) i fa-
lowych, nazywamy dualizmem korpusku-
larno-falowym.

Jednym z najważniejszych kroków na dro-

dze do opracowania kompletnej teorii fizyki
kwantowej było opublikowanie przez Erwina
Schrödingera równania Schrödingera. Przy je-
go wykorzystaniu stało się możliwe opisanie
ewolucji stanu układu kwantowego wraz z
upływem czasu.

Bardzo ważna, z punktu widzenia kon-

strukcji komputerów kwantowych, jest zasa-
da nieoznaczoności Heisenberga. Mówi ona,
że nie można jednocześnie i z dowolną do-
kładnością dokonać pomiaru dwóch wiel-
kości, takich jak pęd i położenie lub czas i
energia. W świecie kwantowym nigdy nie
poznamy wszystkich parametrów cząstecz-
ki – możemy mówić jedynie o prawdopodo-
bieństwie, że cząstka w danej chwili znajduje
się w określonym stanie.

Następne lata przyniosły duże postępy w

zakresie formułowania formalizmu mate-
matycznego, niezbędnego do pełnego opisu
praw fizyki kwantowej. W 1927 roku Paul
Dirac połączył prawa mechaniki kwanto-
wej ze szczególną teorią względności Einste-
ina oraz wprowadził notację stanów układów
kwantowych. W 1932 roku wspominany już
John von Neumann zaproponował komplet-
ny sposób opisu mechaniki kwantowej w ję-
zyku matematyki.

Od tego czasu rozwój fizyki kwantowej

przebiegał już bardzo szybko – wielu na-
ukowców zaangażowanych w jej rozwój pra-
cowało przy projektach zbrojeniowych pro-
wadzonych przez Stany Zjednoczone, mię-
dzy innymi w projekcie Manhattan (mającym
na celu budowę bomby atomowej). Jednym z
najważniejszych, późniejszych dokonań, było
opracowanie teorii elektrodynamiki kwanto-
wej (ang. QED – Quantum Electrodynamics)
przez Richarda Feynmanna.

Pomimo ogromnej drogi, jaką przebyła fi-

zyka kwantowa od momentu jej powstania,
dalej mamy do czynienia z wieloma nie-
wiadomymi. Duże wysiłki ukierunkowa-
ne są również na opracowanie tzw. Teorii
Wszystkiego – wyrażającej wszystkie pra-
wa przyrody i łączącej cztery oddziaływa-
nia podstawowe (grawitację, elektromagne-
tyzm, oddziaływanie silne oraz oddziały-
wanie słabe).

Zastosowanie fizyki kwantowej
Większości osób niezainteresowanych na-
ukami przyrodniczymi i pewnymi dzie-
dzinami techniki fizyka kwantowa kojarzy
się z naukami znacznie bardziej abstrakcyj-
nymi i niemającymi praktycznych zastoso-
wań, np. kosmologią. Rzeczywistość jest
jednak zupełnie inna – bez rozwoju fizy-

Rysunek 1. Przedstawienie maszyny Turinga

Tabela 1. Tabele funktorów logicznych

p

q

p AND q

p OR q

NOT p

p XOR q

1

1

1

1

0

0

1

0

0

1

0

1

0

1

0

1

1

1

0

0

0

0

1

0

11/2009

68

Warsztaty

Komputery kwantowe – przyszłość informatyki?

www.sdjournal.org

69

ki kwantowej nie można mówić o rozwoju
wielu dziedzin chemii oraz – co powinno
być dla nas szczególnie interesujące – elek-
troniki. Okazuje się bowiem, że większość
podzespołów używanych we współcze-
snych komputerach korzysta ze zjawisk
wytłumaczalnych za pomocą mechaniki
kwantowej.

Bez znajomości praw fizyki kwantowej

niemożliwa byłaby produkcja podstawo-
wych podzespołów półprzewodnikowych,
takich jak diody i tranzystory, nie wspomi-
nając o nawet najprostszych układach sca-
lonych. Jeżeli weźmiemy pod uwagę, jak
ogromną rolę odgrywa technologia półprze-
wodnikowa w rozwoju informatyki, oraz jak
duży popyt na nowe technologie elektro-
niczne generuje informatyka, to nie będzie-
my mogli zignorować roli odkryć z dziedzi-
ny fizyki kwantowej dla kształtu wspołcze-
snego świata.

Zastanawiasz się teraz zapewne nad nastę-

pującym problemem – skoro współczesne
komputery w tak dużym stopniu korzystają z
odkryć fizyki kwantowej, to dlaczego nie na-
zywamy ich komputerami kwantowymi? Jest
to bardzo dobre pytanie – aby jednak na nie
odpowiedzieć, przypomnimy najpierw budo-
wę i zasadę działania współczesnych kompu-
terów i algorytmów.

Architektura

współczesnych komputerów

Pełne zrozumienie zasady działania współ-
czesnych komputerów i programów przez nie
przetwarzanych wymaga poznania podstawo-
wych paradygmatów leżących u podstaw in-
formatyki. Zajmiemy się teraz teoretycznymi
i praktycznymi podstawami działania współ-
czesnych komputerów.

Maszyna Turinga
a współczesne komputery
Jednym z podstawowych, abstrakcyjnych mo-
deli komputera jest maszyna Turinga, stwo-
rzona przez matematyka Alana Turinga. Jak
zaraz się przekonasz, jest ona modelem ściśle
teoretycznym – nie do końca oddaje zasadę
działania rzeczywistych komputerów cyfro-
wych. Nie będziemy zajmowali się nią zbyt
długo – matematyczne szczegóły jej działa-
nia są dość skomplikowane, nie mówiąc już o
jej zastosowaniu w celu określania złożoności
obliczeniowej lub rozwiązywalności konkret-
nych problemów.

Maszyna Turinga składa się z nieskoń-

czenie długiej taśmy podzielonej na pola,
służącej jako pamięć (Rysunek 1). Każde z
pól taśmy może znajdować się w jednym z
określonej liczby stanów. W trakcie realiza-
cji procesu obliczeniowego, maszyna Tu-
ringa znajduje się w jednym ze skończonej
liczby stanów, z głowicą ustawioną nad jed-
nym z pól taśmy. Po wykonaniu instrukcji
(polegającej na zmianie wartości pola) gło-
wica przesuwana jest o jedno pole w prawo
lub w lewo.

Z pewnością dostrzegasz już główną ide-

alizację w budowie maszyny Turinga, doty-
czącą nieskończoności taśmy – żaden kom-
puter nie dysponuje nieskończoną pamię-
cią. Maszyna Turinga jest więc jedynie mo-
delem, który z zasadą działania współcze-
snych komputerów ma jedynie kilka wspól-
nych cech charakterystycznych. Najważniej-
szymi z nich są determinizm oraz operowa-
nie na wartościach dyskretnych.

Determinizm jest jedną z podstawowych

cech współczesnych komputerów. Zakłada-
jąc, że maszyna działa poprawnie oraz zna-
jąc kod programu i dane wejściowe, jesteśmy

w stanie dokładnie przewidzieć tok jej dzia-
łania oraz wynik końcowy. Na działanie kom-
putera deterministycznego nie ma wpływu
przypadek, lecz jest ono ściśle zdefiniowa-
ne poprzez jego budowę, przetwarzany kod
oraz dane.

Kolejną ważną cechą komputerów cyfro-

wych jest jest działanie na wartościach dys-
kretnych – czyli należących do skończone-
go zbioru. Elementarną jednostką infor-
macji przechowywanej w komputerze jest
bit (0 albo 1), zaś wszystkie bardziej zło-
żone typy danych są ciągami bitów. Wi-
dać więc, że niezależnie od długości takie-
go ciągu (oznaczmy ją przez n) może on
przyjmować jedynie 2n wartości. Każdy sy-
gnał przed przetworzeniem przez kompu-
ter musi zostać zamieniony na postać cy-
frową – reprezentowaną poprzez skończo-
ną ilość bitów.

Realizacja sprzętowa
Wiemy już, jakie są podstawowe cechy współ-
czesnych komputerów cyfrowych. Zastanów-
my się jednak bliżej nad tym, w jaki sposób
realizowane są w nich wszystkie podstawowe
funkcje związane z przetwarzaniem danych.
Nie będziemy oczywiście opisywali żadnej
konkretnej architektury – posiadają one bar-
dzo wiele cech wspólnych, które nie zmienia-
ją się wraz z coraz to nowszymi i bardziej wy-
dajnymi modelami.

Produkowane obecnie komputery korzy-

stają z podzespołów zbudowanych przy uży-
ciu układów scalonych. Układy scalone za-
wierają (w zależności od skali integracji) od
kilkudziesięciu do setek milionów elemen-
tarnych podzespołów elektronicznych, ta-
kich jak tranzystory, diody, rezystory i kon-
densatory. Dzięki postępowi technologicz-
nemu w elektronice, możliwe jest budowa-
nie układów, w których elementy te mają co-
raz to mniejsze rozmiary, co z kolei prowadzi
do zmniejszenia zużycia energii i zwiększe-
nia mocy obliczeniowej (przynajmniej teo-
retycznie).

Budowa współczesnych układów scalo-

nych jest niezwykle skomplikowana, ma jed-
nak bardzo wiele cech wspólnych z prostymi
układami scalonymi realizującymi funkcje lo-
giczne. Jedną z nich jest wykorzystanie dys-
kretnych poziomów napięć w celu reprezen-
tacji stanów logicznych, np. 1 – 5V, 0 – 0V
(w układach TTL – Transistor-to-Transistor-Lo-
gic). Napięcie podane na dane wejście może
mieć oczywiście dowolną wartość – istnieje
jednak pewien próg, powyżej którego napię-
cie interpretowane jest jako logiczna 1.

Więcej do przeczytania w papierowym wyda-
niu Software Developer’s Journal.

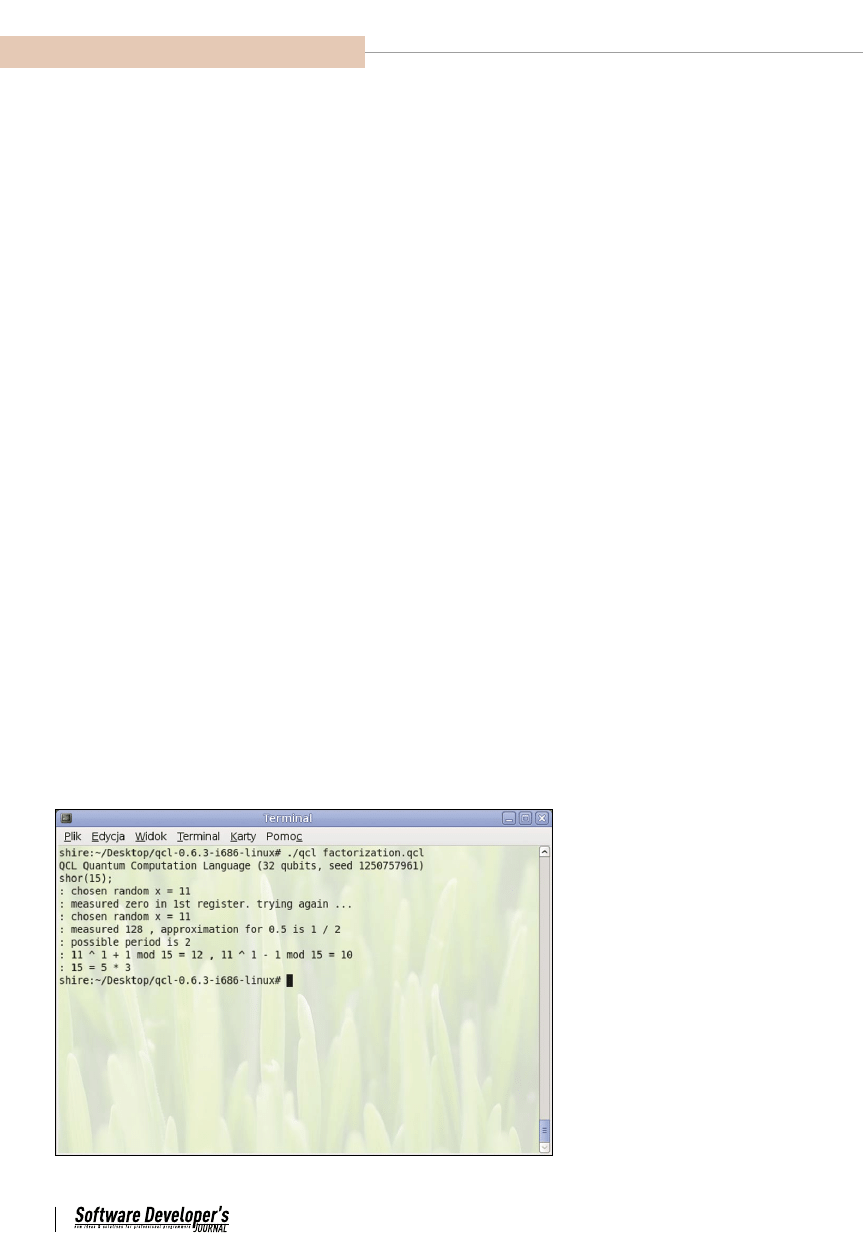
Rysunek 2. Algorytm faktoryzacji Shora w symulatorze QCL