Combustion, Explosion, and Shock Waves, Vol. 37, No. 1, pp. 99–105, 2001

Approximate Method for Calculating the Impact Sensitivity

Indices of Solid Explosive Mixtures

UDC 662.215.4

A. V. Dubovik

1

Translated from Fizika Goreniya i Vzryva, Vol. 37, No. 1, pp. 112–119, January–February, 2001.
Original article submitted September 22, 1999.

An approximate method is proposed to calculate the impact sensitivity indices (critical
initiation pressure and critical charge thickness) for solid explosive mixtures (explo-
sive compositions and mixtures of an oxidizer with a fuel). The calculation is based
on some model concepts of the physicochemical and explosive properties of reactive
mixtures. Test calculations of the sensitivity indices were performed for mixtures of
HMX and TNT and mixtures of ammonium perchlorate with polymethylmethacrylate
(PMMA) and TNT, and the results are compared with data of laboratory experiments
on an impactor.

Calculations of the sensitivity indices of solid ex-

plosive mixtures (SEM) are required to substantiate
the previously proposed mechanisms of initiation of
explosive systems and to predict the sensitivity level
for new mixed compositions.

1. MIXTURES OF SOLID EXPLOSIVES

A rather simple method for calculating the sensi-

tivity indices of individual solid high explosives (HE)
was developed in [1]. This method gives sufficiently
accurate (

±6%) estimates of the critical initiation

pressure p

cr

and the critical charge thickness h

cr

for

HE tested for impact sensitivity by the critical stress
method [2]. For calculations, it is necessary to have
reliable information on a complex of physicochemi-
cal and explosive characteristics, including the den-
sity ρ, the specific heat c

p

, the melting point T

m

, the

piezoelectric coefficient of the melting point β, the
compression strength of the HE charge σ, the heat
of explosion Q, the activation energy of thermal de-
composition E, and the preexponent Z. According
to [1], it is assumed that the stiffness of the load-
ing system of the impact testing machine (impactor
and roller device) ensures a typical time of charge
collapse during which explosion occurs under critical
impact conditions, t

0

= 11.3 µsec. Calculation re-

1

Semenov Institute of Chemical Physics,
Russian Academy of Sciences, Moscow 117977.

duce to solution of the transcendental equation for
the parameter x = (T

m

− T

0

+ βp

m

)/T

0

:

A

x + 1

= B

− ln x,

A =

E

RT

0

,

B = ln

QZt

0

c

p

T

0

.

Here T

0

is the initial temperature,

R is the gas

constant, and p

m

= σ(1 + 2.4(p

cr

/σ

− 1)). The

quantity h

cr

is calculated from the formula h

cr

=

0.385R(p

cr

/σ

− 1), where R is the radius of the im-

pactor.

The method of [1] can be used to calculate the

sensitivity indices for SEM, which, as solid explosives,
explode under fast (brittle) fracture of the charge,
i.e., do not undergo marked viscoplastic or hyperelas-
tic deformation upon impact. Among such SEM are
primarily mechanical mixtures of solid explosives and
solid mixed compositions of the oxidizer–fuel type.

However, particular calculations of the sensitiv-

ity indices of SEM involve serious difficulties due to
the lack of necessary information on the physico-
chemical and explosive characteristics for the major-
ity of such mixtures. Some of these characteristics,
such as ρ, c

p

, and Q, can be calculated from well-

known formulas or simple additive relations using the
composition of the mixture. For the other character-
istics, there are no ready formulas or these charac-
teristics are meaningless in the case of mixtures (for
example, E, Z, and T

m

).

From the aforesaid it becomes obvious that even

approximate information on the physicochemical and
explosive characteristics of SEM can be obtained only

0010-5082/01/3701-0099 $25.00 c

2001

Plenum Publishing Corporation

99

100

Dubovik

using some model concepts on the behavior of mix-
tures upon impact.

It is not necessary that the

model of this or that characteristic of SEM be rather
plausible.

Before detailed theoretical studies, one

can restrict oneself to calculations using approximate
models for the sensitivity indices of SEM, whose re-
sults agree with available experimental data. Models
for the physicochemical and explosive characteristics
of SEM and calculations of sensitivity indices using
these models are considered below.

1.1. Strength of SEM Charges. Processing

of a great body of data on the impact strength of
solid HE obtained by the critical stress method [2]
gives a linear dependence of the quantity σ on the
modulus of bulk compression K = ρc

2

, where c is the

volume speed of sound in the HE material, which is
calculated from the structural formula of substances
by the Rao rule [3]:

σ [MPa] = a

0

+ aK.

(1)

Here a

0

=

−1.45 MPa and a = 0.007. The coeffi-

cient of correlation between the parameters is 0.93.
Because the value of the free term in Eq. (1) is com-
parable to the errors in experimental determination
σ and calculation K, we assume that σ = aK.

We estimate the strength of a mixed composi-

tion. The specific volume of an n-component mixture
is given by the additive relation

V =

X

α

i

V

i

(i = 1, 2, . . . , n),

(2)

where V

i

= 1/ρ

i

is the specific volume of the ith

component and α

i

is the mass content (

P α

i

= 1).

Here and below, the sign

P denotes summation over

all i from 1 to n. Differentiating (2) with respect
to the pressure p, which is considered equal over
the entire mixture, and taking into account that
V

2

i

(dp/dV

i

) =

−c

2
i

(c

i

is the volume speed of sound

in the ith component of the mixture), we obtain

K = V

. X

α

i

V

i

K

−1

i

.

(3)

Substituting V from Eq. (2) into Eq. (3) and assum-
ing that σ

i

= aK

i

, we obtain the following formula

for the strength of the mixture:

σ =

X

α

i

V

i

. X

α

i

V

i

σ

−1

i

= 1

. X

γ

i

σ

−1

i

.

(4)

Here γ

i

= α

i

V

i

/V is the volume content of the ith

component of the mixture.

In tests of impact sensitivity of HE using the

critical stress method [2] to determine the strength
of a charge, a thin layer of the tested material is
pressed under a rather high pressure (to 0.5 GPa).
But because of the poor compressibility of thin layers,
the strength of the HE charges produced is several
(from 10 and more) percent lower than the maximum

value calculated from (2). The decreased density of
the charges cannot be explained only by the presence
of air inclusions between the HE crystals. We assume
that the intercrystalline space is filled with fine par-
ticles — the products resulting from fracture of the
surface layers of the crystals during pressing. We as-
sume that the conglomerate of these dusty particles
is the (n + 1)th independent component of the SEM
charge and its volume content is Π = 1

−

P γ

i

> 0

and strength is σ

0

.

With allowance for the new component of the

mixture, (4) is written as

σ =

(1

− Π)

P α

i

V

i

/σ

i

P α

i

V

i

+

Π

σ

0

−1

.

(5)

The product σ

i

r

i

is called the mechanical stiff-

ness of crystals of size r

i

.

We assume that r

0

=

P α

i

r

i

is the typical size of gaps between the crystals,

and, by analogy with Eq. (3), we write the follow-
ing expression for the stiffness of the intercrystalline
medium:

(σ

0

r

0

)

−1

=

X

α

i

(σ

i

r

i

)

−1

.

(6)

Substituting (6) into (5), we obtain the final formula
for the strength of a SEM charge. In the case of a
binary (n = 2) mixture, it is written as

σ

σ

1

=

R

1

(1

− Π)(1 + R

2

(1 + b))

(7)

b =

Π(1

− α)R

1

R

3

R

4

(1

− Π)R

2

,

where R

1

= 1 + αρ

1

/(1

− α)ρ

2

, R

2

= αρ

1

σ

1

/(1

−

α)ρ

2

σ

2

, R

3

= 1 + αr

1

σ

1

/(1

− α)r

2

σ

2

, R

4

= 1 +

αr

2

/(1

− α)r

1

, σ

1

is the strength of the 1st com-

ponent, and α is the content of the 2nd component
of the mixture. From (7) it follows that σ

→ σ

1

as

α

→ 0 and σ → σ

2

as α

→ 1 for all Π. If the charge is

pressed to the maximum density (Π = 0), Eq. (7) be-
comes Eq. (4). A comparison of Eq. (7) and Eq. (4)
shows that in (7) the quantity b > 0 plays the role
of an adjusting parameter for the main formula (4).
Its role is minor if the particles of the mixture com-
ponents have approximately identical sizes (r

1

≈ r

2

),

but it increases markedly when r

1

r

2

or r

1

r

2

.

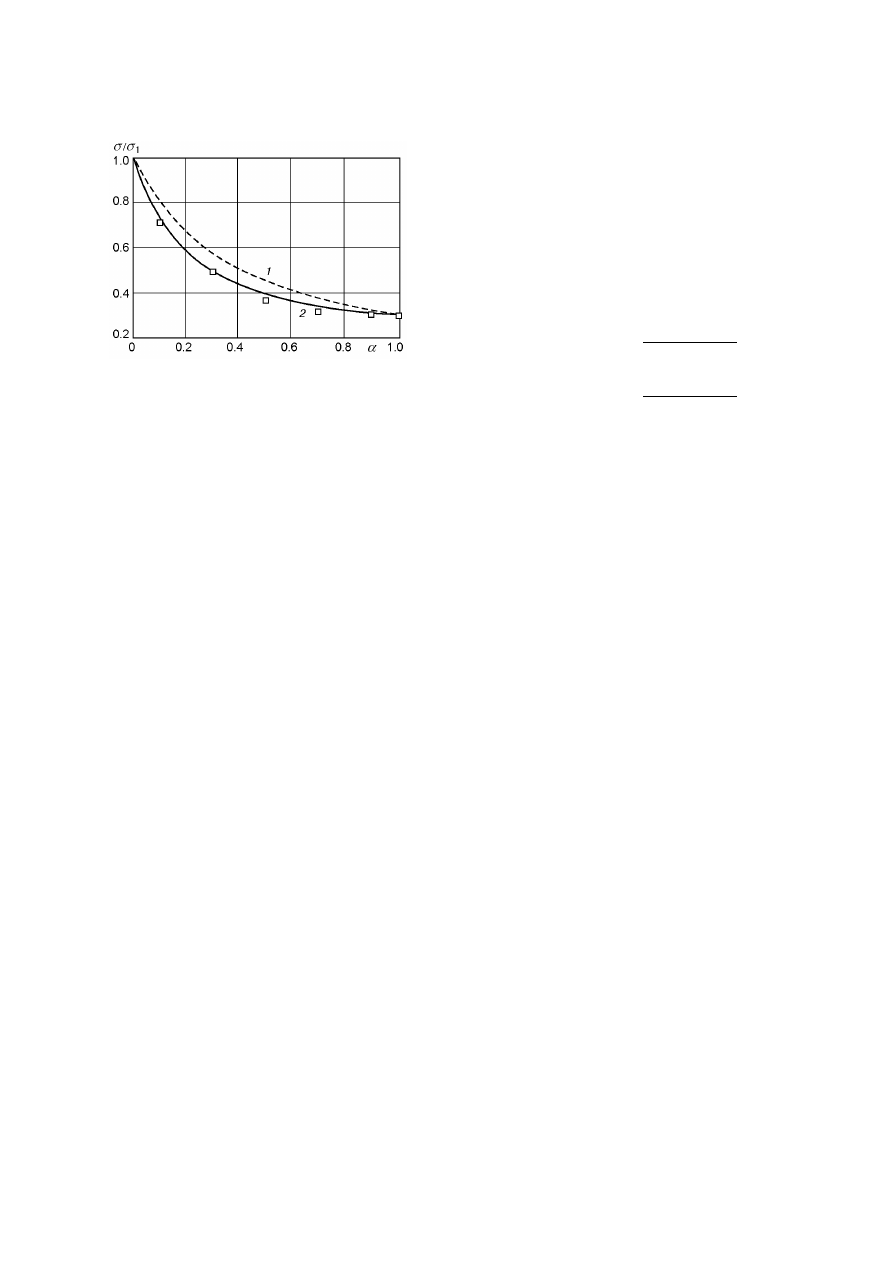
Figure 1 shows values of σ calculated from

Eq. (7) versus α for a mixture of HMX (here and
below indicated by subscript 1) and TNT (subscript
2) for r

1

= 4 µm, r

2

= 70 µm, ρ

1

= 1900 kg/m

3

,

ρ

2

= 1630 kg/m

3

, σ

1

= 130 MPa, and σ

2

= 40 MPa.

Points show the experimental data of [4].

Good

agreement between the theory and experiment is ob-
tained for Π = 0.1. Figure 1 also shows the depen-
dence σ(α) calculated from (4) for charges with ideal
continuity (Π = 0).

Calculating the Impact Sensitivity Indices of Solid Explosive Mixtures

101

Fig. 1. Ultimate strength of an HMX–TNT mixture
depending on the content of a TNT: curves 1 and 2 re-
fer to calculations on Eq. (4) and Eq. (7), respectively;
points refer to experimental data of [4].

1.2.

Chemical-Kinetic Characteristics of

SEM. The kinetic characteristics of HE imply data
from calorimetric studies of the specific (per unit
volume) heat-release rate, which, according to the
Arrhenius law, is determined by the activation en-
ergy E and the preexponent Z.

Considering that

the reactivities of the mixture components are simi-
lar, it is assumed with reasonable accuracy that the
rate of decomposition of the mixture is equal to the
rate of decomposition of each component, and, hence,
the kinetic characteristics of the components approx-
imately coincide and any pair of their values (E

i

, Z

i

)

can be chosen as a kinetic characteristic of SEM.

Difficulties arise when the mixture components

have different thermal stability. In this case, each
of the components decomposes with maximum heat-
release rate in a particular temperature range, and a
unique set of kinetic characteristics of SEM does not
exist. In practice, however, especially if one needs
only an averaged (over temperature) estimate of the
thermal stability of SEM, one uses some gross values
of the parameters E and Z, which are presumably
related to values of E

i

and Z

i

under a particular law.

Indeed, if the content of all components is much lower
than the content of the 1st component, the parame-
ters E and Z of the mixture are approximately char-
acterized by values of E

1

and Z

1

. A similar situation

is also observed when the mixture is dominated by
the 2nd component, etc.

Developing this model for the thermal decompo-

sition of SEM, we assume that as the composition of
the mixture changes gradually, there is a more or less
smooth transition from one mechanism of thermal de-
composition, typical of the predominance of the 1st
component in the mixture, to the mechanism of ther-
mal decomposition of the 2nd component, etc. In the

case of a binary mixture, one can use the following
formulas, in which the gross values of the activation
parameters for the thermal decomposition of the mix-
ture are related to the corresponding parameters of
the individual components:

E(α) = E

1

+ (E

2

− E

1

)/f

E

(α),

(8)

Z(α) = Z

1

+ (Z

2

− Z

1

)/f

Z

(α),

where

f

E

(α) = 1 + C

1

exp

C

2

(1

− α/α

th

)

α(1

− α)

,

f

Z

(α) = 1 + C

3

exp

C

4

(1

− α/α

th

)

α(1

− α)

.

It is easy to see that in the extreme cases α = 0
and α = 1, Eqs. (8) give the activation character-
istics of individual components. At the same time,
they adequately describe the thermal decomposition
of an explosive mixture if one properly choose the
parameters C

1

–C

4

, which describe the smoothness of

the transition from the first thermal-decomposition
mechanism to the second. The parameter α

th

is the

content of the 2nd component near which the indi-
cated transition occurs.

Equations (8) imply that none of the mixture

components is an inert material. In the extreme case,
it can be subjected to pyrolysis, whose mechanism is
also described by a set of some parameters (E and
Z). Unfortunately, there is no adequate method for
a priori estimation of the quantity α

th

. One can only

state that if the mixture components differ strongly
by thermal stability, then α

th

→ 0 or α

th

→ 1. If all

components make identical contributions to the total
rate of heat release due to thermal decomposition of
the mixture, then α

th

≈ 0.5.

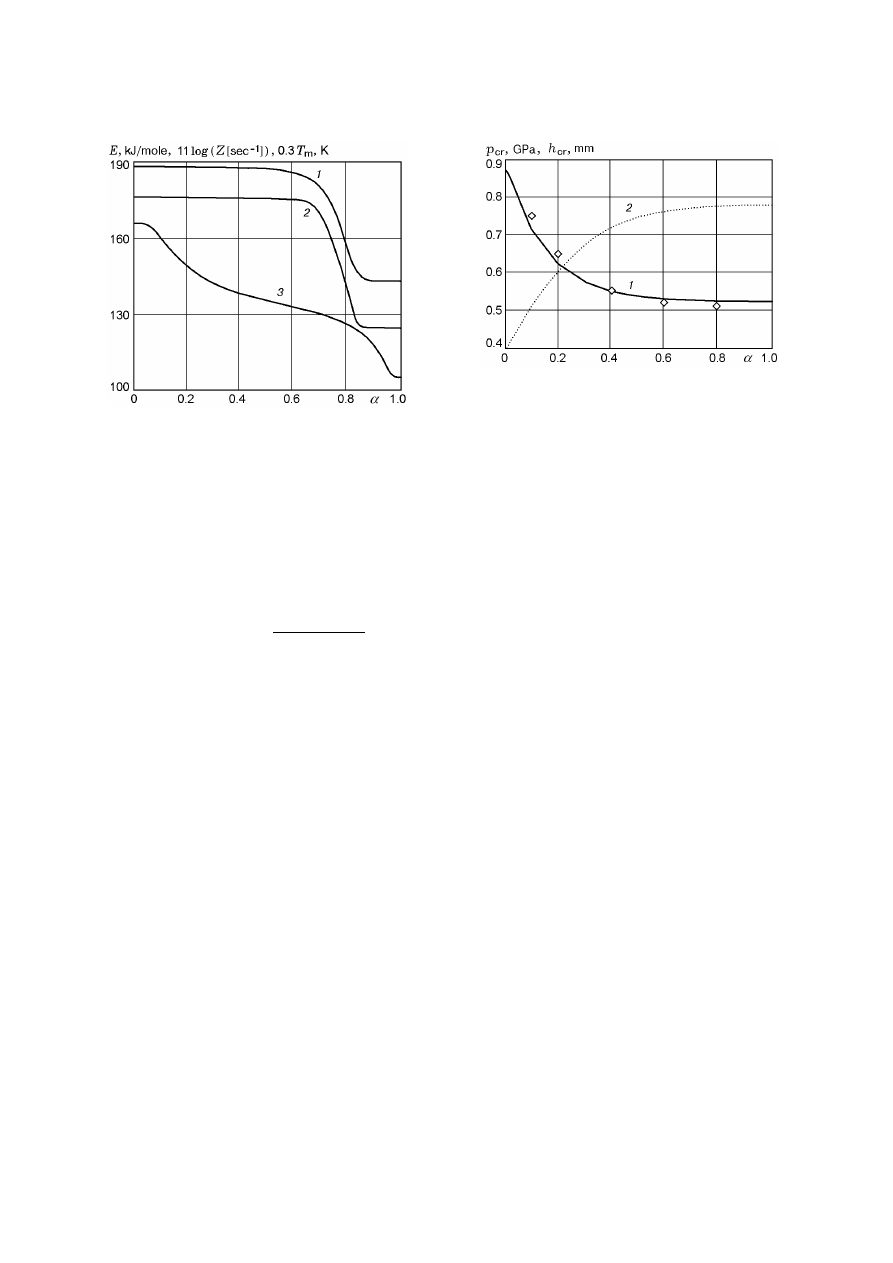
Figure 2 give curves of E(α) and Z(α) calcu-

lated from (8) for an HMX–TNT mixture. They are
obtained for E

1

= 188 kJ/mole, E

2

= 144 kJ/mole,

Z

1

= 10

16

sec

−1

, and Z

2

= 10

11.4

sec

−1

(see [1])

and the following values of the constants: C

1

= 6,

C

2

= 2.7, C

3

= 0.6, C

4

= 7, and α

th

= 0.7. It

is possible to distinguish two typical “zones of influ-
ence” of the components: 0 6 α 6 α

th

for HMX and

α

th

6 α 6 1 for TNT.

1.3. “Melting Point” of the Mixture (T

m

).

The methodical difficulties encountered in Sec. 1.2 in-
crease further in determining the “melting point” of
the mixture T

m

, which implies a certain thermody-

namic characteristic that determines the mechanical
strength of the mixture σ [4]. Taking into account
some similarity between the processes of thermal de-
composition and melting of SEM crystals (initiation
at surface defects, kinetic regime with typical values

102

Dubovik

Fig. 2. Activation energy (1), preexponent (2), and
melting point (3) for an HMX–TNT mixture versus
the TNT content.

of the activation parameters, etc.), we shall arbitrar-
ily describe the quantity T

m

, as a function of the

composition of the mixture, α by formulas similar
to (8) but having different constants C

5

and C

6

and

with transition parameter α

tr

:

T

m

(α) = T

m,1

+ (T

m,2

− T

m,1

)/f

th

(α),

f

th

(α) = 1 + C

5

exp

C

6

(1

− α/α

tr

)

α(1

− α)

.

We note that the quantity T

m

plays no part in cal-

culations of the critical parameters of initiation of
SEM because it enters only as a nonprincipal term
in the sum T

m

+ βp

cr

, which determines the criti-

cal temperature T

cr

of the “hot spot” under impact

[2, 4]. A curve of T

m

(α) for an HMX–TNT mixture

is shown in Fig. 2. It is calculated using values of
T

m,1

= 553 K, T

m,2

= 353.5 K, C

5

= 0.7, C

6

= 0.3,

and α

tr

= 0.7. It is evident that the curve T

m

(α)

is more similar to a strength curve of σ(α) than to
kinetic curves of E(α) and Z(α). The relationship
between the strength σ and the melting point of in-
dividual HE was first indicated in [2].

1.4. Sensitivity Indices for an HMX–TNT

Mixture. If the elemental composition and the en-
thalpy of the composition (∆H

i

) are known, the heat

of explosion of the mixture Q is easily calculated by
well-known rules [5]. The specific heat of the mix-
ture c

p

is usually calculated by the additive relation

c

p

=

P α

i

c

p,i

, which is justified by the small differ-

ence in heat capacities between organic solids. For
the same reason, we assume that the piezoelectric
coefficient of the melting point β is also an additive
function β

i

of the mixture components.

Using the information obtained on the physic-

ochemical and explosive characteristics of SEM, we

Fig. 3. Sensitivity indices for an HMX–TNT mixture
versus TNT content in the mixture: curve 1 and 2
refer to p

cr

and h

cr

, respectively; points refer to the

experimental data of [4].

calculate the sensitivity indices for an HMX–TNT
mixture by the method of [1]. The initial data for
the calculation are given above, except for c

p,1

=

1.05 kJ/(kg

· K), c

p,2

= 1.465 kJ/(kg

· K), β

1

=

0.20 K/MPa, β

2

= 0.29 K/MPa, ∆H

1

= 253 J/kg,

and ∆H

2

=

−328 J/kg [5]. Our calculations show

that the heat of explosion of the mixture depends
practically linearly on the composition and, hence,
Q = (1

− α)Q

1

+ αQ

2

, where Q

1

= 5.53 MJ/kg

and Q

2

= 4.22 MJ/kg. The initiation parameters

of SEM were calculated with a step in the TNT con-
tent ∆α = 0.01. The results are shown in Fig. 3 in
the form of curves of p

cr

(α) and h

cr

(α).

From Fig. 3 it follows that there is a sharp, al-

most jumpwise transition from the value p

cr,1

cor-

responding to the HMX initiation pressure to the
value p

cr,2

typical of TNT when the TNT content in

the mixture is α

≈ 0.7. The obtained value of α coin-

cides with the limiting content of TNT α

th

for which

its influence on the characteristics of thermal decom-
position of the mixture becomes determining (see
Fig. 2). We also note that all physicochemical and
explosive characteristics of SEM, except for thermal-
activation parameters, were assumed to be linearly-
additive in α and, hence, they could not be responsi-
ble for the jumpwise behavior of the curve of p

cr

(α)

(charge strength σ influences the quantity p

cr

only

slightly). Hence it follows that the thermal-activation
parameters play a decisive role in initiation of SEM
by impact. Let us verify this conclusion by calculat-
ing the critical initiation parameters for solid mix-
tures based on ammonium perchlorate (AP).

Calculating the Impact Sensitivity Indices of Solid Explosive Mixtures

103

2. AMMONIUM PERCHLORATE
BASED MIXTURES

The formulas of Sec. 1 cannot be used di-

rectly to calculate the sensitivity indices of AP-based
SEM since the thermal-decomposition mechanism for
AP differs markedly from the thermal-decomposition
mechanism for organic solids. Indeed, the thermal
decomposition of AP proceeds in two stages [6]. In
Stage 1 (low-temperature stage) which proceeds at
crystal defects, a fraction η < 0.3 of the potential
chemical energy of AP is released. The final decom-
position of AP to the end products proceeds at Stage
2 (high-temperature stage) in the bulk of the crystals.

There is the hypothesis [7] that Stage 1 of AP de-

composition is sensitized by perchloric acid (PA) ad-
sorbed at crystal defects. Perchloric acid is thermally
less stable than AP and, hence, acts as an initiator of
AP decomposition. The decomposition of AP begins
with dissociation into ammonia and PA, and then PA
continues the reaction. According to [8], the thermal
decomposition of PA is characterized by parameters
E

PA

= 121 kJ/mole and Z

PA

= 10

12

sec

−1

. The sen-

sitizing effect of PA on AP decomposition is taken
into account by decreasing the activation energy of
AP E

0

= 126 kJ/mole by a value that depends on the

amount of defects in the crystals, i.e., on the quan-
tity η and on the reactivity and content of the fuel
component interacting with AP. As a result, the ac-
tivation energy of AP necessary for the calculations
is written as

E

1

= E

0

(1

− q

1

α

u

th(C

7

η)),

(9)

where q

1

= (E

0

−E

PA

)/E

0

is the relative difference in

activation energy between thermal decompositions of
AP and PA, and u is an empirical constant that de-
scribes the reactivity of the fuel. The constant C

7

is

chosen from the condition that the function tanh(x)
reaches a value close to 1 for a value of η

≈ 0.3 that

corresponds to Stage 1 of AP decomposition. From
this, we find that C

7

= 7–8.

In order that the rate of thermal decomposition

of AP remain unchanged after the introduction of E

1

,

we compensate for the decrease in E

0

by the corre-

sponding increase in the preexponent Z

0

and obtain

Z

1

= Z

0

(1 + q

2

α

v

tanh(C

7

η)),

(10)

where q

2

= (Z

PA

−Z

0

)/Z

0

is the relative difference of

the preexponents of AP and PA and v is a constant
that depends on the reactivity of the fuel. Let us
use the above model concepts of AP thermal decom-
position to calculate some features of the mechanical
initiation of mixtures of AP and fuels.

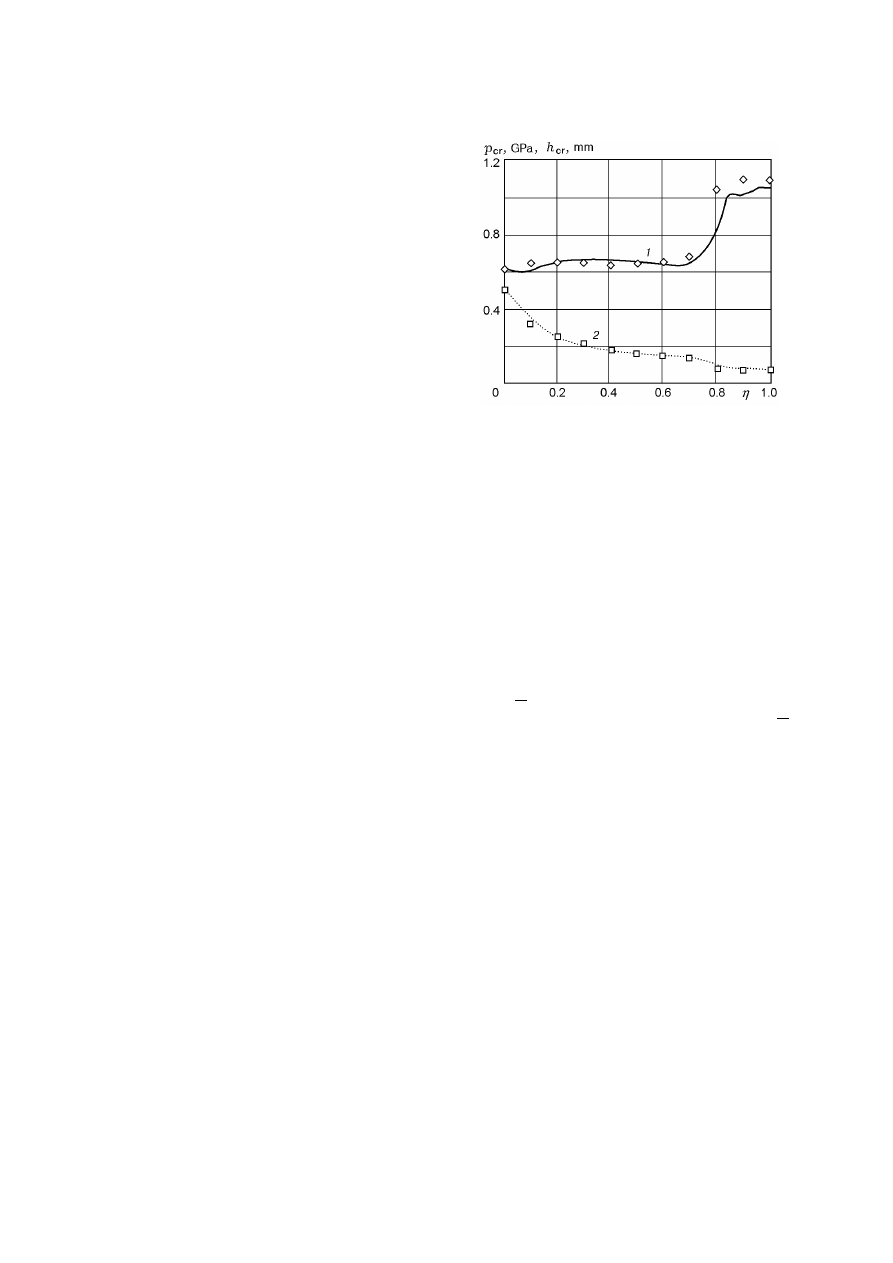
Fig. 4. Calculated and experimental sensitivity in-
dices for an AP–PMMA mixture versus η: curves 1
and 2 refer to p

cr

and h

cr

, respectively; points refer to

the experimental data of [9].

2.1.

A Mixture of AP and an Inexplo-

sive Component (PMMA). In [9], values of p

cr

for an 80/20 AP/PMMA mixture were measured for
0 < η < 0.4.

We recall that PMMA is a linear

polymer compound with density ρ

2

= 1190 kg/m

3

,

strength σ

2

= 118 MPa, and heat capacity c

p,2

=

1.47 kJ/(kg

· K). It is softened at T

m,2

= 393 K and

subjected to pyrolysis at T > 593 K. One reason
for the small thermal stability and light combustibil-
ity of PMMA might be the relatively low strength
of the C

C bond, equal to E

2

= 332 kJ/mole [10].

The characteristic oscillation frequency of the C

C

bond in PMMA estimated from this energy is Z

2

=

8.3

· 10

14

sec

−1

.

Let us calculate the heat effect of chemical in-

teraction between AP and PMMA. Since the active
zones of this reaction are AP crystal defects, whose
fraction in the mass of the material is η, then the
heat release due to interaction of AP with PMMA is
proportional to a certain function η. Therefore, the
heat effect of the reaction is written as

Q = (1

− α)Q

0

+ (Q

m

− (1 − α)Q

0

) tanh(C

7

η)),

(11)

where Q

0

= 1.37 MJ/kg and Q

m

= 4.19 MJ/kg

are the heats of explosion of AP and an 80/20
AP/PMMA mixture, respectively. For η = 0 (defect-
free crystals), there is no interaction between AP and
PMMA and the heat effect is determined only by AP
decomposition. If η > 0.3, interaction of AP with
PMMA proceeds with maximum heat release.

Setting for AP, c

p,1

= 1.3 kJ/(kg

· K), σ

1

=

185 MPa, T

m,1

= 820 K [1], u = 0.5, and v = 3, as-

suming that β

1

= β

2

= 0.26 K/MPa, and character-

izing an 80/20 AP/PMMA mixture by σ = 155 MPa

104

Dubovik

Fig. 5. Calculated and experimental sensitivity in-
dices for an AP–PMMA mixture versus PMMA con-
tent for η = 0.01 (1), 0.1 (2 and 4), and 0.35 (3):
curves 1–3 refer to p

cr

and curve 4 refer to h

cr

; points

refer to the experimental data of [9].

and C

7

= 7, we calculate from [1] the critical initi-

ation parameters of this mixture as functions of the
parameter η. Calculation results for p

cr

(η) and h

cr

(η)

are shown in Fig. 4 together with the experimental
data of [9]. Evidently, there is good agreement be-
tween the theoretical and experimental results. This
is explained primarily by the effect of the heat effect
of reaction (11) on the sensitivity indices and, to a
lesser degree, by the effect of the kinetic characteris-
tics of thermal decomposition of AP because a similar
calculation for E

1

= E

0

and Z

1

= Z

0

gives about the

same agreement of results. From Fig. 4 it also fol-
lows that a mixture of a defectless AP and PMMA
(80/20) is characterized by an initiation pressure of
0.88 GPa, i.e., decreased impact sensitivity (at the
level of pycric acid [1, 2]).

We continue the analysis of impact sensitivity for

a AP/PMMA mixture and calculate the sensitivity
indices as functions of the composition of the mixture
for various fixed values of η. As noted in [9], the de-
gree of decomposition of AP in the 1st stage increases
with increase in the particle size r

1

. This relation

can be written in approximate form η

≈ 10

−2

r

2/3

1

,

where r

1

is given in micrometers.

Therefore, the

TABLE 1

η

r

1

,

µm

r

2

,

µm

Π

p

cr,min

,

GPa

h

cr,min

,

mm

0.01

5

5

0.02

0.825

0.478

0.1

25

5

0.02

0.601

0.712

0.35

250

15

0.03

0.514

0.808

Fig. 6. Calculated and experimental [9, 11] (points)
values of p

cr

for AP–TNT and AP–HMX mixtures

(curves 1 and 2, respectively) versus the HE content.

dependences p

cr

(α, r

1

) and p

cr

(α, η) are equivalent

in the indicated sense. The initial data for calcu-
lating the strengths of charges of AP with PMMA
(r

2

≈ 10 µm) by (7) are shown in Table 1. To calcu-

late the kinetic characteristics of the mixture, in (8)
we set the following values of the constants: C

1

= 1.7,

C

2

= 1.3, C

3

= 400, C

4

= 2.5, C

5

= C

6

= 3,

α

th

= 0.95, and α

tr

= 0.9. From these data, us-

ing the method of [1], we calculated curves of p

cr

(α),

which are shown in Fig. 5 together with the experi-
mental results of [9]. A curve of h

cr

(α) obtained for

the AP-based mixture with r

1

= 25 µm is also given

in Fig. 5.

All calculated dependences are nonmonotonic

and have typical extrema at the point of stoichiom-
etry for the given mixture: α

st

= 0.15. Values of

p

cr,min

and h

cr,max

are listed in Table 1. An analysis

of the results obtained shows the following: 1) the
sensitivity level is determined by the calorific value
of the mixture, which depends on η for all α < α

th

;

2) the effect of the reactivity of the oxidizer as the
AP–PA system on the sensitivity of the mixture is
especially pronounced for small values of α

≈ α

st

.

For the remaining α < α

th

, calculations of the sen-

sitivity indices of the mixture give the same results
as for AP as the oxidizer. In AP–PMMA mixtures,
α

th

≈ α

tr

≈ 0.9. In mixtures of AP with explosive fu-

els, the values of the indicated parameters are much
lower.

2.2. Mixtures of AP and Explosive Com-

ponents. Experimental data on the sensitivity of
mixtures of AP with TNT and HMX are given in
[9, 11], in which “ordinary” AP with η

≈ 0.2 was

used. This value of η was used to calculate the curves
of p

cr

(α) and h

cr

(α) given in Fig. 6. In the calcu-

lations, the following values for the constants were

Calculating the Impact Sensitivity Indices of Solid Explosive Mixtures

105

used: u = 0.2, v = 1.6, C

1

= 0.8, C

2

= 1, C

3

= 400,

C

4

= 2.6, C

5

= C

6

= 3, α

th

= 0.25, and α

tr

= 0.9

for an AP–TNT mixture; u = 0.2, v = 2.3, C

1

= 1.1,

C

2

= 1.2, C

3

= 300, C

4

= 3, C

5

= 0.8, C

6

= 0.7,

α

th

= 0.7, and α

tr

= 0.6 for an AP–HMX mixture.

They differ markedly from the corresponding con-
stants for an AP–PMMA mixture by the values of u
and α

th

, which determine the kinetic characteristics

of the mixtures. The above sets of constants differ
from one another by the values of C

5

, C

6

, and α

tr

,

which determine the strength properties of mixtures.

The above data lead to the following conclu-

sions: 1) the values of u and α

th

show that AP in-

teracts more actively with TNT and HMX than with
PMMA, and the interaction with TNT is more in-
tense than that with HMX; 2) in contrast to mix-
tures of AP with TNT and PMMA, a mixture of AP
and HMX is characterized by high strength, which,
via the store of energy in the loading system, facili-
tates the interaction of the mixture components dur-
ing charge collapse. From this, we have decreased
values for the constants C

5

, C

6

, and α

tr

.

Thus, the approximate physicochemical model

of mechanical initiation of SEM charges proposed in
this paper can be used to calculate the critical pa-
rameters of explosion initiation by an impactor with
accuracy sufficient for applied calculations. Accumu-
lating calculated data supported by experiments, it
will be possible to obtain reliable values for the con-
stants used in the calculation, and, thus, to reliably
predict the sensitivity of new mixed compositions.

REFERENCES

1. A. V. Dubovik, “Calculation of impact sensitivity in-

dices for solid explosives,” Dokl. Akad. Nauk SSSR,

268, No. 2, 377–380 (1986).

2. G. T. Afanas’ev and V. K. Bobolev, Initiation

of Solid Explosives by Impact [in Russian], Nauka,

Moscow (1968).

3. E. A. Stolyarov and N. G. Orlova, Calculation of the

Physicochemical Properties of Liquids [in Russian],

Khimiya, Leningrad (1976).

4. I. A. Karpukhin and V. K. Bobolev, “Critical con-

ditions of impact initiation of an explosion in solid

mixed explosives,” Fiz. Goreniya Vzryva, 3, No. 3,

381–385 (1967).

5. V. I. Pepekin, M. N. Makhov, and Yu. A. Lebedev,

“Heats of explosive decomposition of individual HE,”

Dokl. Akad. Nauk SSSR, 232, No. 4, 852–855 (1977).

6. L. L. Bircumshaw and B. N. Newman, “The ther-

mal decomposition of ammonium perchlorate,” Proc.

Roy. Soc. London, Ser. A, 227, No. 1168, 115–132

(1954); 227, No. 1169, 228–241 (1954).

7. V. Guillory and M. King, “Thermal decomposition

of ammonium perchlorate,” AIAA J., No. 6, 1134–

11362 (1970).

8. V. A. Koroban, V. P. Guk, et al., “Effect of sub-

stituents in the cation on the decomposition of per-

chlorates of ammonium bases,” in: Trans. Mendeleev

Chem. Technol. Inst., No. 104: Chemical Physics of

Condensed Explosive Systems (1979), pp. 44–51.

9. I. A. Karpukhin, V. K. Bobolev, Yu. M. Balinets,

et al., “Certain features of impact initiation of an

explosion and the detonation capability of oxidizer–

fuel mixtures,” Fiz. Goreniya Vzryva,

15, No. 2,

140–146 (1979).

10. A. A. Ravdel’ and A. M. Ponomareva (eds.), Short

Handbook of Physicochemical Quantities [in Russian],

Khimiya, Leningrad (1983).

11. V. K. Bobolev, I. A. Karpukhin, and V. A. Teselkin,

“Role of chemical interaction of components in initi-

ation of an explosion in mixtures of ammonium per-

chlorate and fuel,” in: Combustion and Explosion,

Proc. 3rd All-Union Symp. on Combustion and Ex-

plosion [in Russian], Nauka, Moscow (1972), pp. 515–

518.