Combustion, Explosion, and Shock Waves, Vol. 39, No. 1, pp. 75–79, 2003

Semi-Empirical Method for Estimating the Combustion-Wave

Transition through the Contact Surface in a Composite Explosive

UDC 536.46:662.2

V. T. Kuznetsov

1

Translated from Fizika Goreniya i Vzryva, Vol. 39, No. 1, pp. 87–91, January–February, 2003.
Original article submitted January 22, 2002.

Through a comparison of experimental data on stable ignition and combustion of ini-
tial specimens composing igniter trains of pyrotechnic charges, critical conditions
for combustion-wave transition through the contact surface between neighboring
compound-explosive compacts are found.

The evaluation procedure is tested with

twenty explosives representing different combinations of five compacts of pyroxylin
(gun-cotton), black gunpowder, and three types of pyrotechnic mixtures. Minimal
dimensions of an interfacial protuberance promoting combustion-wave propagation
throughout the charge are found.

Key words:

ignition, combustion, heat flux, pyrotechnic mixtures, composite

charge.

Stable propagation of combustion waves in com-

posite explosives is determined by ignition conditions
at contact surfaces between the neighboring compacts.
The critical values of wave-transition parameters in an
explosive depend on the amount of heat accumulated
in the wave, thermal resistance of the interface, and
thermokinetic properties of the specimen [1–3].

The

present paper proposes an engineering procedure for
predicting the possibility of combustion-wave transi-
tion through the interface between the neighboring com-
pacts, which employs experimental results on stable ig-
nition and combustion of explosive components. The
procedure is based on the concept of the so-called “op-
timal” ignition regime, in which the external source of
heat on the surface of a specimen provides for ignition
conditions identical to those at the surface of this speci-
men during stable burning [4]. Hence, the energy in the
combustion wave and, hence, the associated heat flux
can be estimated from ignition tests performed in the
“optimal” regime.

We consider burning of a pyrotechnic charge con-

sisting of a triggering mixture and a main mixture.
We assume that, in the case of a plane interface be-
tween the mixtures and ideal heat transfer between the

1

Institute of Applied Mathematics and
Mechanics, Tomsk State University,
Tomsk 634050; [e-mail].

neighboring compacts, the combustion wave can pass
through the interface if the energy necessary for ignit-
ing the main mixture (N

main

) at a given heat flux in the

combustion wave traversing the triggering mixture (q

∗

tr

)

does not exceed the energy required for “optimal” igni-
tion of the triggering mixture (N

∗

tr

). The heat flux q

∗

tr

can be found graphically from the experimental depen-
dence N (q) at the minimum value of energy required for
the triggering mixture to be reliably ignited. From the
experimental relation between the stable-ignition time
of the main mixture and the heat flux at a given value
of q

∗

tr

, we can determine the ignition time of the main

mixture (t

ign,main

) and, hence, the energy required for

the mixture to be ignited: N

main

= q

∗

tr

t

ign,main

. Thus,

we can determine the values of N

∗

tr

and N

main

from

the experimental dependences t

ign

(q) for the trigger-

ing and main mixtures and estimate, from their ratio
N

tr

/N

main

, the possibility of combustion-wave transi-

tion through the plane interface between the mixtures.
However, the thermal resistance at the contact surface
caused, for instance, by loose contact between the com-
pacts may result in combustion quenching at the inter-
face even if the above-formulated conditions are fulfilled.
In the case under consideration, the establishment of a
stationary combustion wave as the initial wave traverses
the interface essentially depends on the gap width [3].
Here, stable transition is promoted by conditions under

0010-5082/03/3901-0075 $25.00 c

2003

Plenum Publishing Corporation

75

76

Kuznetsov

TABLE 1

Characteristics of Composite-Explosive Specimens

Specimen

ρ, kg/m

3

a, 10

−8

m

2

/sec

U , mm/sec

t

∗

ign

, sec

N

∗

, 10

4

J/m

2

P

1500

6.77

1.4

0.035

2.5

GP

1700

14.3

9.0

0.020

5.4

A

1700

806

9.6

0.090

]

58.0

]

B

2350

55

3.2

0.045

11.2

C

1800

704

3.5

0.010

]

50.0

]

Note. The values of the parameters were obtained by extrapolating experimental data into
the region of intense heat fluxes are marked by the symbol ].

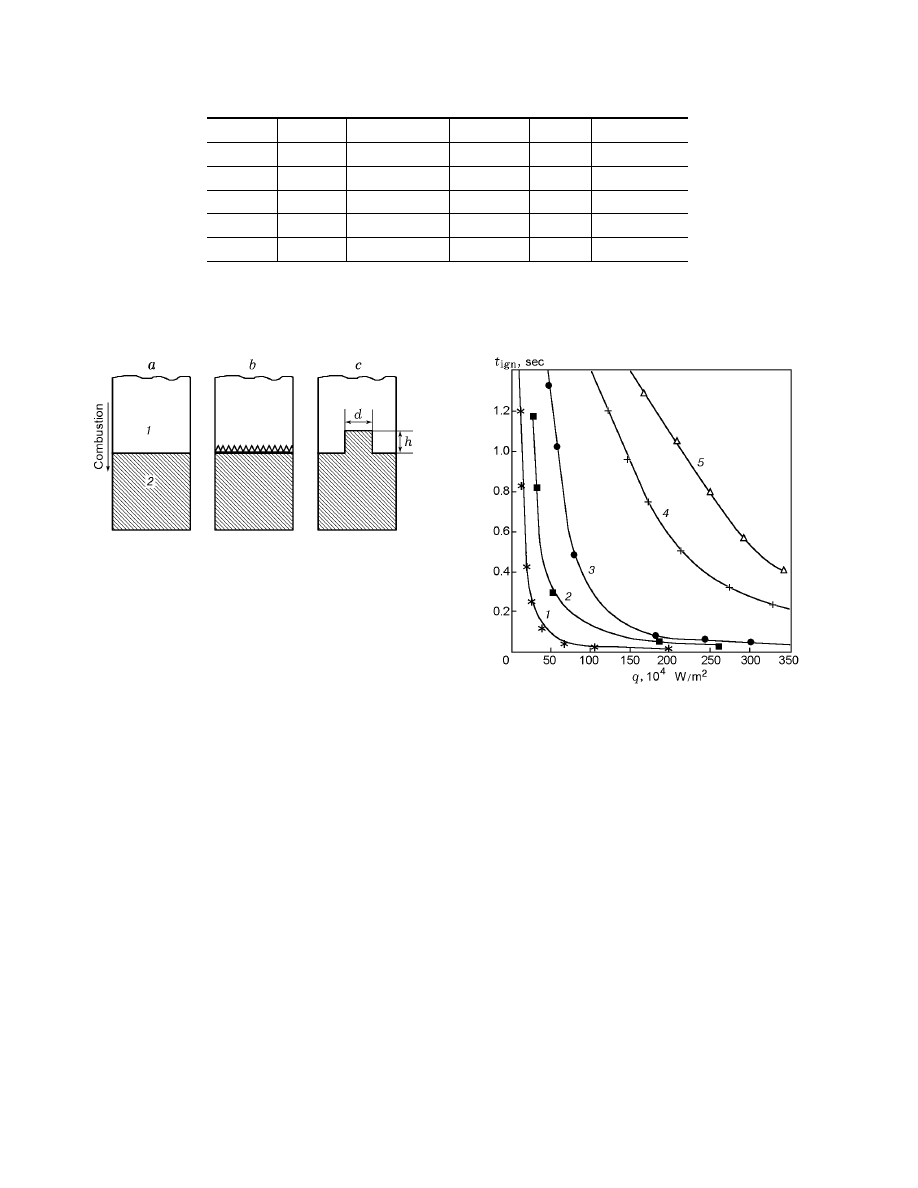
Fig. 1. Diagrams of composite explosives: (a) plane in-
terface between the triggering (1) and main (2) mixtures;
(b) corrugated interface; (c) interfacial main-mixture
protuberance.

which part of the main-mixture surface experiences, for
a certain time, the action by the flame produced by the
triggering mixture. Such conditions can be organized,
for instance, with the help of protuberances prepared
at the interface between the mixtures. Here, we assume
that the burning zone of the triggering mixture is suffi-
ciently wide, and the temperature of combustion prod-
ucts in this zone is higher than the ignition temperature
of the main mixture.

Consider which geometric dimensions of protuber-

ances are critical for stable transition of the combus-
tion wave through the contact surface. Let there be
a cylindrical protuberance of the main mixture at the
interface between the two mixtures. Based on physi-
cal considerations, we can find the minimal height of
the protuberance from the formula h

min

= U

tr

t

ign,main

,

where U

tr

is the burning rate of the triggering mixture

and t

ign,main

is the ignition time of the main mixture at

q = q

∗

tr

. As the minimal diameter of the flame source

in the case of a cylindrical protuberance with allowance
for heat withdrawal through side surfaces, the quantity
d

min

= 6.7(at

∗

ign,main

)

1/2

[5] can be used, where a is the

Fig. 2. Ignition time versus heat-flux density: curve 1
refers to pyroxylin, curve 2 to GP, curves 3, 4, and 5
refer to pyrotechnic mixtures B, C, and A, respectively.

thermal diffusivity of the mixture and t

∗

ign,main

is either

the ignition time of the main mixture in the “optimal”
regime or the thermal relaxation time of the heated
layer. Thus, in the case of interest, a protuberance at
the interface between the neighboring compacts can en-
sure stable transition of the combustion wave through
the contact surface.

The proposed procedure was tested in experiments

with composite charges representing various combina-
tions of five dissimilar compacts with a plane interface
between the mixtures and with a protuberance provided
on the main-mixture contact surface. Part of the explo-
sives had corrugated interfaces. Figure 1 shows various
diagrams of the explosives. Depending on the burning

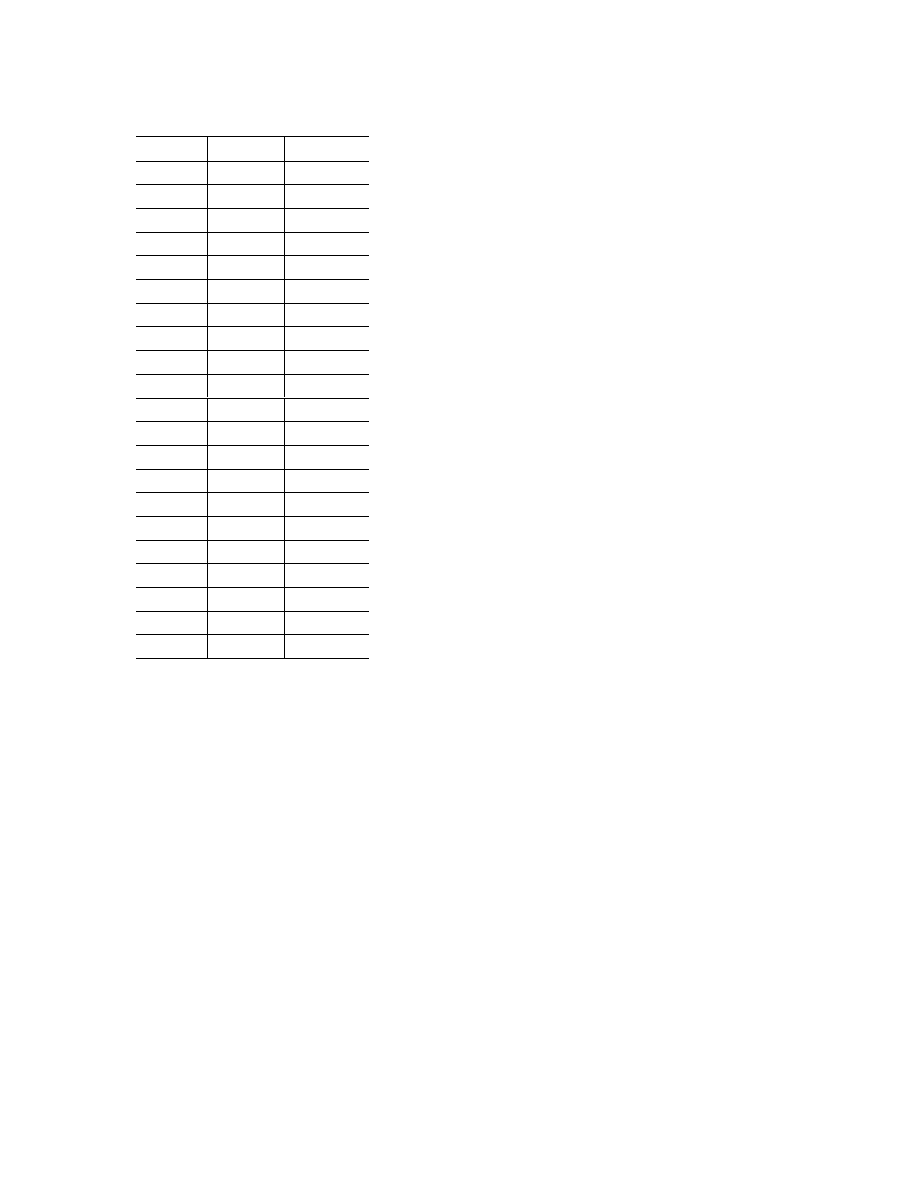
Estimating the Combustion-Wave Transition through the Contact Surface

77

TABLE 2

Combustion of Explosives with

a Plane Interface between the Compacts

Explosive

Test result

N

∗

tr

/N

main

P + GP

+

0.220

P + A

−

0.004

P + B

−

0.065

P + C

−

0.009

GP + P

+

3.552

GP + A

−

0.030

GP + B

−

0.400

GP + B

−

0.060

A + P

+

18.100

A + GP

+

10.069

A + B

−

4.500

A + C

+,

−

1.130

B + P

+

4.978

B + GP

+

1.731

B + A

+,

−

0.060

B + C

+

0.120

C + P

+

16.600

C + GP

+

6.700

C + A

−

0.710

C + B

+

4.000

A + A

−

1.000

Note. The plus and minus denote burning and extinction,
respectively.

direction, the explosives were subdivided into triggering
or main ones. Compacts of gun powder (GP), pyroxylin
No. 1 (P), and pyrotechnic mixtures A, B and, C, based
on sodium, strontium, and barium nitrates containing
up to 60 wt.% of MPF-3 magnesium powder (mixtures
A and C) and up to 40 wt.% of PTM(a) titanium pow-
der (mixture B) were used. To raise the compressibility
of the specimens, various technological additives were
also used. The diameter of the specimens was 15 mm,
and their height was 20 mm.

Explosives with plane

interfaces were prepared by pressing of precompacted
specimens followed by subsequent armoring of their side
surfaces with a linoleum solution in acetone and drying
them at room temperature during three days. Explo-
sives with protuberances at the interfaces between the
triggering and main mixtures were prepared by succes-

sive compacting of mixtures with a puncheon having a
spigot tang. The diameter and height of the tang varied
in the range of 2–6 mm. After compacting, explosives
with interfacial protuberances were also armored with
the linoleum solution. Explosives with corrugated inter-
faces between the neighboring mixtures were prepared
in a similar manner. In the latter case, the surface of
the puncheon had conical tangs 1 mm high with 2-mm
diameter bases. Initial specimens of the composite ex-
plosives were put to tests on stable ignition initiated by
luminous fluxes with intensities (10–300)

· 10

4

W/m

2

.

The testing procedure for the illumination-triggered ig-
nition was described in detail in [6]. The experimental
data for five initial compacts are shown in Fig. 2. Using
these data and assuming that the energy necessary for
stable ignition is minimal in the “optimal” regime, we
determined the critical parameters N

∗

, t

∗

, and q

∗

for all

the compositions. The values of the critical parameters
are listed in Table 1. The same table lists the densities
ρ and thermal diffusivities a of the compacts, and also
the normal burning rates U displayed by the compacts
in air under atmospheric pressure. The mixtures used
in the tests appreciably differ in their characteristics,
and the explosives prepared from them cover a broad
range of the factor under study. The composite explo-
sives were burnt in atmospheric air at room tempera-
ture. The triggering mixture was ignited by a heated
Nichrome spiral. Visual observations of the process were
performed to register the final test result, either com-
plete burn-up of the whole explosive or flame extinction
at the interface between the triggering and main mix-
tures. At least five tests were performed for each pair of
compacts. The experimental data on burning compos-
ite explosives with plane interfaces between the neigh-
boring compacts are listed in Table 2. For each explo-
sive, the same table indicates the energy ratio necessary
for stable ignition of its components. It is seen that
an explosive burns out completely if N

∗

tr

/N

main

> 1;

if N

∗

tr

/N

main

< 1, then the flame fails to penetrate

through the interface between the triggering and the
main mixtures. For N

∗

tr

= N

main

, either propagation

of the combustion wave through the interface or flame
extinction was observed. The only exceptions were the
explosives P + GP and B + C, whose combustion pat-
tern might be affected by the heat-resistant armoring,
and also the compositions A + B and A + A, whose com-
bustion might cause violation of the thermal contacts
between the neighboring compacts. Flame extinction
between similar compacts A + A might also be caused
by the difference between the microstructure of the ex-
plosives at the interface between the compacts and the
microstructure of bulk materials. Indeed, if we have, in-
stead of a plane interface, a corrugated interface, which

78

Kuznetsov

TABLE 3

Minimal Dimensions of the Interfacial Protuberance Ensuring

Stable Propagation of Flame Across Composite Explosives

Explosive

d

min

, mm

h

min

, mm

d

min

, mm

h

min

, mm

composition

Experiment

Calculation

P + A

6

4

5.7

7.0

P + B

3

4

1.0

0.8

P + C

6

6

5.6

5.2

GP+A

6

4

5.7

6.0

GP + B

2

2

1.0

0.4

GP + C

6

4

5.6

3.0

diminishes the probability of violation of the thermal
contact between the compacts, then the combustion
wave does penetrate through the In our tests, we ob-
served stable transition of the combustion wave through
corrugated interfaces in the explosives A + A, A + B,
A + C, and B + A. However, if the ignition energies of
the neighboring compacts considerably differ from each
other, then the interfacial corrugation is insufficient for
the combustion wave to penetrate through the interface.
For instance, corrugation of contact surfaces in the ex-
plosives GP + A, GP + B, and GP + C failed to promote
the propagation of the combustion wave from the trig-
gering to the main mixture. To make the transition
possible, it is required to prepare a main-mixture pro-
tuberance of certain dimensions. Explosives with such
main-mixture protuberances were prepared; the protu-
berances were 2, 3, 4, and 6 mm in diameter and 2, 4,
and 6 mm in height. The specimens were burnt with
atmospheric air at room temperature. No less than 36
tests were performed to determine the minimal dimen-
sions of interfacial protuberances capable of ensuring
stable flame propagation over each composite explosive.
The experimental and predicted minimal diameters of
the interfacial protuberances are listed in Table 3. In
view of the possible difference in compression condi-
tions of the materials in the cylindrical protuberance
and in the main explosives, and also considering the
fact that the firing tests were carried out on explosives
with discrete values of geometrical parameters of the
protuberance, we may consider the agreement between
the experimental and predicted minimal diameters of in-
terfacial protuberances as quite satisfactory. The only
exceptions are explosives with a protuberance 2 mm in
diameter: the thermophysical parameters and ignition
times of the substance (in the protuberance) can differ
from analogous parameters of bulk material of the main
explosive. Thus, a main-mixture protuberance prepared

at the interface of a composite explosive can ensure sta-
ble propagation of the combustion wave through the
contact between the triggering and main mixtures with
sharply differing characteristics (ignition energies, burn-
ing rates, and thermophysical parameters).

Based on the physical concept of ignition and com-

bustion of condensed substances, we proposed an en-
gineering procedure for predicting the possibility of the
combustion-wave transition through the contact surface
in composite explosives. The procedure rests on the
idea of an “optimal” ignition regime under the action of
an external source of heat. Experimental data on igni-
tion and combustion of initial composite-explosive spec-
imens are used. The procedure is tested with twenty
explosives composed of dissimilar compacts differing in
their ignition energies, burning rates, and thermophysi-
cal characteristics. The statements put forward are con-
firmed both qualitatively and quantitatively. Further
development of the procedure and determination of its
applicability limits require a wider range of systems to
be considered. Of special interest here are explosives
with a high metal content and gasless compositions. In
this case, “optimal” ignition conditions can be orga-
nized with the help of heating facilities that can ensure
heating intensities higher than 10

7

W/m

2

.

REFERENCES

1. I. G. Assovsky, “Conditions for the combustion-wave

transition through the contact surface between two fu-

els,” Dokl. Akad. Nauk SSSR,

253, No. 1, 124–128

(1980).

2. V. N. Simonenko, V. E. Zarko, A. B. Kiskin, et al., “Sta-

bility of the combustion of composite metallized sam-

ples,” Combust. Expl. Shock Waves, 19, No. 5, 590–591

(1983).

Estimating the Combustion-Wave Transition through the Contact Surface

79

3. O. Yu. Perevalov, V. T. Kuznetsov, and I. G. Dik,

“Transition of the combustion front through a nonideal

contact of two gasified solid fuels,” Combust. Expl. Shock

Waves, 29, No. 2, 155–157 (1993).

4. Z. I. Aristova and O. I. Leipunskii, “Pre-ignition heating

of gunpowders,” Zh. Fiz. Goreniya Vzryvov, No. 2, 225–

228 (1958).

5. V. N. Vilyunov, Theory of Ignition of Condensed Sub-

stances [in Russian], Nauka, Novosibirsk (1984).

6. V. T. Kuznetsov, V. P. Marusin, and A. I. Skorik, “Igni-

tion mechanism in a heterogeneous system,” Combust.

Expl. Shock Waves, 10, No. 4, 456–458 (1974).