Opracowanie: dr Marian Gewert, dr Zbigniew Skoczylas

◦

∗

Na podstawie wartości kilku początkowych wyrazów podanych ciągów znaleźć ich wzory
ogólne:

(x

n

) = (1, 2, 6, 24, 120, . . .);

(y

n

) =

1,

1

2

, 3,

1

4

, 5,

1

6

, . . .

;

(z

n

) = (1, 3, 7, 15, 31, 63, . . .);

(t

n

) = (1, 1, 1, 2, 2, 2, 3, 3, 3, . . .).

◦

Dla podanych ciągów napisać wzory określające wskazane wyrazy tych ciągów:

x

n

= n

n

, x

2n

;

y

n

=

1

2n

+

1

2n + 1

+

1

2n + 2

+ . . . +

1

3n

, y

n+1

;

z

n

= (2n + 1)!, z

n+3

;

t

n

=

n

2

+ 1

3

, t

2n

−1

.

◦

Zbadać, czy podane ciągi są ograniczone z dołu, z góry, są ograniczone:

x

n

= n

4

− n

2

;

y

n

= (

−1)

n

n!;

z

n

=

n

√

2

n

+ 1;

t

n

=

(

−2)

n

1 + (

−2)

n

.

◦

Zbadać, czy podane ciągi są monotoniczne od pewnego miejsca:

x

n

=

1

n

2

− 6n + 10

;

y

n

=

4

n

2

n

+ 3

n

;

z

n

= tg

100π

2n + 1

;

t

n

=

n!

10

n

.

◦

Korzystając z definicji granicy ciągu uzasadnić podane równości:

lim

n

→∞

2n + 1

n

2

= 0;

lim

n

→∞

n

4

− 1

=

∞;

lim

n

→∞

2

n

− 3

n

2

n

+ 3

n

=

−1;

lim

n

→∞

√

n

− n

=

−∞.

◦

Korzystając z twierdzeń o arytmetyce granic ciągów obliczyć podane granice:

lim

n

→∞

4

n

4

+ 16

− n

;

lim

n

→∞

n

2

+ 1

n! + 1

(2n + 1)(n + 1)!

;

lim

n

→∞

n

20

+ 2

3

(n

3

+ 1)

20

;

lim

n

→∞

3

√

8

n+1

+ 3

2

n

+ 1

.

◦

Korzystając z twierdzenia o trzech ciągach znaleźć podane granice:

lim

n

→∞

n

√

n2

n

+ 1;

lim

n

→∞

E(nπ)

n

;

lim

n

→∞

2

n

sin n

3

n

+ 1

;

lim

n

→∞

1

4

√

n

4

+ 1

+

1

4

√

n

4

+ 2

+ . . . +

1

4

√

n

4

+ n

.

∗

Numeracja zadań z książki

„Analiza matematyczna 1. Przykłady i zadania”.

1

◦

Korzystając z twierdzenia o ciągu monotonicznym i ograniczonym uzasadnić zbieżność
podanych ciągów:

x

n

=

1

· 3 · 5 · . . . · (2n − 1)

2

· 4 · 6 · . . . · 2n

;

y

n

=

n

2

5

n

;

z

n

=

1

1

· 2

1

+

1

2

· 2

2

+ . . . +

1

n

· 2

n

;

t

1

= 2, t

n+1

=

√

6 + t

n

.

◦

Korzystając z definicji liczby e oraz z twierdzenia o granicy podciągu obliczyć podane
granice:

lim

n

→∞

5n + 2

5n + 1

15n

;

lim

n

→∞

n

2

n

2

+ 1

n

2

;

lim

n

→∞

3n + 2

5n + 2

n

·

5n + 3

3n + 1

n

;

lim

n

→∞

3n

3n + 1

n

.

◦

Korzystając z twierdzenia o dwóch ciągach znaleźć granice:

lim

n

→∞

n

√

n

n

+ 5;

lim

n

→∞

(3

n

cos n

− 4

n

);

lim

n

→∞

1

E

√

1

+

1

E

√

2

+. . .+

1

E (

√

n)

;

lim

n

→∞

1

3

+

1

n

n

5

−

1

n

n

.

◦

Korzystając z tabelki działań z symbolem

∞ obliczyć podane granice:

lim

n

→∞

n

4

− 3n

3

− 2n

2

− 1

;

lim

n

→∞

1

− (n + 1)!

n! + 2

;

lim

n

→∞

√

3

− cos

π

n

n

;

lim

n

→∞

arctg n

arcctg n

.

◦

Znaleźć zbiory punktów skupienia (właściwych i niewłaściwych) podanych ciągów:

a

n

=

(

−1)

n

n

n + 1

;

b

n

= sin

2

nπ

4

;

c

n

= [1 + (

−1)

n

]

· 2

n

;

d

n

=

1 +

cos nπ

n

n

.

◦

Znaleźć granice dolne i górne podanych ciągów:

a

n

= (

−1)

n

n

2

+ 1

;

b

n

= tg

(2n + 1)π

4

;

c

n

=

(

−2)

n+1

2

n

+ 1

;

d

n

= (1 + cos nπ) n!.

◦

Korzystając z definicji Heinego granicy funkcji uzasadnić podane równości:

2

lim

x

→3

(x

− 2)

5

= 1;

lim

x

→∞

1

− 2x

3

x

3

+ 1

=

−2;

lim

x

→2

−

4

− x

2

= 0;

lim

x

→1

+

1

(x

− 1)

7

=

∞.

◦

W ostrosłupie trójkątnym prawidłowym krawędź podstawy ma długość b, a kąt nachy-

lenia krawędzi bocznej do podstawy ma miarę x, gdzie 0 < x <

π

2

. Niech r(x) oznacza

promień kuli wpisanej w ten ostrosłup. Obliczyć granice lim

x

→0

+

r(x),

lim

x

→

π

2

−

r(x). Czy

można podać te granice nie wyznaczając funkcji r?

Cząstka pewnego układu drgającego porusza się po osi Ox. Położenie tej cząstki w
chwili t > 0 jest opisane wzorem x(t) = 5

− 4

−3t

cos(2t + 1). Znaleźć jej graniczne

położenie, gdy t

−→ ∞. Co oznacza otrzymany wynik?

Równanie ax

4

− 2x − 8 = 0 ma dla parametru a > 0 dwa pierwiastki rzeczywiste x

1

(a),

x

2

(a). Obliczyć granice lim

a

→0

+

x

1

(a), lim

a

→0

+

x

2

(a), lim

a

→∞

x

1

(a), lim

a

→∞

x

2

(a).

Wskazówka. Narysować wykresy funkcji

y = ax

4

oraz

y = 2x + 8. Następnie zbadać położenie punktów

wspólnych obu wykresów, gdy

a → 0

+

oraz, gdy

a → ∞.

◦

Uzasadnić, że podane granice funkcji nie istnieją:

lim

x

→3

x

2

x

− 3

;

lim

x

→2

E

x

2

;

lim

x

→∞

e

x

cos x;

lim

x

→π

2

1

sin x

.

◦

Zbadać, obliczając granice jednostronne, czy istnieją podane granice:

lim

x

→0

[x sgn x];

lim

x

→0

2

1

x

3

;

lim

x

→

π

2

E (3 sin x);

lim

x

→2

x

2

− 4

|x − 2|

.

◦

Korzystając z twierdzeń o arytmetyce granic funkcji obliczyć podane granice:

lim

x

→1

x

3

− 1

x

4

− 1

;

lim

x

→∞

2

x

+ 1

3

x

+ 2

;

lim

x

→64

3

√

x

− 4

√

x

− 8

;

lim

x

→

π

2

−

tg

2

x + 1

tg

2

x + 5

.

◦

Korzystając z twierdzenia o trzech funkcjach uzasadnić podane równości:

lim

x

→0

x

3

arctg

1

x

= 0;

lim

x

→∞

E

x

√

8

E

x

√

2

= 2;

lim

x

→−∞

2

−x

+ sin x

2

−x

+ cos x

= 1;

lim

x

→2

E(x) sin(xπ) = 0.

◦

Korzystając z twierdzenia o dwóch funkcjach uzasadnić podane równości:

lim

x

→∞

E

x

2

+ 1

E(x)

=

∞;

lim

x

→0

2 + sin

1

x

x

2

=

∞;

lim

x

→0

−

3

− cos

1

x

ctg x =

−∞.

3

◦

Korzystając z granic podstawowych wyrażeń nieoznaczonych obliczyć podane granice:

lim

x

→0

sin

2

3x

x

2

;

lim

x

→−∞

ln (1 + 2

x

)

3

x

;

lim

x

→0

+

2

x

− 1

4

√

x

− 1

;

lim

x

→0

[1 + tg(2x)]

ctg x

.

◦

Znaleźć asymptoty pionowe i ukośne podanych funkcji:

u(x) =

x

3

+ x

2

x

2

− 4

;

v(x) =

x

− 3

√

x

2

− 9

;

w(x) =

sin x

x

− π

;

z(x) =

cos(πx)

2

x

− 8

.

◦

Narysować wykresy funkcji spełniających wszystkie podane warunki:

lim

x

→−∞

u(x) =

∞, lim

x

→0

−

u(x) = 1, u(2) = 0, lim

x

→∞

u(x) =

−1;

lim

x

→∞

v(x) = e, lim

x

→2

v(x) = 0, funkcja v jest parzysta;

prosta y = x + 1 jest asymptotą ukośną funkcji z w

−∞, prosta y = x − 1 asymptotą

ukośną w

∞, a prosta x = 0 jest jej asymptotą pionową obustronną;

Na rysunkach wskazać fragmenty wykresów spełniające poszczególne warunki.

◦

Korzystając z definicji Heinego uzasadnić ciągłość podanych funkcji na

:

u(x) =

x

3

x

2

+ 2

;

v(x) = sin

2

x;

w(x) =

|x − 5|;

z(x) = 2

−x

.

◦

Określić zbiory punktów ciągłości podanych funkcji:

u(x) =

x

3

− x

E(x);

v(x) =

⎧

⎨
⎩

1

dla x = 0 lub π,

π sin x

x(x

− π)

dla x

= 0 i π;

w(x) =

⎧

⎪

⎪

⎪

⎨
⎪

⎪

⎪

⎩

x cos

1

x

dla x < 0,

0

dla x = 0,

√

x sin

1

√

x

dla x > 0;

z(x) =

⎧

⎨
⎩

√

1

− cos 2x

x

dla x

= 0,

2

dla x = 0;

◦

Dobrać parametry a, b

∈

tak, aby podane funkcje były ciągłe we wskazanych punktach:

4

u(x) =

⎧

⎪

⎨
⎪

⎩

sin x

dla

|x|

π

2

,

ax + b dla

|x| <

π

2

,

v(x) =

⎧

⎨
⎩

2

dla x

0,

a

x

+ b dla 0 < x < 1,

3

dla x

1,

x

1

=

−

π

2

, x

2

=

π

2

;

x

1

=

−1, x

2

= 1;

w(x) =

x

2

+ax+b dla

|x| < 2,

x

√

x

2

− 4 dla |x| 2;

z(x) =

⎧

⎪

⎨
⎪

⎩

a sin x + b cos x dla

|x| >

π

4

,

1 + tg x

dla

|x|

π

4

;

x

1

=

−2, x

2

= 2;

x

1

=

−

π

4

, x

2

=

π

4

;

◦

Uzasadnić ciągłość podanych funkcji na wskazanych zbiorach:

u(x) = e

x

cos x,

;

v(x) =

1

√

16

− x

4

, (

−2, 2);

w(x) = arctg

√

x, [0,

∞);

z(x) =

√

sin x,

k

∈

[2kπ, (2k + 1)π] .

◦

Określić rodzaje nieciągłości podanych funkcji we wskazanych punktach:

u(x) =

⎧

⎨
⎩

x

2

−1

√

x

−1

dla x

∈ (0, 1) ∪ (1, ∞),

3

dla x = 1,

v(x) =

⎧

⎪

⎪

⎨
⎪

⎪

⎩

e

1
x

+ 2

e

1
x

+ 1

dla x

= 0,

e

dla x = 0,

x

0

= 1;

x

0

= 0;

w(x) =

⎧

⎨
⎩

|x| + x

x

2

dla x

= 0,

0

dla x = 0,

z(x) =

⎧

⎪

⎪

⎪

⎨
⎪

⎪

⎪

⎩

(1

− x)

1
x

dla x < 0,

e

dla x = 0,

(1 + x)

1
x

dla x > 0,

x

0

= 1;

x

0

= 0;

◦

Korzystając z twierdzenia Weierstrassa o przyjmowaniu kresów przez funkcję ciągłą na
przedziale domkniętym uzasadnić, że podane zagadnienia ekstremalne mają rozwiązania:

wśród stożków wpisanych w kulę o promieniu r istnieje ten, który ma największą ob-
jętość;

wśród trójkątów prostokątnych wpisanych w koło o promieniu r istnieje ten, który ma
najwiekszy obwód;

wśród prostokątów opisanych na danej elipsie istnieje ten, który ma najmniejsze i naj-
większe pole;

◦

Uzasadnić, że podane równania mają jednoznaczne rozwiązania we wskazanych przedzia-
łach:

x

3

+ 6x

− 2 = 0, (0, 1);

x sin x = 7,

2π,

5π

2

;

3

x

+ 5

x

= 9, (1, 2);

x

2

+ ln x = 0,

1

e

, 1

.

5

◦

Korzystając z twierdzenia Darboux o przyjmowaniu wartości pośrednich przez funkcję cią-
głą uzasadnić następujące stwierdzenia:

na każdym szlaku turystycznym wiodącym z Karpacza (800 m nad poziomej morza)
na Śnieżkę (1602 m nad poziomem morza) jest miejsce, które wznosi się 1000 m nad
poziomem morza;

w każdym wielokącie wypukłym istnieje sieczna, która jednocześnie połowi obwód i pole
tego wielokąta;

na dowolnej figurze wypukłej na płaszczyźnie można opisać kwadrat;

◦

Korzystając z definicji zbadać, czy istnieją pochodne podanych funkcji we wskazanych
punktach:

u(x) = 2x

− |x|, x

0

= 0;

v(x) =

|x| sin x, x

0

= 0;

w(x) =

x

2

dla x

2,

2

x

dla x > 2,

z(x) =

⎧

⎪

⎨
⎪

⎩

sin x dla x

π

2

,

1

dla x >

π

2

,

x

0

= 2;

x

0

=

π

2

.

◦

Korzystając z definicji obliczyć pochodne podanych funkcji:

u(x) =

1

x + 1

, gdzie x

= −1;

v(x) =

√

x, gdzie x > 0;

w(x) = tg x, gdzie x

=

π

2

+ kπ dla k

∈

;

z(x) = sh x, gdzie x

∈ .

◦

Napisać równania stycznych do wykresów podanych funkcji we wskazanych punktach:

f (x) = arcsin

x

2

, (1, f (1));

f (x) = ln

x

2

+ e

, (0, f (0));

f (x) = e

tg x

,

π

4

, f

π

4

;

f (x) =

√

2

x

+ 1, (3, f (3)) .

◦

Obliczyć kąty, pod jakimi przecinają się wykresy podanych funkcji:

i) f (x) = x

2

, g(x) =

3

√

x, x > 0;

ii) f (x) = 4

− x, g(x) = 4 −

x

2

2

, x > 0;

iii) f (x) =

1

x

, g(x) =

√

x, x > 0;

iv) f (x) = tg x, g(x) = ctg x, 0 < x <

π

2

.

◦

Na wykresie funkcji y = e

x

znaleźć punkt, który jest położony najbliżej prostej y = ex

−4;

◦

Wskazówka minutowa zegara na ratuszu ma długość 3 m, a godzinowa 2 m. Obliczyć
prędkość, z jaką oddalają się od siebie końce wskazówek zegara o godzinie 6:00;

6

Basen ma kształt odwróconego ostrosłupa ściętego prawidłowego. Dno basenu jest kwa-
dratem o boku 4 m, a jego górna powierzchnia kwadratem o boku 16 m. Głębokość
basenu wynosi 2 m. Do basenu wlewa się woda z prędkością 1 m

3

/min. Z jaką prędko-

ścią będzie się podnosił poziom wody w basenie w chwili, gdy będzie on napełniony do
połowy głębokości?

◦

Badając pochodne jednostronne rozstrzygnąć, czy istnieją pochodne podanych funkcji we
wskazanych punktach:

u(x) =

x

2

− x

, x

0

= 1;

v(x) = sgn (x)

· sin x, x

0

= 0;

w(x) =

ctg

3

x

, x

0

=

π

2

;

z(x) =

⎧

⎨
⎩

tg x dla

−

π

2

< x

0,

sin x dla 0 < x <

π

2

,

x

0

= 1.

◦

Znaleźć parametry a, b, c, dla których podane funkcje mają pochodne na

:

v(x) =

ae

x

+be

−x

dla x < 0,

ch 2x

dla 0

0;

u(x) =

x+1

dla x

0,

a sin x+b cos x dla x > 0.

◦

Zbadać, czy podane funkcje mają pochodne niewłaściwe w punkcie x

0

= 0:

u(x) = 3

−

5

√

x;

v(x) = tg

3

√

x;

w(x) =

| sin x|.

◦

Korzystając z reguł różniczkowania obliczyć pochodne podanych funkcji:

y =

x

3

+

1

x

2

e

x

;

y =

sin x

x

4

+ 4

;

y =

3

arcsin (x

2

);

y = x

tg x

.

◦

Korzystając z twierdzenia o pochodnej funkcji odwrotnej obliczyć:

f

−1

(y) dla:

i) f (x) = 3

−x

, gdzie x

∈ ;

ii) f (x) = cos x, gdzie 0 < x < π;

iii) f (x) = th x, gdzie x

∈ ; iv) f(x) = ln x, gdzie x > 0;

i)

f

−1

(e + 1), gdzie f (x) = x + ln x;

ii)

g

−1

(1), gdzie g(x) = cos x

− 3x;

iii)

h

−1

(3), gdzie h(x) =

3

√

x +

5

√

x +

7

√

x;

iv)

k

−1

(4), gdzie k(x) = x

3

+ 3

x

.

◦

Zakładając, że funkcje f i g mają pochodne właściwe, obliczyć pochodne funkcji:

y = f (x) cos g(x);

y = e

f (x)

g(x)

;

y = arctg [f (x)g(x)];

y = ln

f (x)

g(x)

+ 1

.

7

◦

Korzystając z różniczki funkcji obliczyć przybliżone wartości podanych wyrażeń:

3

√

7.999;

e

0.04

;

ln

2001

2000

;

arccos 0.499.

◦

Fragment terenu ma kształt trójkąta równoramiennego o boku b = 200 m. Kąt przy

wierzchołku tego trójkata, zmierzony z dokładnością 0.01 rad wynosi

π

3

. Z jaką w przy-

bliżeniu dokładnością można obliczyć pole tego terenu?

Objętość kulki metalowej, wyznaczona z dokładnością 1 cm

3

, wynosi 36π cm

3

. Z jaką w

przybliżeniu dokładnością można obliczyć średnicę tej kuli?

Do sztolni puszczono swobodnie kamień i zmierzono czas jego spadania z dokładnością
0.1 s. Z jaką w przybliżeniu dokładnością można wyznaczyć głębokość sztolni, jeżeli
czas spadania kamienia wyniósł 4.1 s? Przyjąć g = 9.8 m/s

2

.

◦

Korzystając z twierdzenia o pochodnej funkcji odwrotnej oraz z różniczki funkcji znaleźć
przybliżone rozwiązania podanych równań:

x

2003

+ 2003x = 2005;

3

x

−

1

2

x

= 8.70;

sin x + arctg x = 0.008;

x + ln x = 3.71.

◦

Obliczyć f

, f

, f

podanych funkcji:

f (x) = x

3

−

2

x

;

f (x) = x sin x;

f (x) =

e

x

x

;

f (x) = arctg x.

◦

Zbadać, czy istnieje f

(n)

(x

0

) dla podanych funkcji i punktów:

f (x) = x

3

|x|, x

0

= 0, n = 3;

f (x) =

(e

x

− 1)

2

dla

x

0,

x

2

dla

x

0,

x

0

= 0, n = 2;

◦

Funkcja f ma pochodne do drugiego rzędu włącznie. Obliczyć y

, y

dla podanych funkcji:

y = e

f (x)

;

y = f (tg x);

y = xf (3x);

y = f

f

x

2

.

◦

Znaleźć wzory ogólne na pochodną n

−tego rzędu podanych funkcji:

u(x) =

1

√

x

;

v(x) = sin

2

x;

w(x) = xe

x

;

z(x) = ln(1 + 2x).

◦

Punkt materialny porusza się po krzywej y = 2

x

w ten sposób, że jego rzut na oś Ox ma

stałą prędkość v

x

= 3. Z jaką prędkością (w kierunku osi Oy) porusza sie ten punkt w

chwili, gdy jest na wysokości 4?

8

◦

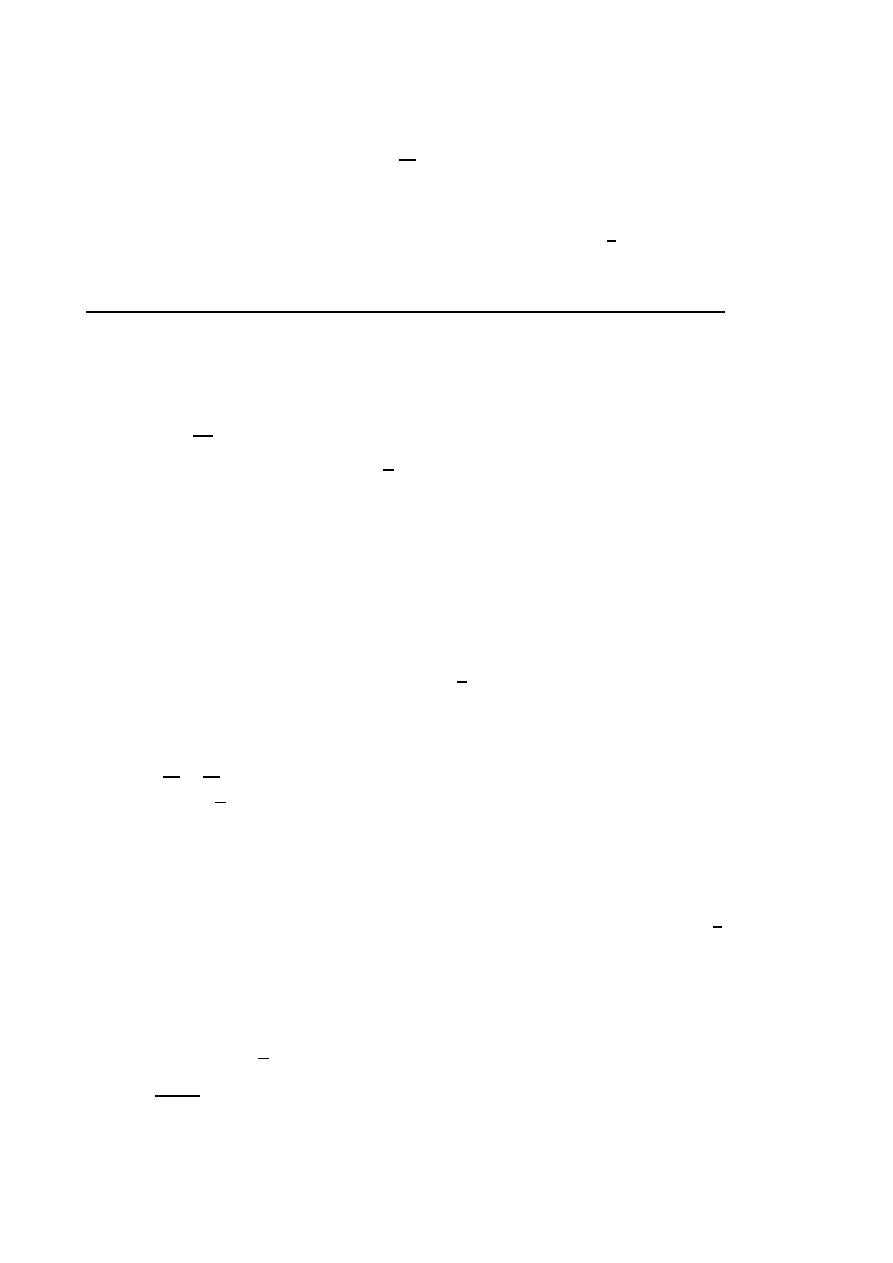
Złożona drabina strażacka ma długość 10 m i jest pozioma. Przy rozkładaniu drabiny

podnosi się ona z prędkością kątową ω =

π

12

rad/min i jednocześnie wysuwa z prędkością

w = 5 m/min. Z jaką prędkością będzie się poruszał strażak w koszu na końcu drabiny
po 3 minutach wznoszenia?

Położenie cząstki w chwili t opisuje wektor wodzący

r

=

e

t

cos t, e

t

sin t, e

t

. Znaleźć

przyspieszenie cząstki w chwili, gdy wektor prędkości miał długość

√

3.

◦

Sprawdzić, czy podane funkcje spełniają założenia twierdzenia Rolle’a na przedziale [

−1, 1].

Narysować wykresy tych funkcji.

u(x) =

cos

πx

2

;

v(x) = 1

− |x|;

w(x) = arcsin

|x|;

z(x) =

x

3

sin

π

x

dla x

= 0,

0

dla x = 0;

◦

Zastosować twierdzenie Lagrange’a do podanych funkcji na wskazanych przedziałach. Wy-
znaczyć odpowiednie punkty:

u(x) = e

x

, [0, 2];

v(x) = x

3

+ x, [

−1, 1] .

◦

Korzystając z twierdzenia Lagrange’a uzasadnić podane nierówności:

| arctg a − arctg b| |a − b| dla a, b ∈ ;

ln

a

b

b − a dla 1 a b.

◦

Znaleźć przedziały monotoniczności podanych funkcji:

u(x) =

x

4

4

−

x

3

3

− x

2

;

v(x) = e

x

(x + 1);

w(x) = x

− 3

3

√

x;

z(x) = x ln

2

x.

◦

Narysować wykresy funkcji f :

−→ , które spełniają wszystkie podane warunki:

f

(x) > 0 dla x

∈ (−∞, 1) ∪ (4, ∞), f

(x) < 0 dla x

∈ (1, 4) ale f

(1), f

(4) nie istnieją;

f

(x) > 0 dla każdego x < 1, f

(x) < 0 dla każdego x > 1, f

−

(1) = 1, f

+

(1) =

−

1

2

,

f (1) = 2;

Na rysunkach zaznaczyć fragmenty wykresów, które spełniają poszczególne warunki.

◦

Uzasadnić podane tożsamości:

arctg x + arcctg x =

π

2

dla x

∈ ;

arcsin

2x

1 + x

2

= 2 arctg x dla x

∈ (−1, 1).

9

◦

Korzystając z reguły de L’Hospitala obliczyć podane granice:

lim

x

→∞

ln (2

x

+ 1)

x

;

lim

x

→1

ln sin

π

2

x

ln x

;

lim

x

→0

(cos x)

1
x

;

lim

x

→∞

x arcctg x.

◦

Obliczyć podane granice. Czy można tu zastosować regułę de L’Hospitala?

lim

x

→0

x

3

sin

1
x

sin

2

x

;

lim

x

→−∞

x + cos 3x

x

− cos 2x

.

◦

Napisać wzory Taylora z resztą Lagrange’a dla podanych funkcji f , punktów x

0

oraz n :

f (x) = x

3

, x

0

=

−1, n = 4;

f (x) =

1

x

2

, x

0

= 1, n = 2;

f (x) = sin 2x, x

0

= π, n = 3;

f (x) = e

−x

, x

0

= 0, n = 5.

◦

Napisać wzór Maclaurina dla podanych funkcji ze wskazaną resztą:

f (x) = sin

x

3

, R

n

;

f (x) = ch x, R

n

.

◦

Oszacować dokładności podanych wzorów przybliżonych na wskazanych przedziałach:

ch x

≈ 1 +

x

2

2

,

|x| 0.1;

tg x

≈ x, |x|

π

12

;

ln(1

− x) ≈ −x −

x

2

2

−

x

3

3

,

|x| < 0.1;

1

√

4 + x

≈

1

2

−

x

16

, 0 < x < 0.1.

◦

Stosując wzór Maclaurina obliczyć:

sin 0.1 z dokładnością 10

−5

;

1

e

z dokładnością 10

−3

.

◦

Korzystając z definicji uzasadnić, że podane funkcje mają ekstrema lokalne we wskazanych
punktach:

u(x) =

|x| dla x = 0,
1

dla x = 0,

x

0

= 0;

v(x) = ch x, x

0

= 0;

w(x) =

|x − 1| + |x + 1|, x

0

= 1;

z(x) =

|sin x|, x

0

= π.

◦

Znaleźć wszystkie ekstrema lokalne podanych funkcji:

u(x) =

2x

2

− 1

x

4

;

v(x) = x ln x;

w(x) = x

−

√

x;

z(x) =

x

2

− 5x − 6

.

10

◦

Znaleźć wartości najmniejsze i największe podanych funkcji na wskazanych przedziałach:

u(x) = 2x

3

− 15x

2

+ 36x, [1, 5];

v(x) = arctg

1

− x

1 + x

, [0, 1];

w(x) =

2x

2

+

2

x

2

dla x

= 0,

1

dla x = 0,

, [

−2, 2];

z(x) = 1

−

9

− x

2

, [

−5, 1] .

◦

Określić przedziały wypukłości oraz punkty przegięcia podanych funkcji:

u(x) = xe

−x

;

v(x) = ln

1 + x

2

;

w(x) = x

−

2

3

x

3

− 4 ln |x|;

z(x) = sin x +

1

8

sin 2x.

◦

Zbadać przebieg zmienności podanych funkcji i następnie sporządzić ich wykresy:

u(x) = x ln x;

v(x) =

√

x

x

− 1

;

w(x) = arcsin

1

− x

2

1 + x

2

;

z(x) = e

2

−x

2

x

2

−1

;

r(x) = 3

−

4

x

−

4

x

2

;

s(x) = x2

1
x

.

◦

Platforma wiertnicza jest zakotwiczona na morzu 10 km od brzegu. Ropa z tej platformy
będzie dostarczana rurociągiem do rafinerii położonej nad brzegiem morza, 16 km od
punktu najbliższego platformie. Koszt ułożenia 1 km rurociągu na dnie morza wynosi 200
000 euro, a na lądzie – 100 000 euro. Do którego miejsca na brzegu należy doprowadzić
rurociąg, aby koszt jego budowy był najmniejszy?

Platforma

wiertnicza

x

16

km

10

km

Rafineria

◦

Kropla deszczu spada pod wpływem siły ciężkości (pomijamy opór powietrza). W czasie
spadku kropla paruje w ten sposób, że jej masa zmniejsza się proporcjonalnie do upływu
czasu. Wiadomo, że po 5 sekundach wyparowała połowa jej masy. Po ilu sekundach energia
kinetyczna kropli będzie największa?

◦

Jaka powinna być miara kąta α przy wierzchołku trójkata równoramiennego o danym polu,
aby promień koła r wpisanego w ten trójkąt był największy?

11

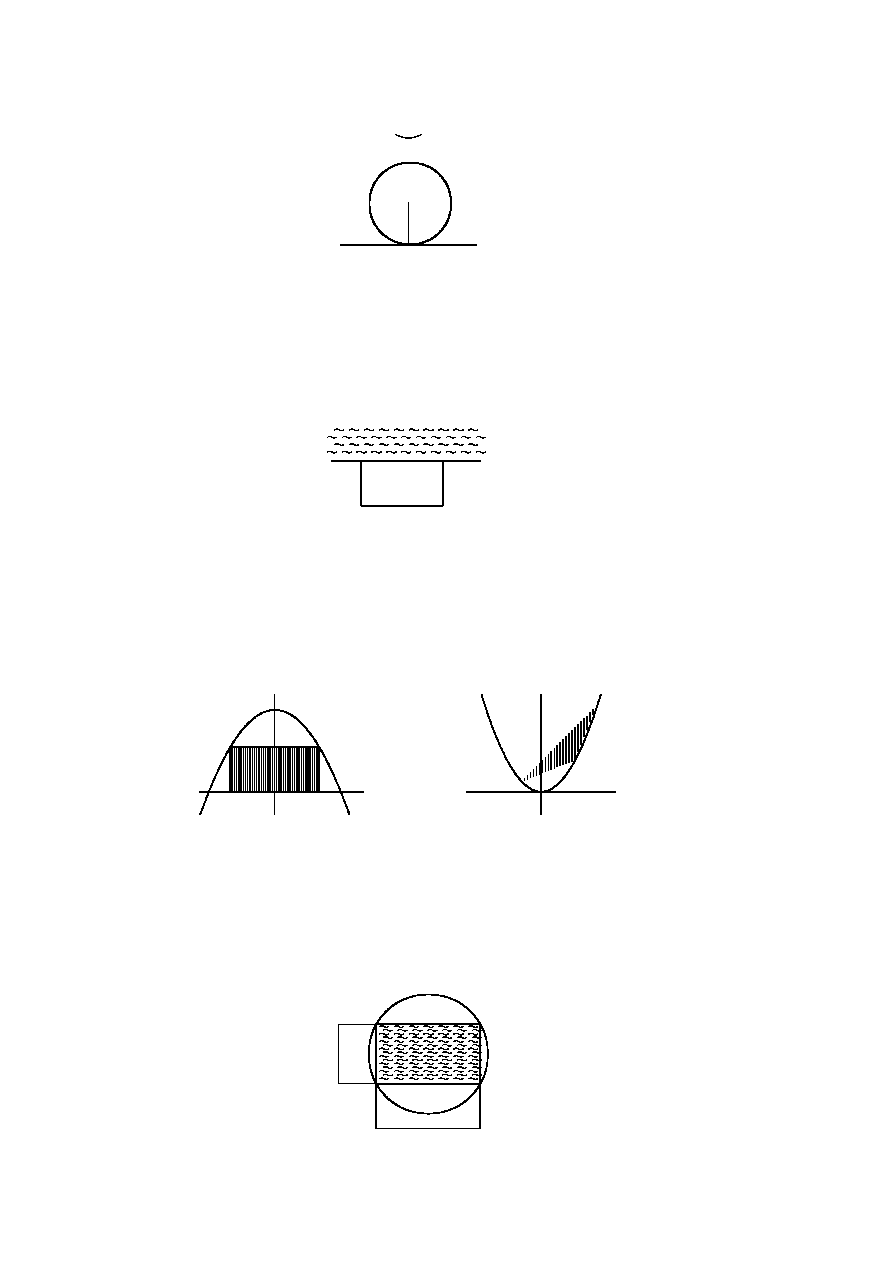
α

r

◦

Prostopadłościenny kontener ma mieć pojemność 22.50 m

3

i kwadratową podstawę. Koszt

1 m

2

blachy potrzebnej do wykonania jego dna i pokrywy wynosi 20 zł, a ścian bocznych

– 30 zł. Jakie powinny być wymiary kontenera, aby koszt jego budowy był najmniejszy?

◦

Jakie powinny być wymiary prostokątnego pola o powierzchni S, którego jednym natural-
nym bokiem jest brzeg rzeki, aby na jego ogrodzenie zużyć jak najmniej siatki?

a

b

rzeka

S

◦

Odcinek o długości l podzielić na dwie części tak, aby suma pól kwadratów zbudowanych
na tych częściach była najmniejsza.

◦

W parabolę o równaniu y = 16

− x

2

wpisano prostokąt, w sposób przedstawiony na

rysunku. Znaleźć wymiary prostokąta, który ma największe pole.

y

x

x

y

O

y=16

−x

2

y

x

O

B

C

A

y=x+2

y=x

2

Na paraboli y = x

2

wyznaczyć punkt A tak, aby pole trójkata, którego wierzchołkami

są punkt A oraz punkty B, C przecięcia paraboli z prostą y = x + 2, było największe.

◦

Wytrzymałość deski o ustalonej długości jest wprost proporcjonalna do jej szerokości oraz
kwadratu grubości. Jakie wymiary powinna mieć deska wycięta z okrągłego pniaka o pro-
mieniu r = 9 cm, aby jej wytrzymałość była największa?

s

h

r

12

◦

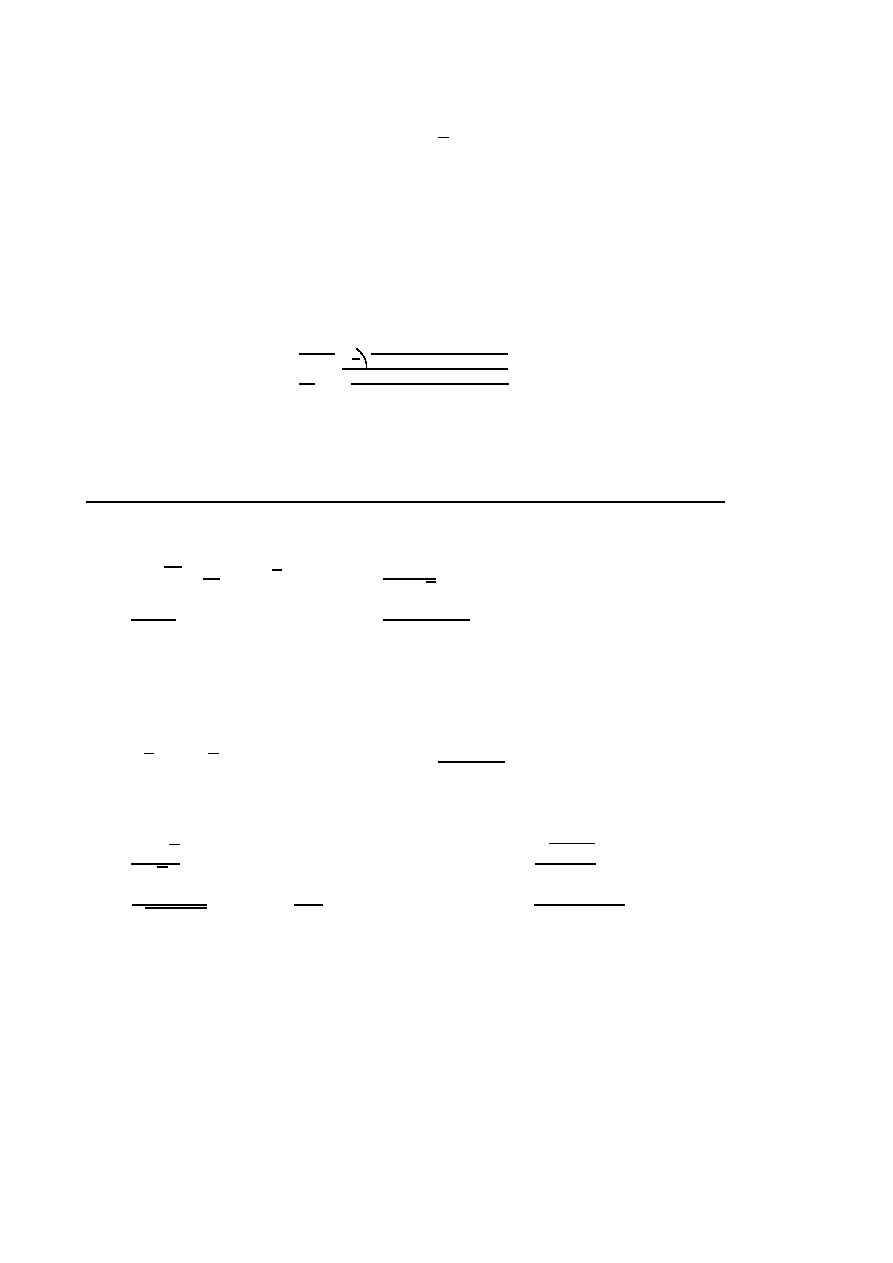
Drogi łączące miasta A i B oraz B i C torzą kąt

π

3

(zobacz rysunek). Samochód osobowy

wyruszył z miasta A do B i poruszał się prędkością v

1

= 80 km/h. Jednocześnie z miasta

B do C wyruszył samochóch ciężarowy i jechał z prędkością v

2

= 50 km/h. Po jakim czasie

samochody te będą najbliżej siebie, jeżeli odległość między miastami A i B wynosi 200
km?

A

B

C

v

1

v

2

π

3

d

◦

Obliczyć podane całki nieoznaczone:

3

3

√

x

2

+

1

x

3

− 2x

√

x

dx;

1

− x

1

−

3

√

x

dx;

x

4

x

2

+ 1

dx;

cos 2x

cos x

− sin x

dx.

◦

Korzystając z twierdzenia o całkowaniu przez części obliczyć całki nieoznaczone:

ln(x + 1) dx;

cos ln x dx;

x

2

2

x

dx;

√

x arctg

√

x dx;

x ch x dx;

(x

− 1)e

x

x

2

dx.

◦

Stosując odpowiednie podstawienia obliczyć podane całki nieoznaczone:

cos

√

x

√

x

dx;

(x+1) sin

x

2

+2x+2

dx;

√

1 + 4x

x

dx;

cos x

√

1 + sin x

dx;

dx

ch x

dx;

3x + 2

3x

2

+ 4x + 7

dx.

◦

Obliczyć podane całki nieoznaczone:

(

|x| + 1) dx;

f (x) dx, gdzie f (x) =

x

dla x < 0,

sin x dla x

0;

min

x, x

2

dx;

arctg

|x| dx.

13

◦

Obliczyć podane całki z funkcji wymiernych:

(x + 2) dx

x(x

− 2)

;

x

2

dx

x + 1

;

dx

(x

− 1)x

2

;

dx

(x

2

+ 1) (x

2

+ 4)

;

(4x + 1) dx

2x

2

+ x + 1

;

(3x

− 1) dx

x

2

− x + 1

.

◦

Obliczyć podane całki z funkcji trygonometrycznych:

dx

sin x + tg x

;

1 + tg x

cos x

dx;

dx

1 + 2 cos

2

x

;

sin

2

x

1 + cos x

dx;

dx

1

− tg x

;

sin

5

x

cos

3

x

dx.

◦

Obliczyć podane całki z funkcji niewymiernych:

dx

(1 + x

2

)

√

1 + x

2

;

x

3

1 + x

2

dx;

x

2

dx

√

x

2

− 1

;

√

9

− x

2

x

.

◦

Korzystając z definicji oraz z faktu, że funkcje ciągłe są całkowalne obliczyć podane całki
oznaczone:

1

−2

(2x

− 1) dx;

2

0

|x − 1| dx.

Wskazówka. Ad.

przedział całkowania podzielić równomiernie parzystą liczbą punktów.

◦

Korzystając z twierdzenia Newtona-Leibniza obliczyć podane całki:

2

1

√

x +

1

√

x

dx;

1

0

x

− 1

x + 1

dx;

9

0

dx

x

2

+ 9

dx;

1

2

−

1

2

dx

x

2

− 1

dx;

e

1

e

ln x dx;

π

0

sin

2

x cos x dx.

◦

Korzystając z definicji całki oznaczonej uzasadnić podane równości:

lim

n

→

∞

1

n

√

n

√

1 + n +

√

2 + n + . . . +

√

n + n

=

2

3

2

√

2

− 1

;

lim

n

→

∞

n

1

n

2

+ n + 1

2

+

1

n

2

+ 2n + 2

2

+ . . . +

1

n

2

+ n

2

+ n

2

=

π

3

√

3

;

14

lim

n

→

∞

π

4n

tg

π

4n

+ tg

2π

4n

+ . . . + tg

nπ

4n

= ln

√

2;

lim

n

→

∞

1

n

ln

(1 + n)(2 + n)

· . . . · (n + n)

n

n

= ln 4

− 1.

◦

Obliczyć podane całki oznaczone dokonując wskazanych podstawień:

6

1

dx

1 +

√

3x

− 2

, 3x

− 2 = t

2

;

3

1

x dx

√

x + 1

, 1 + x = t;

e

1

ln x, ln x = t;

1

4

0

dx

√

x(1

− x)

, x = t

2

;

1

1

3

3

√

x

− x

3

x

4

, x =

1

t

;

1

2

0

1 + x

1

− x

, dx, x = cos t.

◦

Metodą całkowania przez części obliczyć podane całki oznaczone:

1

0

arcsin x dx;

e

√

e

ln x

x

2

dx;

π

0

x(1 + cos x) dx;

1

0

x

2

e

2x

dx.

◦

Obliczyć podane całki oznaczone:

2

1

e

(x

− 1)sgn (ln x) dx;

3

0

f (x) dx, gdzie f (x) =

⎧

⎨
⎩

1

−x

dla 0

x 1,

1

dla 1 < x

2,

(2

−x)

2

dla 2 < x

3;

2

−2

||x| − 1| dx;

4

0

|x − 1| dx

|x − 2| + |x − 3|

.

◦

Oszacować podane całki:

2

0

x

6

+ 5

x

6

+ 2

dx;

1

0

dx

√

2 + x + x

2

dx;

π

2

0

√

sin x dx;

1

0

ln

1 + x

9

dx.

◦

Obliczyć wartości średnie podanych funkcji na wskazanych przedziałach:

15

u(x) =

1

x

2

+ 4

,

0,

π

2

;

v(x) = sin

3

x, [0, π];

w(x) =

|ln x| ,

1

e

, e

;

z(x) = arctg x,

0,

√

3

.

◦

Kamień rzucono z wysokości h = 2 m pionowo do góry z szybkością początkową v

0

=

5 m/s. Obliczyć średnią szybkość kamienia w czasie ruchu (od momentu wyrzucenia do
momentu upadku na ziemię). Nie uwzględniać oporu powietrza, przyjąć g = 10 m/ s

2

;

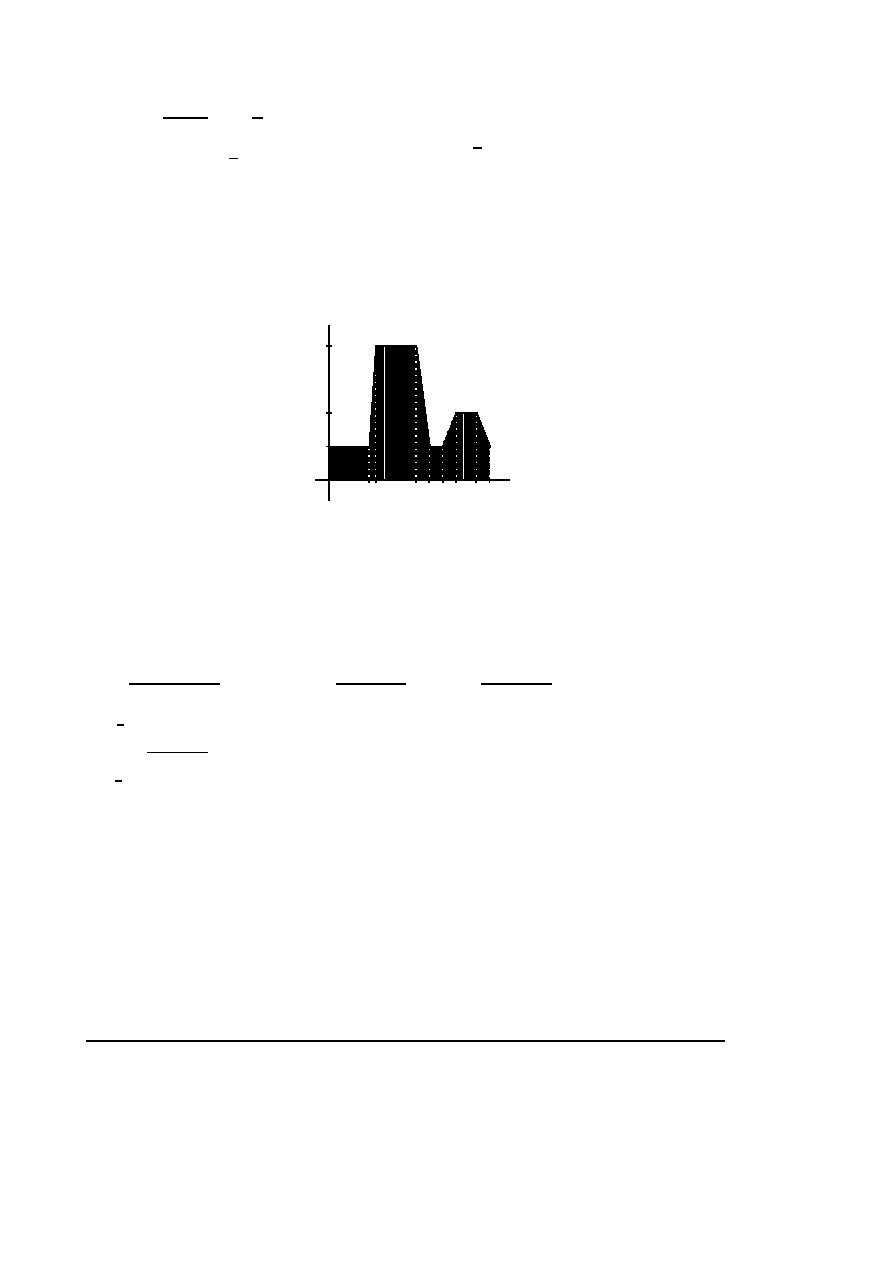
Zapotrzebowanie na energię elektryczną w Polsce 13 kwietnia 2003 r. przedstawiono na
wykresie. Obliczyć średnie zapotrzebowanie na energię w tym dniu.

energia

[MW ]

20

10

5

67

13151719 2224 czas [godz.]

◦

W Nowy Rok średnia temperatura we Wrocławiu była równa 4

◦

C. Przy czym od północy

do godziny 6 rano temperatura była ujemna, a w godz. od 18 do 24 nie przekraczała 2

◦

C.

Uzasadnić, że w pewnej chwili temperatura była równa 7

◦

C.

◦

Wykorzystując własności całek z funkcji parzystych, nieparzystych lub okresowych uza-
sadnić podane równości:

1

−1

x

5

− 3x

3

+ x

x

4

+ 2x

2

+ 1

dx = 0;

π

−π

x sin x

1 + cos x

2

dx = 2

π

0

x sin x

1 + cos x

2

dx;

1

e

−

1

e

ln

1 + sin x

1

− sin x

dx = 0;

n

0

(x

− E(x)) dx = n

1

0

(x

− E(x)) dx, gdzie n ∈

.

◦

Dla podanych funkcji f całkowalnych na przedziale [a, b], znaleźć funkcje górnej granicy
całkowania

F (x) =

x

c

f (t) dt,

gdzie c

∈ [a, b].

Naszkicować wykresy funkcji f i F.

f (x) = sgn

x

− x

2

, [a, b] = [

−1, 2], c = 0;

f (x) = min

1, x

2

[a, b] = [

−2, 3], c = −2.

◦

Obliczyć pola obszarów ograniczonych podanymi krzywymi:

16

√

x +

√

y = 1, x = 0, y = 0;

4y = x

2

, y =

8

x

2

+ 4

;

y = x

3

, y = 2x;

y = x

2

, y =

1

2

x

2

, y = 3x;

y = πx

2

, x = πy

2

;

y = x + sin x, y = x, (0

x 2π).

◦

Obliczyć długości podanych krzywych:

y = ln

e

x

+ 1

e

x

− 1

, gdzie 2

x 3;

y = x

2

, gdzie 0

x 1.

◦

Wyprowadzić wzór na objętość ostrosłupa prawidłowego o wysokości H i podstawie
kwadratowej o boku a.

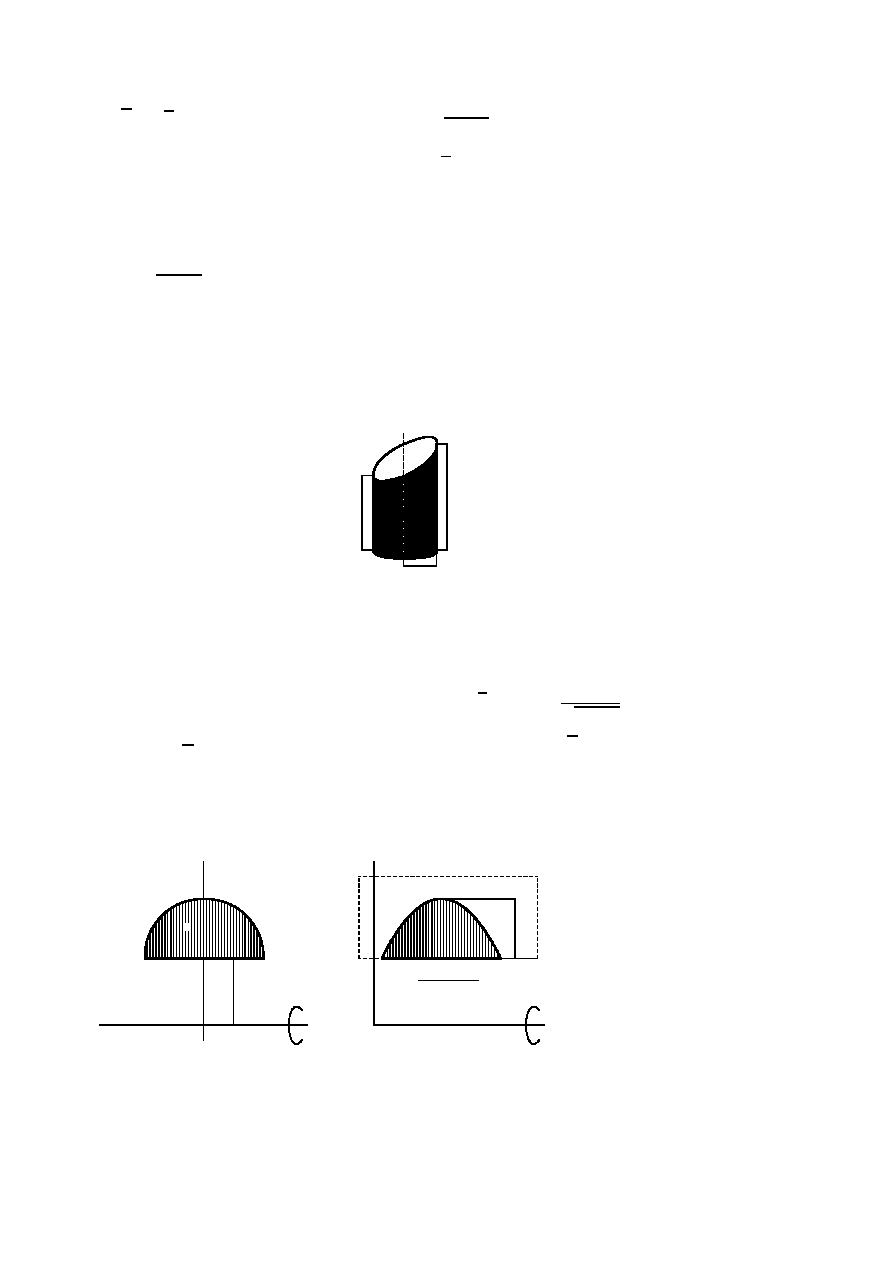
Walec o promieniu podstawy R ścięto ukośnie płaszczyzną (rysunek). Mniejsza wyso-
kość walca wynosi h, a większa H. Obliczyć objętość tego walca.

h

H

R

Obliczyć objętość stożka ściętego o wysokości H i promieniach podstaw r, R, gdzie
r < R.

◦

Obliczyć objętości brył powstałych z obrotu podanych figur T wokół wskazanych osi:

T : 0

x2, 0 y 2x − x

2

, Ox;

T : 0

x

√

5, 0

y

2

√

x

2

+ 4

, Oy;

T : 0

x

π

4

, 0

y tg x, Ox;

T : 0

x1, x

2

y

√

x, Oy.

◦

Obliczyć objętości brył powstałych z obrotu wokół osi Ox figur T przedstawionych na
rysunkach poniżej:

r

y

h

x

O

T

parabola

y

O

z

x

h

a

b

T

◦

Obliczyć pola powierzchni powstałych z obrotu wykresów podanych funkcji wokół wska-
zanych osi:

17

f (x) = cos x, 0

x

π

2

, Ox;

f (x) =

√

4 + x,

−4 x 2, Ox;

f (x) = ln x, 1

x

√

3, Oy;

f (x) =

|x − 1| + 1, 0 x 2, Oy.

◦

Obliczyć pola powierzchni powstałych z obrotu wokół osi Ox krzywych Γ przedstawionych
na rysunkach poniżej:

O

Γ

h

x

y

r

y

O

z

x

r

h

Γ

◦

Przy rozciąganiu sprężyny siła rozciągania jest proporcjonalna do wydłużenia sprężyny
(współczynnik proporcjonalności wynosi k). Obliczyć pracę jaką należy wykonać, aby
sprężynę o długości l rozciągnąć do długości L;

Zbiornik ma kształt walca o osi poziomej. Średnica walca D = 2 m, a długość L = 6 m.
Obliczyć pracę, jaką potrzeba wykonać, aby opróżnić zapełniony całkowicie wodą zbior-
nik. Otwór do opróżnienia zbiornika znajduje się w jego górnej części. Masa właściwa
wody γ = 1000 kg/m

3

.

◦

Punkt materialny zaczął poruszać się prostoliniowo z szybkością początkową v

0

=

10 m/s i przyspieszeniem a

0

= 2 m/s

2

. Po czasie t

1

= 10 s punkt ten zaczął poru-

szać się z opóźnieniem a

1

=

−1 m/s

2

. Znaleźć położenie punktu po czasie t

2

= 20 s od

chwili rozpoczęcia ruchu;

Dwie cząstki elementarne A i B położone w odległości d = 36 zaczynają zbliżać się do
siebie z szybkościami odpowiednio v

A

(t) = 10t + t

3

, v

B

(t) = 6t, gdzie t

0. Po jakim

czasie nastąpi zderzenie tych cząstek?

◦

Do dwóch jednakowych naczyń w kształcie walca włożono dwie bryły. Do naczyń wlewa
się woda z tą samą intensywnością. Pokazać, że jeżeli w każdej chwili poziom wody w
obu naczyniach był jednakowy, to pola przekrojów poziomych obu brył na tych samych
wysokościach są równe.

18