Analiza matematyczna 3

Lista pierwsza

Zadanie

1.1

1

Obliczy¢ podane caªki krzywoliniowe niezorientowane po wskazanych ªukach:
a)

Z

,

dl

p

x

2

+ y

2

, , { odcinek ª¡cz¡cy punkty (0;

,

1), (2;0);

b)

Z

,

xy dl, , { cz¦±¢ okr¦gu x

2

+ y

2

= R

2

le»¡ca w I ¢wiartce ukªadu;

c*)

Z

,

(x + y)dl, , { ¢wiartka okr¦gu x

2

+ y

2

+ z

2

= R

2

, y = x le»¡ca w pierwszym oktancie ukªadu.

Zadanie

1.2

Obliczy¢ dªugo±ci podanych ªuków:

a) , : x = a(t

,

sint); y = a(1

,

cos t); 0

¬

t

¬

2; a > 0;

b) , : jeden zwój linii ±rubowej o skoku h nawini¦tej na walec o promieniu r > 0;

c) , : x = e

,

t cost; y = e

,

t sint; z = e

,

t; 0

¬

t <

1

.

Zadanie

1.3

Znale¹¢ pole powierzchni bocznej walca x

2

+ y

2

= 1 ograniczonej pªaszczyznami z =

,

x; z = 5 + y.

Zadanie

1.4

Znale¹¢ masy podanych ªuków o wskazanych g¦sto±ciach liniowych:

a) , : x = acost; y = bsint; 1

¬

t

¬

2; (x;y) =

j

y

j

;

b) , : x = t; y = t

2

2 ; z =

t

3

3 ; 0

¬

t

¬

1; (x;y;z) =

p

2y;

c) , : x = rcos t; y = r sint; z = bt; 0

¬

t

¬

2; (x;y;z) = x

2

+ y

2

+ z

2

.

Lista druga

Zadanie

2.1

Okre±li¢ wspóªrz¦dne ±rodków masy podanych ªuków jednorodnych:

a) linia ªa«cuchowa y = a2

e

x=a

+ e

,

x=a

,

,

a

¬

x

¬

a;

b) x = r cos t; y = rsint; z = bt; 0

¬

t

¬

2;

c) brzeg trójk¡ta sferycznego x

2

+ y

2

+ z

2

= 1, x

­

0, y

­

0, z

­

0;

Zadanie

2.2

Znale¹¢ momenty bezwªadno±ci podanych ªuków jednorodnych wzgl¦dem wskazanych osi, przyj¡¢

0

= 1:

a) brzeg kwadratu o bokach a, wzgl¦dem przek¡tnej;

b) odcinek AB, gdzie A = (1;2;3), B = (3;5;4), wzgl¦dem osi Oz;

c) , : x = acost; y = asint; z = bt; 0

¬

t

¬

2; wzgl¦dem osi Ox.

Zadanie

2.3

Obliczy¢ nat¦»enie pola elektrycznego pochodz¡cego od ªadunku Q rozªo»onego równomiernie na brzegu kwadratu o boku

a: Nat¦»enie pola obliczy¢ w punkcie poªo»onym w odlegªo±ci d nad jednym z wierzchoªków kwadratu.

1

Zadania z pierwszych siedmiu list pochodz¡ ze skryptu

Elementy analizy wektorowej. Teoria, przykªady, zadania

. Zadania z

pozostaªych list pochodz¡ ze skryptu

Równania ró»niczkowe zwyczajne Teoria przykªady zadania

Przy czym obok kolejnych

Zadanie

2.4

Obliczy¢ siª¦, z jak¡ póªokr¡g o masie M i promieniu R przyci¡ga mas¦ punktow¡ m poªo»on¡ w ±rodku póªokr¦gu.

Zadanie

2.5

Obliczy¢ caªki krzywoliniowe zorientowane z podanych pól wektorowych po wskazanych ªukach (zorientowanych zgodnie

ze swoj¡ parametryzacj¡):

a)

~

F

(x;y) =

,

x

2

+ y

2

;xy

; , : x = t; y = e

t

; t

2

[0;1];

b)

~

F

(x;y;z) = (yz;xz;xy) , : x = cost; y = sint; z = t; t

2

[0;2];

c)

~

F

(x;y;z) = (y;z;x); , { odcinek AB, gdzie A = (1;

,

1;2), B = (0;2;3):

Lista trzecia

Zadanie

3.1

Obliczy¢ caªki krzywoliniowe z podanych pól wektorowych po ªukach okre±lonych wskazanymi równaniami (orientacja

ªuku jest zgodna ze wzrostem parametru x):

a)

~

F

(x;y) = (x

,

y;x + y), , : y = sinx; 0

¬

x

¬

;

b)

~

F

(x;y) = (lnx;lny), , : y = x

2

; 1

¬

x

¬

e:

Zadanie

3.2

Obliczy¢ podane caªki krzywoliniowe zorientowane po wskazanych ªukach zamkni¦tych:
a)

I

,

xy dx + x

2

dy, , { brzeg trójk¡ta o wierzchoªkach w punktach A = (0;0), B = (1;2), C = (

,

1;4); zorientowany

dodatnio;

b)

I

,

x

2

y dx + xy(y + 1) dy, , { okr¡g x

2

+ y

2

+ 2y = 0; zorientowany dodatnio;

c)

I

,

(3x+ 5z) dx+ (x+ 4y) dy + (6x

,

z) dz, , { brzeg trójk¡ta o wierzchoªkach w punktach A = (2;0;0), B = (0;2;0),

C = (0;0;2); obiegany w kolejno±ci ABCA:

Zadanie

3.3

Obliczy¢ caªki krzywoliniowe zorientowane z podanych potencjalnych pól wektorowych po dowolnym ªuku o pocz¡tku A

i ko«cu B:

a)

~

F

(x;y) = (x;y), A = (1;1), B = (

,

1;

,

2);

b)

~

F

(x;y) = (sinxcosy;cos xsiny), A =

2;

2

, B = (;);

c)

~

F

(x;y;z) =

,

x

2

,

2yz;y

2

,

2xz;z

2

,

2xy

, A = (0;0;0), B = (1;1;1):

Zadanie

3.4

Sprawdzi¢, »e podane caªki krzywoliniowe nie zale»¡ od ksztaªtu krzywej caªkowania i nast¦pnie obliczy¢ te caªki:

a)

(

1

;

2

)

Z

(0

;

0)

e

x

cos y dx

,

e

x

siny dy;

b)

(1

;

2)

Z

(2

;

1)

y

x

2

dx

,

1

x dy; wzdªu» ªuku nie przechodz¡cego przez o± Oy;

c)

(2

;

3

;

4)

Z

(1

;

1

;

1)

,

x

2

,

2yz

dx +

,

y

2

,

2xz

dy +

,

z

2

,

2xy

dz:

bezpo±rednio:
a)

I

,

,

1

,

x

2

y dx + x

,

1 + y

2

dy, , { okr¡g x

2

+ y

2

= R

2

; zorientowany dodatnio;

b)

I

,

,

x + y

2

dx +

,

x

2

+ y

2

dy, , { brzeg trójk¡ta o wierzchoªkach w punktach A = (1;1), B = (3;2), C = (2;5);

zorientowany dodatnio;

c)

I

,

e

x

(1

,

cos y) dx

,

e

x

(y

,

siny) dy, , { brzeg obszaru 0

¬

x

¬

, 0

¬

y

¬

sinx; zorientowany dodatnio.

Lista czwarta

Zadanie

4.1

Za pomoc¡ caªki krzywoliniowej zorientowanej obliczy¢ pola obszarów ograniczonych podanymi ªukami zamkni¦tymi:

a) elipsa , : x = acost; y = bsint; t

2

[0;2];

b) kardioida , : x = 2cost

,

cos2t; y = 2sint

,

sin2t; t

2

[0;2]:

Zadanie

4.2

Obliczy¢ prac¦ w podanych polach wektorowych podczas ruchu po wskazanych ªukach zorientowanych:

a)

~

F

(x;y) =

,

2xy;x

2

, dowolny ªuk , ª¡cz¡cy punkty A = (1;0);B = (0;3);

b)

~

F

(x;y;z) = (xy;y+z;z); wzdªu» ªuku , : x = cost; y = sint; z = t od punktu A = (1;0;0) do punktu B = (

,

1;0;);

c)

~

F

(x;y;z) = (

,

x;

,

y;

,

z) wzdªu» dowolnego ªuku , ª¡cz¡cego, nale»¡cy do sfery x

2

+ y

2

+ z

2

= r

2

; punkt A =

(x

1

;y

1

;z

1

); z punktem B = (x

2

;y

2

;z

2

), nale»¡cym do sfery x

2

+ y

2

+ z

2

= R

2

:

Lista pi¡ta

Zadanie

5.1

Obliczy¢ podane caªki powierzchniowe zorientowane:
a)

Z

Z

xy dydz + yz dzdx + xz dxdy, { zewn¦trzna strona powierzchni czworo±cianu ograniczonego pªaszczyznami

x = 0, y = 0, z = 0, x + y + z = 1;

b)

Z

Z

xdydz + yz dzdx + z dxdy , { zewn¦trzna strona powierzchni sze±cianu 0

¬

x

¬

1, 0

¬

y

¬

1, 0

¬

z

¬

1;

c)

Z

Z

x

2

dydz + y

2

dzdx + z

2

dxdy ; { górna strona powierzchni sto»ka z =

p

x

2

+ y

2

, z

¬

1;

d)

Z

Z

z

2

dxdy , { zewn¦trzna strona sfery x

2

+ y

2

+ z

2

= 4:

Zadanie

5.2

Niech funkcje f; g maj¡ wszystkie pochodne cz¡stkowe pierwszego rz¦du na obszarze V

R

3

: Sprawdzi¢, »e :

a)

grad

f

g

= g

grad

f

,

f

grad

g

g

2

;

b)

grad

h(f) = h

0

(f)

grad

f, gdzie h jest funkcj¡ ró»niczkowaln¡ na pewnym przedziale.

Zadanie

5.3

Sprawdzi¢, »e podane to»samo±ci s¡ prawdziwe:

a)

rot

(

grad

U) =

~

0, gdzie U jest funkcj¡ maj¡c¡ ci¡gªe wszystkie pochodne cz¡stkowe drugiego rz¦du na obszarze

V

R

3

;

Zadanie

5.4

Sprawdzi¢, »e podane to»samo±ci s¡ prawdziwe:

a) div

~

F

~

G

=

~

G

rot

~

F

,

~

F

rot

~

G

, gdzie pola wektorowe

~

F

i

~

G

s¡ ró»niczkowalne na obszarze V

R

3

;

b) div

rot

~

F

= 0, gdzie pole wektorowe

~

F

ma skªadowe dwukrotnie ró»niczkowalne w sposób ci¡gªy na obszarze

V

R

3

:

Zadanie

5.5

Przy pomocy twierdzenia Gaussa{Ostrogradskiego obliczy¢ podane caªki powierzchniowe. Sprawdzi¢ otrzymane wyniki

obliczaj¡c te caªki bezpo±rednio:
a)

Z

Z

2xy dydz

,

y

2

dzdx + 2z dxdy , { zewn¦trzna strona brzegu obszaru V : x

2

+y

2

+z

2

¬

9, x

­

0, y

­

0, z

­

0;

b)

Z

Z

(x + z)dydz + (x + y)dzdx + (y + z)dxdy, { zewn¦trzna strona brzegu obszaru V : x

2

+y

2

¬

R

2

, x+y+z

¬

R, z

­

0;

c)

Z

Z

x

3

dydz + y

3

dzdx + z

3

dxdy , { wewn¦trzna strona powierzchni walca V : x

2

+ y

2

¬

R

2

; 0

¬

z

¬

H:

Lista szósta

Zadanie

6.1

Obliczy¢ podane caªki powierzchniowe zorientowane:
a)

Z

Z

xy dydz + yz dzdx + xz dxdy, { zewn¦trzna strona powierzchni czworo±cianu ograniczonego pªaszczyznami

x = 0, y = 0, z = 0, x + y + z = 1;

b)

Z

Z

xdydz + yz dzdx + z dxdy , { zewn¦trzna strona powierzchni sze±cianu 0

¬

x

¬

1, 0

¬

y

¬

1, 0

¬

z

¬

1;

c)

Z

Z

x

2

dydz + y

2

dzdx + z

2

dxdy ; { górna strona powierzchni sto»ka z =

p

x

2

+ y

2

, z

¬

1;

d)

Z

Z

z

2

dxdy , { zewn¦trzna strona sfery x

2

+ y

2

+ z

2

= 4:

Zadanie

6.2

Niech funkcje f; g maj¡ wszystkie pochodne cz¡stkowe pierwszego rz¦du na obszarze V

R

3

: Sprawdzi¢, »e :

a)

grad

f

g

= g

grad

f

,

f

grad

g

g

2

;

b)

grad

h(f) = h

0

(f)

grad

f, gdzie h jest funkcj¡ ró»niczkowaln¡ na pewnym przedziale.

Zadanie

6.3

Sprawdzi¢, »e podane to»samo±ci s¡ prawdziwe:

a)

rot

(

grad

U) =

~

0, gdzie U jest funkcj¡ maj¡c¡ ci¡gªe wszystkie pochodne cz¡stkowe drugiego rz¦du na obszarze

V

R

3

;

b)

rot

(f

~

c

) =

grad

f

~

c

, gdzie f jest funkcj¡ maj¡c¡ wszystkie pochodne cz¡stkowe pierwszego rz¦du na obszarze

V

R

3

; a

~

c

jest ustalonym wektorem.

Zadanie

6.4

Sprawdzi¢, »e podane to»samo±ci s¡ prawdziwe:

a) div

~

F

~

G

=

~

G

rot

~

F

,

~

F

rot

~

G

, gdzie pola wektorowe

~

F

i

~

G

s¡ ró»niczkowalne na obszarze V

R

3

;

Zadanie

6.5

Przy pomocy twierdzenia Gaussa{Ostrogradskiego obliczy¢ podane caªki powierzchniowe. Sprawdzi¢ otrzymane wyniki

obliczaj¡c te caªki bezpo±rednio:
a)

Z

Z

2xy dydz

,

y

2

dzdx + 2z dxdy , { zewn¦trzna strona brzegu obszaru V : x

2

+y

2

+z

2

¬

9, x

­

0, y

­

0, z

­

0;

b)

Z

Z

(x + z)dydz + (x + y)dzdx + (y + z)dxdy, { zewn¦trzna strona brzegu obszaru V : x

2

+y

2

¬

R

2

, x+y+z

¬

R, z

­

0;

c)

Z

Z

x

3

dydz + y

3

dzdx + z

3

dxdy , { wewn¦trzna strona powierzchni walca V : x

2

+ y

2

¬

R

2

; 0

¬

z

¬

H:

Lista siódma

Zadanie

7.1

Korzystaj¡c z twierdzenia Stokesa obliczy¢ podane caªki krzywoliniowe. Sprawdzi¢ otrzymane wyniki obliczaj¡c te caªki

bezpo±rednio:
a)

I

,

x

2

y

3

dx + dy + z dz, , { okr¡g x

2

+ y

2

= R

2

, z = 0; zorientowany dodatnio;

b)

I

,

x dx + (x + y) dy + (x + y + z) dz, , : x = sint; y = cos t; z = sint + cost; t

2

[0;2];

c)

I

,

(y + z) dx + (z + x) dy + (x + y) dz, , { okr¡g x

2

+ y

2

+ z

2

= R

2

, x = y:

Zadanie

7.2

Obliczy¢ strumienie podanych pól wektorowych przez wskazane pªaty:
a)

~

F

(x;y;z) =

x

3;z

2

,

x

2

; 2z3

, { powierzchnia caªkowita walca z = x

2

+ y

2

¬

R

2

, 0

¬

z

¬

H;

b)

~

F

(x;y;z) =

,

x

p

x

2

+ y

2

+ z

2

;

,

y

p

x

2

+ y

2

+ z

2

;

,

z

p

x

2

+ y

2

+ z

2

!

, { powierzchnia zewn¦trzna sfery x

2

+ y

2

+ z

2

=

R

2

;

c)

~

F

(x;y;z) = (5x + z;x

,

3y;4y

,

2z), { górna cz¦±¢ pªaszczyzny x + y + z = 2 odci¦ta pªaszczyznami ukªadu

wspóªrz¦dnych.

Zadanie*

7.3

Wyprowadzi¢ prawo Archimedesa.

Zadanie

7.4

Obliczy¢ cyrkulacje podanych pól wektorowych wzdªu» wskazanych ªuków zamkni¦tych:

a)

~

F

(x;y;z) =

,

y

2

;(x + y)

2

;z

; , { ªamana zamkni¦ta ª¡cz¡c¡ punkty A = (1;0;0), B = (0;1;0), C = (0;0;1);

b)

~

F

(x;y;z) = (y;1

,

x;

,

z); , { ªuk zamkni¦ty otrzymany w wyniku przeci¦cia powierzchni walca (x

,

1)

2

+ y

2

= 1 z

póªsfer¡ (x

,

2)

2

+ y

2

+ z

2

= 4, z

­

0:

Lista ósma

Zadanie

8.1

Z pewnej substancji radioaktywnej po upªywie 4 lat zostaªo 20 gram, a po upªywie dalszych 4 lat tylko 4 gramy. Jaka

byªa masa substancji w chwili pocz¡tkowej ?

a) yy

0

+ 4t = 0;

b) dy = 2ty

2

dt;

c) t

,

y

2

,

1

dt + y

,

t

2

,

1

dy = 0; d) siny

0

= t:

Zadanie

8.3

Wyznaczy¢ rozwi¡zanie zagadnienia pocz¡tkowego

y

0

= 1 + y

2

1 + t

2

, y(1) =

,

1

oraz poda¢ przedziaª na którym jest ono okre±lone.

Zadanie

8.4

Rozwi¡za¢ podane zagadnienia pocz¡tkowe:

a) y

0

sint = y lny, y

2

= e; b) t

p

1

,

y

2

dt + y

p

1

,

t

2

dy = 0, y(0) = 1:

Zadanie

8.5

Wyznaczy¢ rozwi¡zania podanych równa« ró»niczkowych jednorodnych:

a) ty

0

=

p

t

2

,

y

2

+ y; b) (t

,

y)dt + tdy = 0;

c) ty

0

= y (lny

,

lnt); d) ty

0

,

y = ttg yt:

Zadanie

8.6

Rozwi¡za¢ podane zagadnienia pocz¡tkowe:

a)

,

t

2

+ y

2

dt

,

2tydy = 0, y(1) =

p

2; b) ty

0

= t + 12y, y(1) = 0.

Zadanie

8.7

Znale¹¢ krzywe, dla których trójk¡t

OSY (rysunek) utworzony przez o± Oy,

styczn¡ i wektor wodz¡cy punktu stycz-

no±ci jest równoramienny (o podstawie

OY ).

-

6

y

=

y

(

t

)

t

O

y

Q

Q

Q

Q

Q

Q

Q

,

,

,

Q

Q

Q

r

r

r

Y

S

Zadanie

8.8

Wyznaczy¢ rozwi¡zania podanych równa« ró»niczkowych liniowych niejednorodnych:

a) y

0

+ y = sint; b) y

0

+ 2ty = e

,

t

2

; c) ty

0

,

2y = t

3

cos t:

Zadanie

8.9

Wyznaczy¢ rozwi¡zania podanych zagadnie« pocz¡tkowych oraz przedziaªy, na których s¡ one okre±lone:

a) y

0

,

y = 1, y(3) = 3;

b) y

0

= (y + 1)sint, y (t

0

) = y

0

;

c) ty

0

+ y = t + 1, y(1) = 0; d) y

0

sintcos t = y + sin

3

t, y

4

= 0:

Zadanie

8.10

Znale¹¢ równanie krzywej przechodz¡cej

przez punkt (1,1), dla której pole trójk¡ta

OST (rysunek) utworzonego przez o± Ot;

styczn¡ i wektor wodz¡cy punktu styczno-

±ci jest staªe i równa si¦ 1.

-

6

@

@

@

,

,

,

r

t

t

O

y

y

=

y

(

t

)

@

@

@

@

@

@

@

r

r

T

S

y

(

t

)

Zadanie

8.11

Rozwi¡za¢ podane równania Bernoulliego lub zagadnienia pocz¡tkowe:

a) ty

0

+ y = y

2

lnt, y(1) = 1;

b) y

0

,

2y = 2

p

ye

t

lnt, y(1) = 0;

c) y

0

+ 2ty = 2ty

2

;

d) 3ty

2

y

0

,

2y

3

= t

3

;

1

Lista dziewi¡ta

Zadanie

9.1

Znale¹¢ równania ró»niczkowe podanych rodzin krzywych:

a) y

,

Ct = C

,

1; b) y

2

= 2Ct

,

2t

2

:

Zadanie

9.2

Znale¹¢ równania rodzin krzywych ortogonalnych do podanych rodzin krzywych:

a) y = Ct

2

; b) t

2

+ y

2

= 2Cy:

Zadanie

9.3

Basen o pojemno±ci 10.000 litrów zawiera 1.000 litrów czystej wody. Do basenu wlewa si¦ woda o ska»eniu 50% z pr¦dko±ci¡

20 litrów na minut¦. Przez otwór spustowy ciecz wylewa si¦ z pr¦dko±ci¡ 10 litrów na minut¦. Wyznaczy¢ procent ska»enia

wody w chwili napeªnienia zbiornika.

Zadanie

9.4

W hali o obj¦to±ci 200 m

3

powietrze zawiera 0,15 % dwutlenku w¦gla. Wentylator podaje w ci¡gu minuty 20 m

3

powietrza

zawieraj¡cego 0,04 % CO

2

. Po jakim czasie ilo±¢ dwutlenku w¦gla w hali zmniejszy si¦ dwukrotnie ?

Zadanie

9.5

Dwa stulitrowe zbiorniki, z których pierwszy zawiera 10 % wodny roztwór soli, a drugi czyst¡ wod¦ poª¡czono rur¡

umo»liwiaj¡c¡ mi¦dzy nimi przepªyw. Je»eli do pierwszego zbiornika wlewa si¦ ciecz z zadan¡ pr¦dko±ci¡, to wymusza ona

przepªyw roztworu z t¡ sam¡ pr¦dko±ci¡ ze zbiornika pierwszego do drugiego oraz z drugiego na zewn¡trz. Po jakim czasie

st¦»enie soli w drugim zbiorniku b¦dzie najwi¦ksze, je»eli do pierwszego zbiornika wlewa si¦ czysta woda z pr¦dko±ci¡ 5

litrów na minut¦ ?

Zadanie

9.6

Ciaªo, którego temperatura wynosi 220

C jest umieszczone w pomieszczeniu, gdzie termometry wskazuj¡ 60

C. Po

10 minutach od chwili umieszczenia ciaªa w pomieszczeniu jego temperatura obni»yªa si¦ do 140

C. W tym momencie

wª¡czono klimatyzatory, które obni»aj¡ temperatur¦ otoczenia z szybko±ci¡ 1

C na minut¦. Jaka b¦dzie temperatura T

ciaªa po t minutach od chwili uruchomienia klimatyzatorów ?

Zadanie

9.7

W obwodzie elektrycznym poª¡czono szeregowo opornik o oporze R, cewk¦ o indukcyjno±ci L oraz ¹ródªo pr¡du E(t) =

E

0

sint: Wyznaczy¢ nat¦»enie pr¡du i w obwodzie jako funkcj¦ czasu, je»eli i(0) = 0:

Zadanie

9.8

Wyznaczy¢ rozwi¡zania podanych równa«:

a) t

2

y

00

,

(y

0

)

2

= 0; b) ty

00

,

y

0

= t

2

e

t

; c) 2ty

0

y

00

= (y

0

)

2

,

1:

Zadanie

9.9

Wyznaczy¢ rozwi¡zania podanych równa«:

a) y

3

y

00

+ 1 = 0; b) 2yy

00

,

3(y

0

)

2

= 4y

2

; c) (y

,

1)y

00

= 2(y

0

)

2

:

Zadanie

9.10

Rozwi¡za¢ podane zagadnienia pocz¡tkowe:

a) y

00

= y

0

t +

t

2

y

0

, y(2) = 0, y

0

(2) = 4;

b) 2y

00

= 3y

2

, y(

,

2) = 1, y

0

(

,

2) = 1;

c) yy

00

,

(y

0

)

2

= y

2

lny, y(0) = 1, y

0

(0) = 1:

Zadanie

9.11

00

0

2

Zadanie

9.12

Wyznaczy¢ równanie ruchu spadaj¡cego swobodnie ciaªa o masie m z uwzgl¦dnieniem oporu powietrza wyra»aj¡cego si¦

wzorem G = kv

2

; gdzie k jest staª¡ dodatni¡, a v pr¦dko±ci¡ ruchu. Znale¹¢ rozwi¡zanie tego równania przy warunkach

pocz¡tkowych x(0) = x

0

, v(0) = 0:

Zadanie

9.13

Cz¡steczka o masie m porusza si¦ po linii prostej. Niech x(t) oznacza odlegªo±¢ tej cz¡steczki zmierzon¡ w chwili t; od

ustalonego centrum na prostej. Cz¡steczka jest przyci¡gana przez centrum z siª¡ kx

3

; gdzie k > 0: Wyznaczy¢ równa-

nie ruchu cz¡steczki oraz jego rozwi¡zanie, je»eli rozpocz¦ªa ona ruch w odlegªo±ci x

0

od centrum z zerow¡ pr¦dko±ci¡

pocz¡tkow¡. Obliczy¢ czas, po którym cz¡steczka osi¡gnie centrum.

Lista dziesi¡ta

Zadanie

10.1

Wyznaczy¢ przedziaªy, na których podane zagadnienia pocz¡tkowe maj¡ jednoznaczne rozwi¡zania:

a)

,

t

2

,

2

y

00

+ (2t

,

1)y

0

+ y = lnt, y

,

1

= 1, y

0

(1) = 0;

b) y

000

+ (t

,

arcsin t)y = arccos t, y

4

= 1, y

0

4

=

,

1, y

00

4

= 0:

Zadanie

10.2

Pokaza¢, »e podane funkcje tworz¡ na zadanym przedziale ukªady fundamentalne wskazanych równa« ró»niczkowych.

Znale¹¢ rozwi¡znia tych równa« z zadanymi warunkami pocz¡tkowymi:

a) y

1

(t)=lnt, y

2

(t)=t, (0;e), t

2

(1

,

lnt)y

00

+ty

0

,

y=0, y(1)=2, y

0

(1)=1;

b) y

1

(t)=t, y

2

(t)=e

t

, (

,1

;1), (t

,

1)y

00

,

ty

0

+y=0, y(0)=0, y

0

(0)=1.

Zadanie

10.3

Wyznaczy¢ równania ró»niczkowe liniowe jednorodne postaci (LJ

n

) odpowiednich rz¦dów, których ukªady fundamentalne

tworz¡ podane funkcje:

a) y

1

(t) = t, y

2

(t) = t

2

, t

2

(0;

1

);

b) y

1

(t) = t, y

2

(t) = sint, y

3

(t) = cost, t

2

(0;

1

):

Zadanie

10.4

Wykorzystuj¡c metod¦ obni»ania rz¦du równania znale¹¢ rozwi¡zania ogólne podanych równa«:

a) t

2

y

00

,

ty

0

,

3y = 0, '(t) = 1t; b) (t

,

1)y

00

,

(t + 1)y

0

+ 2y = 0, '(t) = e

t

:

Zadanie

10.5

Wyznaczy¢ warto±¢ parametru m

2

R

dla którego funkcja '(t) = e

mt

jest rozwi¡zaniami równania (2t + 1)y

00

+ 2(2t

,

1)y

0

,

8y = 0; a nast¦pnie scaªkowa¢ to równanie.

Zadanie

10.6

Napisa¢ równania charakterystyczne podanych równa« ró»niczkowych:

a) y

00

,

2y

0

+ y = 0;

b) y

00

,

3y = 0;

c) 4y

000

+ y

0

= 0;

d) y

000

,

2y

00

,

2y

0

= 0; e) y

(5)

+ y

000

+ y = 0; f) y

(10)

= 0:

Zadanie

10.7

Wyznaczy¢ ukªady fundamentalne oraz równania ró»niczkowe postaci (LS

n

) mo»liwie najni»szego stopnia dla zadanych

pierwiastków ich równa« charakterystycznych:

a)

1

= 1 +

p

3i;

b)

1

=

2

=

,

2;

c)

1

= 2;

2

= 3;

Zadanie

10.8

Wyznaczy¢ równania ró»niczkowe postaci (LS

n

) mo»liwie najni»szego rz¦du, je»eli podane funkcje wchodz¡ w skªad ich

ukªadów fundamentalnych:

a) cos2t;

b) te

,

t

;

c) e

2

t

, e

t

,

6

= 2;

d) 1, e

,

t

sint; e) t

2

cos 2t; f) t

3

, e

t

:

Zadanie

10.9

Rozwi¡za¢ podane równania o staªych wspóªczynnikach:

a) 6y

00

,

5y

0

+ y = 0;

b) y

00

,

y

0

,

2y = 0;

c) 4y

00

,

4y + y = 0;

d) y

00

+ y

0

+ 14y = 0; e) y

00

,

4y

0

+ 5y = 0;

f) y

00

,

2y

0

+ 5y = 0;

g) y

000

,

8y = 0;

h) y

000

,

2y

00

,

y

0

+ 2y = 0; i) y

(4)

,

y = 0;

j) y

(4)

+ 10y

00

+ 9y = 0; k) y

(6)

+ 2y

(5)

+ y

(4)

= 0; l) y

(5)

+ 8y

000

+ 16y

0

= 0:

Zadanie

10.10

Rozwi¡za¢ podane zagadnienia pocz¡tkowe:

a) y

00

+ y

0

,

6y = 0, y

,

0

= 1;y

0

(0) = 0;

b) y

00

+ 9y = 0, y

3

= 1;y

0

3

= 1;

c) y

00

,

2y

0

+ y = 0, y

,

1

= 2;y

0

(1) = 3;

d) y

000

,

3y

00

+ 3y

0

,

y = 0, y

,

0

= 1; y

0

(0) = 2; y

00

(0) = 3;

e) y

000

+ y

00

= 0, y

,

0

= 1; y

0

(0) = 0; y

00

(0) = 1:

Zadanie

10.11

Punkt materialny o masie m porusza si¦ po linii ªacz¡cej dwa centra i jest przyci¡gany przez nie z siª¡ wprost propor-

cjonaln¡ do jego odlegªo±ci od ka»dego z nich. Wspóªczynnik proporcjonalno±ci jest równy k > 0, a odlegªo±¢ mi¦dzy

centrami wynosi 2b: Znale¹¢ równanie ruchu i rozwi¡za¢ je wiedz¡c, »e w chwili pocz¡tkowej (t

0

= 0) punkt znajdowaª si¦

w odlegªo±ci x

0

od ±rodka linii ªacz¡cej oba centra i miaª zerow¡ pr¦dko±¢.

Zadanie

10.12

Wyznaczy¢ te warto±ci parametru

2

R

; dla których zagadnienie brzegowe

y

00

+ y = 0; y(0) = y(2); y

0

(0) = y

0

(2)

ma niezerowe rozwi¡zanie.

Zadanie*

10.13

Znale¹¢ rozwi¡zania podanych równa« Eulera:

a) t

2

y

00

+ 2ty

0

,

6y = 0;

b) ty

00

+ y

0

= 0;

c) t

2

y

000

,

3ty

00

+ 3y

0

= 0; d) t

3

y

000

,

t

2

y

00

+ 2ty

0

,

2y = 0:

Lista jedenasta

Zadanie

11.1

Sprawdzi¢, »e podane funkcje s¡ rozwi¡zaniami wskazanych równa« ró»niczkowych. Wyznaczy¢ rozwi¡zania podanych

równa« lub zagadnie« pocz¡tkowych:

a) y

00

+ 10y

0

+ 25y = 4e

,5

t

, '(t) = 2t

2

e

,5

t

;

b) y

00

+ 4y = sin2t, '(t) =

,

1

4 tcos2t;

c) y

00

,

y

0

,

2y = 4t

,

2e

t

, '

,

t

= 1

,

2t + e

t

, y(0) = 0, y

0

(0) = 1;

Zadanie

11.2

Podane funkcje s¡ rozwi¡zaniami wskazanych równa« liniowych niejednorodnych. Wyznaczy¢ rozwi¡zania ogólne tych

równa«:

a) '(t) = sint

t +

1

t , (t) =

1

t , y

00

+ 2ty

0

+ y = 1t;

b) '(t) = t, (t) = sine

t

+ t, y

00

,

y

0

+ ye

2

t

= te

2

t

,

1:

Zadanie

11.3

Wyznaczy¢ rozwi¡zania ogólne podanych równa« liniowych niejednorodnych, je»eli znane s¡ ukªady fundamentalne ich

równa« jednorodnych:

a)

,

3t + 2t

2

y

00

,

6(1 + t) y

0

+ 6y = 6, y

1

(t) = t

3

, y

2

(t) = t + 1, t > 0;

b) (t

,

1)y

00

,

ty

0

+ y = (t

,

1)

2

e

t

, y

1

(t) = t, y

2

(t) = e

t

, t > 1;

c) (t + 1)y

00

,

(2 + t)y

0

= e

t

, y

1

(t) = 1, y

2

(t) = te

t

, t >

,

1:

Zadanie

11.4

Metod¡ uzmienniania staªych rozwi¡za¢ podane równania ró»niczkowe:

a) y

00

+ 4y = 1

cos2t; b) y

00

,

y = 4t

2

+ 1

t

p

t ; c) y

00

,

2y

0

tgt = 1:

Zadanie

11.5

Poda¢ postaci rozwi¡za« wskazanych równa« ró»niczkowych:

a) 4y

00

,

4y = t

3

,

24t; b) y

00

,

7y

0

= (t

,

1)

2

;

c) y

00

,

8y

0

+ 16y = (1

,

t)e

4

t

;

d) y

00

+ 3y

0

= 3;

e) y

00

+ 25y = cos5t;

f) y

00

+ y = sint

,

cost;

g) y

000

+ y = t;

h) y

000

+ y

00

= 3;

i) y

(4)

+ 2y

000

+ y

00

= e

,

t

;

j) y

(4)

,

y

0

= 2;

k) y

(4)

+ 4y

00

+ 4y = cost; l) y

(4)

+ 4y

00

+ 4y = tcos 2t:

Zadanie

11.6

Korzystaj¡c z metody wspóªczynników nieoznaczonych rozwi¡za¢ podane równania:

a) y

00

+ 2y

0

+ y =

,

2;

b) y

00

,

4y

0

+ 4y = t

2

;

c) y

00

+ 4y

0

+ 4y = 8e

,2

t

;

d) y

00

+ 3y

0

= 3te

,3

t

;

e) y

00

+ 5y

0

+ 6y = 10(1

,

t)e

,2

t

; f) y

00

+ 4y

0

,

4y = 8sin2t;

g) y

00

+ 9y = 3sin3t + 2cos3t;

h) y

000

,

3y

00

+ 3y

0

,

y = e

t

;

i) y

000

,

y = sint;

j) y

000

,

3y

00

+ 3y

0

,

y = e

t

cos2t;

k) y

(4)

+ y

00

= t + t

2

;

l) y

(4)

+ 2y

00

+ y = cost:

Zadanie

11.7

Rozwi¡za¢ podane równania korzystaj¡c z twierdzenia o superpozycji:

a) y

00

,

y

0

,

2y = e

t

+ e

,2

t

;

b) y

00

,

y = t + sint;

c) y

00

,

4y

0

= 2cos

2

4t;

d) y

00

,

y

0

,

2y = 4t

,

2e

t

;

e) y

000

,

4y

0

= t

2

+ te

2

t

+ sint; f) y

(5)

+ y

000

= t + 2e

,

t

:

Zadanie

11.8

Rozwi¡za¢ podane zagadnienia pocz¡tkowe:

)

00

2(1 t) (0) 2

0

(0)

2

b) y

00

,

6y

0

+ 9y = 9t

2

,

12t + 2, y(0) = 1, y

0

(0) = 3;

c) y

00

+ 6y

0

+ 9y = 10sint, y(0) = 0, y

0

(0) = 0;

d) y

00

+ y

0

= e

,

t

, y

,

0

= 1, y

0

(0) =

,

1;

e) y

000

,

y

0

=

,

2t, y

,

0

= 0, y

0

(0) = 1, y

00

(0) = 2;

f) y

(4)

,

y = 8e

t

, y

,

0

= 0, y

0

(0) = 2, y

00

(0) = 4, y

000

(0) = 6:

Lista dwunasta

Zadanie

12.1

Sprawdzi¢, »e dla podanych ukªadów równa« wskazane ci¡gi funkcji s¡ ich rozwi¡zaniami na zadanych przedziaªach:

a)

8

>

<

>

:

y

0

1

=

,

1

y

2

y

0

2

= 1y

1

; (y

1

(t);y

2

(t)) =

e

,

t

2

; 2e

t

2

!

;

R

;

b)

8

>

<

>

:

y

0

1

= 1

,

2y

1

t

y

0

2

= y

1

+ y

2

+ 2y

1

t

,

1

; (y

1

(t);y

2

(t)) =

t

3

+ 3

3t

2

; 2e

t

,

t

3

+ 3

3t

2

; (0;

1

);

c)

8

>

<

>

:

y

0

1

=

,

y

1

t + y

2

y

0

2

=

,

2y

1

t

2

+ y

2

t

; (y

1

(t);y

2

(t)) =

C

1

+ C

2

t; 2C

2

+ C

1

t

; (0;

1

):

Zadanie

12.2

Zapisa¢ w postaci wektorowej podane ukªady równa« ró»niczkowych liniowych:

a)

8

<

:

y

0

1

= ty

1

+ t

2

y

2

,

lnt

y

0

2

= y

1

t + y

2

; b)

8

<

:

y

0

1

= 2y

1

,

3y

2

+ e

t

y

0

2

= y

1

+ e

,

t

; c)

8

>

>

>

<

>

>

>

:

y

0

1

= y

2

+ 3y

3

,

1

y

0

2

= y

1

+ 2y

3

y

0

3

= y

1

,

y

2

+ t

:

Zadanie

12.3

Korzystaj¡c z twierdzenia o istnieniu i jednoznaczno±ci dla ukªadów równa« okre±li¢ przedziaªy, na których podane

zagadnienia pocz¡tkowe maj¡ jednoznaczne rozwi¡zania:

a)

8

>

<

>

:

y

0

1

= y

1

t + y

2

y

0

2

= y

1

,

y

2

+ 1

t

,

1

; y

1

1

2

= 1; y

2

1

2

= 2;

b)

8

<

:

y

0

1

sint = y

1

,

y

2

+ sint

y

0

2

cost = y

1

+ y

2

+ cos t

; y

1

3

4

= 12; y

2

3

4

= 13:

Zadanie

12.4

Korzystaj¡c z metody eliminacji rozwi¡za¢ podane ukªady równa« ró»niczkowych liniowych ze wskazanymi warunkami

pocz¡tkowymi:

a)

2

4

x

0

y

0

3

5

=

2

4

1 3

,

1 5

3

5

2

4

x

y

3

5

;

2

4

x(0)

y(0)

3

5

=

2

4

3

1

3

5

;

b)

2

4

x

0

y

0

3

5

=

2

4

3

,

2

4 7

3

5

2

4

x

y

3

5

;

2

4

x(0)

y(0)

3

5

=

2

4

1

0

3

5

;

2

x

0

3

2

1 2

3

2

x

3

2

x(0)

3

2

0

3

d*)

2

4

x

0

y

0

3

5

=

2

4

,

t

,1

t

,

2t

,3

t

,1

3

5

2

4

x

y

3

5

;

2

4

x(1)

y(1)

3

5

=

2

4

1

2 +

p

2

3

5

.

Zadanie

12.5

Sprawdzi¢, czy podane funkcje wektorowe tworz¡ ukªady fundamentalne wskazanych ukªadów równa« ró»niczkowych

liniowych na zadanych przedziaªach:

a)

y

1

(t) =

2

4

e

,

t

2e

,

t

3

5

,

y

2

(t) =

2

4

e

3

t

,

2e

3

t

3

5

;

y

0

=

2

4

1

,

1

,

4 1

3

5

y

;

R

;

b)

y

1

(t) =

2

4

t

t

2

3

5

,

y

2

(t) =

2

4

0

t

3

5

,

y

0

=

2

4

t

,1

0

1 t

,1

3

5

y

; (0;

1

);

c)

y

1

(t) =

2

4

1

t

,1

3

5

,

y

2

(t) =

2

4

t

2

3

5

,

y

0

=

2

4

,

t

,1

1

,

2t

,1

1

3

5

y

; (

,1

;0):

Zadanie

12.6

Korzystaj¡c z zadania

12.5

rozwi¡za¢ podane zagadnienia pocz¡tkowe:

a)

y

0

=

2

4

1

,

1

,

4 1

3

5

y

;

y

(0) =

2

4

1

1

3

5

; b)

y

0

=

2

4

t

,1

0

1 t

,1

3

5

y

;

y

(1) =

2

4

0

1

3

5

;

c)

y

0

=

2

4

,

t

,1

1

,

2t

,1

1

3

5

y

;

y

(

,

1) =

2

4

1

,

1

3

5

:

Zadanie

12.7

Przy pomocy metody Eulera wyznaczy¢ ukªad fundamentalny ukªadu równa« ró»niczkowych

y

0

= A

y

, je»eli:

a) A =

2

4

,

3

,

4

,

2

,

5

3

5

; b) A =

2

4

1 5

,

1

,

3

3

5

; c) A =

2

6

6

6

4

1 0 0

0 1

,

1

0 1 1

3

7

7

7

5

:

Zadanie

12.8

Korzystaj¡c z metody Eulera dla ró»nych rzeczywistych warto±ci wªasnych, rozwi¡za¢ ukªad równa«

y

0

= A

y

lub zagad-

nienie pocz¡tkowe

y

0

= A

y

,

y

(0) =

y

0

je»eli:

a) A =

2

4

,

1 8

1 1

3

5

; b) A =

2

6

6

6

4

2

,

1 1

1 2

,

1

1

,

1 2

3

7

7

7

5

; c) A =

2

4

1 1

,

2 4

3

5

;

y

0

=

2

4

0

,

1

3

5

:

Zadanie

12.9

Korzystaj¡c z metody Eulera dla ró»nych zespolonych warto±ci wªasnych rozwi¡za¢ ukªad równa«

y

0

= A

y

lub zagadnienie

pocz¡tkowe

y

0

= A

y

,

y

(0) =

y

0

je»eli:

a) A =

2

4

,

7 1

,

2

,

5

3

5

; b) A =

2

4

0

,

1

2 2

3

5

;

y

0

=

2

4

1

1

3

5

:

Zadanie

12.10

Korzystaj¡c z metody Eulera dla ró»nych rzeczywistych i zespolonych warto±ci wªasnych rozwi¡za¢ ukªad równa«

y

0

= A

y

lub zagadnienie pocz¡tkowe

y

0

= A

y

,

y

(0) =

y

0

je»eli:

a) A =

2

6

6

6

4

0 1 0

0 0 1

3

7

7

7

5

; b) A =

2

6

6

6

4

2 1

,

2

,

1 0 0

3

7

7

7

5

;

y

0

=

2

6

6

6

4

0

,

1

3

7

7

7

5

:

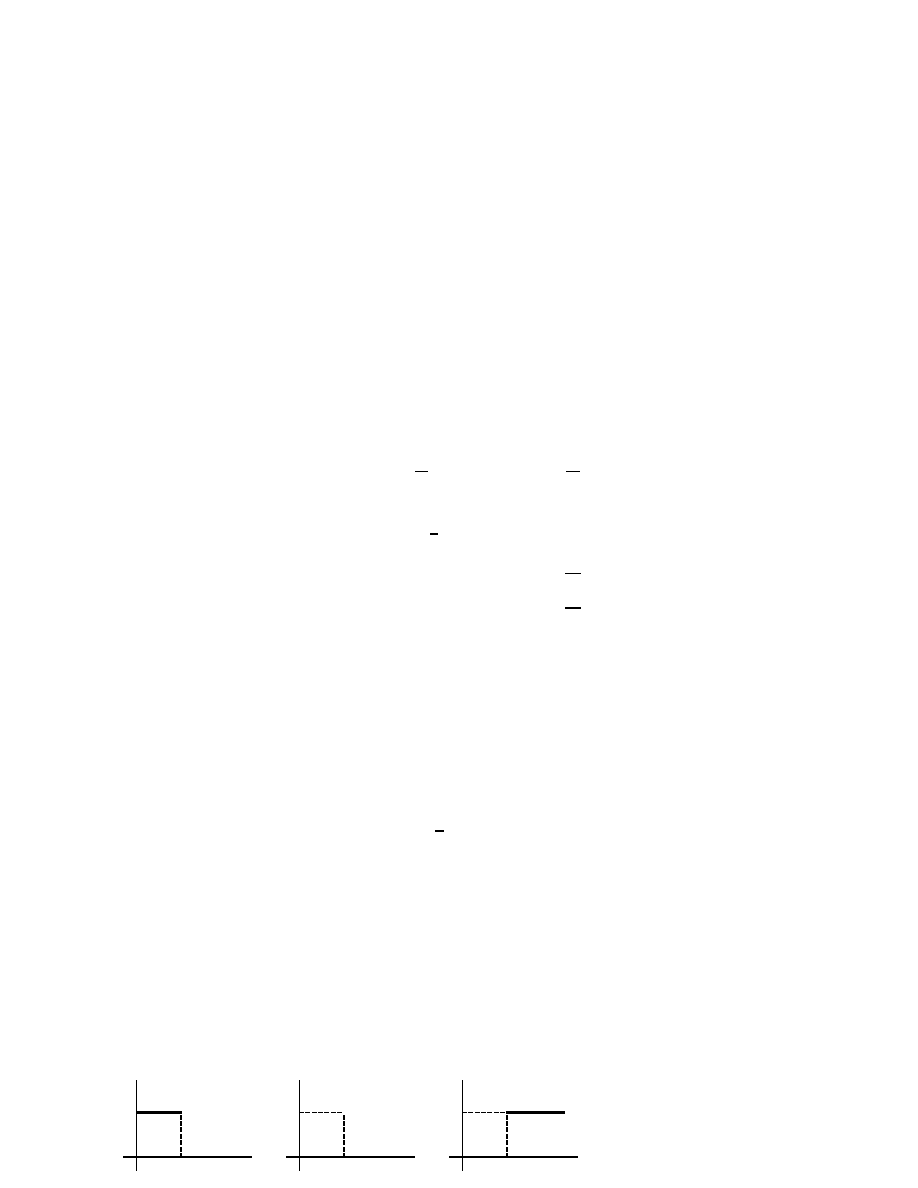
Lista trzynasta

Zadanie

13.1

Metod¡ eliminacji wyznaczy¢ rozwi¡zania ogólne podanych niejednorodnych ukªadów równa« ró»niczkowych lub zagad-

nie« pocz¡tkowych:
a)

8

<

:

x

0

= x

,

2y + e

t

y

0

= x + 4y + e

2

t

; b)

8

<

:

x

0

= x + 2y

y

0

= x

,

5sint

;

c)

8

<

:

x

0

= 4x

,

5y + 4t

,

1

y

0

= x

,

2y +

t

;

8

<

:

x(0) = 0

y(0) = 0

:

Zadanie

13.2

Sprawdzi¢, »e funkcje

y

1

(t) = 1t

3

2

,

1

,

y

2

(t) = 1t

4

,

1

1

s¡ na przedziale (0;

1

) ukªadem fundamentalnym ukªadu jednorodnego odpowiadaj¡cego ukªadowi niejednorodnemu

y

0

= 1t

,

2 2

,

1

,

5

y

+

1

t

:

Rozwi¡za¢ ukªad niejednorodny z warunkiem pocz¡tkowym

y

(1) =

2

6

4

11

30

1

12

3

7

5

:

Zadanie

13.3

Korzystaj¡c z metody uzmienniania staªych rozwi¡za¢ podane ukªady niejednorodne równa« ró»niczkowych liniowych:

a)

8

<

:

x

0

= x + y

,

cos t

y

0

=

,

2x

,

y + sint + cos t

; b)

8

<

:

x

0

=

,

5x

,

y + e

t

y

0

= x

,

3y + e

2

t

.

Zadanie

13.4

Rozwi¡za¢ zagadnienie pocz¡tkowe

y

0

= A

y

+

h

(t),

y

(0) =

y

0

, je»eli:

a) A =

2

4

0 1

,

1 0

3

5

;

h

(t) =

2

4

cos t

1

3

5

;

y

0

=

2

4

1

1

2

3

5

;

b) A =

2

6

6

6

4

,

1

,

2 0

0

,

1

,

1

0 0

,

1

3

7

7

7

5

;

h

(t) =

2

6

6

6

4

2e

,2

t

1

1

3

7

7

7

5

;

y

0

=

2

6

6

6

4

1

1

1

3

7

7

7

5

:

Zadanie

13.5

Korzystaj¡c z denicji obliczy¢ transformaty Laplace'a podanych funkcji:

a) sin2t; b) t

2

; c) te

,

t

; d) e

2

t

cos2t:

Zadanie

13.6

Korzystaj¡c z denicji obliczy¢ transformaty Laplace'a funkcji o podanych wykresach:

-

6

y

t

O

1

y

=

f

(

t

)

a)

-

6

y

t

O

,

,

,@

@

@

1

2

1

y

=

g

(

t

)

b)

-

6

y

t

O

,

,

,

1

1

y

=

h

(

t

)

c)

a) 1

s + 2;

b)

s

s

2

+ 4s + 5; c)

1

s

2

,

4s + 3;

d)

s + 2

(s + 1)(s

,

2)(s

2

+ 4); e)

s

2

+ 1

s

2

(s

2

,

1)

2

:

Lista czternasta

Zadanie

14.1

Metod¡ operatorow¡ rozwi¡za¢ podane zagadnienia pocz¡tkowe dla równa« ró»niczkowych rz¦du pierwszego:

a) y

0

,

y = 1, y(0) = 1; b) y

0

,

2y = sint, y(0) = 0:

Zadanie

14.2

Metod¡ operatorow¡ rozwi¡za¢ podane zagadnienia pocz¡tkowe dla równa« ró»niczkowych rz¦du drugiego:

a) y

00

+ y

0

= 0, y(0) = 1, y

0

(0) = 1;

b) y

00

+ 3y

0

= e

,3

t

, y(0) = 0, y

0

(0) =

,

1;

c) y

00

,

2y

0

+ 2y = sint, y(0) = 0, y

0

(0) = 1;

d) y

00

,

2y

0

+ y = 1 + t, y(0) = 0, y

0

(0) = 0;

e) y

000

+ y

00

= t, y(0) =

,

3, y

0

(0) = 1, y

00

(0) = 0;

f) y

(4)

,

5y

00

+ 10y

0

,

6y = 0, y(0) = 1, y

0

(0) = 0, y

00

(0) = 6, y

000

(0) =

,

14:

Zadanie

14.3

Metod¡ operatorow¡ rozwi¡za¢ podane zagadnienia pocz¡tkowe dla ukªadów dwóch równa« rz¦du pierwszego:

a)

8

<

:

x

0

=

,

y

y

0

=

,

x

;

8

<

:

x(0) = 1

y(0) =

,

1

;

b)

8

<

:

x

0

=

,

y

y

0

= 2x + 2y

;

8

<

:

x(0) = 1

y(0) = 1

;

c)

8

<

:

x

0

=

,

2y + 3t

y

0

= 2x

+ 4

;

8

<

:

x(0) = 2

y(0) = 3

; d)

8

<

:

x

0

,

y

0

=

,

sint

x

0

+ y

0

= cost

;

8

>

<

>

:

x(0) = 12

y(0) =

,

1

2

:

Zadanie

14.4

Metod¡ operatorow¡ rozwi¡za¢ podane zagadnienia pocz¡tkowe dla ukªadów trzech równa« rz¦du pierwszego:

a)

8

>

>

>

<

>

>

>

:

x

0

=

,

2x

,

2y

,

4z

y

0

=

,

2x + y

,

2z

z

0

= 5x + 2y + 7z

;

8

>

>

>

<

>

>

>

:

x(0) = 1

y(0) = 1

z(0) = 1

;

b)

8

>

>

>

<

>

>

>

:

x

0

=

,

x + y + z + e

t

y

0

= x

,

y + z + e

3

t

z

0

= x + y + z + 4

;

8

>

>

>

<

>

>

>

:

x(0) = 0

y(0) = 0

z(0) = 0

:

Zadanie

14.5

Korzystaj¡c z podstawowych wªasno±ci przeksztaªcenia Laplace'a obliczy¢ transformaty podanych funkcji:

a) sin

4

t;

b) cos 4tcos2t; c) t

2

cost;

d) tsh3t;

e) te

t

cost;

f) e

3

t

sin

2

t;

g)

1

(t

,

2)sin(t

,

2); h)

1

(t

,

1)e

t

,1

:

Zadanie

14.6

Obliczy¢ transformat¦ Laplace'a funkcji:

f(t) =

8

>

>

>

>

>

>

<

>

>

>

>

>

>

:

1 dla 0

¬

t < 1

0 dla 1

¬

t < 2

1 dla 2

¬

t < 3

0 dla 3

¬

t < 4

1 dla 4

¬

t < 5

0 dla 5

¬

t <

1

:

Wskazówka. Funkcj¦

f

(

t

) zapisa¢ wykorzystuj¡c jedynk¦ Heaviside'a.

Zadanie

14.7

Korzystaj¡c z podstawowych wªasno±ci przeksztaªcenia Laplace'a wyznaczy¢ funkcje, których transformaty dane s¡ wzo-

rami:

a)

2s + 3

s

3

+ 4s

2

+ 5s; b)

3s

2

(s

3

,

1)

2

; c) e

,

s

s + 1:

Zadanie

14.8

Obliczy¢ podane sploty:

a) e

t

e

2

t

; b) cos3t

cos t:

Zadanie

14.9

Korzystaj¡c ze wzoru Borela wyznaczy¢ funkcje, których transformaty dane s¡ wzorami:

a)

1

s

2

(s

2

+ 1); b)

s

(s

2

+ 1)

2

; c)

1

(s

,

1)

2

(s + 2):

Zadanie

14.10

Przedstawi¢ rozwi¡zania podanych zagadnie« pocz¡tkowych w postaci splotu:

a) y

00

+ y

0

,

2y = cost, y(0) = 0, y

0

(0) = 0;

b) y

00

,

2y

0

+ y = e

t

, y(0) = 0, y

0

(0) = 0: