FILOZOFIA PRZYRODY

Prof. dr hab. Marian Grabowski

WYKŁAD XXI i XXII

Na tym wykładzie wróćmy jeszcze raz do problemu usytuowania matematyki w obrębie metody nowożytnego przyrodoznawstwa. Zajmowaliśmy się tym na rozmaite sposoby. Przyglądaliśmy się strukturom matematycznym jako pewnym modelom rzeczywistości fizykalnej i zrobiliśmy to na przykładzie różnych modeli przestrzeni, które można matematycznie skonstruować i przyglądaliśmy się, jak te modele są coraz precyzyjniejsze. Z drugiej strony, na ostatnim wykładzie pojawiły się też takie teorie fizyczne, które miały charakter wysoce hipotetyczny. Mówiliśmy jak wygląda zmiana pojęcia masy w fizyce itp. To ma taki charakter teorii spekulatywnych, które ciągle nie mają potwierdzeń empirycznych. Odróżnia się te teorie od takich, które te potwierdzenia posiadają. Mówiliśmy także, że to, co charakteryzuje metodę przyrodniczą, to takie intensywne używanie języka matematyki.

Jak zatem wygląda ta relacja między używaniem matematyki w fizyce, a samą matematyką? Bo matematyka też ma swój własny, prywatny sens. Można się nią zajmować niekoniecznie badając przyrodę ożywioną dla niej samej.

W związku z powyższym, matematycy, którzy się zajmują matematyką w sposób taki czysty, nie odniesiony do żadnych obiektów fizykalnych, także natrafiają na masę pytań matematycznych. Czyli mamy matematykę i mamy też filozofię matematyki.

Wywołajmy teraz pytanie o sposób istnienia obiektów matematycznych.

Można uchwycić łatwo, o co w tym pytaniu chodzi, z perspektywy idei Platońskich. Można zadać sobie pytanie: Czy obiekty matematyczne istnieją w jakiś idealny sposób, czy to są po prostu konstrukty, które my wymyślamy? To występuje pod hasłem dwóch przeciwnych poglądów filozoficznych: platonizm kontra konstruktywizm. Z jednej strony jest taki sposób taktowania tych obiektów matematycznych jako obiektów idealnych, które mają jakiś sposób istnienia. A drugi pogląd powiada, że to nie istnieje, nie ma takiego charakteru obiektywnego, niezależnego sposobu istnienia, tylko jest czymś skonstruowanym. No i teraz ten konstrukt matematyczny rozmaicie się rozumie - czy to jest rodzaj jakiegoś instrumentu, który jest nam potrzebny do opisu czegoś, czy ma to taki charakter jak spór o powszechniki? Czy pojęciom ogólnym odpowiadają jakieś konkretnie istniejące byty? Ten spór szedł po linii realizmu pojęciowego - tym pojęciom ogólnym coś odpowiada, a nominalizmem - który mówi, że są nazwy, a za nimi tak naprawdę nic nie stoi.

Przedmiotem refleksji filozofów średniowiecznych nie były twory matematyczne, zaś z tymi pojęciami ogólnymi wiele ludzi się stykało, i stąd te pytanie.

Pewnego rodzaju argumenty na rzecz platonizmu są argumentami, na które w naszej kulturze jest trudno natrafić. W dzisiejszych czasach w różnych pracach, zawierających poglądy filozoficzne, trudno jest natrafić na jakieś poglądy o platonizmie.

W jaki sposób można o tym platonizmie opowiadać? Można to robić w dwojaki sposób. Z jednej strony podawać argumenty wprost za istnieniem tych tworach idealnych, ale można też zastosować strategię przeciwną, wyjść z tego faktu, że matematyka jest intensywnie używana w fizyce i ma tam swoje sukcesy. Można zacząć próbować patrzeć na to użycie matematyki w fizyce, jako na pewnego rodzaju argument na rzecz uznania jakiejś formy istnienia obiektów matematycznych. To jest taki pogląd, który pojawił się u Hilarego Putnama - jest to matematyk, który później zajął się filozofią matematyki. Wymyślił argument z niezbędności. On nie jest platonikiem, i ten argument nie był konstruowany na takiej zasadzie, żeby bezpośrednio był potraktowany na rzecz platonizmu. Jest to jednak taki argument na rzecz realizmu tych obiektów matematycznych. W jaki sposób argumentuje na rzecz tego argumentu z niezbędności?

Co do tego, że mamy całe mnóstwo teorii fizycznych, które nieźle opisują nam świat przyrodniczy, nie ma sporów. Z tego powodu, że w fizyce używa się intensywnie matematyki, to akceptując dowolną teorię fizyczną, jako coś, co rzeczywiście opowiada o świecie, my zarazem chcąc nie chcąc, musimy zaakceptować tą matematykę, która jest w niej użyta. Czyli jak zaakceptujemy teorie fizyczne, to zarazem akceptujemy teorie o istnieniu bytów matematycznych. Mamy realizm w stosunku do teorii fizycznej, i ten realizm pociąga za sobą realizm w odniesieniu do tworów matematycznych.

Drugi argument, jest to taki argument, że jeśli uznalibyśmy fikcyjność w kwestii istnienia tych obiektów matematycznych, to grozi nam, że znowu, ponieważ te teorie matematyczne są używane w fizyce, ta fikcja w kwestii obiektów matematycznych, pociągnie za nami fikcje w kwestii tych teorii fizycznych. Musielibyśmy uznać, że jeśli fikcyjnymi tworami są twory matematyczne, to również fikcjami są teorie fizyczne. No i znowu trudno się na to zgodzić.

Putnam używa jeszcze innego argumentu, który nie odwołuje się już do sukcesów matematyki w przyrodoznawstwie, tylko takiego argumentu co do sposobu uprawiania matematyki. Istnieje sposób aksjomatyczno - dedukcyjny uprawiania matematyki. Teorie czy koncepcje matematyczne są konstruowane w taki sposób, że mamy serię możliwie oczywistych aksjomatów, i teraz za pomocą odpowiednich wnioskowań, wyciągamy z tych aksjomatów jakieś treści matematyczne, których wprost jak się przyglądamy tym aksjomatom, to nie widać. Takim wzorcem dla takiego sposobu uprawiania matematyki, była pierwsza koncepcja geometrii euklidesowej. Była tam seria aksjomatów, a on z niej wywodził kolejne własności. To się nazywa metodą aksjomatyczno - dedukcyjną. Ma ona taką właściwość, że jak się udowodni coś w obrębie tej metody, to my wiemy, że tak będzie zawsze. Jak udowodnię, że suma kątów w trójkącie jest 180^o, to mogę sobie wyrysować milion trójkątów i Mierzym za pomocą kątomierza kąty, które występują w tych trójkątach i je dodawać, to zawsze wyjdzie 180^o. Jak mamy taką sytuację jak z tymi trójkątami, to mamy 2 sposoby postępowania. Z jednej strony możemy udowodnić, że każdy trójkąt, jak go narysujemy na płaszczyźnie, to udowodnimy, że suma tych kątów jest zawsze 180^o. Ale moglibyśmy uprawiać matematykę tak indukcyjnie. Znaczy to, że moglibyśmy wyrysować 100 trójkątów, zmierzyć ich kąty, i jeśli wszędzie wychodzi mi 180^o, to dokonuje uogólnienia, że wszystkie trójkąty mają taką miarę kątów. Te 2 sposoby argumentowania są od strony logicznej zupełnie odmienne. Nic nie gwarantuje, że ktoś wyrysuje taki trójką 101, w którym ta suma kątów nie będzie inna. Natomiast w obrębie tej metody dedukcyjnej, jak ja to starannie zrobię, to wiem, że zawsze suma kątów będzie taka sama. Metoda dedukcyjna jest takim modelem myślenia, który jest niezawodny. Myślenie indukcyjne natomiast może być logicznie zawodne.

Do tego taka anegdotka:

„Był indyk indukcjonista. Miał pogląd, że można dokonać uogólnień. W poniedziałek go nakarmili, we wtorek też, w środę tez itd. Indyk dokonał uogólnienia, że w sobotę też go nakarmią. A w sobotę przyszedł kucharz, upiekł mu głowę i upiekł go.”

Uogólnienie indukcyjne niekoniecznie musi być prawdziwe. W związku z powyższym, matematyka funkcjonowała jako taki wzór, do którego należy dążyć, natomiast fizycy, najczęściej posługiwali się metodą indukcyjną. Z drugiej strony mamy takie twierdzenia, jak zasada zachowania energii, że jeszcze taki mądry się nie znalazł, który by wykazał, że przyroda tej zasady nie honoruje, a sposób uzasadnienia jest typowo indukcyjny, że ona nas nie zawiodła.

Z tego powodu próbowano często opowiadać fizykę w taki sposób dedukcyjny.

Wróćmy teraz do tego uprawiania matematyki. Ktoś może mieć wrażenie matematyki, jako komputerów, które mają swoje zbiory aksjomatów i jadą od twierdzenia do twierdzenia, potem mogą wykorzystywać i te uzyskane twierdzenia, i system w taki harmonijny sposób jest badany. No niestety, tak dobrze nie jest. Bardzo często matematycy też używają takich metod empirycznych. Są tacy fizycy, którzy tego nie lubią.

Przykład dotyczący liczb pierwszych:

Liczby pierwsze są takimi liczbami, które ludzi wprawiają w pewien rodzaj fascynacji. Byli wielbiciele liczb pierwszych.

Co to są liczby pierwsze?

Jak mamy ciąg liczb naturalnych, to niektóre liczby są podzielne przez różne cyfry, a są takie jak 3, którą można podzielić tylko rzez jeden i przez siebie - to jest liczba pierwsza.

Jak mamy ten nieskończony ciąg liczb naturalnych, to teraz wybrać z tego liczby pierwsze jest nie lada zadaniem. Euklides umiał udowodnić, że tych liczb jest nieskończenie wiele. Po drugie, matematycy dość dużo czasu stracili, aby znaleźć formułkę, która by pozwalała kolejne liczby pierwsze generować. Jest taki sposób, który pochodzi od bibliotekarza Biblioteki Aleksandrii, który się nazywa Sitem Erastotenesa.

Jest to dość uciążliwe bawienie się, ale wielu ludzi używając tego sposobu wypisywało kolejne liczby pierwsze. Próbowano szukać jakiejś formuły.

= l.p

Wkładamy w nią ciąg liczb naturalnych i dostajemy liczby pierwsze. Jak się zorientowali, że nie uda się takiej formułki za bardzo sensownie stworzyć, to zadali sobie matematycy pytanie, jak wygląda sprawa gęstości rozkładu liczb pierwszych w tym ciągu wszystkich liczba naturalnych.

Powiedzmy, że wypisujemy ciąg liczb naturalnych do 11 i pytamy, ile do tej liczby pojawiło się liczb pierwszych. Powiedzmy, że nazwiemy tą funkcję, która opisuje ilość liczb pierwszych pojawiających się do miejsca (n), literą pi, będzie to liczba liczb pierwszych do miejsca n w ciągu liczb naturalnych.

Można się bawić i wypisywać, jak ta liczba wygląda. Pojawia się znowu pytanie, czy potrafimy podać wzór na to, jakąś formułę matematyczną, która powie, jak wygląda ta liczba tych liczb pierwszych do tego miejsca n.

Gaus przeglądając te tabele liczb pierwszych, zgadł jak taka formułka wygląda:

ln n- logarytm naturalny z n

Co to jest takiego ten logarytm naturalny z n?

Każdy w szkole się uczył, jak wygląda krzywa

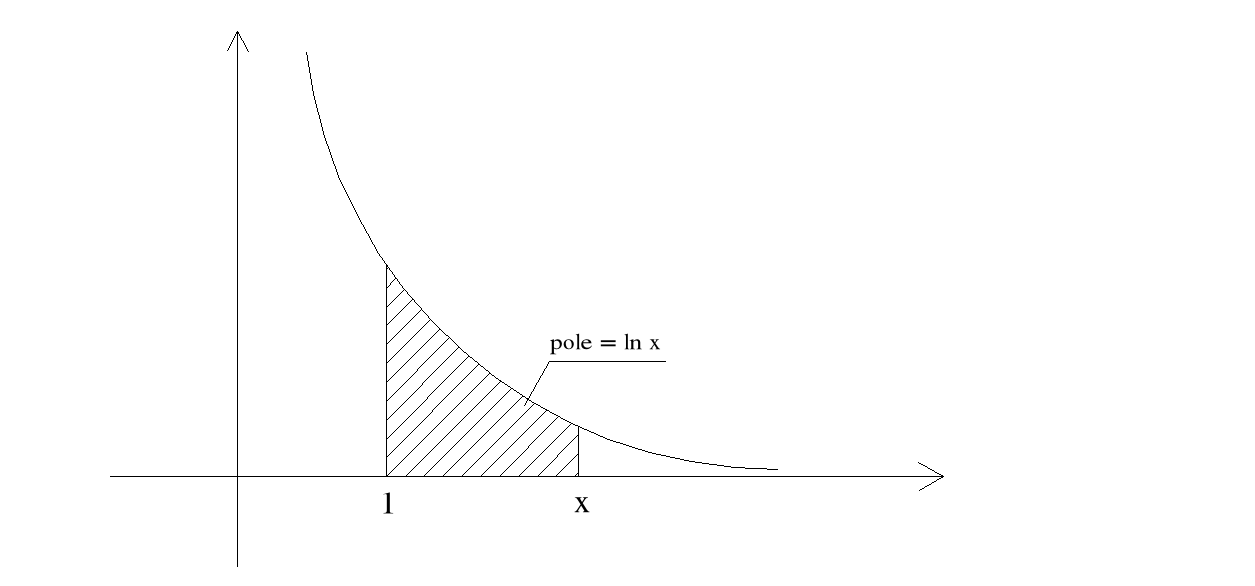
Logarytm naturalny z x, to jest pole zakreskowane na tym obrazku.

W człowieku budzi podziw, ta intuicja Gausa. Jak on wpadł na to, że ten wzór akurat tak a nie inaczej będzie wyglądał? Zostawmy tą sprawę.

Zobaczmy co on zrobił. On nie prowadził żadnej procedury dowodowej, w sensie dedukcyjnym, tylko obserwując dane empiryczne, jakimi były te tabele liczb pierwszych, na podstawie tych danych, zapostulował, dokonał uogólnienia indukcyjnego, że tak będzie wyglądać ta formułka i ona będzie tym lepsza im n będzie większe.

No i jeśli teraz podstawiać te liczby n kolejne i obliczać tą funkcję pi, to jak możemy sprawdzić, że to jest rzeczywiście trafione?

Robimy sobie tabelkę i wyrachowujemy, jak dla tego długiego ciągu wszystkich liczb naturalnych wygląda to
, a z drugiej strony liczymy tą funkcję. Te liczby są do siebie coraz bardziej podobne, jeśli n jest coraz większe. Patrzymy na to w taki sposób indukcyjny, że im więcej n­-ów mamy, to tym lepsza jest zgodność. Ale to jeszcze ciągle nie znaczy, że potrafimy to udowodnić w ramach standardów matematycznych. Jest to uogólnienie indukcyjne, i w tym sensie jest ten moment empiryczny w uprawianiu matematyki, który nie tak rzadko się w matematyce zjawia, że najpierw są jakieś intuicje, a potem próbujemy to udowodnić. Gaus jak sprawdził to na jakiejś sekwencji liczb naturalnych, to próbował to udowodnić w sensie już taki matematycznie poprawnym, dedukcyjnym. Niestety mu się to nie powiodło. Żeby mogło to zostać zrobione, to trzeba było ok. 100 lat czekać, bo w 1896r, została ta hipoteza udowodniona. Dopiero wtedy został uzyskany ten dowód dedukcyjny. Jest to taki przykład, że widać, że matematykę można uprawiać w taki quasi - empiryczny sposób. Mogę w jakiś sposób traktować pewne nieudowodnione jeszcze twierdzenia jako twierdzenia prawdziwe, chociaż dowodu do tego ciągle nie ma, bo mam wystarczająco bogaty zbiór takich sytuacji, na których potrafię pokazać, że to generalnie to twierdzenie wychodzi. Wiele jest taki otwartych ciągle problemów w matematyce. Np. hipoteza Riemanna, że potrafi się wyliczyć to na najszybszych komputerach, wszystko się zgadza, a dowodów dedukcyjnych nie ma.

Tego rodzaju element w metodzie uprawiania matematyki, pozwala twierdzić Putnamowi, że na matematykę można patrzeć jako na coś quasi - empirycznego i znowu jak patrzymy na tą quasi - empiryczność, to mamy taką sytuację, że wtedy myślimy o tym, że to jakoś istnieje, ma jakąś formę bytu, do której my mamy dostęp poznawczy dosyć umiarkowany. Mamy quasi - empiryczny dostęp poznawczy, ale to jest jakieś. Można to w jakiś sposób rozsądzić, czy ta hipoteza jest ostatecznie prawdziwa czy fałszywa.

W ten sposób można jakoś myśleć o tych bytach matematycznych, jako o tworach, które mają samodzielny sposób istnienia.

Myślenie o tych tworach matematycznych przez pryzmat sukcesu matematyki w nowożytnym przyrodoznawstwie, jeszcze inaczej można próbować demonstrować.

Tutaj wywołajmy nazwisko Wignera, który napisał artykuł „O niepojętej skuteczności matematyki w naukach przyrodniczych”. O co tutaj chodzi? Pisze, że jeśli patrzymy na to biorąc abstrakcyjność struktury, w których nie ma żadnego dobrego powodu, żeby sądzić, że one mają jakiś związek ze światem realnie istniejącym, że ostatecznie okazuje się, ze te abstrakcyjne struktury pasują do tego świata realnego, to jest jakiś element cudowności, tajemniczości. Dlaczego tak jest, że twór wymyślony w sposób czysto abstrakcyjny, nagle będzie do rzeczywistości pasował?

Spójrzmy tutaj na taką anegdotkę historyczną:

„Jak rozwijała się mechanika kwantowa na początku XXw., to badacze, kry się tym zajmowali, pracowali na Uniwersytecie w Getyndze. Równocześnie na tym uniwersytecie działał genialny matematyk Hilbert, który miał swoją grupę, która zajmowała się teorią spektralną. Jeden z tych matematyków jechał pociągiem do Getyngi, w przedziale naprzeciw niego siedziało 2 fizyków, którzy dyskutowali nad pomysłami, w jaki sposób opisać ten świat kwantowy, i dyskutowali, że trzeba używać macierzy, tworów matematycznych, które powinny być nieskończone. Zastanawiali się, czy można to zastosować, jakie będą kłopoty itd. Wówczas ten matematyk siedzący naprzeciwko tych fizyków, mówi, że w grupie Hilberta się czymś takim właśnie zajmują i być może ich wyniki będą im pomocne.”

Widać tutaj zupełnie 2 światy. Jedni rozważają taką teorię, gdzie takie nieskończone macierze się pojawiają, badają to tak, jak matematykom przystoi, a ci fizycy aby opisać jakiś nowy kawałek świata, który ich interesuje w danym momencie, natrafiają na pewną sekwencją problemów matematycznych, które tym matematykom w głowie się nie mieściło wcześniej, że to może mieć jakieś zastosowanie do świata, który ich otacza.

To jest taki obrazek, który pokazuje, że to po pierwsze pasuje, a po drugie to jest skuteczne, że jak ta teorię fizycy zaczęli faktycznie używać, to się nagle udało opisywać ten świat kwantowy. Dopóki tej teorii nie dostali w takiej wersji, w jakiej Hilbert ją wypracował, to nie bardzo było wiadomo, jak opisać ten świat tych cząsteczek kwantowych.

Powróćmy teraz do Wignera. Twierdzi on w tym artykule, że jest jakaś tajemnica, podziwia się, że te 2 rzeczywistości na siebie nachodzą, jedna pasuje do drugiej. Symbolicznie możemy to tak narysować:

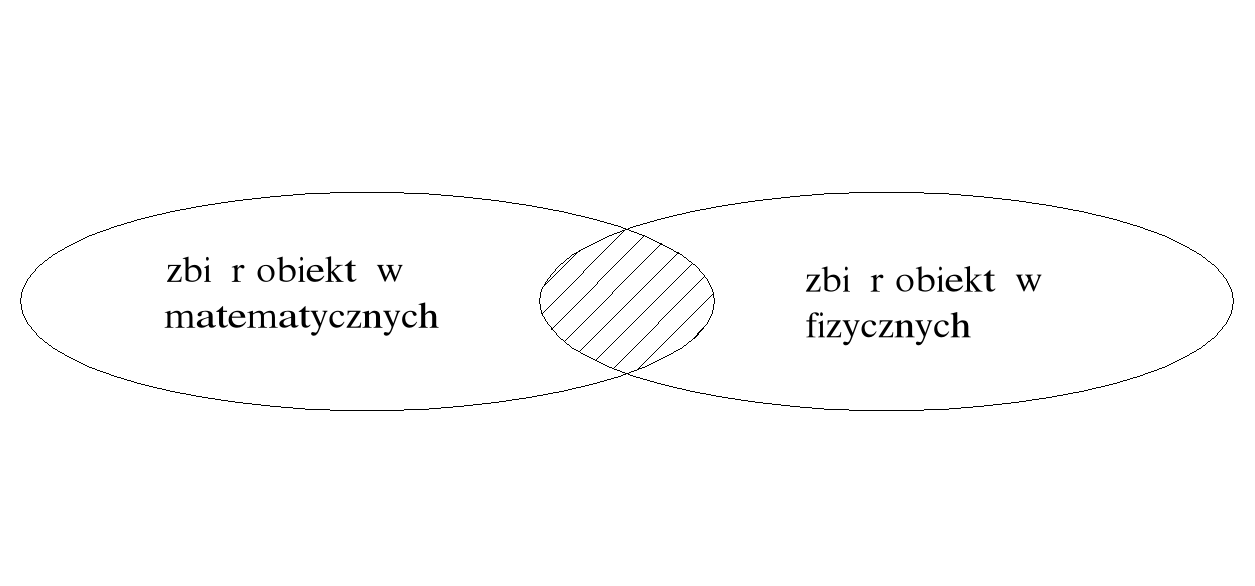
Jest jakaś część wspólna, jest ileś tworów matematycznych, które w żaden sposób nie są stosowane do opisu świata przyrodniczego. Nie można wykluczyć, że istnieją jakieś twory fizykalne, które matematycznie opisywane nie są. W tym sensie właśnie jest bezpiecznie myśleć w taki sposób, że te 2 światy jakoś na siebie nachodzą, jakoś się przecinają, i z powodu faktu tego przecięcia, możemy wnosić o niezależnym istnieniu tych obiektów matematycznych.

Jak inaczej można argumentować sprawę istnienia tych obiektów matematycznych, to stanowisko realizmu, w kwestii przedmiotów matematycznych?

Wywołajmy sobie tutaj argumenty matematyka, genialnego austriackiego logika - Kurta Gödla, który też był platonikiem. W matematyce zapisał się złotymi zgłoskami, bo udowodnił twierdzenia o niezupełności systemów aksjomatyczno dedukcyjnych. O co w tym odkryciu szło?

Mianowicie mamy taką strukturę matematyczną, która jest co najmniej tak bogata jak arytmetyka liczb naturalnych, i matematycy byli święcie przekonani, że każde zdanie z takiego systemu da się udowodnić, czy ono jest prawdziwe czy fałszywe. W tym sensie ten system jest rozstrzygalny. To przekonanie było niezwykle mocne, i Gödel pokazał, że dla systemó, czy struktur matematycznych tak bogatych, jak jest ta arytmetyka liczb naturalnych, istnieją zdania, które są nierozstrzygalne, że my potrafimy podać pewną własność czegoś w tym zbiorze liczb naturalnych i startując z aksjomatów liczb naturalnych, nie jesteśmy w stanie udowodnić, że to zdanie jest fałszywe albo prawdziwe. Po prostu jest nierozstrzygalne. To było szokiem dla matematyków, bo ten taki idealny obraz matematyki, w dużej mierze wiązał się z kwestią tej rozstrzygalności. Nie dosyć, że mamy taką dobrą strukturę dochodzenia, że na pewno wiemy, że coś jest w tym systemie prawdziwe, albo fałszywe, to jeszcze o każdym zdaniu w obrębie danej teorii matematycznej, możemy orzec tą prawdziwość czy fałszywość. Natomiast Gödel pokazał, że przy nawet już ubogich systemach matematycznych, ja arytmetyka, tak dobrze nie jest. Pojawią się stwierdzenia matematycznej natury, które są nierozstrzygalne. Nie potrafimy w obrębie tego systemu aksjomatyczno - dedukcyjnego powiedzieć, czy to zdanie jest prawdziwe czy fałszywe. Jaką receptę Gödel proponował, aby to przezwyciężyć? Proponował po prostu wzbogacenie systemów aksjomatów. Jest to bardzo prosta myśl, a skuteczna. Jak zmienimy system aksjomatów, w jakiś sposób go wzbogacimy, to to zdanie będzie już rozstrzygalne. Oczywiście pojawią się nowe zdania, które nie będą rozstrzygalne, no ale takie już jest życie. Na to już nie ma lekarstwa. Mimo tego, że on myślał i rozważał takie sprawy, które w pewnym sensie pokazują na ograniczoność metody matematycznej, był on bardzo radykalnym platonikiem i uważał, że obiekty matematyczne istnieją:

„Założenie o istnieniu obiektów matematycznych jest równie uzasadnione, jak założenie o istnieniu obiektów fizycznych.”

W jaki sposób argumentował tą tezę?

Używał argumentacji, ze obiekty matematyczne istnieją niezależnie od ludzkiej myśli. One istnieją niezależnie od tego, czy my jakąś wiedzę na temat istnienia tych obiektów mamy czy nie. Może istnieć jakaś cywilizacja, w której nie odkryto twierdzenia Pitagorasa. Ale czy to znaczy, że te twierdzenie Pitagorasa nie istnieje? Mogę czegoś nie znać, a to wcale nie znaczy, że to wcale nie istnieje. No ale jak to istnieje? Istnieje w taki sposób aczasowy, są to twory, które nie istnieją w sposób czasowy, są aczasowe, i są to twory, które nie istnieją przestrzennie. Nikt nie potrafi pokazać w przestrzeni miejsca, gdzie istnieje twierdzenie Pitagorasa. Są to takie byty nie fizyczne. Jak wygląda dostęp poznawczy do tego rodzaju obiektów? Tak, jak Platon twierdził, tak samo twierdzą współcześni platonicy w filozofii matematyki, że dostęp do tych obiektów jest czysto mentalny. My tylko za pomocą rozumu możemy w jakiś kontakt poznawczy z nimi wejść. Możemy wejść z nimi w kontakt poznawczy za pomocą zmysłów. To, że widzimy napisane na tablicy, że 2*2=4, to to postrzeganie zmysłowe nie jest dostępem do tej treści matematycznej, tylko musimy zrozumieć, jakoś uchwycić mentalnie, że dwie dwójki dają czwórkę. W tym sensie to, co napiszemy na tablicy, jest to tylko jakiś wyraz, jakaś forma symbolicznego zapisu tego, co naprawdę w świecie tych bytów matematycznych ma miejsce.

Te obiekty matematyczne, które istnieją aczasowo i przestrzennie, nie mają oddziaływania przyczynowego. Nikt nie odczuwa działania przyczyn jakichś tworów matematycznych. Dalej, te treści matematyczne mają określoną wartość logiczną, która nie zależy od naszej działalności umysłowej. Jak zapiszemy 2*2=5, to te zdanie zostanie fałszywe, wszystko jedno, co będzie się działo w mózgu tego myślącego nad tym zdaniem. Podobnie, jak inne zdania, które mają walor prawdziwości. Te treści matematyczne są fałszywe bądź prawdziwe na mocy znaczenia pojęć, które opisują te obiekty, co nie zależy od świata przedmiotów matematycznych. Gödel będzie bardzo starannie odrzucał tzw. psychologizm, który powiada, że pojęcia matematyczne są tworami naszych myśli. Jak z kolei te tezy argumentować?

Jeden rodzaj argumentów jest platoniczny, że sposób poznania ma charakter intuicyjny, źródłem wiedzy matematycznej wg Gödla jest szczególny rodzaj intuicji, którą matematyk posiada. Jest jeszcze inny argument, który można by nazwać argumentem z owocności. Znaczy to tyle, że jeśli mamy jakiś rodzaj tworu, struktury matematycznej, to ona ma pewne konsekwencje. My z iluś zdań matematycznych jesteśmy w stanie wyprowadzić pewną serię konsekwencji. Tak właśnie wygląda i dział ta metoda aksjomatyczno - dedukcyjna. I teraz ta owocność oznacza pewne bogactwo tych konsekwencji, że mamy pewien system, w ramach którego możemy dowiedzieć się o całej nowej serii faktów matematycznych. Jeśli się o tym argumencie z owocności myśli serio, to z jednej strony może się on wydawać argumentem, który z jednej strony gwarantuje istnienie matematyce, że matematyk ma co robić. Ma serię zdań, czy jakąś ubogą strukturę, że jest ją niesłychani łatwo przebadać, to to z punktu widzenia matematyka jest nieciekawe. Kilka faktów się wypatrzy i sprawa jest jasna jak to wszystko wygląda i koniec. Natomiast jeśli ta struktura matematyczna ma dużą ilość tych konsekwencji, to jest czymś co stwarza taki front, takie pole badawcze, że iluś matematyków może się tym zajmować i ma co robić. Są takie struktury, które będą stwarzać pole pracy dla całych tysięcy ludzi, którzy się będą w danym momencie tym zajmować, gdyż ten system czy struktura okazuje się owocna. Ta owocność ma taki sens, że jest ciekawa, warto się tym zajmować, bo jest co robić, w porządku uprawiania matematyki. Natomiast w porządku argumentów filozoficznych na rzecz platonizmu, to chodzi o to, ze ostatecznie istnieje jakiś świat tych obiektów, do którego pewnego rodzaju seria zdań, wyrażająca pewną sekwencję zdań matematycznych, daje nam lepszy dostęp. Więcej z tego świata można zobaczyć, więcej można się o tym świecie dowiedzieć. W tym sensie ta owocność dla Gödla była takim argumentem na rzecz platonizmu, że dokładasz nowe aksjomaty i masz nową strukturę. Masz wgląd w ten świat, obiektów matematycznych, który jest niezwykle bogaty, nieskończenie bogaty. Nasza wiedza z matematyki jest też jakaś taka fragmentaryczna, ze my kawałek tego świata poznajemy.

Są takie fakty matematyczne, które sugerują, że jest być może ileś równoległych matematyk. Że można jakby rozwijać nie tylko różne systemy o różnych aksjomatykach ( np. geometrie euklidesowe, lub nieeuklidesowe) w zależności jakie aksjomaty przyjmiemy, to również jakieś bardziej ogólne struktury matematyczne, które opierają się na samych fundamentach matematyki, że tam jak się inaczej skonstruuje aksjomaty, to dostaje się jakby 2 równoległe matematyki. I to wszystko, co jakby do tej pory w naszej cywilizacji udało się wypracować, jest rozwinięciem jednej matematyki, ale są też i takie fakty, które być może otwierają nam wgląd w zupełnie nową matematykę.

Skala tego bogactwa rzeczywistości jest taka, że jakby sobie to uświadomić, to trudno sobie uświadomić, że to jest wytwór działania naszej wyobraźni, naszego mózgu. Jest jakieś takie poczucie, że stoję wobec czegoś, co jest niezależne od tego mózgu, w co ten rozum ma wgląd, ale taki, który jest ograniczony, podobnie jak nasz wgląd w to, czym jest ten świat, który zmysłowo dostrzegamy, ten czasoprzestrzenny jest też ograniczony. My się chwalimy, że dużo wiemy, ale przypuszczalnie znacznie więcej nie wiemy niż wiemy. Dokładnie tak samo jest z tymi obiektami matematycznymi. Tego jest takie bogactwo, taka rozmaitość, różnorodność, ze osiągnięcia matematyki są jakby takim zajrzeniem przez okno do takiego ogrodu, w którym jest niezwykłe bogactwo tworów i tylko niektóre z nich widzimy, potrafimy je zbadać.

Jeśli jest takie bogactwo rzeczywistości, to czemu nie wszyscy matematycy są platonikami, albo nie wszyscy filozofowie matematyki są platonikami, tylko część twierdzi uporczywie, że to jest konstrukt ludzkiego umysłu? Jedna z odpowiedzi jest taka, że: Jak zaczynają matematyka pytać, jaki ma pogląd na sprawę istnienia obiektów matematycznych, to zaczyna częściej mieć wątpliwości, czy ten platonizm daje się utrzymać. A spontanicznie jak się długo zajmuje jakimś obiektem, to pojawia się takie naturalne przeświadczenie, które sobie człowiek nawet nie uświadamia, że jakoś jest, to czym ja się zajmuję to jakoś istnieje. Sposób istnienia tego, sposób realności tego obiektu może być różny. Inaczej jest dana kreda, którą czuję, że jest szorstka, bawię się nią itd., a inaczej będzie dana realność tego obiektu matematycznego, ale na swój sposób jakoś każde istnieje.

Natomiast jak się z tego doświadczenia realności obiektu zrezygnuje, czyli zacznie się myśleć o konceptach filozoficznych, to wtedy kręci się szybko w głowie, i traci się takie naturalne poczucie, że to jakoś realnie istnieje.

Platonicy będą często mówić o intuicji, a sam Gödel będzie tak o tym pisał:

„Pomimo oddalenia obiektów matematycznych od danych zmysłowych, mamy coś w rodzaju percepcji obiektów teorii mnogości, co widać z faktu, że aksjomaty narzucają nam się jako prawdziwe. Nie widzę powodu, aby mieć mniej zaufania do tego rodzaju percepcji, do intuicji matematycznej, niż do percepcji zmysłowej, która pozwala nam budować teorie fizyczne w oczekiwaniu, że przyszłe dane zmysłowe będą zgodne z nimi, i co więcej, oczekiwać, że problem, który teraz jest nierozstrzygalny, jest mimo to sensowny i może być rozstrzygnięty w przyszłości.”

Mamy tutaj takie świadectwo, gdzie powiada, że również serio rozważa tą percepcję, która idzie przez intelekt, przez intuicje matematyczną, jak percepcję, która jest związana z percepcją, jaką nam dają nasze zmysły. To porównanie obu sposobów postrzegania obiektów fizykalnych i tych matematycznych, jest warte chwili uwagi. Trzeba sobie uświadomić taką sprawę, ze od kiedy żeśmy się urodzili, to za pomocą zmysłów się kontaktujemy ze światem a sprawa realności tego świata, który jest nam dany przez zmysły, z tego powodu jest dla nas oczywista. Natomiast ile czasu każdy z nas poświęcił na zajmowanie się obiektami matematycznymi w życiu? Jakby poskładać wszystkie lekcje matematyki odbyte w naszym życiu, to by wyszło, że jesteśmy w 2 miesiącu życia. Porównując to bogactwo doświadczenia zmysłowego z postrzeganiem obiektów matematycznych. Wyobraźmy sobie teraz ludzi uzdolnionych matematycznie, którzy są w tym świecie obiektów matematycznych zanurzeni przez całe życie. Ich doświadczenie obiektów matematycznych jest w jakiejś mierze porównywalne z naszym doświadczeniem zmysłowym, które mamy jeśli chodzi o świat obiektów fizycznych. Dla nich to też jest jakoś realne, nie mniej realne niż to, o czym nas informują zmysły: dotyk, wzrok, słuch. W tym sensie, to jest też pewien argument na rzecz tego, że aby zostać platonikiem w jakiejś sprawie, np. w sprawie tworów moralnych, wartości, to niewątpliwie kluczowe znaczenie tutaj ma długość przebywania z tym czymś. Jeśli ja naprawdę mam wolę współbycia z tym fragmentem rzeczywistości, to dopiero wówczas się odsłania jego realność dla nas. Dokładnie tak sam jest z tą realnością rzeczywistości duchowej. Ktoś, kto z tą rzeczywistością nie jest w kontakcie, to dla niego nie wiadomo co to jest. Natomiast jeśli w tej rzeczywistości się tkwi, to sprawa realności tej rzeczywistości w naturalny sposób się odsłania, ujawnia się. Z tego powodu sprawa platonizmu wydaje się w obrębie filozofii chrześcijańskiej zupełnie kluczowa. Wszystko jedno czy to jest platonizm matematyczny, czy aksjologiczny czy jeszcze jakiś inny. Dalej trzeba zobaczyć, że jak mamy to pojęcie dania realności, to możemy zacząć porównywać, jak jest nam dana realność bytów czasoprzestrzennych materialnych, fizykalnych, a jak jest nam dana realność tych bytów matematycznych, do których można mieć tylko dostęp mentalny. Jak wygląda sprawa tego porównania? Od początku widać, że jest różnica w sensie przestrzenności a przestrzenności czy aczasowości a czasowości. Jest jednak też i jakaś forma podobieństwa. Trzeba zobaczyć, że nasz kontakt z bytami realnymi można opisywać za pomocą kategorii oporu. One stawiają nam pewien opór. Chodzi tu o to, że pewne czynności ja z danym bytem mogę wykonać, a pewnych się nie uda wykonać. Mam kawałek kredy, jest to przedmiot dany realnie i za pomocą tej kredy mogę napisać coś na tablicy, mogę kogoś nim cisnąć, ale nie mogę się unieść w powietrze za pomocą tej kredy, Istnieje pewna faktyczność przedmiotu realnego. Daje się go opisać w sensie sposobu manipulacji, jaka jest tu możliwa. Pewien typ manipulacji jest możliwy a pewien jest niemożliwy. Tą realność, tą faktyczność, że to jest kawałek kredy a nie samolot, w ten sposób opisując to odróżniamy. Samolotem jak ktoś się umie posłużyć, to się wzbije w powietrze. Za pomocą kawałka kredy nie da rady. Samolotem nie napisze się niczego na tablicy, a kredą się napisze. Ja mamy tą własność przedmiotów materialnych na uwadze, to można zauważyć, że przedmioty matematyczne też stawiają opór. W tym sensie, że one są konkretne. Twory wyobrażeniowe są niezwykle plastyczne. Ja wyobrażam sobie syrenę, to mogę ją przekształcić w taki sposób, że będzie miała taką a nie inną twarz. Natomiast jak mam obiekt matematyczny, to pewnego typu manipulacji tego rodzaju nie zrobię. Jest pewna wewnętrzna logika, sensowność tego obiektu, która sprawia, że tylko ta to może być potraktowane i nie inaczej. Jest to w pewnym sensie kłopot, jaki ludzie mają z matematyką, że trzeba się do tych reguł dopasować. Podobnie jak się musimy dopasować do reguł tego, co realnie istnieje w sensie przedmiotowym. Jak będą sople wisiały, to będziemy umykać, aby one nam na głowę nie spadły. Tak samo jest w tym świecie przedmiotów matematycznych. Pewne fenomeny zachodzą i ja się muszę do nich dostosować, a pewne fenomeny s atu niemożliwe. Niemożna sobie dowolnie zmienić tego obiektu tak jak np. w wypadku marzenia czy wyobrażenia czegoś. Jest to kolejny argument na rzecz tego, że sposób dana realności tych tworów idealnych, jest jakoś podobny do dania realności tych tworów materialnych. Inny jeszcze rodzaj analogii - jak odkryłem pewien fragment świata realnego, pojechałem do Zakopanego, widziałem jak Giewont wygląda, stanąłem tam przy krzyżu i wróciłem do domu. Mogę teraz opowiedzieć osobie, która tam nigdy nie była, że na Giewoncie krzyż rzeczywiście jest. Jest tu taka pewna stabilność tej sporej części przedmiotów realnych. Podobnie jest z przedmiotami matematycznymi. Też ten moment odkrycia daje się sensownie użyć. Jak pojawia się np. teoria matematyczna, którą kilu ludzi niezależnie od siebie odkrywa, to trudno w tym momencie się powstrzymać przed taką platońską myślą, że ten obiekt jakoś jest. Oni wszyscy widza ten sam obiekt, chociaż tak naprawdę jeden drugiego nie podglądał w tym dochodzeniu do tego obiektu itd. Podobnie jest też i z tymi obiektami matematycznymi, ze one nieraz się pojawiają z takiej odległości, że nieraz wpada się na nie po raz pierwszy.

Teraz spójrzmy na przykład dotyczący pierwiastka z minus jedności.

Widać, że jest to pojęcie nieprawdopodobne. Jak weźmiemy jakąkolwiek liczbę ujemną, np. -5
i podniesiemy ją do kwadratu, to daje nam to 25 w sensie +. Minus razy minus daje plus.

Widać wyraźnie, że w zbiorze liczb rzeczywistych nie istnieje taka liczba, że jak się ją podniesie od kwadratu, to daje nam -1. No bo -1 jak podniesiemy do kwadratu, to mamy +1. Nie potrafimy sobie wyobrazić, co mogłoby być takiego, co podniesione do kwadratu, daje nam -1. A jednak samo pojęcie, jako niedorzeczne w obrębie liczb rzeczywistych, się pojawia. To pojęcie pierwiastka z minus jedności, czyli tego pierwiastka. To x, to jest właśnie to i.

Jak się prześledzi historię pojawiania się liczb zespolonych, to są takie momenty, gdzie przykładowo Leibniz wpadł na pomysł napisania takiej oto równości:

Jak coś takiego jest, to widać, że pojawia się pierwiastek z liczby ujemnej, czyli coś, czego sensu żadną miarą nie potrafił zrozumieć, ale jak na tą równość się popatrzy, jak się ją podniesie do kwadratu, to łatwo się zobaczy, że ona jest prawdziwa. Z lewej strony będzie 6 i z prawej strony będzie 6.

Pojęcie jest niedorzeczne, ale formułka wygląda na prawdziwą, że rzeczywiście tak jest.

Drugi tego samego rodzaju moment miał miejsce, jak badano rozwiązywania równań 3-go stopnia. Jak te formułki równań 3-go stopnia pokazano, to wyszła taka właściwość jak i tutaj, że pierwiastek wychodzi rzeczywisty, a w trakcie manipulacji, używania tych ogólnych wzorów na te pierwiastki 3-go stopnia, po drodze mamy pierwiastki liczb ujemnych. Bezsensowne pojęcie prowadzi do sensownego wyniku matematycznego. Pedros powiada, że to jest też taki moment w historii matematyki, że wyjrzałeś przez okno i coś ci błysnęło. Dobrze nie wiesz co to jest. Zyskujemy dostęp do nowego tworu matematycznego, który nie wygląda na pierwszy rzut oka w ogóle sensownie, jednak przy bliższym przyjrzeniu się, okazuje się, że to jest coś, co ma jakiś sens, co jakoś istnieje. Ten
się okazuje sensownym obiektem matematycznym. Ciągle jeszcze nie wiem jak to zargumentować, ciągle jeszcze nie umiem tego osadzić w jakimś obszarze tworów matematycznych, gdzie bym rozumiał jak to się pojawia, ale nie mniej jakoś na to wpadłem, na trop czegoś.

Inny przykład tego doświadczenia opisuje Pedros odwołując się do odkrycia zbioru Mandelbrota. Jest to rodzaj takich zbiorów fraktalnych, na które ludzie wpadli dzięki używaniu komputerów osobistych. Komputer pomaga w odkryciu pewnego obiektu matematycznego. To doświadczenie Mandelbrota jest doświadczeniem natykania się na coś nowego, czego nikt nie znał do tej pory.

Pedros w taki sposób o tym pisze:

„Zbiór Mandelbrota jest wymownym przykładem tego właśnie odkrywania. Jego cudownie misterna struktura nie była wynalazkiem żadnego człowieka, nie była również dziełem żadnego zespołu matematyków. Sam Mandelbrot, który pierwszy badał ten zbiór, początkowo nie miał żadnego pojęcia o jego faktycznym skomplikowaniu, chociaż zdawał sobie sprawę, że wpadł na trop czegoś bardzo interesującego. Najpierw, gdy jego pierwsze rysunki komputerowe zaczęły się pojawiać, przypuszczał, że rozmyte struktury ukazujące się jego oczom, stanowią wynik złego funkcjonowania komputera. Dopiero później przekonał się, że te struktury rzeczywiście tam są. Stanowią własność zbioru. Co więcej, skomplikowanych szczegółów struktury zbiorów Mandelbrota, nikt z nas nie może w pełni poznać, nie mogą też one zostać w całej pełni ujawnione przez żaden komputer. Świadczyłoby to o tym, że struktura ta nie jest częścią naszych umysłów, lecz posiada swoją własną rzeczywistość. Ilekroć jakiś matematyk lub komputer zdecyduje się poddać zbiór badaniom, odkryje jedynie przybliżenia zawsze tej samej fundamentalnej matematycznej struktury. Jeśli pominąć fakt, że różnice w prędkości, pojemności i graficznych możliwościach komputerów mogą prowadzić do różnic subtelności szczegółów i prędkości, z jaką zostaną one ujawnione, to nie ma najmniejszego znaczenia, jaki komputer zostanie użyty do wykonania obliczeń, byle nie był tylko uszkodzony. Komputer spełnia tutaj zasadniczo taką samą rolę jak w pracy fizyka doświadczalnego spełnia przyrząd eksperymentalny, przy pomocy którego bada on strukturę fizycznego świata. Zbiór Mandelbrota nie jest wynalazkiem ludzkiego umysłu, lecz odkryciem. Zbiór Mandelbrota podobnie jak Mount Everest, po prostu tam jest.”

Jest to kolejny przykład natrafiania na pewien obiekt. To natrafianie jest też sposobem doświadczenia realności tego obiektu. On tam jest. To nie jest tak, że ja go wymyślam. To jest taki obiekt, który jest w jakiejś mierze ujawniany, ale nie jest ujawniany w całości. Natomiast na formułę, którą można wypisać, to jak się na nią patrzy, to nie widać tej struktury samego zbioru tych punktów, które ona generuje, czyli jest to znowu taki element na rzecz platonizmu.

Subtelniejsi platonicy będą swoje stanowisko niuansować w taki sposób, że powiedzą, że nie twierdzą, że wszystko, co w matematyce jest, ma charakter takiego bytu istniejącego, że ewidentnie są takie miejsca, gdzie są to konstrukty. Jest pewien konstrukt, na który matematyk musi wpaść, gdy chce udowodnić jakiś tam fragment twierdzenia, ale to, czego to twierdzenie dotyczy, jest w jakiejś mierze już obiektem.

1

---