Politechnika Wrocławska

Wydział Podstawowych Problemów Techniki

Analiza niepewności pomiarowych

wspomagana komputerowo

Praca inżynierska

Autor:

Grzegorz Zyśko

Kierunek:

Fizyka Techniczna

Specjalność:

Fizyka Komputerowa w Nauce i Technice

Promotor:

Dr hab. inż. Włodzimierz Salejda prof. nadzw. PWr

Wrocław, luty 2002

Chciałbym złożyć serdeczne podziękowania

mojemu promotorowi

dr hab. inż. Włodzimierzowi Salejdzie prof. PWr

za poświęcony czas mojej pracy inżynierskiej.

2

Spis treści

Część pierwsza
„Wprowadzenie”
1.1

Wprowadzenie 4

1.2

Cel pracy 4

Część druga
„Podstawy analizy niepewności pomiarowych”
2.1

Wstęp 6

2.2

Statystyczna analiza niepewności i wyników niepewności pomiarów bezpośrednich

6

2.3

Statystyczna analiza niepewności i wyników niepewności pomiarów pośrednich

7

2.4

Zasady zapisywania i zaokrąglania wyników i niepewności pomiarowych

9

Cześć trzecia
„Opis programu”
3

Uruchomienie programu

10

3.1

Panel „Różne”

11

3.1.1

Niepewność przypadkowa

12

3.1.2

Średnia arytmetyczna

12

3.1.3

Zaokrąglanie wyników

12

3.2

Panel „Statystyczna analiza niepewności i wyników niepewności pomiarów bezpośrednich” 12

3.2.1

Panel „Niepewność standardowa”

12

3.2.1.1

Niepewność standardowa

13

3.2.1.2

Niepewność standardowa dla pojedynczego pomiaru

13

3.2.1.3

Całkowita niepewność standardowa

14

3.2.2

Panel „Niepewność względna”

14

3.2.2.1

Niepewność względna pojedynczego pomiaru

15

3.2.2.2

Niepewność względna wartości średniej

15

3.2.3

Panel „Niepewność całkowita”

15

3.2.3.1

Maksymalna wartość niepewności całkowitej miernika analogowego

15

3.2.3.2

Maksymalna wartość niepewności całkowitej miernika cyfrowego

15

3.3

Panel „Statystyczna analiza niepewności i wyników niepewności pomiarów pośrednich” 16

3.3.1

Współczynnik korelacji

16

3.3.2

Niepewność standardowa niepewności nieskorelowanych

17

3.3.3

Niepewność standardowa niepewności skorelowanych

18

Część czwarta
„Podsumowanie”
4

Podsumowanie

19

Część piąta
„Literatura”
5

Literatura

20

3

1.1 Wprowadzenie

Wynik nawet najstaranniej wykonanego pomiaru lub obserwacji obarczony jest niepewnością

odzwierciedlającą niedokładność wartości wielkości zmierzonej. Dlatego też analiza niepewności pomia-
rowych jest istotnym elementem każdego eksperymentu w fazie jego projektowania, realizacji i opraco-
wania otrzymanych wyników [1,2].

Podstawowym pojęciem przyjętej w 1995 roku międzynarodowej normy dotyczącej technologii

i zasad wyznaczania niepewności pomiarowych jest niepewność pomiaru będąca miarą niedokładności,
z jaką zmierzono daną wielkość fizyczną [1,2].

Do najważniejszych źródeł niepewności pomiaru zaliczamy [1-4]:

a) niepełną definicję wielkości mierzonej (określenie danej wielkości fizycznej jest tymczasowe w

tym sensie, że może ulec zmianie wraz z rozwojem nauki),

b) niedokładną realizację tej definicji (przyrząd, miernik, wzorzec nie jest idealną realizacją definicji

wielkości fizycznej),

c) niereprezentatywność serii wyników pomiarów (np. zbyt mała liczba pomiarów),
d) niedokładną znajomość czynników zewnętrznych (np. wpływ otoczenia na przebieg pomiarów)

lub ich niedokładny pomiar,

e) błędy obserwatora podczas odczytów przyrządów pomiarowych,
f) skończoną zdolność rozdzielczą stosowanych w pomiarach przyrządów,
g) niedokładność stosowanych wzorców i materiałów odniesienia,
h) niedokładne wartości stałych lub parametrów pochodzących z innych źródeł,
i) przybliżenia i założenia upraszczające przyjęte w pomiarach lub procedurze pomiarowej,
j) zmiany kolejnych wyników pomiarów wielkości mierzonej w pozornie identycznych warunkach.

Dokonując pomiaru wielkości fizycznej

X przypisujemy jej liczbę mianowaną postaci

X

X

X

J

r

x

)

(

δ

±

=

, (1)

gdzie

−liczba jednostek (w takim zapisie

jest wartością niemianowaną),

X

r

X

r

X

δ

−niepewność pomiaru

(w takim zapisie

X

δ

jest wartością niemianowaną),

−jednostką wielkości

X

J

X .

O ile nie jest to wielkość bezwymiarowa to podanie wartości wielkości fizycznej w postaci liczby

nie ma sensu.

Wartość niepewności

X

δ

oceniamy [1

− 4]:

a) metodą A, czyli za pomocą analizy statystycznej serii pomiarów,
b) metodą B, czyli wykorzystując dodatkowe niestatystyczne informacje np. wielkość działki elemen-

tarnej lub klasę przyrządu.

1.2 Cel pracy dyplomowej

Studenci odbywający zajęcia w Laboratorium Podstaw Fizyki Instytutu Fizyki muszą niejednokro-

tnie wykonywać dość złożone i czasochłonne obliczenia niepewności pomiarowych [1,2]. Ponadto w osta-
tnich latach XX wieku ustalona została nowa międzynarodowa terminologia z zakresu analizy niepe-
wności pomiarowych oraz zasad szacowania niepewności pomiarowych [1-8].

Z uwagi na powyższe jako cel pracy wybrano zaprojektowanie i zaprogramowanie środowiska

komputerowego do obliczania niepewności pomiarowych zgodnie z międzynarodowymi zasadami.

4

Część druga „Podstawy analizy niepewności pomiarowych” jest poświęcona analizie statystycznej

serii pomiarów (tzw. metoda A), a także zasadom zapisywania i zaokrąglania wyników pomiarów.

Część trzecia „Opis programu” jak nazwa sugeruje jest poświęcona opisowi działania programu

„Analiza niepewności pomiarowych wspomagana komputerowo".

5

2.1 Wstęp

Podstawowym pojęciem analizy niepewności pomiarowych jest niepewność przypadkowa

x

x

x

−

=

=

δ

δ

. (2)

gdzie x jest średnią arytmetyczną serii n pomiarów

∑

=

=

+

+

+

=

n

i

i

n

x

n

n

x

x

x

x

1

2

1

...

. (3)

2.2 Statystyczna analiza niepewności i wyników niepewności pomiarów bezpośrednich

Załóżmy, że n-krotnie powtórzono bezpośredni pomiar wielkości X w jednakowych stabilnych

warunkach. Otrzymaną serię wyników oznaczmy symbolicznie jako

.

)

,

(

2

1

n

x

x

,..., x

W charakterze najlepszej oceny wartości rzeczywistej przyjmuje się średnią arytmetyczną, a za

miarę niepewności pojedynczego pomiaru z próby (

przyjmujemy odchylenie standardowe

pojedynczego pomiaru

)

,...,

,

2

1

n

x

x

x

∑

=

−

−

=

−

+

+

−

+

−

−

=

n

i

i

n

x

x

x

n

x

x

x

x

x

x

n

s

1

2

2

2

2

2

1

)

(

1

1

]

)

(

...

)

(

)

[(

1

1

. (4)

Niepewnością pomiarową

x

s zwaną niepewnością standardową, obarczona jest również wartość

średnia x . Oceną tej niepewności jest

∑

=

−

−

=

=

n

i

i

x

x

x

x

n

n

n

s

s

1

2

)

(

)

1

(

1

. (5)

Jeżeli dostępny jest tylko jeden wynik pomiaru lub wyniki pomiarów nie wykazują rozrzutu, to

w charakterze niepewności wartości średniej przyjmujemy

3

.

.e

d

x

s

∆

=

, (6)

gdzie

∆ jest wielkością działki elementarnej.

.

.e

d

W przypadku, gdy w pomiarach uwzględniamy niepewność statystyczną i niepewność przyrządu

pomiarowego, należy wyznaczyć całkowitą niepewność standardową

)

(c
x

s wartości średniej z wzoru

2

.

.

2

)

(

)

(

3

1

)

(

e

d

x

c

x

s

s

∆

+

=

Oprócz wprowadzonych wielkości w analizie niepewności pomiarowych posługujemy się także

następującymi wielkościami bezwymiarowymi:

a) Niepewność względna pojedynczego pomiaru

i

x

i

x

x

s

=

Ε

)

(

, (8)

gdzie

s definiuje wzór (4).

x

6

b) Niepewność względna wartości względnej

x

s

x

x

=

Ε

, (9)

gdzie

x

s definiuje wzór (5).

Znając klasę

przyrządu analogowego użytego w pomiarach wyznaczymy maksymalną wartość

niepewności całkowitej

korzystając z zależności

a

C

)

(c

δ

100

)

(

Z

C

a

c

=

δ

, (10)

gdzie

Z oznacza używany zakres pomiarowy przyrządu.

Jeżeli stosujemy w pomiarach miernik cyfrowy, to

r

d

d

X

C

δ

δ

+

=

100

)

(

, (11)

gdzie

− klasa (w procentach) miernika cyfrowego,

d

C

r

δ

− rozdzielczość miernika (niepewność dyskre-

tyzacji).

2.3 Statystyczna analiza niepewności i wyników niepewności pomiarów pośrednich

Mierzymy wielkości fizyczne

, z którymi wielkość

)

,...,

,

(

2

1

k

X

X

X

Y mierzona pośrednio jest zwią-

zana relacją postaci

)

,...,

,

(

2

1

k

X

X

X

g

Y

=

. (12)

Dokonując serii pomiarów wyznaczamy wartości średnie

)

,...,

,

(

2

1

k

x

x

x

i na tej podstawie zna-

jdujemy jako ocenę pośrednio wielkości

Y wartości

)

,...,

,

(

2

1

k

x

x

x

g

y

=

. (13)

Przy obliczaniu niepewności standardowych wielkości pośrednich

, należy rozróżnić nieskore-

lowane i skorelowane pomiary wielkości mierzonych bezpośrednio. Pojęcie to przedstawię na przykładzie
dwóch wielkości

y

u

X i Z .

Niech {(

będą wynikami serii pomiarów

i

)}

,

(

),...,

,

(

),

,

2

2

1

1

n

n

z

x

z

x

z

x

X

Z . Współczynnikiem kore-

lacji

(korelacja z próby) nazywamy wielkości

z

x

r

,

∑

∑

∑

=

=

=

−

−

−

−

=

n

i

i

n

i

i

n

i

i

i

z

x

z

z

x

x

z

z

x

x

r

1

2

1

2

1

,

)

(

)

(

)

)(

(

. (14)

Wartości współczynnika korelacji należą do przedziału [-1,1]. Jeżeli

, to punkty

leżą na prostej. Mówimy wtedy, że wielkości

i

1

,

±

=

z

x

r

)

,

(

i

i

z

x

X

Z

są skorelowane. Jeżeli

, to wielkości te nie są

skorelowane.

1

〈〈

=

,z

x

r

7

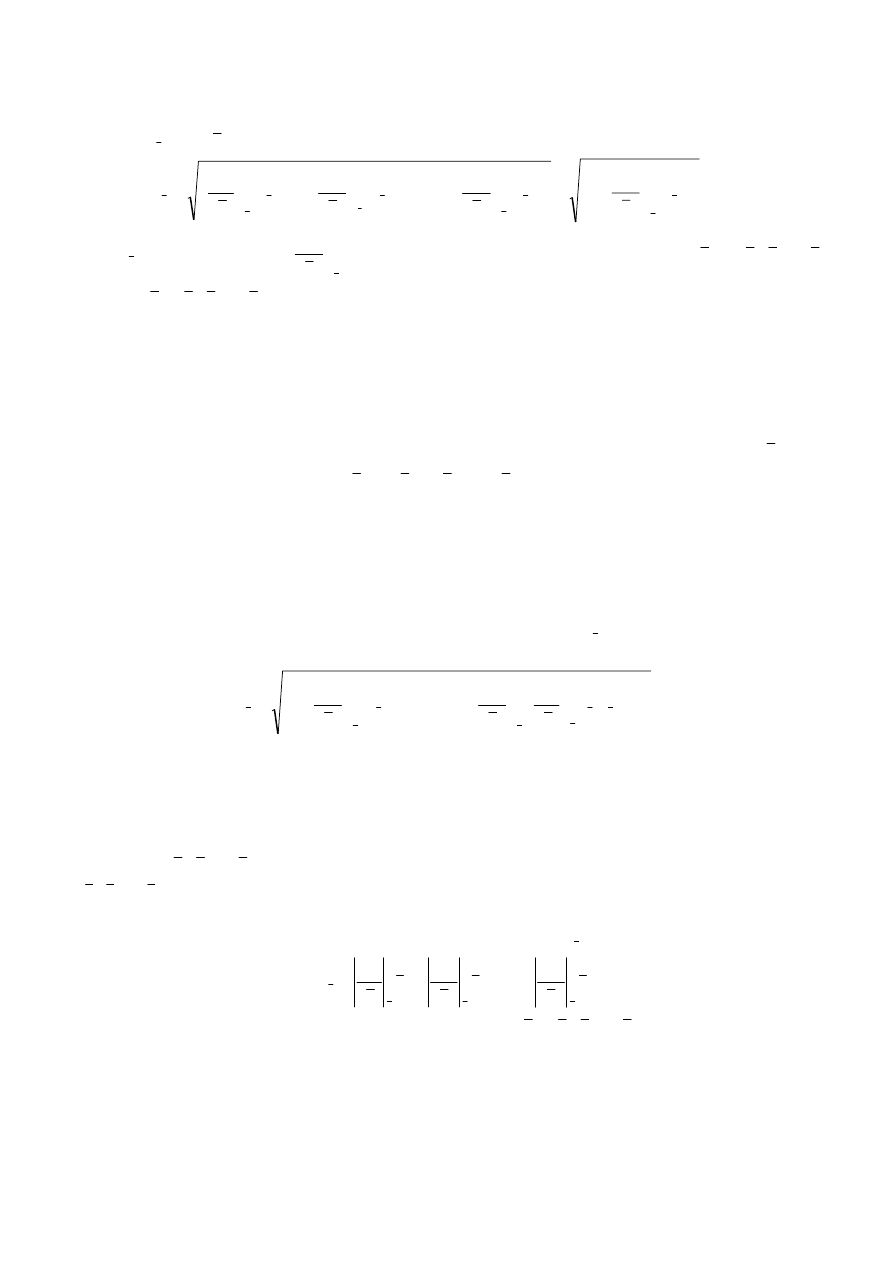
Jeżeli wielkości występujące w poprzednim wzorze są parami nieskorelowane, to niepewność sta-

ndardowa

y

u

oceny y wielkościY wynosi

( )

( )

( )

( )

∑

=















∂

∂

=













∂

∂

+

+













∂

∂

+













∂

∂

=

k

j

x

x

j

x

x

k

x

x

x

y

j

k

x

s

x

g

s

x

g

s

x

g

s

x

g

u

1

2

2

2

2

2

2

2

2

2

1

...

2

1

, (15)

gdzie

x

s

definiuje wzór (5),

x

k

x

g











∂

∂



jest wartością pochodnej cząstkowej funkcji

)

,...,

,

(

2

1

k

x

x

x

g

y

=

w punkcie

)

,...,

,

(

2

1

k

x

x

x

x

=

.

W wielu przypadkach zależność funkcyjna Y

)

,...,

,

(

2

1

k

X

X

X

g

=

ma postać iloczynu

k

k

X

X

X

A

Y

α

α

α

)

...(

)

(

)

(

2

1

2

1

=

, (16)

gdzie

−stała wielkość lub bezwymiarowy współczynnik,

A

j

α

−znane wykładniki (liczby rzeczywiste).

W takim przypadku ocena niepewności złożonej wartości średniej (zakładamy, że

,

0

>

A

0

>

j

x

)

k

k

x

x

x

A

y

α

α

α

)

...(

)

(

)

(

2

1

2

1

=

. (17)

Pomiary wielkości fizycznych należy uznać za skorelowane wtedy, gdy są mierzone wielokrotnie

za pomocą jednego zestawu doświadczalnego. Oznacza to, że praktycznie wszystkie pomiary elektryczne
w pracowniach studenckich są pomiarami skorelowanymi.

W takim przypadku należy uwzględnić korelacje zachodzące pomiędzy poszczególnymi wielko-

ściami mierzonymi bezpośrednio i złożona niepewność standardowa

y

u

wielkościY mierzonej pośrednio

wyrażą się wzorem

∑ ∑

∑

=

+

=

=













∂

∂















∂

∂

+















∂

∂

=

k

j

k

j

i

x

x

x

x

x

i

x

j

k

j

x

x

j

y

i

j

i

j

j

r

s

s

x

g

x

g

s

x

g

u

1

1

,

1

2

2

)

(

, (18)

gdzie

i

j

x

x ,

r

− definiuje wzór (14).

Ocenę niepewności pomiarowych wielkości nieskorelowanych można także wyznaczyć za pomocą

metody różniczki zupełnej.

Niech

)

,...,

,

2

1

k

x

x

x

(

będą ocenami zmierzonych bezpośrednio wielkości

,

a

)

,...,

,

(

2

1

k

X

X

X

)

,...,

,

2

1

k

s

s

s

(

niepewnościami tych ocen.

Jeżeli zachodzi związekY

to niepewność

)

,...,

,

(

2

1

k

X

X

X

g

=

y

u

wielkościY wynosi

k

x

k

x

x

y

s

x

g

s

x

g

s

x

g

u

δ

δ

δ

δ

δ

δ

+

+

+

=

...

2

2

1

1

, (19)

gdzie wartości pochodnych cząstkowych obliczamy w punkcie

)

,...,

,

(

2

1

k

x

x

x

x

=

.

8

2.4 Zasady zapisywania i zaokrąglania wyników i niepewności pomiarowych

Wyniki pomiarów zapisujemy w postaci liczbowej mianowanej

δ

±

x

,

gdzie

x

x

J

r

x

⋅

=

jest teraz wielkością mianowaną.

Postać ta zawiera informacje o ocenie wartości zmierzonej x , jednostkach w jakich jest ona poda-

na, oraz o niepewności pomiaru, której miarą jest mianowana wielkość

x

x

J

⋅

=

δ

δ

.

Wyznaczając wartość średnią lub niepewność pomiaru otrzymujemy liczby wielocyfrowe, w

których wiarygodne są cyfry zwane cyframi znaczącymi.

Cyfry znaczące w średniej ustalamy na podstawie cyfr określających ocenę niepewności

pomiarowej

δ . Wyznaczając niepewność pomiarową δ otrzymujemy także liczbę wielocyfrową, w której

co najwyżej dwie są cyfry znaczące. Ich znajomość pozwala określić sensownie ocenę wartości średniej i
jej cyfry znaczące.

Kierujemy się przy tym następującą regułą zaokrąglania wyników:

Wyniki pomiarów podajemy z dokładnością do miejsca, na którym występuje ostatnia cyfra zna-
cząca niepewności pomiaru.

Reguła ta pozwala zapisać średnią za pomocą tylko cyfr znaczących.

Przy wyznaczaniu wartości liczbowej niepewności pomiarowej oraz jej cyfr znaczących posługu-

jemy się następującymi regułami zaokrąglenia:

a) Wartości niepewności zawsze zaokrąglamy w górę.
b) Wstępnie niepewność zaokrąglamy do jednej cyfry znaczącej.
c) Jeżeli wstępne zaokrąglenie wartości niepewności powoduje wzrost jej wartości o więcej niż 10%,

to niepewność zaokrąglamy z dokładnością do dwóch cyfr znaczących.

Zera występujące w liczbie mogą być lub nie być cyframi znaczącymi. Zera, które określają

w zapisie dziesiętnym liczby położenie przecinka nie są cyframi znaczącymi, jak w liczbach 0,02 lub
0,0056. Liczby te mają odpowiednio jedną i dwie cyfry znaczące. Wartości takie zapisujemy w postaci
wykładniczej, czyli 2

⋅10

-2

i 5,6

⋅10

-4

. W pozostałych przypadkach pod cyframi znaczącymi rozumiemy

cyfry rzeczywiście znane.

Przy podawaniu wyników zaleca się:

a) Opisać jednoznacznie metodę obliczeń wyników i niepewności.
b) Podać składniki niepewności i sposoby ich obliczania
c) Przedstawić w taki sposób, by ich użytkownik miał możliwość powtórzenia obliczeń, a nawet po-

miarów.

d) Podać wszystkie wniesione poprawki i stałe oraz źródła, z których je zaczerpnięto.

W sprawozdaniach studenckich należy podawać:

a) Pełną definicję wielkości mierzonej.
b) Wynik końcowy i niepewność wraz z jednostkami.
c) Poziom ufności zwany przedziałem ufności.
d) Wszystkie poprawki oraz ich źródła.

Przedstawione i opisane w tym rozdziale metody wyznaczania niepewności pomiarowych oraz

zaokrąglenie wyników i niepewności pomiarowych zostały uwzględnione przy projektowaniu programu
komputerowego pt. „Analiza niepewności pomiarowych wspomagana komputerowo". W następnym
rozdziale przedstawimy jego opis.

9

3 Uruchomienie programu

Aby uruchomić program należy:

a) przegrać pliki „analiza_pomiarow.exe” i „snpmk.dll” do stworzonego wcześniej katalogu,
b) wpisać „analiza_pomiarow” lub wybrać plik „analiza_pomiarow.exe” i nacisnąć na klawiaturze

przycisk „Enter”.
Wymagania:

a) Komputer klasy Pentium PC lub nowszy.
b) System operacyjny Microsoft Windows 95 lub nowszy.

Zalecana minimalna rozdzielczość 800x600 i standardowe ustawienia kolorów.

Rys.1 Okno wstępne.

Stworzony program pozwala wyznaczyć następujące wielkości:

1) Niepewności przypadkowe (wzór (2))(rozdział 3.1.1).
2) Średnie arytmetyczne (wzór (3))(rozdział 3.1.2).
3) Zaokrąglenia liczb (według zasad z rozdziału 2.4)(rozdział 3.1.2).
4) Niepewności standardowe pomiarów bezpośrednich (wzór (5))(rozdział 3.2.1.1).
5) Niepewności standardowe pojedynczych wyników pomiarów bezpośrednich (wzór (6))(rozdział

3.2.1.2).

6) Całkowite niepewności standardowe pomiarów bezpośrednich (wzór (7))(rozdział 3.2.1.3).
7) Niepewności względne pomiarów bezpośrednich (wzór (8))(rozdział 3.2.2.1).
8) Niepewności względne wartości średnich pomiarów bezpośrednich (wzór (9))(rozdział 3.2.2.2).
9) Maksymalne wartości niepewności całkowitych mierników analogowych (wzór (10))(rozdział

3.2.3.1).

10) Maksymalne wartości niepewności całkowitych mierników cyfrowych (wzór (11))(rozdział

3.2.3.2).

11) Współczynniki korelacji pomiarów pośrednich (wzór (14)) (rozdział 3.3.1).
12) Niepewności standardowe nieskorelowanych pomiarów pośrednich (wzór (15))(rozdział 3.3.2).

10

13) Złożone niepewności standardowe skorelowanych pomiarów pośrednich (wzór (18))(rozdział

3.3.3).

Po uruchomieniu programu pojawia się okno wstępne programu (rys.1), które gasimy poprzez

kliknięcie lewym przyciskiem myszy przycisku „x” w prawym górnym rogu panelu lub z jego boku. Za-
wiera ono informacje o autorze i nazwie programu. Można je także wyświetlić naciskając przycisk „o pro-
gramie” w prawym dolnym rogu panelu.

Po wygaszeniu okna wyświetlony zostaje panel główny programu. W jego górnej części widzimy

przyciski o następujących nazwach:

1) „Różne”,
2) „Statystyczna analiza wyników i niepewności pomiarów bezpośrednich”,
3) „Statystyczna analiza wyników i niepewności pomiarów pośrednich”.

W dolnej części widzimy panel przedziału ufności. Aby go określić należy nacisnąć kółeczko przy

przedziale w którym chcemy obliczać niepewności.

3.1 Panel „Różne”

Obecnie zajmiemy się omówieniem panelu znajdującego się pod przyciskiem „Różne” (Rys.2).

Rys 2; 1

− przycisk „Różne”, 2 − panel niepewności przypadkowej, 3 − panel średniej arytmetycznej,

4

− panel zaokrąglania wyników, 5 − panel przedziału ufności.

11

3.1.1 Obliczanie niepewności przypadkowej

Pierwszy panel z prawej strony od góry panelu „Różne” służy do obliczania niepewności przypa-

dkowej

x

δ

zmierzonej wielkości fizycznej X (wzór (2)). Aby ją obliczyć należy:

a) wpisać w tabeli znajdującej się po lewej stronie w rubryce „Zmienna” wartości poszczególnych

pomiarów,

b) podać, dla których wpisanych wartości program ma obliczyć niepewność,
c) nacisnąć przycisk „Oblicz”.

Wyniki pojawią się w tabeli w rubryce „Wynik”, a zaokrąglone wyniki do liczb znaczących w rubryce
„Zaokrąglony”.

3.1.2 Obliczanie średniej arytmetycznej

Środkowy panel kontrolny służy do obliczania średniej arytmetycznej (wzór (3)). Aby ją obliczyć

należy:

a) wpisać w tabeli znajdującej się po lewej stronie tego panelu wartości poszczególnych pomiarów,
b) podać, dla których wpisanych wartości chcemy obliczyć niepewność,
c) nacisnąć przycisk „Oblicz”.

Wyniki pojawią się pod przyciskiem „Oblicz”.

3.1.3 Zaokrąglanie wyników

Trzeci dolny panel kontrolny służy do zaokrąglania pojedynczych wyników zgodnie z zasadami

przyjętymi w rozdziale 2.4. Aby ją obliczyć należy:

a) wpisać liczbę pod napisem „Wpisz liczbę…”,
b) nacisnąć przycisk „Wykonaj”.

Wyniki pojawią się pod przyciskiem „Wykonaj”.

3.2 Panel „Statystyczna analiza wyników i niepewności pomiarów bezpośrednich”

Teraz zajmiemy się omówieniem panelu znajdującego się pod przyciskiem drugim nazwanym

„Statystyczna analiza wyników i niepewności pomiarów bezpośrednich” (Rys.3).

Obok tabeli z prawej strony widzimy trzy przyciski:

a) „Niepewność standardowa”,
b) „Niepewność względna”,
c) „Niepewność całkowita”.

3.2.1 Niepewność standardowa

Gdy wciśnięty jest przycisk „Niepewność standardowa”, to ukazuje się nam kolejny panel (Rys.3).

12

Rys.3 Panel „Niepewność standardowa”; 1

− przycisk „Statystyczna analiza wyników i niepewności po-

miarów bezpośrednich”, 2

− przycisk „Niepewność standardowa”, 3 − panel niepewności standardowej

4

− panel niepewności wartości średniej, 5 − panel całkowitej niepewności standardowej.

3.2.1.1 Obliczanie niepewności standardowej

Mamy możliwość obliczania niepewności standardowej (wzór (5)). Aby tego dokonać należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać, dla których wpisanych wartości chcemy obliczyć niepewność,
c) nacisnąć przycisk „Oblicz”.

Wyniki pojawią się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

3.2.1.2 Obliczanie niepewności wartości średniej małej liczby pomiarów

Panel kontrolny w prawym górnym rogu panelu z rysunku 3 służy do wyznaczania niepewności

wartości średniej jeżeli dostępny jest tylko jeden pomiar lub wyniki nie wykazują rozrzutu (wzór (6)).
Aby rozpocząć obliczenia należy:

a) podać wartość działki elementarnej,

13

b) nacisnąć przycisk „Oblicz”.

Wyniki pojawią się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

3.2.1.3 Obliczanie całkowitej niepewności standardowej

Aby obliczyć całkowitą niepewność standardową (wzór (7)) należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać, dla których wpisanych wartości chcemy obliczyć niepewność,
c) wprowadzić wartość działki elementarnej,
d) nacisnąć przycisk „Oblicz”.

Rezultat pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

3.2.2 Niepewności względna

Po wciśnięciu przycisku „Niepewność względna” panelu „Statystyczna analiza wyników i niepe-

wności pomiarów bezpośrednich” widzimy:

Rys.4 Panel „Niepewność względna”; 1

− przycisk „Niepewność względna”, 2 − panel niepewności

względnej pojedynczego pomiaru, 3

− panel niepewności względnej wartości średniej.

14

3.2.2.1 Obliczanie niepewności względnej pojedynczego pomiaru

Za pomocą tego panelu możemy policzyć niepewność względną pojedynczego pomiaru (wzór (8))

W tym celu należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać, dla których wpisanych wartości zmierzonych chcemy obliczyć niepewność,
c) podać, dla której z podanych poprzednio wartości chcemy obliczyć niepewność,
d) nacisnąć przycisk „Oblicz”.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

3.2.2.2 Obliczanie niepewności względnej wartości średniej

Aby obliczyć niepewność względną wartości średniej (wzór (9)) należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać, dla których wpisanych wartości chcemy obliczyć niepewność,
c) nacisnąć przycisk „Oblicz”.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

3.2.3 Niepewności całkowita

Po wciśnięciu przycisku „Niepewność całkowita” panelu „Statystyczna analiza wyników i niepe-

wności pomiarów bezpośrednich” widzimy rysunek 6.

3.2.3.1 Obliczanie maksymalnej wartości niepewności całkowitej miernika analogo-
wego

W celu obliczenia maksymalnej wartości niepewności całkowitej miernika analogowego (wzór

(10)) należy:

a) podać klasę przyrządu w procentach,
b) podać zakres przyrządu,
c) nacisnąć przycisk „Oblicz”.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

3.2.3.2 Obliczanie maksymalnej wartości niepewności całkowitej miernika cyfrowego

Aby obliczyć maksymalną wartość niepewności całkowitej miernika analogowego (wzór (11))

należy:

a) podać klasę przyrządu w procentach,
b) podać zakres przyrządu,
c) podać wartość zmierzonej zmiennej,
d) nacisnąć przycisk „Oblicz”.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

15

Rys.5 Panel „Niepewność całkowita”; 1

− przycisk „Niepewność całkowita”,2 − panel maksymalnej war-

tości niepewności całkowitej miernika analogowego, 3

− panel maksymalnej wartości niepewności całko-

witej miernika cyfrowego.

3.3 Panel „Statystyczna analiza wyników i niepewności pomiarów pośrednich”

Teraz zajmiemy się omówieniem panelu znajdującego się pod przyciskiem trzecim „Statystyczna

analiza wyników i niepewności pomiarów pośrednich” (Rys.6).

3.3.1 Obliczanie współczynnika korelacji

W celu obliczenia współczynnika korelacji (wzór (14)) należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać, dla których wpisanych wartości chcemy obliczyć niepewność, pamiętając aby wielkości

korelujące znajdowały się na tych samych Y,

c) nacisnąć przycisk „Oblicz”.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”.

16

Rys.6 Panel „Statystyczna analiza wyników i niepewności pomiarów pośrednich”; 1

− przycisk

„Statystyczna analiza wyników i niepewności pomiarów pośrednich”, 2

− panel współczynnika korelacji,

3

− zakładka „Nieskorelowane”, 4 − panel niepewności standardowej wielkości nieskorelowanych.

3.3.2 Obliczanie niepewności standardowej wielkości nieskorelowanych

Kiedy jest wciśnięta zakładka „Nieskorelowane” (Rys.6), mamy możliwość obliczania niepewno-

ści standardowych wielkości nieskorelowanych (wzór (15)). W tym celu należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać zakres pierwszej zmiennej i nacisnąć przycisk „Następna”,
c) podać zakres kolejnej zmiennej i nacisnąć przycisk „Następna” w celu wprowadzenia kolejnej

zmiennej (maksymalna dopuszczalna liczba zmiennych wynosi 100), lub przycisk „Oblicz” w celu
obliczenia wartości niepewności standardowej.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”. Jeżeli popełniono błąd podczas wprowadzania danych to należy wcisnąć przycisk „Błąd”
i zacząć wprowadzać dane od początku.

17

Rys.7 Panel „Statystyczna analiza wyników i niepewności pomiarów pośrednich”; 1

− zakładka „Skorelo-

wane”, 2

− panel niepewności standardowej wielkości skorelowanych.

3.3.2 Obliczanie niepewności standardowej wielkości skorelowanych

Przy wciśniętej zakładce „Skorelowane” (Rys.7), mamy możliwość obliczania niepewności

standardowych wielkości skorelowanych (wzór (18)). W tym celu należy:

a) wpisać w tabeli znajdującej się po lewej stronie wartości poszczególnych pomiarów,
b) podać zakres pierwszej zmiennej i nacisnąć przycisk „Następna”,
c) podać zakres kolejnej zmiennej i nacisnąć przycisk „Następna” w celu wprowadzenia kolejnej

zmiennej (maksymalna dopuszczalna liczba zmiennych wynosi 100), lub przycisk „Oblicz” w celu
obliczenia wartości niepewności standardowej.

Wynik pojawi się pod napisem „Wynik”, a zaokrąglony wynik do liczb znaczących pod napisem „Po
zaokrągleniu”. Jeżeli popełniono błąd podczas wprowadzania danych to należy wcisnąć przycisk „Błąd”
i zacząć wprowadzać dane od początku.

18

4 Podsumowanie

Głównym osiągnięciem pracy jest zaprojektowany i przetestowany program nazwany „Analiza

niepewności pomiarowych wspomagana komputerowo” (ANPWK). Jest on wygodnym i efektywnym
narzędziem służącym do prowadzenia podstawowych obliczeń z zakresu analizy niepewności pomiaro-
wych. Uwzględnione zostały w nim wszystkie zalecenia międzynarodowych organizacji dotyczące nowej
i adekwatnej terminologii [1 – 8] oraz sposobów prowadzenia analizy niepewności za pomocą metody A
polegającej na statystycznej analizie skończonej serii pomiarów bezpośrednich i pośrednich.

Omawiany pakiet został zaprogramowany za pomocą obiektowo-zorientowanego języka DELPHI

5.0 [9]. Dzięki temu użytkownik ma możliwość korzystania z przyjaznego mu interfejsu graficznego,
który umożliwia sterowanie pracą programu i wykonywanymi obliczeniami.

Stworzone narzędzie komputerowe pozwala wyznaczać wartości następujących podstawowych,

dla analizy niepewności wielkości:

1) Niepewności przypadkowe (wzór (2)).
2) Średnie arytmetyczne (wzór (3)).
3) Zaokrąglenia liczb (według zasad z rozdziału 2.4).
4) Niepewności standardowe pomiarów bezpośrednich (wzór (5)).
5) Niepewności standardowe pojedynczych wyników pomiarów bezpośrednich (wzór (6)).
6) Całkowite niepewności standardowe pomiarów bezpośrednich (wzór (7)).
7) Niepewności względne pomiarów bezpośrednich (wzór (8)).
8) Niepewności względne wartości średnich pomiarów bezpośrednich (wzór (9)).
9) Maksymalne wartości niepewności całkowitych mierników analogowych (wzór (10)).
10) Maksymalne wartości niepewności całkowitych mierników cyfrowych (wzór (11)).
11) Współczynniki korelacji pomiarów pośrednich (wzór (14)) (rozdział 3.3.1).
12) Niepewności standardowe nieskorelowanych pomiarów pośrednich (wzór (15)).
13) Złożone niepewności standardowe skorelowanych pomiarów pośrednich (wzór (18)).

Uważam, że pakiet ANPWK może być wykorzystywany w Laboratorium Podstaw Fizyki Instytutu

Fizyki Politechniki Wrocławskiej jako pożyteczne narzędzie ułatwiające sporządzanie sprawozdań przez
studentów oraz ich weryfikację przez nauczycieli akademickich.

Niewygórowane wymagania sprzętowe umożliwiają jego używanie, bez konieczności

instalowania, w innych laboratoriach i pracowniach fizycznych.

Do pracy dołączona jest płyta CD-ROM, na której znajdują się:

1. Treść pracy zredagowany za pomocą MS WORD XP.
2. Kod źródłowy programu ANPWK.
3. Skompilowany program ANPWK.

19

5 Literatura

[

1] Ryszard Poprawski, Włodzimierz Salejda, Ćwiczenia laboratoryjne z fizyki. Część I.

Zasady opracowania wyników pomiarów, Wydanie II poprawione i uzupełnione,
Oficyna wydawnicza PWr, Wrocław 1999.

[2] Włodzimierz Salejda, Ryszard Poprawski, Podstawy analizy niepewności pomiarowych

w studenckim laboratorium podstaw fizyki, dokument elektroniczny

http://www.if.pwr.wroc.pl/`dydaktyka/LPF/index.html

, Wrocław 2001

[3] Andrzej Zięba, Natura niepewności pomiaru a jego nowa kodyfikacja, Postępy fizyki
52, Zeszyt 5 (2001).

[4] Henryk Szydłowski, Międzynarodowe normy oceny niepewności pomiarów, Postępy
fizyki 51, Zeszyt 2 (2000).

[5] B.N.Taylor and Ch.E.Kuyatt, Guidelines for Evaluation and Expressing the

Uncertainty of NITS Measurement Results. The National Institute of Standards and
Technology (NITS) Technical Note 1297 (1994), dokument elektroniczny

http://physics.nits.gov/Pubs/guidelines

.

[6] Guide to Expression of Uncertainty in Measurement, opracowanie International
Organization for Standardization (ISO), Genewa 1995.

[7] Essential of expressing measurement uncertainty. The National Institute of Standards

and Technology (NITS) Reference on Constants, Units and Uncertainty, dokument
elektroniczny

http://physics.nits.gov/cuu/Uncertainty

.

[8] Wiktor Konecki, Statystyka dla Inżynierów, PWN, Warszawa 1999.

[9] Andrzej Marciniak, Borland Delhi 5 Professional. Object Pascal, Nakom Poznań 2000.

20