1

ANALIZA NIEPEWNOŚCI

POMIAROWYCH

1.

Pomiary wielkości fizycznych

2.

Błędy i niepewności pomiarowe

3.

Metody określania niepewności pomiarowych

4.

Zapis wyników pomiaru

5.

Przykład opracowania wyników doświadczenia

6.

Dodatek:

Zestawienie najważniejszych elementów Międzynarodowej Normy

Oceny Niepewności Pomiarowej

2

1. Pomiary wielkości fizycznych

Pomiar wielkości fizycznej polega na porównaniu jej z wielkością tego samego rodzaju

przyjętą za jednostkę. Zatem liczba otrzymana jako wynik pomiaru zależy od wyboru

jednostki (przykład: pomiar długości w cm, m, ft, in itp.). Wynik pomiaru musi więc zawsze

składać się z dwóch części: wartości liczbowej oraz jednostki.

Pomiary wielkości fizycznych dzielimy na bezpośrednie i pośrednie. Pomiary

bezpośrednie są najprostsze – polegają wprost na porównaniu danej wielkości z

odpowiednią miarą wzorcową np. pomiar wymiarów ciała za pomocą linijki, suwmiarki,

ś

ruby mikrometrycznej itp., pomiar czasu trwania jakiegoś procesu przy użyciu stopera,

pomiar natężenia prądu amperomierzem. W przypadku pomiarów pośrednich wartość

badanej wielkości wyznaczana jest na podstawie pomiarów bezpośrednich innych wielkości

fizycznych, które są z nią związane znanym nam prawem fizycznym. Na przykład – chcemy

wyznaczyc wartość przyspieszenia ziemskiego na podstawie okresu drgań wahadła

matematycznego. Jak wiadomo okres drgań wahadła opisuje wzór:

g

l

T

/

2

π

=

, st

ą

d

2

2

4

T

l

g

π

=

. W celu wyznaczenia warto

ś

ci

g

musimy zatem dokona

ć

pomiarów

(bezpo

ś

rednich) okresu drga

ń

wahadła (

T

) oraz długo

ś

ci nici (

L

). Innym przykładem jest

wyznaczanie nat

ęż

enia pr

ą

du elektrycznego na podstawie pomiarów spadku napi

ę

cia na

oporniku wzorcowym oraz prawa Ohma

R

U

I

/

=

. Widzimy,

ż

e w zale

ż

no

ś

ci od wyboru

metody pomiarowej, warto

ś

ci niektórych wielko

ś

ci fizycznych mog

ą

by

ć

wyznaczane

zarówno drog

ą

pomiarów bezpo

ś

rednich, jak i po

ś

rednich.

2. Błędy i niepewności pomiarowe

Niezale

ż

nie od metody pomiarów nie mo

ż

emy nigdy bezwzgl

ę

dnie dokładnie wyznaczy

ć

rzeczywistej warto

ś

ci wielko

ś

ci fizycznej. Ró

ż

nic

ę

pomi

ę

dzy wynikiem pomiaru, a

rzeczywist

ą

warto

ś

ci

ą

mierzonej wielko

ś

ci nazywamy

błędem pomiaru

. Bł

ę

dy pomiarów

tradycyjnie dzielimy na grube (omyłki), przypadkowe oraz systematyczne.

Błędy grube

powstaj

ą

zwykle na skutek nieuwagi lub niestaranno

ś

ci obserwatora przy

odczytywaniu lub zapisywaniu wyników lub w wyniku nagłej zmiany warunków pomiaru

(np. wstrz

ą

sy). Je

ś

li mamy seri

ę

pomiarów wyniki obarczone bł

ę

dem grubym s

ą

łatwe do

wykrycia i usuni

ę

cia.

Błędy systematyczne

wynikaj

ą

z niedoskonało

ś

ci przyrz

ą

dów i metod pomiarowych. Mo

ż

na je

redukowa

ć

stosuj

ą

c bardziej doskonałe i precyzyjne metody i przyrz

ą

dy, jednak całkowite

3

wyeliminowanie bł

ę

dów systematycznych jest niemo

ż

liwe. Rozpoznane bł

ę

dy systematyczne

nale

ż

y uwzgl

ę

dnia

ć

poprzez wprowadzenie odpowiednich poprawek do wyniku, np. kiedy

wa

ż

ymy na wadze, której wskazanie bez obci

ąż

enia wynosi

m

0

zamiast 0 to

m

0

jest bł

ę

dem

systematycznym, który nale

ż

y odj

ąć

od wyniku wa

ż

enia, innym typowym przykładem jest

poprawka na opór wewn

ę

trzny woltomierza przy pomiarze napi

ę

cia .

Z

błędami przypadkowymi

mamy do czynienia zawsze. Wynikaj

ą

one z ró

ż

nych

przypadkowych i nie daj

ą

cych si

ę

uwzgl

ę

dni

ć

czynników (np. wahania temperatury, lub ruch

powietrza w pobli

ż

u przyrz

ą

du pomiarowego). Inn

ą

przyczyn

ą

mo

ż

e by

ć

niezgodno

ść

przyj

ę

tego modelu z obiektem mierzonym – np. gdy mamy zmierzy

ć

ś

rednic

ę

pr

ę

ta,

zakładamy milcz

ą

co,

ż

e jest on idealnym walcem, co nie jest prawd

ą

. O istnieniu bł

ę

dów

przypadkowych

ś

wiadczy niepowtarzalno

ść

wyników pomiaru jednej i tej samej wielko

ś

ci.

Bł

ę

dy przypadkowe redukuje si

ę

poprzez wielokrotne powtarzanie pomiaru – zachodzi

wówczas cz

ęś

ciowa kompensacja przypadkowych zawy

ż

aj

ą

cych i zani

ż

aj

ą

cych odchyłek

wyniku.

Poniewa

ż

nigdy nie znamy rzeczywistej warto

ś

ci wielko

ś

ci mierzonej, wi

ę

c

posługiwanie si

ę

w praktyce poj

ę

ciem bł

ę

du pomiaru nie jest wygodne. Obecnie przy

opracowywaniu wyników pomiarów nale

ż

y stosowa

ć

si

ę

do zalece

ń

Mi

ę

dzynarodowej

Normy Oceny Niepewno

ś

ci Pomiaru. Norma ta uzgodniona w 1995 r. i przyj

ę

ta ustawowo w

Polsce w 1999 r. znajduje zastosowanie w ró

ż

nych dziedzinach nauki i techniki.

Mi

ę

dzynarodowa Norma zaleca posługiwanie si

ę

terminem

niepewność pomiarowa

zdefiniowanym jako parametr charakteryzujący wątpliwości dotyczące wartości wyniku

pomiarowego

. Miar

ą

niepewno

ś

ci pomiarowej jest

niepewność standardowa

, która mo

ż

e

by

ć

szacowana na 2 sposoby:

typu A

wykorzystuj

ą

cy analiz

ę

statystyczn

ą

serii pomiarów

oraz

typu B

oparty na naukowym os

ą

dzie obserwatora. Symbolem niepewno

ś

ci standardowej

jest

u

(od ang. uncertainty), który mo

ż

na zapisywa

ć

na 3 ró

ż

ne sposoby, np.

u

,

u

(

x

) lub

u

(st

ęż

enie NaCl). Zalet

ą

tego zapisu jest to,

ż

e informacja o wielko

ś

ci mierzonej mo

ż

e by

ć

wyra

ż

ona słownie, co ułatwia tworzenie dokumentacji pomiaru. Nale

ż

y jednak pami

ę

ta

ć

,

ż

e

u

nie jest funkcj

ą

tylko liczb

ą

!

3. Metody określania niepewności pomiarowych

3.1. Niepewność standardowa pomiarów bezpośrednich

Przypu

ść

my,

ż

e wykonali

ś

my seri

ę

n

pomiarów bezpo

ś

rednich wielko

ś

ci fizycznej

X

otrzymuj

ą

c wyniki

X

1

,

X

2

...

X

n

. Je

ś

li wyniki pomiarów nie s

ą

takie same, wówczas za

4

najbardziej zbli

ż

on

ą

do warto

ś

ci prawdziwej przyjmujemy

ś

redni

ą

arytmetyczn

ą

ze

wszystkich wyników pomiarów:

∑

=

=

≈

n

i

i

X

n

X

X

1

1

(1)

Stwierdzenie to jest tym bardziej słuszne im wi

ę

ksza jest liczba przeprowadzonych pomiarów

(dla

∞

→

n

,

X

X

→

). W celu okre

ś

lenia niepewno

ś

ci standardowej posługujemy si

ę

w tym

wypadku sposobem typu A, czyli korzystamy ze wzoru na odchylenie standardowe

ś

redniej

(

)

)

1

(

)

(

1

2

2

−

−

=

=

∑

=

n

n

X

X

s

X

u

n

i

i

X

(2)

Je

ś

li natomiast wyniki pomiarów nie wykazuj

ą

rozrzutu, czyli

n

X

X

X

=

=

=

...

2

1

, lub te

ż

gdy

istnieje tylko jeden wynik pomiaru, wówczas niepewno

ść

standardow

ą

szacujemy sposobem

typu B. Mo

ż

na np. wykorzysta

ć

informacj

ę

o niepewno

ś

ci maksymalnej

X

∆

okre

ś

lonej przez

producenta przyrz

ą

du pomiarowego, je

ś

li nie mamy innych dodatkowych informacji,

wówczas niepewno

ść

standardow

ą

obliczamy ze wzoru

3

)

(

X

X

u

∆

=

(3)

Dla prostych przyrz

ą

dów (tj. linijka,

ś

ruba mikrometryczna czy termometr) jako

X

∆

mo

ż

na

przyj

ąć

działk

ę

elementarn

ą

przyrz

ą

du. W elektronicznych przyrz

ą

dach cyfrowych

niepewno

ść

maksymalna podawana jest przez producenta w instrukcji obsługi i jest zwykle

kilkakrotnie wi

ę

ksza od działki elementarnej. Najcz

ęś

ciej zale

ż

y ona od wielko

ś

ci mierzonej

X i zakresu na którym mierzymy Z:

Z

c

X

c

X

2

1

+

=

∆

Gdy wyst

ę

puj

ą

oba typy niepewno

ś

ci (tzn. zarówno rozrzut wyników jak i

niepewno

ść

wzorcowania) i

ż

adna z nich nie mo

ż

e by

ć

zaniedbana (tzn. obie s

ą

tego samego

rz

ę

du), wówczas niepewno

ść

standardow

ą

(całkowit

ą

) obliczamy ze wzoru

( )

3

)

(

2

2

X

s

X

u

X

∆

+

=

.

(4)

3.2. Niepewność standardowa pomiarów pośrednich – niepewność złożona (u

c

)

W przypadku pomiarów po

ś

rednich wielko

ść

mierzon

ą

Y obliczamy korzystaj

ą

c ze zwi

ą

zku

funkcyjnego, który mo

ż

na zapisa

ć

w ogólnej postaci:

)

,...,

,

(

2

1

k

X

X

X

f

Y

=

, gdzie symbolami

k

X

X

X

,...,

,

2

1

oznaczamy

k wielko

ś

ci fizycznych mierzonych bezpo

ś

rednio. Zakładamy,

ż

e

5

znane s

ą

wyniki pomiarów tych wielko

ś

ci

k

X

X

X

,...,

,

2

1

oraz ich niepewno

ś

ci standardowe

)

(

),...,

(

),

(

2

1

k

X

u

X

u

X

u

. Wynik (ko

ń

cowy) pomiaru oblicza si

ę

wówczas ze wzoru:

)

,...,

,

(

2

1

k

X

X

X

f

Y

Y

=

≈

W przypadku pomiarów po

ś

rednich nieskorelowanych (tzn. gdy ka

ż

d

ą

z wielko

ś

ci

k

X

X

X

,...,

,

2

1

mierzy si

ę

niezale

ż

nie) niepewno

ść

zło

ż

on

ą

wielko

ś

ci

Y szacujemy przy

pomocy przybli

ż

onego wzoru:

(

) ( )

∑

=















∂

∂

=

k

j

j

k

j

c

X

u

X

X

X

X

f

Y

u

1

2

2

2

1

,...,

,

)

(

(5)

3.3. Niepewność rozszerzona

Niepewno

ść

standardowa całkowicie i jednoznacznie okre

ś

la warto

ść

wyniku, jednak do

wnioskowania o zgodno

ś

ci wyniku pomiaru z innymi rezultatami (np. z warto

ś

ci

ą

tabelaryczn

ą

) oraz dla celów komercyjnych i do ustalania norm przemysłowych, zdrowia,

bezpiecze

ń

stwa itp. Mi

ę

dzynarodowa Norma wprowadza poj

ę

cie

niepewności rozszerzonej

oznaczanej symbolem

U (dla pomiarów bezpo

ś

rednich), lub

U

c

(dla pomiarów po

ś

rednich).

Warto

ść

niepewno

ś

ci rozszerzonej oblicza si

ę

ze wzoru

)

(

)

(

X

ku

X

U

=

lub

)

(

)

(

X

ku

X

U

c

c

=

(6)

Liczba

k, zwana współczynnikiem rozszerzenia, jest umownie przyj

ę

t

ą

liczb

ą

wybran

ą

tak,

aby w przedziale

)

( X

U

X

±

znalazła si

ę

większość

wyników pomiaru potrzebna dla danych

zastosowa

ń

. Warto

ść

współczynnika rozszerzenia mie

ś

ci si

ę

najcz

ęś

ciej w przedziale 2-3. W

wi

ę

kszo

ś

ci zastosowa

ń

zaleca si

ę

przyjmowanie umownej warto

ś

ci

2

=

k

.

4. Zapis wyników pomiaru

Wyniki pomiaru zapisujemy zawsze łącznie z niepewnością i jednostką.

Niepewno

ść

podajemy zawsze z dokładno

ś

ci

ą

do

dwu cyfr

, za

ś

liczb

ę

cyfr znacz

ą

cych wyniku dobieramy

tak, aby o

statnia cyfra rezultatu i niepewności należały do tego samego rzędu

. Dla

niepewno

ś

ci standardowych zalecany jest

zapis z użyciem nawiasów

, za

ś

dla niepewno

ś

ci

rozszerzonej stosowany jest

zapis z użyciem symbolu

±±±±

.

Przykłady zapisu

Dobrze:

Niepewno

ść

standardowa:

====

m

100,0214 g,

====

)

(m

u

3,5 mg

6

====

m

100,0214(35) g

====

m

100,0214(0,0035) g

Niepewno

ść

rozszerzona:

====

m

100,0214 g,

=

)

(m

U

0,0070 g

====

m

(100,0214

0070

,

0

±

) g

Źle:

====

m

100,0214 g – nie podano niepewno

ś

ci,

====

m

100,021(0,0035) g – ostatnie cyfry rezultatu i niepewno

ś

ci nie s

ą

tego samego rz

ę

du,

====

m

100,021 g,

====

)

(m

u

3 mg – przy zapisie niepewno

ś

ci podano zbyt mało cyfr,

====

m

100,02147(0,00352) g - przy zapisie niepewno

ś

ci podano zbyt du

ż

o cyfr.

5. Przykład opracowania wyników doświadczenia

Celem wyznaczenia przyspieszenia ziemskiego przeprowadzono pomiary czasu spadku ciała

z pewnej wysoko

ś

ci. Wysoko

ść

spadku

h zmierzono 3-krotnie ta

ś

m

ą

miernicz

ą

z podziałk

ą

milimetrow

ą

uzyskuj

ą

c za ka

ż

dym razem wynik 1270 mm. Czas spadku

t zmierzono 5 razy

otrzymuj

ą

c nast

ę

puj

ą

ce wyniki (w s)

509

,

0

1

=

t

,

512

,

0

2

=

t

,

510

,

0

3

=

t

,

504

,

0

4

=

t

,

501

,

0

5

=

t

. Dokładno

ść

czasomierza wynosiła 0,001 s, za

ś

niepewno

ść

systematyczn

ą

zwi

ą

zan

ą

z wyborem chwili wł

ą

czenia i wył

ą

czenia oszacowano na 0,01 s. Obliczy

ć

z tych

danych przyspieszenie ziemskie i jego niepewno

ść

.

Przyspieszenie ziemskie b

ę

dziemy oblicza

ć

ze wzoru

2

2

t

h

g

=

. Warto

ść

g

otrzymamy

wstawiaj

ą

c do powy

ż

szego równania

ś

rednie arytmetyczne wysoko

ś

ci spadku ( h ) oraz czasu

spadku ( t ) (wzór (1)). Dla danych z tego przykładu mamy:

1270

=

h

mm = 1,27 m,

)

501

,

0

504

,

0

510

,

0

512

,

0

509

,

0

(

5

1

+

+

+

+

=

t

s = 0,5072 s,

st

ą

d

2

2

s

m

874

,

9

s)

(0,5072

m

27

,

1

2

≈

⋅

=

g

Aby obliczy

ć

niepewno

ść

zło

ż

on

ą

pomiaru po

ś

redniego g musimy najpierw okre

ś

li

ć

niepewno

ś

ci standardowe pomiaru czasu i wysoko

ś

ci.

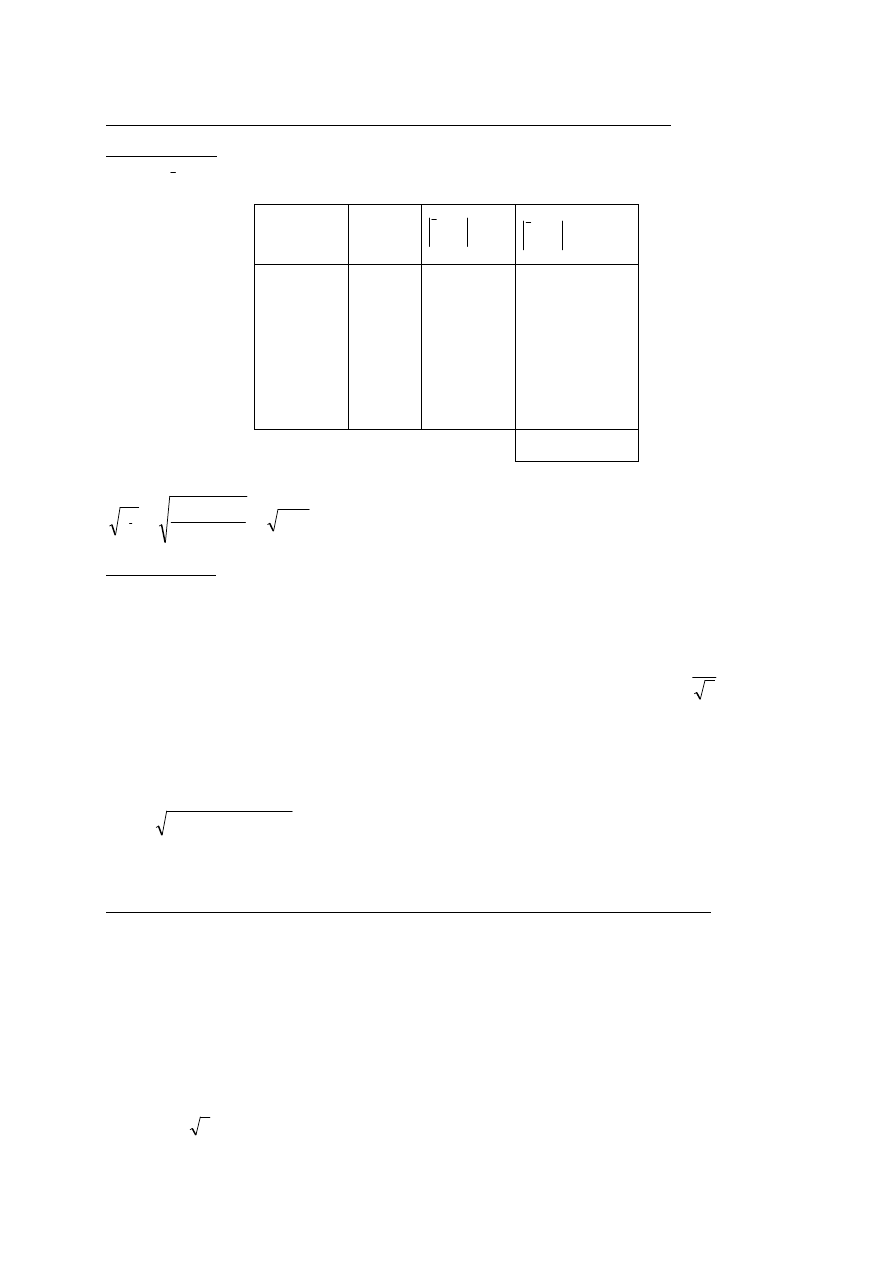
7

Oszacowanie niepewno

ś

ci standardowej (bezpo

ś

redniego) pomiaru czasu u(t):

Ocena typu A:

Korzystaj

ą

c ze wzoru (2) oraz z tabeli obliczamy odchylenie standardowe

ś

redniej t :

Nr pomiaru t

i

[s]

i

t

t

−

[ms]

2

i

t

t

−

[ms

2

]

1

2

3

4

5

0,509

0,512

0,510

0,504

0,501

1,8

4,8

2,8

3,2

6,2

3,24

23,04

7,84

10,24

38,44

Suma: 82,80

ms

14

,

4

4

5

ms

80

,

82

2

2

=

=

⋅

=

t

s

2,0 ms

Ocena typu B: Mo

ż

emy przyj

ąć

,

ż

e niepewno

ść

maksymalna zwi

ą

zana z pomiarem czasu

wynika przede wszystkim z niepewno

ś

ci chwili wł

ą

czenia i wył

ą

czenia, a zatem wynosi

01

,

0

=

∆

t

s = 10 ms (zaniedbujemy przy tym 10-krotnie mniejsz

ą

niepewno

ść

zwi

ą

zan

ą

z

dokładno

ś

ci

ą

czasomierza). Niepewno

ść

standardowa typu B wynosi zatem

=

∆

3

t

5,8 ms

(wzór (3)). Jak wida

ć

w tym wypadku nale

ż

y uwzgl

ę

dni

ć

oba typy niepewno

ś

ci

standardowych (poniewa

ż

s

ą

one tego samego rz

ę

du). Ostatecznie wi

ę

c całkowita niepewno

ść

standardowa pomiaru czasu wynosi (wzór (4)):

1

,

6

ms

)

8

,

5

0

,

2

(

)

(

2

2

2

≈

+

=

t

u

ms = 0,0061 s.

Ko

ń

cowy wynik pomiaru czasu mo

ż

na zapisa

ć

w postaci:

t = 0,5072(0,0061) s

.

Oszacowanie niepewno

ś

ci standardowej (bezpo

ś

redniego) pomiaru wysoko

ś

ci u(h):

Poniewa

ż

w tym wypadku nie wyst

ą

pił rozrzut wyników wi

ę

c poprzestaniemy na okre

ś

leniu

niepewno

ś

ci standardowej typu B. Najmniejsza działka przyrz

ą

du pomiarowego wynosi w

tym wypadku 1 mm. Poniewa

ż

jednak pewien wpływ na wynik pomiaru mo

ż

e mie

ć

równie

ż

sposób ustawienia miarki oraz sposób odczytu, rozs

ą

dnie b

ę

dzie przyj

ąć

,

ż

e niepewno

ść

maksymalna tego pomiaru jest wi

ę

ksza od działki elementarnej np. dwukrotnie:

∆

h = 2 mm.

Zgodnie ze wzorem (3), niepewno

ść

standardowa pomiaru wysoko

ś

ci wynosi zatem:

=

∆

=

3

/

)

(

h

h

u

1,2 mm = 0,0012 m, a wi

ę

c

h = 1270,0(1,2) mm

.

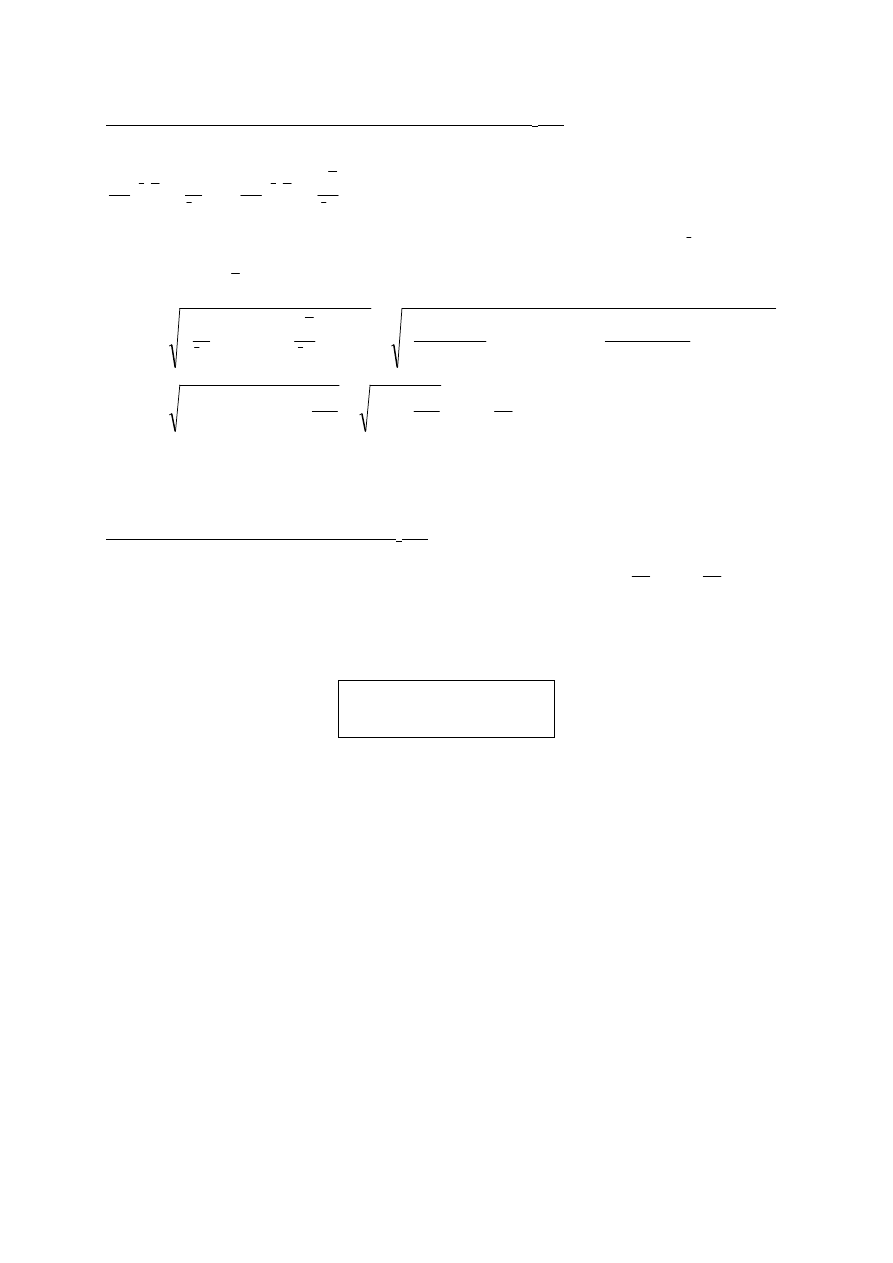
8

Oszacowanie niepewno

ś

ci zło

ż

onej pomiaru po

ś

redniego u

c

(g):

Korzystamy ze wzoru (5). Obliczmy najpierw pochodne cz

ą

stkowe:

2

2

)

,

(

t

h

t

h

g

=

∂

∂

,

3

4

)

,

(

t

h

h

t

t

g

=

∂

∂

. Aby niepewno

ść

)

(g

u

c

wyra

ż

ona była w m/s

2

, przy

podstawianiu danych do wzoru (5) musimy pami

ę

ta

ć

o uzgodnieniu jednostek ( t i u(t) nale

ż

y

wyrazi

ć

w s, za

ś

h i u(h) nale

ż

y wyrazi

ć

w m).

(

)

(

)

2

3

2

2

2

2

3

2

2

2

s

0061

,

0

s

507

,

0

m

2700

,

1

4

m

0012

,

0

s

507

,

0

2

)

(

4

)

(

2

)

(













⋅

⋅

+













⋅

=















+















=

t

u

t

h

h

u

t

g

u

c

(

)

2

4

2

4

2

5

s

m

24

,

0

s

m

057

,

0

s

m

057

,

0

10

7

,

8

)

(

≈

≈

+

⋅

≈

−

g

u

c

Jak wida

ć

, przyczynek do niepewno

ś

ci zło

ż

onej u

c

(g) zwi

ą

zany z niepewno

ś

ci

ą

pomiaru

wysoko

ś

ci okazał si

ę

zaniedbywalnie mały.

Obliczenie niepewno

ś

ci rozszerzonej U

c

(g):

Podstawiaj

ą

c dane do wzoru (6) otrzymujemy:

2

2

s

m

48

,

0

s

m

24

,

0

2

)

(

2

)

(

=

⋅

=

=

g

u

g

U

c

c

.

Ostatecznie ko

ń

cowy rezultat pomiaru przyspieszenia ziemskiego, który mo

ż

emy

porównywa

ć

z wielko

ś

ci

ą

tablicow

ą

, wygl

ą

da nast

ę

puj

ą

co:

g =( 9,87

±

0,48) m/s

2

Literatura

1.

A. Zi

ę

ba, 2001 : Natura rachunku niepewno

ś

ci pomiarowych a jego nowa kodyfikacja.

Post

ę

py fizyki

52

, nr 5, s. 238-247

2.

H. Szydłowski, 2000: Mi

ę

dzynarodowe normy oceny niepewno

ś

ci pomiarowych.

Post

ę

py fizyki

51

, nr 2, s. 92-97

3.

Guide to Expression of Uncertainty in Measurement, ISO 1995, Switzerland.

Tłumaczenie: Wyra

ż

anie niepewno

ś

ci pomiaru. Przewodnik (Główny Urz

ą

d Miar

Warszawa 1999)

9

Dodatek:

Zestawienie najważniejszych elementów Międzynarodowej Normy Oceny

Niepewności Pomiarowej

Wielkość

Symbol i sposób obliczania oraz nr wzoru w tekście

Niepewno

ść

standardowa:

ocena typu A

(pomiary bezpo

ś

rednie)

Podstawa: statystyczna analiza serii pomiarów.

Dla serii n równowa

ż

nych pomiarów (wzory (2) i (1)):

(

)

)

1

(

)

(

1

2

2

−

−

=

=

∑

=

n

n

X

X

s

X

u

n

i

i

X

, gdzie

∑

=

=

≈

n

i

i

X

n

X

X

1

1

Niepewno

ść

standardowa:

ocena typu B

(pomiary bezpo

ś

rednie)

Podstawa: naukowy os

ą

d eksperymentatora.

3

)

(

X

X

u

∆

=

(3)

(gdy znana jest niepewno

ść

maksymalna

∆

X)

Niepewno

ść

standardowa całkowita

ocena typu A oraz typu B

(pomiary bezpo

ś

rednie)

( )

3

)

(

2

2

X

s

X

u

X

∆

+

=

(4)

(gdy niepewno

ś

ci typu A i typu B s

ą

tego samego rz

ę

du)

Niepewno

ść

zło

ż

ona

(pomiary po

ś

rednie)

Dla wielko

ś

ci

)

,...,

,

(

2

1

k

X

X

X

f

Y

=

:

(

)

( )

∑

=

















∂

∂

=

k

j

j

k

j

c

X

u

X

X

X

X

f

Y

u

1

2

2

2

1

,...,

,

)

(

(5)

(gdy wszystkie wielko

ś

ci X

i

s

ą

nieskorelowane)

Współczynnik rozszerzenia

2

≥

k

Niepewno

ść

rozszerzona

)

(

)

(

X

ku

X

U

=

lub

)

(

)

(

X

ku

X

U

c

c

=

(6)

Zalecany

zapis

niepewno

ś

ci

(przykład)

standardowa:

781

,

9

=

g

m/s

2

,

076

,

0

)

(

=

g

u

c

m/s

2

)

76

(

781

,

9

=

g

m/s

2

)

076

,

0

(

781

,

9

=

g

m/s

2

rozszerzona:

78

,

9

=

g

m/s

2

,

15

,

0

)

(

=

g

U

c

m/s

2

)

15

,

0

78

,

9

(

±

=

g

m/s

2

(obowi

ą

zuje zasada podawania 2 cyfr znacz

ą

cych

niepewno

ś

ci)