WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

1

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

1. Kratownice płaskie

1.1. Odpowiedź do zadania 1/1

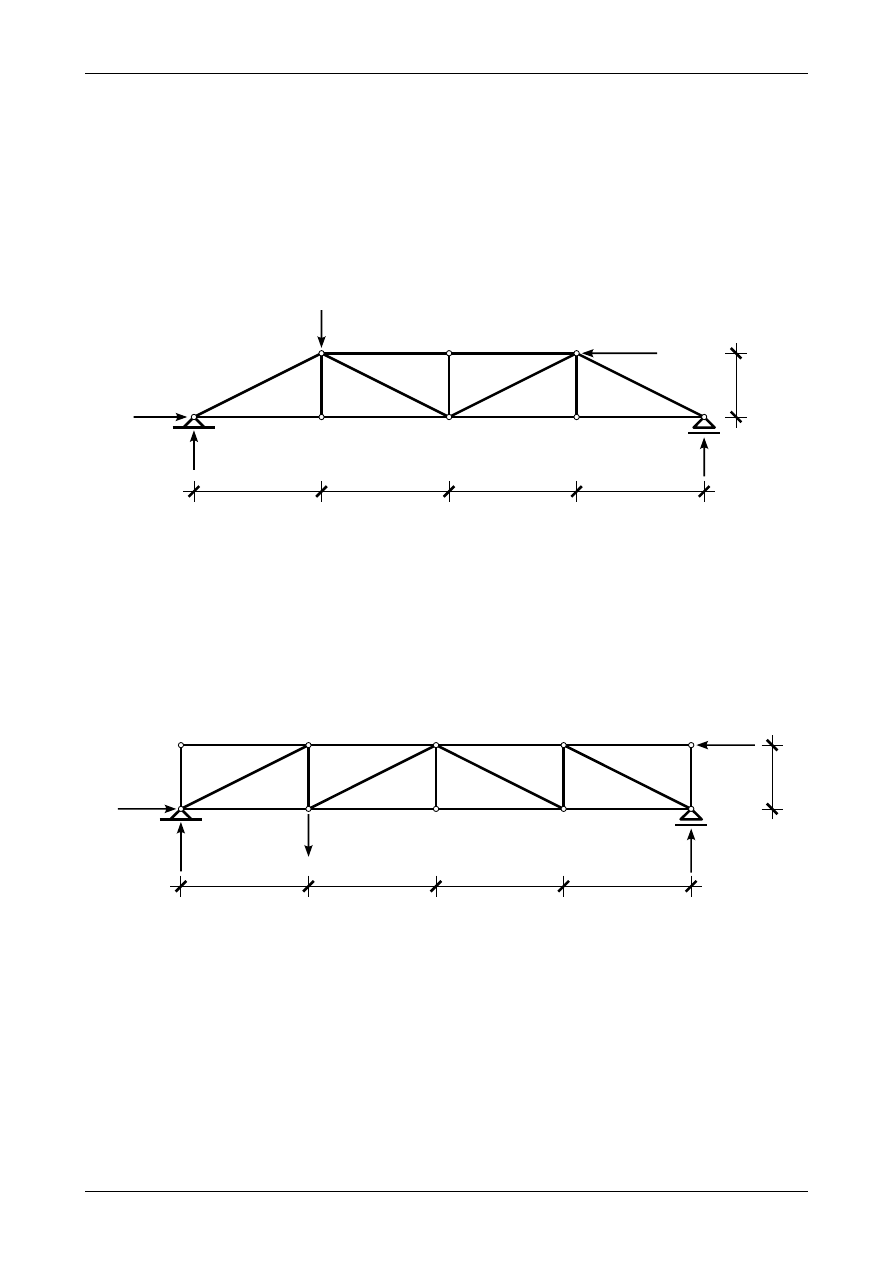
Rysunek 1.1 przedstawia prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej.

Siła normalna w pręcie oznaczonym literą R wynosi

N

R

=−

90,03 kN

.

54,0 kN

36,0 kN

8,0

8,0

8,0

8,0

3,

0

R

[m]

36,0 kN

43,88 kN

10,13 kN

A

Rys. 1.1. Prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej

1.2. Odpowiedź do zadania 1/2

Rysunek 1.2 przedstawia prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej.

Siła normalna w pręcie oznaczonym literą R wynosi

N

R

=

26,33 kN

.

7,0

7,0

7,0

7,0

3,

0

R

[m]

57,0 kN

47,0 kN

57,0 kN

41,36 kN

5,643 kN

A

Rys. 1.2. Prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej

1.3. Odpowiedź do zadania 1/3

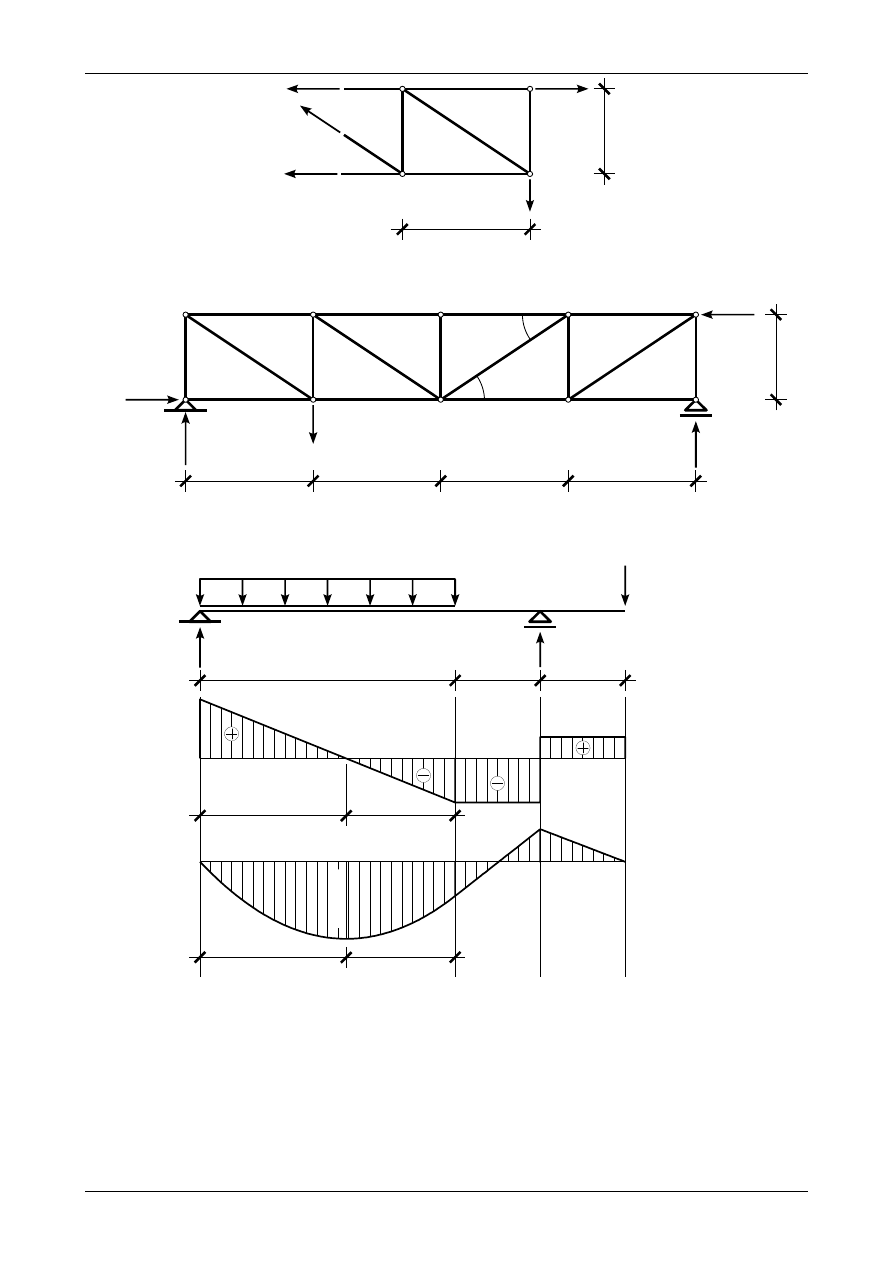
Rysunek 1.3 przedstawia odciętą część kratownicy płaskiej. Do wyznaczenia siły normalnej w pręcie

oznaczonym literą R nie są potrzebne reakcje podporowe. Siła ta wynosi

N

R

=

205,0 kN

.

1.4. Odpowiedź do zadania 1/4

Rysunek 1.4 przedstawia prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej.

Wartość sinusa kąta nachylenia krzyżulca wynosi

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

2

3,0

2,

0

R

90,0 kN

70,0 kN

[m]

A

N

R

Rys. 1.3. Odcięta część kratownicy płaskiej

65,0 kN

105,0 kN

R

7,0

7,0

7,0

7,0

4,

0

[m]

65,0 kN

88,04 kN

16,96 kN

α

α

Rys. 1.4. Prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej

6,0

2,0

2,0

25,0 kN

20,0 kN/m

A

B

D

C

[m]

68,75 kN

76,25 kN

T(x) [kN]

M(x) [kNm]

3,438

2,563

3,438

2,563

68

,7

5

51,25

25,0

0,

0

52

,5

0

50

,0

0

,0

11

8

,2

Rys. 2.1. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

sin







=

0,4961

.

Siła normalna w pręcie oznaczonym literą R wynosi

N

R

=

34,19 kN

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

3

2. Belki

2.1. Odpowiedź do zadania 2/1

Rysunek 2.1 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej. Ten

sam rysunek przedstawia także wykresy siły poprzecznej oraz momentu zginającego.

2.2. Odpowiedź do zadania 2/2

Rysunek 2.2 a) przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce złożonej.

Rysunek 2.2 b) przedstawia wykresy siły poprzecznej oraz momentu zginającego.

2,0

8,0 kN/m

A

B

3,5 kN

9,0 kNm

[m]

25,0 kN

B

C

D

37,5 kN

B

12,5 kN

12,5 kN

12

,5

k

N

1

2,

5

k

N

2,0

1,0

2,0

[m]

2,0

1,0

25,0 kN

8,0 kN/m

A

B

C

D

3,5 kN

37,5 kN

9,0 kNm

T(x) [kN]

M(x) [kNm]

25,0

12,5

3

,5

1,563

0,4375

1,563

0,4375

9

,0

9,

76

6

0,

0

0,

0

25

,0

a)

b)

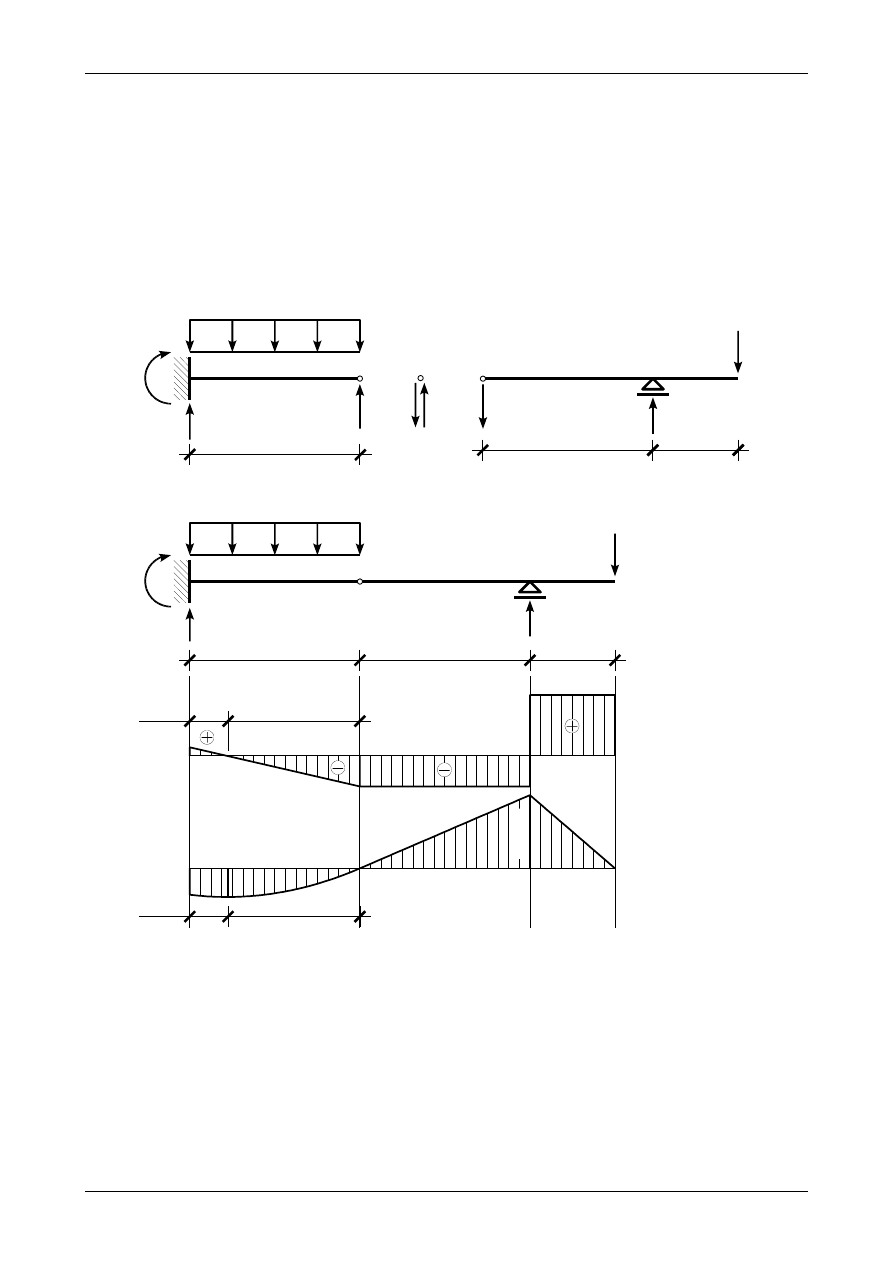
Rys. 2.2. Belka złożona. a) prawidłowe wartości i zwroty reakcji podporowych, b) wykresy siły poprzecznej oraz

momentu zginającego

2.3. Odpowiedź do zadania 2/3

Rysunek 2.3 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej. Ten

sam rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego.

2.4. Odpowiedź do zadania 2/4

Rysunek 2.4 a) przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce złożonej.

Rysunek 2.4 b) przedstawia wykresy siły poprzecznej oraz momentu zginającego.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

4

85

,0

11

0

,0

11

3,

9

4,0

[m]

2,0

2,0

20,0 kN/m

30,0 kN

A

B

C

D

67,5 kN

42,5 kN

T(x) [kN]

M(x) [kNm]

3,375

0,625

3,375

0,625

12,5

42,5

67

,5

0,

0

0

,0

Rys. 2.3. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

3,0

A

B

15,0 kN/m

55,0 kN

97,5 kNm

[m]

3,0

1,0

C

D

30,0 kNm

10,0 kN

B

B

10,0 kN

10,0 kN

10,0 kN

10,0 kN

3,0

[m]

3,0

1,0

A

B

C

D

15,0 kN/m

30,0 kNm

55,0 kN

10,0 kN

97,5 kNm

T(x) [kN]

M(x) [kNm]

55

,0

10,0

0,0

97

,5

0,0

30,0

a)

b)

Rys. 2.4. Belka złożona. a) prawidłowe wartości i zwroty reakcji podporowych, b) wykresy siły poprzecznej oraz

momentu zginającego

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

5

11

3,

0

24,0 kN/m

20,0 kNm

A

B

C

D

[m]

2,0

6,0

2,0

T(x) [kN]

M(x) [kNm]

56,50 kN

87,50 kN

56,50

87

,5

0

0,0

2,354

3,646

2,354

3,646

0,

0

17

9,

5

20,0

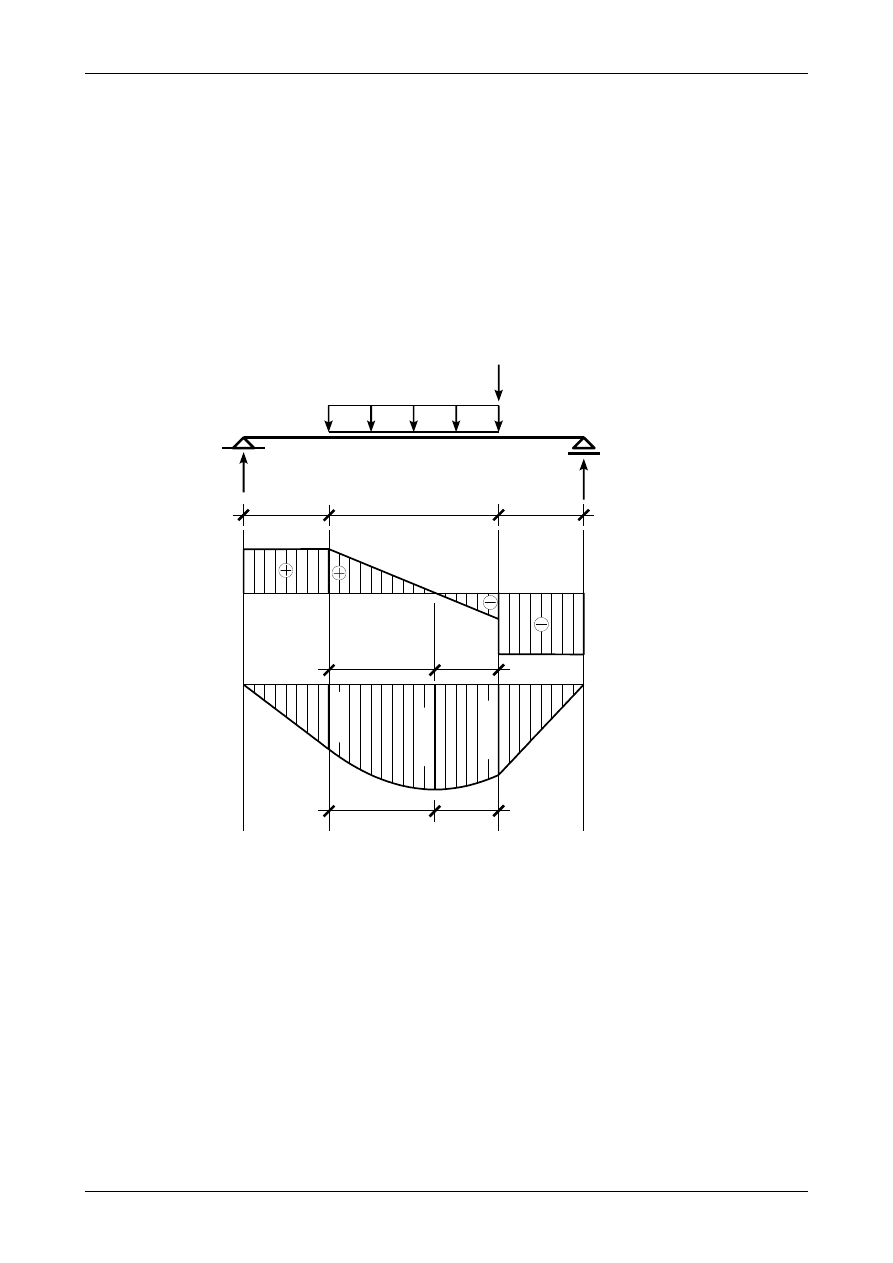
Rys. 2.5. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

2,0

16,0 kN/m

A

B

10,0 kN

20,0 kNm

[m]

12,0 kN

B

C

D

34,0 kN

B

10,0 kN

10

,0

k

N

10

,0

k

N

2,0

1,0

10,0 kN

2,0

[m]

2,0

1,0

12,0 kN

16,0 kN/m

A

B

C

D

10,0 kN

34,0 kN

20,0 kNm

T(x) [kN]

M(x) [kNm]

12,0

10,0

22

,0

0,625

1,375

0,625

1,375

0,

0

12

,0

3,

1

25

0,

0

2

0,

0

a)

b)

Rys. 2.6. Belka złożona. a) prawidłowe wartości i zwroty reakcji podporowych, b) wykresy siły poprzecznej oraz

momentu zginającego

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

6

2.5. Odpowiedź do zadania 2/5

Rysunek 2.5 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej. Ten

sam rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego.

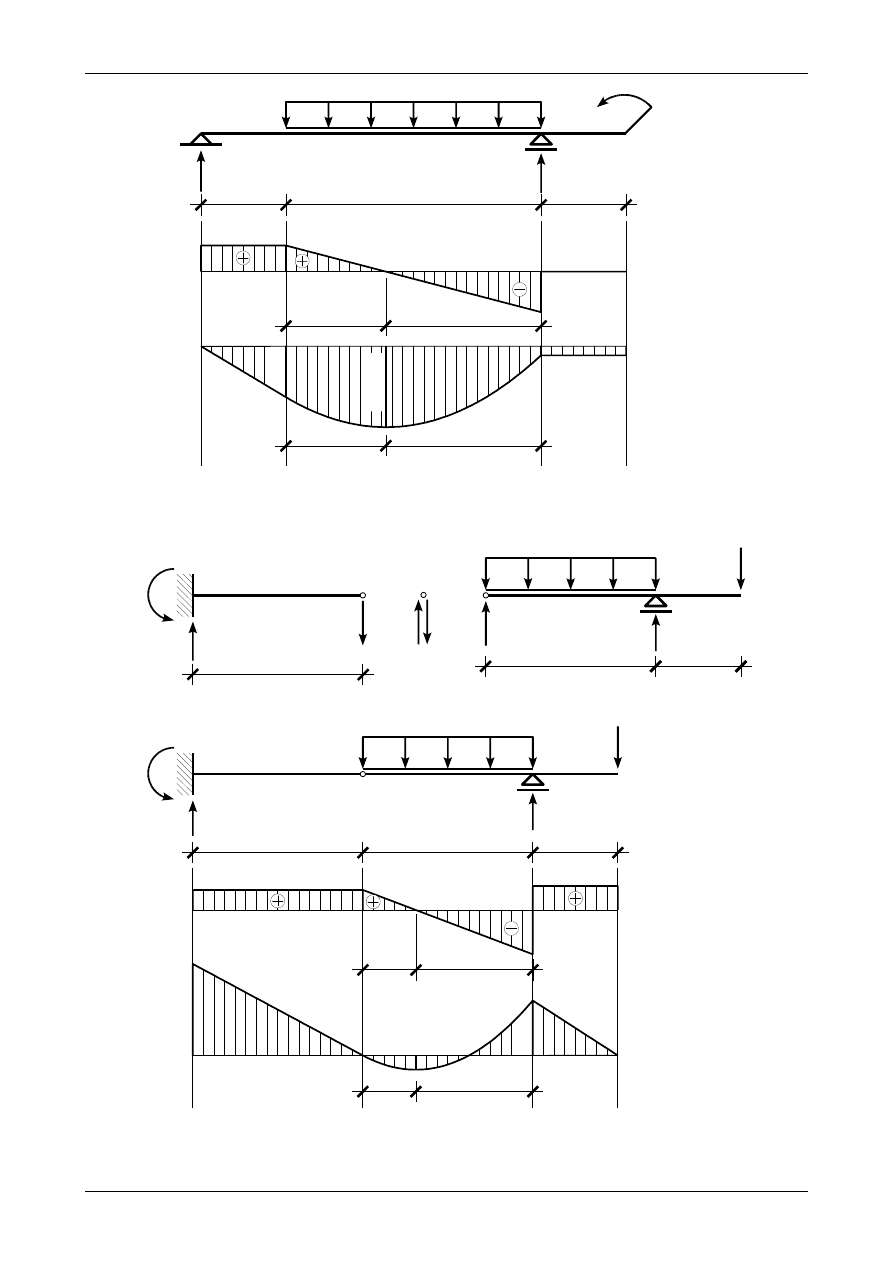
2.6. Odpowiedź do zadania 2/6

Rysunek 2.6 a) przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce złożonej.

Rysunek 2.6 b) przedstawia wykresy siły poprzecznej oraz momentu zginającego.

2.7. Odpowiedź do zadania 2/7

Rysunek 2.7 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej. Ten

sam rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego.

1

46

,3

12

6,

0

90

,0

4,0

[m]

2,0

2,0

18,0 kN/m

36,0 kN

A

B

C

D

45,0 kN

63,0 kN

T(x) [kN]

M(x) [kNm]

2,5

1,5

2,5

1,5

45,0

63,0

27

,0

0

,0

0,

0

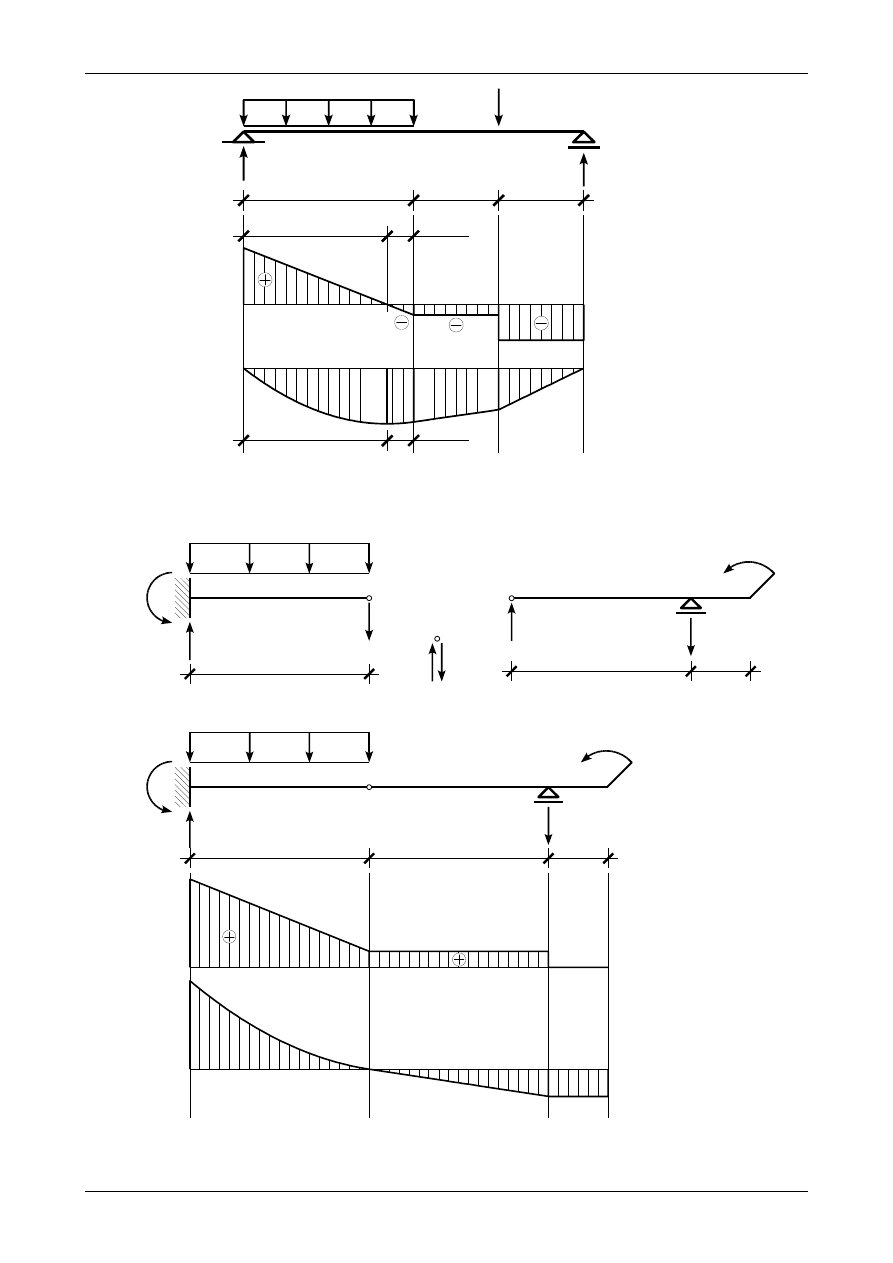
Rys. 2.7. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

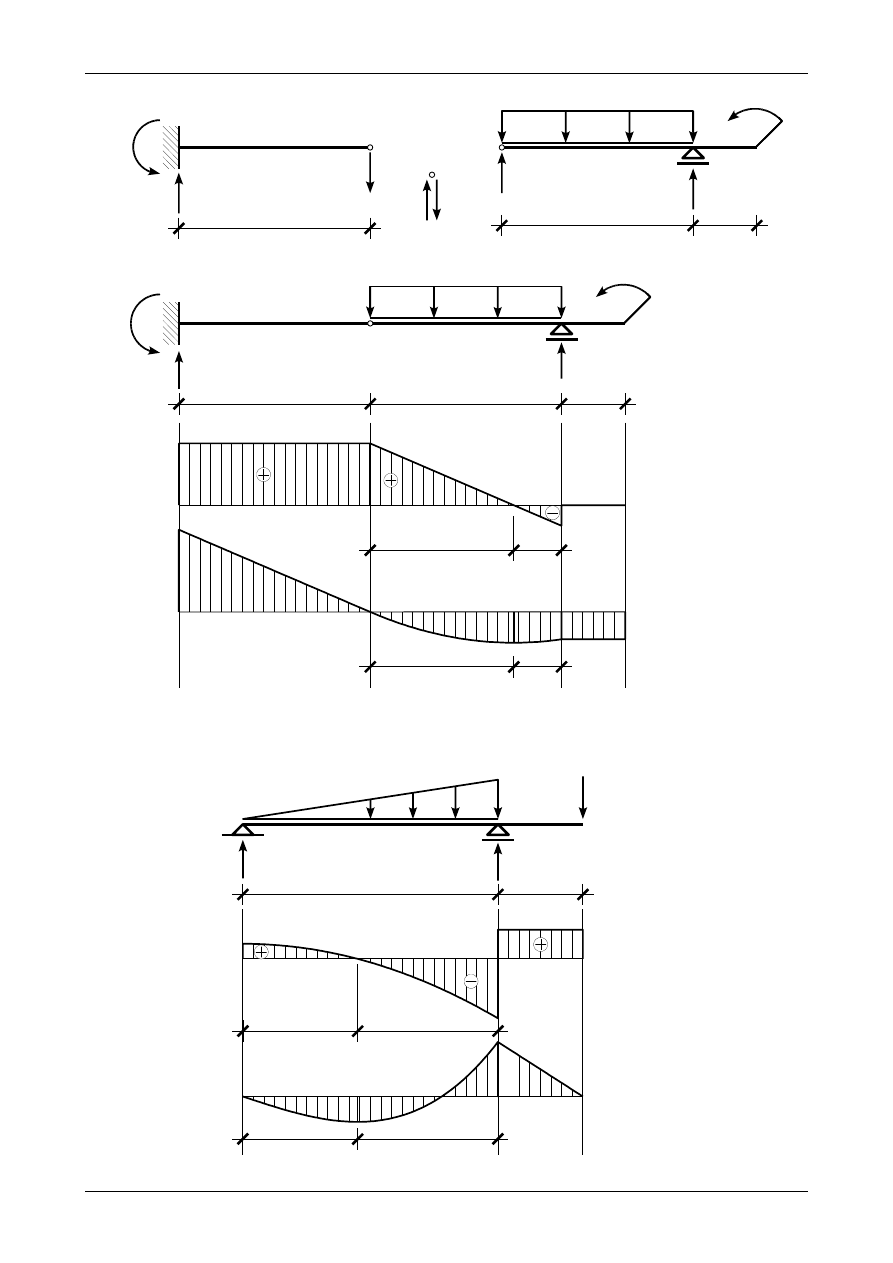
2.8. Odpowiedź do zadania 2/8

Rysunek 2.8 a) przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce złożonej.

Rysunek 2.8 b) przedstawia wykresy siły poprzecznej oraz momentu zginającego.

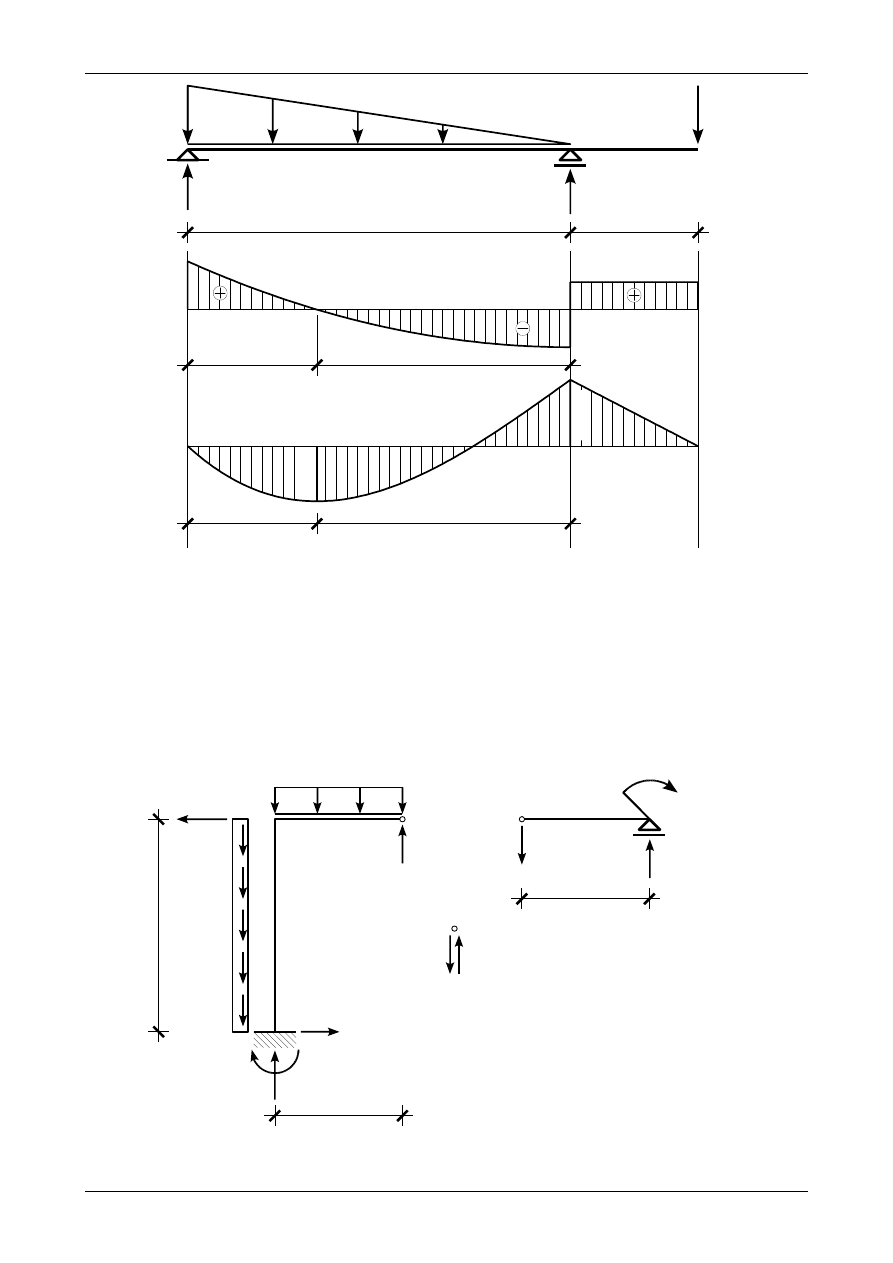
2.9. Odpowiedź do zadania 2/9

Rysunek 2.9 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej. Ten

sam rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego.

2.10. Odpowiedź do zadania 2/10

Rysunek 2.10 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej. Ten

sam rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

7

3,0

A

B

12,0 kN/m

81,0 kNm

[m]

3,0

1,0

C

D

27,0 kNm

9,0 kN

B

B

27,0 kN

2

7,

0

k

N

27

,0

k

N

27,0 kN

27,0 kN

3,0

[m]

3,0

1,0

A

B

C

D

12,0 kN/m

27,0 kNm

27,0 kN

9,0 kN

81,0 kNm

T(x) [kN]

M(x) [kNm]

2,25

0,75

2,25

0,75

27,0

0,0

9

,0

27,0

81

,0

0,

0

30

,3

8

a)

b)

Rys. 2.8. Belka złożona. a) prawidłowe wartości i zwroty reakcji podporowych, b) wykresy siły poprzecznej oraz

momentu zginającego

A

B

C

20,0 kN

17,0 kN/m

6,0

2,0

[m]

60,67 kN

10,33 kN

2,70

3,30

2,70

3,30

T(x) [kN]

M(x) [kNm]

10

,3

3

40

,6

7

20,0

0,

0

18

,6

0

40

,0

0,

0

Rys. 2.9. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

8

1

8,

7

5

A

B

C

15,0 kN

21,0 kN/m

4,5

1,5

[m]

26,5 kN

35,75 kN

T(x) [kN]

M(x) [kNm]

26

,5

20

,7

5

15,0

0,

0

22

,5

1,518

2,982

1,518

2,982

0,

0

Rys. 2.10. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

3. Ramy

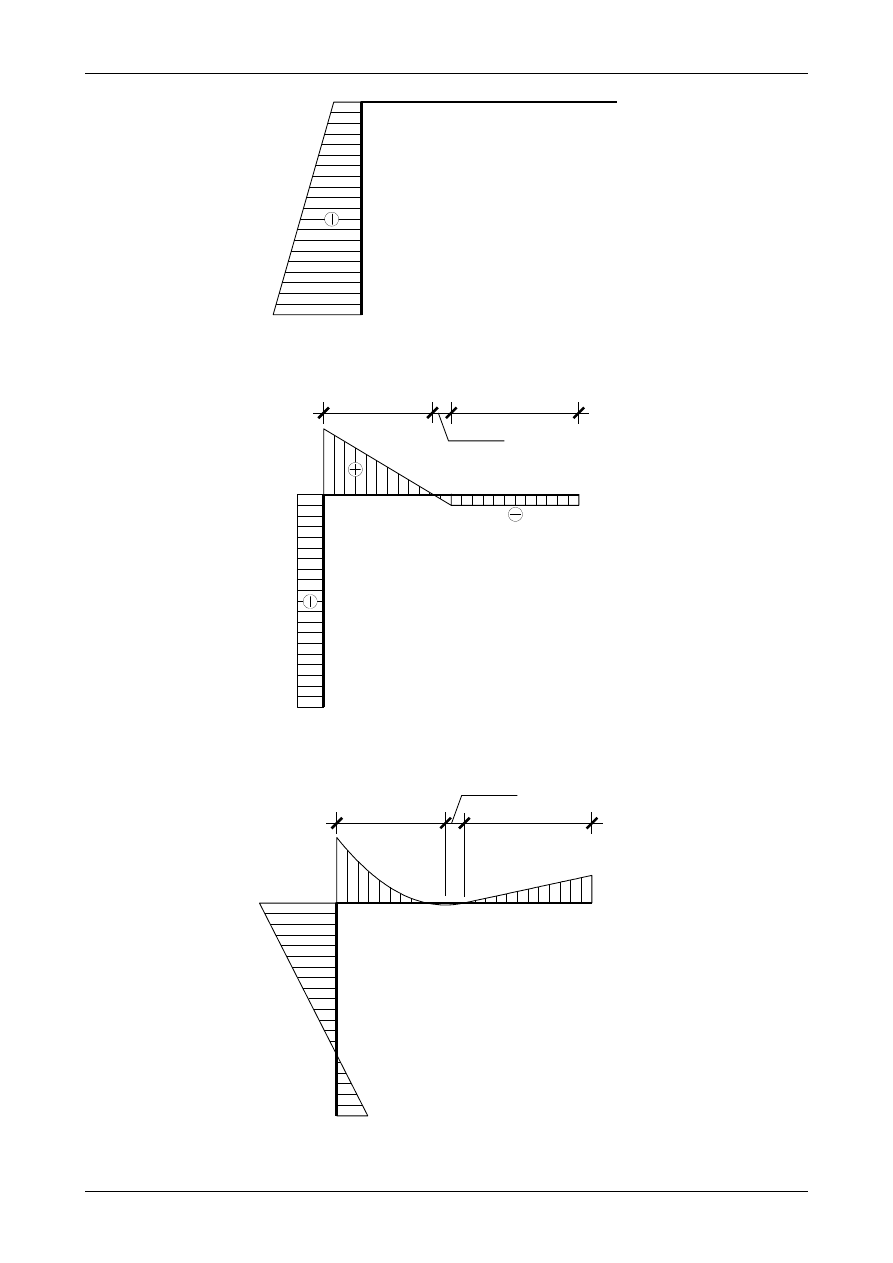
3.1. Odpowiedź do zadania 3/1

Rysunek 3.1 przedstawia prawidłowe wartości i zwroty reakcji podporowych ramie ortogonalnej,

rysunek 3.2 przedstawia wykres siły normalnej, rysunek 3.3 wykres siły poprzecznej, rysunek 3.4 wykres
momentu zginającego natomiast rysunek 3.5 przedstawia węzeł B będący w równowadze.

3,0

[m]

5,

0

A

B

C

18,0 kN/m

2

0,

0

k

N

/m

16,0 kN

146,0 kN

16,0 kN

23,0 kNm

24,0 kNm

C

D

8,0 kN

8,0 kN

8,0 kN

C

8,0 kN 8,0 kN

3,0

Rys. 3.1. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

9

N [kN]

0,0

146,0

46,0

Rys. 3.2. Wykres siły normalnej w ramie ortogonalnej

T [kN]

2,556

[m]

3,0

0,4444

16

,0

46

,0

8,0

Rys. 3.3. Wykres siły poprzecznej w ramie ortogonalnej

M [kNm]

23,0

57,0

2,556

[m]

3,0

0,4444

57

,0

1,

77

8

0,

0

24

,0

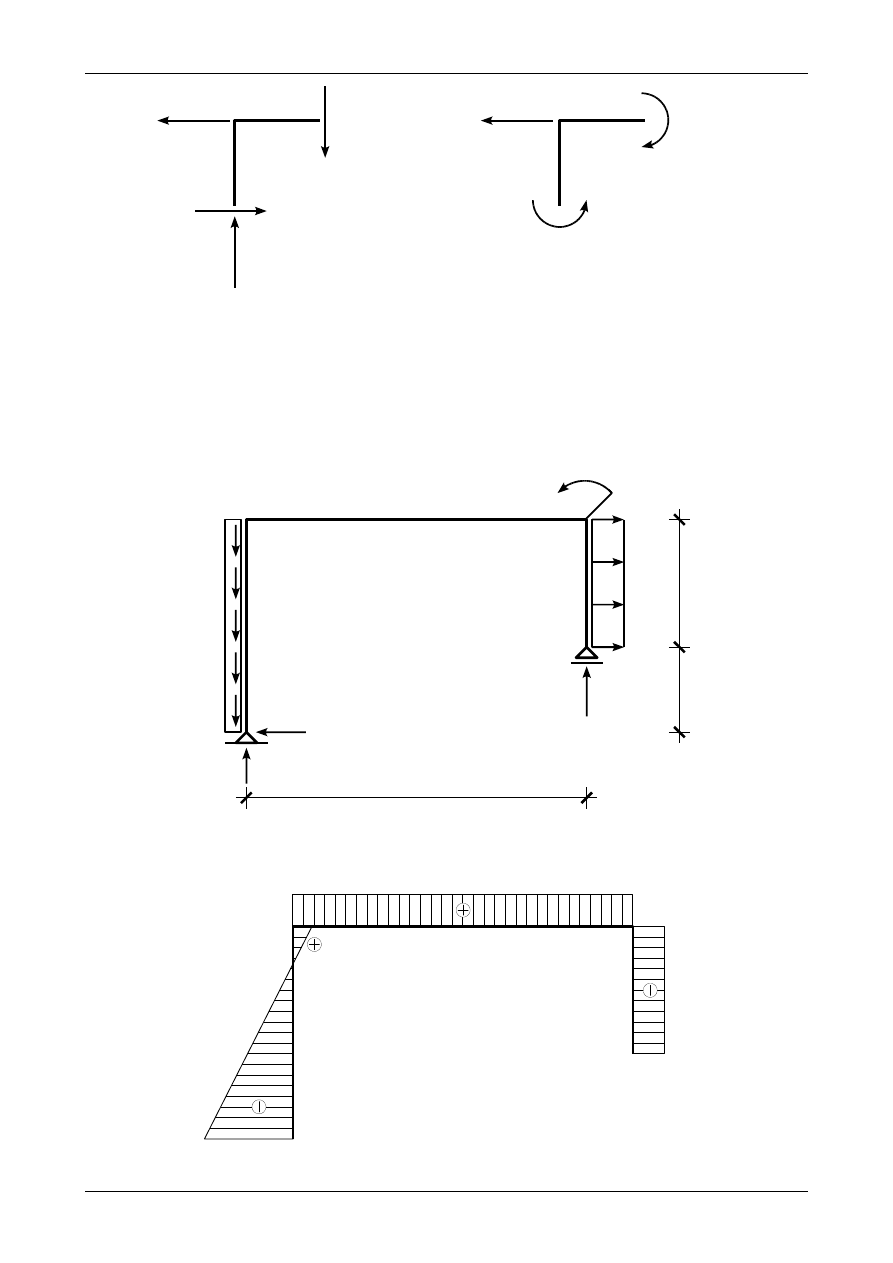
Rys. 3.4. Wykres momentu zginającego w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

10

B

B

16,0 kN

16,0 kN

4

6,

0

kN

46

,0

k

N

16,0 kN

57,0 kNm

57,0 kNm

Rys. 3.5. Węzeł B

3.2. Odpowiedź do zadania 3/2

Rysunek 3.6 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.7 przedstawia wykres siły normalnej, rysunek 3.8 wykres siły poprzecznej, rysunek 3.9 wykres
momentu zginającego natomiast rysunek 3.10 przedstawia węzły B i C będące w równowadze.

8,0

[m]

3

,0

2

,0

20

,0

k

N

/m

15

,0

k

N

/m

19,0 kNm

A

B

C

D

45,0 kN

82,69 kN

17,31 kN

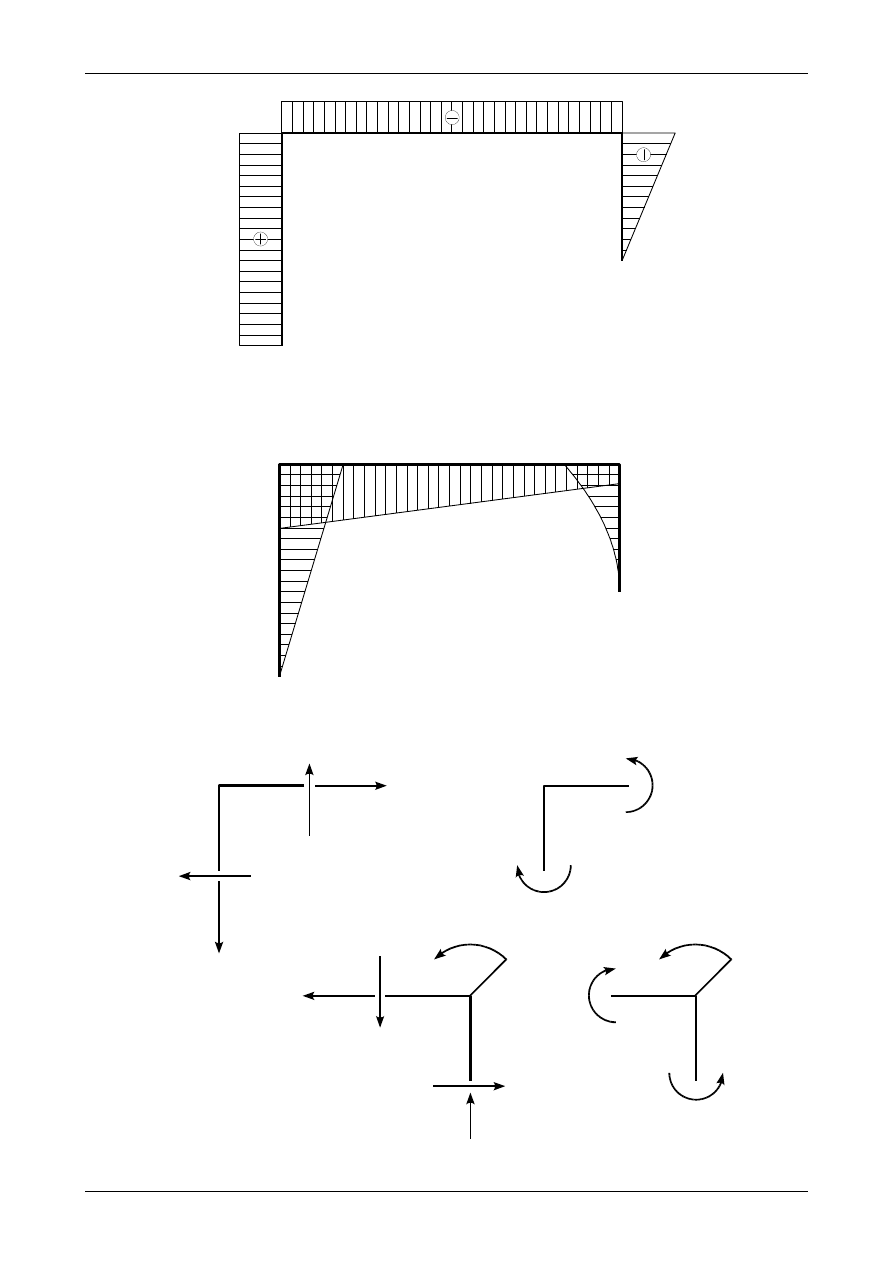
Rys. 3.6. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

N [kN]

82,69

17,31

45,0

1

7,

3

7

Rys. 3.7. Wykres siły normalnej w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

11

T [kN]

17,31

45

,0

0,0

45,0

Rys. 3.8. Wykres siły poprzecznej w ramie ortogonalnej

M [kNm]

0,0

0,0

225,0

22

5,

0

8

6,

5

2

67,5

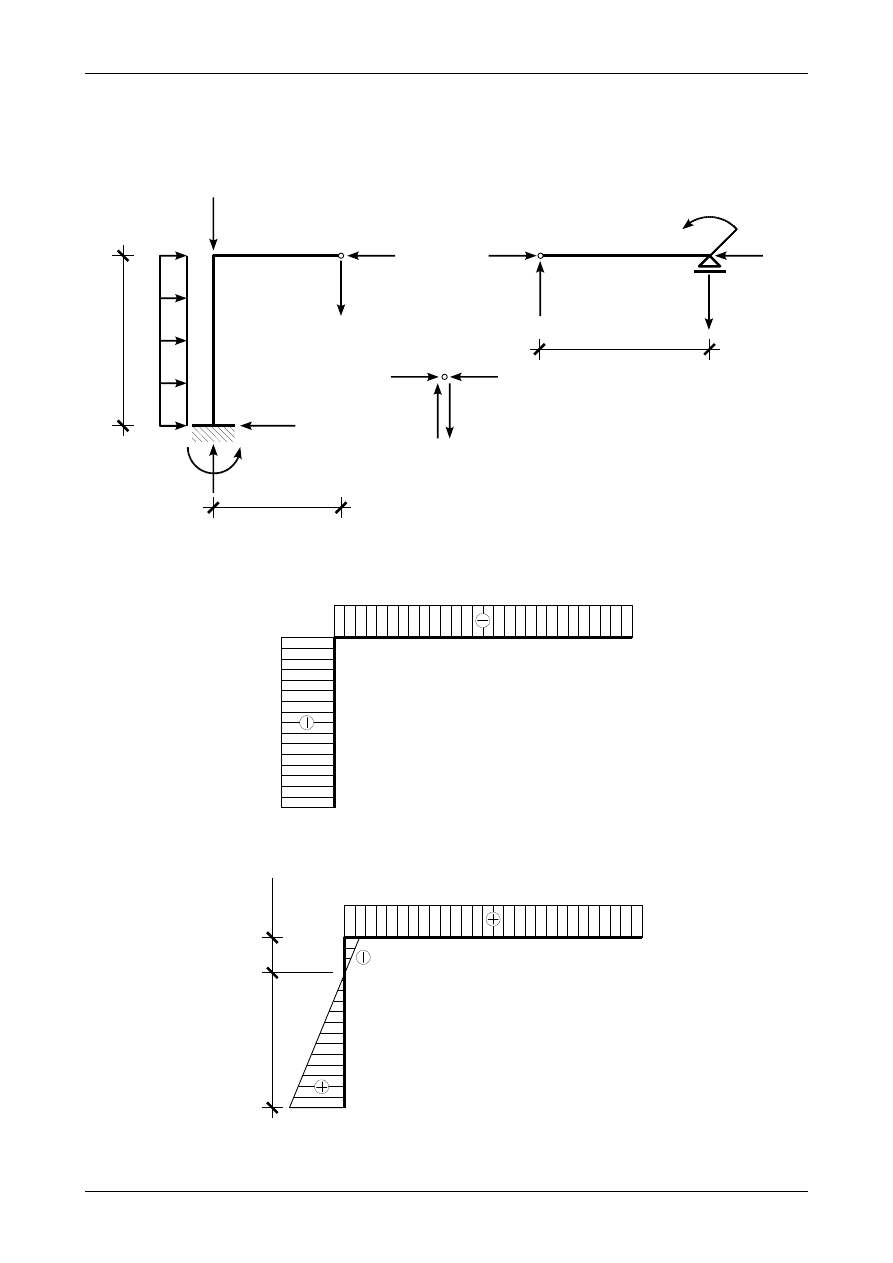
Rys. 3.9. Wykres momentu zginającego w ramie ortogonalnej

B

B

45,0 kN

17

,3

1

kN

225,0 kNm

17

,3

1

kN

45,0 kN

225,0 kNm

C

C

67,5 kNm

86,52 kNm

17

,3

1

kN

45,0 kN

19,0 kNm

19,0 kNm

17,31 kN

45,0 kN

Rys. 3.10. Węzły B i C

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

12

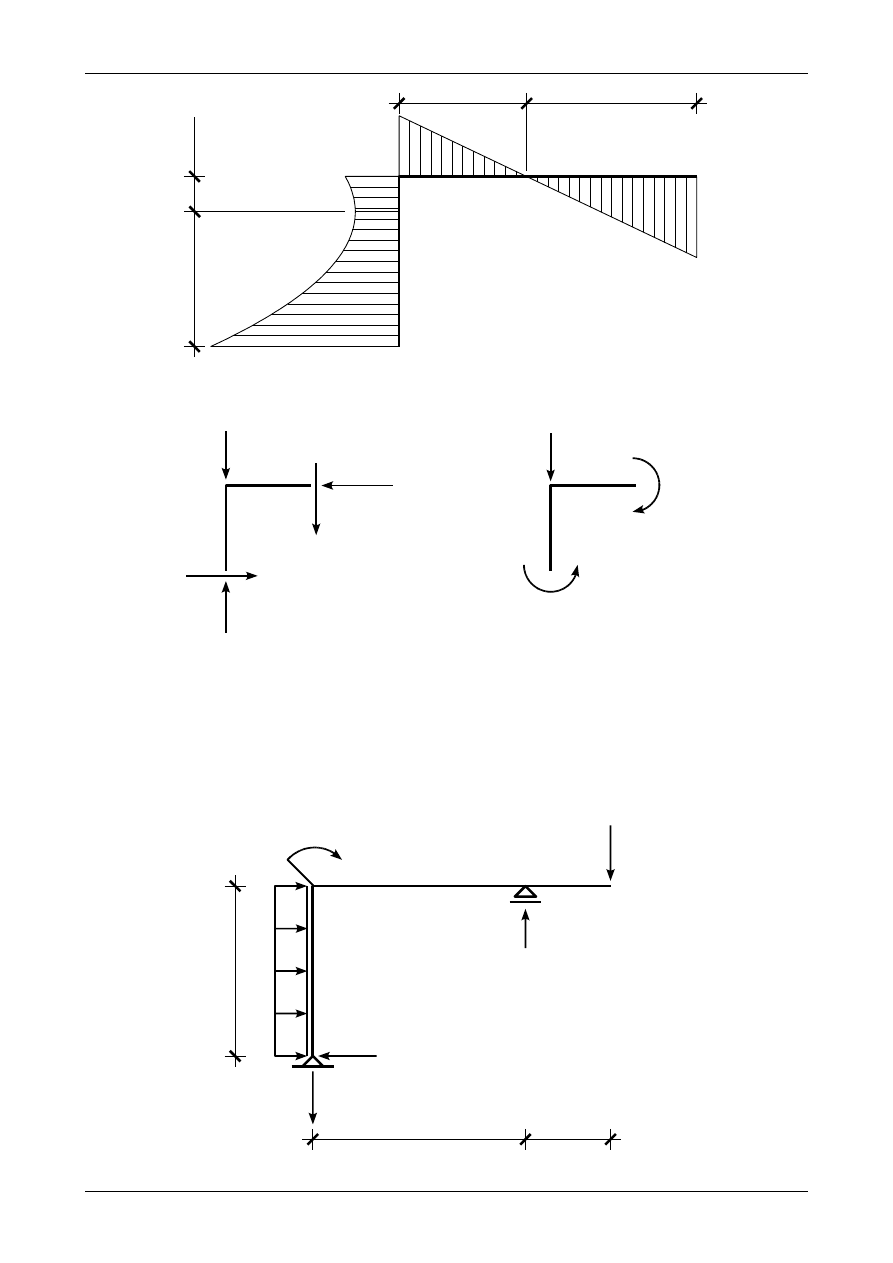
3.3. Odpowiedź do zadania 3/3

Rysunek 3.11 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.12 przedstawia wykres siły normalnej, rysunek 3.13 wykres siły poprzecznej, rysunek 3.14 wykres
momentu zginającego natomiast rysunek 3.15 przedstawia węzeł B będący w równowadze.

A

B

C

[m]

3,0

4,

0

24

,0

k

N

/m

30,0 kN

45,0 kN

76,0 kN

157,0 kNm

C

D

4,0

60,0 kNm

20,0 kN

15,0 kN

C

15,0 kN

15,0 kN

20,0 kN

20,0 kN

20,0 kN

20,0 kN

15,0 kN

15,0 kN

Rys. 3.11. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

N [kN]

20,0

45

,0

Rys. 3.12. Wykres siły normalnej w ramie ortogonalnej

T [kN]

[m]

15,0

20,0

76,0

3

,1

6

7

0

,8

3

33

Rys. 3.13. Wykres siły poprzecznej w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

13

M [kNm]

[m]

45

,0

60

,0

3,0

4,0

3,

16

7

0,

83

33

45,0

157,0

36,67

Rys. 3.14. Wykres momentu zginającego w ramie ortogonalnej

B

B

20,0 kN

45,0 kNm

1

5,

0

kN

45,0 kNm

30,0 kN

30,0 kN

20,0 kN

45,0 kN

Rys. 3.15. Węzeł B

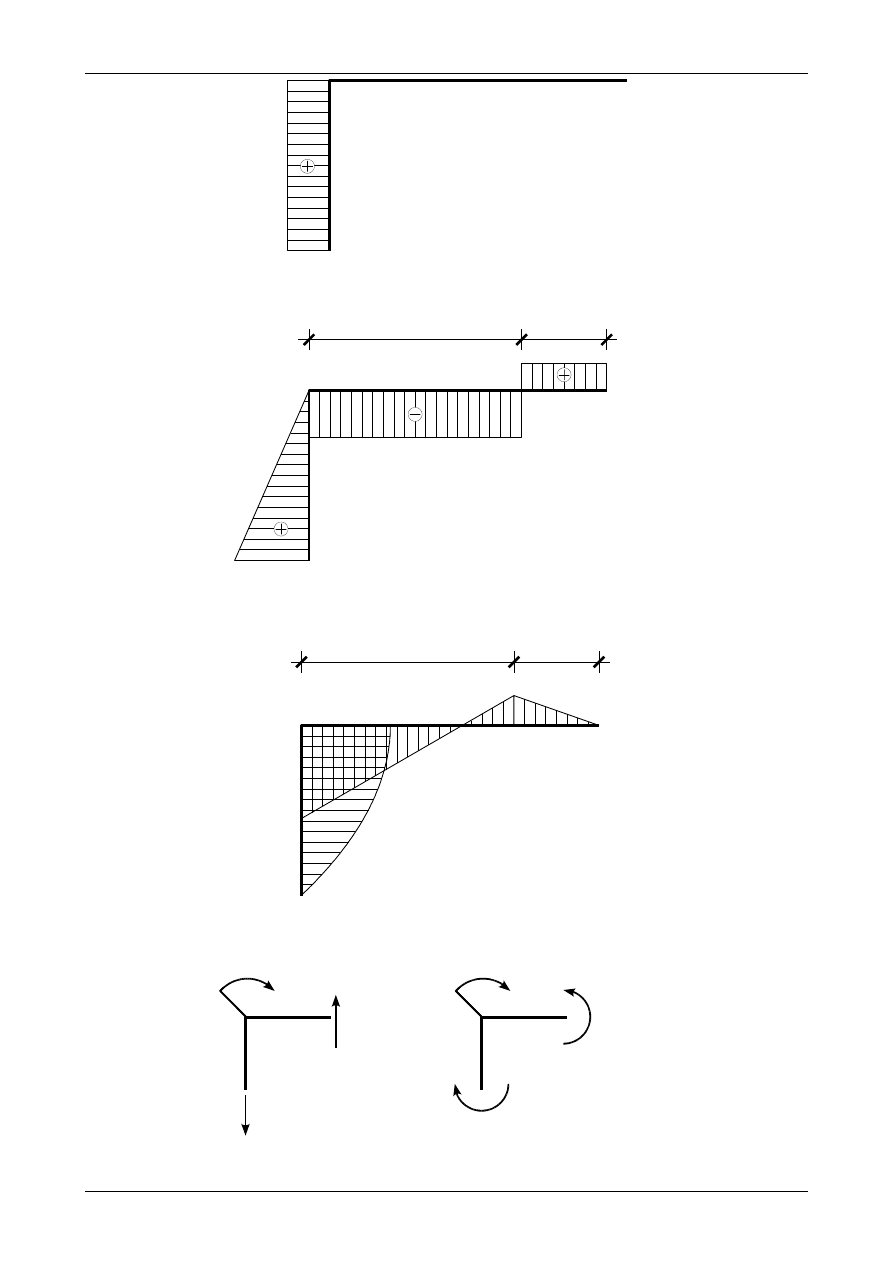
3.4. Odpowiedź do zadania 3/4

Rysunek 3.16 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.17 przedstawia wykres siły normalnej, rysunek 3.18 wykres siły poprzecznej, rysunek 3.19 wykres
momentu zginającego natomiast rysunek 3.20 przedstawia węzeł B będący w równowadze.

25

,0

k

N

/m

35,0 kN

5,0

[m]

2,0

4,

0

A

B

C

D

100,0 kN

92,8 kN

57,8 kN

19,0 kNm

Rys. 3.16. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

14

N [kN]

0,0

57

,8

Rys. 3.17. Wykres siły normalnej w ramie ortogonalnej

T [kN]

100,0

0,0

57,8

35,0

5,0

2,0

[m]

Rys. 3.18. Wykres siły poprzecznej w ramie ortogonalnej

M [kNm]

5,0

2,0

[m]

0,

0

70

,0

21

9,

0

200,0

0,0

Rys. 3.19. Wykres momentu zginającego w ramie ortogonalnej

B

B

200,0 kNm

57

,8

k

N

19,0 kNm

57,8 kN

19,0 kNm

219,0 kNm

Rys. 3.20. Węzeł B

Dr inż. Janusz Dębiński

Budownictwo

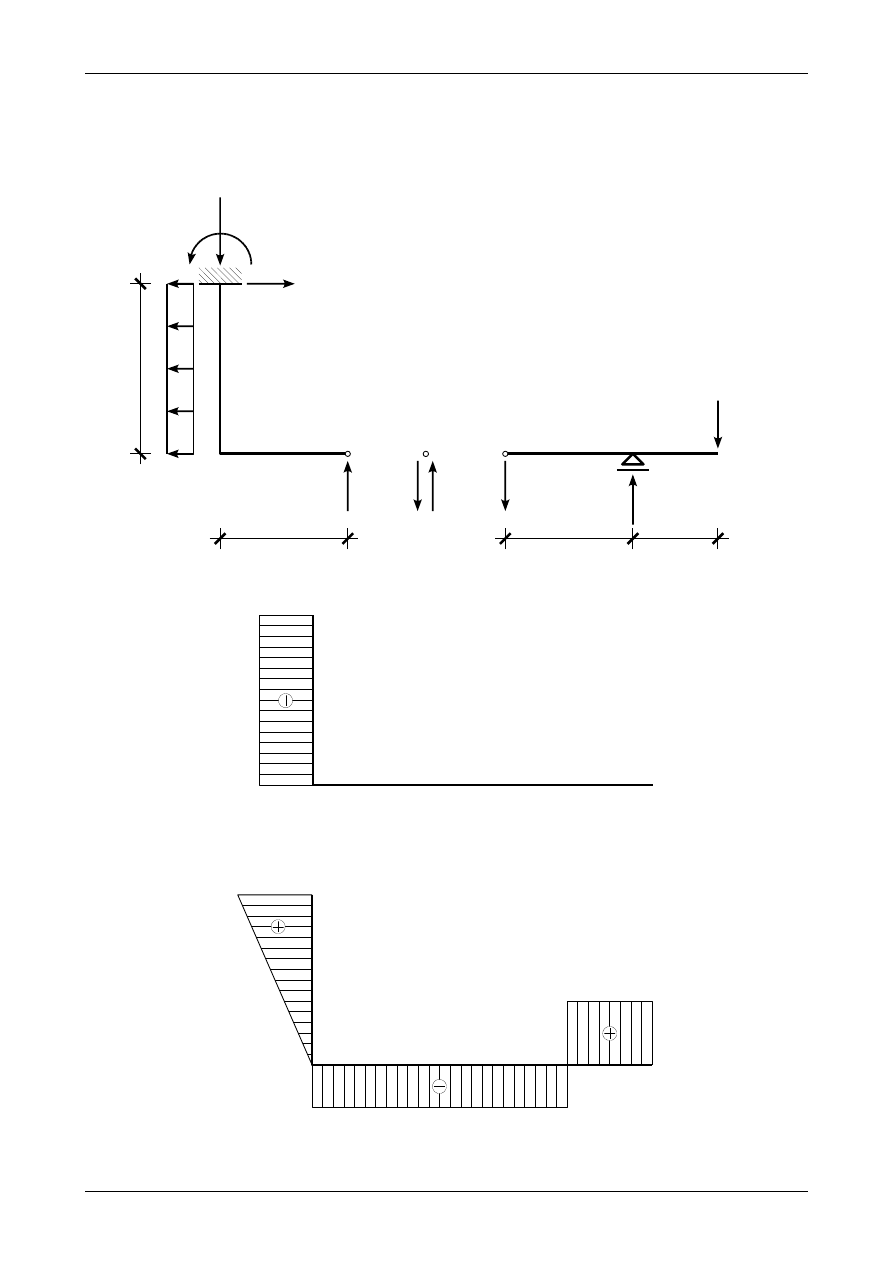
WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

15

3.5. Odpowiedź do zadania 3/5

Rysunek 3.21 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.22 przedstawia wykres siły normalnej, rysunek 3.23 wykres siły poprzecznej, rysunek 3.24 wykres
momentu zginającego natomiast rysunek 3.25 przedstawia węzeł B będący w równowadze.

A

B

C

3,0

4,

0

24

,0

k

N

/m

14,0 kN

96,0 kN

150,0 kNm

C

D

E

[m]

3,0

2,0

21,0 kN

35,0 kN

C

14,0 kN

14,0 kN

14

,0

k

N

14

,0

k

N

Rys. 3.21. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

N [kN]

14

,0

0,0

Rys. 3.22. Wykres siły normalnej w ramie ortogonalnej

T [kN]

96,0

0,0

14,0

21,0

Rys. 3.23. Wykres siły poprzecznej w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

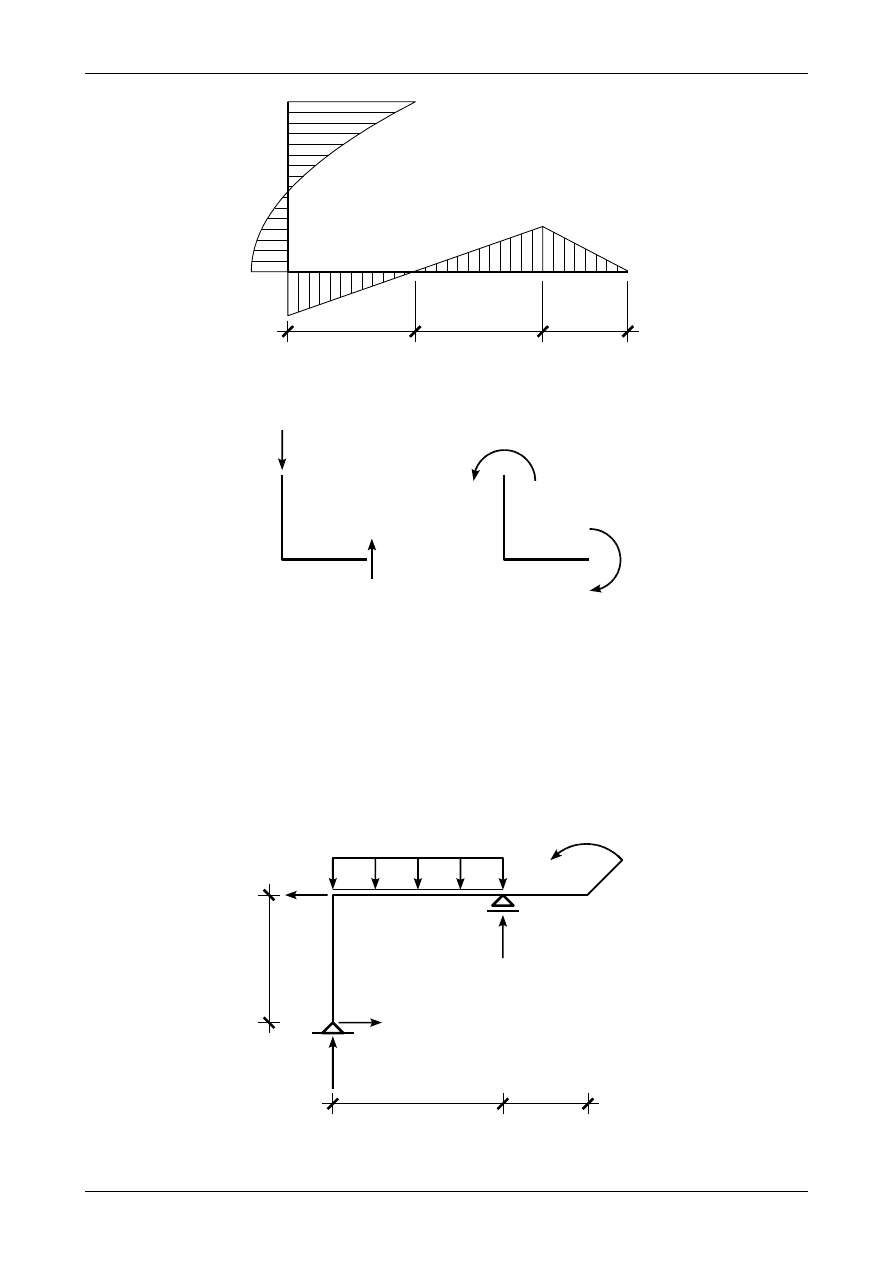
WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

16

M [kNm]

[m]

3,0

3,0

2,0

150,0

42,0

42

,0

0,

0

42

,0

0,

0

Rys. 3.24. Wykres momentu zginającego w ramie ortogonalnej

B

B

14,0 kN

42,0 kNm

14

,0

k

N

42,0 kNm

Rys. 3.25. Węzeł B

3.6. Odpowiedź do zadania 3/6

Rysunek 3.26 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.27 przedstawia wykres siły normalnej, rysunek 3.28 wykres siły poprzecznej, rysunek 3.29 wykres
momentu zginającego natomiast rysunek 3.30 przedstawia węzeł B będący w równowadze.

4,0

2,0

3,

0

34,0 kNm

26,0 kN/m

25,0 kN

A

B

C

D

[m]

25,0 kN

24,75 kN

79,25 kN

Rys. 3.26. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

17

N [kN]

79

,2

5

0,0

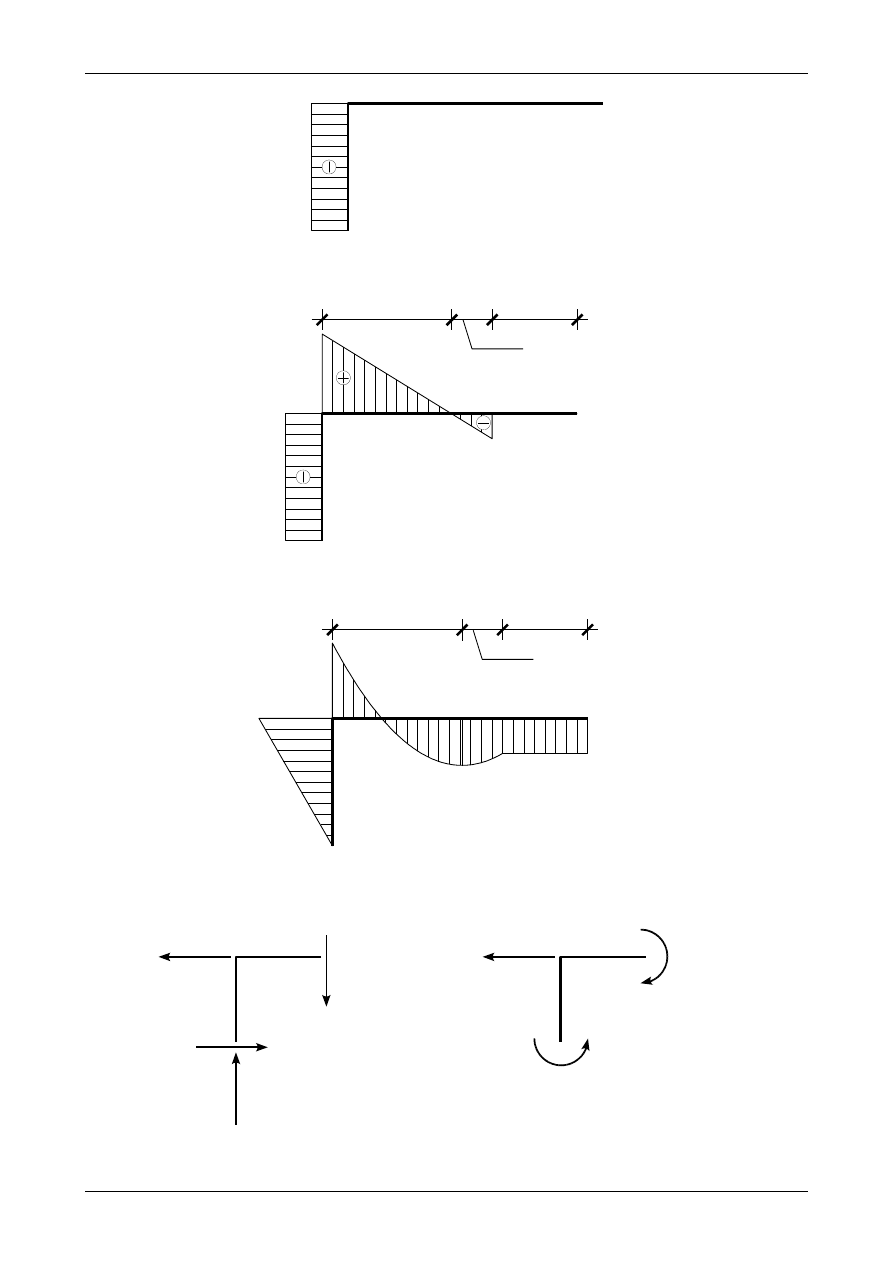
Rys. 3.27. Wykres siły normalnej w ramie ortogonalnej

T [kN]

25

,0

3,048

2,0

[m]

0,9519

7

9,

2

5

24

,7

5

0,0

Rys. 3.28. Wykres siły poprzecznej w ramie ortogonalnej

M [kNm]

0,0

75,0

3,048

2,0

[m]

75

,0

45

,7

8

34,0

0,9519

Rys. 3.29. Wykres momentu zginającego w ramie ortogonalnej

B

B

25,0 kN

75,0 kNm

79

,2

5

kN

75,0 kNm

25,0 kN

79

,2

5

kN

25,0 kN

Rys. 3.30. Węzeł B

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

18

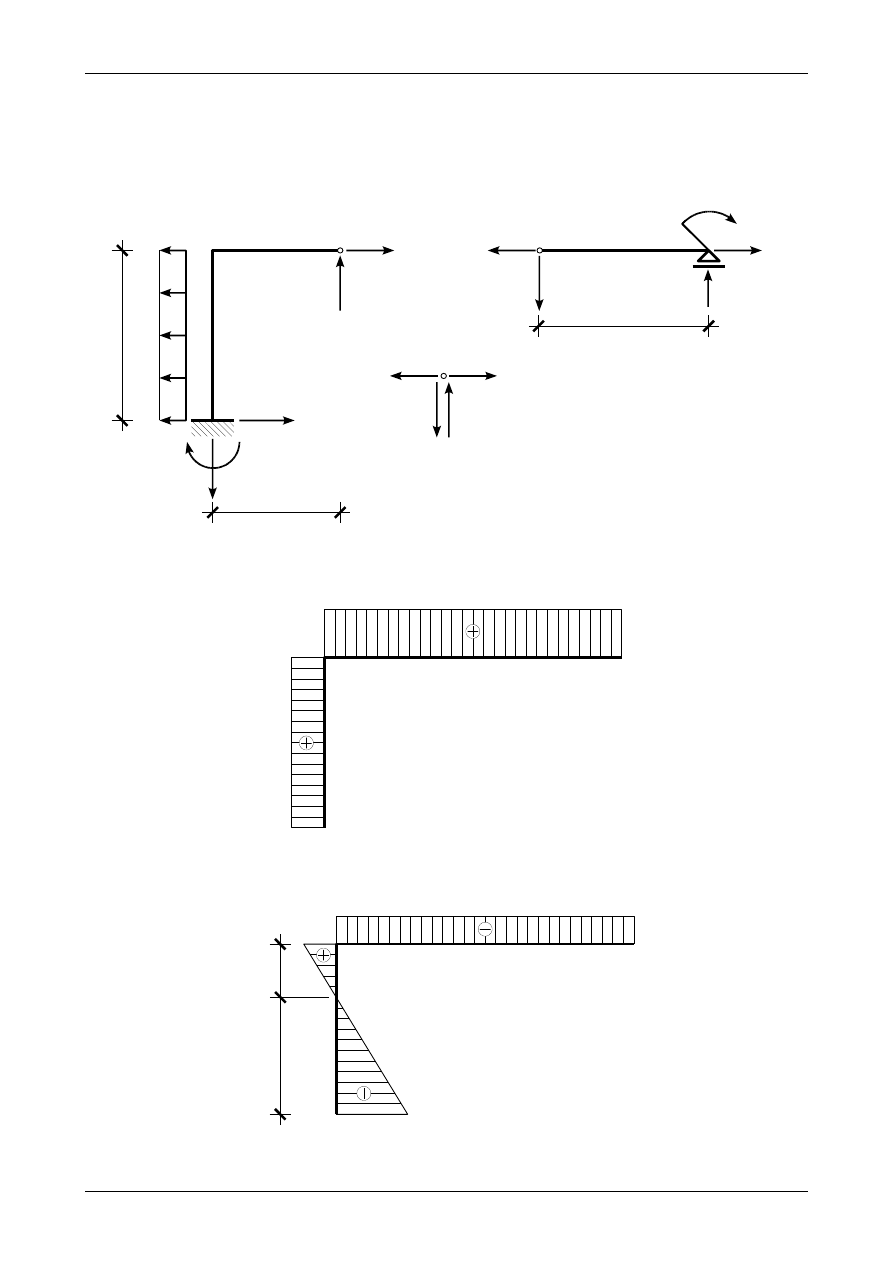
3.7. Odpowiedź do zadania 3/7

Rysunek 3.31 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.32 przedstawia wykres siły normalnej, rysunek 3.33 wykres siły poprzecznej, rysunek 3.34 wykres
momentu zginającego natomiast rysunek 3.35 przedstawia węzeł B będący w równowadze.

A

B

C

[m]

3,0

4,

0

24

,0

k

N

/m

7,5 kN

44,0 kN

70,5 kNm

C

D

4,0

20,0 kN

7,5 kN

C

7,5 kN

20,0 kN

20,0 kN

20,0 kN

20,0 kN

30,0 kNm

7,5 kN

7,5 kN

7,5 kN

Rys. 3.31. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

N [kN]

20,0

7,

5

Rys. 3.32. Wykres siły normalnej w ramie ortogonalnej

T [kN]

[m]

7,5

20,0

44,0

2,

75

1,

25

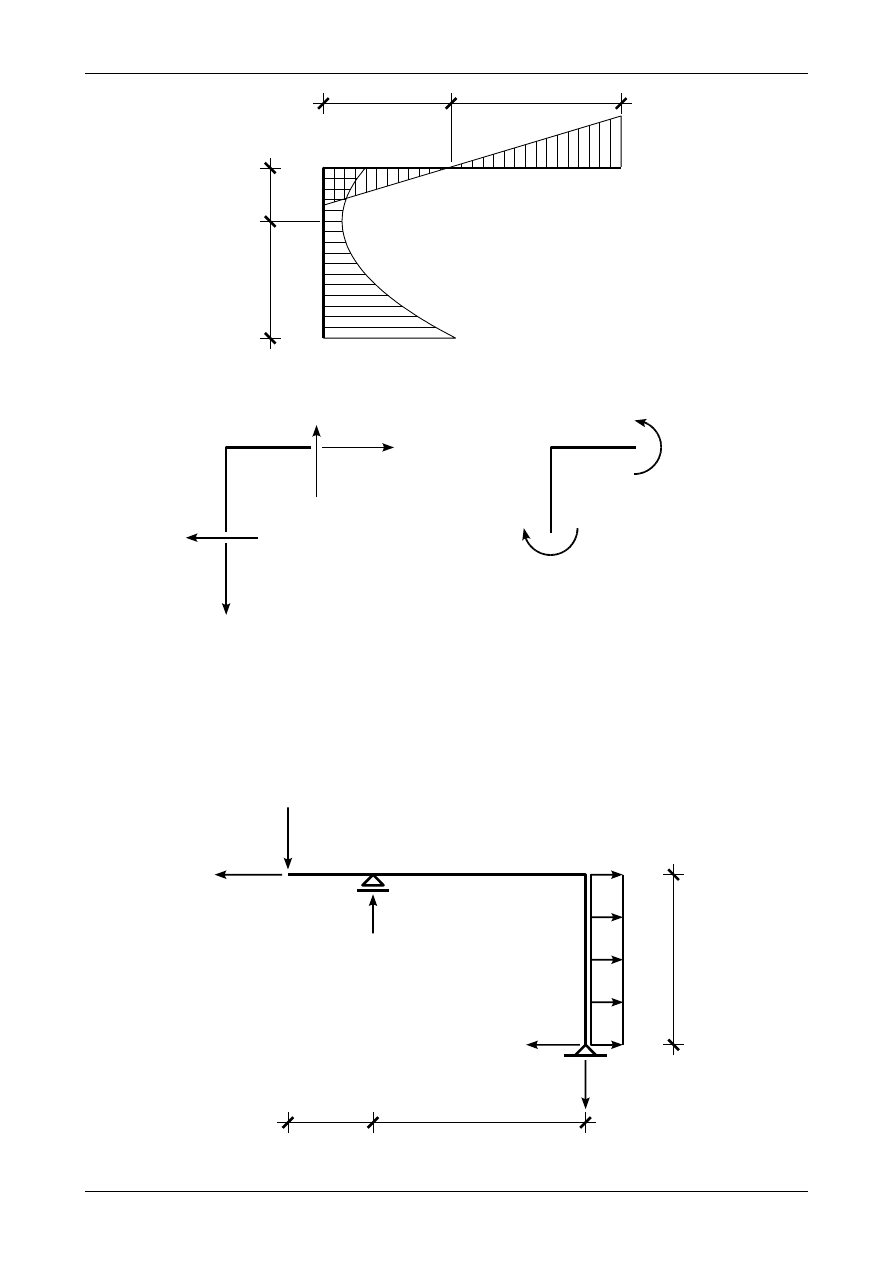
Rys. 3.33. Wykres siły poprzecznej w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

19

M [kNm]

[m]

22

,5

3

0,

0

3,0

4,0

22,5

70,5

2,

75

1,

25

10,0

0,

0

Rys. 3.34. Wykres momentu zginającego w ramie ortogonalnej

B

B

20,0 kN

22,5 kNm

7,

5

kN

22,5 kNm

7,

5

k

N

20,0 kN

Rys. 3.35. Węzeł B

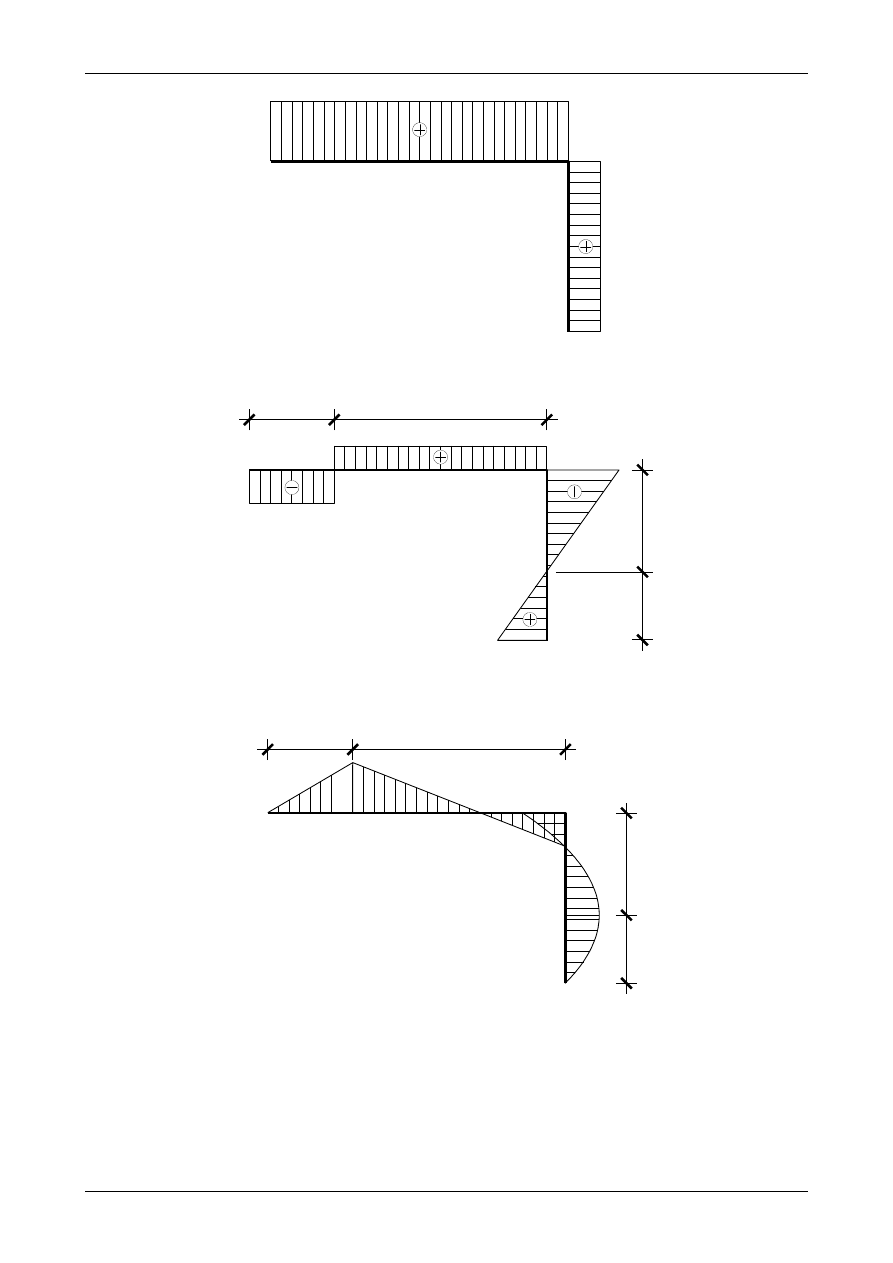
3.8. Odpowiedź do zadania 3/8

Rysunek 3.36 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej,

rysunek 3.37 przedstawia wykres siły normalnej, rysunek 3.38 wykres siły poprzecznej, rysunek 3.39 wykres
momentu zginającego natomiast rysunek 3.40 przedstawia węzeł B będący w równowadze.

15

,0

k

N

/m

18,0 kN

5,0

[m]

2,0

4,

0

A

B

C

D

36,0 kN

30,0 kN

24,0 kN

12,0 kN

Rys. 3.36. Prawidłowe wartości i zwroty reakcji podporowych w ramie ortogonalnej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

20

N [kN]

36,0

12

,0

Rys. 3.37. Wykres siły normalnej w ramie ortogonalnej

T [kN]

[m]

18,0

12,0

5,0

2,0

2,

4

1,

6

36,0

24,0

Rys. 3.38. Wykres siły poprzecznej w ramie ortogonalnej

36

,0

M [kNm]

[m]

5,0

2,0

0,

0

24

,0

24,0

2,

4

1,

6

19,2

0,0

Rys. 3.39. Wykres momentu zginającego w ramie ortogonalnej

3.9. Odpowiedź do zadania 3/9

Rysunek 3.41 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie płaskiej, rysu-

nek 3.42 przedstawia wykres siły normalnej, rysunek 3.43 wykres siły poprzecznej, rysunek 3.44 wykres
momentu zginającego natomiast rysunek 3.45 przedstawia węzeł B będący w równowadze.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

21

B

B

24,0 kNm

1

2,

0

k

N

36,0 kN

24,0 kNm

1

2,

0

k

N

36,0 kN

Rys. 3.40. Węzeł B

C

5,0

[m]

B

A

3,

0

2,

0

17,0 kN

10

,0

k

N

/m

14,0

kN

/m

101,6 kN

30,62 kN

47,62 kN

- 5,8

31 -

Rys. 3.41. Prawidłowe wartości i zwroty reakcji podporowych w ramie płaskiej

N[kN]

101,6

81,60

82

,8

3

40

,8

3

Rys. 3.42. Wykres siły normalnej w ramie płaskiej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

22

3,79

0

2,04

1

T[kN]

30

,6

2

45

,5

0

24

,5

0

Rys. 3.43. Wykres siły poprzecznej w ramie płaskiej

[m]

3,79

0

2,04

1

M[kNm]

61

,2

4

25

,0

0

0,

0

0,0

61,24

Rys. 3.44. Wykres momentu zginającego w ramie płaskiej

B

17,0 kN

81,60 kN

30,62 kN

45

,5

0

kN

82,8

3 kN

B

17,0 kN

61,24 kNm

61,24 kNm

Rys. 3.45. Węzeł B

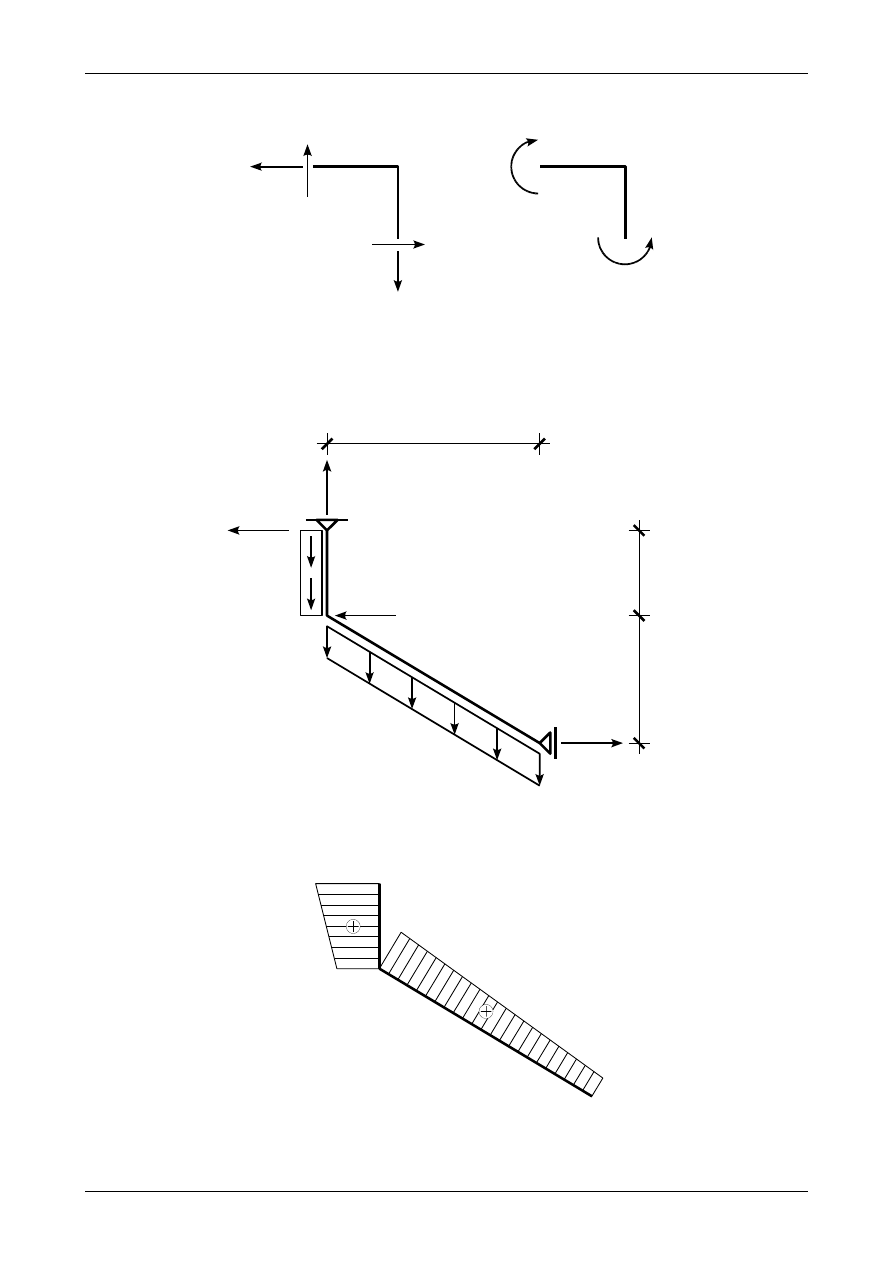
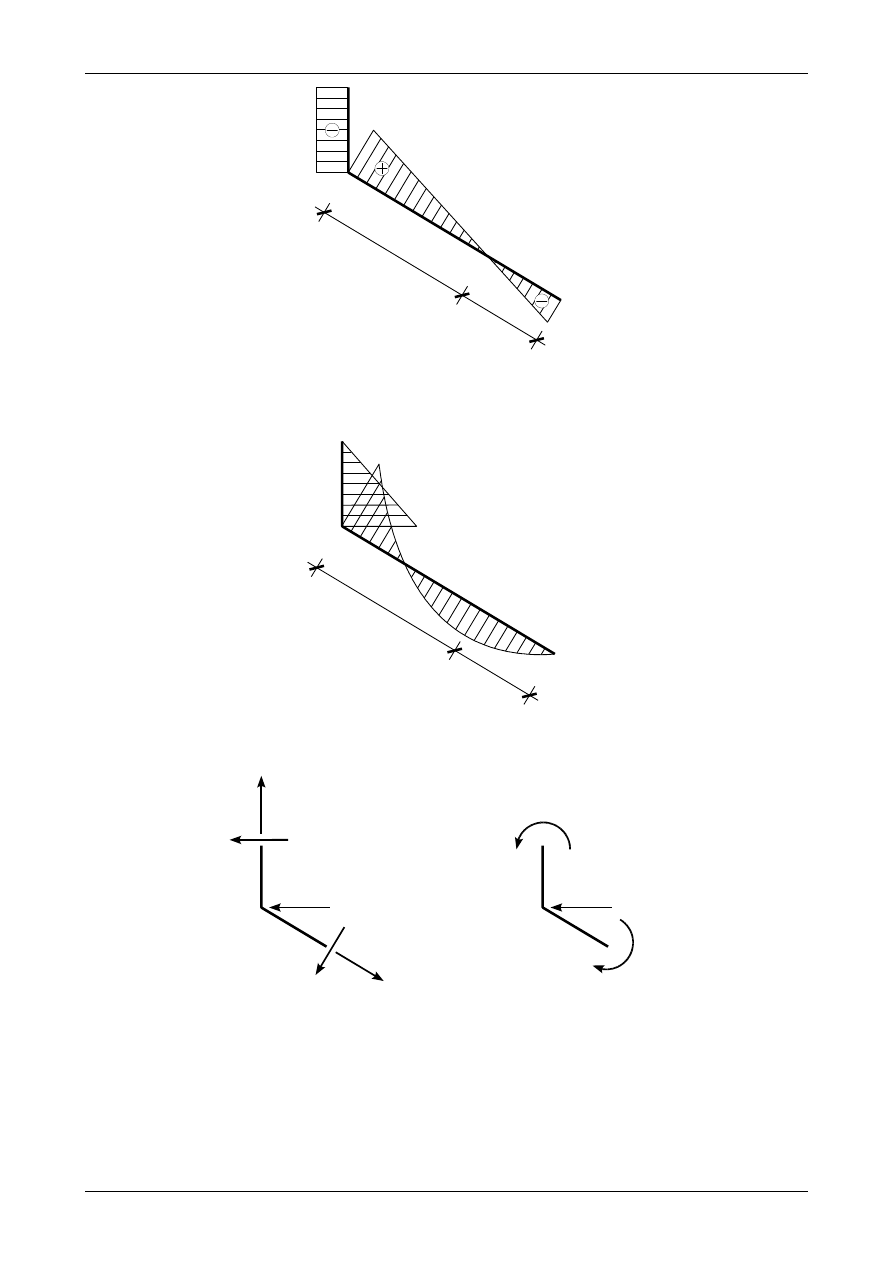
3.10. Odpowiedź do zadania 3/10

Rysunek 3.46 przedstawia prawidłowe wartości i zwroty reakcji podporowych w ramie płaskiej, rysu-

nek 3.47 przedstawia wykres siły normalnej, rysunek 3.48 wykres siły poprzecznej, rysunek 3.49 wykres
momentu zginającego natomiast rysunek 3.50 przedstawia węzeł B będący w równowadze.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

23

A

B

C

3,0

2,0

2,

5

[m]

16,0 kN/m

48,0 kN

67,2 kN

67,2 kN

Rys. 3.46. Prawidłowe wartości i zwroty reakcji podporowych w ramie płaskiej

N[kN]

67,2

51

,62

82

,35

Rys. 3.47. Wykres siły normalnej w ramie płaskiej

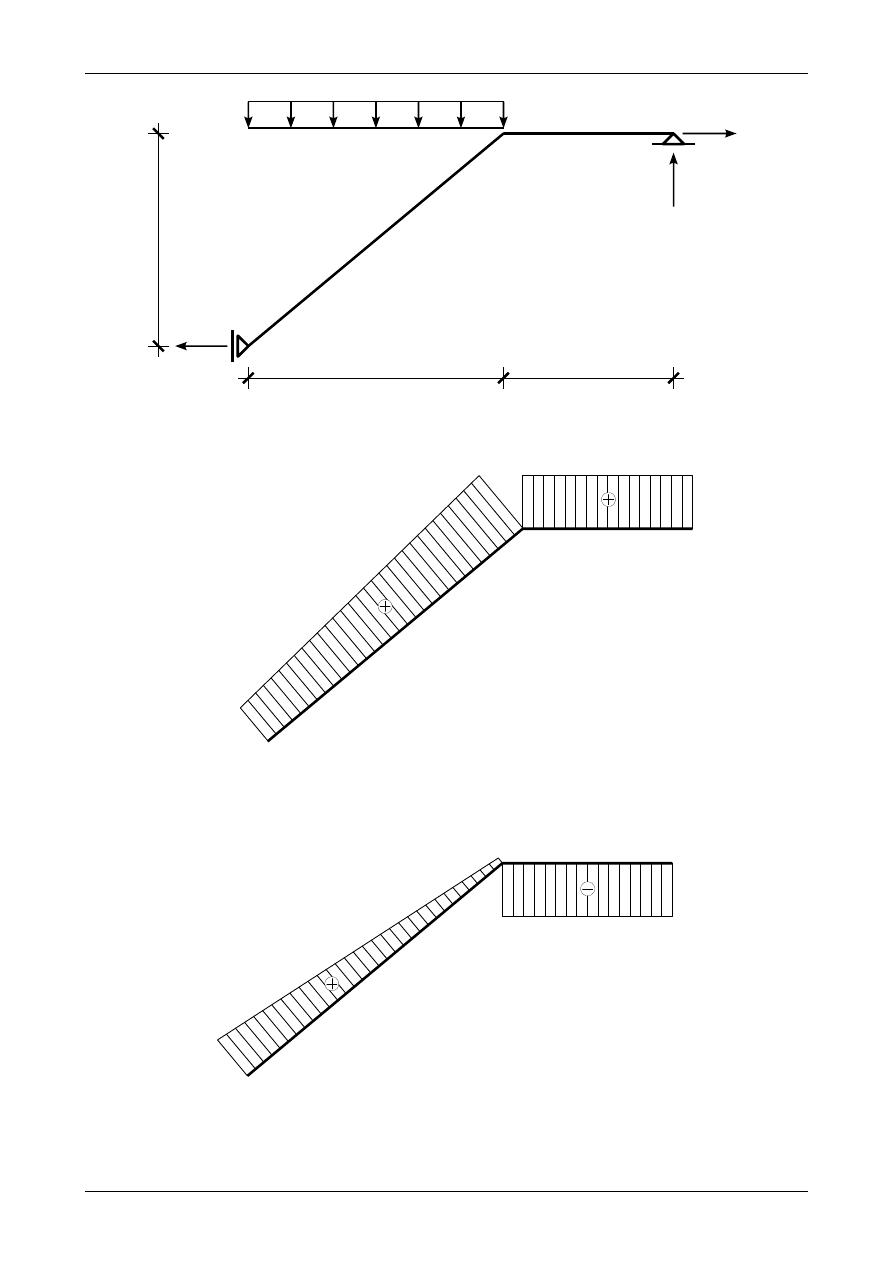
T[kN]

48,0

43

,02

6,1

48

Rys. 3.48. Wykres siły poprzecznej w ramie płaskiej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

24

M[kNm]

0,

0

96

,0

96

,0

0,0

Rys. 3.49. Wykres momentu zginającego w ramie płaskiej

B

67,2 kN

48

,0

k

N

6,1

48

kN

82

,35

kN

B

96,0 kNm

96,0 kNm

Rys. 3.50. Węzeł B

4. Charakterystyki geometryczne przekroju

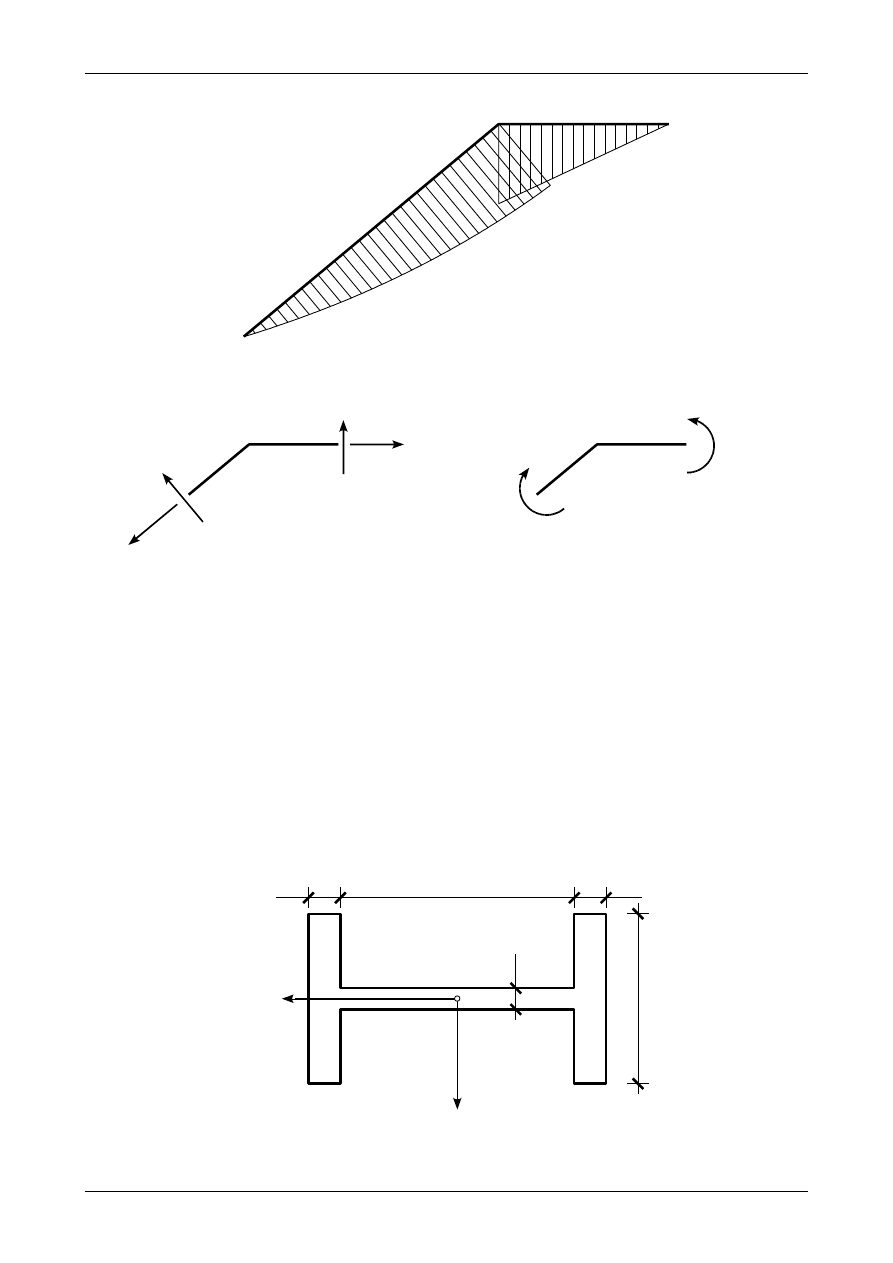
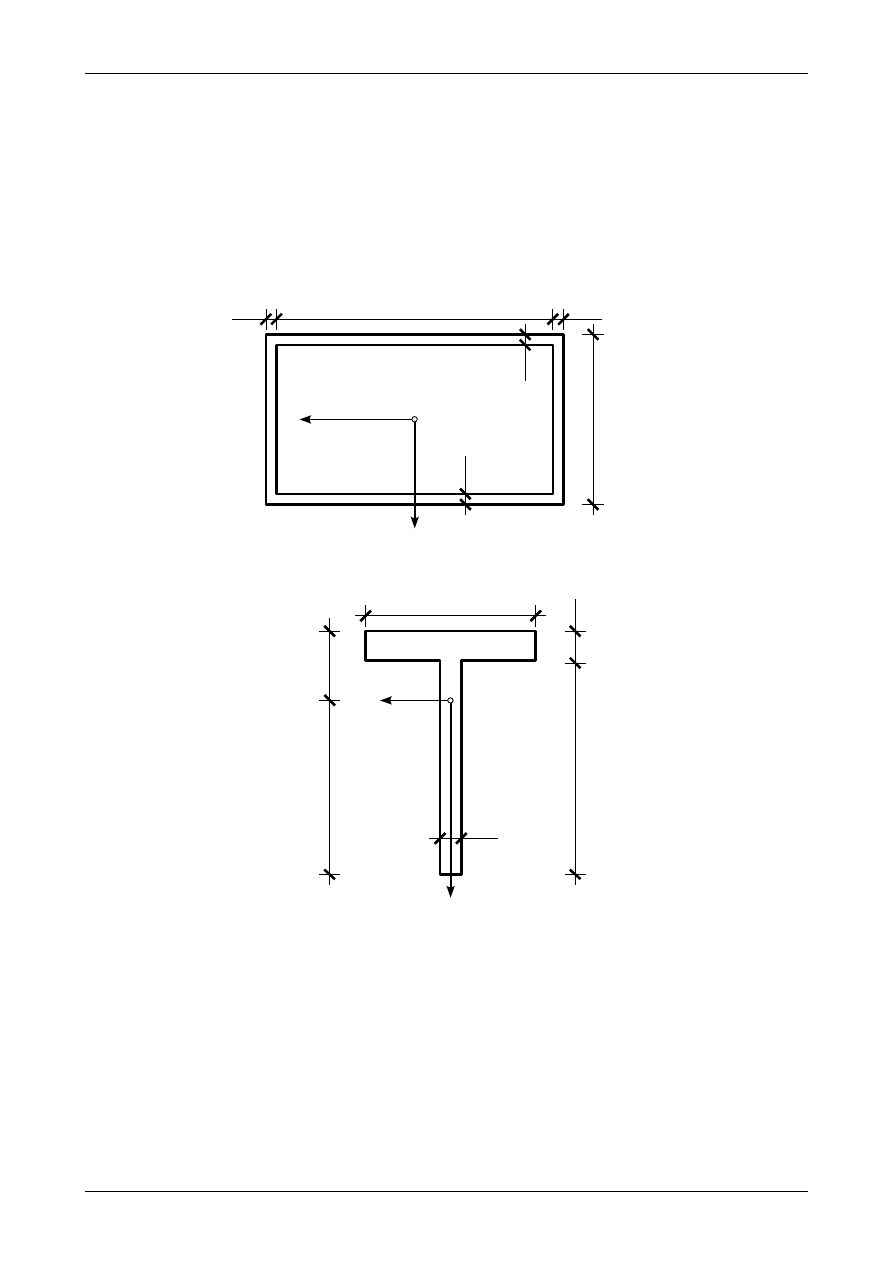
4.1. Odpowiedź do zadania 4/1

Rysunek 4.1 przedstawia wszystkie wymiary blachownicy dwuteowej wyrażone w centymetrach.

Główne momenty bezwładności przekroju wynoszą

J

Ygl

=

578,7 cm

4

,

J

Zgl

=

16620 cm

4

.

Y=Y

gl

Z=Z

gl

32,0

2,0

1,

0

12

,0

sc

2,0

[cm]

Rys. 4.1. Wymiary przekroju dwuteowego w centymetrach

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

25

4.2. Odpowiedź do zadania 4/2

Rysunek 4.2 przedstawia wszystkie wymiary blachownicy skrzynkowej wyrażone w centymetrach.

Główne momenty bezwładności przekroju wynoszą

J

Ygl

=

5361 cm

4

,

J

Zgl

=

33440 cm

4

.

Y=Y

gl

Z=Z

gl

36,0

1,

2

1

5,

0

sc

2,2

1

,2

2,2

[cm]

Rys. 4.2. Wymiary przekroju skrzynkowego w centymetrach

Y=Y

gl

Z=Z

gl

3,

0

1,2

12,0

sc

[cm]

12

,9

6

28

,0

4

38

,0

Rys. 4.3. Wymiary przekroju teowego w centymetrach

4.3. Odpowiedź do zadania 4/3

Rysunek 4.3 przedstawia wszystkie wymiary blachownicy teowej wyrażone w centymetrach. Rysunek

ten przedstawia także położenie głównych osi bezwładności. Główne momenty bezwładności przekroju
wynoszą

J

Ygl

=

5361 cm

4

,

J

Zgl

=

437,5 cm

4

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

26

4.4. Odpowiedź do zadania 4/4

Osiowe momenty bezwładności przekroju względem osi Y oraz Z zadanego układu współrzędnych

wynoszą

J

Y

=

10,0⋅7,0

3

12



3,5

2

⋅

10,0⋅7,0

−



6,0⋅3,0

3

36



3,0

2

⋅

1
2

⋅

6,0⋅3,0





6,117,97

2

⋅

4,79=1368 cm

4

,

J

Z

=

7,0⋅10,0

3

12



3,0

2

⋅

10,0⋅7,0

−



3,0⋅6,0

3

36



4,0

2

⋅

1
2

⋅

6,0⋅3,0





17,26,04

2

⋅

4,79=1243 cm

4

.

Dewiacyjny moment bezwładności kątownika nierównoramiennego 60x40x5 wynosi

J

Y0Z0

L

=

5,979 cm

4

.

Dewiacyjny moment bezwładności całego przekroju wynosi

J

YZ

=

0,03,0⋅3,5⋅10,0⋅7,0−

−



6,0

2

⋅

3,0

2

72



4,0⋅3,0⋅

1
2

⋅

6,0⋅3,0







5,9796,04⋅7,97⋅4,79=859,1 cm

4

.

4.5. Odpowiedź do zadnia 4/5

Osiowe momenty bezwładności przekroju względem osi Y oraz Z zadanego układu współrzędnych

wynoszą

J

Y

=

15,0⋅10,0

3

12



5,0

2

⋅

10,0⋅15,0

−



9,0⋅6,0

3

36



6,0

2

⋅

1
2

⋅

6,0⋅9,0







114,312,03

2

⋅

22,7=7373cm

4

,

J

Z

=

10,0⋅15,0

3

12



7,5

2

⋅

10,0⋅15,0

−



6,0⋅9,0

3

36



9,0

2

⋅

1
2

⋅

6,0⋅9,0







323,011,0

2

⋅

22,7=12010 cm

4

.

Dewiacyjny moment bezwładności kątownika nierównoramiennego 120x80x12 wynosi

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

27

J

Y0Z0

L

=

110,4 cm

4

.

Dewiacyjny moment bezwładności całego przekroju wynosi

J

YZ

=

0,07,5⋅5,0⋅10,0⋅15,0−

−



−

6,0

2

⋅

9,0

2

72



9,0⋅6,0⋅

1
2

⋅

6,0⋅9,0







110,411,0⋅12,03⋅22,7=7322cm

4

.

4.6. Odpowiedź do zadania 4/6

Osiowe momenty bezwładności przekroju względem osi Y oraz Z zadanego układu współrzędnych

wynoszą

J

Y

=

14,0⋅8,0

3

12



4,0

2

⋅

14,0⋅8,0

−



9,0⋅6,0

3

36



4,0

2

⋅

1
2

⋅

6,0⋅9,0







7,598,88

2

⋅

6,89=2454 cm

4

,

J

Z

=

8,0⋅14,0

3

12



7,0

2

⋅

14,0⋅8,0

−



6,0⋅9,0

3

36



9,0

2

⋅

1
2

⋅

6,0⋅9,0







44,98,85

2

⋅

6,89=5593 cm

4

.

Dewiacyjny moment bezwładności kątownika nierównoramiennego 80x40x6 wynosi

J

Y0Z0

L

=−

10,33 cm

4

.

Dewiacyjny moment bezwładności całego przekroju wynosi

J

YZ

=

0,04,0⋅7,0⋅14,0⋅8,0−

−



6,0

2

⋅

9,0

2

72



9,0⋅4,0⋅

1
2

⋅

6,0⋅9,0



−

−

10,338,88⋅8,85⋅6,89=2655cm

4

.

4.7. Odpowiedź do zadania 4/7

Aby główne moment bezwładności przekroju były sobie równe odległość pomiędzy środkami cięż-

kości dwuteowników musi wynosić

a=32,13 cm

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

28

4.8. Odpowiedź do zadania 4/8

Aby główne momenty bezwładności przekroju były sobie równe odległość pomiędzy ściankami ceow-

ników powinna wynosić

a=17,24 cm

.

4.9. Odpowiedź do zadania 4/9

Moment bezwładności przekroju względem osi środkowej Y

0

wynosi

J

Y0

=

267000−20,0

2

⋅

628,3=15680 cm

4

.

Moment bezwładności przekroju względem osi Y

2

wynosi

J

Y2

=

1568025,0

2

⋅

628,3=408 400 cm

4

.

4.10. Odpowiedź do zadania 4/10

Moment bezwładności przekroju względem osi środkowej Z

0

wynosi

J

Z0

=

64170−25,0

2

⋅

100,0=1670 cm

4

.

Moment bezwładności przekroju względem osi Z

2

wynosi

J

Z2

=

167020,0

2

⋅

100,0=41670 cm

4

.

5. Analiza stanu naprężenia i odkształcenia w punkcie przekroju pręta

5.1. Odpowiedź do zadania 5/1

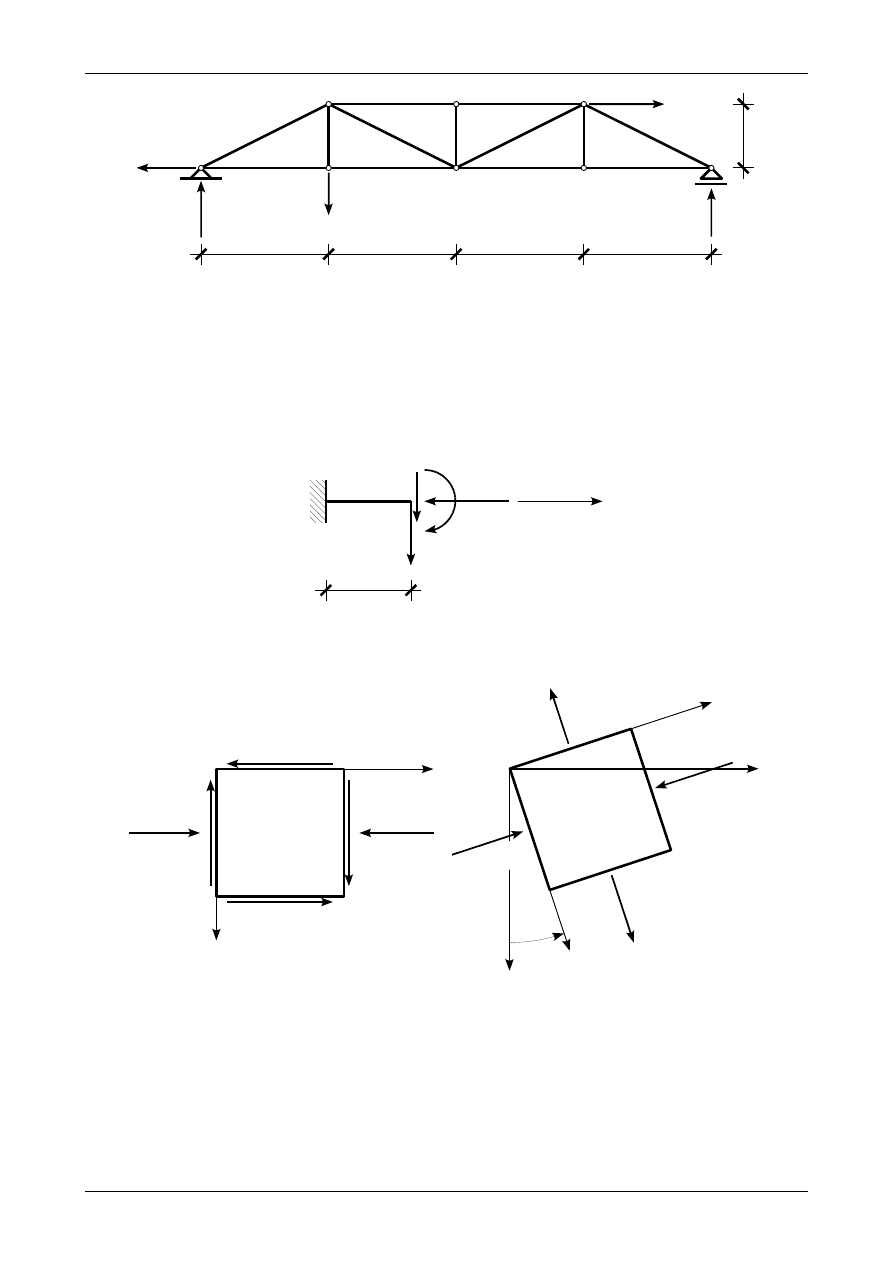
Rysunek 5.1 przedstawia prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej.

Siła normalna w pręcie oznaczonym literą R wyznaczona metodą Rittera wynosi

N

R

=

49,16 kN

.

Naprężenie normalne w pręcie wynosi



X

=

49,16

45,0

=

1,092

kN

cm

2

=

10,92 MPa

.

Całkowite wydłużenie pręta wynosi



L=

49,16⋅8,0

205⋅10

6

⋅

45,0⋅10

−

4

=

0,000426 m=0,426 mm

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

29

64,0 kN

26,0 kN

8,0

8,0

8,0

8,0

3

,0

R

[m]

26,0 kN

45,56 kN

18,44 kN

Rys. 5.1. Prawidłowe wartości i zwroty reakcji podporowych w kratownicy płaskiej

5.2. Odpowiedź do zadania 5/2

Rysunek 5.2 przedstawia prawidłowe wartości i zwroty sił przekrojowych, które działają w przekroju

α

-

α

. Graficzne interpretacje stanu naprężenia w układzie ZX oraz w układzie osi głównych przedstawia

rysunek 5.3.

1,0

[m]

Z=Z

0

=Z

gl

X

20,0 kN

32,0 kN

24,0 kNm

Rys. 5.2. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

36,7

6 MP

a

Z

X

32,79 MPa

12

,0

8

M

P

a

32,79 MPa

12

,0

8

M

P

a

12,08 MPa

12,08 MPa

Z

gl

X

gl

Z

X

18

,1

9

o

36,7

6 MP

a

3,9

70

M

P

a

3,9

70

M

P

a

Rys. 5.3. Graficzne interpretacje stanu naprężenia w punkcie A

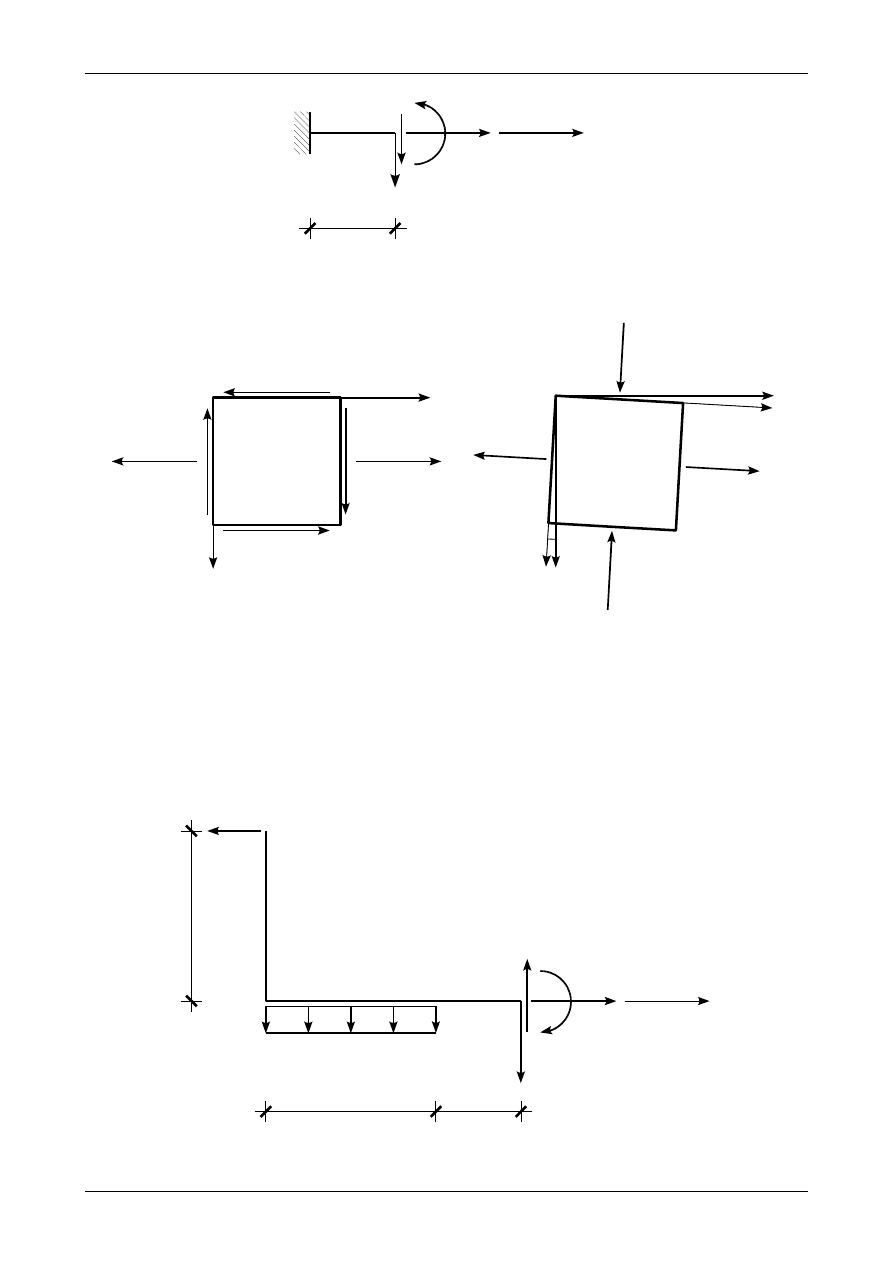
5.3. Odpowiedź na zadanie 5/3

Rysunek 5.4 przedstawia prawidłowe wartości i zwroty sił przekrojowych, które działają w przekroju

α

-

α

. Graficzne interpretacje stanu naprężenie w układzie ZX oraz w układzie osi głównych przedstawia

rysunek 5.5.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

30

Z=Z

0

=Z

gl

X

19,0 kN

8,0 kN

22,0 kNm

1,0

[m]

Rys. 5.4. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

Z

X

33,39 MPa

1

,8

6

2

M

P

a

33,39 MPa

1

,8

6

2

M

P

a

1,862 MPa

1,862 MPa

Z

gl

X

gl

Z

X

33,49 MPa

33,49 MPa

0,

1

03

5

M

P

a

0

,1

0

35

M

P

a

3,181

0

Rys. 5.5. Graficzne interpretacje stanu naprężenia w punkcie A

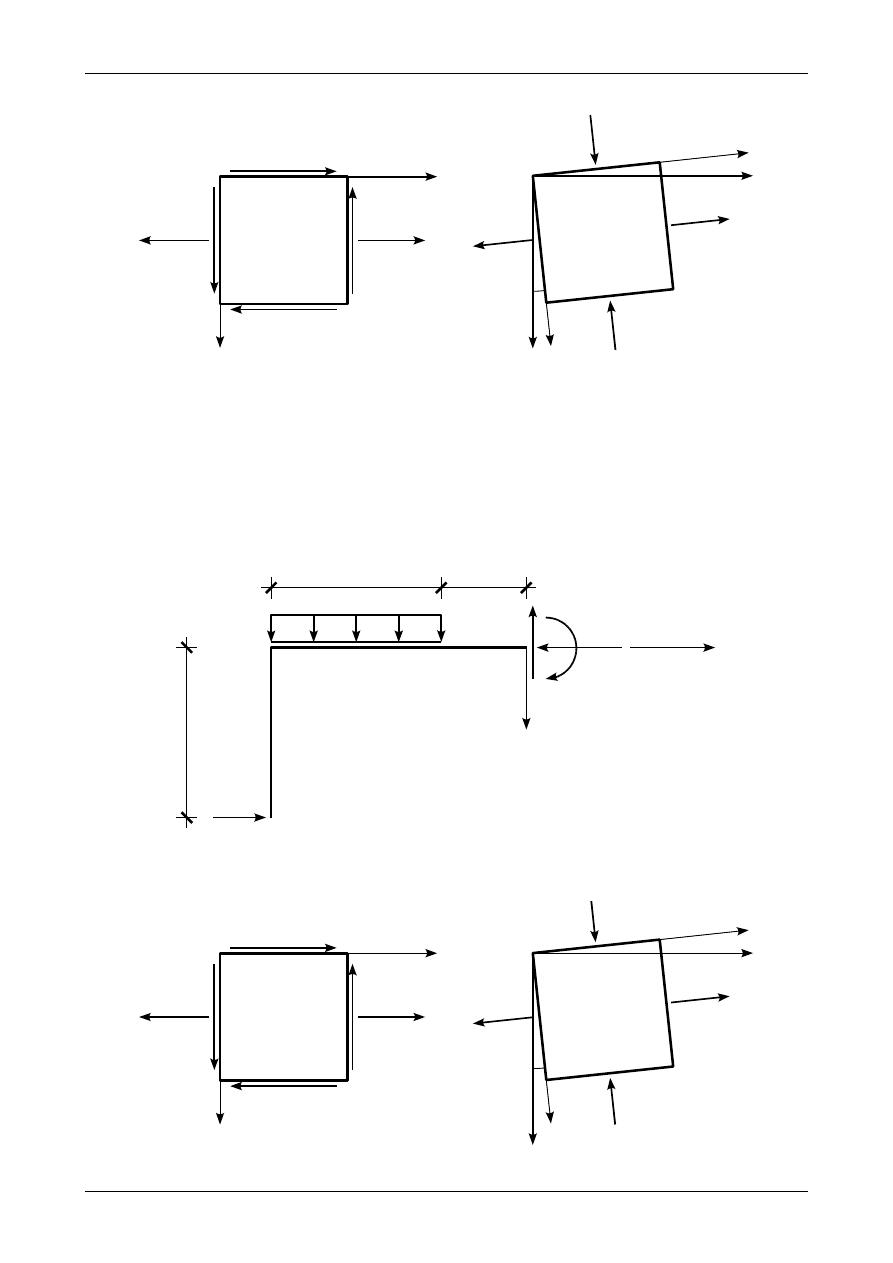
5.4. Odpowiedź do zadania 5/4

Rysunek 5.6 przedstawia prawidłowe wartości i zwroty sił przekrojowych, które działają w przekroju

α

-

α

. Graficzne interpretacje stanu naprężenia w układzie ZX oraz w układzie osi głównych przedstawia

rysunek 5.7.

1,5

3,0

3,

0

19,0 kN/m

15,0 kN

[m]

Z=Z

0

=Z

gl

X

15,0 kN

57

,0

k

N

216,0 kNm

Rys. 5.6. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

31

Z

X

161,7 MPa

1

7,

4

6

M

P

a

161,7 MPa

17

,4

6

M

P

a

17,46 MPa

17,46 MPa

Z

gl

X

gl

163,6 MPa

1,8

64

M

P

a

163,6 MPa

1,8

64

M

P

a

Z

X

6,094

0

Rys. 5.7. Graficzne interpretacje stanu naprężenia w punkcie A

5.5. Odpowiedź do zadania 5/5

Rysunek 5.8 przedstawia prawidłowe wartości i zwroty sił przekrojowych, które działają w przekroju

α

-

α

. Graficzne interpretacje stanu naprężenia w układzie ZX oraz w układzie osi głównych przedstawia

rysunek 5.9.

1,5

3,0

3,

0

8,0 kN/m

11,0 kN

[m]

Z=Z

0

=Z

gl

X

11,0 kN

24,0 kN

105,0 kNm

Rys. 5.8. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

Z

X

89,21 MPa

4

,9

6

2

M

P

a

89,21 MPa

4,

96

2

M

P

a

4,962 MPa

4,962 MPa

Z

gl

X

gl

89,49 MPa

0,2751 MPa

89,49 MPa

0,2751 MPa

Z

X

3,173

0

Rys. 5.9. Graficzne interpretacje stanu naprężenia w punkcie A

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

32

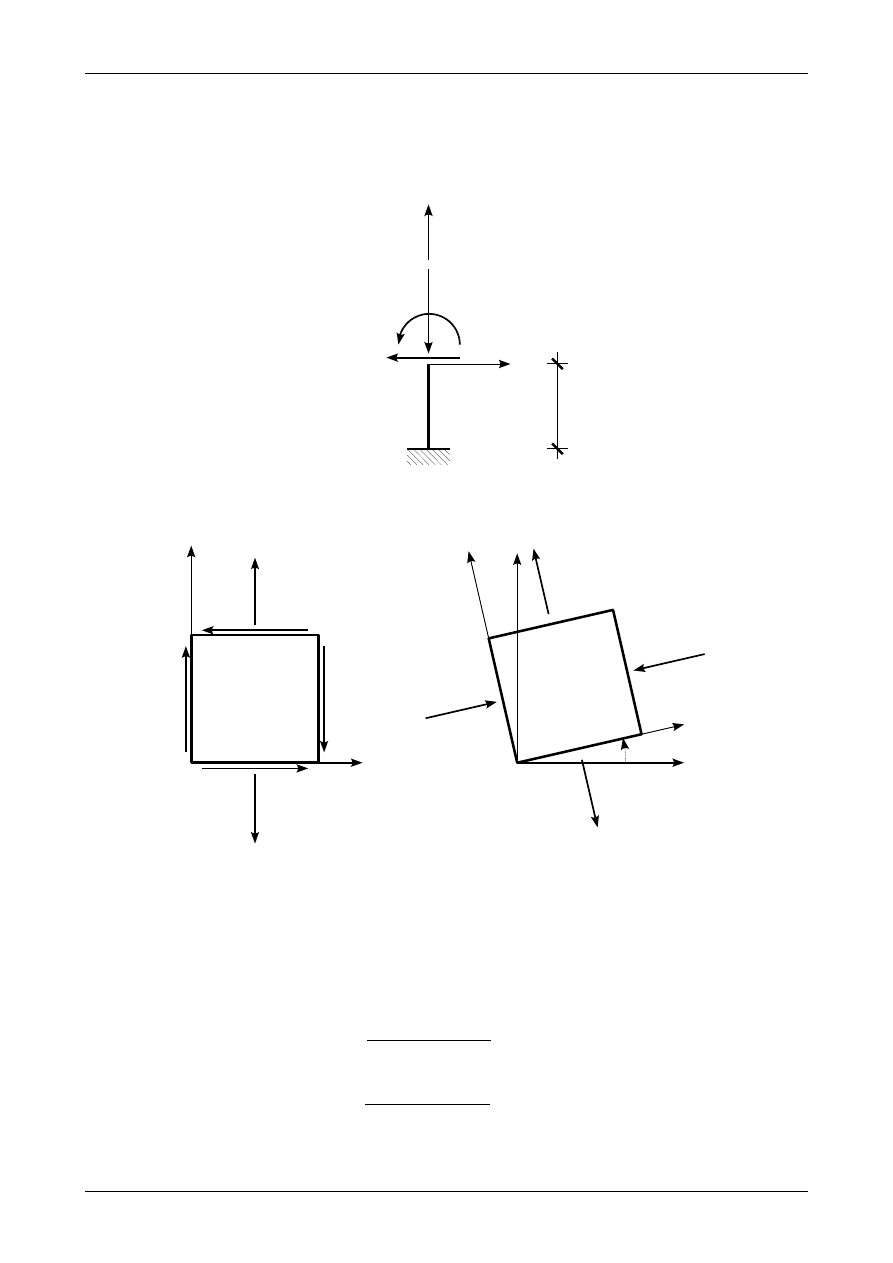
5.6. Odpowiedź do zadania 5/6

Rysunek 5.10 przedstawia prawidłowe wartości i zwroty sił przekrojowych, które działają w przek-

roju

α

-

α

. Graficzne interpretacje stanu naprężenia w układzie ZX oraz w układzie osi głównych

przedstawia rysunek 5.11.

1,

0

[m]

Z=Z

0

=Z

gl

X

20

,0

k

N

44,0 kN

128,0 kNm

Rys. 5.10. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

Z

X

51

,5

1

M

P

a

12,48 MPa

5

1,

5

1

M

P

a

12,48 MPa

12

,4

8

M

P

a

12

,4

8

M

P

a

Z

gl

X

gl

54

,3

7 M

P

a

54

,3

7 M

P

a

2,864

MPa

2,864

MPa

Z

X

12,93

0

Rys. 5.11. Graficzne interpretacje stanu naprężenia w punkcie A

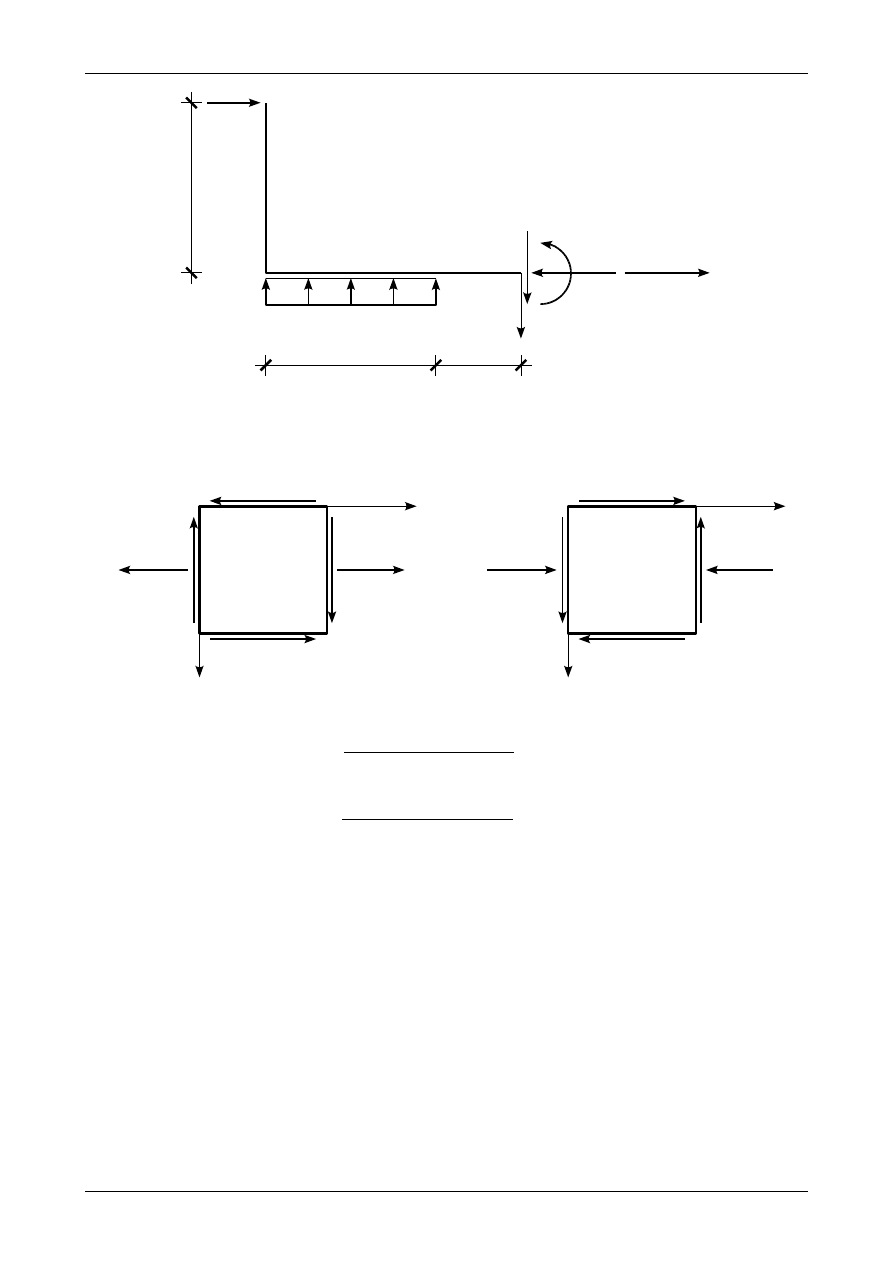
5.7. Odpowiedź do zadania 5/7

Rysunek 5.12 przedstawia prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

.

Graficzną interpretację stanu naprężenia w punkcie A przedstawia rysunek 5.13 a) natomiast w punkcie
B rysunek 5.13 b). Naprężenia zredukowane według hipotez Hubera i Treski w punkcie A wynoszą



red

H A

=



73,04

2



3⋅11,22

2

=

75,58 MPa

,



red

T  A

=



73,04

2



4⋅11,22

2

=

76,41 MPa

.

Naprężenia zredukowane według powyższych hipotez w punkcie B wynoszą

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

33

1,0

2,0

2,

0

17,0 kN/m

15,0 kN

[m]

Z=Z

0

=Z

gl

X

15,0 kN

34,0 kN

98,0 kNm

Rys. 5.12. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

Z

X

73,04 MPa

11

,2

2

M

P

a

73,04 MPa

11

,2

2

M

P

a

11,22 MPa

11,22 MPa

Y

X

127,3 MPa

2,

17

2

M

P

a

127,3 MPa

2,

17

2

M

P

a

2,172 MPa

2,172 MPa

a)

b)

Rys. 5.13. Graficzne interpretacje stanów naprężenia, a) w punkcie A, b) w punkcie B



red

H B

=





−

127,3



2



3⋅



−

2,172



2

=

127,4 MPa

,



red

T  B

=





−

127,3



2



4⋅



−

2,172



2

=

127,4 MPa

.

5.8. Odpowiedź do zadania 5/8

Rysunek 5.14 przedstawia prawidłowe wartości i zwroty sił przekrojowych w przekroju

α

-

α

. Rysu-

nek 5.15 przedstawia graficzną interpretację stanu naprężenia w punkcie A. Odkształcenia liniowe oraz
niezerowe odkształcenia postaciowe odpowiadające stanowi naprężenia w punkcie A wynoszą



X

=−

293,6⋅10

−

6

,



Y

=

Z

=

88,08⋅10

−

6

,



XZ

=

30,76⋅10

−

6

.

Dr inż. Janusz Dębiński

Budownictwo

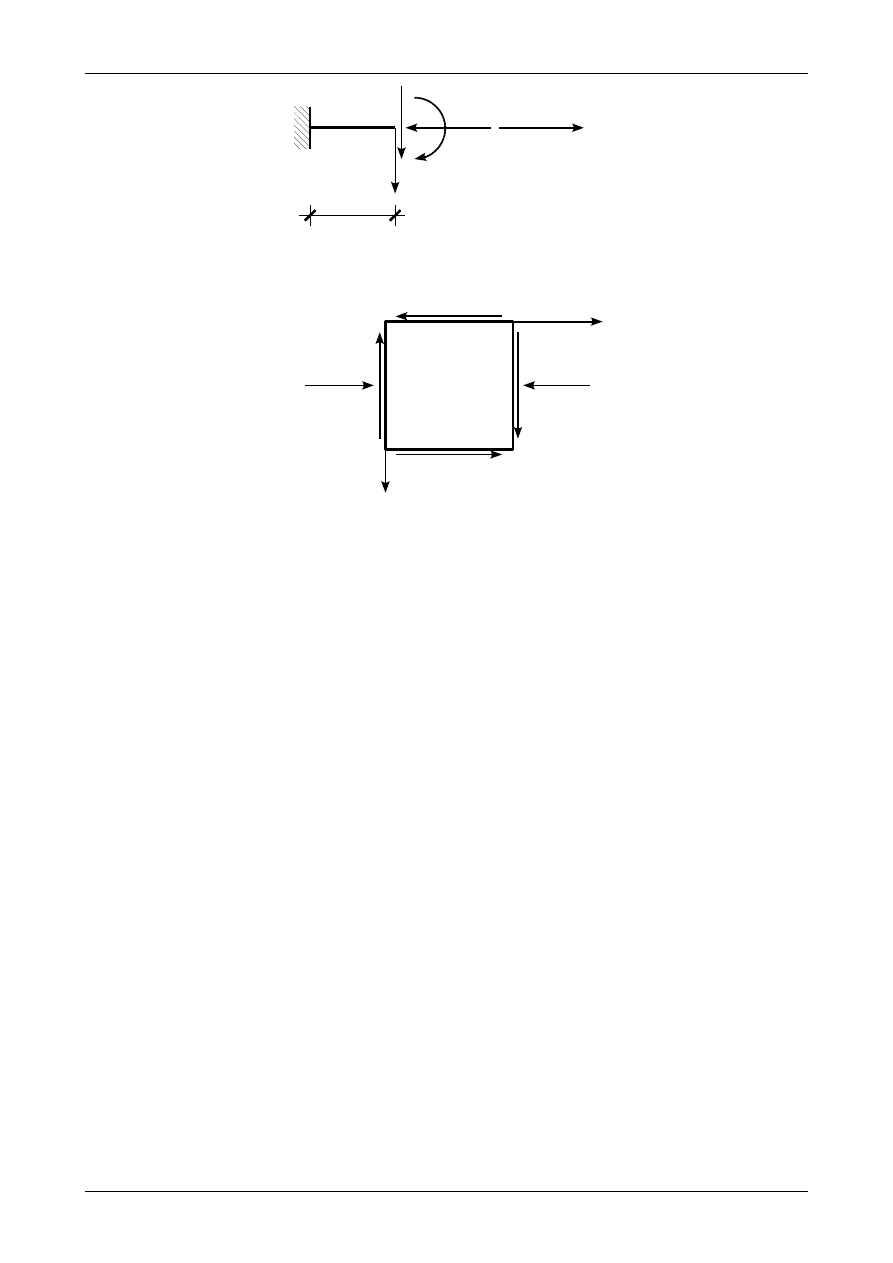
WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

34

1,0

[m]

Z=Z

0

=Z

gl

X

32,0 kN

19,0 kN

70,0 kNm

Rys. 5.14. Prawidłowe wartości i zwroty sił przekrojowych w przekroju

Z

X

60,19 MPa

4,

85

1

M

P

a

60,19 MPa

4

,8

5

1

M

P

a

4,851 MPa

4,851 MPa

Rys. 5.15. Graficzna interpretacja stanu naprężenia w punkcie A

5.9. Odpowiedź do zadania 5/9

Rysunek 5.16 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce swobodnie

podpartej. Ten sam rysunek przedstawia także wykres siły poprzecznej. Ekstremalna bezwzględna wartość
tej siły wynosi

T

EXT

=

36,0 kN

.

Naprężenie styczne w spoinie ciągłej o grubości 3 mm wynosi



sp

=

20,60 MPa

.

Naprężenie styczne w spoinie przerywanej o grubości 4 mm wynosi



sp

=

38,63 MPa

.

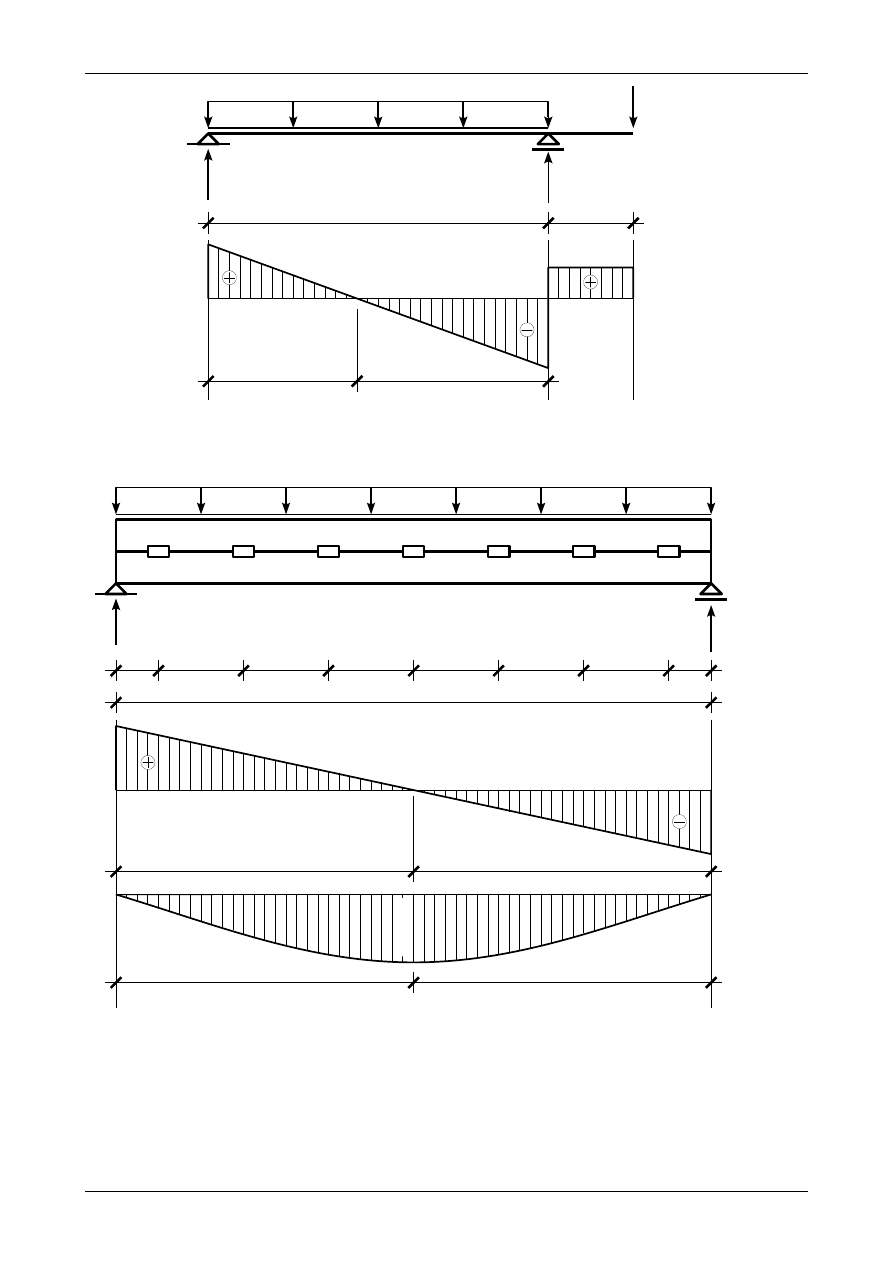
5.10. Odpowiedź do zadania 5/10

Rysunek 5.17 przedstawia wykresy siły poprzecznej oraz momentu zginającego w belce drewnianej.

Maksymalna wartość momentu zginającego wynosi

M

EXT

=

55,13 kNm

.

Rysunek 5.18 przedstawia wykres naprężenia normalnego

σ

X

w najbardziej obciążonym przekroju belki

drewnianej.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

35

2,0

8,0

8,0 kN/m

16,0 kN

A

B

C

[m]

28,0 kN

52,0 kN

T(x) [kN]

3,5

4,5

28

,0

36

,0

16,0

Rys. 5.16. Wykres siły poprzecznej w belce swobodnie podpartej

55

,1

3

7,0

9,0 kN/m

[m]

1,0

1,0

1,0

1,0

1,0

1,0

0,5

0,5

31,5 kN

31,5 kN

T(x) [kN]

M(x) [kNm]

3,5

3,5

3,5

3,5

31

,5

3

1,

5

Rys. 5.17. Wykresy sił przekrojowych w belce drewnianej

Ekstremalna wartość siły poprzecznej wynosi

T

EXT

=

31,5 kN

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

36

15,0

13

,0

13

,0

10

,0

[cm]

Y=Y

gl

Z=Z

gl

[MPa]

σ

X

17,39

4,830

4,830

17,39

55,13 kNm

sc

Rys. 5.18. Wykres naprężenia normalnego

σ

X

w najbardziej obciążonym przekroju

Główny moment bezwładności przekroju pełnego wynosi

J

Ygl

=

15,0⋅36,0

3

12

=

58320 cm

4

Naprężenie styczne w środku ciężkości przekroju pełnego wynosiłoby



XZ

=

31,5⋅18,0⋅15,0⋅9,0

15,0⋅58320

=

0,0875

kN

cm

2

=

0,875 MPa

.

Siła rozwarstwiająca przypadająca na jeden klocek wynosi

R=0,0875⋅100,0⋅15,0=131,3 kN

.

Naprężenie styczne w pojedynczym klocku przy założeniu ich równomiernego rozkładu wynosi



kl

=

131,3

15,0⋅20,0

=

0,4377

kN

cm

2

=

4,377 MPa

.

5.11. Odpowiedź do zadania 5/11

W zadaniu zakładamy, że siła normalna rozkłada się równomiernie na każdą ze śrub. Siłę rozciągającą

przenoszą razem cztery śruby, liczba płaszczyzn ścinania wynosi 8. Pole powierzchni pojedynczej śruby
wynosi

A

sr

=

⋅

2,0

2

4

=

3,142 cm

2

.

Wartość naprężenia stycznego w pojedynczej śrubie wynosi

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

37

2,0

2,0

5,0

5,0

6,0

2,0

2,0

5,0

5,0

6,0

2,

0

2,

0

1,

0

1,

0

b)

a)

[cm]

[cm]

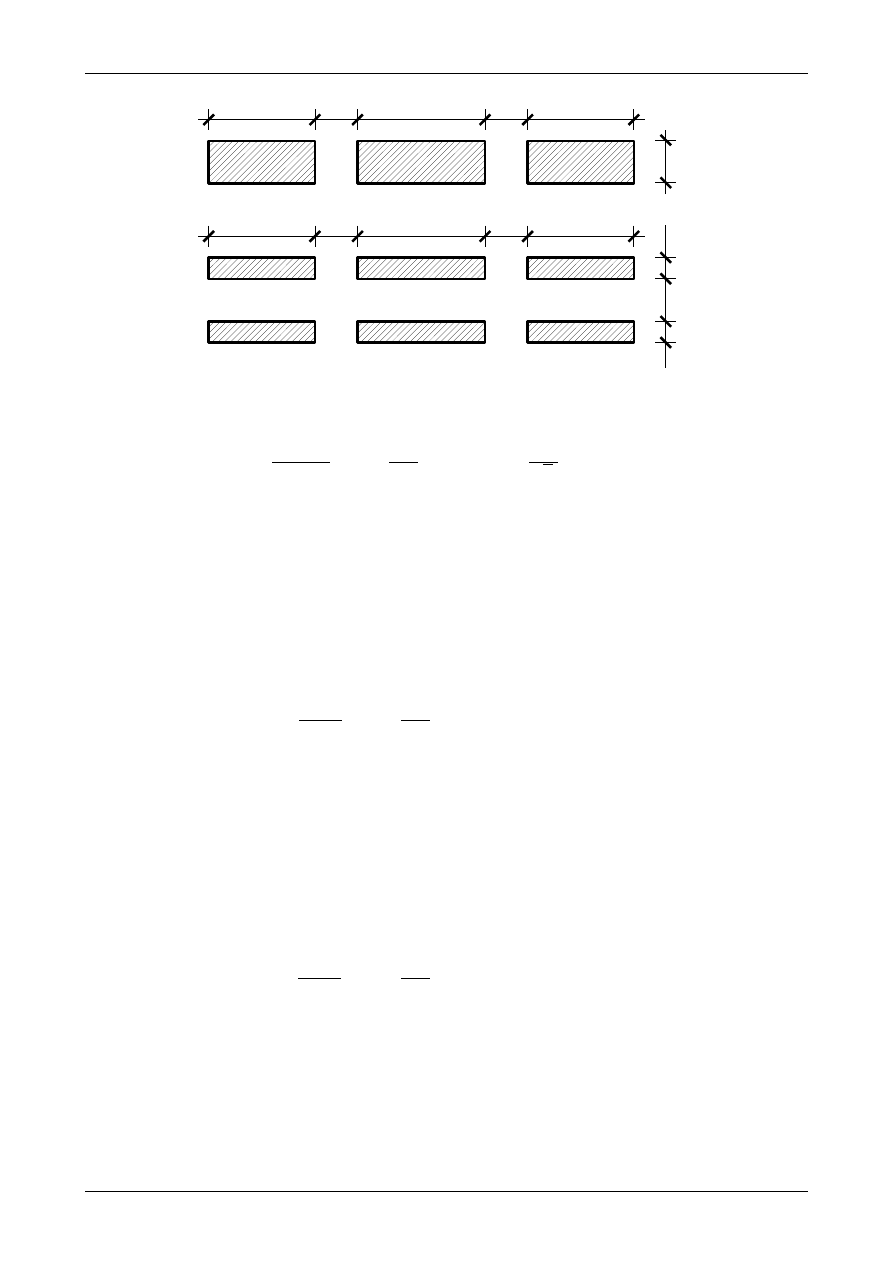
Rys. 5.19. Powierzchnia netto a) rozciąganego pręta, b) nakładek



sr

=

260,0

8⋅3,142

=

10,34

kN

cm

2

=

103,4 MPa

215



3

=

124,1 MPa

.

Rysunek 5.19 przedstawia przekrój netto pręta oraz nakładek. Pole powierzchni netto pręta wynosi

A

p

=

2,0⋅5,02,0⋅6,02,0⋅5,0=32,0 cm

2

.

Wartość naprężenia normalnego

σ

X

w pręcie wynosi



X



p

=

260,0

32,0

=

8,125

kN

cm

2

=

81,25 MPa R=215 MPa

.

Pole powierzchni netto nakładek wynosi

A

n

=

2⋅



1,0⋅5,01,0⋅6,01,0⋅5,0



=

32,0 cm

2

.

Wartość naprężenia normalnego

σ

X

w nakładkach wynosi



X



n

=

260,0

32,0

=

8,125

kN

cm

2

=

81,25 MPaR=215 MPa

.

5.12. Odpowiedź do zadania 5/12

Pole powierzchni czterech spoin pachwinowych łączących pręt z nakładkami (uwzględniamy spoinę

od miejsca połączenia prętów do końca nakładek) wynosi

A

sp

=

4⋅40,0⋅0,3=48,0 cm

2

.

Dr inż. Janusz Dębiński

Budownictwo

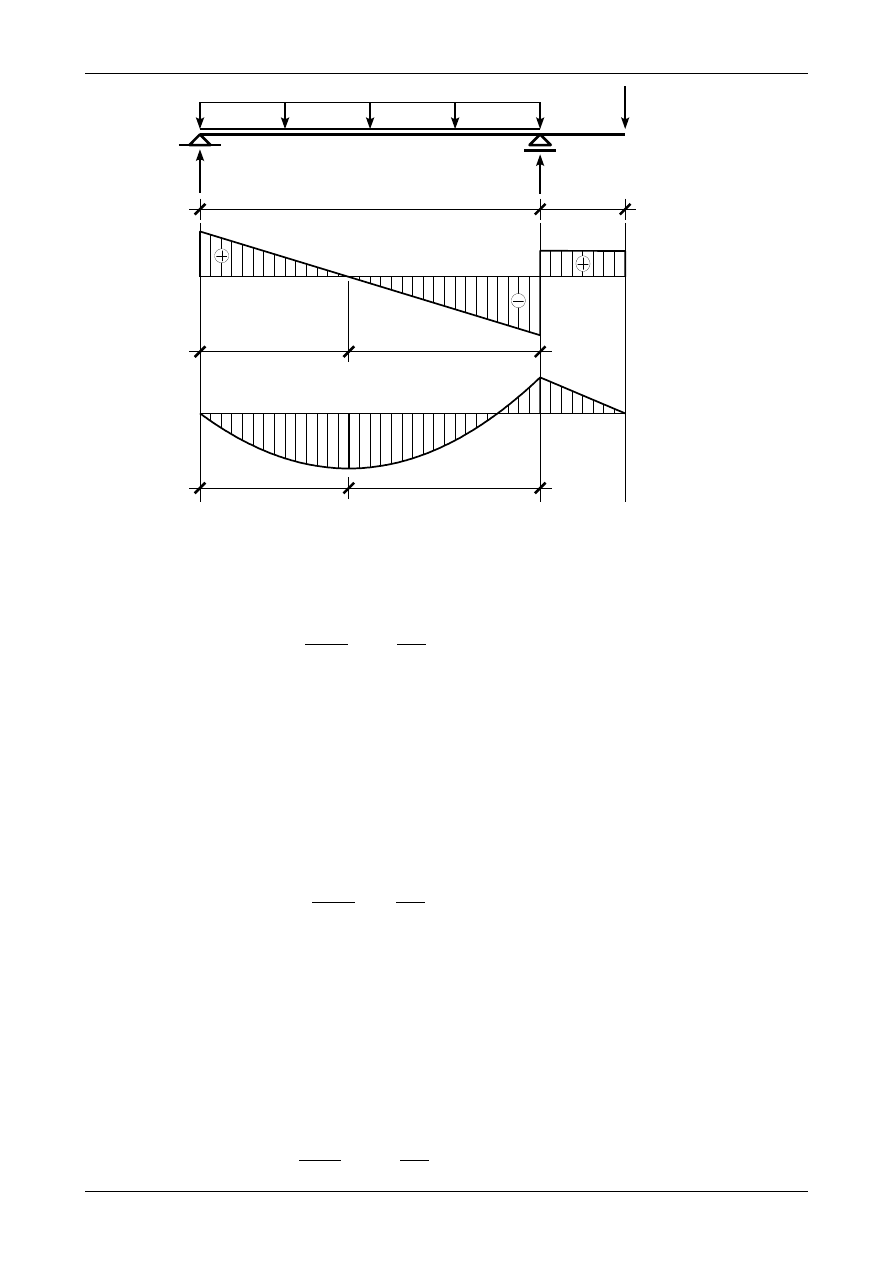
WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

38

2,0

8,0

12,0 kN/m

24,0 kN

A

B

C

[m]

42,0 kN

78,0 kN

T(x) [kN]

M(x) [kNm]

42

,0

54

,0

24,0

0,

0

0,

0

4

8,

0

3,5

4,5

3,5

4,5

73

,5

0

Rys. 6.1. Wykres siły poprzecznej oraz momentu zginającego w belce prostej

Naprężenie styczne w spoinie wynosi więc



sp

=

360,0

48,0

=

7,50

kN

cm

2

=

75,0 MPaR=215 MPa

.

Pole powierzchni pręta wynosi

A

p

=

20,0⋅2,0=40,0 cm

2

.

Naprężenie normalne

σ

X

w pręcie wynosi więc



X



p

=

360,0

40,0

=

9,0

kN

cm

2

=

90,0 MPaR=215 MPa

.

Pole powierzchni nakładek wynosi

A

n

=

2⋅16,0⋅1,0=32,0 cm

2

.

Naprężenie normalne

σ

X

w nakładkach wynosi więc



X



n

=

360,0

32,0

=

11,25

kN

cm

2

=

112,5 MPaR=215 MPa

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

39

6. Zginanie ukośne

6.1. Odpowiedź do zadania 6/1

Rysunek 6.1 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej, ten sam

rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego. Rysunek 6.2 przedstawia wykres
naprężenia normalnego

σ

X

w przekroju belki.

Y=Y

gl

Z=Z

gl

48,11

0

σ

X

[M

Pa

]

43

2,7

43

2,7

20,0

0

7350 kNcm

sc

Rys. 6.2. Wykres naprężenia normalnego

σ

X

w przekroju belki

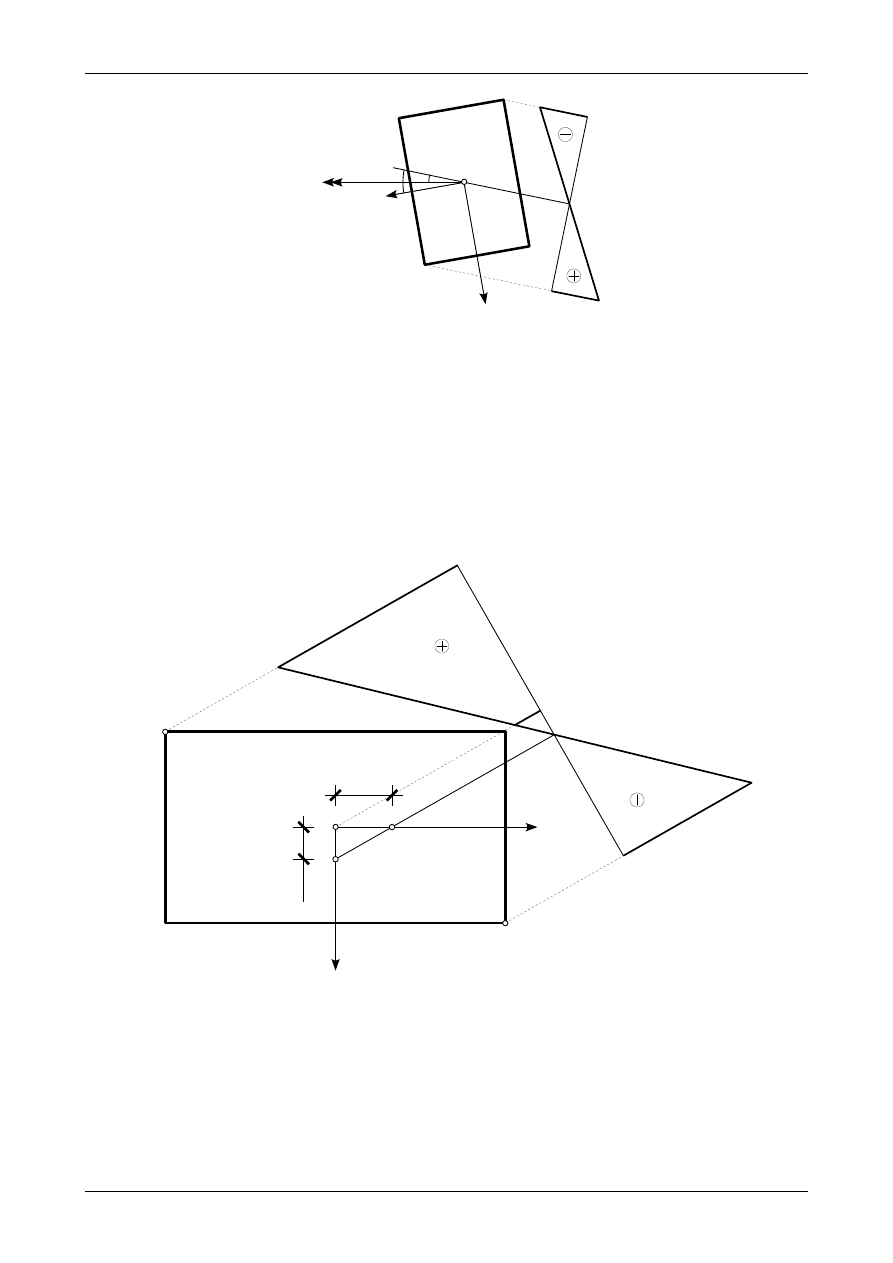
6.2. Odpowiedź do zadania 6/2

Rysunek 6.3 przedstawia prawidłowe wartości i zwroty reakcji podporowych w belce prostej, ten sam

rysunek przedstawia wykresy siły poprzecznej oraz momentu zginającego. Rysunek 6.4 przedstawia wykres
naprężenia normalnego

σ

X

w przekroju belki.

20,0 kN/m

56,0 kNm

8,0

[m]

87,0kN

73,0kN

T(x) [kN]

M(x) [kNm]

4,35

3,65

4,35

3,65

87

,0

73

,0

0,

0

5

6,

0

1

89

,2

Rys. 6.3. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

40

Y=Y

gl

Z=Z

gl

21,63

0

σ

X

[MPa]

153,4

153,4

10,0

0

18920 kNcm

sc

Rys. 6.4. Wykres naprężenia normalnego

σ

X

w przekroju belki

7. Mimośrodowe działanie siły normalnej

7.1. Odpowiedź do zadania 7/1

Rysunek 7.1 przedstawia położenie osi obojętnej oraz wykres naprężenia normalnego

σ

X

w przekroju

pręta.

[cm]

Y=Y

gl

Z=Z

gl

2,

99

9

5,333

σ

X

[MP

a]

48,

61

34,

72

0,0

6,9

44

A

sc

B

Rys. 7.1. Wykres naprężenia normalnego

σ

X

w przekroju pręta

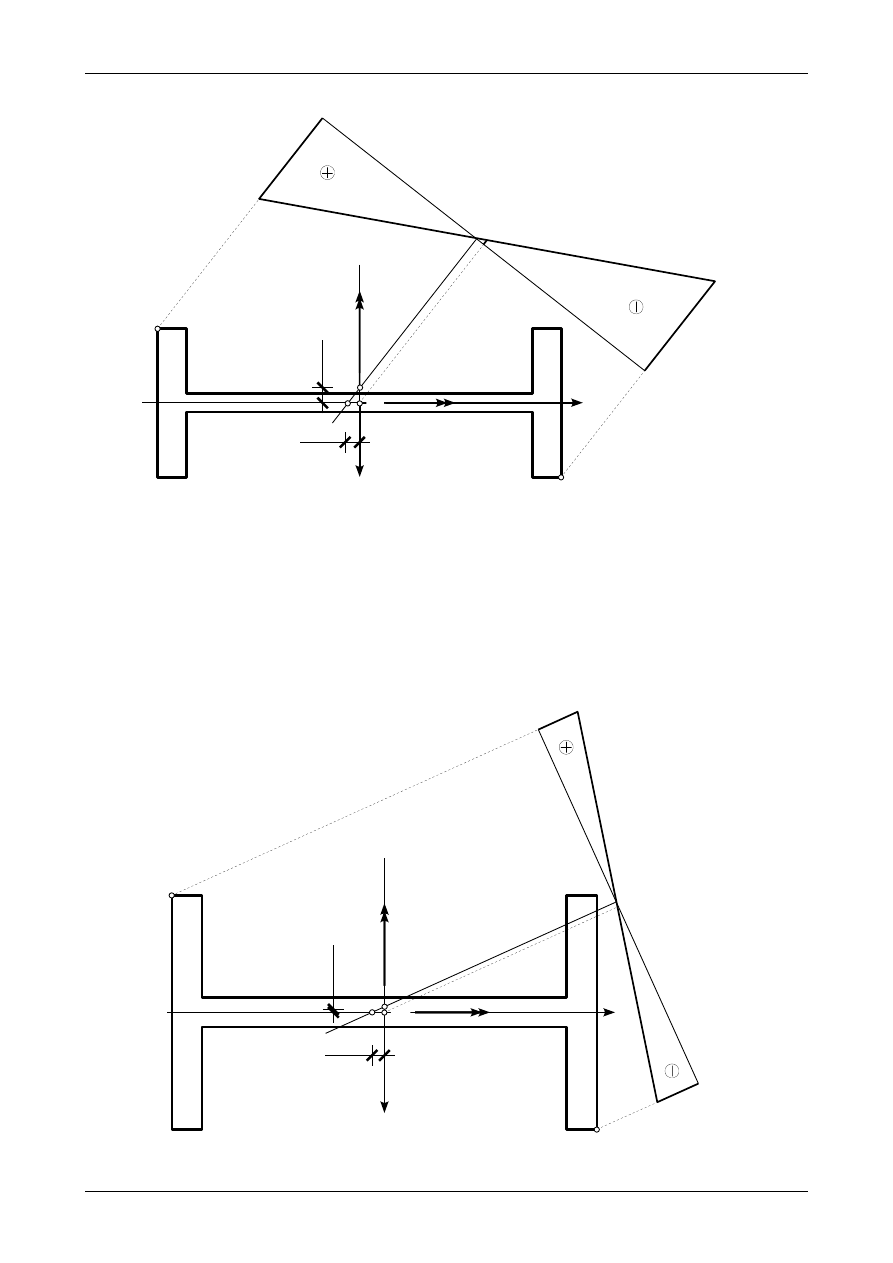
7.2. Odpowiedź do zadania 7/2

Rysunek 7.2 przedstawia przekrój pręta wspornikowego wraz z prawidłowymi wartościami oraz

zwrotami momentów zginających działających w nim. Siła normalna o wartości -40,0 kN jest przyłożona
w środku ciężkości przekroju. Rysunek ten przedstawia także położenie osi obojętnej oraz wykres naprę-
żenia normalnego

σ

X

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

41

[cm]

sc

Y=Y

gl

Z=Z

gl

82

40

k

N

cm

280,0 kNcm

1,

45

6

1,156

A

B

σ

X

[M

Pa

]

89

,9

4

0,

0

98

,8

3

N = -40,0 kN

4,

44

4

Rys. 7.2. Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego

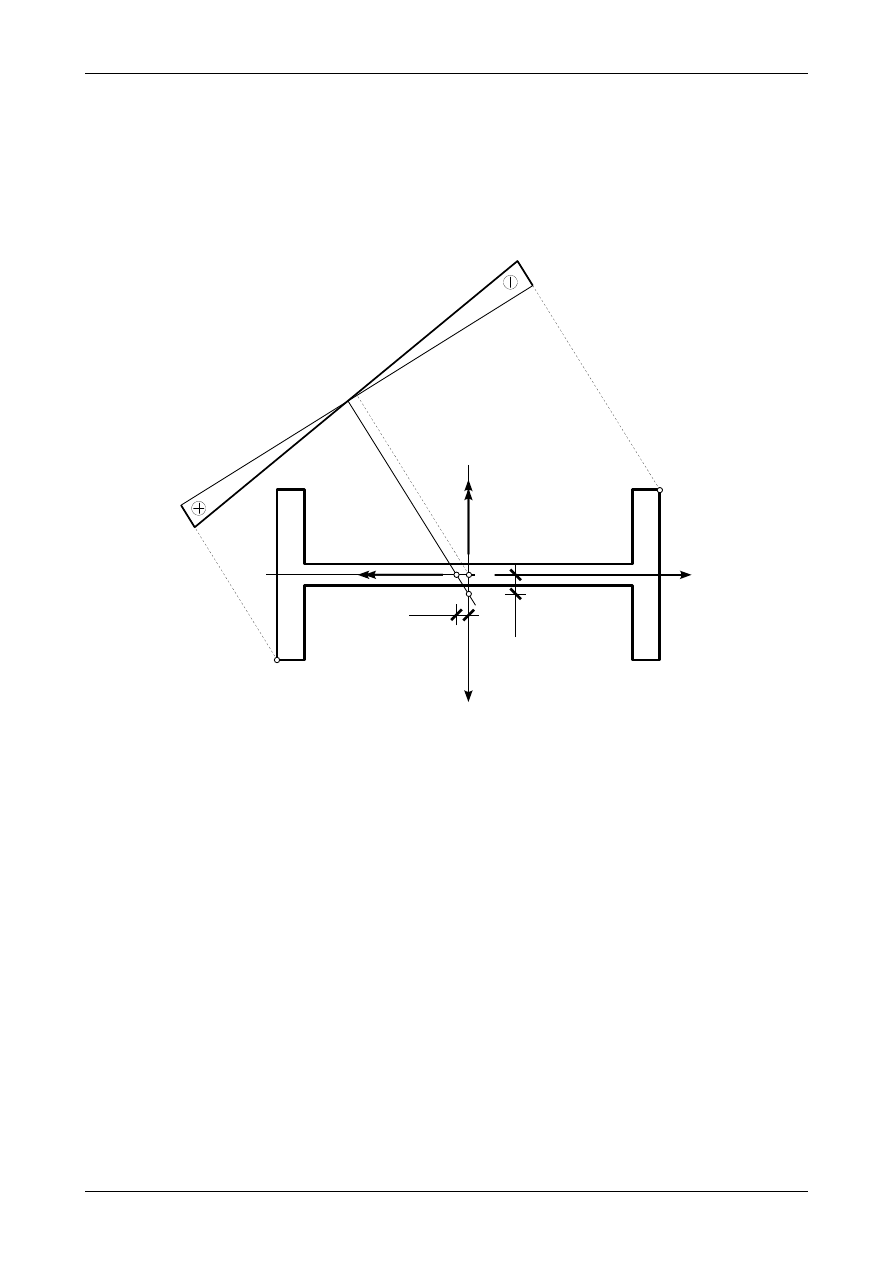
7.3. Odpowiedź do zadania 7/3

Rysunek 7.3 przedstawia przekrój pręta wspornikowego wraz z prawidłowymi wartościami oraz

zwrotami momentów zginających działających w nim. Siła normalna o wartości -40,0 kN jest przyłożona
w środku ciężkości przekroju. Rysunek ten przedstawia także położenia osi obojętnej oraz wykres naprę-
żenia normalnego

σ

X

.

[cm]

Y=Y

gl

Z=Z

gl

sc

0,

28

22

1,175

σ

X

[MP

a]

177

,4

183

,9

N = -40,0 kN

98

00

k

N

cm

4060 kNcm

A

B

0,0

3,2

26

Rys. 7.3. Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

42

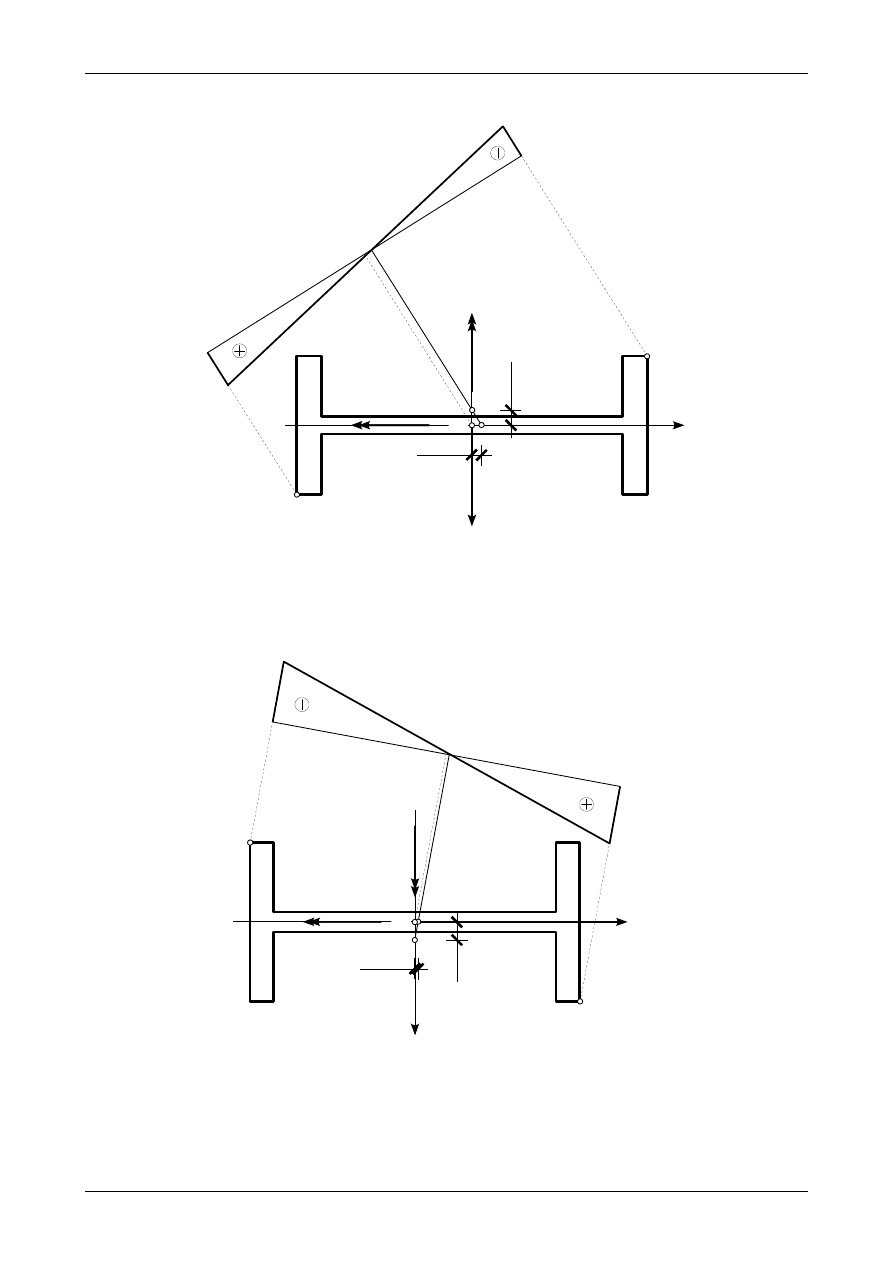
7.4. Odpowiedź do zadania 7/4

Rysunek 7.4 przedstawia przekrój pręta wspornikowego wraz z prawidłowymi wartościami oraz

zwrotami momentów zginających działających w nim. Siła normalna o wartości -30,0 kN jest przyłożona
w środku ciężkości przekroju. Rysunek ten przedstawia także położenie osi obojętnej oraz wykres naprę-
żenia normalnego

σ

X

.

[cm]

Y=Y

gl

Z=Z

gl

sc

1,

78

2

1,114

N = -30,0 kN

B

5

96

0

kN

cm

240,0 kNcm

A

σ

X

[M

P

a]

61

,4

0

67

,6

5

0,0

3,1

25

Rys. 7.4. Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego

7.5. Odpowiedź do zadania 7/5

Rysunek 7.5 przedstawia przekrój pręta wspornikowego wraz z prawidłowymi wartościami oraz

zwrotami momentów zginających działających w nim. Siła normalna o wartości 30,0 kN jest przyłożona
w środku ciężkości przekroju. Rysunek ten przedstawia także położenie osi obojętnej oraz wykres napręże-
nia normalnego

σ

X

.

7.6. Odpowiedź do zadania 7/6

Rysunek 7.6 przedstawia przekrój pręta wspornikowego wraz z prawidłowymi wartościami oraz

zwrotami momentów zginających działających w nim. Siła normalna o wartości -25,0 kN jest przyłożona
w środku ciężkości przekroju. Rysunek ten przedstawia także położenie osi obojętnej oraz wykres napręże-
nia normalnego

σ

X

.

7.7. Odpowiedź do zadania 7/7

Rysunek 7.7 przedstawia przekrój pręta wspornikowego wraz z prawidłowymi wartościami oraz

zwrotami momentów zginających działających w nim. Siła normalna o wartości -30,0 kN jest przyłożona
w środku ciężkości przekroju. Rysunek ten przedstawia także położenie osi obojętnej oraz wykres napręże-
nia normalnego

σ

X

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

43

Y=Y

gl

Z=Z

gl

sc

1,

39

6

0,8969

N = 30,0 kN

A

B

σ

X

[M

P

a]

89

,1

0

81

,6

9

6

00

5

kN

cm

195,0 kNcm

0,0

3,7

04

[cm]

Rys. 7.5. Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego

Y=Y

gl

Z=Z

gl

sc

11

86

0

kN

cm

187,5 kNcm

N = -25,0 kN

A

1,

72

7

0,3460

B

σ

X

[M

P

a]

14

4,

1

2,

87

4

0,

0

13

8,

3

[cm]

Rys. 7.6. Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego

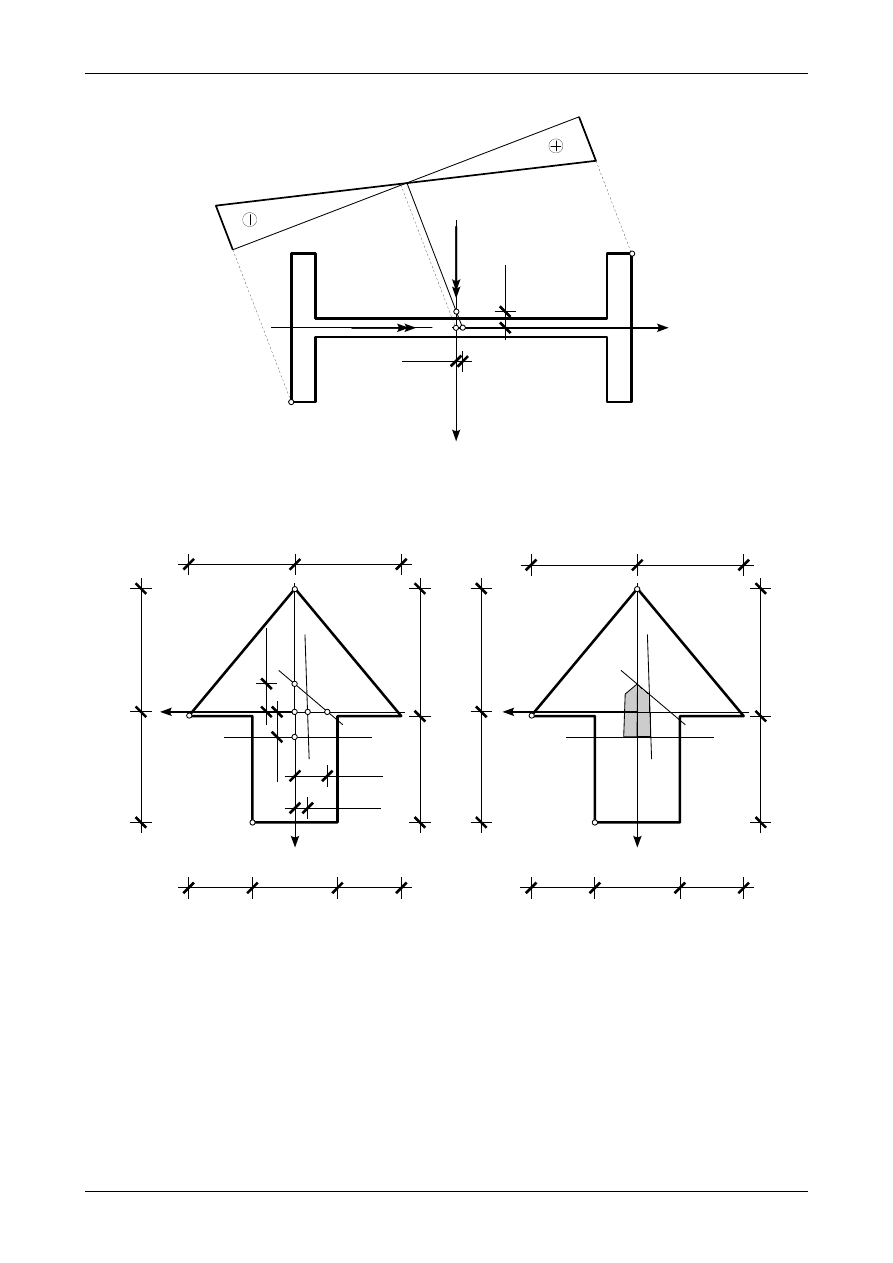
7.8. Odpowiedź do zadania 7/8

Rysunek 7.8 a) przedstawia położenie środka ciężkości przekroju oraz współrzędne odcinkowe osi

obojętnych będących konturem rdzenia przekroju natomiast rysunek 7.8 b) przedstawia rdzeń przekroju.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

44

Y=Y

gl

Z=Z

gl

sc

8

88

0

kN

cm

210,0 kNcm

N = -30,0 kN

1

,5

5

9

0,5811

A

B

σ

X

[M

P

a]

11

7,9

3,5

71

0,0

11

0,8

[cm]

Rys. 7.7. Wykres naprężenia normalnego

σ

X

w przekroju pręta wspornikowego

6,0

6,0

8,0

1

0,

0

1

2,

0

[cm]

1

0,

4

11

,6

Y=Y

gl

Z=Z

gl

1

2

3

2,

37

8

1

1

1,214

2

2

3

3

3,035

2,

6

52

6,0

6,0

8,0

1

0,

0

1

2,

0

[cm]

10

,4

11

,6

Y=Y

gl

Z=Z

gl

1

2

3

1

1

2

2

3

3

a)

b)

10,0

10,0

10,0

10,0

Rys. 7.8. Rdzeń przekroju

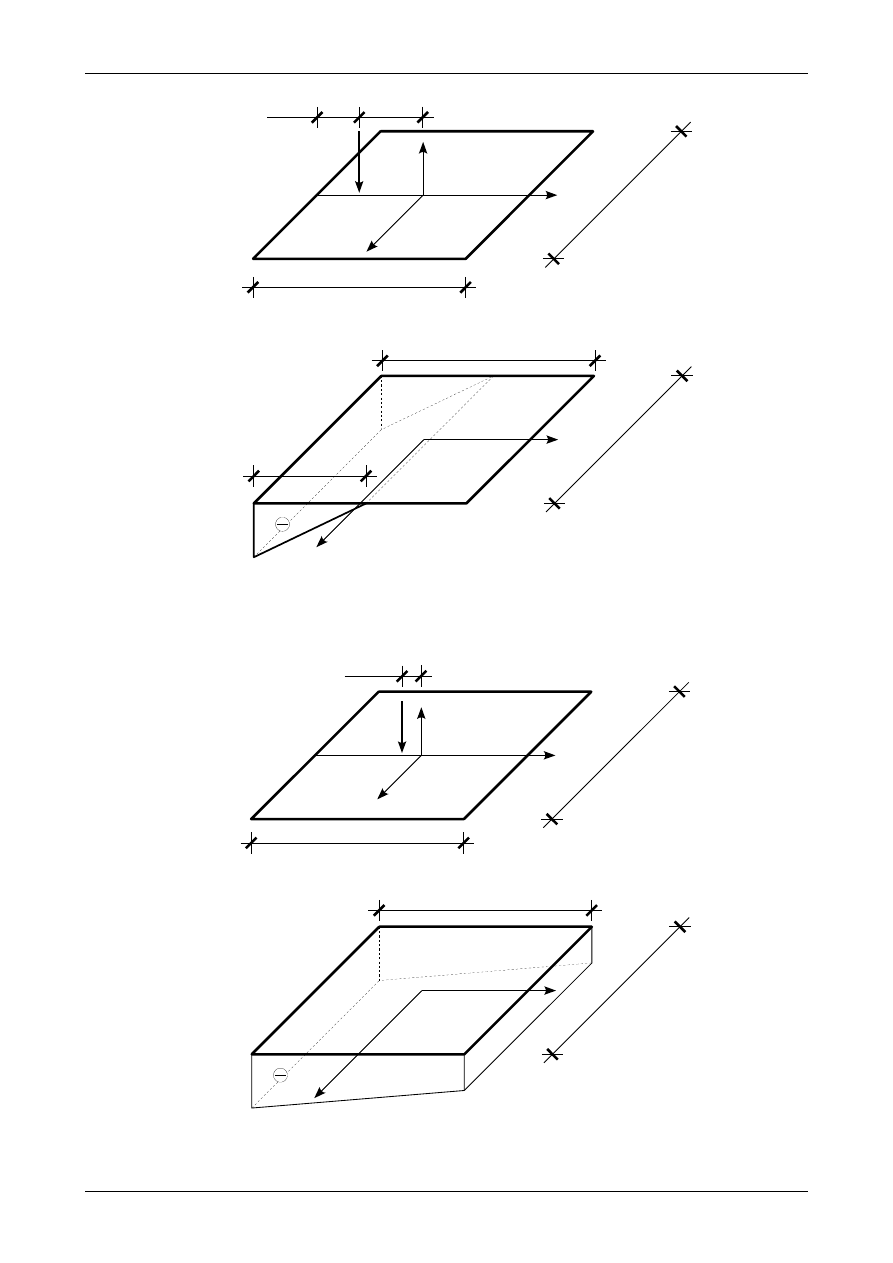
7.9. Odpowiedź do zadania 7/9

Rysunek 7.9 a) przedstawia siłę normalną działającą na mimośrodzie. Siła ta działa poza rdzeniem

przekroju. Rysunek 7.9 b) przedstawia wykres naprężenia normalnego

σ

X

w przekroju betonowej ściany

zbiornika na wodę.

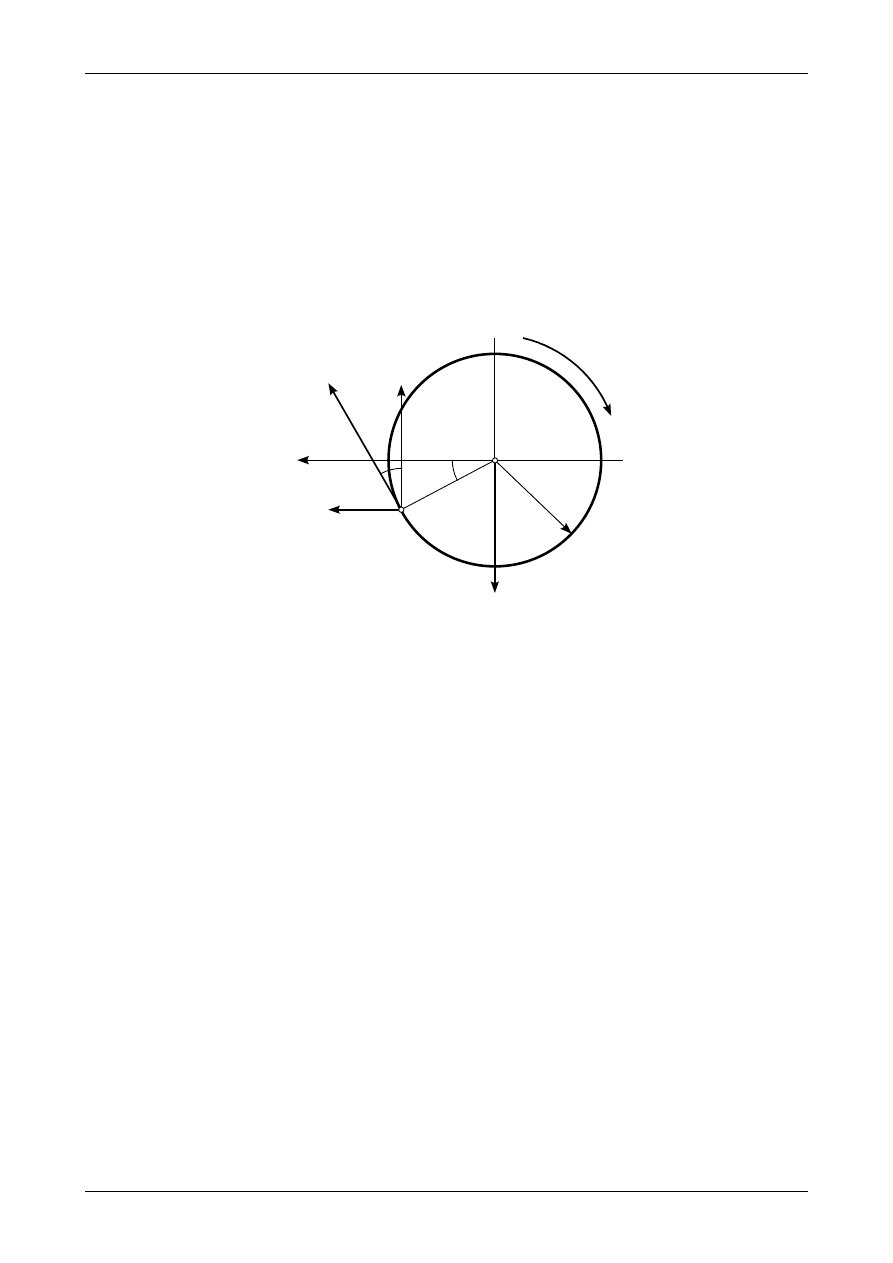
7.10. Odpowiedź do zadania 7/10

Rysunek 7.10 a) przedstawia siłę normalną działającą na mimośrodzie. Siła ta działa w rdzeniu przek-

roju. Rysunek 7.10 b) przedstawia wykres naprężenia normalnego

σ

X

w przekroju betonowej ściany

zbiornika na wodę.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

45

437,5 kN

2,5

1,

0

Z=Z

gl

Y=

Y

gl

[m]

0,8229

0,4271

X

2,5

1,

0

Z=Z

gl

Y=

Y

gl

[m]

1,281

68

3,

1

kP

a

a)

b)

Rys. 7.9. Wykres naprężenia normalnego

σ

X

w przekroju betonowej ściany zbiornika na wodę

4

81

,0

k

N

2,6

1,

0

Z=Z

gl

Y=

Y

gl

[m]

0,1245

X

2,6

1,

0

Z=Z

gl

Y=

Y

gl

[m]

23

8,

2

kP

a

13

1,

8

kP

a

a)

b)

Rys. 7.10. Wykres naprężenia normalnego

σ

X

w przekroju betonowej ściany zbiornika na wodę

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

46

8. Skręcanie

8.1. Odpowiedź do zadnia 8/1

Rysunek 8.1 przedstawia wypadkowe naprężenie styczne

τ

X

oraz składowe naprężenia styczne

τ

XY

i

τ

XZ

działające w punkcie A. Naprężenia składowe mają wartości



XY

=

34,82 MPa

,



XZ

=−

60,30 MPa

.

Y=Y

gl

Z=Z

gl

8,0

[cm]

56

,0

k

N

m

O

30

0

30

0

69

,6

3 M

P

a

34,82 MPa

60

,3

0

M

P

a

sc

Rys. 8.1. Naprężenia styczne działające w punkcie A

8.2. Odpowiedź do zadania 8/2

Rysunek 8.2 przedstawia wypadkowe naprężenie styczne

τ

X

oraz składowe naprężenia styczne

τ

XY

i

τ

XZ

działające w punkcie A. Naprężenia składowe mają wartości



XY

=−

34,63 MPa

,



XZ

=−

49,46 MPa

.

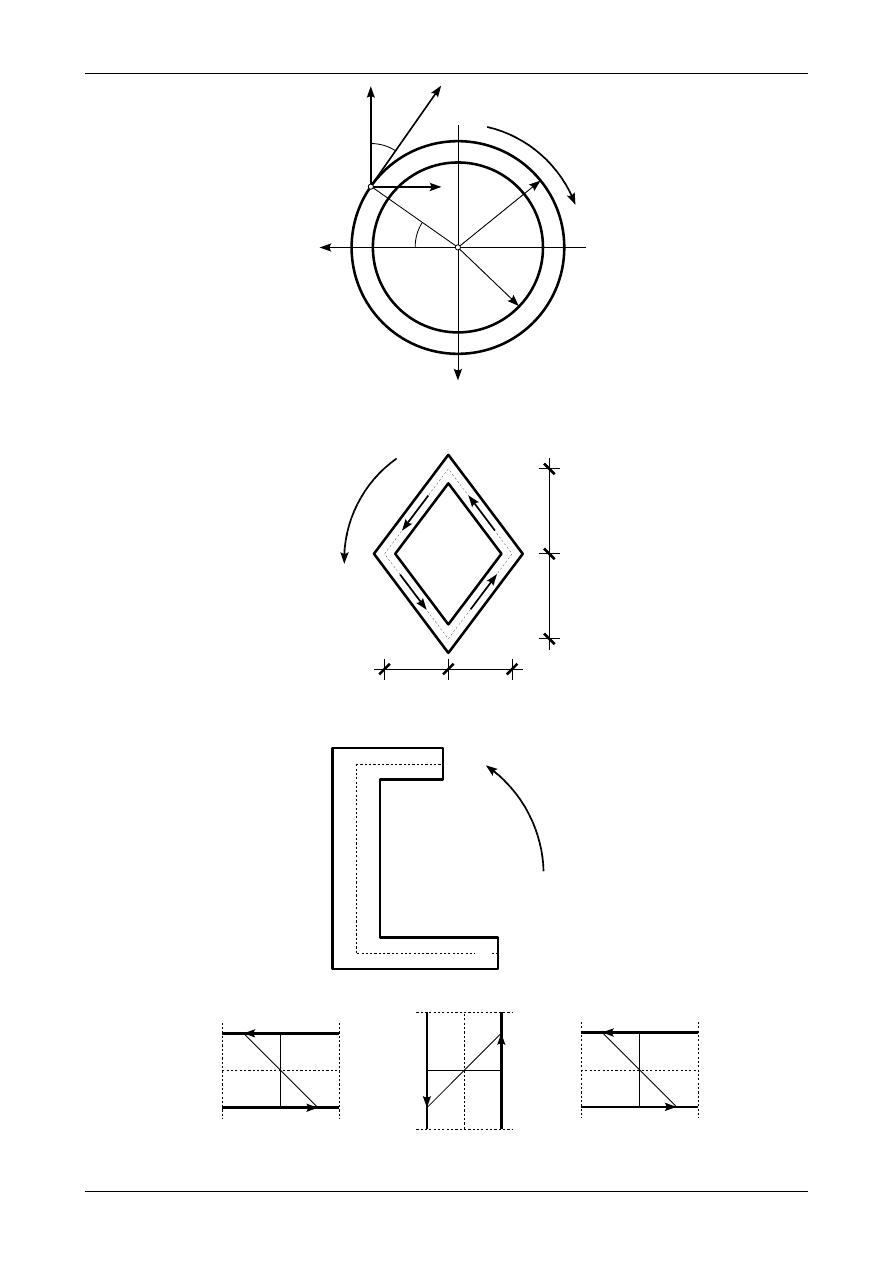
8.3. Odpowiedź do zadania 8/3

Rysunek 8.3 przedstawia stałe na grubości ścianki naprężenia styczne w przekroju o profilu zamknię-

tym.

8.4. Odpowiedź do zadania 8/4

Rysunek 8.4 przedstawia wykresy naprężeń stycznych na poszczególnych ściankach przekroju o profi-

lu otwartym.

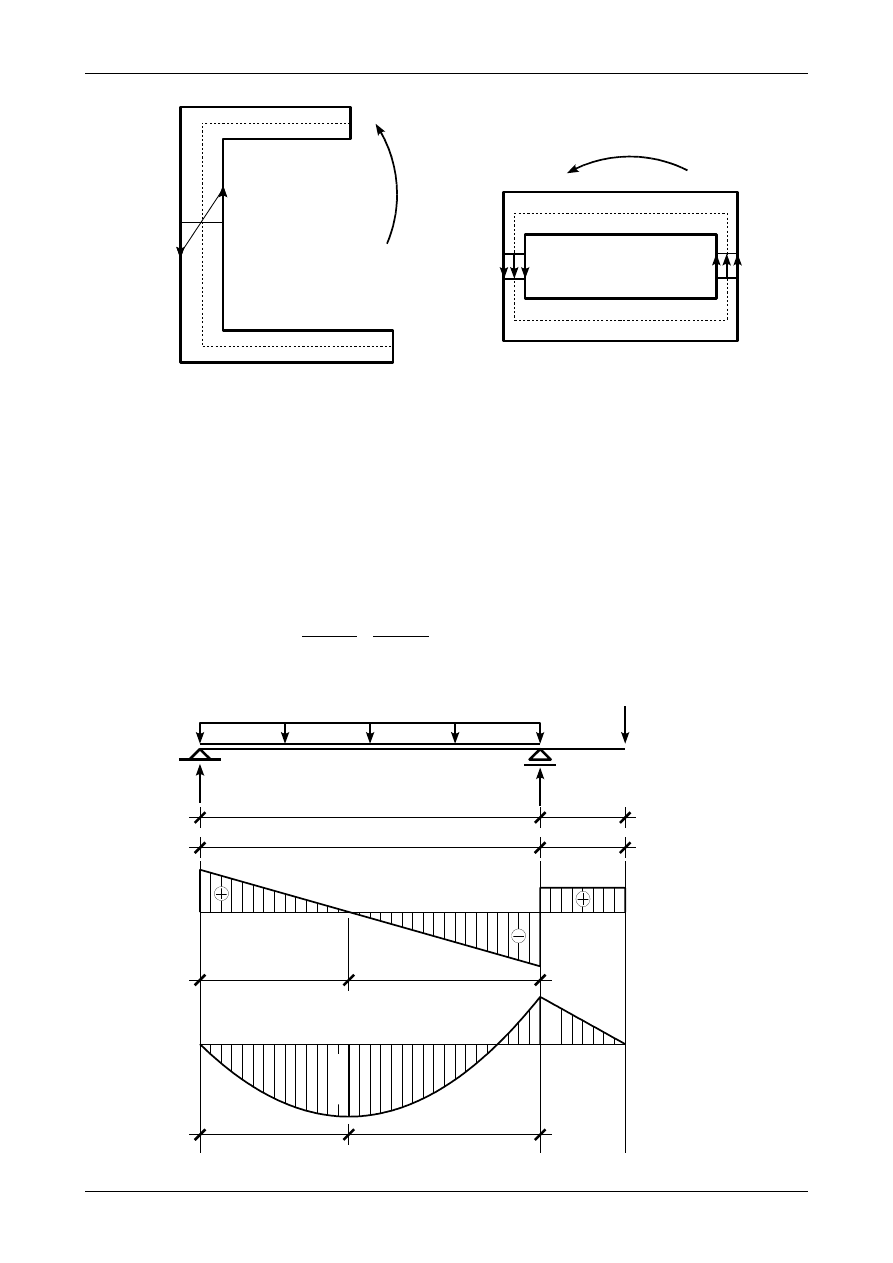
8.5. Odpowiedź do zadania 8/5

Rysunek 8.5 a) przedstawia rozkład maksymalnego naprężenia stycznego w przekroju o profilu

otwartym natomiast rysunek 8.5 b) w przekroju o profilu zamkniętym.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

47

Y=Y

gl

Z=Z

gl

8,0

[cm]

56

,0

k

N

m

10

,0

35

0

sc

O

3

5

0

34,63 MPa

49

,4

6

M

P

a

60,38 MPa

Rys. 8.2. Naprężenia styczne działające w punkcie A

[cm]

5,0

5,0

10

,0

10

,0

20

,0

k

N

m

10

0,0

M

Pa

10

0,

0

M

Pa

10

0,

0

M

Pa

10

0,0

M

Pa

Rys. 8.3. Rozkład naprężeń stycznych w ściankach przekroju o profilu zamkniętym

3

3,5

k

N

m

1

2

137,9 MPa

137,9 MPa

165,5 MPa

165,5 MPa

2

06

,9

M

P

a

2

06

,9

M

P

a

a)

b)

c)

Rys. 8.4. Rozkład naprężeń stycznych. a) prostokąt numer 1, b) prostokąt numer 2, c) prostokąt numer 3

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

48

2,0 kNm

2,0 kNm

19

9,

1

M

P

a

1

99

,1

M

P

a

1

0,

2

0

M

P

a

10

,2

0

M

P

a

a)

b)

Rys. 8.5. Rozkład maksymalnego naprężenia stycznego. a) w przekroju o profilu otwartym, b) w przekroju o profilu

zamkniętym

9. Ugięcia w belkach

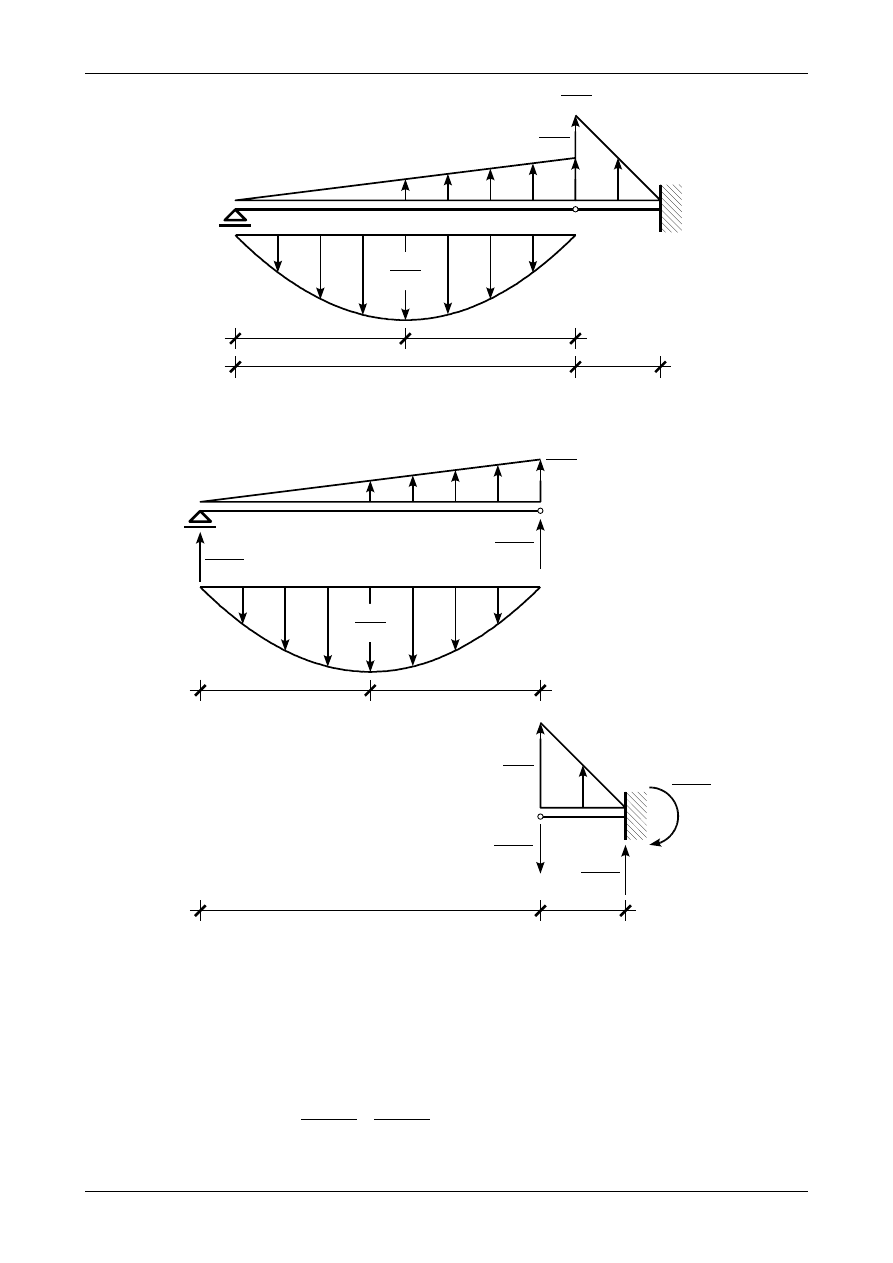
9.1. Odpowiedź do zadania 9/1 - wersja I

Rysunek 9.1 przedstawia wykresy siły poprzecznej oraz momentu zginającego w belce prostej. Jako

porównawczą sztywność na zginanie E∙J

0

przyjęto sztywność na zginanie w przedziale AB. Rysunek 9.2

przedstawia obciążenie wtórne belki fikcyjnej. Rysunek 9.3 przedstawia prawidłowe wartości i zwroty
wtórnych reakcji w belce fikcyjnej. Wartość ugięcia w punkcie C wynosi

w

C

=

−

85,33

E⋅J

0

=

−

85,33

2460

=−

0,03469 m=−3,469 cm

.

2,0

8,0

8,0 kN/m

16,0 kN

A

B

C

[m]

28,0 kN

52,0 kN

T(x) [kN]

M(x) [kNm]

28

,0

36

,0

16,0

0,

0

0,

0

3

2,

0

3,5

4,5

3,5

4,5

4

9,

0

2460 kNm

2

1230 kNm

2

Rys. 9.1. Wykresy siły poprzecznej oraz momentu zginającego w belce prostej

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

49

2,0

8,0

A

B

C

[m]

4,0

4,0

64,0

E⋅J

0

64,0

E⋅J

0

32,0

E⋅J

0

Rys. 9.2. Obciążenie wtórne belki fikcyjnej

A

B

4,0

4,0

64,0

E⋅J

0

32,0

E⋅J

0

2,0

8,0

B

C

[m]

64,0

E⋅J

0

128,0

E⋅J

0

85,33

E⋅J

0

85,33

E⋅J

0

85,33

E⋅J

0

21,33

E⋅J

0

Rys. 9.3. Prawidłowe wartości i zwroty wtórnych reakcji w belce fikcyjnej

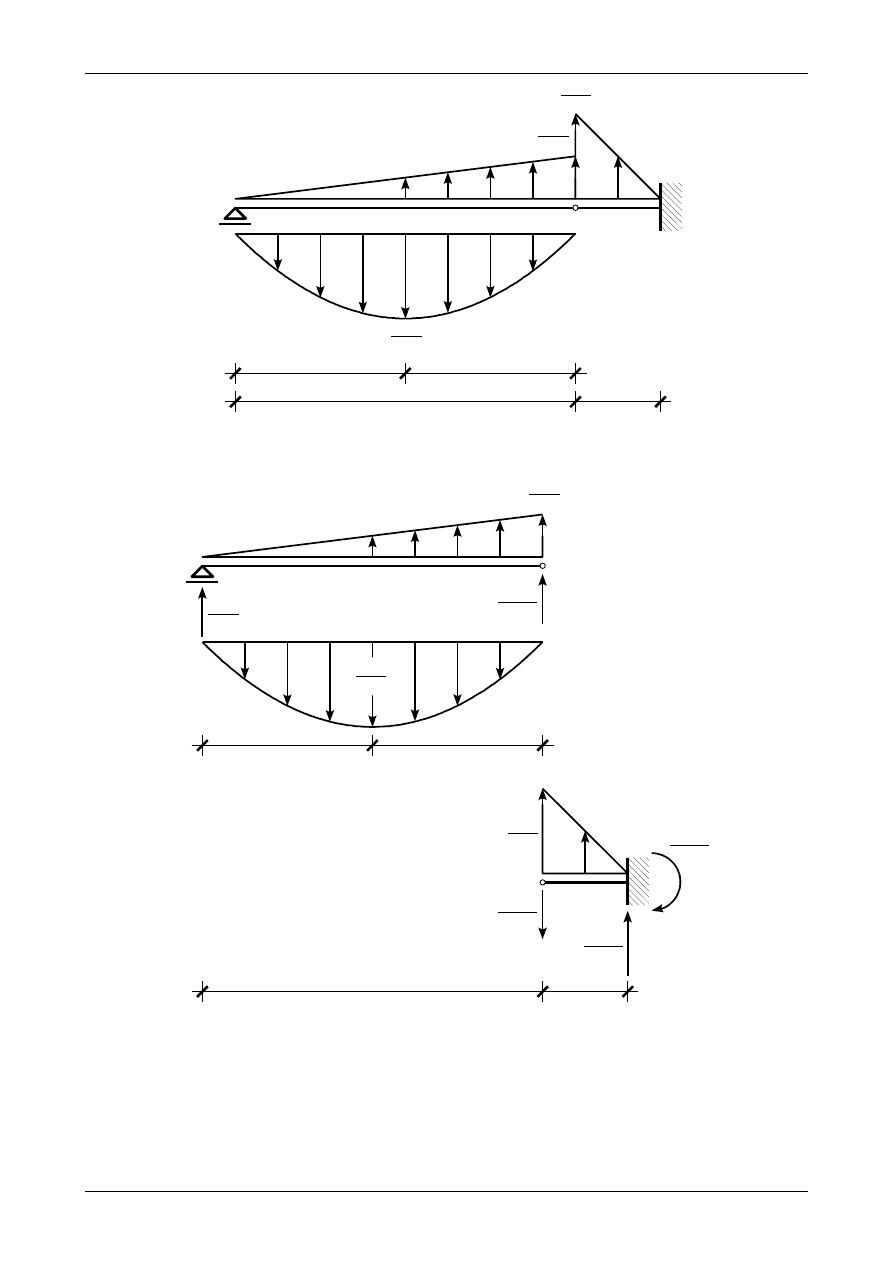
9.2. Odpowiedź do zadania 9/1 - wersja II

Jako porównawczą sztywność na zginanie E∙J

0

przyjęto sztywność na zginanie w przedziale BC.

Rysunek 9.4 przedstawia obciążenie wtórne belki fikcyjnej. Rysunek 9.5 przedstawia prawidłowe wartości
i zwroty wtórnych reakcji w belce fikcyjnej. Wartość ugięcia w punkcie C wynosi

w

C

=

−

42,67

E⋅J

0

=

−

42,67

1230

=−

0,03469 m=−3,469 cm

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

50

2,0

8,0

A

B

C

[m]

4,0

4,0

32,0

E⋅J

0

16,0

E⋅J

0

32,0

E⋅J

0

Rys. 9.4. Obciążenie wtórne belki fikcyjnej

A

B

4,0

4,0

32,0

E⋅J

0

2,0

8,0

B

C

[m]

16,0

E⋅J

0

64,0

E⋅J

0

42,67

E⋅J

0

42,67

E⋅J

0

42,67

E⋅J

0

10,67

E⋅J

0

32,0

E⋅J

0

Rys. 9.5. Prawidłowe wartości i zwroty wtórnych reakcji w belce fikcyjnej

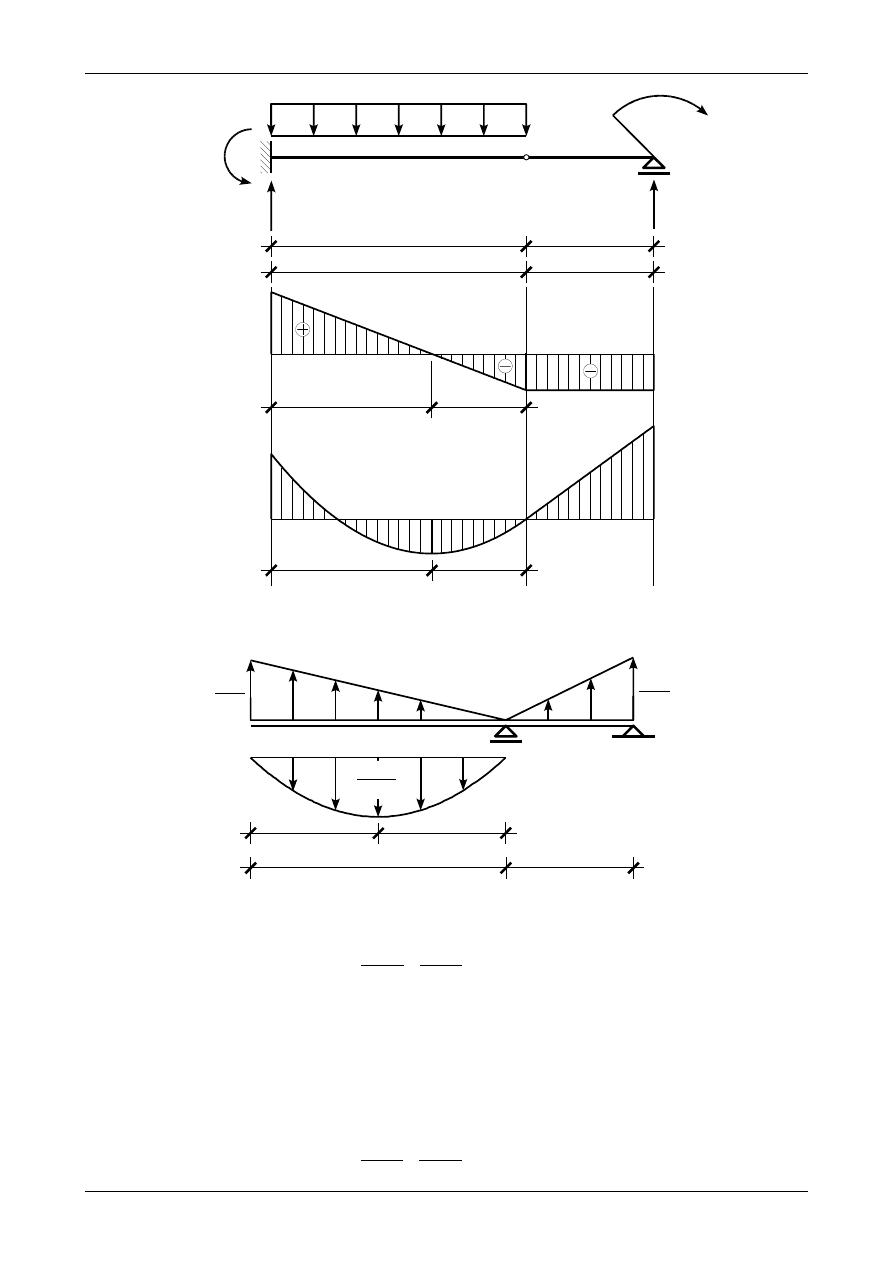
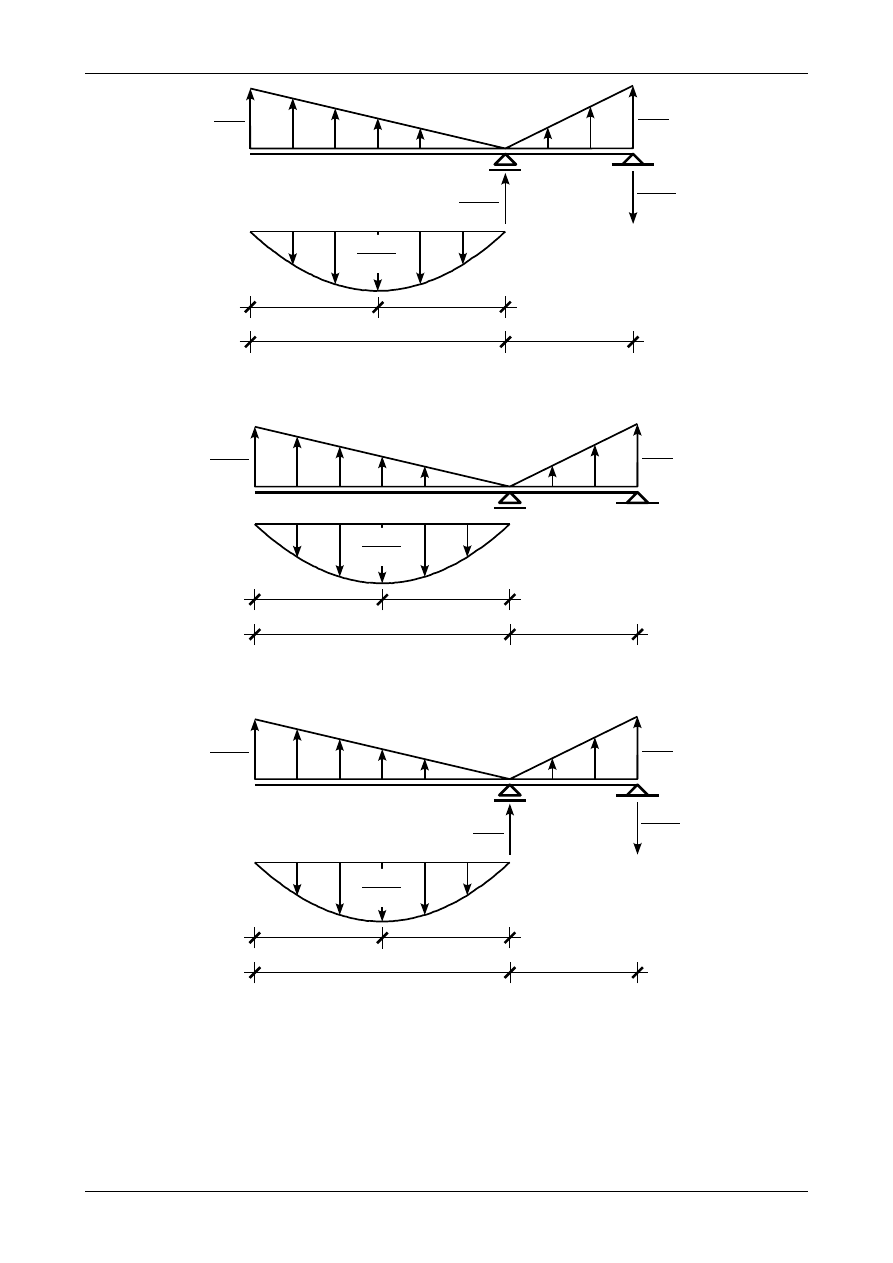
9.3. Odpowiedź do zadania 9/2 - wersja I

Rysunek 9.6 przedstawia wykresy siły poprzecznej oraz momentu zginającego w belce złożonej. Jako

porównawczą sztywność na zginanie E∙J

0

przyjęto sztywność na zginanie w przedziale AB. Rysunek 9.7

przedstawia obciążenie wtórne belki fikcyjnej. Rysunek 9.8 przedstawia prawidłowe wartości i zwroty
wtórnych reakcji w belce fikcyjnej. Wartość kąta obrotu przekroju w punkcie C wynosi

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

51

1,889

1,111

T [kN]

8

,5

5,0

M [kNm]

5

,2

5

0

,0

7,

5

1,889

1,111

2,

7

78

7,5 kNm

3,0

1,5

[m]

4,5 kN/m

A

B

C

5,25 kNm

8,5 kN

5,0 kN

512,5 kNm

2

615,0 kNm

2

Rys. 9.6. Wykresy siły poprzecznej oraz momentu zginającego w belce złożonej

3,0

1,5

[m]

A

B

C

1,5

1,5

5,25

E⋅J

0

5,063

E⋅J

0

6,25

E⋅J

0

Rys. 9.7. Obciążenie wtórne belki fikcyjnej



C

=

6,443

E⋅J

0

=

6,443
512,5

=

0,01257 rad

.

9.4. Odpowiedź do zadania 9/2 - wersja II

Jako porównawczą sztywność na zginanie E∙J

0

przyjęto sztywność na zginanie w przedziale BC.

Rysunek 9.9 przedstawia obciążenie wtórne belki fikcyjnej. Rysunek 9.10 przedstawia prawidłowe wartości
i zwroty wtórnych reakcji w belce fikcyjnej. Wartość kąta obrotu w punkcie C wynosi



C

=

7,725

E⋅J

0

=

7,725
615,0

=

0,01256 rad

.

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

52

3,0

1,5

[m]

A

B

C

1,5

1,5

5,25

E⋅J

0

5,063

E⋅J

0

6,25

E⋅J

0

4,010

E⋅J

0

6,443

E⋅J

0

Rys. 9.8. Prawidłowe wartości i zwroty wtórnych reakcji w belce fikcyjnej

3,0

1,5

[m]

A

B

C

1,5

1,5

7,50

E⋅J

0

6,300

E⋅J

0

6,076

E⋅J

0

Rys. 9.9. Obciążenie wtórne belki fikcyjnej

3,0

1,5

[m]

A

B

C

1,5

1,5

7,50

E⋅J

0

6,300

E⋅J

0

6,076

E⋅J

0

4,80
E⋅J

0

7,725

E⋅J

0

Rys. 9.10. Prawidłowe wartości i zwroty wtórnych reakcji w belce fikcyjnej

10. Wyznaczanie siły krytycznej prętów ściskanych osiowo

10.1. Odpowiedź do zadania 10/1

Pole powierzchni oraz główne momenty bezwładności dla pręta ściskanego osiowo wynoszą odpo-

wiednio

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

53

A

=

156,2cm

2

,

J

Y

=

J

Ygl

=

19620 cm

4

,

J

Z

=

J

Zgl

=

11400 cm

4

Smukłość graniczna wynosi



GR

=

99,35

.

Największa smukłość pręta występuje w płaszczyźnie XZ i ma ona wartość



=



Y

=

107,0

.

Smukłość ta jest większa niż smukłość graniczna. Pręt pracuje więc w zakresie sprężystym. Naprężenie
krytyczne wynosi



KR

=

176,7 MPa

.

Ostatecznie siła krytyczna wynosi

P

KR

=

2760 kN

.

10.2. Odpowiedź do zadania 10/2

Pole powierzchni oraz główne momenty bezwładności dla pręta ściskanego osiowo wynoszą odpo-

wiednio

A=64,4cm

2

,

J

Y

=

J

Ygl

=

2237cm

4

,

J

Z

=

J

Zgl

=

3820cm

4

.

Smukłość graniczna wynosi



GR

=

99,35

.

Największa smukłość pręta występuje w płaszczyźnie XY i ma ona wartość

Dr inż. Janusz Dębiński

Budownictwo

WM

Zbiór zadań z Wytrzymałości materiałów - odpowiedzi

54

=

Z

=

38,95

.

Smukłość ta jest mniejsza niż smukłość graniczna. Pręt pracuje więc w zakresie sprężysto-plastycznym.
Naprężenie krytyczne wynosi



KR

=

223,2 MPa

.

Ostatecznie siła krytyczna wynosi

P

KR

=

1437kN

.

Dr inż. Janusz Dębiński

Budownictwo