-
Granica cia
,
gu
Ostatnia aktualizacja 22 pa´
zdziernika 2012, godz. 23:57
W wielu sytuacjach rozpatrywane sa
,
tzw. cia
,
gi liczbowe. Je´sli np. chcemy zdefi-
niowa´c pole ko la, to mo˙zna rozwa˙za´c np. wieloka
,
ty foremne wpisane w to ko lo o coraz
wie
,
kszej liczbie bok´ow i m´owi´c, ˙ze pole ko la jest liczba
,
, kt´ora
,
mo˙zna przybli˙za´c po-
lami tych wieloka
,
t´ow, przy czym przybli˙zenie jest tym dok ladniejsze im wie
,
ksza jest
liczba bok´ow wieloka
,
ta. Mamy tu wie
,
c do czynienia z cia
,
giem p´ol wieloka
,
t´ow wpi-
sanych w dane ko lo, co oznacza, ˙ze liczbom naturalnym pocza
,
wszy od 3 przypisane
zosta ly pewne liczby rzeczywiste. Te ostatnie nazywamy wyrazami cia
,
gu i oznaczamy
na og´o l symbolem a
n
.
Inny przyk lad by l rozwa˙zany przez Zenona (490-430 p.n.e) z Elei . Twierdzi l on
mianowicie, ˙ze znany w staro˙zytno´sci biegacz Achilles nie jest w stanie dogoni´c ˙z´o lwia.
Rozwa˙zania te przedstawimy oczywi´scie u˙zywaja
,
c wsp´o lczesnego je
,
zyka i stosuja
,
c
wsp´o lczesne oznaczenia. Przyjmijmy na przyk lad, ˙ze pocza
,
tkowa odleg lo´s´c mie
,
dzy
Achillesem i ˙z´o lwiem r´owna jest 100 m. Dla prostoty przyjmiemy, ˙ze pre
,
dko´s´c Achil-
lesa jest dziesie
,
ciokrotnie wie
,
ksza ni˙z pre
,
dko´s´c uciekaja
,
cego ˙z´o lwia. W jakim´s czasie
Achilles przebiegnie 100 m. W tym samym czasie ˙z´o lw przesunie sie
,
o 10 m, wie
,
c
na razie przynajmniej nie zostanie z lapany. Po
1
10
tego czasu Achilles przebiegnie
10 m, jednak zn´ow nie dogoni ˙z´o lwia, kt´ory oddali sie
,
o naste
,
pny metr. Achilles
przebiegnie metr, a ˙z´o lw oddali sie
,
o 10 cm itd. Proces ten mo˙zna kontynuowa´c.
Prowadzi to do rozpatrywania coraz d lu˙zszych odcink´ow przebytych przez Achillesa,
czyli liczb: 100 ; 110 ; 111 ; 111,1 ; . . . – czyli cia
,
gu, kt´orego wyraz o numerze n jest
dany za pomoca
,
wzoru a
n
= 100 + 10 + 1 + . . . +
100
10
n−1
= 111,1 . . . 1 – przy czym w
zapisie dziesie
,
tnym tej liczby wyste
,
puje n jedynek. Zenon po prostu nie potrafi l zsu-
mowa´c niesko´
nczenie wielu sk ladnik´ow. Nie operowa l poje
,
ciem sumy niesko´
nczonej,
nie umiano wtedy takiego poje
,
cia zdefiniowa´c. Tego rodzaju problemy analizowano
ju˙z wtedy, ale ´scis le definicje matematyczne pojawi ly sie
,
dopiero w pierwszej po lowie
XIX wieku (Gauss, Cauchy, Bolzano). Oczywi´scie mo˙zna latwo odpowiedzie´c na py-
tanie po przebiegnie
,
ciu jakiego dystansu Achilles z lapie ˙z´o lwia: 111, 1 . . . =
1000
9
.
Na wszelki wypadek podamy formalne rozumowanie, kt´ore mo˙zna by lo zastosowa´c
r´ownie˙z w staro˙zytno´sci, jednak bez jawnego u˙zycia poje
,
cia sumy niesko´
nczonej, a
wie
,
c omijaja
,
c istotny problem matematyczno-filozoficzny.* Oznaczmy dystans prze-
byty przez ˙z´o lwia do momentu zako´
nczenia pogoni przez x . Achilles w tym samym
czasie przebieg l odleg lo´s´c 10x . R´o˙znica tych wielko´sci to 9x = 100 . Sta
,
d natych-
miast wynika, ˙ze x =
100
9
, zatem 10x =
1000
9
. Oczywi´scie problemem istotnym
*
By ly inne paradoksy zwia,zane z problemem dzielenia w niesko´nczono´s´c na cze,´sci, np. punkt nie ma
d lugo´sci, odcinek sk lada sie, z punkt´ow i ma d lugo´s´c, poruszaja,cy sie, obiekt w niesko´nczenie kr´otkim
czasie nie przebywa ˙zadnej odleg lo´sci, a jednak sie, porusza. Przekonamy sie,, ˙ze dzie,ki poje,ciu granicy
daje sie, w sensowny spos´ob m´owi´c o tego rodzaju kwestiach nie dochodza,c do pozornych sprzeczno´sci.
1

Granica cia
,
gu
Micha l Krych
by lo tu obliczenie tzw. granicy cia
,
gu, czym zajmiemy sie
,
niebawem.
Rozwa˙zymy jeszcze inny przyk lad. Za l´o˙zmy, ˙ze mamy do czynienia z pewna
,
ilo´scia
,
pierwiastka promieniotw´orczego. Niech m oznacza jego mase
,
. Fizycy twierdza
,
,
˙ze ubytek masy pierwiastka promieniotw´orczego jest proporcjonalny do czasu i masy
substancji. Oznaczmy wsp´o lczynnik proporcjonalno´sci przez µ i zastan´owmy sie
,
jaka
,
ilo´s´c tego pierwiastka be
,
dziemy mie´c po czasie t . Na tzw. „zdrowy rozum” masa
w czasie t powinna sie
,
zmniejszy´c o µ · t · m . Jednak substancja promieniuje bez
przerwy. Mogliby´smy wie
,
c rozumowa´c w ten sam spos´ob my´sla
,
c o czasie dwukrotnie
kr´otszym, czyli
t
2
. Wtedy masa zmniejszy laby sie
,
o µ ·
t
2
· m . Wobec tego po czasie
t
2
masa by laby r´owna m − µ ·
t
2
· m = m 1 − µ ·
t
2
) . Ta masa zmniejsza laby sie
,
w
dalszym cia
,
gu zgodnie z tym samym prawem, wie
,
c po czasie
t
2
masa pierwiastka
by laby r´owna m 1 − µ ·
t
2
) − µ ·
t
2
m 1 − µ ·
t
2
) = m 1 − µ ·
t
2
)
2
. Mamy wie
,
c dwa wyniki
1 − µ ·
t
2
)
2
m , je´sli czas „dzielimy ” na p´o l oraz 1 − µ · t
m , je´sli „nie dzielimy”.
Te wyniki sa
,
r´o˙zne, wie
,
c podany opis nie mo˙ze by´c dobry. Na domiar z lego, je´sli
czas podzielimy nie na dwie r´owne cze
,
´sci, to wynik be
,
dzie jeszcze inny: przy podziale
t =
t
3
+
t
3
+
t
3
wywnioskujemy, ˙ze po czasie t masa r´owna jest m 1 − µ ·
t
4
)
3
, przy
podziale t =
t
4
+
t
4
+
t
4
+
t
4
wynik to m 1−µ·
t
4
)
4
. Oczywi´scie rezultat nie mo˙ze zale˙ze´c
od tego, w jaki spos´ob opisujemy zjawisko. Mo˙zna wie
,
c przypu´sci´c, ˙ze zacytowane
prawo fizyki dzia la w przypadku dostatecznie kr´otkiego czasu z b le
,
dem mniejszym ni˙z
dok ladno´s´c pomiaru. Matematyka obliguje to do zadania pytania: czy kolejne liczby
m 1 − µ · t) , m 1 − µ ·
t
2
)
2
, m 1 − µ ·
t
3
)
3
, m 1 − µ ·
t
4
)
4
, . . . przybli˙zaja
,
z coraz
wie
,
ksza
,
dok ladno´scia
,
pewna
,
liczbe
,
, kt´ora mog laby by´c wtedy uwa˙zana za prawdziwy
wynik?
Pytanie okazuje sie
,
tym wa˙zniejsze, ˙ze do tego samego pytania prowadzi analiza
oprocentowanego wk ladu bankowego albo np. wyd lu˙zania sie
,
np. szyn kolejowych
w wyniku wzrostu temperatury lub ich skracania sie
,
w wyniku spadku tempera-
tury. To prawo fizyczne jest znane ka˙zdemu, kto by l przytomny w czasie lekcji fizyki
w szkole podstawowej lub gimnazjum. Jednak nieliczni uczniowie zauwa˙zaja
,
problem,
kt´ory opisali´smy wy˙zej. Stosowanie tego prawa w spos´ob opisany w podre
,
cznikach
szkolny prowadzi do r´o˙znych wynik´ow w zale˙zno´sci od tego czy temperatura zmienia
sie
,
np. o 20
◦
, czy te˙z o 10
◦
+10
◦
, co oczywi´scie nie mo˙ze by´c prawda
,
, bowiem wzrost
temperatury nie jest skokowy, lecz odbywa sie
,
stopniowo. Podsumujmy: opisane wy˙zej
zagadnienia prowadza
,
do rozpatrywania cia
,
gu o wyrazie (1+
x
n
)
n
, w przypadku masy
substancji promieniotw´orczej x = −µ · t . Powy˙zsze rozwa˙zania sugeruja
,
, ˙ze wzrost
liczby naturalnej n powinien powodowa´c wzrost wyra˙zenia (1 +
x
n
)
n
przynajmniej
w przypadku x 6= 0 . W istocie rzeczy latwo mo˙zna sie
,
przekona´c o tym, ˙ze n > −x
2

Granica cia
,
gu
Micha l Krych
wzrost taki ma miejsce, wyka˙zemy to niebawem.
Innym rodzajem cia
,
gu jest tzw. cia
,
g geometryczny: a
n
= a
0
q
n
, gdzie a
0
i q sa
,
dowolnymi liczbami rzeczywistymi. Liczba q jest zwana ilorazem cia
,
gu geometrycz-
nego, bo w przypadku q 6= 0 jest r´owna ilorazowi dw´och kolejnych wyraz´ow cia
,
gu. Do
rozpatrywania tego cia
,
gu prowadza
,
opisane poprzednio zagadnienia, je´sli nie zmniej-
szamy odcink´ow czasu lub temperatury Liczba ludzi w danym kraju w przypadku
sta lego przyrostu naturalnego zachowuje sie
,
jak cia
,
g geometryczny o ilorazie dosy´c
bliskim jedno´sci — dodatni przyrost naturalny oznacza, ˙ze iloraz jest wie
,
kszy ni˙z 1
za´s ujemny przyrost naturalny — ˙ze iloraz jest mniejszy ni˙z 1 .
Jeszcze innym rodzajem cia
,
gu jest cia
,
g arytmetyczny: a
n
= a
0
+ nd , gdzie a
0
oraz d oznaczaja
,
dowolne liczby rzeczywiste. Liczba d zwana jest r´o˙znica
,
cia
,
gu aryt-
metycznego, jest ona r´owna r´o˙znicy dw´och kolejnych wyraz´ow cia
,
gu. Na prze lomie
XVIII i XIX wieku zaobserwowano, ˙ze ilo´s´c zbo˙za zachowuje sie
,
jak wyraz cia
,
gu
arytmetycznego ( n jest numerem roku). Oczywi´scie tego rodzaju obserwacje sa
,
przy-
bli˙zone, bowiem co jaki´s czas zdarzaja
,
sie
,
powodzie, susze i wtedy proces wzrostu
ulega zak l´oceniu. Bywaja
,
te˙z zak l´ocenia innego rodzaju, np. w XIX zauwa˙zono, ˙ze
stosowanie saletry chilijskiej (nawozy azotowe) zwie
,
ksza w istotny spos´ob plony. By ly
te˙z inne zak l´ocenia „naturalnego” tempa wzrostu ilo´sci zb´o˙z.
W ksia
,
˙zce „Liber Abaci” z 1202 r. autorstwa Leonarda z Pizy, zwanego Fibo-
naccim, znajduje sie
,
naste
,
puja
,
ce zadanie: Ile par kr´olik´ow mo˙ze by´c sp lodzonych
przez pare
,
p lodnych kr´olik´ow i jej potomstwo w cia
,
gu roku, je´sli ka˙zda para daje
w cia
,
gu miesia
,
ca ˙zywot jednej parze, para staje sie
,
p lodna po miesia
,
cu, kr´oliki nie
zdychaja
,
w cia
,
gu tego roku. Jasne jest, ˙ze po miesia
,
cu mamy ju˙z dwie pary przy
czym jedna z nich jest p lodna, a druga jeszcze nie. Wobec tego po dw´och miesia
,
cach
˙zyja
,
ju˙z trzy pary kr´olik´ow: dwie p lodne, jedna jeszcze nie. Po trzech miesia
,
cach
˙zyje ju˙z pie
,
´c par kr´olik´ow: trzy p lodne, dwie jeszcze nie. Po czterech miesia
,
cach jest
ju˙z 8 = 5 + 3 par kr´olik´ow. Kontynuuja
,
c to poste
,
powanie stwierdzamy po niezbyt
d lugim czasie, ˙ze po roku ˙zyje ju˙z 377 = 233 + 144 par kr´olik´ow. Naturalnym pro-
blemem jest: znale´z´c wz´or na liczbe
,
a
n
, je´sli a
0
= 1 , a
1
= 2 i a
n
= a
n−1
+ a
n−2
dla
n = 2, 3, 4, . . . . Wz´or taki zosta l znaleziony dopiero po kilkuset latach od napisania
ksia
,
˙zki przez
Fibonacci’ego i wygla
,
da tak:
a
n
=
1+
√
5
2
n+2
−
1−
√
5
2
n+2
√
5
.
Dow´od prawdziwo´sci tego wzoru jest prosty i nie wykracza poza program liceum
3

Granica cia
,
gu
Micha l Krych
— latwa indukcja. Jednak wa˙zniejsze jest pytanie, jak w og´ole mo˙zna tego rodzaju
hipoteze
,
sformu lowa´c. Za kilka miesie
,
cy stanie sie
,
jasne w jaki spos´ob do takiego
dziwnego rezultatu mo˙zna doj´s´c.
Przejdziemy teraz do ´scis lego zdefiniowania cia
,
gu.
Definicja 4.1 (cia
,
gu)
Cia
,
giem nazywamy dowolna
,
funkcje
,
okre´slona
,
na zbiorze z lo˙zonym ze wszystkich tych
liczb ca lkowitych, kt´ore sa
,
wie
,
ksze lub r´owne pewnej liczbie ca lkowitej n
0
. Warto´s´c
tej funkcji punkcie n nazywamy n -tym wyrazem cia
,
gu.
Stosujemy oznaczenie (a
n
) dla oznaczenia cia
,
gu, kt´orego n -tym wyrazem jest
a
n
. Rozpatruja
,
c wieloka
,
ty wpisane w okra
,
g zaczynamy od tr´ojka
,
ta, w tym przy-
padku najmniejszym numerem wyrazu cia
,
gu jest liczba n
0
= 3 (zaczynamy wie
,
c
od a
3
). Rozwa˙zaja
,
c cia
,
gi postaci 1 +
x
n
n
zaczynamy od n
0
= 1 , czyli od a
1
.
Rozpatruja
,
c cia
,
g arytmetyczny, geometryczny oraz cia
,
g Fibonacciego rozpocze
,
li´smy
od n
0
= 0 . Oczywi´scie mo˙zna rozpoczyna´c numeracje
,
od dowolnej liczby ca lkowitej,
r´ownie˙z ujemnej. Terminy cia
,
g arytmetyczny, cia
,
g geometryczny u˙zywane be
,
da
,
nie
tylko w przypadku cia
,
g´ow rozpoczynaja
,
cych sie
,
od wyrazu a
0
, r´ownie˙z w tym przy-
padku n
0
mo˙ze by´c dowolna
,
liczba
,
ca lkowita
,
. Chodzi jedynie o to, by by ly prawdziwe
r´owno´sci a
n
= a
n−1
+ d lub — w przypadku cia
,
gu geometrycznego — a
n
= a
n−1
· q
dla wszystkich liczb ca lkowitych n ≥ n
0
. Zazwyczaj jednak numeracje
,
be
,
dziemy roz-
poczyna´c od 0 lub od 1 . Je´sli nie zaznaczymy tego wyra´znie, symbol n oznacza´c
be
,
dzie liczbe
,
ca lkowita
,
nieujemna
,
, czyli naturalna
,
.*
Rozpatrywanie cia
,
g´ow niesko´
nczonych wymaga precyzji. Wiele os´ob nie mo˙ze
pogodzi´c sie
,
z tym, ˙ze 1 = 0, 9999 . . . = 0,9 + 0,09 + 0,009 + 0,0009 + . . . , bo wy-
daje im sie
,
, ˙ze prawa strona jest mniejsza, cho´c wiedza
,
jaka mia laby r´o˙znica le-
wej i prawej strony. Om´owimy jeszcze jeden przyk lad, kt´ory w przekonaniu autora
tekstu wyra´znie sugeruje konieczno´s´c dok ladnego zdefiniowania poje
,
´c, kt´orymi sie
,
pos lugujemy i wyja´snienia, co wolno, a czego nie wolno robi´c. Rozwa˙zmy sume
,
s = 1 −
1
2
+
1
3
−
1
4
+
1
5
−
1
6
+
1
7
−
1
8
+
1
9
−
1
10
+
1
11
−
1
12
+
1
13
−
1
14
+
1
15
−
1
16
+
1
17
−
1
18
+ . . .
W sumie wyste
,
puje niesko´
nczenie wiele sk ladnik´ow. Jest jasne, ˙ze
s = 1−
1
2
+
1
3
−
1
4
+
1
5
−
1
6
+
1
7
−
1
8
+
1
9
−
1
10
+
1
11
−
1
12
+
1
13
−
1
14
+
1
15
−
1
16
+
1
17
−
1
18
+. . . = =(1−
1
2
)+(
1
3
−
1
4
)+(
1
5
−
1
6
)+(
1
7
−
1
8
)+(
1
9
−
1
10
)+(
1
11
−
1
12
)+(
1
13
−
1
14
)+(
1
15
−
1
16
)++(
1
17
−
1
18
)+
. . . > 1 −
1
2
, bo r´o˙znice w nawiasach sa
,
dodatnie. Podobnie mo˙zna uzasadni´c, ˙ze
*
Cze,´s´c matematyk´ow uwa˙za, ˙ze liczby naturalne to 1 , 2 ,
. . .
Inni uwa˙zaja,, ˙ze zaczyna´c nale˙zy od 0 .
W momencie pisania tego tekstu autor przychyli l sie, do tej drugiej koncepcji: liczby naturalne s lu˙za,
przede wszystkim do ustalania liczby element´
ow danego zbioru sko´
nczonego, poniewa˙z rozwa˙zamy
niejednokrotnie zbi´
or pusty, wie,c liczbe, 0 uwa˙za´c be,dziemy za naturalna,.
4

Granica cia
,
gu
Micha l Krych
s > (1−
1
2
)+(
1
3
−
1
4
) =: s
4
lub s > (1−
1
2
)+(
1
3
−
1
4
)+(
1
5
−
1
6
)+(
1
7
−
1
8
)+(
1
9
−
1
10
) =: s
10
.
Rozpatrywana
,
sume
,
mo˙zemy te˙z zapisa´c tak:
s = 1 −
1
2
+
1
3
−
1
4
+
1
5
−
1
6
+
1
7
−
1
8
+
1
9
−
1
10
+
1
11
−
1
12
+
1
13
−
1
14
+
1
15
−
1
16
+
1
17
−
1
18
+ . . . =
=1 + (−
1
2
+
1
3
) + (−
1
4
+
1
5
) + (−
1
6
+
1
7
) + (−
1
8
+
1
9
) + (−
1
10
+
1
11
) + (−
1
12
+
1
13
) +
+(−
1
14
+
1
15
)+(−
1
16
+
1
17
)+(−
1
18
+
1
19
)+. . . < 1 =: s
1
— ostatnia nier´owno´s´c wynika
z tego, ˙ze sumy we wszystkich nawiasach sa
,
ujemne. Podobnie jak poprzednio mo˙zemy
wykaza´c wie
,
cej: s = 1 + (−
1
2
+
1
3
) + (−
1
4
+
1
5
) + (−
1
6
+
1
7
) + (−
1
8
+
1
9
) + (−
1
10
+
1
11
) +
+(−
1
12
+
1
13
) + (−
1
14
+
1
15
) + (−
1
16
+
1
17
) + (−
1
18
+
1
19
) + . . . < 1 + (−
1
2
+
1
3
) =: s
3
Og´olnie, je´sli s
n
oznacza sume
,
pierwszych n sk ladnik´ow sumy niesko´
nczonej s ,
to dla ka˙zdej liczby naturalnej n zachodzi nier´owno´s´c s
2n
< s < s
2n+1
. Jasne jest
te˙z, ˙ze istnieje tylko jedna taka liczba σ , ˙ze s
2n
< σ < s
2n+1
dla wszystkich liczb
naturalnych n . Poprzekszta lcamy jeszcze troche
,
:
s = 1 −
1
2
+
1
3
−
1
4
+
1
5
−
1
6
+
1
7
−
1
8
+
1
9
−
1
10
+
1
11
−
1
12
+
1
13
−
1
14
+
1
15
−
1
16
+
1
17
−
1
18
+ . . . =
=1 −
1
2
−
1
4
+
1
3
−
1
6
−
1
8
+
1
5
−
1
10
−
1
12
+
1
7
−
1
14
−
1
16
+
1
9
−
1
18
−
1
20
+ . . . =
=
1
2
−
1
4
+
1
6
−
1
8
+
1
10
−
1
12
+
1
14
−
1
16
+
1
18
−
1
20
+ . . . =
=
1
2
1 −
1
2
+
1
3
−
1
4
+
1
5
−
1
6
+
1
7
−
1
8
+
1
9
−
1
10
+ . . .
=
1
2
s — zmienili´smy kolejno´s´c
sk ladnik´ow nie pozbywaja
,
c ani jednego, pogrupowali´smy i w ko´
ncu, po wy la
,
czeniu
1
2
przed nawias, doprowadzili´smy do r´owno´sci s =
1
2
s , kt´ora mia laby zachodzi´c
pomimo tego, ˙ze
1
2
< s < 1 . Wida´c wie
,
c, ˙ze je´sli chcemy operowa´c sumami nie-
sko´
nczenie wielu sk ladnik´ow, to musimy zdefiniowa´c dok ladnie poje
,
cia, np. sumy
niesko´
nczonej, a potem sformu lowa´c i udowodni´c odpowiednie twierdzenia pozwa-
laja
,
ce na przekszta lcanie sum niesko´
nczonych.
Kluczowym poje
,
ciem jest granica cia
,
gu – poje
,
cia zasygnalizowanego przy okazji
omawiania paradoksu Zenona. Warto stwierdzi´c od razu, ˙ze w definicji pojawi sie
,
zdanie wielokrotnie z lo˙zone, a takie zdania osobom, kt´ore ich na co dzie´
n nie u˙zywaja
,
moga
,
sprawia´c k lopoty. Zreszta
,
ludzie przez d lugi czas m´owili o granicach nie podaja
,
c
precyzyjnej definicji, co prowadzi lo do r´o˙znych nieporozumie´
n, ale poda´c definicje
,
u˙zyteczna
,
i jednocze´snie ´scis la
,
, nie by lo latwo.
Definicja 4.2 (granicy cia
,
gu)
a. Liczba g nazywana jest granica
,
cia
,
gu (a
n
) wtedy i tylko wtedy, gdy dla
dowolnej liczby dodatniej ε > 0 istnieje liczba ca lkowita n
ε
, taka ˙ze je´sli
n > n
ε
, to |a
n
− g| < ε .
b. +∞ (czytaj: plus niesko´
nczono´s´c) jest granica
,
cia
,
gu (a
n
) wtedy i tylko
wtedy, gdy dla ka˙zdej liczby rzeczywistej M istnieje liczba ca lkowita n
m
taka, ˙ze je´sli n > n
M
, to a
n
> M.
5

Granica cia
,
gu
Micha l Krych
c. −∞ (czytaj: minus niesko´
nczono´s´c) jest granica
,
cia
,
gu (a
n
) wtedy i tylko
wtedy, gdy dla ka˙zdej liczby rzeczywistej M istnieje liczba ca lkowita n
m
taka, ˙ze je´sli n > n
M
, to a
n
< M.
d. Je´sli g jest granica
,
cia
,
gu (a
n
) , sko´
nczona
,
lub nie, to piszemy g = lim
n→∞
a
n
lub
a
n
−−−−−→
n→∞
g . Mo˙zna te˙z pisa´c a
n
→ g , gdy n → ∞ lub kr´otko
a
n
→ g . M´owimy, ˙ze cia
,
g jest zbie˙zny, je´sli jego granica jest sko´
nczona.
Skomentujemy po pierwsze cze
,
´s´c a. Chodzi tam o to, ˙ze wyrazy cia
,
gu, kt´orych
numery sa
,
dostatecznie du˙ze ( n > n
ε
) przybli˙zaja
,
granice
,
g z dopuszczalna
,
dok-
ladno´scia
,
( |a
n
− g| < ε ). Stwierdzimy tu wyra´znie, ˙ze przej´scie do naste
,
pnego
wyrazu nie musi zwie
,
kszy´c dok ladno´sci przybli˙zenia, przeciwnie chwilowo mo˙ze sie
,
ta dok ladno´s´c zmniejszy´c, dopiero dostatecznie du˙zy wzrost numeru wyrazu musi
zwie
,
kszy´c dok ladno´s´c przybli˙zenia (je´sli cia
,
g jest sta ly, np. a
n
= 33 dla ka˙zdej
liczby naturalnej n , to b la
,
d jest zerowy zawsze, niezale˙znie od numeru wyrazu, wie
,
c
dok ladno´s´c nie mo˙ze by´c poprawiona). O liczbie ε my´sle´c nale˙zy jako o ma lej liczbie
dodatniej (chodzi o to, ˙ze je´sli dla ma lego ε umiemy wskaza´c moment, od kt´orego
b la
,
d jest mniejszy ni˙z ε , to od tego momentu nier´owno´s´c jest r´ownie˙z spe lniona
z wie
,
kszym ε ). Pamie
,
tajmy r´ownie˙z o tym, ˙ze liczba |x − y| mo˙ze by´c traktowana
jako odleg lo´s´c dw´och punkt´ow prostej. Wobec tego nier´owno´s´c |a
n
− g| < ε oznacza,
˙ze punkt a
n
znajduje sie
,
w przedziale o d lugo´sci 2ε i ´srodku g . W szczeg´olno´sci cia
,
g,
kt´orego wszystkie wyrazy sa
,
takie same (lub nawet nie wszystkie, tylko wszystkie od
pewnego momentu, tj. dla dostatecznie du˙zych n sa
,
identyczne), jest zbie˙zny, przy
czym granica
,
takiego cia
,
gu jest wsp´olna warto´s´c jego wyraz´ow.
Cze
,
sto zamiast m´owi´c istnieje n
ε
, takie ˙ze dla n > n
ε
zachodzi . . . be
,
dziemy
m´owi´c, ˙ze dla dostatecznie du˙zych n zachodzi . . . lub ˙ze dla prawie wszystkich n za-
chodzi . . . . Tak wie
,
c dla prawie wszystkich n . . . oznacza dla wszystkich , z wyja
,
tkiem
sko´
nczenie wielu n . . . .
Podobnie mo˙zna interpretowa´c cze
,
´s´c b definicji granicy. Tym razem wyraz cia
,
gu,
kt´orego numer jest dostatecznie du˙zy ( n > n
M
) powinien by´c blisko plus nie-
sko´
nczono´sci, wie
,
c ma by´c du˙za
,
liczba
,
dodatnia
,
( a
n
> M ). Interpretacje
,
cze
,
´sci
c pozostawiamy czytelnikom – jest ona w pe lni analogiczna do cze
,
´sci b. Niekt´orzy
autorzy u˙zywaja
,
terminu „cia
,
g jest rozbie˙zny do +∞ ”, a inni m´owia
,
, ˙ze „cia
,
g jest
zbie˙zny do +∞ ”. My be
,
dziemy stosowa´c raczej pierwsza
,
terminologie
,
.
Przyk lad 4.1
0 = lim
n→∞
1
n
. Aby przekona´c sie
,
o prawdziwo´sci tej tezy wystarczy
przyja
,
´c, ˙ze n
ε
jest dowolna
,
liczba
,
ca lkowita
,
wie
,
ksza
,
ni˙z
1
ε
. Mo˙zna wie
,
c przyja
,
´c np.
n
1
= 2 , n
1/2
= 3 , n
0,41
= 3 , ale mo˙zna te˙z powie
,
kszy´c niekt´ore z tych liczb lub
6

Granica cia
,
gu
Micha l Krych
nawet wszystkie i przyja
,
´c n
1
= 10 , n
1/2
= 207 , n
0,41
= 3 . Mamy wie
,
c mo˙zliwo´s´c
wyboru: liczbe
,
n
ε
mo˙zna zawsze zasta
,
pi´c wie
,
ksza
,
.
Przyk lad 4.2
1
2
= lim
n→∞
2n+3
4n−1
. Wyka˙zemy, ˙ze wz´or ten jest prawdziwy. Bez trudu
stwierdzamy, ˙ze nier´owno´s´c
1
2
−
2n+3
4n−1
=
−7
2(4n−1)
≤
7
6n
zachodzi dla dowolnej
liczby ca lkowitej n ≥ 1 . Wystarczy wie
,
c, by n
ε
>
7
6ε
. To zdanie oznacza , ˙ze dla
tak dobranego n
ε
i n > n
ε
prawdziwa jest nier´owno´s´c
1
2
−
2n+3
4n−1
< ε — nie zna-
czy to jednak, ˙ze tylko dla tych liczb ca lkowitych n nier´owno´s´c ta ma miejsce! Nie
musieli´smy rozwia
,
zywa´c nier´owno´sci, cho´c w tym przypadku by lo to mo˙zliwe — wy-
starczy lo udowodni´c, ˙ze nier´owno´s´c ma miejsce dla wszystkich dostatecznie du˙zych
liczb naturalnych n .
Przyk lad 4.3
Je´sli d > 0 , to +∞ = lim
n→∞
(a
0
+ nd) . Postaramy sie
,
wykaza´c,
˙ze r´owno´s´c ta ma miejsce. Je´sli M jest dowolna
,
liczba
,
rzeczywista
,
, n
ε
>
M −a
0
d
i
n > n
ε
, to n >
M −a
0
d
, zatem a
n
= a
0
+nd > M , co dowodzi prawdziwo´sci r´owno´sci,
kt´ora
,
dowodzimy.
Wyka˙zemy teraz bardzo u˙zyteczna
,
nier´owno´s´c.
Twierdzenie 4.3 (Nier´
owno´s´
c Bernoulli’ego)
Za l´o˙zmy, ˙ze n jest liczba
,
ca lkowita
,
dodatnia
,
za´s a > −1 liczba
,
rzeczywista
,
. Wtedy
(1 + a)
n
≥ 1 + na
przy czym r´owno´s´c ma miejsce wtedy i tylko wtedy, gdy a = 0 lub gdy n = 1 .
Dow´
od. Je´sli n = 1 , to oczywi´scie niezale˙znie od wyboru liczby a ma miejsce
r´owno´s´c. Poniewa˙z (1 + a)
2
= 1 + 2a + a
2
≥ 1 + 2a , przy czym r´owno´s´c ma miejsce
wtedy i tylko wtedy, gdy a=0, wie
,
c teza zachodzi dla n = 2 i wszystkich liczb
rzeczywistych a (nie tylko a > −1 ). Otrzymana
,
nier´owno´s´c (1 + a)
2
≥ 1 + 2a
mo˙zemy pomno˙zy´c stronami przez liczbe
,
dodatnia
,
(1+a) – tu korzystamy z za lo˙zenia
a > −1 . W wyniku otrzymujemy (1 + a)
3
≥ (1 + 2a)(1 + a) = 1 + 3a + 2a
2
≥ 1 + 3a .
Tak˙ze w tym przypadku jest widoczne, ˙ze dla a 6= 0 otrzymujemy nier´owno´s´c ostra
,
.
Z tej nier´owno´sci w taki sam spos´ob jak poprzednio wynika, ˙ze
(1 + a)
4
≥ (1 + 3a)(1 + a) ≥ 1 + 4a + 3a
2
≥ 1 + 4a .
Teraz w ten sam spos´ob wnioskujemy prawdziwo´s´c twierdzenia dla n = 5 i wszystkich
a > −1 , potem dla n = 6 itd. Og´olnie je´sli (1 + a)
n
≥ 1 + na dla wszystkich liczb
a > −1 przy ustalonej liczbie naturalnej n , to
(1 + a)
n+1
≥ (1 + na)(1 + a) = 1 + (n + 1)a + na
2
≥ 1 + (n + 1)a
7

Granica cia
,
gu
Micha l Krych
i zn´ow bez trudu stwierdzamy, ˙ze r´owno´s´c ma miejsce jedynie dla a = 0 . Oczywi´scie
jest to latwe rozumowanie indukcyjne, nazwy nie u˙zyto wcze´sniej, by nie odstrasza´c
tych, kt´orzy jeszcze boja
,
sie
,
indukcji.
Twierdzenie 4.4 (Granica cia
,
gu geometrycznego)
Niech a
n
= q
n
. Cia
,
g ten ma granice
,
0 , je´sli |q| < 1 , ma granice
,
1 , je´sli q = 1 , ma
granice
,
+∞ , je´sli q > 1 . Je´sli q ≤ −1 , to cia
,
g granicy nie ma.
Dow´
od. W przypadku q = 0 oraz q = 1 teza jest oczywista, bo cia
,
g jest sta ly
(jego wyrazy nie zale˙za
,
od numeru). Za l´o˙zmy teraz, ˙ze 0 < |q| < 1 . Niech ε > 0
be
,
dzie liczba
,
rzeczywista
,
. Je´sli n
ε
>
1
ε
−1
1
|q|
−1
jest liczba
,
ca lkowita
,
i n > n
ε
, to
♣
1
|q|
n
=
1 +
1
|q|
− 1
n
≥ 1 + n
1
|q|
− 1
> 1 +
1
ε
− 1 =
1
ε
.
Z otrzymanej nier´owno´sci wynika, ˙ze dla n > n
ε
zachodzi
1
|q|
n
>
1
ε
, czyli |q
n
| < ε ,
a to oznacza, ˙ze lim
n→∞
q
n
= 0 .
Kolejny przypadek to q > 1 . Mamy teraz q
n
= (1 + (q − 1))
n
≥ 1 + n(q − 1) .
Wobec tego, je´sli n > n
M
i n
M
>
M −1
q−1
, to q
n
> 1 + (M − 1) = M . Jasne jest wie
,
c,
˙ze lim
n→∞
q
n
= +∞ .
Pozosta l przypadek ostatni: q ≤ −1 . W tym przypadku mamy q
n
≤ −1 dla
ka˙zdej liczby ca lkowitej nieparzystej n oraz q
n
≥ 1 dla ka˙zdej liczby ca lkowitej pa-
rzystej n . Gdyby istnia la sko´
nczona granica g , to wyrazy cia
,
gu o dostatecznie du˙zych
numerach le˙za lyby w odleg lo´sci mniejszej ni˙z 1 od granicy g — to natychmiastowa
konsekwencja istnienia granicy sko´
nczonej. Je´sli jednak odleg lo´sci q
n
i q
n+1
od gra-
nicy g sa
,
mniejsze od 1 , to odleg lo´s´c mie
,
dzy nimi jest mniejsza ni˙z 1 + 1 = 2 , co
oznacza, ˙ze |q
n
− q
n+1
| < 2 . To jednak nie jest mo˙zliwe, bowiem jedna z liczb q
n
,
q
n+1
jest mniejsza lub r´owna −1 , a druga wie
,
ksza lub r´owna 1 . Sta
,
d za´s wynika,
˙ze odleg lo´s´c mie
,
dzy q
n
i q
n+1
nie jest mniejsza ni˙z 1 − (−1) = 2 *. Otrzymali´smy
sprzeczno´s´c, wie
,
c cia
,
g granicy sko´
nczonej nie ma. +∞ granica
,
tego cia
,
gu te˙z nie jest,
bowiem wtedy wyrazy cia
,
gu o dostatecznie du˙zych numerach musia lyby by´c wie
,
ksze
od 0 (przyjmujemy M = 0 ), a tak nie jest, bo te, kt´orych numery sa
,
nieparzyste,
sa
,
ujemne. Analogicznie −∞ nie jest granica
,
tego cia
,
gu, bo wyrazy o numerach
parzystych sa
,
dodatnie, co wyklucza to, ˙ze wyrazy o dostatecznie du˙zych numerach
sa
,
ujemne (i w tym przypadku przyjmujemy M = 0 ).
Wykazali´smy wie
,
c, ˙ze cia
,
g nie ma ani granicy sko´
nczonej ani niesko´
nczonej, co
♣
Nie u˙zywamy tu logarytmu, bo chcemy pokaza´
c, ˙ze konkretne oszacowania mo˙zna uzyska´
c bardzo
elementarnie. Gdyby´smy jednak zechcieli go u˙zy´
c, to mogliby´smy napisa´
c n
ε
>(log
10
ε)/(log
10
|q|) ,
przyp. log
10
|q|<0 .
*
Mo˙zna to rozumowanie zapisa´
c wzorami: 2≤|q
n
−q
n+1
|≤|q
n
−g|+|g−q
n+1
|<1+1=2 dla dostatecznie
du˙zych n .
8

Granica cia
,
gu
Micha l Krych
ko´
nczy badanie granicy cia
,
gu geometrycznego.
Cia
,
gi monotoniczne i ´sci´sle monotoniczne, cia
,
gi ograniczone
Definicja 4.5 (cia
,
g´
ow monotonicznych)
Cia
,
g (a
n
) nazywamy niemaleja
,
cym (rosna
,
cym) wtedy i tylko wtedy, gdy dla
ka˙zdego numeru n zachodzi nier´owno´s´c a
n
≤ a
n+1
( a
n
< a
n+1
). Podobnie cia
,
g nie-
rosna
,
cy (maleja
,
cy) to taki, ˙ze dla ka˙zdego numeru n zachodzi nier´owno´s´c a
n
≥ a
n+1
( a
n
> a
n+1
). Cia
,
gi niemaleja
,
ce i nierosna
,
ce maja
,
wsp´olna
,
nazwe
,
: cia
,
gi monoto-
niczne. Cia
,
gi rosna
,
ce i maleja
,
ce nazywamy cia
,
gami ´sci´sle monotonicznymi.
W niekt´orych podre
,
cznikach stosowana jest nieco inna terminologia: cia
,
gi niema-
leja
,
ce zwane sa
,
tam rosna
,
cymi, a rosna
,
ce – ´sci´sle rosna
,
cymi. Jest oczywi´scie oboje
,
tne,
kt´ora z dwu koncepcji jest stosowana, je´sli tylko jest to robione konsekwentnie. Mo˙zna
te˙z, dla uniknie
,
cia nieporozumie´
n, m´owi´c o cia
,
gach niemaleja
,
cych i ´sci´sle rosna
,
cych.
Cia
,
g geometryczny zaczynaja
,
cy sie
,
od wyrazu a
1
= q jest monotoniczny w
przypadku q ≥ 0 : dla q = 0 oraz dla q = 1 cia
,
g geometryczny jest sta ly, wie
,
c
niemaleja
,
cy i jednocze´snie nierosna
,
cy. W przypadku 0 < q < 1 jest on maleja
,
cy,
dla q > 1 jest on rosna
,
cy. Cia
,
g arytmetyczny jest rosna
,
cy, gdy jego r´o˙znica d jest
dodatnia, maleja
,
cy – gdy d < 0 , sta ly (wie
,
c jednocze´snie niemaleja
,
cy i nierosna
,
cy),
gdy d = 0 .
Definicja 4.6 (cia
,
g´
ow ograniczonych)
Cia
,
g (a
n
) nazywany jest ograniczonym z g´ory wtedy i tylko wtedy, gdy istnieje
liczba rzeczywista M , taka ˙ze dla ka˙zdej liczby naturalnej n zachodzi nier´owno´s´c:
a
n
≤ M . Analogicznie (a
n
) jest ograniczony z do lu wtedy i tylko wtedy, gdy ist-
nieje liczba rzeczywista m taka, ˙ze dla ka˙zdego n zachodzi nier´owno´s´c a
n
≥ m .
Cia
,
g ograniczony z g´ory i z do lu nazywamy ograniczonym. Cia
,
giem nieograniczonym
nazywamy ka˙zdy cia
,
g, kt´ory nie jest ograniczony.
Cia
,
g (n) jest ograniczony z do lu np. przez −13 lub 0 , ale nie jest ograniczony
z g´ory, wie
,
c jest nieograniczony. Cia
,
g (−1)
n
jest ograniczony z g´ory np. przez 1 lub
przez
√
1000 oraz z do lu, np przez −1 , ale r´ownie˙z przez −13 .
Cia
,
g (a
n
) jest ograniczony wtedy i tylko wtedy, gdy istnieje liczba nieujemna
M , taka ˙ze |a
n
| ≤ M dla ka˙zdego n . Jest oczywisty wniosek z definicji cia
,
gu ogra-
niczonego: M musi by´c tak du˙ze, by liczba −M by la ograniczeniem dolnym cia
,
gu
(a
n
) i jednocze´snie liczba M by la jego ograniczeniem, g´ornym.
Przyk lad 4.4
Cia
,
g (1 +
x
n
)
n
Wypiszmy przybli˙zenia dziesie
,
ciu pierwszych wyraz´ow cia
,
gu
9
Granica cia
,
gu
Micha l Krych
w przypadku x = 1 :
oraz w przypadku x = −4 :
1 +
1
1
1
= 2
1 +
−4
1
1
= −3
1 +
1
2
2
=
9
4
= 2, 25
1 +
−4
2
2
= 1
1 +
1
3
3
=
64
27
≈ 2, 37
1 +
−4
3
3
=
−1
27
≈ −0, 37
1 +
1
4
4
=
625
256
≈ 2, 44
1 +
−4
4
4
= 0
1 +
1
5
5
=
7776
3125
≈ 2, 49
1 +
−4
5
5
=
1
3125
≈ 0, 00032
1 +
1
6
6
=
117649
46656
≈ 2, 52
1 +
−4
6
6
=
1
729
≈ 0, 0014
1 +
1
7
7
=
2097152
823543
≈ 2, 55
1 +
−4
7
7
=
2187
823543
≈ 0, 0027
1 +
1
8
8
=
43046721
16777216
≈ 2, 56
1 +
−4
8
8
=
1
256
≈ 0, 0039
1 +
1
9
9
=
1000000000
387420489
≈ 2, 58
1 +
−4
9
9
=
1953125
387420489
≈ 0, 0050
1 +
1
10
10
=
25937424601
10000000000
≈ 2, 59
1 +
−4
10
10
=
59049
9765625
≈ 0, 0060
Latwo mo˙zna przekona´c sie
,
, ˙ze cia
,
g o wyrazie a
n
= (1 +
x
n
)
n
nie jest ani geo-
metryczny , ani arytmetyczny z wyja
,
tkiem jednego przypadku: x = 0 .
Wyka˙zemy, ˙ze je´sli n > −x 6= 0 , to a
n+1
> a
n
, czyli ˙ze cia
,
g ten jest
rosna
,
cy od pewnego momentu. W przypadku x > 0 jest rosna
,
cy. Gdy x < 0 ,
to mo˙ze sie
,
zdarzy´c, ˙ze pocza
,
tkowe wyrazy zmieniaja
,
znak, wie
,
c o monotoniczno´sci
nie mo˙ze by´c nawet mowy. Je´sli jednak wszystkie wyrazy cia
,
gu sa
,
dodatnie, to jest
niemaleja
,
cy. Wyka˙zemy to. Z nier´owno´sci n > −x wynika od razu nier´owno´s´c n+1 >
−x . Z pierwszej z nich wnioskujemy, ˙ze 1 +
x
n
> 0 , z drugiej — ˙ze 1 +
x
n+1
> 0 .
Nier´owno´s´c a
n
< a
n+1
r´ownowa˙zna jest nier´owno´sci
1 +
x
n
n
<
1 +
x
n+1
n+1
,
a ta — dzie
,
ki temu, ˙ze 1 +
x
n
> 0 — nier´owno´sci
1+
x
n+1
1+
x
n
n+1
>
1
(
1+
x
n
)
=
n
n+x
.
Skorzystamy teraz z nier´owno´sci Bernoulli’ego, by udowodni´c, ˙ze ostatnia nier´owno´s´c
ma miejsce dla n > −x . Mamy
1+
x
n+1
1+
x
n
n+1
=
1 −
x
(n+x)(n+1)
n+1
≥ 1 − (n + 1)
x
(n+x)(n+1)
= 1 −
1
n+x
=
x
n+x
.
Dla jasno´sci nale˙zy jeszcze zauwa˙zy´c, ˙ze liczba
−x
(n+x)(n+1)
, pe lnia
,
ca role
,
a w nier´ow-
no´sci Bernoulli’ego, jest wie
,
ksza od −1 — jest to oczywiste w przypadku x ≤ 0 , bo
w tym przypadku jest ona nieujemna, za´s dla x > 0 jej warto´s´c bezwzgle
,
dna, czyli
x
(n+x)(n+1)
jest mniejsza od
1
n+1
< 1 . Wykazali´smy wie
,
c, ˙ze od momentu, w kt´orym
wyra˙zenie (1 +
x
n
) staje sie
,
dodatnie, cia
,
g zaczyna rosna
,
´c (gdy x = 0 jest sta ly).
Dodajmy jeszcze, ˙ze je´sli x > 0 , to wyrazy cia
,
gu sa
,
dodatnie, je´sli za´s x < 0 , to sa
,
one dodatnie dla n parzystego oraz dla n nieparzystego, o ile n > −x .
Pozostaje pytanie: czy w przypadku x > 0 wzrost wyrazu cia
,
gu (1 +
x
n
)
n
jest
nieograniczony, czy te˙z dla ustalonego x znale´z´c mo˙zna liczbe
,
wie
,
ksza
,
od wszyst-
10

Granica cia
,
gu
Micha l Krych
kich wyraz´ow tego cia
,
gu. Wyka˙zemy, ˙ze cia
,
g
(1 +
x
n
)
n
jest ograniczony z g´ory
dla dowolnej liczby rzeczywistej x . Dla ujemnych x tak jest, bo od pewnego miej-
sca, jak to stwierdzili´smy wcze´sniej, wyrazy cia
,
gu sa
,
dodatnie i mniejsze od 1 . Je´sli
n > x > 0 , to 1 +
x
n
n
=
1−
x2
n2
n
(
1−
x
n
)
n
<
1
(
1−
x
n
)
n
. Wyra˙zenie
1
(
1−
x
n
)
n
maleje wraz
ze wzrostem n (gdy rozpatrujemy n > x ), bo licznik nie zmienia sie
,
, a mianow-
nik — jak to wykazali´smy wcze´sniej — ro´snie. Wynika sta
,
d, ˙ze je´sli n(x) jest naj-
mniejsza
,
liczba
,
ca lkowita
,
wie
,
ksza
,
od x , to wszystkie wyrazy cia
,
gu sa
,
mniejsze ni˙z
1
1−
x
n(x)
n(x)
=
n(x)
n(x)−x
n(x)
.
Np. n(1) = 2 , zatem wszystkie wyrazy cia
,
gu 1 +
1
n
n
sa
,
mniejsze ni˙z
2
2−1
2
= 4 .
W przypadku x = −4 wszystkie wyrazy cia
,
gu pocza
,
wszy od pia
,
tego sa
,
dodatnie i
mniejsze od 1, rozwa˙zywszy cztery pierwsze przekonujemy sie
,
o tym, ˙ze najwie
,
kszym
wyrazem cia
,
gu jest wyraz drugi, r´owny 1 , a najmniejszym — pierwszy, r´owny −3 .
W istocie rzeczy z tego, co zosta lo napisane wynika, ˙ze dla ka˙zdej liczby naturalnej
k ≥ n(x) liczba
1
(
1−
x
k
)
k
=
k
k−x
k
jest ograniczeniem g´ornym cia
,
gu 1 +
x
n
n
—
zache
,
camy do samodzielnego uzasadnienia tego prostego stwierdzenia.
Wyka˙zemy teraz naste
,
pujace
Twierdzenie 4.7 (o istnieniu granicy cia
,
gu monotonicznego)
Ka˙zdy cia
,
g monotoniczny ma granice
,
.
Dow´
od. Za l´o˙zmy, ˙ze cia
,
g (a
n
) jest niemaleja
,
cy, tzn. dla ka˙zdego n zachodzi
nier´owno´s´c a
n
≤ a
n+1
. Je´sli cia
,
g nie jest ograniczony z g´ory, to dla ka˙zdej liczby rze-
czywistej M istnieje liczba naturalna n
M
taka, ˙ze a
n
M
≥ M . Wtedy dla ka˙zdej
liczby naturalnej n ≥ n
M
zachodzi nier´owno´s´c a
n
≥ a
n
M
≥ M . Wobec tego
lim
n→∞
a
n
= +∞ . Za l´o˙zmy teraz, ˙ze cia
,
g (a
n
) jest ograniczony z g´ory przez liczbe
,
b
0
. Dla ka˙zdej liczby naturalnej n ≥ 0 mamy wie
,
c a
0
≤ a
n
≤ b
0
. Je´sli w prze-
dziale
a
0
+b
0
2
, b
0
, znajduja
,
sie
,
jakiekolwiek wyrazy cia
,
gu (a
n
) , to przyjmujemy
c
1
=
a
0
+b
0
2
i b
1
= b
0
. Je´sli w przedziale
a
0
+b
0
2
, b
0
wyraz´ow cia
,
gu (a
n
) nie ma,
to przyjmujemy c
1
= a
0
i b
1
=
a
0
+b
0
2
. W obu przypadkach otrzymujemy prze-
dzia l [c
1
, b
1
] ⊆ [a
0
, b
0
] dwa razy kr´otszy od przedzia lu [a
0
, b
0
] zawieraja
,
cy prawie
wszystkie wyrazy cia
,
gu (a
n
) . W taki sam spos´ob otrzymujemy przedzia l [c
2
, b
2
] ⊆
[c
1
, b
1
] dwa razy kr´otszy od przedzia lu [c
1
, b
1
] , czyli cztery razy kr´otszy od prze-
dzia lu [a
0
, b
0
] zawieraja
,
cy prawie wszystkie wyrazy cia
,
gu (a
n
) . Powtarzaja
,
c te
,
kon-
strukcje
,
wielokrotnie okre´slamy zste
,
puja
,
cy cia
,
g przedzia l´ow domknie
,
tych [c
n
, b
n
]
taki, ˙ze ka˙zdy przedzia l [c
n
, b
n
] jest dwa razy kr´otszy od swego poprzednika (i
11

Granica cia
,
gu
Micha l Krych
jest w nim zawarty). Niech g be
,
dzie punktem wsp´olnym wszystkich przedzia l´ow
[c
n
, b
n
] , n = 1, 2, . . . . Jasne jest, ˙ze ta cze
,
´s´c wsp´olna sk lada sie
,
z tylko jednej liczby
(je´sli g
1
6= g
2
, to dla dostatecznie du˙zych liczb naturalnych n zachodzi nier´owno´s´c
|g
1
− g
2
| >
b
0
−a
0
2
n
= b
n
− c
n
). Wyka˙zemy, ˙ze lim
n→∞
a
n
= g . Niech ε > 0 . Istnieje
liczba naturalna m taka, ˙ze b
m
− c
m
< ε . Niech a
n
∈ [c
m
, b
m
] . Wtedy r´ownie˙z
a
n+1
, a
n+2
, a
n+3
, . . . ∈ [c
m
, b
m
] i oczywi´scie g ∈ [c
m
, b
m
] . Ka˙zde dwa punkty prze-
dzia lu [c
m
, b
m
] sa
,
odleg le o nie wie
,
cej ni˙z b
m
− c
m
< ε , w szczeg´olno´sci odleg lo´s´c
g od ka˙zdego z punkt´ow a
n
, a
n+1
, a
n+2
, a
n+3
, . . . jest mniejsza ni˙z ε . Oznacza to,
˙ze lim
n→∞
a
n
= g . Je´sli cia
,
g (a
n
) jest nierosna
,
cy, to mo˙zna ju˙z udowodniona
,
cze
,
´s´c
twierdzenia zastosowa´c do cia
,
gu (−a
n
) , kt´ory jest niemaleja
,
cy. Ma on zatem jaka
,
´s
granice
,
g . Bez trudu wykazujemy, ˙ze lim
n→∞
a
n
= −g .
Ten dow´od zosta l zamieszczony po to, by studenci mogli zrozumie´c, jak mo˙zna
przeprowadza´c rozumowania matematyczne. Nie nale˙zy uczy´c sie
,
go na pamie
,
´c, warto
go jednak go przemy´sle´c.
Zauwa˙zmy jedynie, ˙ze gdyby´smy ograniczyli sie
,
do liczb wymiernych, tj. u lamk´ow
o ca lkowitych licznikach i mianownikach, to twierdzenie nie by loby prawdziwe — ist-
nieja
,
bowiem cia
,
gi liczb wymiernych, kt´orych granice sa
,
niewymierne. Twierdzenie
to podaje wie
,
c istotna
,
informacje
,
o zbiorze wszystkich liczb rzeczywistych. Chodzi
o to mianowicie, ˙ze nie ma w nim dziur, geometrycznie jest to ca la prosta. Wypro-
wadzili´smy to twierdzenie z lematu o przedzia lach zste
,
puja
,
cych, bo by l on jedynym
do tej pory twierdzeniem m´owia
,
cym w istocie rzeczy, ˙ze „mie
,
dzy” liczbami rzeczy-
wistymi ˙zadnych luk nie ma w odr´o˙znieniu od dziurawego zbioru liczb wymiernych.
Mie
,
dzy ka˙zdymi dwiema r´o˙znymi liczbami wymiernymi c i d znajduje sie
,
liczba
niewymierna, np. c +
d−c
√
2
— jej niewymierno´s´c wynika latwo z tego, ˙ze
√
2 > 1 jest
liczba
,
niewymierna
,
, za´s c 6= d sa
,
wymierne. Jest te˙z jasne, ˙ze le˙zy ona mie
,
dzy c
i d — od punktu c przesuwamy sie
,
w kierunku punktu d o wektor
d−c
√
2
, kt´orego
d lugo´s´c jest mniejsza ni˙z odleg lo´s´c |c − d| punkt´ow c i d .
Z twierdzenia tego wynika np. od razu, ˙ze cia
,
g geometryczny, kt´orego zbie˙zno´s´c
zbadali´smy wcze´sniej ma granice
,
w przypadku q ≥ 0 . Nie wynika natomiast istnienie
tej granicy w przypadku q < 0 , bo w przypadku ujemnego ilorazu cia
,
g geometryczny
nie jest monotoniczny. Z tego twierdzenia wynika r´ownie˙z, ˙ze dla ka˙zdej liczby rze-
czywistej x cia
,
g
(1 +
x
n
)
n
ma granice
,
— nie zawsze jest on monotoniczny, ale
zawsze jest monotoniczny od pewnego momentu, co w oczywisty spos´ob r´ownie˙z wy-
starcza, bowiem zmiana sko´
nczenie wielu wyraz´ow cia
,
gu nie ma wp lywu na istnienie
lub warto´s´c granicy, bowiem w definicji granicy mowa jest jedynie o wyrazach cia
,
gu,
12

Granica cia
,
gu
Micha l Krych
kt´orych numery sa
,
dostatecznie du˙ze, zatem zmiana sko´
nczenie wielu wyraz´ow cia
,
gu
mo˙ze jedynie mie´c wp lyw na znaczenie s l´ow dostatecznie du˙ze.
Oznaczenie 4.8 (wa˙znej granicy)
exp(x) oznacza´c be
,
dzie w dalszym cia
,
gu granice
,
cia
,
gu (1 +
x
n
)
n
, tzn.
exp(x) = lim
n→∞
1 +
x
n
n
.
Wobec tego symbol exp oznacza funkcje
,
, kt´ora jest okre´slona na zbiorze wszystkich
liczb rzeczywistych, jej warto´scia
,
w punkcie x jest liczba dodatnia lim
n→∞
1 +
x
n
n
.
Obliczanie granic i stwierdzanie zbie˙zno´sci cia
,
gu
Sformu lujemy teraz kilka twierdze´
n, kt´ore u latwiaja
,
obliczanie granic, ich sza-
cowanie lub stwierdzanie ich istnienia. Potem poka˙zemy jak mo˙zna je stosowa´c. W
ko´
ncu udowodnimy cze
,
´s´c z nich, tak by wyja´sni´c mechanizm dowodzenia. Najpierw
zdefiniujemy niekt´ore dzia lania z u˙zyciem symboli ±∞ . Przypominamy, ˙ze nie sa
,
to
liczby rzeczywiste, lecz nowe obiekty.
Definicja 4.9 (dzia la´
n z u˙zyciem ±∞ )
−(+∞) = −∞ , +(+∞) = +∞ , −(−∞) = +∞ , +(−∞) = −∞ .
+∞ ± a = ±a + (+∞) = +∞
−∞ ± a = ±a + (−∞) = −∞ dla ka˙zdej liczby
rzeczywistej a.
+∞+(+∞) = +∞ , −∞+(−∞) = −∞ , +∞−(−∞) = +∞ , −∞−(+∞) = −∞ .
+∞ · a = +∞ i −∞ · a = −∞ dla ka˙zdego a > 0 .
(+∞) · (+∞) = (−∞) · (−∞) = +∞ .
+∞ · a = −∞ i −∞ · a = +∞ dla ka˙zdego a < 0 .
a
±∞
= 0 dla dowolnej liczby rzeczywistej a.
±∞
a
= ±∞ ·
1
a
dla dowolnej liczby a 6= 0 .
a
+∞
= +∞ , a
−∞
= 0 dla dowolnej liczby a > 1 .
a
+∞
= 0 i a
−∞
= +∞ dla dowolnej liczby 0 < a < 1 .
−∞ < a < +∞ dla dowolnej liczby rzeczywistej a .
−∞ < +∞ .
ln(+∞) = +∞ , ln 0 = −∞ .
Twierdzenie 4.10 (o arytmetycznych w lasno´sciach granicy)
A1. Je´sli istnieja
,
granice lim
n→∞
a
n
, lim
n→∞
b
n
i okre´slona jest ich suma, to istnieje
granica lim
n→∞
(a
n
+b
n
) i zachodzi wz´or: lim
n→∞
(a
n
+b
n
) = lim
n→∞
a
n
+ lim
n→∞
b
n
.
A2. Je´sli istnieja
,
granice lim
n→∞
a
n
, lim
n→∞
b
n
i okre´slona jest ich r´o˙znica, to ist-
nieje granica lim
n→∞
(a
n
−b
n
) i zachodzi: lim
n→∞
(a
n
−b
n
) = lim
n→∞
a
n
− lim
n→∞
b
n
.
13

Granica cia
,
gu
Micha l Krych
A3. Je´sli istnieja
,
granice lim
n→∞
a
n
, lim
n→∞
b
n
i okre´slony jest ich iloczyn, to ist-
nieje granica lim
n→∞
(a
n
· b
n
) i zachodzi: lim
n→∞
(a
n
· b
n
) = lim
n→∞
a
n
· lim
n→∞
b
n
.
A4. Je´sli istnieja
,
granice lim
n→∞
a
n
, lim
n→∞
b
n
i okre´slony jest ich iloraz, to istnieje
granica lim
n→∞
a
n
b
n
i zachodzi wz´or lim
n→∞
a
n
b
n
=
lim
n→∞
a
n
lim
n→∞
b
n
. ×
Zanim udowodnimy to twierdzenie, sformu lujemy naste
,
pne.
Twierdzenie 4.11 (o szacowaniu)
N1. Je´sli C < lim
n→∞
a
n
, to dla dostatecznie du˙zych numer´ow n zachodzi nie-
r´owno´s´c C < a
n
.
N2. Je´sli C > lim
n→∞
a
n
, to dla dostatecznie du˙zych numer´ow n zachodzi nie-
r´owno´s´c C > a
n
.
N3. Je´sli lim
n→∞
b
n
< lim
n→∞
a
n
, to dla dostatecznie du˙zych numer´ow n zachodzi
nier´owno´s´c b
n
< a
n
.
N4. Je´sli b
n
≤ a
n
dla dostatecznie du˙zych numer´ow n , to zachodzi nier´owno´s´c
lim
n→∞
b
n
≤ lim
n→∞
a
n
. ×
Wniosek 4.12 (z twierdzenia o szacowaniu — jednoznaczno´s´
c granicy)
Cia
,
g ma co najwy˙zej jedna
,
granice
,
.
Dow´
od. Gdyby mia l dwie np. g
1
< g
2
, to wybra´c mogliby´smy liczbe
,
C le˙za
,
ca
,
mie
,
dzy g
1
i g
2
: g
1
< C < g
2
. Wtedy dla dostatecznie du˙zych n by loby jednocze´snie
a
n
< C (zob. N2) oraz a
n
> C (zob. N1), co oczywi´scie nie jest mo˙zliwe.
Wniosek 4.13 (
z tw. o szacowaniu — ograniczono´
s´
c cia
,
gu o granicy sko´
nczonej)
Je´sli granica lim
n→∞
a
n
jest sko´
nczona, to istnieja
,
liczby rzeczywiste C, D takie, ˙ze dla
wszystkich n zachodzi nier´owno´s´c C < a
n
< D , czyli cia
,
g (a
n
) jest ograniczony
z do lu liczba
,
C za´s z g´ory liczba
,
D . ×
Twierdzenie 4.14 (o trzech cia
,
gach)
Je´sli a
n
≤ b
n
≤ c
n
dla dostatecznie du˙zych n i cia
,
gi (a
n
) oraz (c
n
) maja
,
r´owne
granice, to cia
,
g (b
n
) te˙z ma granice
,
i zachodzi wz´or
lim
n→∞
a
n
= lim
n→∞
b
n
= lim
n→∞
c
n
. ×
Definicja 4.15 (podcia
,
gu)
Je´sli (n
k
) jest ´sci´sle rosna
,
cym cia
,
giem liczb naturalnych, to cia
,
g (a
n
k
) nazywany
jest podcia
,
giem cia
,
gu (a
n
) .
14
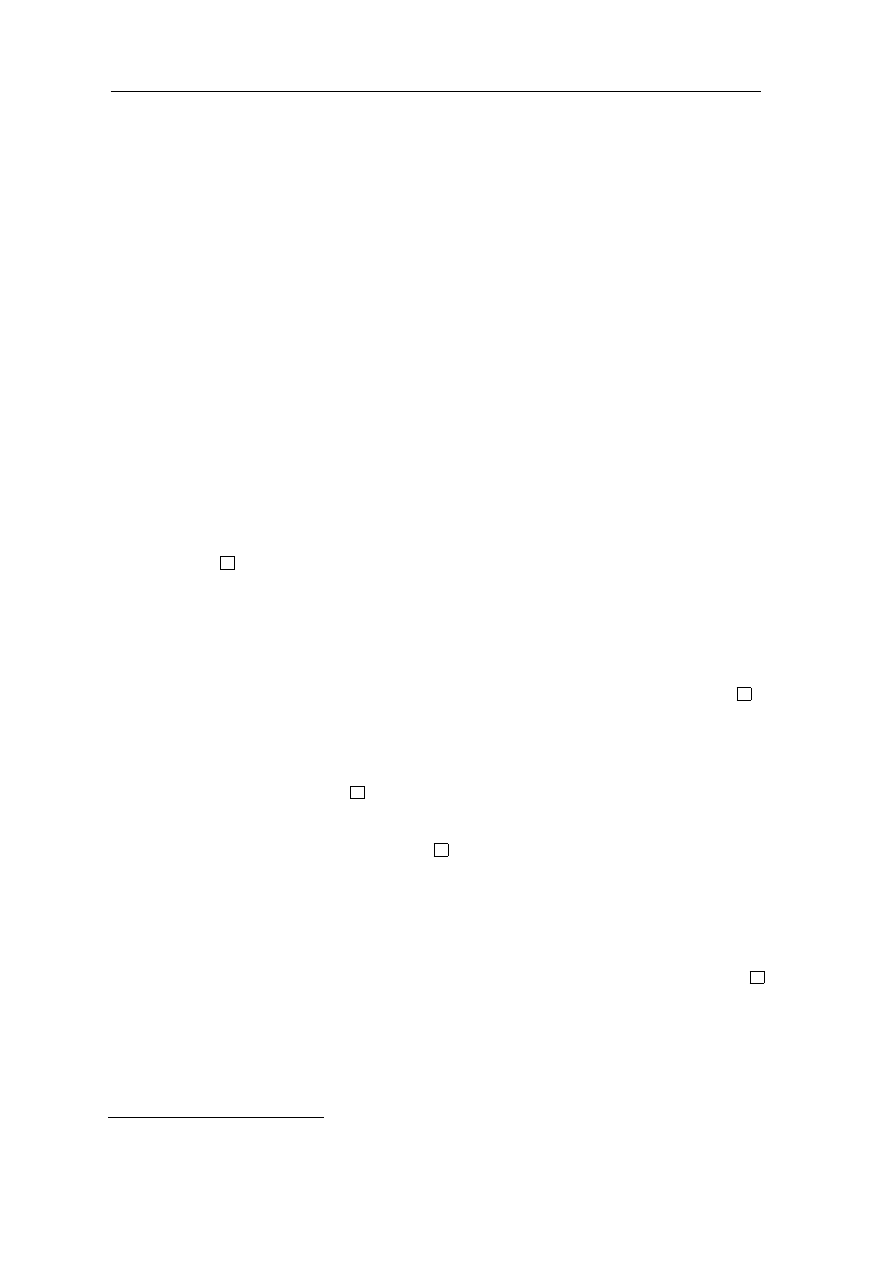
Granica cia
,
gu
Micha l Krych
Na przyk lad cia
,
g a
2
, a
4
a
6
, . . . , czyli cia
,
g (a
2k
) jest podcia
,
giem cia
,
gu (a
n
)
— w tym przypadku n
k
= 2k . Cia
,
g a
2
, a
3
, a
5
, a
7
, a
11
, . . . jest podcia
,
giem cia
,
gu
(a
n
) — w tym przypadku n
k
jest k –ta
,
liczba
,
pierwsza
,
. Przyk lady mo˙zna mno˙zy´c,
ale zapewne starczy powiedzie´c, ˙ze chodzi o wybranie niesko´
nczenie wielu wyraz´ow
wyj´sciowego cia
,
gu bez zmiany kolejno´sci w jakiej wyste
,
powa ly.
Jest jasne, ˙ze je´sli g jest granica
,
cia
,
gu, to jest r´ownie˙z granica
,
ka˙zdego jego
podcia
,
gu, wynika to od razu z definicji granicy i definicji podcia
,
gu. Latwe w dowodzie
jest te˙z twierdzenie pozwalaja
,
ce na zbadanie sko´
nczenie wielu podcia
,
g´ow danego
cia
,
gu, w la´sciwie wybranych, i wnioskowanie istnienia granicy z istnienia wsp´olnej
granicy wybranych podcia
,
g´ow.
Twierdzenie 4.16 (o scalaniu) *
Za l´o˙zmy, ˙ze z cia
,
gu (a
n
) mo˙zna wybra´c dwa podcia
,
gi (a
k
n
) i (a
l
n
) zbie˙zne do
tej samej granicy g , przy czym ka˙zdy wyraz cia
,
gu (a
n
) jest wyrazem co najmniej
jednego z tych podcia
,
g´ow, tzn. dla ka˙zdego n istnieje m , takie ˙ze n = k
m
lub
n = l
m
. Wtedy ta wsp´olna granica obu tych podcia
,
g´ow jest granica
,
cia
,
gu (a
n
) :
lim
n→∞
a
n
= g . ×
Sformu lujemy teraz bardzo wa˙zne twierdzenie, kt´ore be
,
dzie wielokrotnie stoso-
wane w dowodach.
Twierdzenie 4.17 (Bolzano – Weierstrassa)
Z ka˙zdego cia
,
gu mo˙zna wybra´c podcia
,
g, kt´ory ma granice
,
(sko´
nczona
,
lub nie). ×
Wniosek 4.18 (z twierdzenia Bolzano – Weierstrassa)
Cia
,
g ma granice
,
wtedy i tylko wtedy, gdy granice wszystkich tych jego podcia
,
g´ow,
kt´ore maja
,
granice, sa
,
r´owne. ×
Naste
,
pne twierdzenie, w zasadzie ju˙z cze
,
´sciowo udowodnione, wykaza l A.Cauchy,
jeden z tw´orc´ow analizy matematycznej. ×
Twierdzenie 4.19 (Cauchy’ego) Cia
,
g (a
n
) ma granice
,
sko´
nczona
,
wtedy i tylko
wtedy, gdy spe lniony jest naste
,
puja
,
cy warunek Cauchy’ego:
(wC)
dla ka˙zdego ε > 0 istnieje taka liczba naturalna n
ε
,
˙ze je´sli k, l > n
ε
, to |a
k
− a
l
| < ε . ×
Twierdzenie to, podobnie jak twierdzenie o istnieniu granicy cia
,
gu monotonicz-
nego, pozwala czasem stwierdzi´c istnienie granicy bez ustalania jej warto´sci, co jest
bardzo wa˙zne w licznych przypadkach. Pozwala ono te˙z wykazywa´c nieistnienie gra-
nic — w istocie rzeczy wykazuja
,
c, ˙ze cia
,
g geometryczny o ilorazie q ≤ −1 nie ma
*
Ta nazwa to pomys l autora, kt´
ory ma nadzieje,, ˙ze nie jest to ca lkiem g lupi termin.
15

Granica cia
,
gu
Micha l Krych
granicy, wykazywali´smy, ˙ze nie spe lnia on warunku Cauchy’ego, role
,
ε pe lni la tam
liczba 2 .
Teraz poka˙zemy jak mo˙zna stosowa´c twierdzenia, kt´ore sformu lowali´smy wcze´s-
niej. Przyk lady 4.8 — 4.13 sa
,
wa˙zne, wyniki tam opisane be
,
da
,
p´o´zniej wykorzysty-
wane.
Przyk lad 4.5
Rozpoczniemy od przyk ladu ju˙z om´owionego, ale teraz cia
,
g zba-
damy inaczej. Zajmiemy sie
,
mianowicie cia
,
giem
2n+3
4n−1
. Udowodnili´smy poprzed-
nio, ˙ze granica
,
cia
,
gu jest liczba
1
2
nie wyja´sniaja
,
c, ska
,
d wiedzieli´smy, ˙ze akurat ta
liczba ma by´c granica
,
. Zauwa˙zmy, ˙ze zar´owno licznik jak i mianownik maja
,
granice,
mianowicie +∞ . Jeste´smy wie
,
c w sytuacji niedobrej:
+∞
+∞
. W tym przypadku mo˙zna
jednak bez trudu przekszta lci´c wyra˙zenie okre´slaja
,
ce wyraz cia
,
gu:
2n+3
4n−1
=
2 +
3
n
4 −
1
n
.
Teraz mo˙zemy zastosowa´c twierdzenie o granicy sumy cia
,
g´ow (A1), potem o granicy
r´o˙znicy cia
,
g´ow (A2), by stwierdzi´c, ˙ze lim
n→∞
(2 +
3
n
) = 2 + lim
n→∞
3
n
= 2 + 0 = 2 oraz
lim
n→∞
(4 −
1
n
) = 4 − lim
n→∞
1
n
= 4 − 0 = 4 — wiemy ju˙z przecie˙z, ˙ze lim
n→∞
1
n
= 0 ,
zatem lim
n→∞
3
n
= 3 · lim
n→∞
1
n
= 3 · 0 = 0 . Teraz mamy do czynienia z ilorazem, kt´orego
licznik ma granice
,
2 , za´s mianownik — granice
,
4 , wie
,
c r´o˙zna
,
od 0 , co umo˙zliwia
skorzystanie z twierdzenia o granicy ilorazu (A4). Z niego wynika od razu, ˙ze granica
,
jest
2
4
=
1
2
. Oczywi´scie nic wie
,
cej ju˙z robi´c nie trzeba, bo twierdzenie o arytmetycz-
nych w lasno´sciach granicy gwarantuje zar´owno istnienie granic, jak i odpowiednie
r´owno´sci.
Przyk lad 4.6
Rozwa˙zymy naste
,
pny prosty przyk lad: lim
n→∞
(n
5
−100n
4
−333978) .
Wyka˙zemy mianowicie, ze cia
,
g ten ma granice
,
+∞ . Czytelnik zechce zwr´oci´c uwage
,
na to, ˙ze na pewno pierwszych 100 wyraz´ow to liczby ujemne — nie twierdzimy
wcale, ˙ze tylko 100 , ale n
5
− 100n
4
= n
4
(n − 100) ≤ 0 dla n ≤ 100 , a od tej liczby
odejmujemy jeszcze 333978 , wie
,
c te wyrazy sa
,
ujemne, a o znaku dalszych nic nie
m´owimy. Zapiszmy wyraz cia
,
gu w postaci n
5
(1 −
100
n
−
333978
n
5
) . Oczywi´scie
lim
n→∞
n
5
= ( lim
n→∞
n) · ( lim
n→∞
n) · ( lim
n→∞
n) · ( lim
n→∞
n) · ( lim
n→∞
n) =
= (+∞) · (+∞) · (+∞) · (+∞) · (+∞) = +∞
na mocy twierdzenia o granicy iloczynu (A3). Na mocy twierdzenia o granicy ilorazu
(A4) stwierdzamy, ˙ze lim
n→∞
100
n
= 0 oraz lim
n→∞
333978
n
5
= 0 . Mo˙zemy wie
,
c zastosowa´c
twierdzenie o granicy r´o˙znicy (A2) dwukrotnie, by stwierdzi´c, ˙ze
lim
n→∞
1 −
100
n
−
333978
n
5
= 1 − 0 − 0 = 1 .
16

Granica cia
,
gu
Micha l Krych
Nasz cia
,
g zosta l wie
,
c przedstawiony jako iloczyn dw´och cia
,
g´ow, z kt´orych pierwszy
da
,
˙zy do +∞ a drugi do liczby dodatniej, do 1 . Z definicji mno˙zenia symboli nie-
sko´
nczonych przez liczby dodatnie i twierdzenia o granicy iloczynu wynika, ˙ze jego
granica
,
jest +∞ .
Oczywi´scie i w tym przypadku mo˙zna posta
,
pi´c nieco inaczej. Mo˙zemy napisa´c nie-
r´owno´s´c:
n
5
− 100n
4
− 333978 ≥ n
5
− 334078n
4
= n
4
(n − 334078)
— otrzymali´smy cia
,
g, kt´ory jest iloczynem dw´och cia
,
g´ow: (n − 334078) i (n
4
) . Oba
da
,
˙za
,
do +∞ , wie
,
c ich iloczyn da
,
˙zy do +∞ · +∞ = +∞ .
Przyk lad 4.7
Pokazali´smy wcze´sniej, ˙ze wyraz cia
,
gu geometrycznego o ilorazie
z przedzia lu (−1, 1) jest zbie˙zny do 0 . Poka˙zemy jak mo˙zna uzyska´c ten sam rezul-
tat bez szacowa´
n stosuja
,
c w zamian twierdzenie o istnieniu granic pewnych cia
,
g´ow.
Za l´o˙zmy na pocza
,
tek, ˙ze 0 ≤ q < 1 . Wtedy oczywi´scie q
n+1
≤ q
n
, wie
,
c cia
,
g jest
nierosna
,
cy, zatem ma granice
,
. Oznaczmy ja
,
symbolem g . Poniewa˙z wszystkie wy-
razy cia
,
gu le˙za
,
w przedziale (0, 1) , wie
,
c granica le˙zy w przedziale [0, 1] . Jest jasne,
˙ze je´sli granica
,
cia
,
gu jest liczba g , to ka˙zdy jego podcia
,
g jest te˙z zbie˙zny do g .
Wobec tego g = lim
n→∞
q
n+1
= lim
n→∞
(q · q
n
) = q · lim
n→∞
q
n
= q · g , czyli g = qg . Sta
,
d,
poniewa˙z q 6= 1 , natychmiast wynika, ˙ze g = 0 . Za l´o˙zmy teraz, ˙ze −1 < q < 0 .
Wtedy −|q|
n
≤ q
n
≤ |q|
n
. Z ju˙z udowodnionej cze
,
´sci twierdzenia i z twierdzenia
o trzech cia
,
gach wynika, ˙ze 0 = lim
n→∞
(−|q|
n
) = lim
n→∞
q
n
= lim
n→∞
|q|
n
= 0 .
W ten sam spos´ob mo˙zna rozwa˙zy´c przypadek q > 1 . Cia
,
g (q
n
) jest ´sci´sle rosna
,
cy,
wie
,
c ma granice
,
g . Spe lniona musi by´c r´owno´s´c g = qg , co jest mo˙zliwe jedynie
wtedy, gdy g = 0 lub g = ±∞ . Wiemy oczywi´scie, ˙ze g > 0 — granica rosna
,
cego
cia
,
gu liczb dodatnich musi by´c wie
,
ksza ni˙z 0 , wobec tego g = +∞ . W przypadku
q ≤ −1 cia
,
g nie ma granicy, bo mo˙zemy wybra´c podcia
,
g, kt´ory ma granice
,
g
1
≤ −1 ,
np. q
2n−1
= q · (q
2
)
n
oraz podcia
,
g, kt´ory ma granice
,
g
2
≥ 1 , np. q
2n
= (q
2
)
n
,
istnienie podcia
,
g´ow o r´o˙znych granicach przeczy istnieniu granicy cia
,
gu, zar´owno
sko´
nczonej jak i niesko´
nczonej.
Przyk lad 4.8
Niech a > 0 be
,
dzie liczba
,
rzeczywista
,
. Wyka˙zemy, ˙ze lim
n→∞
n
√
a = 1.
Podobnie jak w poprzednich przypadkach poka˙zemy dwie metody. Tym razem za-
czniemy od sposobu z mniejsza
,
liczba
,
rachunk´ow, czyli „bardziej teoretycznego”.
Za l´o˙zmy, ˙ze a > 1 . Cia
,
g
n
√
a
jest w tym przypadku ´sci´sle maleja
,
cy, jego wy-
razy sa
,
wie
,
ksze ni˙z 1 , wie
,
c ma granice
,
g , sko´
nczona
,
, kt´ora nie mo˙ze by´c mniejsza
ni˙z 1 . Ka˙zdy podcia
,
g tego cia
,
gu jest zbie˙zny do g . Mie
,
dzy innymi g = lim
n→∞
2n
√
a .
17

Granica cia
,
gu
Micha l Krych
Skorzystamy teraz z twierdzenia o iloczynie granic:
g
2
= g · g = lim
n→∞
2n
√
a · lim
n→∞
2n
√
a = lim
n→∞
(
2n
√
a)
2
= lim
n→∞
n
√
a = g ,
zatem g
2
= g . Sta
,
d wynika, ˙ze g = 0 < 1 lub g = 1 (ju˙z wiemy, ˙ze g nie jest
r´owne ±∞ ). Poniewa˙z pierwsza mo˙zliwo´s´c zosta la wcze´sniej wykluczona, wie
,
c zo-
staje druga, czyli g = 1 .
Dla a = 1 teza jest prawdziwa w oczywisty spos´ob. Za l´o˙zmy teraz, ˙ze 0 < a < 1 .
Mamy lim
n→∞
n
√
a = lim
n→∞
1
n
p
1/a
=
1
lim
n→∞
n
p
1/a
=
1
1
= 1 — skorzystali´smy z twier-
dzenia o ilorazie granic oraz z ju˙z udowodnionej cze
,
´sci tezy.
Teraz udowodnimy, ˙ze lim
n→∞
n
√
a = 1 w przypadku a > 1 , za pomoca
,
szacowa´
n.
Niech ε be
,
dzie dowolna
,
liczba
,
rzeczywista
,
dodatnia
,
. Chcemy wykaza´c, ˙ze dla do-
statecznie du˙zych liczb naturalnych n zachodzi nier´owno´s´c |
n
√
a − 1| < ε , czyli ˙ze
1 − ε <
n
√
a < 1 + ε . Poniewa˙z a > 1 , wie
,
c nier´owno´s´c podw´ojna sprowadza sie
,
do
nier´owno´sci
n
√
a < 1 + ε , czyli do nier´owno´sci a < (1 + ε)
n
. Ta z kolei wynika z
nier´owno´sci a < 1+nε , bo 1+nε < (1+ε)
n
— nier´owno´s´c Bernoulli’ego. Wystarczy
wie
,
c, by n
ε
>
a − 1
ε
. To ko´
nczy dow´od.
Uwaga 4.20
Nie rozwia
,
zywali´smy nier´owno´sci
n
√
a < 1 + ε , bo wymaga loby
to zastosowania logarytm´ow, n >
log a
log (1 + ε)
, wskazali´smy jedynie moment, od
kt´orego nier´owno´s´c jest prawdziwa, nie troszcza
,
c sie
,
o to, co sie
,
dzieje w przypadku
wcze´sniejszych n .
Uwaga 4.21 Zauwa˙zmy, ˙ze w definiuja
,
c pote
,
ge
,
o wyk ladniku rzeczywistym wyka-
zali´smy, ˙ze dla ka˙zdej liczby a > 1 i dowolnej liczby naturalnej n zachodzi nier´owno´s´c
2m
√
a < 1 +
a−1
2
m
. Sta
,
d wynika, ˙ze je˙zeli n ≥ 2
m
, to 1 <
n
√
a ≤
2m
√
a < 1 +
a−1
2
m
. Maja
,
c
dane ε > 0 dobieramy m ∈ N tak, ˙ze 1 +
a−1
2
m
< 1 + ε , wie
,
c dla n > 2
m
mamy
n
√
a < 1 + ε . Oznacza to, ˙ze lim
n→∞
n
√
a = 1 .
Przyk lad 4.9
Teraz wyka˙zemy, ˙ze granica
,
cia
,
gu
n
√
n
jest liczba 1 . Zacznijmy
od wypisania kilku pierwszych wyraz´ow cia
,
gu:
1
√
1 = 1 ,
√
2 ,
3
√
3 ,
4
√
4 =
√
2 , . . . .
Bez trudu mo˙zna stwierdzi´c, ˙ze
3
√
3 >
√
2 — mo˙zna np. podnie´s´c te
,
nier´owno´s´c
obustronnie do pote
,
gi 6 . Oznacza to, ˙ze
√
2 <
3
√
3 >
4
√
4 . Wynika sta
,
d, ˙ze cia
,
g
ten nie jest maleja
,
cy ani rosna
,
cy. Nie wyklucza to monotoniczno´sci od pewnego miej-
sca. Udowodnimy wie
,
c , ˙ze lim
n→∞
n
√
n = 1 korzystaja
,
c z definicji granicy cia
,
gu, inny
spos´ob poka˙zemy p´o´zniej.
Niech ε be
,
dzie dodatnia
,
liczba
,
dodatnia
,
. Poniewa˙z wszystkie wyrazy cia
,
gu sa
,
wie
,
ksze
18

Granica cia
,
gu
Micha l Krych
lub r´owne od 1 , wie
,
c wystarczy wykaza´c, ˙ze dla dostatecznie du˙zych n zacho-
dzi nier´owno´s´c
n
√
n < 1 + ε , czyli n < (1 + ε)
n
. Tym razem nier´owno´s´c Ber-
noulli’ ego jest niewystarczaja
,
ca, ale poniewa˙z ε > 0 , wie
,
c dla n ≥ 2 mamy
(1 + ε)
n
≥ 1 +
n
1
ε +
n
2
ε
2
>
n
2
ε
2
. Wystarczy wie
,
c, ˙zeby n <
n
2
ε
2
=
n(n−1)
2
ε
2
,
czyli
2
ε
2
+ 1 < n , co ko´
nczy dow´od.
Teraz poka˙zemy, jak mo˙zna uzyska´c ten sam wynik bez szacowa´
n. Nier´owno´s´c
n+1
√
n + 1 <
n
√
n jest r´ownowa˙zna nier´owno´sci n >
n+1
n
n
=
1 +
1
n
n
. Ot´o˙z
wykazali´smy wcze´sniej, ˙ze cia
,
g 1 +
1
n
n
jest ograniczony. Wobec tego nier´owno´s´c
n > 1 +
1
n
n
zachodzi dla wszystkich dostatecznie du˙zych liczb naturalnych n —
nie mamy powodu ustala´c w tej chwili, od kt´orego momentu jest ona prawdziwa.
Wobec tego cia
,
g (
n
√
n) jest maleja
,
cy od pewnego momentu, jest te˙z ograniczony z
do lu przez liczbe
,
1 , a co zatem idzie zbie˙zny. Oznaczmy przez g jego granice
,
. Ka˙zdy
podcia
,
g tego cia
,
gu, np.
2n
√
2n jest zbie˙zny do tej samej granicy g . Wobec tego
g
2
= g · g = lim
n→∞
2n
√
2n · lim
n→∞
2n
√
2n = lim
n→∞
2n
√
2n
2
= lim
n→∞
n
√
2 ·
n
√
n
=
= lim
n→∞
n
√
2 ·
n
√
n = 1 · g .
Otrzymali´smy r´owno´s´c g
2
= g a poniewa˙z 1 ≤ g < +∞ , wie
,
c g = 1 , co ko´
nczy
dow´od. Okaza lo sie
,
, ˙ze r´ownie˙z w tym przypadku mo˙zna omina
,
´c rachunki, wymaga lo
to tylko nieco wie
,
cej zachodu ni˙z poprzednio, bo cia
,
g nie jest monotoniczny, a tylko
maleja
,
cy od pewnego momentu.
Przyk lad 4.10
Niech k be
,
dzie dowolna
,
liczba
,
ca lkowita
,
dodatnia
,
, q liczba
,
rze-
czywista
,
wie
,
ksza
,
od 1 . Wyka˙zemy, ˙ze lim
n→∞
n
k
q
n
= 0 . Niech r = 1 − q . Oczywi´scie
r > 0 . Za l´o˙zmy, ˙ze n > k + 1 . Mamy wtedy
q
n
= (1 + r)
n
=
= 1 +
n
1
r +
n
2
r
2
+
n
3
r
3
+ · · · +
n
k
r
k
+
n
k+1
r
k+1
+ · · · +
n
n
r
n
>
n
k+1
r
k+1
.
Wobec tego
0 <
n
k
q
n
<
n
k
(
n
k+1
)
r
k+1
=
n
k
(k+1)!
n(n−1)·...·(n−k)r
k+1
=
(k+1)!
n(1−
1
n
)(1−
2
n
)·...·(1−
k
n
)r
k+1
−−−−→
n→∞
0 ,
a sta
,
d i z twierdzenia o trzech cia
,
gach teza wynika od razu.*
Przyk lad 4.11
Niech a
n
=
q
n
n!
i niech q oznacza dowolna
,
liczbe
,
rzeczywista
,
.
Wyka˙zemy, ˙ze lim
n→∞
a
n
= 0 .
Z definicji cia
,
gu (a
n
) wynika, ˙ze a
n
=
q·q·q·...·q
1·2·3·...·n
. Iloraz
|q|
n
maleje wraz ze wzrostem
*
Na prze lomie XVIII i XIX w. angielski ekonomista Th.R.Malthus twierdzi l, ˙ze liczba ludno´sci wzrasta
jak cia,g geometryczny, za´s ilo´s´c ˙zywno´sci jak cia,g arytmetyczny, tzw. prawo Malthusa. Wynika loby
sta,d i z tego, co w la´snie wykazali´smy, ˙ze ilo´s´c ˙zywno´sci przypadaja,ca na jedna, osobe, maleje w czasie
i to do 0 , co prawda w bardzo d lugim, bo w przypadku liczby ludno´sci q≈1 , ale to i tak nie wygla,da lo
dobrze.
19
Granica cia
,
gu
Micha l Krych
liczby n . Jest nawet lim
n→∞
|q|
n
= 0 . Oznacza, to ˙ze je´sli n jest du˙ze, to wyraz a
n+1
jest znikomo ma la
,
cze
,
´scia
,
wyrazu a
n
. Sta
,
d powinna wynika´c zbie˙zno´s´c cia
,
gu do 0 .
Rzeczywi´scie, niech m ≥ 2|q| be
,
dzie liczba
,
naturalna
,
i niech n > m . Wtedy
0 <
q
n
n!
=
|q
m
|
m!
·
|q|
m + 1
·
|q|
m + 2
· . . . ·
|q|
n
<
|q
m
|
m!
·
1
2
n−m
.
Ostatnie wyra˙zenie da
,
˙zy do 0 , bo jest to wyraz cia
,
gu geometrycznego o ilorazie
1
2
.
Stosujemy twierdzenie o trzech cia
,
gach. Z niego wynika, ˙ze lim
n→∞
q
n
n!
= 0 . Dow´od
zosta l zako´
nczony.
Przyk lad 4.12
lim
n→∞
n!
n
n
= 0 . Wynika to sta
,
d, ˙ze 0 <
n!
n
n
=
1
n
·
2
n
· . . . ·
n
n
≤
1
n
i tego, ˙ze lim
n→∞
1
n
= 0 . Dow´od zosta l zako´
nczony.
.
Przyk lad 4.13
Je˙zeli k > 1 jest liczba
,
naturalna
,
, x
1
, x
2
, . . . sa
,
liczbami
nieujemnymi i lim
n→∞
x
n
= g , to lim
n→∞
k
√
x
n
=
k
√
g . Je´sli bowiem
k
√
x
ln
jest pod-
cia
,
giem zbie˙znym do granicy x cia
,
gu
k
√
x
n
, to na mocy twierdzenia o granicy
iloczynu cia
,
g´ow zachodzi x
k
=
lim
n→∞
k
√
x
ln
k
= lim
n→∞
x
ln
= g . Poniewa˙z x ≥ 0 ,
jako granica cia
,
gu liczb nieujemnych, wie
,
c x =
k
√
g . Wykazali´smy wie
,
c, ˙ze wszyst-
kie te podcia
,
gi cia
,
gu
k
√
x
n
, kt´ore maja
,
granice, sa
,
zbie˙zne do
k
√
g . Z wniosku z
twierdzenia Bolzano – Weierstrassa wynika, ˙ze granica
,
cia
,
gu
k
√
x
n
jest
k
√
g . To
twierdzenie z latwo´scia
,
mo˙zna rozszerzy´c na przypadek cia
,
gu liczb ujemnych i pier-
wiastka stopnia nieparzystego.
Mo˙zna te˙z wykaza´c to twierdzenie korzystaja
,
c z latwej do uzasadnienia nier´owno´sci
k
√
x −
k
√
y
≤
k
p
|x − y|
Przyk lad 4.14
Teraz kilka s l´ow wyja´sniaja
,
cych dlaczego pewne dzia lania z u˙zy-
ciem symboli niesko´
nczonych sa
,
zdefiniowane, a inne — nie. Wypiszmy kilka r´owno´sci
latwych do dowodu:
lim
n→∞
n − (n −
1
n
)
= lim
n→∞
1
n
= 0 , co sugeruje, ˙ze powinno by´c +∞ − (+∞) = 0 ;
lim
n→∞
(n − (n − 1)) = lim
n→∞
1 = 1 , co sugeruje, ˙ze powinno by´c +∞ − (+∞) = 1 ;
lim
n→∞
n − (n −
n
2
)
= lim
n→∞
n
2
= +∞ , zatem powinno by´c +∞ − (+∞) = +∞ ;
lim
n→∞
(n − (2n)) = lim
n→∞
(−n) = −∞ , zatem powinno by´c +∞ − (+∞) = −∞ .
Okazuje sie
,
wie
,
c, ˙ze z tego, ˙ze dwa cia
,
gi da
,
˙za
,
do +∞ , nic nie wynika na temat
warto´sci granicy ich r´o˙znicy. Przyja
,
wszy a
n
= n i b
n
= n + (−1)
n
przekonujemy sie
,
z latwo´scia
,
, ˙ze mo˙ze sie
,
te˙z zdarzy´c, ˙ze lim
n→∞
a
n
= +∞ , lim
n→∞
b
n
= +∞ , natomiast
20

Granica cia
,
gu
Micha l Krych
r´o˙znica (a
n
− b
n
) cia
,
g´ow (a
n
) i (b
n
) granicy w og´ole nie ma, w tym przypadku
jest ona cia
,
giem geometrycznym o ilorazie −1 . Innymi s lowy na podstawie tego,
˙ze dwa cia
,
gi maja
,
granice
,
+∞ , nic o istnieniu granicy ich r´o˙znicy lub jej warto´sci
w przypadku, gdy granica istnieje, powiedzie´c nie mo˙zna! To samo dotyczy innych
symboli nieoznaczonych np.
0
0
,
±∞
±∞
, 1
±∞
, 0
0
. . . Zache
,
camy czytelnika do samo-
dzielnego wymy´slenia odpowiednich przyk lad´ow w celu lepszego zrozumienia tych
kwestii.
Uwaga 4.22 (o cie
,
˙zkim ˙zyciu studenta) Wielu student´ow miewa lo w przesz lo´sci
— przysz lo´s´c nie jest autorowi znana — k lopoty z symbolami nieoznaczonymi; wg.
autora samodzielne wymy´slenie kilku przyk lad´ow ilustruja
,
cych niemo˙zno´s´c rozsze-
rzenia definicji dzia la´
n z u˙zyciem niesko´
nczono´sci to jedna z najpewniejszych dr´og
uniknie
,
cia tego rodzaju trudno´sci.
Ostatnia rzecz, o kt´orej wspomnie´c wypada przed przej´sciem do dowod´ow, to
twierdzenie o przenoszeniu sie
,
nier´owno´sci na granice
,
(N4). Ot´o˙z mo˙zna by pomy´sle´c,
˙ze je´sli dla wszystkich dostatecznie du˙zych liczb naturalnych n zachodzi ostra nie-
r´owno´s´c b
n
< a
n
, to r´ownie˙z w granicy nier´owno´s´c jest ostra. Tak mo˙ze by´c, ale nie
musi. ´
Swiadczy´c mo˙ze o tym naste
,
puja
,
cy przyk lad: a
n
=
1
2n
, b
n
=
1
n
— wobec
tego a
n
< b
n
dla n = 1, 2, 3, . . . i jednocze´snie lim
n→∞
a
n
= 0 = lim
n→∞
b
n
.
Opuszczone dowody
Przejdziemy teraz do dowod´ow twierdze´
n sformu lowanych na pocza
,
tku tego roz-
dzia lu. Zaczniemy od nier´owno´sci. Zache
,
camy student´ow do przejrzenia przynajmniej
cze
,
´sci dowod´ow i do lo˙zenia stara´
n w celu zrozumienia wnioskowania. Wnioskowanie
to jedna z najwa˙zniejszych rzeczy w matematyce. Rozpowszechniany pogla
,
d, ˙ze jest
to potrzebne tylko matematykom, jest tylko w pewnym sensie prawdziwy. Bez za-
poznania sie
,
z metodami stosowanymi w matematyce nie spos´ob zapewne zrozumie´c
sformu lowa´
n wielu twierdze´
n i wobec tego trudno je stosowa´c, na pewno grozi to
b le
,
dami i zmusza student´ow do zbe
,
dnego zapamie
,
tywania jakich´s szczeg´o l´ow, kt´ore
z punktu widzenia os´ob, kt´ore zrozumia ly podstawowe kwestie sa
,
po prostu oczywi-
ste i w og´ole o nich nie warto wspomina´c. Poza tym cze
,
´s´c dowod´ow m´owi o tym,
jak nale˙zy poste
,
powa´c w r´o˙znych sytuacjach: dow´od twierdzenia o granicy iloczynu
lub ilorazu cia
,
g´ow to po prostu opis podstawowej (i najprostszej) metody szacowania
iloczynu lub ilorazu.
Dow´
od twierdzenia o szacowaniu
Zaczniemy od N1. Przypomnijmy, ˙ze liczba
C jest mniejsza od granicy cia
,
gu (a
n
) . Mamy wykaza´c, ˙ze dla dostatecznie du˙zych
21
Granica cia
,
gu
Micha l Krych
n zachodzi nier´owno´s´c C < a
n
. Za l´o˙zmy najpierw, ˙ze granica lim
n→∞
a
n
jest nie-
sko´
nczona. Jest ona wie
,
ksza od liczby rzeczywistej C , wie
,
c lim
n→∞
a
n
= +∞ (bo
−∞ < C ). Z definicji od razu wynika, ˙ze dla ka˙zdej liczby rzeczywistej M , np. dla
M = C , pocza
,
wszy od pewnego momentu, zachodzi nier´owno´s´c a
n
> M = C .
Przejd´zmy do naste
,
pnego przypadku: granica lim
n→∞
a
n
jest sko´
nczona. Przyj-
mijmy ε = lim
n→∞
a
n
− C . Z definicji od razu wynika, ˙ze dla dostatecznie du˙zych n
zachodzi nier´owno´s´c |a
n
− lim
n→∞
a
n
| < ε , wie
,
c a
n
> lim
n→∞
a
n
− ε = C .
W taki sam spos´ob udowodni´c mo˙zna N2 — trzeba jedynie zmieni´c kierunki
niekt´orych nier´owno´sci i zasta
,
pi´c +∞ przez −∞ .
Teraz za l´o˙zmy, ˙ze lim
n→∞
b
n
< lim
n→∞
a
n
. Niezale˙znie od tego, czy granice sa
,
sko´
n-
czone czy nie, istnieje liczba C taka, ˙ze lim
n→∞
b
n
< C < lim
n→∞
a
n
. Na mocy ju˙z
udowodnionej cze
,
´sci twierdzenia dla dostatecznie du˙zych n zachodza
,
nier´owno´sci
b
n
< C oraz C < a
n
. Z nich wynika od razu, ˙ze dla dostatecznie du˙zych liczb
naturalnych n mamy b
n
< a
n
, co ko´
nczy dow´od cze
,
´sci N3.
Za l´o˙zmy, ˙ze od pewnego momentu zachodzi nier´owno´s´c b
n
≤ a
n
, chcemy nato-
miast wykaza´c, ˙ze lim
n→∞
b
n
≤ lim
n→∞
a
n
. Je´sli tak nie jest, to lim
n→∞
b
n
> lim
n→∞
a
n
. Sta
,
d
jednak wynika, ˙ze dla dostatecznie du˙zych liczb naturalnych n zachodzi nier´owno´s´c
b
n
> a
n
sprzeczna z za lo˙zeniem. Zako´
nczyli´smy dow´od twierdzenia o szacowaniu.
Z udowodnionego w la´snie twierdzenia ju˙z wcze´sniej wywnioskowali´smy, ˙ze je´sli
cia
,
g ma granice
,
, to tylko jedna
,
.
Teraz udowodnimy, ˙ze cia
,
g zbie˙zny do granicy sko´
nczonej jest ograniczony za-
r´owno z g´ory jak i z do lu. Niech c i d be
,
da
,
takimi liczbami rzeczywistymi, ˙ze
c < lim
n→∞
a
n
< d . Z twierdzenia o szacowaniu wynika, ˙ze dla dostatecznie du˙zych liczb
naturalnych n , powiedzmy wie
,
kszych od odpowiednio dobranej liczby m , zachodzi
nier´owno´s´c c < a
n
< d . Wystarczy teraz przyja
,
´c, ˙ze C jest najmniejsza
,
z liczb a
0
,
a
1
, . . . , a
m
, c , by dla wszystkich liczb naturalnych n by lo C ≤ a
n
. Analogicznie
przyjmujemy, ˙ze D jest najwie
,
ksza
,
z liczb a
0
, a
1
, . . . , a
m
, d — wtedy a
n
≤ D
dla wszystkich liczb naturalnych n . Dow´od tego wniosku zosta l zako´
nczony.
Uwaga 4.23 Ten dow´od jest bardzo prosty. Prosze
,
jednak zwr´oci´c uwage
,
na to,
˙ze spo´sr´od sko´
nczenie wielu liczb mo˙zna zawsze wybra´c najmniejsza
,
a spo´sr´od nie-
sko´
nczenie wielu niekoniecznie, np. w´sr´od liczb 1,
1
2
,
1
3
, . . . najmniejszej nie ma!
Uwaga 4.24 (o zbie˙zno´sci cia
,
gu przeciwnego)
Zauwa˙zmy teraz, ˙ze cia
,
g (c
n
) ma granice
,
wtedy i tylko wtedy, gdy cia
,
g (−c
n
) ma
22

Granica cia
,
gu
Micha l Krych
granice
,
, niezale˙znie od tego, czy granica ta jest sko´
nczona, czy niesko´
nczona oraz ˙ze
zachodzi wtedy r´owno´s´c
lim
n→∞
(−c
n
) = − lim
n→∞
c
n
.
Ta bardzo prosta uwaga wielokrotnie pozwoli nam na zmniejszenie liczby przy-
padk´ow rozwa˙zanych w dowodach.
Teraz zajmiemy sie
,
twierdzeniem o arytmetycznych w lasno´sciach granicy cia
,
gu.
Udowodnimy, ˙ze suma granic dw´och cia
,
g´ow jest granica
,
sumy tych cia
,
g´ow. Za l´o˙zmy,
˙ze g
a
= lim
n→∞
a
n
i g
b
= lim
n→∞
b
n
. Nale˙zy rozwa˙zy´c trzy przypadki: g
a
, g
b
sa
,
liczbami
rzeczywistymi, g
a
jest liczba
,
rzeczywista
,
za´s g
b
jest symbolem niesko´
nczonym, g
a
, g
b
sa
,
symbolami niesko´
nczonymi tego samego znaku.
Rozpoczniemy od granic sko´
nczonych, przypadku znanego pewnej cze
,
´sci stu-
dent´ow ze szko ly. Niech ε be
,
dzie dodatnia
,
liczba
,
rzeczywista
,
i niech n
0
ε
be
,
dzie
taka
,
liczba
,
naturalna
,
, ˙ze dla n > n
0
ε
zachodzi nier´owno´s´c |a
n
− g
a
| <
ε
2
. Niech
|b
n
− g
b
| <
ε
2
dla n > n
00
ε
, gdzie n
ε
jest odpowiednio dobrana
,
liczba
,
naturalna
,
.
Wtedy dla n > n
ε
:= max(n
0
ε
, n
00
ε
) zachodza
,
obydwie nier´owno´sci, zatem
|a
n
+ b
n
− (g
a
+ g
b
)| ≤ |a
n
− g
a
| + |b
n
− g
b
| <
ε
2
+
ε
2
= ε.
Oznacza to, ˙ze dla dostatecznie du˙zych numer´ow n r´o˙znica (a
n
+ b
n
) − (g
a
+ g
b
)
ma warto´s´c bezwzgle
,
dna
,
mniejsza
,
ni˙z ε , wie
,
c lim
n→∞
(a
n
+ b
n
) = g
a
+ g
b
. Dow´od
twierdzenia o granicy sumy cia
,
g´ow w tym przypadku zosta l zako´
nczony.
Zajmiemy sie
,
teraz naste
,
pnym przypadkiem: niech liczba g be
,
dzie granica
,
cia
,
gu
(a
n
) , czyli g = lim
n→∞
a
n
i niech +∞ = lim
n→∞
b
n
. Wyka˙zemy, ˙ze lim
n→∞
(a
n
+b
n
) = +∞ .
Niech M be
,
dzie dowolna
,
liczba
,
rzeczywista
,
. Istnieje liczba naturalna n
00
M −g+1
taka,
˙ze dla n > n
00
M −g+1
zachodzi nier´owno´s´c b
n
> M −g+1 . Istnieje te˙z liczba naturalna
n
0
1
taka, ˙ze dla n > n
0
1
zachodzi nier´owno´s´c |a
n
− g| < 1 . Niech n
M
be
,
dzie wie
,
ksza
,
z liczb n
00
M −g+1
i n
0
1
. Dla n > n
M
obie nier´owno´sci zachodza
,
, wie
,
c
a
n
+ b
n
= b
n
+ g + (a
n
− g) ≥ b
n
+ g − |a
n
− g| > (M − g + 1) + g − 1 = M .
Wykazali´smy , ˙ze dla dostatecznie du˙zych liczb naturalnych n zachodzi nier´owno´s´c
a
n
+ b
n
> M , wie
,
c lim
n→∞
(a
n
+ b
n
) = +∞ . Dow´od zosta l zako´
nczony.
Je´sli wie
,
c cia
,
g (a
n
) ma granice
,
sko´
nczona
,
i lim
n→∞
b
n
= −∞ , to na mocy po-
przednio wykazanej cze
,
´sci twierdzenia o granicy sumy cia
,
g −a
n
+(−b
n
)
ma granice
,
i zachodzi r´owno´s´c lim
n→∞
(−a
n
− b
n
) = − lim
n→∞
a
n
+ lim
n→∞
(−b
n
) = +∞ , co w ´swietle
uwagi poprzedzaja
,
cej to zdanie oznacza, ˙ze granica lim
n→∞
(a
n
+ b
n
) istnieje i jest
23
Granica cia
,
gu
Micha l Krych
r´owna −∞ . Dow´od zosta l zako´
nczony.
Kolej na ostatni przypadek: obie granice sa
,
r´owne +∞ lub obie sa
,
r´owne −∞ .
Z uwagi o zbie˙zno´sci cia
,
gu przeciwnego wynika, ˙ze dow´od przeprowadzi´c wystarczy
zak ladaja
,
c, ˙ze lim
n→∞
a
n
= +∞ = lim
n→∞
b
n
. Je´sli M jest dowolna
,
liczba
,
rzeczywista
,
,
to istnieja
,
takie liczby naturalne n
0
M/2
oraz n
00
M/2
, ˙ze je´sli n > n
0
M/2
, to a
n
>
M
2
,
za´s je´sli n > n
00
M/2
, to b
n
>
M
2
. Przyjmijmy, ˙ze n
M
jest wie
,
ksza
,
z liczb n > n
0
M/2
,
n > n
00
M/2
. Wtedy zachodza
,
obie nier´owno´sci i wobec tego a
n
+ b
n
>
M
2
+
M
2
= M ,
wie
,
c dla dostatecznie du˙zych liczb naturalnych n zachodzi nier´owno´s´c a
n
+ b
n
> M ,
a to oznacza, ˙ze lim
n→∞
(a
n
+ b
n
) = +∞ . Dow´od zosta l zako´
nczony.
Z uwagi o zbie˙zno´sci cia
,
gu przeciwnego i twierdzenia o granicy sumy (A1) wynika
od razu twierdzenie o granicy r´o˙znicy (A2).
Zajmiemy sie
,
teraz iloczynem. Podobnie jak poprzednio jest wiele przypadk´ow,
kt´orych liczbe
,
mo˙zna zredukowa´c stosuja
,
c uwage
,
o zbie˙zno´sci cia
,
gu przeciwnego do
naste
,
puja
,
cych: obie granice sa
,
sko´
nczone, obie granice sa
,
r´owne +∞ , jedna granica
jest dodatnia
,
liczba
,
rzeczywista
,
a druga jest niesko´
nczona, np. +∞ .
Rozpoczniemy od rozpatrzenia granicy iloczynu dw´och cia
,
g´ow, kt´orych gra-
nice sa
,
sko´
nczone. Z twierdzenia o szacowaniu wynika, ˙ze ka˙zdy z tych cia
,
g´ow jest
ograniczony, wie
,
c istnieje liczba K
0
> 0 taka, ˙ze |a
n
| ≤ K
0
i istnieje te˙z liczba
K
00
taka, ˙ze |b
n
| < K
00
dla ka˙zdej liczby naturalnej n . Przyjmuja
,
c, ˙ze K to
wie
,
ksza z liczb K
0
, K
00
znajdujemy liczbe
,
, kt´orej nie przekracza warto´s´c bezwzgle
,
dna
˙zadnego wyrazu kt´oregokolwiek z dw´och rozpatrywanych cia
,
g´ow: |a
n
|, |b
n
| ≤ K .
Niech g
a
= lim
n→∞
a
n
, g
b
= lim
n→∞
b
n
. Z twierdzenia o szacowaniu wnioskujemy, ˙ze
r´ownie˙z |g
a
|, |g
b
| ≤ K . Niech ε oznacza dowolna
,
liczbe
,
dodatnia
,
. Istnieje wtedy
liczba naturalna n
ε
, taka ˙ze je´sli n > n
ε
, to |a
n
− g
a
| <
ε
2K
i jednocze´snie
|b
n
− g
b
| <
ε
2K
. Wtedy
|a
n
b
n
− g
a
g
b
| = |(a
n
− g
a
)b
n
+ g
a
(b
n
− g
b
)| ≤ |a
n
− g
a
| · |b
n
| + |g
a
| · |b
n
− g
b
| <
<
ε
2K
· K + K ·
ε
2K
= ε .
Udowodnili´smy wie
,
c, ˙ze dla dostatecznie du˙zych n odleg lo´s´c liczby a
n
b
n
od liczby
g
a
g
b
jest mniejsza ni˙z ε , co oznacza, ˙ze g
a
g
b
= lim
n→∞
a
n
· lim
n→∞
b
n
, a to w la´snie by lo
naszym celem.
Teraz zajmiemy sie
,
granica
,
iloczynu cia
,
g´ow, z kt´orych jeden ma granice
,
sko´
nczo-
na
,
i dodatnia
,
, a granica
,
drugiego jest +∞ . Niech g
a
= lim
n→∞
a
n
be
,
dzie liczba
,
dodat-
nia
,
i niech +∞ = lim
n→∞
b
n
. Niech M be
,
dzie dowolna
,
liczba
,
rzeczywista
,
. Z twierdze-
nia o szacowaniu wynika, ˙ze istnieje liczba naturalna n
M
taka, ˙ze je´sli n > n
M
, to
a
n
>
1
2
g
a
> 0 i b
n
>
2|M |
g
a
> 0 . Wtedy a
n
b
n
>
1
2
g
a
2|M |
g
a
= |M | ≥ M . Dow´od w tym
24

Granica cia
,
gu
Micha l Krych
przypadku zosta l zako´
nczony. Rozpatrzymy teraz iloczyn cia
,
g´ow (a
n
) i (b
n
) przy
za lo˙zeniu, ˙ze lim
n→∞
a
n
= +∞ = lim
n→∞
b
n
. Je´sli M jest dowolna
,
liczba
,
rzeczywista
,
, to
istnieje liczba naturalna n
M
, taka ˙ze dla n > n
M
zachodza
,
nier´owno´sci a
n
> 1+|M |
i b
M
> 1+|M | . Wtedy dla n > n
M
mamy a
n
b
n
> (1+|M |)
2
> 2·|M | ≥ |M | ≥ M ,
co dowodzi r´owno´sci +∞ = lim
n→∞
a
n
b
n
. Twierdzenie o granicy iloczynu cia
,
g´ow zo-
sta lo w ten spos´ob udowodnione.
Pozosta la ostatnia cze
,
´s´c — twierdzenie o granicy ilorazu. Zn´ow zaczniemy od
granic sko´
nczonych. Niech g
a
= lim
n→∞
a
n
i niech 0 6= g
b
= lim
n→∞
b
n
. Wyka˙zemy,
˙ze lim
n→∞
a
n
b
n
=
g
a
g
b
. Niech ε be
,
dzie dowolna
,
liczba
,
dodatnia
,
. Z poczynionych za lo˙ze´
n
wynika, ˙ze istnieje taka liczba naturalna n
ε
, ˙ze je´sli n > n
ε
, to
|b
n
| >
|g
b
|
2
, |a
n
− g
a
| <
ε·|g
b
|
4
, |b
n
− g
b
| <
ε·|g
b
|
2
4(|g
a
|+1)
.*
Dla n > n
ε
mamy wie
,
c
a
n
b
n
−
g
a
g
b
=
|a
n
g
b
−g
a
b
n
|
|g
b
b
n
|
≤
|a
n
g
b
−g
a
g
b
|+|g
a
g
b
−g
a
b
n
|
|g
b
|
2
/2
=
2
|g
b
|
|a
n
− g
a
| +
2|g
a
|
|g
b
|
2
|g
b
− b
n
| < ε .
Twierdzenie zosta lo udowodnione w przypadku granic sko´
nczonych.
Je´sli lim
n→∞
a
n
= +∞ a cia
,
g (b
n
) ma granice
,
sko´
nczona
,
i r´o˙zna
,
od 0 , to cia
,
g
1
b
n
ma granice
,
sko´
nczona
,
i r´o˙zna
,
od 0 – wynika to z ju˙z udowodnionej cze
,
´sci twier-
dzenia o granicy ilorazu. Mo˙zna zastosowa´c twierdzenie o granicy iloczynu cia
,
g´ow:
lim
n→∞
a
n
b
n
= lim
n→∞
a
n
·
1
b
n
= lim
n→∞
a
n
· lim
n→∞
1
b
n
= +∞ · lim
n→∞
1
b
n
. Ten ostatni iloczyn
jest oczywi´scie dobrze okre´slony.
Ostatni przypadek: granica cia
,
gu (a
n
) jest sko´
nczona a granica cia
,
gu (b
n
) jest
niesko´
nczona. W tym przypadku cia
,
g (a
n
) jest ograniczony, tzn. istnieje liczba
K > 0 , taka ˙ze dla ka˙zdego n zachodzi nier´owno´s´c |a
n
| < K . Je´sli ε > 0 , to istnieje
liczba naturalna n
ε
, taka ˙ze je´sli n > n
ε
, to |b
n
| >
K
ε
. Wtedy
a
n
b
n
< K ·
ε
K
= ε .
Wykazali´smy wie
,
c, ˙ze dla dostatecznie du˙zych n iloraz
a
n
b
n
ma warto´s´c bezwzgle
,
dna
,
mniejsza
,
ni˙z ε , a to oznacza, ˙ze lim
n→∞
a
n
b
n
= 0 . Dow´od zosta l zako´
nczony.
Uwaga 4.25 (o ilorazie z ograniczonym licznikiem)
Z dowodu twierdzenia o granicy ilorazu wynika natychmiast, ˙ze je´sli cia
,
g (a
n
) jest
ograniczony i lim
n→∞
|b
n
| = +∞ , to lim
n→∞
a
n
b
n
= 0 — nie zak lada sie
,
tu, ˙ze cia
,
g (b
n
)
w og´ole ma granice
,
, starczy za lo˙zy´c, ˙ze cia
,
g jego warto´sci bezwzgle
,
dnych ma granice
,
niesko´
nczona
,
, o cia
,
gu (a
n
) te˙z nie trzeba zak lada´c, ˙ze jest zbie˙zny — wystarcza
ograniczono´s´c.
*
Nie za lo˙zyli´smy, ˙ze g
a
6=0 , wie,c w mianowniku umie´scili´smy |g
a
|+1 , by na pewno mianownik by l
r´
o˙zny od 0 .
25

Granica cia
,
gu
Micha l Krych
Teraz zajmiemy sie
,
twierdzeniem o trzech cia
,
gach. Wiemy, ˙ze dla dostatecznie
du˙zych n zachodzi nier´owno´s´c podw´ojna a
n
≤ b
n
≤ c
n
oraz ˙ze cia
,
gi a
n
i c
n
maja
,
wsp´olna
,
granice
,
g . Mamy dowie´s´c, ˙ze ta wsp´olna granice jest r´ownie˙z granica
,
cia
,
gu
(b
n
) . Za l´o˙zmy najpierw, ˙ze granica g jest sko´
nczona. Niech ε > 0 be
,
dzie dowolna
,
liczba
,
. Istnieje taka liczba naturalna n
ε
, ˙ze |a
n
− g| < ε i |c
n
− g| < ε dla n > n
ε
.
Wynika sta
,
d, ˙ze g − ε < a
n
≤ b
n
≤ c
n
< g + ε , zatem |b
n
− g| < ε . Udowodnili´smy
wie
,
c, ˙ze g = lim
n→∞
b
n
. Teraz mo˙zemy sie
,
zaja
,
´c przypadkiem granicy niesko´
nczonej.
Jak zwykle wystarczy zaja
,
´c sie
,
jedna
,
z dwu niesko´
nczono´sci, tym razem dla odmiany
g = −∞ . Niech M be
,
dzie liczba
,
rzeczywista
,
. Poniewa˙z lim
n→∞
c
n
= −∞ , wie
,
c istnieje
liczba naturalna n
M
, taka ˙ze dla n > n
M
zachodzi nier´owno´s´c b
n
≤ c
n
< M , wie
,
c
w szczeg´olno´sci b
n
< M . Dow´od zosta l zako´
nczony.
Uwaga 4.26 (o trzech cia
,
gach w przypadku granic niesko´
nczonych)
Z dowodu wynika, ˙ze w przypadku granicy niesko´
nczonej, np. r´ownej −∞ , u˙zycie
jednego z dw´och zewne
,
trznych cia
,
g´ow, w tym przypadku cia
,
gu (a
n
) , jest zbe
,
dne.
Prawdziwe jest wie
,
c twierdzenie: je´sli dla dostatecznie du˙zych n zachodzi nier´owno´s´c
b
n
≤ c
n
i cia
,
g (c
n
) ma granice
,
−∞ , to r´ownie˙z cia
,
g (b
n
) ma granice
,
−∞ i — ana-
logicznie — je´sli dla dostatecznie du˙zych n zachodzi nier´owno´s´c a
n
≤ b
n
i granica
,
cia
,
gu (a
n
) jest +∞ , to r´ownie˙z +∞ = lim
n→∞
b
n
.
Dow´
od twierdzenia o scalaniu. Ten dow´od jest bardzo prosty. Za l´o˙zmy, ˙ze gra-
nica g jest sko´
nczona i niech ε > 0 . Istnieja
,
liczby n
0
ε
i n
00
ε
, takie ˙ze dla n > n
0
ε
zachodzi nier´owno´s´c |a
kn
− g| < ε , dla n > n
00
ε
zachodzi nier´owno´s´c |a
ln
− g| < ε .
Poniewa˙z k
n
→ ∞ i l
n
→
∞
, wie
,
c istnieje n
ε
, takie ˙ze je´sli n > n
ε
i m jest
tak dobrane, ˙ze a
n
= a
km
lub a
n
= a
lm
, to m > n
0
ε
oraz m > n
00
ε
i wobec tego
|a
n
−g| < ε . To oznacza, ˙ze g = lim
n→∞
a
n
. Nieznaczne modyfikacje tego rozumowania
dadza
,
dow´od w przypadku granicy niesko´
nczonej.
Dow´
od twierdzenia Bolzano – Weierstrassa. Je´sli cia
,
g (a
n
) nie jest ogra-
niczony z g´ory, to mo˙zna z niego wybra´c podcia
,
g ´sci´sle rosna
,
cy: niech n
1
= 1 ;
poniewa˙z cia
,
g jest nieograniczony z g´ory, wie
,
c w´sr´od wyraz´ow naste
,
puja
,
cych po a
n
1
sa
,
wie
,
ksze od a
n
1
; niech n
2
be
,
dzie numerem jednego z nich — mamy wie
,
c n
2
> n
1
oraz a
n
2
> a
n
1
; poniewa˙z cia
,
g (a
n
) jest nieograniczony z g´ory, wie
,
c w´sr´od wy-
raz´ow, kt´ore naste
,
puja
,
po a
n
2
jest wyraz wie
,
kszy ni˙z a
n
2
, wybierzmy jeden z nich
i przyjmijmy, ˙ze n
3
jest jego numerem; mamy wie
,
c n
3
> n
2
oraz a
n
3
> a
n
2
; pro-
ces ten mo˙zna kontynuowa´c nieograniczenie. Ca lkowicie analogicznie poste
,
pujemy
w przypadku cia
,
gu nieograniczonego z do lu z tym, ˙ze teraz wybieramy podcia
,
g ´sci´sle
maleja
,
cy. Cia
,
g monotoniczny ma, jak wiemy, granice
,
. Pozosta l do rozpatrzenia przy-
26

Granica cia
,
gu
Micha l Krych
padek cia
,
gu ograniczonego (z g´ory i z do lu).
Niech c, d be
,
da
,
takimi liczbami rzeczywistymi, ˙ze dla ka˙zdego liczby naturalnej n
zachodzi nier´owno´s´c c ≤ a
n
≤ d , c jest ograniczeniem dolnym cia
,
gu (a
n
) a d —
g´ornym. Bez straty og´olno´sci rozwa˙za´
n mo˙zna przyja
,
´c, ˙ze cia
,
g (a
n
) nie zawiera pod-
cia
,
gu sta lego — je´sli zawiera, to ten w la´snie podcia
,
g jest zbie˙zny. Dalej zak ladamy,
˙ze (a
n
) nie zawiera podcia
,
gu sta lego, wie
,
c ˙ze ka˙zda liczba mo˙ze wysta
,
pi´c jako wyraz
cia
,
gu jedynie sko´
nczenie wiele razy. Zreszta
,
to za lo˙zenie nie jest istotne dla rozu-
mowania przeprowadzanego poni˙zej, jednak pozwala unikna
,
´c pyta´
n o szczeg´o lowa
,
interpretacje
,
u˙zywanych sformu lowa´
n. Niech n
1
= 1 , c
1
= c , d
1
= d . Jedna
z po l´owek przedzia lu [c, d] (lub obie) zawiera niesko´
nczenie wiele wyraz´ow cia
,
gu
a
n
, niech [c
2
, d
2
] be
,
dzie ta
,
w la´snie po l´owka
,
(je´sli np. w przedziale
c,
c+d
2
jest nie-
sko´
nczenie wiele wyraz´ow cia
,
gu (a
n
) , to przyjmujemy c
2
= c
1
= c i d
2
=
c+d
2
,
je´sli w przedziale
c,
c+d
2
jest sko´
nczenie wiele wyraz´ow cia
,
gu (a
n
) , to w przedziale
c+d
2
, d
musi by´c ich niesko´
nczenie wiele, w tym przypadku przyjmujemy c
2
=
c+d
2
i d
2
= d
1
= d ) i niech n
2
> n
1
be
,
dzie takim numerem, ˙ze a
n
2
∈ [c
2
, d
2
] . Powta-
rzamy przeprowadzone rozumowanie w odniesieniu do przedzia lu [c
2
, d
2
] i wyraz´ow
cia
,
gu naste
,
puja
,
cych po a
n
2
. W wyniku tego otrzymujemy liczbe
,
naturalna
,
n
3
> n
2
oraz liczby rzeczywiste c
3
, d
3
takie, ˙ze c
3
≤ a
n
3
≤ d
3
. Dla j = 1, 2, 3 mamy wobec
tego c
j
≤ a
n
j
≤ d
j
i d
j
− c
j
=
d−c
2
j
oraz c
1
≤ c
2
≤ c
3
i d
1
≥ d
2
≥ d
3
. Kontynuuja
,
c
to poste
,
powanie otrzymujemy niemaleja
,
cy cia
,
g (c
j
) oraz nierosna
,
cy cia
,
g (d
j
) , przy
czym d
j
−c
j
=
d−c
2
j
. Cia
,
gi te maja
,
granice, bo sa
,
monotoniczne. Granice te sa
,
r´owne,
bo lim
n→∞
(d
j
− c
j
) = lim
n→∞
1
2
j
· (d − c) = 0 . Poniewa˙z c
j
≤ a
n
j
≤ d
j
dla ka˙zdej liczby
naturalnej j , wie
,
c — na mocy twierdzenia o trzech cia
,
gach — cia
,
g (a
n
j
) te˙z ma te
,
sama
,
granice
,
. Dow´od zosta l zako´
nczony.
Dow´
od wniosku z twierdzenia Bolzano – Weierstrassa Udowodnimy teraz,
˙ze z cia
,
gu (a
n
) , kt´ory nie ma granicy mo˙zna wybra´c dwa podcia
,
gi maja
,
ce r´o˙zne
granice. Za l´o˙zmy,˙ze cia
,
g (a
n
) zawiera podcia
,
g o granicy +∞ . Poniewa˙z +∞ nie
jest granica
,
cia
,
gu (a
n
) , wie
,
c istnieje liczba rzeczywista B , taka ˙ze dla niesko´
nczenie
wielu n zachodzi nier´owno´s´c a
n
< B . Niech a
kn
oznacza podcia
,
g cia
,
gu (a
n
) z lo˙zony
z tych wszystkich wyraz´ow cia
,
gu a
n
, kt´ore sa
,
mniejsze ni˙z B . Na mocy twierdze-
nia Bolzano–Weierstrassa mo˙zna z cia
,
gu (a
kn
) wybra´c podcia
,
g kt´ory ma granice
,
g . Oczywi´scie g ≤ B . Wobec tego w tym przypadku istnieja
,
dwa podcia
,
gi: jeden
o granicy +∞ , drugi o granicy g ≤ B < +∞ , co ko´
nczy dow´od w tym przypadku.
Je´sli cia
,
g (a
n
) zawiera podcia
,
g o granicy −∞ , to teza wynika z poprzednio udowod-
nionego fragmentu: cia
,
g (−a
n
) zawiera dwa podcia
,
gi o r´o˙znych granicach. Pozosta l
do rozpatrzenia przypadek cia
,
gu (a
n
) , kt´ory nie zawiera podcia
,
g´ow o granicach nie-
27
Granica cia
,
gu
Micha l Krych
sko´
nczonych. Poniewa˙z cia
,
g (a
n
) nie zawiera podcia
,
gu o granicy +∞ , wie
,
c jest
ograniczony z g´ory, a poniewa˙z nie zawiera podcia
,
g´ow zbie˙znych do −∞ , wie
,
c jest
ograniczony r´ownie˙z z do lu. Mamy wie
,
c do czynienia z cia
,
giem ograniczonym. Mo˙zna
ze´
n wybra´c podcia
,
g zbie˙zny do granicy g . Poniewa˙z g nie jest granica
,
cia
,
gu (a
n
) ,
wie
,
c istnieje ε > 0 , takie ˙ze poza przedzia lem (g −ε, g +ε) znajduje sie
,
niesko´
nczenie
wiele wyraz´ow cia
,
gu. Wybieramy z tych w la´snie wyraz´ow podcia
,
g zbie˙zny. Ma on
oczywi´scie granice
,
6= g , dok ladniej odleg lo´s´c mie
,
dzy granicami tych podcia
,
g´ow nie
mo˙ze by´c mniejsza ni˙z ε . Dow´od zosta l zako´
nczony.
Uwaga 4.27 (o odleg lo´sci do ±∞ ) Z punktu widzenia zbie˙zno´sci wyr´o˙znianie
granic niesko´
nczonych jest nieco sztuczne, zwia
,
zane g l´ownie z tym, ˙ze nie wprowa-
dzili´smy poje
,
cia odleg lo´sci od ±∞ . To mo˙zna zrobi´c i to w ten spos´ob, by cia
,
g
zbie˙zny wg. definicji podanych przez nas poprzednio do pewnej granicy, by l takim
cia
,
giem, ˙ze odleg lo´s´c jego wyrazu od granicy da
,
˙zy do 0 . Niech f (x) =
x
√
1+x
2
dla
ka˙zdej liczby rzeczywistej x oraz f (+∞) = 1 i f (−∞) = −1 . Mo˙zna bez trudu wy-
kaza´c, ˙ze lim
n→∞
x
n
= g wtedy i tylko wtedy, gdy lim
n→∞
f (x
n
) = f (g) , a to ma miejsce
wtedy i tylko wtedy, gdy lim
n→∞
|f (x
n
)−f (g)| = 0 . Wida´c wie
,
c, ˙ze po przyje
,
ciu, ˙ze od-
leg lo´scia
,
punkt´ow x i y prostej uzupe lnionej niesko´
nczono´sciami jest |f (x) − f (y)| ,
be
,
dzie mo˙zna rozpatrywa´c wy la
,
cznie cia
,
gi o wyrazach z przedzia lu [−1, 1] — zamiast
cia
,
gu (x
n
) mo˙zna rozwa˙za´c cia
,
g (f (x
n
)) . Wada
,
tego podej´scia jest np. to, ˙ze przy
przej´sciu od x do f (x) liczbie x + y odpowiada f (x + y) 6= f (x) + f (y) .
Dow´
od. (twierdzenia Cauchy’ego) Zajmiemy sie
,
warunkiem Cauchy’ego. Je-
˙zeli cia
,
g ma granice
,
sko´
nczona
,
g i ε > 0 , to dla dostatecznie du˙zych liczb naturalnych
n zachodzi nier´owno´s´c |a
n
− g| <
ε
2
. Je´sli wie
,
c liczby naturalne k i l sa
,
dostatecznie
du˙ze, to
|a
k
− a
l
| = |a
k
− g + g − a
l
| ≤ |a
k
− g| + |g − a
l
| <
ε
2
+
ε
2
= ε .
Wykazali´smy wie
,
c, ˙ze z istnienia granicy sko´
nczonej wynika warunek Cauchy’ego.
Za l´o˙zmy teraz, ˙ze cia
,
g spe lnia warunek Cauchy’ego. Istnieje wtedy n
1
, takie ˙ze dla
k, l > n
1
mamy |a
k
− a
l
| < 1 . Niech l = n
1
+ 1 i niech k > l . Wtedy zachodzi
nier´owno´s´c |a
k
| − |a
l
| ≤ |a
k
− a
l
| < 1 , zatem |a
k
| < |a
l
| + 1 . Znaczy to, ˙ze cia
,
g
(a
n
) jest ograniczony. Wybierzmy z cia
,
gu (a
n
) podcia
,
g zbie˙zny (a
n
m
) . Niech g
oznacza jego granice
,
. Wyka˙zemy, ˙ze g jest granica
,
ca lego cia
,
gu. Je´sli ε > 0 , to dla
dostatecznie du˙zych k, l, m zachodza
,
nier´owno´sci |a
k
− a
l
| <
ε
2
oraz |a
n
m
− g| <
ε
2
. Poniewa˙z m, l sa
,
wybierane dowolnie, byle by ly dostatecznie du˙ze, i n
m
≥ m ,
wie
,
c mo˙zna wybra´c je tak, by l = n
m
. Wtedy dla dostatecznie du˙zego k zachodzi
nier´owno´s´c |a
k
− g| ≤ |a
k
− a
l
| + |a
n
m
− g| <
ε
2
+
ε
2
= ε , co oznacza, ˙ze g = lim
n→∞
a
n
.
28
Granica cia
,
gu
Micha l Krych
Dow´od zosta l zako´
nczony.
Troche
,
zada´
n do domu i na ´
cwiczenia
1. 01 Czy prawda
,
jest, ˙ze nier´owno´s´c 3
n
− 2,999
n
< 10000 zachodzi dla wszystkich
liczb n ∈ N ?
1. 02 Oblicz sze´s´c pocza
,
tkowych wyraz´ow cia
,
gu, kt´orego wyraz og´olny wyra˙za sie
,
wzorem:
a) a
n
=
n
2
+2n+1
n
,
b) b
n
= 1 −
1
10
n
,
c) c
n
= cos(n · 90
◦
) ,
d) d
n
= (−1)
n
·
3−n
n
, e) u
n
= [sin(n · 45
◦
)]
n
,
f) v
n
=
n
2
n+2
.
1. 03 Kt´ore wyrazy cia
,
gu (a
n
) sa
,
r´owne zeru
a) a
n
= n
2
− 5n − 6 , b) a
n
=
n
2
−30n+200
n
2
+n−1
,
c) a
n
= n
2
− n − 20 ?
1. 04 Kt´ore wyrazy cia
,
gu (a
n
) sa
,
r´owne liczbie: 1, −2 , 0, je˙zeli:
a
n
=
n
2
,
a
n
= 3n − 5 ,
a
n
= n − n
2
?
1. 05 Kt´ore wyrazy cia
,
gu (a
n
) sa
,
r´owne liczbie:
1
2
,
3
5
,
7
4
, je˙zeli
a
n
=
2n−1
5
,
a
n
=
7
n
,
a
n
=
3n−2
n+1
?
1. 06 Cia
,
g (a
n
) jest okre´slony wzorem rekurencyjnym: a
n+1
= a
n
+ 8n , przy czym
a
1
= 1 . Wykaza´c, ˙ze a
n
= (2n − 1)
2
.
1. 07 Cia
,
g (b
n
) jest okre´slony wzorem rekurencyjnym: b
n+1
= b
n
+ 2n + 1 , przy czym
b
1
= 1 . Wykaza´c, ˙ze b
n
= n
2
.
1. 08 Cia
,
g (x
n
) okre´slony jest wzorem rekurencyjnym:
a)
x
1
= 2
x
n+1
= x
n
+
1
3
b)
x
1
= 1
x
n+1
= 2x
n
c)
(
x
1
=
3
2
x
n+1
=
4
3
x
n
d)
(
x
1
= 0; x
2
= −
1
2
x
n+2
= (x
n
)
2
· x
n+1
W ka˙zdym z tych przypadk´ow poda´c wz´or og´olny na jego wyraz i uzasadni´c jego
poprawno´s´c.
1. 09 Zbada´c, kt´ore wyrazy podanych cia
,
g´ow sa
,
wie
,
ksze od danej liczby M :
a) a
n
= 3n + 4 , M = 1000 ;
b) b
n
= n
2
− 1 , M = 730 ;
c) c
n
=
10n
n
2
+1
, M = 4 ;
d) d
n
=
2n+5
2n+3
, M =
3
4
.
1. 10 Zbada´c, kt´ore wyrazy podanych cia
,
g´ow sa
,
mniejsze od danej liczby m :
a) a
n
=
1
n
, m =
1
100
;
b) b
n
=
3n
n
2
+1
, m = 0,001, c) c
n
=
100n
100+n
2
, m =
23
53
.
1. 11 Wykaza´c, ˙ze dla dowolnej liczby naturalnej n i dowolnych liczb rzeczywistych
a, b zachodza
,
r´owno´sci:
(i) (a + b)
n
= a
n
+
n
1
a
n−1
b +
n
2
a
n−2
b
2
+ · · · +
n
n−2
a
2
b
n−2
+
n
n−1
ab
n−1
+ b
n
,
gdzie
c
k
=
c(c−1)(c−2)... c−(k−1)
k!
dla ka˙zdego c ∈ R i ka˙zdego k ∈ {1, 2, 3, . . .} ,
29
Granica cia
,
gu
Micha l Krych
(ii) a
n
− b
n
= (a − b) a
n−1
+ a
n−2
b + a
n−3
b
2
+ · · · + ab
n−2
+ b
n−1
.
(iii) a
2n+1
+ b
2n+1
= (a + b) · a
2n
− a
2n−1
b + a
2n−2
b
2
− a
2n−3
b
3
+
+ · · · + a
2
b
2n−2
− ab
2n−1
+ b
2n
.
1. 12 Niech wyrazy cia
,
gu (a
n
) spe lniaja
,
r´ownanie: a
n+1
= qa
n
. Wykaza´c, ˙ze dla
dowolnej liczby naturalnej n zachodzi r´owno´s´c a
n
= a
1
q
n−1
. Udowodni´c, ˙ze
wz´or
a
1
+ a
2
+ ... + a
n
= a
1
1 − q
n
1 − q
zachodzi dla dowolnej liczby q 6= 1 i dowolnej liczby naturalnej n ≥ 1 .
1. 13 Zapisa´c liczbe
,
0,12345123451234512345 . . . = 0, (12345) jako iloraz dwu liczb
ca lkowitych.
1. 14 Co jest wie
,
ksze: liczba 1 czy liczba 0,99999 . . . = 0,(9) ? — odpowied´z dok ladnie
uzasadni´c.
1. 15 Dowie´s´c, ˙ze je´sli dla ka˙zdej liczby naturalnej n zachodzi r´owno´s´c a
n+1
= qa
n
+p ,
gdzie p oraz q sa
,
dowolnymi, niezale˙znymi od n liczbami rzeczywistymi, to
dla ka˙zdej liczby naturalnej n zachodzi r´owno´s´c a
n
=
p
1−q
+ (a
1
−
p
1−q
)q
n−1
.
W szczeg´olno´sci, je´sli a
1
=
p
1−q
, to wyraz cia
,
gu (a
n
) jest niezale˙zny od n .
1. 16 Wykaza´c, ˙ze cia
,
g (a
n
) jest zbie˙zny do 0 wtedy i tylko wtedy, gdy cia
,
g (|a
n
|)
jest zbie˙zny do 0 .
1. 17 Wykaza´c, ˙ze iloczyn (a
n
b
n
) cia
,
gu (a
n
) zbie˙znego do 0 i cia
,
gu ograniczonego
(b
n
) jest cia
,
giem zbie˙znym do liczby 0 .
1. 18 Znale´z´c wszystkie takie liczby naturalne n , ˙ze
n
n
2
+1
<
1
7
.
1. 19 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n > k , to
n+666
7n
2
−13
<
1
33
.
1. 20 Znale´z´c wszystkie takie liczby naturalne n , ˙ze
√
n
2
+ 1 − n <
1
7
.
1. 21 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
2n
2
+15n+2007
n
2
−2006n+13
− 2
<
1
4
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 22 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
n
2
+5n
1,2
n
<
1
10
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 23 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
sin n
√
n
<
1
3
√
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 24 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
sin n
√
n
<
1
3
√
n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 25 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
sin(1/n)
√
n
<
1
3
√
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 26 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
sin(1/n)
√
n
<
1
3
√
n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
30

Granica cia
,
gu
Micha l Krych
1. 27 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c sin
1
n
− sin
1
n+1
<
1
n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 28 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c sin
1
n
− sin
1
n+1
>
1
n
3
; lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 29 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
√
n + 2 −
√
n <
1
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 30 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
√
n + 2 −
√
n <
1
√
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 31 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
2n
n
> n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 32 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
2n
n
< n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 33 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
n
2
<
1
3
n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 34 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
n
2
>
1
3
n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 35 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c
n
2
<
√
2
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 36 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c n! <
√
n
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 37 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c n! >
√
n
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 38 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c n! < 100
n
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 39 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c n! > 1 +
1
n
n
2
lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 40 Wskaza´c jaka
,
kolwiek liczbe
,
naturalna
,
k taka
,
, ˙ze je´sli n ≥ k , to zachodzi
nier´owno´s´c ln n <
10
√
n lub wykaza´c, ˙ze taka liczba nie istnieje.
1. 41 Wykaza´c, ˙ze dla n > 1000000 zachodzi nier´owno´s´c
n
√
2 < 1.000001 .
1. 42 Wykaza´c, ˙ze dla dostatecznie du˙zych liczb naturalnych n zachodza
,
nier´owno´sci:
n! > 1000000
n
oraz 1.000001
n
> n
1000000
. W obu przypadkach sprawdzi´c, ˙ze
dla n = 2, 3, 4, 5 zachodzi nier´owno´s´c przeciwna i wskaza´c liczbe
,
n
0
(nie szuka´c
najmniejszej!) taka
,
, ˙ze dla n > n
0
zachodza
,
nier´owno´sci wypisane w pierwszym
zdaniu.
1. 43 W kraju dotknie
,
tym ostrym kryzysem inflacja wynosi 5% miesie
,
cznie. Oblicz
wska´znik inflacji rocznej z dok ladno´scia
,
do 1%. Do oszacowania mo˙zna u˙zy´c
31
Granica cia
,
gu
Micha l Krych
dwumian Newtona.
1. 44 Zak ladaja
,
c, ˙ze ´sredni przyrost naturalny na Ziemi r´owny jest 1,3% rocznie ob-
liczy´c po jakim czasie liczba ludzi na planecie sie
,
podwoi.
1. 45 Wypisa´c trzy pierwsze wyrazy cia
,
gu (a
n
) . Obliczy´c granice
,
cia
,
gu (a
n
) , o ile
istnieje, je´sli a
n
=
α.
1+n+3n
7
+n
2
n
2
−n+13
;
β.
1+n+3n+n
2
n
2
−n+13
;
γ.
1+n+3n
7
+n
2
n
2
−n
8
+13
;
δ.
√
n + 13 −
√
n ;
a.
p
n +
√
n −
√
n ;
b.
p
n +
3
√
n −
√
n ;
c.
n
√
3
n
+ sin n ;
d.
n
√
3
n
− 2
n
;
e. 1 +
n
n + 1
cos
nπ
2
;
f. sin n ;
g.
n
2
+ n + 1000
n
1000
+ 999n − 1
;
h.
ln n
2
+ n + 1000
ln (n
1000
+ 999n − 1)
;
i.
3
n
− 2
n
3
n
+ n
2
· 2
n
;
j.
3
n
+ 2
n
· sin n
3
n+1
+ n
2002
k.
10 · 11 · 12 · .... · (n + 9)
1 · 3 · 5 · ... · (2n − 1)
;
l.
n
√
n! ;
m. 1 −
1
2
1 −
1
3
... 1 −
1
n
;
n. 1 −
1
2
2
1 −
1
3
2
... 1 −
1
n
2
.
o.
n
2
n
;
p. lim
n→∞
n
13
2
n
;
q.
√
1 + 2
(−1)
n
;
r.
n
√
1
k
+ 2
k
+ · · · + n
k
;
s.
1
√
n
2
+1
+
1
√
n
2
+2
+ · · · +
1
√
n
2
+n
;
t.
1
2
+2
2
+3
2
+···+n
2
n
3
−n+13
u. lim
n→∞
n
k
q
1 +
1
n
− 1
, tu k ∈ N ;
v. lim
n→∞
(−2)
n
+3
n
(−2)
n+1
+3
n+1
1. 46 Znale´z´c granice
,
lim
n→∞
a
n
cia
,
gu (a
n
) , o ile istnieje, je´sli a
n
=
(1)
1 +
2
n+2
n
,
(2) 0.999999 +
1
n
n
,
(3)
n
2
+5n−3
n
2
+13
n
,
(4) 1.000001 +
1
n
n
,
(5)
1000000
n
n!
,
(6)
n
100000
1.000001
n
.
(7)
1 + sin
1
n
2
n
;
(8)
1 +
sin n
n
n
.
1. 47 Wykaza´c, ˙ze cia
,
g (a
n
) ma granice
,
i zbada´c, czy jest ona sko´
nczona, czy jest
r´owna 0 , je´sli cia
,
g (a
n
) zdefiniowany jest wzorem a
n
=
(a)
1
n+1
+
1
n+2
+ · · · +
1
n+n
.
(b) 1 +
1
1·2
+
1
2·3
+ · · · +
1
n(n+1)
.
(c)
1
1
2
+
1
2
2
+
1
3
2
+ · · · +
1
n
2
.
(d)
1
1
+
1
2
+
1
3
+ · · · +
1
n
.
(e)
√
6 + a
n−1
dla n = 1, 2, 3, . . . przy czym a
0
jest tu dowolna
,
liczba
,
rzeczy-
wista
,
nieujemna
,
, znale´z´c lim
n→∞
a
n
.
(e)
1
2
a
n−1
+
5
a
n−1
dla n = 1, 2, 3, . . . przy czym a
0
jest tu dowolna
,
liczba
,
32
Granica cia
,
gu
Micha l Krych
rzeczywista
,
dodatnia
,
, znale´z´c lim
n→∞
a
n
.
Wskaz´owka: wykaza´c, ˙ze a
n+1
≥
√
5 oraz a
n+1
≥ a
n+2
dla n = 0, 1, 2 . . . .
(g)
∗
1 +
1
1
2
1 +
1
2
2
1 +
1
3
2
. . . 1 +
1
n
2
.
Wskaz´owka: skorzysta´c z tego, ˙ze 1 + x ≤ e
x
dla ka˙zdej liczby x .
(h)
∗
1 −
1
2
1
1 −
1
2
2
1 −
1
2
3
. . . 1 −
1
2
n
, czy lim
n→∞
a
n
= 0 ?
Wskaz´owka: wykaza´c, ˙ze dla x < 1 zachodzi nier´owno´s´c
1 − x =
1
1 +
x
1−x
≥ e
−x/(1−x)
.
1. 48 Znale´z´c granice
,
lim
n→∞
a
n
cia
,
gu (a
n
) , je´sli a
n
=
(1)
1 +
n
√
2
n
;
(2)
1 +
n
√
2
n
n
;
(3)
ln n
n
;
(10)
1 −
1
n
2
n
;
(11)
1 −
1
3
√
n
5
n
;
(12)
1 +
2n
n
2
−n+1
n
;
(4)
e
bn
−1
b
n
, gdzie b
n
oznacza n − ty wyraz pewnego cia
,
gu zbie˙znego do 0 ,
przy czym b
n
6= 0 dla n = 1, 2, . . .
Wskaz´owka: dla x < 1 zachodzi nier´owno´s´c 1 + x ≤ e
x
≤
1
1−x
;
(5)
n
√
2−1
1/n
;
(6)
1+
n
√
2
2
n
;
(7)
n − ln n ;
(8)
1
3
+2
3
+3
3
+···+n
3
−
1
4
n
4
n
3
;
(9)
1
(n+1)
2
+
1
(n+2)
2
+ · · · +
1
(2n)
2
;
1. 49 Znale´z´c granice
,
cia
,
gu (a
n
) , je´sli a
0
=
1
10
oraz a
n+1
=
(1)
sin a
n
;
(2)
−a
n
+
1
2
a
3
n
;
(3)
2
a
n
− 1
– istnienie poszukiwanej granicy nale˙zy oczywi´scie wykaza´c!
1. 50 Czy lim
n→∞
a
n
istnieje? Je´sli ta granica istnieje, to czy jest sko´
nczona?
(1) a
n
=
1
√
2
+
1
3
√
3
+
1
4
√
4
+ · · · +
1
n
√
n
;
(2)
1
2
2
+
1
3
3
+
1
4
4
+ · · · +
1
n
n
;
(3) a
n
=
1
2
+
1
2·2
2
+
1
3·3
3
+ · · · +
1
n·n
n
;
(4) a
n
=
1
2
+
2
2
2
+
3
2
3
+ · · · +
n
2
n
;
(5)
a
n
= 1 +
1
2
−
1
3
−
1
4
+
1
5
+
1
6
−
1
7
−
1
8
+ · · · +
1
4n−3
+
1
4n−2
−
1
4n−1
−
1
4n
.
1. 51 Znale´z´c lim
n→∞
nq
n
dla q ∈ (−1, 1) , je´sli ta granica istnieje.
1. 52 Znale´z´c lim
n→∞
1 + q + q
2
+ · · · + q
n−1
dla q ∈ (−1, 1) , je´sli ta granica istnieje.
1. 53 Znale´z´c lim
n→∞
1+2q +3q
2
+· · ·+nq
n−1
dla q ∈ (−1, 1) , je´sli ta granica istnieje.
1. 54 Niech a
1
=
√
2 , a
2
=
p
2 +
√
2 , a
2
=
q
2 +
p
2 +
√
2 , . . . Wykaza´c, ˙ze cia
,
g
(a
n
) ma sko´
nczona
,
granice
,
.
1. 55 Niech x ∈ R be
,
dzie liczba
,
dodatnia
,
. W zale˙zno´sci od x znale´z´c
lim
n→∞
(1 + x)(1 + x
2
)(1 + x
4
) · . . . · (1 + x
2
n
) .
33
Wyszukiwarka
Podobne podstrony:
5 Ciagi,granica i ciaglosc funkcji
11. Zagadnienia granic poznania II, Archiwum, Filozofia
ciagi-granice-przyklady
11 Zagadnienia granic poznania IIid 12272 ppt
3 Indukcja matematyczna, ciągi granice
Ciągi, granica ciągu
W03 Ciągi c.d, granice
11 Zagadnienia granic poznania II
(3683) ciągi, granice ciągów, granice funkcji, ciągłość funkcji
ch10 11 geoman
5 Ciagi,granica i ciaglosc funkcji
11. Zagadnienia granic poznania II, Archiwum, Filozofia
3 Matematyka ciągi i granice ciągu
5 Ciagi,granica i ciaglosc funkcji
3 Indukcja matematyczna, ciągi granice
ciągi granice
więcej podobnych podstron