
Wanda Gryglewicz-Kacerka
Matematyka
————————————————————————————————————————
Semestr 1 Informatyka
Ciągi i granice ciągu

2
Matematyka Ciągi i granice
Spis treści
WIERDZENIE O CIĄGU OGRANICZONYM

Ciągi i granice
3
Matematyka Ciągi i granice
1. Ciągi i granice ciągu
Wykład obejmuje pojęcia dotyczące ciągów, granic ciągów i wyznaczania granic
ciągów.
1.1
Ciąg liczbowy
Ciąg – w matematyce pojęcie oddające intuicję ponumerowania, czy też
uporządkowania elementów zbioru. W zależności od rodzaju elementów zbioru stosuje
się różne nazwy: w przypadku liczb mówi się o ciągach liczbowych, bądź bardziej
precyzyjnie, np. w przypadku zbioru liczb całkowitych, rzeczywistych czy zespolonych,
ciąg nazywa się wtedy odpowiednio ciągiem całkowitoliczbowym, rzeczywistym i
zespolon
ym. Jeśli elementami zbioru są funkcje, to ciąg nazywa się ciągiem funkcyjnym.
Ciąg powstały poprzez wybranie elementów innego ciągu nazywa się podciągiem.

Ciągi i granice
4
Matematyka Ciągi i granice
Przykładami ciągów mogą być następujące:
ciąg pięciu elementów zbioru liczb naturalnych;
ciąg liczb całkowitych 1 oraz − 1 przyjmowanych naprzemiennie;
ciąg kolejnych liczb pierwszych;
ciąg wszystkich liczb wymiernych uporządkowanych w jakiś sposób.
Nieskończony ciąg liczbowy określa się jako przyporządkowanie każdej liczbie
naturalnej jednej liczby rzeczywistej u
n
.
Zapis ciągu
,...
,...
,
,
n
3
2
1
u
u
u
u

Ciągi i granice
5
Matematyka Ciągi i granice
lub
n
u
,..
,
,
3
2
1
u
u
u
nazywane są wyrazami ciągu,
n
u
wyraz ogólny ciągu.
Przykład

Ciągi i granice
6
Matematyka Ciągi i granice
Wyraz ogólny ciągu
,...
,
, 3
2
1
n
n
1
n
u
n
Wyrazy ciągu
,..
,
,
3
4
u
2
3
u
2
u
3
2
1
1.2
Granica ciągu
Definicja Cauchy’ego
Liczbę g nazywa się granicą ciągu u
n
, jeżeli dla każdego
>0 istnieje taka liczba
, że
dla każdego n>
spełniona jest nierówność

Ciągi i granice
7
Matematyka Ciągi i granice
Granica ciągu
g
u
n
Zapisuje się granicę
Granica ciągu
g
u
n
n
lim
Zapis zwięzły
Granica ciągu
g
u
g
u
n
n
0
n
lim
(oznaczenia:
g
u
n
lim
wtedy i tylko wtedy

Ciągi i granice
8
Matematyka Ciągi i granice
0
dla każdego epsilon większego od zera
istnieje takie
delta, że
n
dla każdego n> delta
Spełniony jest warunek
g
u
n
Przykład
Dowód, że liczba 1 jest granicą ciągu o ogólnym wyrazie

Ciągi i granice
9
Matematyka Ciągi i granice
,...
,
, 3
2
1
n
n
1
n
u
n
Poszukiwana jest liczba
, dla której spełniony jest warunek
Granica ciągu
n
1
n
1
n
Oznaczenie:
dla każdego
Wyrażenie w nawiasie można zapisać w postaci

Ciągi i granice
10
Matematyka Ciągi i granice
n
1
1
n
1
n
1
n
n
1
1
n
1
n
Istnieje liczba
spełniająca podany warunek a 1 jest granicą ciągu.
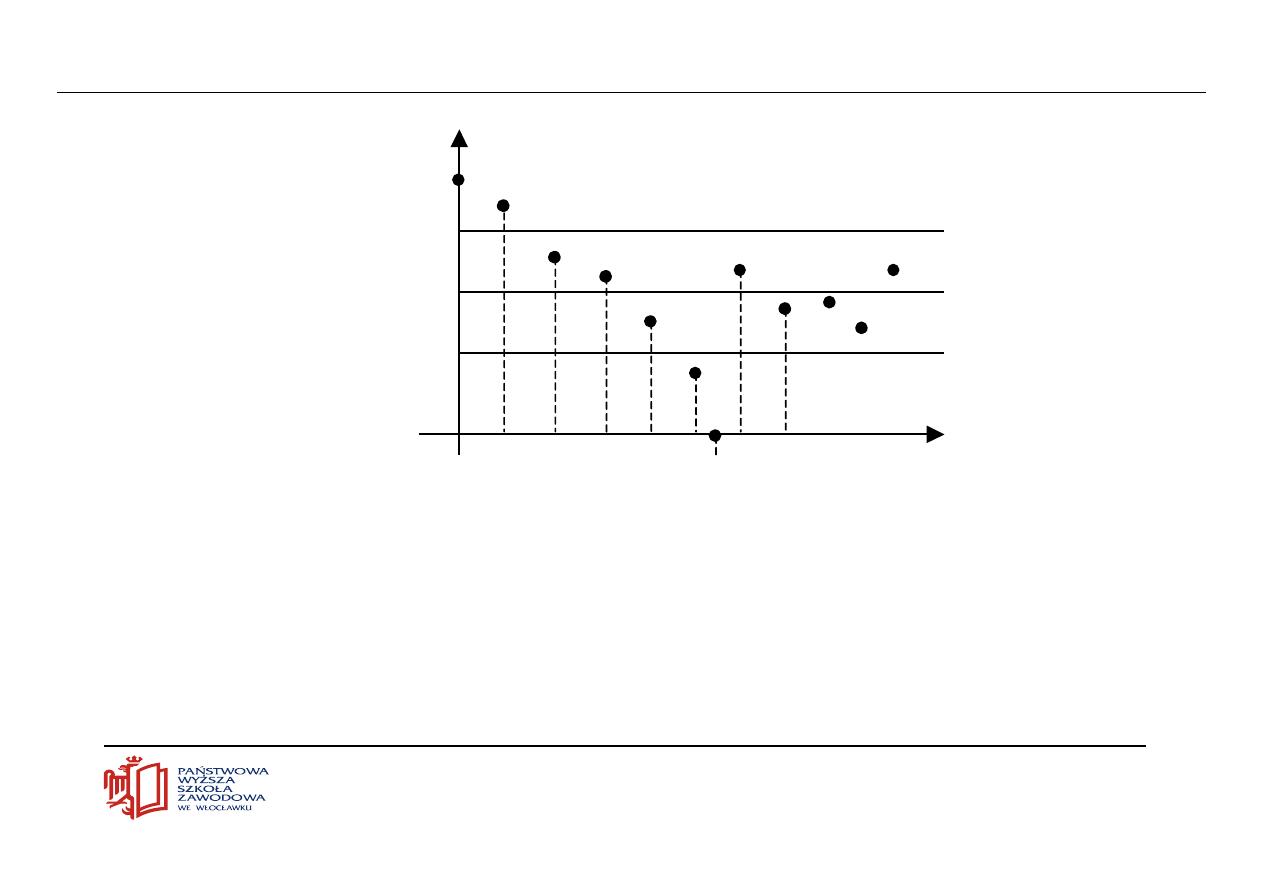
Ciągi i granice
11
Matematyka Ciągi i granice
g
g-
g+
1 2 3
7
4
n
Prawie wszystkie elementy mieszczą się w pasku epsylonowym. Oznacza to dla
ciągu nieskończonego, że mieszczą się poza skończoną liczbą wyrazów.
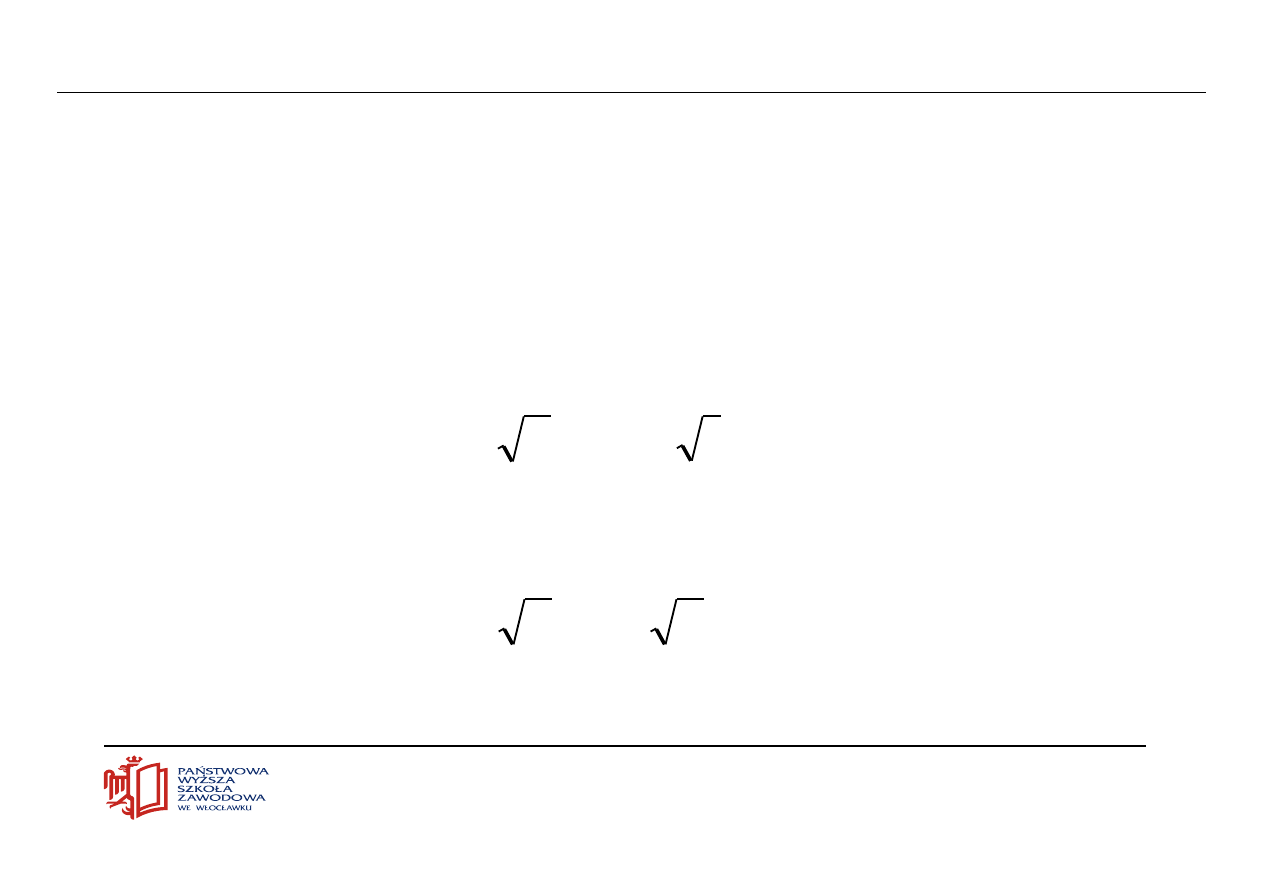
Ciągi i granice
12
Matematyka Ciągi i granice
Definicja
Liczba g jest granicą ciągu, jeżeli prawie wszystkie elementy ciągu leżą w otoczeniu
punktu g na osi liczbowej.
Przykład
Wyznaczyć granicę ciągu
Ciąg
1
1
1
1
u
n
u
n
n
Rozwiązanie
Rozważa się wyraz pomocniczy
Wyraz pomocniczy
1
1
n
n
n
n
a
n
n
a

Ciągi i granice
13
Matematyka Ciągi i granice
Dwumian
Newtona
n
n
n
n
n
n
n
n
a
a
n
a
n
a
n
n
...
1
2
1
1
1
1
2
2
1
Pominięcie
wyrazów
0
1
2
1
2
2
n
n
a
a
n
n
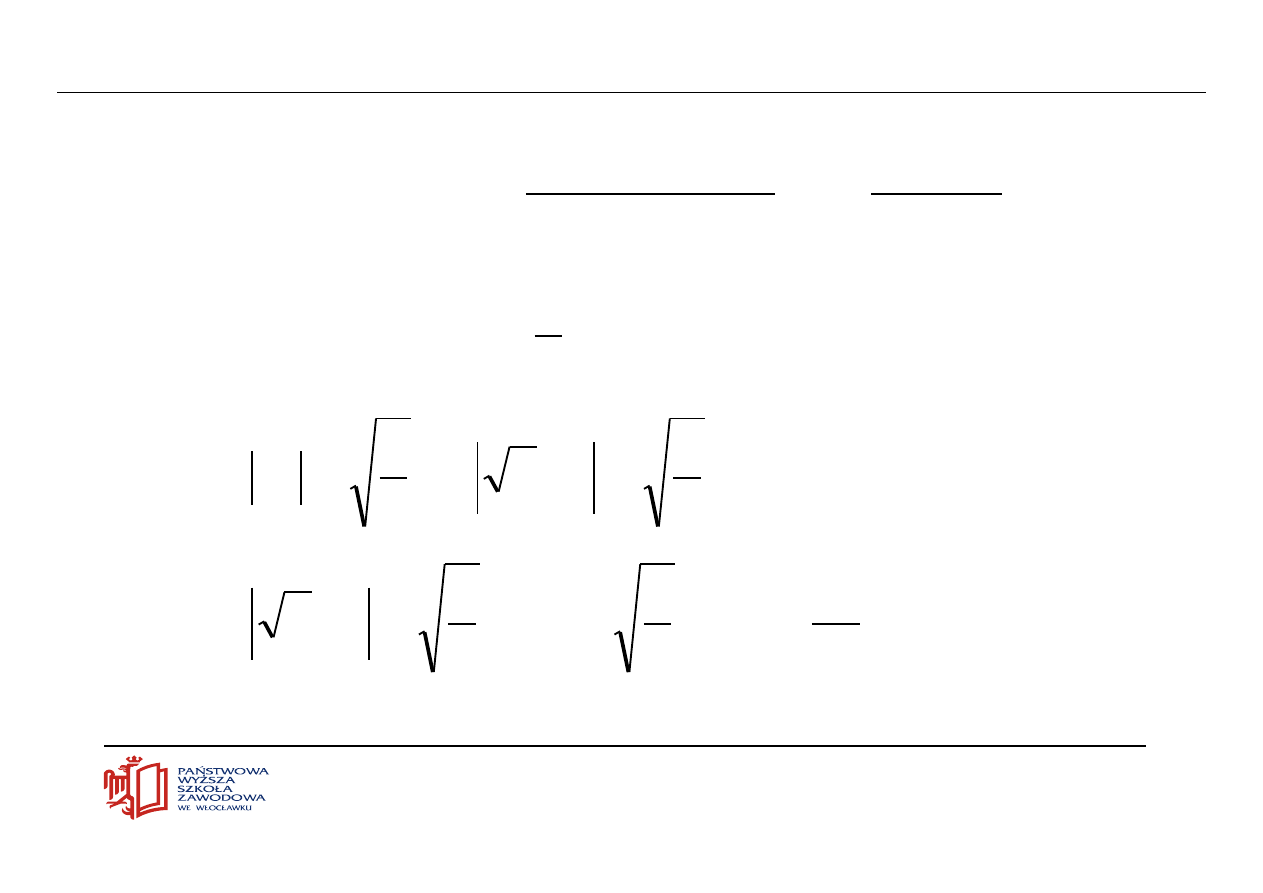
Ciągi i granice
14
Matematyka Ciągi i granice
Przeksz-
tałcenie
2
2
2
2
1
!
2
!
2
!
2
1
2
1
n
n
n
a
n
n
a
n
n
n
n
a
n
n
n
a
na
n
n
2
2
2
2
n
n
n
a
n
n
2
1
2
2
2
2
2
1
n
n
n
n

Ciągi i granice
15
Matematyka Ciągi i granice
Spełniona jest zależność
1
2
0
2
n
n
n
Granicą ciągu jest 1.
Oznaczenie:
dl
a każdego epsilon większego od zera
istnieje takie
delta, że
2
2

Ciągi i granice
16
Matematyka Ciągi i granice
Dla każdego
n
Spełniona jest zależność:
1
n
n
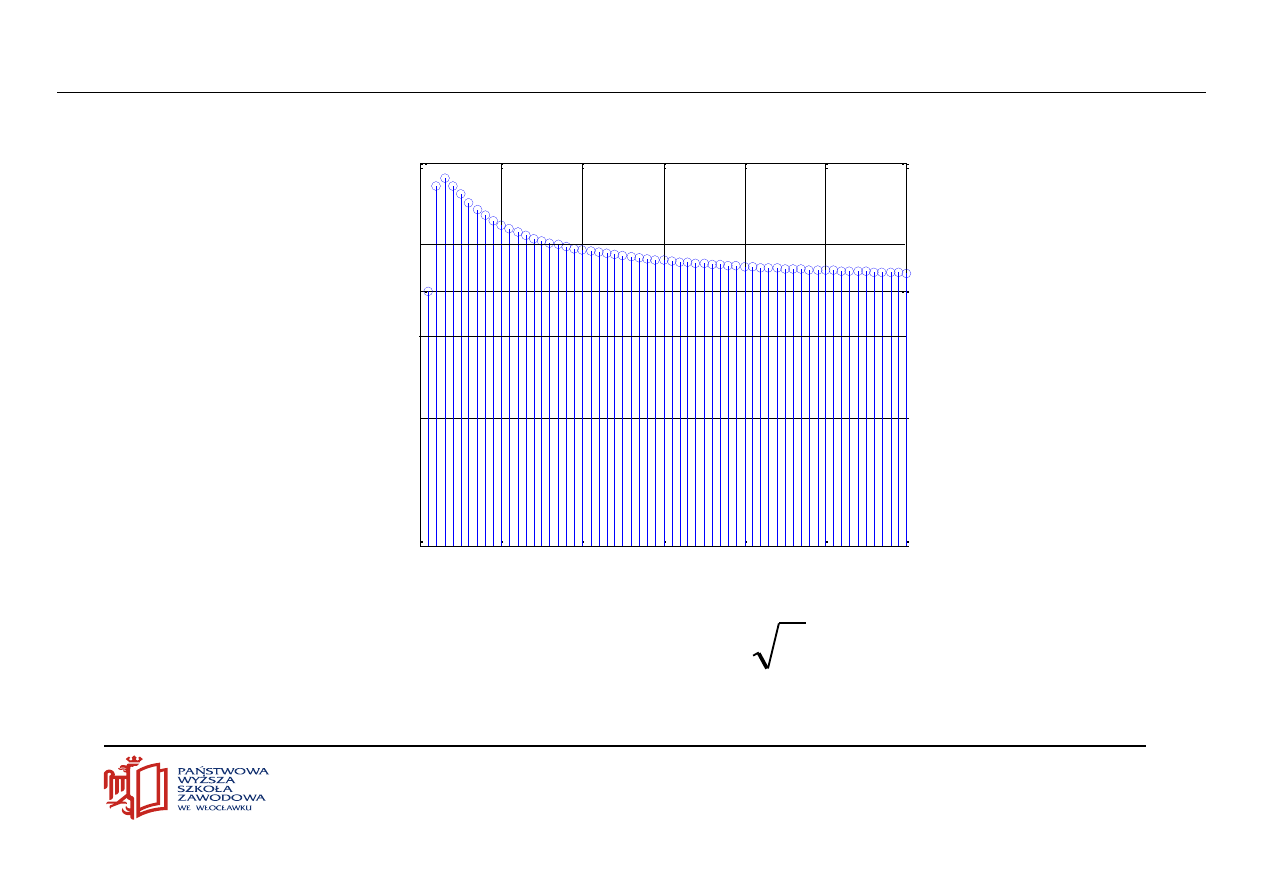
Ciągi i granice
17
Matematyka Ciągi i granice
0
10
20
30
40
50
60
0
0.5
1
1.5
1+0.2
1-0.2
delta
Wyrazy ciągu
n
n
n
u

Ciągi i granice
18
Matematyka Ciągi i granice
Wybrano
1
50
50
2
2
.
0
2
n
n
n
Definicja
Ciąg, który ma granicę nazywa się ciągiem zbieżnym
Ciąg, który nie ma granicę nazywa się ciągiem rozbieżnym
Ciągi mogą być rozbieżne do -
lub +
.
1.3
Ciągi rozbieżne do
Definicja ciągu rozbieżnego do +

Ciągi i granice
19
Matematyka Ciągi i granice
Rozbieżny
M
u
n
n
M
n
u
lim
Rozbieżny
M
u
n
n
M
n
u
lim
Przykład ciągu rozbieżnego do
Ciągi i granice
20
Matematyka Ciągi i granice
2
1
lim
n
n
Dowód
Trzeba znaleźć liczbę M i
.
2
2
1
1
n
M
M
n
także
M
M
n
n
M
1
1
1
2
Niech M=
3.
2
3
1
1
M
Ciągi i granice
21
Matematyka Ciągi i granice
3
1
2
2
n
n
1
1.5
2
2.5
3
3.5
4
4.5
5
-25
-20
-15
-10
-5
0
-3
delta>2

Ciągi i granice
22
Matematyka Ciągi i granice
1.4
Twierdzenie o ciągu ograniczonym
Twierdzenie
Jeżeli ciąg jest zbieżny, to jest ograniczony.
Ograniczoność jest warunkiem koniecznym, ale niewystarczającym zbieżności.
Przykład
Ciąg
n
n
u
1
Jest ograniczony, ale nie jest zbieżny
Ciągi i granice
23
Matematyka Ciągi i granice
0
2
4
6
8
10
12
14
16
18
20
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
Ciąg ograniczony i rozbieżny

Ciągi i granice
24
Matematyka Ciągi i granice
Twierdzenie
Ciąg monotoniczny i ograniczony jest zbieżny
Jeżeli ciąg jest np. niemalejący i ograniczony z góry, to istnieje kres górny
n
u
K
sup
Dowód, że
K
u
n
lim
Z określenia kresu górnego wynika, że
u
K
N
0
:
Ciąg jest niemalejący, więc

Ciągi i granice
25
Matematyka Ciągi i granice
n
n
n
u
K
u
u
Poni
eważ
K
u
n
K
u
K
u
K
K
K
u
n
n
n
n
lim
Ciąg o wyrazie ogólnym
n
n
n
1
1
u

Ciągi i granice
26
Matematyka Ciągi i granice
jest ograniczony i rosnący.
Dowód, że jest ograniczony
n
3
2
n
n
n
n
1
n
n
n
1
3
n
n
1
2
n
n
1
1
n
1
n
1
1
u
...
n
n
3
2
n
n
n
n
n
1
1
n
n
n
3
n
3
n
3
n
n
2
n
2
n
1
1
u
!
!
!
!
!
...
!
!
!
!
!
!
Ciągi i granice
27
Matematyka Ciągi i granice
!
...
!
!
...
!
!
!
)
(
n
n
1
n
1
n
2
1
n
1
1
2
n
1
1
2
n
n
1
n
n
2
n
1
n
n
n
2
n
2
2
n
1
n
n
2
u
n
2
n
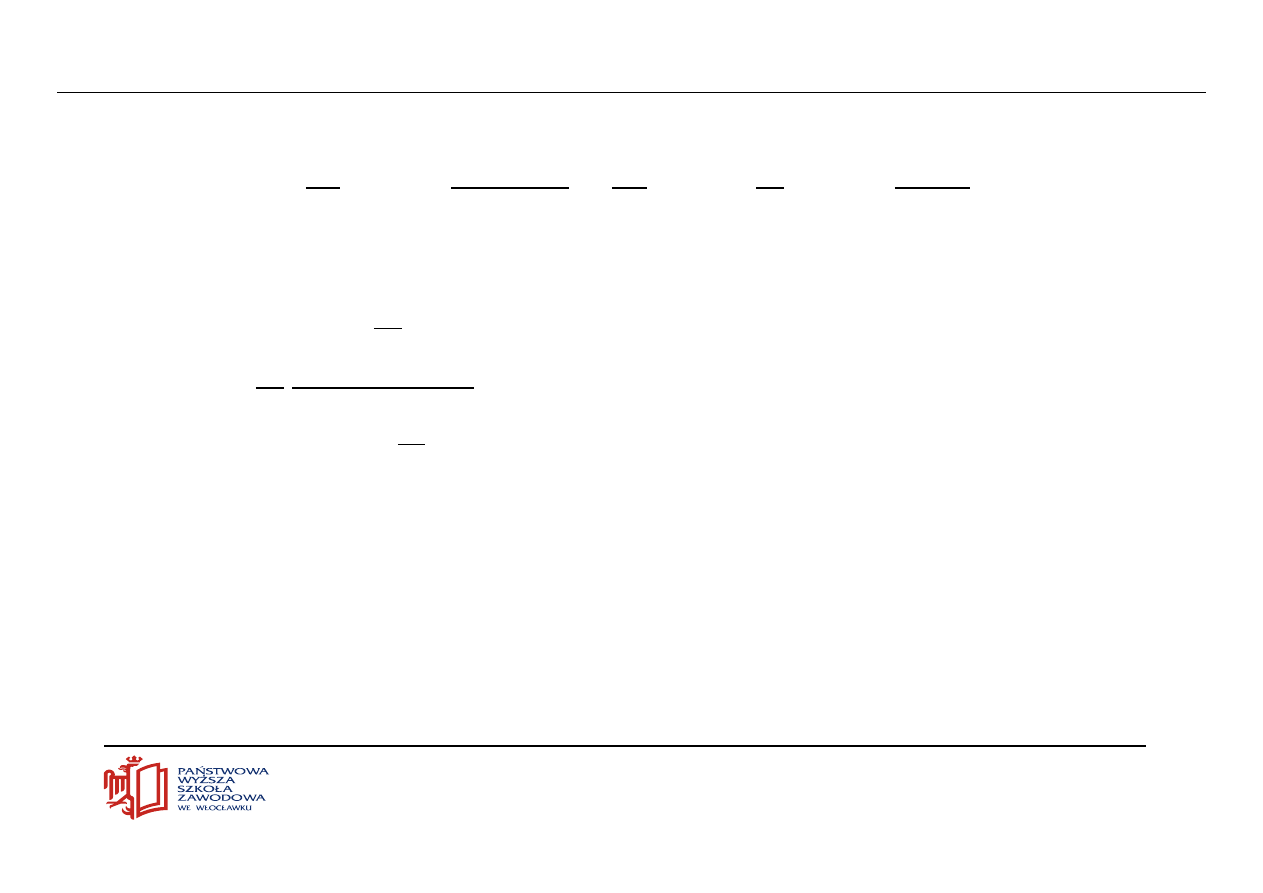
Ciągi i granice
28
Matematyka Ciągi i granice
3
2
1
1
2
1
1
2
1
2
2
1
2
1
2
n
1
1
n
1
2
1
2
u
1
n
1
n
n
...
!
!
...
!
Ciąg jest ograniczony.
Dowód, że ciąg u
n
jest rosnący.
W tym celu dla dowolnego
N
n
należy obliczyć iloraz:

Ciągi i granice
29
Matematyka Ciągi i granice
1
n
1
n
1
n
1
n
n
1
n
n
1
n
n
1
1
1
n
1
1
n
1
n
n
1
1
1
n
1
1
n
1
1
n
1
1
1
n
1
1
n
1
1
n
1
1
1
n
1
1
u
u

Ciągi i granice
30
Matematyka Ciągi i granice
1
n
2
2
2
1
n
2
1
n
1
n
1
1
n
1
1
n
2
n
n
n
1
n
1
n
2
n
n
n
1
n
n
1
n
1
n
2
n
n
1
n
Stosując nierówność Bernoulliego stwierdza się, że

Ciągi i granice
31
Matematyka Ciągi i granice
1
1
n
1
n
1
n
1
n
1
n
1
1
n
1
n
2
1
n
2
czyli ciąg u
n
j
est rosnący.
Przypomnienie
Nierówność Bernoulliego - oszacowanie z dołu wielomianu
nx
x
x
R
x
N
n
n
1
1
1
0
Ciąg jest ograniczony i rosnący. Istnieje zatem granica tego ciągu. Granicą ciągu jest
liczba e

Ciągi i granice
32
Matematyka Ciągi i granice
...
.
59
7182818284
2
e
Przykład
Obliczyć granicę ciągu o wyrazie ogólnym
n
n
n
u
4
1
Rozwiązanie. Wiadomo, że
e
n
u
n
n
n
n
1
1
lim
lim
Wzór ogólniejszy

Ciągi i granice
33
Matematyka Ciągi i granice
e
a
u
n
a
n
n
n
n
1
1
lim
lim
jeżeli
)
0
(
)
0
lim
(
n
n
n
a
a
W danym przypadku:
)
0
(
)
0
lim
(
;
4
n
n
n
n
a
a
n
a
;
4
4
1
n
n
a
n
4
4
4
1
4
4
1
lim
1
lim
lim
e
n
a
u
n
n
a
n
n
n
n
n
Koniec przykładu

Ciągi i granice
34
Matematyka Ciągi i granice
1.5 Twierdzenie o trzech ciągach
Jeżeli
g
v
u
n
n
lim
lim
a oprócz tego
g
w
v
w
u
n
n
n
n
n
lim
0
0
Przykład
Dany jest ciąg
n
7
5
3
w
n
n
n
n
n
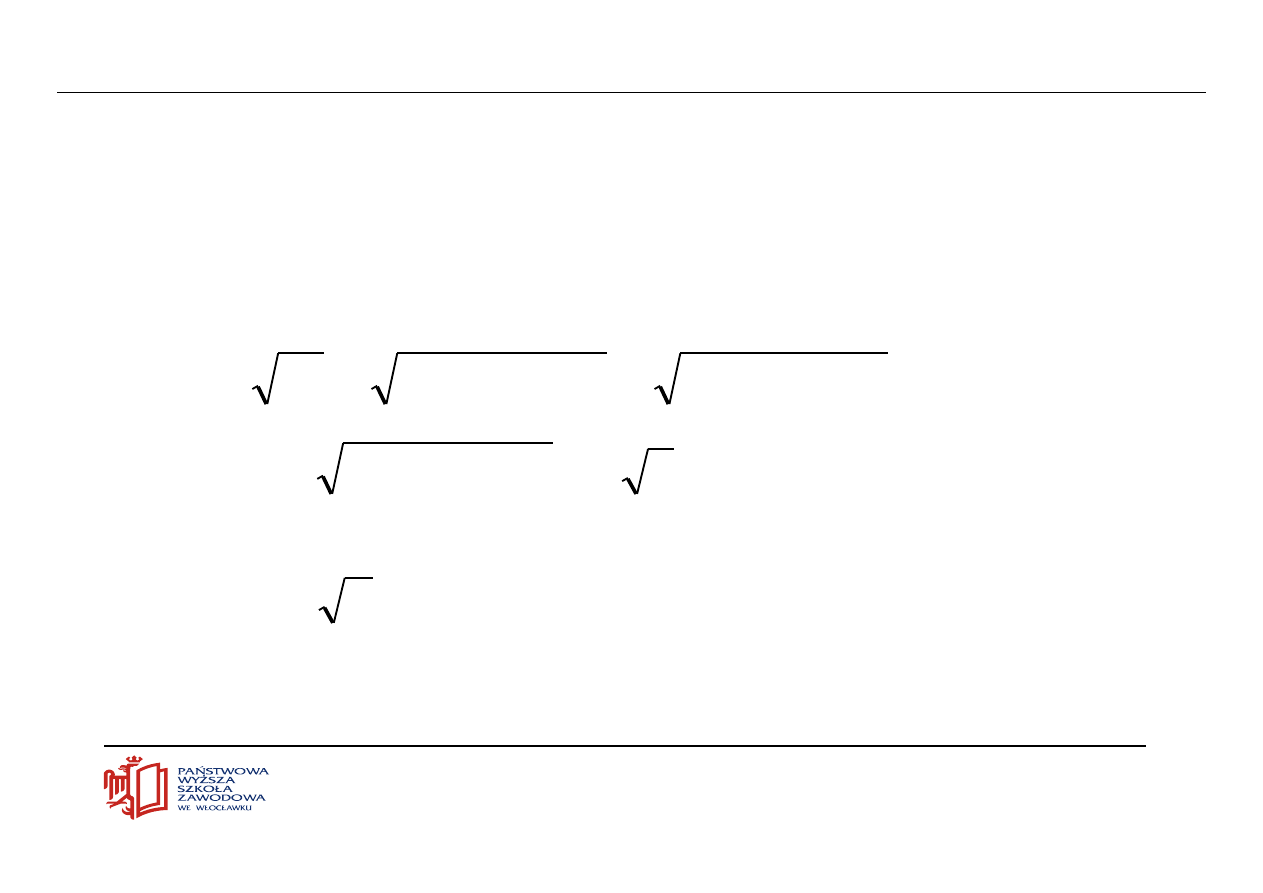
Ciągi i granice
35
Matematyka Ciągi i granice
Rozwiązanie
Spełniona jest nierówność
n
n
n
n
n
n
n
7
7
7
7
5
3
7
n
n
n
n
n
n
n
n
n
n
7
7
7
7
5
3
7
n
n
n
n
n
3
7
7
5
3
7
Można dowieść, że
1
a
n
n
lim
Zatem
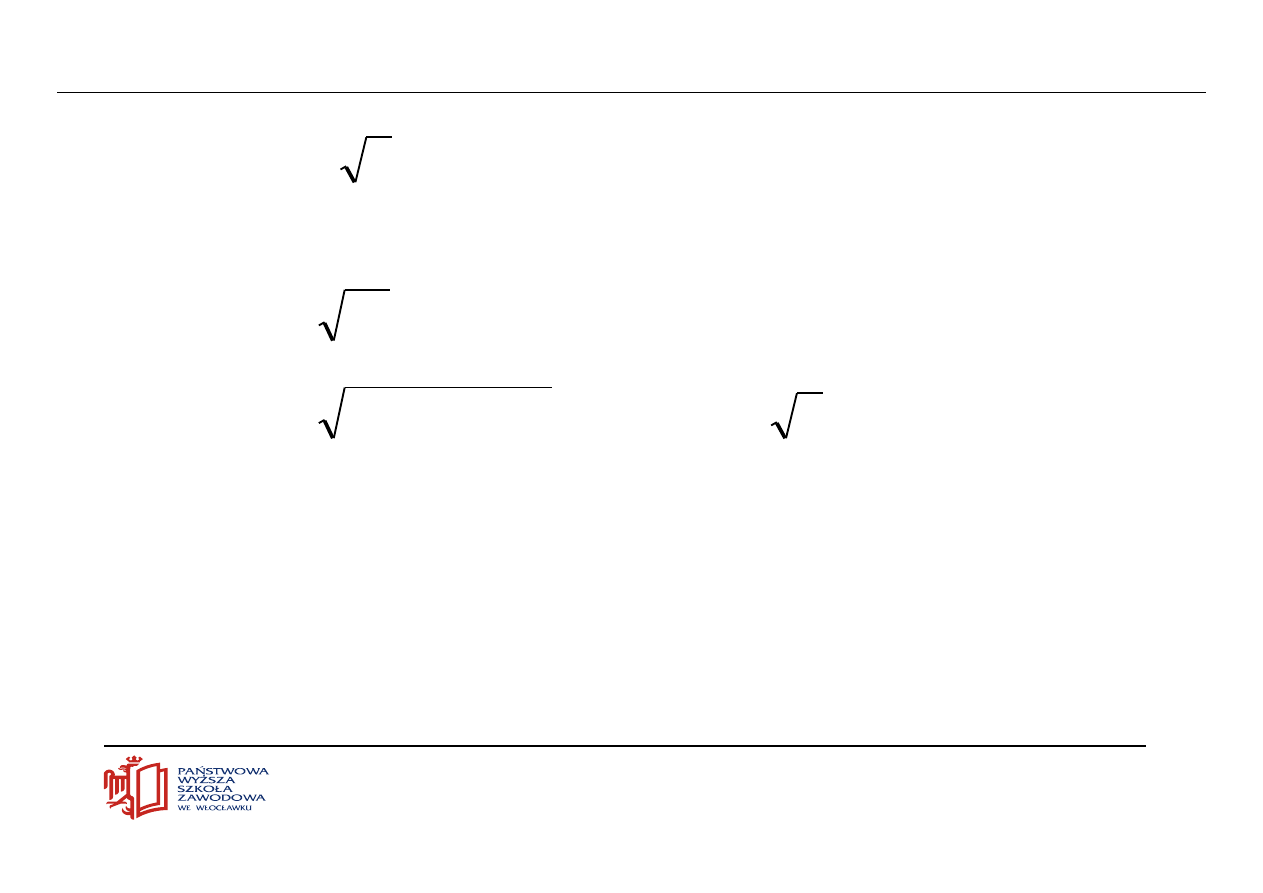
Ciągi i granice
36
Matematyka Ciągi i granice
7
1
7
3
7
n
n
lim
Granice ciągów
n
n
n
n
n
n
n
n
n
n
n
n
n
3
7
v
7
7
7
7
u
7
lim
lim
lim
lim
Spełniona jest zależność

Ciągi i granice
37
Matematyka Ciągi i granice
7
w
7
v
u
v
w
u
n
n
n
n
n
n
n
n
n
lim
lim
lim
1.6 Twierdzenie o granicach sumy, różnicy, iloczynu i ilorazu ciągów
Jeżeli ciągi
n
n
v
u ,
są zbieżne i mają granice

Ciągi i granice
38
Matematyka Ciągi i granice
b
v
a
u
n
n
lim
,
lim
to istnieją następujące granice dla wyrazów tworzących sumę, różnicę, iloczyn i
iloraz:
0
b
b
a
v
u
b
a
v
u
b
a
v
u
b
a
v
u
n
n
n
n
n
n
n
n
lim
lim
lim
lim

Ciągi i granice
39
Matematyka Ciągi i granice
Oznaczenie:
wynika że
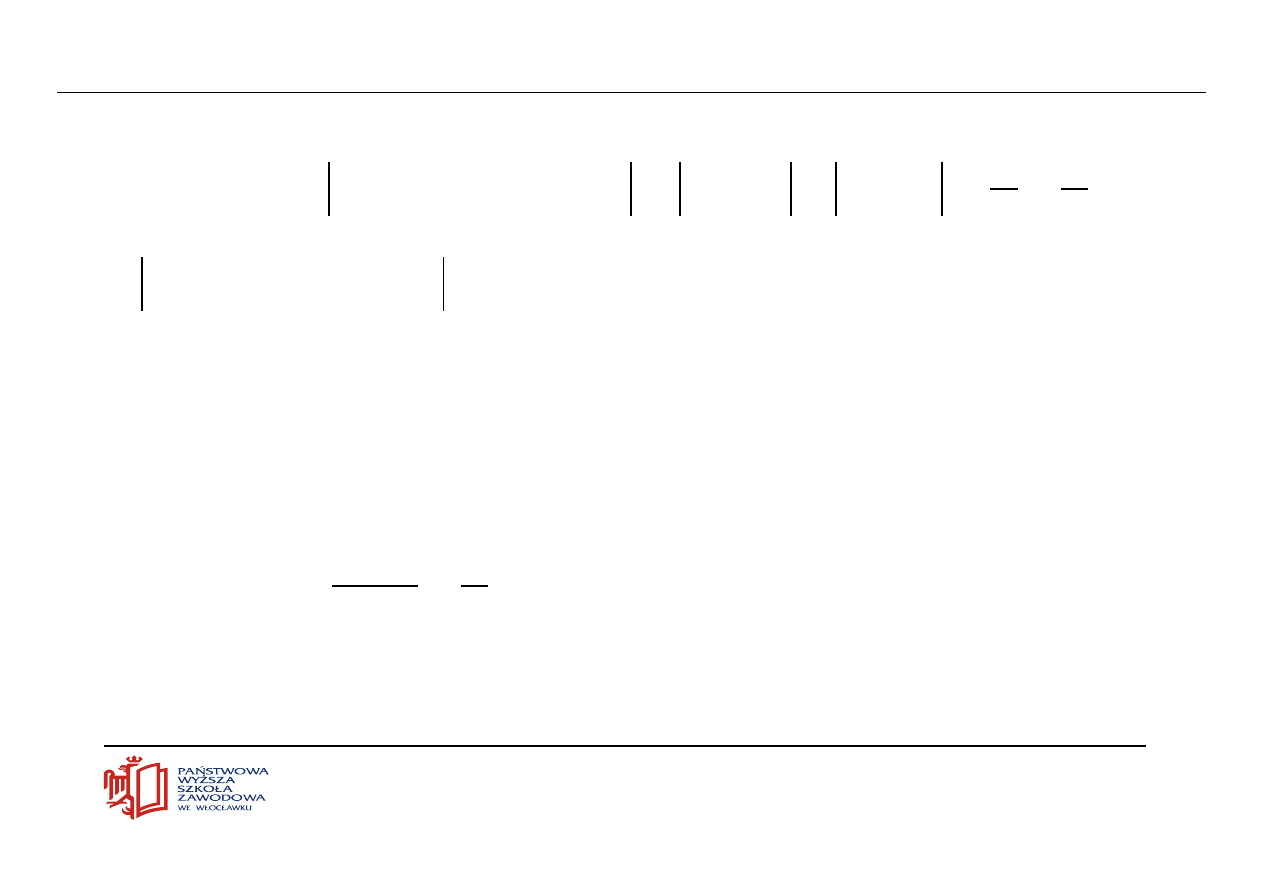
Dowód dla sumy
2
b
v
b
v
2
a
u
a
u
n
n
n
n
n
n
2
2
1
1
lim
lim
Ciągi i granice
40
Matematyka Ciągi i granice
b
a
v
u
2
2
b
v
a
u
b
a
v
u
n
n
n
n
n
n
n
2
1
,
max
a+b jest granicą ciągu.
Przykład
1
0
1
n
1
1
n
n
lim

Ciągi i granice
41
Matematyka Ciągi i granice
1.7 Twierdzenie o granicach ciągów rozbieżnych do
0
u
0
u
u
1
0
u
n
n
n
n
lim
lim
Przykład
1
lim
1
lim
0
lim
;
1
1
2
2
n
u
u
n
u
n
n
n
Koniec przykładu.
0
u
1
u
n
n
lim
lim

Ciągi i granice
42
Matematyka Ciągi i granice
Granica iloczynu wyrazów ogólnych, z których jeden ma granicę +
a drugi ciąg jest
zbieżny
0
a
0
a
v
u
a
v
u
n
n
n
n
lim
lim
lim
Przykład
1
4
2
3
1
1
2
lim
lim
1
4
2
3
lim
lim
;
2
1
1
2
lim
lim
2
2
n
n
n
n
v
u
n
n
u
n
n
v
n
n
n
n

Ciągi i granice
43
Matematyka Ciągi i granice
Koniec przykładu
0
v
u
0
v
M
u
n
n
n
n
lim
lim
,
0
v
M
u
n
n
v
u
n
n
lim
lim
,
a
v
u
a
v
u
n
n
n
n
lim
lim
lim

Ciągi i granice
44
Matematyka Ciągi i granice
a
v
a
v
a
u
n
n
n
lim
lim
lim
0
a
a
0
a
We wzorach oznaczono przez 0
+
liczbę zbliżającą się do 0 przez wartości dodatnie,
przez 0
-
liczbę zbliżającą się do 0 przez wartości ujemne.

Ciągi i granice
45
Matematyka Ciągi i granice
a
0
0
a
a
0
0
a
0
a
0
a
0
a
0
a

Ciągi i granice
46
Matematyka Ciągi i granice
0
u
1
a
0
0
a
n
0
u
1
a
0
0
a
n
a
1
0
a
a
1
a
0
b
0
b
b
0
b
Istnieje kilka symboli nieoznaczonych, dla których nie można od razu podać wyniku i
Ciągi i granice
47
Matematyka Ciągi i granice
trzeba analizować je w konkretnej sytuacji.
0
0
0
1
0
0
0
Przykładowo
e
n
n
1
1
lim
chociaż
1
1
1
lim
n
oraz
n
lim
Przykład
1
1
lim
1
2
2
2
2
n
n
n
v
n
u
n
n
n

Ciągi i granice
48
Matematyka Ciągi i granice
Często korzysta się w tych przypadkach z reguł opartych na rachunku różniczkowym.
0
0
0
1
0
n
n
lim
0
a
n
0
1
a
n
n
lim

Ciągi i granice
49
Matematyka Ciągi i granice
0
n
a
R
a
n
n
!
lim
1
a
0
a
n
n
lim
1
n
n
n
lim

Ciągi i granice
50
Matematyka Ciągi i granice
1
a
1
a
1
1
a
0
1
a
istnieje
nie
a
n
n
lim
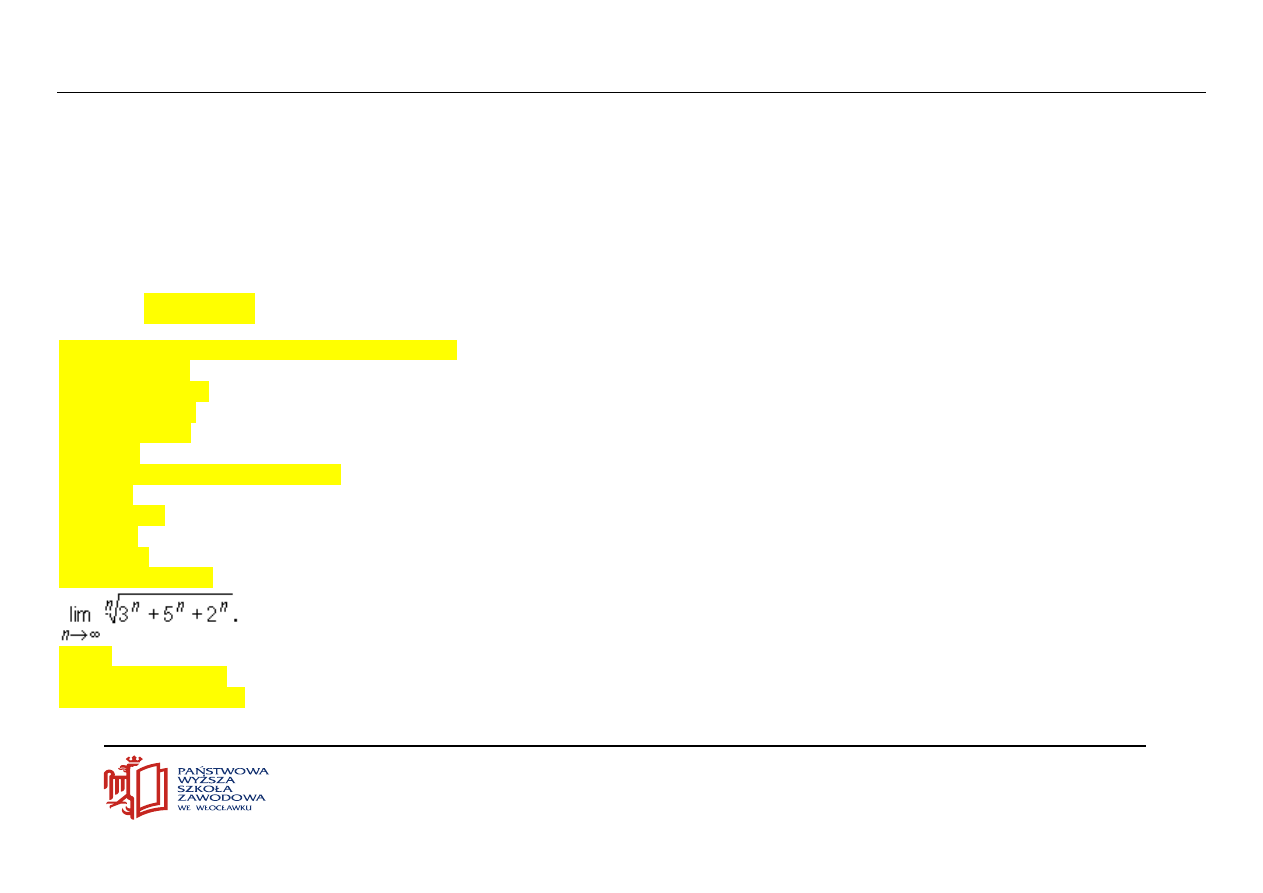
Literatura
51
Matematyka Ciągi i granice
Literatura
[1]
Decewicz G., Żakowski W.: Matematyka. Cz.I Analiza matematyczna. WNT 2005.
[2]
Krysicki W., Włodarski L.: Analiza matematyczna w zadaniach. Cz. 1. PWN 2006.
[3] Analiza matematyczna_1. www.wazniak.mimuw.edu.pl
Zadanie:
Które z podanych ciągów są arytmetyczne (uzasadnij)?
a). 1, 2, 3, 4, 5, ...
b). 2, 4, 8, 16, 32, ...
c). -2, -4, -6, -8, ...
d). 1, 2, 5, 7, 8, ...
e). 1, 2,1,1
Podaj 5 początkowych wyrazów ciągu:
a). a
n
=3n
b). a
n
=5n-1
c). a
n
=n+1
d). a
n
=2n-2
Oblicz granicę ciągu:
Oblicz:
Sumą ciągów (a
n
), (b
n
)
Różnicą ciągów (a
n
), (b
n
)

Literatura
52
Matematyka Ciągi i granice
Iloczynem ciągów (a
n
), (b
n
)
Ilorazem ciągów (a
n
), (b
n
)
Dla a
n
=3n , b
n
=5n-1
Wyszukiwarka
Podobne podstrony:
matematyka, File173, GRANICA CIĄGU
3 Indukcja matematyczna, ciągi granice
Ciągi, granica ciągu
3 Indukcja matematyczna, ciągi granice
6 Granica ciągu liczbowego Ciągi monotoniczne Zbieżność ciągów monotonicznych Liczba ex
Granica ciągu 1, PWR, semestr I, analiza matematyczna, materiały do nauki od DOROTY
Przykłady obliczania granicy ciągu, Analiza matematyczna
matematyka, GRANICA CIĄGU, GRANICA CIĄGU
5 Ciagi,granica i ciaglosc funkcji
granica ciagu zad przykl
Matematyka Funkcja granice
granice ciągu
Analiza matematyczna Wykłady, GRANICE FUNKCJI
Matematyka cw5 Granice funkcji Ciaglosc funkcji Asymptoty
Liczbę g nazywamy granicą ciągu
matematyka ciągi
więcej podobnych podstron